中性原子系综内量子非破坏(quantum nondemolition, QND)测量方式, 通过测量光与原子系综相互作用后产生的相移, 获得原子布居数信息, 而不分辨单个原子的状态, 是产生自旋压缩和多粒子纠缠的一种重要手段. 利用预测量和后测量的差分模式, 可将原子自旋分量上的量子涨落作为共模项消除, 获得优于量子投影噪声的相位灵敏度, 产生自旋压缩态(spin squeezed state, SSS)^[1,2]. 压缩增强的量子传感器件可突破量子投影测量过程中的散粒噪声限制, 达到优于标准量子极限(standard quantum limit, SQL)的灵敏度, 已经在原子微波钟^[3,4]、原子光钟^[5,6]、原子干涉仪^[7,8]、原子磁力仪^[9]、里德伯原子阵列^[10]和量子精密测量网 络^[11]等领域验证了优于SQL的灵敏度^[12]. 原子自旋压缩度可使用Wineland参数来表征^[13], 通常和光与原子相互作用强度呈正相关. 相比于利用自由空间高功率、强聚焦光束进行QND测量的方式^[14], 谐振腔在光功率放大和信号提取等方面具有优势, 因而被广泛用于腔增强型量子精密测量中. 如常用的两腔镜Fabry-Perot (FP)腔, 已经验证了在腔-原子耦合系统中, 通过QND测量^[15,16], 或光介质中的单轴扭转(one-axis twisting, OAT)相互作用^[3,5]等方式产生原子自旋压缩态.

在原子干涉应用中, 目前报道的谐振腔多属于两腔镜的FP腔构型^[7,17]. 然而, FP腔内存在光场强度空间分布不均匀的驻波场结构, 会导致光与原子相互作用不均匀. 在冷原子光钟应用领域, 因原子通常被俘获在光晶格势阱中, 相对位置基本不变, 故驻波场结构对自旋压缩态产生的影响较小. 并且, 可以利用与探测光波长互补的腔内晶格光俘获原子的方法, 保证探测光与原子相互作用的均匀性^[4]. 但在原子干涉仪中, 原子系综存在自由空间演化, FP腔内驻波光场结构导致光与原子相互作用不均匀, 会降低原子自旋压缩度并限制其灵敏度增益. 针对此问题, 2016年, Cox等^[17]提出时间平均的方法, 使原子在下落过程中经过多个探测光模式, 通过时间平均获得均匀相互作用, 观测到了11 dB的自旋压缩. 但这种方法, 需对谐振腔内晶格光进行调制产生多边带并形成干涉, 在局部范围内提供均匀偶极力势阱以限制原子横向扩散. 2018年, Salvi等^[18]提出使用行波场环形腔进行探测, 在保证光与原子强耦合相互作用条件的同时, 规避相互作用不均匀的影响. 这为原子干涉仪中自旋/动量压缩态的产生和应用提供了新思路^[19].

尽管谐振腔制造工艺已较为成熟, 研制一款满足冷原子干涉仪中QND测量需求的窄束腰、高精细度和高真空兼容光学谐振腔, 仍面临谐振腔设计、约束条件限制和真空兼容性等多方面的挑战. 因此, 根据特定科学问题中光与原子相互作用的需求, 设计并实现一款非标准化谐振腔, 往往是解决问题的关键. 例如, 2018年, Cox等^[20]设计并研制了一款抛物线环形腔, 用于增强光与原子耦合强度和腔稳定性, 为腔量子电动力学实验提供了一种实用平台. 2019年, Kawasaki等^[21]研制了一款非对称腔, 获得了极小的模式体积, 并在镱原子光钟内产生接近幺正的自旋压缩, 实现压缩增强的原子光钟^[22]. 2022年, Chen等^[23]研制了一款高精细度蝶形腔, 用于产生里德伯原子阵列中光与原子的强耦合相互作用. 本文针对原子干涉仪中利用QND测量产生自旋/动量压缩的需求, 采用行波场光学环形腔, 在提供光与原子强耦合相互作用的同时, 保持其相互作用均匀性.

在非真空应用环境下, 如激光倍频领域, 环形腔具有广泛应用, 其研制手段也多有报道^[24]. 非真空环境下利用可调节镜架, 可对环形腔四个腔镜独立进行调节; 在某些对稳定度要求较高的场合, 可在环形腔调节完成后用胶水固定其腔镜自由度. 然而, 在原子干涉仪等冷原子应用领域, 需提供高真空环境以延长原子相干时间并降低碰撞率. 在真空条件下使用谐振腔, 面临谐振腔调节和高真空度维持两方面的挑战. 真空条件限制使得唯一可调节自由度为谐振腔腔长, 并且普通胶水出气率高会导致真空度恶化. 利用光学接触方法^[25]可以使表面抛光的高反射率镜片通过分子间作用力与超低膨胀率腔体两端接触面贴合. 采用这种工艺的FP超稳腔展示了超过百万量级的精细度和超低热噪声, 可作为频率基准^[26,27]. 然而, 基于光学接触工艺的谐振腔仅限于两腔镜平行的FP腔, 且一般制作完成后腔长不可调节, 或只能通过主动控温进行慢调节. 对于环形腔, 同样面临腔长调节和真空维持等难题. 一种可行的方法是利用低出气率真空兼容型树脂将腔镜固定到腔体基座上, 并利用基座上的压电陶瓷(piezoelectric transducer, PZT)调节腔长^[28,29]. 这些研究为设计并实现一种满足高真空兼容条件的高精细度光学环形腔提供了借鉴.

本文从产生原子干涉仪动量压缩态的需求出发, 综合考虑光与原子相互作用均匀性、原子干涉光学系统兼容性和真空兼容性等因素, 设计并研制一款高精细度、高真空兼容型光学环形腔, 并研究环形腔内QND测量产生动量压缩态的方法. 利用光学环形腔行波场特性, 有效解决FP腔内驻波场导致的光与原子相互作用不均匀难题; 提出适用于真空系统中的光学环形腔制备方法, 并成功研制出高真空兼容型环形腔, 解决了高真空条件下环形腔可调性和稳定性之间的矛盾. 实验测试结果表明, 环形腔各项参数达到了预期的设计指标, 并在与原子相互作用的实验中, 验证了环形腔QND测量的可行性. 本文提出的设计方案和实验结果, 为研制高精细度、高真空兼容型光学环形腔, 克服QND测量中光与原子相互作用不均匀性影响, 提供了关键技术支撑, 有利于推动压缩增强的量子精密测量领域研究.

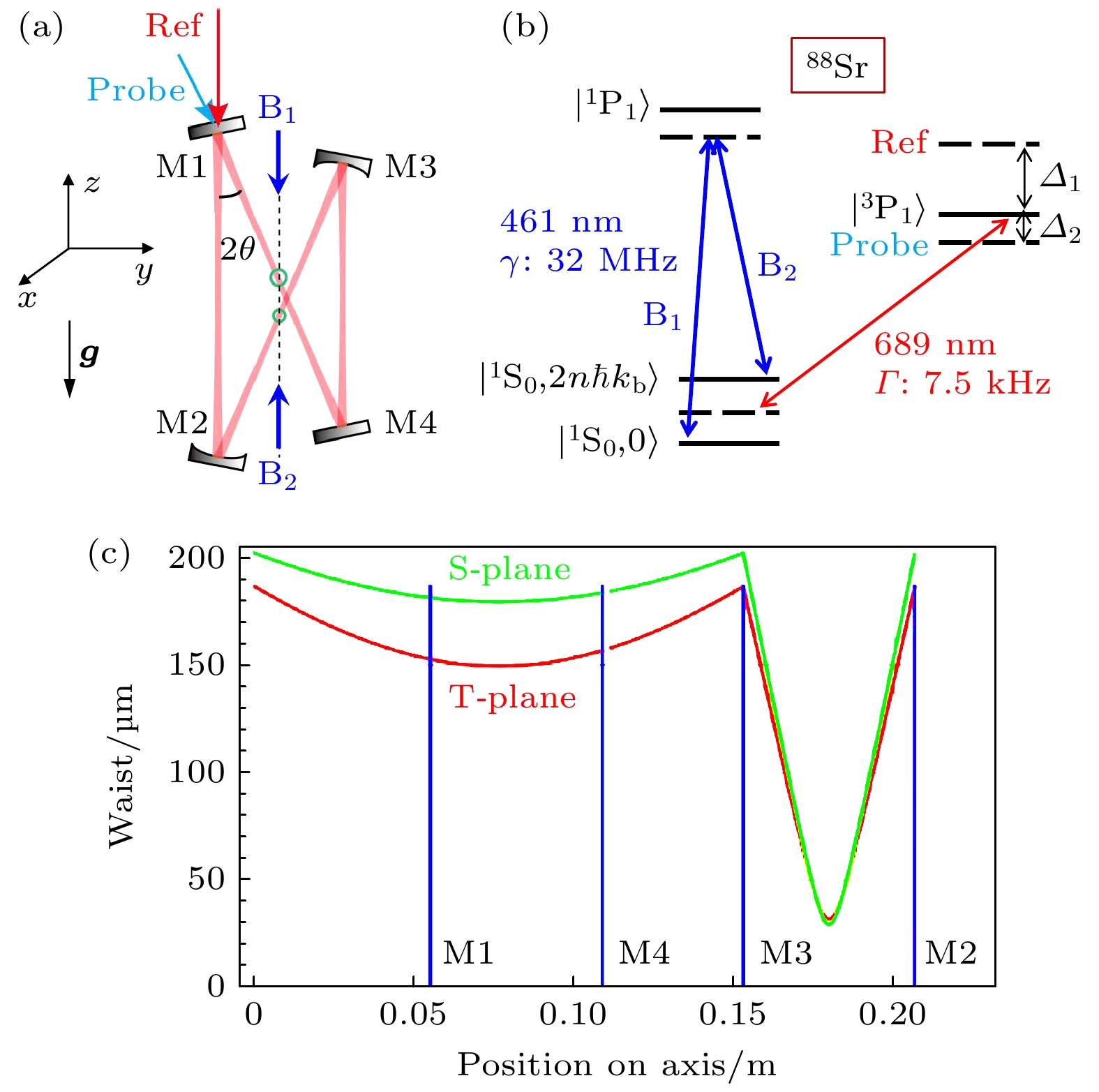
利用光学环形腔QND测量在原子干涉仪中产生动量态压缩的原理方法如图1所示^[18]. 以$ ^{88}\text{Sr} $玻色子为研究对象, 使用一对相向传播的Bragg激光$ (\text{B}_{1} $和$ \text{B}_{2} )$激发$ ^{1} {\mathrm{S}} _{0} $—$ ^{1} {\mathrm{P}} _{1} $之间的Bragg跃迁, 制备动量叠加态$ \left| {{^{1}\text{S}_{0}, 0}} \right\rangle $和$ \left| {{^{1}\text{S}_{0}, 2 n\hbar k_{\text{b}}}} \right\rangle $, 其中n为Bragg跃迁的衍射级数, $ k_{\text{b}} $为光子动量. 然后, 通过$ ^{1} {\mathrm{S}} _{0} $—$ ^{3} {\mathrm{P}} _{1} $窄线宽跃迁对动量叠加态上的原子数目进行QND测量, 制备动量态的条件压缩. QND方法利用频率失谐处于光腔色散区的探测光(probe)测量耦合进腔模内的原子对腔内光场产生的集体相移, 非破坏地测量原子数目, 以制备原子数目的压缩态. 然后利用具有特定相位的光脉冲, 将原子数目压缩态旋转为相位方向上的动量压缩态.

考虑自由空间散射等退相干效应后, 利用 Wineland参数可估计压缩带来的灵敏度增益近似 为^[4,30]

其中, N为耦合进腔模内并参与相互作用的原子数目; η定义为单原子协同因子, 其几何意义为原子散射至腔模内的光子数与散射到自由空间光子数的比值^[31]; Γ和ω 分别为原子上能级自然线宽和基态两个能级之间的跃迁频率. 由(1)式可知, 谐振腔的集体协同因子$ N\eta $是决定灵敏度增益的关键因素. 本节从谐振腔集体协同因子出发, 进行环形腔几何结构设计, 并分析光与原子相互作用均匀性的影响.

传统两腔镜的FP腔内具有驻波场结构, 单原子协同因子最大值为^[31]

其中, $ 2 g $为腔内光场与原子相互作用的有效Rabi频率, κ和Γ分别为腔的半高全宽(full width half maximum, FWHM)和原子对应跃迁的自然线宽, $ {\cal{F}} $为谐振腔精细度, $ k= {2\pi}/{\lambda} $为波长为λ的探测光波数, w为腔模束腰半径.

在行波场环形腔内, η的取值略有不同. 考虑环形腔内光与原子电偶极相互作用的哈密顿量为

其中, 电偶极作用算符为

其中$ \left| {{g}} \right\rangle $, $ \left| {{e}} \right\rangle $分别表示二能级原子的基态和激发态. 环形腔内单模电场算符为

其中, $ \omega_{{\mathrm{c}}} $为腔共振频率, V是腔模式体积, $ {\boldsymbol{e}} $是单位原子极化矢量, $ \hat{c} $是腔湮灭算符且有$ [\hat{c}, \hat{c}^{\dagger}] = 1 $, $ {\cal{E}}(\boldsymbol r) $是腔内$ \text{TEM}_{00} $高斯模式归一化的模式方程. 于是, 电偶极相互作用的哈密顿量可以写为

其中, 包含非共振因子$ {\mathrm{e}}^{-{\mathrm{i}}\omega t}\left| {{g}} \right\rangle\langle {{e}} | $和$ {\mathrm{e}}^{{\mathrm{i}}\omega t}\left| {{e}} \right\rangle\langle {{g}} | $的两项可以忽略. 而腔与原子耦合的Jaynes-Cummings哈密顿量为

其中$ 2 g $是单光子Rabi频率. 联立(6)式和(7)式得到

当偶极矩与电场极化方向平行时(如图1(b)中$ \left| {{^{1}\text{S}_{0}, m = 0}} \right\rangle \leftrightarrow \left| {{^{3}\text{P}_{1}, m = 0}} \right\rangle $), $ -{\boldsymbol{D}}\cdot {\boldsymbol{e}} = -D $. 这里m为磁量子数.

因此, 对协同因子的计算转化为对腔有效模式体积V的计算. 在真空中,

其中, $ {\cal{E}} $为归一化电场强度且$ \text{max}(|{\cal{E}}|^{2}) = 1 $.

在腔内束腰最小的点,

其中, L为总的腔长.

最后, 利用电偶极矩和原子跃迁线宽Γ的关系$ D^{2} = {3\pi\varepsilon_{0}\hbar \varGamma}/{k^{3}}\; $, 以及腔长L与腔线宽κ和精细度$ {\cal{F}} $的关系$ L = {2\pi c}/({\kappa{\cal{F}}}) $, 得到

因此, 在束腰最窄处, 环形腔单原子协同因子计算为

由于入射光与环形腔存在夹角θ, 因此, 环形腔内为非典型高斯光束, $ w_{0 xm} $和$ w_{0 ym} $分别为光传播方向上沿切平面和矢状面的最小半径. 比较(2)式和(13)式发现, 在相同腔参数条件下, FP腔和环形腔的单原子协同因子有4倍的差距, 可以理解为FP腔内驻波场干涉增强造成的结果. 而在环形腔内光场沿单一方向传播, 可有效保持原子和腔内光场耦合过程中相互作用的均匀性.

在谐振腔与原子耦合系统中, 通常来说$ N\eta \gg 1 $是产生光与原子强耦合相互作用的条件, 这既需要较大的原子数目N, 也需要较高的单原子协同因子η. 根据(13)式, 提高谐振腔精细度$ {\cal{F}} $是增加η的一种方法, 降低腔模束腰半径w是另一种渠道. 然而, 使用强聚焦的光束虽然可以增加η, 但对$ N\eta $的贡献却是有限的. 因$ \eta\propto1/w^{2} $, 而在腔模内与探测光相互作用的有效原子数目也与$ w^{2} $成正比, 故$ N\eta $与w是无关的. 另外, 较大的束腰半径可保证在整个测量过程中, 光与原子横向耦合的均匀性. 因此, 选择与原子团线性尺寸相当的腔模束腰半径, 是优化集体协同因子$ N\eta $的关键.

针对QND测量和动量压缩态原子干涉需求, 环形腔可采用由四个腔镜组成的蝶形腔结构, 其中, 两个腔镜为平面镜, 另两个为凹面镜, 在腔内形成具有两个焦点的稳定光场模式, 如图1(a)所示. 利用高斯光束传播的ABCD矩阵理论^[32]计算腔内光场束腰半径的演化规律. 光场在环形腔内的传播主要涉及到以下3个传输矩阵:

其中, $ {\cal{M}}_{{\mathrm{f}}}(d) $描述了自由空间传播距离为d的传输矩阵, $ {\cal{M}}_{{\mathrm{t}}}(R_{m}, \theta) $和$ {\cal{M}}_{{\mathrm{s}}}(R_{m}, \theta) $分别描述了经由曲率半径为$ R_{m} $、入射角为 θ的反射镜面的反射光在切平面(tangential plane, T-plane)和矢状面(sagittal plane, S-plane)的传输矩阵. 其中, 切平面平行于环形腔所在平面, 而矢状面正交于腔平面.

通常, 激光冷却的磁光阱(magneto optical trap, MOT)中原子团尺寸约200 μm, 因此, 所设计的环形腔内应存在束腰直径与原子团几何尺寸相当的区域. 选取合适的腔镜参数, 将入射镜(M1)和出射镜(M4)设为平面镜, 而M2和M3为曲率半径$ R_{m} = 50 $ mm的凹面镜, 使得环形腔内模式存在一个与原子尺寸相近的束腰. 经计算, 环形腔内束腰尺寸演化规律如图1(c)所示, 其中, 绿色和红色曲线分别为矢状面和切平面上光束演化规律, 蓝色竖线指示腔镜的相对位置. 可以看出, 设计的环形腔具有一个半径约$ 169\; $μm的焦点和另一个半径约$ 30\; $μm的焦点, 可满足与原子团尺寸相近的需求, 并且对入射光准直性具有较强的稳定度^[33].

研制具备高精细度和高真空兼容性的光学环形腔是本文的一个重要工作. 传统两腔镜的FP腔结构简单且研制手段较为成熟, 而环形腔的研制涉及到更多自由度的调控. 并且, 在真空环境下, 唯一可调节自由度为环形腔腔长. 为了保证环形腔装配到真空系统之后的稳定性, 利用真空兼容型树脂将腔镜固定到基座上, 并在腔镜底部衬以PZT进行腔长调节. 本节首先阐述环形腔研制过程, 包括可释放腔镜支架设计、光腔模式匹配和环形腔装配等, 重点解决真空兼容型环形腔研制过程中腔稳定性和可调节性之间的矛盾. 其次, 详细阐述应用光学环形腔进行QND测量的实验装置和原理.

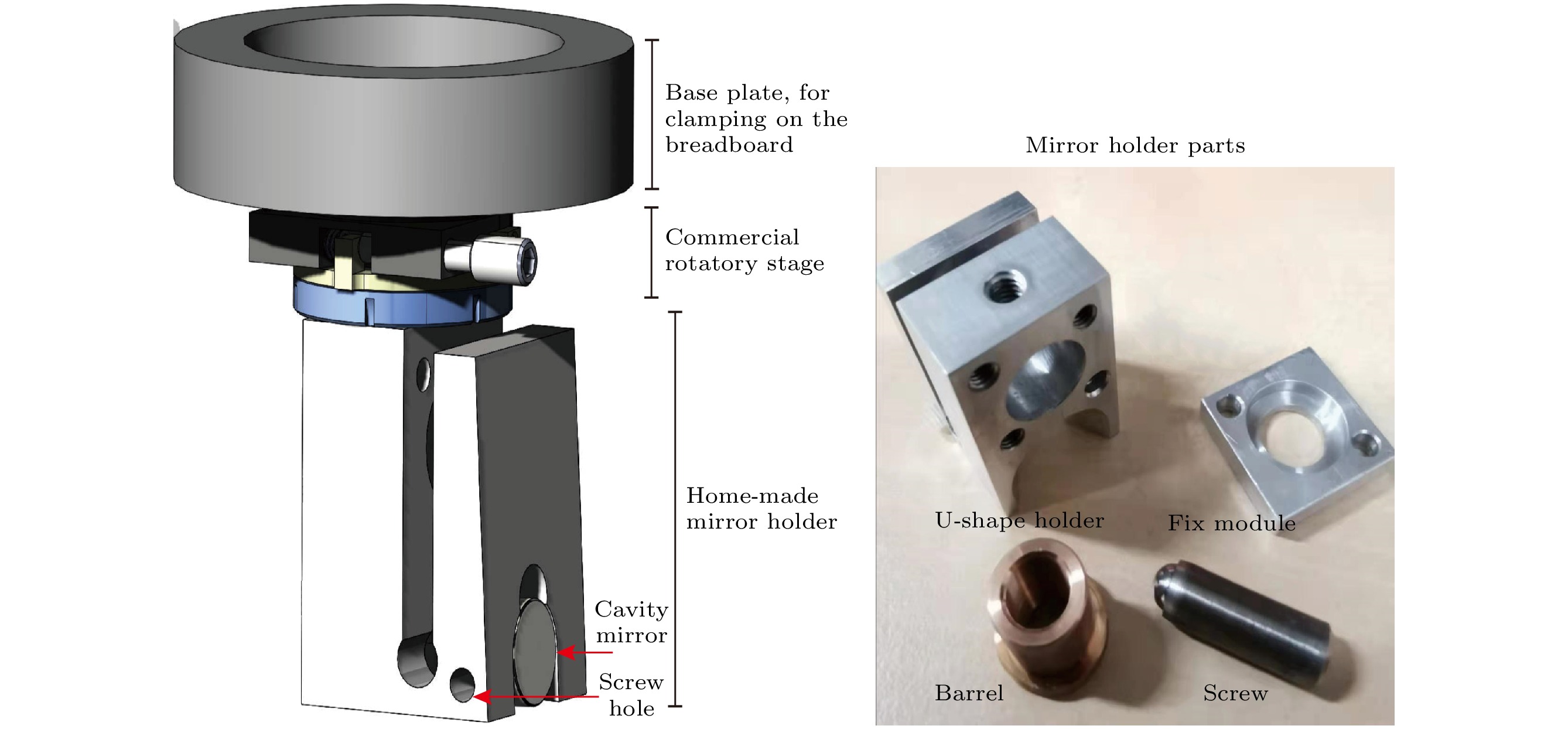
实验中使用的腔镜为定制的直径7.5 mm、厚度4 mm的高反镜, 尺寸小以满足真空装配需求, 腔镜表面抛光并镀以特定波长的高反射膜, 以满足高精细度要求. 由于腔镜尺寸小, 且需满足可释放的需求, 目前未有商用镜架可供使用. 因此, 设计了一种腔镜支架, 以实现环形腔共振模式调节过程中, 每个腔镜具备独立水平和俯仰两个自由度的调节, 并可整体释放以将调配完成的环形腔整体粘连至腔基座上. 该腔镜支架主要由三部分组成, 如图2所示, 自下而上分别为自制镜架、商用转台和支撑基底. 其中, 自制镜架结构零件如插图所示, 底部拱型槽用于放置腔镜(直径7.5 mm), 拱型槽两边小孔用于固定腔镜. 自制镜架采用U型模式, 可通过背部精细螺纹结构(Thorlabs NO.F25USA1和 NO.F25US075)实现俯仰角度精细调节. 中部商用转台(Edmund Optics, ID:2399) 可提供360°范围粗调节和17°范围精细调节. 顶部支撑基底用于连接商用转台, 并固定在光学平台上. 通过此镜架, 可实现腔镜俯仰和水平(旋转)自由度的控制, 用于调节环形腔TEM00共振模式, 并在模式稳定后, 利用拱型槽接触面将四个腔镜同时粘连至腔基座. 待真空树脂凝固后, 通过松开固定螺丝实现腔镜和支架的分离.

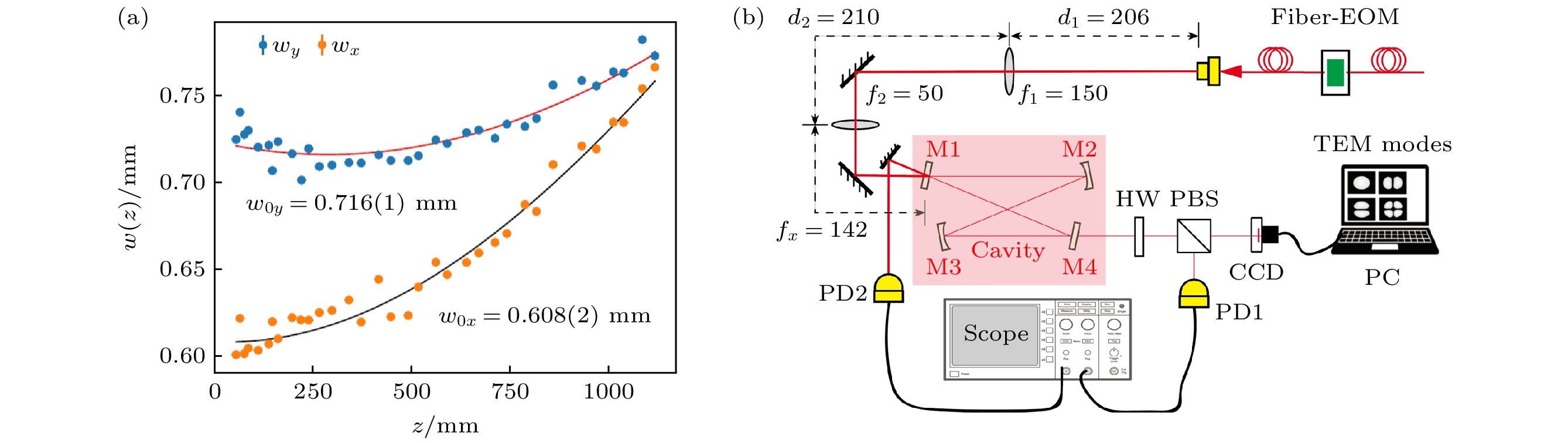
光-腔模式匹配保证探测光和环形腔耦合效率, 提高腔内共振时的循环功率. 环形腔内部模式对应的腔模半径演化规律如图1(c)所示, 其束腰半径约为169 μm, 设为模式匹配的目标尺寸. 根据探测光传播路径上束腰半径演化规律, 计算光-腔模式匹配所需的光学透镜组合. 实验中使用的探测光光源为波长$ \lambda = 689 $ nm的窄线宽激光, 对应于锶原子$ ^{1} {\mathrm{S}} _{0} $—$ ^{3} {\mathrm{P}} _{1} $跃迁频率, 通过光纤电光调制器(fiber electro-optic modulator, Fiber-EOM) (Jenoptik PM705)输出. 对光纤输出路径上光斑演化规律进行测量分析, 如图3(a)所示. 其中蓝色点和橙色点分别表示光斑在y方向上和x方向上束腰半径随传输距离的变化, 实线为高斯光束传播拟合曲线,

其中, $ w_{0} $为高斯光束的腰斑半径, $ x_{{\mathrm{f}}} $是光束焦点位置, $ z_{{\mathrm{R}}} = {\pi w_{0}^{2} n_{0}}/{\lambda} $为光束的瑞利长度, $ n_{0} $为空气折射率. 通过拟合光束传播方向上的光斑尺寸, 得到探测光在x方向上和y方向上束腰半径分别为$ w_{x} \approx 0.608 $ mm和$ w_{y} \approx 0.716 $ mm. 因此, 焦点处的束腰半径取为其几何平均$ \sqrt{w(x)^{2}+w(y)^{2}}\approx 0.660 $ mm.

在一块尺寸为$ 300\; \text{mm} \times 600\; \text{mm} $的光学面板上搭建探测光与环形腔模式匹配光路. 选取$ f_{1} = 150 \; \text{mm}$和$ f_{2} = 50 \; \text{mm}$透镜组合, 基于高斯光束ABCD传输矩阵理论, 以最小化模式匹配误差为优化目标, 理论计算得到光纤EOM和透镜之间的间距$ d_{1} $和$ d_{2} $. 根据计算结果, 搭建模式匹配光路, 如图3(b)所示. 其中, 红色阴影内为光学环形腔, 腔镜使用3.1.1节中研制的支架固定. 腔反射信号和透射信号分别用光电探测器(PD2 和PD1)采集, 并输入示波器; 同时, 利用CCD相机观察腔透射信号以确定环形腔共振模式. 扫描探测光频率, 调节各腔镜俯仰和旋转角度, 使得环形腔透射信号最大, 且共振模式处在$ \text{TEM}_{00} $模式. 此时, 环形腔腔镜相对位置为理想位置, 但各个腔镜由支架独立控制, 还须进一步将腔镜整体粘连到腔基座上, 以保持环形腔共振模式并装配至真空腔体中.

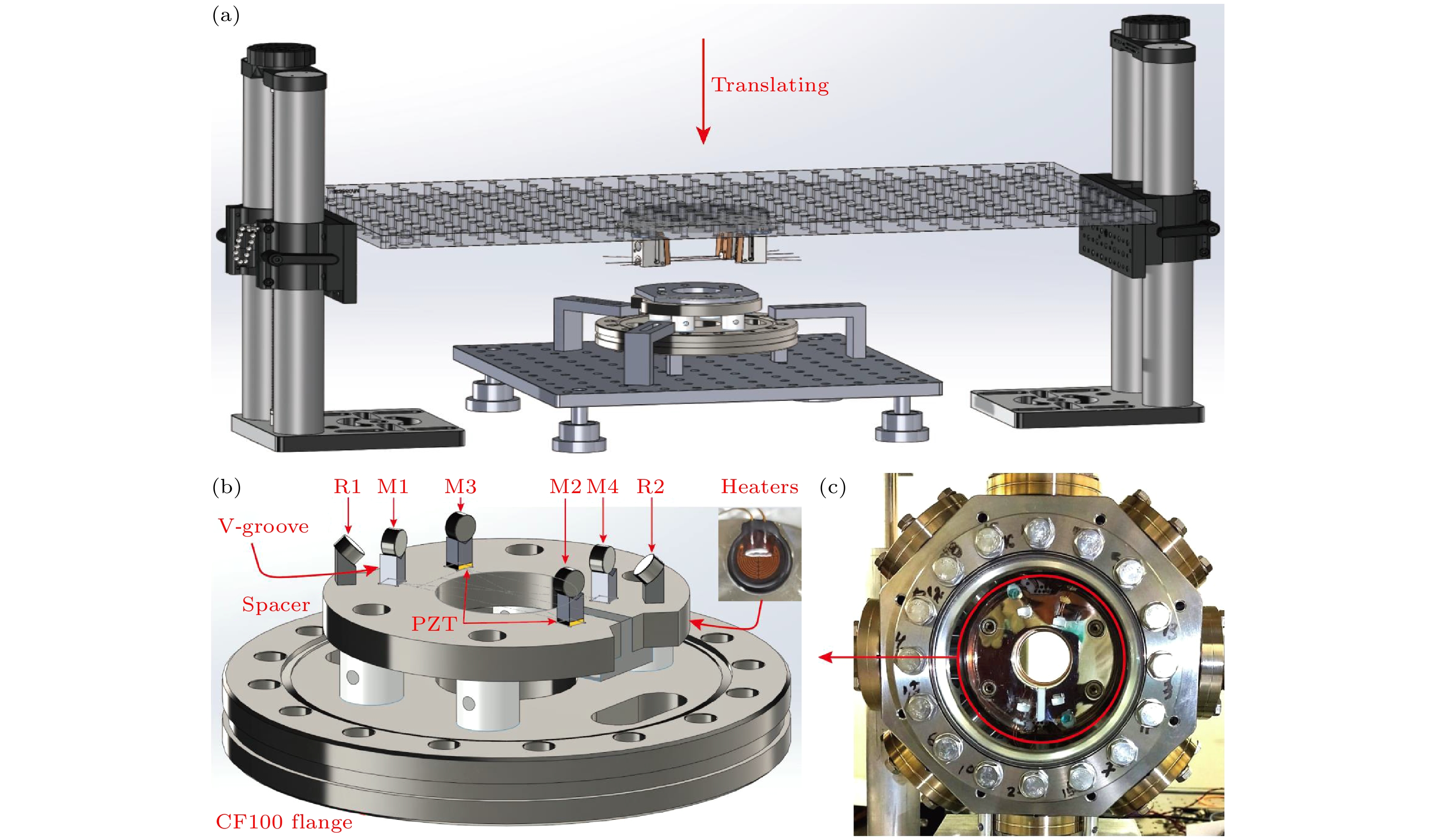
采用翻转光学面板的方式, 将光学环形腔的四个腔镜整体粘连到腔基底上, 并通过法兰实现真空装配, 如图4(a)所示. 总体思路为: 将承载光-腔模式匹配光路的光学面板翻转, 固定在垂直升降台(Thorlabs VAP10/M)上. 升降台下方放置固定在法兰基底上的环形腔基座, 腔基座上粘连了四个V形槽, 分别对应四个腔镜的位置. V形槽通过真空导电树脂在120 ℃条件下粘连到腔基座上, 其中两个V形槽下方还粘连了剪切力压电陶瓷(PZT, Noliac NAC2402-H2.3), 用于调节腔长. 同时, 为了实现腔基座的温度控制, 使用Pt100传感器测量基座温度, 并在其背面粘连了四个高真空兼容型加热片(Birk Manufacturing, P/N 3503-57.5-L00-00)进行温度反馈调节. 腔镜通过Torrseal树脂在室温下粘连到V形槽上, 在Torrseal树脂固化过程中, 监测环形腔透射信号强度, 维持环形腔$ \text{TEM}_{00} $模式共振. 待腔镜与V形槽完全固定后, 通过腔镜支架释放腔镜, 上移升降台, 实现腔镜与支架的分离. 此时, 具备高耦合效率的共振$ \text{TEM}_{00} $模式环形腔完全固定于基座上. 同时, 在腔基座上还粘连了两个倾角为45°的平面反射镜, 用于将环形腔的入射光和反射光导出至与腔基座平面垂直的方向, 以通过真空玻璃窗口.

环形腔粘连完成后, 通过法兰装配到真空系统中, 在较低温度(80 ℃)下烘烤系统以制备真空. 烘烤主要是为了增加真空树脂的出气率, 而采用较低温度是防止腔镜在高温下发生形变. 经过约20天的低温烘烤和抽真空, 可达到$ 1\times10^{-10}\; {\mathrm{mbar}} (1\;{\mathrm{mbar}} = 100\;{\mathrm{Pa}})$真空度. 装配完成的真空兼容型环形腔结构示意图和实物图如图4(b)和图4(c)所示.

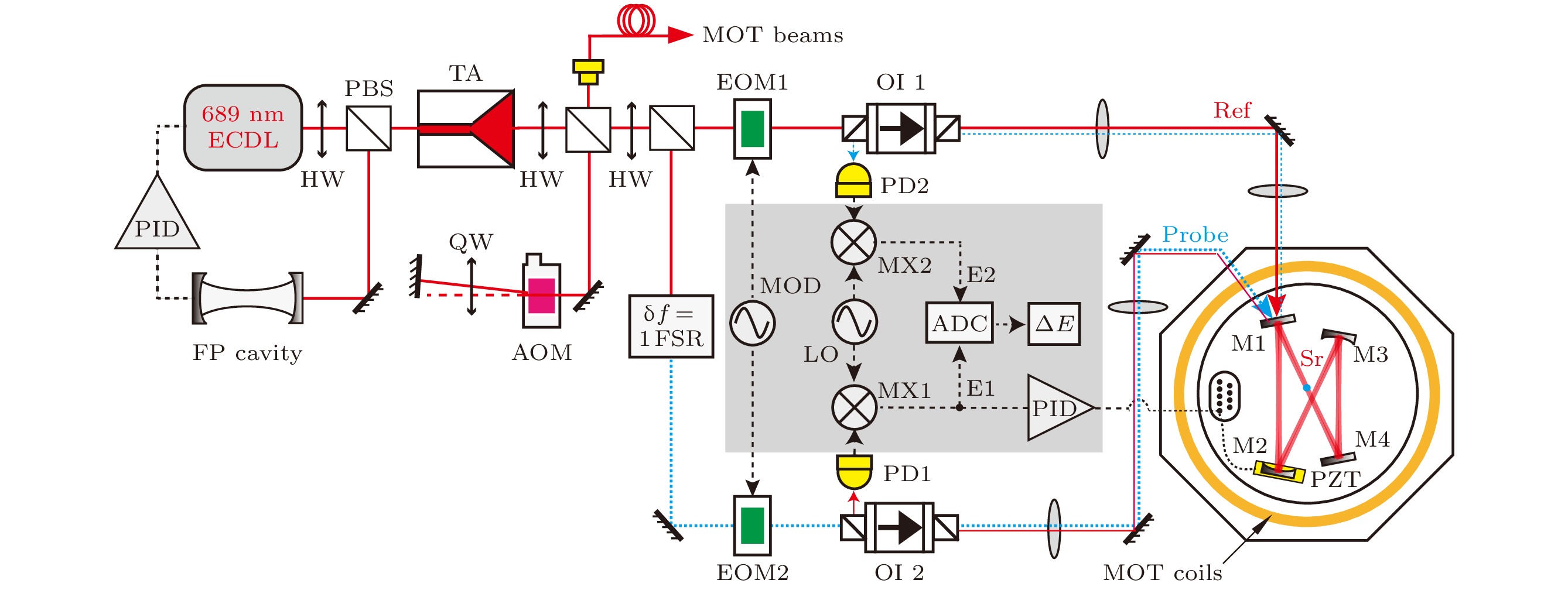
利用光学环形腔进行非破坏测量的主要实验测试装置如图5所示. 用于QND测量的光源采用689 nm外腔半导体(ECDL)激光器. 该激光器通过Pound-Drever-Hall (PDH)方法^[34]与高精细度($ {\cal{F}}^{\prime}= 8600 $) FP腔锁定, 以获得约20 Hz的窄线宽输出^[35]. 激光经锥形放大器(TA)进行功率放大后, 按照功能分为两束: 一束经声光调制器(AOM)双次通过移频后, 作为锶原子二级冷却的MOT光; 另一束作为非破坏测量的探测光(Probe)和参考光(Ref). 探测光经声光移频系统获得与参考光频率相差1倍环形腔自由光谱区(free spectral range, FSR)($ \text{FSR}\approx 1.45 $ GHz)的频率, 使得两束光可同时与环形腔共振. 在此配置下, 探测光频率相对原子跃迁处于腔色散区, 可利用PDH误差信号获取原子对腔内探测光场产生的相移, 非破坏测量原子数目; 而参考光远失谐于原子共振跃迁, 几乎不与原子发生作用, 但可作为共模项, 用以消除环形腔腔长抖动等产生的共模噪声, 提升环形腔QND测量的灵敏度.

环形腔差分测量方法在文献[35]中详细报道. 简单来说, 探测光和参考光采用对称结构, 沿相反方向经M1入射进环形腔, 探测光的入射与参考光的反射重合. 光路中采用两个光学隔离器(OI1和OI2), 一方面保证耦合进环形腔的光偏振相同; 另一方面, 使得反射光与入射光分离并可被探测器测得. 采用两套PDH装置, 即用两个电光调制器(EOM1和EOM2)对探测光和参考光分别进行调制(MOD), 腔反射信号经探测器(PD1和PD2)采集后, 与本振信号(LO)在混频器(MX)中混频以获得PDH误差信号($ E_{1} $和$ E_{2} $). 参考光误差信号($ E_{2} $)经PID反馈到环形腔的PZT上, 实现参考光和探测光与环形腔的同时锁定. 而原子对腔产生的色散相移信号, 可通过差分PDH误差信号$ \Delta E = E_{1} + \alpha E_{2} $获得, 其中$ \alpha = -{\text{Cov}(E_{1}, E_{2})}/ \text{Var}(E2) $, $ \text{Var}(\cdot) $和$ \text{Cov}(\cdot) $分别为方差和协方差的计算符号. 根据文献[35], 在差分测量方法下, 环形腔腔长抖动等共模噪声可降低至探测系统本底噪声水平.

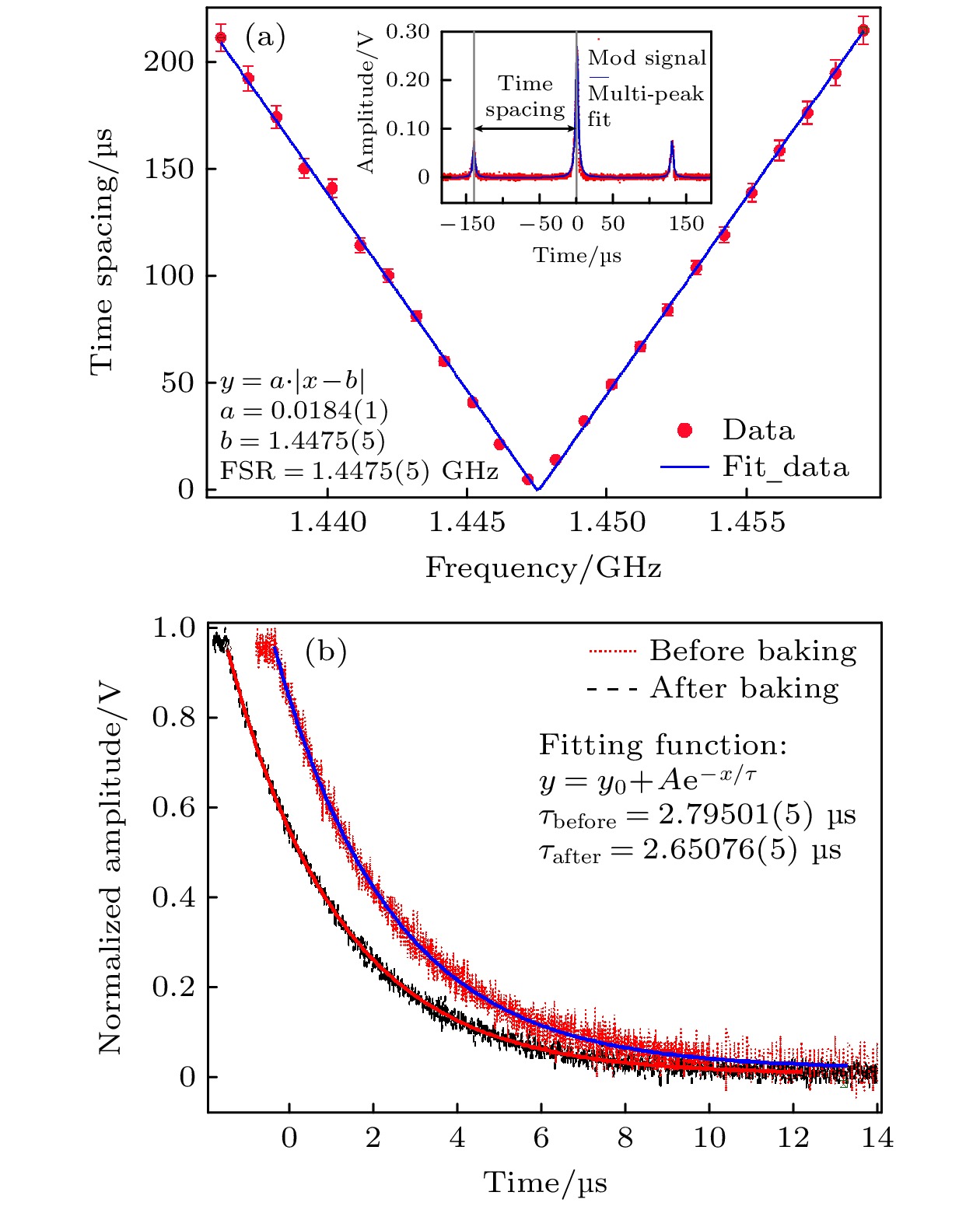
光学环形腔装配完成后, 对环形腔基本参数进行测试. 根据设计腔长$ L\approx 206 $ mm, 估计腔$ \text{FSR}= {c}/{L}\approx 1.455 $ GHz, 其中c为真空中光速. 实际测量中, 可通过对入射光进行相位调制产生边带的方法, 精确确定FSR值, 如图6(a)所示. 改变相位调制的频率, 腔透射光载波和边带的间距会随之改变, 当调制频率为FSR整数倍时, 载波和边带重合. 因此, 通过拟合载波-边带间距随调制频率的变化规律, 可得到该环形腔$ \text{FSR}= 1.4475(5) $ GHz.

利用PDH方法实现入射光与环形腔的频率锁定, 并可直接利用谐振腔衰减振荡方法确定环形 腔内光子耗散时间和腔线宽^[36]. 对于高精细度谐振腔, 光子衰减振荡方法相比传统频率扫描测试 法^[37]具有更高的准确度. 当入射光与环形腔共振时, 利用声光调制器(acousto-optic modulator, AOM)快速关断入射光, 谐振腔内光子在腔内振荡一段时间后耗散. 通过快速光电探测器监测腔透射信号在入射光关断之后的强度变化, 可得到腔内光子耗散的时间常数$ \tau = 2.79501(5) \;{\rm μs}$, 如图6(b)中红色点线所示, 谐振腔线宽即为$ {\text{δ}}\nu = {1}/{2\pi\tau} = 56.9(4) $ kHz. 由FSR和$ {\text{δ}}\nu $可得到环形腔精细度为$ {\cal{F}} = {\text{FSR}}/{{\text{δ}}\nu}= 2.5(4)\times10^{4} $. 由此, 可估算在腔束腰处$ (w\approx 169 \;{\rm μm})$单原子协同因子$ \eta\approx {6{\cal{F}}}/({\pi k^{2} {w}^{2}}) = 0.025 $.

测量真空制备前后光学环形腔主要参数的变化, 对比结果如表1所列. 真空制备后腔精细度$ {\cal{F^{\prime}}}= 2.4(1)\times10^{4} $, 相比于制备前略有下降, 可归咎于腔镜反射率在真空制备和低温烘烤过程中的恶化. 但是, 考虑到冷原子团内原子数目通常$ N > 10^{5} $, 该精细度条件下, 依然满足$ N\eta\gg 1 $的需求. 综上所述, 研制的光学环形腔满足高精细度和高真空兼容性等设计需求.

利用真空系统制备冷原子系综, 与腔内光场相互作用, 验证环形腔内量子非破坏测量效果. 利用磁光阱技术, 制备锶原子($ ^{88}\text{Sr} $)两级冷却, 其时序如图7(a)所示. 其中, 一级冷却采用$ ^{1} {\mathrm{S}} _{0} $—$ ^{1} {\mathrm{P}} _{1} $偶极跃迁, 对应波长461 nm, 并通过497 nm重泵浦光将暗态原子重新泵浦进入循环^[38]; 二级冷却采用$ ^{1} {\mathrm{S}} _{0} $—$ ^{3} {\mathrm{P}} _{1} $组间跃迁, 对应波长689 nm, 其冷却过程包括宽带(broadband, BB)冷却和单频(single frequency, SF)冷却两个阶段^[39]. 配合磁场梯度的变化, 两级冷却后的锶原子温度约为1 μK.

冷原子团释放后, 在重力作用下自由下落, 经过环形腔模式, 如图1(a)所示. 环形腔内探测光与参考光通过PDH锁频方式同时与腔共振, 且频率相差一个腔FSR^[35]. 匹配环形腔与冷原子团空间位置, 使得原子下落过程中经过腔模半径约为169 μm的焦点. 原子的存在改变了腔内介质的折射率, 对环形腔共振模式产生色散相移. 考虑到本实验中, 参考光远失谐于原子共振跃迁, 故环形腔的色散相移主要由探测光产生, 可以表示为原子对腔共振模式产生的色散频移$ {\text{δ}}\omega_{{\mathrm{c}}} $相对于环形腔半线宽$ \kappa/2 $的比值, 即

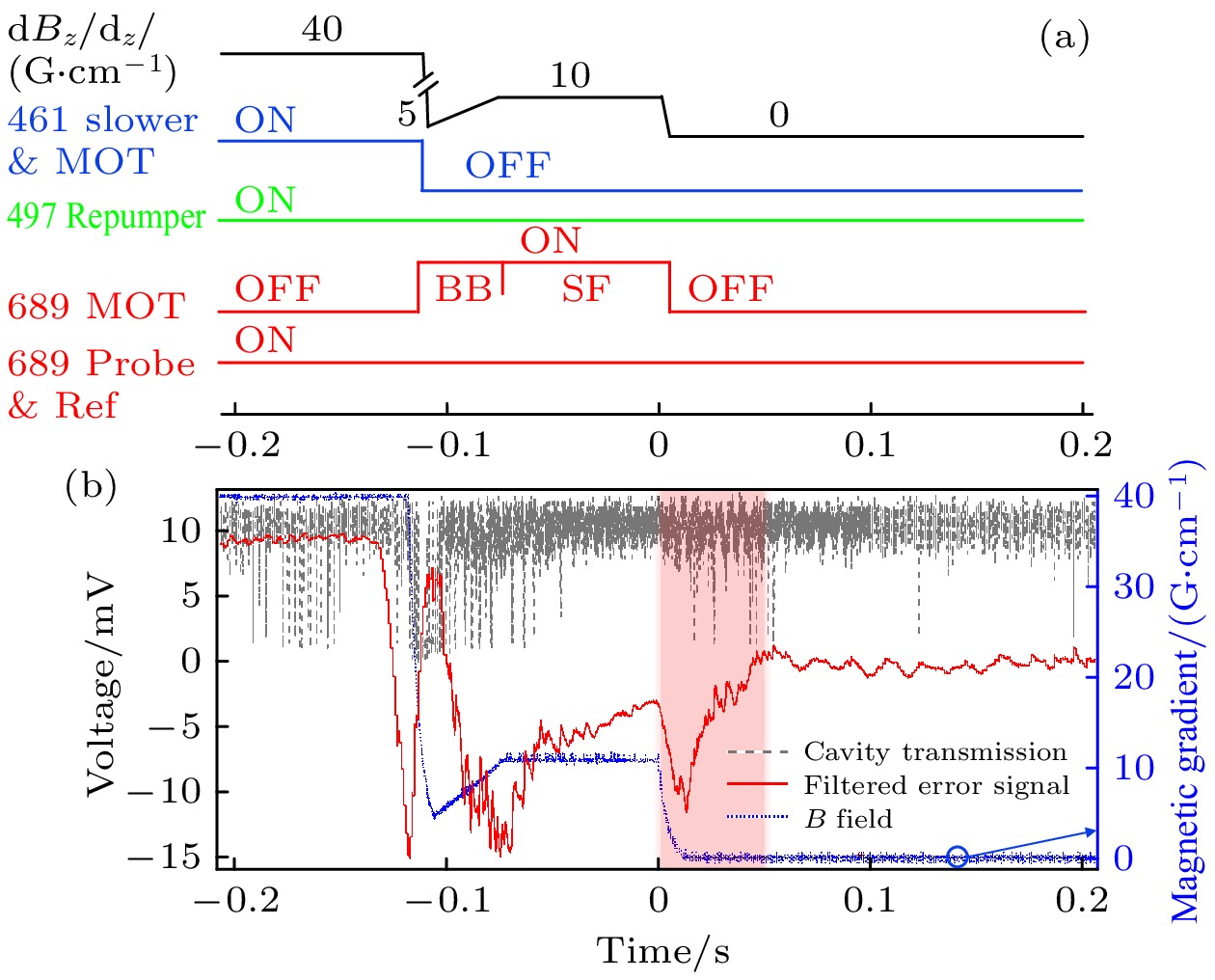
式中, $ \kappa = 2\pi \times60.4(1) $ kHz是环形腔线宽角频率, $ \varGamma = 2\pi \times 7.5 $ kHz为$ ^{1} {\mathrm{S}} _{0} $—$ ^{3} {\mathrm{P}} _{1} $跃迁对应的上能级自发辐射率, $ \varDelta_{2}=-2\pi \times 110 $ MHz 为探测光相对于$ ^{1} {\mathrm{S}} _{0} $—$ ^{3} {\mathrm{P}} _{1} $跃迁的频率失谐量, 如图1(b)所示.

根据3.2节中阐述的方法, 环形腔色散相移 可通过PDH误差信号提取, 并可利用差分测量方法, 抑制谐振腔长度抖动等共模噪声^[35]. 在探测光功率20 μW条件下, 利用基于PIN二极管的低噪声探测器^[35], 探测得到原子下落经过腔模过程中, 对腔内光场产生的色散相移信号, 如图7(b)所示. 其中, 蓝色点线代表霍尔元件探测到的磁场梯度, 可作为时序参考; 灰色虚线为环形腔透射信号, 用于监测环形腔PDH锁定状态; 红色实线为差分PDH误差信号, 包含了原子对腔内光场产生的色散相移信息. 可以看出, 当磁场梯度从$ 40\; \text{G}/\text{cm} $快速下降到约$ 5\; \text{G}/\text{cm} $时, 环形腔透射信号降低, 表示腔短暂失锁, 随后重新自动锁定, 此时的PDH误差信号不具备参考性. 而当原子冷却完成并释放后, 原子经过腔模引起腔色散相移, 可由图7(b)中红色阴影处的信号表示. 腔色散相移量可通过该PDH误差信号幅值变化量($ \text{δ} E $)与PDH误差信号峰峰值的比值确定, 即

其中, $ V_{\text{pp1}} \approx 2 \;{\rm V}$是环形腔扫描时探测光PDH误差信号($ E_{1} $)的峰峰值. 联立(18)式和(19)式, 可估计参与腔内相互作用的有效原子数目约为

其中, $ \eta \approx 0.025 $. 考虑腔色散相移信号幅值$ \text{δ} E\approx 0.1 $V, 由(20)式可估计参与作用的原子数目约为$ 1 \times 10^{5} $.

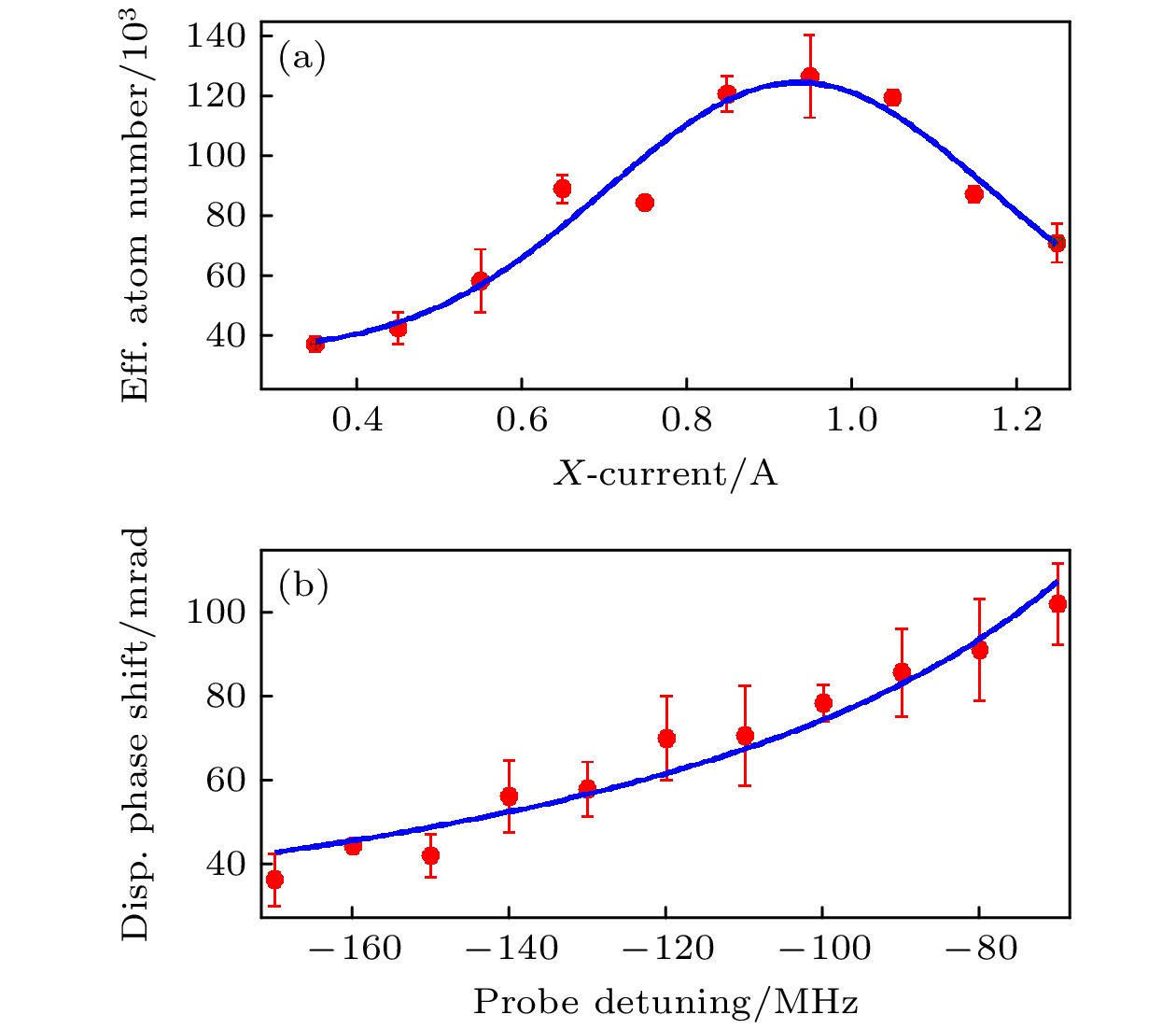
基于以上结果, 可通过环形腔色散相移优化原子与腔的耦合效率. 根据图1(a)的坐标, 原子在$ y{\text{-}}z $平面下落, 因此, 可通过改变x方向补偿磁场的大小, 调节原子团位置以优化原子与腔的耦合. 固定探测光失谐量为$ \varDelta_{2}=-2\pi\times110 $ MHz, 扫描x方向补偿磁场线圈电流大小, 测得环形腔色散相移量并计算有效原子数目, 如图8(a)所示. 其中, 每个点为三次重复测量的平均值. 当电流约0.95 A时, 原子与腔模的耦合效率最高, 耦合进腔模内的原子数目约为$ 1.2 \times10^{5} $.

其次, 通过改变探测光失谐量验证环形腔对原子数目的非破坏测量. 利用AOM改变探测光失谐量, 并保持探测光和参考光同时锁定在环形腔上. 当探测光失谐量在–170 MHz至–70 MHz范围内改变时, 环形腔色散相移如图8(b)所示. 其中, 每个点为三次重复测量的平均值. 根据(18)式, 腔色散相移与探测光失谐量存在反比关系. 因此, 图8(b)中蓝色实线为基于函数$ y=a+b/x $的拟合. 拟合结果与(18)式较好符合, 验证了通过环形腔内色散相移非破坏测量原子数目的能力.

实验结果表明, 利用光学环形腔差分测量方式, 可非破坏地测量耦合进腔模内的有效原子数目, 且环形腔内行波光场结构保证了光与原子相互作用均匀性, 这为制备原子数目压缩态提供了基础. 进一步地, 利用具有特定相位的光脉冲, 可将原子数目压缩转换为动量压缩, 并通过干涉测量结果评估压缩度. 对于目前的装置, 由于探测器灵敏度限制, 腔内色散相移测量灵敏度偏低, 在探测光入射功率为20 μW的条件下, 可测得环形腔色散相移为40 mrad. 可进一步采用更低噪声的单光子探测器, 以获得更高的相位灵敏度, 从而提高原子自旋/动量压缩度. 另一方面, 原子团下落过程中的扩散, 是限制原子自旋/动量压缩度和干涉灵敏度的重要因素, 可以考虑在环形腔内注入晶格光, 限制原子团扩散, 并引导原子团在晶格势场内运动以延长干涉时间, 提高原子干涉灵敏度.

本文研究基于光学环形腔的QND测量方法, 消除光与原子相互作用不均匀影响, 可用于产生原子自旋/动量压缩态, 提升原子干涉灵敏度. 建立以环形腔集体协同因子为主要指标的设计方法, 得到与原子团尺寸相近的环形腔模式. 在此基础上, 利用自行设计和研制的腔镜支架进行环形腔调节和光-腔模式匹配, 采用翻转面板的方式将四腔镜同步粘连至真空法兰基座, 并实时监测调节环形腔$ {\rm TEM}_{00} $共振模式, 解决了环形腔真空装配稳定性和可调性之间的矛盾. 环形腔测试结果表明, 真空制备后腔精细度$ {\cal{F^{\prime}}}\approx 2.4(1)\times10^{4} $, 相比于装配前的$ {\cal{F}}\approx 2.5(4)\times10^{4} $略有下降, 但依然满足$ N\eta\gg 1 $的需求. 利用环形腔测得原子对腔内光场产生的色散相移, 验证了QND测量的可行性, 为原子干涉仪中自旋/动量压缩态产生提供重要技术支撑.