高级搜索

镍同位素链原子核低能四极态的微观研究

,  ,  ,  , 

downloadPDF

上一篇

下一篇

孙帅, 安荣, 祁淼, 曹李刚, 张丰收. 镍同位素链原子核低能四极态的微观研究[J]. 物理学报, 2025, 74(3): 032101-1. doi: 10.7498/aps.74.20240991
引用本文: 孙帅, 安荣, 祁淼, 曹李刚, 张丰收. 镍同位素链原子核低能四极态的微观研究[J]. 物理学报, 2025, 74(3): 032101-1. doi: 10.7498/aps.74.20240991
shu
Shuai SUN, Rong AN, Miao QI, Ligang CAO, Fengshou ZHANG. Microscopic study on low-energy quadrupole states in Ni isotope chain atomic nuclei[J]. Acta Physica Sinica, 2025, 74(3): 032101-1. doi: 10.7498/aps.74.20240991
Citation: Shuai SUN, Rong AN, Miao QI, Ligang CAO, Fengshou ZHANG. Microscopic study on low-energy quadrupole states in Ni isotope chain atomic nuclei[J]. Acta Physica Sinica, 2025, 74(3): 032101-1. doi: 10.7498/aps.74.20240991
shu

镍同位素链原子核低能四极态的微观研究

  • 1.

    北京师范大学物理与天文学院, 射线束技术教育部重点实验室, 北京　100875

  • 2.

    宁夏大学物理学院, 银川　750021

  • 3.

    北京市科学技术研究院, 辐射技术研究所, 北京　100875

  • 4.

    兰州重离子加速器国家实验室, 原子核理论研究中心, 兰州　730000

    • 作者简介: 孙帅: suns186@mail.bnu.edu.cn .
    通讯作者: E-mail: caolg@bnu.edu.cn;  E-mail: fszhang@bnu.edu.cn

  • 中图分类号: 21.60.-n, 21.60.Jz, 24.30.Cz

Microscopic study on low-energy quadrupole states in Ni isotope chain atomic nuclei

  • 1.

    Key Laboratory of Beam Technology of Ministry of Education, School of Physics and Astronomy, Beijing Normal University, Beijing 100875, China

  • 2.

    School of Physics, Ningxia University, Yinchuan, 750021, China

  • 3.

    Institute of Radiation Technology, Beijing Academy of Science and Technology, Beijing 100875, China

  • 4.

    Center of Theoretical Nuclear Physics, National Laboratory of Heavy Ion Accelerator of Lanzhou, Lanzhou 730000, China

    • Corresponding authors: E-mail: caolg@bnu.edu.cn;  E-mail: fszhang@bnu.edu.cn

  • MSC: 21.60.-n, 21.60.Jz, 24.30.Cz

  • 摘要: 利用Skyrme HF+BCS理论以及自洽的QRPA方法研究了镍同位素链原子核的第一个2+态以及矮四极态的性质随中子数增加的演化情况. 研究中分别采用了SGII, SLy5以及SkM*三种能量密度泛函以及密度依赖的零程对相互作用. 计算得到的镍同位素链原子核第一个2+态的激发能以及电磁跃迁强度能较好地再现实验值. 发现$^{70—76}{\rm{Ni}}$的同位旋标量矮四极态共振能量 (跃迁强度) 随着中子数增加而降低 (增加). 这是由于中子$1{{\mathrm{g}}}_{9/2}$态的占有概率的增加, 由该中子态产生的准粒子激发组态占比增加, 组态激发由质子主导渐变为由中子主导产生. 并发现镍同位素链原子核矮四极态对壳结构的改变比较敏感, 可以为丰中子核的壳演化提供信息.
    Abstract: This work mainly investigates the properties of the low-energy quadrupole strength in Ni isotopes, especially the evolution of the pygmy quadrupole states with the increase of neutron number. And the effect of shell evolution on the pygmy resonance is also discussed in detail. Based on the Skyrme Hartree-Fock+Bardeen-Cooper-Schrieffer (HF+BCS) theory and the self-consistent quasiparticle random phase approximation (RPA) method, the evolution in the nickel isotope chain with the increase of neutron number is studied. And in the calculations, three effective Skyrme interactions, namely SGII, SLy5 and SKM*, and a density-dependent zero-range type force are adopted. The properties of the first 2+ state in Ni isotopes are studied. A good description on the experimental excited energies of the first 2+ states are achieved, and the SGII and SLy5 can well describe the reduced electric transition probabilities for $^{58-68}{\rm{Ni}}$. It is found that the energy value of the first 2+ state for $^{68}{\rm{Ni}}$ and $^{78}{\rm{Ni}}$ are obviously high than those of other nuclei, reflecting the obvious shell effect. In addition to the first 2+ states, pygmy quadrupole states between 3 MeV and 5 MeV with relatively large electric transition probabilities are evidently found for $^{70-76}{\rm{Ni}}$ in the isoscalar quadruple strength distribution. The pygmy quadrupole states have the energy values decreasing with the number of neutrons increasing, but their strengths increase gradually. Therefore, they are more sensitive to the change in the shell structure. This is due to the fact that the gradual filling of the neutron level $1{{\mathrm{g}}}_{9/2}$ has a significant effect on the pygmy quadrupole states of $^{70-76}{\rm{Ni}}$, and it leads to switching from proton-dominated excitations to neutron-dominated ones. The pygmy quadrupole states for $^{70-76}{\rm{Ni}}$ are sensitive to the proton and neutron shell gaps, so they can provide the information about the shell evolution in neutron-rich nuclei.
  • 加载中

  • 图 1  利用SGII, SLy5和SkM*相互作用计算的镍同位素链原子核的中子对能隙与实验值[40]的对比

    Figure 1.  Neutron pairing gaps in Ni isotopes calculated by using SGII, SLy5, and SkM* interactions, and compared with the experimental values[40].

    下载: 全尺寸图片 幻灯片

    图 2  (a)利用SGII, SLy5和SkM*相互作用计算的镍同位素链原子核的第一个2+态激发能与实验值的对比; (b)对应的电磁跃迁强度与实验值的对比. 实验数据取自文献[46]

    Figure 2.  (a) Energies of the first 2+ state in Ni isotopes obtained by using SGII, SLy5, and SkM* interactions, and compared with the experimental data; (b) corresponding electromagnetic transition strengths. The experimental data is taken from Ref. [46].

    下载: 全尺寸图片 幻灯片

    图 3  镍同位素链原子核的同位旋标量四极强度分布(计算采用了SGII相互作用)　(a) $^{60—68}{\rm{Ni}}$; (b) $^{70—78}{\rm{Ni}}$

    Figure 3.  Isoscalar quadrupole strength distributions in Ni isotopes: (a) $^{60-68}{\rm{Ni}}$; (b) $^{70-78}{\rm{Ni}}$. The SGII interaction is employed in the calculations.

    下载: 全尺寸图片 幻灯片

    图 4  镍同位素链原子核低能区跃迁强度(计算采用了SGII相互作用)

    Figure 4.  Transition strength for the low-energy region in Ni isotopes. The SGII interaction is employed in the calculations.

    下载: 全尺寸图片 幻灯片

    图 5  组态$\nu 1\text{g}_{9/2} \to \nu 1\text{g}_{9/2}$和$\nu 1\text{g}_{9/2} \to \nu 2\text{d}_{5/2}$对$^{64—76}{\rm{Ni}}$矮四极共振态的(a)贡献百分比与(b)跃迁概率幅, 其中计算采用了SGII相互作用

    Figure 5.  (a) Contribution percentage and (b) reduced transition amplitudes ${b}_{ cd}$ of configurations $\nu 1\text{g}_{9/2}\to \nu 1\text{g}_{9/2}$ and $\nu 1\text{g}_{9/2}\to \nu 2\text{d}_{5/2}$ contributed to the pygmy quadrupole states in $^{64-76}{\rm{Ni}}$. The SGII interaction is employed in the calculations.

    下载: 全尺寸图片 幻灯片

    表 1  利用SGII相互作用计算的$^{64, 68, 72, 76}{\rm{Ni}}$费米面附近中子态的准粒子能$E_{{\mathrm{q.p}}.}$ (MeV)、占据概率$\upsilon^{2}$以及中子费米面$\lambda_n$ (MeV)

    Table 1.  Quasi-particle energies ($E_{{\mathrm{q.p}}.}$ in MeV), occupation probabilities ($\upsilon^{2}$) of neutron states around the Fermi level and neutron Fermi energies ($\lambda_n$ in MeV) in $^{64, 68, 72, 76}{\rm{Ni}}$, which are calculated by using SGII interaction.

    States $^{64}{\rm{Ni}}$ $^{68}{\rm{Ni}}$ $^{72}{\rm{Ni}}$ $^{76}{\rm{Ni}}$
    $E_{{\mathrm{q.p}}.}$ $\upsilon^{2}$ $E_{{\mathrm{q.p}}.}$ $\upsilon^{2}$ $E_{{\mathrm{q.p}}.}$ $\upsilon^{2}$ $E_{{\mathrm{q.p.}}}$ $\upsilon^{2}$
    $1{\rm{f}}_{7/2}$ 7.43 0.98 8.89 0.99 10.47 0.99 11.47 1.00
    $2{\rm{p}}_{3/2}$ 2.51 0.86 3.60 0.96 5.17 0.98 6.20 0.99
    $1{\rm{f}}_{5/2}$ 1.95 0.55 2.66 0.89 4.34 0.95 5.48 0.98
    $2{\rm{p}}_{1/2}$ 1.70 0.47 2.04 0.86 3.53 0.95 4.57 0.99
    $1{\rm{g}}_{9/2}$ 4.30 0.05 2.59 0.12 1.84 0.44 1.68 0.80
    $2{\rm{d}}_{5/2}$ 8.45 0.00 6.65 0.01 4.91 0.01 3.61 0.01
    $\lambda_{n}$ –9.34 –7.98 –6.66 –5.84
    下载: 导出CSV

    表 2  对$^{64, 70, 76}{\rm{Ni}}$的第一个2+态以及矮四极共振态作出主要贡献的准粒子组态的组态能量${{E}}_{{\rm{conf}}.}$ (MeV)、贡献百分比以及对应的跃迁概率幅${{b}}_{{{cd}}}$ (fm2), 其中计算采用了SGII相互作用; π和ν分别代表质子态和中子态.

    Table 2.  Quasiparticle configurations giving the major contribution to the first 2+ and pygmy quadrupole states in Ni isotopes. For each transition, configuration energies (${{E}}_{{\rm{conf}}.}$ in MeV), their contribution to the norm of the state (in percentage) and the corresponding reduced transition amplitudes (${{b}}_{{{cd}}}$ in fm2) are given for $^{64}{\rm{Ni}}$, $^{70}{\rm{Ni}}$, and $^{76}{\rm{Ni}}$, respectively. The SGII interaction is employed in the calculations. Herein, the superscripts π and ν refer to the proton and neutron states, respectively.

    $^{64}{\rm{Ni}}$ $^{70}{\rm{Ni}}$ $^{76}{\rm{Ni}}$
    Configurations ${{E}}_{\rm{conf.}}$ Percentage/% ${{b}}_{{{cd}}}$ Configurations ${{E}}_{\rm{conf.}}$ Percentage/% ${{b}}_{{{cd}}}$ Configurations ${{E}}_{\rm{conf.}}$ Percentage/% ${{b}}_{{{cd}}}$
    第一个2+态 1.46 MeV 2.52 MeV 2.08 MeV
    $\nu 1{\rm{f}}_{5/2}-\nu 2{\rm{p}}_{1/2}$ 3.65 27.85 –7.45 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 4.07 68.71 17.43 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 3.37 71.34 –16.45
    $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 3.89 24.67 –9.02 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.12 15.53 7.55 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 5.30 11.88 –8.64
    $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 4.83 18.58 –10.52 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 7.68 4.39 3.00 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.54 8.92 –6.30
    $\nu 2{\rm{p}}_{3/2}-\nu 2{\rm{p}}_{1/2}$ 4.22 12.75 –5.10 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 6.15 2.40 1.49 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 5.79 2.21 –1.49
    $\nu 2{\rm{p}}_{3/2}-\nu 1{\rm{f}}_{5/2}$ 4.46 3.27 –1.27 $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 7.22 1.42 0.84 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{7/2}$ 8.75 0.70 –0.83
    $\nu 2{\rm{p}}_{3/2}-\nu 2{\rm{p}}_{3/2}$ 5.03 2.35 –1.50 $\nu 1{\rm{f}}_{5/2}-\nu 2{\rm{p}}_{1/2}$ 6.48 1.13 0.53
    矮四极共振态 5.16 MeV 4.98 MeV 4.11 MeV
    $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 4.83 61.35 –10.38 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.12 57.89 10.52 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 5.30 45.03 –13.35
    $\nu 2{\rm{p}}_{3/2}-\nu 2{\rm{p}}_{3/2}$ 5.03 22.68 3.22 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 4.07 28.57 –8.98 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 3.37 26.99 7.85
    $\nu 2{\rm{p}}_{3/2}-\nu 2{\rm{p}}_{1/2}$ 4.22 6.20 1.97 $\nu 1{\rm{f}}_{5/2}-\nu 2{\rm{p}}_{1/2}$ 6.48 3.85 1.23 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.54 20.62 –6.82
    $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 3.89 4.72 2.14 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 7.68 3.77 2.46 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 5.79 3.27 –1.29
    $\nu 2{\rm{p}}_{3/2}-\nu 1{\rm{f}}_{5/2}$ 4.46 2.78 0.70 $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 7.22 1.75 1.18 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{7/2}$ 8.75 0.64 –0.71
    $\nu 1{\rm{f}}_{5/2}-\nu 2{\rm{p}}_{1/2}$ 3.65 1.62 0.93 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 6.15 1.15 0.80
    矮四极共振态 6.89 MeV 6.46 MeV 6.31 MeV
    $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 6.59 90.06 –5.54 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 6.15 75.16 –5.15 $\pi 1{\rm{f}}_{7/2}-\pi 1{\rm{f}}_{5/2}$ 5.79 51.09 –4.34
    $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 8.60 2.14 –1.48 $\nu 1{\rm{f}}_{5/2}-\nu 2{\rm{p}}_{1/2}$ 6.48 12.00 1.83 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 5.29 30.23 9.29
    $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 4.83 2.06 1.49 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.12 4.39 2.44 $\pi 1{\rm{f}}_{7/2}-\pi 2{\rm{p}}_{3/2}$ 5.54 16.37 –5.49
    $\nu 2{\rm{p}}_{3/2}-\nu 2{\rm{p}}_{1/2}$ 4.22 1.07 0.82 $\nu 1{\rm{g}}_{9/2}-\nu 2{\rm{d}}_{5/2}$ 7.68 3.47 –2.21 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{7/2}$ 8.75 1.04 –0.63
    $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 3.89 0.9 1.02 $\nu 1{\rm{f}}_{5/2}-\nu 1{\rm{f}}_{5/2}$ 7.22 1.42 –0.88
    $\nu 1{\rm{f}}_{7/2}-\nu 1{\rm{f}}_{5/2}$ 9.37 0.9 –0.45 $\nu 1{\rm{g}}_{9/2}-\nu 1{\rm{g}}_{9/2}$ 4.07 1.38 1.69
    下载: 导出CSV
  • [1] Paar N, Vretenar D, Khan E, Colò G 2007 Rep. Prog. Phys. 70 691 doi: 10.1088/0034-4885/70/5/R02
    [2] Garg U, Colò G 2015 Prog. Part. Nucl. Phys. 84 124 doi: 10.1016/j.ppnp.2015.06.003
    [3] Horowitz C J, Pollock S J, Souder P A, Michaels R 2001 Phys. Rev. C 63 025501 doi: 10.1103/PhysRevC.63.025501
    [4] Roca-Maza X, Cao L G, Colò G, Sagawa H 2016 Phys. Rev. C 94 044313 doi: 10.1103/PhysRevC.94.044313
    [5] Chen L W, Ko C M, Li B A 2005 Phys. Rev. C 72 064309 doi: 10.1103/PhysRevC.72.064309
    [6] Fang D Q 2023 Nucl. Tech. 46 080016 doi: 10.11889/j.0253-3219.2023.hjs.46.080016
    [7] An R, Sun S, Cao L G, Zhang F S 2023 Nucl. Sci. Tech. 34 119 doi: 10.1007/s41365-023-01269-1
    [8] Cao L G, Ma Z Y 2004 Eur. Phys. J. A 22 189 doi: 10.1140/epja/i2004-10029-5
    [9] Ma C W, Liu Y P, Wei H L, Pu J, Cheng K X, Wang Y T 2022 Nucl. Sci. Tech. 33 6 doi: 10.1007/s41365-022-00997-0
    [10] Ren Z Z, Mittig W, Chen B Q, Ma Z Y 1995 Phys. Rev. C 52 R20(R doi: 10.1103/PhysRevC.52.R20
    [11] Meng J, Ring P 1996 Phys. Rev. Lett. 77 3963 doi: 10.1103/PhysRevLett.77.3963
    [12] Zhou S G, Meng J, Ring P, Zhao E G 2010 Phys. Rev. C 82 011301(R doi: 10.1103/PhysRevC.82.011301
    [13] Zhong S Y, Zhang S S, Sun X X, Smith M S 2022 Sci. China Phys. Mech. Astron. 65 262011 doi: 10.1007/s11433-022-1894-6
    [14] Tian Y J, Liu Q, Heng T H, Guo J Y 2017 Phys. Rev. C 95 064329 doi: 10.1103/PhysRevC.95.064329
    [15] Piekarewicz J 2006 Phys. Rev. C 73 044325 doi: 10.1103/PhysRevC.73.044325
    [16] Vretenar D, Paar N, Ring P, Lalazissis G A 2001 Phys. Rev. C 63 047301 doi: 10.1103/PhysRevC.63.047301
    [17] Yang D, Cao L G, Tian Y, Ma Z Y 2010 Phys. Rev. C 82 054305 doi: 10.1103/PhysRevC.82.054305
    [18] Sun S, Yu R Q, Cao L G, Zhang C L, Zhang F S 2024 Eur. Phys. J. A 60 61 doi: 10.1140/epja/s10050-024-01288-5
    [19] Cao L G, Ma Z Y 2004 Mod. Phys. Lett. A 19 2845 doi: 10.1142/S0217732304015233
    [20] Pei J C, Kortelainen M, Zhang Y N, Xu F R 2014 Phys. Rev. C 90 051304 doi: 10.1103/PhysRevC.90.051304
    [21] Khan E, Paar N, Vretenar D, Cao L G, Sagawa H, Colò G 2013 Phys. Rev. C 87 064311 doi: 10.1103/PhysRevC.87.064311
    [22] Tao C, Ma Y G, Zhang G Q, Cao X G, Fang D Q, Wang H W 2013 Nucl. Sci. Tech. 24 030502 doi: 10.13538/j.1001-8042/nst.2013.03.001
    [23] Zhang Z, Chen L W 2014 Phys. Rev. C 90 064317 doi: 10.1103/PhysRevC.90.064317
    [24] Cao L G, Ma Z Y 2008 Chin. Phys. Lett. 25 1625 doi: 10.1088/0256-307X/25/5/028
    [25] Cortés M L, Rodriguez W, Doornenbal P, et al. 2020 Phys. Lett. B 800 135071 doi: 10.1016/j.physletb.2019.135071
    [26] Allmond J M, Brown B A, Stuchbery A E, et al. 2014 Phys. Rev. C 90 034309 doi: 10.1103/PhysRevC.90.034309
    [27] Marchi T, de Angelis G, Valiente-Dobón J J, et al. 2014 Phys. Rev. Lett. 113 182501 doi: 10.1103/PhysRevLett.113.182501
    [28] Pellegri L, Bracco A, Tsoneva N, et al. 2015 Phys. Rev. C 92 014330 doi: 10.1103/PhysRevC.92.014330
    [29] Spieker M, Tsoneva N, Derya V, et al. 2016 Phys. Lett. B 752 102 doi: 10.1016/j.physletb.2015.11.004
    [30] Yüksel E, Colò G, Khan E, Niu Y F 2018 Phys. Rev. C 97 064308 doi: 10.1103/PhysRevC.97.064308
    [31] Tsoneva N, Lenske H 2011 Phys. Lett. B 695 174 doi: 10.1016/j.physletb.2010.11.002
    [32] Langanke K, Terasaki J, Nowacki F, Dean D J, Nazarewicz W 2003 Phys. Rev. C 67 044314 doi: 10.1103/PhysRevC.67.044314
    [33] Ansari A, Ring P 2006 Phys. Rev. C 74 054313 doi: 10.1103/PhysRevC.74.054313
    [34] Colò G, Cao L G, Giai N V, Capelli L 2013 Comput. Phys. Commun. 184 142 doi: 10.1016/j.cpc.2012.07.016
    [35] Liu L, Liu S, Zhang S S, Cao L G 2021 Chin. Phys. C 45 044105 doi: 10.1088/1674-1137/abdfbc
    [36] Shang X L, Zuo W 2013 Phys. Rev. C 88 025806 doi: 10.1103/PhysRevC.88.025806
    [37] Yan Y J, Shang X L, Dong J M, Zuo W 2021 Chin. Phys. C 45 074105 doi: 10.1088/1674-1137/abf99a
    [38] Zhang S S, Cao L G, Lombardo U, Schuck P 2016 Phys. Rev. C 93 044329 doi: 10.1103/PhysRevC.93.044329
    [39] Zhang S S, Cao L G, Lombardo U, Zhao E G, Zhou S G 2010 Phys. Rev. C 81 044313 doi: 10.1103/PhysRevC.81.044313
    [40] Wang M, Audi G, Kondev F G, Huang W J, Naimi S, Xu X 2017 Chin. Phys. C 41 030003 doi: 10.1088/1674-1137/41/3/030003
    [41] Giai N V, Sagawa H 1981 Phys. Lett. B 106 379 doi: 10.1016/0370-2693(81)90646-8
    [42] Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R 1998 Nucl. Phys. A 635 231 doi: 10.1016/S0375-9474(98)00180-8
    [43] Bartel J, Quentin P, Brack M, Guet C, Håkansson H B 1982 Nucl. Phys. A 386 79 doi: 10.1016/0375-9474(82)90403-1
    [44] Colò G, Roca-Maza X 2021 arXiv: 2102.06562 [nucl-th]
    [45] Sun S, Zhang S S, Zhang Z H, Cao L G 2021 Chin. Phys. C 45 094101 doi: 10.1088/1674-1137/ac0b39
    [46] Pritychenko B, Birch M, Singh B, Horoi M 2016 At. Data Nucl. Data Tables 107 1 doi: 10.1016/j.adt.2015.10.001
    [47] Severyukhin A P, Voronov V V, Giai N V 2008 Phys. Rev. C 77 024322 doi: 10.1103/PhysRevC.77.024322
  • 加载中
图( 5) 表( 2)
计量
  • 文章访问数:  53
  • HTML全文浏览数:  53
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-16
  • 刊出日期:  2025-02-05

镍同位素链原子核低能四极态的微观研究

    通讯作者: E-mail: caolg@bnu.edu.cn; 
    通讯作者: E-mail: fszhang@bnu.edu.cn
    作者简介: 孙帅: suns186@mail.bnu.edu.cn
  • 1. 北京师范大学物理与天文学院, 射线束技术教育部重点实验室, 北京　100875
  • 2. 宁夏大学物理学院, 银川　750021
  • 3. 北京市科学技术研究院, 辐射技术研究所, 北京　100875
  • 4. 兰州重离子加速器国家实验室, 原子核理论研究中心, 兰州　730000
  • 收稿日期:  2024-07-16

摘要: 利用Skyrme HF+BCS理论以及自洽的QRPA方法研究了镍同位素链原子核的第一个2+态以及矮四极态的性质随中子数增加的演化情况. 研究中分别采用了SGII, SLy5以及SkM*三种能量密度泛函以及密度依赖的零程对相互作用. 计算得到的镍同位素链原子核第一个2+态的激发能以及电磁跃迁强度能较好地再现实验值. 发现$^{70—76}{\rm{Ni}}$的同位旋标量矮四极态共振能量 (跃迁强度) 随着中子数增加而降低 (增加). 这是由于中子$1{{\mathrm{g}}}_{9/2}$态的占有概率的增加, 由该中子态产生的准粒子激发组态占比增加, 组态激发由质子主导渐变为由中子主导产生. 并发现镍同位素链原子核矮四极态对壳结构的改变比较敏感, 可以为丰中子核的壳演化提供信息.

English Abstract

    全文HTML

    1.   引　言

    • 巨共振现象是原子核的一种集体激发行为, 它为人们探索核物质性质、约束状态方程以及理解原子核结构提供了有效途径[1,2]. 20世纪80年代以来, 随着世界范围内放射性束流大科学装置的使用以及先进探测技术的蓬勃发展, 核物理的研究对象从传统的稳定原子核扩展到远离稳定线的不稳定核. 研究发现不稳定核具有一系列不同于稳定核的奇特性质, 如中子 (质子) 皮现象[3-9]、中子 (质子) 晕现象[10-14]以及软模式共振[15-21]等. 在过去的几十年里, 低能共振态受到了人们广泛的关注, 例如原子核的低能偶极共振态是由中子皮 (晕) 与核芯的相对运动引起的, 这种低能偶极共振的性质与丰中子核的中子皮厚度以及核物质对称能之间存在很强的相关性[22-24].

      由于低能四极态的能量和强度对于壳结构的改变比较敏感, 因此可以为壳结构的演化提供信息[25]. 进入新世纪以来, 人们为低能四极态的实验与理论研究付出了大量的努力. 实验上, 探测技术的不断改进提高了低能四极态的测量精度[26,27]. 特别是, 美国橡树岭实验室在2014年通过库仑激发技术精确地测量出了$ ^{58, 60, 62, 64} {\rm{Ni}}$的第一个2+态的跃迁强度[26]. 运用同样的技术美国密歇根州立大学核物理实验组测量了丰中子核$ ^{74} {\rm{Ni}}$的第一个2+态的跃迁强度[27]. 此外, 实验上对能量略高于第一个2+态的矮四极共振态的测量也取得一定进展[28,29]. Pellegri等[28]利用340 MeV的$ ^{17} {\rm{O}}$非弹性散射测得$ ^{124} {\rm{Sn}}$在2—5 MeV的矮四极共振态. 这一结果被基于$ ^{124} {\rm{Sn}}$进行的 (α, $ \alpha'\, \gamma $) 与 (γ, $ \gamma' $) 反应所验证[29]. 随着放射性束装置和探测技术的发展, 不稳定原子核低能四极态数据将越来越丰富, 为人们研究原子核的壳演化提供了机遇和挑战.

      理论上, 能量密度泛函理论被广泛应用于低能四极态的研究. 文献[30,31]分别使用基于Skyrme能量密度泛函的准粒子无规位相近似 (QRPA) 以及准粒子声子模型 (QPM) 详细地研究了锡同位素链原子核低能四极态随中子数增加的演化情况, 并探讨了低能四极态对壳演化的敏感性. 文献[32]通过低能四极态性质的研究着重讨论了$ ^{68} {\rm{Ni}}$是否为双幻原子核, 并发现$ ^{68} {\rm{Ni}}$中能量高于4 MeV的低能态对于$ N = 40 $壳隙比较敏感. 采用相对论能量密度泛函, 镍同位素链原子核第一个2+态的激发能以及对应的跃迁强度可以较好地再现实验值[33].

      目前, 关于镍同位素链原子核的低能四极态的研究工作仅有少量的理论研究来讨论第一个2+态的性质, 并与实验值进行对比, 尚未系统地讨论第一个2+态随中子数增加的演化情况. 另外, 文献[31]仅对锡同位素链原子核中的矮四极共振做了理论研究, 对于镍同位素链原子核矮四极共振态性质的理论研究鲜有文献报道. 基于此, 本文采用基于Skyrme能量密度泛函的QRPA理论详细地研究镍同位素链原子核中的低能四极态性质, 特别是矮四极共振的性质随中子数演化情况, 并从微观角度解释壳关联影响的物理机制.

      本文分为4个部分, 第2部分简要地介绍理论模型; 第3部分首先讨论镍同位素链原子核的对关联性质, 然后重点讨论镍同位素链原子核低能四极态性质的演化情况; 第4部分为文章的结论.

    2.   理论模型

    • 本文中, 原子核的基态性质由Skyrme Hartree-Fock + Bardeen-Cooper-Schrieffer (HF + BCS) 方法来描述, QRPA理论方法应用于研究镍同位素链原子核的低能四极态性质. 基于Skyrme能量密度泛函的HF + BCS方法发展得比较成熟, 在许多文献中已经做了详细介绍, 这里不再赘述, 可参考文献[34,35]. 目前, 对于对相互作用的多体关联机制还在进一步的研究中, 如文献[36—39]讨论了核物质中对关联的多体关联以及同位旋依赖性. 由于计算的复杂性, 该方法还不能直接应用于有限原子核对关联的计算中. 对于有限原子核对关联的计算, 一般采用唯象的有效对相互作用, 本文采用了密度依赖的零程对相互作用:

      其中, $ \rho({\boldsymbol{r}}) $是核子密度; $ \rho_{0} = 0.16\; {\rm{fm}}^{-3} $代表核物质饱和点密度; η的取值决定对相互作用类型, 当η为0.0, 0.5和1.0时, 分别对应体型、混合型和面型对相互作用, 本文采用混合型对相互作用, 即η = 0.5; $ V_{0} $代表对相互作用强度, 通过拟合$ ^{68} {\rm{Ni}}$的实验中子对能隙来确定$ V_{0} $的大小[40], 计算中分别采用SGII[41], SLy5[42]和SkM*[43]三种有效的Skyrme能量密度泛函, 对应的$ V_{0} $分别为453.9, 495.4和413.5 $ {\rm{MeV}}{\cdot} {\rm{fm}}^{3} $. 获得的$ V_{0} $值可推广应用到整个镍同位素链的基态和集体激发态性质的计算中. HF + BCS方程在球坐标空间中进行数值求解, 其中径向长度取24 fm, 步长取0.1 fm. 经检验, 这一数值设置可以确保计算结果的收敛性.

      原子核的集体激发行为可以通过QRPA方程描述. QRPA方程的矩阵形式为[44]

      其中, A与B为剩余相互作用矩阵元, $ E_{\nu } $为第ν个集体态的本征能量, $ X^{\nu } $与$ Y^{\nu } $为本征波矢. 对于给定的激发态ν, 则准粒子组态贡献到该集体激发态的百分比可以通过对应$ E_{\nu } $的本征波矢$ X^{\nu }_{ab} $与$ Y^{\nu }_{ab} $得到:

      归一化方程为

      对于给定的外场算符$ \hat{F}_{J} $, 其跃迁强度为

      其中, $ \mid \nu \rangle $代表激发态, $ \mid \widetilde{0} \rangle $代表基态, $ b_{cd}(EJ) $为准粒子组态$d\rightarrow c $的跃迁概率幅, $EJ $表示电跃迁类型, $v\;(u) $为准粒子态的占据率(非占据率).

      离散的QRPA谱可通过Lorentzian展开方程

      展开为连续的四极强度分布, 其中$ \varGamma $代表Lorentzian宽度, 本文中$ \varGamma = 1 $ MeV.

    3.   结果与讨论

      3.1.   镍同位素链原子核的对关联性质

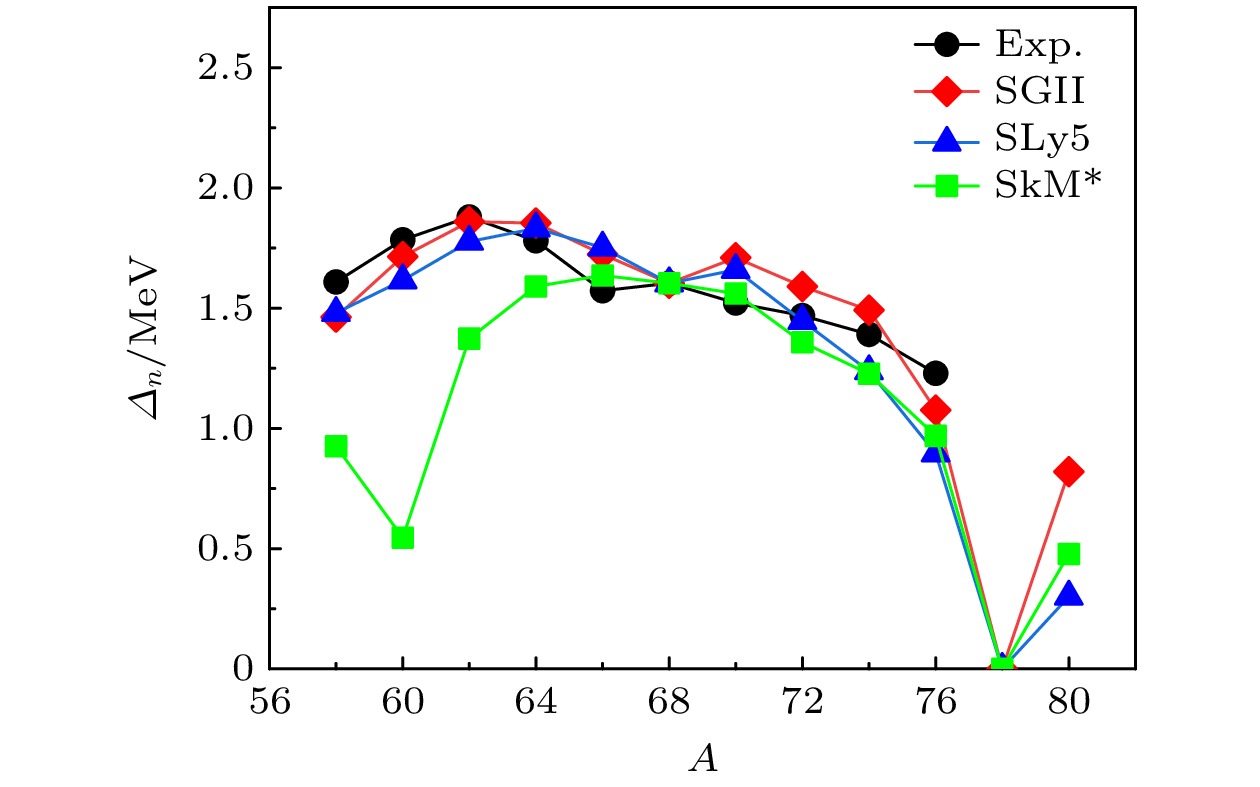
    • 同位旋标量巨四极共振低能态主要由费米面附近准粒子的激发所形成, 因此它对于对关联效应比较敏感[45]. 为了反映中子对关联的同位素依赖性, 图1展示了利用SGII, SLy5和SkM*相互作用计算的镍同位素链原子核的中子对能隙与实验值[40]的对比. 发现SGII与SLy5的结果整体上能较好地再现实验值, 而SkM*能较好地描述$ ^{64—76} {\rm{Ni}}$的中子对能隙实验值. 以SGII的计算结果为例, 中子对能隙从$ ^{58} {\rm{Ni}}$随中子数的增加而逐渐上升, 在$ ^{62} {\rm{Ni}}$时达到最大值. 随着中子的继续填充, 能隙逐渐下降直到$ ^{68} {\rm{Ni}}$达到较低值, 此时中子$ N = 40 $亚壳被填满. $ ^{70} {\rm{Ni}}$的能隙值相对于$ ^{68} {\rm{Ni}}$有所升高是由少量中子填充至更高能级$ 1{\rm{g}}_{9/2} $造成的. 随着轨道$ 1{\rm{g}}_{9/2} $内中子的增加, $ N = 50 $壳层趋向于闭合, 能隙值由$ ^{70} {\rm{Ni}}$至$ ^{76} {\rm{Ni}}$逐渐减小.

      由于费米面附近准粒子态的性质对同位旋标量巨四极共振低能态的影响比较大, 因此在研究镍同位素链原子核的低能四极态之前, 首先来研究费米面附近准粒子态的性质随中子数增加的演化情况. 表1展示了利用SGII相互作用计算的$ ^{64, 68, 72, 76} {\rm{Ni}}$费米面附近中子态的准粒子能、占据概率以及每个核的中子费米能$ \lambda_{n} $. 准粒子能的表达式为$ \sqrt{(\varepsilon_{i}-\lambda)^{2}+\varDelta_{i}^{2}} $, 发现能量低于费米面的能级$ 1{\rm{f}}_{7/2} $, $ 2{\rm{p}}_{3/2} $, $ 1{\rm{f}}_{5/2} $和$ 2{\rm{p}}_{1/2} $的准粒子能随着中子数的增加而增大, 而能量高于费米面的能级$ 1 {\mathrm{g}}_{9/2} $和$ 2 {\mathrm{d}}_{5/2} $随着中子数的增加而减小. 对于远离费米面的能级, 由于$ |\varepsilon_{i}-\lambda|\gg\varDelta_{i} $, 因此准粒子能的行为由$ |\varepsilon_{i}-\lambda| $主导; 而对于靠近费米面的能级, $ |\varepsilon_{i}-\lambda| $与$ \varDelta_{i} $比较接近, 对能隙$ \varDelta_{i} $也对准粒子能有明显影响. 至于准粒子占据概率$ \upsilon^{2} $, 能级$ 1 {\mathrm{g}}_{9/2} $的变化最为明显, 从$ ^{64} {\rm{Ni}}$的0.05上升到到$ ^{76} {\rm{Ni}}$的0.80, 当$ A = 78 $时, 该能级被完全占据. 同时, 发现使用SLy5和SKM*计算的$ ^{64, 68, 72, 76} {\rm{Ni}}$的准粒子能和占据概率与SGII的结果基本相似, 计算结果具有类似的随中子数增加的变化趋势.

      • 3.2.   镍同位素链原子核的低能四极激发态性质

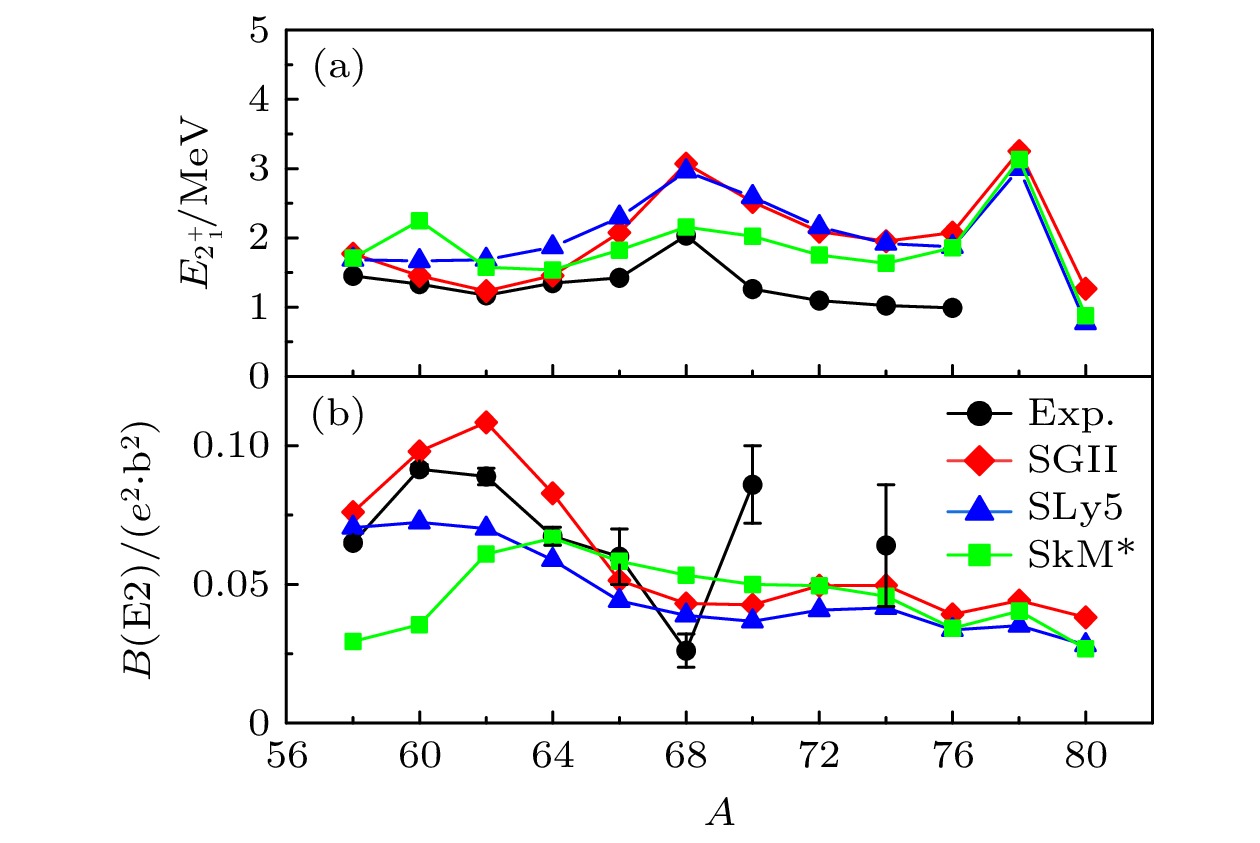
    • 图2展示了计算得到的镍同位素链原子核第一个2+态的激发能和电磁跃迁强度与实验值的对比. 发现三种Skyrme相互作用预言的第一个2+态的激发能整体略高于实验值, 但是基本上可再现实验值随中子数增加的变化趋势. 不同Skyrme相互作用的预言值尽管存在差别, 但是这种差别对于大多数原子核都比较小. 对于电磁跃迁强度, 不同的Skyrme相互作用给出的理论值在$ ^{58—62} {\rm{Ni}}$差异比较大而在$ ^{64—80} {\rm{Ni}}$差异比较小, SGII与SLy5相比于SkM*能更好地再现实验值的变化趋势, 尤其是SGII参数基本能再现$ ^{58—68} {\rm{Ni}}$的实验结果. 对于质量数大于68的核, 只有$ ^{70} {\rm{Ni}}$和$ ^{74} {\rm{Ni}}$有实验结果, 且比理论结果大. 结合上述分析, 第一个2+态激发能以及电磁跃迁强度的理论结果依赖于采用的Skyrme相互作用. 对比三种Skyrme相互作用给出的计算值, SGII的结果总体上与实验值符合得最好. 接下来将以SGII的结果为例进行分析.

      从图2(a) 可以看到SGII参数计算的镍同位素链原子核的第一个2+态激发能介于1—3 MeV之间. 随着质量数增加第一个2+态激发能先减小, 在$ ^{62} {\rm{Ni}}$达到较小值之后随着质量数增加而增加, 在$ ^{68} {\rm{Ni}}$达到相对较大值之后又随着质量数增加而减小, 在$ ^{74} {\rm{Ni}}$达到较小值之后又开始增加, 直到在$ ^{78} {\rm{Ni}}$达到较高能量. 由于原子核的费米能量以及费米面附近单粒子占有概率随着质量数的增加发生变化, 因此第一个2+态激发能的变化主要受到中子pfg亚壳中的准粒子组态以及中子$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $准粒子组态的影响, 另外还有来自低能质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $和$ \pi 1{\rm{f}}_{7/2} \to \pi 1{\rm{f}}_{5/2} $组态的贡献. 对于$ ^{68} {\rm{Ni}}$, 第一个2+激发态比相邻的$ ^{66} {\rm{Ni}}$和$ ^{70} {\rm{Ni}}$激发能要高, 下面给出可能的原因: 这几个原子核的第一个2+激发态主要受到质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $和$ \pi 1{\rm{f}}_{7/2} \to \pi 1{\rm{f}}_{5/2} $, 中子组态$ \nu 1{\rm{f}}_{5/2} \to \nu 2{\rm{p}}_{1/2} $, $ \nu 1{\rm{f}}_{5/2} \to \nu 1{\rm{f}}_{5/2} $, $ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{1/2} $及$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $的影响. 我们发现质子组态的能量随着质量数的增加变化很小, 影响主要来自中子组态的变化. 例如$ ^{66} {\rm{Ni}}$中, 上面列出的中子组态能量分别为3.68, 4.10, 4.52和7.03 MeV, 贡献百分比分别为34.42%, 23.78%, 10.98%和2.38%. $ ^{68} {\rm{Ni}}$中, 由于费米能和单粒子态占有概率的变化, 这些中子组态能量分别为4.69, 5.32, 5.64和5.18 MeV, 贡献百分比分别为19.55%, 12.79%, 6.18%和24.44%. 相较于$ ^{66} {\rm{Ni}}$, 准粒子能的增大以及占有百分比的变化, 使得$ ^{68} {\rm{Ni}}$激发能 略高于$ ^{66} {\rm{Ni}}$. 而$ ^{70} {\rm{Ni}}$中, 基于同样的原因, 这些中子组态能量和百分比也发生了变化, 分别为6.49, 7.23, 7.39和4.09 MeV, 贡献百分比分别为1.14%, 1.41%, 0.7%和68.35%. 尽管$ \nu 1{\rm{f}}_{5/2} \to \nu 2{\rm{p}}_{1/2}, \nu 1{\rm{f}}_{5/2} \to \nu 1{\rm{f}}_{5/2} $, $ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{1/2} $组态的准粒子能量较$ ^{68} {\rm{Ni}}$变大, 但是它们的占有百分比变得很小. 另外$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $组态的准粒子能量较$ ^{68} {\rm{Ni}}$中的变小, 而且占有百分比升高了很多, 这使得$ ^{70} {\rm{Ni}}$的激发能低于$ ^{68} {\rm{Ni}}$. 类似地, 对于$ ^{78} {\rm{Ni}}$, 中子$ N = 50 $壳层闭合, $ 1{\rm{g}}_{9/2} $轨道内的核子跨越$ N = 50 $壳隙向更高能级$ \nu 2{\rm{d}}_{5/2} $跃迁, 组态$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $ (能量为4.53 MeV) 的贡献百分比达到67.43%, 显著提升了$ ^{78} {\rm{Ni}}$的第一个2+态激发能.

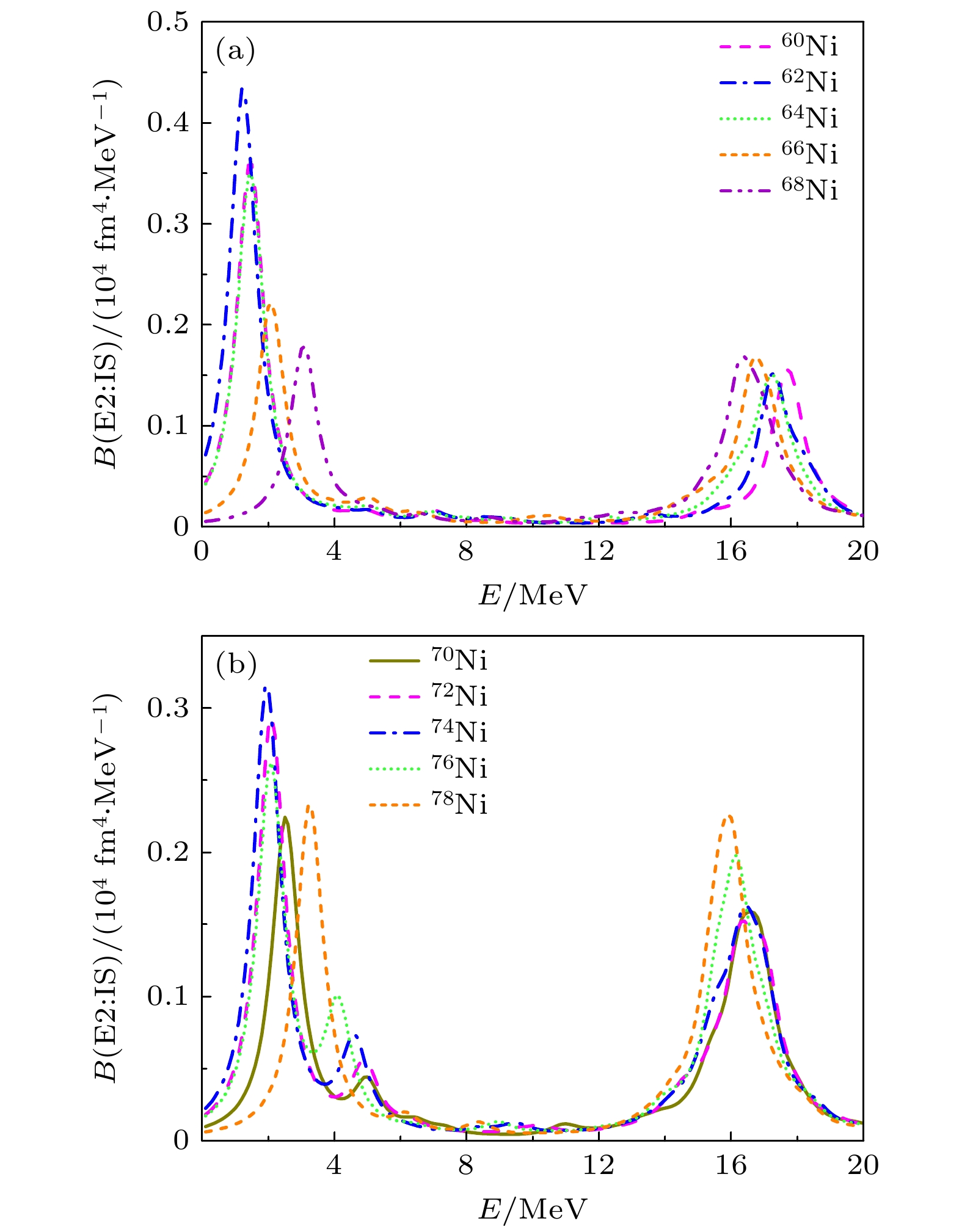
      从图2(b) 可以看到, 利用SGII参数计算得到的镍同位素链原子核第一个2+态的电磁跃迁强度从$ ^{58} {\rm{Ni}}$开始随中子数的增加而逐渐上升, 到$ ^{62} {\rm{Ni}}$达到最大值. 随着中子数的进一步增加, 镍原子核的电磁跃迁强度显著下降, 在$ A = 68 $附近达到较小值. 对于质量数$ A > 68 $的镍原子核, 计算得到的电磁跃迁强度的变化幅度较小. 镍原子核第一个2+态的电磁跃迁强度由质子激发所贡献. 其中, $ ^{58—66} {\rm{Ni}}$的电磁跃迁强度由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $主导. 这一质子组态的跃迁概率幅由$ ^{58} {\rm{Ni}}$的10.67 fm2上升至$ ^{62} {\rm{Ni}}$的12.12 fm2, 再下降至$ ^{66} {\rm{Ni}}$的8.51 fm2, 造成电磁跃迁强度先增大后减小. 对于质量数为$ 68\leqslant A\leqslant 76 $的镍原子核, 电磁跃迁强度随中子数增加而出现的涨落来自于质子组态总跃迁概率幅的轻微变化. 当$ A = 78 $时, 电磁跃迁强度相对于$ ^{76} {\rm{Ni}}$有所增大主要来自质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $的跃迁概率幅的上升, 这可能与$ N = 50 $壳层闭合引起的对关联消失有关[47]. 而$ ^{80} {\rm{Ni}}$的电磁跃迁强度则由于质子跃迁$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $贡献的降低而产生回落.

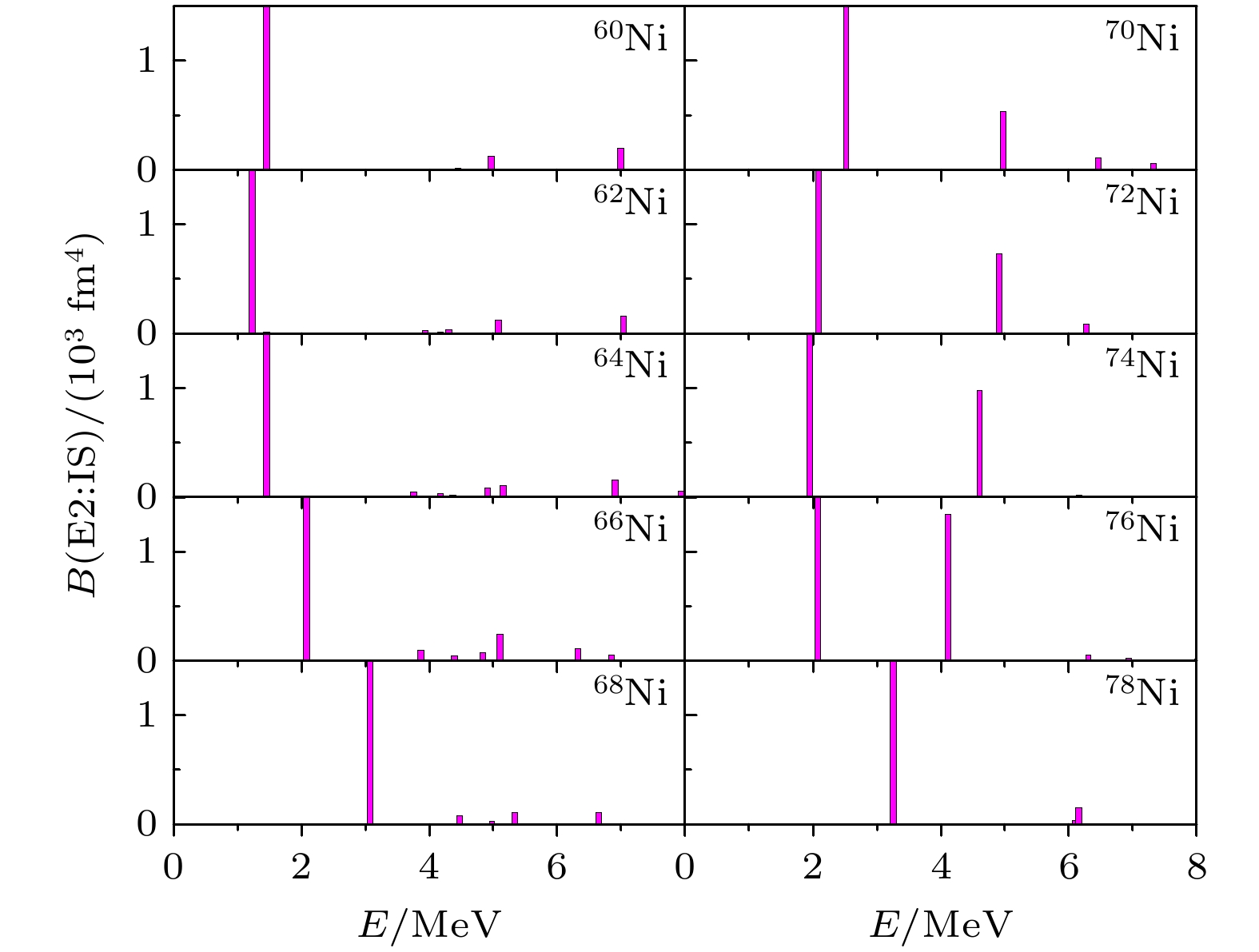
      图3给出了镍同位素链原子核的同位旋标量四极强度分布, 发现巨四极共振分布在16—18 MeV能区, 共振能量随中子数的增加而减小, 响应强度则随着中子数的增加而增加. 在1—3 MeV能区分布着镍同位素链原子核的第一个2+态, 由于第一个2+态能量受壳关联的影响, 在接近幻数时能量较大, 在远离幻数时则能量相对较低, 响应强度则与能量有一定的关系, 能量较低则响应强度较强, 能量较高则响应强度较弱. 表2展示了对$ ^{64, 70, 76} {\rm{Ni}}$第一个2+态作出主要贡献的准粒子组态的组态能量、贡献百分比以及对应的跃迁概率幅. 对于$ ^{60—68} {\rm{Ni}}$的第一个2+态, 如表2所列, 主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $以及中子准粒子组态$ \nu 1{\rm{f}}_{5/2} \to \nu 2{\rm{p}}_{1/2} $, $ \nu 1{\rm{f}}_{5/2} \to \nu 1{\rm{f}}_{5/2} $及$ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{1/2} $激发所贡献. 随着中子数的增加, 中子态$ \nu 1{\rm{g}}_{9/2} $的占有概率增加, 由$ \nu 1{\rm{g}}_{9/2} $中子准粒子激发的占比也随着增加. 对于$ ^{70—76} {\rm{Ni}}$的第一个2+态, 如表2所列, 主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $以及中子准粒子组态$ \nu 1{\rm{9}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $和$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $激发所贡献. 由于壳效应, $ ^{78} {\rm{Ni}}$中子态$ \nu 1{\rm{g}}_{9/2} $填满, 中子$ \nu 1{\rm{9}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $组态跃迁不存在, 它的第一个2+态则主要由质子$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $和中子$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $的跨壳跃迁所贡献, 激发能相对于$ ^{76} {\rm{Ni}}$变大, 有很强的壳效应. 同时发现镍同位素链原子核第一个2+态不存在不同组态之间跃迁概率幅的抵消, 集体性比较好.

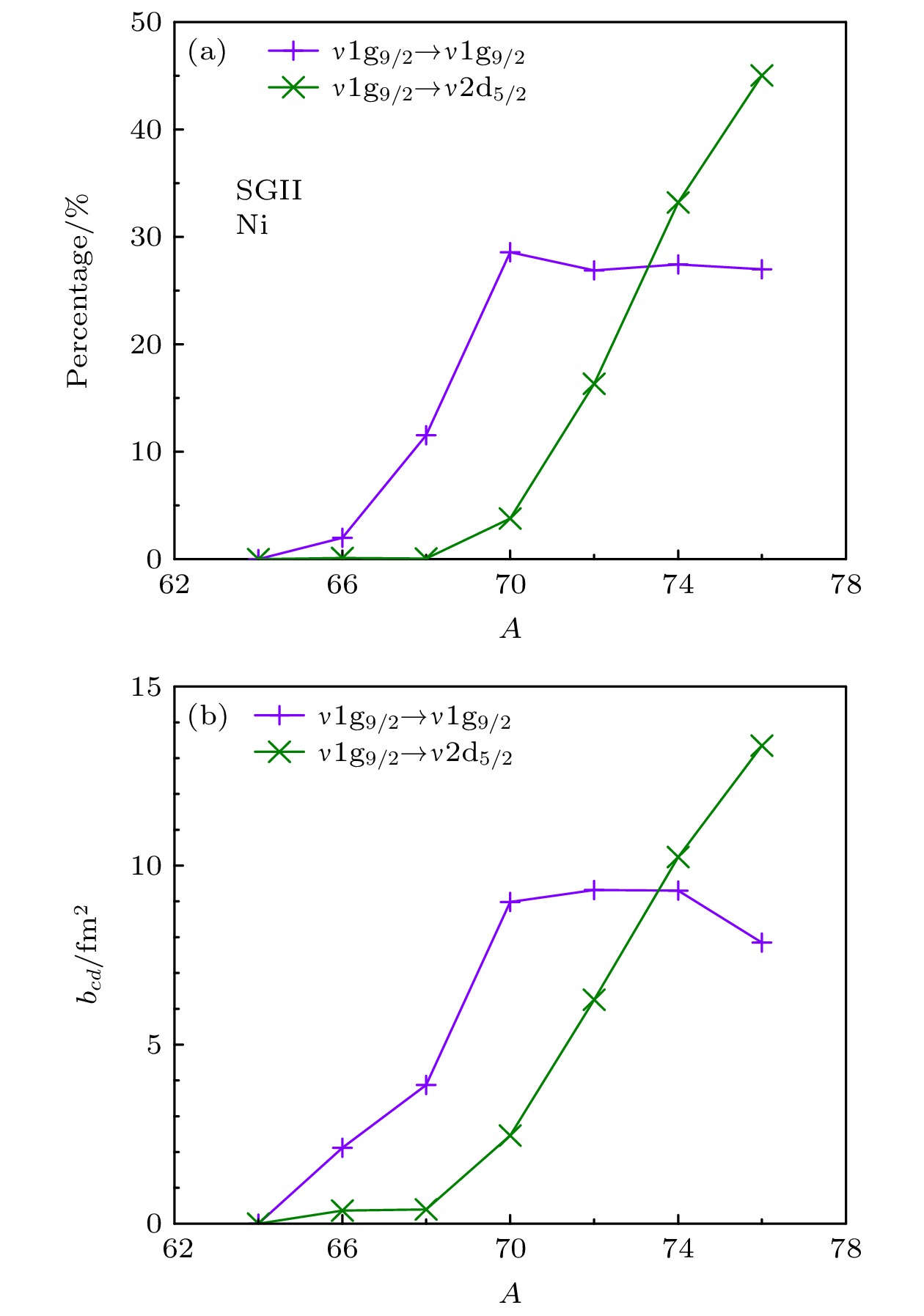
      由图3发现在低能区除了强度很高的第一个2+态以外, 在4—7 MeV能区还存在强度较小的矮四极共振态, 尤其对于$ ^{70—76} {\rm{Ni}}$原子核, 相对于$ ^{60—68} {\rm{Ni}}$原子核具有较强的矮四极跃迁强度. 为了详细地研究矮四极共振态随中子数增加的演化情况, 图4展示了镍原子核在8 MeV以下能区的跃迁强度分布. 如图4所示, $ ^{60—68} {\rm{Ni}}$的矮四极共振态主要分布于$ 4—7$ MeV, 能量分布比较弥散且具有较小的跃迁强度, 随着中子数的增加矮四极态的数量也有所增加, 例如$ ^{66} {\rm{Ni}}$有6个可见的矮四极态, 其中3个具有较强的跃迁强度, 分别位于3.86, 4.84, 5.10 MeV. 这些矮四极共振态主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $和$ \pi 1{\rm{f}}_{7/2} \to \pi 1{\rm{f}}_{5/2} $以及处于中子$ N = 28 — 50 $壳层内的准粒子组态所贡献, 例如$ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{1/2} $, $ \nu 1{\rm{f}}_{5/2} \to \nu 1{\rm{f}}_{5/2} $, $ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{3/2} $, $ \nu 1{\rm{f}}_{7/2} \to \nu 2{\rm{p}}_{3/2} $以及$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $, 这些组态对每一个矮四极态的贡献依赖于组态的能量. 一般来说, 组态能量越接近矮四极态的能量, 这个组态所贡献的百分比越大, 同时也给出较大的跃迁概率幅. 表2列出了$ ^{64, 70, 76} {\rm{Ni}}$中具有较强跃迁强度的矮四极共振态的组态信息. 例如$ ^{64} {\rm{Ni}}$中能量为5.16 MeV的矮四极态, 它主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $以及中子准粒子组态$ \nu 2{\rm{p}}_{3/2} \to \nu 2{\rm{p}}_{3/2} $跃迁形成, 它们的组态能量分别为4.83 MeV和5.03 MeV, 与这个矮四极态的能量很接近, 因此这两个组态贡献的占比和跃迁概率幅也相对于表中其他组态的值大, 占比分别为61.35%和22.68%, 跃迁概率幅分别为–10.38 fm2和3.22 fm2. 对于能量为6.89 MeV的矮四极态, 主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 1{\rm{f}}_{5/2} $跃迁形成, 它的组态能量为6.59 MeV, 占比和跃迁概率幅分别为90.06%和–5.04 fm2, 是所有组态中最高的. 另外, 对于$ ^{64—68} {\rm{Ni}}$, 随着中子数的增加, 中子态$ \nu 1{\rm{g}}_{9/2} $的占有概率变大, 中子$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $准粒子组态对镍同位素矮四极态的贡献增加. 图5给出了中子$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $和$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $组态的占比和跃迁概率幅, 可以看出, $ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $组态的占比和跃迁概率幅从$ ^{64} {\rm{Ni}}$到$ ^{68} {\rm{Ni}}$逐渐上升.

      图4显示$ ^{70—76} {\rm{Ni}}$的矮四极共振态的数量较少, 但是紧挨着第一个2+态的矮四极态具有较强的跃迁强度, 能量介于$ 4—5$ MeV之间, 随着中子数量的增加, 激发能量降低, 跃迁强度变强. 通过分析发现这个矮四极态主要由质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $和$ \pi 1{\rm{f}}_{7/2} \to \pi 1{\rm{f}}_{5/2} $, 以及中子准粒子组态$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $和$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $激发所贡献, 并且由质子主导激发逐渐转变为中子主导激发. 例如$ ^{70} {\rm{Ni}}$和$ ^{76} {\rm{Ni}}$分别处于4.98 MeV和4.11 MeV的矮四极态, 前者占比最高的是质子组态$ \pi 1{\rm{f}}_{7/2} \to \pi 2{\rm{p}}_{3/2} $, 占比为57.89%, 后者占比较高的是两个中子组态$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $和$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $, 占比分别为45.03%和26.99%. 这是中子态$ \nu 1{\rm{g}}_{9/2} $的占有概率随着中子数增加的结果. 如图5所示, 中子组态$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $的贡献百分比随着中子数的增加在增加, 在A = 70时最大, 之后则基本不变. 相比于$ ^{68} {\rm{Ni}}$中的跃迁概率辐, $ ^{70—76} {\rm{Ni}}$中$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $组态的跃迁概率辐变大, 但随中子数增加变化很小. 对于$ ^{70—76} {\rm{Ni}}$, 中子$ \nu 1{\rm{g}}_{9/2} \to \nu 2{\rm{d}}_{5/2} $组态对矮四极共振态的贡献百分比与跃迁概率幅随着中子数的增加而增加. 由于$ ^{78} {\rm{Ni}}$中不存在$ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $的组态激发, 因此在$ ^{78} {\rm{Ni}}$中不存在跃迁强度较强能量接近第一个2+态的矮四极态, 这些行为表明矮四极态具有一定的壳效应. 另外发现矮四极态的组态中存在跃迁概率幅符号不一致的情况, 一定程度上削弱了该四极态的跃迁强度.

    4.   结　论

    • 本文基于Skyrme HF+BCS理论以及自洽的QRPA方法研究了镍同位素链原子核的低能四极态性质随中子数增加的演化情况, 计算中分别采用SGII, SLy5和SkM*三种Skyrme相互作用以及密度依赖的零程对相互作用. 发现理论计算能够基本上符合镍同位素链原子核第一个2+态激发能量的变化趋势, SGII参数能较好地符合$ ^{58-68} {\rm{Ni}}$电磁跃迁强度的实验值. 同时发现$ ^{68} {\rm{Ni}}$和$ ^{78} {\rm{Ni}}$第一个2+态激发能比相邻同位素核的第一个2+态激发能高, 表现出较强的壳效应.

      本文还研究了矮四极态随中子数增加的演化情况. $ ^{58—68} {\rm{Ni}}$的矮四极共振态随中子数增加变化并不明显. 对于$ ^{70—76} {\rm{Ni}}$, 发现存在较强同位旋标量跃迁强度的矮四极态, 共振能量随着中子数增加而降低, 跃迁强度则随着中子数增加而增加. 随着中子数的增加, 中子$ 1{\rm{g}}_{9/2} $态占有概率增加, 由中子$ 1{\rm{g}}_{9/2} $态的准粒子激发组态占比增加, 组态激发由质子主导渐变为由中子主导. 在$ ^{78} {\rm{Ni}}$中, 由于中子$ 1{\rm{g}}_{9/2} $态填满, $ \nu 1{\rm{g}}_{9/2} \to \nu 1{\rm{g}}_{9/2} $的组态激发不存在, $ ^{78} {\rm{Ni}}$中的矮四极共振态消失, 因此镍同位素链原子核矮四极态对壳结构的改变比较敏感, 可以为丰中子核的壳演化提供信息. 使用SLy5和SKM*相互作用的计算值相比于SGII的结果存在数值上的轻微差别, 但是矮四极共振态的演化趋势与SGII的结论基本一致. 因此镍同位素链原子核矮四极共振态随中子数增加的演化与Skyrme相互作用的选择无关.

    参考文献 (47)

目录

/

返回文章
返回