高级搜索

两个系列铍反射层临界基准实验的一致性分析与核数据检验

, 

downloadPDF

上一篇

下一篇

陈胜利, 王天翔. 两个系列铍反射层临界基准实验的一致性分析与核数据检验[J]. 物理学报, 2025, 74(6): 062801-1. doi: 10.7498/aps.74.20241685
引用本文: 陈胜利, 王天翔. 两个系列铍反射层临界基准实验的一致性分析与核数据检验[J]. 物理学报, 2025, 74(6): 062801-1. doi: 10.7498/aps.74.20241685
shu
Shengli CHEN, Tianxiang WANG. Consistency analysis and nuclear data validation for two series of beryllium reflector critical benchmark experiments[J]. Acta Physica Sinica, 2025, 74(6): 062801-1. doi: 10.7498/aps.74.20241685
Citation: Shengli CHEN, Tianxiang WANG. Consistency analysis and nuclear data validation for two series of beryllium reflector critical benchmark experiments[J]. Acta Physica Sinica, 2025, 74(6): 062801-1. doi: 10.7498/aps.74.20241685
shu

两个系列铍反射层临界基准实验的一致性分析与核数据检验

  • 中山大学中法核工程与技术学院, 珠海　519082

    • 通讯作者: E-mail: chenshli23@mail.sysu.edu.cn.; 

  • 中图分类号: 28.20.-v, 28.20.Gd, 28.41.-i, 28.41.Ak

Consistency analysis and nuclear data validation for two series of beryllium reflector critical benchmark experiments

  • Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-sen University, Zhuhai 519082, China

    • Corresponding author: E-mail: chenshli23@mail.sysu.edu.cn.; 

  • MSC: 28.20.-v, 28.20.Gd, 28.41.-i, 28.41.Ak

  • 摘要: 铍金属与氧化铍都是重要核材料, 铍的中子核反应数据对核能研发具有重大意义. 宏观检验是核数据评价过程的重要环节, 对确保核数据的可靠性与精确度至关重要. 临界基准实验是目前核数据宏观检验最重要的标准. 但此前研究发现, 两个高度相似的铍反射层临界基准实验系列HMF-058与HMF-066在检验铍的中子反应数据时给出了矛盾的结论, 不能指出铍相关数据的改进方向, 导致这两个系列共14个实验无法被用于高精度的核数据检验. 出射中子角分布是反应堆物理计算中的关键物理量, 但核数据宏观检验中对其的关注度较低. 本文通过改进铍(n, n)与(n, 2n)反应的出射中子角分布数据提升了两个系列的理论计算与实验测量值的一致性. 基于改进的核数据, 所有计算与实验测量值的偏差均在1σ实验不确定度范围内, 因此无法在此不确定度内拒绝两个系列实验的一致性. 结合最新的整套铀核数据, 两者的一致性还有少许提升. 若要得出两个系列期望值系统性差异的结论, 仍需降低实验不确定度或开展更高精度的实验.
    Abstract: Beryllium metal and beryllium oxide are important nuclear materials, with neutron-induced nuclear reaction data on beryllium playing a crucial role in nuclear energy research and development. Macroscopic validation is an essential step in the nuclear data evaluation process, providing a means to assess the reliability and accuracy of such data. Critical benchmark experiments serve as the most important references for this validation. However, discrepancies have been observed in two closely related series of beryllium-reflector fast-spectrum critical benchmark experiments, HMF-058 and HMF-066, which are widely used in current nuclear data validation. A previous systematic study indicates that these two series of experiments reache contradictory conclusions in validating the neutron-induced nuclear reaction data of beryllium, creating ambiguity in improving beryllium nuclear data. As a result, the total of 14 experiments in these two series cannot currently support high-accuracy validation of nuclear data. Although most researches on nuclear data validation and adjustment mainly focus on cross sections, the angular distribution of emitted neutrons is a key factor in reactor physics calculations. In this work, we address these inconsistencies by improving the secondary angular distributions of the (n, n) and (n, 2n) reactions of beryllium, thereby making the theoretical calculations (C) and experimental results (E) of these two series more consistent, and reducing the cumulative χ2 value from 7.58 using the ENDF/B-VII.1 evaluation to 4.52. All calculations based on the improved nuclear data agree with the experimental measurements within 1σ experimental uncertainty. With these enhancements, the consistency between the HMF-058 and HMF-066 series cannot be rejected within the 1σ experimental uncertainty. Based on the latest comprehensive evaluation of uranium nuclear data, this consistency is slightly improved, and the cumulative χ2 value decreases to 4.36 once again. Despite these advances, systematic differences in the expected values of C/E between the two series still exist. The C/E values of the HMF-066 series are generally 230–330 pcm lower than those of the HMF-058 series, comparable to their experimental uncertainties of 200–400 pcm. Therefore, drawing a definitive conclusion about this systematic difference remains challenging. If the current improvement of differential nuclear data based on experimental data of 9Be is accurate, then the HMF-058 series experiments seem to be more reliable than the HMF-066 series. Ultimately, to achieve this goal, either reducing experimental uncertainty or designing and executing higher-precision integral experiments is required.
  • 加载中

  • 图 1  HMF-058-002与HMF-066-007实验的示意图(中心小球为不随实验改变的铍球-镍层)

    Figure 1.  Schematic of HMF-058-002 and HMF-066-007 experiments (the sphere in the core represents Be core-Ni layer that keeps unchanged in different experiments).

    下载: 全尺寸图片 幻灯片

    图 2  HMF-058与HMF-066系列的keff实验结果以及不确定度

    Figure 2.  Experimental measurements and uncertainties of keff for HMF-058 and HMF-066 series experiments.

    下载: 全尺寸图片 幻灯片

    图 3  9Be(n, n)与(n, 2n)反应的出射中子角分布

    Figure 3.  Angular distributions of outgoing neutrons for 9Be(n, n) and (n, 2n) reactions.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 9Be的中子吸收截面; (b)热中子吸收截面与实验值的比较[20]

    Figure 4.  (a) Neutron capture cross section of 9Be; (b) the comparison with experimental data for thermal neutron[20].

    下载: 全尺寸图片 幻灯片

    图 5  HMF-058系列先前的keff计算与实验结果比值(C/E )[12]以及改进后的结果

    Figure 5.  Ratio of calculation to experimental measurement (C/E ) of keff for HMF-058 series: previous [12] and improved results.

    下载: 全尺寸图片 幻灯片

    图 6  HMF-066系列先前的keff计算与实验比值结果(C/E )[12]以及改进后的结果

    Figure 6.  Ratio of calculation to experimental measurement (C/E ) of keff for HMF-066 series: previous [12] and improved results.

    下载: 全尺寸图片 幻灯片

    图 7  高度相似实验的keff的C/E结果比较

    Figure 7.  Comparison of C/E for keff of highly similar experiments.

    下载: 全尺寸图片 幻灯片
  • [1] Hou M D, Zhou X W, Liu B 2022 Nucl. Eng. Technol. 54 4393 doi: 10.1016/j.net.2022.07.017
    [2] Chen S L, Yuan C X 2020 Nucl. Mater. Energy 22 100728 doi: 10.1016/j.nme.2020.100728
    [3] Chen S L, He X J, Yuan C X 2020 Nucl. Sci. Tech. 31 32 doi: 10.1007/s41365-020-0741-9
    [4] Brown D A, Chadwick M B, Capote R, et al. 2018 Nucl. Data Sheets 148 1 doi: 10.1016/j.nds.2018.02.001
    [5] Plompen A J M, Cabellos O, De Saint Jean C, et al. 2020 Eur. Phys. J. A 56 181 doi: 10.1140/epja/s10050-020-00141-9
    [6] Iwamoto O, Iwamoto N, Kunieda S, et al. 2023 J. Nucl. Sci. Technol. 60 1 doi: 10.1080/00223131.2022.2141903
    [7] 葛智刚, 陈永静 2020 原子核物理评论 37 309 doi: 10.11804/NuclPhysRev.37.2019CNPC42 Ge Z G, Chen Y G 2020 Nucl. Phys. Rev. 37 309 doi: 10.11804/NuclPhysRev.37.2019CNPC42
    [8] Ge Z, Xu R, Wu H, et al. 2020 EPJ Web Conf. 239 09001 doi: 10.1051/epjconf/202023909001
    [9] Zabrodskaya S V, Ignatyuk A V, Koshcheev V N, Manochin V N, Nikolaev M N, Pronyaev V G 2007 RUSFOND-Russian National Library of Evaluated Neutron Data https://vant.ippe.ru/en/year2007/neutron-constants/774-1.html
    [10] Briggs J B, Scott L, Nouri A 2003 Nucl. Sci. Eng. 145 1 doi: 10.13182/NSE03-14
    [11] 吴海成, 张环宇 2024 原子能科学技术 58 1271 Wu H C, Zhang H Y 2024 At. Energy Sci. Tech. 58 1271
    [12] 胡泽华, 尹延朋, 叶涛 2016 物理学报 65 212801 doi: 10.7498/aps.65.212801 Hu Z H, Yin Y P, Ye T 2016 Acta Phys. Sin. 65 212801 doi: 10.7498/aps.65.212801
    [13] NEA 2024 “ICSBEP Handbook 2022-23”, International Criticality Safety Benchmark Evaluation Project Handbook (Database) https://www.oecd-nea.org/jcms/pl_20291 [2024-11-27]
    [14] Romano P K, Horelik N E, Herman B R, Nelson A G, Forget B, Smith K 2015 Ann. Nucl. Energy 82 90 doi: 10.1016/j.anucene.2014.07.048
    [15] Chen S L, Vandermeersch E, Tamagno P, Bernard D, Noguere G, Blaise P 2021 Ann. Nucl. Energy 163 108553 doi: 10.1016/j.anucene.2021.108553
    [16] Otuka N, Dupont E, Semkova V, et al. 2014 Nucl. Data Sheets 120 272 doi: 10.1016/j.nds.2014.07.065
    [17] Zerkin V V, Pritychenko B 2018 Nucl. Instrum. Methods Phys. Res. A 888 31 doi: 10.1016/j.nima.2018.01.045
    [18] Shibata K, Iwamoto O, Nakagawa T, et al. 2011 J. Nucl. Sci. Technol. 48 1 doi: 10.1080/18811248.2011.9711675
    [19] Chadwick M B, Herman M, Obložinský P, et al. 2011 Nucl. Data Sheets 112 2887 doi: 10.1016/j.nds.2011.11.002
    [20] Wang T X, Chen S L, Xu S Q, Li Z, Chen S Y, Wu X F 2023 Ann. Nucl. Energy 192 110017 doi: 10.1016/j.anucene.2023.110017
    [21] Chadwick M B, Capote R, Trkov A, et al. 2018 Nucl. Data Sheets 148 189 doi: 10.1016/j.nds.2018.02.003
    [22] Capote R, Trkov A, Sin M, et al. 2018 Nucl. Data Sheets 148 254 doi: 10.1016/j.nds.2018.02.005
    [23] Carlson A D, Pronyaev V G, Capote R, et al. 2018 Nucl. Data Sheets 148 143 doi: 10.1016/j.nds.2018.02.002
    [24] Broadhead B L, Rearden B T, Hopper C M, Wagschal J J, Parks C V 2004 Nucl. Sci. Eng. 146 340 doi: 10.13182/NSE03-2
    [25] Nouri A, Nagel P, Briggs J B, Ivanova T 2003 Nucl. Sci. Eng. 145 11 doi: 10.13182/NSE03-15
    [26] Wang T X, Xu S Q, Li Z, Chen S L 2025 Ann. Nucl. Energy 210 110851 doi: 10.1016/j.anucene.2024.110851
    [27] Cabellos O, Hursin M, Palmiotti P 2023 EPJ Web Conf. 284 14012 doi: 10.1051/epjconf/202328414012
  • 加载中
图( 7)
计量
  • 文章访问数:  147
  • HTML全文浏览数:  147
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-05
  • 刊出日期:  2025-03-20

两个系列铍反射层临界基准实验的一致性分析与核数据检验

  • 收稿日期:  2024-12-05

摘要: 铍金属与氧化铍都是重要核材料, 铍的中子核反应数据对核能研发具有重大意义. 宏观检验是核数据评价过程的重要环节, 对确保核数据的可靠性与精确度至关重要. 临界基准实验是目前核数据宏观检验最重要的标准. 但此前研究发现, 两个高度相似的铍反射层临界基准实验系列HMF-058与HMF-066在检验铍的中子反应数据时给出了矛盾的结论, 不能指出铍相关数据的改进方向, 导致这两个系列共14个实验无法被用于高精度的核数据检验. 出射中子角分布是反应堆物理计算中的关键物理量, 但核数据宏观检验中对其的关注度较低. 本文通过改进铍(n, n)与(n, 2n)反应的出射中子角分布数据提升了两个系列的理论计算与实验测量值的一致性. 基于改进的核数据, 所有计算与实验测量值的偏差均在1σ实验不确定度范围内, 因此无法在此不确定度内拒绝两个系列实验的一致性. 结合最新的整套铀核数据, 两者的一致性还有少许提升. 若要得出两个系列期望值系统性差异的结论, 仍需降低实验不确定度或开展更高精度的实验.

English Abstract

    全文HTML

    1.   引　言

    • 铍(Be)是除锂(Li)之外最轻的非气体元素, 具有良好的物理、化学和核反应性能. 在快中子慢化过程中, 慢化效果随慢化剂原子量的减小而增强, 由于Li的化学性质过于活泼, Be是可用的固体慢化剂中慢化效果最好的材料之一. Be在自然界中仅存在9Be一种同位素. 9Be具有较大的热中子散射截面以及较小的热中子吸收散射比, 可作为良好的中子反射剂. 此外, 9Be可以通过(n, 2n)核反应实现中子增殖, 可作为中子倍增剂. 因此, 金属Be已成为备受关注的关键核材料. 除金属Be外, 其氧化物形态的BeO也在核反应堆中广泛应用[1], 特别是因其良好的导热性被掺杂在核燃料中以提高燃料的导热性[2,3]. 因此, Be相关的中子反应特性研究至关重要.

      由于缺乏系统性描述全能区中子诱发核反应的微观机理模型, 目前应用核反应的研究主要基于核反应数据开展. 鉴于核素数量庞大、反应道多、核反应相关物理量多(包括反应截面、角分布、能量分布等)、入射能量相关等特点, 常用的核反应数据在经过专业评价、检验后形成评价核数据库. 目前国际上已有五大通用评价核数据库, 分别是美国的ENDF/B[4], 欧共体的JEFF[5], 日本的JENDL[6], 中国的CENDL[7,8]和俄罗斯的ROSFOND[9], 其中美国的ENDF/B评价库在全球范围内使用最为广泛.

      在核数据评价建库的过程中, 为确保中子反应数据的可靠性, 宏观检验是一个重要步骤. 宏观检验主要基于微观中子反应数据计算宏观物理量, 通过计算结果与实验测量结果的比较来评估微观核数据的准确性. 宏观检验的目标物理量也称为积分量, 通常为中子能谱与反应堆物理参数, 其中最典型的是国际核临界安全基准评价项目 (International Criticality Safety Benchmark Evaluation Project, ICSBEP) 手册[10]收录的有效增殖因子(keff)实验值. keff的计算值(C )与实验值(E )比较已成为当今评价核数据检验的标准流程. 我国也基于ICSBEP建立了包含2237个临界基准实验的计算模型库ENDITS-2.1[11]以进一步推动核数据的检验工作.

      但此前的研究发现, ICSBEP中高度相似的HMF-058与HMF-066两个快中子能谱系列的铍反射层临界基准实验, 在核数据检验中给出了不自洽的结论, 因此其中至少一个系列基准实验的测量或评价可能存在系统性的问题[12]. 此外, 基于当时最新评价核数据的HMF-058系列计算结果在1σ实验不确定度内大于实验结果[12]. 鉴于这两个系列的临界基准实验在评价核数据库宏观检验中的广泛应用, 对其进行系统性的分析与评价对于核数据评价以及后续应用至关重要. 本研究将通过改善关键核数据, 特别是此前关注较少的中子散射角分布数据, 使得HMF-058与HMF-066的一致性大幅提升, 且两个系列的计算结果均在1σ的实验不确定度内.

    2.   临界基准实验

      2.1.   实验设置与参数

    • 截至2022年, ICSBEP手册已收录了598个系列共计5159个临界基准实验[13]. 手册中每个系列的每个实验都有对应的编号, 包括表示实验特点的3层字母缩写(核裂变燃料类型-燃料物理形态-中子能谱)、紧随其后的系列数字编号、以及每个系列内部的实验数字编号. 本研究聚焦于两个系列的铍反射层临界基准实验, 其ICSBEP手册编号分别是HEU-MET-FAST-058与HEU-MET-FAST-066. 其中HEU表示高富集度铀(highly enriched uranium), MET代表金属(metal)燃料, FAST则指快(fast)中子能谱, 058与066为HEU-MET-FAST类别下的具体编号. 针对每个系列中的临界基准实验, ICSBEP会在系列名称后附加从001开始的顺序编号, 如HEU-MET-FAST-058-001. 出于简化考虑, 通常可用HMF-058与HMF-066指代这两个实验系列.

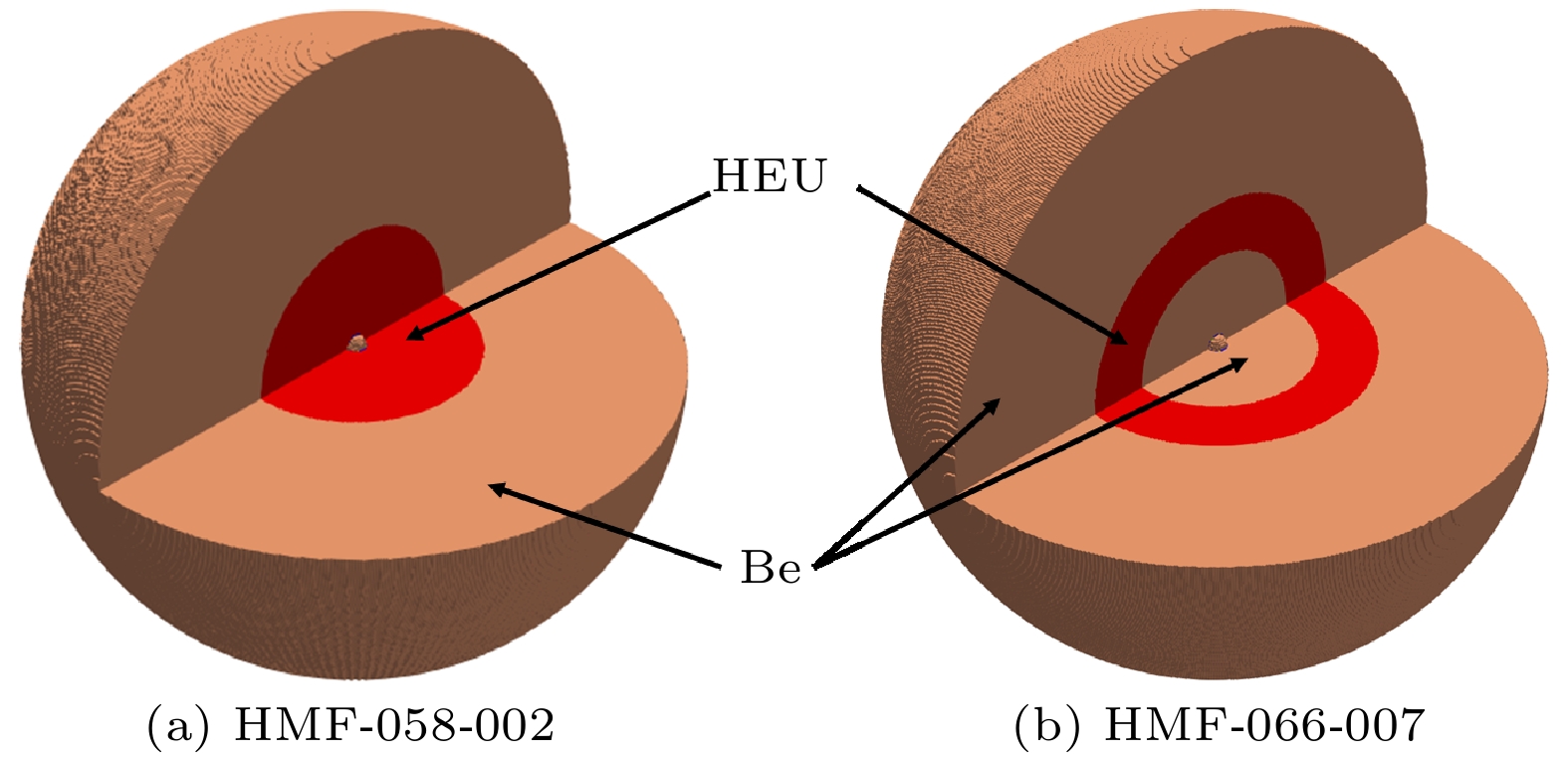
      HMF-058系列的5个实验于1958—1959年间开展, 而HMF-066系列的9个实验在1960年进行. 两个系列实验都是球形几何设计, 其中HMF-058系列由内到外依次是铍球(半径4.98 mm)、镍壳层(外径5.21 mm)、空隙层(外径5.56 mm)、燃料壳层及铍反射壳层, 不同实验仅改变燃料层与铍反射壳层的厚度使得装置达到临界状态; HMF-066系列与HM-F058高度相似, 仅在空隙和燃料层间增加了一个铍壳层, 不同实验改变内外两层铍反射层以及燃料层的厚度. 图1展示了整体尺寸最为接近的HMF-058-002 (半径152.11 mm)与HMF-066-007 (半径151.49 mm)的1/4截面示意图. 这两个系列简单的几何与材料设计也使得它们在核数据宏观检验中被广泛应用.

      • 2.2.   实验结果

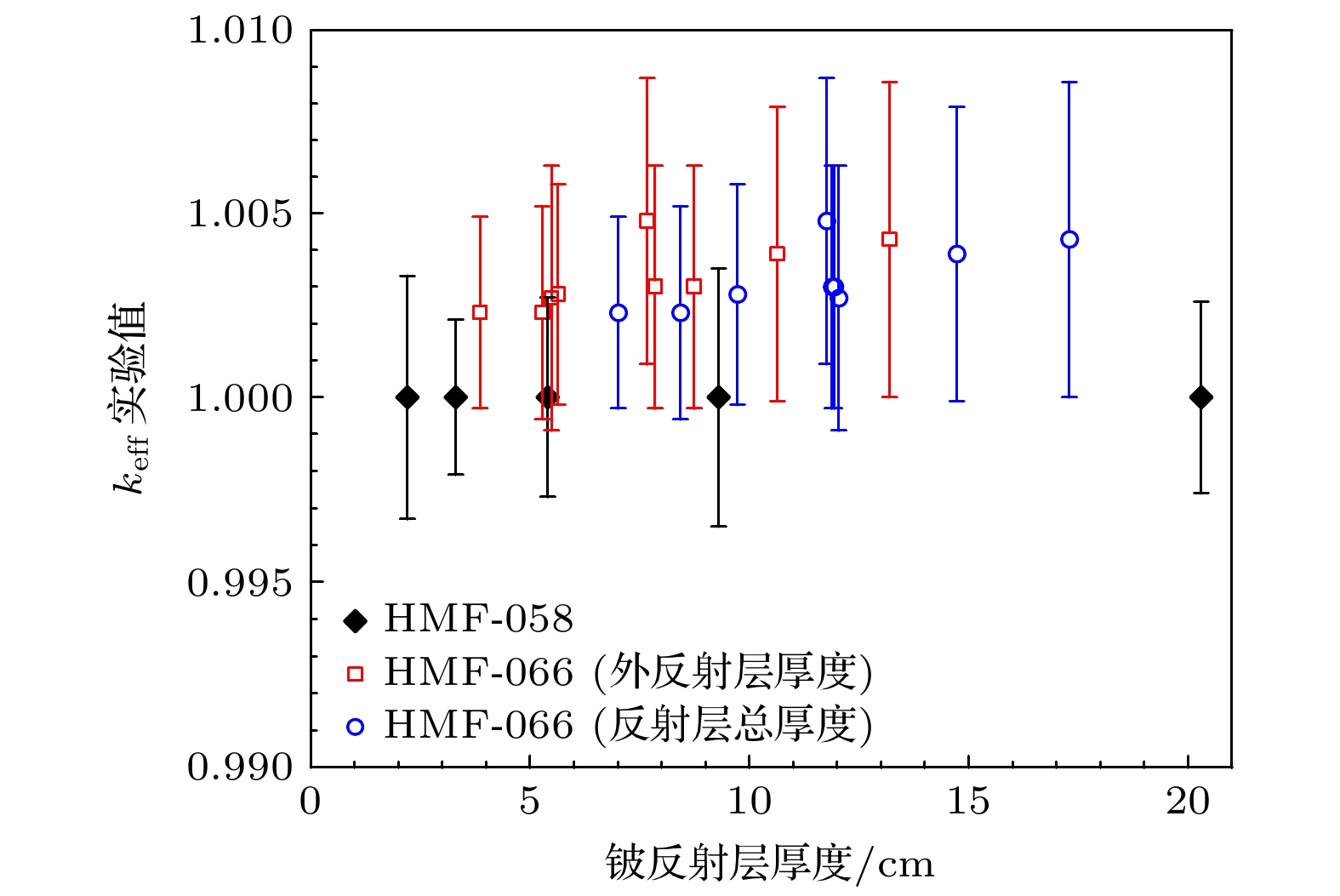
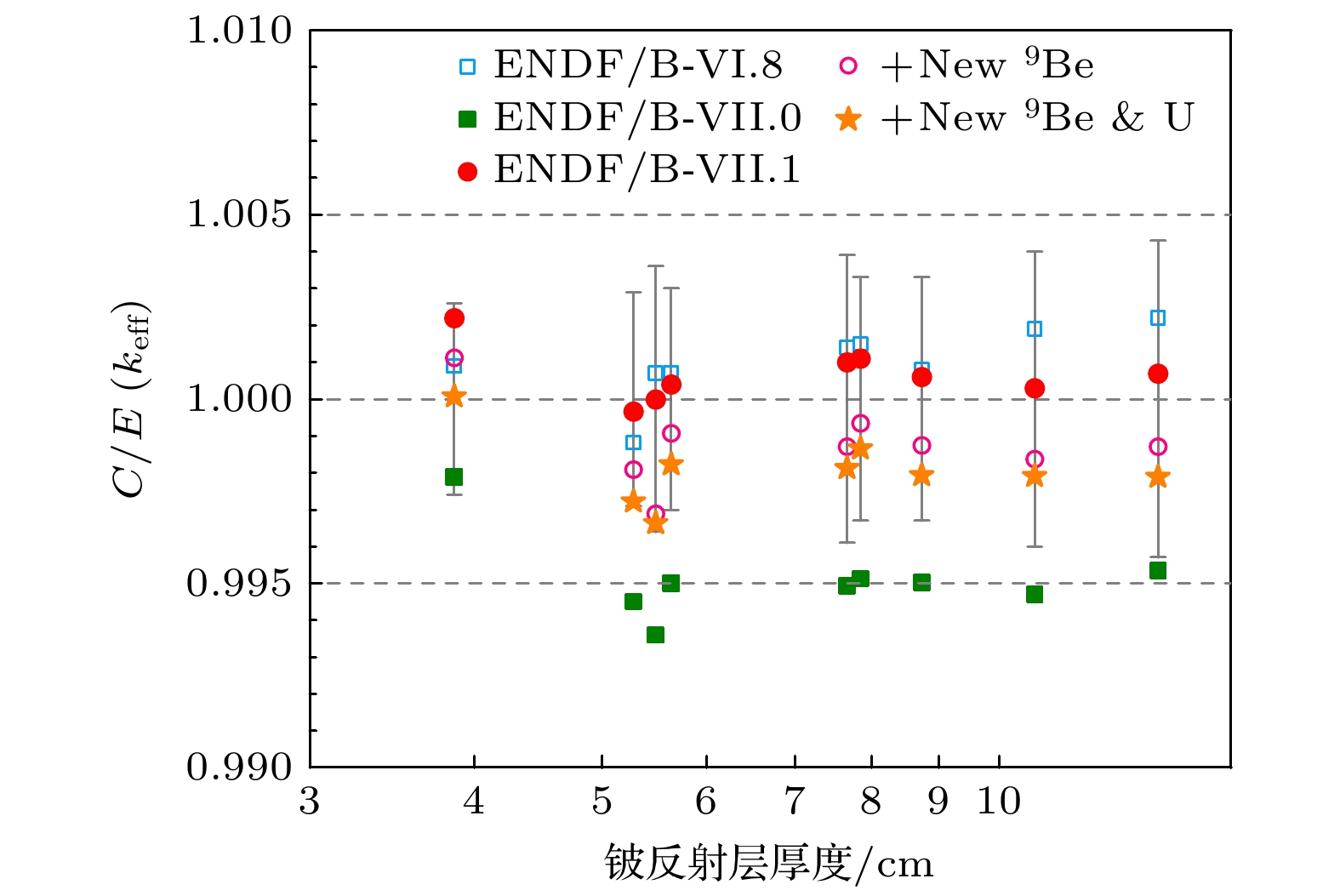
    • 参照此前的分析研究[12], 本文根据铍反射层厚度将实验的keff测量值在图2中展示. 由于HMF-066系列有内外两层铍反射层, 因此分别以外反射层厚度(与HMF-058系列一致)以及内外反射层总厚度为变量进行展示. 值得注意的是, HMF-058系列的5个基准实验均为临界状态, 而HMF-066系列基准实验则处于略超临界状态. 对应本研究中涉及的基于评价核数据的keff理论计算都通过蒙特卡罗中子输运程序OpenMC[14]开展.

    3.   计算结果的改进

      3.1.   HMF-058结果的改进

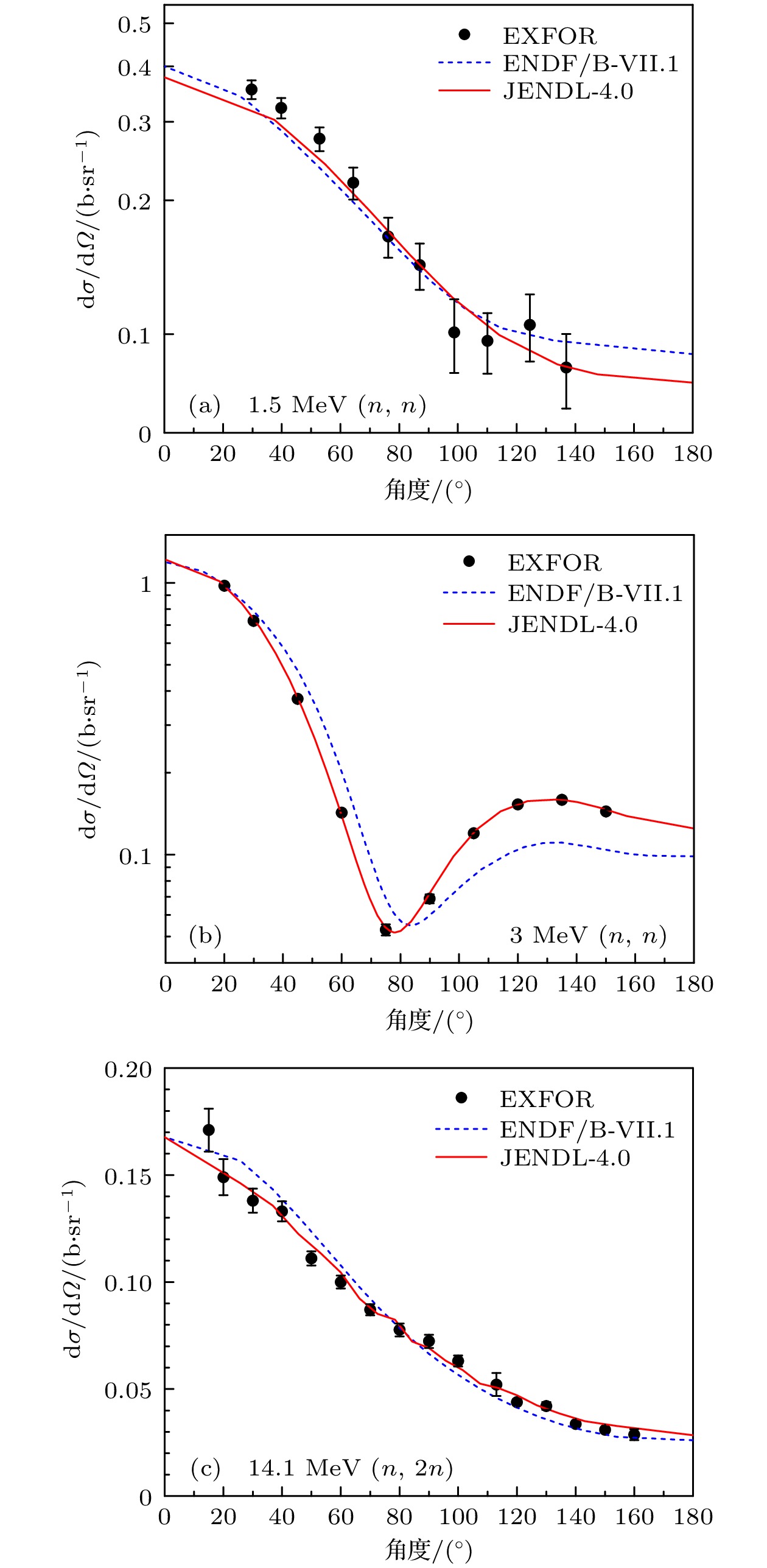
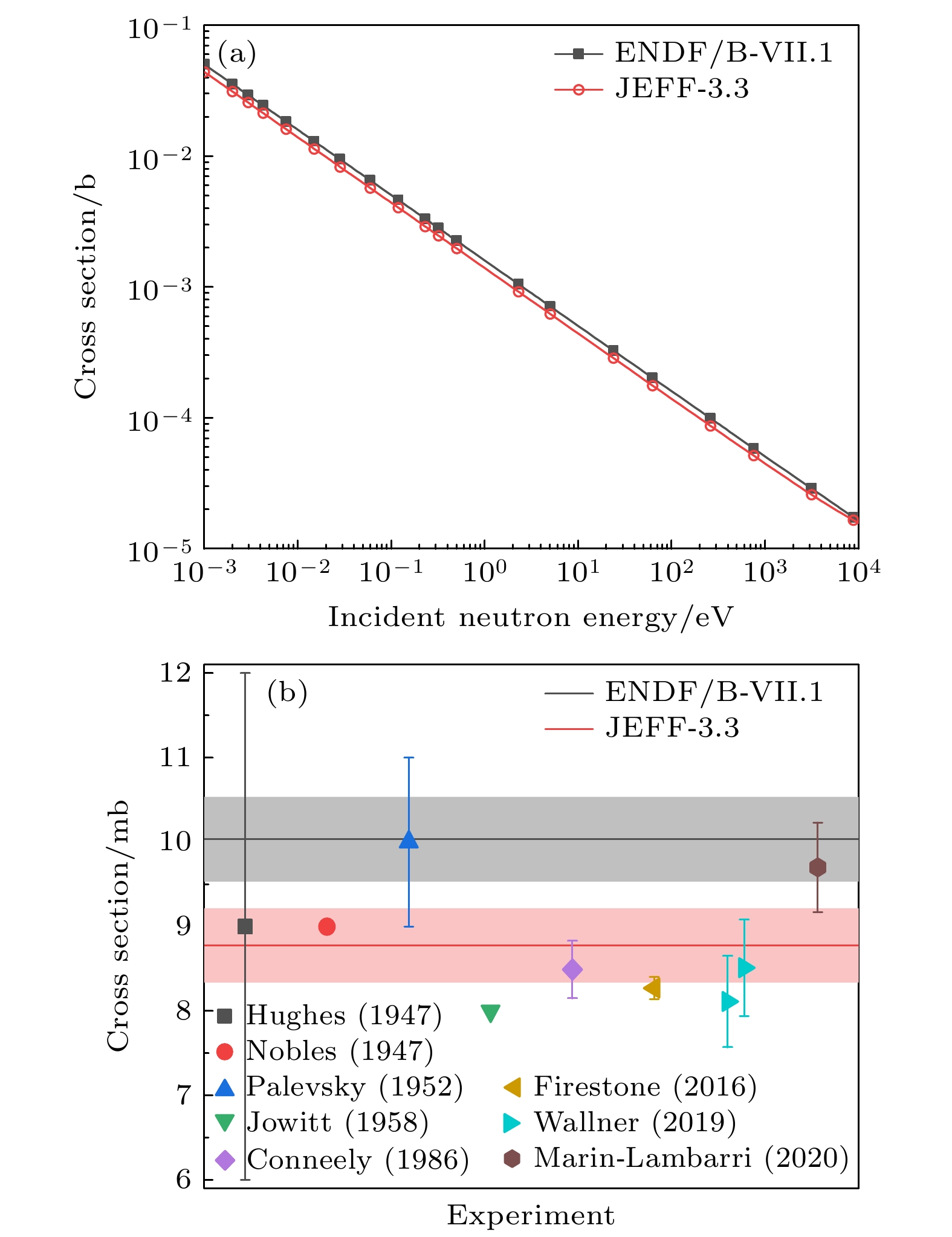
    • 此前研究表明HMF-058与HMF-066之间关于9Be反应截面的敏感性系数相近, 因此, 仅通过反应截面数据无法提高的两者间的一致性[12]. 实际上, 虽然当前的核数据检验与调整研究主要关注反应截面数据, 但出射中子角分布是影响keff计算的重要因素[15]. 对于9Be, 如图3所示, 以EXFOR[16,17]收录的实验值为参照, JENDL-4.0[18]评价的(n, n)与(n, 2n)反应的出射中子角分布总体上优于ENDF/B-VII.1[19]的评价. 基于更优的角分布数据得到的计算结果的准确度更高. 此外, 如图4所示, ENDF/B-VII.1中9Be的热中子吸收截面((10.03±0.50) mbarn)明显高于实验值(平均为(8.4±0.1) mbarn), 其准确性不如JEFF-3.3的评价((8.78±0.44) mbarn)[20]. 因此, ENDF/B-VII.1的9Be中子吸收截面也替换为JEFF-3.3的评价数据.

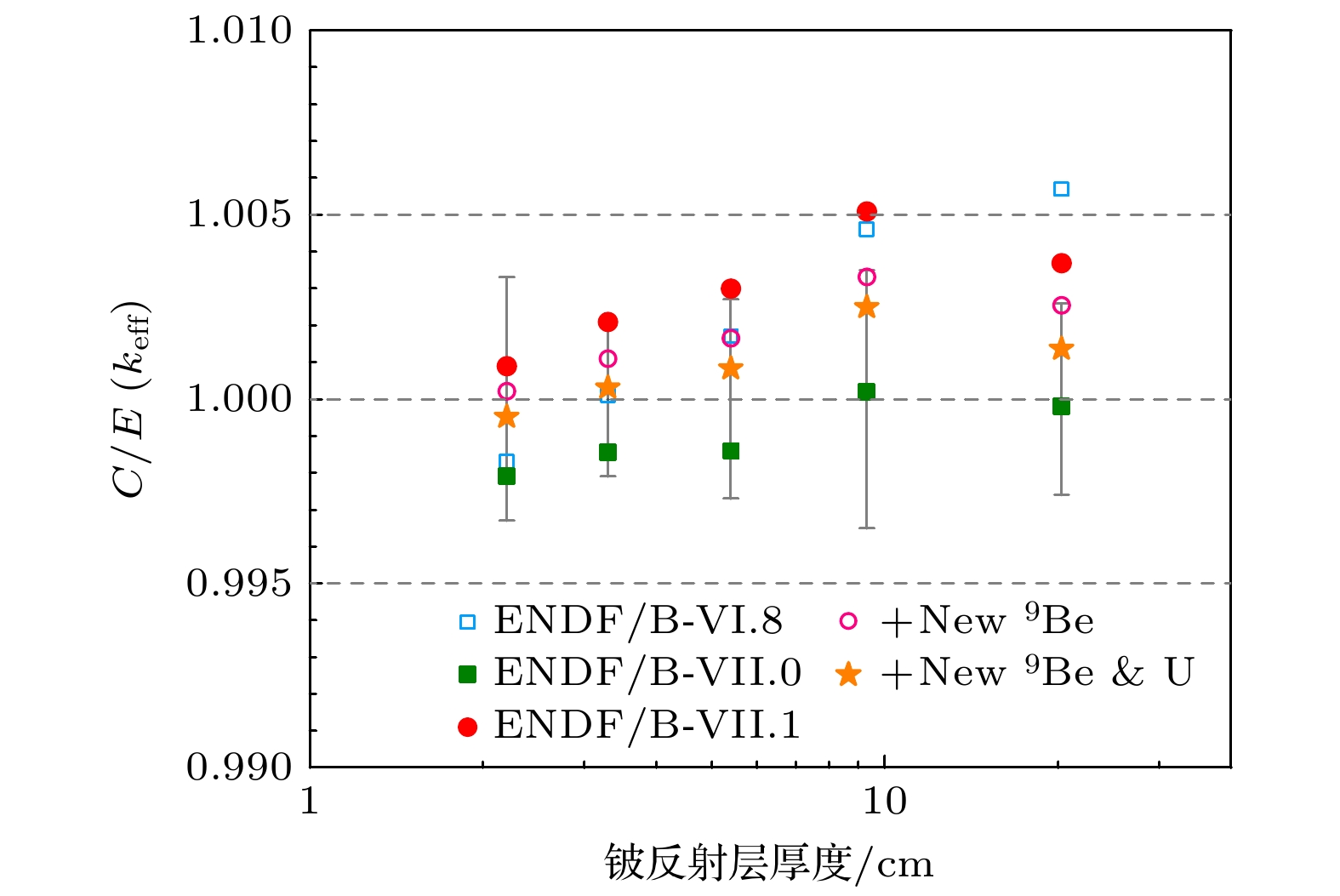
      图5所示为HMF-058系列的计算与实验比值(C/E )结果, 基于更新的角分布数据, 计算值显著减小, 减小量为70—180 pcm (平均减小120 pcm), 且5个实验的计算与测量值均在1σ的实验不确定度内吻合, 累积χ2由基于ENDF/B-VII.1评价数据库的6.46降至2.52. 实际上, 由于减小中子吸收截面会导致keff计算值增大, 因此9Be角分布的影响比图5中的变化稍大. 由此可以推断, 此前基于ENDF/B-VII.1的HMF-058系列基准实验计算值总体大于实验值极有可能是由9Be的(n, n)与(n, 2n)反应道的角分布导致的. 基于微分截面实验的9Be角分布改进与临界基准实验积分量keff的计算准确度提升一致.

      虽然HMF-058临界基准实验对9Be数据的敏感性较高, 但其高富集度235U的实验设置对235U数据的敏感性整体上更高. 在ENDF/B-VII.1发布后, 经合组织核能署(OECD/NEA)组织了国际协作评价库机构(Collaborative International Evaluation Library Organization, CIELO)项目来对核技术应用影响较大的氢(H)、氧(O)、铁(Fe)、铀(U)与钚(Pu)同位素的核数据进行评价[21]. 其中铀同位素的全套数据均得到了重新评价[22]. 虽然235U的中子诱发裂变截面有国际标准[23], 但其余无标准的数据对临界计算仍有较大的影响, 如裂变中子数. 因此, 本文采用CIELO评价的铀(包括235U和238U)的全套评价数据对HMF-058系列基准实验进行计算. 如图5所示, 计算结果减小了70—120 pcm (平均减小约90 pcm), 计算结果与实验值的吻合度进一步提升. 该结论与新评价的235U诱发裂变中子数减少[22]一致, 理论keff对后者的敏感性系数接近1.

      HMF-058系列基准实验因其独特的材料设计, 仅对9Be与235U的中子诱发核反应数据敏感. 上述9Be出射中子角分布的改进以及235U全套数据的重新评估均使得keff的计算与实验测量值吻合度的大幅提升, 累积χ2由基于ENDF/B-VII.1评价数据库的6.46降至0.92. 这一结果表明, 相关角分布等微分实验数据以及HMF-058系列临界基准积分实验是一致的.

      • 3.2.   HMF-058与HMF-066的一致性

    • 经过上述核反应数据的更新, HMF-058的计算结果与实验测量结果能较好符合. 但此前研究表明, HMF-058与HMF-066之间存在系统性偏差, 提升HMF-058的计算结果会导致HMF-066的计算与实验间偏差增大[12]. 图6展示了HMF-066系列9个临界基准实验基于更新核数据的C/E结果. 与基于原ENDF/B-VII.1数据的结果比较, 计算结果系统性减小, 与文献[12]的结论一致. 更新 9Be数据与U数据带来的减小量为分别为110— 320 pcm (平均减小190 pcm)与30—100 pcm (平均减小70 pcm).

      但无论仅更新9Be的角分布与吸收截面还是同时更新U的全套核数据, HMF-066系列的计算与实验测量结果基本在1σ实验不确定度内符合. 9个实验的累积χ2值由基于ENDF/B-VII.1评价数据库的1.12分别增大到2.01与3.44. 因此, 在统计意义上, 仍可以认为HMF-066系列的计算与测量值在1σ实验不确定度内是符合的.

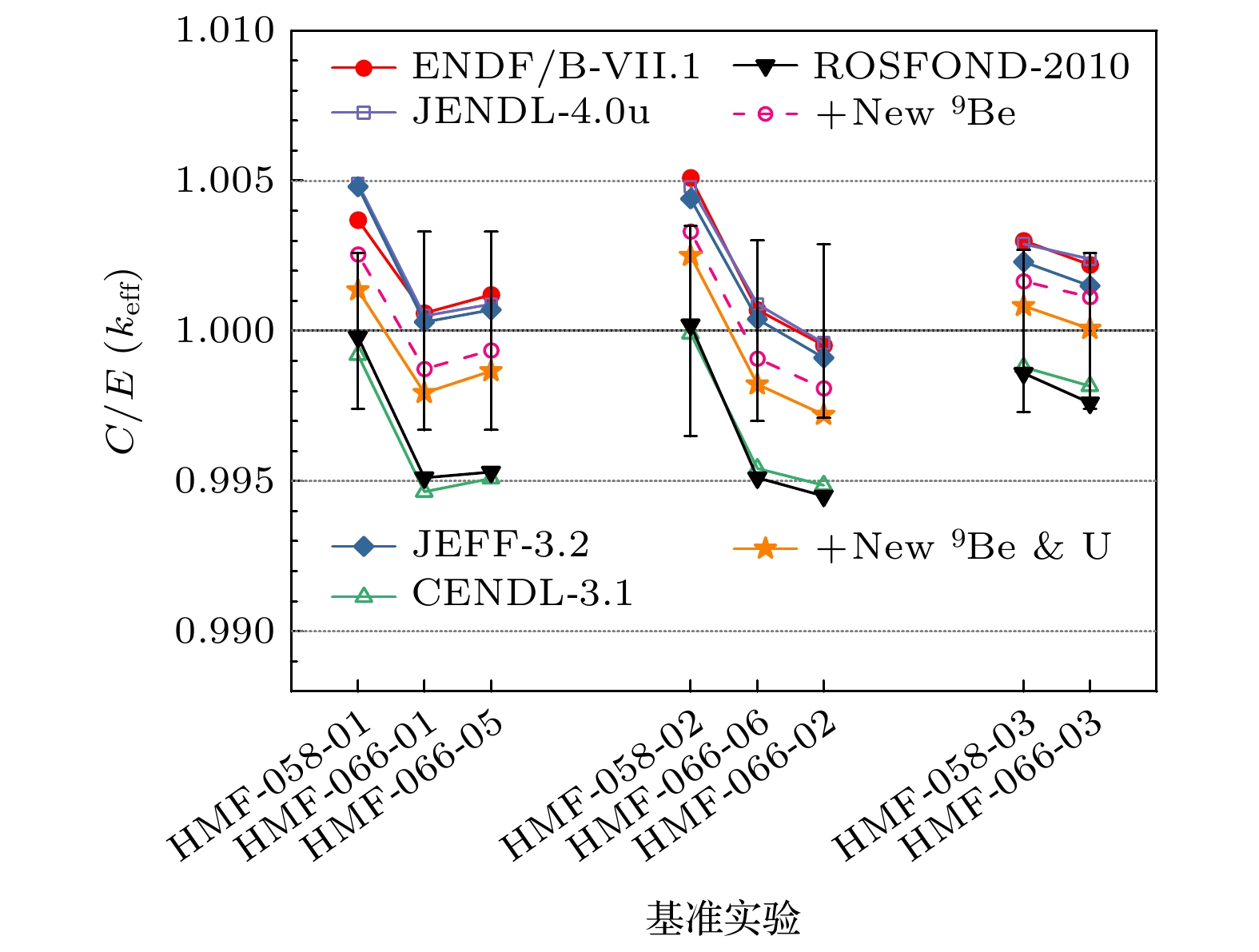
      鉴于HMF-058与HMF-066系列实验设计的较高相似度, 可用量化的相似性指标进行相似性分析. 此前研究已系统地计算了HMF-058系列5个实验与HMF-066系列9个实验两两之间的相似度(两个敏感性系数向量间的余弦值, 也称E指标[24]或余弦相似度), 并以HMF-058-001, HMF-058-002, HMF-058-003为例, 分别选取了与之高相似度的HMF-066-001 (相似度99.4% )与HMF-066-005 (相似度99.3% )、HMF-066-006 (相似度99.8% )与HMF-066-002 (相似度99.8% )、HMF-066-003 (相似度99.5% )作为对比[12].

      图7展示了这3组高相似度临界基准实验的keff的C/E结果. 此前基于5个不同评价核数据库的计算结果[12]可归为2类: ENDF/B-VII.1, JENDL-4.0u以及JEFF-3.2结果相似, CENDL-3.1与ROSFOND-2010结果相近. 前者高估了HMF-058系列多数实验的keff, 但与HMF-066系列实验的keff符合较好; 后者则与HMF-058系列实验的keff符合较好, 但低估了HMF-066系列多数实验的keff. 基于本研究更新的数据, 两个系列间虽仍有差异, 但在1σ实验不确定度内, 所有计算与实验结果的一致性得到了保证.

    4.   讨　论

    • 临界基准实验的数值模拟与计算依赖于相关的全套核反应数据. 其中计算结果关于反应截面的敏感性分析受到了广泛的关注, 包括DICE数据库[25]收录的部分ICSBEP基准实验的敏感性. 出射中子角分布对keff计算也有较大影响[15], 但目前相关的研究较为缺乏. 其中一个重要原因是每个反应截面仅随入射中子能量变化, 因此其对应的扰动计算以及敏感性表示相对容易. 然而, 角分布涉及入射中子能量与出射中子角度两个自由变量, 因此相关分析与表示的复杂性显著提升. 由于角分布变化对keff计算的影响对反应堆或临界基准实验设计极为敏感, 对于相对复杂的系统, 该影响的定性预测仍存在困难[26]. 因此, 角分布对keff计算的影响不可忽视.

      针对HMF-058与HMF-066两个系列的铍反射层临界基准实验, 此前基于截面敏感性分析的研究表明两者之间存在系统性偏差[12]. 本研究通过更新9Be(n, n)与(n, 2n)反应道的角分布与中子吸收截面提升了原ENDF/B-VII.1中9Be这两方面核数据的准确性. 基于更新的9Be核数据, 两个系列的计算结果与实验测量值在1σ实验不确定度内均符合较好. 两个系列共14个实验的累积χ2由基于ENDF/B-VII.1评价数据库的7.58降至4.52. 因此, 在统计意义上, 在1σ实验不确定度内无法拒绝两个系列是一致的.

      在更新9Be核数据同时, 用CIELO评价的全套U (包括235U和238U)核数据替换ENDF/B-VII.1中的数据, HMF-058的计算结果与实验测量结果的符合度进一步提升, 且两个系列间的一致性也有些许提升(累积χ2由4.52降至4.36). 但U数据改进对HMF-058与HMF-066两个系列的影响不如9Be核数据显著. 由于CIELO的全套U数据几乎都是重新评价的, 包括裂变中子数目随入射中子能量振荡变化的拟合[22], 因此我们未量化特定U核数据对临界基准实验计算的影响. 但本研究仍然验证了CIELO全套U中子反应核数据总体上优于ENDF/B-VII.1, 因此其很合理地被ENDF/B-VIII.0数据库直接采纳.

      当然, 从图7的前两组结果可用看出, HMF-058与HMF-066两个系列的C/E期望值仍存在系统性的差异, 尤其是更新核数据后HMF-066的C/E整体上更偏离1. 若当前基于微分实验数据的核数据改进方向是正确的, 则可以推断HMF-058系列实验的可信度相对更高. 但由于两个系列的计算与测量结果均在1σ实验不确定度内符合, 且两个系列共14个实验的累积χ2仅为4.36, 无法在统计意义上拒绝两个系列在1σ实验不确定度内是一致的. 若要得到两个系列一致性进一步的结论, 需要降低实验不确定度或开展新的更高精度实验.

    5.   结　论

    • 此前基于多个评价核数据库的研究表明, 高度相似的HMF-058与HMF-066两个系列的铍反射层临界基准实验之间存在系统性偏差[12]. 出射中子角分布对临界计算具有重要影响[15], 但相关的研究较为缺乏. 本研究通过改进9Be(n, n)与(n, 2n)反应道的角分布数据, 发现两个系列的理论计算结果与实验测量值在1σ实验不确定度内均符合, 因此无法在1σ实验不确定度内拒绝两者的一致性. 该一致性在使用CIELO评价的U全套数据后有进一步的轻微提升, 也说明了核数据优化对于临界基准实验一致性判断的重要性.

      但同时需要注意的是, 虽然改进的核数据使得HMF-058与HMF-066两个系列的计算与实验结果均在1σ实验不确定度内符合, 但总体上HMF-066的C/E期望值比HMF-058仍低了230—300 pcm. 基于微分实验数据的9Be(n, n)和(n, 2n)反应角分布以及U全套数据的改进方向与HMF-058系列积分实验验证结论是一致的. 该两个系列临界基准实验keff的测量误差为200—400 pcm, 与上述差异相当, 并接近于快中子反应堆计算中由核数据协方差引入的不确定度目标[27]. 因此, 降低实验不确定度或开展更高精度的积分实验对更深入分析这两个系列实验的一致性以及检验核反应堆计算的准确性尤为重要.

      感谢北京应用物理与计算数学研究所胡泽华研究员的深入讨论、提供文献[12]的数据以及对本文的修订.

    参考文献 (27)

目录

/

返回文章
返回