高级搜索

镍钴铬多主元合金高温高压相图与相变动力学模拟

, 

downloadPDF

上一篇

下一篇

熊浩智, 王云江. 镍钴铬多主元合金高温高压相图与相变动力学模拟[J]. 物理学报, 2025, 74(8): 086101-1. doi: 10.7498/aps.74.20250097
引用本文: 熊浩智, 王云江. 镍钴铬多主元合金高温高压相图与相变动力学模拟[J]. 物理学报, 2025, 74(8): 086101-1. doi: 10.7498/aps.74.20250097
shu
Haozhi XIONG, Yunjiang WANG. Kinetic simulation of phase diagram and phase transitions in NiCoCr multi-principal element alloy at high temperature and high pressure[J]. Acta Physica Sinica, 2025, 74(8): 086101-1. doi: 10.7498/aps.74.20250097
Citation: Haozhi XIONG, Yunjiang WANG. Kinetic simulation of phase diagram and phase transitions in NiCoCr multi-principal element alloy at high temperature and high pressure[J]. Acta Physica Sinica, 2025, 74(8): 086101-1. doi: 10.7498/aps.74.20250097
shu

镍钴铬多主元合金高温高压相图与相变动力学模拟

  • 1.

    中国科学院力学研究所, 超常环境非线性力学全国重点实验室, 北京　100190

  • 2.

    中国科学院大学工程科学学院, 北京　100049

    • 作者简介: 熊浩智 E-mail: xionghaozhi@imech.ac.cn .
    通讯作者: E-mail: yjwang@imech.ac.cn.

  • 中图分类号: 61.66.Dk, 05.70.Fh, 05.70.-a, 87.10.Tf

Kinetic simulation of phase diagram and phase transitions in NiCoCr multi-principal element alloy at high temperature and high pressure

  • 1.

    State Key Laboratory of NonLinear Mechanics, Institute of Mechanics, Chinses Academy of Sciences, Beijing 100190, China

  • 2.

    School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China

    • Corresponding author: E-mail: yjwang@imech.ac.cn.

  • MSC: 61.66.Dk, 05.70.Fh, 05.70.-a, 87.10.Tf

  • 摘要: 多主元合金概念的提出颠覆了传统物理冶金的理念, 极大地拓展了材料设计空间. 合金相图从热力学角度揭示成分、热力学与结构之间的关系, 对指导材料优化具有重要意义. 传统实验方法测定相图费时耗力, 且面临着测量条件、成分控制、高温高压等因素限制, 系统评估相图和热力学性质困难. 在此工作中, 我们以典型等原子比镍钴铬合金为原型材料, 采用元动力学、动态概率增强采样和扩展系综模拟相结合的方法, 克服原子尺度模拟的时间尺度限制, 系统地绘制了镍钴铬在高温、高压条件下的温度-压力相图, 并计算了不同热力学条件下该材料体心立方晶体与液体相变的自由能面. 基于自由能路径, 量化了晶化和熔化相变过程中, 激活能、激活体积、激活熵与温度、压力的关系, 从而揭示了压力和温度分别通过影响激活体积和激活熵, 进而影响熔化和晶化动力学的物理机制. 该研究为理解多主元合金的热力学与相变动力学提供了理论支持, 探索了其在极端条件下结构稳定性.
    Abstract: Understanding the phase stability and transformation kinetics of multi-principal element alloys (MPEAs) under extreme conditions is critical for optimizing their performance under extreme conditions such as high-temperature and high-pressure environment. In this work the high pressure-temperature (p-T) phase diagram and solid-liquid transition mechanism of an equiatomic NiCoCr alloy are investigated based on embedded atom method (EAM) potential, through advanced molecular dynamics (MD) simulation combined with enhanced sampling techniques. In order to overcome the timescale limitations of traditional MD in capturing phase transitions as rare events, a hybrid approach integrating well-tempered metadynamics (WTMetaD) and the on-the-fly probability-enhanced sampling with expanded ensembles is used in this work. Collective variables such as enthalpy per atom SH, and two-body entropy SS are used to explore the polymorphic states of the NiCoCr alloy. The crystallinity senv, potential energy U, and volume V are utilized to drive phase transitions, and sampling configurations are performed in the range of 1550–1750 K and 0–10 GPa by using multithermal-multibaric-multiumbrella simulation.Several key results about liquid-solid phase transition in NiCoCr alloy are obtained as follows.1) Phase diagram prediction. NiCoCr alloy exhibits a stable body-centered cubic (BCC) phase under high-pressure condition (e.g. 10 GPa) at elevated temperatures (up to 1750 K), rather than a face-centered cubic stable (FCC) phase at room temperature and ambient pressure. The solid-liquid coexistence line shifts upward with the increase of pressure, raising the melting temperature from ~1400 K (ambient pressure) to about 1750 K (over 10 GPa).2) Free energy landscape. The free energy curves corresponding to different thermodynamic conditions are obtained using reweighting techniques and block averaging methods, which reveal that the increase of pressure and decrease of temperature can reduce the free-energy difference ΔGL→BCC, while simultaneously increasing $ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ required for melting. The combined effects of these changes enhance the stability of the BCC phase in NiCoCr under high-temperature and high-pressure condition.3) Activation parameters and kinetic mechanism. For the activation parameters of solid-liquid dynamic mechanics, $ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ of NiCoCr alloy decreases with the increase of temperature and the decrease of pressure ( from (–4.32 ± 0.16) J·mol–1·K–1 at 1550 K to (–6.71 ± 0.48) J·mol–1·K–1 at 1750 K, 0 GPa ), and |$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $| increases with temperature increasing and pressure decreasing ( from (–88.21 ± 2.57) Å3 at 0 GPa to (–26.09 ± 6.35) Å3 at 10 GPa, 1600 K). At constant temperature, increasing pressure lowers $S^* $ sensitivity to temperature change, whereas higher temperatures amplify pressure’s role in reducing |$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|, the change of pressure has no significant effect on $ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $.These results demonstrate that the synergistic effects of pressure and temperature on $S^* $ and $V^* $ dictate the phase stability and transformation kinetics of NiCoCr alloys under extreme conditions. The predicted p-T phase diagram and quantitative activation parameters provide critical ideas for designing MPEAs with tailored microstructures for high-pressure applications. Limitations of the EAM potential in describing magnetic interactions and non-equilibrium states are discussed, and the necessity of of future validation through first-principles calculations and high-pressure experiments is emphasized.
  • 加载中

  • 图 1  等原子比镍钴铬合金体系在高温常压下的二维吉布斯自由能面关于每原子焓(SH)和每原子两体熵(SS)的函数　(a) 1750 K和1 bar; (b) 1550 K和1 bar

    Figure 1.  2D Gibbs free energy surface of the equiatomic NiCoCr alloy system at high temperature and atmospheric pressure, plotted as a function of the enthalpy per atom (SH) and two-body entropy per atom (SH): (a) 1750 K and 1 bar; (b) 1550 K and 1 bar.

    下载: 全尺寸图片 幻灯片

    图 2  优化核函数最佳展宽参数　(a)基于最小重叠确定最佳展宽参数; (b)最佳展宽参数下(σ = 0.047), 镍钴铬合金体系液相与体心立方晶体相的核函数分布情况

    Figure 2.  The optimization of the kernel function’s optimal broadening parameter: (a) The optimal broadening parameter is determined by minimizing the overlap; (b) under the optimal broadening parameter (σ = 0.047), the distribution of the kernel functions for the liquid phase and body-centered cubic phase of the NiCoCr alloy system.

    下载: 全尺寸图片 幻灯片

    图 3  多温-多压-多伞增强采样中物理量及构型随时间的演化　(a)势能; (b)盒子体积; (c)类体心立方原子数; (d)偏置势; (e) c(t); (f)构型

    Figure 3.  Collective variables, bias, c(t) and configuration as a function of simulation time in the multithermal-multibaric-multiumbrella simulations: (a) Energy vs. time; (b) volume vs. time; (c) NBCC-like vs. time; (d) bias vs. time; (e) c(t) vs. time; (f) configuration vs. time.

    下载: 全尺寸图片 幻灯片

    图 4  多温-多压-多伞模拟在NiCoCr构型空间中采样　(a) 结晶度在能量-体积空间中的分布; (b)偏置势随体积-结晶度的变化

    Figure 4.  Configuration space of NiCoCr sampled during the multithermal-multibaric-multiumbrella simulation: (a) The distribution of crystallinity in the energy-volume space; (b) the variation of the bias potential with respect to volume-crystallinity.

    下载: 全尺寸图片 幻灯片

    图 5  一维自由能曲线作为结晶度的函数　(a) 5 GPa下, 不同温度的自由能曲线; (b) 1650 K下, 不同压力的自由能曲线. 自由能误差约等于线宽

    Figure 5.  1D Free energy landscape as a function of crystallinity CV: (a) Free energy landscapecurves at different temperatures under 5 GPa; (b) free energy landscape curves under different pressures at 1650 K. Error bars are approximately equal to the linewidth.

    下载: 全尺寸图片 幻灯片

    图 6  等原子比镍钴铬高温、高压相图的多温-多压-多伞模拟　(a)不同热力学条件下液相与体心立方相的自由能差ΔGL→BCC, 黑色实线表示固液共存线; (b)不同压力下液相与体心立方相的自由能差ΔGL→BCC随温度的变化

    Figure 6.  Phase digram of equiatomic NiCoCr sampled by the multithermal-multibaric-multiumbrella simulations: (a) The free energy difference between the Liquid and the BCC ΔGL→BCC under different thermodynamic conditions, the black solid line represents the solid-liquid coexistence line; (b) the change of the free energy difference ΔGL→BCC between liquid phase and BCC crystal at different pressures with increasing temperature.

    下载: 全尺寸图片 幻灯片

    图 7  晶化和熔化过程中, 不同压力下激活自由能和激活熵随温度的变化　(a)晶化激活自由能$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $; (b)熔化激活自由能$ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $; (c)晶化激活熵$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $; (d)熔化激活熵$ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $

    Figure 7.  Activation free energy and activation entropy of crystallization and melting, as a function of temperature under different pressures: (a) The activation free energy $ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ during crystallization; (b) the activation free energy $ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ during melting; (c) the activation entropy $ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ of crystallization process; (d) the activation entropy $ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ of melting process.

    下载: 全尺寸图片 幻灯片

    图 8  晶化和熔化过程中, 不同温度下激活自由能和激活体积随压力的变化　(a)晶化激活自由能$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $; (b)熔化激活自由能$ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $; (c)晶化激活体积$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $; (d)熔化激活体积$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $

    Figure 8.  Activation free energy and activation volume of crystallization and melting, as a function of pressure under different temperatures: (a) The activation free energy $ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ during crystallization; (b) the activation free energy $ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ during melting; (c) the activation volume $ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ of crystallization process; (d) the activation volume $ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $ of melting process

    下载: 全尺寸图片 幻灯片
  • [1] Peng J, Chen B, Wang Z, Guo J, Wu B, Hao S, Zhang Q, Gu L, Zhou Q, Liu Z, Hong S, You S, Fu A, Shi Z, Xie H, Cao D, Lin C J, Fu G, Zheng L S, Jiang Y, Zheng N 2020 Nature 586 390 doi: 10.1038/s41586-020-2783-x
    [2] Du J, Jiang S, Cao P, Xu C, Wu Y, Chen H, Fu E, Lu Z 2023 Nat. Mater. 22 442 doi: 10.1038/s41563-022-01260-y
    [3] Bai X, Xie H, Zhang X, Zhao D, Rong X, Jin S, Liu E, Zhao N, He C 2024 Nat. Mater. 23 747 doi: 10.1038/s41563-024-01884-2
    [4] George E P, Curtin W A, Tasan C C 2020 Acta Mater. 188 435 doi: 10.1016/j.actamat.2019.12.015
    [5] Ma E, Wu X 2019 Nat. Commun. 10 5623 doi: 10.1038/s41467-019-13311-1
    [6] George E P, Raabe D, Ritchie R O 2019 Nat. Rev. Mater. 4 515 doi: 10.1038/s41578-019-0121-4
    [7] Yeh J W, Chen S K, Lin S J, Gan J Y, Chin T S, Shun T T, Tsau C H, Chang S Y 2004 Adv. Eng. Mater. 6 299 doi: 10.1002/adem.200300567
    [8] Hsu W L, Tsai C W, Yeh A C, Yeh J W 2024 Nat. Rev. Chem. 8 471 doi: 10.1038/s41570-024-00602-5
    [9] Wang M, Ma Z L, Xu Z Q, Cheng X W 2021 Scr. Mater. 191 131 doi: 10.1016/j.scriptamat.2020.09.027
    [10] Kumar N A P K, Li C, Leonard K J, Bei H, Zinkle S J 2016 Acta Mater. 113 230 doi: 10.1016/j.actamat.2016.05.007
    [11] Zhao S, He L xin, Fan X xia, Liu C hai, Long J ping, Wang L, Chang H, Wang J, Zhang W 2019 Surf. Coat. Technol. 375 215 doi: 10.1016/j.surfcoat.2019.07.033
    [12] Wu Z, Bei H, Pharr G M, George E P 2014 Acta Mater. 81 428 doi: 10.1016/j.actamat.2014.08.026
    [13] Gludovatz B, Hohenwarter A, Thurston K V S, Bei H, Wu Z, George E P, Ritchie R O 2016 Nat. Commun. 7 10602 doi: 10.1038/ncomms10602
    [14] Ding J, Yu Q, Asta M, Ritchie R O 2018 Proc. Natl. Acad. Sci. U. S. A. 115 8919 doi: 10.1073/pnas.1808660115
    [15] Smith T M, Kantzos C A, Zarkevich N A, Harder B J, Heczko M, Gradl P R, Thompson A C, Mills M J, Gabb T P, Lawson J W 2023 Nature 617 513 doi: 10.1038/s41586-023-05893-0
    [16] Panagiotopoulos A Z, Quirke N, Stapleton M, Tildesley D J 1988 Mol. Phys. 63 527 doi: 10.1080/00268978800100361
    [17] Frenkel D, Ladd A J C 1984 J. Chem. Phys. 81 3188 doi: 10.1063/1.448024
    [18] Grochola G 2004 J. Chem. Phys. 120 2122 doi: 10.1063/1.1637575
    [19] Zhang L, Wang H, Car R, E W 2021 Phys. Rev. Lett. 126 236001 doi: 10.1103/PhysRevLett.126.236001
    [20] Kruglov I A, Yanilkin A, Oganov A R, Korotaev P 2019 Phys. Rev. B 100 174104 doi: 10.1103/PhysRevB.100.174104
    [21] Chen T, Yuan F, Liu J, Geng H, Zhang L, Wang H, Chen M 2023 Phys. Rev. Mater. 7 053603 doi: 10.1103/PhysRevMaterials.7.053603
    [22] Pártay L B, Bartók A P, Csányi G 2010 J. Phys. Chem. B 114 10502 doi: 10.1021/jp1012973
    [23] Dorrell J, Pártay L B 2020 J. Phys. Chem. B 124 6015 doi: 10.1021/acs.jpcb.0c03882
    [24] Marchant G A, Caro M A, Karasulu B, Pártay L B 2023 npj Comput. Mater. 9 131 doi: 10.1038/s41524-023-01081-w
    [25] Unglert N, Carrete J, Pártay L B, Madsen G K H 2023 Phys. Rev. Mater. 7 123804 doi: 10.1103/PhysRevMaterials.7.123804
    [26] Laio A, Parrinello M 2002 Proc. Natl. Acad. Sci. U. S. A. 99 12562 doi: 10.1073/pnas.202427399
    [27] Barducci A, Bussi G, Parrinello M 2008 Phys. Rev. Lett. 100 020603 doi: 10.1103/PhysRevLett.100.020603
    [28] Valsson O, Parrinello M 2014 Phys. Rev. Lett. 113 090601 doi: 10.1103/PhysRevLett.113.090601
    [29] Dama J F, Rotskoff G, Parrinello M, Voth G A 2014 J. Chem. Theory Comput. 10 3626 doi: 10.1021/ct500441q
    [30] Piaggi P M, Parrinello M 2019 Phys. Rev. Lett. 122 050601 doi: 10.1103/PhysRevLett.122.050601
    [31] Piaggi P M, Parrinello M 2019 J. Chem. Phys 150 244119 doi: 10.1063/1.5102104
    [32] Piaggi P M, Valsson O, Parrinello M 2017 Phys. Rev. Lett. 119 015701 doi: 10.1103/PhysRevLett.119.015701
    [33] Invernizzi M, Valsson O, Parrinello M 2017 Proc. Natl. Acad. Sci. U. S. A. 114 3370 doi: 10.1073/pnas.1618455114
    [34] Piaggi P M, Parrinello M 2018 Proc. Natl. Acad. Sci. U. S. A. 115 10251 doi: 10.1073/pnas.1811056115
    [35] Oganov A R, Pickard C J, Zhu Q, Needs R J 2019 Nat. Rev. Mater. 4 331 doi: 10.1038/s41578-019-0101-8
    [36] Niu H, Bonati L, Piaggi P M, Parrinello M 2020 Nat. Commun. 11 2654 doi: 10.1038/s41467-020-16372-9
    [37] Invernizzi M, Piaggi P M, Parrinello M 2020 Phys. Rev. X 10 041034
    [38] Tribello G A, Bonomi M, Branduardi D, Camilloni C, Bussi G 2014 Comput. Phys. Commun. 185 604 doi: 10.1016/j.cpc.2013.09.018
    [39] Li Q J, Sheng H, Ma E 2019 Nat. Commun. 10 3563 doi: 10.1038/s41467-019-11464-7
    [40] Dai S C, Yang Y, Wang Y J 2024 Phys. Rev. Mater. 8 033607 doi: 10.1103/PhysRevMaterials.8.033607
    [41] Cao F H, Wang Y J, Dai L H 2020 Acta Mater. 194 283 doi: 10.1016/j.actamat.2020.05.042
    [42] Bussi G, Donadio D, Parrinello M 2007 J. Chem. Phys. 126 014101 doi: 10.1063/1.2408420
    [43] Parrinello M, Rahman A 1981 J. Appl. Phys. 52 7182 doi: 10.1063/1.328693
    [44] Flyvbjerg H, Petersen H G 1989 J. Chem. Phys. 91 461 doi: 10.1063/1.457480
    [45] Rein Ten Wolde P, Ruiz-Montero M J, Frenkel D 1996 J. Chem. Phys. 104 9932 doi: 10.1063/1.471721
    [46] Du J P, Yu P, Shinzato S, Meng F S, Sato Y, Li Y, Fan Y, Ogata S 2022 Acta Mater. 240 118314 doi: 10.1016/j.actamat.2022.118314
    [47] Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704 doi: 10.1063/1.2210932
    [48] Gusev V V, Adamson D, Deligkas A, Antypov D, Collins C M, Krysta P, Potapov I, Darling G R, Dyer M S, Spirakis P, Rosseinsky M J 2023 Nature 619 68 doi: 10.1038/s41586-023-06071-y
  • 加载中
图( 8)
计量
  • 文章访问数:  74
  • HTML全文浏览数:  74
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-20
  • 刊出日期:  2025-04-20

镍钴铬多主元合金高温高压相图与相变动力学模拟

    通讯作者: E-mail: yjwang@imech.ac.cn.
    作者简介: 熊浩智 E-mail: xionghaozhi@imech.ac.cn
  • 1. 中国科学院力学研究所, 超常环境非线性力学全国重点实验室, 北京　100190
  • 2. 中国科学院大学工程科学学院, 北京　100049
  • 收稿日期:  2025-01-20

摘要: 多主元合金概念的提出颠覆了传统物理冶金的理念, 极大地拓展了材料设计空间. 合金相图从热力学角度揭示成分、热力学与结构之间的关系, 对指导材料优化具有重要意义. 传统实验方法测定相图费时耗力, 且面临着测量条件、成分控制、高温高压等因素限制, 系统评估相图和热力学性质困难. 在此工作中, 我们以典型等原子比镍钴铬合金为原型材料, 采用元动力学、动态概率增强采样和扩展系综模拟相结合的方法, 克服原子尺度模拟的时间尺度限制, 系统地绘制了镍钴铬在高温、高压条件下的温度-压力相图, 并计算了不同热力学条件下该材料体心立方晶体与液体相变的自由能面. 基于自由能路径, 量化了晶化和熔化相变过程中, 激活能、激活体积、激活熵与温度、压力的关系, 从而揭示了压力和温度分别通过影响激活体积和激活熵, 进而影响熔化和晶化动力学的物理机制. 该研究为理解多主元合金的热力学与相变动力学提供了理论支持, 探索了其在极端条件下结构稳定性.

English Abstract

    全文HTML

    1.   引　言

    • 金属材料作为重要的结构和功能材料, 在工程应用中常常面临多种极端环境. 例如, 在海洋工程领域, 金属材料需抵御海水腐蚀与高应力的叠加影响[1]; 在核工业领域, 金属材料则需承受强辐射和高温的复合作用[2]; 在航空航天领域, 金属材料必须承受高温、高应力以及强辐射的共同作用[3]. 这些极端条件的联合作用可能对金属材料的微观结构产生更加复杂且严重的影响, 从而显著降低材料性能和服役寿命.

      近年来, 多主元合金(multi-principal elemental alloys, MPEAs)作为一种新型合金材料, 逐渐成为金属材料研究的热点[4–6]. 与传统合金中仅含有一种或两种主要元素的设计理念不同, MPEAs通常由5—13种合金元素以等原子比或近等原子比(5%—35%)混合而成, 形成单相固溶体[7]. 这一创新设计理念打破了传统合金材料设计的局限, 聚焦于由多种元素共混而成的合金体系. MPEAs独特的成分设计赋予其一些显著不同于传统合金的特性, 包括高熵效应、大晶格畸变、迟滞扩散效应及“鸡尾酒”效应等[8]. 此外, MPEAs具有广泛的成分设计空间和可调节范围, 使其能够展现出优异的综合性能, 在高温、高辐照以及强腐蚀等极端环境下具有广阔的应用前景[9–11].

      镍钴铬合金作为MPEAs家族中的佼佼者, 其突出特点是结合了高强度、延展性和断裂韧性, 显示 出超过大多数多相合金和MPEAs的强度-韧性性能, 在一定条件下镍钴铬合金兼备了很好的极限抗拉强度(约1 GPa), 塑性应变(约0.6)[12]以及断裂韧性(约200 MPa·m1/2)[13]. 为了更好地开发镍钴铬合金的潜力, 近年来, 研究人员从原子分布、组织结构等相关机制针对该合金展开了一系列研究. Ding等[14]发现可以利用微观的化学有序度调节层错能, 影响相变诱导塑性的发生, 进而影响镍钴铬合金宏观力学性能. Smith等[15]使用模型驱动的合金设计和基于激光的增材制造工艺, 将纳米级Y2O3颗粒弥散强化到镍钴铬基合金, 与传统多晶锻造镍基合金相比, 新合金高温强度提高了2倍, 抗氧化性能提高了近3倍, 蠕变性能提高了3个数量级.

      相图描述材料在不同成分与热力学条件的相稳定性, 是材料科学和工业生产的基础及重要工具. 了解MPEAs的温度-压力(p-T)相图, 尤其在高温高压下的材料稳定相结构, 对改善材料性能, 提高极端条件下的服役可靠性尤为重要. 但是, 通过实验得到极端条件下的相图往往受到测量条件等客观因素制约. 为了克服实验条件的限制, 自20世纪80年代以来, 已有多种计算模拟方法应用于相图构建. 吉布斯系综方法可用于计算液气相图, 但不适于研究固-液体系[16]. 热力学积分方法可用于计算每相的单个状态点的绝对吉布斯自由能. 比如, Frenkel和Ladd[17]以此为基础利用爱因斯坦晶体作为参考, 计算固体自由能. Grocholar[18]提出一种建立一条连接液相和固相的热力学积分路径. 这些方法及其变体已用于模拟水的相图[19], 计算铀极端条件下的相图[20], 三相点锡的相图[21]等. 以上方法都需要对控制变量空间中的每个点进行至少一次蒙特卡罗(Monte Carlo, MC)或分子动力学(molecular dynamics, MD)模拟, 如对每个具体的温度和压力条件. 并且, 研究者需事先了解待测体系的相结构, 因此无法预测相图中可能存在的新结构. 相比而言, 嵌套采样方法[22]则无需对体系有先验知识. 它通过克隆现有样本, 然后使用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)随机行走生成新样本, 采用迭代方法直接通过样本的加权平均得到自由能. 因此, 该方法能够有效地得到每个状态点的自由能函数, 已经被用以计算锂、碳、硅的p-T相图[23–25]. 虽然嵌套采样方法无需了解待测体系的相结构, 但其计算复杂, 仅适用于计算几十个原子的小模型. 并且, 小体系在低压下易受到有限尺寸效应的影响, 导致共存线偏差, 计算结果难以保障.

      最近, Parrinello等提出了元动力学(metadynamics)[26]及相应变体[27–29]的增强采样方法, 可以克服以一阶相变为代表的稀有事件时间尺度限制, 并且结合多温、多压系综[30]计算相间自由能差, 获得材料的温度-压力相图和相变自由能面. 在计算精度上, 其方法与嵌套采样一致[31]. 元动力学通过采用可探索多晶态的集体变量(collective variables, CVs)[32,33]或晶体结构预测算法[34,35], 得到感兴趣体系的多形态. 随后, 针对其不同物质结构定制驱动相变的结晶度CV, 提高采样效率. 此类方法已在研究钠、铝、镓等材料的相图上得到应用, 兼顾了计算精度和效率[31,36,37].

      本文基于分子动力学模拟方法, 采取两步研究策略[31]计算等原子比镍钴铬多主元合金高温、高压相图与相变自由能面. 我们采用温和元动力学方法(well-tempered metadynamics, WTMetaD)[27], 选用两体熵和每原子焓[32]作为集体变量, 在1550—1750 K温度范围内探索发现了其多形态. 然后, 使用具有扩展系综的动态概率增强采样方法(on-the-fly probability enhanced sampling with expanded ensembles, OPES_EXPAND), 并结合多温、多压、多伞模拟[37]得到镍钴铬在1550—1750 K, 0—10 GPa热力学条件下的相图. 进一步, 我们给出模拟过程中集体变量、偏置势及原子构型随模拟时间的演化特征, 获得不同热力学条件下的液固自由能差及自由能, 分析了激活函数对压力和温度的依赖性, 探讨了多主元合金高温高压相变的物理机制.

    2.   计算方法

    • 本研究模拟基于LAMMPS软件结合增强采样插件PLUMED 2[38]实现. 所采用的镍钴铬EAM势函数[39]通过大型的从头算数据库开发, 对内聚能、晶格参数、弹性常数和声子等有着相对准确的描述, 已经在局部化学短程序对镍钴铬扩散抑制[40], 原子尺度解释初始塑性[41]等方面进行了广泛的使用与验证.

      • 2.1.   寻找多形态

    • 本研究采用Piaggi等[32]建议以熵和焓作为集体变量的采样方法. 首先, 对具有498个原子的等原子比镍钴铬体系进行等温、等压分子动力学模拟, 牛顿运动方程的积分步长为2 fs. 使用随机速度缩放恒温器[42]控制温度, 弛豫时间为0.1 ps. 使用Panrinello-Rahman恒压器[43]将压力控制到标准大气压值, 弛豫时间为0.1 ps. 模拟中保持盒子接近立方体形状, 但仍然允许应力张量的非对角线分量变化, 以适应晶体和液体的不同原子结构涨落. 对于WTMetaD 模拟[27], 偏置因子设置为30. 采样过程中的偏置势每1 ps沉积一次, 焓与熵的高斯偏置势宽度分别为0.7 kJ/mol和0.2kB, 高度为7.5 kJ/mol.

      本文采用焓SH和两体熵SS作为集体变量搜索多形态, 二者分别基于分子动力学状态函数与原子结构定义为[32]

      其中U(R)表示势能; P为压力; V为体积; N = 498为体系采用的原子数. 此外, gm(r)为修正径向分布函数:

      其中ρ为数密度; σ为展宽参数; rij为原子i与j间的距离, 截止距离rmax = 0.7 nm.

      自由能面G(SH, SS)可由关于SH和SS边际分布概率P (SH, SS)表示为

      其中P(R)为等温等压系综中观测到构型R的概率.

      • 2.2.   OPES_EXPAND重新加权和块平均方法

    • OPES_EXPAND方法对定义的扩展目标系综, 采用扩展集体变量$ \Delta {u_\lambda }({\boldsymbol{x}}) $[37] (expansion collective variables, ECVs), 通过动态估计所需的概率分布, 迭代地构建一个偏置势, 第n步的偏置势表示为

      其中$ {N_{\{ \lambda \} }} $为定义目标参数的λ∈∆λ集合{λ}点的数量; $ \Delta {u_\lambda }({\boldsymbol{x}}) = {u_\lambda }({\boldsymbol{x}}) - {u_0}({\boldsymbol{x}}) $为势能差; ΔFn(λ)为每迭代n步更新加权估计的自由能.

      当估计分子动力学系综平均不确定度时, 必须考虑样品之间的时间相关性, 即样本量有效性变小的问题. 本文采用块平均[44]方法处理, 避免因简单取方差平方根除以样本数导致低估不确定性. 为了正确估计不确定性, 将数据分成M个子集或块, 每个子集或块包含相同数量的样本n/M, 通过加权平均计算每个块的估计值$ {\hat O_i} $以及第i块的权重$ {W_i} $. 从偏置系综中估计可观测到的O = O(x)的系综平均值, 可用基于重新加权方法表示为

      其中Ok≡O(xk); $ {w_k}(\lambda ) \equiv {{\mathrm{e}}^{ - \Delta u_\lambda ^{(k)} + v_{k - 1}^{(k)}}} $为偏置势权重值; $ {W_i} = \displaystyle \sum\nolimits_{k = (i - 1)(n/M)}^{i(n/M)} {{w_k}} $为第i块的权重. 根据块平均过程估计块之间的无偏方差, 在这种情况下为加权方差:

      其中$ {M_{{\mathrm{eff}}}} = {{\bigg({{\displaystyle \sum\nolimits_{i = 1}^M {{W_i} \bigg)} }^2}} {\Big/ } {\displaystyle \sum\nolimits_{i = 1}^M {W_i^2} }} $为有效块大小, 使用有效块大小Meff < M, 而不是块总数M计算方差. 因为当M很小, 或者当权重Wi不平衡时, 使用M代替Meff可能会大大低估实际的不确定性.

      • 2.3.   结晶度CV

    • 为了驱动相变, 必须明确引入适当的CV. 在相图的研究中, 我们采用Piaggi和Parrinelo[31]设计的结晶度CV. 该CV定义的起点为给定原子周围的局部原子密度. 考虑该原子周围的环境为χ, 并定义密度:

      其中i为遍历环境χ中的近邻原子; σ是展宽参数, 其最佳的情况下, 不同近邻原子之间的重叠可以忽略不计; ri是近邻原子相对于中心原子的坐标.

      测量包含n个参考位置$ \left\{ {{\boldsymbol{r}}_1^0, \cdots, {\boldsymbol{r}}_n^0} \right\} $的当前环境和参考环境χ和χ0之间的差异, 使用核函数进行比较:

      将上述两个方程结合, 进行解析积分, 并归一化使$ {\tilde k_{{\chi _0}}}({\chi _0}) = 1 $

      对于N原子的体系, 每原子i的核函数表示为$ {\tilde k_{{\chi _0}}}({\chi _i}) $, 其中$ {i = 1, \cdots , N} $. 这个量是所考虑的特定相的每个原子的结晶度$ \left( {{s_i}} \right) $, 采用连续可微分的三次开关函数区分其处于晶体或液体状态, 即

      其中$ {k_{\mathrm{L}}} ( {{\chi _i}} ) = 0.41 $; $ {k_{{\mathrm{BCC}}}} ( {{\chi _i}} ) = 0.80 $, 由图2(b)中确定的核函数分布的最大值分别得到. $ {s_i} $取值在0到1之间平滑变化, 液体中的原子$ {s_i} \approx 0 $, 而完美结晶环境下的原子$ {s_i} \approx 1 $. 故而, 体系的结晶度CV(senv)可计算为

      由于MD模拟中晶体取向可能会在与模拟盒子不一样, 因此引入以下物理量以避免此现象出现:

      其中$ {Q_6} $为全局Steinhardt参数[45], 设其计算截止为0.35. $ \overline{k}=\displaystyle\sum\nolimits _{i=1}^{N}\tilde{k}\left({\chi }_{i}, {\chi }^{\prime }\right)/N $为核函数平均值. (13)式中符号的上标表示为A相(A)和B相(B)中的参数. sc背后的基本原理是: 只有当$ {Q_6} $和$ \bar k $同时增加时, sc才接近于零. 通过sc保持接近于零, 避免了与期望取向不同的晶体. 因此, 采用约束势$ V({s_{\mathrm{c}}}) $:

      其中κ = 105 kJ/mol; $ s_{\text{c}}^{0} = 0.1 $.

      • 2.4.   多温-多压-多伞模拟

    • 在相图研究中, 我们采用动态概率增强采样及多温-多压-多伞系综模拟[37]. 此框架下, 每个伞窗口的约化势为

      其中$ {u_0}({\boldsymbol{x}}) = {\beta _0}U({\boldsymbol{x}}) + {\beta _0}{p_0}V({\boldsymbol{x}}) $, $ \Delta {u_\lambda }({\boldsymbol{x}}) $为多温-多压-多伞模拟中的ECVs, 并使用倒温度β = 1/(kBT). 压力p以及结晶度senv作为λ的参数:

      自由能估计值∆Fn(β, p, senv)表示为倒温度β、压力p及结晶度senv的函数. 偏置势v = v(U,V,senv) 表示为势能U、体积V和结晶度CVsenv的函数. 在T0 = 1650 K和p0 = 5 GPa 条件下, 对432个原子进行模拟, 以对应体心立方结构的原子数. 模拟时间为200 ns. 在温度区间1550—1750 K, 压 力区间0—10 GPa (100 kbar, 1 bar = 105 Pa)的范围内, 我们对液体和固体结构进行取样. β和p区间分别用6和9个网格平均划分. 多伞高斯值$\sigma_{\rm umb} = 16 $, 用以确定28个伞均匀放置在$\langle s_{\rm env} \rangle_{\min} = 0 $ (液体)和$\langle s_{\rm env} \rangle_{\max} =1$ (固体)之间. 故而, 待估算的自由能面∆Fn(β, p, senv)网格点为6×9×28 = 1512.

    3.   结果与讨论

      3.1.   等原子比镍钴铬合金的多形态

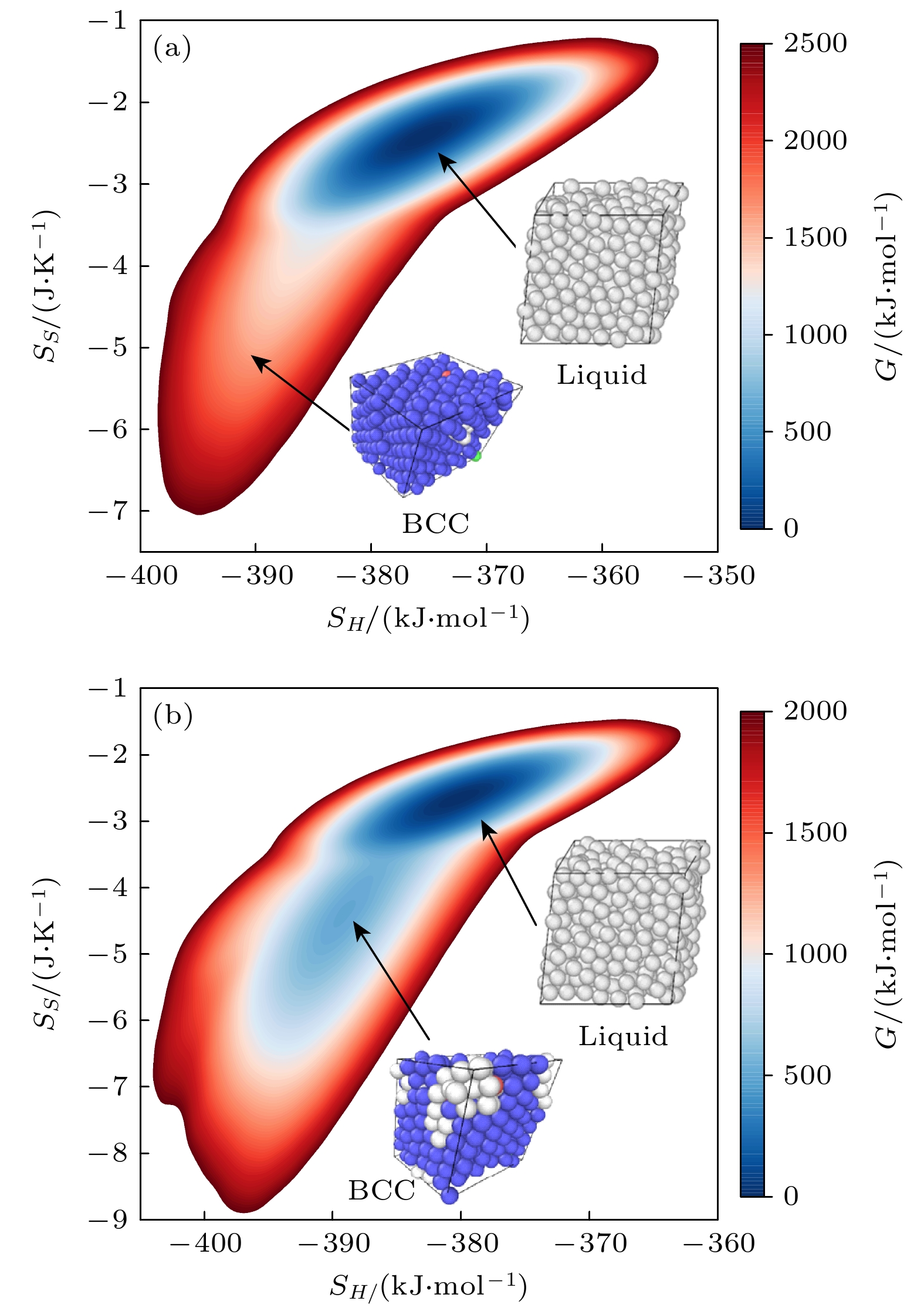
    • 本文采用的EAM势函数熔点估计为(1390 ± 20) K[46], 低于实验测定值1690 K[12]. 温和元动力学(WTMetaD)模拟通过动态偏置“熵”和“焓”函数, 对常压条件下, 1550和1750 K温度区间的等原子比镍钴铬合金相变过程采样. 由于合金在常温常压下为FCC相, 为保证等原子比, 采用的原子数为5×5×5×4 – 2 = 498的体系(3的倍数). 然后, 通过记录模拟中施加的偏置势, 重建自由能面(free energy surface, FES). 此处, MD模拟时长为 500 ns, 自由能在300 ns时收敛. 图1(a)和图1(b)分别显示了常压下温度分别为1750和1550 K时的二维自由能面, 以偏置的集体变量SH和SS表示. 我们可明显地观察到两个温度的FES皆存在两 个明显的自由能盆地, 分别对自由能盆地处构型 进行弛豫, 并采用共近邻分析(common neighbor analysis, CNA)算法辨识不同盆地的结构, 发现高熵高焓处为液态, 而低熵低焓处对应固态体心立方相结构. 不同于常温常压下等原子比镍钴铬合金存在的FCC稳定相.

      • 3.2.   核函数最佳展宽参数

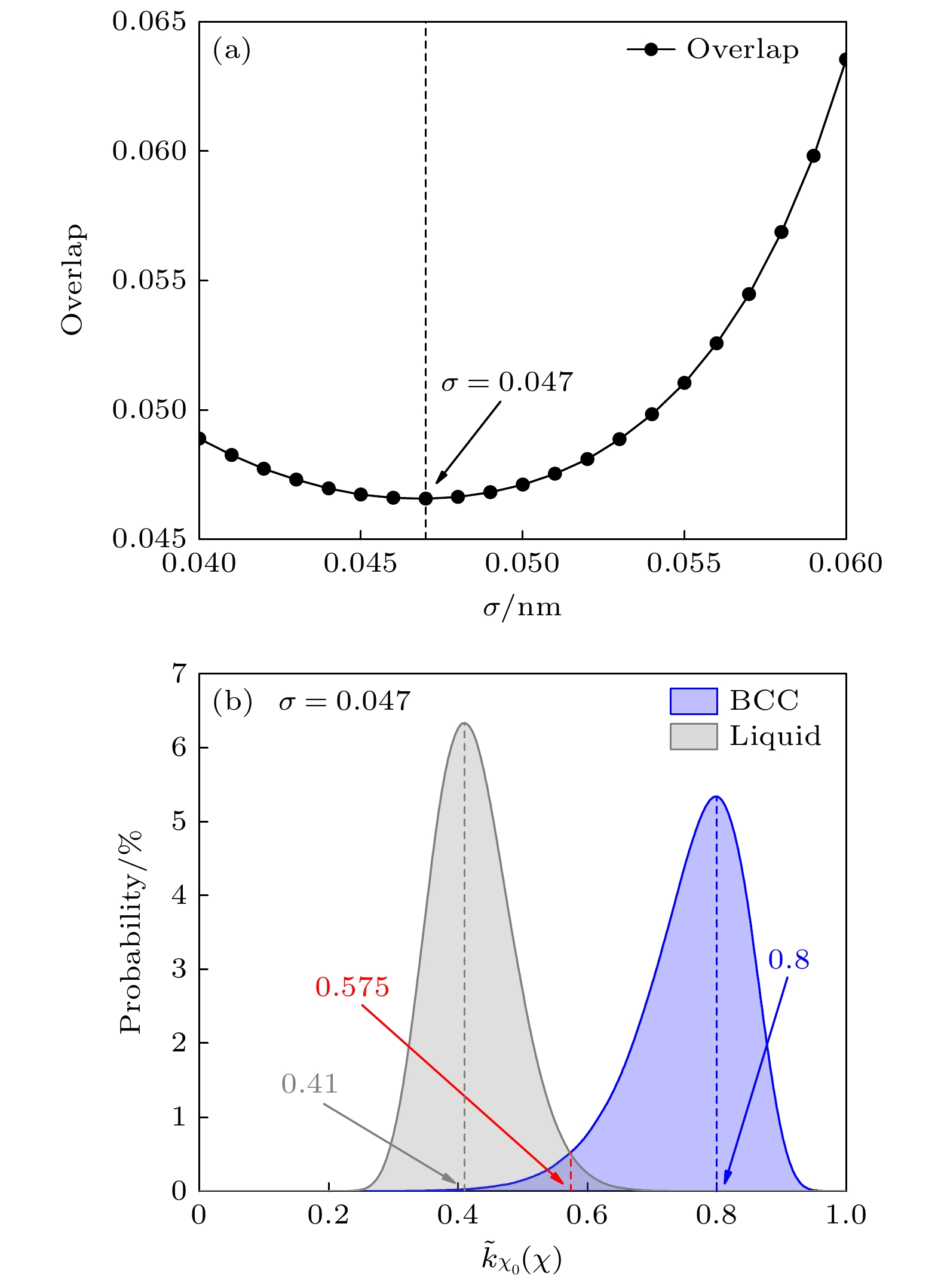
    • 在采用能量、体积、结晶度集体变量构成的偏置势探索镍钴铬p-T相图之前, 为了清楚区分液相和BCC相, 需构造合适的结晶度核函数. 按照(8)式—(10)式的要求, 展宽参数σ选择的宗旨是确保不同相的环境相似核函数$ {\tilde k_{{\chi _0}}}(\chi ) $的重叠部分最小[26]. 图2(a)绘制了液相与BCC相$ {\tilde k_{{\chi _0}}}(\chi ) $核函数重叠区域随展宽参数σ的变化. 我们发现σ = 0.047时重叠部分最小, 所以确定该值为最佳展宽参数. 图2(b)显示了在最佳展宽参数σ = 0.047时, 液相与BCC相核函数$ {\tilde k_{{\chi _0}}}(\chi ) $的分布情况. 液相和BCC相的最大值分布位于$ {\tilde k_{{\chi _0}}}(\chi ) = 0.41 $及$ {\tilde k_{{\chi _0}}}(\chi ) = 0.8 $处, 两相在$ {\tilde k_{{\chi _0}}}(\chi ) = 0.575 $时分布概率相同.

      • 3.3.   多温-多压-多伞系综模拟

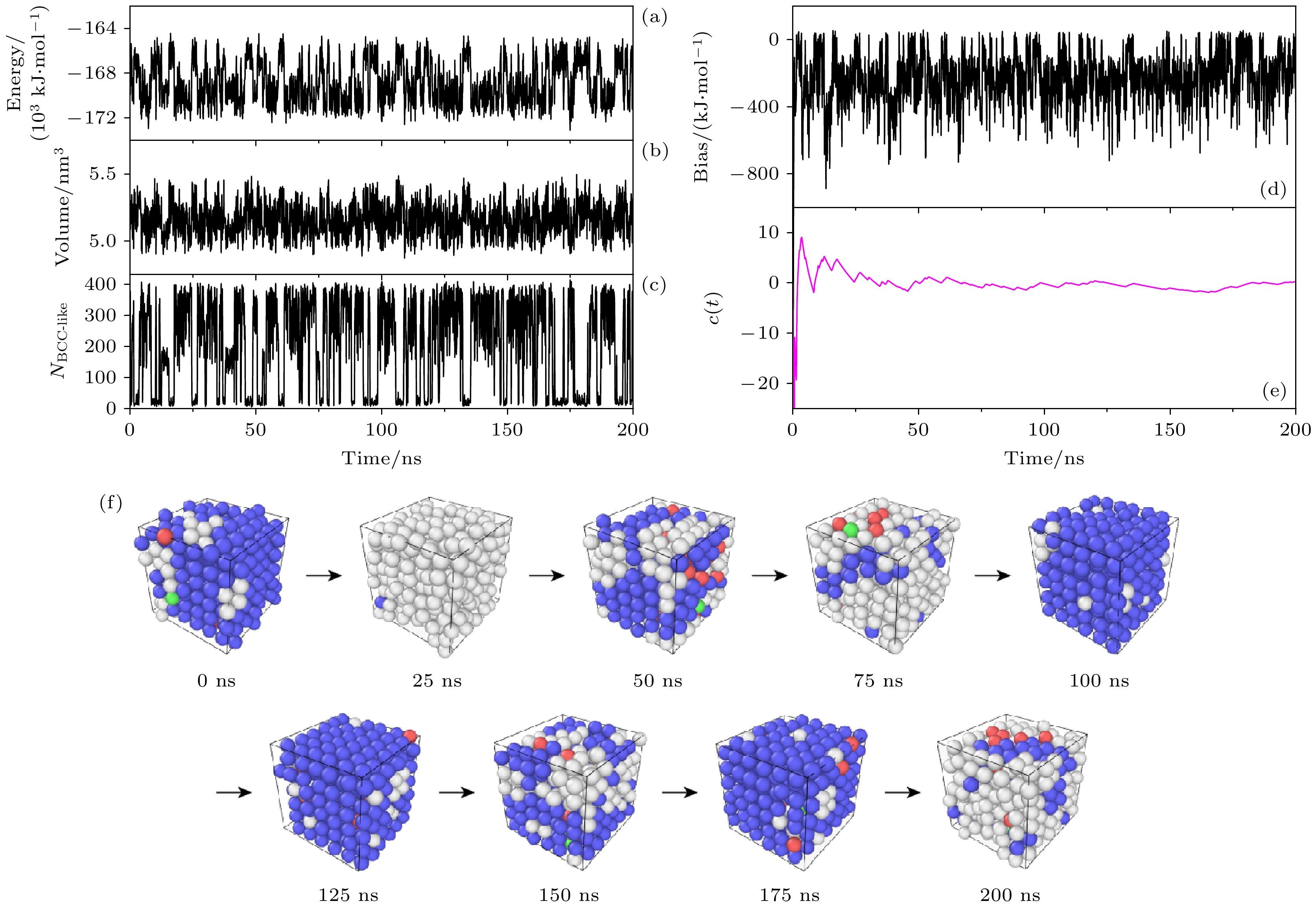
    • 我们选取合适的参数, 基于多温-多压-多伞系综模拟不同温度和压力条件下的相图与相变过程. 图3(a)—(e)分别绘制了采样过程中能量、体积、类BCC原子数、偏置势、重加权因子c(t)与模拟时间的关系. 由图3(a)和图3(b)可以看出, 在多温-多压-多伞模拟中, 体系的能量和体积随模拟时间波动剧烈, 侧面反映出体系在不同温度、压力及构型间不断转变. 图3(c)反映了类BCC原子数$ {N_{\text{BCC-like}}} $在0到原子总数432间进行了广泛采样, 表明液相和BCC相二者间在模拟过程中进行了有效可逆转变, 自由能差趋于稳定. 类BCC原子数$ {N_{\text{BCC-like}}} $定义为:

      图3(d)表示偏置势v(U, V, senv)作为模拟时间的函数. 它从模拟一开始便急剧上升, 并在–800—0 kJ/mol的能量范围内附近剧烈振荡, 这是体系的温度和能量不断地变化的体现, 表明模拟在不同的温度和压力下不断采样. 重加权因子c(t)作为偏置势的函数表示为$ c(t)=1/\beta\ln\left\langle\mathrm{e}^{\beta v}\right\rangle $. 随着偏置势收敛, c(t)达到在固定值, 因此可以将其作为衡量模拟收敛的标准. 图3(e)中c(t)在模拟起始很快上升, 并不断振荡接近稳定值, 在50 ns后随模拟时间保持恒定, 说明模拟收敛.

      图3(f)显示了200 ns采样过程中构型在液体与BCC晶相之间的转换, 显示的构型用CNA算法分析原子环境, 每25 ns输出一个构型的变化. 注意每个输出的构型, 都经过了能量最小化, 排除了热涨落的干扰. 模拟显示构型在BCC和液相之间等概率存在, 直观地证明了该采样方法对固液相变采样的遍历性和有效性.

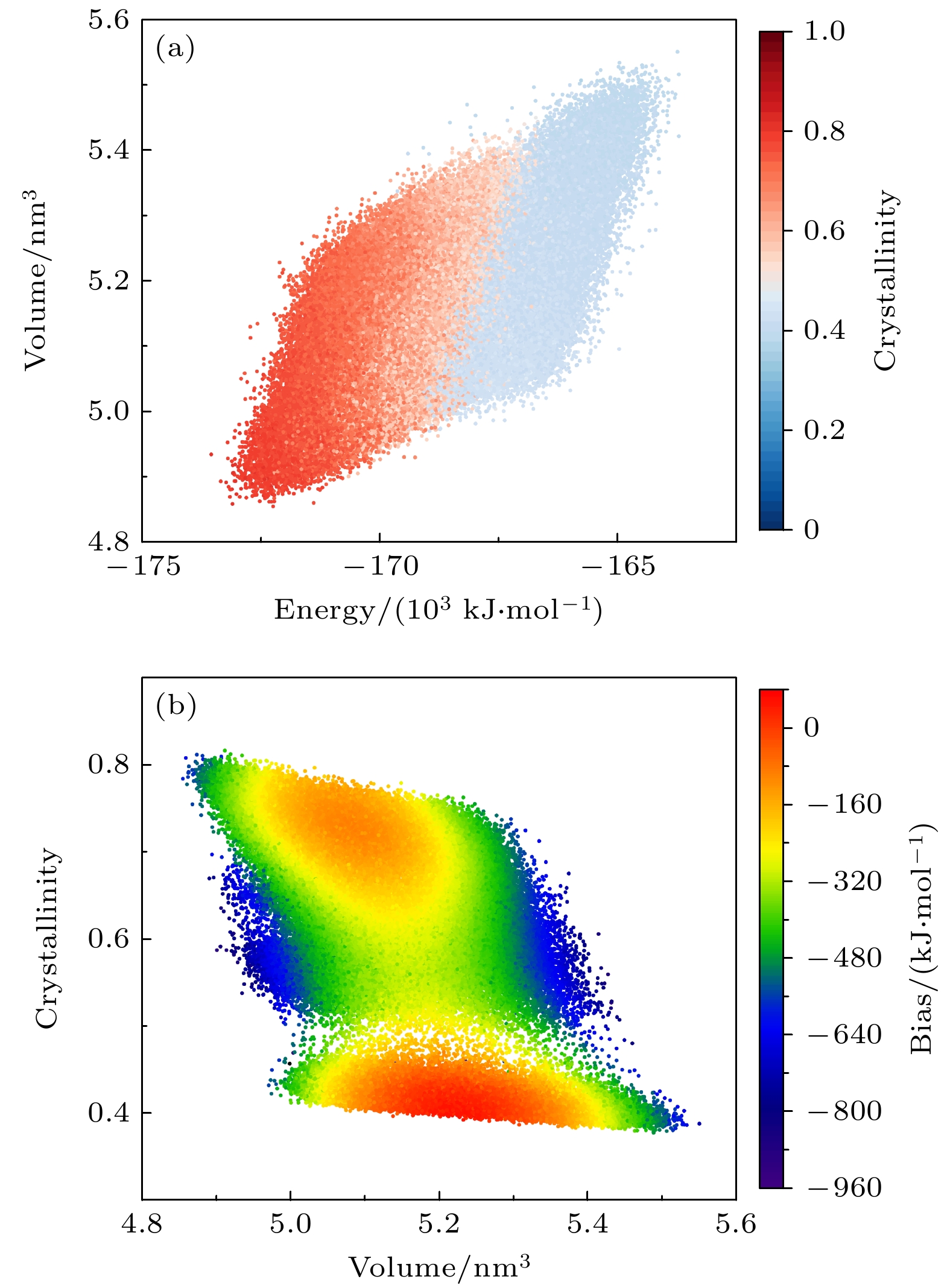
      图4(a)与图4(b)分别展示了在能量-体积空间和体积-结晶度空间中的采样点分布情况, 并分别用结晶度和偏置势对采样点进行着色. 由图4(a)可以看到, 在采样的时间尺度内结晶度在能量-体积空间中连续变化, 表明体系固液相变转换过程中采样连续性和一致性, 空间显著被区分为两个区域. 图4(b)中采样点用偏置势染色, 采样点组成了沙漏形状, 清晰地展示了一阶相变过程中. 基于结晶度对BCC相与液相间转换过程采样, 面临显著的动力学瓶颈, 体系需克服该动力学瓶颈才能进行相变. 在瓶颈附近, 采样点相较于两端处略显稀疏, 反映出一阶相变中动力学瓶颈对采样过程的阻碍. 若是采用传统MD方法, 很难克服动力学瓶颈, 从而导致采样遍历性受限，无法有效模拟相变过程.

      • 3.4.   等原子比镍钴铬相图及一维自由能曲线

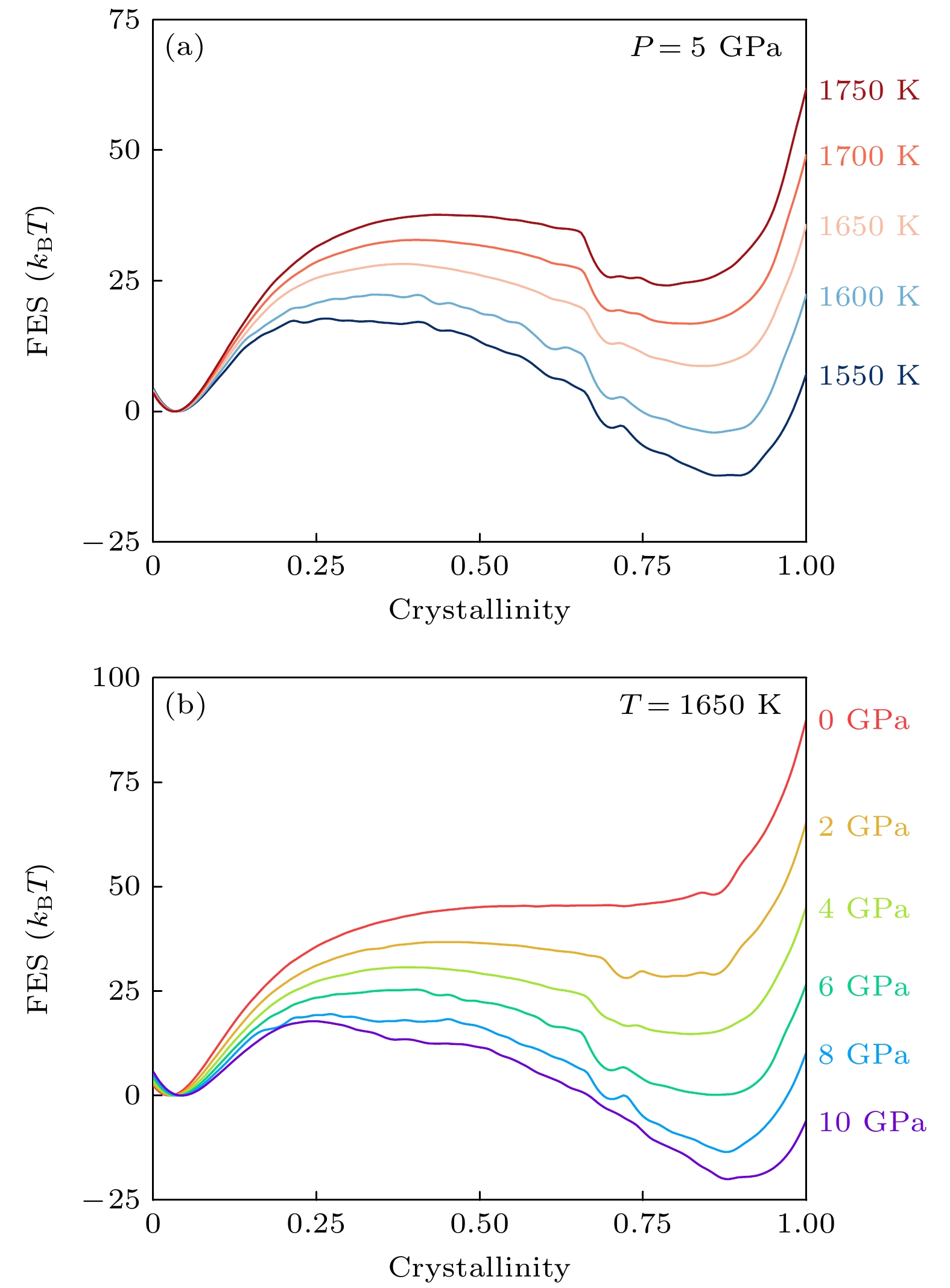
    • 利用重新加权算法可得到不同热力学条件下的自由能景观, 例如作为集体变量结晶度(senv)的函数. 可以将该函数在液体的自由能盆地处设为0, 基于此我们分别绘制了5 GPa压力下变化温度, 以及1650 K温度下变化压力的一维自由能曲线, 如图5(a)和图5(b)所示. 自由能曲线的误差采用加权块平均方法计算, 计算结果显示所有曲线的误差近似等于线宽. 在高温、高压状态下, 镍钴铬合金的BCC晶态是稳定相. 压力改变相较于温度改变更能促使镍钴铬液体向BCC转变, 因为低压下几乎不存在BCC镍钴铬亚稳态. 从动力学角度出发, 改变温度或改变压力对晶化(或熔化)的自由能垒影响作用基本等同.

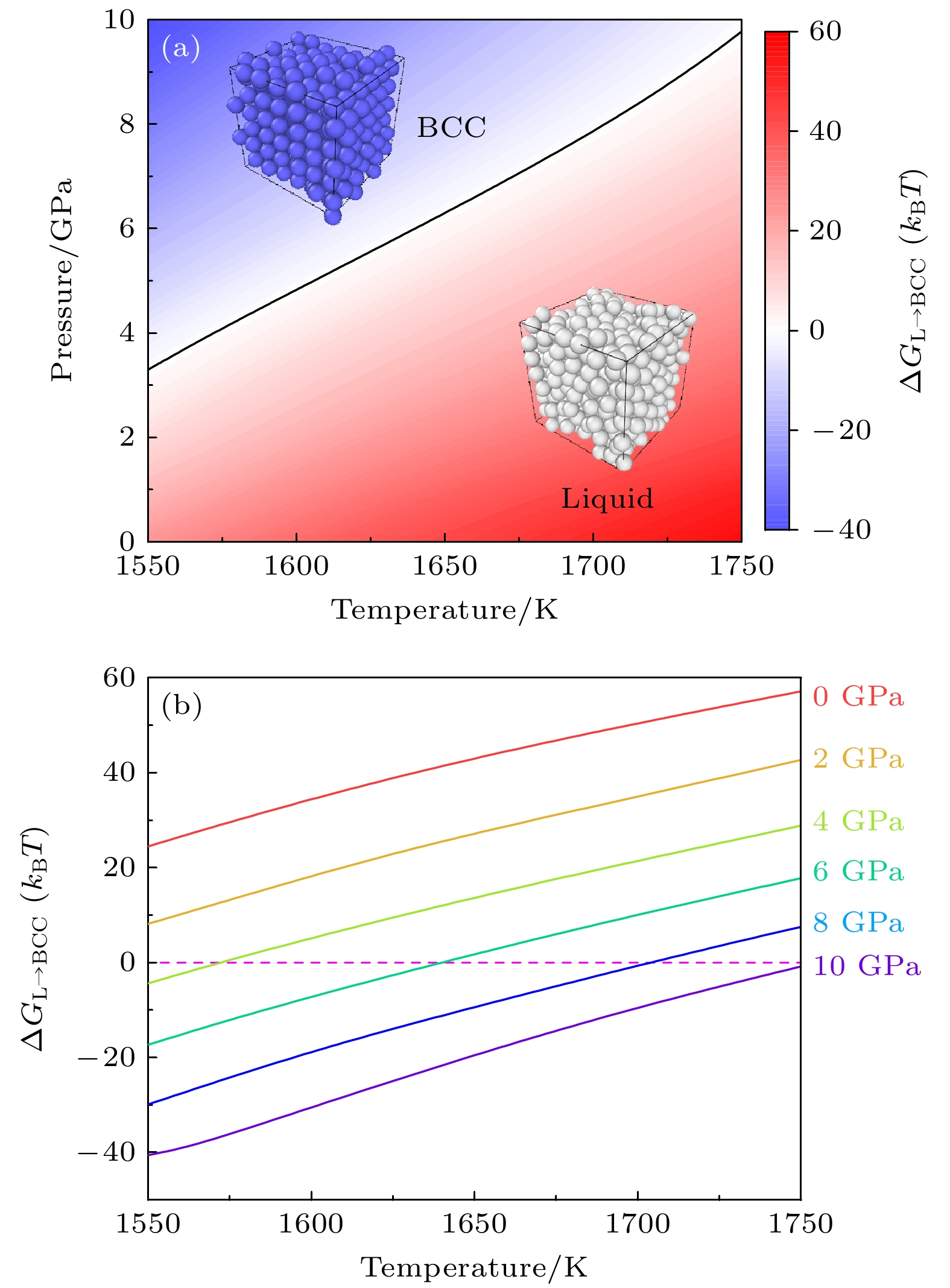
      进一步, 图6(a)显示了在1550—1750 K, 0—10 GPa热力学区间, 等原子比镍钴铬合金的相图. 任意温度和压力条件下, BCC晶体相与液相间的自由能差为

      其中H为Heaviside函数. 如果体系中包含有一半以上的类BCC晶体原子, 则构型被判断为BCC晶体(固相), 此时H = 1; 否则, 构型被认为是液相, 即H = 0. 图6(a)所示的相图中, 固液两相共存线$ \Delta G_{\mathrm{L}\to\mathrm{BCC}}(T,p)=0 $用黑色实线表示. 图6(b)则显示了不同压力下, 固液自由能差$ \Delta {G_{{\mathrm{L}} \to {\mathrm{BCC}}}}(T, p) $随温度的变化趋势. 可见, 在低温高压条件下, BCC晶体的自由能显著低于液体相, 所以固体是稳定相; 而在高温低压条件下, 晶体相自由能高于液体相, 镍钴铬合金系统趋向于以液体的状态存在. 图6(b)中自由能曲线与自由能差为0的交点, 定义了不同压力下系统的熔点. 晶体的熔点随压力升高而增加的现象非常普遍, 从热力学角度上看，压力抑制熔化过程中体积的增大；从结构层面分析，压力使原子间距缩小, 原子间的结合力增强, 导致固态结构更稳定, 需要更高的能量(比如温度激励)才能破坏化学键使晶体无序化(即熔化). 显而易见, 熔点随着压力的增加而升高. 比如, 10 GPa压力的条件下, 镍钴铬合金的熔点已经从1400 K提高到近1750 K.

      • 3.5.   激活参数对相变动力学的影响

    • 通过计算得到不同热力学条件下的一维自由能曲线, 我们可以获得相应热力学条件下的晶化和熔化过程自由能势垒$G^* $, 从而推演动力学信息并揭示相变的物理图像. 图7(a)和图7(b)分别表示晶化过程和熔化过程不同压力下的激活自由能随温度的变化趋势. 同样地, 我们也将晶化过程和熔化过程不同温度下的激活自由能随压力的变化于图8(a)和图8(b)表示. 根据热力学状态函数关系式, 在等压条件下, 对激活能求温度偏导,

      分别可以得到图7(c)和图7(d)所示等压条件下晶化和熔化过程中不同温度下的激活熵. 等温条件下对激活能求压力偏导,

      分别可以得到图8(c)和图8(d)所示等温条件下晶化和熔化过程中不同压力下的激活体积. 故而可以定量讨论激活熵与激活体积对于相变动力学的影响.

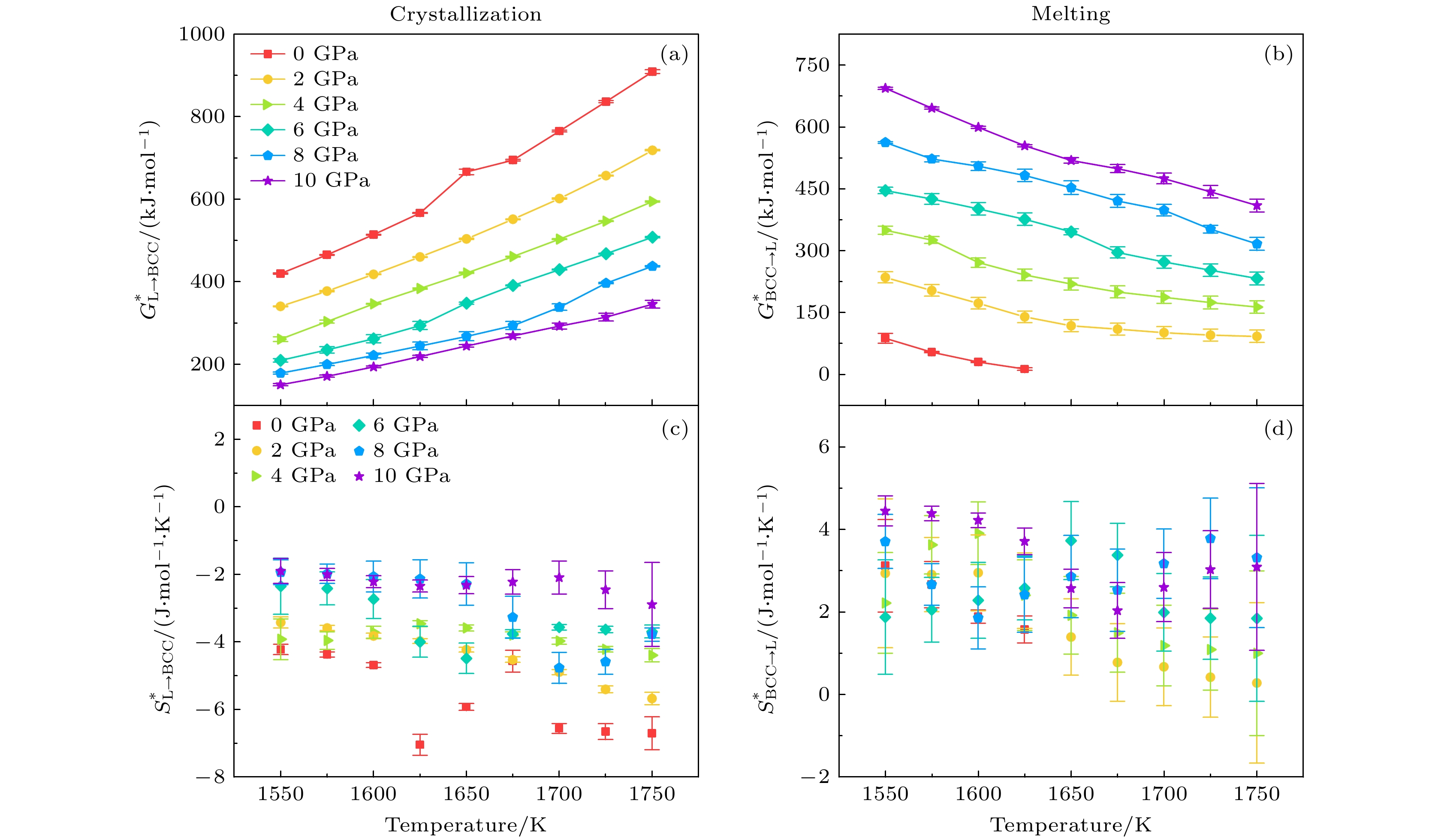
      对于晶化过程, 图7显示了固液相变中不同压力条件(0, 2, 4, 6, 8, 10 GPa)下, $G^* $和$S^* $随温度的变化. 从图7(a)可以看出, $ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $随温度升高而加速上升, 高温下晶化变得困难, 这与常识相符. 压力的增加会抑制这种效果, 使$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $随温度的变化从非线性变化趋向于线性变化. 而对于熔化过程, 图7(b)则可以看出$ G_{{ {\mathrm{BCC}} \to\mathrm{L}} }^* $随温度升高而减速下降, 高温降低激活自由能促进熔化发生, 而压力抑制了$ G_{{\mathrm{BBC}} \to {\mathrm{L}}}^* $随温度的下降速率, 使$ G_{{\mathrm{BBC}} \to {\mathrm{L}}}^* $随温度的变化同样地从非线性趋于线性. 相比于图7(a)的晶化过程, 图7(b)熔化过程中$ G_{{\mathrm{BBC}} \to {\mathrm{L}}}^* $随温度的变化更加线性化. 总结而言, 在等温条件下, 压力的增加有利于固相向BCC相转变; 在等压条件下, 温度的升高不利于固相向BCC相转变. 压力在固液相变过程中对$G^* $的影响随温度的升高而变得显著, 降低了$G^* $对温度变化的敏感性, 即熵对动力学的作用.

      具体而言, 激活熵$S^* $作为描述相变过程中原子或分子的无序自由度的物理量, 并且直接作为$G^* $关于温度的偏导数, 可以直观地反映等压条件下$G^* $对温度变化的敏感性. 晶化和熔化过程中$S^* $随温度的变化趋势如图7(c)和图7(d)所示. 在所模拟的温度和压力范围内, $ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $<0, $ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $>0, 这说明液相转变为BCC晶态相是无序度降低的过程, 其逆过程无序度增加, 这是符合常识的. 以图7(c)中晶化过程为例, 0 GPa压力条件下, 体系的晶化激活熵由1550 K时$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–4.32 ± 0.16) J·mol–1·K–1变化至1750 K时$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–6.71 ± 0.48) J·mol–1·K–1; 10 GPa下1550 K体系$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–1.90 ± 0.37) J·mol–1·K–1变化至1750 K的$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–2.89 ± 1.24) J·mol–1·K–1. 相较于0 GPa的情况, 10 GPa的$\Delta S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $更小. 而以图7(d)熔化过程为例, 2 GPa下1550 K体系$ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ = (2.94 ± 1.81) J·mol–1·K–1变化至1750 K $ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ = (0.28 ± 1.95) J·mol–1·K–1; 10 GPa下的1550 K体系$ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ = (4.45 ± 0.36) J·mol–1·K–1变化至1750 K$ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $ = (3.09 ± 2.03) J·mol–1·K–1. 相较2 GPa情况下, 10 GPa时$\Delta S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $更小. 图7(c)和图7(d)的结果表明, 等温条件下, 压力的升高使得$ S_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $趋于减小, $ S_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $趋于升高. 在等压条件下, 温 度升高使$S^* $趋于减小; 更高的压力下, $S^* $随温度 变化的梯度趋于降低, 即弱化了S*对温度变化的敏感性.

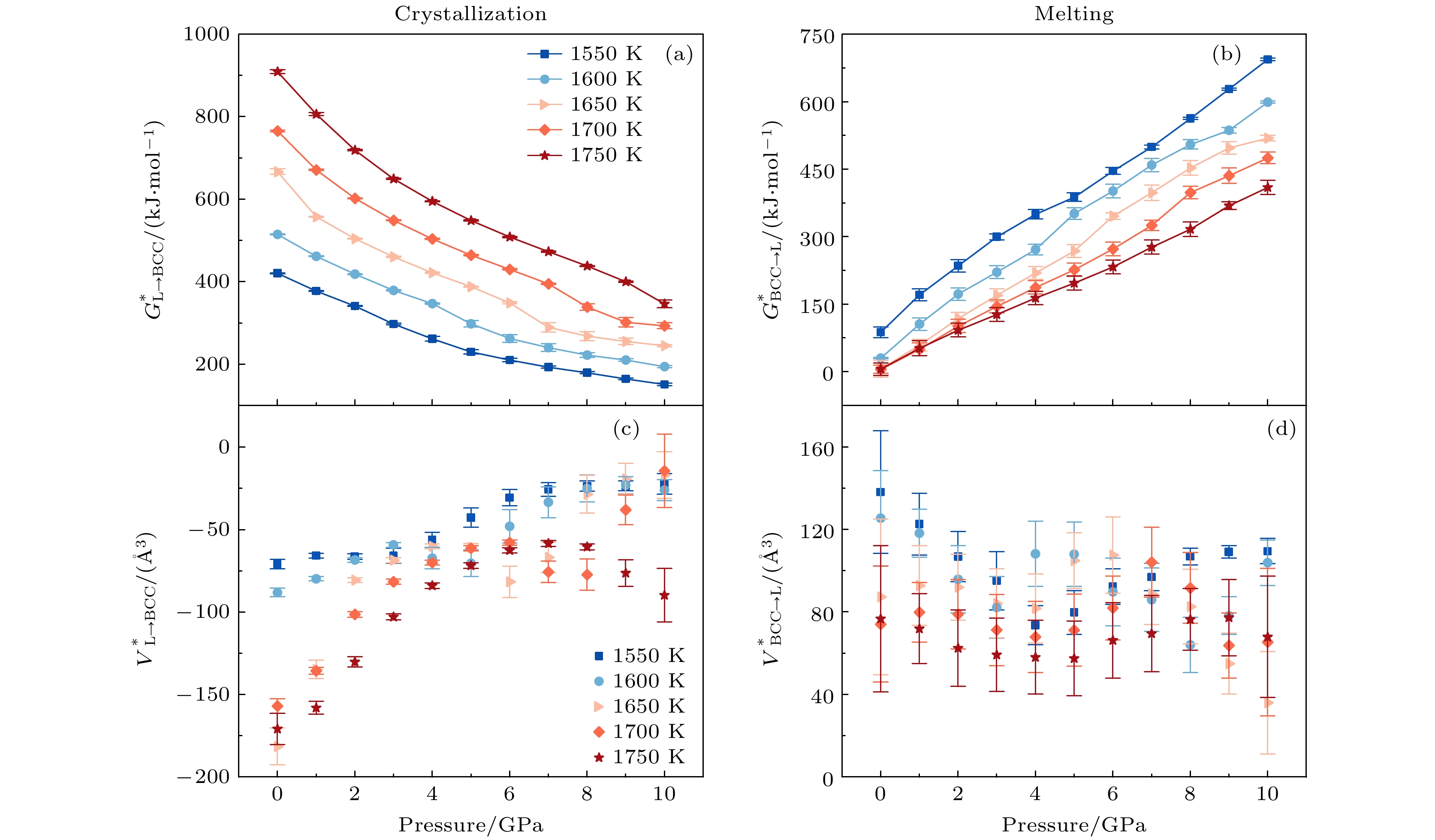
      图8显示了固液相变中不同温度条件(1550, 1600, 1650, 1700, 1750 K)下, 激活自由能$G^* $和激活体积$V^* $随压力的变化. 由图8(a)可以看出, 对于晶化过程,$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $随压力的升高而减速下降, 促进晶化, 而温度升高会加速这种效果, 使$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $随压力的变化趋于非线性. 对于熔化过程, 图8(b)则可以看出$ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $随压力的升高而近乎于线性升高, 即压力使熔化变困难. 温度升高降低了$ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $随压力升高而升高的变化趋势, 且不会改变等温条件下$\Delta G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $随压力的变化趋势. 总结而言, 在等温条件下, 更高的温度提升了晶化过程中$ G_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $对压力变化的敏感性; 对于熔化过程, $ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $随压力升高而线性增加, $\Delta G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $随温度的升高而增加.

      激活体积$V^* $作为描述相变过程中体系所需克服的多余体积, 并且它是$G^* $关于压力的偏导数, 所以激活体可以直观地反映等温下$G^*$对压力变化的敏感性. 晶化和熔化过程$V^*$随温度的变化如图8(c)和图8(d)所示. 在所模拟的温度和压力范围内, $ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $<0, $ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $>0, 即液固相变是体积减小的过程, 其逆过程(熔化)体积增加, 这是符合常识的. 以图8(c)中晶化过程1600 和1700 K的条件为例, 1600 K体系0 GPa时$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–88.21 ± 2.57) Å3变化至10 GPa时$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–26.09 ± 6.35) Å3; 1700 K体系0 GPa时$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–157.04 ± 4.44) Å3变化至10 GPa时$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $ = (–14.40 ± 22.37) Å3, 相较于1600 K时0到10 GPa |$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|减少近1/3的情况下, 1700 K的|$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|可变化至原先的1/10. 以图8(d)中熔化过程1600和1700 K的条件为例, 1600 K体系0 GPa时$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $ = (125.47 ± 23.07) Å3变化至10 GPa时$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $ = (103.87 ± 10.98) Å3; 1700 K体系0 GPa时$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $ = (74.03 ± 28.09) Å3变化至10 GPa时$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $ = (65.36 ± 35.73) Å3, 相同温度下, $ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $随压力的变化不显著. 图8(c)和图8(d)的结果表明, 在等压条件下, 温度升高使得晶化过程中体系的|$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|增加, 熔化过程中体系$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $减小; 更高的压力使得|$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|减小, 但对于熔化过程$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $无明显影响. 等温条件下, 晶化过程中|$ V_{{\mathrm{L}} \to {\mathrm{BCC}}}^* $|随压力的升高呈现下降趋势; 对于熔化过程$ V_{{\mathrm{BCC}}\to {\mathrm{L}}}^* $随压力无显著变化.

    4.   讨　论

    • 高温高压相图与相变动力学依赖于选用势函数的精确性, 由于所采用的EAM势是基于非磁性密度泛函理论(density functional theory, DFT)计算和基态或平衡态的实验数据, 没有包含对高温及非平衡态等相关数据的训练集, 在模拟高温高压相图及研究相变动力学时不足够准确. 在高温、高压下计算相关激活势垒$G^* $, 激活熵$S^* $和激活体积$V^* $时可能存在一定的误差. 该势函数和从头计算方法比较了对不同化学有序度镍钴铬合金之间的内聚能, 具有较高的一致性, 因此在保证精确结果下的使用范围应是在常压及0—1650 K附近的热力学条件. 在相图及BCC相稳定性的预测方面, 由于势函数的参数化基于平衡态数据, 可能无法准确描述非平衡态下亚稳BCC相形成, 导致相图预测可能与将来的实验观测的产生偏差. DFT计算表明, 磁性差异可能导致能量差达15 meV/atom, EAM非磁性简化模型可能影响相图中相应热力学平衡态BCC相的准确性. 另外, 相图的预测高度依赖于化学短程序的模拟精度, 该EAM势在描述Co-Cr有序化时与DFT结果趋势一致, 但局部Ni偏析的动力学过程可能因势函数的截断半径假设而误差增大, 进而影响相图准确性. 对动力学参数的影响上, EAM势的原子间相互作用基于对势截断和平均场近似, 导致对自由能面的局部起伏描述不足, 导致激活体积$V^* $低估. 所采用的EAM势未考虑电子熵和磁熵的贡献, 仅依赖构型熵近似. 在高温下的热激活过程的激活熵$S^* $可能被低估, 导致计算误差.

      对于高温高压的BCC相可靠稳定性的研究, 未来在模拟方面可采用第一性原理计算, 将总能量从头计算与进化算法相结合的晶体结构预测方法[47], 寻找能量最低的周期性晶格原子排列的搜索程序[48]等方法进行验证, 在实验方面可采用静高压与XRD, TEM相结合的手段进行直接观察.

      增强采样手段相比于传统分子动力学, 在相同计算步长上所需更多的硬件及计算资源, 因此兼具效率和准确性的EAM势函数成为首选, 开发适用于高温高压及非平衡态的势函数成为当务之急. 在今后对于MPEAs高温高压及非平衡态的研究中, 相应的势函数的模型建立, 应考虑DFT计算的结果, 以提供对亚稳态和液态结构更准确的描述.

    5.   结　论

    • 本文首先采用温和元动力学方法发现了等原子比镍钴铬合金在高温高压下的BCC晶态稳定相, 有别于常温常压下的FCC晶态稳定相. 通过具有扩展系综的动态概率增强采样方法, 结合多温-多压-多伞系综模拟, 绘制了镍钴铬合金p-T相图并提取了相应的热力学和动力学信息, 比如一维自由能曲线, 不同温度、压力条件下的激活自由能、激活熵、激活体积等, 系统评估了温度和压力对合金高温、高压固液相变过程中热力学性质的影响, 得出了以下结论.

      1) 预测等原子比镍钴铬合金在高温情况下存在BCC相和液相, 不存在常温下稳定的FCC相.

      2) 给出了等原子比镍钴铬合金在1550— 1750 K, 0—10 GPa下的p-T相图, 发现高温高压下存在BCC稳定相的情况, 为实验相图测试提供理论参考.

      3) 由重新加权法和块平均法得到不同热力学条件下误差极小的一维自由能曲线, 从中得到的晶化和熔化激活势垒$G^* $, 通过热力学状态函数关系式可得到相应的激活熵$S^* $和激活体积$V^* $.

      4) 压力升高和温度降低, 可降低两相自由能差ΔGL→BCC, 且提高熔化过程中所需$ G_{ {\mathrm{BCC}} \to{\mathrm{L}}}^* $, 二者变化的共同作用使得镍钴铬合金在高温高压下, BCC相稳定性得到提升.

      5) 熔化过程中压力变化对$V^* $无显著影响, 温度和压力均会通过对熔化及晶化过程中$S^* $和$V^* $影响, $S^* $及$V^* $下降影响相变动力学, 加快相变过程.

    参考文献 (48)

目录

/

返回文章
返回