-
传统的微波探测器采用金属天线, 在校准、自干扰等方面有一定局限性. 近年来, 里德伯原子已成为众多原子-场相互作用体系中备受关注的量子体系, 它具有主量子数高、偶极矩强、原子半径大、极化率高、寿命长等特点, 将其与微波场强耦合, 可实现对微波场的精密测量. 基于里德伯原子的微波测量技术, 不仅利用了里德伯能级之间与微波场的强耦合作用, 还借助原子相干效应将布居于基态的原子激发到里德伯高激发态, 为原子与微波相干耦合与转换提供了重要条件, 从而可借助低能态实现微波到光频场的有效转换, 并利用光场极易探测和操控的特点, 实现由光场对微波场的操控与测量. 基于里德伯原子的光谱探测技术是可涵盖从直流到太赫兹场灵敏检测的重要光学技术[1–9]. 研究表明, 利用里德伯原子可实现相比传统金属天线更高精度的测量技术[10].
最早实现微波测量的里德伯原子结合了四能级原子体系中的电磁诱导透明(electromagnetically induced transparency, EIT)量子相干效应和AT分裂(Autler-Townes splitting)效应, 实现了可溯源至普朗克常数的微波电场功率的精密测量[11]. 此后一系列方案的提出与实现如基于频率失谐[12]、塞曼分裂频率调制光谱[13]、幅度调制光谱[14]、多载波调制[15]、冷原子[16]、原子体系参数[17,18]以及超外差等, 进一步促进了里德伯原子微波探测的实用化和趋近于散粒噪声极限的高精度探测技术[19]. 此外, 利用斯塔克位移技术, 可同时提高测量精度和测量带宽[20].
基于EIT-AT方法的无线电微波测量精度和灵敏度主要与EIT和AT光谱宽度相关, 为了提升里德伯原子微波电场测量精度和灵敏度, 获得较窄EIT和AT谱至关重要[21–27]. 通过调节探针强度和更强的耦合场, 控制原子光学厚度(optical densities, ODs)等可优化EIT谱宽[28,29]. 此外由于超精细分裂能级间的布居再分配, 光泵浦(optical pumping, OP)效应也可以通过优化EIT提高光束的频率转换效率, 从而有助于提高测量灵敏度[30–36]. 利用内腔压窄EIT线宽的技术也可用于实现无线电波测量灵敏度的提升[37–39]. 因此, 实现一个峰高增强、线宽压窄的高对比度EIT光谱对里德伯原子微波探测相关技术的应用与研究有直接作用.
我们在铯原子气体中研究了里德伯原子微波探测中多能级体系引入OP效应对改善EIT线宽的最佳泵浦机理, 及其对提高微波测量精度和灵敏度的重要作用, 并由此实现了可实时微波探测的宽带测量, 阐明了在铯原子中D1线OP机制、D2线和里德伯态形成的EIT是一个多能级多光束场相互作用过程, 通过改善EIT线宽, 提高里德伯原子EIT-AT谱, 实现对微波探测的增强效应.
-
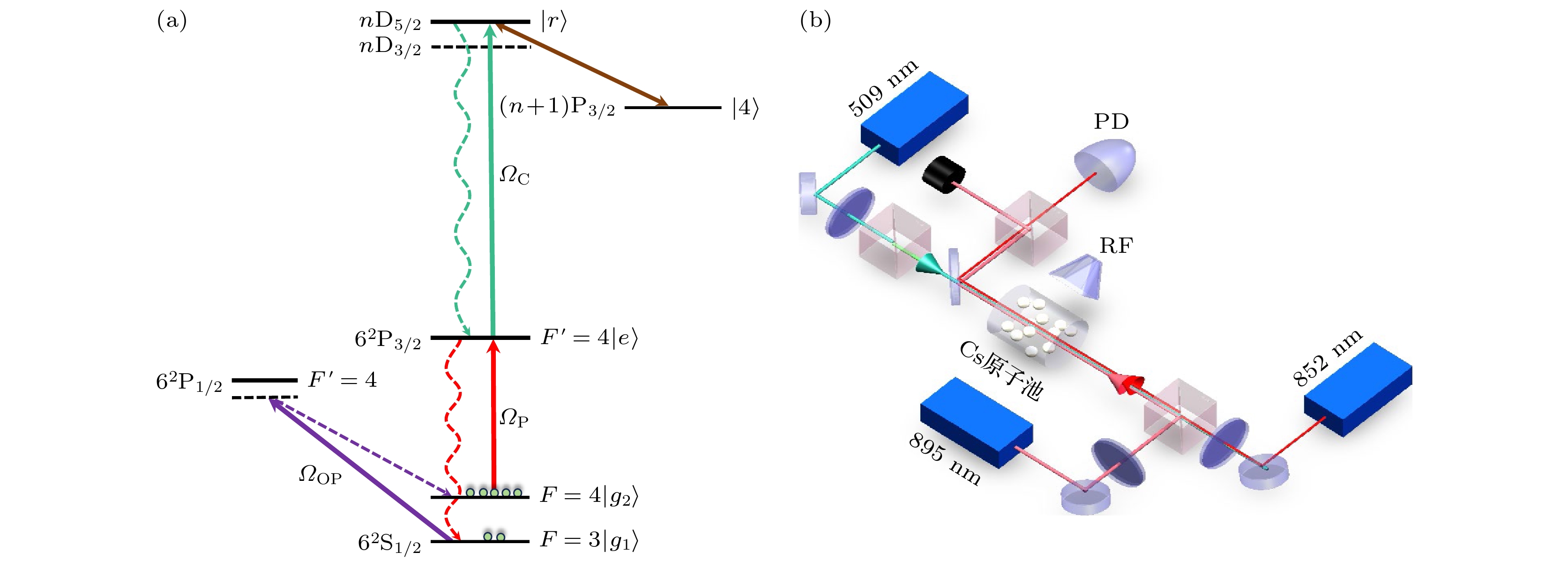
图1为在133CS原子气体中开展里德伯EIT和EIT-AT谱实现微波场测量的原子能级结构以及实验装置图. 该测量系统由铯原子的6个能级组成, 包含2个基态
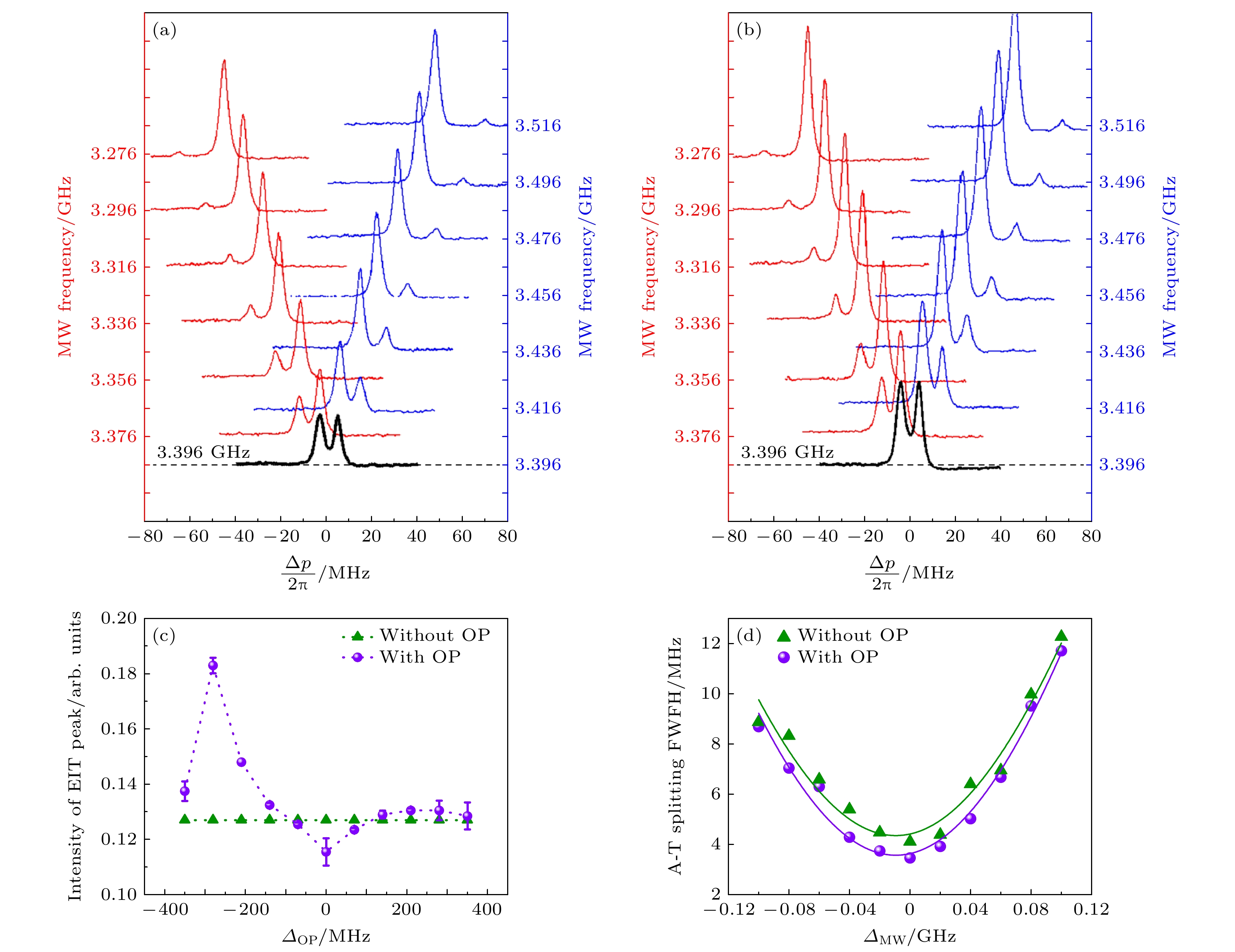
$ \left| {{g_1}} \right\rangle $ 和$ \left| {{g_2}} \right\rangle $ ($\left| {6{{\text{S}}_{1/2}}, F = 3} \right\rangle $ 和$\left| {6{{\text{S}}_{1/2}}, F = 4} \right\rangle $ ), 2个中间态$ \left| e \right\rangle $ (D2线的$ |6{\text{P}}_{3/2}, {F}' = 4\rangle $ 和D1线的$ \left| {6{\text{P}}{}_{1/2}, F' = 4} \right\rangle $ ), 以及2个里德伯高激发态$ \left| r \right\rangle $ 和$ \left| 4 \right\rangle $ ($59{{\text{D}}_{5/2}}$ 和$60{{\text{P}}_{3/2}}$ ). 一束拉比频率为$ {\varOmega _{\text{P}}} $ 的探测光和一束拉比频率为$ {\varOmega _{\text{C}}} $ 的耦合光将原子从基态$ \left| {{g_2}} \right\rangle $ 经中间态$ \left| e \right\rangle $ 泵浦到里德伯态$ \left| r \right\rangle $ , 构成阶梯型EIT系统, 在双光子共振条件下EIT效应导致原子对探测光吸收减小, 扫描耦合场频率可得到输出探测光的光谱, 呈现出EIT透明峰. 当微波电场(RF)与里德伯能态$ \left| r \right\rangle $ 和$ \left| 4 \right\rangle $ 之间发生近共振跃迁时, 由于高激发里德伯态(n = 59, 60)与微波场的强相干耦合特性, 引起里德伯态$ \left| r \right\rangle $ 产生显著AT分裂, EIT谱也随之分裂, 称其为EIT-AT分裂[40], 如图2(a)中的黑线探测谱所示, 其分裂间隔为$ {{\Delta }}f = ( - {\varDelta _{{\text{MW}}}} \pm \sqrt {\varDelta _{{\text{MW}}}^2 + \varOmega _{{\text{MW}}}^2}) /2 $ ,$ {\varDelta _{{\text{MW}}}} = {\omega _4} - {\omega _{4, r}} $ 和$ {\varOmega _{\rm MW}} $ 是微波电场的频率失谐和拉比频率,${\varDelta _{\text{P}}} = {\omega _{\text{P}}} - {\omega _{e{, }{g_{2}}}}$ 为探测光失谐. 因此通过对分裂光谱的测量实现对微波场强度${E_{{\text{MW}}}} = 2\pi \hbar \Delta f/{\wp _{4 r}}$ 的有效探测.实验测量装置如图1(b)所示. 852 nm外腔半导体激光器(Toptica)作为探测光, 其中心波长设置为852.36 nm, 经半波片和偏振分光棱镜(PBS)分束后, 选择水平偏振光作用于铯原子气体. 509 nm激光器(频准)作为耦合光与探测光反向作用于原子气体, 其偏振经半波片和PBS分束后选择水平偏振. 探测光(852 nm)功率为400 μW, 光斑直径大小为790 μm. 耦合光(509 nm)功率为30 mW, 光斑直径大小为980 μm. 微波(RF)信号场经喇叭天线从铯原子气室正上方输入, 天线距离原子12 cm, 微波功率为–10 dBm. 微波场、探针和耦合场均以水平偏振作用于原子. 895 nm外腔半导体激光器(toptica)作为再泵浦光, 选择垂直偏振光作用于原子产生OP效应, 将EIT-AT谱探测过程中因自发辐射跃迁到基态
$ \left| {{{\text{g}}_1}} \right\rangle $ 的原子再泵浦到循环跃迁中. 895 nm的OP光最佳功率为316 μW, 光斑直径大小为1060 μm. 在EIT-AT分裂谱实验过程中, 耦合光扫描覆盖了从$\left| {n{{\text{D}}_{3/2}}} \right\rangle $ 到$\left| {n{{\text{D}}_{5/2}}} \right\rangle $ 的两套EIT-AT分裂谱, 由探测器(PD)探测. 利用两能态之间的固有频率差作为参考, 定标微波测量过程中的频率失谐. -
微波测量所参与的能级为约化的四能级体系(
$ \left| {{g_2}} \right\rangle \leftrightarrow \left| e \right\rangle \leftrightarrow \left| r \right\rangle \leftrightarrow \left| 4 \right\rangle $ ), 如图1(a)所示. 实验选择将852 nm探测光锁定于$ \left| {{g_{2}}} \right\rangle \leftrightarrow \left| e \right\rangle $ ($\left| {6{{\text{S}}_{1/2}}, F = 4} \right\rangle $ ↔$ |6{\text{P}}_{3/2}, {F}' = 4\rangle $ )跃迁能级, 509 nm耦合光在中间态和里德伯态跃迁能级间扫描$ \left| e \right\rangle \leftrightarrow \left| r \right\rangle $ ($ |6{\text{P}}_{3/2}, {F}' = 4\rangle $ ↔$\left| {59{{\text{D}}_{5/2}}} \right\rangle $ ). 同时微波场作用于里德伯跃迁能级$ \left| r \right\rangle \leftrightarrow \left| 4 \right\rangle $ ($\left| {59{{\text{D}}_{5/2}}} \right\rangle $ ↔$\left| {60{{\text{P}}_{3/2}}} \right\rangle $ ), 其共振跃迁频率为3.4 GHz. 在该中心频率附近调节微波场频率, 即可实现微波场与里德伯态之间从共振到失谐耦合的操控与测量. 图2(a)所示为扫描探测光频率时的微波场与里德伯原子共振耦合和可调谐耦合的EIT-AT谱. 在加入3.4 GHz共振微波电场时, EIT-AT谱呈现出对称分裂(黑线). 当加入的微波电场为红失谐或蓝失谐时, EIT-AT谱呈现出不对称分裂. 与共振谱相比, AT分裂谱出现明显非对称结构, 如果微波频率为蓝色失谐, 则左峰高于右峰, 否则谱线呈现相反情况. 这一现象与微波场产生的里德伯态$ \left| r \right\rangle $ 的AT分裂$ {{\Delta }}f = ( - {\varDelta _{{\text{MW}}}} \pm \sqrt {\varDelta _{{\text{MW}}}^2 + \varOmega _{{\text{MW}}}^2} )/2 $ 相关. 当里德伯态与微波场共振耦合时, AT分裂${{\Delta }}f = \pm {\varOmega _{{\text{MW}}}}/2$ 使$ \left| r \right\rangle $ 态分裂成正负失谐对称的两个能态, 间隔等于微波场拉比频率, 因此AT呈现对称结构. 当微波场为正失谐(蓝移)或负失谐(红移), AT分裂使$ \left| r \right\rangle $ 态出现不对称分裂态$ \Delta f = ( - {\varDelta _{{\text{MW}}}} \pm \sqrt {\varDelta _{{\text{MW}}}^2 + \varOmega _{{\text{MW}}}^2} )/2 $ , 或$ \Delta f = ({\varDelta _{{\text{MW}}}} \pm \sqrt {\varDelta {}_{{\text{MW}}}^2 + \varOmega _{{\text{MW}}}^2} )/2 $ , 因此EIT-AT谱出现不对称型谱, 左右峰对应于接近和远离$ \left| r \right\rangle $ 态的EIT峰, 近共振EIT效应优于远共振EIT效应, 导致EIT-AT谱出现左右不等的峰高现象.在图2(a)的EIT-AT谱探测过程中, 原子从基态
$ \left| {{g_2}} \right\rangle $ 经探测光和耦合光激发到里德伯态$ \left| r \right\rangle $ , 原子会因自发辐射返回到基态$ \left| {{g_2}} \right\rangle $ 和$ \left| {{g_1}} \right\rangle $ (图1(a)虚线). 处于基态$ \left| {{g_1}} \right\rangle $ 的原子不会继续参与到EIT和AT循环跃迁过程中, 因此通过引入OP效应将退居于$ \left| {{g_1}} \right\rangle $ 的原子抽运回循环跃迁中. 采用895 nm再泵浦OP光, 将$ \left| {{g_1}} \right\rangle $ 态原子泵浦到D1线能态$\left| {6{\text{P}}{}_{1/2}, F' = 4} \right\rangle $ , 经自发跃迁回到$ \left| {{g_2}} \right\rangle $ 态, 提高参与EIT过程的原子数, 在不改变EIT相互作用的情况下等效于增加了原子数密度和原子的光学厚度, 从而增强EIT效应, 进而提高微波探测灵敏度. 图2(b)是引入OP时的EIT-AT光谱, 与图2(a)未引入OP光时相同条件的EIT-AT光谱相比, 谱线出现明显增强效应.OP光的参与使得EIT-AT谱线宽得到压窄, 从而提高了微波测量精度. 因此基于里德伯原子的微波电场测量的灵敏度也会随之得到提高. 在优化EIT谱的过程中, 我们发现OP光频率须在非共振处, 可得到最强的EIT效应, 如图2(c)实验结果所示. 增强EIT的最佳OP光频率锁定于失谐
${\varDelta _{{\text{OP}}}} = {\omega _{{\text{OP}}}} - {\omega _{{\text{OP}}, {g_{1}}}}$ 约为–294 MHz, 是由于相比其他原子体系如铷原子, EIT铯原子能级结构尤其是D2线的超精细能级分裂较多而且较密, 因此其复杂能级结构导致在引入D1线OP光时, 会带来一系列多能级体系引起的电磁诱导吸收, 相对于–294 MHz在OP光失谐较大, 可以考虑为Raman泵浦过程, 不会产生其他能级的电磁诱导吸收相干效应.从图2(a)和图2(b)谱线对比可以看出: 无论是近共振微波电场耦合的EIT-AT谱, 还是具有一定失谐的微波场EIT-AT谱, 在引入895 nm再泵浦OP光后, 均可获得显著压窄的谱线. 根据电场强度与谱宽
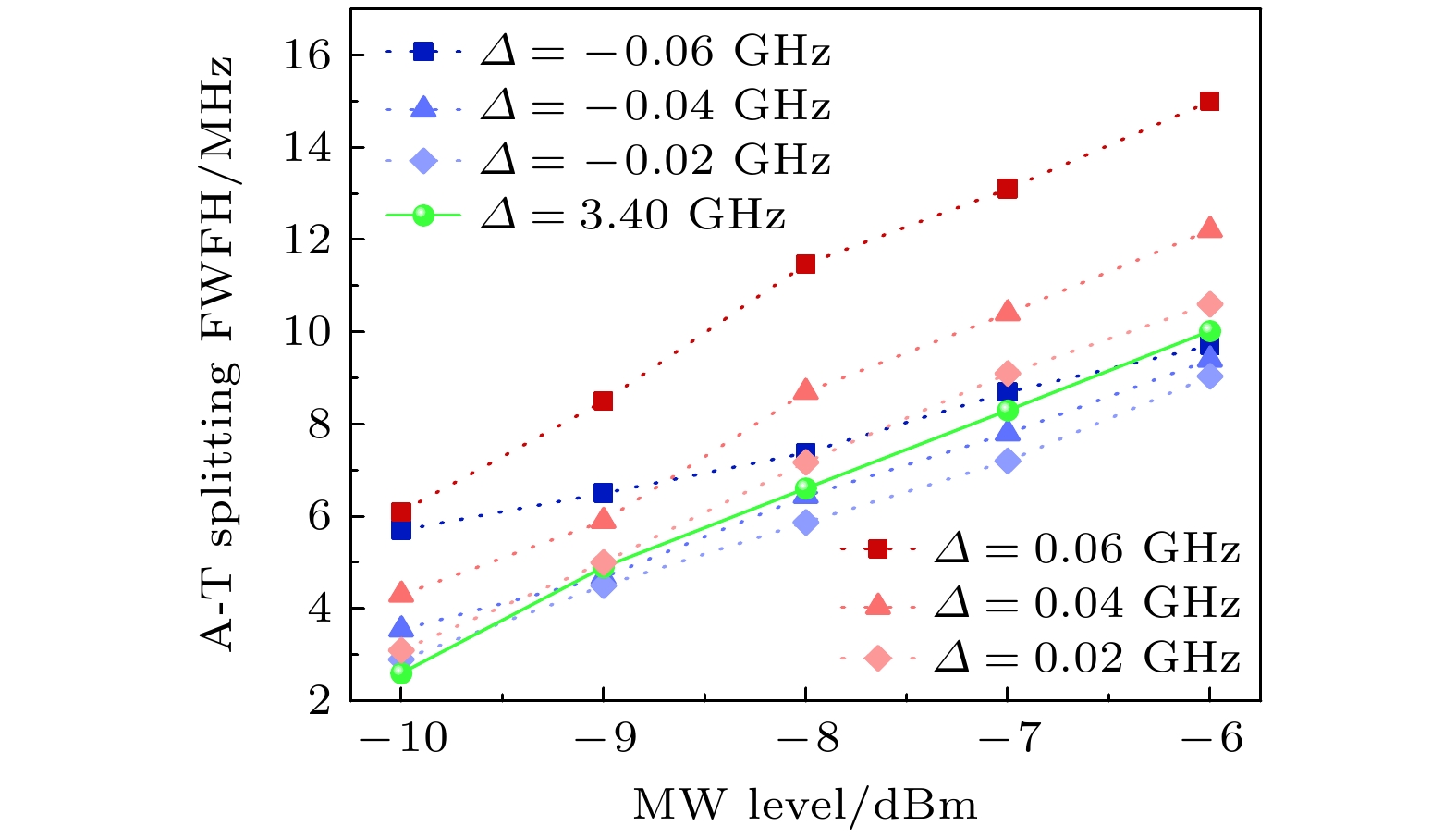
${{\Delta }}f$ 公式:${E_{{\text{MW}}}} = 2\pi \hbar {{\Delta }}f{\text{/}}{\wp _{4 r}}$ , 其中普朗克常量$ \hbar $ 和微波的跃迁偶极矩$ {\wp _{4 r}} $ , 谱宽压窄正比于微波场的灵敏度(即增强测量), 从而提高微波测量精度. 如图2(d)所示, 从优化的EIT-AT谱半高宽线宽可得到对应的微波电场强度的优化指标. 在微波近共振附近, EIT-AT谱宽压窄约1.3倍, 对应于微波电场测量的灵敏度提高1.3倍. 因此通过优化EIT振幅以及EIT-AT谱, 基于里德伯原子的电测传感的灵敏度也将得到提高.图3为加入再泵浦OP光后, EIT-AT分谱宽与不同微波信号源输出功率的关系. 我们分别测试了共振频率3.4 GHz、蓝失谐Δ = –0.06 GHz, Δ = –0.04 GHz, Δ = –0.02 GHz, 红失谐Δ = 0.02 GHz, Δ = 0.04 GHz, Δ = 0.06 GHz时的EIT-AT谱宽. 横坐标为微波信号源输出功率
$P({\text{mW}})$ 从–10 dBm增大到–6 dBm (相应的微波电压$ {E_{{\text{mV}}}} $ 由功率和 电压关系式$ P=-10\lg(E_{\text{mV}}^2/R) $ 确定, 为0.071—0.112 V)的谱宽. 因此在微波信号源电压mV量级实现EIT-AT分裂探测. 在固定微波失谐的情况下, 图3测试结果显示, 随着微波功率的增加, 谱宽不断增大, 符合理论预测即微波功率增加, 对应于微波场拉比频率增加, 谱宽$\Delta f = \big( - {\varDelta _{{\text{MW}}}} \pm \sqrt {\varDelta _{{\text{MW}}}^2 + \varOmega _{{\text{MW}}}^{2}} \,\big)/2$ 也会相应增大. 此外, 结果显示对于红失谐和蓝失谐, 谱宽变化对于拉比频率的响应有所不同, 红移的变化情况较蓝移更为显著. 这一效应也许说明了铯原子超精细能态谱间隔较密, 会引起EIT-AT谱产生一定影响. 实验中我们选取铯原子D2线的超精细态F' = 4作为EIT效应中间态, 其附近超精细态F' = 3相比F' = 5距离F' = 4更近, 因此会引起EIT-AT谱中蓝移和红移的不同谱宽. -
基于原子系统的微波测量, 取决于微波场与原子的相干耦合, 通过耦合利用原子介质将微波场测量转变为光频波段的测量, 既改善了微波场测量的操控性又提高了其精度和灵敏度. 虽然利用里德伯原子EIT-AT分裂效应测量微波电场较传统天线有不可比拟的优势, 但当下限制约束微波场测量精度进一步提升在很大程度上取决于更窄线宽、更高信噪比里德伯原子EIT-AT分裂光谱的获得. 本文主要研究了OP效应对于改善基于里德伯原子微波电场测量的EIT-AT谱的实验实现. 实验结果表明在阶梯型里德伯EIT系统中, 通过OP可以压窄EIT和微波场EIT-AT谱宽, 因此提高微波电场测量灵敏度. 在优化EIT振幅后加入单频微波, 通过A-T分裂间隔观察到微波电场测量的灵敏度得到了1.3倍的提升. 不仅对于原子微波探测的应用有实际意义, 同时也可用于研究高激发里德伯态偶极-偶极相互作用、激光频率稳定和环境电磁场作为量子传感器的可追溯检测.
多能级里德伯原子中实现3.4 GHz微波增强测量
Enhanced sensing of 3.4 GHz microwave in multi-level Rydberg atomic system
-
摘要: 里德伯原子微波测量系统是不同于传统电子微波测量的新型全光学测量技术, 它利用里德伯原子与微波场的强相干耦合效应, 将微波场转化为原子相干光谱的特性测量, 目前已成为高灵敏度高精度微波测量的主要研究领域. 微波场与里德伯原子相干耦合过程中的退相干机理会极大地影响微波场与相干光谱的转换效率, 从而影响微波电场测量灵敏度. 我们实验研究了在多能级里德伯铯原子系统中, 实现中心频率为3.4 GHz微波测量的最佳增强条件以及0.3 GHz动态范围测量. 利用铯原子D1线和D2线构成的多能级光学泵浦效应减小里德伯原子的退相干, 从而增强里德伯原子的电磁诱导透明(EIT)量子相干特性, 以及增强微波场作用产生的EIT-AT分裂谱, 实现微波场的增强测量.Abstract: The Rydberg-based microwave detection is an all-optical technology that uses the strong coherent interaction between Rydberg atoms and microwave field. Different from the traditional microwave meter, the Rydberg atomic sensing is a new-type microwave detector that transforms the microwave spectrum into a coherent optical spectrum, and arouses increasingly the interests due to its high sensibility. For this kind of sensor, the coherence effect induced by coupling atoms with microwave plays a key role, and the decoherence may reduce the sensitivity. A multi-level Rydberg atomic scheme with optimized quantum coherence, which enhances both the bandwidth and the sensitivity for 4 GHz microwave sensing, is demonstrated experimentally in this work. The enhanced quantum coherence of Rydberg electromagnetically induced transparency (EIT) and microwave induced Autler-Townes (AT) splitting in EIT windows are shown using optical pumping at D1 line. The enhanced sensitivity at 3.4 GHz with 0.3 GHz bandwidth can be realized, based on the enhanced EIT-AT spectrum. The experimental results show that in the stepped Rydberg EIT system, the spectral width of EIT and microwave field EIT-AT can be narrowed by optical pumping (OP), so the sensitivity of microwave electric field measurement can be improved. After optimizing the EIT amplitude and adding single-frequency microwaves, the sensitivity of the microwave electric field measurement observed by the AT splitting interval is improved by 1.3 times. This work provides a reference for utilizing atomic microwave detection.
-
Key words:
- quantum coherence effect /
- Rydberg /
- microwave measurements /
- optical pumping .
-

-
图 2 微波探测实验结果 (a)四能级EIT-AT分裂谱, 黑线为微波与里德伯态共振耦合的EIT-AT谱(3.4 GHz), 红线和蓝线分别为微波频率发生红移或蓝移的耦合谱(3.276—3.516 GHz); (b) OP效应增强的EIT和EIT-AT谱; (c)不同再泵浦光频率失谐对EIT峰增强特性; (d) OP效应和无OP效应时EIT-AT谱宽的对比
Figure 2. Experimental results of microwave detection: (a) Four-level EIT-AT fission spectra; the black line is the EIT-AT spectrum (3.4 GHz) of microwave and Rydberg state resonance coupling, the red line and blue line are the coupling spectrum of microwave frequency with red shift or blue shift (3.276–3.516 GHz); (b) EIT and EIT-AT spectra with enhanced OP effect; (c) the enhancement characteristics of EIT peak by different repump optical frequency detuning; (d) the comparison of EIT-AT spectral width between OP effect and no OP effect.
-
[1] Song Z F, Liu H P, Liu X C, Zhang W F, Zou H Y, Zhang J, Qu J F 2019 Opt. Express 27 8848 doi: 10.1364/OE.27.008848 [2] Holloway C, Simons M, Haddab A H, Gordon J A, Anderson D A, Raithel G 2021 IEEE Antennas Propag. Mag. 63 63 doi: 10.1109/MAP.2020.2976914 [3] Holloway C L, Simons M T, Gordon J A, Novotny D 2019 IEEE Antennas Wirel Propag. Lett. 18 1853 doi: 10.1109/LAWP.2019.2931450 [4] Meyer D H, Kunz P D, Cox K C 2021 Phys. Rev. A 15 014053 [5] Otto J S, Hunter M K, Kjærgaard N, Deb A B 2021 Appl. Phys. 129 154503 [6] Anderson D A, Sapiro R E, Raithel G 2021 IEEE Trans. Antennas Propag. 69 2455 doi: 10.1109/TAP.2020.2987112 [7] Robinson A K, Prajapati N, Senic D, Simons M T, Holloway C L 2021 Appl. Phys. Lett. 118 114001 doi: 10.1063/5.0045601 [8] A. Gürtler; A. S. Meijer; W. J. van der Zande 2003 Appl. Phys. Lett. 014053 [9] Holloway C L, Prajapati N, Artusio-Glimpse A B, et al. 2022 Appl. Phys. Lett. 120 204001 doi: 10.1063/5.0088532 [10] Fan H Q, Kumar S, Sedlacek J, Kübler H, Karimkashi S, Shaffer J P 2015 J. Phys. B: At. Mol. Opt. Phys. 48 202001 doi: 10.1088/0953-4075/48/20/202001 [11] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819 doi: 10.1038/NPHYS2423 [12] Simons M T, Gordon J A, Holloway C L, Anderson D A, Miller S A, Raithel G 2016 Appl. Phys. Lett. 108 174101 doi: 10.1063/1.4947231 [13] Jia F D, Yu Y H, Liu X B, Zhang X, Zhang L, Wang F, Mei J, Zhang J, Xie F, Zhong Z P 2020 Appl. Opt. 59 8253 doi: 10.1364/AO.401945 [14] Liu X B, Jia F D, Zhang H Y, Mei J, Yu Y H, Liang W C, Zhang J, Xie F, Zhong Z P 2021 Appl. Phys. Lett. 11 085127 [15] Li S H, Yuan J P, Wang L R 2020 Appl. Sci. 10 8110 [16] Liao K Y, Tu H T, Yang S Z, Chen C J, Liu X H, Liang J, Zhang X D, Yan H, Zhu S L 2020 Phys. Rev. A 101 053432 [17] Chopinaud A, Pritchard J D 2021 Phys. Rev. Appl. 16 024008 doi: 10.1103/PhysRevApplied.16.024008 [18] Meyer D H, O'Brien C, Fahey D P, Cox K C, Kunz P D 2021 Phys. Rev. A 104 043103 [19] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911 [20] Hu J L, Li H Q, Song R, Bai J X, Jiao Y C, Zhao J M, Jia S T 2022 Appl. Phys. Lett. 121 011101 [21] Mohapatra A K, Jackson T R, Adams C S 2007 Phys. Rev. Lett. 98 113003 [22] Zhao J M, Zhu X B, Zhang L J, Feng Z G, Li C Y, Jia S T 2009 Opt. Express 17 15821 doi: 10.1364/OE.17.015821 [23] Kumar S, Fan H, Kübler H, Sheng J, Shaffer J P 2017 Sci. Rep. 7 42981 doi: 10.1038/srep42981 [24] Simons M T, Gordon J A, Holloway C L 2018 Appl. Opt. 57 6456 [25] Jia F D, Zhang J, Zhang L, Wang F, Mei J, Yu Y H, Zhong Z P, Xie F 2020 Appl. Opt. 59 2108 doi: 10.1364/AO.384315. [26] Fancher C T, Scherer D R, St. John M C, Marlow B L S 2021 IEEE Trans. Quantum Eng. 2 1 doi: 10.1109/TQE.2021.3065227 [27] 李敬奎, 杨文广, 宋振飞, 张好, 张临杰, 赵建明, 贾锁堂 2015 物理学报 64 163201 doi: 10.7498/aps.64.163201 Li J K, Yang W G, Song Z F, Zhang H, Zhang L J, Zhao J M, Jia S T 2015 Acta Phys. Sin. 64 163201 doi: 10.7498/aps.64.163201 [28] Wu B H, Chuang Y W, Chen Y H, Yu J C, Chang M S, Yu I A 2017 Sci. Rep. 7 9726 doi: 10.1038/s41598-017-09953-0 [29] Su H J, Liou J Y, Lin I C, Chen Y H 2022 Opt. Express 30 1499 doi: 10.1364/OE.444894 [30] He Z S, Tsai J H, Chang Y Y, Liao C C, Tsai C C 2013 Phys. Rev. A 87 033402 [31] Moon H S, Lee L, Kim J B 2008 Opt. Express 16 12163 doi: 10.1364/OE.16.012163 [32] Yang B D, Liang Q B, He J, Zhang T C, Wang J M 2010 Phys. Rev. A 81 043803 [33] Zhang L J, Bao S X, Zhang H, Raithel G, Zhao J M, Xiao L T, Jia S T 2018 Opt. Express 26 29931 [34] Prajapati N, Robinson A K, Berweger S, et al. 2021 Appl. Phys. Lett. 119 214001 doi: 10.1063/5.0069195 [35] Prajapati N, Akulshin A M, Novikova I 2018 J. Opt. Soc. Am. B: Opt. Phys. 35 1133 doi: 10.1364/JOSAB.35.001133 [36] Akulshin A M, Orel A A, McLean R J 2012 J. Phys. B: At. Mol. Phys. 45 015401 doi: 10.1088/0953-4075/45/1/015401 [37] Yang A H, Zhou W P, Zhao S C, Xu Y, Fedor J , Li Y X, Peng Y D 2020 J. Opt. Soc. Am. B: Opt. Phys. 37 1664 [38] Li S H, Yuan J P, Wang L R, Xiao L T, Jia S T 2022 Front. Phys. 10 846687 doi: 10.3389/fphy.2022.846687 [39] Wang Q X, Wang Z H, Liu Y X, Guan S J, He J, Zhang P F, Li G, Zhang T C 2023 Acta Phys. Sin. 72 087801 [王勤霞, 王志辉, 刘岩鑫, 管世军, 何军, 张鹏飞, 李刚, 张天才 2023 物理学报 72 087801] doi: 10.7498/aps.72.20230039 Wang Q X, Wang Z H, Liu Y X, Guan S J, He J, Zhang P F, Li G, Zhang T C 2023 Acta Phys. Sin. 72 087801 doi: 10.7498/aps.72.20230039 [40] Moon H S, Lee W K, Lee L, Kim J B 2004 IEEE Conf. Publ. 85 3965 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: