-
锂金属因具备高理论容量、低密度以及低氧化还原电位等特性, 成为极具潜力的阳极材料, 在众多领域与行业中得以应用并逐步普及. 近年来, 全球范围内锂离子电池的使用量呈逐年递增态势. 锂离子电池在新能源汽车和航空航天等领域发挥着主导性作用, 深刻影响着相关产业的技术革新与发展走向, 对推动全球能源转型以及高端制造业的进步意义重大. 固态锂电池由于采用了不泄露、不挥发、不易腐蚀、不易燃烧以及对锂稳定性高的固态电解质, 使得其相比于采用电解液的锂电池, 在安全性和电化学性能等方面都有了显著的提高[1,2], 拥有更好的热稳定性、机械稳定性和更高的电池能量密度[3]. 因此, 作为重要的储能装置, 固态锂电池在发展国民经济、减少碳排放、降低对化石能源的依赖、解决环境污染等方面意义重大, 被视为未来最有发展前景的战略性新能源[4,5]. 然而, 锂枝晶生长问题一直是制约其性能提升和安全应用的关键因素. 锂枝晶生长不仅会降低电池的库仑效率, 还可能刺穿隔膜导致电池内部短路, 从而引发严重的安全事故. 此外, 枝晶不仅会破坏固体电解质界面(SEI), 增强电极-电解质界面的副反应, 还会产生死锂, 不断消耗锂源, 大幅降低电池使用寿命[6,7]. 因此有必要研究固态电解质对锂枝晶生长的影响.
在锂枝晶研究中, 可借助多种实验方法, 诸如原位或非原位显微镜、光学显微镜以及电子显微镜等展开研究. 然而, 受实验设备的局限, 锂枝晶研究多只能在宏观层面进行, 难以深入至微观尺度去捕捉其反应过程. 此外, 实验方法还存在时间成本高昂、对环境条件极为敏感等问题, 这些不足致使部分研究学者运用数值模拟方法来开展锂枝晶的相关研究. 相场法是一种广泛应用在材料科学、物理学和化学等领域的数值模拟方法, 其以金兹堡-朗道理论(Ginzburg-Landau theory)为物理基础, 通过引入一个或多个连续变化的相场变量, 基于非均相系统中弥散界面, 借助微分方程来描述物质系统中各个相的状态和相变过程, 该方法可以克服电化学沉积过程中负极和电解质运动界面跟踪的难题[8]. 这些相场变量可以是浓度c、温度T、外力F等物理量, 也可以是表述相结构或相组成的序参量[9–11]. 在模拟锂枝晶的生长方面, 通过求解相场方程, 可以揭示锂枝晶生长的微观机制, 如锂离子在电极表面的不均匀沉积、电池内部的应力分布等, 还可以揭示不同内部/外部条件下锂枝晶的生长形态和演化规律, 从而预测锂枝晶的生长趋势, 最终为电池设计和优化提供理论指导.
国内外学者针对锂电池枝晶生长问题开展大量的研究. Guyer等[12]最早将相场法应用于锂枝晶的研究, 基于一维相场模型构建了电化学系统模型, Kobayashi[13]通过相场法模拟了枝晶生长, 二者将得到的仿真结果与实验结果对比, 均验证了实验结果与仿真结果的一致性. Liang等[14]建立一维的非线性相场模型, 用于描述电极/电解质界面在高度非平衡电化学过程中的演变过程, 验证了该模型在高过电位电化学过程中能有效预测界面运动和微观结构演变, 且与经典Butler-Volmer动力学相符. Chen等[15]提出在液态电解质中锂枝晶的非线性相场模型, 通过对3种枝晶形态进行分析, 研究发现较大的外加电压或界面处扁平突起会导致枝晶侧分支的形成, 甚至会导致不稳定的尖裂. 基于该模型, Shen等[16]提出了固体电解质中锂枝晶的相场模型, 并研究了不同外部压力对锂枝晶生长行为的影响, 研究结果表明, 外压会抑制电镀反应的进行而不利于电池的速率性能, 并且会使锂枝晶形貌光滑, 增大其力学不稳定性. Yan等[17]将非线性相场锂枝晶模型[15]与传热模型相耦合, 进一步研究了锂枝晶的热效应, 发现环境温度的升高会使归一化枝晶长度减小, 且温度梯度会阻止横向分支的形成. 内热分布不均匀使枝晶形貌由树形变化至菱形. Hong和Viswanathan[18]在此基础上, 进一步提出完全热耦合的电化学沉积相场模型, 发现较低的电化学反应势垒有利于抑制枝晶生长. Yurkiv等[19]提出了电化学-力相耦合的相场模型来研究表面能与枝晶形貌之间的关系, 发现低充电速率或高界面Li+扩散能力有利于保持界面稳定性. Qi等[20]和Arguello等[21]都在三维尺度上进一步对锂枝晶进行了模拟, 发现高各向异性强度会增加枝晶的最大高度, 而高温有助于锂枝晶的均匀沉积并有效抑制其生长, 并且枝晶的形成与锂离子扩散和电迁移力之间的竞争有关, 如枝晶尖端附近更大的电场, 会引发更高的锂离子浓度, 从而触发树枝状锂的尖端生长. Jiang等[22]通过构建固体电解质中枝晶生长和裂纹扩展的力-电-化学耦合相场模型, 发现增大固体电解质的机械强度, 能使枝晶生长速度减慢, 枝晶尖端的应力变得更高, 但未研究热效应对枝晶的影响. Liang等[23]通过模拟死锂的生长过程, 发现较大充放电循环周期数能减缓充电时的锂枝晶生长, 降低锂沉积面积, 但也使放电过程中的死锂面积增大. 但较高环境温度在抑制锂枝晶生长的同时也能减少死锂的形成.
目前, 关于锂枝晶的数值仿真研究主要基于单一物理场或双物理场耦合作用[8], 而研究不同影响因素之间的相互作用、从力-热-电化学耦合角度分析锂枝晶变化的研究较少. 因此, 有必要建立一个同时耦合应力场、热场以及电化学场的锂枝晶生长模型来探究锂枝晶的动态生长过程. 基于此, 本文通过构建锂枝晶在固态电解质中的相场模型, 采用COMSOL Multiphysics有限元模拟软件, 系统研究外界压力和温度对锂枝晶生长行为的影响. 研究针对不同外压力与温度条件的组合, 通过参数化讨论揭示其对锂枝晶形貌演化与生长规律的调控机制. 探讨外界物理场对锂金属沉积动力学和枝晶生长特性的耦合作用, 明确关键影响因素的作用规律. 研究重点聚焦于多场耦合下锂枝晶的生长模式, 包括外压力对界面稳定性和应力分布的调控作用, 以及加入势垒时不同环境温度对锂离子扩散速率的影响. 研究结果不仅揭示不同参数下锂枝晶的生长规律和差异, 还为进一步优化锂金属电池的设计提供理论指导和数据支持. 通过对锂枝晶生长机理的定量化分析, 旨在探索有效的枝晶抑制策略, 从而提高锂金属电池的安全性和电化学性能, 为下一代高能量密度储能器件的发展提供可靠的技术依据.
-
基于Chen等[15]提出的相场法, 通过引入力学场, 建立力-电化学耦合模型来模拟固态电解质中锂枝晶的生长情况. 在充电过程中, 锂离子通过固态电解质扩散到负极, 与锂金属界面的电子相结合形成锂. 相场模型建立的基础是系统的吉布斯自由能, 固态电解质中锂枝晶生长的总吉布斯自由能, 可以表示为
其中,
$ {f_{{\text{ch}}}}\left( {\xi , {c_i}} \right) $ 为化学自由能密度,$ {f_{{\text{grad}}}}\left( \xi \right) $ 为梯度自由能密度,$ {f_{{\text{elec}}}}\left( {\xi , {c_i}, \varphi } \right) $ 为静电能密度,$ {f_{{\text{els}}}}\left( {\xi , u} \right) $ 弹性自由能能量密度, 4个变量ξ, ci, φ, u分别表示锂枝晶生长界面的相场序变量、化学物质i (i = Li, Li+, A–)的摩尔分数、系统电势和位移. 在相场模型中, 相场序变量ξ作为一个非守恒参数来追踪锂枝晶生长界面的变化, 其范围从0到1, 当ξ = 1时, 代表锂电极相, 当ξ = 0时, 代表电解质相.化学自由能密度
$ {f_{{\text{ch}}}}\left( {\xi , {c_i}} \right) $ 表示为其中, R为摩尔气体常数, T为绝对温度,
$\mu _i^\varTheta $ 为物质i的参考化学势,$g\left( \xi \right) = W{\xi ^2}{\left( {1 - \xi } \right)^2}$ 表示一个双阱函数.${c_{{\text{L}}{{\text{i}}^{+}}}}$ 表示电解质中Li+的浓度, canion表示电解质中的阴离子浓度, c0为电解质的初始浓度,${{{c_{{\text{L}}{{\text{i}}^{+}}}}} {/ } {{c_0}}}$ 和${{{c_{{\text{anion}}}}} {/ } {{c_0}}}$ 分别表示归一化的Li+和阴离子的浓度.梯度自由能密度
$ {f_{{\text{grad}}}}\left( \xi \right) $ 表示为其中
$k = {k_0}\left[ {1 + \delta \cos \left( {\omega \theta } \right)} \right]$ , k0为梯度能量系数, δ为各向异性强度, ω表示各向异性模态, θ为界面法向量与参考轴的夹角, 以模拟系统中的因金属负极缺陷、电极和电解质不完全接触等原因造成的局部不均匀性.静电能密度
$ {f_{{\text{elec}}}}\left( {\xi , {c_i}, \varphi } \right) $ 表示为其中, n表示离子电荷数, 对于锂离子取n = 1, F为法拉第常数.
弹性自由能能量密度
$ {f_{{\text{els}}}}\left( {\xi , u} \right) $ 表示为其中,
$\varepsilon _{ij}^{\text{E}} = \varepsilon _{ij}^{\text{T}}{\lambda _i}h\left( \xi \right){\delta _{ij}}$ 表示弹性应变张量,$\varepsilon _{ij}^{\text{T}}$ 为总应变, λi为Vegard应变系数,$ h\left( \xi \right) = {\xi ^3}( 6{\xi ^2} - 15\xi + 10 ) $ 为插值函数. Cijkl为局部弹性张量, 单一物质可表示为对于锂金属和固态电解质的复合材料, 局部弹性张量也可写为
对锂金属和固态电解质的弹性模量和泊松比进行复合计算, 可得有效弹性模量
$ {E^{{\text{eff}}}} = {E^{\text{e}}}h\left( \xi \right) + {E^{\text{s}}}\left[ {1 - h\left( \xi \right)} \right] $ , 有效泊松比为${v^{{\text{eff}}}} = {v^{\text{e}}}h\left( \xi \right) + {v^{\text{s}}}[ 1 - h\left( \xi \right) ]$ . 其中Ee, ve分别表示锂金属的弹性模量和泊松比, Es, vs分别表示电解质的弹性模量和泊松比, δilδjk为克罗内克函数.用相场描述锂枝晶沉积过程时[24,25], 可通过非守恒变量方程来描述锂电极/电解质界面的相场演化方程, 可表示为
其中, Li为动力学系数, F1为吉布斯自由能. Γ为电化学反应引起的电化学沉积速率, 可由Butler-Volmer方程求得
其中, i0为与反应有关的常数, n1为参与反应的电子数, a1为对称因子, ηa为活化过电位.
联立(8)式和(9)式可得电化学反应驱动的序参量演化方程, 即锂枝晶的控制方程:
其中, Lσ为界面迁移率, Lη为反应常数.
电解质中Li+的扩散可用Nernst-Planck方程表示[15]:
其中,
${D^{{\text{eff}}}} = {D^{\text{e}}}h\left( \xi \right) + {D^{\text{s}}}\left[ {1 - h\left( \xi \right)} \right]$ 为有效扩散系数,${D^{\text{e}}}, {D^{\text{s}}}$ 分别为电极和电解质的扩散系数, K = 0.025为金属锂的点密度.对于电势分布, 假设系统中的电荷为中性, 则电流密度可用泊松方程描述, 由源项IR组成, 表示由于电化学反应离开或进入的电荷:
其中,
$ {\sigma ^{{\text{eff}}}} = {\sigma ^{\text{e}}}h\left( \xi \right) + {\sigma ^{\text{s}}}\left[ {1 - h\left( \xi \right)} \right] $ 为有效电导率.${\sigma ^{\text{e}}}, {\sigma ^{\text{s}}}$ 分别为电极和电解质的电导率. ρs为金属锂的点密度, IR只出现在系统偏离平衡状态时.锂电池体系内部呈力学平衡状态, 可表示为
其中,
$\varepsilon _{kl}^{\text{T}}$ 表示总应变,${\lambda _i}h\left( \xi \right){\delta _{ij}}$ 表示锂离子插入时化学层面产生的膨胀所导致的局部本征应变, 弹性应变张量$\varepsilon _{kl}^{\text{T}}$ 为总应变和局部应变之差. 静水压力、主压力和von Mises应力被用来可视化应力的演变[16,26]. -
温度通过控制Li+在电解质中的扩散速率来影响锂枝晶在电极上的生长情况. 为了探讨电池内部产热对锂枝晶生长过程的影响, 有必要对温度随时间和坐标的变化情况进行研究[17]. 电池的温度变化通常是由电池内部的热量产生和周围环境的热量传递引起的, 因此, 温度控制方程为
其中, Cp为单位体积比热容, ρ为质量密度, 二者取值与电极、电解质的特征相关. Ra为有效导热率, Re和Rs分别为电极和电解质溶液中的导热系数. Q为内部热生成率, 包括可逆热和不可逆热. 与不可逆热相比[27], 可逆热的影响可以忽略不计. 因此, 不可逆热占内部产热率的主导地位, 表示为
其中, qohmic为离子电阻产生的焦耳热, qover为过电位产生的焦耳热. De为电极中Li+的扩散系数, Ds为电解质中Li+的扩散系数, 通过扩散系数将温度与锂枝晶的生长联系起来, 实现了温度场与相场模型的耦合. Doyle等[28]通过假设电极颗粒为球形来估计电极单位体积的比表面积as. φe, φs分别为电极和电解质的静电电位. Uj为开路电位, 可视为常数, j为电流密度.
首先对系统施加初始条件T = T0, 其中T0为环境温度. 在每个时间步长中, 辐射边界条件更新并应用于系统的外边界, 温度控制方程可表示为
其中, nx和ny表示边界处外法向量的两个方向余弦值, h = 10 W/(m2·K)为对流换热系数. 定义初始温度T0 = 298 K.
${\varepsilon _{\text{R}}} = 0.49$ , σR = 5.67$ \times $ 10–8 W/(m2·K4)分别为辐射率和斯蒂芬-玻尔兹曼常数(Stefan-Boltzmann constant). -
由于传热模型与相场模型的耦合依赖于确定锂离子扩散系数与温度之间的相关性. 因此, 可以通过锂离子的扩散系数与温度场的耦合关系来实现:
其中, pe = 2.582
$ \times $ 10–9 m2/s和ED分别表示与温度无关的前置指数和活化能[29], b = 2.735$ \times $ 103 mol/m3为实验数据的拟合因子.电池内部的温度分布主要受外部环境及其产热和散热条件的影响. 温度通过影响离子传递、反应动力学和原子扩散显著影响锂枝晶的形成和生长. 为了耦合热效应, 可采用Arrhenius方程来量化温度敏感参数X (X = D, Lη). Hong和Viswanathan [18]提供了基于反应动力学更详细的热方程, 并对传热方程进行补充. 结合Zhang等[30]的研究, 可以得到:
其中, XT与
${X_{{T_{{\text{ref}}}}}}$ 分别表示温度T与参考温度Tref时的温度敏感参数值. Ea, X是对应参数X的活化能. 为了更准确分析温度对锂枝晶的影响, 本文引入锂离子扩散势垒${E_{{\text{a}}, D_{{\text{Li}}}^{+}}}$ 与电化学反应势垒${E_{{\text{a}}, {L_{\mathrm{η}} }}}$ . -
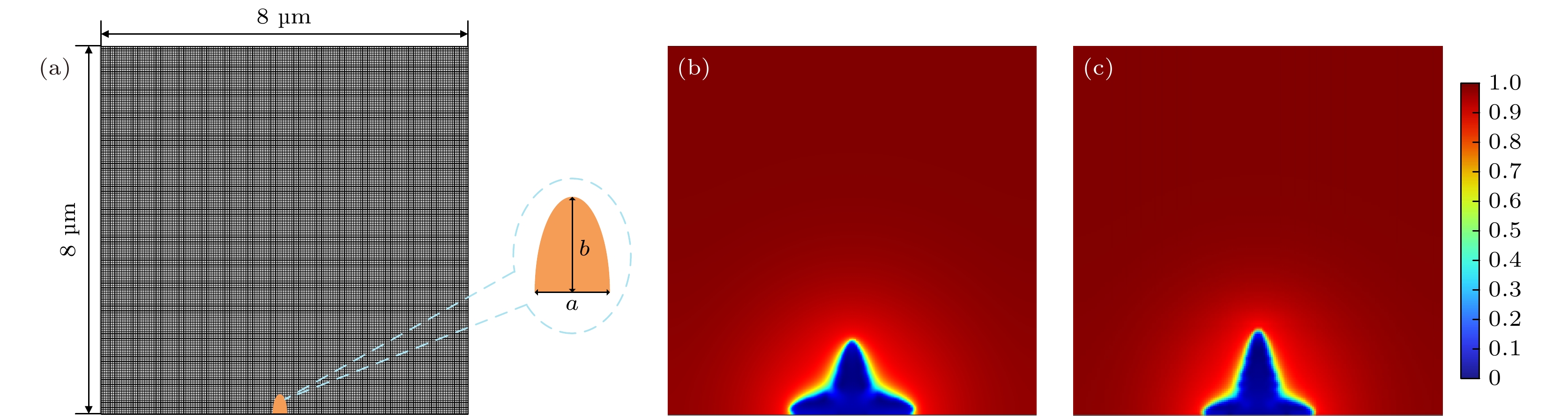
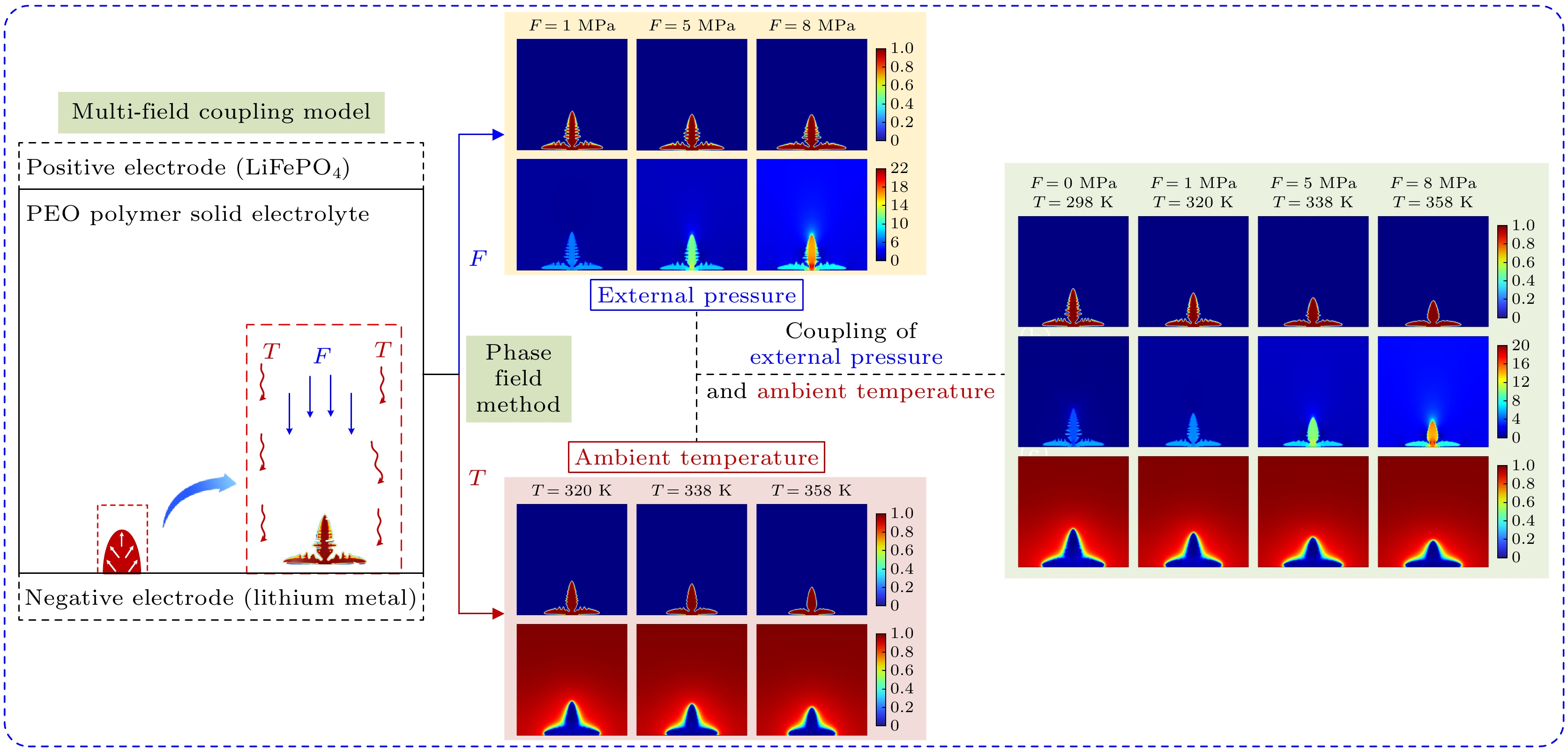
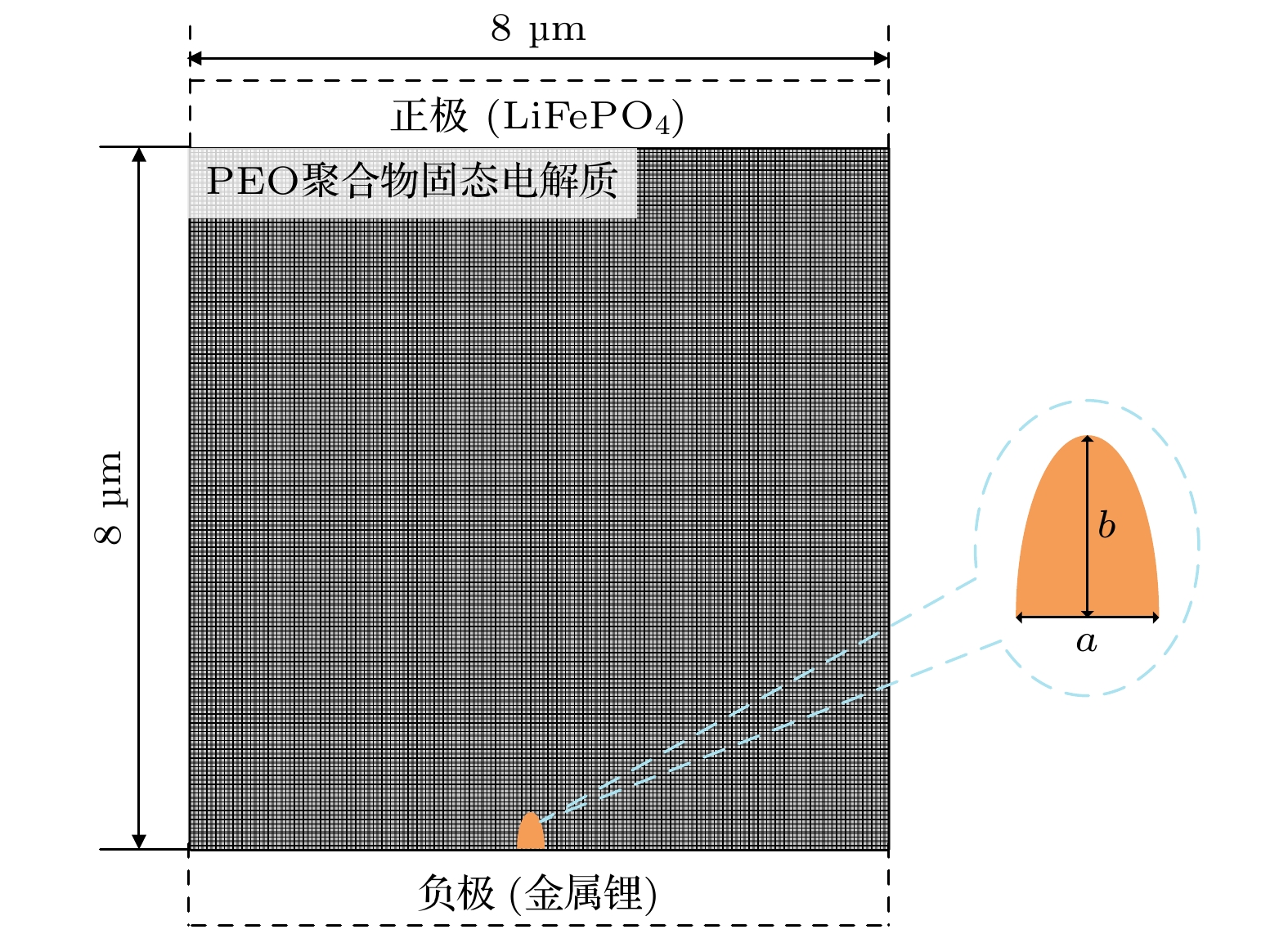
采用COMSOL Multiphysics软件建立非线性相场模型来模拟微米级锂枝晶的生长. 考虑到固态锂电池的锂枝晶生长属于局部变化, 相对于整个电池的几何尺寸很小, 因此构建8 μm×8 μm的二维正方形电解质模型来模拟锂枝晶向电解质中的生长过程及复杂的物理和化学变化, 如图1所示, 下侧为金属锂负极, 上侧为LiFePO4正极, 中间为聚氧化乙烯(PEO)聚合物固态电解质. 电解质上侧的初始锂离子浓度为c0, 在上侧施加0.1 V的电压, 下侧不施加电压, 可以通过空间电荷效应诱导锂枝晶形成, 锂离子会由于电势差从正极向负极沉积, 这会导致金属锂负极表面局部空间电荷累积, 形成较强的电场, 诱导锂离子形核生长, 假设初始单点形核形状为半椭圆状, 短轴和长轴的一半分别为a和b. 相场初始值、锂离子浓度初始值和电压初始值都设置为阶跃函数. 相场初始值为
$ \text{step1}\left( {x^2}/{0.2}+ {y^2}/{1.2}\right) $ ; 锂离子浓度初始值为$ \left[1-\text{step1}\left({x^2}/{0.2} + {y^2}/{1.2}\right)\right]\cdot c_0 $ ; 电压初始值为$ \left[1-\text{step1}\left({x^2}/{0.2} + {y^2}/{1.2}\right)\right]\cdot0.1 $ . 此外, 对称性和规则性网格有利于数值计算上更高效, 有助于结果的观察和分析. 在选择偏微分方程模块, 网格选用自定义的自由四边形网格, 其中最大单元格大小设置为0.05 μm, 最小单元格大小设置为0.005 μm, 最大单元格生长速率和曲率因子设置为1.3和0.3, 窄区分辨率设置为1. 求解过程采用隐式的向后差分公式以确保数值解的稳定性和精确性. 设定计算时间为80 s, 时间步长为1 s. 有限元模型采用的相场参数见表1. -
为了验证有限元模型的有效性, 通过建立与Yang等[31]研究相同的有限元模型, 如图2(a)所示, 并与其有限元结果进行对比. 构建8 μm×8 μm的二维正方形模型, 考察锂枝晶的初始成核为单点成核, 形核点设于模型下边界的中心位置, 初始形核设置为椭圆状, 其中b2/a2 = 1.5. 基于锂枝晶生长过程, 当t = 40 s时, 本文得到的锂离子浓度(图2(b))与Yang等[31]得到的锂离子浓度(图2(c))基本一致. 所以, 当前的有限元模型是可以进行锂枝晶生长的模拟计算.
-
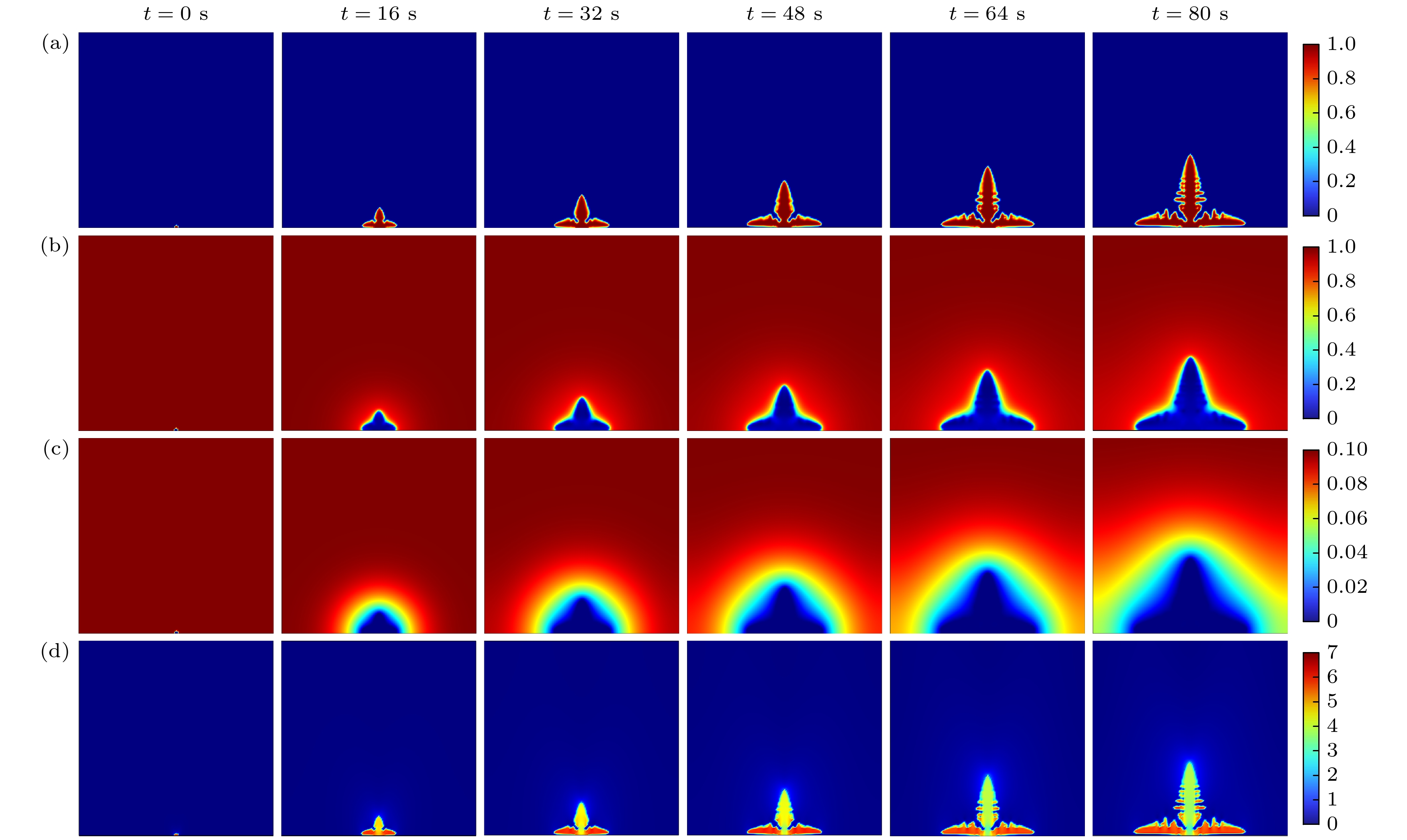
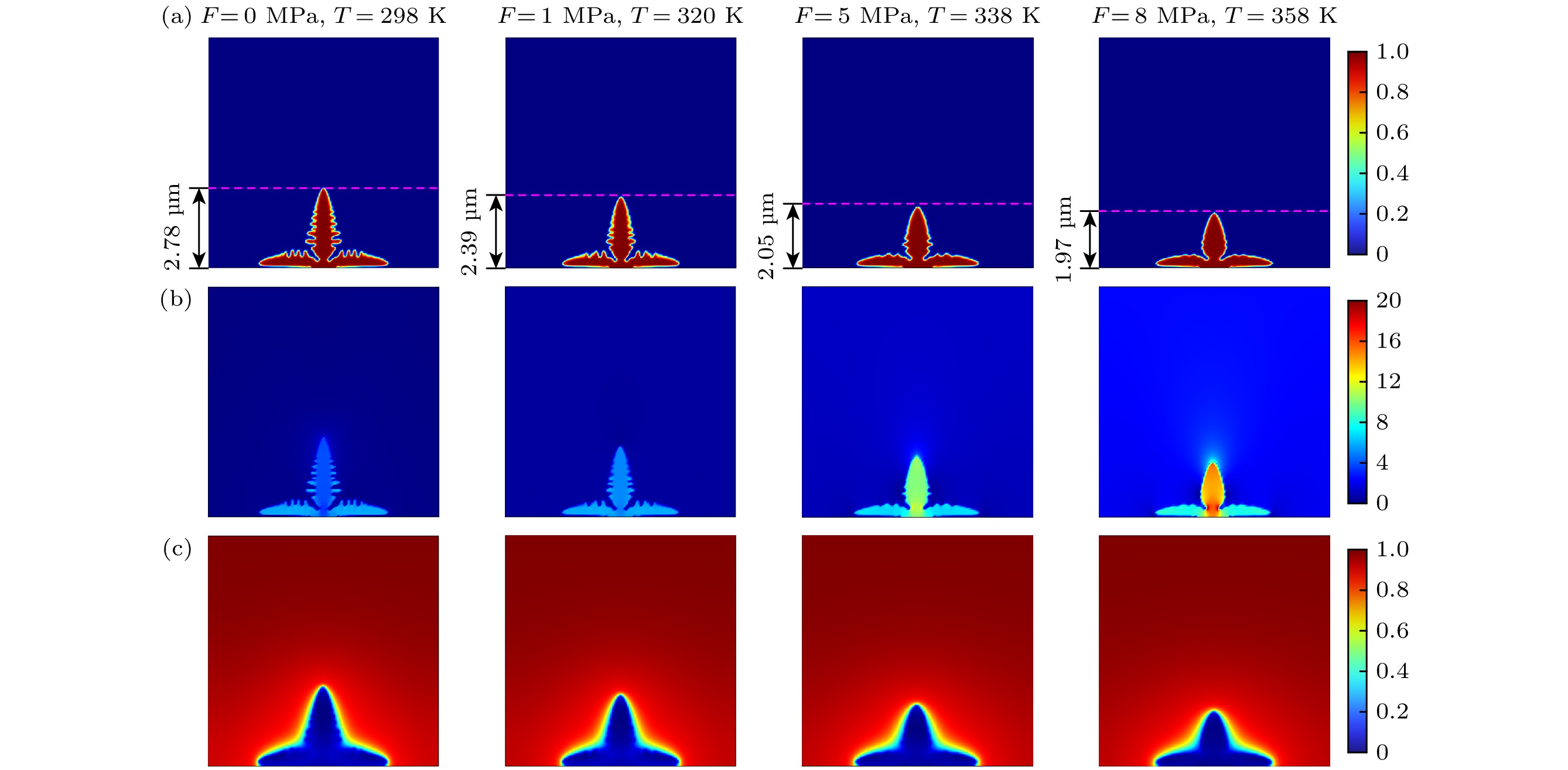
通过在上侧施加0.1 V的电压、下侧不施加电压, 来诱导锂枝晶的形成. 当温度为常温(T = 298 K)以及不施加外力(F = 0 MPa)时, 锂枝晶生长形貌、锂离子浓度、电势分布和von Mises应力分布如图3所示. 在电势差驱动下, 当t = 0 s时, 锂枝晶开始在金属锂负极表面形核, 且在形核尖端造成空间电荷累积形成较强电场, 诱导锂枝晶在固态电解质内部生长. 反过来, 生长的锂枝晶对固态电解质挤压导致内部应力的产生, 固态电解质中的应力引起弹性应变能继续驱动界面反应, 使锂枝晶生长持续演化. 当前研究结果与Chen等[15]、Yang和Wang[31]的研究结论相似. 由图3(a)可以看出, 当锂沉积16 s后, 负极界面出现明显的锂枝晶生长, 并且沿电解质生长, 枝晶呈对称形状生长, 并且在对称轴两侧, 枝晶的生长速率和形态相似. 经过80 s的生长过程后, 锂枝晶逐渐出现明显的侧枝, 侧枝是锂枝晶主干上分支出来的较小结构. 图3(b), (c)分别为相应的锂离子浓度和电势分布. 侧枝的形成可增大锂枝晶表面积并改变电流分布. 锂在电解质中的不均匀分布、局部浓度梯度等原因导致在锂枝晶/电解质界面处有明显的锂离子浓度和电势梯度, 枝晶生长驱动力较大, 锂枝晶生长更快. 另外, 锂枝晶内部(0 V)与固体电解质(0.1 V)之间存在电位差, 也会加快界面处生长速度. 图3(d)为枝晶内部的von Mises应力演化情况, 可以看出von Mises逐渐增大, 在根部与底部分支处尤为集中. 由于电解质的弹性模量较低, 对锂枝晶的抑制作用不强, 应力值越大, 电解质的变形越大.
-
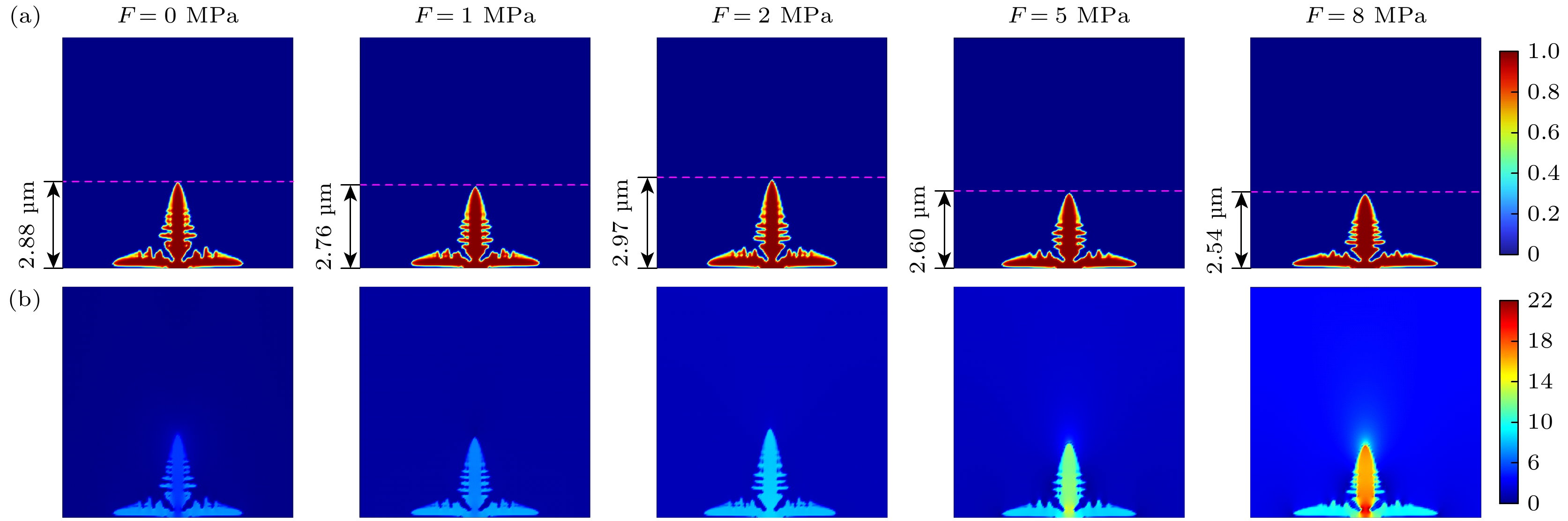
外部压力可以增大电极与电解质的接触面积, 改善界面稳定性, 从而有助于抑制锂枝晶的生长. 而内部应力, 由锂沉积和剥离引起的体积变化, 会通过影响锂离子在电解质界面层中的扩散和电极表面的电化学反应, 进而反过来影响锂沉积和溶解的过程[32]. 为了探讨不同外压力对锂枝晶生长产生的影响, 在模型上边界分别施加不同的外压力1 MPa, 2 MPa, 5 MPa和8 MPa. 图4分别给出了不施加外力(F = 0 MPa)和施加不同外压力时的锂枝晶生长演化结果. 由图4(a)可以看出, 随着外压力的增大, 锂枝晶的纵向生长受到抑制, 而横向扩展趋势逐渐增强, 呈压缩状态. 值得注意的是, 当外力为F = 2 MPa时, 锂枝晶高度b = 2.97 μm, 出现增大的情况, 即较小外压力对锂枝晶的抑制作用不明显, 这与Shen等[16]的研究结果相一致. 此外, 由F = 5 MPa和F = 8 MPa的结果观察到, 锂枝晶的高度发生明显变化, 分别为2.60 μm和2.54 μm, 枝晶主干宽度增大, 侧枝减少. 这种光滑粗实的枝晶可以显著降低比表面积, 提高致密性, 从而为优化锂负极界面稳定性提供了潜在的物理机制. 由图4(b)可以看出, 枝晶主干和根部的应力值相对其他地方较大些, 这种应力集中现象对锂离子在枝晶根部的沉积行为产生抑制, 从而进一步调控枝晶的生长方向. 通过比较不同压力下的应力场分布, 可以看出, 高压力条件下的应力集中度更强, 这是导致枝晶横向扩展增加、纵向生长受限的关键因素. 另外, 根据Yin等[33]的实验研究发现, 外压也会影响锂离子运输速率进而影响电化学反应进程, 使电池的循环性能提高, 具体表现为更均匀的锂溶解和更密集的锂生长. 当外压逐渐增大时, 锂离子的扩散和传输受到一定抑制, 导致枝晶中的锂离子浓度局部减小. 这是因为锂电池的生长依赖于锂离子的不断供应, 当锂离子的扩散和传输受阻时, 锂枝晶的尖端和表面可能无法获得足够的锂离子来支持其持续生长. 即固体电解质发生压缩变形而导致锂离子的传输通道受阻.
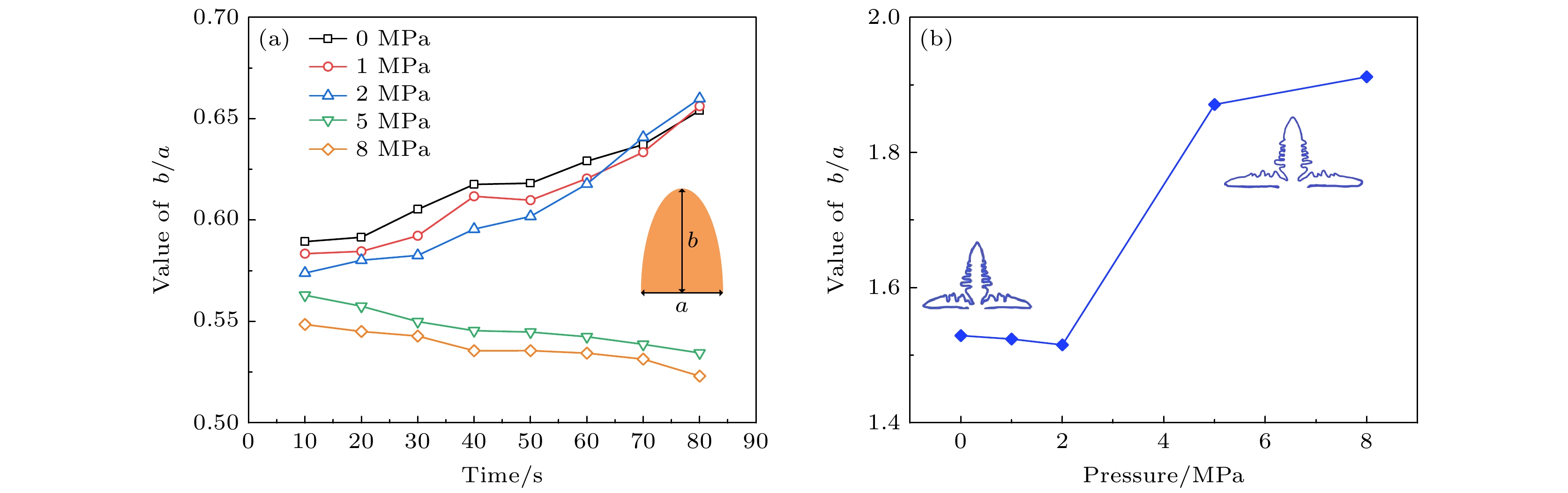
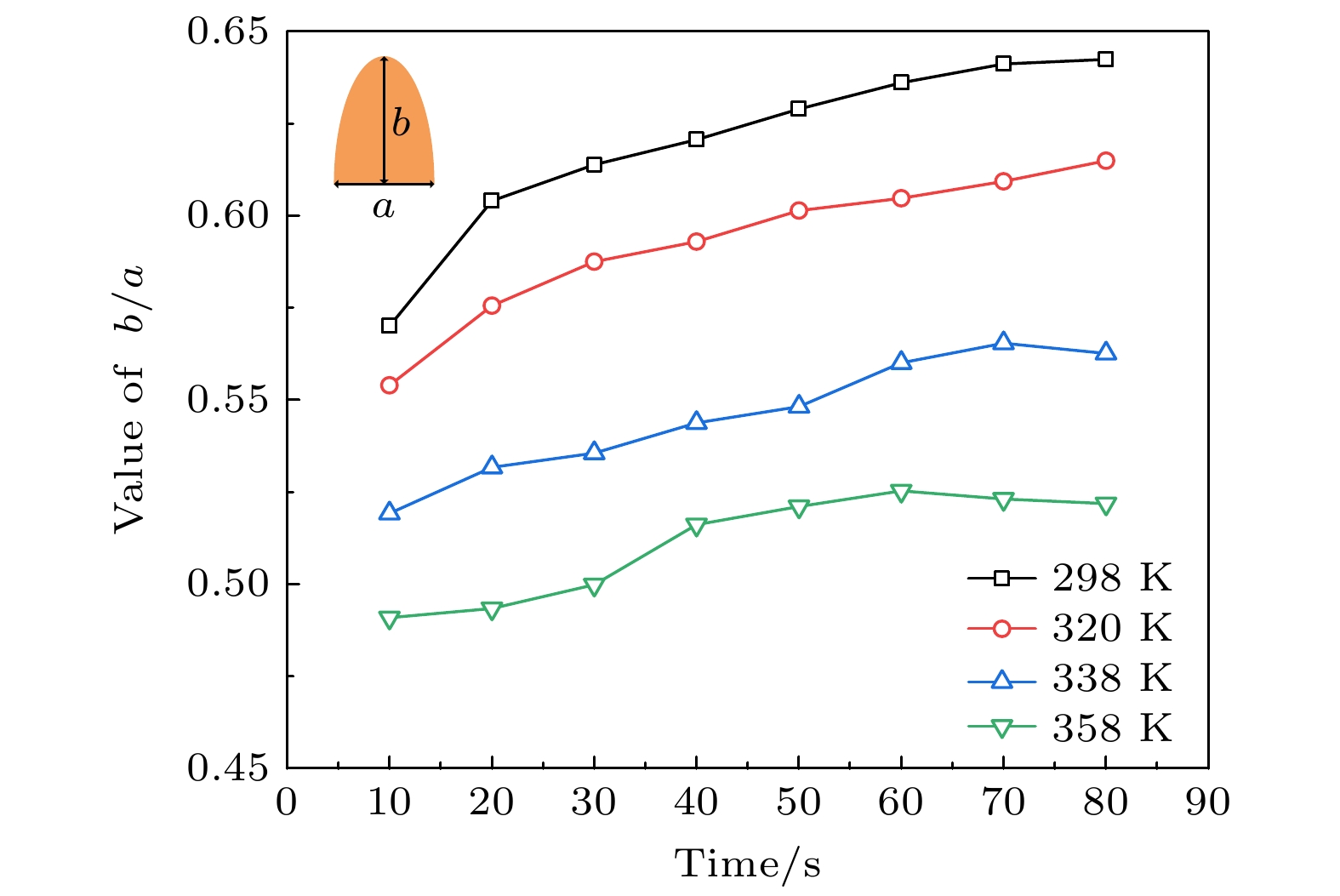
图5(a)为锂枝晶在不同外压力下高度与宽度的比值(b/a)随时间的变化曲线. 可以看到, 当施加较小压力时, 锂枝晶形态未发生明显变化; 但施加较大压力时, 比值随时间延长而减小, 说明枝晶横向生长较大, 纵向生长受抑制更多, 进一步证实了较大压力能够显著改变锂枝晶的形貌演变趋势. 图5(b)为不同外压力下, 锂枝晶宽度与高度的比值(a/b)随不同外压力的变化情况. 当外压力较小时, 对锂枝晶的抑制作用不明显; 当外压力超过2 MPa时, 锂枝晶的生长受到了抑制. 当施加外压增大时, 锂枝晶生长受抑制逐渐明显, 且水平方向生长趋势大于竖直方向. 外压虽有效地抑制了锂枝晶生长, 但也带来材料失效的风险[34]. 当 von Mises 应力超过材料的屈服强度时, 锂枝晶会因为承受不住压力而发生塑性变形或破坏, 导致电解质无法随锂枝晶的剥离而发生回弹, 但本文只讨论理想的弹性应变. 在图4(b)中, 当外力为F = 8 MPa时, 枝晶根部von Mises应力值最大, 因此断裂风险更大. 断裂的锂枝晶会失去与固态电解质的电接触, 无法再参与电化学反应, 从而转变为死锂. 死锂的形成不仅减少了活性锂的数量, 还可能导致电池内部电阻的增加, 进一步降低电池的库仑效率. 一个合理的外部压力范围对锂电池的电化学性能和力学性能产生很好的影响, 外部压力下限可以确保锂金属电池中均匀且稳定的进行锂沉积反应, 而超过外部压力上限, 电池性能则不再对外部压力敏感甚至导致性能退化[32].
-
锂电池在服役过程中涉及到复杂的力-热-电化学耦合变化, 温度对锂枝晶的影响也较复杂. 在已有传热模型的基础上, 考虑反应动力学与温度的耦合有助于从微观角度方面深度分析离子传输和电化学反应速率之间的相互作用与温度的关系. 图6给出了结合扩散势垒和电化学势垒时, 在298 K, 320 K, 338 K和358 K四种环境温度下锂枝晶形貌与锂离子浓度变化. 图6(a)可以看到, 在338 K和358 K的高环境温度下, 枝晶高度明显比在298 K和320 K时低, 并且生长速度受到抑制, 但枝晶主干的宽度略有增大. 图6(b)中电解质到枝晶尖端处的锂离子浓度缓慢下降, 枝晶与电解质界面处的浓度梯度减小, 这与乔东格等[35]、Hong和Viswanathan[18]的研究结果相似, 这种变化可以归因于温度升高增强了锂离子的迁移能力, 降低了局部浓度梯度. 高温对锂枝晶形貌的影响可以从多方面解释. 首先, 温度的升高提高了锂离子的扩散系数和电化学反应速率, 从而促进了锂离子的均匀沉积, 使成核密度降低而核径增大[36]. 其次, 温度升高导致电解质材料的稳定性下降, 因此对锂枝晶的生长产生一定的抑制作用. 当环境温度达到358 K时, 温度的升高对锂枝晶生长的抑制作用更加明显. 锂枝晶主茎上几乎没有侧分支, 枝晶表面也趋于光滑. 高温还可能引起电解质与锂枝晶之间的界面反应加剧, 导致界面能增加, 抑制锂枝晶的侧枝生长[17]. 图7为不同环境温度下, 锂枝晶高度与宽度的比值(b/a)随时间的变化. 可以看出, 比值随着时间的延长而增大, 随着温度的升高而减小. 这表明高温条件下枝晶的横向生长相较于纵向生长更为显著, 使其形貌趋于宽而矮的结构特征.
-
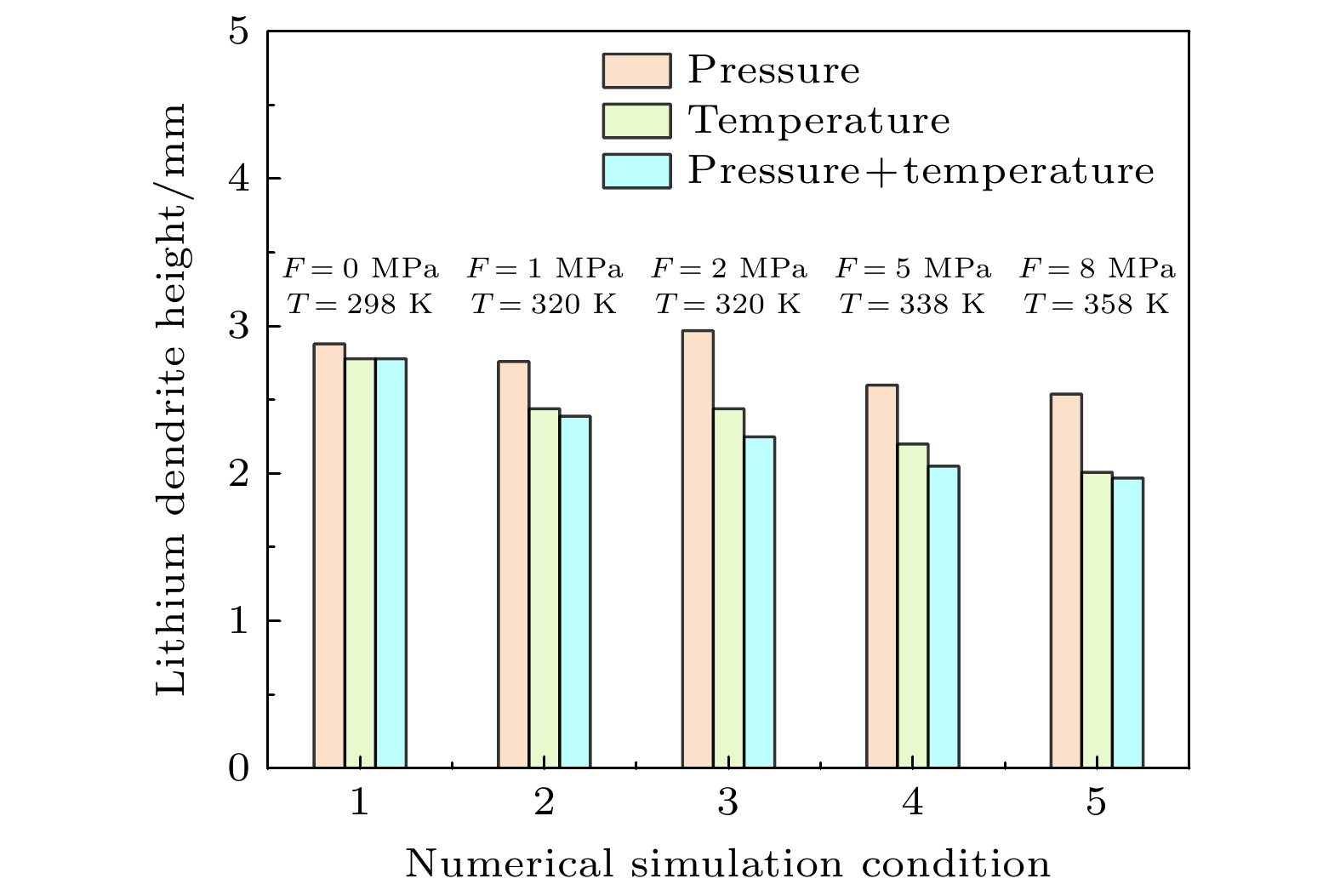
为了考察环境温度和外压力对抑制锂枝晶生长的协同作用, 图8给出了不同环境温度和外压力耦合作用下锂枝晶生长演化结果. 由图8(a)可以观察到, 当两个条件耦合作用时, 固态电解质中对锂枝晶的抑制相较于单一条件作用下更明显. 施加在竖直方向的较大外力F = 8 MPa和较高温度T = 358 K的共同作用明显抑制了锂枝晶的垂直生长趋势, 锂枝晶向水平方向生长, 进而呈现出明显的尖锥状. 由图8(b)可以看出, von Mises应力集中发生在枝晶根部和主干, 有利于形成平坦和密集的锂沉积, 这是由于枝晶生长首先对固态电解质挤压造成了局部应力集中. 施加的压力使得整个枝晶结构受到机械压缩, 由于体积较大且为整个枝晶承载力的中心, 压力会优先传递到主干区域. 在锂枝晶尖端, 由于曲率较高的尖锐形状产生了明显的“尖端效应”, 导致应力集中现象更加显著, 在枝晶的尖端有较高的锂离子浓度累积(图8(c)). 特别在高压力(F = 8 MPa)与高温(T = 358 K)的情况下, 根部与主干的von Mises应力值更大, 枝晶尖端处的锂离子浓度累积更集中. 图9给出了在外压、环境温度以及这两种条件耦合作用下锂枝晶生长高度对比. 与单一条件下的结果相比, 锂枝晶生长在受到两种条件影响下, 枝晶生长整体呈现出更强的抑制效应, 并且不呈线性变化. 在von Mises应力分布中, 将耦合条件下(图8(b))与只施加外压力下的应力值(图4(b))相比, 耦合条件下的最大von Mises应力为20 MPa, 小于只施加外压力下的应力值22 MPa. 这是由于温度的升高也会抑制枝晶生长, 而部分抵消了由外压力引起的应力集中, 耦合条件下的应力更多的向宽度方向分散. 由于温度与电化学势垒更多使枝晶的整体尺寸变小, 因此水平方向上部分抵消了压力导致的横向生长. 耦合条件下的枝晶高度小于只施加外压力下的枝晶高度, 表明温度和压力的耦合作用对抑制锂枝晶生长具有显著的协同效应, 但也有一定的竞争效应.
-
本文通过建立相场模型, 模拟了固态电解质锂电池中锂枝晶的生长过程. 调整外部载荷与温度数值, 以观察不同外压力与环境温度对锂枝晶的影响. 研究了环境温度、外压力以及该两种条件耦合作用下的锂枝晶生长形态以及演化规律.
1)随着外压力的增大, 锂枝晶生长受到抑制. 较高的外压力会导致电极材料的应力集中区域减少, 从而使得锂离子在电极表面的沉积更加均匀, 有助于减少锂枝晶的形成. 随着外压力的增大, 锂枝晶的形态也会发生变化. 锂枝晶由“针状”转变为短粗形态, 表面区域光滑, 致密性更高. 而这种形态变化有利于减少锂枝晶的表面积和界面能, 从而进一步抑制其生长. 因此, 较高的外压力有利于促进固态电解质电池中均匀的电沉积, 从而抑制锂枝晶的生长. 粗的锂枝晶结构在力学上更加稳定, 不容易因外界因素而断裂或脱落, 从而提高了电池的稳定性和安全性. 此外, 枝晶根部的von Mises应力相较来说更大些, 出现应力集中现象, 进一步影响枝晶的生长方向. 但也需关注材料可承受的最大应力与屈服强度, 避免应力值大的地方出现枝晶断裂而形成死锂.
2)在研究环境温度对锂枝晶生长时, 将传热模型与扩散系数和反应常数相关联, 可从更微观的角度去分析热效应对锂枝晶生长的影响. 在电化学反应势垒大于扩散势垒时, 随着环境温度的升高, 锂枝晶尺寸逐渐减小, 其生长速度受到抑制. 而且, 锂枝晶主茎上的侧枝逐渐减少, 表面趋于光滑. 高温环境下, 电解质材料的稳定性严重下降, 导致锂枝晶的生长受到极大的抑制. 较高的环境温度会提高锂离子的扩散率, 即锂离子在电解质中的传输速度更快, 从而降低界面上的锂离子浓度差. 还会引起电解质与枝晶界面处的反应加剧, 提高界面能, 这对锂枝晶的生长起到了一定的抑制作用.
3)单一因素(温度或外压力)对锂枝晶生长均表现出一定的抑制作用, 但当两者耦合作用时, 枝晶的生长形态可能变得更加复杂和难以预测. 这表明, 在研究锂枝晶生长时, 需要对多物理场的耦合作用进行更加全面和系统的分析. 然而, 从整体趋势来看, 较高的外压力与较高的环境温度对锂枝晶生长仍具有显著的抑制效果. 具体表现为枝晶的水平生长占主导, 相较于纵向生长趋势有所减弱, 同时枝晶形状呈现出更明显的压缩状态. 这种形貌变化有助于形成更加平坦且致密的锂沉积层, 为优化固态锂电池的性能提供了有利条件.
本文采用弹性力学模型对锂枝晶生长中的应力分布进行模拟, 并使用von Mises应力作为评价指标. 然而, von Mises应力的定义通常用于描述材料的屈服行为, 因此特别指出, 本研究未考虑锂金属和固态电解质的塑性行为, 仅基于弹性假设分析了不同条件下的应力集中效应. 在实际应用中, 锂金属在高应力区域可能表现出明显的塑性变形或蠕变, 而温度升高可能进一步改变其屈服行为和弹性模量. 因此, 未来研究可在现有模型基础上引入塑性力学行为, 通过结合弹性和塑性本构关系, 利用实验验证, 以更全面地描述压力对锂枝晶的生长影响作用与应力分布.
基于力-热-电化学耦合下固态锂电池枝晶生长的相场模拟
Phase field simulation of dendrite growth in solid-state lithium batteries based on mechaincal-thermo-electrochemical coupling
-
摘要: 固态电解质锂电池具有能量密度大、循环稳定性强、机械强度高、不易燃、安全性高、使用寿命长等优点, 广泛应用于航空航天、新能源汽车和移动设备等领域. 但是在锂电池的电极/电解质界面处存在的锂枝晶生长问题一直是制约其性能提升和安全应用的关键因素, 锂枝晶在电解质中生长不仅会降低电池的库仑效率, 而且可能刺穿电解质导致电池内部正负极短路. 本文针对固态锂电池中的锂枝晶生长问题, 基于相场理论进行数值模拟研究, 建立了耦合应力场、热场和电化学场的锂枝晶生长相场模型, 研究了环境温度、外压力以及该两种条件耦合作用下的锂枝晶生长形态以及演化规律. 研究结果表明, 在较高温度和较大外应力作用下, 锂枝晶生长缓慢, 侧枝数量减少, 表面更光滑, 电沉积较为均匀. 施加外压越大时, 锂枝晶纵向生长受到抑制, 呈压缩状态, 致密度更高, 但机械不稳定性也会增强; 环境温度越高, 锂离子的扩散速率和反应速率越大, 锂枝晶生长速率和大小也受到抑制, 且二者耦合作用对枝晶生长有明显的抑制效果, 应力集中在根部, 使得枝晶更侧重于横向生长, 有利于形成平坦和密集的锂沉积.Abstract: Solid-state lithium batteries possess numerous advantages, such as high energy density, excellent cycle stability, superior mechanical strength, non-flammability, enhanced safety, and extended service life. These characteristics make them highly suitable for applications in aerospace, new energy vehicles, and portable electronic devices. However, the growth of lithium dendrite at the electrode/electrolyte interface remains a critical challenge, limiting both performance and safety. The growth of lithium dendrites in the electrolyte not only reduces the Coulombic efficiency of the battery but also poses a risk of puncturing the electrolyte, leading to internal short circuits between the anode and cathode. This study is to solve the problem of lithium dendrite growth in solid-state lithium batteries by employing phase-field theory for numerical simulations. A phase-field model is developed by coupling the mechanical stress field, thermal field, and electrochemical field, to investigate the morphology and evolution of lithium dendrites under the condition of different ambient temperatures, external pressures, and their combined effects. The results indicate that higher temperature and greater external pressure significantly suppress lithium dendrite growth, leading to fewer side branches, smoother surfaces, and more uniform electrochemical deposition. Increased external pressure inhibits longitudinal dendrite growth, resulting in a compressed morphology with higher compactness, but at the cost of increased mechanical instability. Similarly, elevated ambient temperature enhances lithium-ion diffusion and reaction rate, which further suppress dendrite growth rate and size. The combined effect of temperature and pressure exhibits a pronounced inhibitory influence on dendrite growth, with stress concentrating at the dendrite roots. This stress distribution promotes lateral growth, facilitating the formation of flatter and denser lithium deposits.
-

-
图 2 有限元结果验证 (a) 有限元网格与初始形核点位置设置; (b) 当t = 40 s时当前模型的锂离子浓度; (c) 当t = 40 s时Yang等[31]得到的锂离子浓度
Figure 2. Verification of finite element results: (a) Setting of finite element mesh and initial nucleation point; (b) lithium-ion concentration (mol/m3) of current model when t = 40 s; (c) lithium-ion concentration (mol/m3) morphology obtained by Yang et al. [31] when t = 40 s.
图 5 不同外压力下锂枝晶生长趋势结果 (a) 锂枝晶高度与宽度的比值(b/a)随时间的变化; (b) 锂枝晶宽度与高度的比值(a/b)随压力的变化
Figure 5. Results of lithium dendrite growth trend under different external pressures: (a) The ratio of height to width (b/a) of lithium dendrite changes with time; (b) the ratio of width to height (a/b) of lithium dendrite changes with pressure.
图 8 不同环境温度和外压力耦合作用下锂枝晶生长演化结果 (a) 锂枝晶生长形貌; (b) von Mises应力分布(MPa); (c) 锂离子浓度(mol/m3)
Figure 8. Evolution results of lithium dendrite growth under coupling of external pressure and ambient temperature: (a) Growth morphology of lithium dendrites; (b) von Mises stress (MPa); (c) lithium-ion concentration (mol/m3).
参数名 参数符号 数值 参数名 参数符号 数值 界面迁移率 Lσ/(m3·J–1·s–1) 1×10–6 化学反应常数 Lη/s–1 0.5 各向异性强度 δ 0.05 各项异性模数 ω 4 电极扩散系数 De/(m2·s–1) 1.7×10–15 电解质扩散系数 Ds/(m2·s–1) 2×10–15 电极电导率 σe/(S·m–1) 1×107 电解质电导率 σs/(S·m–1) 0.1 电荷转移系数 α 0.5 势垒高度 W/(J·m–3) 105 电解质初始浓度 c0/(mol·m–3) 1000 电极初始浓度 cs/(mol·m–3) 7.69×104 梯度能量系数 k/(J·m–1) 1×10–10 电极杨氏模量 Ee/GPa 7.8 电解质杨氏模量 Es/GPa 1 电极泊松比 Ve 0.42 电解质泊松比 Vs 0.3 电极比热容 Cpe/(J·kg–1·K–1) 1200 Vegard 应变系数 λi –0.866×10–3 电解质比热容 Cps/(J·kg–1·K–1) 133 –0.773×10–3 电极导热系数 Re/(W·m–1·K–1) 1.04 –0.529×10–3 电解质导热系数 Rs/(W·m–1·K–1) 0.45 扩散势垒 ${E_{{\text{a}}, D_{{\text{Li}}}^{+}}}$ /eV0.34 电化学反应势垒 ${E_{{\text{a}}, {L_{\mathrm{η}}}}}$ /eV0.3 -
[1] Goodenough J B, Singh P 2015 J. Electrochem. Soc. 162 A2387 doi: 10.1149/2.0021514jes [2] Peters B K, Rodriguez K X, Reisberg S H, Beil S B, Hickey D P, Y Kawamata, Collins M, Starr J, Chen L, Udyavara S, Klunder K, Gorey T J, Anderson S L, Neurock M, Minteer S D, Baran P S 2019 Science. 363 838 doi: 10.1126/science.aav5606 [3] 耿晓彬, 李顶根, 徐波 2023 物理学报 72 220201 doi: 10.7498/aps.72.20230824 Geng X B, Li D G, Xu B 2023 Acta Phys. Sin. 72 220201 doi: 10.7498/aps.72.20230824 [4] Viswanathan V, Epstein A H, Chiang Y M, Esther T, Bradley M, Langford J, Winter M 2022 Nature. 601 519 doi: 10.1038/s41586-021-04139-1 [5] Lee M J, Han J, Lee K, Lee Y J, Kim B G, Jung K N, Kim B J, Lee S W 2022 Nature. 601 217 doi: 10.1038/s41586-021-04209-4 [6] Hao F, Verma A, Mukherjee P P 2018 J. Mater. Chem. A 6 19664 doi: 10.1039/C8TA07997H [7] Liu Z, Qi Y, Lin Y X, Chen L, Lu P, Chen L Q 2016 J. Electrochem. Soc. 163 A592 doi: 10.1149/2.0151605jes [8] 张更, 王巧, 沙立婷, 李亚捷, 王达, 施思齐 2020 物理学报 69 226401 doi: 10.7498/aps.69.20201411 Zhang G, Wang Q, Sha L T, Li Y J, Wang D, Shi S Q 2020 Acta Phys. Sin. 69 226401 doi: 10.7498/aps.69.20201411 [9] Sripad S, Viswanathan V 2017 Electrochem. Soc. 164 E3635 doi: 10.1149/2.0671711jes [10] Sripad S, Viswanathan V 2017 ACS Energy Lett. 2 1669 doi: 10.1021/acsenergylett.7b00432 [11] Guttenberg M, Sripad S, Viswanathan V 2017 ACS Energy Lett. 2 2642 doi: 10.1021/acsenergylett.7b01022 [12] Guyer J E, Boettinger W J, Warren J A, McFadden G B 2004 Phys. Rev. E 69 021603 doi: 10.1103/PhysRevE.69.021603 [13] Kobayashi R 1993 Physica D 63 410 doi: 10.1016/0167-2789(93)90120-P [14] Liang L Y, Qi Y, Xue F, Bhattacharya S, Harris S J, Chen L Q 2012 Phys. Rev. E 86 051609 doi: 10.1103/PhysRevE.86.051609 [15] Chen L, Zhang H W, Liang L Y, Liu Z, Qi Y, Lu P, Chen J, Chen L Q 2015 J. Power Sources 300 376 doi: 10.1016/j.jpowsour.2015.09.055 [16] Shen X, Zhang R, Shi P, Chen X, Zhang Q 2021 Adv. Energy Mater. 11 2003416 doi: 10.1002/aenm.202003416 [17] Yan H H, Bie Y H, Cui X Y, Xiong G P, Chen L 2018 Energy Convers Manag. 161 193 doi: 10.1016/j.enconman.2018.02.002 [18] Hong Z J, Viswanathan V 2019 ACS Energy Lett. 4 1012 doi: 10.1021/acsenergylett.9b00433 [19] Yurkiv V, Foroozan T, Ramasubramanian A, Shahbazian-Yassar R, Mashayek F 2018 MRS Commun. 8 1285 doi: 10.1557/mrc.2018.146 [20] Qi G Q, Liu X L, Dou R F, Wen Z, Zhou W N, Liu L 2024 J. Energy Storage 101 113899 doi: 10.1016/j.est.2024.113899 [21] Arguello M E, Labanda N A, Calo V M, Gumulya M, Utikar R, Derksen J 2022 J. Energy Storage 53 104892 doi: 10.1016/j.est.2022.104892 [22] Jiang W J, Wang Z H, Hu L Z, Wang Y, Ma Z S 2024 J. Energy Storage 86 111126 doi: 10.1016/j.est.2024.111126 [23] 梁辰, 邢鹏飞, 吴孟武, 秦训鹏 2024 储能科学与技术 1125 2095 doi: 10.19799/j.cnki.2095-4239.2024.1125 Liang C, Xing P F, Wu M W, Qin X P 2024 Energy Storage Sci. Techn. 1125 2095 doi: 10.19799/j.cnki.2095-4239.2024.1125 [24] Cahn J W, Allen S M 1977 J. Phys. IV 38 C7 doi: 10.1051/jphyscol:1977709 [25] Allen S M, Cahn J W 1979 Acta Metall. 27 1085 doi: 10.1016/0001-6160(79)90196-2 [26] 梁宇皓, 范丽珍 2020 物理学报 69 226201 doi: 10.7498/aps.69.20200713 Liang Y H, Fan L Z 2020 Acta Phys. Sin. 69 226201 doi: 10.7498/aps.69.20200713 [27] Wu W, Xiao X, Huang X S 2012 Electrochim. Acta 83 227 doi: 10.1016/j.electacta.2012.07.081 [28] Doyle M, Newman J, Góźdź A S, Schmutz C, Tarascon J M 1996 J. Electrochem. Soc. 143 1890 doi: 10.1149/1.1836921 [29] Stewart S G, Newman J 2008 J. Electrochem. Soc. 155 F13 doi: 10.1149/1.2801378 [30] Zhang Y X, Li Y F, Shen W J, Li K, Lin Y X 2023 ACS Appl. Energy Mater. 6 1933 doi: 10.1021/acsaem.2c03864 [31] Yang H D, Wang Z J 2023 J. Solid State Electr. 27 2607 doi: 10.1007/s10008-023-05560-4 [32] 崔锦, 石川, 赵金保 2021 化工学报 72 3511 doi: 10.11949/0438-1157.20210145 Cui J, Shi C, Zhao J B 2021 CIESC J. 72 3511 doi: 10.11949/0438-1157.20210145 [33] Yin X S, Tang W, Jung I D, Phua K C, Adams S., Lee S W, Zheng G W 2018 Nano Energy 50 659 doi: 10.1016/j.nanoen.2018.06.003 [34] 王其钰, 王朔, 周格, 张杰男, 郑杰允, 禹习谦, 李泓 2018 物理学报 67 128501 doi: 10.7498/aps.67.128501 Wang Q Y, Wang S, Zhou G, Zhang J N, Zheng J Y, Yu X Q, Li H 2018 Acta Phys. Sin. 67 128501 doi: 10.7498/aps.67.128501 [35] 乔东格, 刘训良, 温治, 豆瑞峰, 周文宁 2022 储能科学与技术 11 1008 doi: 10.19799/j.cnki.2095-4239.2021.0629 Qiao D G, Liu X L, Wen Z, Dou R F, Zhou W N 2022 ESST 11 1008 doi: 10.19799/j.cnki.2095-4239.2021.0629 [36] Yan K, Wang J Y, Zhao S Q, Zhou D, Sun B, Cui Y, Wang G X 2019 Angew Chem. Int. Edit. 58 11364 doi: 10.1002/anie.201905251 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: