大尺寸精密测距技术在科学研究、航空航天和工业生产等领域具有重要应用价值. 光频梳凭借其短脉冲、宽光谱、多纵模及频率稳定可溯源等特性, 为解决传统激光测距中大量程与高精度的矛盾提供了创新方案. 因此, 基于光频梳的大尺寸绝对测距技术已成为当前激光测距领域的研究热点.

光频梳在时域上为飞秒量级脉宽的超短脉冲光, 在频域上为数百万条等间隔光谱线, 使其在绝对测距领域具有超强的优势, 近年来国内外学者围绕光频梳测距技术开展了深入研究^[1–5]. 在时域内, 飞行时间法通过脉冲互相关实现大尺寸测距, 但需要机械扫描位移平台或激光器腔长导致测量效率受限^[6–9]. 双光频梳测距技术通过互相关信号实现无盲区测距且无需机械扫描, 提高了测量速度, 但双光源系统导致成本较高^[10–13]. 在频域内, 合成波长法通过参考光和测量光的相位差获取被测距离的粗测值和精测值, 经过测量值合成实现大范围高精度测距, 但构建多尺度合成波长链导致其测量系统相对复杂且成本较高^[14–16]. 光谱干涉法利用光谱仪采样频域干涉信号, 再通过傅里叶变换或小波变换解析相位, 系统简单但受限于商用光谱仪频率分辨力的限制导致其非模糊范围较小^[17–19]. 为了扩展光谱干涉测距的非模糊范围, 可以采用VIPA光谱仪进行采样但价格较为昂贵; 结合高速光电探测器的啁啾脉冲频域干涉法也是一种有效方法, 但需搭配额外的高精度光纤延迟线以消除测量盲区; 另外, 选用高重复频率的微腔孤子光频梳作为光源同样可以消除测量盲区, 但是其超高重复频率难以精确测量和控制, 对使用环境提出了较高要求^[20–24].

因此, 鉴于工业现场及室外环境等应用场景的需求, 研究一种系统简单、量程大、精度高的任意长绝对测距技术显得尤为重要. 本文提出了一种基于光频梳的多脉冲光谱干涉绝对测距方法, 构建了相应的数学模型, 仅对多脉冲光谱干涉信号进行一次傅里叶变换, 即可利用伪时域同步确定测量光路的群折射率和被测长度; 进一步利用微调重复频率和差分计算的方法, 可将测距范围由传统光谱干涉测距的非模糊范围拓展至任意长度. 针对所提出的方法进行了大量的数值模拟分析, 结果表明, 本文提出的多脉冲光谱干涉测距方法能够实现大量程、高精度绝对测距.

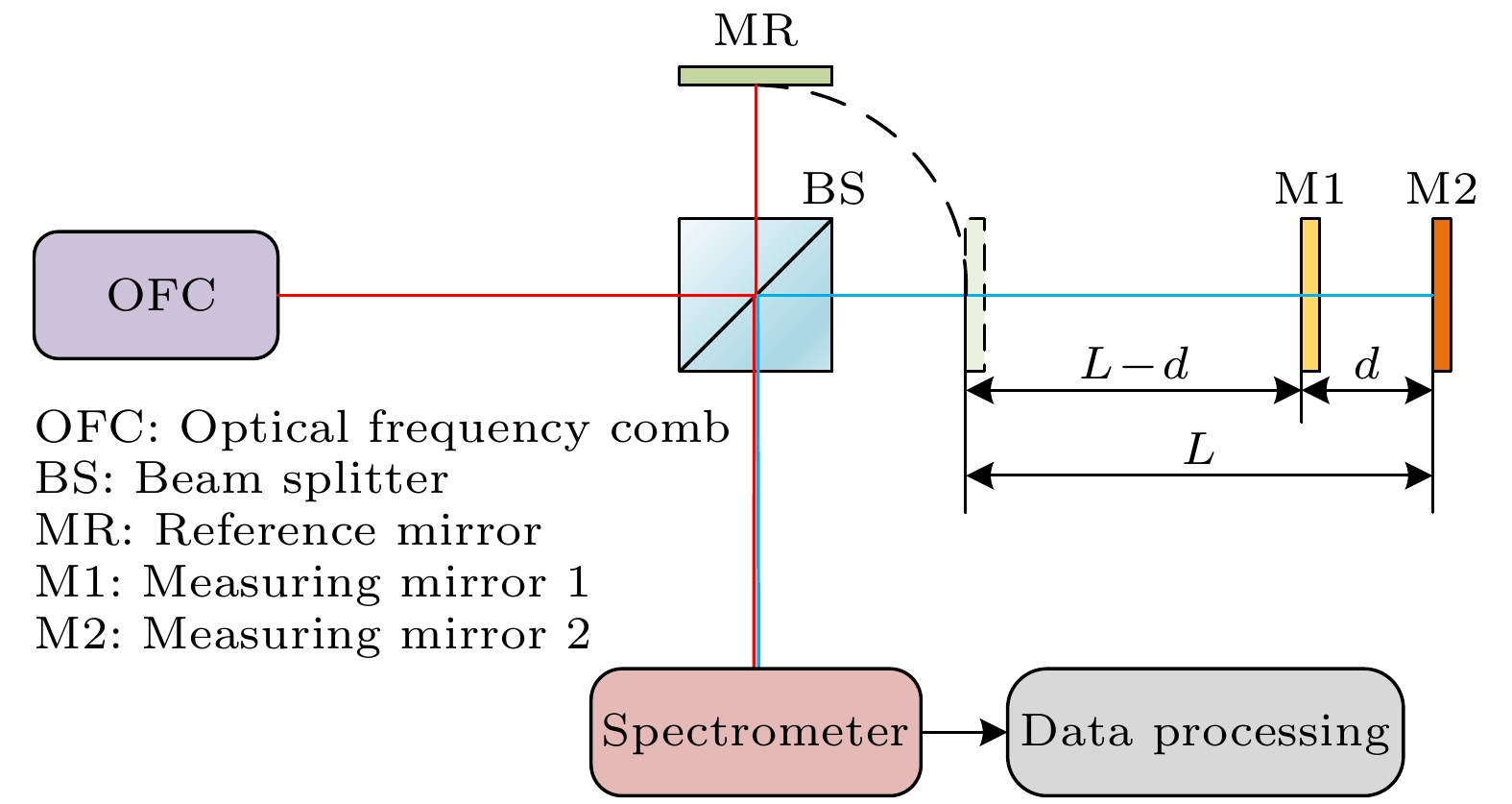
光频梳具有宽光谱且频率稳定的优势, 其包含的众多纵模能够相互干涉, 相比于其他测距方式, 光谱干涉测距系统简单且精度高, 展现出一定的优势. 因此, 本文设计了基于多脉冲光谱干涉的测距系统, 如图1所示. 利用光频梳OFC作为测距光源, 其发出的一系列脉冲光在分束器BS处被分为两束光, 一束进入参考臂被参考镜MR反射, 作为参考光, 另一束进入测量臂分别被两个测量镜反射, 作为两个测量光, 其中测量镜M1为半反半透镜, 测量镜M2和参考镜MR都为平面镜, 两个测量镜之间的距离为d, 被测绝对距离为L.

由于两个测量脉冲的光程不同, 因此各自的光谱会分别携带与距离相关的相位信息. 假设光频梳的光谱为理想高斯光谱, 记为$ E(\omega ) $, 则参考光、测量光1、测量光2的光谱可分别表示为$ \alpha E(\omega ) $, $ {\beta _1}E(\omega )\exp ( - {\text{i}}\omega {\tau _1}) $和$ {\beta _2}E(\omega )\exp ( - {\text{i}}\omega {\tau _2}) $. 其中, $ \alpha $, $ {\beta _1} $和$ {\beta _2} $分别为参考脉冲和两个测量脉冲的功率因子, $ {\tau _1} $和$ {\tau _2} $分别为两个测量脉冲相对于参考脉冲的时间延迟, 表示为

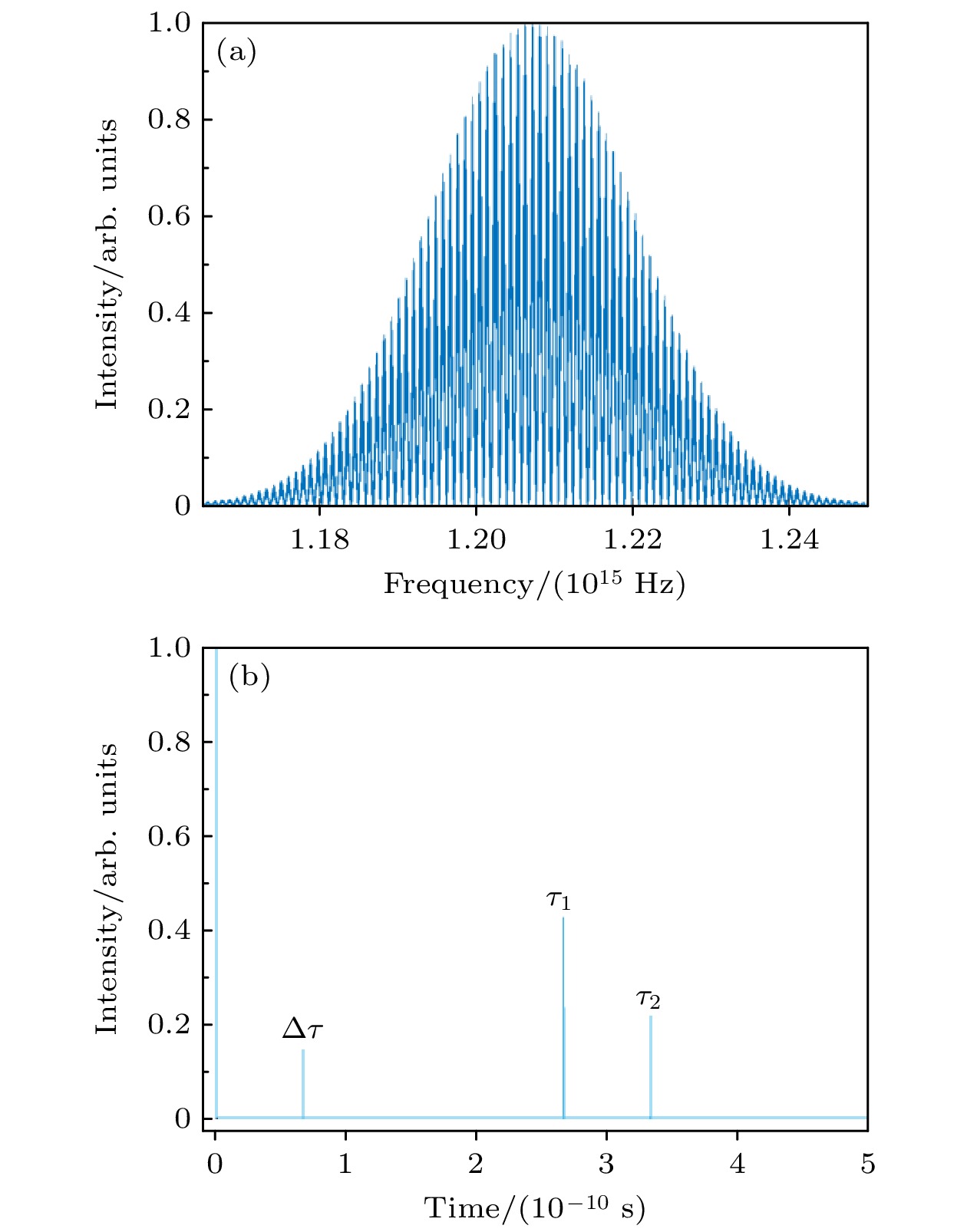
式中, $ {n_{\text{g}}} $为群折射率, $ c $为真空中光速.

参考光与两束测量光会在频域内同时发生光谱干涉, 因此由光谱仪记录到的信号为多脉冲光谱干涉条纹如图2(a)所示, 可表示为

式中, $ \Delta \tau $表示两个测量脉冲之间的时间延迟, 其与两个测量镜之间的距离d有关, 即$ \Delta \tau = {\tau _2} - {\tau _1} = 2{n_{\text{g}}}d{\text{/}}c $.

由(3)式可见, 多脉冲光谱干涉信号包含直流项和交流项两部分, 其中直流项为光谱干涉信号的背景项, 而交流项与时间延迟$ {\tau _1} $和$ {\tau _2} $有关. 对光谱干涉信号进行傅里叶变换可得到伪时域谱, 表示为

由(4)式可知, 伪时域谱的右侧(即t > 0时)共包含3个脉冲, 分别对应${\tau _1}$, ${\tau _2}$和$\Delta \tau $, 其强度依次为$ 2\alpha {\beta _1} $, $ 2\alpha {\beta _2} $和$ 2{\beta _1}{\beta _2} $, 只需保证$\alpha \ne {\beta _1} \ne {\beta _2}$, 即可通过峰值大小区分出${\tau _1}$, ${\tau _2}$, $\Delta \tau $的具体位置, 如图2(b)所示.

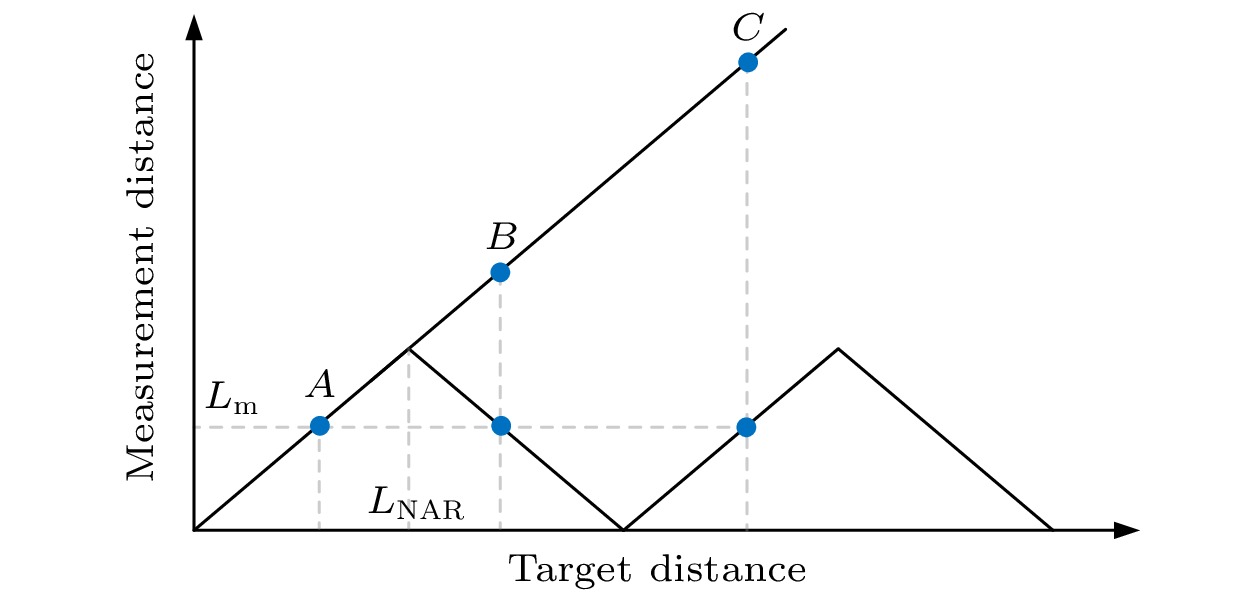
理论上将${\tau _2}$代入(2)式即可得到被测距离L, 但是由于光频梳在时域内为周期性脉冲, 被测距离的变化导致了参考脉冲和测量脉冲的前后相对位置变化, 因此利用光谱干涉测距时, 被测距离L与非模糊范围$ {L_{{\text{NAR}}}} $之间的关系呈周期性变化, 如图3所示. 光谱干涉测距的非模糊范围为

式中, $ {l_{{\text{pp}}}} $为脉冲间距, $ {f_{\text{r}}} $为重复频率.

当被测距离较小时, 即$L \lt {L_{{\text{NAR}}}}$时, 如图3中的A点, 此时未出现混叠, 被测距离为${L_{\text{m}}} = c{\tau _2}{\text{/}}{n_{\text{g}}}$. 随着被测距离L逐渐增大, 如图3中的B点和C点, 此时测量发生混叠, 但光谱干涉信号对应的光程差与实际值之间仍有直接关系. 最终被测距离L可表示为

其中, L为被测距离, $ {L_{\text{m}}} $为伪时域法测距结果, N为整数. 根据以上分析, 被测距离L通过N, $ {L_{{\text{NAR}}}} $和$ {L_{\text{m}}} $三个分量被拓展为任意长绝对距离. 由(6)式可见, 被测距离L包含小数和整数两部分, 小数部分为$ {L_{\text{m}}} $或$ {L_{{\text{NAR}}}} - {L_{\text{m}}} $, 整数部分为$ N \cdot {L_{{\text{NAR}}}} $, 需要确定N值, 可以通过微调光频梳的重复频率由${f_{\text{r}}}$变为$f_{\text{r}}'$, 当小数部分处于图3中的递增阶段时, 被测距离可以表示为

通过差分方式计算可得整数N的表达式为

同理, 当小数部分处于图3中的递减阶段时, 整数N的表达式为

另外, 本文采用两束测量光同时与参考光在频域内进行干涉, 其优点在于两束测量光共用同一个测量光路, 对于单次测量来说, 在忽略测量光路不均匀性的情况下可认为两束测量光都是在相同介质中传输的, 其在测量光路中的传输速度是一致的, 对应相同的群折射率$ {n_{\text{g}}} $. 合理选择两个测量镜之间的距离d作为参考间距并进行标定, 即可获得真空中两个测量脉冲之间的参考时间延迟$\Delta {\tau _0} = 2 d/c$, 对比$\Delta {\tau _0}$和$\Delta \tau $可以直接计算出实际测量光路的群折射率$ {n_{\text{g}}} $, 即

综上所述, 通过测量群折射率$ {n_{\text{g}}} $, 整数N和时间延迟${\tau _2}$, 即可由(6)式计算出被测距离L.

假设光频梳在真空中的中心波长为1560 nm, 脉宽90 fs, 对应的理想高斯光谱的半高宽为4.9 THz, 重复频率为5 GHz, 初始频率偏移为0, 采样点数为10⁶, 采样率为重复频率, 温度为20 ℃, 湿度为50%, 大气压为101.325 kPa, 二氧化碳的体积分数为4.5×10^–4.

由(6)式可以看出, 被测距离L由N, ${L_{{\text{NAR}}}}$和$ {L_{\text{m}}} $组成, 其中${L_{{\text{NAR}}}}$和$ {L_{\text{m}}} $都与群折射率$ {n_{\text{g}}} $有关, 可见群折射率$ {n_{\text{g}}} $直接影响到被测距离L的测量精度, 有必要对本文方法中群折射率$ {n_{\text{g}}} $的测量精度进行分析. 由(10)式可知, 群折射率$ {n_{\text{g}}} $与两个测量镜之间的参考间距d有关, 因此在标准大气环境条件下, 以0.01 m的间隔改变参考间距d的大小, 对群折射率$ {n_{\text{g}}} $的测量结果进行模拟. 模拟时假设重复频率${f_{\text{r}}} = 5 \;{\text{GHz}}$, 对应的非模糊范围${L_{{\text{NAR}}}}$近似等于0.03 m, 此时伪时域谱横轴对应的最大值为1/(2×5×10⁹) = 10^–10 s, 在参考间距d大于非模糊范围${L_{{\text{NAR}}}}$时, 利用伪时域谱求得两个测量脉冲之间的时间延迟$\Delta \tau $会发生混叠, 其与实际的时间延迟之间同样存在直接联系, 实际时间延迟的计算公式如下:

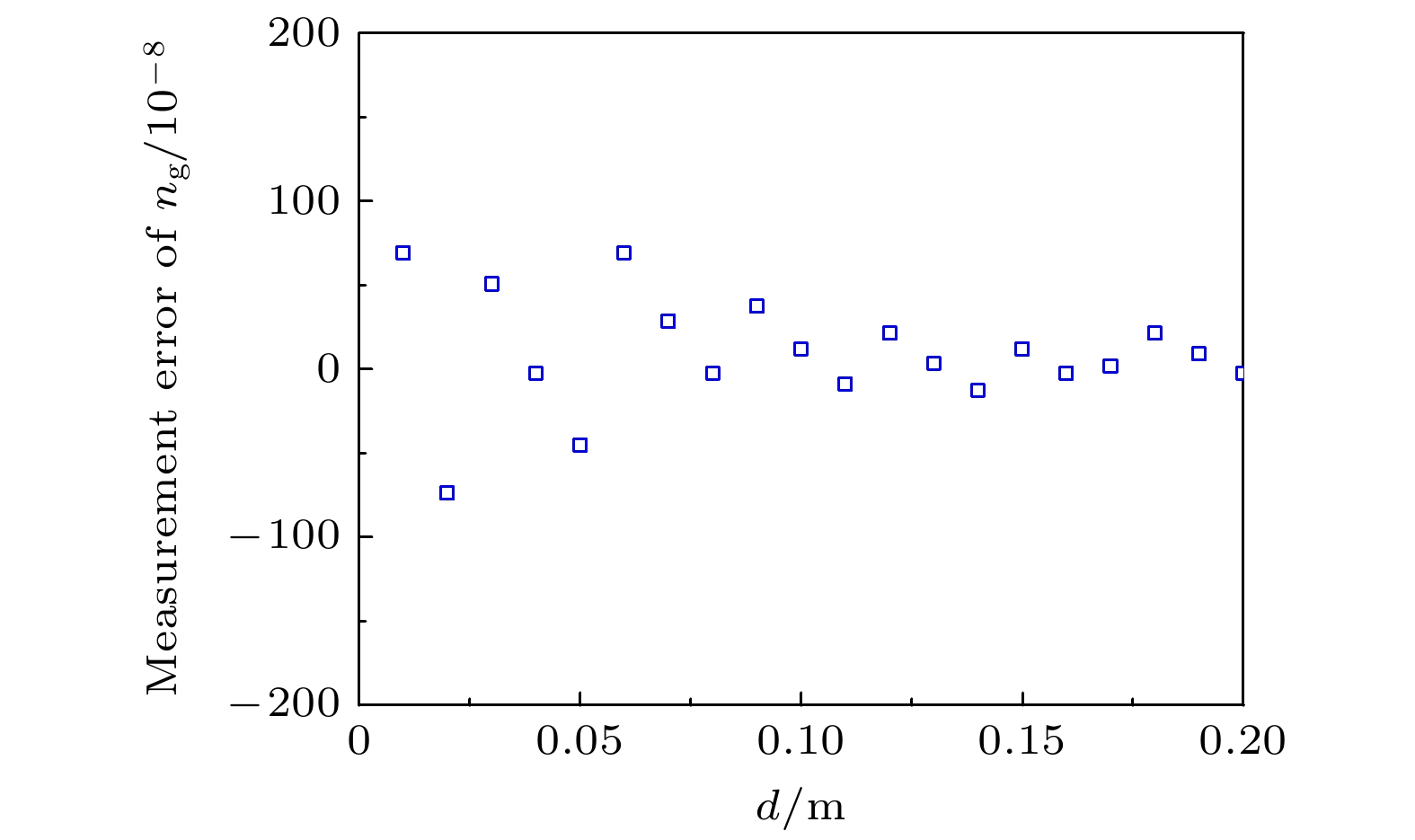
式中, $ \Delta \tau ' $和$ \Delta \tau $分别表示两个测量脉冲之间实际的时间延迟和在伪时域中的时间延迟, m为自然数, 由参考间距d和$ {L_{{\text{NAR}}}}/2 $的比值向下取整即可获得. 最终, 将$ \Delta \tau ' $代入(10)式就可以计算出实际测量光路中的群折射率$ {n_{\text{g}}} $.

结果如图4所示, 随着参考间距d的增大, 群折射率的测量误差逐渐收敛, 当d≥0.1 m时, 群折射率测量的绝对误差可以稳定在±0.21×10^–6以内, 当d = 0.12 m时, 群折射率测量的绝对误差最大为0.21×10^–6, 当d = 0.17 m时, 群折射率测量的绝对误差最小为0.02×10^–6, 当d = 0.1 m时, 群折射率测量的绝对误差为0.12×10^–6. 在理想仿真情况下, 影响群折射率测量精度的主要因素是采样点数, 在参考间距d = 0.1 m的情况下, 当采样点为4×10⁶时, 群折射率的测量误差可以达到0.5×10^–8. 因此, 基于多脉冲光谱干涉测量群折射率的方法在理论上具有极高的精度, 局限性在于实际应用中一方面对于光谱仪的性能要求极高, 以确保能够采集到准确的光谱干涉信号, 另一方面对于光谱干涉信号需要进行插值处理, 增加了数据处理的复杂性和计算负担.

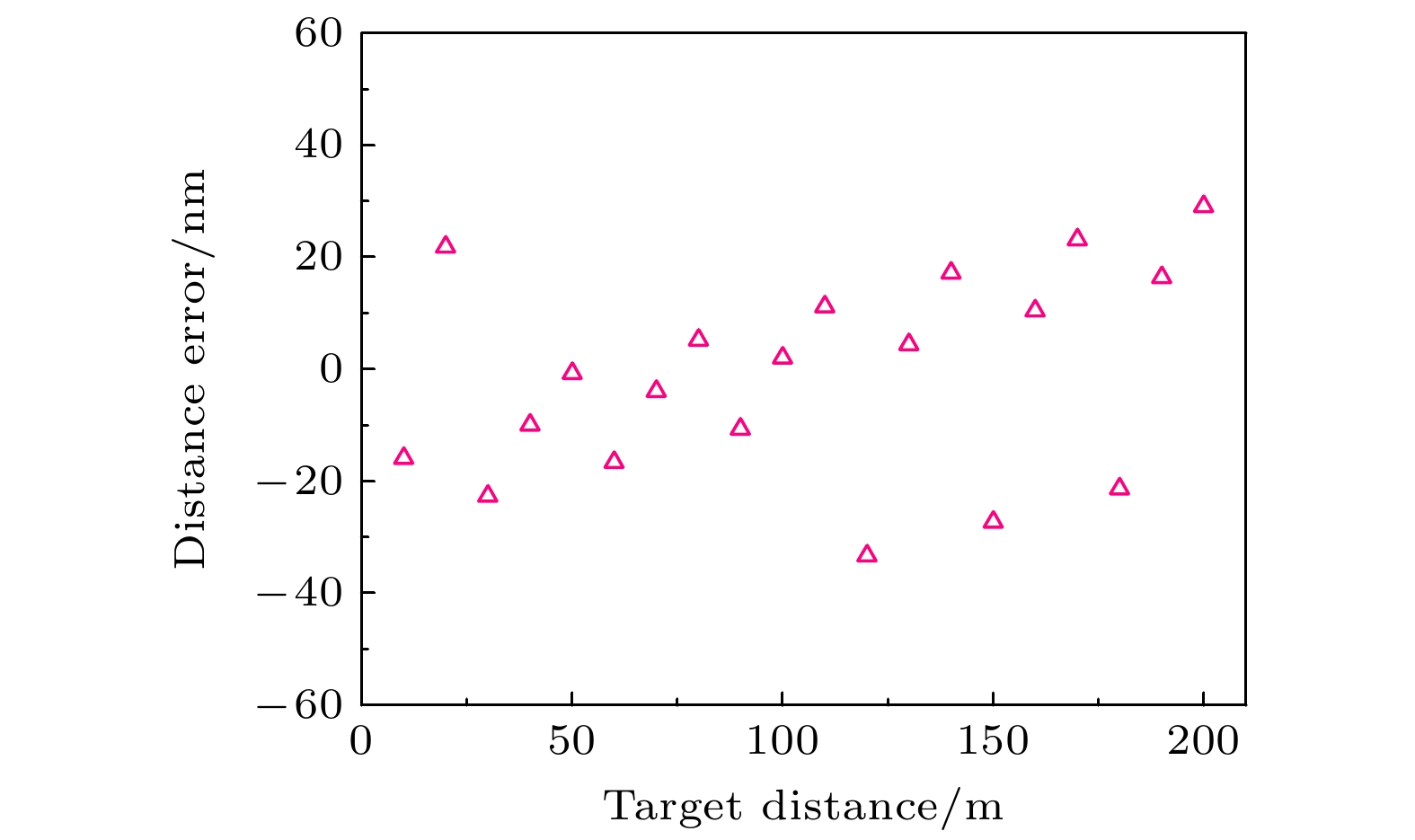
在绝对距离测量中测距精度是关键参数之一, 传统的光谱干涉测距在实验室环境下可实现纳米量级的测距精度, 但是在室外长距离测量情况下空气折射率难以准确测量, 无法保证最终的测距精度. 本文在标准大气条件下对被测距离在0—200 m内的测距精度进行了数值模拟, 仿真分析中取参考间距d = 0.1 m, 采样点数为10⁶, 测距间隔为10 m, 对20个被测距离进行了测距仿真, 模拟结果如图5所示, 被测距离在0—200 m内, 测距误差保持在–33—29 nm之间, 测量误差的PV值为62 nm, 标准偏差为18 nm. 结果表明, 在考虑空气折射率测量不准确的影响下, 当被测距离L = 120 m时, 最大测距误差仅为33 nm, 多脉冲光谱干涉测距在0—200 m大量程内的测距精度可以达到0.1 μm以内.

为了验证本文方法的测距分辨力, 在被测距离L = 100 m时, 每次增大0.1 μm, 移动100次, 对测距结果进行仿真, 仿真结果如图6所示, 在0—10 μm范围内, 测距误差保持在–12—6 nm之间, 测量误差的PV值为18 nm, 标准偏差为7 nm. 结果表明, 多脉冲光谱干涉测距在大量程内的测距分辨力能够达到0.1 μm以内.

由(5)式和(6)式可知, 被测距离L由非模糊范围$ {L_{{\text{NAR}}}} $和伪时域法测距结果$ {L_{\text{m}}} $组成, 并且这两者都与群折射率有关, 在空气中群折射率可以表示为

式中, $ {f_{\text{c}}} $为中心频率, $ n({f_{\text{c}}}) $为中心波长的空气折射率.

在实际应用场景中, 温度、湿度、气压、二氧化碳含量等条件发生改变, 都将影响光频梳各波长的空气折射率, 进而导致群折射率发生变化, 而群折射率的波动是影响大尺寸测距精度的关键因素之一, 因此有必要对本文提出的方法在大气条件变化下的测距精度进行分析.

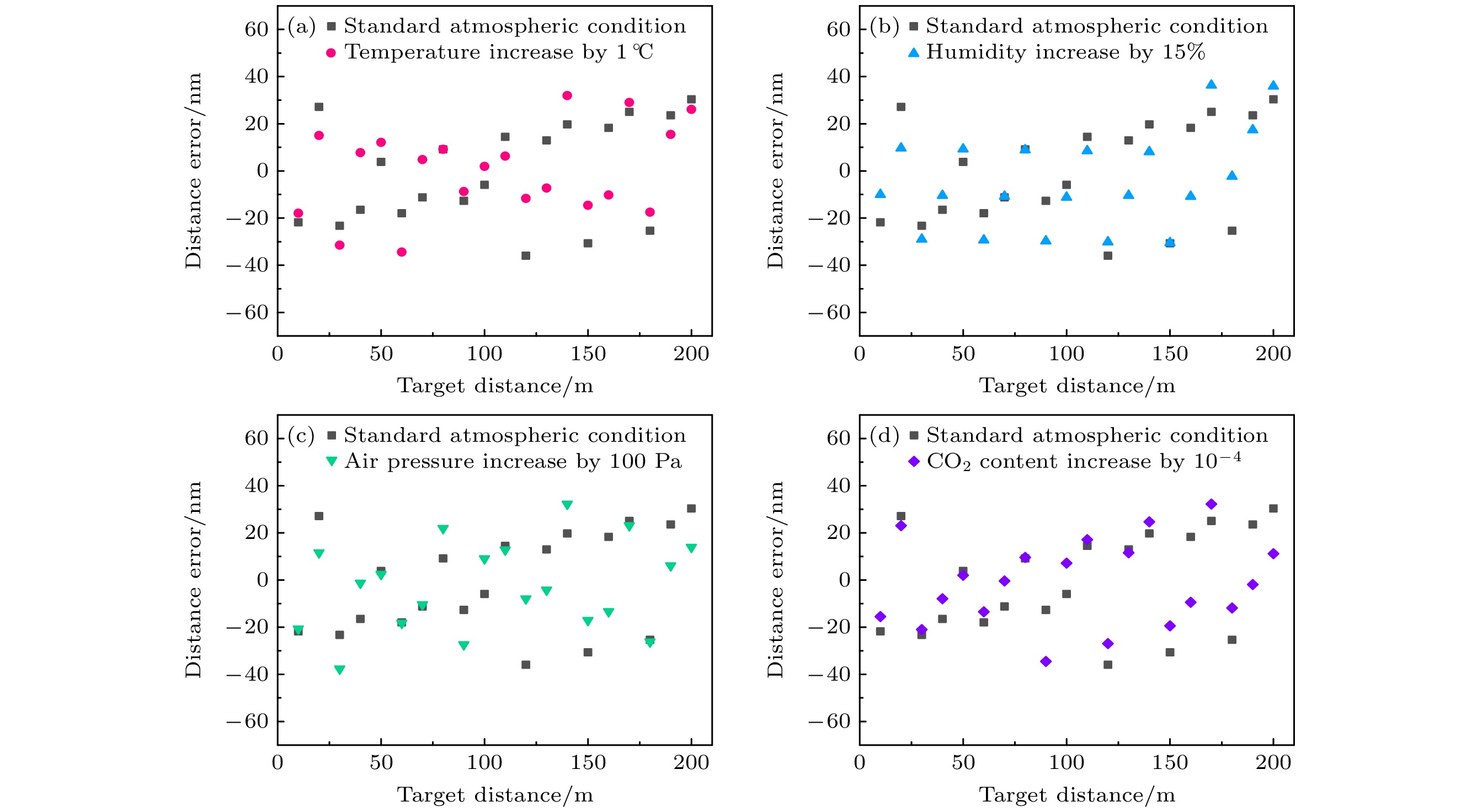
在0—200 m范围内, 以10 m的测量间距进行模拟, 分别将温度提高1 ℃、湿度增加15%、气压提高100 Pa、二氧化碳的体积分数提高10^–4时, 模拟出测距结果并与标准大气环境下的测距结果进行对比, 结果如图7所示.

可以看出, 当被测距离L = 0—200 m时, 标准环境时的测距误差在–33—29 nm之间, 测量误差的PV值为62 nm, 标准偏差为18 nm; 温度提高1 ℃时的测距误差在–34—32 nm之间, 测量误差的PV值为66 nm, 标准偏差为19 nm; 湿度增大15%时的测距误差在–31—36 nm之间, 测量误差的PV值为67 nm, 标准偏差为21 nm; 气压升高100 Pa时的测距误差在–38—32 nm之间, 测量误差的PV值为70 nm, 标准偏差为19 nm; 二氧化碳的体积分数增大10^–4时的测距误差在–35—32 nm之间, 测量误差的PV值为67 nm, 标准偏差为18 nm. 对比以上5种情况, 多脉冲光谱干涉测距由于可以利用伪时域直接测量出测量光路 中的群折射率$ {n_{\text{g}}} $, 并对被测距离L进行修正, 所以温度、湿度、气压、CO₂含量等大气环境条件的改变对于本文测距方法的影响并不大, 在0—200 m的测距范围内其测距误差不超过±40 nm, 依然可以在大量程范围内实现亚微米级的测距精度.

本文提出了一种基于光频梳的多脉冲光谱干涉绝对测距方法, 构建了相应的数学模型, 通过对多脉冲光谱干涉信号进行一次傅里叶变换, 即可同步确定测量光路中的群折射率和被测距离. 通过微调重复频率和差分计算, 可将测距范围从传统光谱干涉测距的非模糊范围拓展至任意长度, 解决了大量程与高精度测距之间的矛盾.

模拟结果表明: 两个测量镜之间的参考间距对于群折射率的测量精度具有重要影响, 当参考间距为0.1 m时, 群折射率测量的绝对误差最大为0.12×10^–6, 另外增加采样点数可以进一步提高群折射率的测量精度. 在考虑空气折射率测量不准确引入测距误差的情况下, 在0—200 m的测量范围内, 测距误差可以保持在–33—29 nm之间. 在大气条件发生改变时, 通过实时修正群折射率波动引入的测距误差, 在0—200 m的测距范围内测距误差不超过±40 nm, 所以温度、湿度、气压、二氧化碳含量等大气环境条件的改变对于测距精度的影响并不大. 理论分析和数值模拟表明, 本文提出的多脉冲光谱干涉测距方法可以实现大量程内亚微米量级的绝对测距.