高级搜索

基于深度学习方法的圆柱绕流实验缺失数据重构

,  ,  ,  , 

downloadPDF

上一篇

下一篇

张帆, 张恒, 李卓越, 文俊, 胡海豹. 基于深度学习方法的圆柱绕流实验缺失数据重构[J]. 物理学报, 2025, 74(7): 074701-1. doi: 10.7498/aps.74.20241689
引用本文: 张帆, 张恒, 李卓越, 文俊, 胡海豹. 基于深度学习方法的圆柱绕流实验缺失数据重构[J]. 物理学报, 2025, 74(7): 074701-1. doi: 10.7498/aps.74.20241689
shu
Fan ZHANG, Heng ZHANG, Zhuoyue LI, Jun WEN, Haibao HU. Reconstruction of gappy data in cylindrical flow experiments based on deep learning method[J]. Acta Physica Sinica, 2025, 74(7): 074701-1. doi: 10.7498/aps.74.20241689
Citation: Fan ZHANG, Heng ZHANG, Zhuoyue LI, Jun WEN, Haibao HU. Reconstruction of gappy data in cylindrical flow experiments based on deep learning method[J]. Acta Physica Sinica, 2025, 74(7): 074701-1. doi: 10.7498/aps.74.20241689
shu

基于深度学习方法的圆柱绕流实验缺失数据重构

  • 1.

    西北工业大学航海学院, 西安　710072

  • 2.

    西北工业大学深圳研究院, 深圳　518063

    • 通讯作者: E-mail: huhaibao@nwpu.edu.cn

  • 中图分类号: 47.15.-x, 47.80.Cb, 07.05.Mh, 47.50.Ef

Reconstruction of gappy data in cylindrical flow experiments based on deep learning method

  • 1.

    School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China

  • 2.

    Shenzhen Research Institute of Northwestern Polytechnical University, Shenzhen 518063, China

    • Corresponding author: E-mail: huhaibao@nwpu.edu.cn

  • MSC: 47.15.-x, 47.80.Cb, 07.05.Mh, 47.50.Ef

  • 摘要: 对流动现象进行精确预测与有效控制的前提在于对流动现象的深入理解, 而实验研究在此过程中提供了宝贵的数据支撑. 粒子图像测速(PIV)技术作为当前流场测量的主流手段之一, 在钝体绕流等复杂流动现象的实验研究中发挥着不可或缺的作用. 然而, 在PIV实验中, 由于光路遮挡等问题的存在, 获取完整且准确的流场数据往往极具挑战性. 鉴于此, 提出了一种基于机器学习的流场数据重构方法, 该方法采用以卷积神经网络为核心的深度学习模型, 旨在解决流场数据中缺失部分的重构问题. 首先探讨了不同缺失区域对数值计算流场重构效果的影响, 并从瞬时流场、速度统计量等多个维度, 对重构流场与真实值之间的差异进行了细致的比较分析. 结果显示, 对于瞬时流场的重构, 最大$ L_2 $误差维持在约0.02的水平. 进一步发现, 当缺失区域在流向方向上的尺寸增大时, 重构的难度也随之显著增加; 而相比之下, 缺失区域在垂直于流向方向上的尺寸变化, 对重构精度的影响则相对有限. 在此基础上, 进一步研究了深度神经网络对噪声的泛化性, 通过在数值计算结果中人为添加噪声来测试网络, 发现重构数据的误差随着噪声等级的提升呈指数型增长趋势. 最终, 将提出的网络模型应用于实际的PIV实验数据中, 从瞬时流场和时间平均结果两个方面进行了验证. 结果表明, 该网络模型不仅能够成功重构缺失位置的速度信息, 还能有效修正回流区部分因测量不准确而产生的数据偏差. 经过神经网络重构的实验结果, 在统计意义上更加接近数值仿真的结果, 这充分说明, 本文提出的模型仅需使用数值计算数据进行训练, 便可以具备重构PIV实验中缺失信息的能力.
    Abstract: The prerequisite for accurate prediction and effective control of flow phenomena lies in the understanding of flow dynamics, and experimental studies provide essential data to support this process. Particle image velocimetry (PIV), as one of the important methods of measuring flow fields, plays a critical role in experimental investigations such as flow passing through a circular cylinder. PIV is a non-contact laser-optical measurement technique, however, it often faces challenges in obtaining complete and accurate flow field data when the optical path is obstructed. Particularly in PIV experiments involving flow passing through a circular cylinder, the presence of the cylinder itself and the supporting structure can significantly obscure the optical path, making it highly challenging to acquire complete PIV data. To solve this problem, we propose a deep learning-based flow field data reconstruction method, in which a deep learning framework centered on convolutional neural networks (CNNs) is used. The method aims to solve the reconstruction problem of gappy regions in flow field data by establishing a mapping relationship between flow fields with gappy regions and complete flow fields. First, the influence of gappy regions with different characteristics on the reconstruction accuracy of numerically simulated flow fields is investigated. The reconstructed flow fields are carefully compared with ground truth data through multi-dimensional assessments of instantaneous flow fields and velocity time statistics. The results indicate that the maximum L2 error between the reconstructed flow field and the ground truth is still about 0.02. Furthermore, it is observed that as the size of the gappy region increases along the flow direction, the difficulty in reconstructing flow field increases significantly. In contrast, changes in the size of the gappy region perpendicular to the flow direction have minimum influence on the accuracy of flow field reconstruction. Additionally, the robustness of the proposed deep neural network against noise is systematically evaluated. When clean numerical simulation data are used for training, test data are generated by artificially introducing varying levels of Gaussian noise to assess the network performance under noisy conditions. The results demonstrate that the error between the reconstructed data and the ground truth increases exponentially as the noise level rises. Finally, the proposed deep neural network model is applied to real PIV experimental data, with the training data remaining clean and numerically simulated. Both instantaneous flow fields and time-averaged statistics are analyzed and compared. The results show that the network model successfully reconstructs velocity information in the missing regions and effectively corrects data errors caused by measurement inaccuracies in the backflow zones. The reconstructed experimental results show closer statistical agreement with numerical simulation data, demonstrating that the model proposed in this work, when trained solely on numerical simulation data, is capable of reconstructing missing physical information in PIV experiments. This method provides a novel approach for addressing the challenge of data reconstructionin PIV experiments.
  • 加载中

  • 图 1  使用深度神经网络模型将圆柱绕流不完整的速度场重构为完整速度场　(a) 有缺失区域的速度场; (b) 本文使用的卷积神经网络模型; (c) 完整的速度场

    Figure 1.  A deep neural network model is used to reconstruct the incomplete velocity field of a flow past a cylinder into the complete one: (a) The velocity field with gappy area; (b) the CNN model used in this work; (c) the complete velocity field.

    下载: 全尺寸图片 幻灯片

    图 2  本文使用的神经网络模型中的Reduction模块

    Figure 2.  Reduction block in the neural network used in this work.

    下载: 全尺寸图片 幻灯片

    图 3  几种不同的数据缺失区域　(a) 无缺失的流场; (b) 缺失区域为$ 60\times 120 $; (c) 缺失区域为$ 60\times 200 $; (d) 缺失区域为$ 80\times 160 $; (e) 缺失区域为$ 100\times 120 $; (f) 缺失区域为$ 100\times 200 $

    Figure 3.  Gappy regions of several different areas: (a) The complete flow filed; (b) gappy region of $ 60\times 120 $; (c) gappy region of $ 60\times 200 $; (d) gappy region of $ 80\times 160 $; (e) gappy region of $ 100\times 120 $; (f) gappy region of $ 100\times 200 $.

    下载: 全尺寸图片 幻灯片

    图 4  不同的缺失区域对于训练误差收敛的影响

    Figure 4.  The influence of gappy regions on training loss convergence.

    下载: 全尺寸图片 幻灯片

    图 5  不同缺失区域的速度重构瞬时流场对比

    Figure 5.  The instantaneous reconstruction flow fields of different gappy regions.

    下载: 全尺寸图片 幻灯片

    图 6  不同缺失区域对尾流中线流向速度重构结果对比　(a)流向速度统计; (b)流向速度绝对误差

    Figure 6.  Comparison of reconstruction results of midline wake flow velocity of different gappy areas: (a) Streamwise velocity statistics; (b) absolute error of streamwise velocity.

    下载: 全尺寸图片 幻灯片

    图 7  不同缺失区域对圆柱下方$ y=-1 $和$ y=-2 $处速度重构结果对比　(a)流向速度统计; (b)流向速度绝对误差; (c)法向速度统计; (d)法向速度绝对误差

    Figure 7.  Comparison of reconstruction results at y = –1 and y = –2 below the cylinder of different gappy regions: (a) Streamwise velocity stcatistics; (b) absolute error of streamwise velocity; (c) normal velocity stcatistics; (d) absolute error of normal velocity.

    下载: 全尺寸图片 幻灯片

    图 8  不同缺失区域的重构结果的POD结果对比　(a)流向速度; (b)法向速度

    Figure 8.  Comparison of POD of flow of different gappy regions: (a) Streamwise velocity; (b) normal velocity.

    下载: 全尺寸图片 幻灯片

    图 9  噪声等级对重构结果的影响　(a)平均$ L_2 $误差随噪声等级的变化; (b)几个不同噪声等级的重构结果对比

    Figure 9.  Effect of noise level on reconstruction results: (a) The mean $ L_2 $ error varies with noise level; (b) comparison of reconstruction results of several different noise levels.

    下载: 全尺寸图片 幻灯片

    图 10  实验中获得的PIV粒子图像

    Figure 10.  An image of PIV particles obtained in the experiment.

    下载: 全尺寸图片 幻灯片

    图 11  两个不同瞬时时刻的实验数据重构结果

    Figure 11.  Reconstruction results of experimental data at two different times.

    下载: 全尺寸图片 幻灯片

    图 12  实验、神经网络重构和数值计算的时均流场对比

    Figure 12.  Comparison of experimental, neural network reconstruction and numerically time-averaged flow fields.

    下载: 全尺寸图片 幻灯片

    图 13  圆柱下方$ y=-1 $和$ y=-2 $处实验、神经网络重构和数值仿真结果对比　(a)流向速度统计; (b)法向速度统计

    Figure 13.  Comparison of reconstruction results at y = –1 and y = –2 below the cylinder of different gappy regions: (a) Streamwise velocity stcatistics; (b) normal velocity stcatistics.

    下载: 全尺寸图片 幻灯片
  • [1] Ragni D, Ashok A, van Oudheusden B W, Scarano F 2009 Meas. Sci. Technol. 20 074005 doi: 10.1088/0957-0233/20/7/074005
    [2] Gunes H, Rist U 2008 Phys. Fluids 20 104109 doi: 10.1063/1.3003069
    [3] Tan B T, Damodaran M, Willcox K E 2004 AIAA J. 42 1505 doi: 10.2514/1.2159
    [4] 李天一, Buzzicotti Michele, Biferale Luca, 万敏平, 陈十一 2021 力学学报 53 2703 doi: 10.6052/0459-1879-21-464 Li T Y, Buzzicotti M, Biferale L, Wan M P, Chen S Y 2021 Chin. J. Mech. 53 2703 doi: 10.6052/0459-1879-21-464
    [5] Sciacchitano A, Dwight R P, Scarano F 2012 Exp. Fluids 53 1421 doi: 10.1007/s00348-012-1366-5
    [6] Zimmermann R, Vendl A 2014 AIAA J. 52 255 doi: 10.2514/1.J052208
    [7] Ruscher C J, Dannenhoffer J F, Glauser M N 2017 AIAA J. 55 255 doi: 10.2514/1.J054785
    [8] Deng Z W, He C X, Wen X, Liu Y Z 2018 J. Vis. 21 1043 doi: 10.1007/s12650-018-0508-0
    [9] Li T X, He C X, Wen X, Liu Y Z 2023 J. Vis. 26 815 doi: 10.1007/s12650-022-00906-y
    [10] 何创新, 邓志文, 刘应征 2021 航空学报 42 524704 He C X, Deng Z W, Liu Y Z 2021 Acta Aeronautica et Astronautica Sinica 42 524704
    [11] 袁昊, 寇家庆, 张伟伟 2024 力学学报 56 2799 doi: 10.6052/0459-1879-24-223 Yuan H, Kou J Q, Zhang W W 2024 Chin. J. Mech. 56 2799 doi: 10.6052/0459-1879-24-223
    [12] 张伟伟, 王旭, 寇家庆 2023 力学进展 53 433 doi: 10.6052/1000-0992-22-050 Zhang W W, Wang X, Kou J Q 2023 Adv. Mech. 53 433 doi: 10.6052/1000-0992-22-050
    [13] 任峰, 高传强, 唐辉 2021 航空学报 42 524686 Ren F, Gao C Q, Tang H 2021 Acta Aeronautica et Astronautica Sinica 42 524686
    [14] Vinuesa R, Brunton S L, McKeon B J 2023 Nat. Rev. Phys 5 536 doi: 10.1038/s42254-023-00622-y
    [15] Brunton S L 2021 Acta Mech. Sin. 37 1718 doi: 10.1007/s10409-021-01143-6
    [16] Wen Z K, Shu W P, Zhang H, Liu S B, Zhang L Q, Liu L, Wang T, Zhang Q J, Li S 2024 Space Sci. Technol. 4 0080 doi: 10.34133/space.0080
    [17] 徐启伟, 王佩佩, 曾镇佳, 黄泽斌, 周新星, 刘俊敏, 李瑛, 陈书青, 范滇元 2020 物理学报 69 014209 doi: 10.7498/aps.69.20190982 Xu Q W, Wang P P, Zeng Z J, Huang Z B, Zhou X X, Liu J M, Li Y, Chen S Q, Fan D Y 2020 Acta Phys. Sin. 69 014209 doi: 10.7498/aps.69.20190982
    [18] Taira K, Hemati M S, Brunton S L, Sun Y Y, Duraisamy K, Bagheri S, Dawson S T M, Yeh C A 2020 AIAA J. 58 998 doi: 10.2514/1.J058462
    [19] 郑天韵, 王圣业, 王光学, 邓小刚 2020 物理学报 69 204701 doi: 10.7498/aps.69.20200563 Zheng T Y, Wang S Y, Wang G X, Deng X G 2020 Acta Phys. Sin. 69 204701 doi: 10.7498/aps.69.20200563
    [20] Wang H P, Yang Z X, Li B L, Wang S Z 2020 Phys. Fluids 32 115105 doi: 10.1063/5.0023786
    [21] Morimoto M, Fuakmi K, Fukagata K 2021 Phys. Fluids 33 087121 doi: 10.1063/5.0060760
    [22] Zhang F, Hu H B, Ren F, Zhang H, Du P 2022 Phys. Fluids 34 127117 doi: 10.1063/5.0130955
    [23] Luo Z H, Wang L Y, Xu J, Wang Z L, Chen M, Yuan J P 2023 Phys. Fluids 35 085115 doi: 10.1063/5.0158235
    [24] Luo Z H, Wang L Y, Xu J, Yuan J P, Chen M, Li Y, Andy C T 2024 Ocean Eng. 293 116605 doi: 10.1016/j.oceaneng.2023.116605
    [25] Zheng Q M, Li T Y, Ma B T, Fu L, Li X M 2024 Phys. Rev. Fluids 9 024608 doi: 10.1103/PhysRevFluids.9.024608
    [26] Muharrem H A, Ilker G, Murat I, Abdullah C 2023 Phys. Fluids 35 114110 doi: 10.1063/5.0176637
    [27] He K M, Zhang X Y, Ren S Q, Sun J 2016 ICCV Santiago, Chile, December 13–16, 2015 p1026
    [28] Szegedy C, Ioffe S, Vanhoucke V, Alemi A 2017 AAAI California, USA, February 4–9, 2017 p1
    [29] Lin M, Chen Q, Yan S C 2013 arXiv: 13124400 [cs.NE]
    [30] He K M, Zhang X Y, Ren S Q, Sun J 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Las Vegas, USA, June 26–July 1, 2016 p770
    [31] Zhang F, Hu H B, Zhang H, Zhang M, Song J, Meng Y Z 2024 Ocean Eng. 309 118578 doi: 10.1016/j.oceaneng.2024.118578
    [32] 陈蒋力, 丁海艳, 胡海豹, 张帆, 文俊 2024 实验流体力学 39 1 doi: 10.11729/syltlx20240027 Chen J L, Ding H Y, Hu H B, Zhang F, Wen J 2024 Experimental Fluid Mechanics 39 1 doi: 10.11729/syltlx20240027
  • 加载中
图( 13)
计量
  • 文章访问数:  53
  • HTML全文浏览数:  53
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-06
  • 刊出日期:  2025-04-05

基于深度学习方法的圆柱绕流实验缺失数据重构

    通讯作者: E-mail: huhaibao@nwpu.edu.cn
  • 1. 西北工业大学航海学院, 西安　710072
  • 2. 西北工业大学深圳研究院, 深圳　518063
  • 收稿日期:  2024-12-06

摘要: 对流动现象进行精确预测与有效控制的前提在于对流动现象的深入理解, 而实验研究在此过程中提供了宝贵的数据支撑. 粒子图像测速(PIV)技术作为当前流场测量的主流手段之一, 在钝体绕流等复杂流动现象的实验研究中发挥着不可或缺的作用. 然而, 在PIV实验中, 由于光路遮挡等问题的存在, 获取完整且准确的流场数据往往极具挑战性. 鉴于此, 提出了一种基于机器学习的流场数据重构方法, 该方法采用以卷积神经网络为核心的深度学习模型, 旨在解决流场数据中缺失部分的重构问题. 首先探讨了不同缺失区域对数值计算流场重构效果的影响, 并从瞬时流场、速度统计量等多个维度, 对重构流场与真实值之间的差异进行了细致的比较分析. 结果显示, 对于瞬时流场的重构, 最大$ L_2 $误差维持在约0.02的水平. 进一步发现, 当缺失区域在流向方向上的尺寸增大时, 重构的难度也随之显著增加; 而相比之下, 缺失区域在垂直于流向方向上的尺寸变化, 对重构精度的影响则相对有限. 在此基础上, 进一步研究了深度神经网络对噪声的泛化性, 通过在数值计算结果中人为添加噪声来测试网络, 发现重构数据的误差随着噪声等级的提升呈指数型增长趋势. 最终, 将提出的网络模型应用于实际的PIV实验数据中, 从瞬时流场和时间平均结果两个方面进行了验证. 结果表明, 该网络模型不仅能够成功重构缺失位置的速度信息, 还能有效修正回流区部分因测量不准确而产生的数据偏差. 经过神经网络重构的实验结果, 在统计意义上更加接近数值仿真的结果, 这充分说明, 本文提出的模型仅需使用数值计算数据进行训练, 便可以具备重构PIV实验中缺失信息的能力.

English Abstract

    全文HTML

    1.   引　言

    • 完整的流场信息是理解和控制复杂流体问题的基础. 为了获取完整的信息, 科研人员已经研发和改进了大量的实验装置, 如热线、激光多普勒测速仪、粒子图像测速仪(PIV)等. 在这些技术中, PIV凭借其非侵入式、全流域测速的特性, 在实验流体研究中占据了重要地位. PIV的工作原理赋予了其独特的优势, 但同时也意味着其测量流场的能力极大地依赖于高质量的光源和示踪粒子. 然而, 在实际实验中, 特别是钝体绕流实验中, 常会遇到因光路受阻等因素导致的流场信息缺失现象, 这使得钝体近壁区流动信息获取变得极为复杂和富有挑战性.

      为解决上述问题, Ragni等[1]尝试在实验过程中采用多角度照明, 旨在规避模型周边光路受阻的现象, 然而, 这一策略会不可避免地牺牲上游区域的信息完整性. Gunes和Rist[2]在探索Kriging方法应用于PIV数据平滑与空间增强方面的研究中发现, 该方法能有效减少PIV测量中的异常值, 并且在数据相关性良好的情况下, 还能估算出PIV实验中因光路受阻而缺失的区域的信息, 从此Kriging方法也被广泛应用于流场中缺失信息的估计. 此外, Tan等[3]开创性地将本征正交分解法(POD)引入空气动力学领域, 用以补充缺失的流场信息. 他们成功地在定常流动条件下, 运用Gappy POD方法从不完整的数据中重构流场. 尽管该方法高度依赖于特定的物理问题和参数设置, 且计算成本高昂, 但为后续研究者提供了宝贵的应用范例. 例如, 李天一等[4]深入研究了Gappy POD重构数据过程中的误差产生机制, 并推导了相应的误差公式, 进一步加强了该方法在流场缺失信息重构领域的应用. 同时, 也有学者采用物理求解的方法来补充物理信息, Sciachitano等[5]尝试通过求解Navier-Stokes (N-S)方程来重构流场的缺失信息, 并将该方法应用于翼型绕流实验中. 他们指出, 该方法对噪声极为敏感, 因此要求实验数据具有较高的质量.

      随着计算机性能的逐步提升, 计算流体力学(CFD)迅猛发展, 学者们发现可以采用数据同化的方法, 从CFD中获取实验条件下难以直接获取的数据, 以重构全面的流场信息. 早期的研究工作主要围绕Gappy POD及其衍生方法展开. 例如, Zimmermann和Vendl[6]基于Gappy POD方法, 改进了一种新的降阶模型, 并将其应用于数据融合领域, 旨在优化空气动力学载荷的预测手段. 同样, Ruscher等[7]使用一种基于Gappy POD的fusion POD方法, 针对轴对称射流工况, 成功将PIV数据与速度场关于中心轴对称的知识融合, 从而修复了因压力传感器遮挡而缺失的流场区域. 邓志文 等[8]则采用了基于集合卡尔曼滤波(EnKF)的数据同化策略. 研究选用了一个自由圆形射流作为案例, 通过局部测量数据来恢复整个流场信息, 结果显示, 即便仅依赖单点数据, 所提出的同化方法仍能有效地复原流场数据. 同团队的Li等[9]使用基于EnKF的数据同化方法预测了更为复杂的双叶片转子附近的三维流场. 数据同化可以弥补单纯的实验测量或CFD的缺陷[10], 但其计算时长和计算资源与问题的复杂度相关.

      近年来, 机器学习凭借其处理非线性问题的能力, 在流体力学领域得到了广泛的应用[11-18], 经过训练的机器学习模型能够迅速预测流场, 兼具了效率与性能优势[19]. 针对槽道湍流PIV实验中近壁面速度场难以准确测量的难题, 王洪平等[20]提出了一种基于卷积神经网络(CNN)来改进近壁面速度的预测, 并提升空间分辨率的方法, 取得了很好的效果. Morimoto等[21]也使用CNN网络, 从方柱绕流流场中粒子缺失的图像中重新估计速度场. 他们通过人工生成的粒子图像模拟真实PIV图像, 重构出的速度场数据密度高达互相关方法的40倍, 这充分展示了机器学习相较于传统方法在捕捉流场精细结构和隐藏特征方面的优势. Zhang等[22]同样利用CNN对PIV实验中随机位置缺失的数据进行了重构, 该网络模型不受时间因素的限制, 能够预测任意随机时刻任意缺失位置的数据, 从而提高了数据重构的灵活性和准确性. 罗朝晖等[23,24]则提出了一种多尺度的自动编码器框架来进行数据重构, 并与Fused POD方法进行了对比, 结果显示, 该框架在重构效果上显著优于POD方法. Zheng等[25]提出了一种基于生成对抗网络的大面积缺失数据高保真重构框架. 他们以完整的流场作为网络的物理约束条件, 重构出的流场在统计规律上与原始流场保持高度一致性, 进一步验证了机器学习在流场数据重构方面的潜力.

      尽管机器学习方法在流场缺失信息重构领域已经取得了诸多应用成果, 但专门针对圆柱绕流PIV实验的相关研究仍较为匮乏. Muharrem等[26]尝试使用机器学习算法来重构圆柱绕流PIV实验中缺失的流场数据, 并通过对比各种时均数据展示了算法的有效性. 然而, 他们并未展示瞬时流场的结果, 而瞬时流场对于后续的流场分析和理解流动机理具有重要意义. 基于此, 本文以圆柱绕流PIV实验为研究对象, 建立了以CNN为核心的深度神经网络模型, 先探究了不同尺度的缺失区域对重构结果的影响; 随后讨论了网络模型在面对噪声干扰时, 其鲁棒性能力的边界; 最后, 将所构建的模型应用于实际的实验数据中, 从瞬时和时均数据角度, 全面评估其在解决实际问题中的效能与表现.

    2.   深度神经网络模型

      2.1.   问题描述

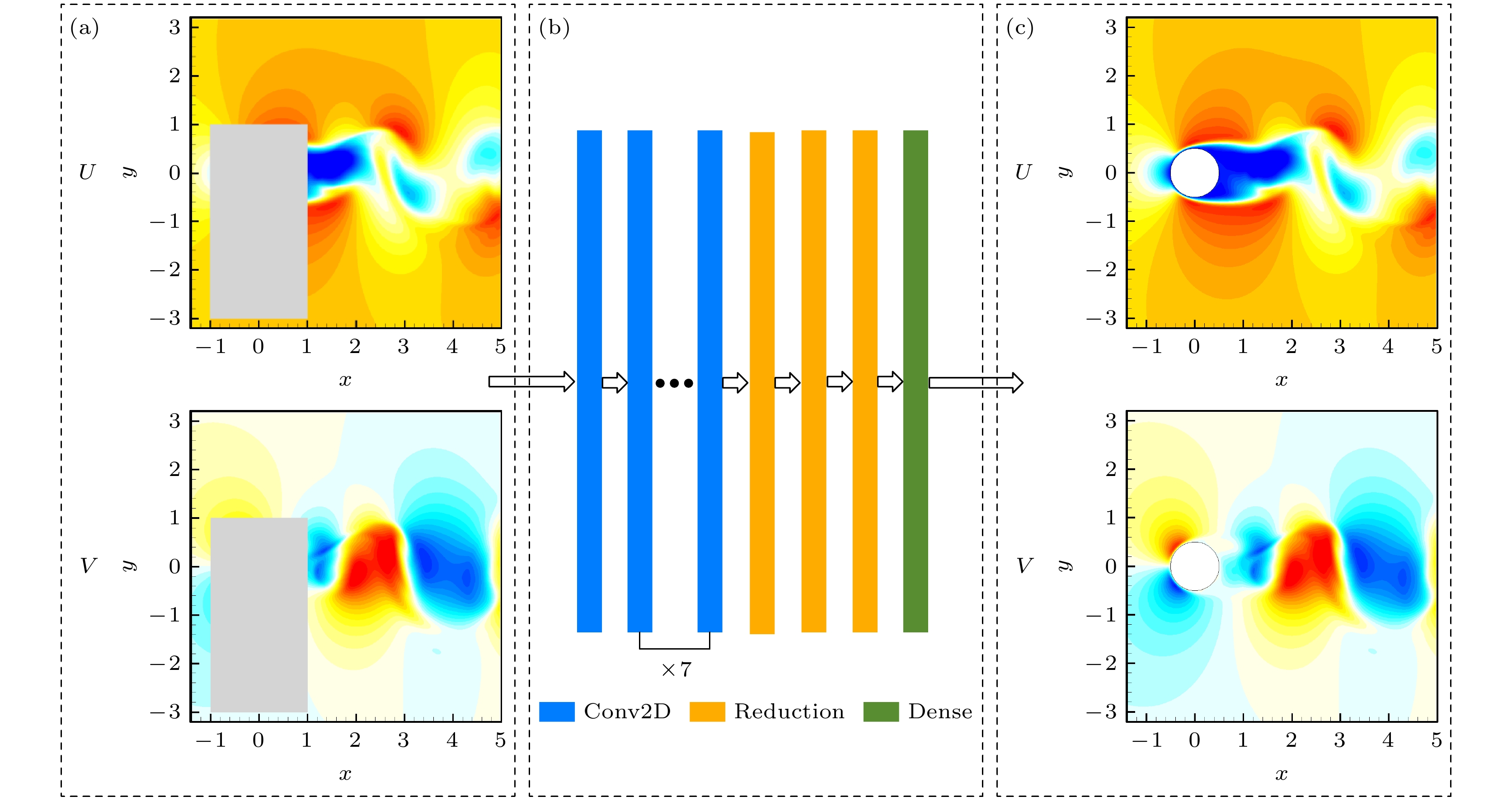
    • 本文以圆柱绕流为例, 重构PIV实验中可能缺失的速度场信息, 具体思路如图1所示. 为了实现这一目标, 搭建一个以CNN为基础的深度神经网络模型(图1(b)), 来建立输入数据$ {\boldsymbol{x}}\in \mathbb{R}^r $(图1(a)中有缺失区域的速度场)和期待的输出数据$ {\boldsymbol{y}}\in\mathbb{R}^n $(图1(c)中完整的速度场)之间的拟合关系. 给定一个输入数据$ {\boldsymbol{x}} $和期待的输出数据$ {\boldsymbol{y}} $, 希望找到深度学习模型$ \mathcal{F} $的最优权重$ {\boldsymbol{\omega}} $, 非线性关系为$ \mathcal{F}({\boldsymbol{x}};{\boldsymbol{\omega}})\approx{\boldsymbol{y}} $. 通过训练神经网络来优化权重$ {\boldsymbol{\omega}} $, 使期望的输出$ {\boldsymbol{y}} $和深度学习模型的输出$ \mathcal{F}({\boldsymbol{x}};{\boldsymbol{\omega}}) $之间的$ {L_2} $范数最小化, 如(1)式. 当权重$ {\boldsymbol{\omega}} $通过训练数据确定下来之后, 深度神经网络模型$ \mathcal{F} $就训练完成.

      • 2.2.   网络结构

    • 卷积层是卷积神经网络的基础之一, 卷积层通过卷积操作((2)式)来提取数据的特征信息,

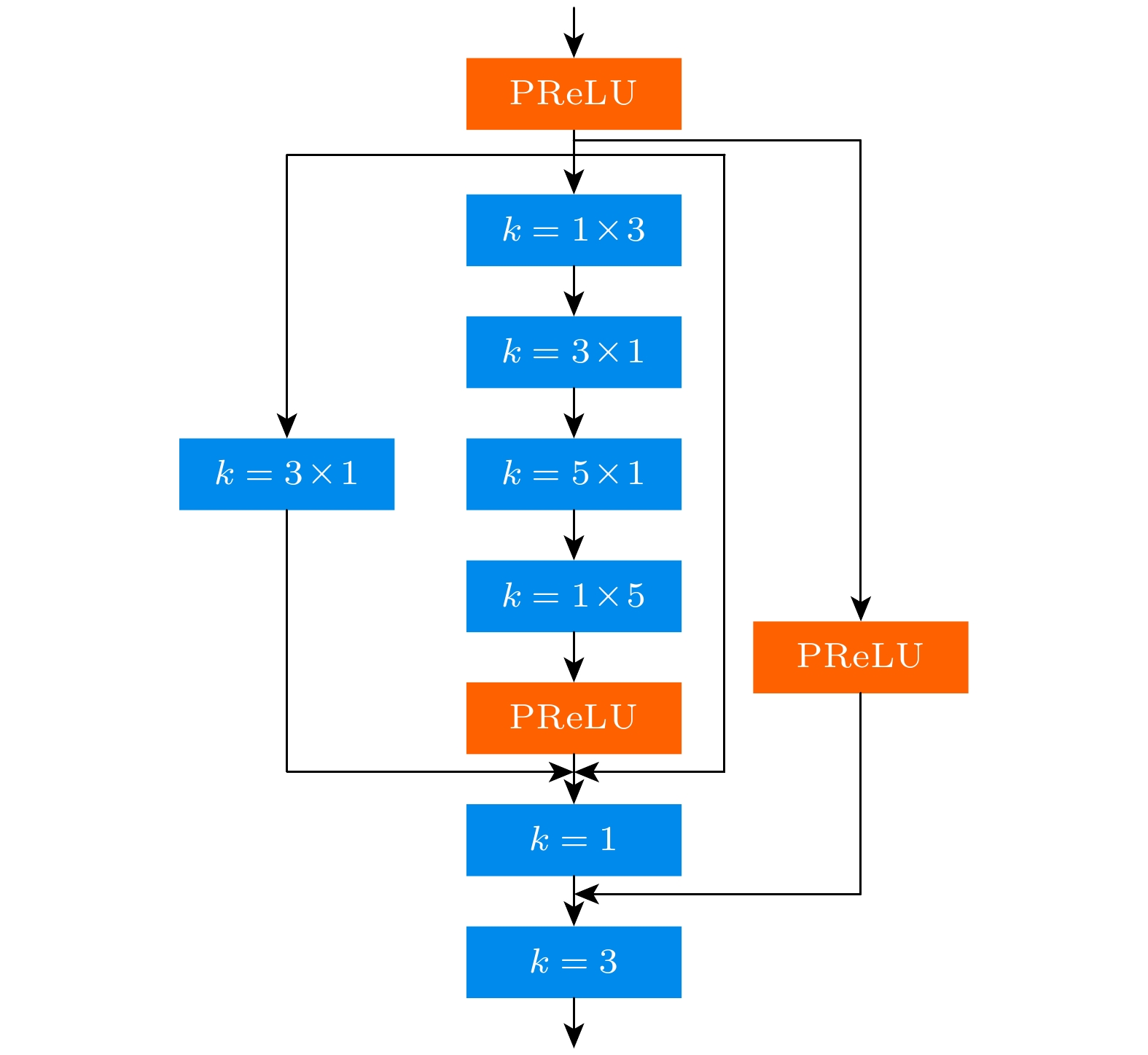
      其中, $ q^{(l)} $和$ q^{(l-1)} $分别是卷积层l的输入和输出, $ h_{pskm} $代表卷积核, Ψ代表激活函数, 本文使用的激活函数为PReLU[27]. 输入数据的尺寸是$ L \times L \times C $, 其中L是每个方向的像素数量, C是分量的个数. 比如在RGB图像中$ C = 3 $(红色、绿色和蓝色). 在本工作中, 分量为流向速度和法向速度两个, 所以$ C = 2 $.

      图1(b)是本文采用的CNN架构, 该架构在整体设计上沿袭了先前的研究[22], 包含卷积层、Reduction模块以及一个全连接层, 但具体的卷积层数和模块数量依据待学习的数据规模来决定, 经过一系列前期的实验验证, 本文最终确定的网络为一个包含8个卷积层和3个Reduction模块的架构. 其中, 8个卷积层均采用$ 7\times 7 $大小的卷积核, 步长统一设定为1. 图1(b)中的Reduction模块是本架构的核心部分, 其详细结构如图2所示. 图中蓝色框是卷积层, 框内的数字具体代表各层的卷积核尺寸. Reduction模块具有多个分支, 通过在不同的分支间实施特征融合, 不仅增强了网络对于细节信息的敏感度, 还有效促进了网络对复杂尺度信息的识别能力. 此外, 引入两个连续的卷积核尺寸为$ N\times1 $和$ 1\times N $的卷积层, 来代替卷积核尺寸为$ N\times N $的卷积层, 在减少计算负荷和缩短计算周期的同时, 能够保持相同的感受野[28]. 另外, 引入卷积核为$ 1\times1 $的卷积层, 能够进一步增强网络的非线性表达能力, 使网络具备学习复杂非线性映射关系的能力[29]. 最后, 为了缓解大规模参数网络可能面临的梯度消失和梯度爆炸问题, 本架构还在网络中加入了一些“短链接”[30].

      超参数是在网络学习过程开始之前人为设定的参数, 对网络模型的训练效率和效果有显著影响. 他们并非通过训练获取的数据, 因此选择一组恰当的网络超参数对于提升网络模型训练的有效性至关重要. 本文选择Nadam优化器来优化网络权重, 并采用指数衰减学习率策略, 其中衰减指数设定为0.95, 初始衰减率设置为$ 10^{-5} $. 然而值得注意的是, 这种超参数配置并非唯一最优解, 其他组合在统计意义上同样也有可能达到相近的准确度. 网络模型使用开源的Python语言基于TensoFlow v2.3搭建, 并使用由两个Intel Xeon CPU和四个NVIDIA Titan V GPU搭建的工作站来训练和测试.

    3.   对网络性能的评估

      3.1.   数据集获取

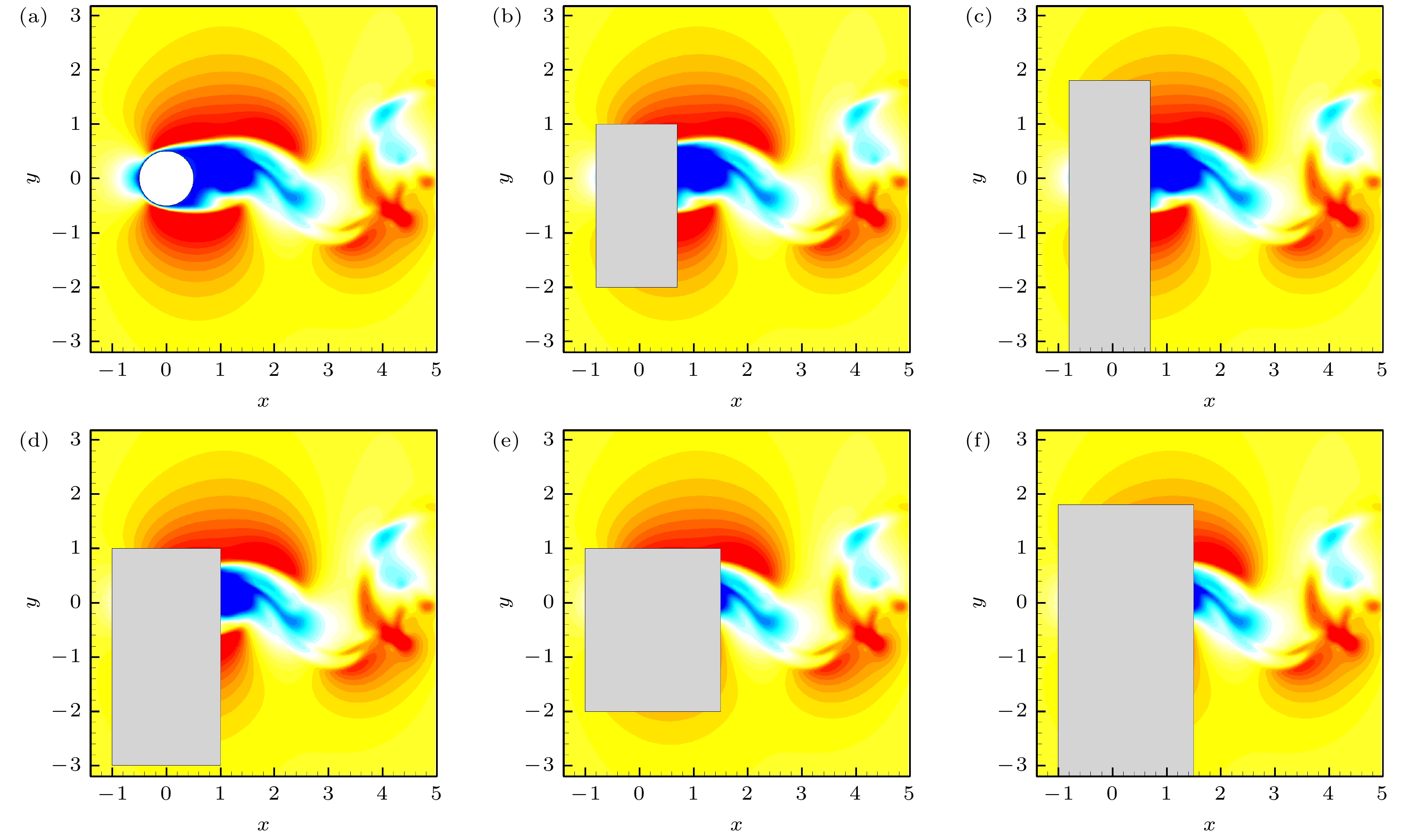
    • 为了评估网络性能, 首先考虑使用$ Re = 500 $的非定常圆柱绕流的CFD数据. 该CFD数据源自直接数值模拟结果, 数据的有效性在前面的工作中已经进行了验证[31]. 采用格子Boltzmann方法作为核心求解器, 雷诺数Re根据来流速度U、圆柱直径D以及流体的运动黏度ν进行定义, 具体表达式为$ Re=UD/\nu $. 通过数值求解不可压Navier-Stokes方程, 获取了三维的圆柱绕流的流场信息, 并沿展向方向(z方向)提取二维数据, 以此构建神经网络模型需要的数据样本集. 本文中, 所有结果均已基于来流速度U、圆柱直径D以及特征时间$ T=D/U $进行无量纲化处理. 所截取的用于本工作的数据范围为$ x\in[-3.2 D, 3.2 D] $, $ y\in [-1.4 D, 5 D] $, 圆柱中心位于坐标原点(0, 0), 流场的分辨率为$ 256\times256 $. 随后, 依据实验中常见的光路遮挡现象, 设置了长方形的数据缺失区域, 图3为本文的几种缺失区域的设置方案, 图3(a)为完整的流场, 并在此基础上设定了5种不同长(沿流向方向)和高(沿法向方向)的数据缺失区域, 图中的灰色区域即数据缺失的区域, 图3(b)—(f)的缺失区域尺寸分别为$ 60\times 120 $, $ 60\times 200 $, $ 80\times 160 $, $ 100\times 120 $以及$ 100\times 200 $. 在选择数据缺失区域的位置时, 遵循的原则是确保缺失区域将圆柱完全遮盖.

      • 3.2.   网络训练结果

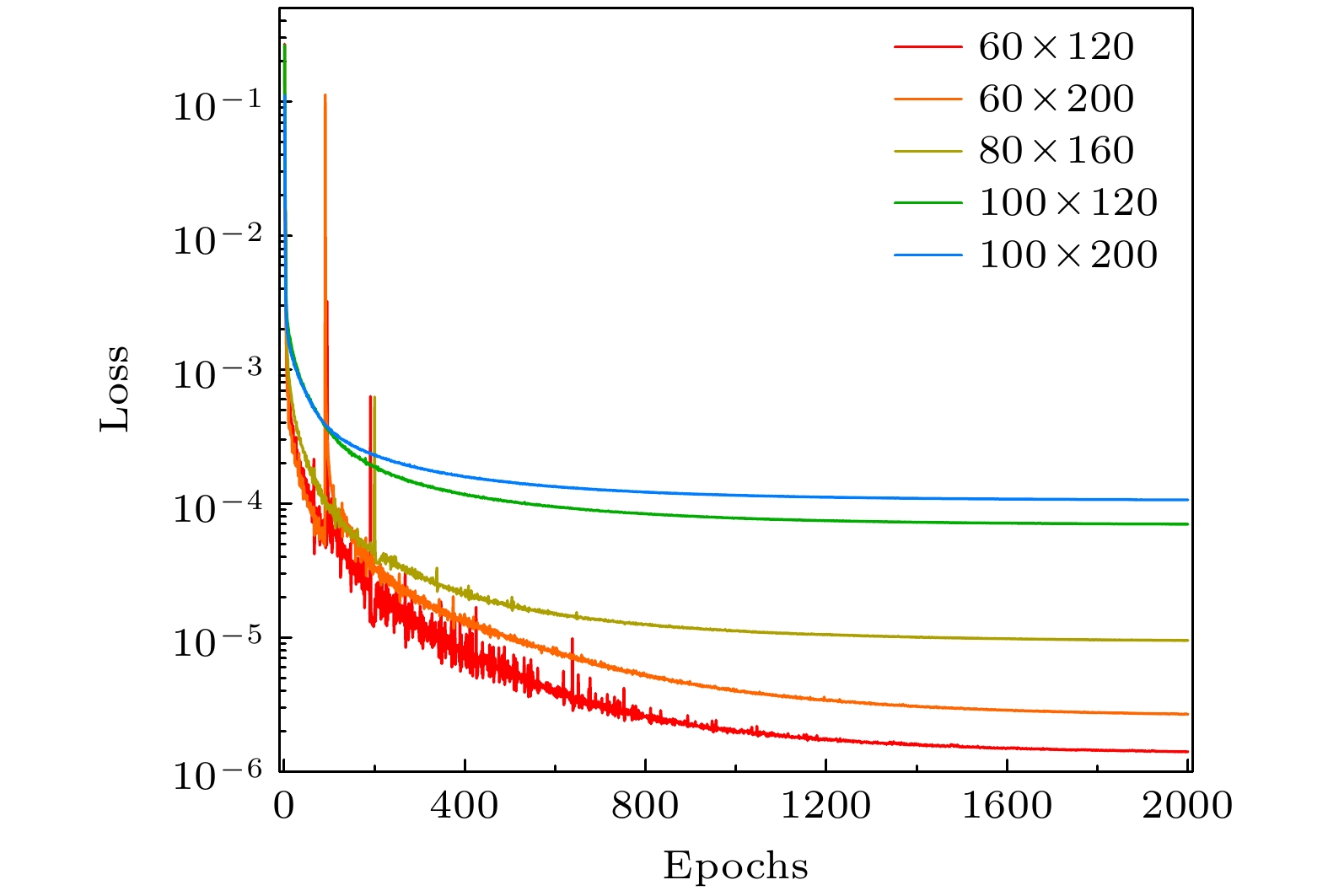
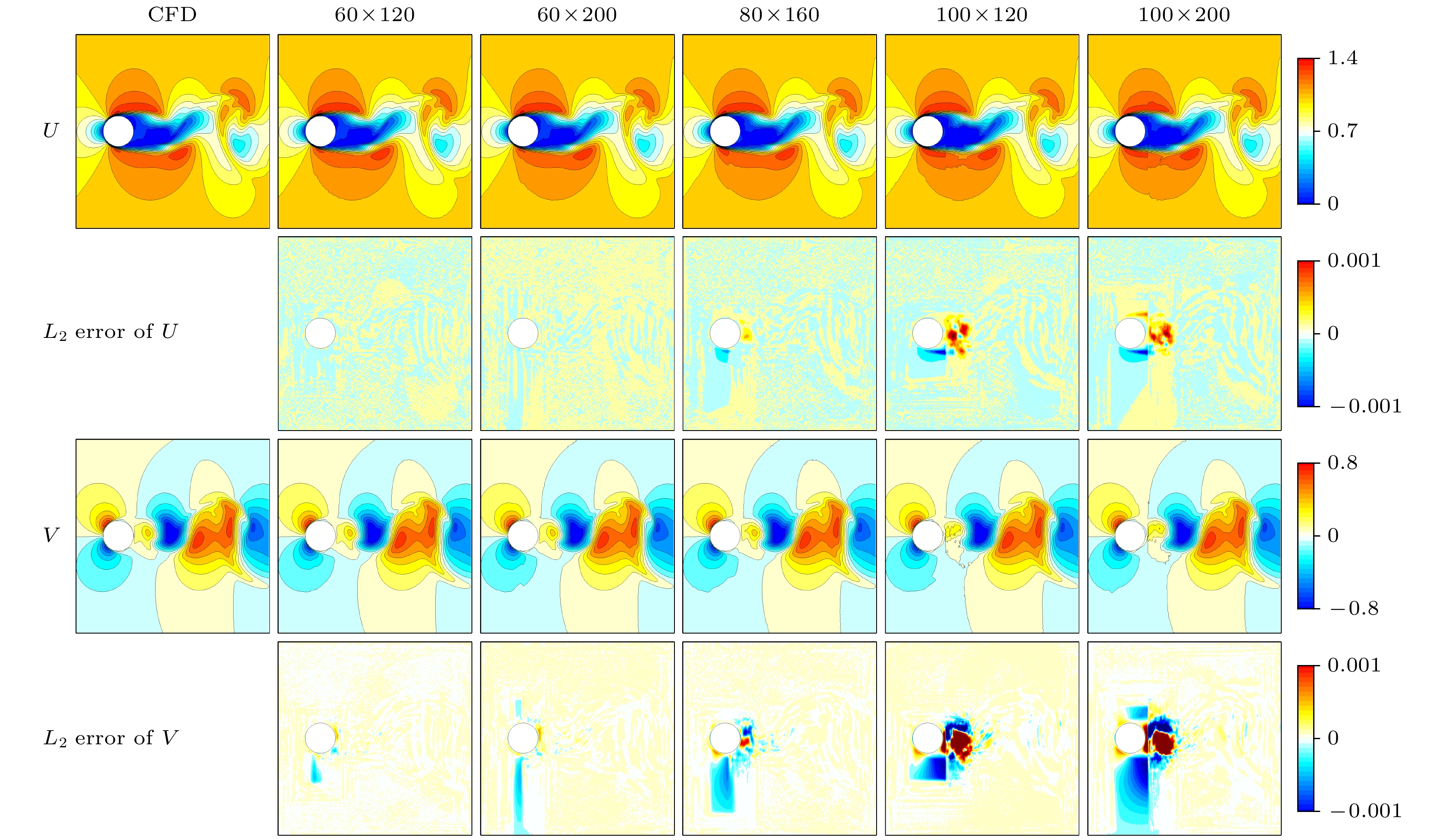
    • 网络模型的训练误差收敛情况如图4所示. 红色、粉色、黄色、绿色和蓝色线条分别对应图3(b)—(f)描述的5种不同的数据缺失区域的类型. 在这些线条中, 红色和粉色线条代表的数据缺失区域为$ 60\times 120 $和$ 60\times 200 $, 他们的误差收敛至最低水平, 具体数值为$ 8.09\times10^{-5} $和$ 8.79\times10^{-5} $. 黄色线条代表的数据缺失区域为$ 80\times 160 $, 其训练误差收敛至中等水平, 约为$ 1.51\times10^{-4} $. 而绿色和蓝色线条代表的数据缺失区域的训练误差收敛情况最差, 尺寸分别为$ 100\times 200 $和$ 100\times 120 $. 通常认为, 随着数据缺失面积的增加, 重构误差会随之增大. 然而, 图4中的数据说明, 数据缺失的面积并非决定重构难度的因素. 比如, 尽管尺寸为$ 60\times 200 $和$ 100\times 120 $的两种数据缺失区域的面积在数值上相等, 但两者在训练误差收敛上的表现有很大差异. 根据图中的数据来看, 随着数据缺失区域沿流向长度的递增, 误差收敛值也呈现出逐渐增大的趋势, 这说明数据缺失区域沿流向的长度或许是影响重构难度的一个关键因素.

      几种不同缺失区域的瞬时流场的重构结果对比如图5所示, 从上到下分别为流向速度、流向速度的重构$ L_2 $误差、法向速度以及法向速度的重构$ L_2 $误差. $ L_2 $误差的定义为$ \varepsilon = \| {\boldsymbol{q}}_{{\mathrm{ref}}}-{\boldsymbol{q}}_{{\mathrm{pre}}} \| / \| {\boldsymbol{q}}_{{\mathrm{pre}}} \| $, 其中$ {\boldsymbol{q}}_{{\mathrm{ref}}} $和$ {\boldsymbol{q}}_{{\mathrm{pre}}} $分别代表作为参考的CFD数据和CNN重构的数据. 图5中从左到右分别为数值计算结果以及5种不同缺失情况下的数据, 对应的$ L_2 $误差依次为0.001587, 0.002239, 0.006790, 0.02194, 0.02198, 缺失区域尺寸为$ 60\times 120 $的瞬时流场的$ L_2 $误差最小. 从流向速度及其误差来看, 网络能够较为准确地重构出不同程度的数据缺失情况. 然而, 从细节来看, 随着缺失区域在法向方向上尺寸的增大, 圆柱上下壁面的流动并未出现显著的重构误差. 这表明神经网络通过学习已基本掌握了该区域速度的梯度分布, 即便对于$ 100\times 120 $和$ 100\times 200 $这两种大面积缺失情况, 尽管圆柱下壁面的小尺度流动几乎被完全遮挡, 网络仍能从已知区域提取有效信息, 从而给出合理且完整的重构结果. 然而, 随着缺失区域在x方向上长度的增加, 神经网络对回流区的重构精度逐渐降低. 从法向速度的结果可以更清晰地观察到与流向速度重构相似的规律. 此外还发现, x方向的数据缺失尺度对重构结果的影响尤为显著. 具体而言, $ 100\times 120 $和$ 100\times 200 $的误差明显大于$ 80\times 160 $, 而$ 80\times 160 $的误差又显著大于$ 60\times 120 $和$ 60\times 200 $. 这进一步说明, 重构精度与缺失区域沿流向的长度密切相关. 例如, 尽管$ 60\times 200 $和$ 100\times 120 $的缺失面积完全相同, 但他们的重构精度却大相径庭.

      • 3.3.   速度统计

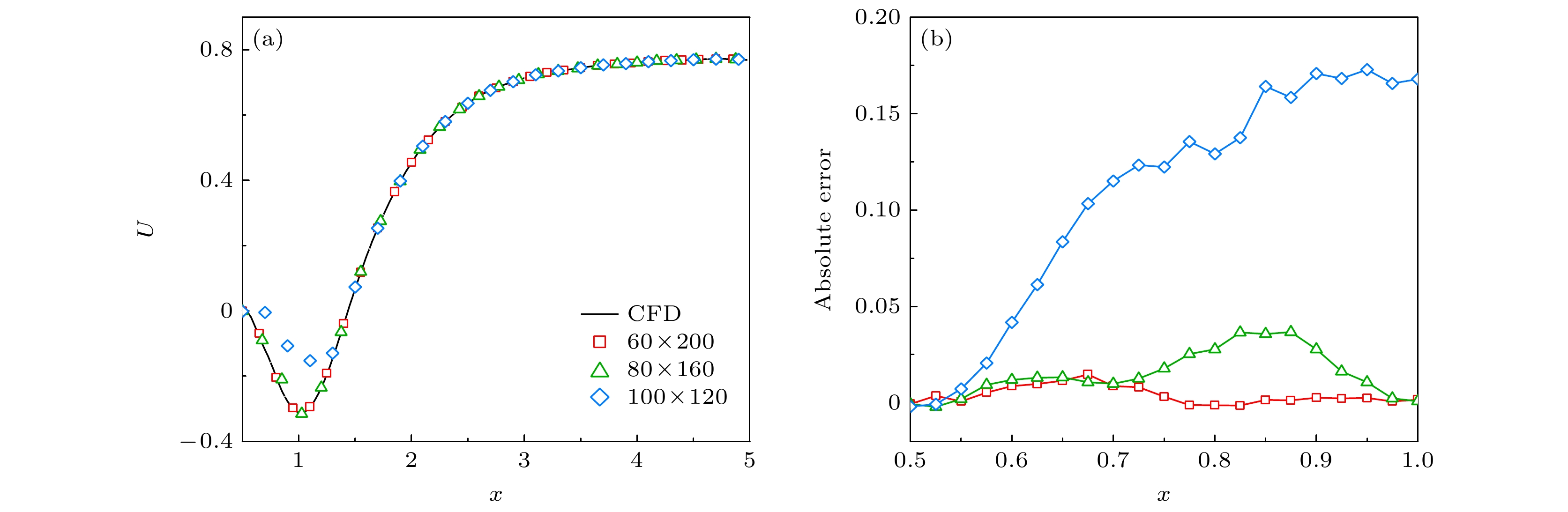
    • 为了深入分析不同缺失区域对流场重构精度的影响, 选取了三组代表性的缺失区域的重构结果, 统计了圆柱尾流中线($ y = 0 $)的数据来定量地评估重构精度, 如图6所示. 具体地, 图6(a)展示了流向速度的时间统计结果, 而图6(b)则展示了重构数据相对于CFD数据的绝对误差. 黑色实线代表作为参考的CFD数据, 红色、绿色和蓝色则分别对应3种不同缺失区域(尺寸分别为$ 60\times 200 $, $ 80\times 160 $和$ 100\times 120 $)的重构结果. 通过图6(a)可以明显看出蓝色组的重构结果与CFD数据存在显著偏差, 而其余两组则与CFD结果拟合得相对较好. $ 100\times 120 $的最大绝对误差约为0.175, 这相当于近50%的相对误差, 且其误差从$ x = 0.55 $开始显著上升, 直至$ x = 1.0 $时仍未下降. 相比之下, $ 80\times 160 $的误差虽然在x∈[0.7, 1.0]范围内有所上升, 但最大误差仅约为0.04, 相当于10%的相对误差, 因此表现明显优于$ 100\times 120 $. 而尺寸为$ 60\times 200 $的数据误差则几乎为零, 表现出极高的重构精度.

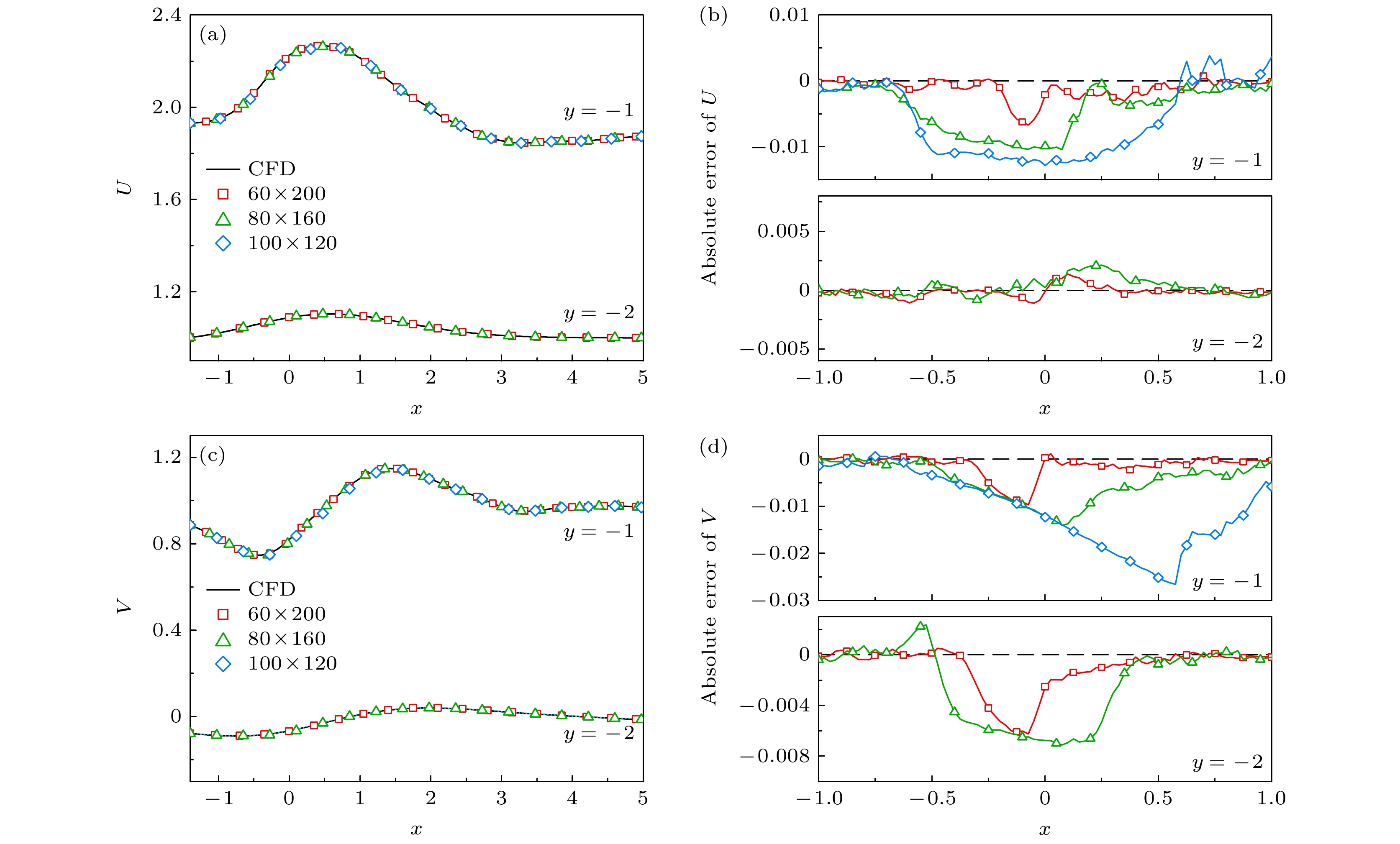
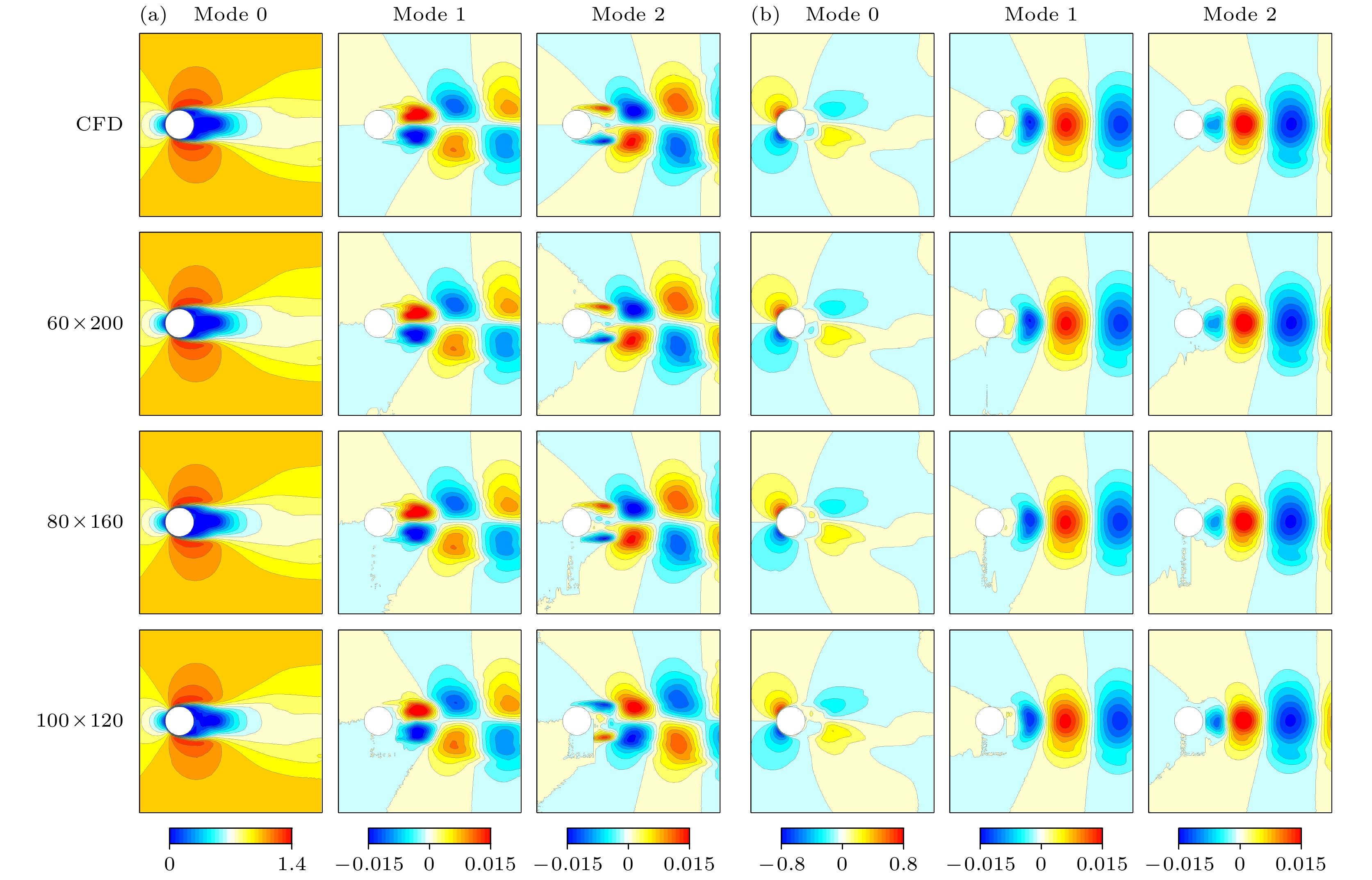
      为了更全面地评估不同缺失区域对流场重构精度的影响, 还绘制了在$ y=-1 $和$ y=-2 $位置处的速度统计量, 如图7所示. 与图6类似, 图7中的黑色实线代表CFD的基准结果, 而其他3种颜色则分别对应三组不同缺失区域的重构结果. 其中, 图7(a)和图7(c)展示了速度统计量, 图7(b)和图7(d)展示了相应的绝对误差. 值得注意的是, 由于$ y=-2 $位置处于$ 100\times 120 $缺失区域的范围之外, 因此在该位置处未统计该工况的数据和误差. 从两个速度统计量图来看, 三组重构数据均与CFD基准结果符合得很好. 从误差图可以看到三组的差别, 流向速度的重构误差随着统计位置与圆柱距离的增加而逐渐减少. 即使在$ y=-2 $位置处, 蓝色曲线也表现出了相对较好的重构精度. 然而, 当$ y=-1 $时, 蓝色线在$ x\in[-0.5, 0.5] $范围内(即圆柱所在的x轴范围)出现了明显的误差. 相比之下, 绿色曲线的表现略优于蓝色, 从$ x = 0 $开始, 其精度有了一定程度的提升. 而红色曲线的误差则始终接近于零, 表现出极高的重构精度. 从图7(d)来看, 与图7(b)类似, 蓝色曲线在法向速度重构中的表现仍然最差, 绿色曲线次之. 然而, 与流向速度的重构误差不同的是, 红色曲线在法向速度重构中也出现了误差. 这在一定程度上说明了法向速度的重构难度远大于流向速度的重构难度. 同样地, 出现明显误差的区域仍然集中在圆柱所在的x轴范围内. 随着接近圆柱中心, 误差逐渐增大; 而随着远离圆柱中心, 误差则逐渐减小至零附近.

      为了更直观地分析不同尺寸的缺失区域对数据重构效果的影响, 采用了本征正交分解(POD)方法对流场进行了降阶处理, 并将对比结果展示于图8中. POD作为一种基于奇异值分解的流场降阶技术, 能够有效地将高维流场信息近似描述为低维空间中的若干模态, 且这些模态按照包含的能量大小进行排序[18]. 针对低雷诺数条件下的圆柱绕流问题, 通常前两阶模态已能涵盖超过50%的流场能量, 因此, 本研究仅展示了平均场(Mode 0)以及前两阶模态的对比结果. 与图6一样, 选取了3个具有代表性的缺失区域进行对比分析. 在平均场的重构方面, 可以观察到回流区附近的误差从上至下逐渐增大, 这一趋势在流向速度和法向速度的重构中均有所体现. 进一步观察模态1和模态2的重构误差, 可以发现表现更为显著. 具体而言, $ 60\times 200 $尺寸缺失区域的重构数据与CFD结果保持高度一致; 然而, 当缺失区域尺寸增大至$ 80\times 160 $时, 数据缺失的区域开始出现噪点; 而当缺失区域尺寸为$ 100\times 120 $时, 重构数据中甚至出现了明显的长方形缺失形状.

      整体来说, 缺失区域为$ 60\times 120 $和$ 60\times 200 $的两组数据在各个评估维度上均展现出了更高的重构精度. 相比之下, 缺失区域为$ 80\times 160 $的组别次之, 而缺失区域为$ 100\times 120 $和$ 100\times 200 $的两组数据, 在各个维度上均存在显著的重构误差. 这表明, 缺失信息的流场区域沿流向方向的长度对重构结果产生了关键的影响. 回流区附近的流动复杂, 速度梯度较大. 当该区域的信息被遮挡时, 神经网 络的学习难度显著增加, 从而导致重构精度下降. 相反, 圆柱上方和下方的流动则呈现出较强的规 律性. 即便这些区域的大量信息被遮盖, 神经网络仍能够较好地捕捉其流动特征, 并实现较为准确的重构.

      • 3.4.   噪声泛化性分析

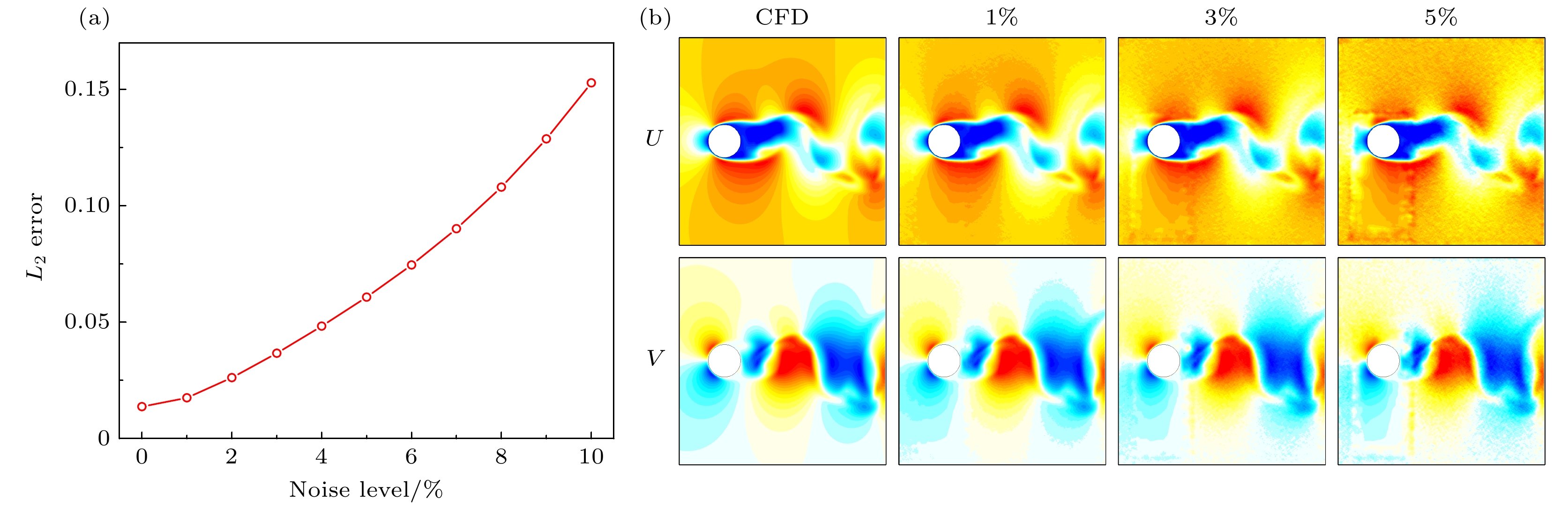
    • 为了评估网络模型的泛化性能, 在测试数据中加入了不同等级的高斯噪声, 以模拟真实实验环境中普遍存在的噪声干扰, 并据此考察网络模型对噪声的敏感程度. 测试了噪声等级0—10%的测试数据集, 并计算了平均$ L_2 $误差, 相关结果如图9所示. 这里选取了缺失区域尺寸为$ 80\times 160 $的数据集进行分析. 图9(a)展示了不同噪声等级下误差的变化趋势, 图9(b)则呈现了噪声等级分别为1%, 3%和5%时的数据重构结果. 观察发现, 随着噪声等级的增加, 平均误差呈现出指数型增长的趋势, 这充分说明了噪声对网络性能有很大影响. 当噪声级别为1%时, 重构图像的边缘区域已出现轻微噪声, 但网络并未展现出明显的降噪效果, 输出数据中仍保留有噪声. 当噪声级别提升至3%时, 从云图中可以清晰看到, 缺失区域的数据被成功重构为无噪声的平滑数据, 而其他区域的数据则保持了与输入数据相同的噪声级别. 这一现象在噪声级别为5%的云图中更为显著. 这说明噪声的输入对于网络在缺失位置的信息预测并未产生明显干扰, 网络依然能够准确识别并重构出缺失的流场数据. 然而, 对于未缺失的位置, 网络则倾向于保留与测试数据相同级别的噪声, 这反映了网络在处理含噪输入时的一种平衡策略.

    4.   重构圆柱绕流PIV实验缺失数据

      4.1.   实验设置

    • 基于对网络性能的评估结果, 测试了真实PIV实验中的数据重构情况. 搭建了一个拖曳水池来进行圆柱绕流实验, 具体的实验设置与之前的工作相同[32]. 其中圆柱的特征长度为10 mm, 水池的长宽高尺寸为$ 2400\; {\mathrm{mm}}\times 500 \; {\mathrm{mm}}\times 400 \; {\mathrm{mm}} $, 装置的阻塞比为0.02, 实验雷诺数为$ Re = 200 $. 图10为实验中获得的PIV粒子图像, 圆柱近壁面存在反光现象, 圆柱下方有清晰的黑色阴影, 这些反光和阴影都会导致该区域的信息缺失.

      • 4.2.   瞬时时刻流场

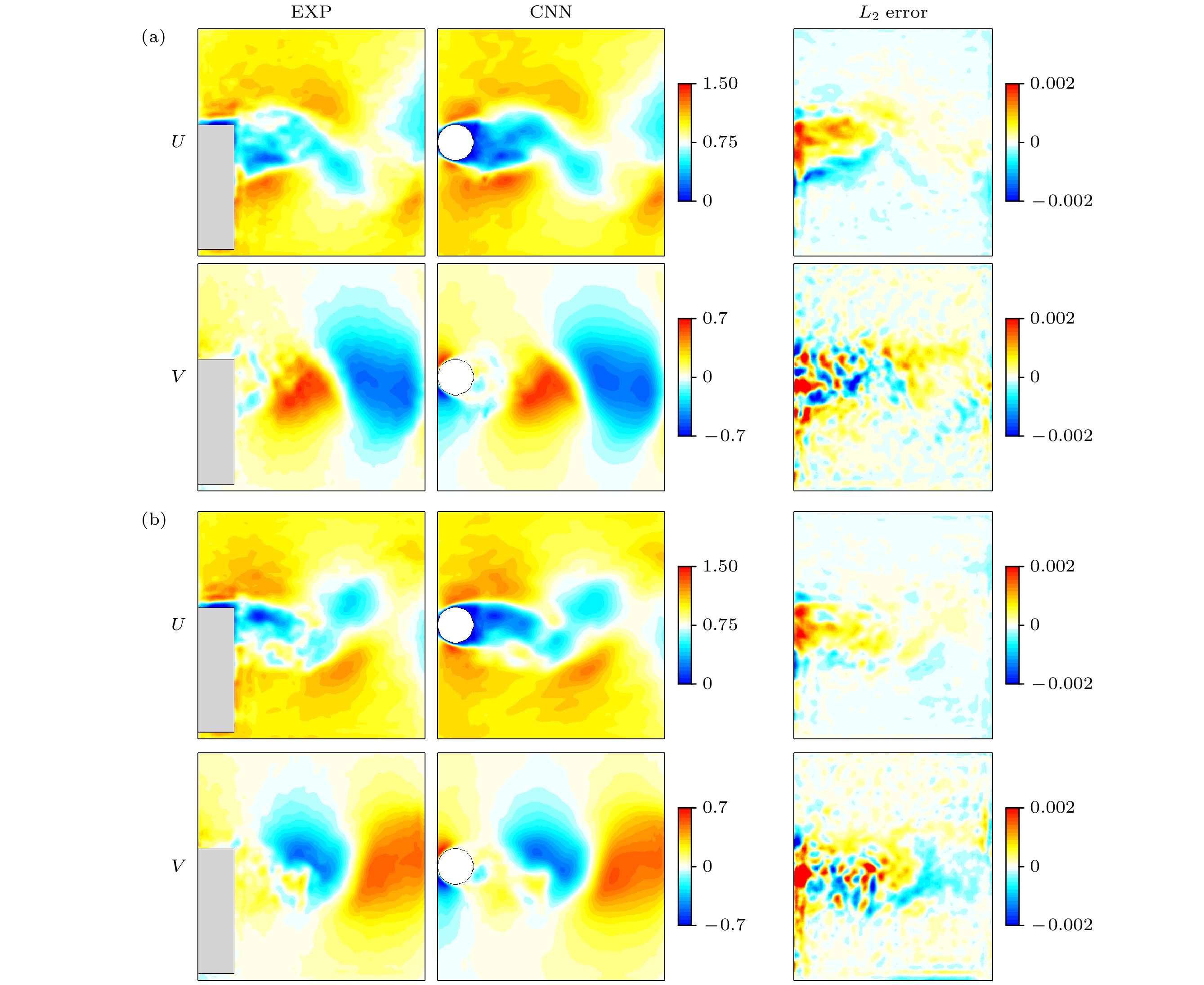
    • 图11展示了两个随机时刻的流场数据对比, 其中EXP代表实验数据, CNN表示通过神经网络重构的结果, 两者之间的差异通过$ L_2 $误差进行量化. 实验数据经由PIVlab软件处理得到. 其中, 灰色区域是PIVlab中绘制的遮挡部分, 表明该区域在PIVlab的识别下无显著速度变化. 整体来看, 网络模型在重构缺失区域数据方面展现出良好的性能, 使得圆柱右侧的流场分布更加合理. 此外, 在实验数据中, 除了灰色遮挡区域外, 回流区的数据获取同样存在明显的数据缺失现象. 而网络模型不仅重构了这一缺失部分的数据, 还进一步平滑了流场分布. 误差图特别关注了圆柱尾流的速度场, 通过误差图的对比分析, 可以清晰看到实验数据与CNN数据在回流区存在显著的差异, 说明CNN凭借已学习到的数据规律, 对这一缺失部分的流场数据进行了合理的补充. 而对于尾流更远端的部分, 两者之间的差异相对较小, 此时CNN主要起到了降噪的效果.

      • 4.3.   速度统计

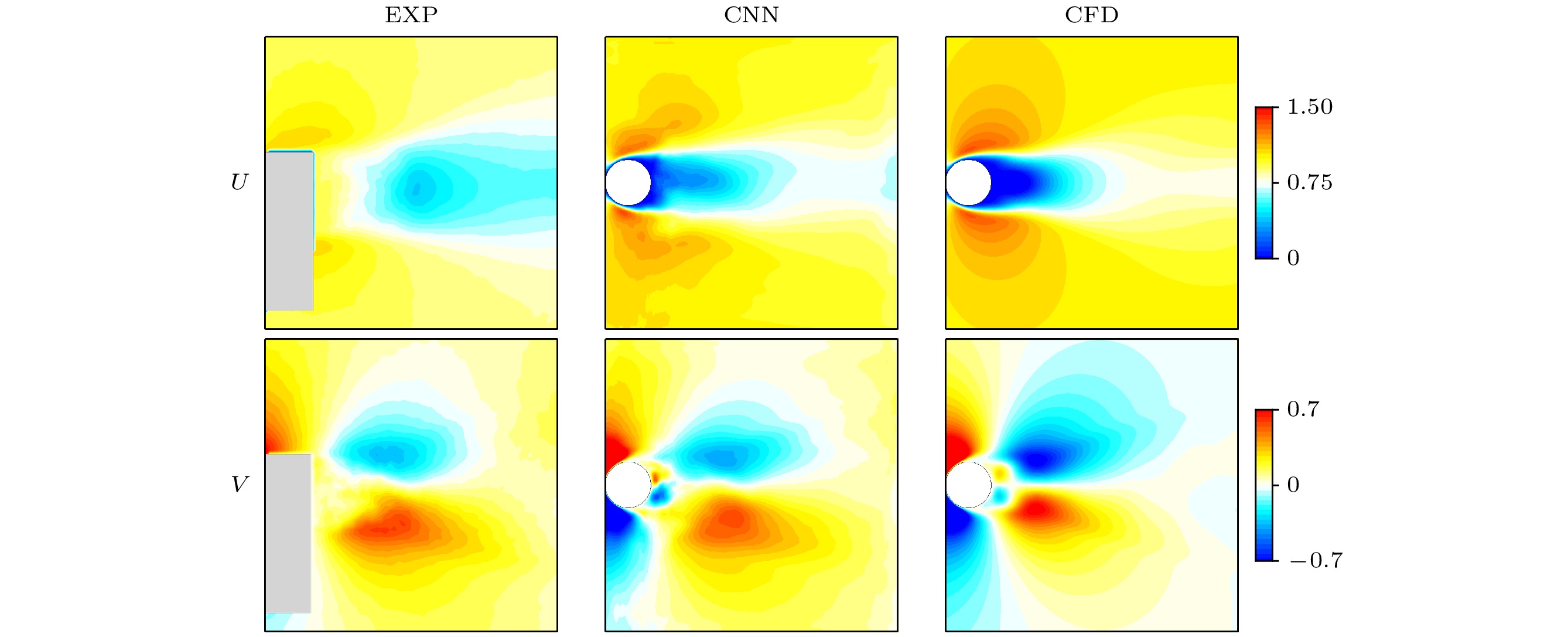
    • 统计了3个涡脱落周期的数据来获取时均流场, 如图12所示. 从上到下分别为实验数据、神经网络的重构结果和数值计算的数据. 可以看到因为实验中很难获得圆柱下方和回流区部分的流场, 所以时均的数据中, 流向数据中只能看到远离圆柱位置的速度场. 经过神经网络测试以后, 重构数据更接近数值计算数据, 能够在云图中看到圆柱上下方的速度变化, 圆柱后方的速度也可以被重构出来. 尤其是法向速度靠近圆柱后方的速度场, 这部分数据在实验结果中完全获取不到.

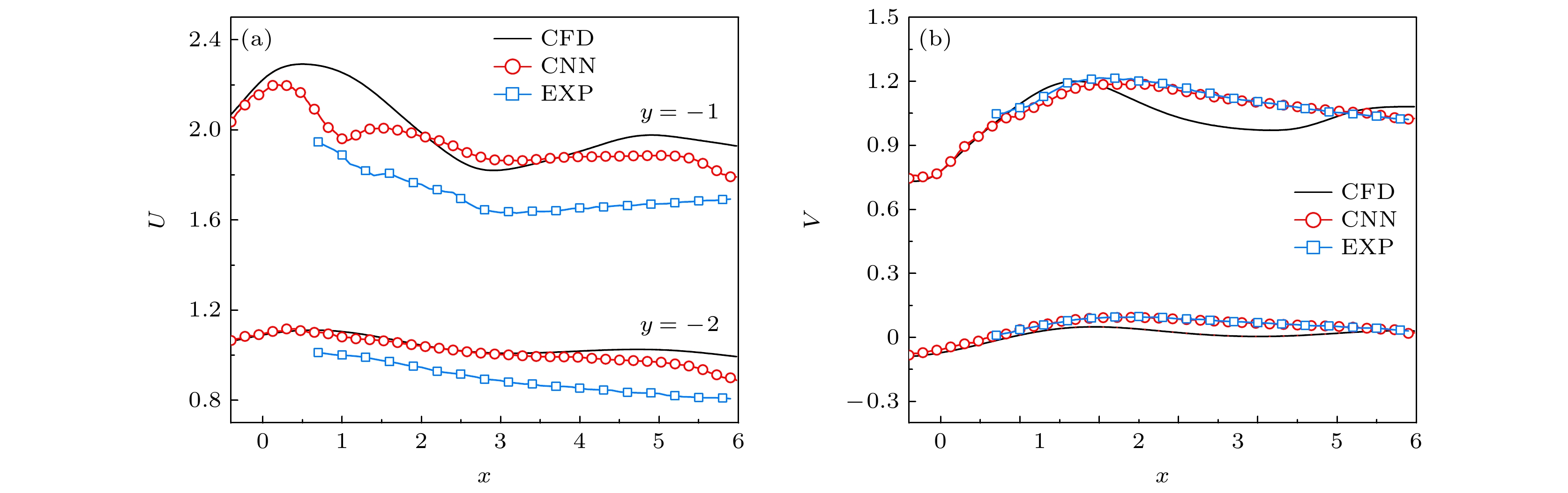
      图13展示了圆柱下方两个特定位置的速度统计对比图, 其中黑色曲线代表数值计算结果, 红色和蓝色曲线分别代表通过神经网络重构的结果与实验测量数据. 以CFD数据为参考数据, 可以明显观察到原始实验数据与CFD数据之间存在显著的误差, 特别是在$ x < 0.5 $的区域, 实验数据缺失. 通过神经网络进行数据重构后, 在原本缺乏实验数据的区域神经网络成功地生成了与数值计算结果高度接近的数据. 而在实验数据存在的区域, 神经网络重构的结果有效拉近了实验数据与数值计算数据之间的距离. 这不仅验证了神经网络在补充缺失数据方面的有效性, 还进一步展示了其在提升实验数据质量方面的潜力, 提升了准确性和可靠性.

    5.   结　论

    • 本文使用深度神经网络技术, 针对圆柱绕流实验中流场信息缺失的问题, 开展了流场重构研究, 并得出以下主要结论.

      1) 缺失区域的尺寸会对重构的精度产生影响, 对于圆柱绕流问题而言, 缺失区域在来流方向(即x方向)上的尺寸增加, 会显著增加信息重构的难度. 相比之下, 缺失区域在法向上增加对重构精度的影响有限. 最大瞬时流场的$ L_2 $误差约为0.02. 因此在开展PIV实验时, 应尽可能地控制缺失信息的范围, 特别是在流向方向上保持较小的缺失区域, 可以获得更好的数据重构效果.

      2) 当测试数据含有噪声时, 重构误差会随着噪声等级的增加呈指数型增加. 尽管网络对于噪声有一定的泛化能力, 但当噪声水平过高时, 重构数据会出现明显的非物理的误差, 影响结果的准确性.

      3) 利用数值计算数据训练的网络模型, 在实际PIV实验数据的应用中展现出了良好的性能. 该模型不仅能够重构出被PIVlab软件识别为静止物体部分的流场信息, 还能够有效地恢复出圆柱后方回流区复杂的流动信息, 使得实验结果与仿真数据更加接近, 这一结果表明, 本文提出的网络在重构PIV实验中缺失的数据方面有很好的效果.

      鉴于PIV实验中的流场缺失问题一直是实验流体研究领域的难点, 本文的研究为这一问题的解决提供了新的思路和方法, 有望为相关研究提供有力支持.

    参考文献 (32)

目录

/

返回文章
返回