首页
登录
注册
-
随着科技的不断发展, 新一代检测装备对高灵敏检测器的需求日益迫切. 在航空航天、装备检测等尖端领域, 检测器的性能直接决定设备的检测 精度和可靠性. 然而, 当前传统硅基检测器由于其灵敏度的限制和沟道尺寸的瓶颈[1], 已无法满足未来高灵敏的检测需求. 为突破这一瓶颈, 研究人员开始寻求新的材料和技术, 以提高检测器的灵敏 度性能. 为此, 金刚石烯材料因具有高载流子迁 移率和宽带隙等优异性能成为了研究热点, 金刚石烯基检测器有望利用高载流子迁移率和低频噪 声的优势来提高检测器的灵敏度, 进而为下一代 高性能检测器的发展提供新的可能. 然而, 尽管 金刚石烯在检测领域展现出诸多潜力, 但其检测 机理仍未完全明晰. 当前的研究主要集中于金刚石烯的制备方法与基本物理特性分析, 对于其在实际检测器中的应用, 特别是如何将其优异电子特性转化为实际检测灵敏度的提升, 仍需进行理论探索 研究.
场效应晶体管(FET)是检测电路的基本组成单元之一. 在二维FET中, 当半导体表面施加垂直外加电场时, 半导体沟道会发生带弯曲[2]. 同时, 二维半导体的载流子在原子级平面内可进行输运调控, 这使得二维FET成为检测灵敏性提升的理想选择[3]. 其中具有代表性的二维材料石墨烯, 具有卓越的电子和机械性能, 在高性能检测灵敏器件等领域被寄予厚望[4]. 但石墨烯也被认为是半金属的零带隙材料[5], 该特性限制了其应用, 特别是在半导体技术中的应用[6]. 为此, 寻找兼具高载流子迁移率和带隙的二维半导体是实现超灵敏检测的可行性方案. 近年来, 研究人员发现, 石墨烯的同素异形体——金刚石烯可兼具所需特性(如宽带隙、高载流子迁移率、极高导热率等)[7,8]. 因此, 以金刚石烯作为核心沟道材料有望在超灵敏检测领域实现应用突破.
目前, 国内外在超敏晶体管检测器的结构设计、器件性能与材料研究等方面已有一些研究成果[9,10], 但大部分研究主要关注于通过替换或改善栅极/沟道材料、优化栅极结构等方面来提升器件的检测能力, 对于超敏检测的机理及碳基低维晶体管的性能等方面还缺乏探索. 因此, 本文首先从晶体管超敏检测工作原理出发, 针对沟道材料中电子工作状态, 构建表面电位及电子分布模型, 深入分析其电子分布特性, 针对性提出经典晶体管沟道电子理论与二维材料电子特性相结合的二维材料晶体管电流理论模型. 以此为基础, 进一步开展理论模型的计算验证, 量化对比不同基底材料晶体管器件的电流灵敏度, 证实了金刚石烯基超敏检测的可行性, 为实现金刚石烯基超敏检测提供理论指导与技术支撑, 对新一代碳基超敏检测器件的设计和应用具有重要意义.
-
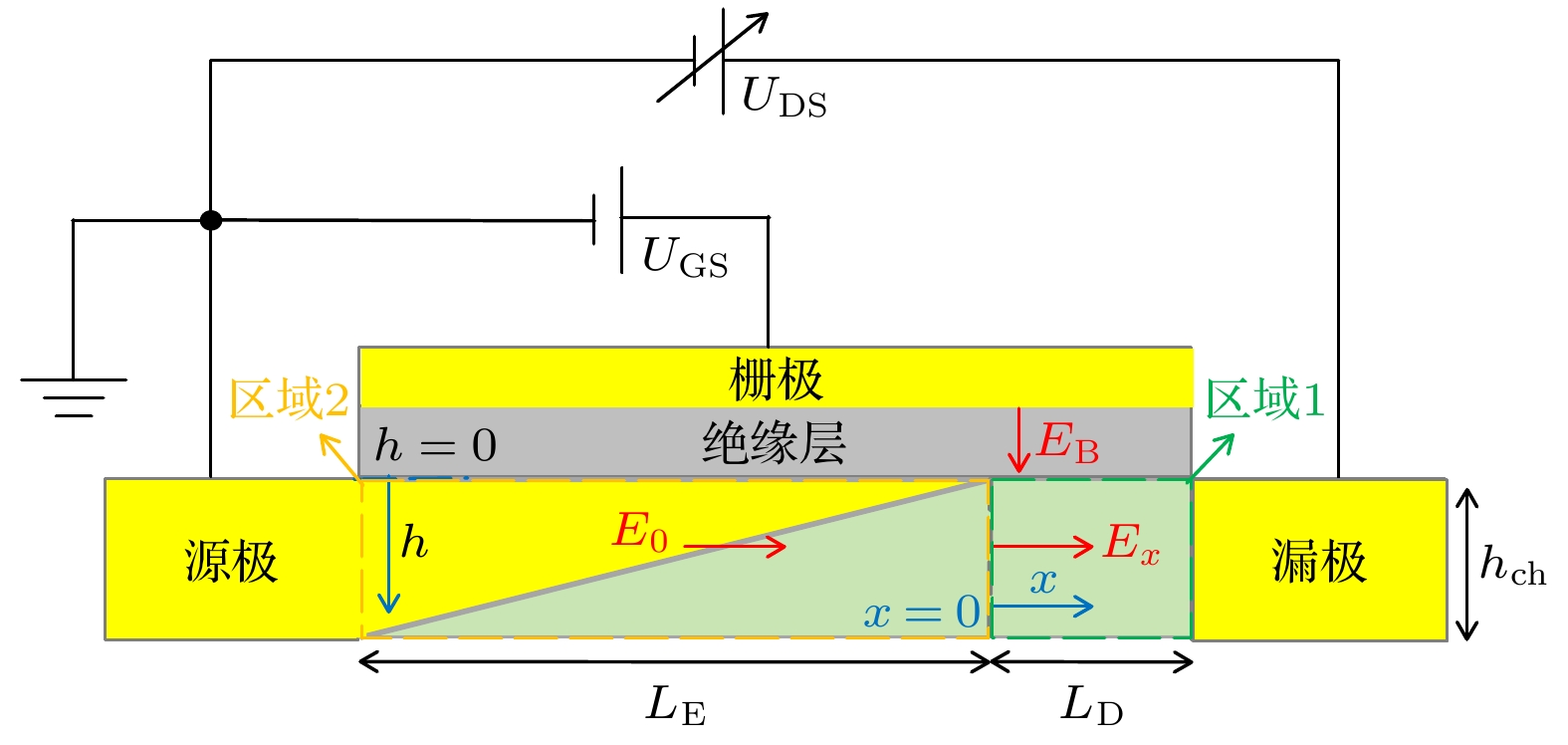
在晶体管工作时, 考虑正常工作状态. 当漏极电压高于漏极饱和电压时, 漏极结点附近电场高于临界场强, 使得载流子速度饱和. 如图1所示, 定义
$ {L_{\text{D}}} $ 区域为饱和区域.$ {E_{\text{B}}} $ ,$ {E_{0}} $ 和$ {E_x} $ 分别代表栅极介质电场、饱和电场和侧向电场.根据高斯定律, 利用电荷量守恒存在以下关系:
进一步求导可得
式中,
$ {0} \leqslant x \leqslant {L_{\text{D}}} $ 为沟道内的表面电位,$ \lambda $ 为特征栅极长度, 平带电压$ {V_{{\text{FB}}}} $ 表达式为[11]式中,
$ {\nu _{\text{F}}} \approx {1}{{0}^{6}}\;{\text{m/s}} $ 为费米速度, 热电压$ {V_{\text{T}}} = {k_{\text{B}}}T/q $ . 根据高斯定律中高斯曲面上的封闭电荷为利用
$ Q{\text{/}}{h_{{\text{ch}}}}x $ 替代$ q\left( {N + n} \right) $ , (1)式可写为二维载流子浓度
$ {n_{{\text{2D}}}} $ 表达式为对(6)式进行近似处理[12,13],
$ {E_{{F_{\text{s}}}}} = {E_{\text{F}}} $ ,$ {E_{{F_{\text{d}}}}} = {E_{\text{F}}} - q{\nu _{{\text{ds}}}} $ ,$ {E_{\text{F}}} = q{V_{{\text{ch}}}} $ . 其中,$ {V_{{\text{ch}}}} $ 为沟道势[14].接下来对表面电位和侧向电场进行解析计算. 定义区域1中
$ {\phi _{1}}\left( x \right) $ 的边界条件:$ {\phi _{1}}\left( x \right) = {V_0} + {V_{{\text{bi}}}} $ ,$ {\phi _{1}}\left( {{L_{\text{D}}}} \right) = {V_{{\text{bi}}}} + {V_{{\text{ds}}}} $ ,$ {\varsigma _{1}}\left( {0} \right) = {\varsigma _{0}} $ . 其中,$ {V_{0}} $ ,$ {V_{{\text{ds}}}} $ ,$ {L_{\text{D}}} $ ,$ {V_{{\text{bi}}}} $ ,$ {\varsigma _{0}} $ 分别为饱和区起始的饱和电压、漏极电压、饱和区长度、漏极内置电压、饱和表面电场. 通过求解微分方程可得存在以下关系:
$ x\left( x \right) = - \partial \phi \left( x \right)/\partial x $ , 则表面电场分布$ \varsigma \left( x \right) $ 可表示为同理, 为模拟源点和饱和点之间的表面电位
$ {\phi _{2}}\left( x \right) $ , 在区域2内应用高斯定律, 同样边界条件设定为$ {\varsigma _{2}}\left( {0} \right) = {\varsigma _{0}} $ 和$ {\phi _{2}}\left( x \right) = {V_0} + {V_{{\text{bi}}}} $ . 假设$ {\phi _{2}}\left( x \right) = {V_0} + {V_{{\text{bi}}}} $ ,$ {\phi _{2}}\left( {L/2} \right) = {\phi _{2}}\left( {L/2 - {L_{\text{D}}}} \right) $ . 因此,$ {\phi _{{\text{ch}}}} $ 可表示为对
$ {\phi _{1}}\left( x \right) $ 进行数值求解, 取$ x = {L_{\text{D}}} $ , 最终可得到有效沟道长度$ {L_{\text{E}}} = L - {L_{\text{D}}} $ 为 -
在二维材料中, 导电性可通过掺杂或施加静电场来调控. 因此, 栅控电压可调控二维材料电子在带内和带间的跃迁. 如果施加能量小于带隙, 则发生带内跃迁, 如果施加能量大于带隙, 则发生带间跃迁. 进一步, 这些带内和带间跃迁可直接影响沟道材料的带电导率, 因此可通过栅压实现对沟道材料电导率的可控性[15].
二维电导率具有复值, 值的大小与外界调控的能量有关[16], 由带间和带内电导率两部分组成. 二维电导率与电子-空穴对的产生/复合有关, 其表达式为
式中,
$ {\sigma _{{\text{intra}}}} $ 和$ {\sigma _{{\text{inter}}}} $ 分别代表水平跃迁电导率和带间电导率.根据Kubo公式, 二维材料的电导率写为[17]
其中, e,
$ \omega $ ,$ {\mu _{\text{c}}} $ ,$ \hbar $ ,$ T $ ,$ \xi $ ,$ f\left( \xi \right) $ ,$ \varGamma $ 分别为电子电荷、辐射频率、费米能级、普朗克常数、温度、能量、费米分布函数和色散率. 根据式中每一部分与带内/带间电导率的关系. 上述方程也可写为色散率
$ \varGamma $ 与电子弛豫时间$ \tau $ 有关, 表达式为[18]式中,
$ \mu $ 为载流子迁移率. 波长$ \lambda $ 、角频率$ \omega $ 和频率$ f $ 存在以下关系:$ \lambda = c/f, {\text{ }}\omega = 2{\text{π}}f $ . 费米能级$ {\mu _{\text{c}}} $ 和费米分布函数分别定义为[19]式中,
$ {n_{\text{s}}} $ 为材料的掺杂水平, 与偏置电压的关系为[20]式中,
$ {\varepsilon _{\text{d}}} $ 和$ {\varepsilon _{0}} $ 分别为介质相对介电常数和空间介电常数,$ d $ 为栅极介电层材料厚度.$ {V_{{\text{Dirac}}}} $ 为沟道材料掺杂所产生的偏置电压,$ {V_{\text{g}}} $ 是栅控电压.当在栅控工作状态时, 沟道材料存在以下关系:
$ \mu \gg {k_{\text{B}}}T $ ,$ {\text{exp}}\left( { - \dfrac{{{\mu _{\text{c}}}}}{{{k_{\text{B}}}T}}} \right) - 1 \cong 0 $ . 对(17)式进一步简化可以得到:在超敏检测中, 参数介电常数
$ {\varepsilon _{\text{g}}} $ 和折射率$ {n_{\text{g}}} $ 也同样重要, 会随费米能量的变化而变化, 接下来分析这些参数. 介电位移矢量$ {\boldsymbol{D}} $ 与电流密度矢量$ {\boldsymbol{J}} $ 随电场矢量$ {\boldsymbol{E}} $ 的关系为其中,
$ {\boldsymbol{k}} $ 为波矢量,$ {\varepsilon _{\text{r}}} $ 为介电函数. 结合电导率运算条件, 可以得到介电常数和折射率的表达式[21]: -
在上述分析基础上, 接下来分析晶体管迁移率等相关参数. 在晶体管工作中, 电流曲线可分为两个部分: 非饱和区(线性区)和饱和区. 它们的表达式分别为
其中,
$ {\mu _{\text{c}}} $ 为沟道材料电子迁移率,$ W $ 为有效沟道宽度,$ {V_{\text{s}}} $ 为源极电压.对于场效应晶体管的工作性能, 可用场效应迁移率
$ {\mu _{\text{i}}} $ 表示[22]:其中,
$ {C_{\text{b}}} $ 为栅极电容,$ \sigma $ 为电导.为表征晶体管对电流的灵敏度, 在此利用亚阈值摆幅参数
$ S $ , 该参数定义为: 非饱和区电流对数与栅极电压关系($ \log {I_1}{{ - }}{V_{\text{g}}} $ )中斜率的倒数. 表达式为[23]根据亚阈值摆幅参数的定义, 该值代表着晶体管在非饱和区域输出电流的线性度, 输出饱和电流减小10倍时所需要改变的栅控电压的大小.
$ S $ 越小, 说明晶体管在非饱和区的栅压变化越小, 即检测电流相对于栅压变化是非常灵敏的, 在很小的栅压变化下就能引起电流一个数量级的变化, 说明该晶体管的灵敏度更高. 因此, 最终评估晶体管电流灵敏度特性的方程组为可以发现, 该电流值大小依赖于与沟道材料相关的物理参数. 灵敏度的数值大小以及金刚石烯基检测器的优势将在后文仿真中做量化对比.
-
由于金刚石烯与石墨烯为同素异形体, 根据金刚石烯的最小组成层数, 对应为3层石墨烯, 其主要参数: 单层厚度
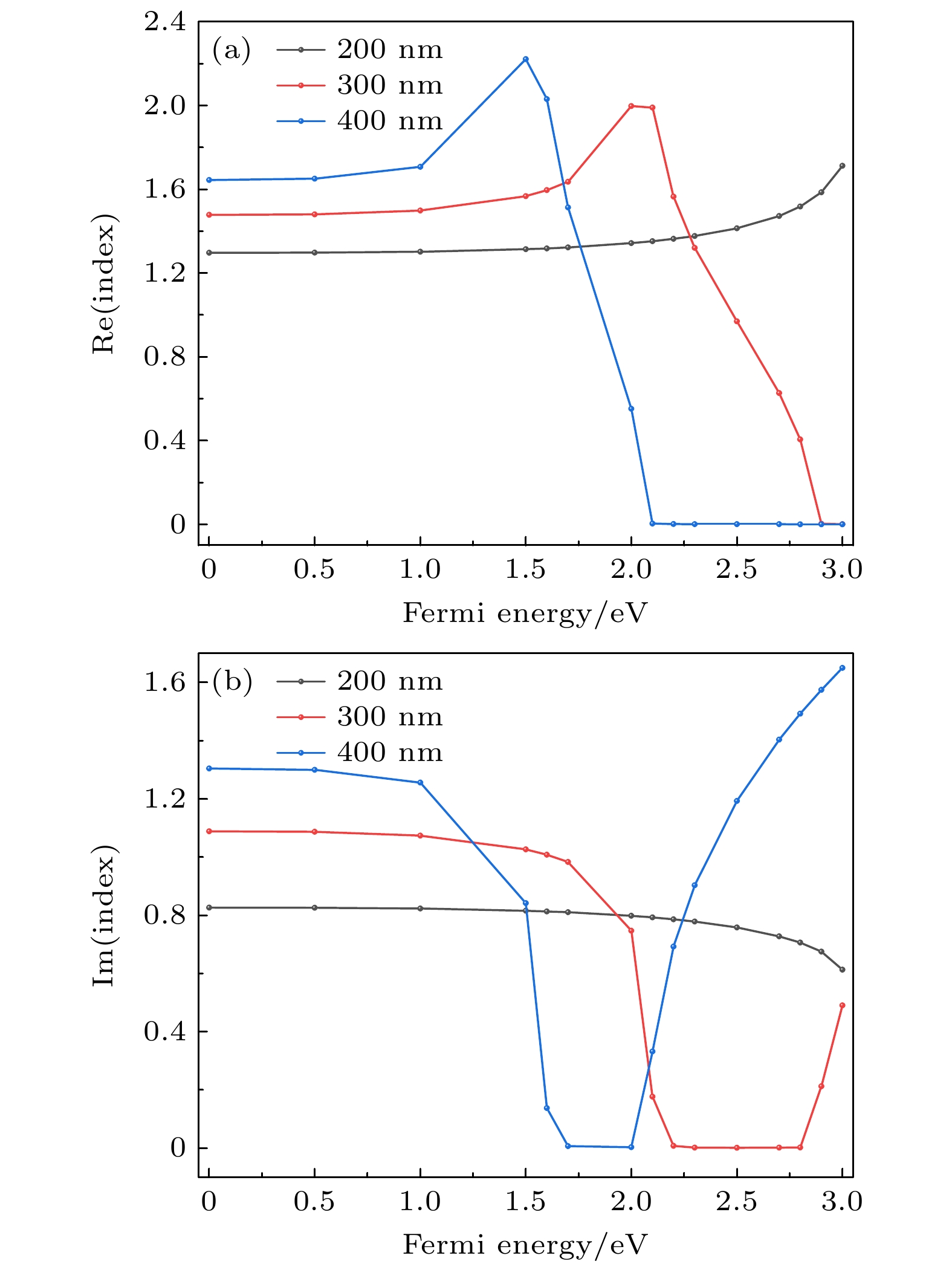
$ {h_{\text{g}}} $ 为0.34 nm, 层数为3, 散射率$ \varGamma $ 为0.514 meV, 温度$ T $ 为300 K, 费米能级$ {\mu _{\text{c}}} $ 为0—3 eV.本文计算了在200 nm, 300 nm和400 nm波长下, 材料折射率随费米能级的变化关系, 并对其灵敏性进行分析.
由图2可知, 在0—3 eV费米能量范围内, 图2(b)所示的虚部折射率存在一定范围的近零区域(300 nm和400 nm). 以300 nm为例, 费米能量范围在2.2—2.8 eV的虚部折射率为近零区域, 此区域也称为泡利阻挡区, 此时材料对光是透明 的[24]. 通过增大电压进一步提升费米能量, 当费米能量大于2.8 eV时打破泡利阻塞, 此时材料呈导体特性[25]. 因此, 由于泡利阻挡与费米能量有关, 只要改变费米能量, 其介电常数和折射率也会随之变化[26]. 在超敏电子检测和光电检测等应用中也都依赖于这一特性[25].
-
基于金刚石烯基晶体管电流沟道理论模型, 接下来进一步仿真金刚石烯基超敏检测器工作中的电势分布情况以及电子/空穴流动状态, 并将其性能与传统硅基检测器进行对比. 仿真中金刚石烯与硅材料设定的具体物理参数见表1. 二者器件尺寸等相关参数完全相同(1.5 × 3 μm).
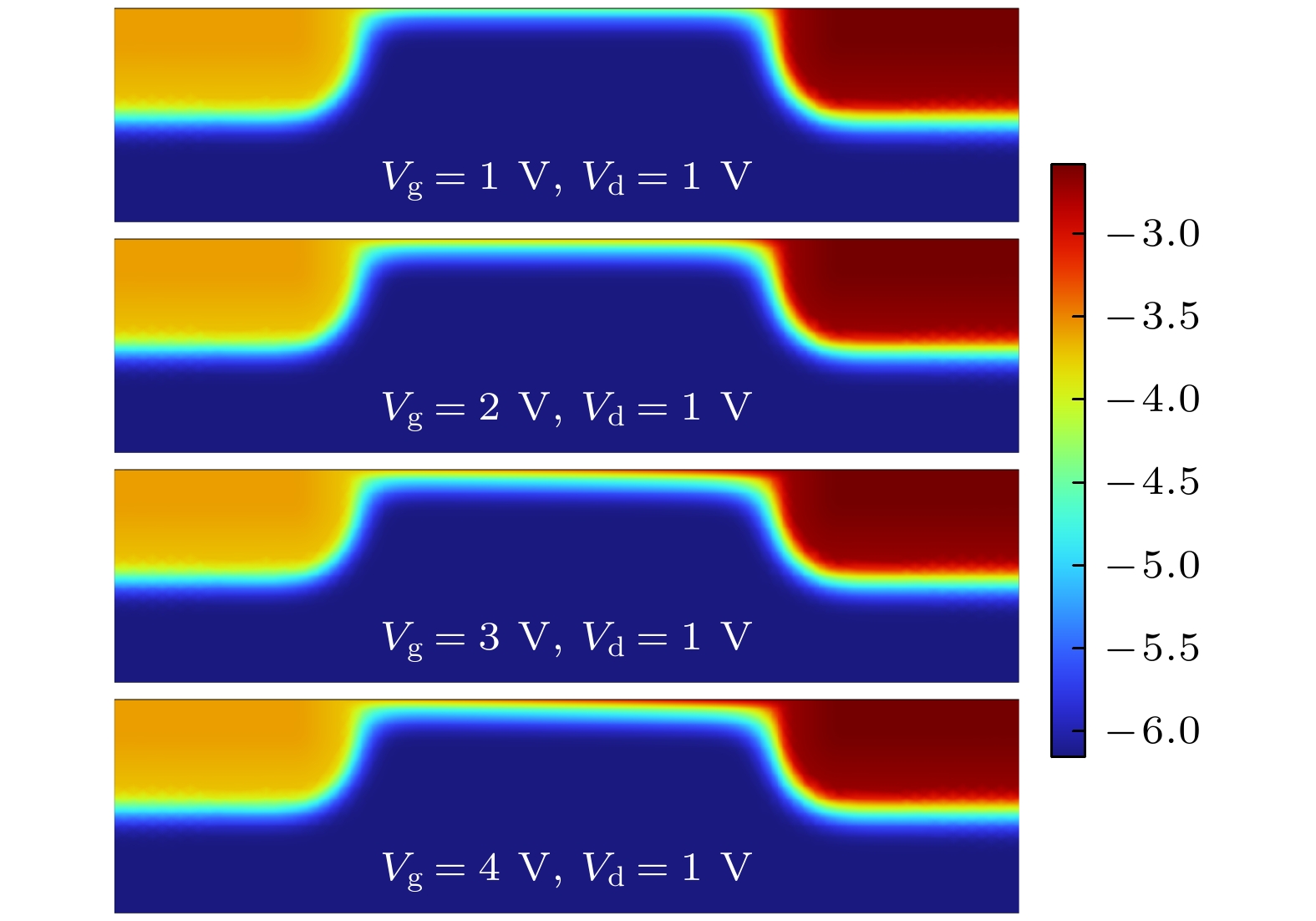
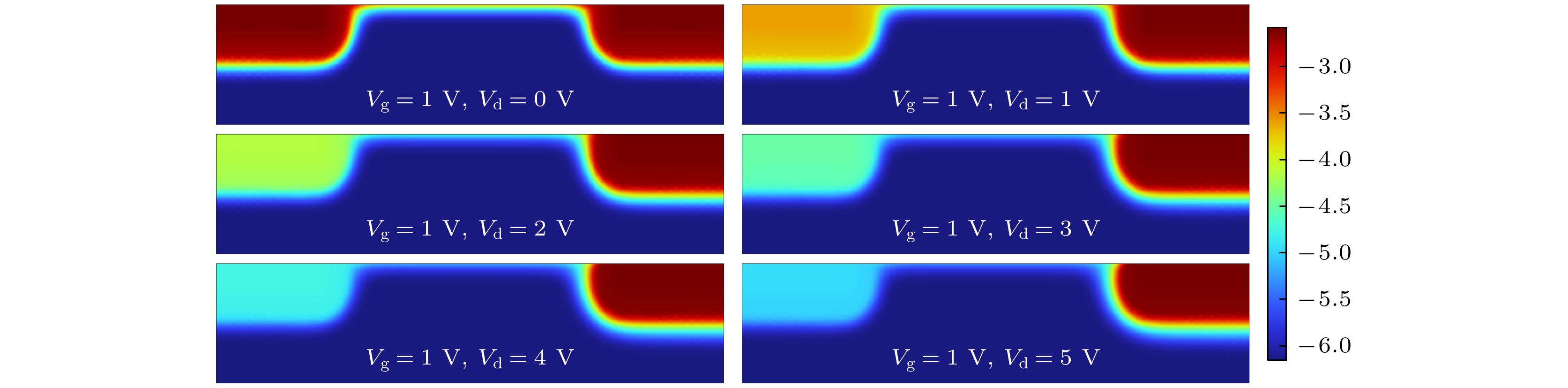
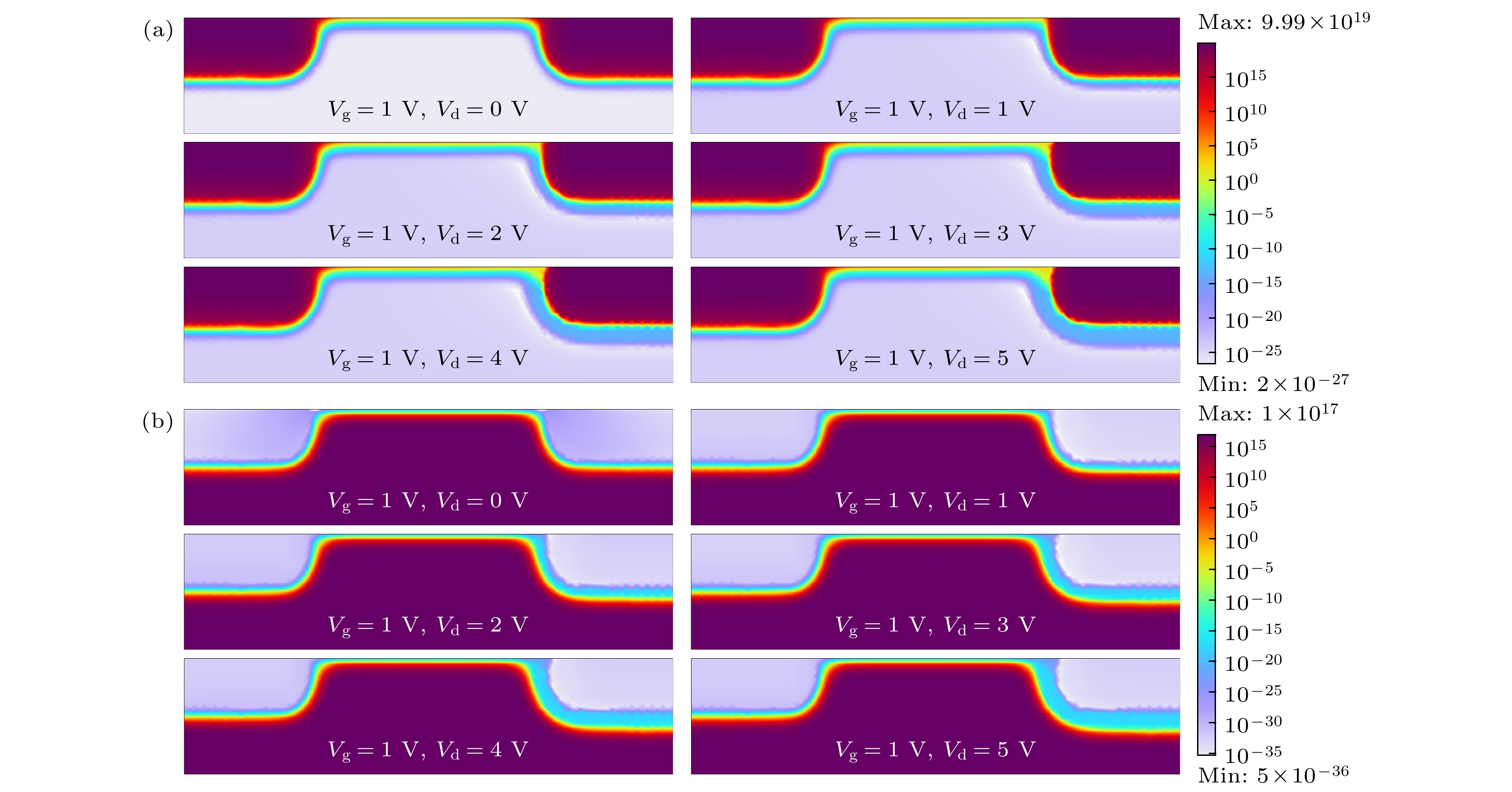
通过有限元仿真, 并对金刚石烯基超敏检测器工作中的电势、电子/空穴分布进行可视化研究. 首先分析电势的变化关系(见图3). 根据(10)式计算出的饱和区域长度
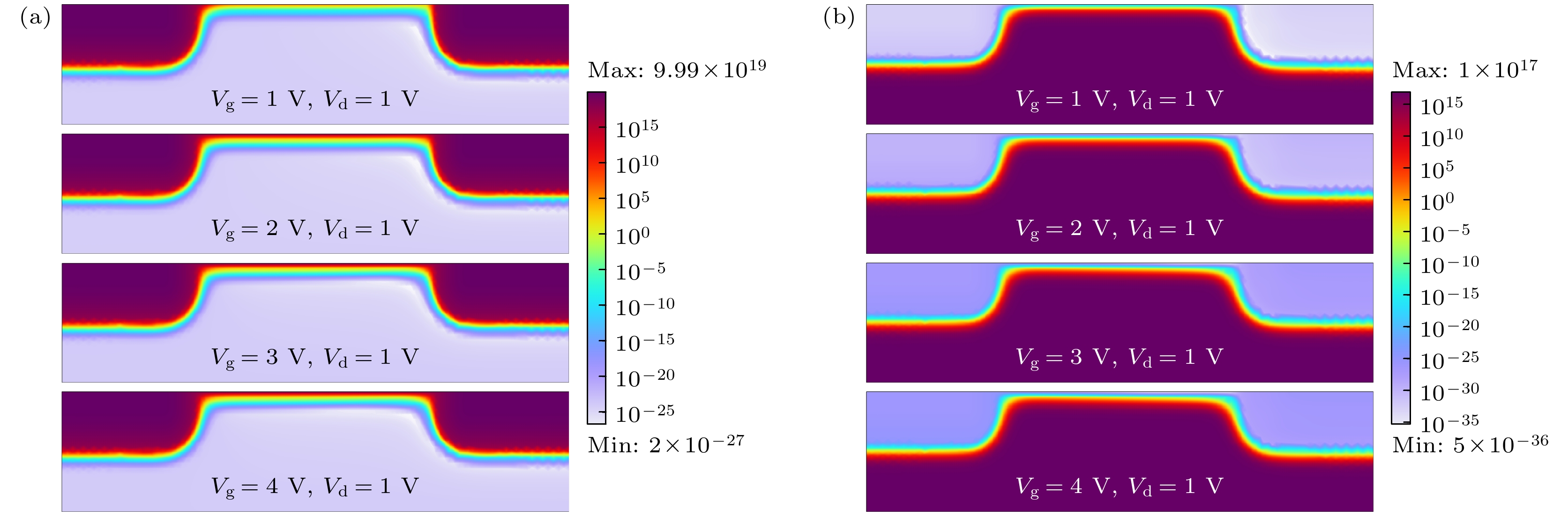
$ {L_{\text{D}}} $ . 可以验证, 在一定范围内,$ {L_{\text{D}}} $ 随栅压增大, 但当栅压达到饱和值后,$ {L_{\text{D}}} $ 不再变化. 因此, 栅控最佳范围为0—4 V. 接下来进一步分析工作中电势随漏压的作用关系, 如图4所示. 可以发现, 在栅压恒定情况下, 随着漏压的增大, 两级电势差逐渐增大, 进而产生电子流动, 同时沟道电势逐渐减弱. 因此, 漏压对电势分布作用敏感. 影响检测器电学性能的核心是内部的电子和空穴, 为进一步分析工作状态中的增敏特性, 接下来分析电子和空穴的分布情况. 图5展示了电子和空穴随栅压的变化情况.由图5(a)可知, 当栅压由1 V增至2 V后, 沟道电子显著增加, 说明金刚石烯沟道电子对栅压敏感性较强. 受栅控作用影响, 沟道电子“被激活”, 增强了沟道电子/空穴的“流动”性. 其内部电场会随着栅极电压的增大而增大, 增大的电场会导致载流子的动能增大, 从而加速它们在沟道中的作用[27], 由于金刚石烯本身具有高载流子迁移率等优异特性, 在输运中电流承载能力更强. 因此, 为提升检测器性能, 需采用高灵敏电子材料作为沟道敏感材料, 而金刚石烯具备高敏感电子特性, 满足超敏性能需求. 接下来进一步分析随漏压的变化关系. 随着漏压的加入, 初始平衡态被打破, 施加的漏压为工作极源源不断输入流动电荷. 由图6可知, 对于金刚石烯超敏材料来说, 电子/空穴分布易受漏源调控, 沟道流动平稳, 实现超敏检测性能.
-
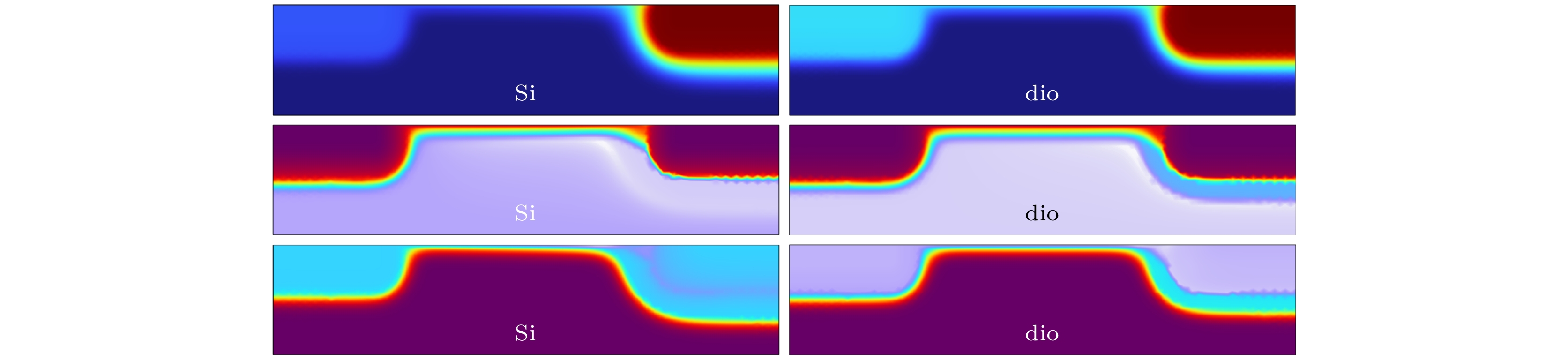
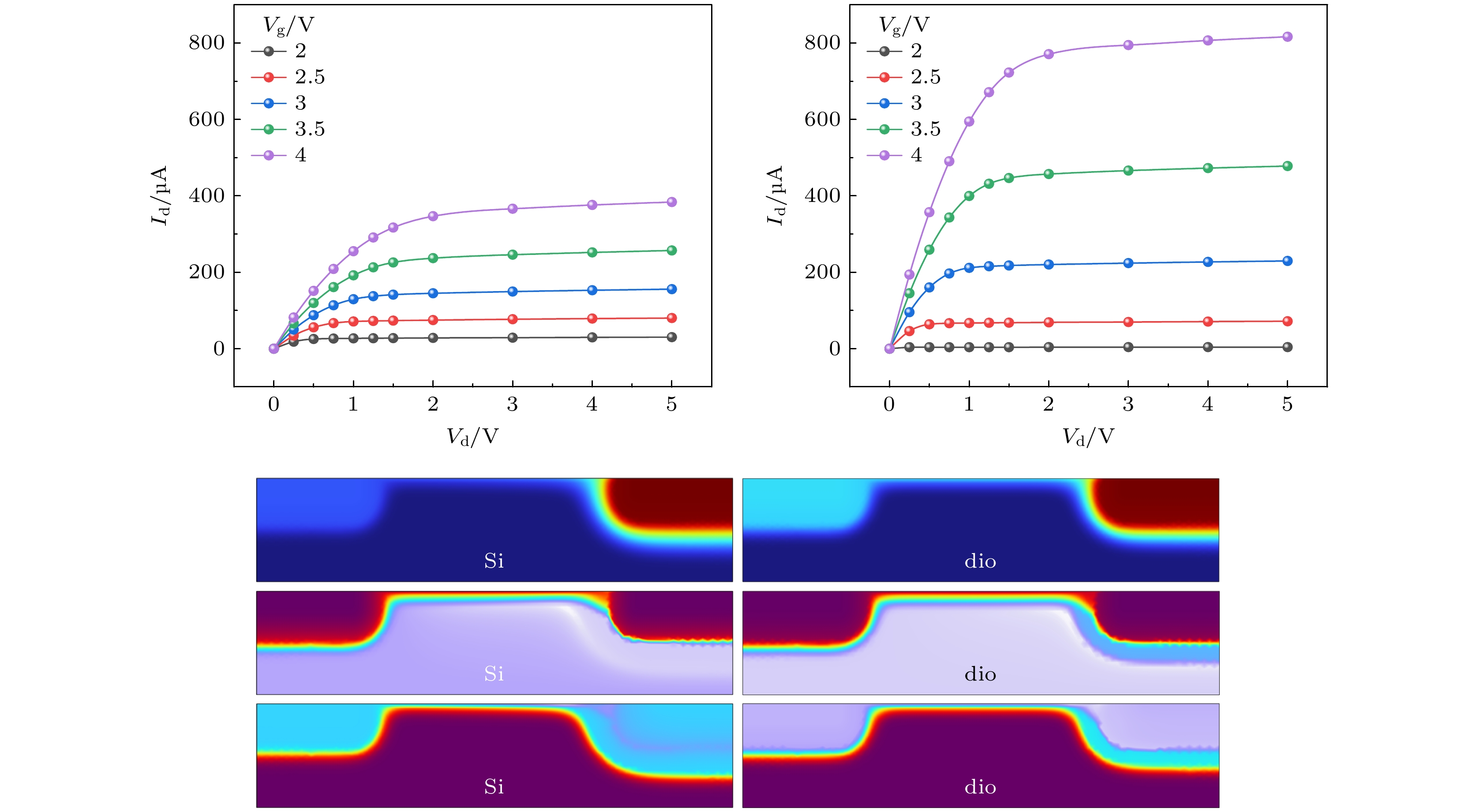
接下来仿真传统硅基检测器的电子电流特性并与金刚石烯基检测器进行对比. 图7展示了二者在相同外界调控下(
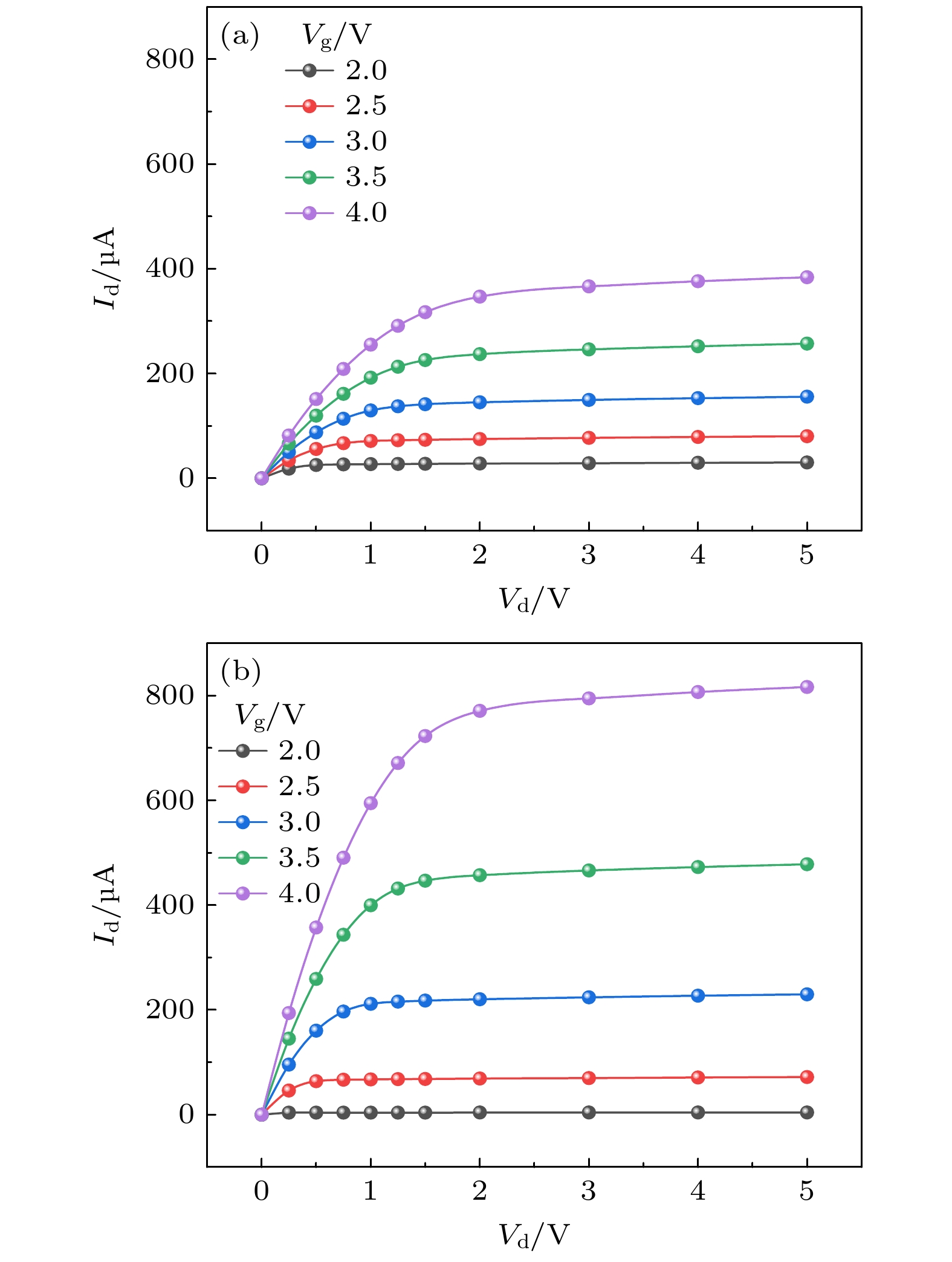
$ {V_{\text{g}}} = 2 {\text{V}}, {V_{\text{d}}} = 5 {\text{V}} $ )的电势、电子和空穴的分布特性. 从电子分布情况分析, 金刚石烯基检测器分布差低于硅基检测器. 在工作过程中, 由图7可知, 硅基两级处的电子/空穴分布差比金刚石烯基较大, 硅基源极漏极电子分布存在较大偏差, 对其性能影响较大[28]. 相比之下, 金刚石烯基检测器两级压降较低, 电路的效率和性能较高.为进一步评估二者的检测性能, 同时对二者的检测电流进行了仿真对比, 如图8所示. 可以发现, 在相同栅控电压下, 金刚石烯的电流高于硅基检测器. 为方便对比, 仿真中用到的仿真模型尺寸保持一致, 仅沟道材料不同. 因此, 利用场效应迁移率的对比可反映出沟道材料的检测水平, 根据(23)式, 可得金刚石基与硅基检测器迁移率之比
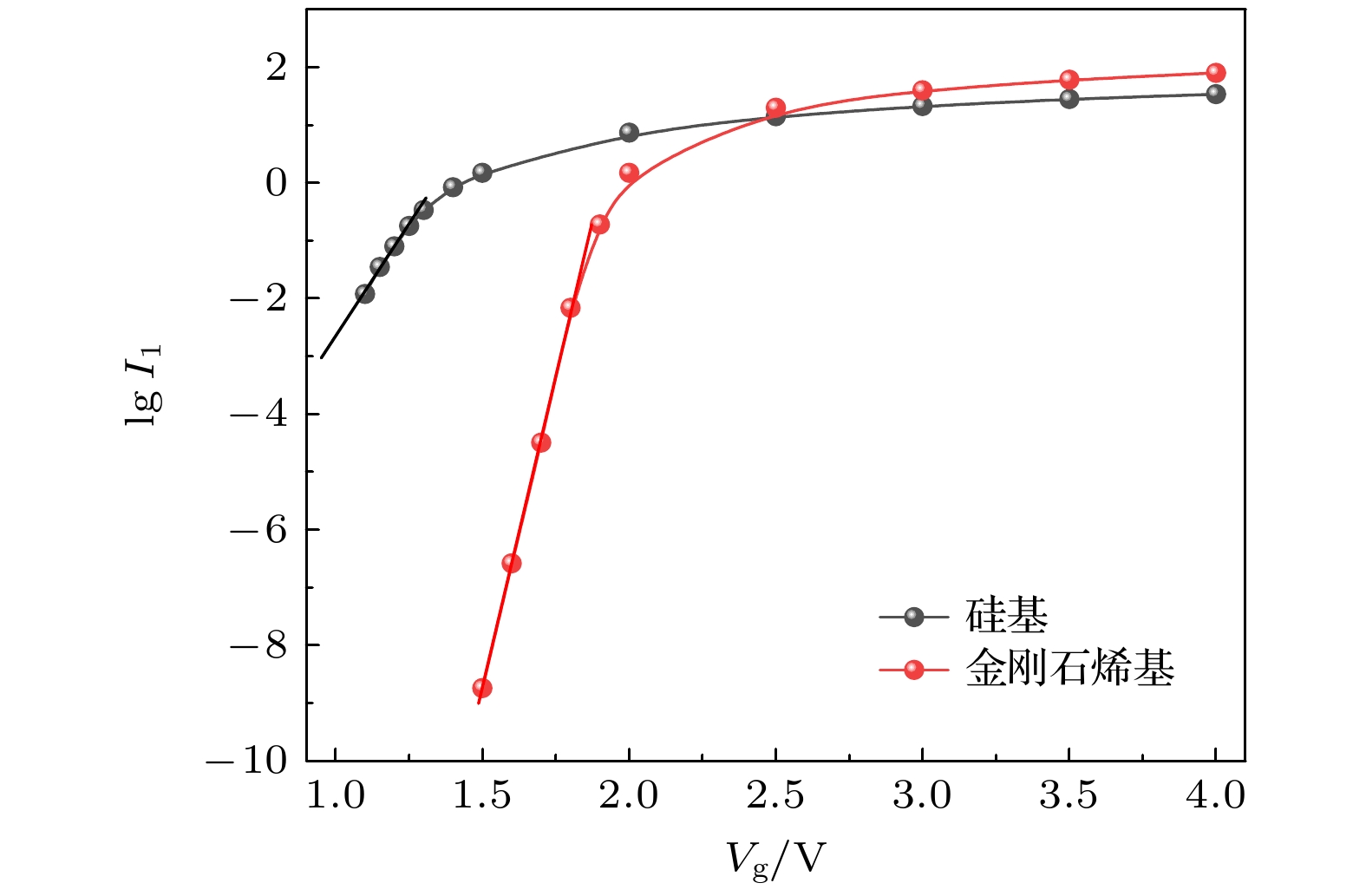
$ {n_{\text{μ }}} $ 为通过对比发现, 金刚石烯基比硅基检测器迁移率性能要高2.5倍, 明显优于硅基材料. 接下来利用(24)式进一步分析二者的电流灵敏度. 硅基与金刚石烯基
$ \log {I_1}{\text{-}}{V_{\text{g}}} $ 对比如图9所示.根据图9和(24)式, 亚阈值摆幅参数
$ S $ 为拟合斜率的倒数, 通过计算可以得出硅基和金刚石烯基的$ S $ 值之比$ {n_S} $ 为可以发现, 硅基的亚阈值摆幅参数
$ S $ 值是金刚石烯基的2.5倍, 也就是说, 在相同数量级电流的检测下, 硅基所需施加的栅压是金刚石烯基的2.5倍. 因此, 金刚石烯的栅控电流较为灵敏, 在较小的栅压下可引起电流在相同数量级上的变化. 转换成检测电流灵敏度, 金刚石烯基检测电流灵敏度约为硅基检测器的$ {1}{{0}^{{n_{\text{s}}}}} \approx {316} $ 倍. 在相同结构中, 金刚石烯基检测器的$ {S_{{\text{dio}}}} $ 值约为$ {49}{\text{.6 mV/decade}} $ , 优于传统硅基检测器[29]. 因此, 金刚石烯材料在超敏检测中具有突出优势, 可实现更灵敏的高性能检测. -
针对传统硅基晶体管检测灵敏度不能满足现代装备发展需求且沟道材料尺寸受限的问题, 本文开展了金刚石烯基超敏检测理论与特性研究. 首先开展了晶体管沟道解析模型及机理研究, 通过分析工作状态中电流沟道表面电势分布情况、有效沟道尺寸的关系以及沟道二维材料电子的敏感特性, 构建了一种基于沟道材料电子特性的晶体管检测器理论模型, 揭示了检测器件的工作特性. 基于有限元仿真模拟了晶体管检测器的工作机制及电势、电子分布, 仿真结果显示金刚石烯基检测器的迁移率水平是传统硅基检测器的2.5倍, 检测电流灵敏度是传统硅基的316倍, 从理论层面验证了金刚石烯基检测器的超敏检测特性. 本文研究工作, 可为实现金刚石烯基超敏检测提供理论指导与技术支撑, 对新一代碳基超敏检测器件的设计和应用具有重要意义.
金刚石烯基晶体管沟道解析模型与电流超敏特性
Channel analysis model and current hypersensitivity characteristics of diamondene-based transistor
-
摘要: 新一代检测装备对高灵敏检测器提出了迫切需求. 纵观半导体检测器件的发展现状, 目前传统硅基检测器灵敏度及沟道尺寸已不满足未来所需, 金刚石烯具有高载流子迁移率、宽带隙等优异性能, 其优异的电子特性有望有效提升检测器的灵敏度性能, 为下一代检测器发展提供新途径. 但基于金刚石烯的检测机理还尚不明晰. 基于上述问题, 本文通过建立晶体管电流沟道理论模型, 分析了检测器工作状态下电子流动机制, 进一步结合沟道材料电子特性, 建立一种基于沟道材料电子流动的晶体管电流理论模型, 并开展金刚石烯基晶体管检测器的机理仿真验证、电子特性分析研究, 证明了碳基二维材料——金刚石烯在超敏电子检测中的潜力, 为新一代高性能检测器的研制提供技术基础.Abstract: The new generation of detection equipment urgently requires high-sensitivity detectors. Traditional silicon-based detectors cannot meet the requirements for sensitivity and channel size. Diamondene has excellent performance such as high carrier mobility and wide band gap. Its excellent electronic characteristics are expected to effectively improve the sensitivity of the detector and provide a new way for developing the next generation of detectors. However, the detection mechanism based on diamondene is still unclear. Based on the above problems, the analytical model and mechanism of the transistor channel are first studied. By analyzing the relationship between the surface potential distribution of the current channel and the effective channel size in the working state and the sensitive characteristics of the two-dimensional material electrons of the channel, a theoretical model of the transistor detector is constructed based on the electronic characteristics of the channel material, and the working characteristics of the detector are investigated. The finite element simulation of the working mechanism, potential and electron distribution of the transistor detector is carried out. The simulation results show that the mobility level of the diamondene-based detector is 2.5 times that of the traditional silicon-based detector, which theoretically verifies the hypersensitive detection characteristics of the diamondene-based detector. This study is of great significance in designing and applying a new generation of carbon-based ultra-sensitive detection devices.
-
Key words:
- high-sensitivity detector /
- channel electronics /
- sensitivity /
- migration rate .
-
-
图 1 晶体管工作电子流动原理图
Figure 1. Schematic diagram of the electron flow principle of the transistor.
图 2 折射率实部(a)和虚部(b)随费米能量的变化关系
Figure 2. Relationship between the real part (a) and the imaginary part (b) of the refractive index with Fermi energy.
图 3 晶体管内截面电势分布随栅压的变化情况
Figure 3. Distribution of the cross-section potential distribution in the transistor with the gate voltage.
图 4 晶体管内截面电势分布随漏压的变化情况
Figure 4. Distribution of the cross-section potential distribution in the transistor with the drain voltage.
图 5 电子(a)和空穴(b)随栅压的分布关系
Figure 5. Distribution of electrons (a) and holes (b) with gate voltage.
图 6 电子(a)和空穴(b)随漏压的分布关系
Figure 6. Distribution of electrons (a) and holes (b) with drain voltage.
图 7 硅基和金刚石烯基检测器的电势、电子和空穴分布对比
Figure 7. Comparison of electric potential, electron, and hole distributions of silicon-based and diamondene-based transistors.
图 8 硅基(a)和金刚石烯基(b)检测器的检测电流性能对比
Figure 8. Comparison of the current performance of silicon-based (a) and diamondene-based (b) transistors.
图 9 硅基与金刚石烯基
$ \log {I_1}{\text{-}}{V_{\text{g}}} $ 图Figure 9. The
$ \log {I_1}{\text{-}}{V_{\text{g}}} $ of silicon-based and diamondene-based transistors.表 1 金刚石烯与硅沟道材料仿真参数
Table 1. Simulation parameters of diamondene and silicon channel materials.
材料 金刚石烯 硅 带隙/eV 2.7 1.12 电子迁移率/m–3 4500 1450 空穴迁移率/m–3 1000 500 电子亲和能/eV 3.64 4.05 
下载: 导出CSV
-
[1] Jiang J F, Xu L, Qiu C G, Peng L M 2023 Nature 616 470 doi: 10.1038/s41586-023-05819-w [2] Dwivedi P, Soneja S, Dhanekar S 2018 IEEE Sensors New Delhi, India, October 28–31, 2018 [3] Liu K L, Jin B, Han W, et al. 2021 Nat. Electron. 4 906 doi: 10.1038/s41928-021-00683-w [4] Grigorenko A N, Polini M, Novoselov K S 2012 Nat. Photonics 6 749 doi: 10.1038/nphoton.2012.262 [5] Gui G, Li J, Zhong J X 2008 Phys. Rev. B 78 075435 doi: 10.1103/PhysRevB.78.075435 [6] Lu G H, Yu K H, Wen Z H, Chen J H 2013 Nanoscale 5 1353 doi: 10.1039/c2nr32453a [7] He Q, Su K, Zhang J F, Ren Z Y, Xing Y F, Zhang J C, Lei Y Q, Hao Y 2022 IEEE T. Electron Dev. 69 1206 doi: 10.1109/TED.2022.3147738 [8] Zhen J P, Huang Q S, Shen K, et al. 2024 PNAS 121 e2403726121 doi: 10.1073/pnas.2403726121 [9] Su K, Ren Z Y, Peng Y, Zhang J F, Zhang J C, Zhang Y C, He Q, Zhang C F, Hao Y 2020 IEEE Access 8 20043 doi: 10.1109/ACCESS.2020.2968742 [10] Sasama Y, Kageura T, Imura M, Watanabe K, Taniguchi T, Uchihashi T, Takahide Y 2022 Nature Electronics 5 37 [11] Zhang Q, Fang T, Xing H, Seabaugh A, Jena D 2008 IEEE Electron. Device Lett. 29 1344 doi: 10.1109/LED.2008.2005650 [12] Cheli M, Michetti P, Iannaccone G 2010 IEEE Electron. Devices Trans 57 1936 doi: 10.1109/TED.2010.2051487 [13] Liang G, Neophytou N, Lundstrom M S, Nikonov D E 2008 J. Comput. Electron 7 394 doi: 10.1007/s10825-008-0243-1 [14] Xing H L, Fang T, Konar A, Jena D 2007 Appl. Phys. Lett. 91 092109 doi: 10.1063/1.2776887 [15] Hanson G W 2008 J. Appl. Phys. 103 064302 doi: 10.1063/1.2891452 [16] Jabbarzadeh F, Heydari M, Sharif A H 2019 Mater. Res. Express 6 086209 doi: 10.1088/2053-1591/ab1e02 [17] Gusynin V P, Sharapov S G, Carbotte J P 2007 J. Phys.: Condens. Matter 19 026222 doi: 10.1088/0953-8984/19/2/026222 [18] Xu W, Zhu Z H, Liu K, et al. 2015 Opt. Express 23 5147 doi: 10.1364/OE.23.005147 [19] Luo X G, Teng Q, Lu W B, Ni Z H 2013 Mater. Sci. Eng. R 74 351 doi: 10.1016/j.mser.2013.09.001 [20] Hua L, Gan X T, Mao D, Zhao J L 2017 Photonics Res. 5 162 doi: 10.1364/PRJ.5.000162 [21] Lima A W, Sombra A 2014 Opt. Commun. 321 150 doi: 10.1016/j.optcom.2014.01.052 [22] Frank S 2010 Nat. Nanotech. 5 487 doi: 10.1038/nnano.2010.89 [23] 季启政, 刘峻, 杨铭, 马贵蕾, 胡小锋, 刘尚合 2023 电子学报 51 1486 Ji Q Z, Liu J, Yang M, Ma G L, Hu X F, Liu S H 2023 Chinese Journal of Electronics 51 1486 [24] Chakraborty I, Roy S, Dixit V, Debnath K 2021 Photonic Nanostruct. 43 100865 doi: 10.1016/j.photonics.2020.100865 [25] Jabbarzadeh F, Habibzadeh S A 2019 JOSA B 36 690 doi: 10.1364/JOSAB.36.000690 [26] Liu M, Yin X B, Erick U A, Geng B S, Zentgraf T, Ju L, Wang F, Zhang X 2011 Nature 474 64 doi: 10.1038/nature10067 [27] Heidari M, Orouji A A, Bozorgi S A 2023 J Mater Sci: Mater Electron 34 1708 doi: 10.1007/s10854-023-11104-3 [28] Santini T, Morand S, Fouladirad M, et al. 2014 Microelectronics Reliability 54 1718 doi: 10.1016/j.microrel.2014.07.082 [29] Sreevani A, Swarnakar S, Krishna S V 2022 Silicon 14 9223 doi: 10.1007/s12633-022-01674-y -
计量
- 文章访问数: 35
- HTML全文浏览数: 35
- PDF下载数: 0
- 施引文献: 0