-
高载流子迁移率的半导体材料在现代电子器件的发展中扮演着至关重要的角色, 这些材料同时具有合适的带隙、长载流子寿命和高可见光吸收系数等优点, 为制造低成本、高效率的光电材料、太阳能电池材料和光催化剂提供了可能[1–3]. 低维层状半导体材料作为未来纳米电子和光电器件的一个重要组成部分, 具有传统三维块状半导体所不具备的特性, 如高速、高灵活性和低功耗, 正日益受到关注[4,5]. 例如, 具有带状结构的Sb2Se3的载流子迁移率呈现出明显的各向异性, 其中沿着以较强的共价键连接的方向的载流子迁移率远高于以较弱的范德瓦耳斯力连接的另外两个方向[6]. 二维层状结构的黑磷因其x, y方向分别呈扶手椅状和锯齿状, 从而形成各向异性的带状结构, 具有各向异性的光学、电学和热学特性[7,8]. 而具有链状结构的准一维范德瓦耳斯层状材料Nb4P2S21表现出较强的各向异性光学、光电特性, 可以应用于新型光电探测器[9].
近些年有研究表明, 三元氮化物在光伏和光电化学能源转换领域有很大的应用潜力[10–17]. 很多具有化学计量比的三元氮化物AMN2以准二维的层状结构结晶[18,19]. 例如, SrHfN2和SrZrN2具有α-NaFeO2型结构[20,21] (空间群
$R \bar {3} m $ ), MgZrN2和MgHfN2具有γ-LiFeO2型结构[14] (空间群$I4_1/amd $ ), BaCeN2[22]具有β-RbScO2型结构(空间群$P6_3/ mmc $ ), CaTiN2[23]和SrTiN2[24,25]具有KCoO2型结构. 其中, KCoO2型结构又分为正交和四方两种结构类型. 迄今为止, 实验仅仅报道了具有正交对称性(空间群Pnmm)的CaTiN2[23]和3种具有四方对称性(空间群P4/nmm)的SrTiN2[24,25], BaZrN2和BaHfN2化合物[26–28]. 由于特殊的层状结构, 这些氮化物展现了丰富的各向异性的介电常数[20,29]、热电输运性质[30,31]、光电性质[20].近期, 我们采用第一性原理计算的方法研究了具有KCoO2型层状结构的氮化物ATiN2 (A为碱土金属元素Ca, Sr和Ba)的力学性质、电子结构、载流子输运性质和光学性质, 发现这些材料都具有合适的带隙和带边位置、超高各向异性的载流子迁移率、良好的可见光吸收能力和较低的激子结合能, 是光电子、光伏和光催化领域有前景的半导体材料[32]. 尽管目前没有BaTiN2的实验报道, 但三元层状氮化物BaMN2 (M = Zr, Hf)已经被固态实验合成[26–28], 并且在(001)SrTiO3衬底上可以生长BaMN2外延薄膜[33]. BaMN2氮化物的电子结构[17]、介电常数[34]、热电性质[35]已经被广泛研究, 特别是最近理论预测BaMN2材料的超低热导率[35]和不同节点线声子的非平庸拓扑特征[36]吸引了研究者的兴趣, 但是其光学性质和电输运性质尚未被系统地研究. 考虑到BaMN2氮化物独特的层状晶体结构和丰富的物理性质, 本文通过第一性原理计算和分析系统研究了BaMN2 (M为同族的Ti, Zr和Hf元素)氮化物的力学性质、电子结构、载流子迁移率、可见光吸收系数和介电性质. 研究结果为理解具有准二维层状结构的BaMN2氮化物中各向异性物理性质提供了新的思路, 为这些氮化物材料在光电子、光伏和光催化领域中的进一步应用提供理论参考.
-
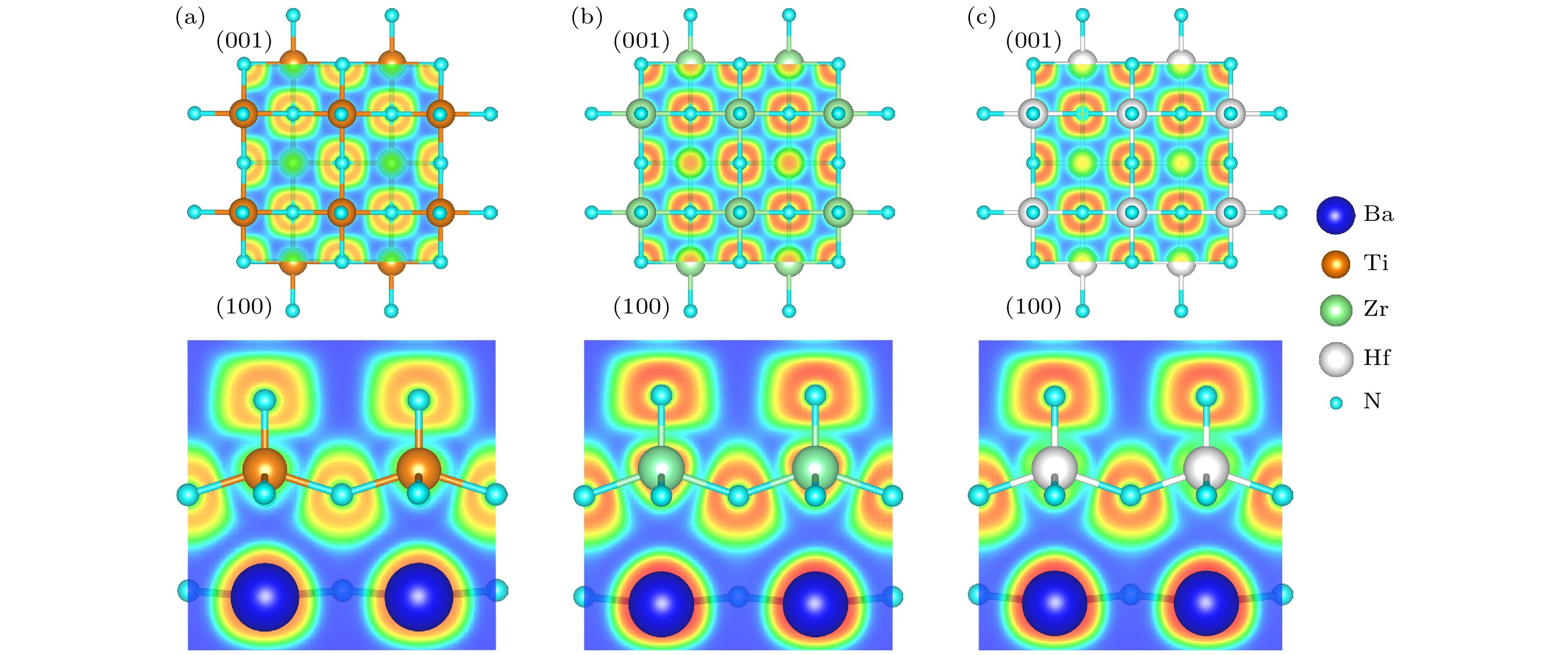
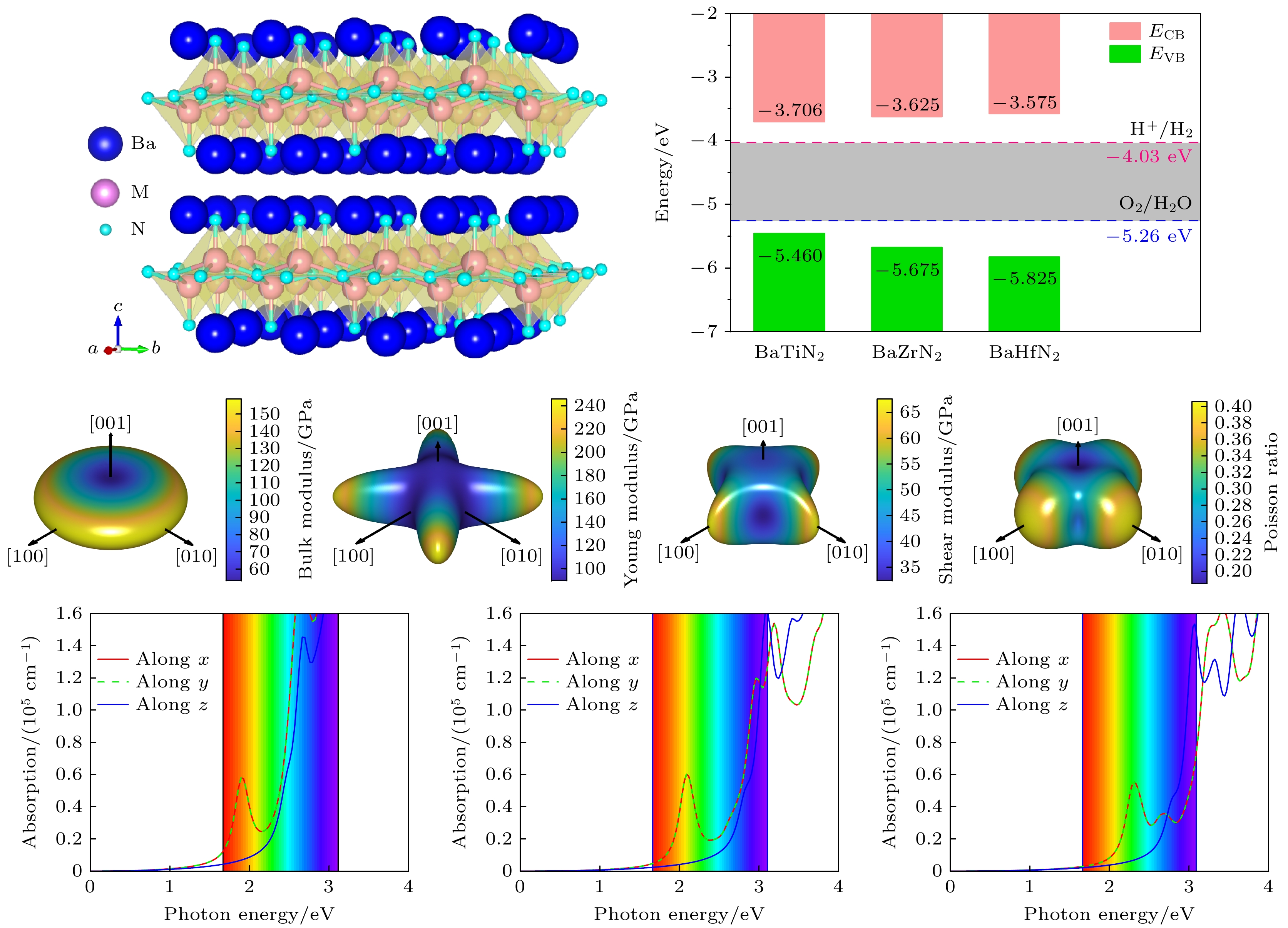
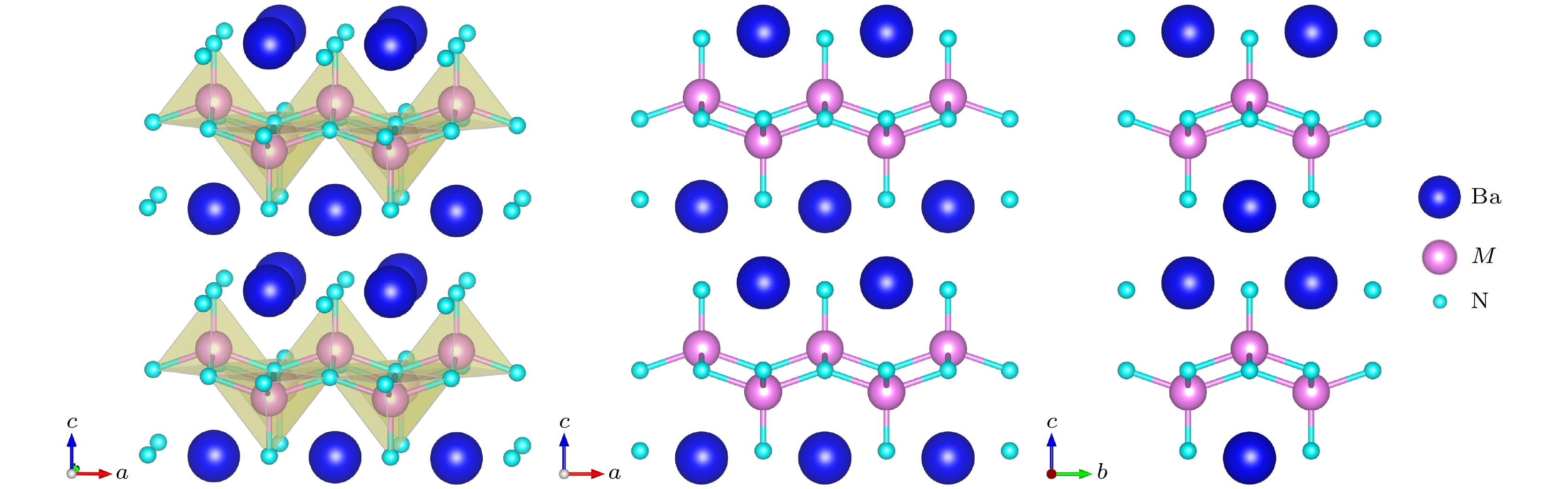
BaMN2氮化物具有四方对称性(空间群 P4/nmm). 如图1所示, BaMN2氮化物中的N3–与
$M^{4+} $ 离子形成共边连接的金字塔结构基元, Ba2+离子位于金字塔顶端之间. BaMN2中具有两种不同的N位, 记为N1 (位于Ba平面附近)和N2 (位于M平面附近), 所以BaMN2的晶体结构由几乎共面的[BaN1]–层和波纹状的[MN2]+层组成, 且M离子交替的位于N2层的上、下方. -
本文理论计算使用基于投影增强波(PAW)势[37,38]的VASP (Vienna ab initio simulation package)[39,40]计算软件包进行. 其中平面波截断能为520 eV, 采用Monkhorst-Pack方法[41]对原胞进行布里渊区积分, 布里渊区k点网格取8×8×4. 选择广义梯度近似(GGA)[42]作为交换关联势进行电子结构计算. 为克服GGA对带隙的低估, 进行了杂化泛函(HSE06)[43]计算. 为了减少计算成本, 采用HSE@GGA模式[44], 通过假设在应用HSE06杂化函时导带相对于价带发生刚性平移, 从而获得带隙. 采用密度泛函微扰理论(DFPT)[45,46]结合VASP软件包以及局域密度近似(LDA)[47]计算波恩有效电荷张量和宏观介电张量[48,49]. 静态介电张量ε包括电子
$ {\varepsilon }_{{\mathrm{e}}{\mathrm{l}}{\mathrm{e}}} $ 和离子$ {\varepsilon }_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $ 的贡献($ \varepsilon ={\varepsilon }_{{\mathrm{e}}{\mathrm{l}}{\mathrm{e}}}+ {\varepsilon }_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}}) $ [50,51]. 通过对ε的对角线分量求平均值, 得到介电常数$ {\varepsilon }_{{\mathrm{r}}} $ .基于Bardeen和Shockley首次提出的形变势理论[52], 可以由(1)式计算得到三维晶体的载流子迁移率:
其中e为电子电荷,
$\hbar $ 为约化普朗克常数, kB为玻尔兹曼常数, T为温度(本文设置为室温, T = 300 K),$ {m}_{{\mathrm{e}}}^{*} $ 是有效质量,$ {C}_{ij} $ 为沿载流子传输方向的弹性常数, Ei为形变势. 用有限差分法通过下式计算$ {m}_{{\mathrm{e}}}^{*} $ :Ei表达式为
式中,
$\partial $ E(k)是导带底或价带顶的能量由晶格形变引起的变化,$ {{\Delta }}V $ 是晶体体积在压缩或拉伸膨胀下的变化量,$ {V}_{0} $ 为晶胞平衡状态下的体积. -
表1为BaMN2氮化物结构优化后晶格常数、晶格体积和M—N的键长, 与文献[26–28]报道的实验值吻合较好, 确保了晶体结构的可靠性. 此外, 顶端的M—N1键长比底部的M—N2键长短, 说明M原子与顶端N1原子的键作用更强, 而M原子与N2原子之间的键作用较弱. 如图2所示, 可以通过电子局域函数(ELF)进一步研究离子间的成键相互作用. Ba原子之间的ELF表现出局域化特征, 而N原子周围的ELF表明这些区域有很强的电子密度, 并且有电子将M原子和相邻的N原子连接起来, 表明它们之间存在很强的共价键.
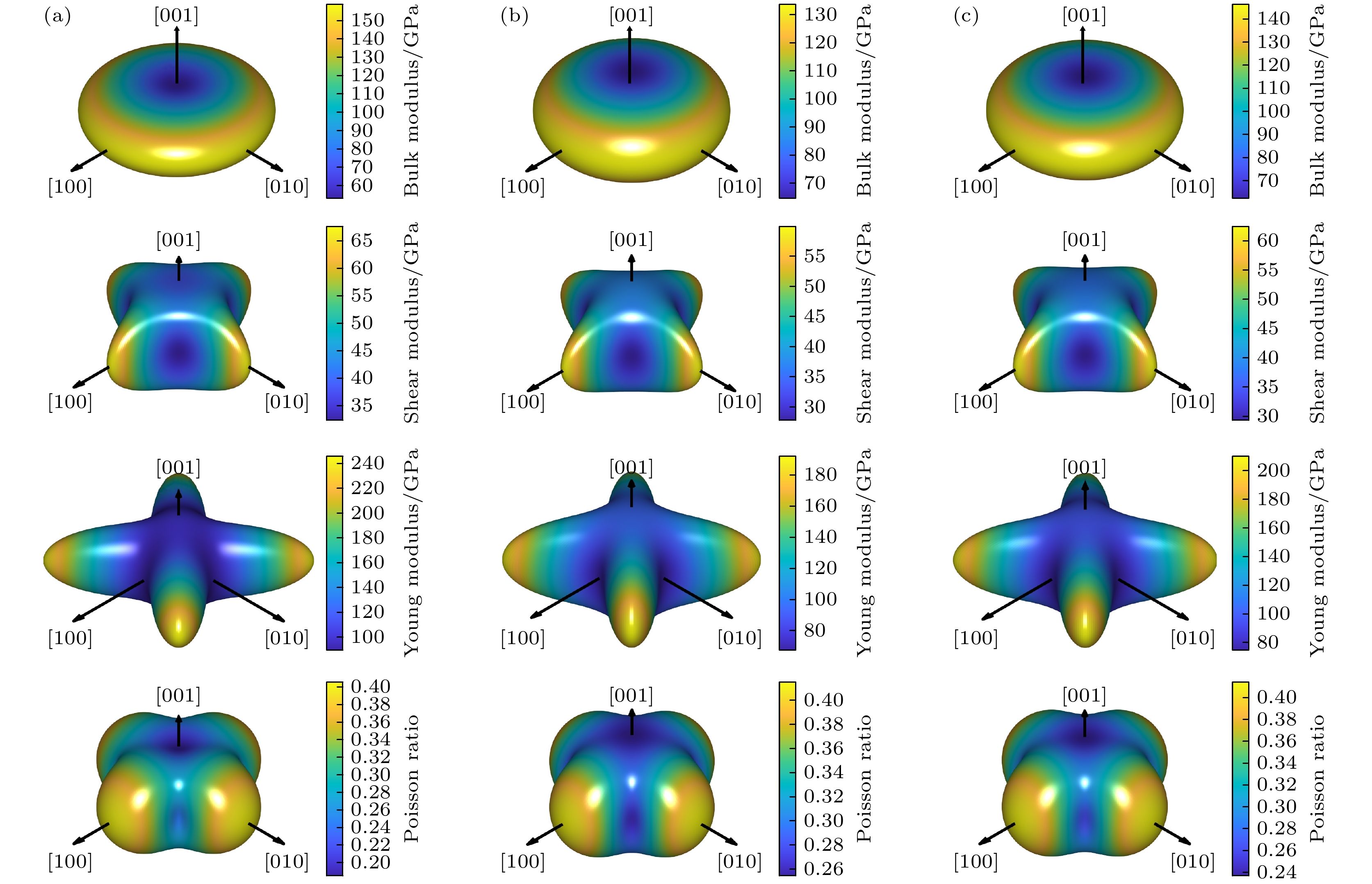
本文首先研究了BaMN2的力学性质, 它们都为四方结构, 有6个独立的弹性常数
$ {C}_{ij} $ . 表2列出了计算结果, 弹性常数满足四方晶系的Born力学稳定判据[53,54]. 使用Voigt-Reuss-Hill模型的近似法从$ {C}_{ij} $ 推导出体模量B和剪切模量G[55], 杨氏模量Y和泊松比ν定义为[54]:$ Y={9 BG}/{(3B+G)} $ ,$ \nu = (3 B-G)/[2\left(3 B+G\right)] $ . BaTiN2, BaZrN2以及BaHfN2的平均体模量B分别为101.175, 100.555和105.066 GPa, 平均杨氏模量Y分别为126.253, 109.580和115.194 GPa. 此外, 由于BaMN2是由准二维[MN2]2–板层排列组成, 其抵抗切应变的能力较弱, 这导致其平均剪切模量G均较低, 分别为48.900, 41.610和43.773 GPa. 较低的B, G和Y表明BaMN2氮化物对外部变形的抵抗能力较弱. BaTiN2, BaZrN2和BaHfN2的泊松比ν分别为0.294, 0.318和0.317, Pugh模量比(B/G)分别为2.070, 2.420和2.400. 根据Pugh定则, ν大于0.26, B/G大于区分塑性和脆性材料的临界值1.75[56,57], 表明它们都具有良好的延展性.为了进一步研究BaMN2的准二维层状结构特征引起的各向异性力学性质, 图3给出了采用ElasticPost软件[58]处理的三维模量图. BaMN2的所有力学性质都表现出明显的各向异性. BaMN2的体模量最大值在a-b平面内(分别为158.707, 133.524, 146.240 GPa), 最小值沿着平面外c轴([001])方向(分别为53.140, 64.774, 62.5569 GPa), 主要是由于准二维[MN2]2–板层在平面外的c轴方向键合作用较弱, 在外部应力作用下最容易产生沿着这一方向的变形. 剪切模量最大值沿着平面内的a和b轴([100]和[010])方向(分别为67.561, 59.860, 62.368 GPa), 最小值沿着平面内的a和b轴对角线([110]和[
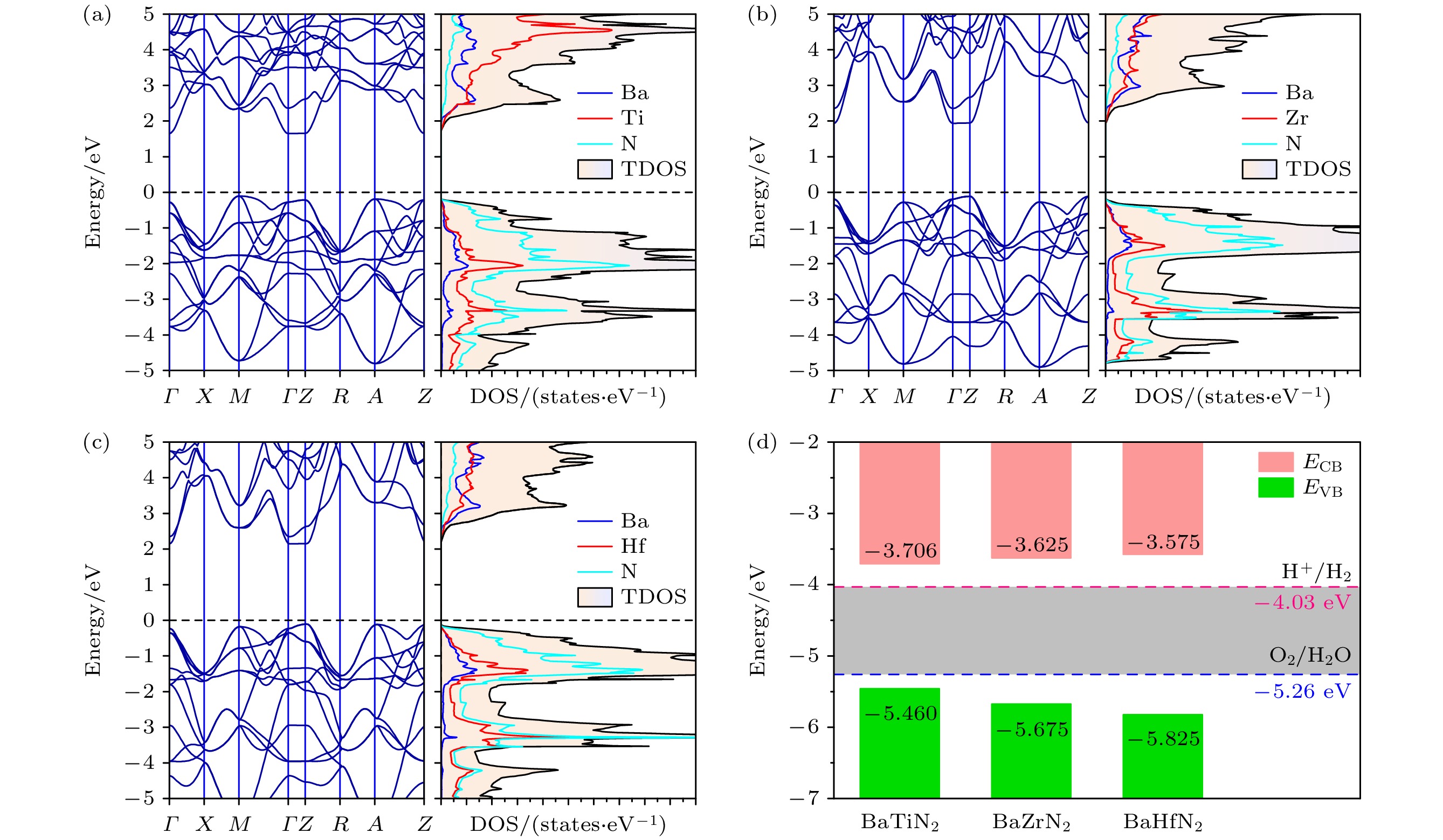
$ \bar{1} $ 10])方向(分别为32.403, 27.844, 29.340 GPa), 主要是由于M 4+和N3– 在平面内的a和b轴方向电子云重叠形成较强的共价键作用, 在剪切力作用下不容易产生变形. 杨氏模量最大值沿着平面内的a和b轴对角线([110]和[$ \bar{1}10 $ ])方向(分别为245.415, 191.855, 209.816 GPa), 最小值沿着平面内的a和b轴([100]和[010])方向(分别为89.737, 67.701, 74.978 GPa), 主要是由于M 4+和N3–在平面内的a和b轴方向电子云重叠形成较强的共价键作用, 在拉伸力作用下不容易产生变形. 泊松比最大值沿着平面内的a和b轴([100]和[010])方向(分别为0.405, 0.415, 0.414), 最小值沿着平面外c轴([001])方向(分别为0.185, 0.255, 0.237), 主要是由于准二维[MN2]2–板层在平面外的c轴方向键合作用较弱, 在外部应力作用下这一方向的变形容易被板层之间的空隙所吸收而不容易引起垂直方向的晶格变形. BaMN2氮化物显著的各向异性力学性能和良好延展性意味着它们在柔性器件中的潜在应用价值.BaMN2的电子结构如图4所示. BaMN2均为间接带隙半导体, BaTiN2, BaZrN2和BaHfN2的带隙分别为1.7541 eV, 2.0498 eV和2.2520 eV. 价带顶(VBM)主要由N的电子态贡献, 而导带底(CBM)则由Ba与M的电子态贡献. BaMN2的带隙值满足水分解对光催化剂的带隙基本要求(大于1.23 eV). 同时, 水分解光催化剂需要合适的带边位置, 即导带底要高于H+还原为H2的电位(H+/H2: –4.03 eV, pH = 7), 价带顶要低于H2O生成O2的氧化电位(O2/H2O: –5.26 eV, pH = 7). 为了判断BaMN2的带边位置是否满足这一要求, 需要知道其电子亲和势A和电离势I. 本质上费米能级是半导体电负性(–χ)的绝对值, 该值对应于导带底和价带顶之间的能量中间值[59], 可以利用相对电化学电位参考真空能级计算BaMN2的带边位置. 带边位置和电负性的关系可表示为:
$ {E}_{{\mathrm{C}}}= -A=-\chi +0.5{E}_{{\mathrm{g}}} $ ;$ {E}_{{\mathrm{V}}}=-I=-\chi -0.5{E}_{{\mathrm{g}}} $ ,其中,
$ {E}_{{\mathrm{C}}} $ 和$ {E}_{{\mathrm{V}}} $ 分别为导带底和价带顶的能量,$ {E}_{{\mathrm{g}}} $ 为带隙值. 随着M元素原子质量的增大, BaMN2氮化物的带隙逐渐增大, VBM逐渐升高, CBM逐渐降低, 均满足可见光催化水分解反应的带边位置要求, 如图4(d)所示, 是可见光催化水分解潜在的催化剂[60].通过观察图4(a)—(c)中Γ点CBM及VBM的能带变化趋势可知, CBM能带沿a-b平面(即Γ-X和Γ-M)的曲率较大, 而沿面外(即Γ-Z)方向的能带较为平坦, 表明在a-b平面上有较小的电子有效质量和较大的迁移率, VBM同样也有类似的特征. 通过对能带结构做抛物线拟合计算得到的电子有效质量(
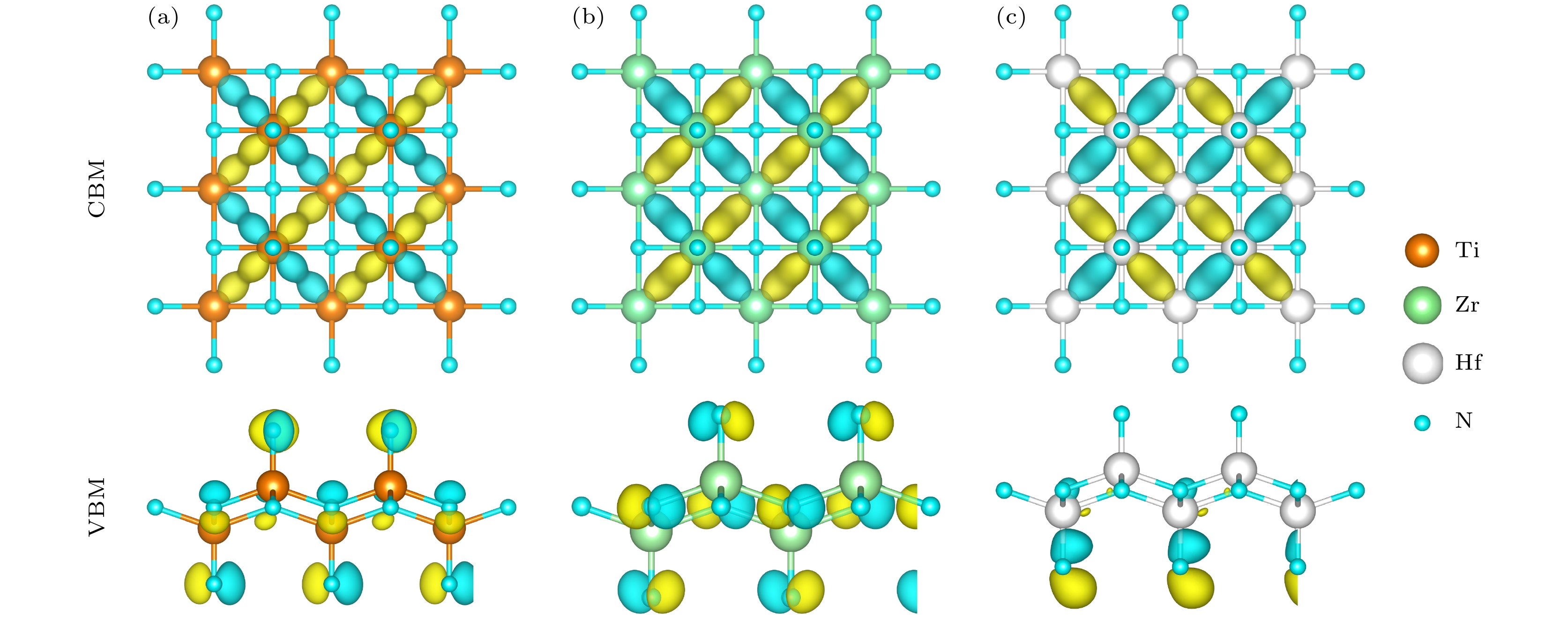
$ {m}_{{\mathrm{e}}}^{*} $ )和空穴有效质量($ {m}_{{\mathrm{h}}}^{*} $ ) 在表3列出. BaTiN2, BaZrN2和BaHfN2沿Γ-X (Γ-Z)的$ {m}_{{\mathrm{e}}}^{*} $ 分别为0.237m0 (29.929m0), 0.229m0 (32.657m0)和0.223m0(30.268m0), 而沿Γ-X (Γ-Z)的$ {m}_{{\mathrm{h}}}^{*} $ 分别为0.536m0(2.560m0), 0.400m0(5.435m0)和0.415m0 (3.608m0). BaMN2的载流子(电子和空穴)的有效质量沿面内(Γ-X)方向均小于1, 而在面外(Γ-Z)方向上均有较大的有效质量, 这意味着电子几乎只能在a-b平面上进行传输. 如图5实空间中的波函数所示, CBM主要由M-dxy轨道形成, 这将为具有较轻$ {m}_{{\mathrm{e}}}^{*} $ 的电子提供高度各向异性和二维平面内的输运通道, 而VBM主要由N-2p轨道贡献, 较轻的$ {m}_{{\mathrm{h}}}^{*} $ 将有利于二维平面中的空穴输运[32].根据三维材料载流子迁移率的计算表达式(1)式, 只需知道该材料的弹性常数、形变势和有效质量等参数, 即可得到在温度T下的载流子迁移率. 在输运方向上三维弹性常数
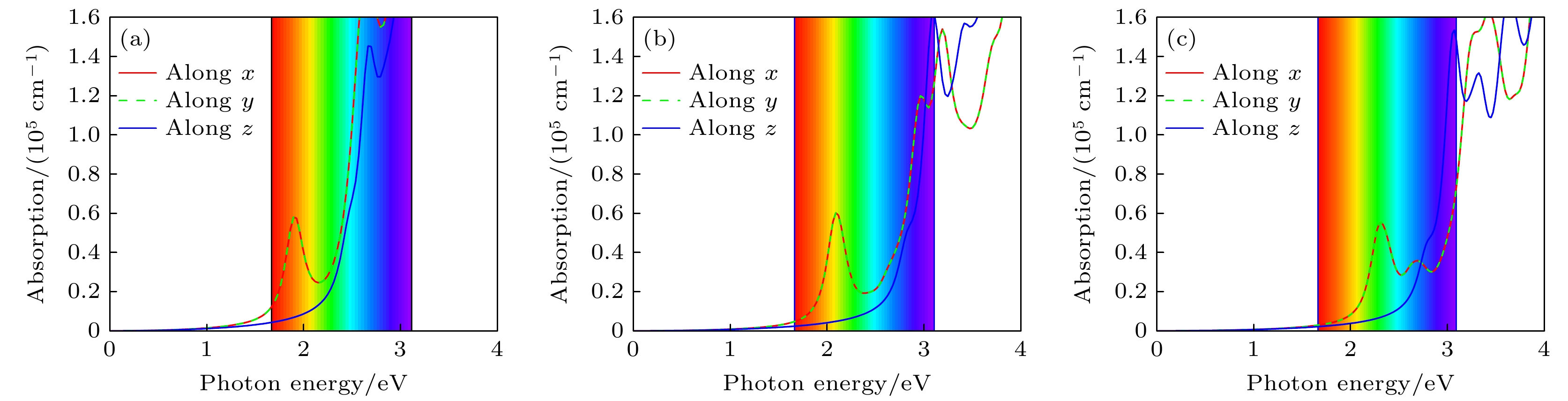
$ {C}_{ij} $ 的数值见表2(在x, y, z方向上的弹性常数标记为C11, C22, C33). 为计算形变势, 对3种结构沿不同方向施加了从–1.5%—1.5%的应变, 步长为0.5%. 如表3所示, BaMN2在a-b平面上具有较轻的载流子有效质量$ {m}^{*} $ , 而在面外方向上具有较重的$ {m}^{*} $ . Ei同样表现出强烈的各向异性, 平面内Ei较大, 表明它们对应变的敏感性较高, 平面外z方向的Ei较小. 平面内电子迁移率µ达到了非常高的数量级(~ 103 cm2/(s·V)), 而平面外方向的电子迁移率µ接近于零. 这些平面内异常高的(平面外异常低的)µ与较轻(较重)的电子有效质量($ {m}^{*} $ )密切相关. BaTiN2的电子和空穴沿x(z)输运方向的迁移率$ {\mu }_{{\mathrm{e}}} $ 和$ {\mu }_{{\mathrm{h}}} $ 分别为7439.406 (0.088)和791.781(23.277) cm2/(s·V), BaZrN2的电子和空穴沿x(z)输运方向的迁移率$ {\mu }_{{\mathrm{e}}} $ 和$ {\mu }_{{\mathrm{h}}} $ 分别为6313.601 (0.225)和1426.402 (5.267) cm2/(s·V), BaHfN2的电子和空穴沿x(z)输运方向的迁移率分别为7286.037 (3.429)和1457.158 (23.152) cm2/(s·V). BaMN2表现出超高各向异性的载流子迁移率, 超过了典型的氮化物半导体GaN的电子迁移率(~1200 cm2/(s·V))[61]. 此外, 各向异性比($ {R}_{{\mathrm{a}}{\mathrm{i}}{\mathrm{n}}}=\dfrac{{\mu }_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}}{{\mu }_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}}} $ )是衡量迁移率各向异性的关键参数, 其中$ {\mu }_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $ 和$ {\mu }_{{\mathrm{m}}{\mathrm{i}}{\mathrm{n}}} $ 分别是最大和最小的载流子迁移率[62]. 因为沿平面外方向的电子迁移率$ {\mu }_{{\mathrm{e}}} $ 几乎为零, 显然$ {\mu }_{{\mathrm{e}}} $ 的各向异性比较大, 这将把电子限制在二维平面内. 此外, BaTiN2, BaZrN2和BaHfN2的空穴迁移率$ {\mu }_{{\mathrm{h}}} $ 的各向异性比也分别达到了34, 270和60. BaMN2的各向异性的电输运特征与CaTiN2和SrTiN2非常类似[32], 如表3所示, BaMN2的载流子在不同方向上的迁移率存在巨大差异, 即电子和空穴在空间中沿着不同的路径迁移, 这种载流子迁移率的差异导致电子和空穴在同一位置相遇的概率显著降低, 如此大的各向异性表明电子和空穴会发生剧烈的分离, 这有利于抑制光生载流子的复合[63].此外, BaMN2在可见光能量范围内具有明显的光吸收能力, 光吸收系数达到105 cm–1数量级(图6), 沿着面内x(y)和面外z方向的光学响应存在显著的差异: 在能量较低的区域中, 可见光与BaMN2的相互作用主要是通过激发价带电子到导带, 同时由于BaMN2的四方结构对称性和层状晶体结构, 沿平面内x(y)方向和面外z方向的原子排列和化学键合作用存在显著差异, 导致沿平面内x(y)方向相对于沿平面外z方向具有非常强的光吸收能力; 而在较高的能量区域中, 电子从占据态到非占据态的跃迁机会增多, 导致对光的吸收情况变得更复杂, 各向异性相对减弱, 使得BaMN2在各个方向上都表现出明显的吸收峰. 优异的可见光吸收性能, 合适的带隙值和带边位置表明BaMN2可以作为潜在太阳能电池吸收层和水分解的光催化剂, 是光电子、光伏和光催化领域有前景的半导体材料[10,60,64].
进一步用激子结合能(Eb)来衡量电子与空穴之间的耦合效应, 其计算公式为
其中,
$ {\varepsilon }_{{\mathrm{o}}{\mathrm{p}}{\mathrm{t}}{\mathrm{i}}{\mathrm{c}}} $ 为静态介电常数,$ {m}_{0} $ 为自由电子质量,$ {m}_{{\mathrm{r}}}^{*}= {{m}_{{\mathrm{e}}}^{*}{m}_{{\mathrm{h}}}^{*}}/({{m}_{{\mathrm{e}}}^{*}+{m}_{{\mathrm{h}}}^{*}})$ 是约化有效质量,$ {m}_{{\mathrm{e}}}^{*} $ 和$ {m}_{{\mathrm{h}}}^{*} $ 分别为3个输运方向上电子和空穴的平均有效质量($ {m}_{{\mathrm{a}}}^{*} $ ):BaTiN2, BaZrN2和BaHfN2的静态介电常数电子贡献部分如表4所示, 分别为9.55, 8.16和7.63, 激子结合能分别为35, 44和50 meV, 比块体Si(20 meV)[65]和层状GaN(21—24 meV)[66]稍大.
$ {E}_{{\mathrm{b}}} $ 越小说明将空穴-电子对(激子)拆分成两个自由粒子所需要的能量越小, 表明电子与空穴之间的结合力越弱, 意味着电子和空穴更容易被分离, 从而增加了激子解离的可能性, 在光照下更容易产生自由载流子, 提高太阳能电池的效率.进一步研究BaMN2的介电响应, 得到了基于DFPT的波恩有效电荷张量和宏观介电张量. 表4总结了BaMN2氮化物的介电常数, 包括电子和离子贡献. BaTiN2, BaZrN2和BaHfN2的平均介电常数分别为39.48, 40.42和35.98, 主要来源于离子贡献, 介电常数平面内的分量
$ {\varepsilon }_{x} $ 和$ {\varepsilon }_{y} $ 比平面外c轴方向$ {\varepsilon }_{z} $ 更大, 显示出显著的各向异性, 这与另外两种层状氮化物SrZrN2和SrHfN2并非完全类似[20]. SrZrN2和SrHfN2的介电常数的电子贡献在各个方向差别不大, 离子贡献是电子贡献的数十倍, 介电常数平面内的分量比平面外分量大一个数量级. 两类氮化物的介电常数差异与他们的结构是密切相关的, 如图1所示, BaMN2氮化物具有四方KCoO2型层状结构, 该结构由准二维[MN2]2–板层组成, 在层间间隙中嵌入Ba2+离子. SrZrN2和SrHfN2具有α-NaFeO2型结构, 该结构也由准二维[MN2]2–板层组成, 与BaMN2氮化物结构的显著区别在于层间间隙嵌入的Sr2+离子远离[MN2]2–板层形成相对独立的一层阳离子. 这些氮化物特殊的层状结构可能导致沿垂直于板层的z方向(即c轴)的较低极化率和较高振动频率. 表5列出了BaMN2氮化物所有位点的波恩有效电荷. Ba, M和N离子的形式电荷分别为2, 4和–3. Ba和N1的极化电荷在a-b平面内比沿c方向小很多, 而M和N2的极化电荷在a-b平面内比沿c方向大很多. 四方BaMN2氮化物在a-b平面内有垂直于c轴偏振的8Eg+6Eu振动模和沿c轴偏振的3A1g+3A2u+1B1g振动模(其中Eu和Eg是二重简并)[20,34]. 其中A1g, B1g和Eg为拉曼活性模(Raman), A2u和Eu是红外活性模(IR). 表6列出了每种红外和拉曼活性模的声子频率和相应的模有效电荷$ \widetilde{{Z}_{\lambda }^{*}} $ . 在21个光学支中, a-b平面中最活跃的模式是第15支, 对应3种BaMN2氮化物的IR频率$ {\omega }_{\lambda } $ 分别为332, 359和363 cm–1, 有效电荷$ \widetilde{{Z}_{\lambda }^{*}} $ 分别为6.10, 4.38和3.84|e|, 主要来源于N2离子在a-b平面内的振动, 其波恩有效电荷相当大, 分别为–5.650, –4.926和–4.763. 而在c方向中最活跃的模式是第20支, 对应3种BaMN2氮化物的IR频率$ {\omega }_{\lambda } $ 分别为682, 588和605 cm–1, 有效电荷$ \widetilde{{Z}_{\lambda }^{*}} $ 分别为2.90, 3.07和2.53|e|, 主要来源于N1离子在面外c方向的振动, 其波恩有效电荷分别为–4.357, –4.839和–4.552. 介电常数的离子贡献与$ {( \widetilde{{Z}_{\lambda }^{*}}/{\omega }_{\lambda })}^{2} $ ($ {\omega }_{\lambda } $ 为红外活性模频率)成正比[20,34], 因此四方相BaMN2氮化物介电常数表现出显著的各向异性. 随着M元素原子质量的增大, M的极化电荷平均值逐渐减小, a-b平面最活跃的IR模式的频率逐渐升高而有效电荷逐渐减小, 在c方向最活跃的IR模式的频率和有效电荷没有表现出单调变化, 最终BaZrN2介电常数的离子贡献部分比另外两种BaMN2氮化物的略微大一点. -
基于密度泛函理论的第一性原理计算系统地研究了三元层状氮化物BaMN2(M = Ti, Zr, Hf)的力学、电子、载流子传输、光学和介电响应性质. BaMN2氮化物由准二维[MN2]2– 板层排列组成独特的层状晶体结构, 且Ba2+和N3– 之间形成离子键, [MN2]2– 板层之间的键合作用较弱, 使得其具有各向异性的力学性质, 具有良好的塑性. 此外, BaMN2的带隙值处于可见光能量范围内, 带边位置符合水分解光催化剂的要求. 更有趣的是, 它们具有超高各向异性的载流子迁移率和较高的可见光吸收系数, 其平面内电子迁移率达到了103 cm2/(s·V)的数量级, 而平面外方向的电子迁移率几乎为零, 可见光吸收系数达到了105 cm–1数量级, 且都表现出较低的激子结合能. 此外, 这些氮化物具有较大的介电常数, 且具有显著的各向异性. 三元层状氮化物BaMN2各向异性的物理性质与其准二维层状晶体结构以及在不同方向的不同键合作用密切相关, 可以作为光电子、光伏和光催化领域有前景的半导体材料.
层状氮化物BaMN2(M = Ti, Zr, Hf)各向异性物理性质的第一性原理研究
First-principles study of anisotropic physical properties of layered nitride BaMN2 (M = Ti, Zr, Hf)
-
摘要: 三元层状氮化物因其独特的电学、光学和光电性质而受到广泛关注, 有希望用于制造低成本、高效率的光电材料、太阳能电池材料和光催化剂. 三元层状氮化物BaZrN2和BaHfN2已经被固态实验合成, 但其光学性质和电输运性质尚未被系统地研究. 本文采用基于密度泛函理论的第一性原理计算系统地研究了BaMN2(M = Ti, Zr, Hf)氮化物的力学、电子、光吸收、载流子传输和介电响应性质. 由于BaMN2氮化物由准二维[MN2]2–板层排列组成独特的层状晶体结构, 且板层内的电子云重叠较多形成强共价键, 板层之间的成键作用较弱, 使得其物理性质表现出显著的各向异性. 首先, BaMN2的体模量、剪切模量、杨氏模量和泊松比等力学性质表现出各向异性, 具有较低的模量、较高的泊松比和Pugh模量比, 表明其具有良好的塑性. 此外, BaMN2具有处于可见光能量范围内的间接带隙值(1.75—2.25 eV), 适宜用于太阳能电池吸收层, 且带边位置满足水分解光催化剂的要求. 由于其载流子在不同方向上的有效质量存在巨大差异, 使得它们还具有超高各向异性的载流子迁移率(103 cm2/(s·V)数量级)和较低的激子结合能. 同时, 沿平面内方向和面外方向的原子排列和成键作用存在显著差异, 导致在低能量区域沿平面内具有非常强的光吸收能力和较高的各向异性可见光吸收系数(105 cm–1数量级); 而在较高的能量区域中, 电子从占据态到非占据态的跃迁概率增大, 导致对光的吸收情况变得更复杂, 各向异性相对减弱. 此外, 特殊的层状结构沿垂直于板层的方向具有较低极化率和较高振动频率, 使得BaMN2有较高的介电常数. 这些优异的各向异性的力学、光电和输运性质使得BaMN2层状氮化物可以作为光电子、光伏和光催化领域有前景的半导体材料.Abstract: Ternary layered nitrides have received widespread attention due to their unique electrical, optical and optoelectronic properties, which are promising for the fabrication of low-cost and high-efficiency optoelectronic materials, solar cell materials and photocatalysts. Although there is a lack of experimental reports on BaTiN2 so far, BaZrN2 and BaHfN2 have been synthesized experimentally by solid state methods. However, their optical and electrical transport properties have not been investigated systematically. This work is to systematically investigates the mechanical, electronic, optical absorption, carrier transport, and dielectric response properties of BaMN2 (M = Ti, Zr, Hf) nitrides through first-principles calculations based on density functional theory. Due to the quasi-two-dimensional layered arrangement of [MN2]2– slabs, the ionic bonds between Ba2+ and N3–, and the weak interactions between the slabs, the deformation along this direction is most likely to occur under the action of external stress. BaMN2 nitrides exhibit significant anisotropic physical properties. Firstly, the mechanical properties of BaMN2, such as bulk modulus, shear modulus, Young’s modulus, and Poisson’s ratio, show prominent anisotropy. The lower modulus, higher Poisson’s ratios and Pugh’s modulus ratios indicate good flexibility of the BaMN2 nitrides. In addition, BaMN2 has indirect bandgap values (1.75–2.25 eV) within the visible-light energy range, which meets the basic requirement for the band gap of a photocatalyst for water splitting (greater than 1.23 eV). Moreover, BaMN2 has suitable band-edge positions. The appropriate bandgap values and band-edge positions indicate their broad application prospects in the absorber layer of solar cells and photocatalytic water decomposition. Due to the significant difference in the effective mass of its charge carriers between different directions, BaMN2 exhibits ultrahigh anisotropic carrier mobility (on the order of 103 cm2⋅s–1⋅v–1) and lower exciton binding energy. At the same time, there are significant differences in atomic arrangement and bonding interactions between the in-plane direction and out of plane direction, resulting in high anisotropic visible-light absorption coefficient (on the order of 105 cm–1) in the low energy region. In contrast, the increase of the opportunity for electrons to transition from occupied to unoccupied states leads to more complex light absorption and relatively reduced anisotropy in higher energy region. Furthermore, the special layered structure has lower polarizability and higher vibration frequency along the vertical direction perpendicular to the [MN2]2– layers, rendering BaMN2 nitrides show high dielectric constants. These excellent anisotropic mechanical, optoelectronic, and transport properties allow BaMN2 layered nitrides to be used as promising semiconductor materials in the fields of optoelectronics, photovoltaics, and photocatalysis.
-
Key words:
- nitrides /
- carrier mobility /
- anisotropy /
- first-principles study .
-

-
表 1 BaMN2的晶格常数, 晶格体积和M—N键长的理论计算值与实验(括号中数据)对比
Table 1. Comparison of theoretically calculated and experimental measured (in parenthesis) lattice constants, lattice volumes and the M—N bond lengths of BaMN2.
表 2 BaMN2的弹性常数Cij、体模量B、剪切模量G、杨氏模量Y、泊松比ν、Pugh模量比(B/G). 模量下标V和R分别表示Voigt-Reuss-Hill模型近似中Voigt和Reuss模型的结果, 没有下标的B和G定义为Voigt和Reuss值的平均值
Table 2. Elastic constants Cij, bulk modulus B, shear modulus G, Young’s modulus Y, Poisson’s ratio ν, Pugh’s ratio (B/G) of BaMN2. The subscripts V and R of the moduli denote results from the Voigt and Reuss models, while B and G moduli without subscripts are defined as the average of the Reuss and Voight values from the Voigt-Reuss-Hill approximations.
Materials C11/GPa C12/GPa C13/GPa C22/GPa C23/GPa C33/GPa C44/GPa C55/GPa C66/GPa BaTiN2 180.639 126.136 56.702 180.639 56.702 121.448 38.493 38.493 118.834 BaZrN2 151.829 110.797 66.919 151.829 66.919 129.396 37.723 37.723 95.162 BaHfN2 163.876 118.407 69.072 163.876 69.072 130.419 37.811 37.811 103.077 Materials BV/GPa BR/GPa B GV GR G/GPa Y/GPa ν B/G BaTiN2 106.870 95.480 101.175 55.380 42.420 48.900 126.253 0.294 2.070 BaZrN2 102.480 98.630 100.555 46.680 36.539 41.610 109.580 0.318 2.420 BaHfN2 107.920 102.211 105.066 49.180 38.366 43.773 115.194 0.317 2.400 表 3 BaMN2的有效质量m*、形变势常数Ei和载流子迁移率μ
Table 3. Effective mass m*, deformation potential constants Ei, and carrier mobility μ of BaMN2.
Material Carrier m*/m0 Ei/eV μ/(cm2·s–1·V–1) x/y z x/y z x/y z BaTiN2 Electron 0.237 29.929 –7.366 –4.159 7439.406 0.088 Hole 0.536 2.560 –8.141 –5.514 791.781 23.277 BaZrN2 Electron 0.229 32.657 –7.652 –2.399 6313.601 0.225 Hole 0.400 5.435 –8.017 –4.669 1426.402 5.267 BaHfN2 Electron 0.223 30.268 –7.650 –0.679 7286.037 3.429 Hole 0.415 3.608 –7.870 –3.731 1457.158 23.152 表 4 介电张量的对角线分量的电子和离子贡献和介电常数
Table 4. Diagonal components of the dielectric tensor from the electronic and ionic contributions and dielectric permittivity.
Material $ {\varepsilon }_{{\mathrm{e}}{\mathrm{l}}{\mathrm{e}}} $ $ {\varepsilon }_{{\mathrm{i}}{\mathrm{o}}{\mathrm{n}}} $ $ {\varepsilon }_{{\mathrm{r}}} $ x/y z x/y z BaTiN2 10.59 7.48 35.70 18.40 39.48 BaZrN2 8.30 7.88 39.08 18.61 40.42 BaHfN2 7.71 7.46 34.37 16.32 35.98 表 5 BaMN2的波恩有效电荷张量及平均值(
$ {Z}^{*} $ )Table 5. Born effective charges tensors along three directions (x, y and z) and the average value (
$ {Z}^{*} $ ) of BaMN2.BaTiN2 BaZrN2 BaHfN2 x/y z $ {Z}^{*} $ x/y z $ {Z}^{*} $ x/y z $ {Z}^{*} $ Ba 2.884 3.094 2.954 2.687 3.233 2.869 2.751 3.130 2.877 M 5.355 2.689 4.466 4.811 3.362 4.328 4.617 3.098 4.111 N1 –2.611 –4.357 –3.193 –2.582 –4.839 –3.334 –2.613 –4.552 –3.259 N2 –5.650 –1.433 –4.244 –4.926 –1.764 –3.872 –4.763 –1.672 –3.733 表 6 声子模及其频率
$ {\omega }_{\lambda } $ (以cm–1为单位)和有效电荷$ \widetilde{{Z}_{\lambda }^{*}} $ (以|e|表示)Table 6. The mode, mode frequencies
$ {\omega }_{\lambda } $ (in cm–1) and effective charges$ \widetilde{{Z}_{\lambda }^{*}} $ (in |e|).Mode Symmetry Active Polarization BaTiN2 BaZrN2 BaHfN2 $ {\omega }_{\lambda } $ $ \widetilde{{Z}_{\lambda }^{*}} $ $ {\omega }_{\lambda } $ $ \widetilde{{Z}_{\lambda }^{*}} $ $ {\omega }_{\lambda } $ $ \widetilde{{Z}_{\lambda }^{*}} $ 1-2 Eu IR x-y 119 0.52 67 0.34 62 0.24 3-4 Eg Raman x-y 80 0 73 0 76 0 5 A2u IR z 110 0.52 99 0.43 89 0.30 6 A1g Raman z 115 0 109 0 109 0 7-8 Eg Raman x-y 225 0 157 0 139 0 9 A1g Raman z 285 0 222 0 166 0 10-11 Eu IR x-y 286 0.23 204 0.31 213 0.48 12-13 Eg Raman x-y 336 0 262 0 234 0 14 B1g Raman z 300 0 311 0 325 0 15-16 Eu IR x-y 332 6.10 359 4.38 363 3.84 17 A2u IR z 496 0.04 462 0.69 452 0.78 18-19 Eg Raman x-y 560 0 541 0 572 0 20 A2u IR z 682 2.90 588 3.07 605 2.53 21 A1g Raman z 769 0 679 0 683 0 -
[1] Ahmed S, Yi J B 2017 Nano-Micro Lett. 9 106313 doi: 10.1007/s40820-017-0152-6 [2] Liao L, Lin Y C, Bao M Q, Cheng R, Bai J W, Liu Y, Qu Y Q, Wang K L, Huang Y, Duan X F 2010 Nature 467 305 doi: 10.1038/nature09405 [3] Mitta S B, Choi M S, Nipane A, Ali F, Kim C, Teherani J T, Hone J, Yoo W J 2021 2D Mater. 8 012002 doi: 10.1088/2053-1583/abc187 [4] Lu C C, Lin Y C, Yeh C H, Huang J C, Chiu P W J A N 2012 Nanscale 6 4469 doi: 10.1021/nn3059828 [5] Allain A, Kang J, Banerjee K, Kis A J N M 2015 Nat. Mater. 14 1195 doi: 10.1038/nmat4452 [6] 张冷, 张鹏展, 刘飞, 李方政, 罗毅, 侯纪伟, 吴孔平 2024 物理学报 73 047101 doi: 10.7498/aps.73.20231406 Zhang L, Zhang P Z, Liu F, Li F Z, Luo Y, Hou J W, Wu K P 2024 Acta Phys. Sin. 73 047101 doi: 10.7498/aps.73.20231406 [7] Ling X, Wang H, Huang S X, Xia F N, Dresselhaus M S 2015 PNAS 112 4523 doi: 10.1073/pnas.1416581112 [8] Qiao J S, Kong X H, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475 doi: 10.1038/ncomms5475 [9] 程秋振, 黄引, 李玉辉, 张凯, 冼国裕, 刘鹤元, 车冰玉, 潘禄禄, 韩烨超, 祝轲, 齐琦, 谢耀锋, 潘金波, 陈海龙, 李永峰, 郭辉, 杨海涛, 高鸿钧 2023 物理学报 72 218102 doi: 10.7498/aps.72.20231539 Cheng Q Z, Huang Y, Li Y H, Zhang K, Xian G Y, Liu H Y, Che B Y, Pan L L, Han Y C, Zhu K, Qi Q, Xie Y F, Pan J B, Chen H L, Li Y F, Guo H, Yang H T, Gao H J 2023 Acta Phys. Sin. 72 218102 doi: 10.7498/aps.72.20231539 [10] Xue P Y, Chu D D, Xie C W, Tikhonov E, Butler K T 2022 J. Phys. Chem. C 126 17398 doi: 10.1021/acs.jpcc.2c05458 [11] Greenaway A L, Ke S, Culman T, Talley K R, Mangum J S, Heinselman K N, Kingsbury R S, Smaha R W, Gish M K, Miller E M, Persson K A, Gregoire J M, Bauers S R, Neaton J B, Tamboli A C, Zakutayev A 2022 J. Am. Chem. Soc. 144 13673 doi: 10.1021/jacs.2c04241 [12] Szymanski N J, Walters L N, Hellman O, Gall D, Khare S V 2018 J. Mater. Chem. A 6 20852 doi: 10.1039/C8TA07536K [13] Arca E, Perkins J D, Lany S, Mis A, Chen B R, Dippo P, Partridge J L, Sun W, Holder A, Tamboli A C, Toney M F, Schelhas L T, Ceder G, Tumas W, Teeter G, Zakutayev A 2019 Mater. Horiz. 6 1669 doi: 10.1039/C9MH00369J [14] Bauers S R, Holder A, Sun W, Melamed C L, Woods-Robinson R, Mangum J, Perkins J, Tumas W, Gorman B, Tamboli A, Ceder G, Lany S, Zakutayev A 2019 PNAS 116 14829 doi: 10.1073/pnas.1904926116 [15] Hinuma Y, Hatakeyama T, Kumagai Y, Burton L A, Sato H, Muraba Y, Iimura S, Hiramatsu H, Tanaka I, Hosono H J N C 2016 Nat. Commun. 7 11962 doi: 10.1038/ncomms11962 [16] Kangsabanik J, Alam A 2019 Phys. Rev. Mater. 3 105405 doi: 10.1103/PhysRevMaterials.3.105405 [17] Shiraishi A, Kimura S, He X, Watanabe N, Katase T, Ide K, Minohara M, Matsuzaki K, Hiramatsu H, Kumigashira H, Hosono H, Kamiya T 2022 Inorg. Chem. 61 6650 doi: 10.1021/acs.inorgchem.2c00604 [18] Zakutayev A, Jankousky M, Wolf L, Feng Y, Rom C L, Bauers S R, Borkiewicz O, LaVan D A, Smaha R W, Stevanovic V 2024 Nat. Synth 3 1471 doi: 10.1038/s44160-024-00643-0 [19] Ming X, Kuang X J 2024 Nat. Synth. 3 1444 doi: 10.1038/s44160-024-00666-7 [20] Liu J W, Lu S L, Wang Y H, Li C, Ming X, Kuang X J 2022 Chem. Mater. 34 4505 doi: 10.1021/acs.chemmater.2c00298 [21] Gregory D H, Barker M G, Edwards P P, Siddons D J 1996 Inorg. Chem. 35 7608 doi: 10.1021/ic9607649 [22] Seeger O, Strähle J 1994 Z. Naturforsch. B 49 1169 doi: 10.1515/znb-1994-0903 [23] Li X H, Wang X M, Han Y F, Jing X P, Huang Q Z, Kuang X J, Gao Q L, Chen J, Xing X R 2017 Chem. Mater. 29 1989 doi: 10.1021/acs.chemmater.6b05226 [24] Farault G, Gautier R, Baker C F, Bowman A, Gregory D H 2003 Chem. Mater. 15 3922 doi: 10.1021/cm034502y [25] Gregory D H, Barker M G, Edwards P P, Siddons D J 1998 Inorg. Chem. 37 3775 doi: 10.1021/ic971556z [26] Seeger O, Hofmann M, Strähle J, Laval J P, Frit B 1994 Z Anorg. Allg. Chem. 620 2008 doi: 10.1002/zaac.19946201129 [27] Gregory D H, Barker M G, Edwards P P, Slaski M, Siddons D J 1998 J. Solid. State. Chem. 137 62 doi: 10.1006/jssc.1997.7686 [28] Gregory D H, O’Meara P M, Gordon A G, Siddons D J, Blake A J, Barker M G, Hamor T A, 2001 J. Alloys Compd 317-318 237 doi: 10.1016/S0925-8388(00)01340-2 [29] Yao M, Zhang Y Y, Ban J M, Hou J J, Zhang B W, Liu J W, Ming X, Kuang X J 2023 PCCP 25 19158 doi: 10.1039/D3CP01907A [30] Ohkubo I, Mori T 2015 Chem. Mater. 27 7265 doi: 10.1021/acs.chemmater.5b02015 [31] Ohkubo I, Mori T 2016 APL Mater. 4 104808 doi: 10.1063/1.4955399 [32] Liang H L, Lu J, Zhang W Y, Ming X 2025 Mater. Sci. Semicond. Process. 185 108955 doi: 10.1016/j.mssp.2024.108955 [33] Luo H M, Wang H Y, Bi Z X, Zou G F, McCleskey T M, Burrell A K, Bauer E, Hawley M E, Wang Y Q, Jia Q X 2009 Angew. Chem. Int. Ed. 48 1490 doi: 10.1002/anie.200805394 [34] Kaur A, Ylvisaker E R, Li Y, Galli G, Pickett W E 2010 Phys. Rev. B 82 155125 doi: 10.1103/PhysRevB.82.155125 [35] Yao M L, Li M, Zhang L, Wang H 2024 Phys. Rev. B 110 115202 doi: 10.1103/PhysRevB.110.115202 [36] Yang X F, Wang Z Q, Fu H H 2024 Phys. Rev. B 109 155414 doi: 10.1103/PhysRevB.109.155414 [37] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [38] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758 doi: 10.1103/PhysRevB.59.1758 [39] Kresse G, Furthmüller J 1996 P Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [40] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 doi: 10.1016/0927-0256(96)00008-0 [41] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188 [42] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865 [43] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207 doi: 10.1063/1.1564060 [44] Yim K, Yong Y, Lee J, Lee K, Nahm H H, Yoo J, Lee C, Seong Hwang C, Han S 2015 NPG Asia Mater. 7 e190 doi: 10.1038/am.2015.57 [45] Gonze X, Lee C 1997 Phys. Rev. B 55 10355 doi: 10.1103/PhysRevB.55.10355 [46] Giannozzi P, de Gironcoli S, Pavone P, Baroni S 1991 Phys. Rev. B 43 7231 doi: 10.1103/PhysRevB.43.7231 [47] Ceperley D M, Alder B J 1980 Phys. Rev. Lett. 45 566 doi: 10.1103/PhysRevLett.45.566 [48] Bokdam M, Sander T, Stroppa A, Picozzi S, Sarma D D, Franchini C, Kresse G 2016 Sci. Rep. 6 28618 doi: 10.1038/srep28618 [49] Gajdoš M, Hummer K, Kresse G, Furthmüller J, Bechstedt F 2006 Phys. Rev. B 73 045112 doi: 10.1103/PhysRevB.73.045112 [50] Zhao X, Vanderbilt D 2002 Phys. Rev. B 65 075105 doi: 10.1103/PhysRevB.65.075105 [51] Cockayne E, Burton B P 2000 Phys. Rev. B 62 3735 doi: 10.1103/PhysRevB.62.3735 [52] Bardeen J, Shockley W 1950 Phys. Rev. 80 72 doi: 10.1103/PhysRev.80.72 [53] Mouhat F, Coudert F X 2014 Phys. Rev. B 90 224104 doi: 10.1103/PhysRevB.90.224104 [54] Wu Z J, Zhao E J, Xiang H P, Hao X F, Liu X J, Meng J 2007 Phys. Rev. B 76 054115 doi: 10.1103/PhysRevB.76.054115 [55] Wang V, Xu N, Liu J C, Tang G, Geng W T 2021 Comput. Phys. Commun. 267 108033 doi: 10.1016/j.cpc.2021.108033 [56] Yu R, Xiao F, Lei W, Wang W, Ma Y P, Gong X J, Ming X 2023 PCCP 25 30066 doi: 10.1039/D3CP03676F [57] Pugh S F 2009 Lond. Edinb. Phil. Mag. 45 823 doi: 10.1080/14786440808520496 [58] Liao M Q, Liu Y, Min L J, Lai Z H, Han T Y, Yang D N, Zhu J C 2018 Intermetallics 101 152 doi: 10.1016/j.intermet.2018.08.003 [59] Xu Y, Schoonen M A A 2000 Am. Mineral. 85 543 doi: 10.2138/am-2000-0416 [60] Zhang H, Guégan F, Wang J, Frapper G 2024 PCCP 26 14675 doi: 10.1039/D4CP00544A [61] Heying B, Smorchkova I, Poblenz C, Elsass C, Fini P, Den Baars S, Mishra U, Speck J S 2000 Appl. Phys. Lett. 77 2885 doi: 10.1063/1.1322370 [62] Lang H F, Zhang S Q, Liu Z R 2016 Phys. Rev. B 94 235306 doi: 10.1103/PhysRevB.94.235306 [63] Kosarev I, Kistanov A 2024 Nanoscale 16 10030 doi: 10.1039/D4NR01292E [64] Zhang H, Wang J J, Guégan F, Frapper G 2023 Nanoscale 15 7472 doi: 10.1039/D2NR07239D [65] Dvorak M, Wei S H, Wu Z 2013 Phys. Rev. Lett. 110 016402 doi: 10.1103/PhysRevLett.110.016402 [66] Muth J F, Lee J H, Shmagin I K, Kolbas R M, Casey H C, Keller B P, Mishra U K, DenBaars S P 1997 Appl. Phys. Lett. 71 2572 doi: 10.1063/1.120191 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: