-
传统合金通常以某一种金属作为主元, 在其中加入其他微量元素形成合金提高性能, 而Yeh等[1]在2004年提出的高熵合金打破了传统合金概念. 高熵合金是以多种主元金属以5%—35%的比例形成的固溶体合金, 又被称为多主元合金. 相较于传统合金而言, 多主元合金表现出更优异的高温力学性能和抗辐照性能, 有望在航天航空以及核领域发挥重要作用[2–9].
以Ti, V, Ta三种难熔金属为主元制备的难熔多主元合金TiVTa相比其他难熔高熵合金较好地平衡了高温强度与室温塑性, 其中等原子比TiVTa合金具有最高的相稳定性. 同时该合金满足核应用领域要求的低活化性能, 已被证明是极具潜力的核应用材料[9].
核材料在服役条件下经受长期辐照作用, 基体内生成大量辐照缺陷, 包括位错环、空洞、层错四面体等, 这些辐照缺陷与位错发生相互作用, 通过阻碍位错运动导致基体硬化和脆化, 研究位错与缺陷之间的相互作用对于解释材料的辐照性能演化至关重要. 而对TiVTa合金展开的离子辐照实验表明, 在纯V中辐照诱导产生的主要是1/2
$ \left\langle {111} \right\rangle $ 环, 但是在TiVTa等比合金中, 产生的位错环以$ \left\langle {100} \right\rangle $ 环为主[10]. 但是目前纯V和TiVTa中$ \left\langle {100} \right\rangle $ 环和$ \left\langle {111} \right\rangle $ 环的存在对于材料辐照硬化的影响机理以及二者之间存在的差异尚不明确. 又考虑到体心立方(body centered cubic, BCC)金属的力学性能主要由位错决定, 因此, 本文选择对刃位错以及刃位错与$ \left\langle {111} \right\rangle $ 环和$ \left\langle {100} \right\rangle $ 环的相互作用展开详细的模拟探究[11–14].Bacon等[15]给出了BCC Fe中刃位错与不同尺寸位错环之间的两种相互作用机制: 小尺寸位错环与位错接触后被位错吸收形成割阶, 大尺寸位错环则与位错反应生成
$ \left\langle {100} \right\rangle $ 位错段,$ \left\langle {100} \right\rangle $ 位错段不易滑动导致位错的运动被阻碍. Marian等[16]发现低应力下螺位错会被$ \left\langle {100} \right\rangle $ 环钉扎, 高应力下螺位错则切过位错环. Rong等[17]研究了BCC Fe中刃位错与一排位错环之间的相互作用, 发现位错环被位错拖动, 且环对位错的阻力随着环密度的增加而增加. Nomoto等[18]模拟了不同应力下刃位错与自间隙环的相互作用, 发现间隙环对位错的阻碍与施加的应力有关: 应力越大, 位错挣脱位错环时的临界角越小, 相应的位错环的阻碍作用也越大. 因为临界角越小, 位错挣脱束缚时两侧位错臂上的Peach-Koehler力越大, 而该力对位错的运动起阻碍作用. 林盼栋等[19]和王瑾等[20,21]则研究了温度和位错环尺寸对于位错与位错环之间相互作用以及临界剪切应力的影响.Yu等[22]模拟了FeCrAl合金中间隙环与刃位错的相互作用, 发现Cr元素容易偏析到环上, 并促进Al的偏析, 导致移动性很强的
$ \left\langle {111} \right\rangle $ 环固着, 增强了环对位错的阻碍作用. Li等[23]研究了Co25Ni25Fe25Al7.5Cu17.5合金中刃位错与沉淀物之间的相互作用, 结果显示, 在不同温度下, 临界应力表现出不同的对沉淀物间距的依赖性. Dou等[24]对比了Fe10Ni20Cr和Fe33Ni33Cr合金中1/2$ \left\langle {110} \right\rangle $ 刃位错与空洞之间的相互作用, 并以此解释了Fe33Ni33Cr优异的抗辐照性能.本文以TiVTa等比合金为主体, 对合金中刃位错运动以及刃位错与位错环之间的相互作用展开模拟, 探究合金的微观形变机理, 以期为后续合金优化奠定良好基础. 第2节介绍了模拟构型以及模拟方法; 第3节给出模拟结果, 其中3.1节聚焦纯V和TiVTa合金中纯刃位错的运动; 3.2节给出位错与位错环之间的相互作用结果, 包括合金成分、位错环类型、温度以及位错环尺寸对于纯V和TiVTa合金中刃位错与位错环之间相互作用的影响; 最后第4节给出结论.
-
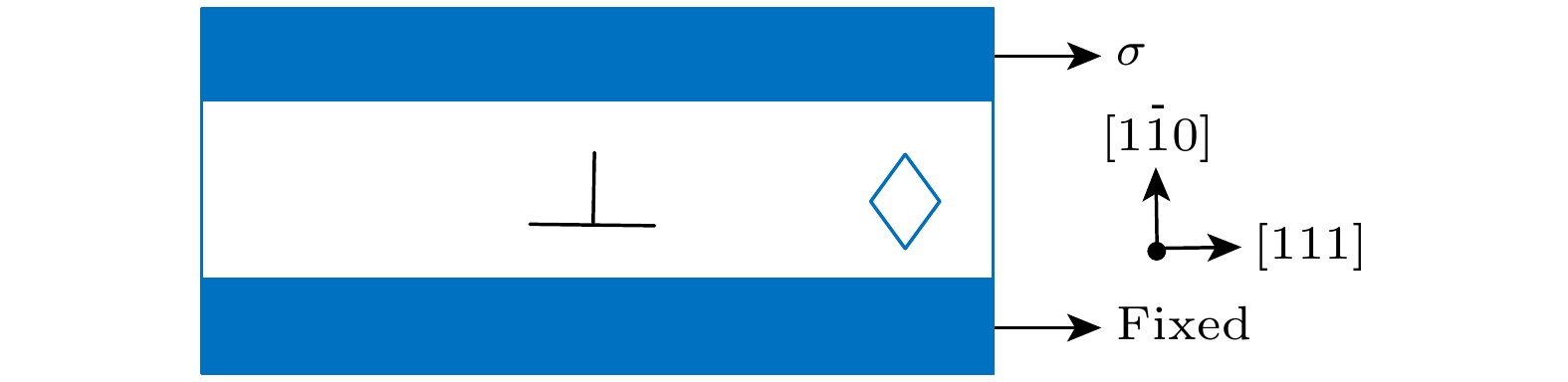
本文所有模拟均通过LAMMPS软件展开[25]. 首先利用基于Daw等[26]提出的周期性位错阵列(periodic array of dislocations, PAD)方法在纯V体系中构建刃位错: 通过令模拟盒子沿y方向分为上下两部分并相对滑移一个伯格斯矢量b的距离在模拟盒子中心生成刃位错. 模拟盒子的x, y, z分别沿[111],
$ \left[ {1\bar 10} \right] $ 和$ \left[ {11\bar 2} \right] $ 方向, 模拟盒子大小为148x0×70y0×27z0 ($ {x}_{0}=\sqrt{3}/2{a}_{0} $ ,$ {y}_{0}= \sqrt{2}{a}_{0}, {z}_{0}=\sqrt{6}{a}_{0} $ , a0是晶体的晶格常数), 位错线沿z方向, x方向为位错滑移方向, y方向是滑移面法线方向. 模拟时沿y方向将模拟盒子分为三个部分: 底层原子固定、中间层原子为可动粒子、对顶层粒子沿x方向施加恒应力驱使位错运动. 沿x方向和z方向使用周期性边界条件, 前者确保位错能够在无限长的距离上移动, 后者则使得可以在理论上模拟无限长的刃位错的运动, y方向使用非周期性边界条件.模拟开始前先在NVT系综下进行弛豫, 使用速度标定法控温, 弛豫的时间为50 ps, 然后在NVE系综下施加恒应力模拟位错运动, 输出模拟过程中的可视化文件. 利用开源可视化工具(OVITO)中的位错分析模块分析位错在不同时刻的位置, 得到位错运动速度随温度、应力的变化[27].
-
根据2.1节建立纯V中的刃位错模型, 在距离刃位错沿滑移方向约14 nm处放置位错环. 对于间隙
$ \left\langle {100} \right\rangle $ 环, 分别加入60, 144和416个间隙原子, 对应环半径分别约为1.1, 1.7和3.0 nm; 对于间隙$ \left\langle {111} \right\rangle $ 环, 分别加入64, 144和400个间隙原子, 对应环半径分别约为1.2, 2.0和3.3 nm. 后续采取的模拟设置与纯刃位错相同, 通过对模拟盒子顶部施加恒定的应力驱使刃位错运动并与环发生相互作用.对于TiVTa合金体系, 通过将含有纯刃位错以及含有刃位错和位错环的纯V模拟盒子合金化后生成, 将其中33%和34%的V原子替换成Ti和Ta从而生成TiVTa等比合金. 图1为模型示意图. 本文所进行的模拟采用Qiu等[28]公开发表的V-Ti-Ta合金的势函数, 该势函数已被证明可以很好地再现V-Ti-Ta合金中缺陷的演化行为.
-
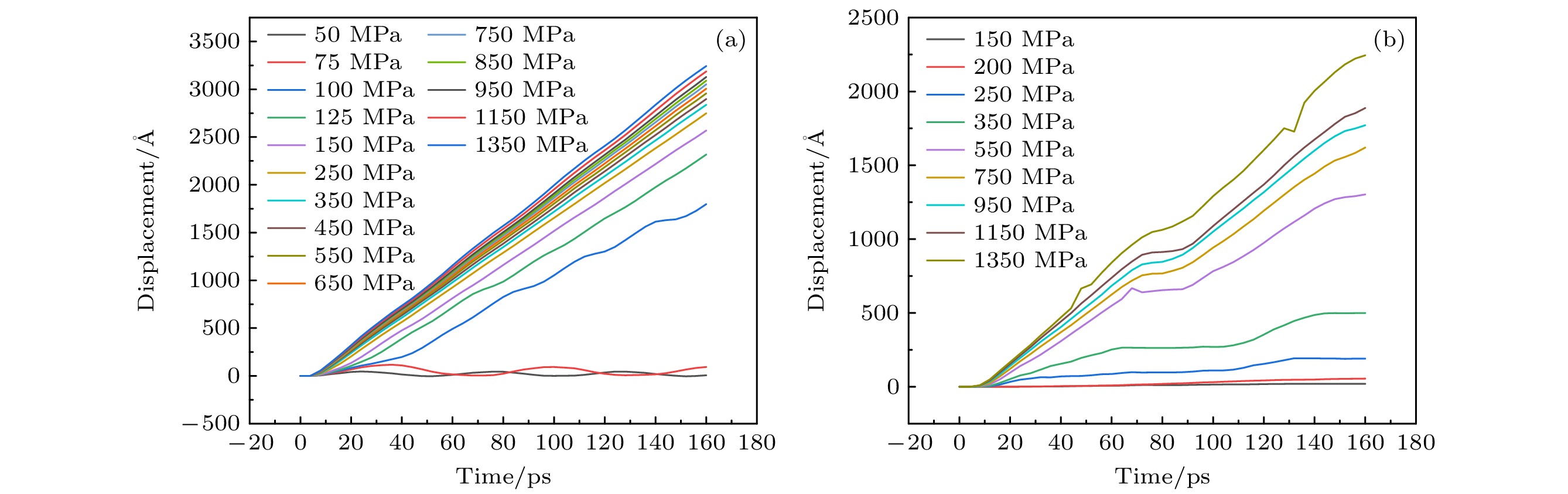
首先在0 K下对晶体施加不同剪切应力, 确认晶体中刃位错启动的派纳力, 得到如图2所示的位错运动的时间位移曲线图. 根据图2可以初步判定: 首先, 纯V中刃位错的启动力在75—100 MPa之间, TiVTa合金中刃位错的启动力在250—350 MPa之间, 以上对比说明TiVTa合金中刃位错的启动力要远高于纯V. 其次, 观察时间位移曲线还可以发现, 在纯V中, 刃位错运动的时间位移曲线是平滑的直线, 表明纯V中刃位错进行的是平滑的连续的匀速运动; 而在TiVTa合金中, 位错运动的时间位移曲线出现弯曲和不连续的拐点, 说明TiVTa合金中刃位错在运动全过程中并非一直保持匀速状态, 在某些区域, 位错运动的速度会减缓或停止, 造成刃位错运动的急停急动状态.
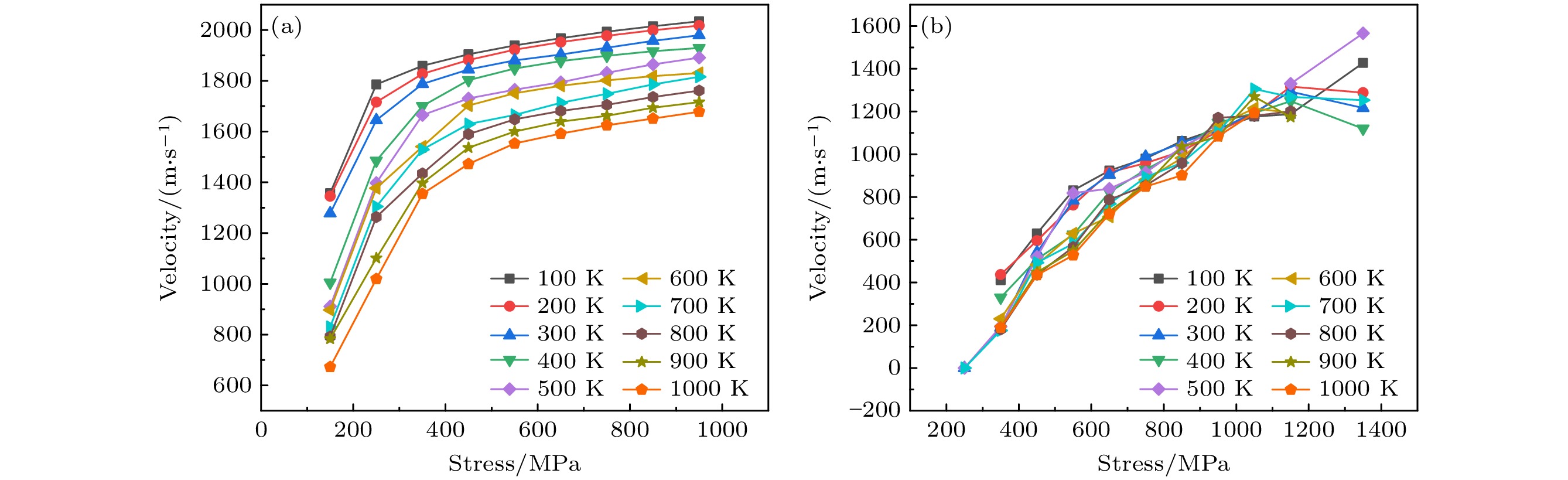
随后, 改变模拟温度, 计算位错运动速度随温度和应力的变化, 得到图3. 可以看出: 在纯V中, 位错运动速度随着应力的增加而增加, 随着温度的上升而降低, 且增幅随着应力的升高而降低; 而在TiVTa合金中, 位错运动速度同样随着应力的增加而增加, 但是位错运动速度随温度的变化关系与纯V不同. 在TiVTa合金中, 位错运动速度与温度之间无明显关联性, 说明TiVTa合金中可能存在与纯V中不同的控制刃位错运动的机制.
在BCC纯金属中, 控制刃位错运动的是声子拖拽机制, 随着温度升高, 声子阻力系数增加, 位错运动速度减缓. 但在本次模拟的TiVTa合金中, 位错运动速度与温度之间没有强烈的关联关系, 说明TiVTa合金中存在其他控制位错运动的机制与声子拖拽机制之间相互竞争. 而TiVTa合金与纯V之间最大的不同在于TiVTa合金中存在显著的晶格畸变, 因此猜想可能是晶格畸变对刃位错的运动产生影响, 造成TiVTa合金中刃位错运动机制的变化. 为验证该猜想, 对TiVTa合金中的刃位错运动行为进行深入探究并与纯V进行比较. 首先, 观察位错运动过程中的可视化图像可以发现, 不同于纯V, 在TiVTa合金中, 刃位错线并不是一条直线, 其呈现出极大的扭曲形态, 如图4所示.
为量化TiVTa合金中刃位错线的弯曲程度, 引用了Chen等[29]提出的波动参数Ra:
其中N代表位错线处的粒子数, si代表位错线处粒子的位置,
$ \stackrel{-}{s} $ 代表位错线处粒子的平均位置. 以300 K, 550 MPa下位错运动状态中弯曲度最大的一帧位错作为研究对象, 计算得到纯V中位错的波动参数为1.28, TiVTa合金中位错的波动参数为7.26, TiVTa合金中位错的波动参数可以达到纯V的5—6倍, 说明相较于纯V, TiVTa中刃位错在运动过程中发生了极大的扭曲.导致位错线发生扭曲的主要原因在于TiVTa合金中由于原子尺寸和模量错配导致的显著的晶格畸变和局部化学波动. 在TiVTa合金中, 不同区域之间的原子组成不同, 导致不同区域的化学性质发生波动, 位错线上各个位错段位于性质不同的区域, 因此位错线自发弯曲从而保证处于能量最低态. 所以相较于纯V, TiVTa合金中刃位错在克服派纳能垒运动的同时还需要额外克服从一个稳定的低能区域过渡到一个较高能量区域的能垒, 因此TiVTa合金中的刃位错运动速度也要显著低于纯V, 这一点可以通过对比图3(a)和图3(b)的横纵坐标轴得到. 且这种位错线上不同位错段克服额外能垒的运动状态与位错克服派纳能垒运动相似, 需要温度的激活, 相关位错运动机制已在多种多主元合金中报道, 被称为纳米段脱陷机制[12,13,29–33]. 因此, 在TiVTa合金中, 刃位错运动一方面受到声子拖拽机制的控制, 随着温度的升高, 阻力系数升高, 位错运动速度降低; 另一方面又受到纳米段脱陷机制的控制, 随着温度的升高, 位错速度也升高; 最终导致位错运动呈现出图3(b)所示的与温度之间的不强相关性.
-
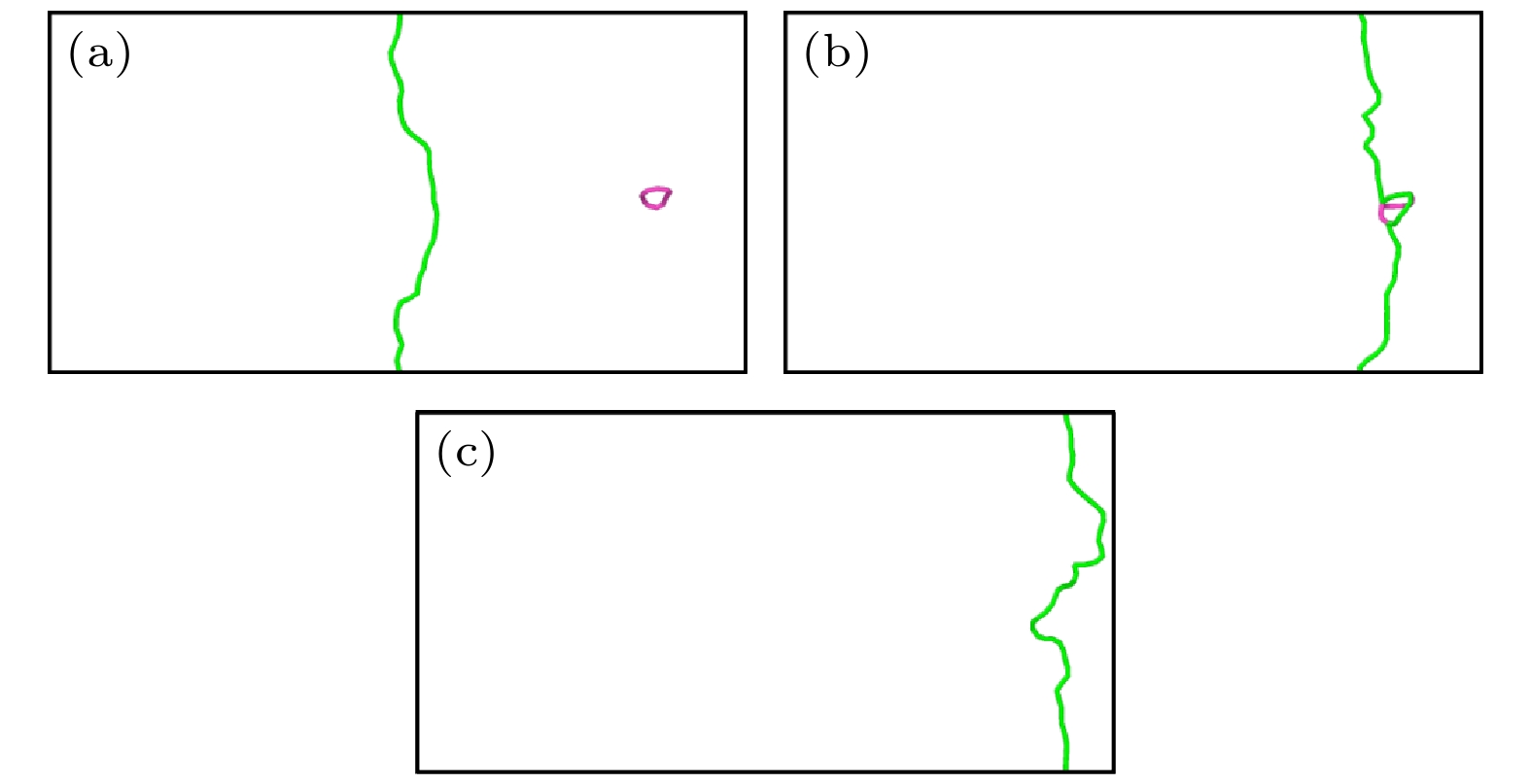
已知纯V中刃位错启动力在75—100 MPa之间, 因此在模拟纯V中位错与位错环之间相互作用时施加150 MPa的应力(如无特殊说明, 纯V中位错与位错环之间的相互作用均在150 MPa的应力下进行), 确保位错能够进行长程运动. 以300 K下的结果为例展开位错环尺寸和类型对位错与位错环相互作用影响分析. 对于最小尺寸的
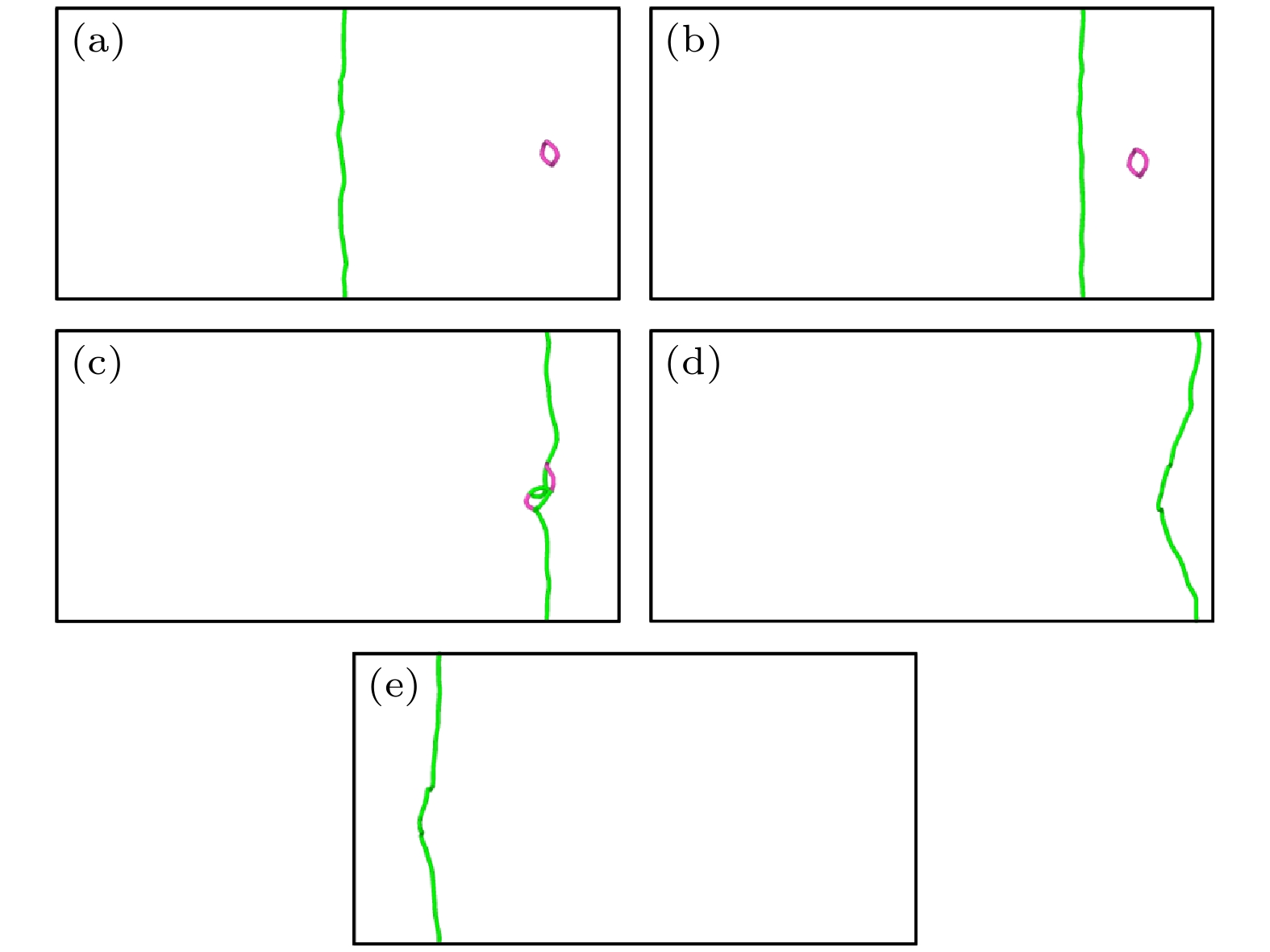
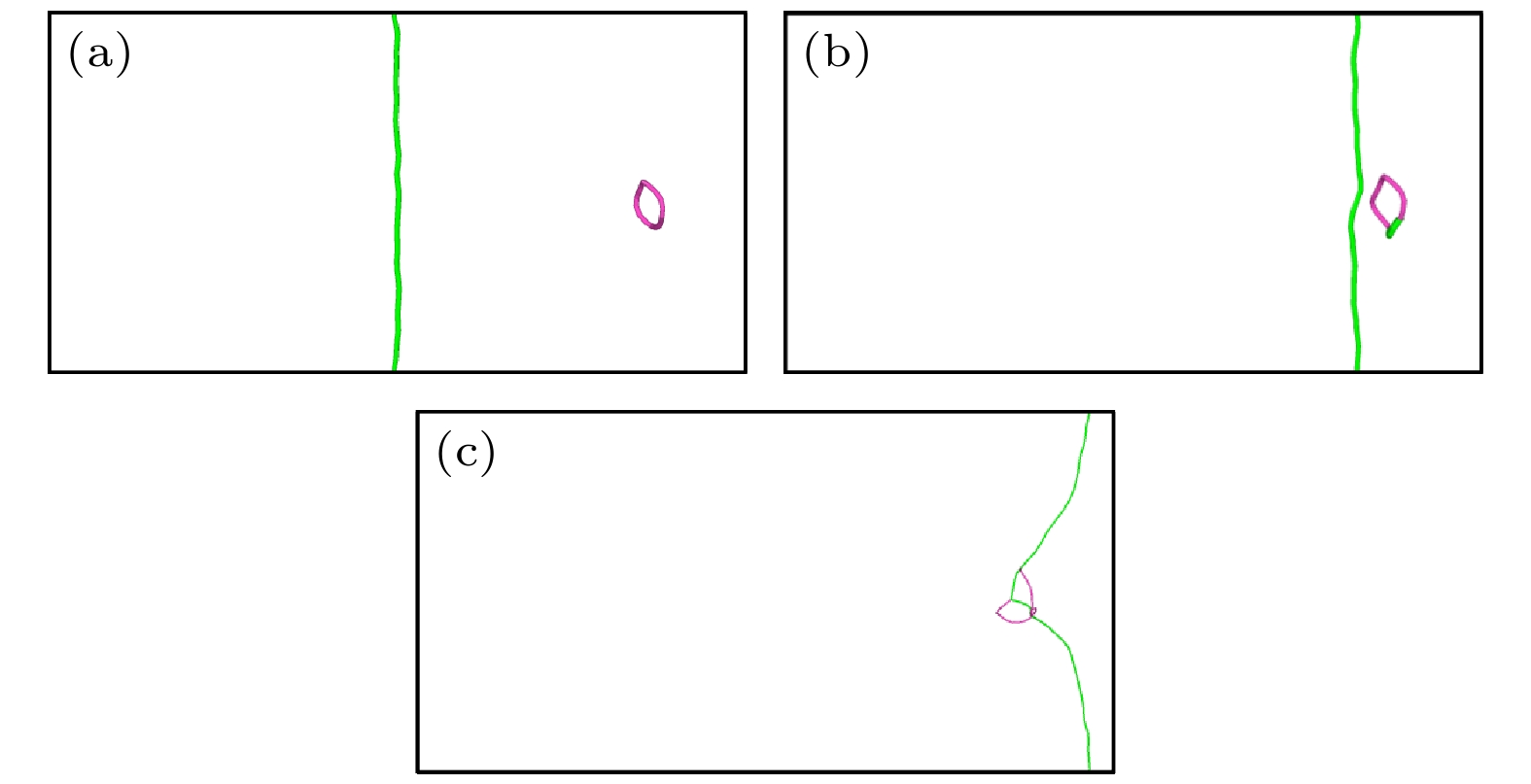
$ \left\langle {100} \right\rangle $ 环, 位错在恒应力驱使下靠近环并将环吸收, 在位错线上形成割阶, 最终含有割阶的位错在应力作用下继续重复匀速直线运动, 如图5所示. 改变环尺寸, 对应间隙数目为144的环, 在相同应力下(150 MPa), 位错的运动在模拟时间内被位错环所阻碍, 如图6所示. 将应力增加至200 MPa, 此时位错吸收间隙环形成割阶, 并继续向前运动.对应尺寸最大的
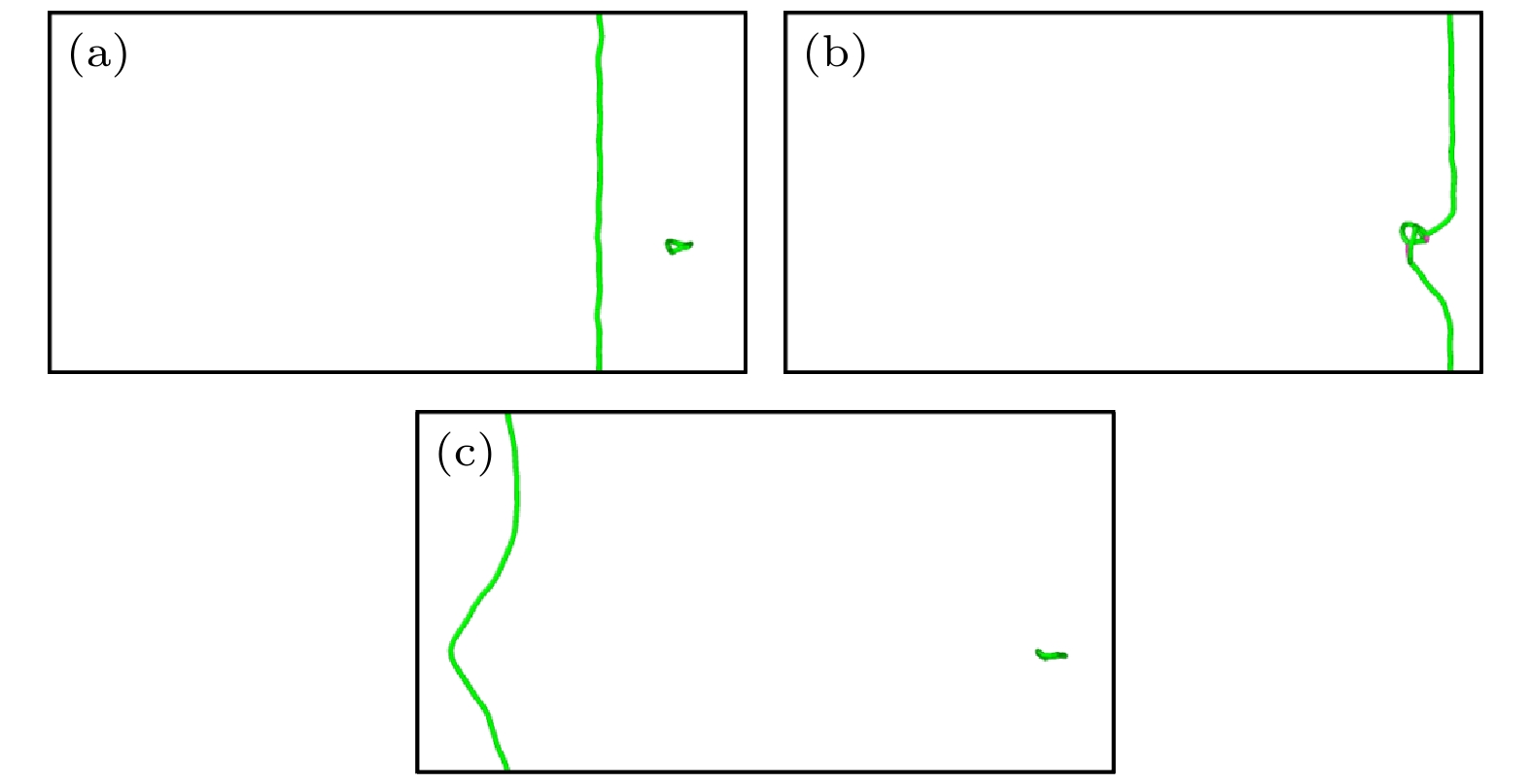
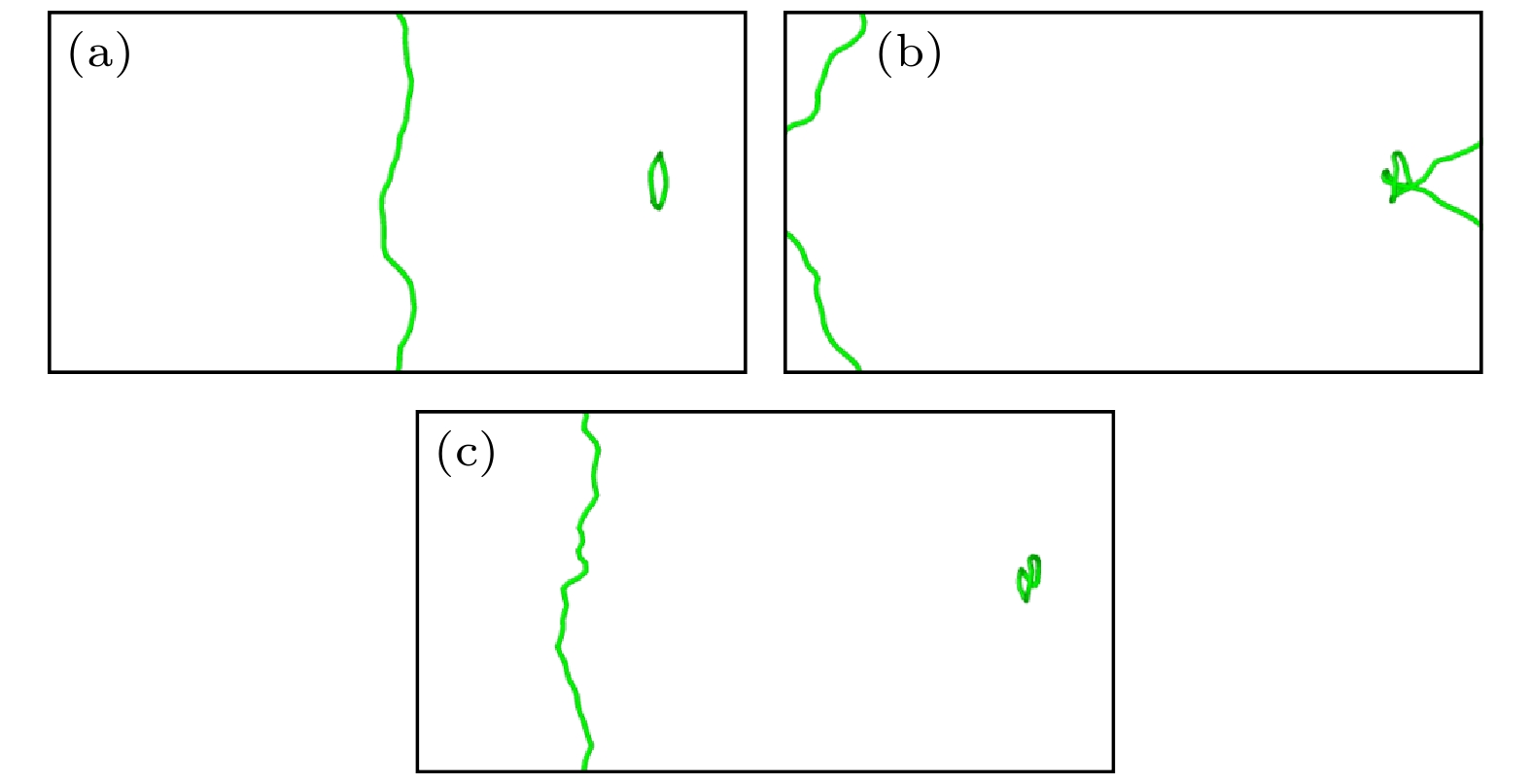
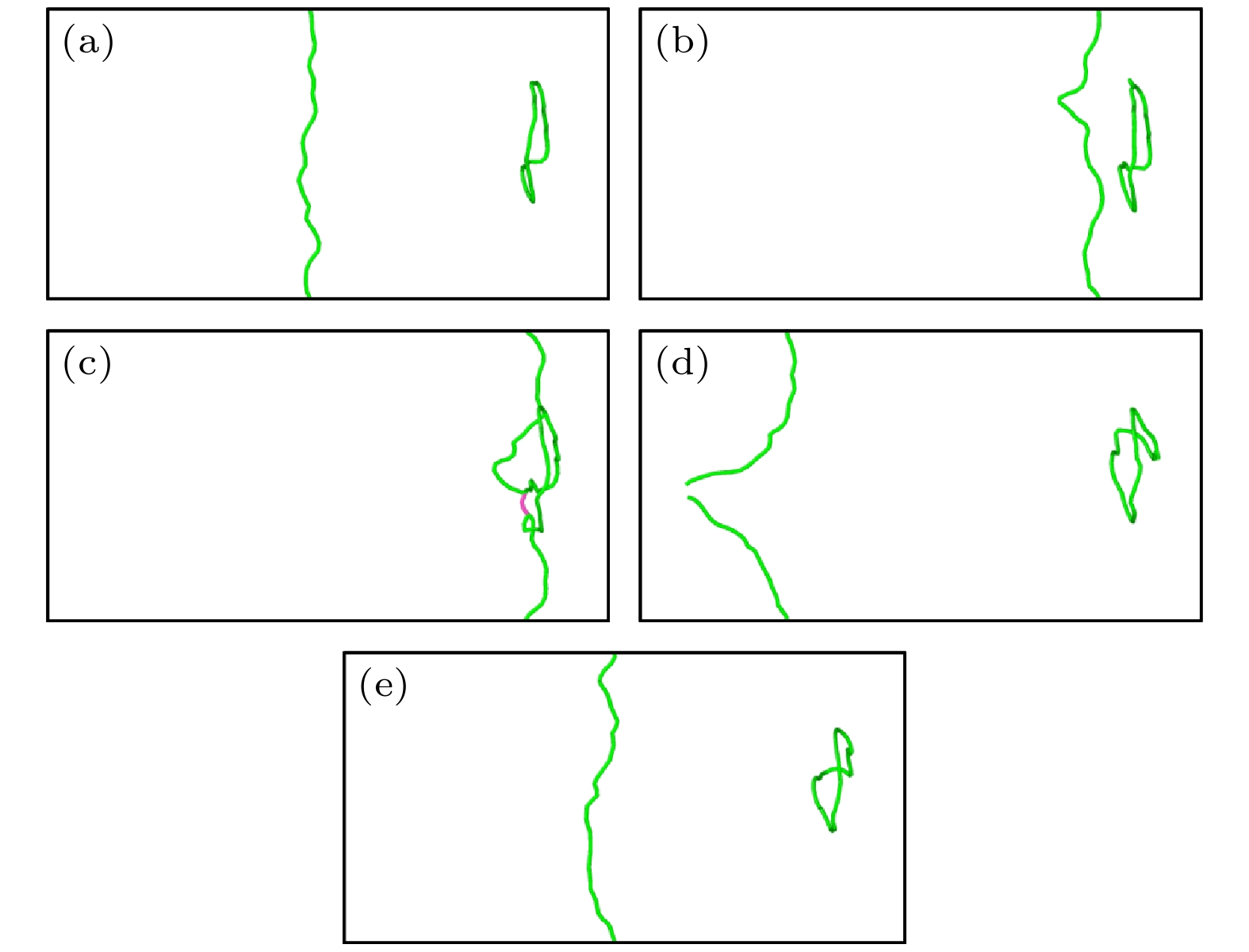
$ \left\langle {100} \right\rangle $ 环, 位错在150 MPa和200 MPa下的运动均被环阻碍, 只有当应力增加到250 MPa时, 位错才切过位错环向前运动, 说明$ \left\langle {100} \right\rangle $ 环对刃位错运动的阻碍随着位错环尺寸的增加而增加. 同样研究不同尺寸$ \left\langle {111} \right\rangle $ 环对位错运动产生的阻碍作用, 对于尺寸最小的$ \left\langle {111} \right\rangle $ 环, 位错切过位错环向前运动, 如图7所示. 而对于间隙数为144和400的$ \left\langle {111} \right\rangle $ 环, 环在位错移动过程中被位错带动一起向前运动, 如图8所示. 位错在应力作用下靠近并与$ \left\langle {111} \right\rangle $ 环相互接触, 随后$ \left\langle {111} \right\rangle $ 环附着在位错线上跟随位错一起向前运动. 同时由于$ \left\langle {111} \right\rangle $ 环存在极强的移动性, 环自身沿着位错线向下移动, 最后当环与位错线相互分离时, 位错环被位错线带到模拟盒子左侧部分(图8(f)). 间隙数为400的$ \left\langle {111} \right\rangle $ 环与位错之间的相互作用与上述情况相同. 根据上述纯V中位错与位错环之间相互作用的模拟结果可以得到以下结论, 在纯V中, 1)随着位错环尺寸的增加, 环与位错接触部分增加, 位错环对位错运动的阻力也增加; 2)$ \left\langle {111} \right\rangle $ 环由于极强的移动性对位错的阻碍作用要明显低于$ \left\langle {100} \right\rangle $ 环.考虑到TiVTa合金中纯刃位错的启动力, 对TiVTa合金施加350 MPa的应力研究位错与环之间的相互作用. 首先, 可以明显地观察到在TiVTa合金中位错线的弯曲和位错环形状的畸变, 如图9所示. 这是由TiVTa合金中显著的晶格畸变和局部化学波动导致的. 其次, 研究环尺寸对位错与位错环相互作用的影响发现, 对于间隙数为60的
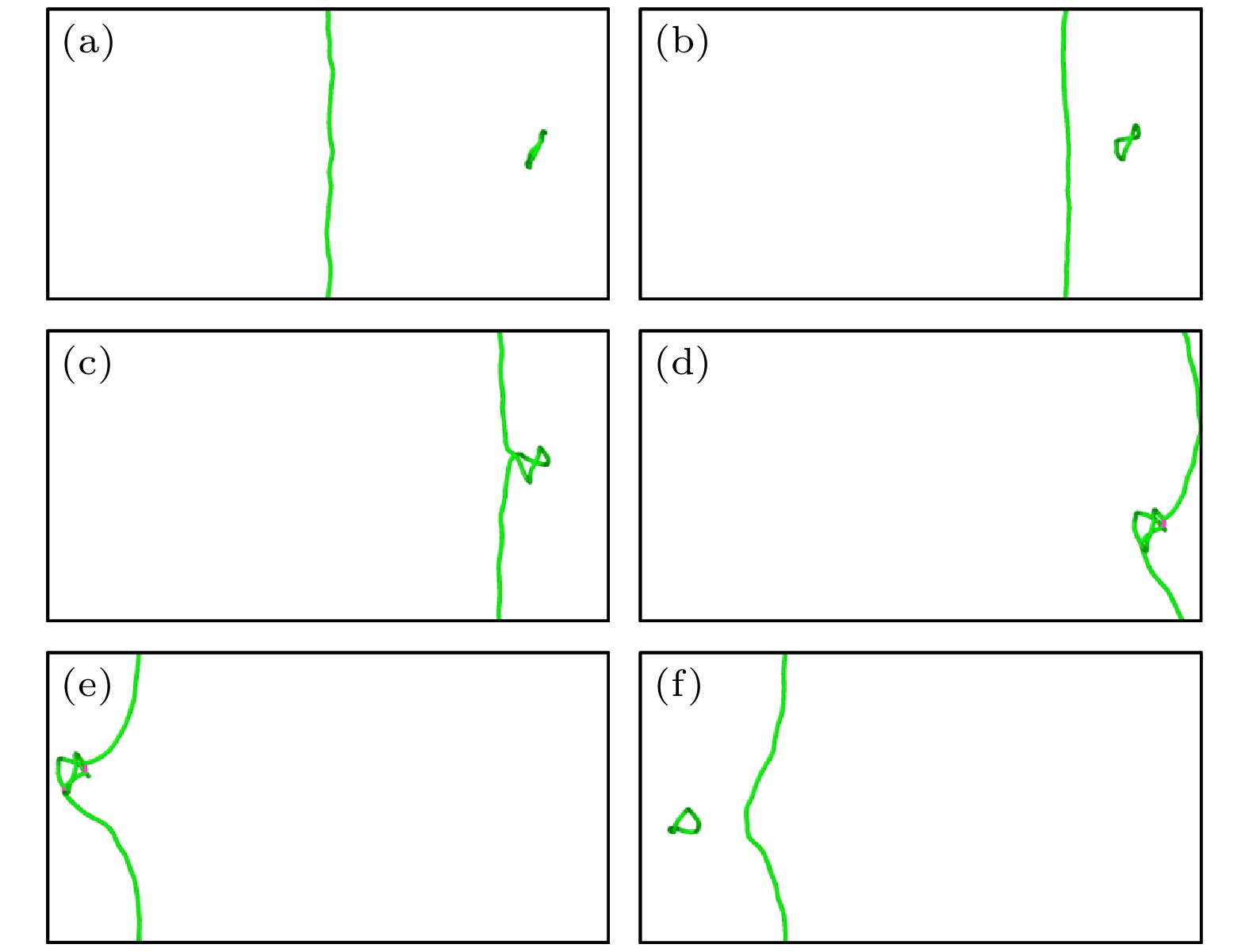
$ \left\langle {100} \right\rangle $ 环, 位错在移动过程中将环吸收, 在位错线上形成割阶; 对于间隙数为64的$ \left\langle {111} \right\rangle $ 环, 位错切过位错环后继续运动, 如图10和图11所示.当环上的间隙数增加到144时, 位错切过
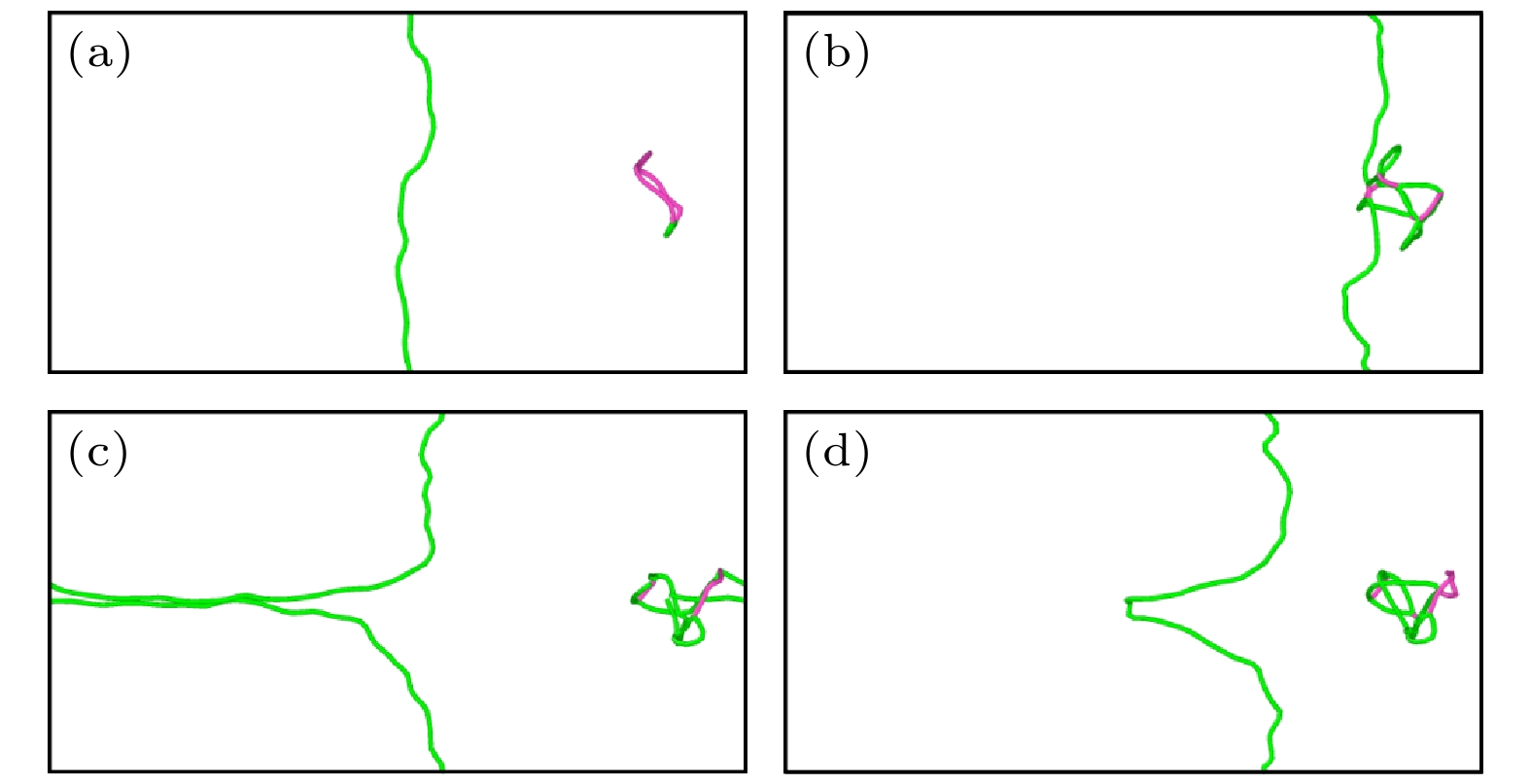
$ \left\langle {100} \right\rangle $ 环和$ \left\langle {111} \right\rangle $ 环向前移动. 而对于尺寸最大的两种位错环(间隙数为416的$ \left\langle {100} \right\rangle $ 环和间隙数为400的$ \left\langle {111} \right\rangle $ 环), 在350 MPa的施加应力下, 位错的运动均被位错环所阻碍. 将应力增加为550 MPa, 发现此时位错切过两种位错环继续向前运动, 如图12和图13所示.对比图12和图13中位错挣脱两种位错环束缚时两侧位错臂的夹角(图12(d)和图13(c))可以明显看出, 位错挣脱
$ \left\langle {100} \right\rangle $ 环时两侧位错臂的夹角小于$ \left\langle {111} \right\rangle $ 环. 而障碍物对位错运动的阻力与位错挣脱束缚时的临界角$ \varphi $ 存在一定的关系[12]:式中,
$ {F}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $ 代表障碍物对位错运动的钉扎力; L代表障碍物之间的间距, 对于本次模拟而言, 即环与经过一个周期后的环的距离, 也就是模拟盒子在x方向的长度. (2)式表明, 临界角$ \varphi $ 越小, 障碍物的阻力越大, 所以在TiVTa合金中尺寸最大的$ \left\langle {100} \right\rangle $ 环对位错的钉扎作用大于相应尺寸的$ \left\langle {111} \right\rangle $ 环.综上可以得到在TiVTa合金中, 1)
$ \left\langle {111} \right\rangle $ 环对位错的阻碍作用低于$ \left\langle {100} \right\rangle $ 环, 因为$ \left\langle {111} \right\rangle $ 环的移动性大于$ \left\langle {100} \right\rangle $ 环. 但是考虑到TiVTa合金中显著的晶格畸变带来的影响, 相较于纯V, TiVTa合金中$ \left\langle {111} \right\rangle $ 环的移动性被明显减弱, 因此在TiVTa合金中$ \left\langle {111} \right\rangle $ 环和$ \left\langle {100} \right\rangle $ 环对位错产生的阻碍作用的差异性要低于纯V; 2)位错环对位错的阻碍作用依旧随着位错环尺寸的增加而增加, 与纯V相同. -
为考虑温度对位错与位错环之间相互作用的影响, 在700 K的温度下研究了纯V中间隙数为144的
$ \left\langle {100} \right\rangle $ 环在150 MPa的恒应力下与位错之间的相互作用以及TiVTa合金中尺寸最大的$ \left\langle {100} \right\rangle $ 环和$ \left\langle {111} \right\rangle $ 环在350 MPa的恒应力下与位错之间的相互作用, 其余模拟条件与300 K下相同.首先根据3.2.1节得知在300 K, 150 MPa下纯V中刃位错的运动被间隙数为144的
$ \left\langle {100} \right\rangle $ 环阻碍. 而当温度升高到700 K时, 如图14所示, 位错切过位错环并吸收$ \left\langle {100} \right\rangle $ 环上的位错段形成割阶, 含有割阶的刃位错继续向前运动, 同时留下的$ \left\langle {100} \right\rangle $ 环转变成$ \left\langle {111} \right\rangle $ 环, 该结果表明温度升高后纯V中$ \left\langle {100} \right\rangle $ 环对位错的阻碍作用降低. 同理, 在300 K, 350 MPa下, TiVTa合金中位错的运动被尺寸最大的$ \left\langle {100} \right\rangle $ 环和$ \left\langle {111} \right\rangle $ 环阻碍, 而当温度升高到700 K时, 刃位错的运动仍然被$ \left\langle {100} \right\rangle $ 环阻碍, 但是对于$ \left\langle {111} \right\rangle $ 环, 位错挣脱环的束缚继续向前移动. 上述结果一方面证明在TiVTa合金中升高温度可以降低位错环对位错的阻碍作用, 另一方面证明了在TiVTa合金中,$ \left\langle {100} \right\rangle $ 环对位错运动的阻碍作用要高于$ \left\langle {111} \right\rangle $ 环.综合恒应力下两种金属中位错与位错环之间的相互作用结果最终可以得到以下结论: 1)纯V和TiVTa合金中存在两种位错与位错环之间的相互作用: 当施加的应力超过临界剪切应力时, 对于尺寸较小的位错环, 位错倾向于吸收位错环形成割阶; 而对于尺寸较大的位错环, 位错倾向于切过位错环继续向前运动. 位错环尺寸越大, 环与位错接触部分面积越大, 因此环对位错的阻碍作用也越强. 2)在纯V和TiVTa合金中,
$ \left\langle {111} \right\rangle $ 环对位错产生的阻碍作用均低于$ \left\langle {100} \right\rangle $ 环, 因为相较于$ \left\langle {100} \right\rangle $ 环,$ \left\langle {111} \right\rangle $ 环具有更高的移动性. 但是这种移动性由于TiVTa合金中显著的晶格畸变和局部化学波动而降低, 因此在TiVTa合金中,$ \left\langle {100} \right\rangle $ 环与$ \left\langle {111} \right\rangle $ 环对位错运动的阻碍强度差异减弱. 3)升高温度可以降低位错环对位错的阻碍作用, 因为温度升高, 原子振动加快. -
本文利用分子动力学模拟技术对纯V和TiVTa合金中刃位错的运动以及刃位错与位错环之间的相互作用展开研究, 根据模拟结果可以得到以下结论:
1)纯V中刃位错运动受到声子拖拽机制的控制, 位错运动速度随着应力的增加而增加, 随着温度的升高而降低;
2) TiVTa合金中由于存在显著的晶格畸变和局部化学波动, 刃位错运动同时受到声子拖拽机制与纳米段脱陷机制的控制, 前者导致位错运动速度随温度升高而降低, 而后者导致位错运动速度随温度升高而升高, 因此最终TiVTa合金中位错运动速度随着应力的增加而增加, 与温度则无明显关系;
3)纯V和TiVTa合金中存在两种位错与位错环的相互作用: 位错吸收位错环或位错切过位错环向前运动;
4)纯V和TiVTa合金中位错环对位错的阻碍作用随着位错环尺寸的增加而增加, 随着温度的升高而降低;
5)在纯V中,
$ \left\langle {111} \right\rangle $ 环对位错运动的阻碍作用明显低于$ \left\langle {100} \right\rangle $ 环, 但在TiVTa合金中, 由于显著的晶格畸变降低了$ \left\langle {111} \right\rangle $ 环的移动性, 所以相对于纯V, TiVTa合金中$ \left\langle {111} \right\rangle $ 环和$ \left\langle {100} \right\rangle $ 环对位错运动的阻碍作用的差异性降低.
纯V和TiVTa合金中刃位错运动及其与位错环之间相互作用的模拟研究
Simulation study on edge dislocation motion and its interaction with dislocation loop in pure V and TiVTa alloy
-
摘要: 利用分子动力学对纯V和TiVTa等比合金中的刃位错运动以及刃位错与位错环之间的相互作用开展模拟研究. 结果表明, 纯V中控制刃位错运动的是声子拖拽机制; 而在TiVTa合金中, 由于存在显著的晶格畸变和局部化学波动, 声子拖拽机制和纳米段脱陷机制同时控制刃位错运动. 在纯V和TiVTa合金中加入不同尺寸的间隙$ \left\langle {100} \right\rangle $环和$ \left\langle {111} \right\rangle $环, 发现位错与环之间存在两种相互作用机制: 对于小尺寸位错环, 位错倾向于吸收位错环后继续运动; 对于大尺寸位错环, 位错倾向于切过位错环后继续运动. 位错环对位错的阻碍作用随着位错环尺寸的增加而增加、随着温度的升高而降低. $ \left\langle {111} \right\rangle $环由于极强的移动性, 对位错运动产生的阻碍作用低于$ \left\langle {100} \right\rangle $环, 而这种差异在TiVTa合金中降低, 因为TiVTa合金中显著的晶格畸变降低了$ \left\langle {111} \right\rangle $环的移动性.Abstract:
The motion of edge dislocations and the interaction between edge dislocations and dislocation loops in pure V and TiVTa alloy are simulated in this work, with the aim to reveal the influences of the existence of $ \left\langle {111} \right\rangle $ dislocation loops, which are dominant in pure V, and $ \left\langle {100} \right\rangle $ dislocation loops, which are dominant in TiVTa alloy, on the irradiation properties of materials and the differences between the irradiation properties influenced by the two types of dislocation loops. The edge dislocations and $ \left\langle {100} \right\rangle $ loops and $ \left\langle {111} \right\rangle $ loops with different sizes are introduced into pure V and TiVTa alloy by using molecular dynamics simulation technology. The effects of loop type, loop size, and temperature on the interaction between edge dislocations and dislocation loops in pure V and TiVTa alloy are compared with each other and analyzed. The differences in interaction between dislocations and dislocation loops are summarized, and the reasons are revealed. The simulation results of edge dislocation motion reveal that the velocity of edge dislocations in the pure V decreases with temperature increasing, while the velocity of edge dislocations in the TiVTa alloy shows no significant relation to temperature. This is due to phonon-drag mechanism controlling the motion of edge dislocations in the pure V. In the TiVTa alloy, due to inevitable local chemical fluctuations, the phonon-drag mechanism and the nanoscale segment detrapping mechanism simultaneously control the motion of edge dislocations. The simulation results of the interaction between edge dislocations and dislocation loops show that there are two kinds of interaction mechanisms between dislocations and loops in pure V and TiVTa alloy: for small dislocation loops, dislocations tend to absorb the loops and continue to move; for large dislocation loops, dislocations tend to go through the loops and then move forward. With the size of dislocation loop increasing, the stress required for dislocations to detach from the dislocation loops also increases. With the increase of temperature, the stress required for dislocations to detach from the dislocation loops decreases. This is because the larger the size of the loops, the larger the contact area between dislocations and loops, and the greater the obstacle presented by the loops. With the increase in temperature, atomic vibrations are accelerated, and the hindrance of the loops is reduced. When comparing the interaction between $ \left\langle {100} \right\rangle $ loops and $ \left\langle {111} \right\rangle $ loops and dislocations, it is found that the hindrance of $ \left\langle {111} \right\rangle $ loops to dislocation movement is lower than that of $ \left\langle {100} \right\rangle $ loops, and the difference in the hindrance to dislocation between $ \left\langle {100} \right\rangle $ loops and $ \left\langle {111} \right\rangle $ loops is more significant in pure V than what is observed in TiVTa alloy. This is because the mobility of $ \left\langle {111} \right\rangle $ loops is higher than that of $ \left\langle {100} \right\rangle $ loops, the hindrance to dislocation motion of $ \left\langle {111} \right\rangle $ loops is lower than that of $ \left\langle {100} \right\rangle $ loops. However, in the TiVTa alloy, significant lattice distortion reduces the mobility of $ \left\langle {111} \right\rangle $ loops. Therefore, the hindrance of $ \left\langle {111} \right\rangle $ loops in the TiVTa alloy is lower than that of $ \left\langle {100} \right\rangle $ loops, but the difference between them is reduced compared with what is observed in pure V. -
Key words:
- molecular dynamics /
- TiVTa alloy /
- edge dislocation /
- dislocation loop .
-

-
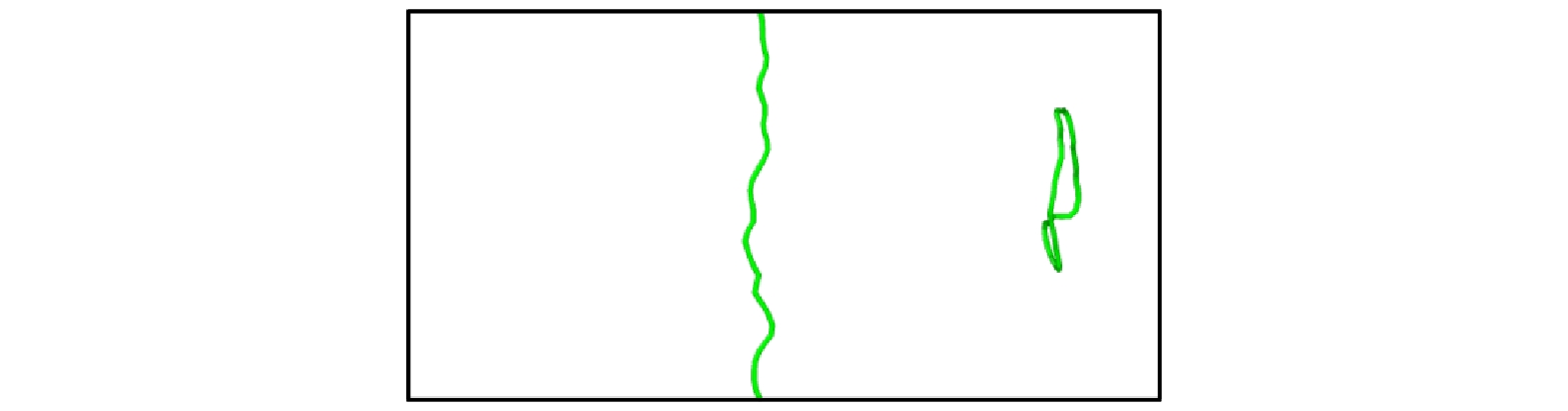
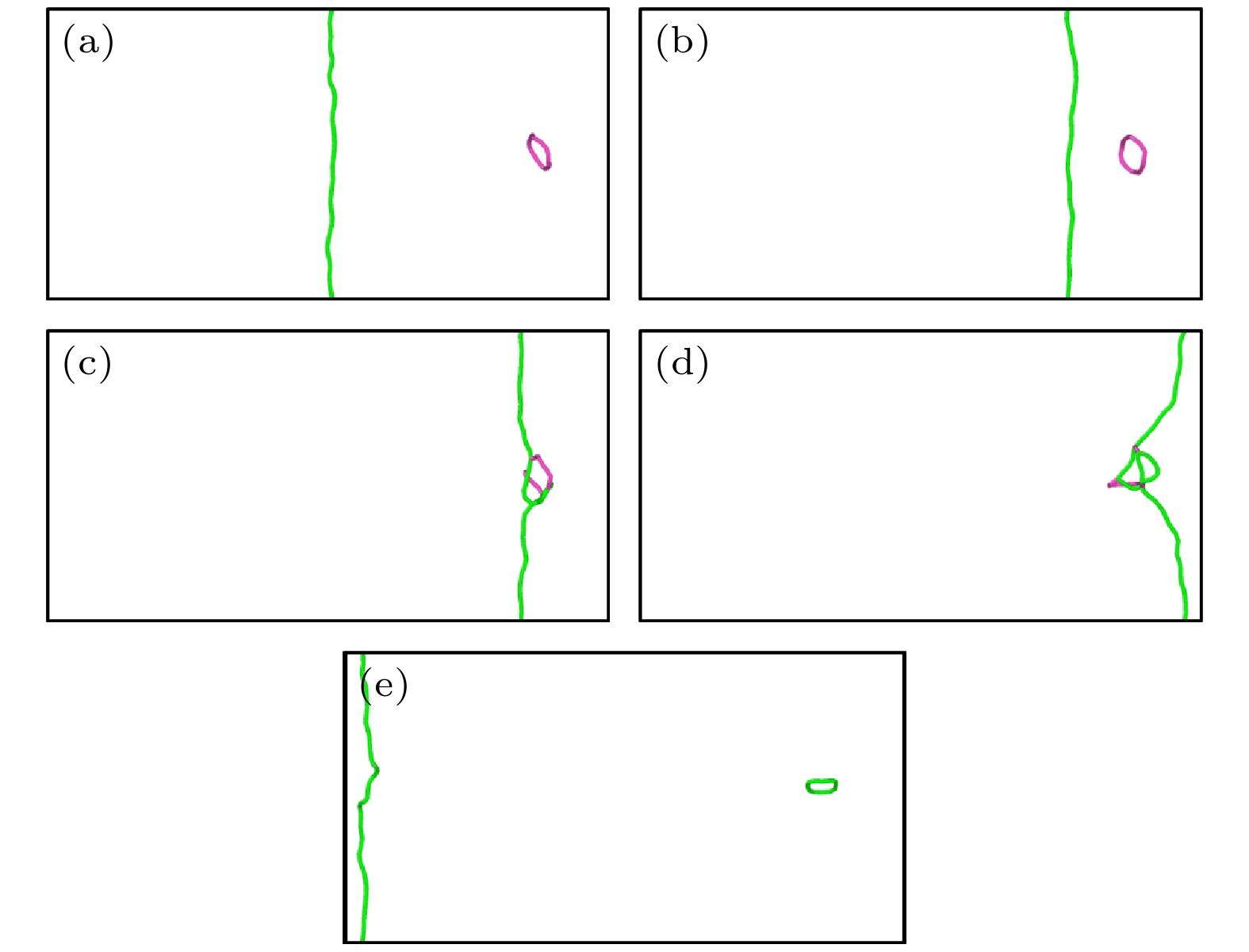
图 5 纯V中位错与间隙数为60的
$ \left\langle {100} \right\rangle $ 环在150 MPa下相互作用的可视化图像 (a) t = 0 ps; (b) t = 20 ps; (c) t = 24 ps; (d) t = 28 ps; (e) t = 36 psFigure 5. Interaction between dislocation and
$ \left\langle {100} \right\rangle $ loop with 60 self interstitial atoms at 150 MPa in pure V: (a) t = 0 ps; (b) t = 20 ps; (c) t = 24 ps; (d) t = 28 ps; (e) t = 36 ps.图 8 纯V中位错与间隙数为144的
$ \left\langle {111} \right\rangle $ 环的相互作用(a) t = 0 ps; (b) t = 20 ps; (c) t = 22 ps; (d) t = 76 ps; (e) t = 118 ps; (f) t = 124 psFigure 8. Interaction between dislocation and
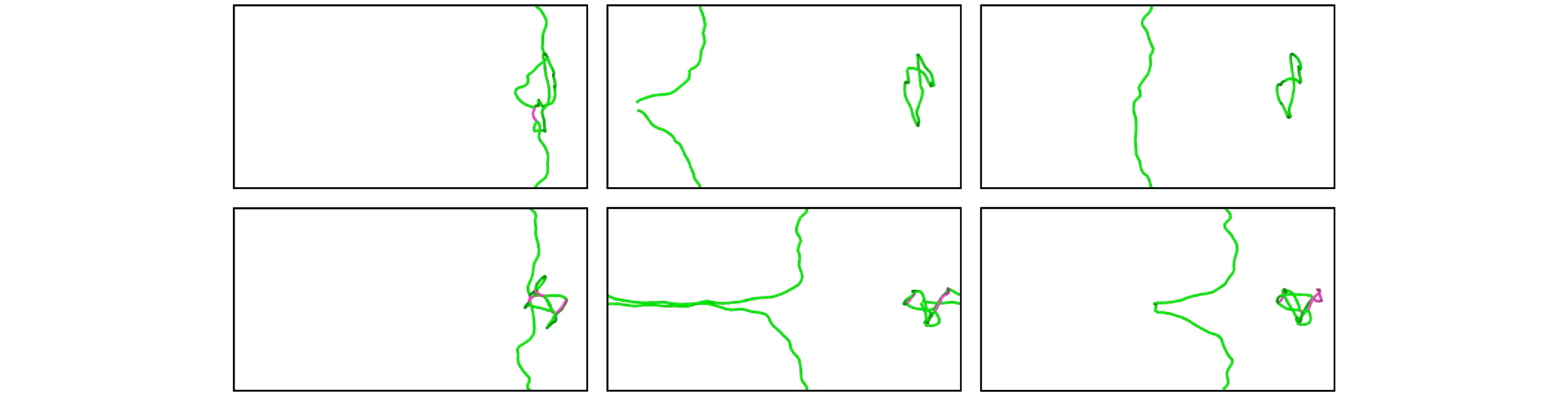
$ \left\langle {111} \right\rangle $ loop with 144 self interstitial atoms in pure V: (a) t = 0 ps; (b) t = 20 ps; (c) t = 22 ps; (d) t = 76 ps; (e) t = 118 ps; (f) t = 124 ps.图 12 550 MPa下TiVTa合金中位错与间隙数为400的
$ \left\langle {111} \right\rangle $ 环的相互作用 (a) t = 0 ps; (b) t = 32 ps; (c) t = 36 ps; (d) t = 52 ps; (e) t = 60 psFigure 12. Interaction between dislocation and
$ \left\langle {111} \right\rangle $ loop with 400 self interstitial atoms in TiVTa alloy at 550 MPa: (a) t = 0 ps; (b) t = 32 ps; (c) t = 36 ps; (d) t = 52 ps; (e) t = 60 ps.图 13 550 MPa下TiVTa合金中位错与间隙数为416的
$ \left\langle {100} \right\rangle $ 环的相互作用 (a) t = 0 ps; (b) t = 28 ps; (c) t = 60 ps; (d) t = 68 psFigure 13. Interaction between dislocation and
$ \left\langle {100} \right\rangle $ loop with 416 self interstitial atoms in TiVTa alloy at 550 MPa: (a) t = 0 ps; (b) t = 28 ps; (c) t = 60 ps; (d) t = 68 ps.图 14 700 K下纯V中位错与间隙数为144的
$ \left\langle {100} \right\rangle $ 环的相互作用 (a) t = 0 ps; (b) t = 24 ps; (c) t = 28 ps; (d) t = 40 ps; (e) t = 48 psFigure 14. Interaction between dislocation and
$ \left\langle {100} \right\rangle $ loop with 144 self interstitial atoms at 700 K in pure V: (a) t = 0 ps; (b) t = 24 ps; (c) t = 28 ps; (d) t = 40 ps; (e) t = 48 ps. -
[1] Yeh J W, Chen S K, Lin S J, Gan J Y, Chin T S, Shun T T, Tsau C H, Chang S Y 2004 Adv. Eng. Mater. 6 299 doi: 10.1002/adem.200300567 [2] Senkov O N, Wilks G B, Scott J M, Miracle D B 2011 Intermetallics 19 698 doi: 10.1016/j.intermet.2011.01.004 [3] Couzinié J P, Dirras G 2019 Mater. Charact. 147 533 doi: 10.1016/j.matchar.2018.07.015 [4] Fu A, Guo W M, Liu B, Cao Y K, Xu L Y, Fang Q H, Yang H, Liu Y 2020 J. Alloys Compd. 815 152466 doi: 10.1016/j.jallcom.2019.152466 [5] Yang C, Aoyagi K, Bian H K, Chiba A 2019 Mater. Lett. 254 46 doi: 10.1016/j.matlet.2019.07.027 [6] Sadeghilaridjani M, Ayyagari A, Muskeri S, Hasannaeimi V, Salloom R, Chen W Y, Mukherjee S 2020 J. Nucl. Mater. 529 151955 doi: 10.1016/j.jnucmat.2019.151955 [7] Kareer A, Waite J C, Li B, Couet A, Armstrong D E J, Wilkinson A J 2019 J. Nucl. Mater. 526 151744 doi: 10.1016/j.jnucmat.2019.151744 [8] El-Atwani O, Alvarado A, Unal K, Fensin S, Hinks J A, Greaves G, Baldwin J K S, Maloy S A, Martinez E 2021 Mater. Today Energy 19 100599 doi: 10.1016/j.mtener.2020.100599 [9] Lu Y P, Huang H F, Gao X Z, Ren C L, Gao J, Zhang H Z, Zheng S J, Jin Q Q, Zhao Y H, Lu C Y, Wang T M, Li T J 2019 J. Mater. Sci. Technol. 35 369 doi: 10.1016/j.jmst.2018.09.034 [10] Mei L, Zhang Q, Dou Y, Fu E G, Li L, Chen S, Dong Y, Guo X, He X, Yang W, Xue Y, Jin K 2023 Scr. Mater. 223 115070 doi: 10.1016/j.scriptamat.2022.115070 [11] George E P, Raabe D, Ritchie R O 2019 Nat. Rev. Mater. 4 515 doi: 10.1038/s41578-019-0121-4 [12] Chen B, Li S Z, Zong H X, Ding X D, Sun J, Ma E 2020 Proc. Natl. Acad. Sci. U. S. A. 117 16199 doi: 10.1073/pnas.1919136117 [13] Lee C, Maresca F, Feng R, Chou Y, Ungar T, Widom M, An K, Poplawsky J D, Chou Y C, Liaw P K, Curtin W A 2021 Nat. Commun. 12 5474 doi: 10.1038/s41467-021-25807-w [14] Yin X, Dou Y K, He X F, Jin K, Wang C L, Dong Y G, Wang C Y, Xue Y F, Yang W 2023 Acta Metall. Sin. (Engl. Lett. ) 36 405 doi: 10.1007/s40195-022-01494-4 [15] Bacon D J, Osetsky Y N, Rong Z 2006 Philos. Mag. 86 3921 doi: 10.1080/14786430600570527 [16] Marian J, Wirth B D, Schäublin R, Odette G R, Perlado J M 2003 J. Nucl. Mater. 323 181 doi: 10.1016/j.jnucmat.2003.08.037 [17] Rong Z, Osetsky Y N, Bacon D J 2005 Philos. Mag. 85 1473 doi: 10.1080/14786430500036371 [18] Nomoto A, Soneda N, Takahashi A, Ishino S 2005 Mater. Trans. 46 463 doi: 10.2320/matertrans.46.463 [19] 林盼栋, 聂君锋, 刘美丹 2022 清华大学学报 (自然科学版) 62 2029 doi: 10.16511/j.cnki.qhdxxb.2022.25.003 Lin P D, Nie J F, Liu M D 2022 J. Tsinghua Univ. (Sci. Technol. ) 62 2029 doi: 10.16511/j.cnki.qhdxxb.2022.25.003 [20] 王瑾, 贺新福, 曹晗, 王东杰, 豆艳坤, 杨文 2021 原子能科学技术 55 1210 doi: 10.7538/yzk.2021.youxian.0080 Wang J, He X F, Cao H, Wang D J, Dou Y K, Yang W 2021 At. Energy Sci. Technol. 55 1210 doi: 10.7538/yzk.2021.youxian.0080 [21] 王瑾, 贺新福, 曹晗, 贾丽霞, 豆艳坤, 杨文 2021 物理学报 70 068701 doi: 10.7498/aps.70.20201659 Wang J, He X F, Cao H, Jia L X, Dou Y K, Yang W 2021 Acta Phys. Sin. 70 068701 doi: 10.7498/aps.70.20201659 [22] Yu M S, Wang Z Q, Wang F, Setyawan W, Long X H, Liu Y, Dong L M, Gao N, Gao F, Wang X L 2023 Acta Mater. 245 118651 doi: 10.1016/j.actamat.2022.118651 [23] Li J, Chen H T, Fang Q H, Jiang C, Liu Y, Liaw P K 2020 Int. J. Plast. 133 102819 doi: 10.1016/j.ijplas.2020.102819 [24] Dou Y K, Cao H, He X F, Gao J, Cao J L, Yang W 2021 J. Alloys Compd. 857 157556 doi: 10.1016/j.jallcom.2020.157556 [25] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, in't Veld P J, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Commun. 271 108171 doi: 10.1016/j.cpc.2021.108171 [26] Daw M S, Foiles S M, Baskes M I 1993 Mater. Sci. Rep. 9 251 doi: 10.1016/0920-2307(93)90001-U [27] Stukowski A 2009 Modell. Simul. Mater. Sci. Eng. 18 015012 doi: 10.1088/0965-0393/18/1/015012 [28] Qiu R Y, Chen Y C, Liao X C, He X F, Yang W, Hu W Y, Deng H Q 2021 J. Nucl. Mater. 557 153231 doi: 10.1016/j.jnucmat.2021.153231 [29] Chen B, Li S Z, Ding J, Ding X D, Sun J, Ma E 2023 Scr. Mater. 222 115048 doi: 10.1016/j.scriptamat.2022.115048 [30] Ma E 2020 Scr. Mater. 181 127 doi: 10.1016/j.scriptamat.2020.02.021 [31] Wang F L, Balbus G H, Xu S Z, Su Y Q, Shin J, Rottmann P F, Knipling K E, Stinville J C, Mills L H, Senkov O N, Beyerlein I J, Pollock T M, Gianola D S 2020 Science 370 95 doi: 10.1126/science.aba3722 [32] Kubilay R E, Ghafarollahi A, Maresca F, Curtin W A 2021 npj Comput. Mater. 7 112 doi: 10.1038/s41524-021-00577-7 [33] Bu Y Q, Wu Y, Lei Z F, Yuan X Y, Wu H H, Feng X B, Liu J B, Ding J, Lu Y, Wang H T, Lu Z P, Yang W 2021 Mater. Today 46 28 doi: 10.1016/j.mattod.2021.02.022 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: