-
随着对微纳机电系统(M/NEMS)器件在更高功率密度、更高频和更高光强度下工作需求的增加, 人们进一步拓展了超宽禁带半导体在M/NEMS中的应用. β相氧化镓(β-Ga2O3)作为近年来备受瞩目的超宽禁带半导体材料, 展现出独特的物理特性. β-Ga2O3禁带宽度约为4.8 eV, 理论计算表明, 它具备高达8 MV/cm的临界击穿场强, 使其在电力电子和紫外传感等领域具有广阔的应用前景[1]. β-Ga2O3作为功率器件材料具有极大的潜力, 例如将锡(Sn)掺杂的β-Ga2O3沟道层转移到碳化硅(SiC)衬底上, 并制成β-Ga2O3射频金属氧化物半导体场效应晶体管(RF metal-oxide-semiconductor field-effect transistor, RF MOSFET), 可实现高达70 mS/mm的最大跨导以及1.1 A/mm的最大漏极电流[2]. 此外, 由于其约4.8 eV的直接带隙, β-Ga2O3光电探测器可以选择性地吸收波长小于约260 nm的光, 使其成为日盲紫外线探测的天然材料, 与需要通过金属掺杂来调整带隙的AlGaN和MgZnO相比具有显著优势[3]. 另外, β-Ga2O3还具有优异的机械性能, 其杨氏模量EY = 261 GPa 和质量密度ρ = 5950 kg/m3 决定了材料的声速c = 6623 m/s, 这些特性使β-Ga2O3成为制造高频率微纳机电谐振器的理想材料[4]. 更重要的是, β-Ga2O3单晶可以通过熔融方式生长, 具有较高的潜在成本效益, 这些特点赋予了其在M/NEMS领域强大的应用前景[5].
微纳米机电谐振器是M/NEMS领域的重要器件结构之一, 能够实现电能、磁能、光能与机械能之间的转换, 以及高灵敏度、高工作频率和高品质因数等性能参数, 在精密测量、生物传感、航空电子、射频通信甚至太赫兹通信[6,7] 等领域备受关注. 由于其极小的尺寸和极高的灵敏度, 纳米机电谐振器还可应用于量子信息领域[8]和光子芯片等新兴领域[9]. 谐振器的常见基本结构包括悬臂梁结构(cantilever)、双端固支结构(doubly-clamped beam)、圆形鼓面结构(circular drumhead)等, 结构的选择决定了谐振器能适用的制备和驱动方式[10].
在微纳机电谐振器中, 品质因数(quality factor, Q值)是衡量器件性能的重要参数, 其与谐振器的能量耗散密切相关[11]. Q值正比于器件所存储的能量E与一个振动周期内耗散的能量ΔE的比值, Q值越高代表器件的能量耗散率越小, 即系统的 储能效率越高[12]. 通常, 谐振器的Q值越高, 其谐振信号就越强, 在相同背景噪声(包括热机械噪声、相位噪声等)下, 器件的信噪比和信号选择性也就越高. 因此, 能量耗散是影响微纳机电谐振 器性能提升和应用发展的关键之一, 如何有效减小能量耗散成为设计高性能谐振器的核心挑战. 谐 振器的总能量耗散由不同耗散机制综合决定, 其 中主要包括空气阻尼(air damping)[13]、热弹性阻尼(thermoelastic damping, TED)[14]、支撑阻尼(clamping loss)[15]、表面阻尼(surface loss)[16]、Akhiezer阻尼(AKE)[17]以及其他阻尼所引起的能量耗散. 在设计谐振器时, 需要考虑各种耗散机制, 尽量降低耗散值以提高Q值. 在对谐振器的能量耗散进行研究时, 需要将不同耗散机制下的能量耗散叠加, 以得到整体耗散.
本文基于双端固支与圆形鼓面两种不同结构的β-Ga2O3微纳机电谐振器, 采用理论、仿真分析与实验测量相结合的方式, 系统地研究谐振器中的能量耗散现象. 通过对不同结构和尺寸的谐振器能量耗散进行理论分析, 并利用COMSOL软件进行有限元仿真, 探究能量耗散的途径及其控制方法. 此外, 为验证理论分析和仿真结果的准确性, 采用激光干涉法对器件的谐振特性进行测量, 并将实验数据与理论分析和仿真结果进行对比验证, 从而分析β-Ga2O3微纳机电谐振器中能量耗散的主要途径, 并推导出优化设计方法.
-
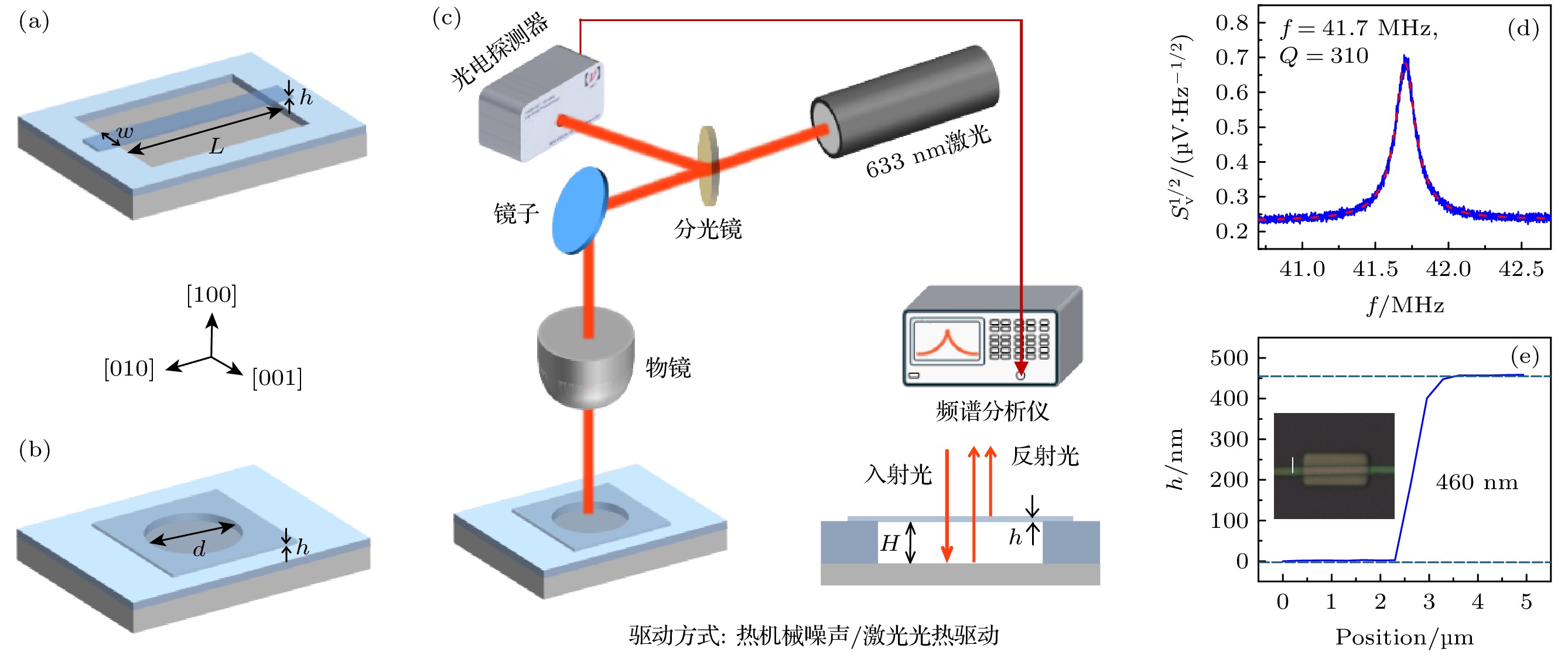
根据晶体的不同获取方式, β-Ga2O3谐振器的制备方式呈现多样性, 具体可参考文献[18]. 本文采用其中一种典型的制备方式, 以实现β-Ga2O3纳米机电谐振器的快速原型制备, 即机械剥离与干式转移结合的方式, 将机械剥离的β-Ga2O3薄膜转移到预先定义有沟槽的衬底上, 进而制备出双端固支与圆形鼓面两种结构的谐振器, 其示意图分别如图1(a), (b)所示. 机械剥离法是指利用胶带撕扯β-Ga2O3晶体, 使晶体中较弱的化学键断裂并发生机械剥离, 通过反复撕扯使β-Ga2O3晶体减薄至所需厚度, 形成带状β-Ga2O3结构. 随后, 借助干式转移法, 利用聚二甲基硅氧烷(polydimethylsiloxane, PDMS)片作为媒介, 将β-Ga2O3带转移到衬底上, 结合衬底上预先定义的沟槽, 形成β-Ga2O3悬空结构. 利用该方法能够避免制备过程中的化学污染, 减小对器件表面的影响, 从而削弱表面阻尼对器件Q值的影响.
随后使用激光干涉法对器件进行测量, 测量装置如图1(c)所示. 当激光到达谐振器表面时, 入射激光在β-Ga2O3层和衬底表面同时发生反射, 不同界面的反射光叠加后被送到光电探测器并转化成电信号. 当谐振器发生振动时, 不同反射光之间的光程差(相位)发生变化, 从而通过干涉效应调制总反射光的光强, 并随谐振器的周期性振动发生周期性的波动. 高精度光电探测器接收到反射光后, 将其转化为电信号, 输入到网络分析仪或频谱分析仪中, 实现对纳米机电谐振器机械振动信号的读取. 对于谐振器机械振动的驱动, 优先利用器件本身的热机械运动, 当热机械运动无法产生激光干涉足以测量的振动幅度时, 则引入可调制蓝(405 nm)激光, 利用光热效应对谐振器进行振动激励. 经过激光干涉测量后, 得到谐振器的谐振频谱数据, 如图1(d)中的蓝色曲线所示, 根据洛伦兹(Lorentzian)分布模型拟合提取谐振频率f和Q值. 谐振器的厚度采用原子力显微镜(atomic force microscopy, AFM)进行测量, 如图1(e)所示, 沿扫描路径探测后得到测量曲线, 曲线两端的差值即谐振器厚度.
在微纳机电谐振器中, 高Q值对器件性能十分重要, 通常用其来表征系统储存能量的能力. Q值定义为Q = 2π(E/ΔE), 其中E为谐振器中存储的总能量, ΔE为每周期的能量耗散. 谐振器的Q值由不同的耗散过程综合决定, 其倒数1/Q与能量耗散速率成正比. 假设各耗散机制独立, 谐振器的总能量耗散和不同物理过程引起的能量耗散的关系可表示为
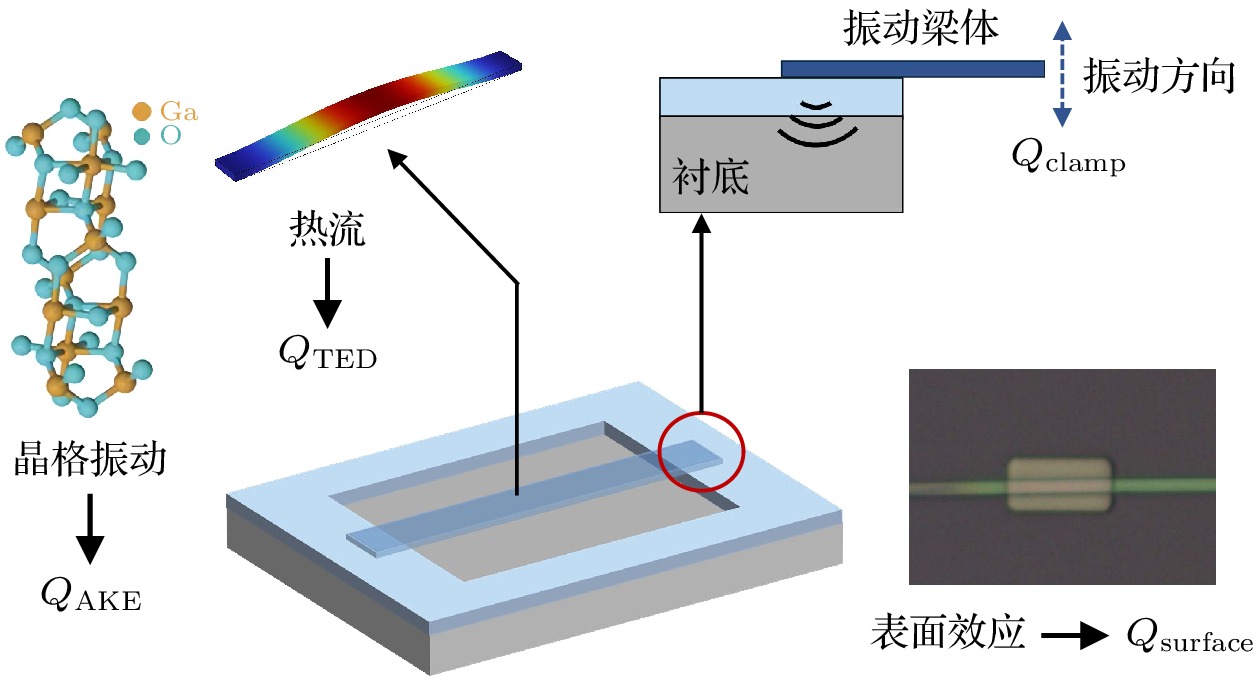
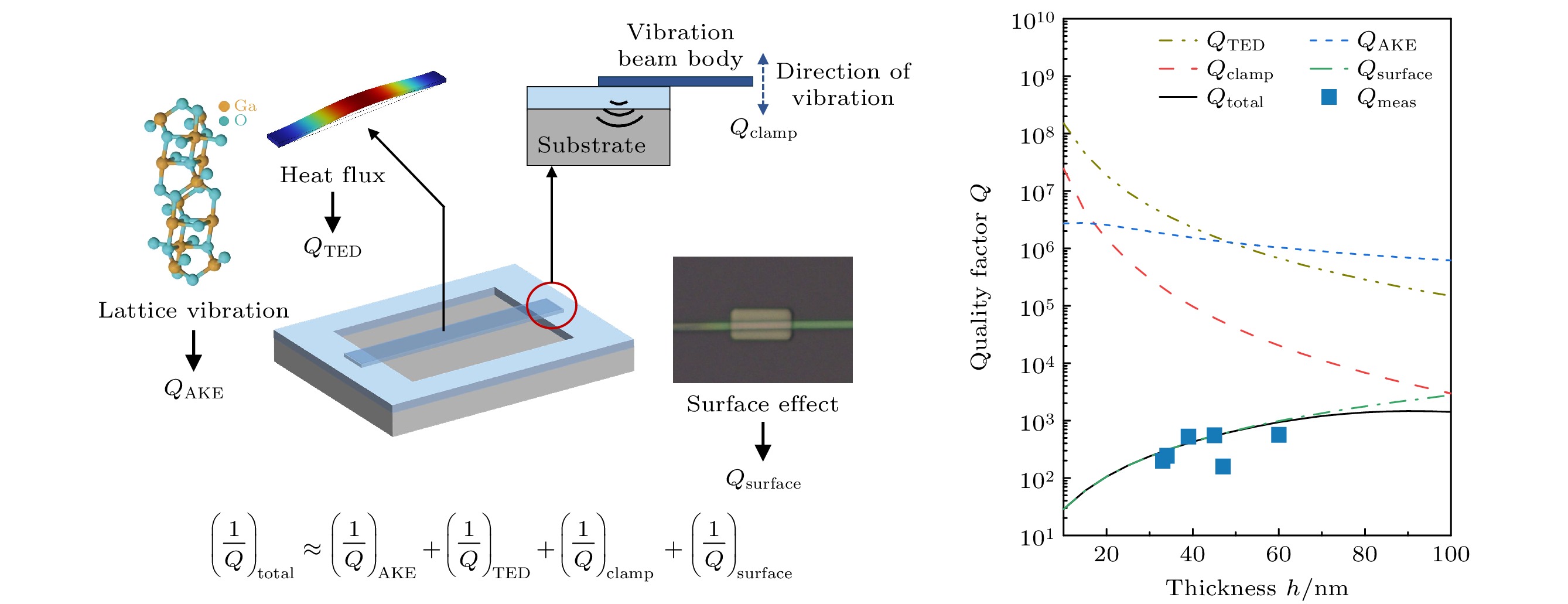
其中(1/Q)total为总能量耗散, 等式右侧其余项分别为空气阻尼(1/Q)air、Akhiezer效应(1/Q)AKE、热弹性阻尼(1/Q)TED、支撑阻尼(1/Q)clamp、表面阻尼(1/Q)surface以及其他阻尼(1/Q)other所引起的能量耗散. 为研究β-Ga2O3谐振器的机械能量耗散现象, 本文将利用双端固支和圆形鼓面两种简单的悬空机械结构, 从理论、仿真和实验的角度, 探讨材料、器件的不同参数对β-Ga2O3谐振器的机械耗散的影响. 图2以双端固支结构为例展示了主要的能量耗散途径.
为研究谐振器在谐振状态下的机械能量耗散, 首先需要确定谐振器的谐振频率. 双端固支结构弯曲模态(flexural mode)的机械谐振频率为[19]
其中n为模态数, I = wh3/12为转动惯量, L, w, h分别为谐振梁的长度、宽度和厚度, EY和ρ分别为β-Ga2O3的杨氏模量和质量体密度, σ为内应力.
圆形鼓面结构弯曲模态的谐振频率表示为[20]
其中m为模态数,
$D = E_{\mathrm{Y}}h^3/[12(1 - \nu^2)] $ 为弯曲刚度, ν为泊松比; d, h分别为谐振器的直径与厚度; (kmd/2)是与模态有关的参数, 在基模下(k1d/2)2可由下式近似表示:其中Z = σhd 2/D; α = 5.7832, β = 10.215, λ = 0.1148, δ = 0.4868是与振动模态相关的参数.
根据(1)式, 总能量耗散由不同能量耗散叠加而成. 其中, 空气阻尼是指在谐振器振动过程中, 振动部分与周围的气体分子碰撞发生能量交换, 阻碍了谐振器的振动, 从而引起能量耗散[21]. 本文所研究的器件均在较高真空条件下(p < 50 mTorr)测量, 因此空气阻尼可以忽略不计. 值得一提的是, 对于圆形鼓面器件, 初始抽真空的过程中会出现鼓膜腔内外压强不一致的现象, 但研究表明随着时间推移, 气体泄漏会使内外压强逐渐趋于一致[22]. 本文测量的圆形鼓面谐振器均已置于真空环境中足够长时间, 并通过多次测量以获得不受此现象影响的Q值.
当固体材料的微观振动模态被量子化为声子时, 声子的能量耗散分别源自声子的散射和输运, 前者被称为Akhiezer效应(AKE) [23], 后者是热弹性阻尼(TED)的量子形式体现, 也可用经典的热传递和其导致的熵增来解释. 与(1)式中所列的其他能量耗散途径不同, AKE无法通过调整谐振器结构设计或控制外部环境进行有效调控, 其完全取决于谐振器材料的性质, 因此限制了机械谐振器f-Q乘积的极大值. 当晶格畸变的周期(τv)长于声子散射的弛豫时间(τs), 即τv > τs时, 在AKE作用下, 声子的散射过程会导致器件中的声子重新分布, 并在到达新的动态热平衡过程中产生熵增, 从而引起能量耗散[24], 这种耗散是由声子-声子相互作用引起的. 在频率非常高的谐振器中, 晶格畸变的振动周期可能会短于声子的平均散射时间, τv < τs, 此时声子没有足够的散射时间来重新分布, AKE被抑制[25]. AKE限制下的Q值可以通过以下公式计算[26]:
其中, Cv和c分别为单位体积热容和平均声速, γavg为平均Grüneisen参数[27], τs = 3k/(Cvc2)为声子散射的弛豫时间, k为热导率[28], 其具有各向异性, 不同晶向的k值见表1. 根据图1, 双端固支结构谐振器的热传导主要沿[010]晶向进行, 因此k值选取[010]晶向的值, kbeam = 27.0 W/(m⋅K); 而圆形鼓面结构谐振器的热传导发生在(100)面内, k值选取[010]和[001]两个晶向的平均值, kdrum = 20.75 W/(m K). 已知c = 6623 m/s, 单位质量热容Cp = 491 J/(kg·K)[29], 则单位体积热容Cv = Cp·ρ = 2.92 × 106 J/(m3 K). 经过计算, 对于双端固支器件, τs-beam = 6.37×10–13 s, 对于圆形鼓面器件, τs-drum = 4.89×10–13 s.
TED是在谐振器振动过程中, 为恢复热平衡产生的热传导所导致的熵增现象. 谐振器材料发生形变时, 一部分被压缩而温度升高, 另一部分被拉伸而温度降低, 由温度梯度引起的热传导在不同应变区间之间产生[30]. 由于热传导的不可逆性, 系统熵增大, 从而导致能量耗散. 热弹性阻尼可以通过理论计算或有限元仿真进行模拟, 其解析公式为[31,32]
其中Δθ是与谐振器结构有关的系数, T = 300 K为温度, α为热膨胀系数[33], Cp为质量热容, k为热导率. 与上文类似, 由于β-Ga2O3的热参数具有各向异性, 在进行计算或仿真时, 双端固支结构谐振器的热参数选取[010]晶向的值, 而圆形鼓面结构谐振器选取[010]和[001]两个晶向的平均值.
支撑阻尼是指在谐振器的振动过程中, 振动能量通过锚点传递到衬底, 造成的能量耗散[34]. 在M/NEMS谐振器中, 振动部分需要通过固定结构与衬底连接, 这些结构称为锚点. 如图2所示, 在振动过程中, 锚点发生应变, 能量以弹性波的形式传播到衬底并逐渐被吸收. 本文采用完美匹配层(PML)的仿真方法对支撑阻尼进行研究, PML通过在仿真区域的边界上设置一层特殊的吸收层, 来模拟无限大衬底对弹性波的吸收效果.
机械能的表面阻尼是指由表面效应引起的能量耗散. 在微纳机电谐振器中, 随着器件尺寸减小, 表面积与体积比增大, 表面效应愈加突出. 谐振器表面的杂质、晶格缺陷、吸附物等因素会产生表面应力[35], 此外当表面粗糙度较大时, 表面波相互作用, 这些都将导致器件的表面阻尼[36]. 表面阻尼的物理机理十分复杂, 目前尚无确切的理论模型可以解释, 但已有研究表明表面阻尼与谐振器表面积成线性正相关[37], 假定β为表面阻尼系数, 利用如下经验公式进行推算[38]:
其中, Meff为谐振模态的有效质量, ω为角谐振频率, 表面阻尼γsurface = β·S, S为器件悬空结构的表面积. 结合(2)式和(3)式, 可以通过计算得到双端固支谐振器的表面阻尼:
式中A, B为比例系数.
对于圆形鼓面谐振器的表面阻尼, 有
式中, K = k1d/2, C和D为比例系数. 其他阻尼包括介电耗散和声子-电子相互作用, 然而由于本文所研究的器件中没有电流通过, 因此这部分阻尼可以忽略[39]. 表1总结了本文用到的β-Ga2O3的一系列材料性能参数.
-
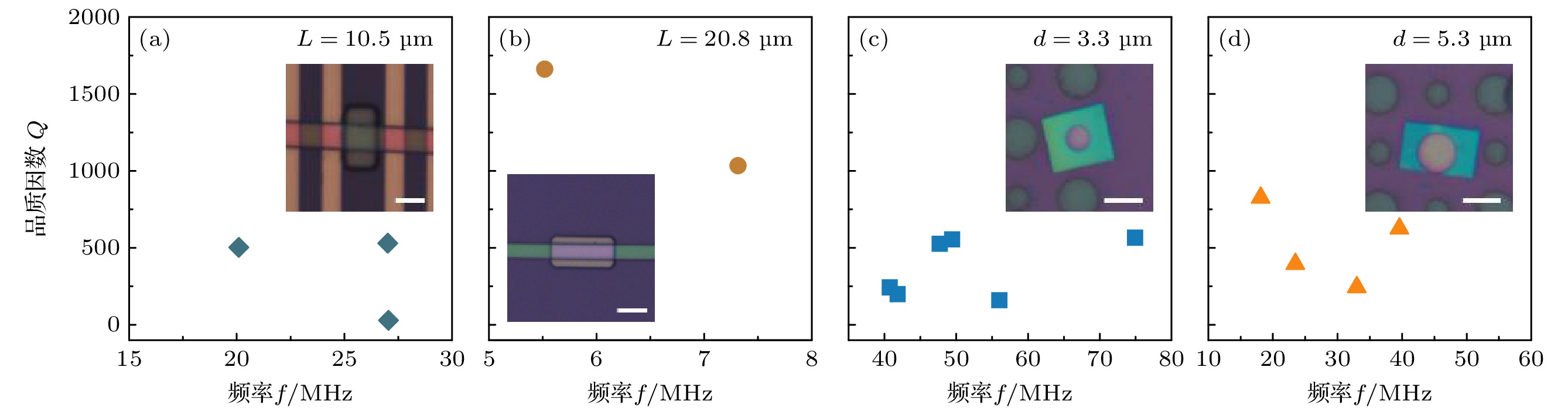
本文制备双端固支和圆形鼓面两种结构的β-Ga2O3谐振器进行测量, 同时整合前期课题组的测量结果, 整理出不同器件在第一面外弯曲模态下谐振频率f和Q的测量值, 结果如图3所示.
利用(2)式和(3)式计算和COMSOL仿真, 绘制了两种不同结构的器件在不同内应力下的频率分布(红、蓝色曲线), 并与测量值(散点)进行比较, 如图4(a), (b)和图5(a), (b)所示. 通过对比, 我们发现对于双端固支器件, 其谐振频率受谐振梁的长度L和厚度h影响, 与宽度w无关: L减小或h增大时, f增大. 对于圆形鼓面器件, 其谐振频率受振动部分的直径d和厚度h影响: d减小或h增大时, f增大. 此外, 两种器件的f都受到内应力σ的影响, σ越大, f越大.
双端固支器件与圆形鼓面器件在不同能量耗散机制下的Q值以及Qtotal如图4(c), (d)和图5(c), (d)所示. 在本文所研究的多个谐振器中, 谐振频率范围均低于100 MHz, τv为晶格畸变的周期, 即谐振器的振动周期[25], 因此τv > 10–8 s, 且根据前文对声子弛豫时间的计算, τs的量级为10–13 s, 因此τv
$ \gg $ τs, 这保证了声子能够在晶格畸变的周期内相互作用达到新的平衡, 能量耗散受Akhiezer效应影响. 根据图中蓝色虚线, 两种结构的谐振器的QAKE都随着厚度h的增大而减小; 同时, 随着器件平面尺寸(长度L或直径d)的增大, QAKE增大.如图4(c), (d)和图5(c), (d)中棕黄色点划线所示, TED效应表现为: 当两种器件的厚度h增大, QTED减小; 而随着器件平面尺寸(长度L或直径d)的增大, QTED增大. 究其原因, 由(6)式可以得知, QTED与f是逆相关的. Qclamp与谐振器结构和器件尺寸相关, 如图4(c), (d)和图5(c), (d)中红色虚线所示, h和Qclamp呈负相关, 而器件的平面尺寸(长度L或直径d)和Qclamp成正相关.
(8)式和(9)式描述了Qsurface与谐振器尺寸的关系, 将它们及其他已求得的Q值分别代入(1)式中, 并通过选取合适的比例系数完成基于(1)式的拟合函数, 使其与测量值Qmeas (图中散点)相匹配. 当分别采用σ = 5与50 MPa进行拟合时, 拟合函数变化不大. 因此, 仅选取σ = 50 MPa作为取值依据, 令A = 2.65 × 1011, B = 1.5 × 107, C = 1.88 × 1010, D = 1 × 107, 得到图4(c), (d)和图5(c), (d)中的Qsurface曲线(绿色点划线). 对于双端固支器件, h增大, Qsurface增大; 而L增大, Qsurface减小. 对于圆形鼓面器件, h增大, Qsurface增大; d增大, Qsurface减小. 可能原因是器件的能量存储能力与体积正相关, 当器件的上下表面一定时, 厚度h增大, 表面积-体积比降低, 每周期耗散的能量基本不变的同时系统储存的能量增加, 由表面阻尼限制的Qsurface增大. 而当两种器件的厚度h一定, 双端固支结构的L和圆形鼓面结构的d增大时, 谐振器的表面积增大, 表面积-体积比增大, 同理在表面阻尼限制下的Qsurface减小.
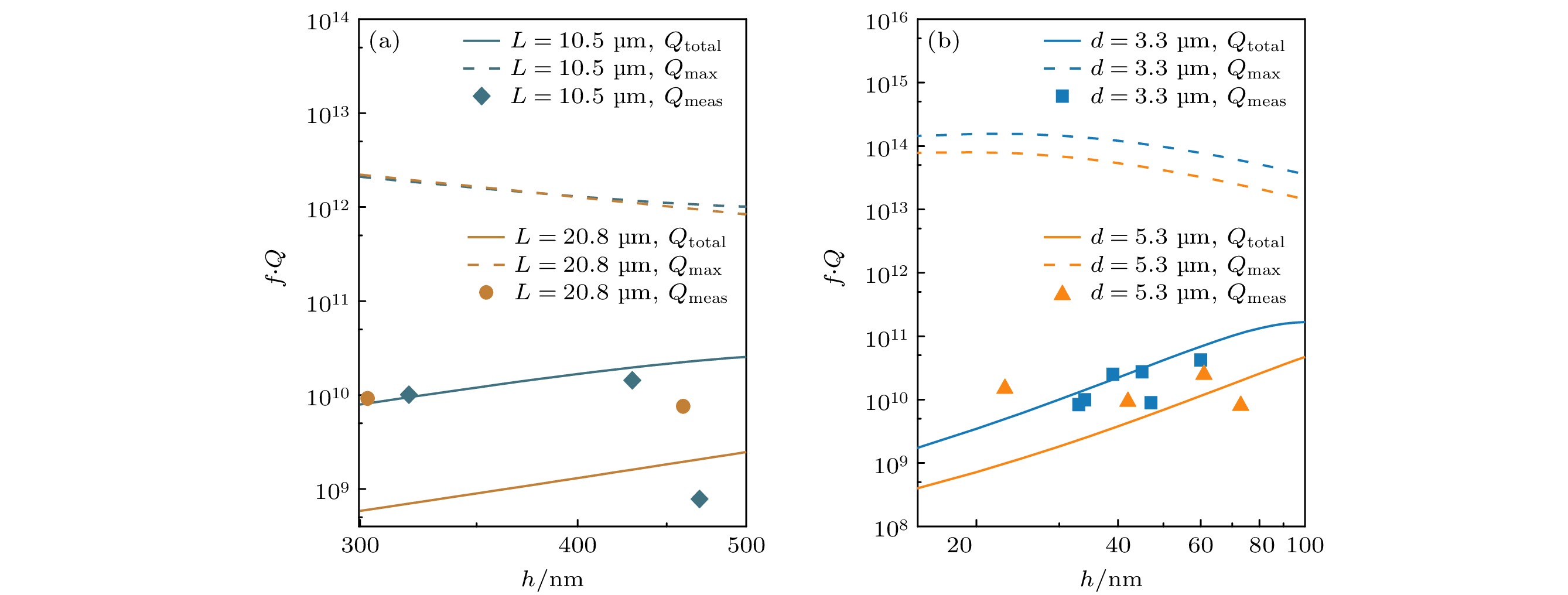
微纳米机械谐振器中的总能量耗散受到各个耗散机制的综合影响, 各途径下的能量耗散(1/Q)i相加得到总的能耗散(1/Q)total. 由图4(c), (d)和图5(c), (d)可知, (1/Q)total主要受表面阻尼(1/Q)surface的限制, 当h增大时, 支撑阻尼(1/Q)clamp也变得明显. 表面阻尼主要源自表面吸附、晶格缺陷、表面杂质等因素, 在本文的研究中, 所有器件的测量都在真空环境下进行, 这有助于有效降低表面吸附对测量结果的影响. 此外, 已有研究证实, 通过优化材料的晶体生长条件、对谐振器表面进行热退火及增加表面镀层的方式, 可以有效降低器件表面晶格缺陷的存在, 同时减少表面杂质, 从而显著提高Qsurface[40–42]. 支撑阻尼作为影响谐振器能量耗散的次要因素, 主要受锚点结构的影响, 本文中所研究的两种结构的谐振器的Qclamp受悬空结构的长度L与厚度h之比和直径d与厚度h之比的影响. 通过优化锚点结构, 采用1/4波长 带[43]、声子晶体带(PC)[44]等结构可以减少弹性波向衬底的传播, 从而提高Qclamp. 由AKE引起的能量耗散(1/Q)AKE与TED引起的耗散(1/Q)TED主要受器件的材料特性影响, 是制约Q值上限的因素. 当表面阻尼和支撑阻尼通过上述手段得到有效抑制的时候, AKE和TED效应限制下的Qmax 即为特定结构下Ga2O3微纳机电谐振器Q值的上限. 图6展示了不同器件的f×Q值, 其中实线表示f×Qtotal, 散点表示f×Qmeas, 虚线表示f×Qmax. 从图6可以观察到, 当不考虑支撑阻尼和表面阻尼时, f ×Q值显著提高. 可以发现Ga2O3微纳机电谐振器的f ×Q值上限极高, 能够达到1014 Hz的水平. 若需进一步提高Q值, 可以通过增加器件内 应变的方式, 在保持每周期能量耗散基本不变的情况下, 增大系统的总机械势能, 达到耗散稀释的效果. 实现应力调控的方式有: 设置沟槽底部的栅极与连接悬空结构的接触电极, 可通过在栅极与悬空结构之间施加电压来引发拉伸应变, 进一步提高Q值.
-
本文制备了两种不同结构的β-Ga2O3纳米机电谐振器, 并对其谐振频率和能量耗散机制进行理论分析和仿真模拟. 通过与实验测量数据的对比, 深入探讨了能量耗散机理及其降低途径. 在双端固支谐振器与圆形鼓面谐振器中, 表面阻尼(1/Q)surface为能量耗散的主要限制因素, 在谐振器厚度较大时支撑阻尼(1/Q)clamp的影响也变得明显. 通过优化器件结构, 可以提高支撑阻尼限制下的Qclamp, 而表面阻尼限制下的Qsurface则可以通过表面和退火处理得到改善, 从而提升器件的总品质因数. AKE与TED是制约谐振器Q值上限的因素, 在有效抑制表面和支撑阻尼耗散的情况下, β-Ga2O3纳米机电谐振器的理论仿真显示f ×Q值可以达到1014 Hz. 在微纳机电谐振器中, 能量耗散是限制器件性能提升与应用拓展的关键因素之一, 但其详细机理尚未完全阐明和量化. 因此, 深入研究频率分布规律及能量耗散机理具有重要的科学意义. 本文结合理论分析、仿真模拟与实验验证, 研究了β-Ga2O3纳米机电谐振器的能量耗散特性, 为微纳谐振器的优化设计与性能提升提供了理论和实验的依据与参考.
Ga2O3纳米机电谐振器机械能量耗散途径研究
Mechanical energy dissipation pathways in Ga2O3 nanoelectromechanical resonators
-
摘要: β相氧化镓(β-Ga2O3)因具有超宽禁带特性、卓越的机械性能和潜在的成本优势, 在高功率、高频率及光电微纳机电器件领域展现出极佳的应用前景. 本文详细探讨了双端固支结构与圆形鼓面结构的β-Ga2O3纳米机电谐振器的能量耗散机制及如何通过设计优化提高其品质因数(Q值). 首先通过理论分析和COMSOL软件仿真, 深入探讨了Akhiezer效应、热弹性阻尼、支撑阻尼和表面阻尼等能量耗散过程, 并制备了器件, 采用激光干涉法对β-Ga2O3纳米机电谐振器进行实验验证. 结果表明, 表面阻尼与支撑阻尼是当前限制β-Ga2O3纳米机电谐振器Q值的主要因素, 而Akhiezer效应和热弹性阻尼则决定了Q值的上限. 本研究不仅阐明了Ga2O3微纳机电谐振器能量耗散的复杂机制, 也为其带宽调控提供了有价值的指导.Abstract:
Beta-gallium oxide (β-Ga2O3), an emerging ultrawide bandgap (~4.8 eV) semiconductor, exhibits excellent electrical properties and cost advantages, being made as a promising candidate for high-power, high-frequency, and optoelectronic applications. Furthermore, its superior mechanical properties, including a Young’s modulus of 261 GPa, a mass density of 5950 kg/m³, and an acoustic velocity of 6623 m/s, make it particularly attractive for realizing high-frequency micro- and nanoelectromechanical system (M/NEMS) resonators. In this work, the energy dissipation mechanisms are investigated in two different β-Ga2O3 NEMS resonator geometries – doubly-clamped beams (10.5–20.8 μm length) and circular drumheads (3.3–5.3 μm diameter) – through theoretical analysis, finite element model (FEM) simulations, and experimental measurements under vacuum condition (<50 mTorr). The dominant energy dissipation mechanisms in resonators are investigated, including Akhiezer damping (AKE), thermoelastic damping (TED), clamping loss, and surface loss, by using a combined theoretical and FEM approach. Experimentally, the resonators are made by employing mechanical exfoliation combined with dry transfer techniques, yielding device thickness of 30–500 nm as verified by atomic force microscopy (AFM). Subsequently, laser interferometry is used to characterize the resonator dynamics. The resonant frequency f is obtained in a range of 5–75 MHz and the quality factor Q is approximately 200–1700 obtained through Lorentzian fitting of the resonant spectra, thus verifying the theoretical and simulation results. Our analysis indicates that surface loss and clamping loss are the main limiting factors for the Q values of current β-Ga2O3 resonators. Conversely, AKE and TED are mainly affected by material properties and resonator geometry, thus setting an upper limit for the achievable Q values with f×Q product reaching up to 1014 Hz. Our study provides a comprehensive framework integrating both theoretical analysis and experimental validation for understanding the complex energy dissipation mechanism inside a β-Ga2O3 NEMS resonator, and optimizes Q value through strain engineering and phonon crystal anchoring. These findings provide essential guidance for optimizing the performance and modulating the bandwidth of β-Ga2O3 NEMS resonator in high-frequency and high-power applications. -
Key words:
- β-Ga2O3 /
- nanoelectromechanical resonator /
- quality factor /
- energy dissipation mechanism .
-

-
图 1 (a) 双端固支谐振器结构示意图; (b) 圆形鼓面谐振器结构示意图; (c) 激光干涉测量系统原理图, 其中h, H分别表示材料厚度与沟槽深度; (d) 谐振器典型频谱曲线及其洛伦兹拟合, 该器件为d = 3.3 μm, h = 45 nm的圆形鼓面谐振器; (e) AFM扫描曲线, 插图为所测量的双端固支结构谐振器, 其中短实线为AFM探针的扫描路径
Figure 1. (a) Illustration of a doubly-clamped resonator; (b) illustration of a circular drumhead resonator; (c) schematic of the laser interferometry measurement system, where h and H denote the material thickness and trench depth, respectively; (d) typical spectrum of a circular drumhead resonator with d = 3.3 μm, h = 45 nm and its Lorentzian fitting; (e) AFM scanning curve with inset showing the scanning path, where the short solid line is the scanning path of the AFM probe.
图 3 不同谐振器的f和Q测量值, 插图显示了对应典型器件的显微图, L与d分别表示双端固支悬空结构的长度与圆形鼓面悬空结构的直径 (a), (b) L = 10.5 μm和20.8 μm的双端固支器件, 比例尺为10 μm; (c), (d) d = 3.3 μm和5.3 μm的圆形鼓面器件, 比例尺为5 μm
Figure 3. Measured values of f and Q for various resonators, with the insets showing the corresponding micrographs of typical devices: (a), (b) Doubly-clamped resonators with L = 10.5 μm and 20.8 μm, each with a scale bar of 10 μm; (c), (d) circular drumhead resonators with d = 3.3 μm and 5.3 μm, each with a scale bar of 5 μm.
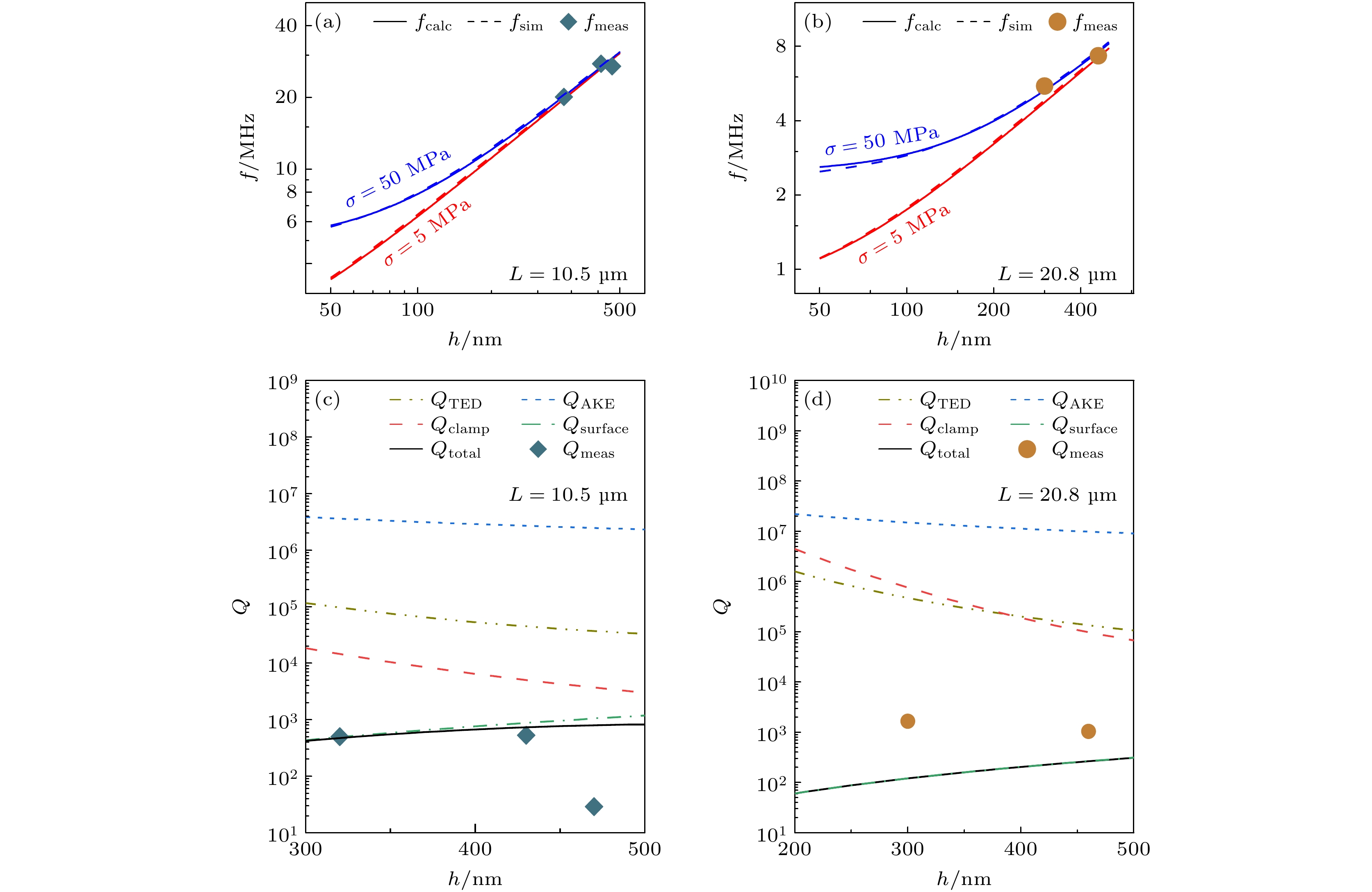
图 4 (a) L = 10.5 μm和(b) L = 20.8 μm两种双端固支器件在不同内应力 (红色曲线为σ = 5 MPa, 蓝色曲线为σ = 50 MPa) 下谐振频率f的计算值fcalc(实线)、仿真值fsim(虚线)与测量值fmeas(散点); (c) L = 10.5 μm和(d) L = 20.8 μm两种双端固支谐振器在不同耗散机制限制下的Q值、通过(1)式计算得到的Qtotal以及测量值Qmeas
Figure 4. Calculated value fcalc (solid line), simulated value fsim (dashed line), and measured value fmeas (scattered symbols) of the resonant frequency f under different internal stresses (σ = 5 MPa for red curve and σ = 50 MPa for blue curve) for doubly-clamped resonators: (a) L = 10.5 μm and (b) L = 20.8 μm, Q values limited by different loss mechanisms, Qtotal calculated by Eq. (1), and measured Qmeas for doubly-clamped resonators of (c) L = 10.5 μm and (d) L = 20.8 μm.
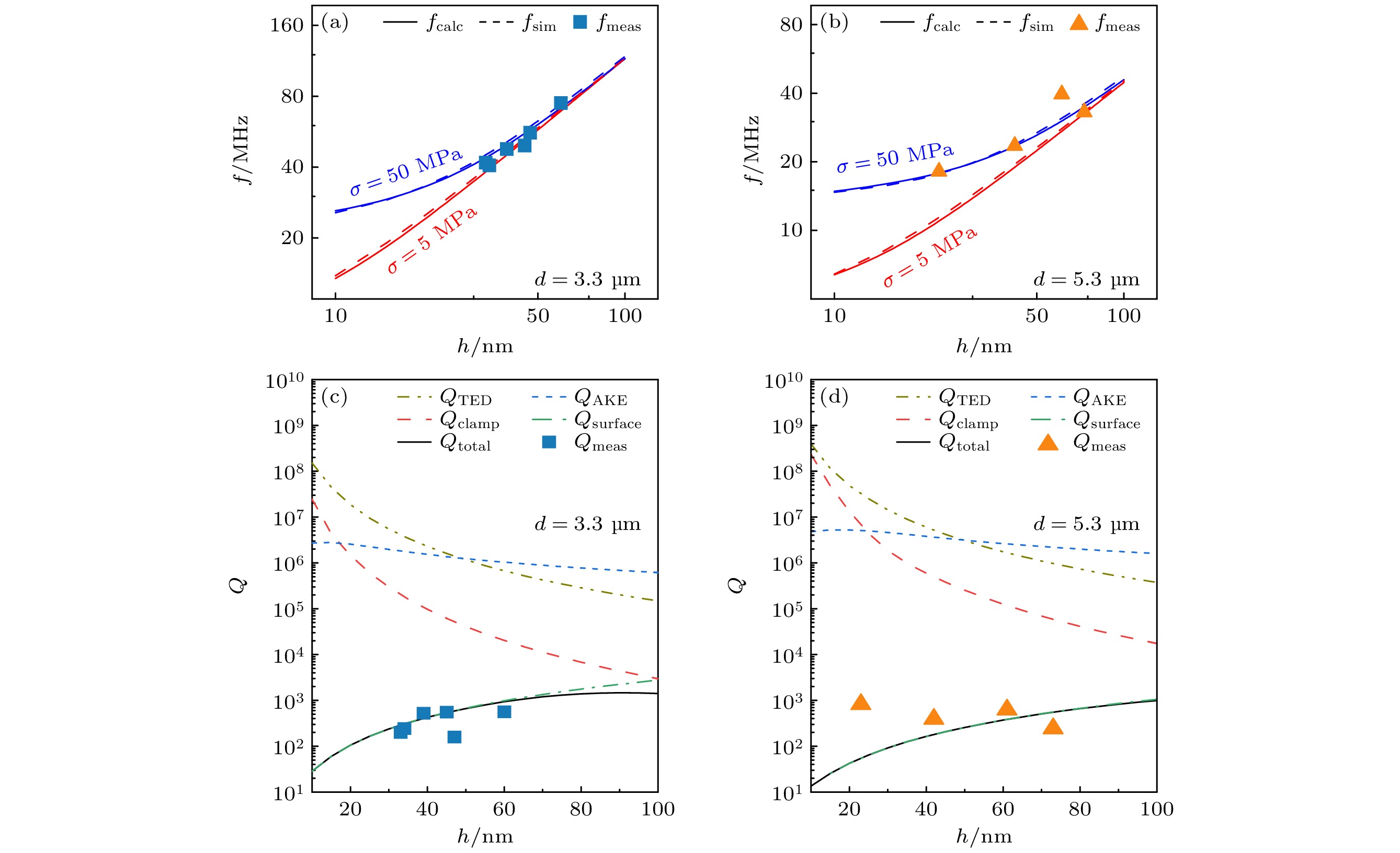
图 5 (a) d = 3.3 μm和(b) d = 5.3 μm两种圆形鼓面器件在不同内应力(红色曲线为σ = 5 MPa, 蓝色曲线为σ = 50 MPa)下谐振频率f的计算值fcalc(实线)、仿真值fsim(虚线)与测量值fmeas(散点), 其中实线为计算值, 虚线为仿真值; (c) d = 3.3 μm和(d) d = 5.3 μm两种圆形鼓面器件在不同耗散机制限制下的Q值、通过(1)式计算得到的Qtotal以及测量值Qmeas
Figure 5. Calculated value fcalc (soild line), simulated value fsim (dashed line), and measured value fmeas (scattered line) of the resonant frequency f under different internal stresses (σ = 5 MPa for red curve and σ = 50 MPa for blue curve) of drumhead resonators: (a) d = 3.3 μm and (b) d = 5.3 μm. Q values limited by different loss mechanisms, Qtotal calculated by Eq. (1), and measured Qmeas for drumhead resonators of (c) d = 3.3 μm and (d) d = 5.3 μm.
表 1 β-Ga2O3的材料性能参数
Table 1. Material properties of β-Ga2O3.
物理量 值 杨氏模量EY[4]/GPa 261 密度ρ[4] /(kg·m–3) 5950 泊松比ν[4] 0.2 声速c[4]/(m·s–1) 6623 声子散射时间τs/s 双端固支: 6.37×10–13
圆形鼓面: 4.89×10–13平均Grüneisen参数γavg[27] 1.018 质量热容Cp[29] /(J·kg–1·K–1) 491 热膨胀系数α[33]/K–1 [100]: 0.10×10–6
[010]: 1.68×10–6
[001]: 1.74×10–6热导率k[28]/(W·m–1·K–1) [100]: 10.9
[010]: 27.0
[001]: 14.5 -
[1] Ning S T, Huang S, Zhang Z Y, Zhao B, Zhang R Q, Qi N, Chen Z Q 2022 Phys. Chem. Chem. Phys. 24 12052 doi: 10.1039/D2CP01003H [2] Zhou M, Zhou H, Huang S, Si M W, Zhang Y H, Luan T T, Yue H Q, Dang K, Wang C L, Liu Z H, Zhang J C, Hao Y 2023 2023 International Electron Devices Meeting Francisco, CA, USA, December 9–13, 2023 p1 [3] Chen H, Li Z, Zhang Z Y L, Liu D H, Zeng L R, Yan Y R, Chen D Z, Feng Q, Zhang J C, Hao Y, Zhang C F 2024 Semicond. Sci. Technol. 39 063001 doi: 10.1088/1361-6641/ad42cb [4] Zheng X Q, Zhao H P, Feng P X L 2022 Appl. Phys. Lett. 120 040502 doi: 10.1063/5.0073005 [5] Labed M, Sengouga N, Prasad C V, Henini M, Rim Y S 2023 Mater. Today Phys. 36 101155 doi: 10.1016/j.mtphys.2023.101155 [6] Liang Y, Yu H, Wang H, Zhang H C, Cui T J 2022 Chip 1 100030 doi: 10.1016/j.chip.2022.100030 [7] Li H, Zhou Z H, Zhao Y Z, Li Y 2023 Chip 2 100049 doi: 10.1016/j.chip.2023.100049 [8] Soref R, Leonardis F D 2022 Chip 1 100011 doi: 10.1016/j.chip.2022.100011 [9] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025 doi: 10.1016/j.chip.2022.100025 [10] Wang L M, Zhang P C, Liu Z H, Wang Z H, Yang R 2023 Chip 2 100038 doi: 10.1016/j.chip.2023.100038 [11] Abdolvand R, Bahreyni B, Lee J E Y, Nabki F 2016 Micromachines 7 160 doi: 10.3390/mi7090160 [12] Feng T R, Yuan Q, Yu D L, Wu B, Wang H 2022 Micromachines 13 2195 doi: 10.3390/mi13122195 [13] Aoust G, Levy R, Bourgeteau B, Traon O L 2015 Sens. Actuators A: Phys. 230 126 doi: 10.1016/j.sna.2015.04.004 [14] Sun Y X, Tohmyoh H 2009 J. Sound Vib. 319 392 doi: 10.1016/j.jsv.2008.06.017 [15] Schmid S, Hierold C 2008 J. Appl. Phys. 104 093516 doi: 10.1063/1.3008032 [16] Imboden M, Mohanty P 2014 Phys. Rep. 534 89 doi: 10.1016/j.physrep.2013.09.003 [17] Rodriguez J, Chandorkar S A, Watson C A, Glaze G M, Ahn C H, Ng E J, Yang Y S, Kenny T W 2019 Sci. Rep. 9 2244 doi: 10.1038/s41598-019-38847-6 [18] Pearton S J, Yang J C, Cary P H, Ren F, Kim J, Tadjer M J, Mastro M A 2018 Appl. Phys. Rev. 5 011301 doi: 10.1063/1.5006941 [19] Bokaian A 1990 J. Sound Vib. 142 481 doi: 10.1016/0022-460X(90)90663-K [20] Suzuki H, Yamaguchi N, Izumi H 2009 Acoust. Sci. Technol. 30 348 doi: 10.1250/ast.30.348 [21] Cimalla V, Foerster C, Will F, Tonisch K, Brueckner K, Stephan R, Hein M E, Ambacher O, Aperathitis E 2006 Appl. Phys. Lett. 88 253501 doi: 10.1063/1.2213950 [22] Lee J, Wang Z H, He K L, Shan J, Feng P X L 2014 Appl. Phys. Lett. 105 023104 doi: 10.1063/1.4890387 [23] Kunal K, Aluru N R 2011 Phys. Rev. B 84 245450 doi: 10.1103/PhysRevB.84.245450 [24] Ghaffari S, Chandorkar S A, Wang S S, Ng E J, Ahn C H, Hong V, Yang Y S, Kenny T W 2013 Sci. Rep. 3 3244 doi: 10.1038/srep03244 [25] Tabrizian R, Rais-Zadeh M, Ayazi F 2009 Solid-state Sensors, Actuators & Microsystems Conference Denver, CO, USA, June 21–25, 2009 p2131 [26] Chen Z J, Jia Q Q, Liu W L, Zhu Y F, Yuan Q, Yang J L, Yang F H 2021 IEEE MEMS 2021 Virtual Conference Gainesville, FL, USA, January 25–29, 2021 p964 [27] Yan S H, Liu Z, Tan C K, Zhang X Y, Li S, Shi L, Guo Y F, Tang W H 2023 Appl. Phys. Lett. 123 142202 doi: 10.1063/5.0174977 [28] Guo Z, Verma A, Wu X F, Sun F Y, Hickman A, Masui T, Kuramata A, Higashiwaki M, Jena D, Luo T F 2015 Appl. Phys. Lett. 106 111909 doi: 10.1063/1.4916078 [29] Safieddine F, Hassan F E H, Kazan M 2022 J. Solid State Chem. 312 123272 doi: 10.1016/j.jssc.2022.123272 [30] Prabhakar S, Vengallatore S 2007 J. Micromech. Microeng. 17 532 doi: 10.1088/0960-1317/17/3/016 [31] Lifshitz R, Roukes M L 2000 Phys. Rev. B 61 5600 [32] Sun Y X, Saka M 2010 J. Sound Vib. 329 328 doi: 10.1016/j.jsv.2009.09.014 [33] Cheng Z Z, Hanke M, Galazka Z, Trampert A 2018 Appl. Phys. Lett. 113 182102 doi: 10.1063/1.5054265 [34] Ko J H, Jeong J, Choi J, Cho M 2011 Appl. Phys. Lett. 98 171909 doi: 10.1063/1.3575560 [35] Yang J L, Ono T, Esashi M 2002 J. Microelectromech. Syst. 11 775 doi: 10.1109/JMEMS.2002.805208 [36] Mohanty P, Harrington D A, Ekinci K L, Yang Y T, Murphy M J, Roukes M L 2002 Phys. Rev. B 66 085416 doi: 10.1103/PhysRevB.66.085416 [37] Villanueva L G, Schmid S 2014 Phys. Rev. Lett. 113 227201 doi: 10.1103/PhysRevLett.113.227201 [38] Zheng X Q, Tharpe T, Enamul Hoque Yousuf S M, Rudawski N G, Feng P X L 2022 ACS Appl. Mater. Interfaces 14 36807 doi: 10.1021/acsami.2c08414 [39] Bercioux D, Buchs G, Grabert H, Groning O 2011 Phys. Rev. B 83 165439 doi: 10.1103/PhysRevB.83.165439 [40] Wang C H, Ning Y H, Zhao W Y, Yi G X, Huo Y 2023 Sens. Actuator A: Phys. 359 114456 doi: 10.1016/j.sna.2023.114456 [41] Ahamed M J, Senkal D, Shkel A M 2014 2014 International Symposium on Inertial Sensors and Systems (INERTIAL) Laguna Beach, CA, USA, February 25–26, 2014 p59 [42] Zheng X Q, Lee J, Rafique S, Han L, Zorman C A, Zhao H P, Feng P X L 2017 ACS Appl. Mater. Interfaces 9 43090 doi: 10.1021/acsami.7b13930 [43] Li S S, Lin Y W, Xie Y, Ren Z Y, Nguyen C T C 2004 17th Int. IEEE Micro Electro Mechanical Systems Conf Maastricht, The Netherlands, January 25–29, 2004 p821 [44] 郑贤德, 甄嘉鹏, 邱静, 刘冠军 2023 仪器仪表学报 44 206 doi: 10.19650/j.cnki.cjsi.J2311681 Zheng X D, Zhen J P, Qiu J, Liu G J 2023 Chin. J. Sci. Instrum. 44 206 doi: 10.19650/j.cnki.cjsi.J2311681 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: