-
温稠密物质(warm dense matter, WDM)通常指质量密度接近常规固体(1—100 g/cm³量级), 温度横跨0.1电子伏至数百电子伏(对应103—106 K温区)[1,2]的特殊物质. 这种独特密度温度参数空间使得离子呈现强耦合的类流体特性, 而电子则处于完全或部分简并态[3,4], 在理想等离子体中通常被忽略的量子效应变得至关重要[5], 传统凝聚态理论与经典等离子体模型在此区域同时失效, 导致WDM在理论描述上面临极大挑战[6]. WDM广泛存在于强激光驱动实验[7,8]、冲击压缩物理[9,10]、惯性约束核聚变[11,12]等极端物理过程中, 对其物性演化规律的研究不仅是理解极端条件下物质行为的科学基础, 更可以为惯性约束聚变点火优化、高能粒子束输运调控、Z箍缩装置设计等重大工程技术提供关键物理参量. 这种基础研究与工程应用的深度耦合, 使得WDM研究成为连接极端条件物理与先进国防科技的重要桥梁.
随着高能量超短激光脉冲技术的发展, 利用激光脉冲对金属薄膜进行等容加热产生温稠密态[13-15]逐渐成为研究WDM非平衡动力学的重要手段. 在激光瞬态加载过程中, 电子经历从光激发、非平衡热化到弛豫平衡的演化, 这一过程跨越阿秒至飞秒量级的超快时空尺度, 呈现复杂的多体相互作用特征. 作为表征WDM物理特性的关键参数, 电导率不仅反映载流子的动态响应行为, 更通过其频率依赖特性编码了传导电子密度、电子交换关联势、离子结构因子以及电子-离子相互作用势等丰富的微观物理信息[16]. 这使得电导率测量成为揭示WDM体系中量子效应与经典效应相互竞争、电子-离子能量弛豫机制等基础物理问题的重要途径. 实验上通常通过监测体系对探测光的瞬态反射率与透射率来研究WDM的直流[17,18]及交流电导率随时间演化规律. 由于电导率演化过程具有飞秒量级的超快特性, 必须采用飞秒激光泵浦-探测技术[19-21]通过重复扫描获取电子分布随时间的演化. 然而, 温稠密实验对泵浦激光能量稳定性要求极高, 不同发次激光之间的抖动可能给实验数据带来巨大误差[22]. 加之强激光脉冲激发样品至温稠密状态的过程通常具有破坏性, 实验需要在单发泵浦光损伤样品之前完成所有延时点的测量. 因此, 研究者们发展了各种测量WDM交流电导率随时间演化的单发测量技术.
电子仪器通常只具备纳秒或者皮秒量级以上的时间采样能力, 所以飞秒动力学单发测量的核心机制是将时间信息映射到其他维度上. 比如可以将时间映射到探测光的频率上[22,23]: 在宽带探测脉冲中引入啁啾, 把不同频率成分的载波在时间上依次分开, 这样探测光进入温稠密物质后, 不同频率成分的光就会“看见”体系在不同时刻的状态, 通过光谱测量中不同频率成分的强度实现不同时刻电导率的提取. 但引入啁啾会展宽探测光的脉冲宽度, 导致实验系统时间分辨本领降低, 只适用于皮秒及以上较慢动力学过程的测量, 无法胜任电子激发与热化等飞秒尺度电子动力学的测量. 而采用把时间映射到空间上的空间啁啾探测技术[24,25]可以克服这一缺点. 在该方案中, 泵浦光与探测光成一定角度入射至样品, 使得不同空间位置处的泵浦-探测延时不同, 然后通过成像实现单发时间分辨测量. Chen等[26]基于空间啁啾方案实现了温稠密金交流电导率的单发测量, 时间分辨率优于100 fs, 其主要限制因素在于泵浦光和探测光的脉冲宽度. 随着超短脉冲技术的持续进步, 脉宽小于10 fs的紫外光脉冲[27-29]和脉冲宽度小于5 fs的近红外少周期探测光脉冲[30,31]的产生与操控技术已十分成熟, 将其应用于交流电导率单发测量实验有望进一步提升系统的时间分辨率.
本研究基于少周期激光脉冲的空间啁啾单发测量技术, 在脉冲宽度得到大幅缩短的前提下, 搭建了具有13.8 fs时间分辨率的实验系统, 详细分析了单发测量实验中绝对延时零点标定、成像系统景深及低通滤波效应等因素对时间分辨率的影响, 为实现超高精度WDM非平衡电子动力学测量奠定了基础.
-
根据Chen等[26]提出的实验方案可以搭建基于超短激光脉冲的交流电导率单发测量实验系统, 如图1(a)所示. 该系统主要为研究温稠密金非平衡电子动力学而设计, 泵浦光选择中心波长为400 nm、脉冲宽度为
$ {\tau }_{1}=9.7\;{\mathrm{f}}{\mathrm{s}} $ 的紫外脉冲, 其光子能量大于金的5d电子跃迁至6sp的激发能. 探测光为中心波长800 nm的近红外少周期光场, 脉冲宽度为$ {\tau }_{2}=5\;{\mathrm{f}}{\mathrm{s}} $ . 为了实现空间啁啾, 泵浦光以$ \alpha = 28^{\circ}$ 的入射角聚焦至金膜表面, 探测光从法线另一侧以$ \beta = 10^{\circ}$ 的入射角与泵浦光在金膜表面交汇, 从而把不同延时映射在不同的空间位置上, 进而通过成像实现时域上的单发测量. 计算电导率需要同时获取反射率和透射率, 所以系统在探测光的反射方向和透射方向各放置一个显微物镜(工作距离56.3 mm, 放大2倍, 数值孔径为0.1)收集出射光线, 再由对应的反射成像相机(RCam)和透射成像相机(TCam)对图像进行记录.为了保证每个延时点的实验条件一致, 整个交汇区域内各点的泵浦光强度要保持一致, 因此泵浦光的焦点应该呈现长条形的均匀分布. 在实验中, 首先利用一个可调狭缝从圆形高斯光束中选出水平方向上中间均匀的区域(约2 mm), 而后利用两个柱面镜实现矩形聚焦, 其中柱面镜1(CM1)用于在水平方向上将狭缝处的光斑成缩小约1/16的像, 即
$ \left|AC\right|=2\;{\mathrm{m}}{\mathrm{m}}/16=125\;\text{μm} $ ; 柱面镜2(CM2)用于在竖直方向上将光斑聚焦, 最终形成一个$ 142\;\text{μm}\times 50\;\text{μm} $ 的长方形焦点. 整个交汇区域的最大延时为其中
$ {c}_{0} $ 为真空下的光速. 根据系统参数, 延时窗口的大小约为303 fs, 足够覆盖电子从激发到热化平衡的整个动力学过程[26].实验中, 我们将厚度为30 nm的自支撑金膜放置在两束光重合处, 利用TCam和RCam同时测量金膜在泵浦光激发下对800 nm探测光的透射率
$ T $ 和反射率$ R $ . 根据光在多层介质中的传播理论可求得T和R对介质电导率$ \sigma $ 的依赖关系$ T\left(\sigma \right) $ 和$ R\left(\sigma \right) $ [32], 然后通过最小化误差函数:便可以求得电导率
$ \sigma $ , 其中$ {R}_{{\mathrm{m}}} $ 和$ {T}_{{\mathrm{m}}} $ 为反射率和透射率的实验测量值. 当探测光早于泵浦光到达金膜时, 探测光测量的是未加热的金膜, 此时$ {R}_{{\mathrm{m}}}= 84.6{\text{%}} $ ,$ {T}_{{\mathrm{m}}} = 7.2{\text{%}} $ , 对应的电导率实部为$ {\sigma }_{{\mathrm{r}}} = 0.58\times {10}^{15}\;{{\mathrm{s}}}^{-1} $ , 虚部为$ {\sigma }_{{\mathrm{i}}}=4.5\times {10}^{15}\;{{\mathrm{s}}}^{-1} $ . 当探测光晚于泵浦光到达时, 金膜中的电子受到泵浦光激发被迅速加热, 导致电导率的实部和虚部上升, 引起$ R $ 和$ T $ 的急剧减小. 在温稠密状态下,$ R $ 和$ T $ 达到极小值$ {R}_{{\mathrm{m}}}=73.7{\text{%}} $ ,$ {T}_{{\mathrm{m}}}=2.6{\text{%}} $ , 求出的电导率实部为$ {\sigma }_{{\mathrm{r}}}=4.0\times {10}^{15}\;{{\mathrm{s}}}^{-1} $ , 虚部为$ {\sigma }_{{\mathrm{i}}}=5.4\times {10}^{15}\;{{\mathrm{s}}}^{-1} $ . 对电导率的进一步分析涉及光激发、电子碰撞激发、电子俄歇等诸多极端非平衡物理过程, 我们将在后续的工作中进一步讨论. -
在空间啁啾测量中, 若只考察泵浦-探测两束光相交的一个特定空间点, 二者具有确定的相对延时, 对特定点进行动力学测量的时间分辨率——即单点时间分辨率——由两束激光的脉冲宽度决定. 由于采用了少周期超短的泵浦激光和探测激光, 单点时间分辨率为
$ {\tau }_{{\mathrm{p}}}=\sqrt{{\tau }_{1}^{2}+{\tau }_{2}^{2}}\approx 11\;{\mathrm{fs}} $ . 此外, 在光束相交的整片区域内, 不同的空间位置点具有不同的相对延时, 系统通过单发成像实现对所有延时点的同时测量, 因而, 成像系统的空间分辨率则对应不同延时点的时间分辨率, 我们将其标记为延时分辨率$ {\tau }_{{\mathrm{d}}} $ , 系统的总体时间分辨率为$ \tau =\sqrt{{\tau }_{{\mathrm{p}}}^{2}+{\tau }_{{\mathrm{d}}}^{2}} $ . 为了估算延时分辨率$ {\tau }_{{\mathrm{d}}} $ , 定义系统的空间啁啾系数如下:式中,
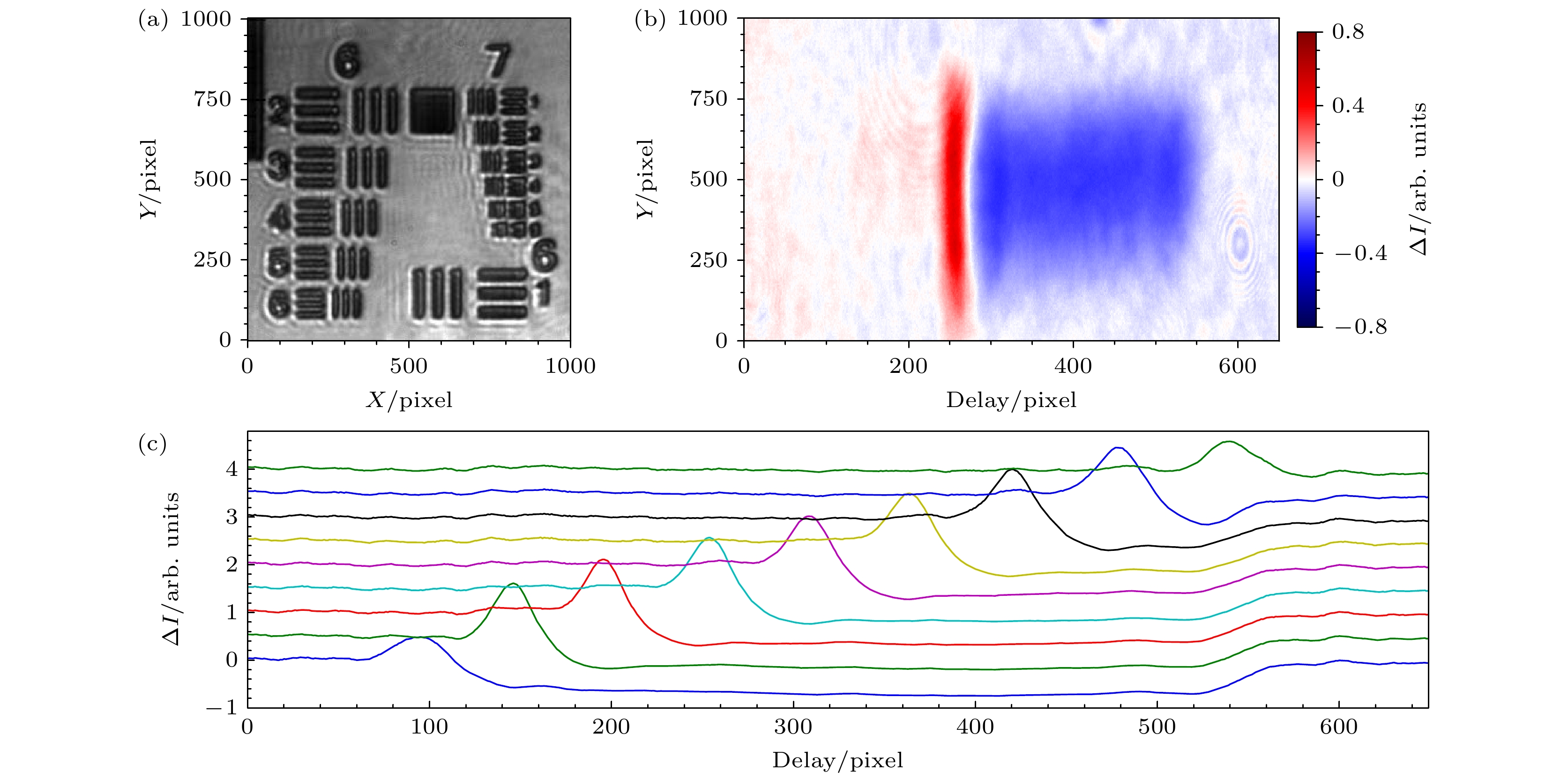
$ \chi $ 表示在作用区域每单位长度内泵浦-探测光延时的改变. 根据实验参数可得到系统的$ \chi \approx 2.1\;{\mathrm{f}}{\mathrm{s}}/\text{μm} $ . 只要测出系统的空间分辨率$ \Delta x $ , 便可求出延时分辨率$ {\tau }_{{\mathrm{d}}}=\chi \Delta x $ . 实验采用USAF 1951分辨率板来测试成像系统的空间分辨率, 将分辨率板置于样品处, 在相机上得到的图像如图2(a)所示, 可以得出系统在水平方向上的空间极限分辨是128 lp/mm, 对应的空间分辨率为$ \Delta x=4\;\text{μm} $ . 结合空间啁啾系数, 对应的延时分辨率为$ {\tau }_{{\mathrm{d}}}=8.4\;{\mathrm{f}}{\mathrm{s}} $ . 实验系统旨在研究激光等容加热金膜的超快过程, 期间金膜来不及发生空间上的形变, 因而激光加热金膜形成的温稠密状态并不影响系统的时间分辨率. 采用更高数值孔径的显微物镜有利于进一步提升空间分辨率, 但这种物镜通常具有更短的工作距离, 泵浦光的夹角就要相应增大, 造成$ \chi $ 的增大, 反而不利于提升时间分辨率. 在目前的参数下, 成像系统的空间分辨率在理论上不是时间分辨率的显著制约因素. 综上所述, 本系统的时间分辨率$ \tau =\sqrt{{\tau }_{{\mathrm{p}}}^{2}+{\tau }_{{\mathrm{d}}}^{2}}=13.8\;{\mathrm{fs}} $ .空间啁啾系数给出了理论上的空间-时间映射关系, 但真实系统中两束光线的入射角难免存在误差, 因此, 实验必须对系统进行精确的延时标定. 实验采用偏振门方案来确定两束光的重合位置. 利用一片厚度小于50 μm的超薄融石英片代替样品放在焦点处, 当没有泵浦光时, 探测光透过样品并被相机探测. 在相机前放置一个检偏器, 并调节至接近完全消光的状态. 然后, 让泵浦光照射样品, 并利用精密平移台调节两束光的延时, 当两束光在石英片上达到时空重合时, 泵浦光诱导的非线性克尔效应会将融石英片变成一个瞬时的双折射波片, 造成探测光偏振的改变, 进而增强透过检偏器的光束强度, 如图2(b)所示. 图中狭窄的透射光增强区域(
$ {{\Delta }}I > 0 $ , 红色区域)代表两束光重合的位置(零延时), 而其右侧蓝色的区域代表正延时(泵浦光在前, 探测光在后). 这是由于泵浦光在介质中激发了较多的载流子, 从而造成透过率的下降, 更高的泵浦光强甚至可以损伤样品. 因而, 当两束光的延时相差较大, 在样品上完全不重合时, 该方法可以判断两束光到达样品的时间先后. 在此基础上, 利用精密平移台以10 μm光程步进量(33.3 fs)在整个延时测量窗口(303 fs)精确调整两束光的相对延时, 可以观察到重合点在对应空间上的线性移动, 如图2(c)所示. 利用线性拟合, 可以确定相机相素点与延时的对应系数$ k=0.6\;{\mathrm{ }}{\mathrm{f}}{\mathrm{s}}/{\mathrm{p}}{\mathrm{i}}{\mathrm{x}}{\mathrm{e}}{\mathrm{l}} $ . -
根据上述分析, 限制单发测量系统最优时间分辨率的主要因素仍是泵浦光脉冲宽度. 实验搭建的装置虽然可以达到13.8 fs的时间分辨率, 但在实际操作过程中还受到零延时标定、成像景深以及成像过程中的衍射振荡等诸多因素的影响. 下面对这些因素进行详细讨论.
-
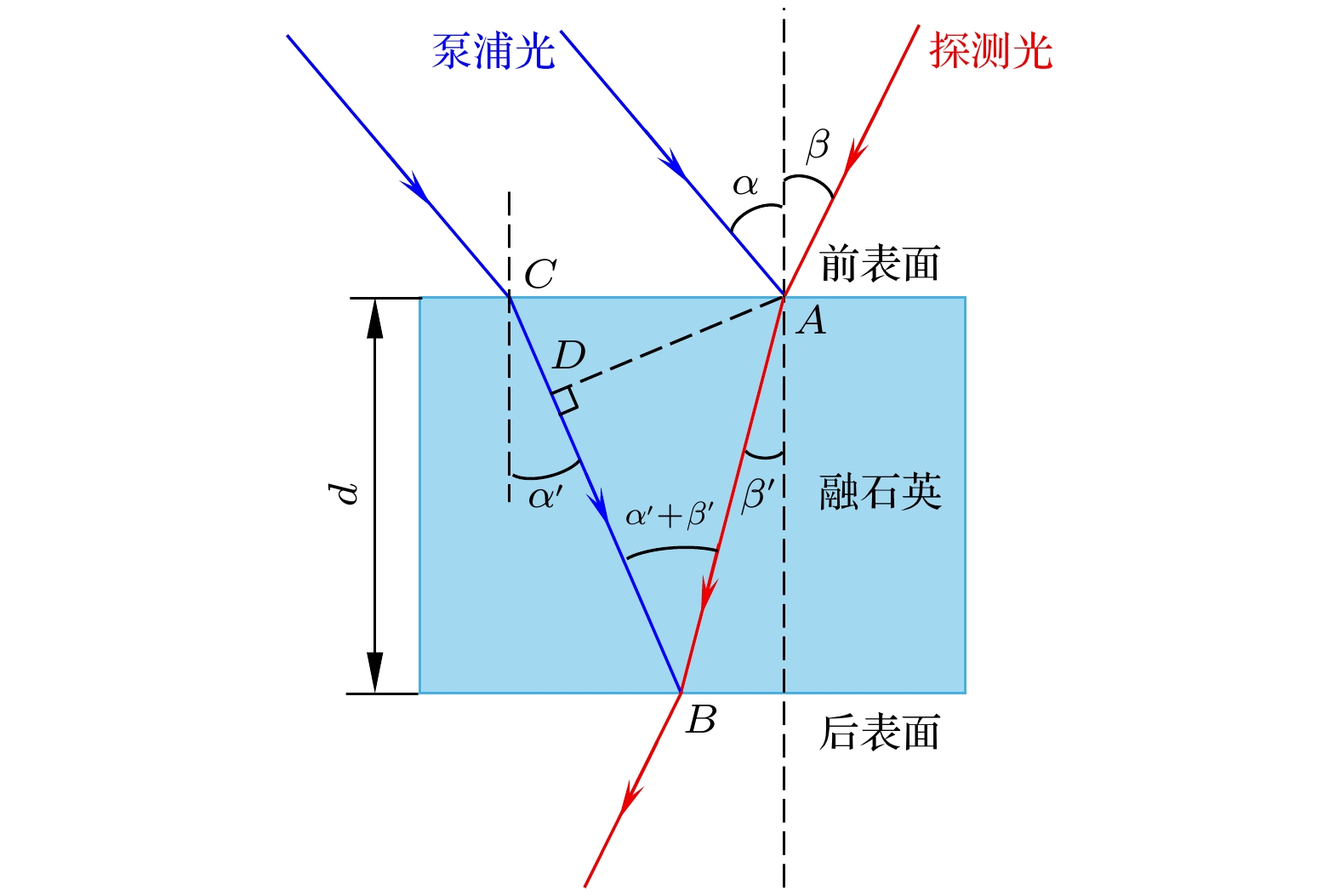
前文中提到利用偏振门方案可以精确标定泵浦-探测光的时间重合位置, 但仅限于两束光在一个理想平面上交汇的情况, 忽略了用于检测的融石英片厚度的影响. 如图3所示, 探测光从融石英片的A点入射, 经前表面折射穿过厚度为
$ d $ 的石英片从B点出射, 最后进入成像系统被探测. 这里, A和B两点在成像系统中对应同一空间位置, 却具有截然不同的泵浦-探测延时. 实际上, 探测光到达B点时将与从前表面C点入射的泵浦光相遇. 当探测光达到A点时, 从C点进入的泵浦光已传播至D点, 因此, B点泵浦-探测延时相对A点的变化实际上就等于探测光从A点传播至B点的时间减去泵浦光从D点传播至B点的时间:其中
$ {n}_{{\mathrm{r}}} $ 和$ {n}_{{\mathrm{b}}} $ 分别是近红外探测光和紫外泵浦光在石英片中的折射率, 而$ \alpha ' $ 和$ \beta ' $ 分别是泵浦光和探测光在介质中的折射角. 根据系统的实验参数, 可以估算$ {{\Delta }}\tau \left[{\mathrm{f}}{\mathrm{s}}\right]\approx 0.42 d\left[\text{μm}\right] $ . 实验中, 用于标定延时的石英片厚度为30 μm, 对应的零延时标定精度为12.7 fs. 要进一步提升精度, 必须使用厚度为24 μm以下的超薄无衬底融石英片. 这里讨论的精度只涉及到利用石英片标定延时零点的过程, 在金膜实验中, 金膜的厚度只有约30 nm, 其厚度带来的时间分辨率展宽效应可以忽略不计. -
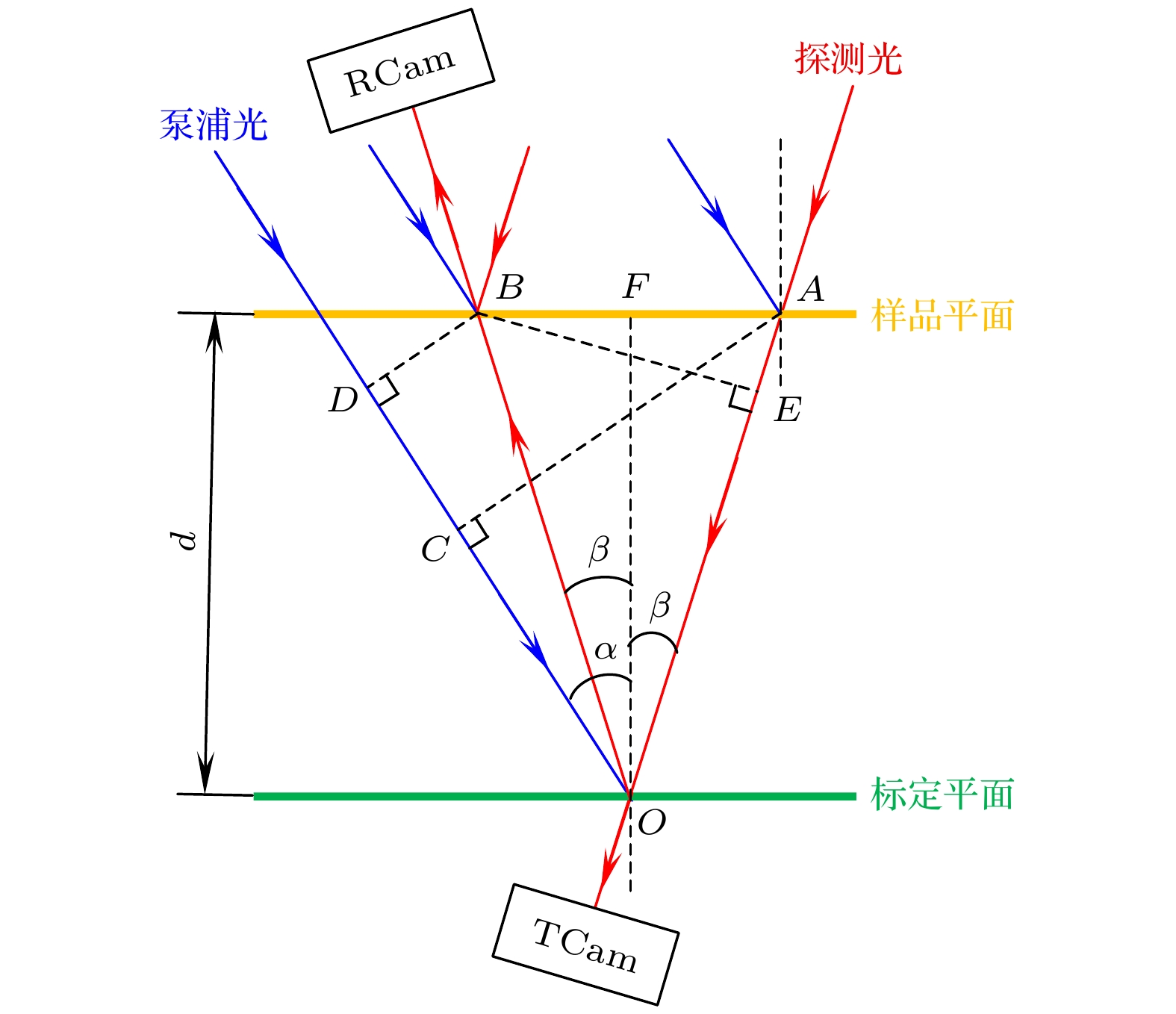
在完成延时标定后, 就可以把金膜样品放入光路进行实验. 但样品所在的物平面很有可能和标定过程中融石英片所在的平面不重合, 进而带来延时零点的漂移. 如图4所示, 假设O点是延时标定过程中确定的零点位置, 其所在的水平面为标定平面. 放入样品后, 样品不会严格与标定平面重合, 而是移动到了距离为
$ d $ 的样品平面. 此时样品上的A点会被透射相机当作延时零点位置, 而B点会被反射相机当作延时零点位置, 由图中的几何关系可以得出透射延时零点($ {{{\Delta }}\tau }_{0{\mathrm{T}}} $ )和反射延时零点($ {{{\Delta }}\tau }_{0{\mathrm{R}}} $ )的真实时间延时分别为根据实验系统参数, 有
$ {{{\Delta }}\tau }_{0{\mathrm{T}}}\left[{\mathrm{f}}{\mathrm{s}}\right]\approx -0.72 d\left[\text{μm}\right] $ ,$ {{{\Delta }}\tau }_{0{\mathrm{R}}}\left[{\mathrm{f}}{\mathrm{s}}\right]\approx 0.038 d\left[\text{μm}\right] $ . 以50 μm偏离距离$ d $ 为例, 在透射测量中会带来36 fs的延时零点漂移, 而在反射测量中的延时零点漂移只有1.9 fs. 所以, 样品定位不准不仅会引入延时零点误差, 还会导致透射测量与反射测量的数据无法对准, 即金膜上同一位置在两个相机上的对应关系会和标定时不一致. 因此, 实验中样品的定位精度至关重要.实验中, 样品的位置是根据两个相机的像平面来确定的, 即把样品移动至两个相机成像最清晰最锐利的位置. 但这个位置并不精确, 其精度受到成像系统景深(depth of field, DOF)的限制. 成像系统DOF可以估计为[33]
其中
$ \lambda $ 为探测光的中心波长,$ n=1 $ 为折射率,$ {{NA}}= 0.1 $ 为显微物镜的数值孔径. 实验系统的DOF估算为70 μm, 即根据成像的定位精度为35 μm, 这会引入约25 fs的延时零点误差和透射反射时间轴的对齐误差. -
在激光加热金膜最初的几个飞秒到几十飞秒的时间内, 电子的光激发及俄歇等过程对理解温稠密状态的建立和演化十分重要, 至今仍没有相关的实验研究, 这也是发展超高时间分辨单发探测技术的主要目的之一. 激光脉冲加载到金膜上时, 电导率可能会在延时零点附近5 μm左右 (约10 fs)的空间区域发生透过率或反射率的突变. 虽然成像系统具备相当的空间分辨本领, 但这样的突变结构, 在通过数值孔径有限的成像系统时会丢失大量空间高频成分, 从而在像中出现衍射振荡. 根据光传播的角谱理论, 从物平面出射的中心波长为
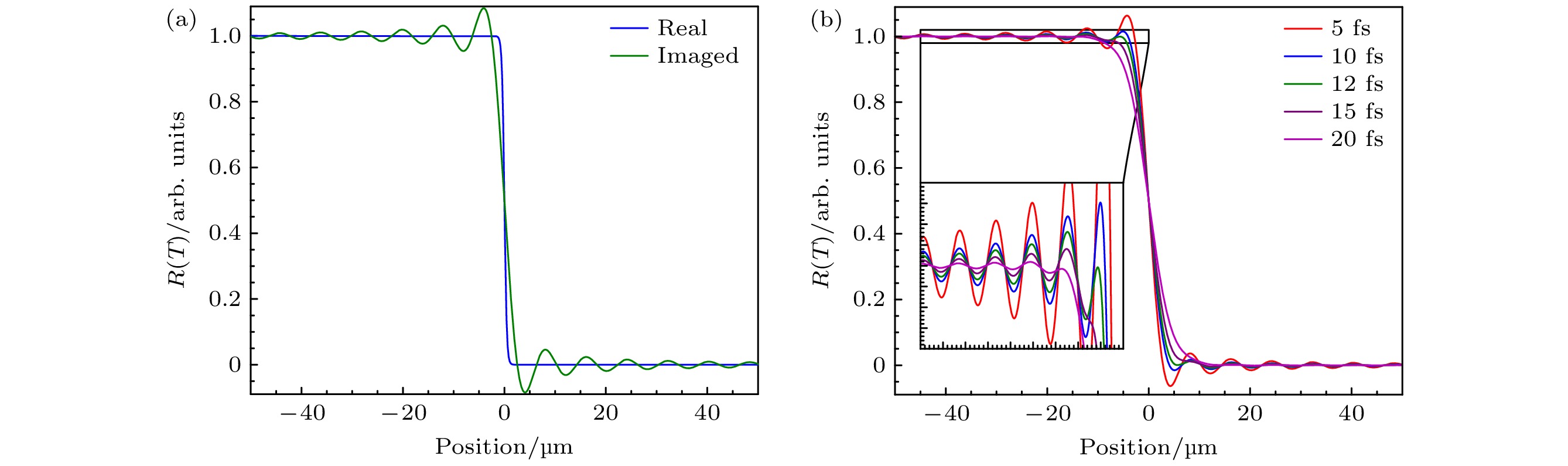
$ {\lambda }_{0} $ 的光波可以看成一系列不同空间频率沿不同方向传播的平面波的叠加, 特定空间频率$ {f}_{x} $ 对应的空间平面波方向角为$ \theta ={\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{s}}{\mathrm{i}}{\mathrm{n}}\left({f}_{x}{\lambda }_{0}\right) $ , 而成像系统可以看作是一个低通滤波器. 因此, 空间频率越大, 方向角也越大, 就越容易被数值孔径有限的成像系统滤掉, 进而造成成像失真.基于角谱传播理论可以对成像系统探测突变结构进行仿真. 首先考察透过率(T )或反射率(R)发生瞬时突变的情形, 在空间上是一个类似于阶跃函数的跳变, 如图5(a)中的蓝线所示(real), 对其作傅里叶变换得到空间频谱, 然后只保留NA = 0.1能接收的角谱成分, 最后通过逆傅里叶变换重建物体的像, 如图中绿线所示(imaged). 图中横坐标由空间啁啾系数将时间延迟转化成了空间位置. 可以看出, 系统成的像带有明显的振荡结构. 这是由于突变结构含有大量的高频成分, 经过成像系统滤波后造成较大失真. 接着改变R(T )的跳变时间, 分别对5 fs, 10 fs, 12 fs, 15 fs和20 fs五种情况重复上述过程. 仿真中R(T )曲线由S函数
$ f\left(x\right)=1/(1+ {{\mathrm{e}}}^{x}) $ 来模拟, 跳变时间定义为信号从最高幅值的90%下降到10%的时间. 仿真结果如图5(b)所示, 只有当信号变化时间在20 fs以上时, 系统成的像才没有明显的振荡. 因此, 虽然系统有13.8 fs的时间分辨率, 但只能对20 fs以上的透射率和反射率快速变化得到无畸变的测量结果.综上所述, 系统时间分辨率∆τ、延时零点标定误差
$ \Delta {\tau }_{0} $ 、透射延时零点定位误差$ \Delta {\tau }_{0{\mathrm{T}}} $ 、反射延时零点定位误差$ \Delta {\tau }_{0{\mathrm{R}}} $ 和动力学突变的时间分辨率$ \Delta {\tau }_{{\mathrm{f}}} $ 是影响系统时间分辨能力的重要因素, 将其主要误差的来源、依赖关系以及典型值汇总成表1. -
本文利用空间啁啾单发泵浦-探测原理, 设计了基于超短泵浦与探测光的WDM交流电导率单发测量装置, 并深入揭示了影响时间分辨能力的关键因素. 分析表明, 在实验装置参数下系统可实现13.8 fs的时间分辨率, 相比传统空间啁啾单发测量技术的时间分辨率提升近一个量级. 该系统在实际应用中存在3个关键约束: 1)延时零点标定精度受石英片厚度制约, 需要使用尽可能薄的石英片; 2)成像系统景深限制使金膜定位精度为35 μm, 由此在透射光路中产生25 fs的延时偏差; 3)受数值孔径约束的光学系统对快于20 fs的透/反射率突变响应不足, 引发探测信号振荡. 本研究不仅阐述了空间啁啾单发测量技术的实验原理, 更通过时间分辨精度的定量分析为提升实验系统时间测量精度指明了技术路径. 该工作为强场条件下材料的超快动力学研究提供了可靠的测量方案, 提出的时间分辨率限制因素对极端条件下物质特性的精密测量具有重要的参考价值.
温稠密物质交流电导率单发测量的时间精度提升与分析
Improvement and analysis of time accuracy in single-shot measurement of ac conductivity of warm dense matter
-
摘要: 基于空间啁啾的单发泵浦-探测技术是探究物质在强激光泵浦下达到温稠密态过程中电子非平衡动力学的重要手段, 其时间分辨率已达到百飞秒量级. 本文详细阐述了温稠密物质交流电导率的空间啁啾单发测量原理及高时间分辨实验装置, 并对影响系统时间分辨率的关键因素进行深入剖析. 分析表明, 基于超短泵浦-探测脉冲, 该系统可实现13.8 fs的时间分辨率. 然而, 在实际实验中, 延时零点的精确标定、成像系统的景深限制以及低通滤波效应等因素, 均会对系统的时间分辨能力产生显著影响. 本研究不仅为提升温稠密物质交流电导率单发测量的时间精度提供了理论依据和实践指导, 而且为探索强场条件下材料的超快动力学过程奠定了坚实的技术基础.Abstract: The spatial chirp based single-shot pump-probe technique represents a pivotal technology for studying electron non-equilibrium dynamics in warm dense matter created with intense laser pulses. Notably, its time resolution can reach tens of femtoseconds. In this work, we introduce the single-shot measurement technique of ac conductivity of warm dense matter, as well as a detailed account of the experimental setup. In addition, the main factors limiting the time resolution of the system are discussed in depth. We show the system can achieve a resolution of 13.8 femtoseconds. Nevertheless, during practical application, several aspects, namely the calibration of the zero-delay, the depth of field of the imaging system, and the low-pass filtering effect inherent in the imaging system, will exert a substantial influence on the time-resolution. This research has important reference for enhancing the time accuracy of single-shot measurement of ac conductivity of warm dense matter. Moreover, it serves as a potent tool for the in-depth study of the ultrafast dynamic processes of materials under strong-field conditions.
-
Key words:
- warm dense matter /
- single-shot pump-probe measurement /
- spatial chirp /
- ac conductivity .
-

-
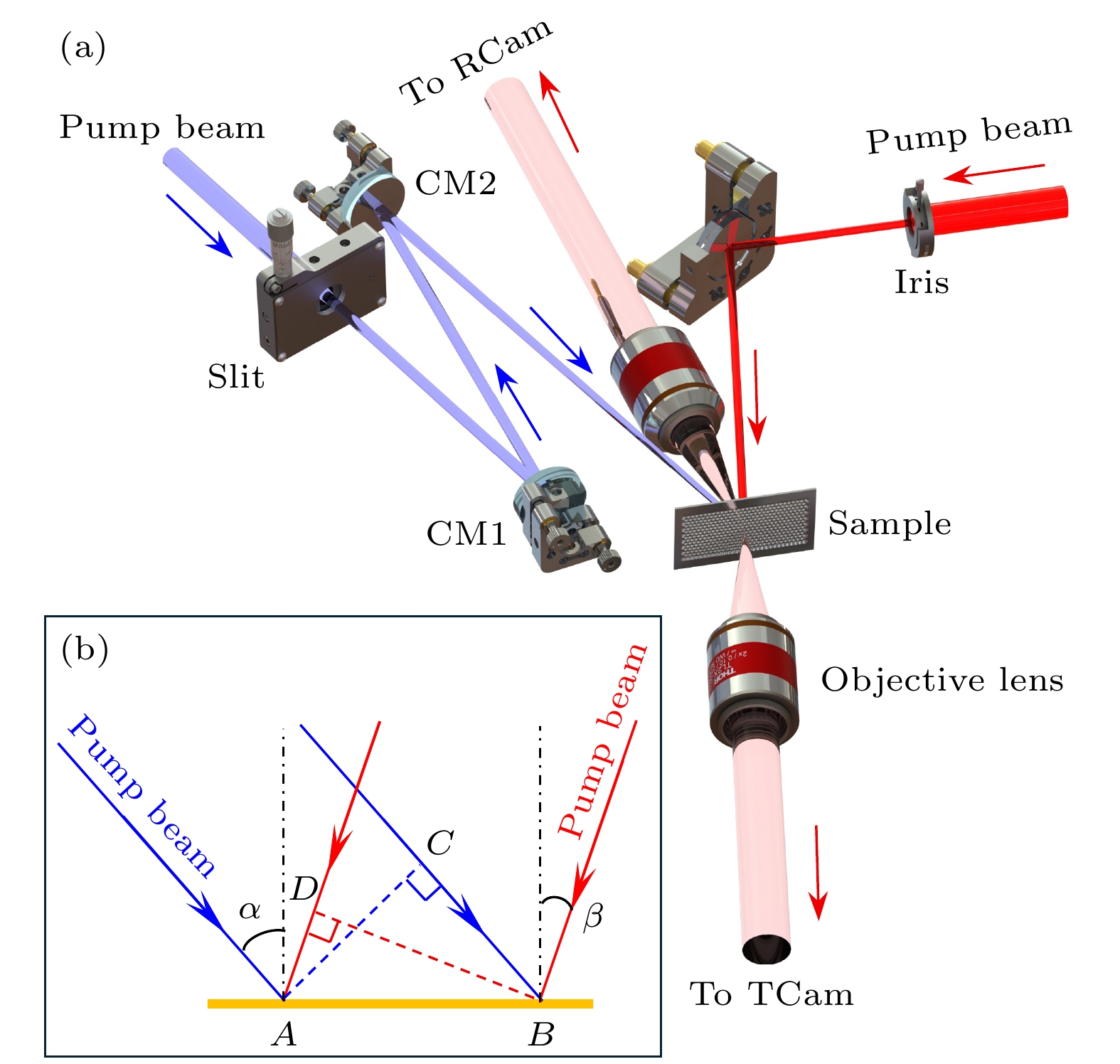
图 1 WDM交流电导率时间演化的单发测量原理 (a) 实验系统示意图, 其中CM1和CM2为两个柱面镜, RCam和Tcam分别为反射光成像相机和透射光成像相机; (b) 空间啁啾把不同延时映射在不同空间位置上的原理
Figure 1. Single-shot measurement principle for time-dependent AC conductivity evolution in WDM: (a) Schematic of the experimental system, where CM1 and CM2 are two cylindrical mirrors, and RCam and Tcam are the reflection light imaging camera and transmission light imaging camera, respectively; (b) principle of spatial chirp which maps different time delays to different spatial positions.
图 2 成像分辨率与延时标定 (a) USAF 1951分辨率板的像, 成像系统在水平方向能分辨至第7组第1个元素 (128 lp/mm); (b) 在偏振选通法(PG)中测得的透射光光强变化(
$ \Delta I $ )随空间的分布; (c) 利用PG标定延时, 图中9条曲线代表9个间隔为33.3 fs的不同延时点测得的$ \Delta I $ 的空间分布Figure 2. Imaging resolution and time delay calibration: (a) Image of the USAF 1951 resolution target, where the imaging system resolves down to the Group 7 Element 1 (128 lp/mm) in the horizontal direction; (b) spatial distribution of transmitted light intensity variation (∆I ) measured via the polarization gating (PG) method; (c) time delay calibration using PG, where the 9 curves represents 9 different measurements of ∆I vs. space with delay increment of 33.3 fs.
图 4 样品平面与标定平面不重合时带来的延时误差, 其中O点是利用偏振门方案标定的延时零点, A点是透射相机“认为”的样品上的延时零点, B点是反射相机“认为”的样品上的延时零点
Figure 4. Delay error introduced when sample plane and calibration plane do not coincide. Point O is the delay zero point calibrated using the polarization gate method, Point A is the delay zero point on the sample perceived by the transmission camera, Point B is the delay zero point on the sample perceived by the reflection camera.
图 5 突变结构的成像模拟 (a)一个瞬时突变结构(real)经过成像系统后的像(imaged)带有衍射振荡结构; (b) 5—20 fs缓变结构的像
Figure 5. Imaging simulation of abrupt structures: (a) An instantaneous abrupt structure (real) after passing through the imaging system, the image (imaged) exhibits a diffractive oscillatory structure; (b) images of 5, 10, 12, 15 and 20 fs gradually varying structures.
表 1 单发测量温稠密交流电导率演化的误差分析
Table 1. Error analysis of conductivity evolution in single-shot measurements of warm dense matter.
系统物理量 误差来源 依赖关系 典型值 系统时间分辨率 $ \Delta \tau $ 泵浦光脉宽 $ {\tau }_{1} $ $ \Delta \tau =\sqrt{{\tau }_{1}^{2}+{\tau }_{2}^{2}+{\left(\chi {{\Delta }}x\right)}^{2}} $ $ {\tau }_{1}=9.7\;{\mathrm{fs}}; {\tau }_{2}=5\;{\mathrm{fs}} $ $ \chi =2.1\;{\mathrm{fs/μm}}, $
$ \Delta x=4\;\text{μm},\; \Delta \tau =13.8\;{\mathrm{fs}} $ 探测光脉宽 $ {\tau }_{2} $ 成像系统分辨率 $ \Delta x $ 延时零点标定误差 $ \Delta {\tau }_{0} $ 融石英片厚度 $ L $ $ \Delta {\tau }_{0}[{\mathrm{fs}}]\approx 0.42 L\;[\text{μm}] $ $ L=30\text{ μm},\; \Delta {\tau }_{0}=12.7\;{\mathrm{fs}} $ 透射延时零点定位误差 $ \Delta {\tau }_{\rm 0T} $ 成像定位精度 $ d $ $ {\Delta \tau }_{\rm 0T}\left[{\mathrm{fs}}\right]\approx -0.72 d\left[\text{μm}\right] $ ,$ d=35\text{ μm}, \; \Delta {\tau }_{\rm 0T}=25.2\;{\mathrm{fs}} $ 反射延时零点定位误差 $ \Delta {\tau }_{\rm 0R} $ $ {\Delta \tau }_{\rm 0R} \left[{\mathrm{fs}}\right]\approx 0.038 d\left[\text{μm}\right] $ $ d=35\text{ μm} ,\; \Delta {\tau }_{\rm 0T}=1.33\;{\mathrm{fs}} $ 动力学突变的时间分辨率 $ \Delta {\tau }_{{\mathrm{f}}} $ 成像系统数值孔径 $ NA $ $ \Delta {\tau }_{{\mathrm{f}}}\propto {1}/{{{NA}}} $ $ {{NA}}=0.1 ,\; \Delta {\tau }_{{\mathrm{f}}} > 20\;{\mathrm{fs}} $ -
[1] 陈其峰, 顾云军, 郑君, 李江涛, 李治国, 权伟龙, 付志坚, 李成军 2017 科学通报 62 812 doi: 10.1360/N972016-00471 Chen Q F, Gu Y J, Zheng J, Li J T, Li Z G, Quan W L, Fu Z J, Li C J 2017 Chin. Sci. Bull. 62 812 doi: 10.1360/N972016-00471 [2] Kang D, Dai J 2018 J. Phys. Condens. Matter 30 073002 doi: 10.1088/1361-648X/aa9e29 [3] Ichimaru S 1982 Rev. Mod. Phys. 54 1017 doi: 10.1103/RevModPhys.54.1017 [4] Koenig M, Benuzzi-Mounaix A, Ravasio A, Vinci T, Ozaki N, Lepape S, Batani D, Huser G, Hall T, Hicks D, MacKinnon A, Patel P, Park H S, Boehly T, Borghesi M, Kar S, Romagnani L 2005 Plasma Phys. Control. Fusion 47 B441 doi: 10.1088/0741-3335/47/12B/S31 [5] Falk K 2018 High Power Laser Sci. Eng. 6 e59 doi: 10.1017/hpl.2018.53 [6] 康冬冬, 曾启昱, 张珅, 王小伟, 戴佳钰 2020 强激光与粒子束 32 092006 doi: 10.11884/HPLPB202032.200121 Kang D D, Zeng Q Y, Zhang S, Wang X W, Dai J Y 2020 High Power Laser Part. Beams 32 092006 doi: 10.11884/HPLPB202032.200121 [7] Lee R W, Moon S J, Chung H K, Rozmus W, Baldis H A, Gregori G, Cauble R C, Landen O L, Wark J S, Ng A, Rose S J, Lewis C L, Riley D, Gauthier J C, Audebert P 2003 J. Opt. Soc. Am. B 20 770 doi: 10.1364/JOSAB.20.000770 [8] Wu D, Yu W, Sheng Z M, Fritzsche S, He X T 2020 Phys. Rev. E 101 051202 doi: 10.1103/PhysRevE.101.051202 [9] Fletcher L B, Lee H J, Döppner T, Galtier E, Nagler B, Heimann P, Fortmann C, LePape S, Ma T, Millot M, Pak A, Turnbull D, Chapman D A, Gericke D O, Vorberger J, White T, Gregori G, Wei M, Barbrel B, Falcone R W, Kao C C, Nuhn H, Welch J, Zastrau U, Neumayer P, Hastings J B, Glenzer S H 2015 Nat. Photonics 9 274 doi: 10.1038/nphoton.2015.41 [10] Graziani F, Moldabekov Z, Olson B, Bonitz M 2022 Contrib. Plasma Phys. 62 e202100170 doi: 10.1002/ctpp.202100170 [11] Dornheim T, Böhme M, Kraus D, Döppner T, Preston T R, Moldabekov Z A, Vorberger J 2022 Nat. Commun. 13 7911 doi: 10.1038/s41467-022-35578-7 [12] Mercadier L, Benediktovitch A, Krušič Š, Kas J J, Schlappa J, Agåker M, Carley R, Fazio G, Gerasimova N, Kim Y Y, Le Guyader L, Mercurio G, Parchenko S, Rehr J J, Rubensson J E, Serkez S, Stransky M, Teichmann M, Yin Z, Žitnik M, Scherz A, Ziaja B, Rohringer N 2024 Nat. Phys. 20 1564 doi: 10.1038/s41567-024-02587-w [13] Forsman A, Ng A, Chiu G, More R M 1998 Phys. Rev. E 58 R1248 doi: 10.1103/PhysRevE.58.R1248 [14] Ping Y, Correa A A, Ogitsu T, Draeger E, Schwegler E, Ao T, Widmann K, Price D F, Lee E, Tam H, Springer P T, Hanson D, Koslow I, Prendergast D, Collins G, Ng A 2010 High Energy Density Phys. 6 246 doi: 10.1016/j.hedp.2009.12.009 [15] Ofori-Okai B K, Descamps A, McBride E E, Mo M Z, Weinmann A, Seipp L E, Ali S J, Chen Z, Fletcher L B, Glenzer S H 2024 Phys. Plasmas 31 042711 doi: 10.1063/5.0193854 [16] Ng A, Sterne P, Hansen S, Recoules V, Chen Z, Tsui Y Y, Wilson B 2016 Phys. Rev. E 94 03321 doi: 10.1103/PhysRevE.94.03321 [17] 孙旭, 吴海忠, 王小伟, 吕治辉, 张栋文, 刘东晓, 范伟, 粟敬钦, 周维民, 谷渝秋, 赵增秀, 袁建民 2023 中国激光 50 1714013 doi: 10.3788/CJL230791 Sun X, Wu H Z, Wang X W, Lü Z H, Zhang D W, Liu D X, Fan W, Su J Q, Zhou W M, Gu Y Q, Zhao Z X, Yuan J M 2023 Chin. J. Lasers 50 1714013 doi: 10.3788/CJL230791 [18] Ofori-Okai B K, Descamps A, Lu J, Seipp L E, Weinmann A, Glenzer S H, Chen Z 2018 Rev. Sci. Instrum. 89 10D109 doi: 10.1063/1.5038944 [19] Ao T, Ping Y, Widmann K, Price D F, Lee E, Tam H, Springer P T, Ng A 2006 Phys. Rev. Lett. 96 055001 doi: 10.1103/PhysRevLett.96.055001 [20] Widmann K, Ao T, Foord M E, Price D F, Ellis A D, Springer P T, Ng A 2004 Phys. Rev. Lett. 92 125002 doi: 10.1103/PhysRevLett.92.125002 [21] Ping Y, Hanson D, Koslow I, Ogitsu T, Prendergast D, Schwegler E, Collins G, Ng A 2006 Phys. Rev. Lett. 96 255003 doi: 10.1103/PhysRevLett.96.255003 [22] Chen Z, Holst B, Kirkwood S E, Sametoglu V, Reid M, Tsui Y Y, Recoules V, Ng A 2013 Phys. Rev. Lett. 110 135001 doi: 10.1103/PhysRevLett.110.135001 [23] Chen Z, Sametoglu V, Tsui Y Y, Ao T, Ng A 2012 Phys. Rev. Lett. 108 165001 doi: 10.1103/PhysRevLett.108.165001 [24] Dhar L, Fourkas J T, Nelson K A 1994 Opt. Lett. 19 643 doi: 10.1364/OL.19.000643 [25] Lindenberg A M, Larsson J, Sokolowski-Tinten K, Gaffney K J, Blome C, Synnergren O, Sheppard J, Caleman C, MacPhee A G, Weinstein D, Lowney D P, Allison T K, Matthews T, Falcone R W, Cavalieri A L, Fritz D M, Lee S H, Bucksbaum P H, Reis D A, Rudati J, Fuoss P H, Kao C C, Siddons D P, Pahl R, Als-Nielsen J, Duesterer S, Ischebeck R, Schlarb H, Schulte-Schrepping H, Tschentscher Th, Schneider J, Von Der Linde D, Hignette O, Sette F, Chapman H N, Lee R W, Hansen T N, Techert S, Wark J S, Bergh M, Huldt G, Van Der Spoel D, Timneanu N, Hajdu J, Akre R A, Bong E, Krejcik P, Arthur J, Brennan S, Luening K, Hastings J B 2005 Science 308 392 doi: 10.1126/science.1107996 [26] Chen Z, Hering P, Brown S B, Curry C, Tsui Y Y, Glenzer S H 2016 Rev. Sci. Instrum. 87 11E548 doi: 10.1063/1.4962057 [27] Liu Y Y, Zhao K, He P, Huang H D, Teng H, Wei Z Y 2017 Chin. Phys. Lett. 34 074204 doi: 10.1088/0256-307X/34/7/074204 [28] Wang Y, Wang S, Rockwood A, Luther B M, Hollinger R, Curtis A, Calvi C, Menoni C S, Rocca J J 2017 Opt. Lett. 42 3828 doi: 10.1364/OL.42.003828 [29] Xiao F, Fan X H, Wang L, Zhang D W, Wu J H, Wang X W, Zhao Z X 2020 Chin. Phys. Lett. 37 114202 doi: 10.1088/0256-307X/37/11/114202 [30] Chang H T, Zürch M, Kraus P M, Borja L J, Neumark D M, Leone S R 2016 Opt. Lett. 41 5365 doi: 10.1364/OL.41.005365 [31] Wang X W, Wang L, Xiao F, Zhang D W, Lue Z H, Yuan J M, Zhao Z X 2020 Chin. Phys. Lett. 37 023201 doi: 10.1088/0256-307X/37/2/023201 [32] Born M, Wolf E 1999 Principles of Optics (Cambridge: Cambridge University Press [33] Shillaber C P 1945 Photomicrography: In Theory and Practice (New York: Wiley -


 首页
首页 登录
登录 注册
注册



 下载:
下载: