激光干涉测量技术以其非接触、高精度、高动态以及测量结果可溯源等特点, 被广泛应用于各种精密测量场景^[1]. 近年来, 随着科技的快速发展, 高端装备制造对激光干涉测量技术提出了更高的测量需求. 如: 在未来引力波探测器的升级改造中, 提出了${\text{pm/}}\sqrt {{\text{Hz}}} $级的远距离高精度探测测距精度需求^[2–8]; 在光刻机的空间精确定位中, 实现纳米级节点光刻技术需要动态测量精度至少达到亚纳米级^[9,10]; 在太空探测任务中, 航天器的精确指向控制要求微角秒甚至纳角秒级的测量精度, 换算为距离则需要达到皮米甚至飞米级^[11,12]. 而精密制造的基础是精密测量的实现. 为了应对上述需求, 国际上顶级的计量机构部署了诸如NANOTRACE等工程, 并制定了测量不确定度在10 pm以下的激光干涉测量技术的研发战略^[13,14]. 常见的激光干涉测量方式主要有零差激光干涉测量与外差激光干涉测量. 相比于零差激光干涉测量, 外差激光干涉测量通过混频的方式产生外差频率, 使信号频谱转移到高频区域, 从而避免了激光低频噪声对测量的影响. 外差激光干涉测量能够提供高信噪比的光电信号, 具有抗干扰能力强, 并且易于实现高精度测量的优势, 因此更适用于上述精密测量领域^[15].

双频激光光源作为外差干涉测量系统的核心部件^[16–19], 其频率稳定性、双频频差稳定性决定了干涉测量系统所能达到的极限测量精度. 目前, 双频激光光源的研究主要集中在其频率稳定性的提升. 以Keysight为首的国内外公司, 制造的双频激光器频率稳定性最高可以达到10^–9@1 s, 10^–8@1000 s量级, 由此引入的测量误差为纳米量级. 然而要满足皮米级干涉测量需求, 激光光源引入的测量误差应至少达到亚皮米量级, 这要求激光光源的频率稳定性达到10^–12以下. 目前基于Pound-Drever-Hall (PDH)稳频技术的超稳激光^[20,21], 其频率稳定性可优于10^–12@1 s, 10^–12@1000 s量级. 而基于硅基F-P超稳腔的PDH稳频技术可以实现频率稳定性达4×10^–17@1 s, 1×10^–16@1000 s的超稳激光输出^[22,23]. 该技术将超稳腔置于独立的真空系统中, 确保残余气压低于10^–9 mbar (1 bar = 10⁵ Pa), 同时将腔体控制于124 K的低温条件. 激光器与稳频系统均置于主动隔振平台上, 进行严格的隔音和隔温处理. 基于该稳频技术, 可以将双频激光光源频率稳定性引入的测量误差降低至飞米量级以下.

双频激光光源的频率稳定性影响波长的真值, 会在波长转换为位移的过程中引入额外误差; 而双频频差稳定性影响多普勒频移的测量值, 会在探测端引入相位解析误差(详见正文第2部分). 经过理论计算, 皮米级的干涉测量, 需求双频激光光源的频率稳定性优于10^–12, 同时频差稳定性至少为10^–7; 飞米级的干涉测量, 需求双频激光光源的频率稳定性优于10^–15, 同时频差稳定性至少为10^–10. 为此, 在提升频率稳定性的同时, 需研究双频激光光源的频差稳定性. 2014年, Köchert等^[24]通过数字锁定的方式将两台氦氖激光器的激光频率进行锁定, 得到了频差短期波动为8.6 Hz的双频激光. 2020年, Yang等^[25]利用两台氦氖单频激光器生成双频激光, 理论分析并实验验证了频差稳定性长期漂移会引起位移测量的漂移, 通过偏频锁定将频差稳定性控制在10^–6@1000 s量级, 从而将频差稳定性引入的测量误差控制在皮米量级. 目前, 仅上述工作对双频频差的长期稳定性进行了分析与实验测试, 但尚未见到关于双频频差稳定性的系统分析与评估方案的相关报道.

为此, 本文建立了双频激光频差稳定性与外差干涉测量误差之间的演化模型. 同时搭建了基于双声光调制的双频激光光源及其频差稳定性评估系统, 并针对优化频差稳定性这一目标, 分析了影响频差稳定性的主要因素. 根据分析结果, 对各单元技术进行了升级与改进, 最终实现了频差稳定性为9×10^–11@1 s, 6×10^–10@1000 s的高频差稳定双频激光输出, 由频差稳定性引起干涉测量的短期波动仅为5.3×10^–2 fm, 长期漂移仅为2.8×10^–1 fm, 充分满足皮米级激光干涉测量对双频激光频差稳定性提出的要求.

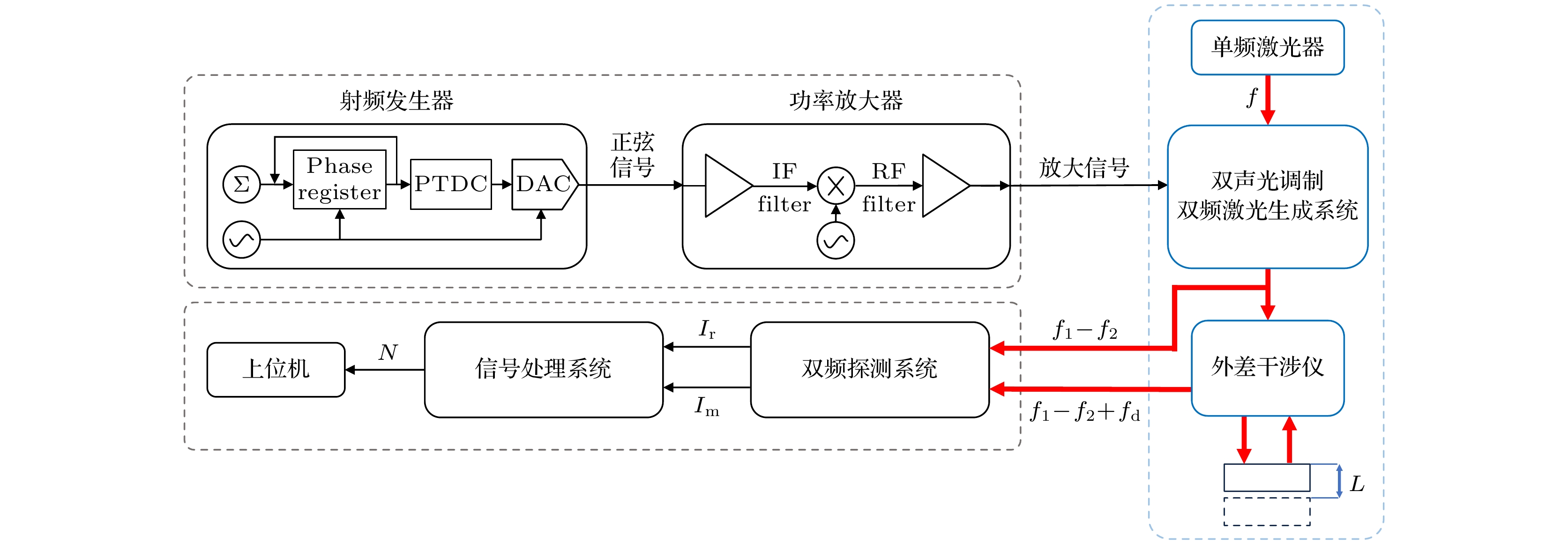
为了系统性分析双频激光频差稳定性对外差干涉测量误差的影响, 本文首先建立了双频激光频差稳定性与外差干涉测量误差之间的演化模型. 图1为双声光调制双频激光测量系统的整体框架图, 其中主要包括光学(蓝色方框)与电学(黑色方框)两部分, 电学部分分为射频信号生成部分与干涉信号处理部分. 单频激光器输出频率为f的自由空间光进入双声光调制双频激光生成系统生成一对正交线偏振光$ f + {f_1} $和$ f + {f_2} $, 这束双频光的一部分经过拍频干涉$ ({f_1} - {f_2}) $后进入双频探测系统成为参考信号I_r, 另一部分进入外差干涉仪后携带待测物体的位移信息返回(物体运动产生多普勒频移$ {f_{\text{d}}} $), 经过拍频干涉$ ({f_1} - {f_2} + {f_{\text{d}}}) $后进入双频探测系统形成测量信号I_m, 通过对I_r与I_m的解调处理, 得到输出的脉冲数N, 最终通过计算得到位移信息L.

待测目标在运动时会产生多普勒频移, 设其运动速度为v, 此时参考信号I_r与测量信号I_m可以表示为

其中A₁和A₂分别为双频激光中正交偏振的两束光的振幅; $ \Delta f = {f_1} - {f_2} $为双频频差; $ {{\boldsymbol{k}}_1} $和$ {{\boldsymbol{k}}_2} $分别为双频光的波矢; L_r和L_m分别为参考信号与测量信号的空间传输距离; $ {\varphi _{{\text{r}}1}} $和$ {\varphi _{{\text{r}}2}} $分别为参考信号处两束正交偏振光的初相位; $ {\varphi _{{\text{m}}1}} $和$ {\varphi _{{\text{m}}2}} $分别为测量信号处两束正交偏振光的初相位. 输出脉冲数N与被测位移L关系如下:

式中, c为光速, n为空气折射率, λ(n)为测量光在折射率为n的介质中的波长, λ为光的真空波长. 在理想情况下待测位移L为

对(5)式求微分有

根据(6)式计算可得, 双频激光光源的频率稳定性为$ \delta f/f =\text{ }1\times {10}^{-12} $时, 测量1 m的位移引入的干涉位移测量误差为1 pm. 其激光频率稳定性相对误差将引起干涉位移测量的等量级的相对误差. 同时, 正交偏振的双频激光在拍频干涉后形成拍频信号, 其频差稳定性也会引起干涉位移测量的误差. 因此, 本文继续对测量误差模型作进一步分析.

上述模型建立在双频频差$ \Delta f $无变化的理想状况下. 为进一步分析频差稳定性对测量精度的影响, 将参考信号与测量信号的频差值分别设为$ \Delta f + \Delta {f_{\text{r}}} $和$ \Delta f + \Delta {f_{\text{m}}} $, 除此之外$ \Delta f $的漂移会导致波矢差$ \Delta k = {k_1} - {k_2} $产生变化, 由$ k = {\text{ }}2\pi /\lambda = {\text{ }}2\pi f/c $则(3)式可改写为

则(7)式第1项$ \displaystyle \int_{{t_0}}^{{t_1}} {\left( {\Delta {f_{\text{m}}} - \Delta {f_{\text{r}}}} \right)} {\text{d}}t $与第2项$ \dfrac{{2{\text{π}}}}{c} \times \left[ {\left( {\Delta f + \Delta {f_{\text{m}}}} \right){L_{\text{m}}} - \left( {\Delta f + \Delta {f_{\text{r}}}} \right){L_{\text{r}}}} \right] $对于位移测量的影响项可以写为

在(8)式第1项中, 尽管$ \Delta f + \Delta {f_{\text{r}}} $和$ \Delta f + \Delta {f_{\text{m}}} $为同一束双频光经分光后产生的拍频信号, 但由于两者在空间中的传输距离不同, 因此$ \Delta {f_{\text{m}}} - \Delta {f_{\text{r}}} $的值并不为0. 这意味着频差的波动会造成测量值L的波动, 形成误差. 在传输过程中, c为真空中的光速, 则两者到达探测器的时间由待测物与外差干涉仪的距离相关, 时间差一般为$\Delta t = ({{{L_{\text{m}}} - L{}_{\text{r}}}})/{c} \approx {10^{ - {8} }}~{\text{s}}$, 由于∆t很小, 频率计的采样率较低只能采集到平滑后的数据, 因此不能直接使用测量值进行分析; (8)式中第2项在频差随时间漂移的过程中造起测量值的零点漂移.

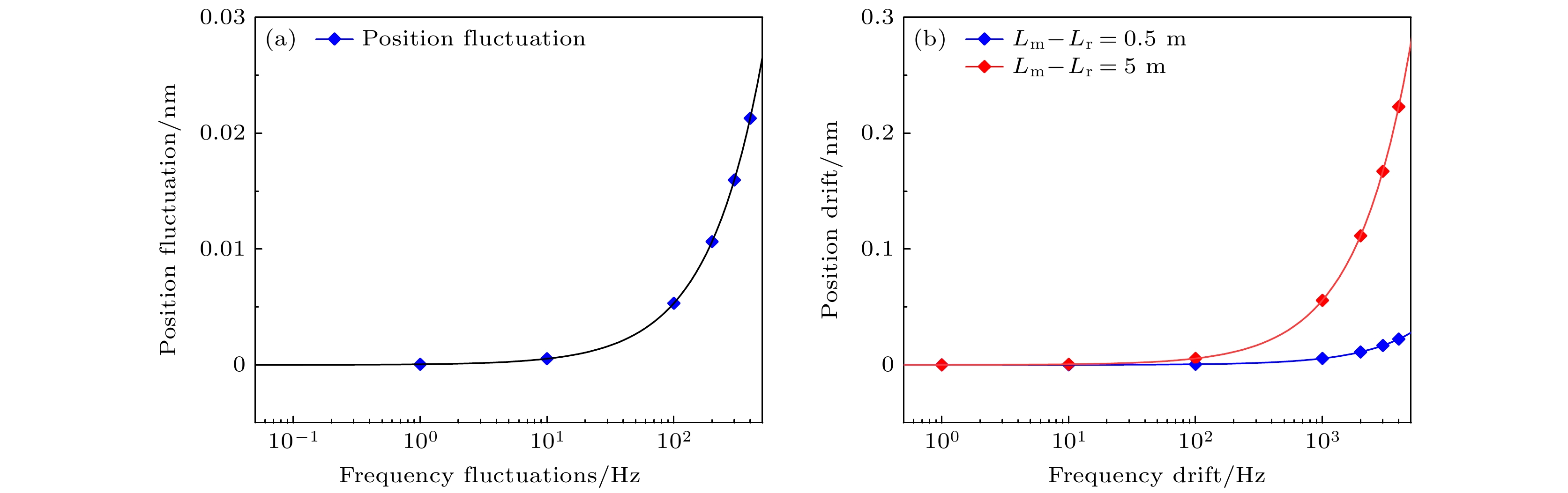
分析(8)式中的第1项, 在参考端由频率计数器测量得到的数据为$ \Delta f + \Delta {f_{\text{r}}} $, 采样率为10 Hz. 忽略测量信号由于温度、振动等环境因素导致的频差稳定性恶化, 将折射率n取为1, 那么测量端和参考端的频差差值$ \Delta {f_{\text{m}}} - \Delta {f_{\text{r}}} $可表示为$ \Delta {f_{\text{r}}}/{10^7} $. 从参考信号本身的频差稳定性出发, 将模型简化为

分析(8)式中的第2项, 经简化可写为^[25]

分别根据(9)式和(10)式建模可得到双频频差短期波动引起的测量误差(图2(a))以及双频频差长期漂移引起的测量误差(图2(b)). 如图2(a)所示, 双频频差存在100 mHz的短期波动会引起位移测量产生约5 fm的短期波动, 100 Hz的短期波动会引起位移测量产生约5 pm的短期波动. 如图2(b)所示, $ {L_{\text{m}}} - {L_{\text{r}}} = 0.5{\text{ m}} $时(蓝色曲线)双频频差存在1 Hz长期漂移会引起位移测量产生约5 fm的长期漂移, 1 kHz长期漂移会引起位移测量产生约5 pm的长期漂移. $ {L_{\text{m}}} - {L_{\text{r}}} = 5{\text{ m}} $时(红色曲线)双频频差存在1 Hz长期漂移会引起位移测量产生约50 fm的长期漂移, 1 kHz长期漂移会引起位移测量产生约50 pm的长期漂移. 因此, 为实现皮米甚至飞米级精度的测量, 双频频差稳定性成为另一制约因素. 基于此, 本文进一步对影响双声光双频激光频差稳定性的各项因素进行理论分析.

对于文中的双声光调制双频激光光源, 其射频信号的传输过程如图1所示, 射频发生器输出高稳定正弦射频信号至功率放大器, 功率放大器将输入的射频信号放大至可驱动负载的功率级别. 被放大的射频信号进入声光调制器(AOM), 经电声换能器转化为超声波. 当光波通过工作中的声光调制介质后会发生布拉格衍射, 通过调节声波频率可以实现对入射光的相位和频率进行调制, 而声波频率与施加在介质上的射频驱动信号相同, 因此射频驱动信号的频率稳定性与光学移频的准确度与稳定度直接相关. 研究发现, 射频信号稳定性和功率放大器引入的高阶谐波是影响频差稳定性的主要因素.

AOM的调制原理是光作为载体, 通过AOM把移频信号加到载波上. 光频的改变量等于外加射频功率信号的频率. 输出光取正一级衍射光时, 输出光的频率为原激光频率加电信号频率, 输出光取负一级衍射光时, 输出光的频率为原激光频率减电信号频率. 改变输入信号的频率, 即可控制输出光的频移量, 或者保持驱动频率不变, 取不同衍射级次作为输出. AOM在实际应用中要求输出光的功率尽可能高, 所以AOM一般工作在布拉格衍射模式.

AOM的移频量和移频精度主要由射频驱动信号决定^[26], 声光器件本身对频率基本没有影响. 所以为保证AOM的移频精度和移频稳定度, 驱动源必须采用高稳定度的晶体振荡器或高稳定性的信号发生器. 高稳定射频发生器能够输出高稳定性的射频正弦波形, 但驱动能力较差, 因此需要功率放大器来配合使用. 射频发生器输出的正弦信号${\nu}(t) = {\nu_0}\cos \left( {\omega t + \varphi } \right)$, 经功率放大器放大后的输出功率为$ {P_{{\text{out}}}} = {{{\nu_0^2}}}/({{8 R}}) = {{{\nu_0^2}}}/{{400}} $, 式中R为负载阻抗. 放大的射频信号输出到AOM, 调制器中的电声换能器将电信号转化为超声波. 换能器置于两个电极之间, 上电极决定了换能器的工作极限, 接地电极与晶体相连. 调制器内部设置阻抗匹配电路, 将换能器与驱动器进行耦合(50 Ω)以避免功率返回损耗, 在最佳匹配状态下功率放大器工作在线性区域内. 生成的超声场作用于介质时, 介质中的各点将出现随时间和空间周期性变化的弹性应变. 由于弹光效应, 介质中各点的折射率也会产生相应的疏密周期性变化, 于是晶体变成了一个等效的相位光栅, 在光束通过时产生衍射. 衍射光受到超声场的调制, 产生移频. 在双声光调制双频激光方案中, 两束光分别受到两个AOM的调制, 得到频差为$ \Delta f = {f_1} - {f_2} $的双频激光. 当器件引起的频率稳定性恶化远小于射频信号的稳定度时, 由公式$ \Delta f = {f_1} - {f_2} $可见, 双频激光的频差即两声光调制器驱动频率之差, 其射频信号稳定性直接决定了双频激光光源的频差稳定性.

对于理想的放大器, 其输出信号应当如实反映输入信号, 即波形应该是相同的. 但是实际上由于多种原因, 输入信号不可能与输入信号的波形完全相同, 这称为放大器失真^[27].

放大器失真主要有频率失真(线性失真)和波形失真(非线性失真)两种. 前者主要指对于不同的频率成分, 放大器的增益和延时有差异; 后者指对于同一频率, 输出信号与输入信号不呈线性关系. 频率失真表现在频域上的频谱改变, 而非线性失真则表现在时域波形上的变化. 非线性失真区别于线性失真主要是会产生大量新的频率分量. 根据两种失真的定义, 频差稳定性受到非线性失真的影响. 对于非线性失真而言, 其具有多种表现形式, 比如经过功率放大后得到额外的高阶谐波会对信号的幅度和相位造成一定的失真.

利用函数表示功放的输出幅度与输入幅度之间的关系, 将按照幂级数的形式展开:

假定输入为单频信号, 即:

将(12)式代入(11)式得

从(13)式可以看出, 除了直流分量和基频分量ω以外, 输出信号中还存在二次谐波2ω和三次谐波3ω等高阶分量, 这些高阶谐波会恶化射频信号的频率稳定性并以噪声形式引入到移频后的移频光中. 两束移频光在干涉时这些高阶分量之间会相互耦合, 从而额外产生许多在信号频域附近的噪声, 最终造成双频频差稳定性的恶化.

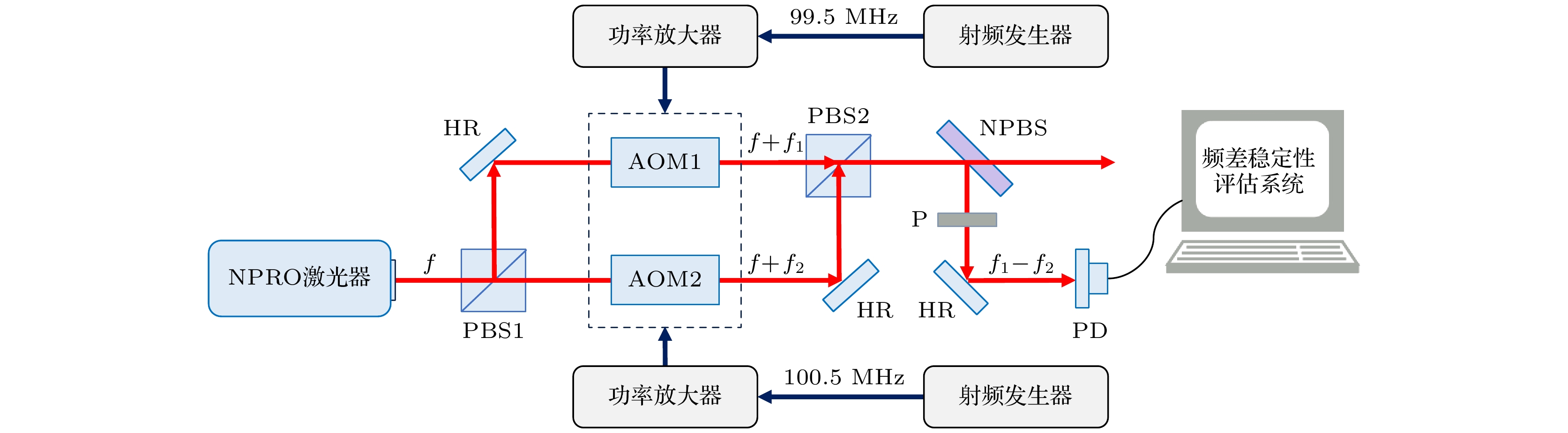
图3所示为基于双声光调制的双频激光光源及其频差稳定性评估系统装置图. 电路部分: 由同一射频发生器(图中的两个射频发生器为方便描述, 实际采用同一射频发生器输出两路信号)输出频率分别为99.5 MHz与100.5 MHz的两路射频信号, 这两路射频信号经功率放大器(PA)放大后具备驱动能力, 输入到AOM1与AOM2中. 光路部分: 由NPRO激光器输出的基频光经偏振分光棱镜PBS1分为两路, 反射光经高反射镜反射进入AOM1发生衍射, 受到AOM1的调制产生99.5 MHz的频移; 透射光进入AOM2发生衍射, 受到AOM2的调制产生100.5 MHz的频移. 两路光在偏振分光棱镜PBS2处汇合, 形成一对双频正交线偏振光, 其频差为1 MHz. 进入外差干涉仪的双频光经过无偏分束镜BS1分为两路, 一路双频光经过起偏器后拍频干涉进入光电探测器PD1作为参考信号, 另一路双频光进入外差干涉仪用于干涉测量. 参考信号接入频差稳定性评估系统, 系统由双频探测器、Keysight 53220 A频率计数器与Allan方差分析软件Stable32组成, 该系统能够对参考信号的频差稳定性进行测量并进行Allan方差分析. NPRO激光器波长为1064 nm, 线宽为1.3 kHz, 腔体温度采用自研的温度控制模块进行控温, 精度可达0.001 ℃. 实验室整体环境温度控制在22—23 ℃, 双频激光光源及其频差稳定性评估系统均独立安装金属外壳, 并整体置于气浮光学平台上(Newport S-2000A), 可实现垂直隔振94%@5 Hz和98%@10 Hz的隔振效率.

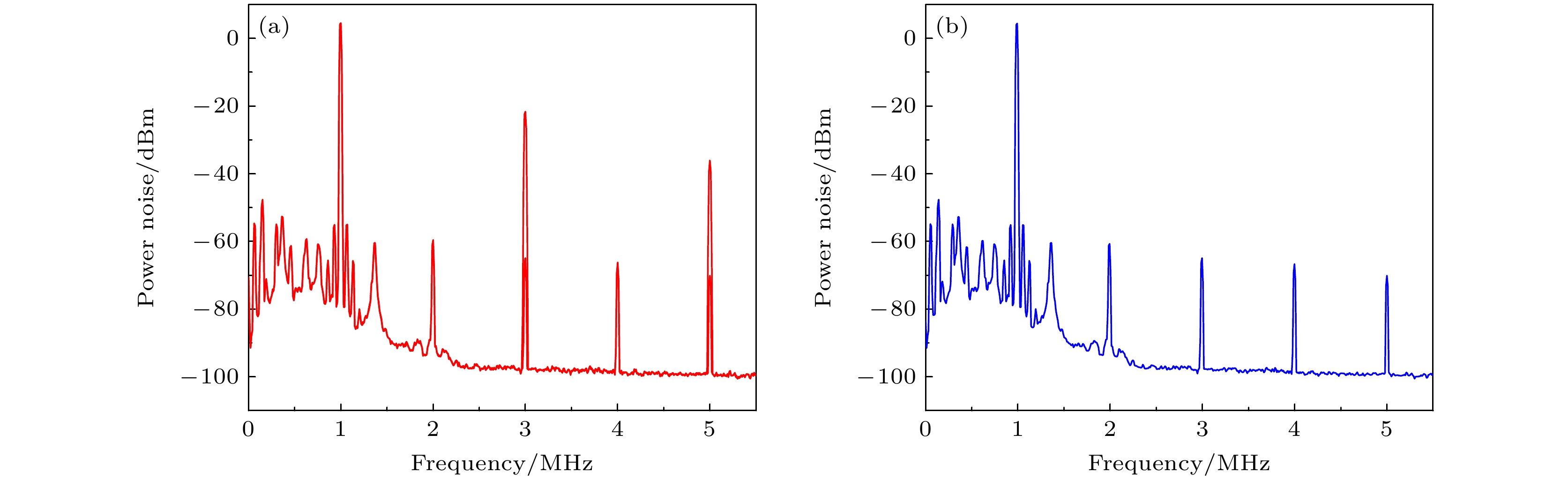
实验中, 首先使用RIGOL DG 4202作为AOM的射频发生器生成双频激光, 经频差稳定性评估系统测量评估, 其短期频率波动为300 Hz, 与射频发生器的频率稳定性差距较大. 对信号进行频域分析, 在1 MHz的载波信号附近存在2, 3, 4 MHz, ···的高阶谐波, 如图4(a)所示.

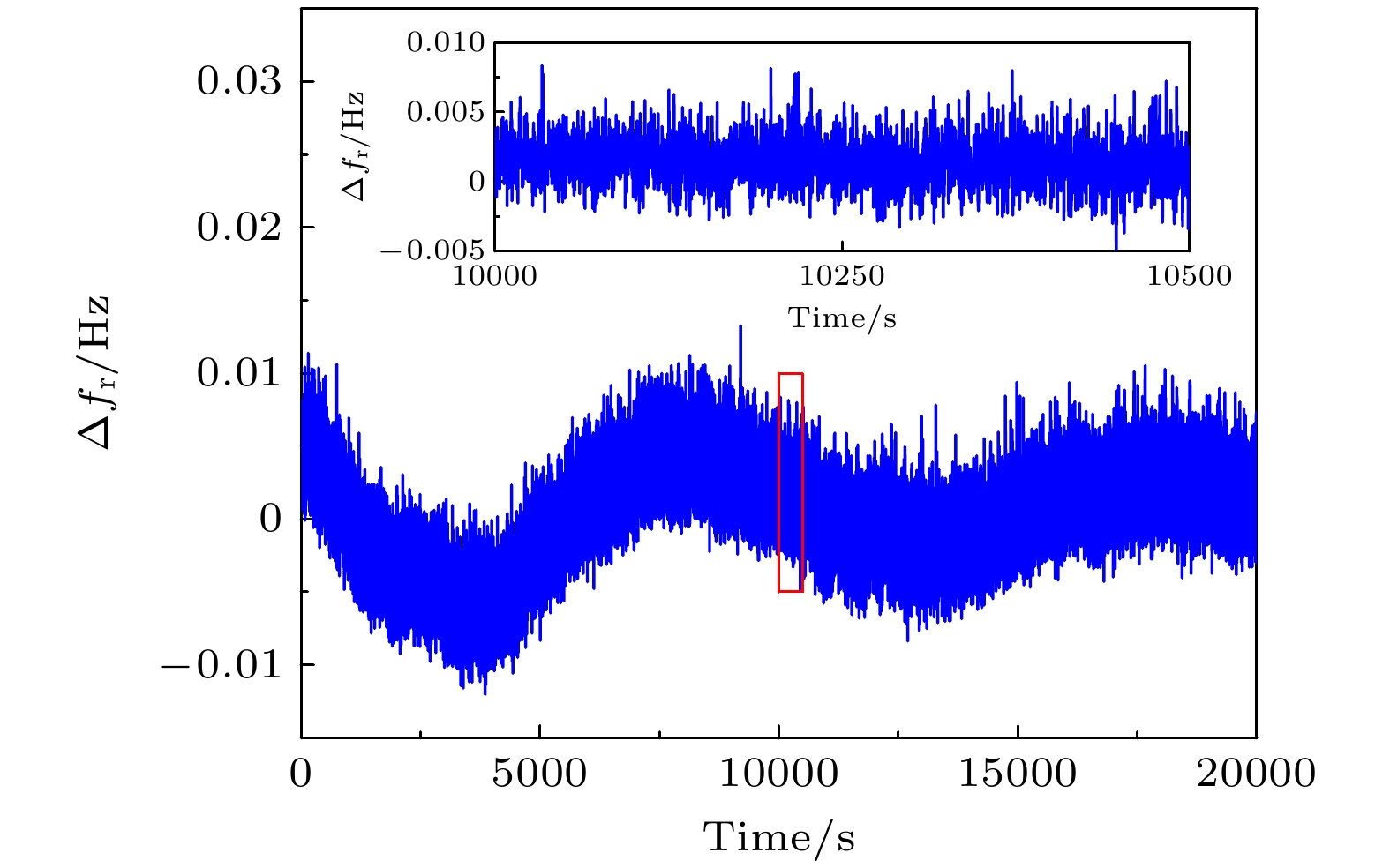
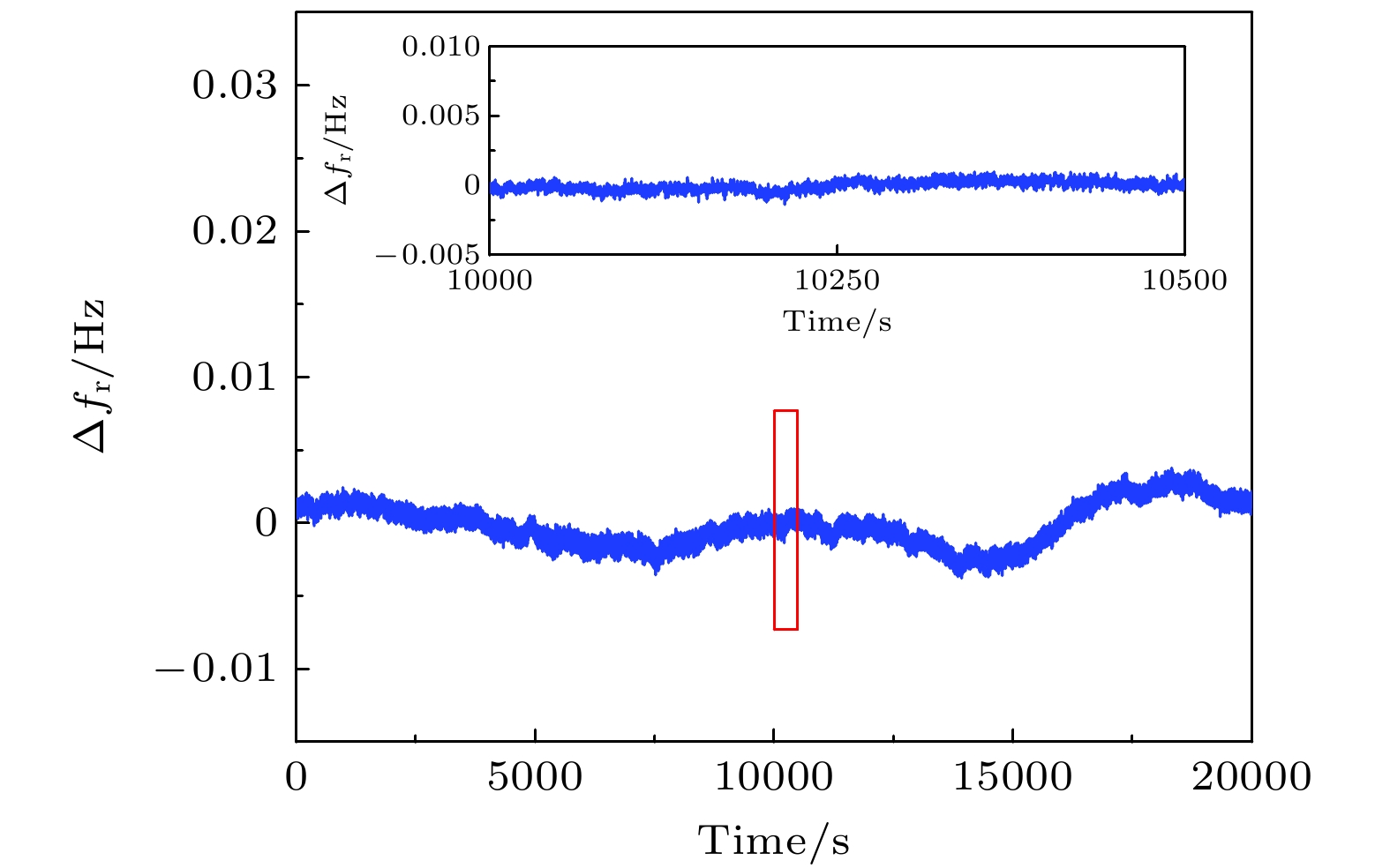
此时对放大后的单路射频信号进行频谱分析, 发现在199, 298.5, 398 MHz, ···处存在高阶谐波, 与理论分析一致; 而另一射频信号同样如此, 在201, 301.5, 402 MHz, ···处存在高阶谐波. 这些高阶谐波会叠加在移频后的光束中, 并在光束拍频干涉时相互耦合, 使得信号中存在1 MHz的整数倍高阶谐波, 导致信号频率稳定性的恶化. 为此, 在双频探测器中增加了对应的滤波电路设计, 有效滤除了这些高阶谐波, 抑制水平达30 dBm以上, 如图4(b)所示. 此时再次测量双频激光的拍频信号, 得到双频频差值随时间的变化如图5所示, 测量总时长为20000 s, 内插图为红色方框部分对应截取的一段测量数据, 可以更加清晰地看到数据的短期稳定性, 截取时长为500 s. 其短期频率波动为10 mHz, 长期漂移最高为20 mHz. 由(9)式和(10) 式分别计算得到, 双频频差短期波动引起的位移测量短期波动为5.3×10^–1 fm, 双频频差长期漂移引起的位移测量长期漂移为1.12 fm. 此时, 双频激光的频差稳定性接近射频发生器DG 4202的频率稳定性. 为进一步提高频差稳定性, 我们对射频发生器进行升级, 以提升射频信号的稳定性.

在正文第3部分中, 提到双频频差稳定性与射频信号的稳定性直接相关. 为验证双频频差稳定性与射频信号频率稳定性的相关性, 我们设计了基于铷钟的高稳定射频发生器, 来满足高稳定双频激光的生成. 其主要结构包含: 铷钟、伺服电路、频率调制和倍频电路, 其中铷钟提供频率基准, 伺服电路用来将输出的射频信号锁定至频率基准, 频率调制和倍频电路结合提供两路频率可调的射频信号输出. 测试双频激光的频差稳定性, 得到的频差稳定性测试结果如图6所示, 测量总时长为20000 s, 内插图为红色方框部分对应截取的一段测量数据. 可以更加清晰地看到数据的短期稳定性, 截取时长为500 s. 其短期频差波动小于1 mHz, 长期漂移约为5 mHz. 由(9)式和(10) 式分别计算得到, 双频频差短期波动引起的位移测量短期波动仅为5.3×10^–2 fm, 双频频差长期漂移引起的位移测量长期漂移仅为2.8×10^–1 fm. 此时, 该双频激光光源生成方案将频差稳定性对外差干涉测量引入的误差降低至亚飞米量级.

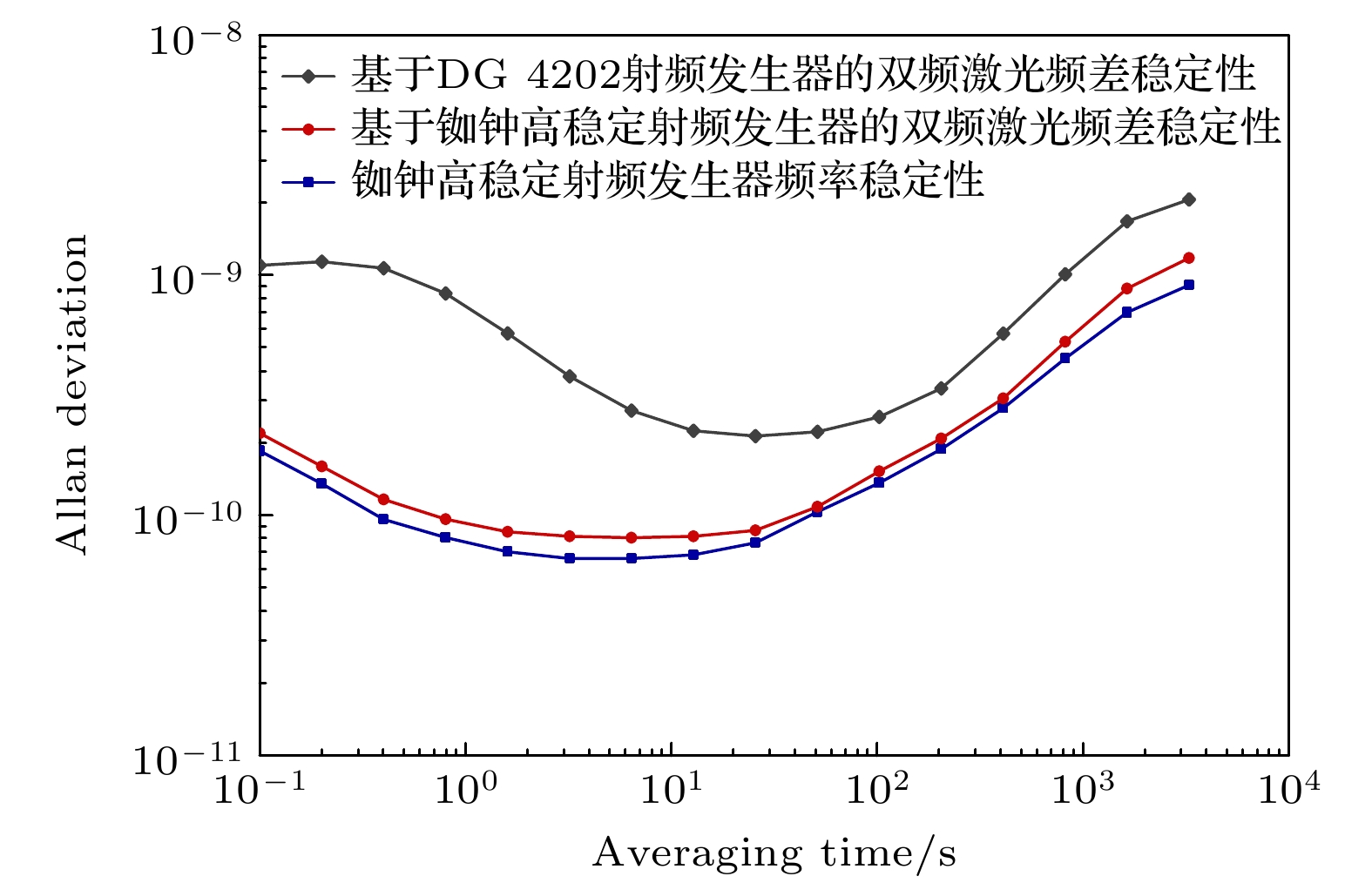
为了更加清晰地明确频差稳定性的提升过程, 利用Allan方差来表征频差稳定性, 并对比了几种技术方案的Allan方差, 结果如图7所示. 其中黑色曲线是对功率放大器高阶谐波进行滤波处理后的双频频差稳定性Allan方差曲线, 此时双频激光的频差稳定性为7.5×10^–10@1 s, 1.2×10^–9@1000 s; 红色曲线是替换频率稳定性更好的基于铷钟的高稳定射频发生器后得到的双频频差稳定性Allan方差曲线, 此时双频激光的频差稳定性为9×10^–11@1 s, 6×10^–10@1000 s; 蓝色曲线是铷钟频率稳定性Allan方差曲线, 频率稳定性为7.5×10^–11@1 s, 5×10^–10@1000 s. 对比黑色和红色曲线可知, 基于铷钟的高稳定射频发生器可以实现频差稳定性高一个量级的双频激光输出; 对比红色和蓝色曲线可知, 此时双频激光的频差稳定性接近铷钟的频率稳定性, 射频信号发生器的稳定性再次成为提升双频频差稳定性的限制因素. 上述实验结果证明了射频信号的稳定性是决定双声光调制双频激光频差稳定性的关键因素. 此后, 通过提高射频信号的稳定性, 可进一步提升频差稳定性, 减小外差干涉测量误差. 结合当前最先进的超稳腔稳频技术(4×10^–17@1 s, 5×10^–16@1000 s)^[22,23], 以及频率噪声主动反馈控制技术^[28,29], 本文高稳定双频激光光源引入的干涉测量误差可降低至亚飞米量级, 预期将满足皮米甚至亚飞米级的超精密干涉测量对双频激光光源的需求.

本文基于外差干涉测量系统, 首先建立了双频激光频差稳定性与外差干涉测量误差之间的演化模型. 该模型定义了双频频差稳定性并分析了频差稳定性对外差干涉位移测量精度的影响. 随后, 针对优化频差稳定性这一目标, 从双声光调制生成双频激光的理论模型出发, 深入分析了影响频差稳定性的各项因素. 最后, 基于上述分析搭建了基于双声光调制的双频激光光源及其频差稳定性评估系统, 并针对性地进行了实验研究. 研究发现, 双频频差稳定性的主要影响因素是功率放大器非线性失真和射频信号稳定性. 针对功率放大器的非线性失真问题, 我们设计了高阶谐波滤除技术, 将双频激光光源的频差短期波动抑制至10 mHz, 同时将频差长期漂移降低至20 mHz. 此时, 频差稳定性提升至7.5×10^–10@1 s, 1.2×10^–9@1000 s, 接近商用射频发生器的频率稳定性, 对外差干涉测量引入的误差从亚纳米降低至飞米量级, 满足了外差干涉皮米级位移测量对双频激光光源频差稳定性的要求. 进一步提升射频信号稳定性, 通过将商用射频发生器替换为基于铷钟的高稳定射频发生器, 将双频激光光源的频差短期波动抑制至1 mHz, 同时将频差长期漂移降低至5 mHz. 此时, 频差稳定性提升至9×10^–11@1 s, 6×10^–10@1000 s, 接近铷钟的频率稳定性, 将频差稳定性对外差干涉测量引入的误差降低至亚飞米量级. 此项研究结合最先进的超稳腔稳频技术^[22,23], 以及频率噪声主动反馈控制技术^[28,29], 能够将高稳定双频激光光源引入的干涉测量误差降低至亚飞米量级, 预期将满足皮米甚至亚飞米级的超精密干涉测量对双频激光光源的需求.