首页
登录
注册
-
金刚石涂层具有接近天然金刚石的硬度、高弹性模量、高热导率、低摩擦系数、低热膨胀系数和极好的抗腐蚀性能, 是一种理想的新型耐磨涂层材料[1–4]. 随着硬质合金基体上沉积金刚石涂层技术日益成熟, 金刚石涂层工具和各种耐磨器件的制备已经进入产业化阶段. 然而, 金刚石涂层工具的实际应用效果与涂层的质量优劣尤其是涂层的膜基界面结合强度密切相关, 否则容易引起涂层早期失效从而影响涂层工具的实际使用寿命[5–7]. 因而, 如何切实有效地在硬质合金基体上提高金刚石涂层膜基界面结合强度已成为金刚石涂层工具制备与应用相关领域中的关键问题之一, 同时也是多年来困扰金刚石涂层制备和产业化应用的关键难题.
金属Co因其良好的综合性能, 是硬质合金应用最广泛的黏结金属. 大量试验表明, 在金刚石涂层沉积过程中, 基底表面的黏结相Co会催生中间石墨层, 严重削弱基底与涂层的结合强度[8–12], 影响工具的使用寿命. 为削弱这一影响, 可以通过化学刻蚀法去除基底表层Co元素[13,14], 一定程度上可改善金刚石涂层膜基界面的结合强度, 但在金刚石涂层沉积过程中, 基底深层Co元素会扩散至基底表面与涂层中[15,16], 影响基底与涂层的结合强度. 因此要彻底解决这一问题, 就必须研究硬质合金基底表层所嵌入的Co原子促石墨化机理及其微观作用过程.
有鉴于此, 本文采用基于密度泛函理论的第 一性原理方法, 借助CASTEP计算工具, 从微观角度对嵌入不同深度Co原子的孕镶金刚石基底及涂层界面作用模型进行理论计算, 以探究基底中Co的嵌入深度对金刚石涂层膜基界面结合强度的影响规律及其作用机制, 为消除基底表层Co原子对界面结合强度的消极影响, 提高孕镶金刚石涂层工具的使用寿命提供理论依据和参考.
-
由于Co促金刚石石墨化作用是其影响金刚石涂层与基底结合强度的主要因素, 因此将基底模型简化为金刚石与Co, 以集中研究Co的深度对结合强度的影响. [100]面是CVD金刚石涂层沉积过程中的主要生长面[17,18], 所以采用Materials Studio软件建立了[100]晶向的金刚石基底、金刚石涂层及两者界面的简化计算模型.
考虑到表面效应, 研究表面和界面时, 必须建立足够的表面厚度[19], 但表面层数越多, 计算的成本就越高. 为此, 采用层间距变化的方法测试表面收敛性, 层间距变化的定义公式如(1)式所示[20]:
式中,
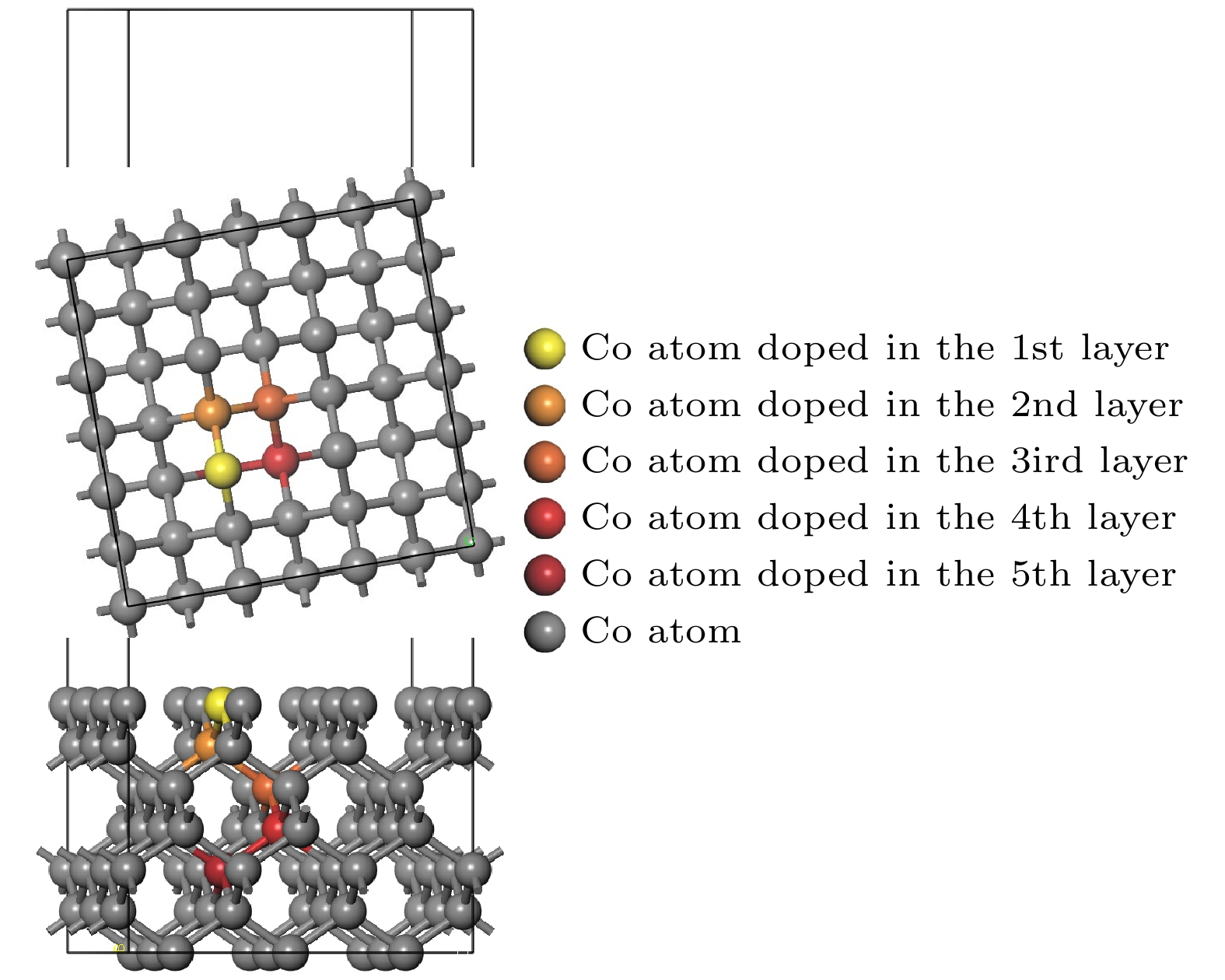
$d_{ij}^0$ 表示弛豫前理想晶体相邻层$i$ 层与$j$ 层的间距,${d_{ij}}$ 表示弛豫后相邻层$i$ 层与$j$ 层的间距. 计算的模型层间距变化随模型原子层数的变化如表1所示, 随着层数的增加,${\varDelta _{12}}$ 和${\varDelta _{23}}$ 趋于收敛, 层数为7时, 层间距的变化表现出良好的收敛性, 再增加层数,${\varDelta _{12}}$ 和${\varDelta _{23}}$ 的波动变化远小于1%, 因此, 选取7层[100]晶向的Diamond构建界面模型.图1为建立金刚石基底与涂层界面模型的流程图. 首先, 将金刚石单晶胞模型沿[100]晶向切取层数为7的表面, 并以3×3的方式扩胞, 沿Z方向建立1.5 nm的真空层, 以消除晶胞间的周期性影响, 得到沿X, Y, Z方向尺寸为0.75 nm×0.754 nm×2.033 nm的基底、涂层模型. 之后按图2分别将基底1—5层中的一个C原子替换为Co原子, 得到Co分别嵌入1—5层的基底模型, 并设置不含Co的基底模型作为对照, 之后分别优化基底与涂层模型. 计算过程中, 模型底部两层碳原子固定, 表面五层原子自由弛豫. 最后, 建立图3所示的界面模型, 真空层厚度为1.7 nm, 膜基界面间距为0.2 nm.
-
采用Materials Studio软件的CASTEP[21]模块进行基于第一性原理的模型结构优化、能量计算及电荷分析. 选用OTFG Ultrosoft赝势描述电子-离子间的交互作用, 交换关联能量泛函采用广义梯度近似GGA[22](generalized gradient approximation)的PBE[23](Perdew Burke Ernzerhof)形式, 同时引入TS色散矫正描述模型中的弱相互作用. 平面波截断能设置为400 eV, 布里渊区采用Monkhorst-Pack[24]的精细精度, 自动生成3×3×1的K点网格进行计算. 能量、原子应力与原子位移的收敛容差分别设置为10–5 eV/atom, 0.03 eV/Å与0.001 Å. 所有计算均在零温、真空条件下, 基于系统的基态进行分析.
-
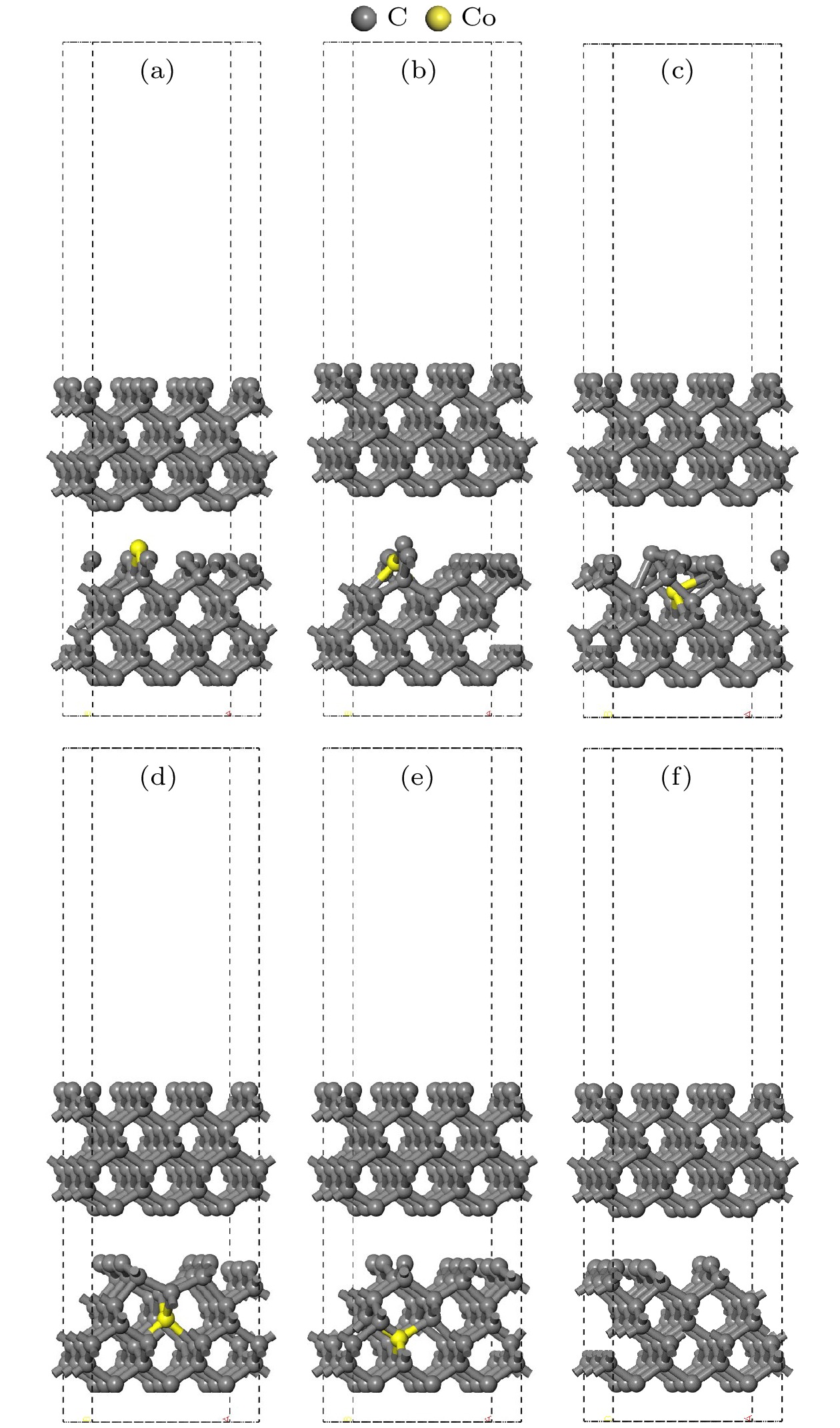
孕镶金刚石基底优化后的结构如图4所示, 根据图4(a)—(d), 当Co位于基底表面前4层时, 与不含Co相比, 基底表层结构变化明显. 特别地, 当Co位于第3层时, 基底表层中心的C原子由空间三维的金刚石结构转变为平面的石墨结构, 相邻C—C键键长为1.466 Å, 1.454 Å, 1.433 Å三种, 接近石墨中层内C—C键长1.42 Å. 由图4(e), (f)可知, 当Co位于第5层时, 基底表层结构与没有Co作用下的一致, 表面出现重构现象.
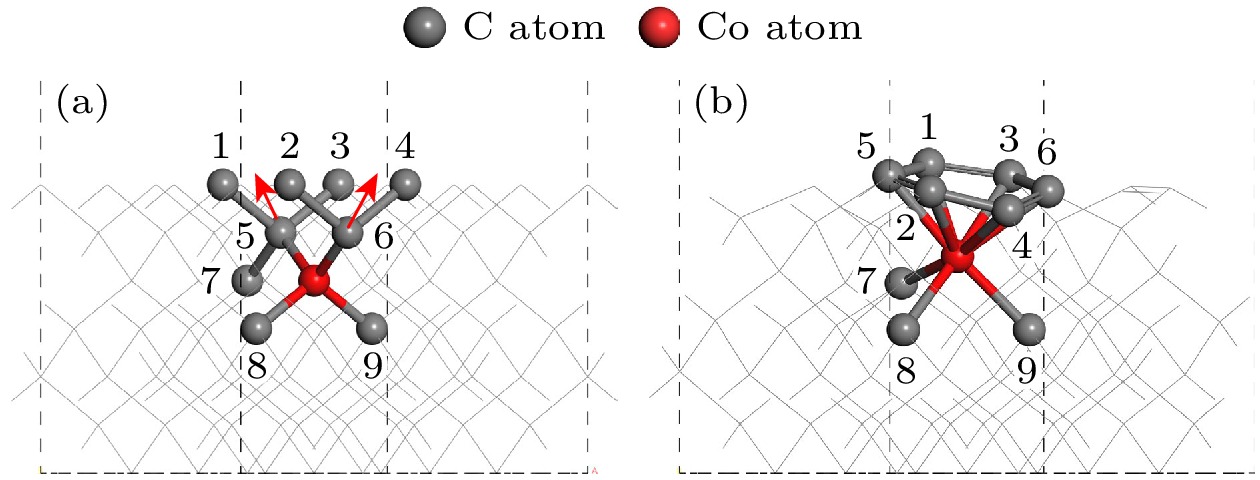
优化后的基底结构中, Co—C键键长均值约为1.90 Å, 大于金刚石中C—C键键长1.54 Å, 这是由于Co原子半径大于C, 且Co—C键是金属-非金属的键合方式, 相比于金刚石中sp3杂化C原子强烈的电子共享, 其电子共享程度较低, 导致Co—C键键长大于C—C键键长, Co在结构优化后表现为“排斥”周围C原子. 因此, 当Co位于基底表面第3层时, 如图5所示, 优化后Co与5, 6, 8, 9原子所成Co—C键键长增大, 由于深层原子趋向于体块特征, 受表面效应影响较小, 所以结构优化前后8, 9原子位置变化较小, Co原子向表层移动, 5, 6原子沿与Co成键方向(如箭头所示)移动至1, 2, 3, 4原子所在平面, 经表面重构, 最终形成平面六元环结构. 而当Co位于第1, 2层时, 如图4(a), (b)所示, Co上层的C原子数量不足以形成六元环; 当Co位于更深层时, 如图4(d), (e)所示, Co原子所在位置的块体特征显著, 状态更稳定, 此外由于Co原子距基底表层较远, 难以显著影响其结构, 也不会形成平面六元环. 因此, 只有当Co嵌入第3层时, 才会使金刚石表面呈现平面六元环.
-
界面结合能可以反映界面相互作用强度, 结合能越大, 表面结合力越强, 界面越稳定, 计算公式为[25]
其中,
${W_{{\text{ad}}}}$ 为界面结合能;${E_{{\text{slab1}}}}$ ,${E_{{\text{slab2}}}}$ 和${E_{{\text{interface}}}}$ 分别为金刚石基底、金刚石涂层和界面结构优化后的能量, A为界面面积.由表2可知, 膜基界面结合能大小为
${W_{{\text{ad}}}}$ (Co在第3层)<${W_{{\text{ad}}}}$ (Co在第2层)<${W_{{\text{ad}}}}$ (Co在第1层)<${W_{{\text{ad}}}}$ (Co在第4层)<${W_{{\text{ad}}}}$ (Co在第5层)≈${W_{{\text{ad}}}}$ (不含Co), 膜基界面结合能随基底中Co深度的增大呈先降低后升高的趋势. 与不含Co时相比, 基底表面1—4层的Co均会削弱膜基界面结合能, 第3层含Co时界面结合能为不含Co的63.7%, 削弱作用最显著, 第5层含Co时的界面结合能为不含Co的99.2%. 说明基底中黏结相Co对金刚石涂层膜基结合能的削弱程度受Co深度的影响, 第3层的Co削弱作用最显著, 第5层甚至更深层的Co不再影响金刚石涂层的膜基结合能. -
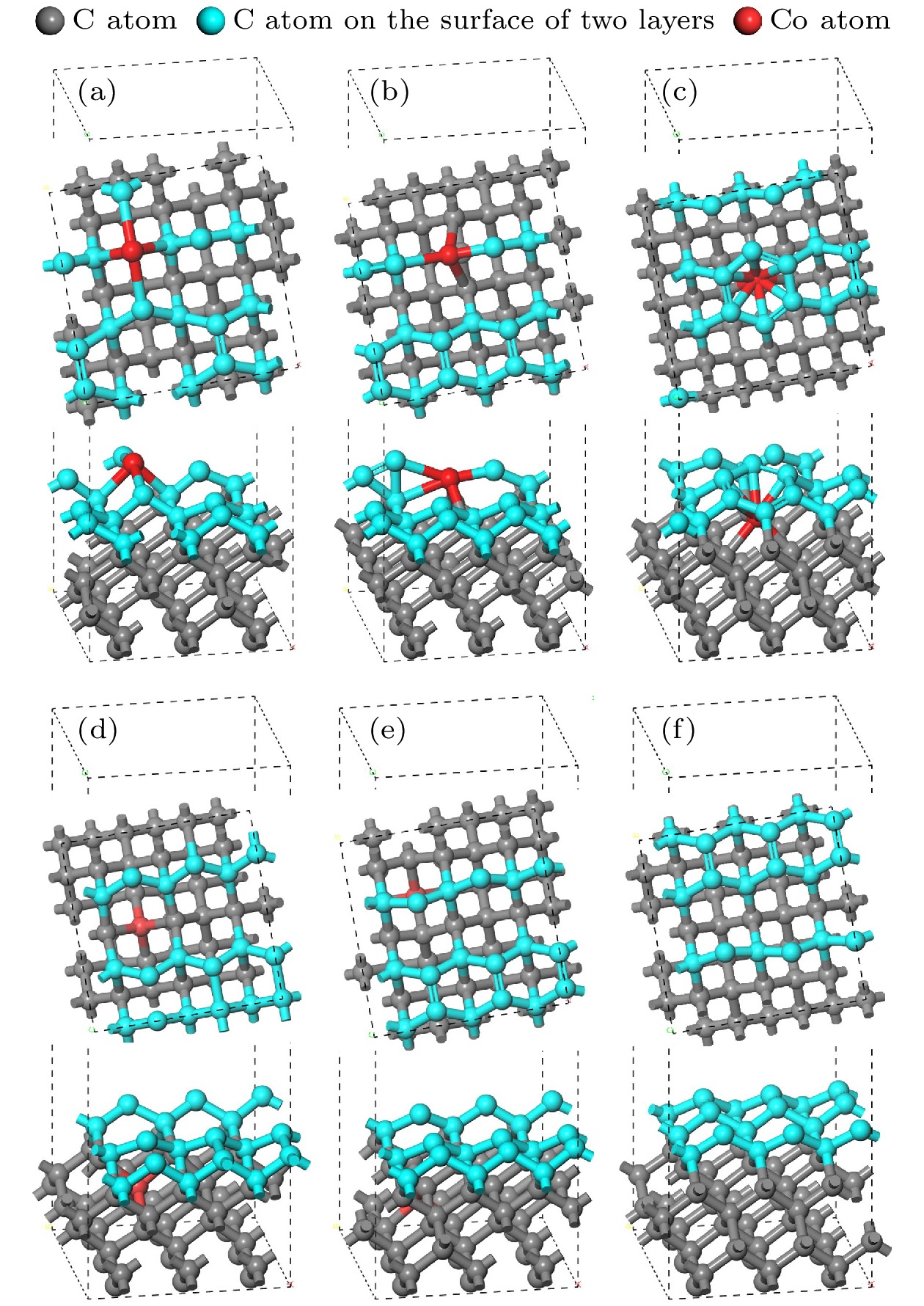
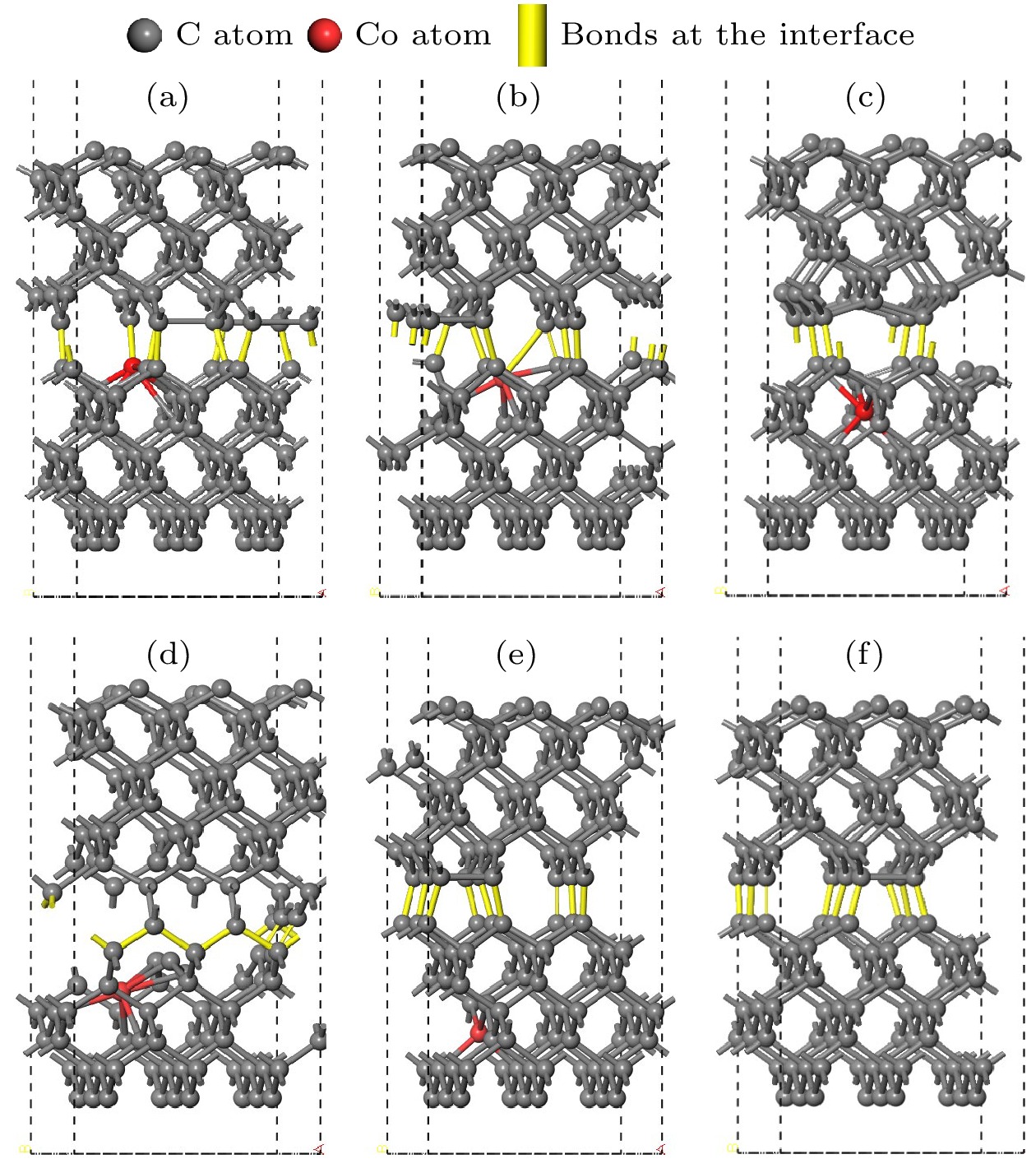
结构优化后的膜基界面模型如图6所示, 明显地, 图6(a)—(d)中的界面间距大于图6(e), (f)中的界面间距. 其中, 当Co位于基底表面第3层时, 界面间成键数目最少; 当Co位于基底表面第5层时, 界面成键情况与不含Co时几乎一致, 这与优化后的基底结构以及界面结合能结果相符, 可知基底中Co深度的变化会引起基底表层结构变化, 进而影响界面成键, 造成金刚石涂层膜基界面结合强度的变化.
-
差分电荷密度可以反映体系中电子的转移和分布情况, 为进一步研究Co的深度对金刚石表层结构的影响机理, 选取Co原子及靠近表层与Co作用的C原子, 分析其差分电荷密度. 特别地, 由图5(b)可知, 当Co位于第3层时, Co共与表层6个C原子、内部3个C原子成键, 且这9个C原子分3组绕中心Co对称分布, 每组C原子与Co的作用相似, 因此取一组C (图5(b)中1, 4, 7原子)所在截面进行分析, 最终得到Co在不同位置时基底差分电荷密度如图7所示, 其中蓝色部分表示电子富集, 红色部分表示电子贫化.
结果表明, Co—C键的形成伴随着明显的电子转移, 除图7(c)外, 电子转移方向均为由Co向C转移, 主要是因为C原子电负性更高, 吸引电子的能力更强. 特别地, 由图7(c)可知, 当Co位于第3层时, 由于Co—C键数目的增多, 每个键的电子转移程度有所减弱, 且表层C原子与Co的成键过程涉及不同的电子转移方向. 其中, 表层半数的C原子(如图7(c)中4所示)与7原子关于中心Co近似成对称分布, 电子由Co向两侧C转移; 而表层另一半C原子(如图7(c)中1所示)则表现为电子由C向Co转移, 两类不同电子转移方向的键间隔排布. 表明此时由于第2层C移动至表层, Co原子与周围C的作用空间扩大、成键数目增多、且体系呈现较高的几何对称性, 加之Co价层结构具有较多的未配对电子, 因此Co的电子轨道产生了更为显著的混合与重排, 最终得以形成稳定的金刚石表面Co促石墨化结构.
-
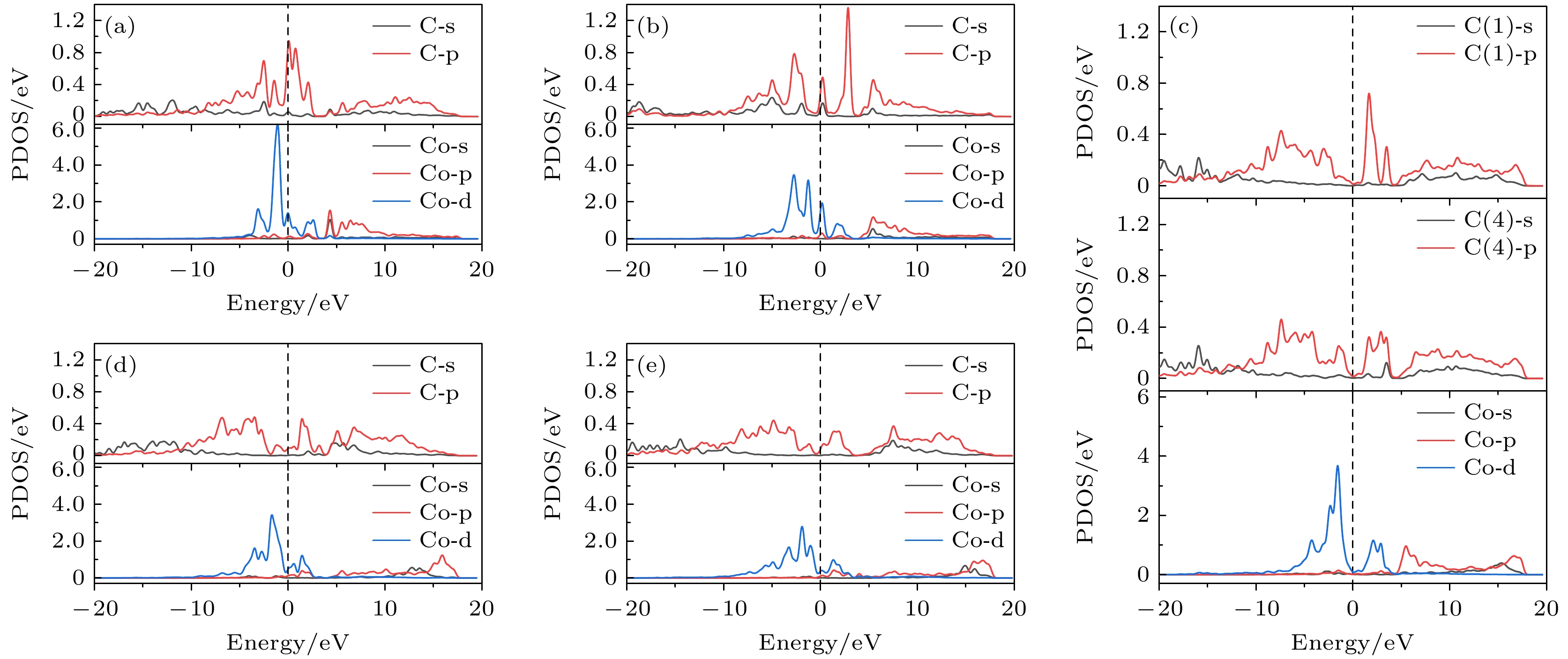
为进一步了解Co原子与相邻C原子的深层作用机理, 选取Co原子及靠近基底表层与Co作用的C原子, 分析其部分态密度(partial density of state, PDOS)如图8所示. 由于当Co位于第3层时, Co与上层的6个C原子涉及两种方向的电子转移, 因此图8(c)给出了这两种C原子的PDOS分布, 对应图7(c)中的1, 4两种C原子.
图8结果显示, Co—d轨道与C—p轨道在费米能级附近峰型相似, 两轨道电子云重叠形成了强的成键键合作用. 其中, 与图8(d), (e)相比, 当Co位于基底表面前3层时, C—p轨道电子态密度在0—3 eV区间分布更多, 表明由于表面效应, C原子杂化方式由sp3转变为sp2, 产生了离域π电子; Co—p轨道与C在5—10 eV表现出明显的电子态密度分布, 表明Co—p轨道与C通过π杂化成键, 进一步印证了这一结果. 当Co位于第4, 5层时, C—s, p轨道、Co—p轨道分别在5—15 eV, 15—18 eV区间表现出明显的电子态密度分布, 表明两轨道产生了一定的σ反键作用, 这是由于较短的C—Co键键长促进了轨道相互作用, 导致形成反键杂化.
特别地, 由图8(c)可知, 当Co位于第3层时, Co—p轨道在5—15 eV, 15—18 eV区间均有电子分布, 表明此时Co的电子轨道产生了更显著的混合和重排, 结合表3和表4可知, Co与周围C原子的电荷转移相对均衡且成键键长近似, 这与差分电荷密度的分析结果一致, 即Co的电子轨道产生了更大程度的混合和重排, 以与周围更多的C成键. 其中, Co—p轨道、C—p轨道在15—18 eV的电子态密度分布表明Co与表层C原子产生了π反键杂化作用, 表4中Co与表层C原子的化学键布居数均为负数, 证明了反键的作用, 进一步支持了这一结论.
-
采用基于密度泛函理论的第一性原理方法计算并分析了孕镶金刚石基底表面1—5层深度分别嵌入Co原子的几何结构及电子分布, 并计算了其与金刚石涂层的界面结合能与界面作用结构, 以研究孕镶金刚石基底中黏结相Co的深度对沉积金刚石涂层膜基界面结合强度的影响, 得到以下结论:
1) Co嵌入基底表面1—4层时会影响基底表层的稳定构型, Co位于第3层时, 表层形成平面六元环结构的石墨相; 第5层深度的Co不再影响基底表层的稳定构型.
2)膜基界面结合能大小为
${W_{{\text{ad}}}}$ (Co在第3层)<${W_{{\text{ad}}}}$ (Co在第2层)<${W_{{\text{ad}}}}$ (Co在第1层)<${W_{{\text{ad}}}}$ (Co在第4层)<${W_{{\text{ad}}}}$ (Co在第5层)≈${W_{{\text{ad}}}}$ (不含Co), 基底表面1—4层的Co会削弱膜基界面结合能, 且Co位于第3层时削弱效果最显著, 第5层的Co不再削弱膜基界面结合能.3) Co嵌入基底表面第3层时, 受表面效应影响, Co周围的C原子重新分布, 第2层的C移至表层, 且由sp3杂化转变为sp2杂化, Co与周围C原子的作用空间增大、作用数量增多, 加之Co价层未配对电子较多, 其电子轨道可以实现显著的混合和重排, 因此与周围9个C原子作用, 使得基底表面稳定为石墨结构.
孕镶金刚石基底Co原子嵌入深度对金刚石涂层膜基界面结合强度的影响
Influence of Co atom embedding depth in impregnated diamond substrate on bonding strength of diamond coating film substrate interface
-
摘要: 采用第一性原理方法, 对孕镶金刚石基底表层Co原子金刚石涂层膜基界面结合作用进行仿真计算分析, 以探究基底中黏结相Co的嵌入深度对金刚石涂层膜基界面结合强度的影响. 计算结果表明, 膜基界面结合能随基底中Co嵌入深度的增大呈先降低后升高的趋势. 当Co原子排列位于第3层时, 涂层生长易出现明显的石墨结构, Co促金刚石石墨化作用最为显著, 膜基界面结合强度达到最小值. 分析结构及电荷发现, 此时在表面效应及Co—C键键长的共同作用下基底第2层C移至表层, 并由sp3杂化转变为sp2杂化, 且C的移动导致Co与周围C原子的作用空间增大、作用数量增多, 加之Co价层未配对电子较多, 易与周围多个碳原子发生电子轨道的混合与重排, 最终使得基底表面呈现为石墨结构. Co位于第5层时不再影响基底表面的稳定构型及膜基界面结合强度.Abstract: Diamond coating has many excellent properties such as extreme hardness, high elastic modulus, high thermal conductivity, low friction coefficient, low thermal expansion coefficient, and good corrosion resistance. Those properties are close to natural diamond’s, thereby making the diamond coating an ideal new type of wear-resistant tool coating material. However, a large number of experiments have proved that during the deposition of diamond coating, the bonding phase cobalt on the surface of impregnated diamond substrate will generate a layer of graphite at the interface, which seriously weakens the adhesive strength between the substrate and the coating. To thoroughly solve this problem, it is necessary to investigate the microscopic process of graphitization caused by the Co element embedded on the substrate surface. Therefore, the first principle theory is adopted to simulate and analyze the interfacial adhesive strength of diamond coating when Co atom is embedded at different depths on the surface of impregnated diamond substrate, thereby exploring the mechanism of the influence of bonding phase Co element in the substrate on the diamond coating and the mechanism of Co promoting diamond graphitization. The calculation results show that the interfacial binding energy first decreases and then increases with the increase of Co embedding depth in the substrate. When Co atom is embedded in the third layer, obvious graphite structures are prone to appear at the interface, and Co promotes diamond graphitization most significantly, resulting in the minimum bonding strength between the film and substrate interface. The results of structure and charge indicate that under the influence of surface effect and Co—C bond length, the C atoms in the second layer of the substrate move to the first layer and the hybridization mode changes from sp3 to sp2. Meanwhile, this movement leads to an increase in the interaction space and quantity between Co atoms and the surrounding C atoms. In addition, there are many unpaired electrons in the Co valence layer, which can easily mix and rearrange electron orbitals with the surrounding C atoms, ultimately resulting in a graphite structure on the substrate surface. When Co atoms are embedded in the fifth layer, the stable configuration of the substrate surface and the interfacial adhesive strength are no longer affected.
-
Key words:
- diamond coating /
- Co element /
- adhesive strength /
- graphitization .
-
-
图 1 孕镶金刚石基底金刚石涂层膜基界面建模流程
Figure 1. Interfacial modeling process between impregnated diamond substrate and diamond coating.
图 2 Co原子嵌入不同深度的孕镶金刚石基底模型
Figure 2. Impregnated diamond substrate models with Co atom doped in different depths.
图 3 孕镶金刚石基底金刚石涂层膜基界面模型 (a) Co在第1层; (b) Co在第2层; (c) Co在第3层; (d) Co在第4层; (e) Co在第5层; (f)不含Co
Figure 3. Interface model between impregnated diamond substrate and diamond coating: (a) Co atom doped in the first layer; (b) Co atom doped in the second layer; (c) Co atom doped in the third layer; (d) Co atom doped in the fourth layer; (e) Co atom doped in the fifth layer; (f) without Co atom.
图 4 结构优化后的孕镶金刚石基底模型 (a) Co在第1层; (b) Co在第2层; (c) Co在第3层; (d) Co在第4层; (e) Co在第5层; (f)不含Co
Figure 4. Impregnated diamond substrate model after structural optimization: (a) Co atom doped in the first layer; (b) Co atom doped in the second layer; (c) Co atom doped in the third layer; (d) Co atom doped in the fourth layer; (e) Co atom doped in the fifth layer; (f) no Co atom.
图 6 结构优化后的孕镶金刚石基底和金刚石涂层的界面模型 (a) Co在第1层; (b) Co在第2层; (c) Co在第3层; (d) Co在第4层; (e) Co在第5层; (f)不含Co
Figure 6. Interface model between impregnated diamond substrate and diamond coating after structural optimization: (a) Co atom doped in the first layer; (b) Co atom doped in the second layer; (c) Co atom doped in the third layer; (d) Co atom doped in the fourth layer; (e) Co atom doped in the fifth layer; (f) no Co atom.
图 7 基底差分电荷密度图 (a) Co在第1层; (b) Co在第2层; (c) Co在第3层; (d) Co在第4层; (e) Co在第5层
Figure 7. Differential charge density of substrate: (a) Co atom doped in the first layer; (b) Co atom doped in the second layer; (c) Co atom doped in the third layer; (d) Co atom doped in the fourth layer; (e) Co atom doped in the fifth layer.
图 8 基底中Co与成键C原子的部分态密度图 (a) Co在第1层; (b) Co在第2层; (c) Co在第3层; (d) Co在第4层; (e) Co在第5层
Figure 8. Partial density of states of Co and bonded C atoms in the substrate: (a) Co atom doped in the first layer; (b) Co atom doped in the second layer; (c) Co atom doped in the third layer; (d) Co atom doped in the fourth layer; (e) Co atom doped in the fifth layer.
表 1 不同原子层数金刚石表面结构优化后的层间距变化
Table 1. Variation of layer spacing after structural optimization of diamond models with different numbers of atomic layers.
原子层数/N 层间距变化/% ${\varDelta _{12}}$ ${\varDelta _{23}}$ ${\varDelta _{34}}$ ${\varDelta _{45}}$ ${\varDelta _{56}}$ ${\varDelta _{67}}$ 3 –10.852 5 –11.142 4.606 7 –10.716 4.643 –0.429 9 –10.708 4.643 –0.701 0.933 11 –10.701 4.688 –0.702 0.825 0.472 13 –10.718 4.688 –0.704 0.862 0.330 –0.613 
下载: 导出CSV
表 2 Co原子嵌入不同深度的孕镶金刚石基底/金刚石涂层界面结合能
Table 2. Interface binding energy of impregnated diamond substrates with Co atoms doped in different depths /diamond coating.
基底中
Co位置Eslab1
/eVEslab2
/eVEinterface
/eVA/Å2 Wad/
(J·m–2)表面第1层 –10822.680 –9874.157 –20740.528 56.903 12.302 表面第2层 –10824.324 –20739.004 11.410 表面第3层 –10820.914 –20725.527 8.575 表面第4层 –10816.048 –20735.417 12.730 表面第5层 –10816.702 –20738.245 13.342 不含Co –9879.266 –19801.206 13.454
下载: 导出CSV
表 3 Co位于第3层的原子布居数
Table 3. Atomic population when Co is doped in the third layer.
Atom Mulliken atomic populations Total electron/e Transfer charge/e s p d Co 0.05 –0.77 7.79 7.06 1.94 C(1) 1.32 2.82 0.00 4.14 –0.14 C(2) 1.19 2.91 0.00 4.10 –0.10 C(3) 1.22 2.94 0.00 4.15 –0.15 C(4) 1.18 3.00 0.00 4.17 –0.17 C(5) 1.22 2.94 0.00 4.15 –0.15 C(6) 1.18 2.91 0.00 4.10 –0.10 C(7) 1.22 2.90 0.00 4.12 –0.12 C(8) 1.17 3.04 0.00 4.20 –0.20 C(9) 1.17 3.04 0.00 4.20 –0.20
下载: 导出CSV
表 4 Co位于第3层的化学键布居数
Table 4. Bond population when Co is doped in the third layer.
Bond Population Length/Å Co—C(1) –0.22 1.94970 Co—C(2) –0.22 2.02913 Co—C(3) –0.31 1.93623 Co—C(4) –0.19 1.98079 Co—C(5) –0.13 1.93626 Co—C(6) –0.22 2.02911 Co—C(7) 0.41 2.07074 Co—C(8) 0.34 1.88913 Co—C(9) 0.34 1.88915
下载: 导出CSV
-
[1] Yan B, He N, Chen N, Weigold M, Chen H W, Sun S C, Wu Y, Fu S Y, Li L, Abele E 2025 Int. J. Extrem. Manuf. 7 015106 doi: 10.1088/2631-7990/ad8d92 [2] Du Y F, Xie F M, Wang J, Xu B, Chen H Y, Yan B N, Wu Y J, Huang W F, Li H 2023 Materials 16 3640 doi: 10.3390/ma16103640 [3] Wheeler D W, Wood R J K 2024 Wear 556–557 205488 doi: 10.1016/j.wear.2024.205488 [4] 简小刚, 张允华 2015 物理学报 64 046701 doi: 10.7498/aps.64.046701 Jian X G, Zhang Y H 2015 Acta Phys. Sin. 64 046701 doi: 10.7498/aps.64.046701 [5] Wang X L, Wu X, Lu K, Ye J W 2025 Diam. Relat. Mater. 152 111886. doi: 10.1016/j.diamond.2024.111886 [6] Liu X W, Zhang H, Lin G L, Wang Z G, Zhang J L, Shi H Y 2023 Vacuum 217 112562 doi: 10.1016/j.vacuum.2023.112562 [7] Tian Q Q, Huang N, Yang B, Zhuang H, Wang C, Zhai Z F, Li G H, Jia X Y, Liu L S, Jiang X 2017 J. Mater. Sci. Technol. 33 1097 doi: 10.1016/j.jmst.2017.06.005 [8] Li X J, He L L, Li Y S, Yang Q 2019 Surf. Coat. Technol. 360 20 doi: 10.1016/j.surfcoat.2018.12.120 [9] Saiki Y, Bando T, Harigai T, Takikawa Hirofumi, Hattori T, Sugita H, Kawahara, N, Tanaka K 2023 Diam. Relat. Mater. 132 109643 doi: 10.1016/j.diamond.2022.109643 [10] Qiao Y, Nie S Y, Li W H, Liu E Z, Wang X C 2023 Appl. Surf. Sci. 633 157589 doi: 10.1016/j.apsusc.2023.157589 [11] Sedov V, Martyanov A, Ashkinazi E, Tiazhelov I, Savin S, Sovyk D, Mandal S, Fedorov S, Grigoriev S, Ralchenko V 2023 Surf. Interfaces 38 102861 doi: 10.1016/j.surfin.2023.102861 [12] 简小刚, 陈军 2015 物理学报 64 216701 doi: 10.7498/aps.64.216701 Jian X G, Chen J 2015 Acta Phys. Sin. 64 216701 doi: 10.7498/aps.64.216701 [13] Sarangi S K, Chattopadhyay A, Chattopadhyay A K 2008 Appl. Surf. Sci. 254 3721 doi: 10.1016/j.apsusc.2007.10.104 [14] Hu J B, Jian X G 2022 Mod. Phys. Lett. B 36 2250086 doi: 10.1142/S0217984922500865 [15] 范舒瑜, 匡同春, 林松盛, 代明江 2023 材料导报 37 28 doi: 10.11896/cldb.21110003 Fan S Y, Kuang T C, Lin S S, Dai M J 2023 Mater. Rep. 37 28 doi: 10.11896/cldb.21110003 [16] Donnet J B, Paulmier D, Oulanti H 2004 Carbon 42 2215 doi: 10.1016/j.carbon.2004.04.034 [17] Lloret F, Soto B, Rouzbahani R, Gutiérrez M, Haenen K, Araujo D 2023 Diam. Relat. Mater. 133 109746 doi: 10.1016/j.diamond.2023.109746 [18] Zhu P, Zhang Q, Xia Y X, Ma Y F, Gou H S, Liang X, Wu G H 2024 Mater. Today Phys. 48 101563 doi: 10.1016/j.mtphys.2024.101563 [19] Hu J B, Jian X G, Yang T, Peng X Y 2022 Diam. Relat. Mater. 123 108864 doi: 10.1016/j.diamond.2022.108864 [20] Bi K, Liu J, Dai Q X 2012 Appl. Surf. Sci. 258 4581 doi: 10.1016/j.apsusc.2012.01.033 [21] Pang X Z, Yang X Y, Yang J B, Zhao Y J, Pang M J 2021 Diam. Relat. Mater. 113 108297 doi: 10.1016/j.diamond.2021.108297 [22] Ernzerhof M, Scuseria G E 1999 J. Chem. Phys. 110 5029 doi: 10.1063/1.478401 [23] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865 [24] Chadi D J 1977 Phys. Rev. B 16 1746 doi: 10.1103/PhysRevB.16.1746 [25] Jin S S, You Z Y, Han P D, Jiang A X, Sun C L, Wang L B, Zhang T, Liu S L 2024 Comput. Mater. Sci. 244 113235 doi: 10.1016/j.commatsci.2024.113235 -
计量
- 文章访问数: 28
- HTML全文浏览数: 28
- PDF下载数: 0
- 施引文献: 0