首页
登录
注册
-
板状结构广泛应用于航空航天、船体制造及建筑等大型结构, 当结构由于长期使用出现腐蚀、泄露或者发生外物撞击等损伤时, 结构稳定性受到影响, 如果不及时定位出损伤位置并进行修复, 可能会引发经济损失甚至人身安全事故[1]. 无损检测是一种可以在不破坏结构的前提下[2,3], 利用结构因受损产生的声、热、光、电、磁等物理现象进行检测, 从而知道损伤的位置以及受损情况的技术[4–6]. 其中基于兰姆波的检测技术具有巨大的应用潜 力[7–9], 兰姆波具有传播距离远, 对损伤敏感等特点, 适用于大型结构的损伤定位[10–12]. 利用兰姆波进行检测时, 通常在板状材料表面布置传感器主动激发激励信号, 同时在其他位置布置传感器接收兰姆波信号, 并将采集到的信号进行数据处理、分析, 从而可以检测板中损伤[13,14].
随着基于兰姆波的检测技术的快速发展[15], 各种阵列信号处理方法也在快速发展. 波束成形由于其在信号定向传输和接收方面的卓越性能, 近年来被广泛应用于无损检测领域中[16]. 其通过对阵列接收到的信号进行相移后叠加等操作, 可以使叠加信号在特定方向上形成较强的波束, 集中接收来自目标方向的信号, 减少其他方向信号的干扰, 从而定位出损伤位置. 对于此技术, 传感器排列方式多样, 例如线性阵列、圆形阵列、星形阵列等[17–19], 但线性阵列由于使用简便, 而被大量应用[20]. He等[21]使用等间距线性阵列(ULA), 利用近场波束成形技术预测声发射源的位置. Li等[22]利用ULA实现了CO2气体连续泄漏源的定位. 为了避免振动噪声影响, Zhang等[23]提出了AF-MUSIC方法, 此方法可以在振动条件下, 对复合材料板的冲击源进行预测. Jung等[24]提出了一种不等间距的线性阵列, 避免了空间混叠, 提高了定位的鲁棒性. 波束成形在垂直方向有着较高的分辨率, 因此可以准确预测位于阵列垂直方向上的声源, 但在水平方向存在着不可避免的定位盲区. 为了消除定位盲区, 常采用二维结构来克服该缺点. 例如Wang等[25]提出了一种十字形阵列, 此方法可以全方位检测损伤. Zhong和Xiang [26]在线性阵列的上方和下方各增加一个传感器来避免水平方向盲区. Yu和Giurgiutiu [27]提出了一种矩形阵列, 可以进行全方位的检测. 以上方法虽可以减少定位盲区, 但需使用大量传感器, 使成本明显增加.
Kundu等[28,29]提出的L形传感器簇(LSSC)定位方法是一种基于传感器间接收信号的到达时差(TDOA)来预测到达方向(DOA)的有效方法. 这种方法不需要材料特性的先验知识以及复杂的数据处理方法, 在无损检测领域中有着巨大的发展潜力[30]. Yin等[31]对LSSC进行改进, 提出了Z形传感器, 提高了定位的精度; 并提出了十字形传感器簇[32], 并将其应用于微裂纹的定位, 该方法高效准确; Sen等[33]提出了由4个传感器组成的方形传感器簇, 每组方形传感器簇可以得到4个DOA, 进一步地减小误差; Zhou等[34]通过在两组LSSC的基础上增加一个发射激励信号的传感器, 实现了对复合材料板损伤的主动检测. LSSC定位方法是一种快速且简便的定位方法, 但是由于TDOA与到DOA之间的非线性关系, 使LSSC无法准确定位出阵列垂直方向上的损伤.
定位盲区一直是无损检测领域中一个值得重点关注的问题. 为了消除定位盲区, Gao等[35–37]提出了T形传感器簇定位方法与不等间距T形传感器簇定位方法, 此方法将波束成形与LSSC方法相结合, 有效减小了定位盲区, 提高了定位的精度以及稳定性.
为了进一步减小损伤定位盲区, 在以上工作的基础上, 本文提出了一种扇形传感器簇损伤定位方法, 通过两组扇形传感器簇以及一个用于发射激励信号的传感器, 将波束成形与LSSC定位方法联合起来, 实现了无盲区损伤定位, 且无需进行复杂的迭代求解. 进行了仿真与实验验证, 并将利用此方法的损伤定位结果与利用T形传感器簇的损伤定位结果进行对比. 仿真与实验结果显示, 扇形传感器簇损伤定位方法具有更高的稳定性, 可以实现无盲区的损伤定位. 此方法可以为大型结构的损伤检测提供新的思路.
-
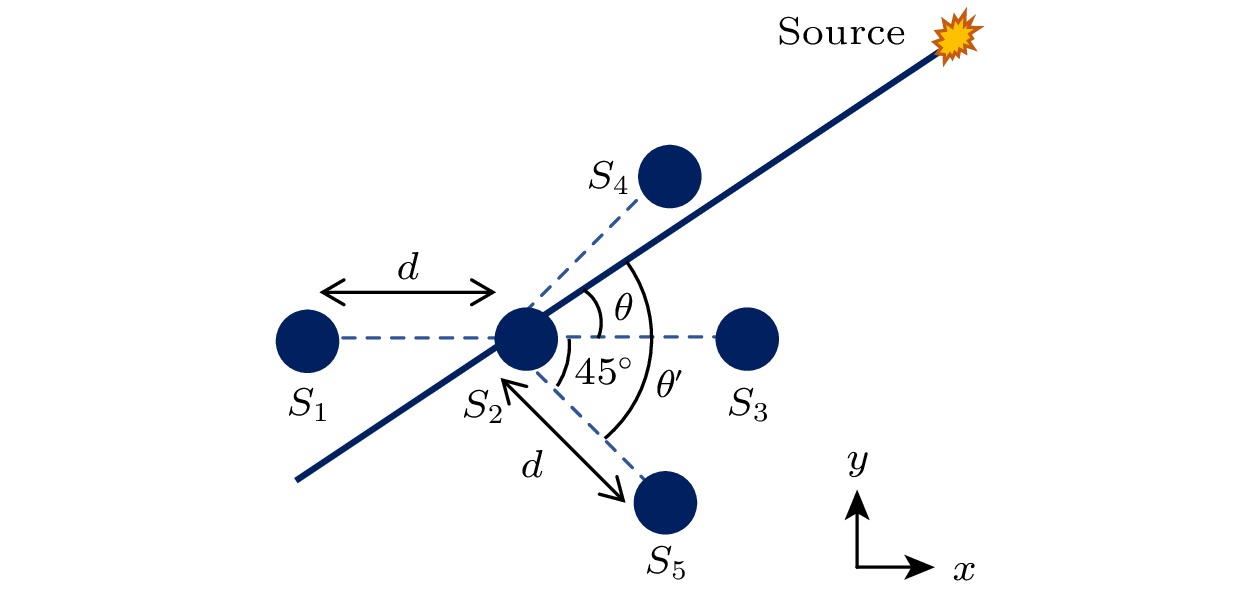
本文所提出的扇形传感器簇结构由5个传感器组成, 其中3个传感器排列呈等间距的线性阵列, 其余两个传感器以线性阵列中心处的传感器为顶点, 组成一组对称的L形结构, 该L形传感器簇呈等腰直角三角形结构, 直角边的边长与线性阵列的间距相同. Xue等[38]通过公式推导以及实验验证发现, 当声源与L形阵列的顶点之间的连线与L形阵列的直角边呈45°夹角时, LSSC定位方法可以准确定位出此声源. 因此对于扇形传感器簇, 将等腰三角形的直角边与线性阵列之间的夹角设置为45°, 扇形传感器簇的排列方式如图1所示.
当已经形成损伤后, 损伤位置不再产生应力波, 此时可以通过额外放置激励源主动激发检测信号, 利用激励信号与损伤相互作用产生的散射波进行后续处理, 因此将此散射波看作一个二次声源. 由于仅考虑远场情况, 即:
其中, r为损伤与阵列参考点间距, l为阵列长度, λ为信号波长. 当使用扇形传感器簇进行损伤定位时, 首先利用波束成形对线性阵列(S1S2S3)接收到的信号进行初次预测, 将线性阵列接收到的信号沿各个方向进行延迟与求和处理后, 可以得到与角度有关的能量函数E(θ):
其中,
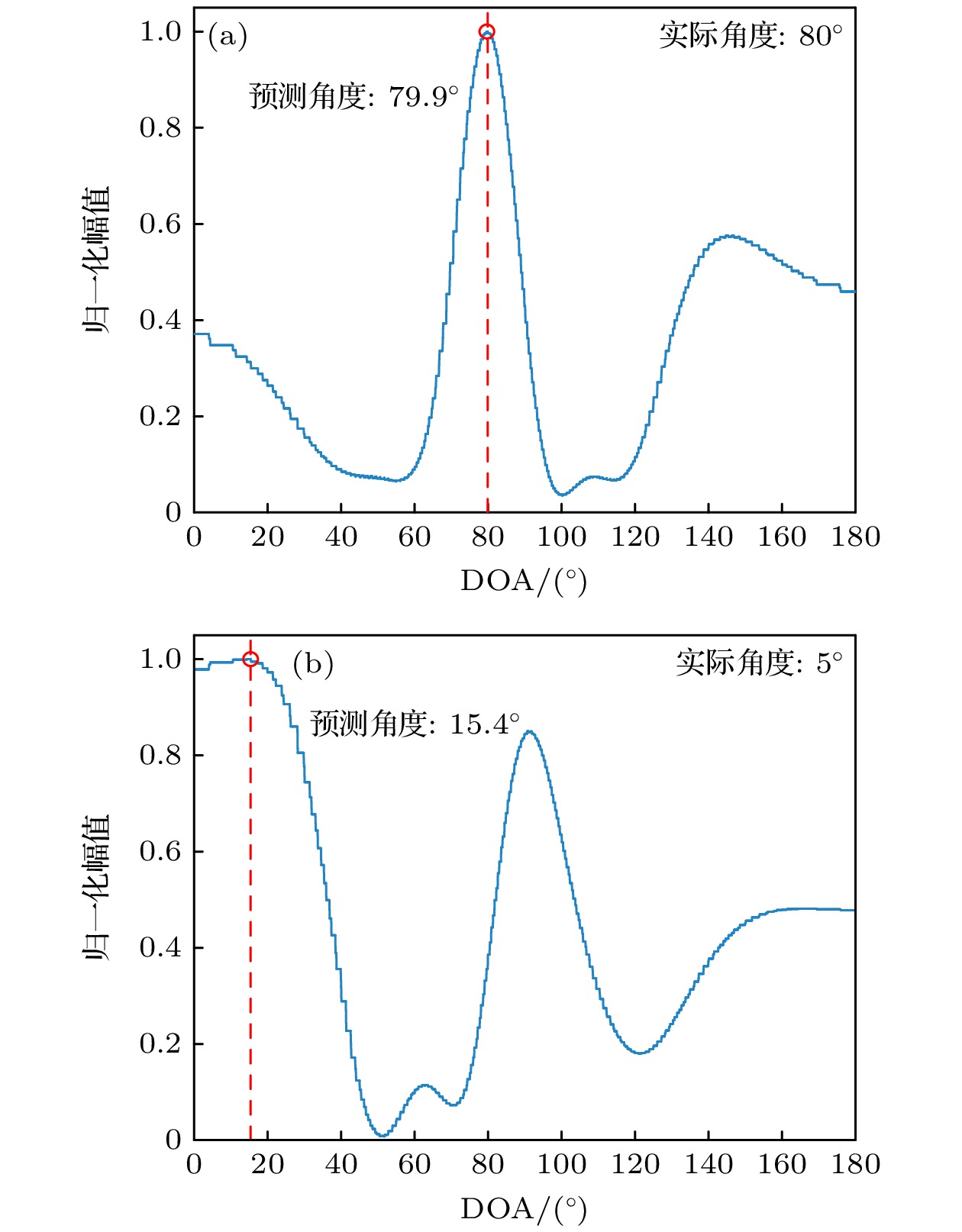
${S'_i}(t)$ 为延迟处理后的信号,${\beta _i}$ 为与信号无关的权重系数. 对于损伤所在的方向, 阵列信号经过延迟与求和处理后, 由于相位对齐, 此时输出能量为最大值. 以能量为纵坐标, 角度为横坐标绘制曲线图, 并将纵坐标按能量最大值进行归一化处理, 能量最大值所对应的角度即为初步预测角度, 如图2所示. 如果能量最大值所对应的角度不在0°或180°附近, 且有明显主瓣, 如图2(a)所示, 表明此损伤位置不在线性阵列的损伤定位盲区中, 此角度即为最终预测角度; 反之, 如果能量最大值所对应的角度在0°或180°的附近, 且有平坦区不易区分具体角度, 如图2(b)所示, 表明此损伤位于线性阵列的定位盲区中, 需要使用LSSC定位方法对(S4S2S5)接收到的信号进行二次预测.二次预测需要利用传感器间接收到的TDOA, 可由互相关求得. 利用以下公式可以得到损伤位置-S2直线与S2-S5直线的夹角
$\theta '$ :其中,
$\Delta {t_{ij}}$ 表示不同传感器之间的TDOA,$\left( {{x_0}, {y_0}} \right)$ 表示损伤坐标,$\left( {{x_2}, {y_2}} \right)$ 表示传感器S2的坐标,$c\left( {\theta '} \right)$ 表示$\theta '$ 方向上的波速.二次预测后, 最终损伤预测角度
$\theta $ 可表示为每组扇形传感器簇可以得到一个预测角. 因此, 当使用此方法对板中损伤进行定位时, 可在板上放置两组扇形传感器簇, 将得到的两个预测角与传感器位置进行联立, 以此预测损伤位置.
-
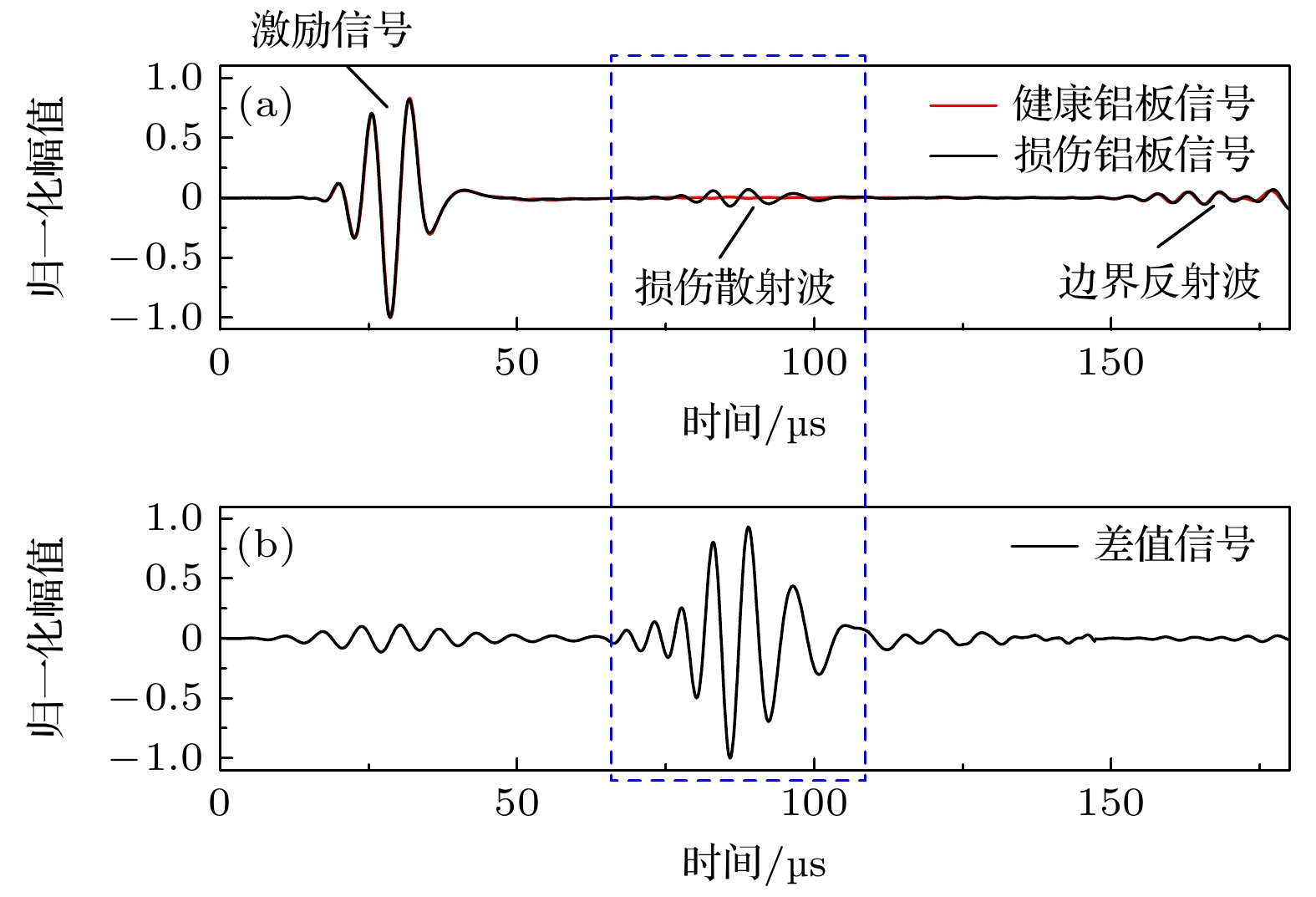
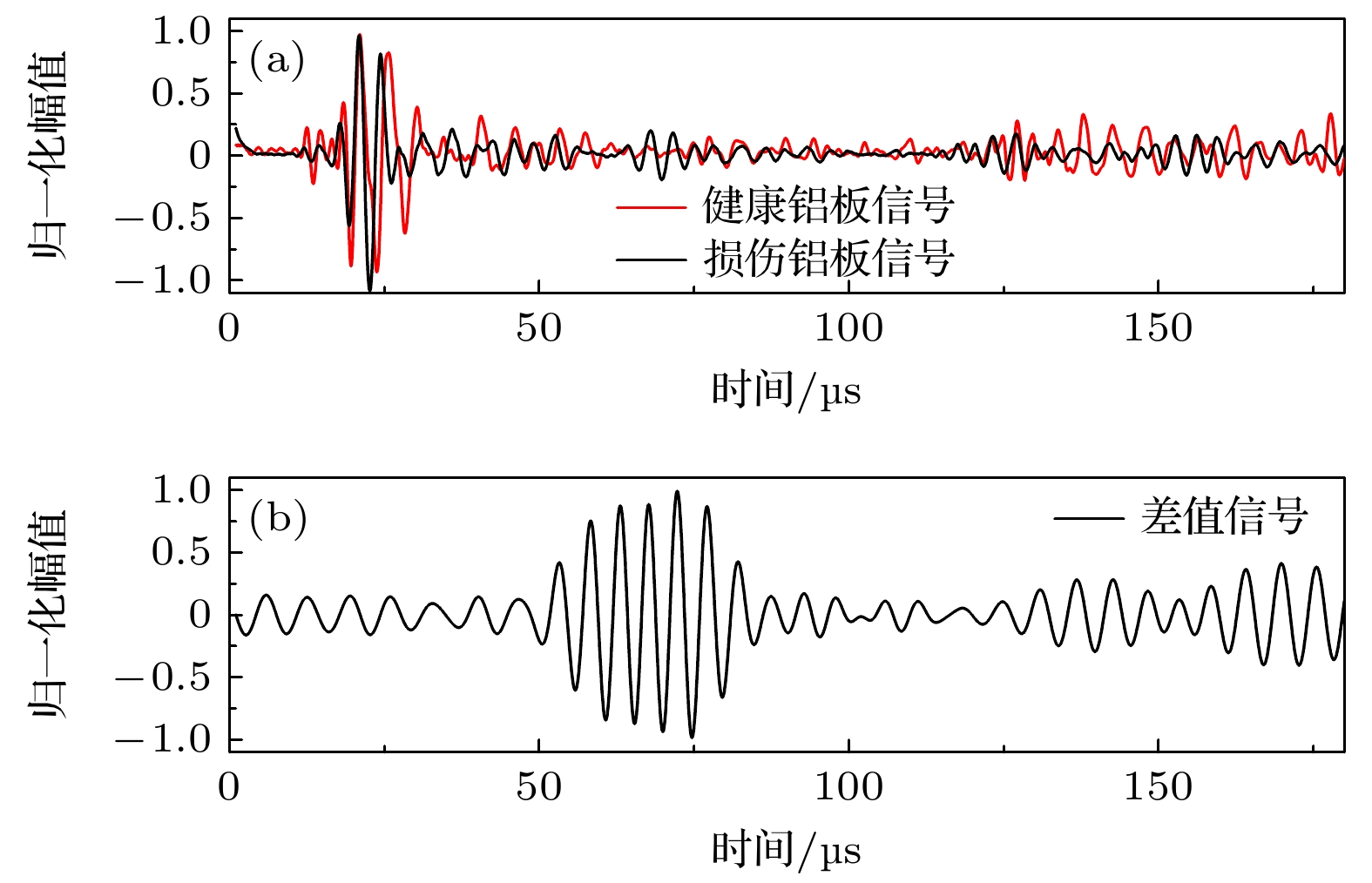
在运用本方法检测板结构损伤时, 需要用到 不同传感器所接收到的损伤散射信号的波形及 到达时间差. 由于损伤尺寸往往较小, 缺陷与激 励信号相互作用产生的损伤散射波强度会远低于原始激励信号与边界反射信号. 因此借助受损结构中接收到的信号和无损结构中接收到的基线信 号进行相减得到的差值信号, 能够让损伤散射信号在其中更清晰地呈现出来, 从而更易于后续的数 据处理.
-
使用扇形传感器簇定位方法检测损伤时, 预 测的损伤位置与实际的损伤位置之间的误差用 二者间的欧式距离来表示, 具体误差计算公式可 表示为
其中,
$\left( {{x_{\text{p}}}, {y_{\text{p}}}} \right)$ 为预测损伤坐标,$\left( {{x_{\text{a}}}, {y_{\text{a}}}} \right)$ 为实际损伤坐标. -
鉴于仿真软件的便利性, 在实验开始前, 首先使用有限元仿真软件COMSOL Multiphysics进行数值模拟以验证扇形传感器簇定位方法的可行性.
-
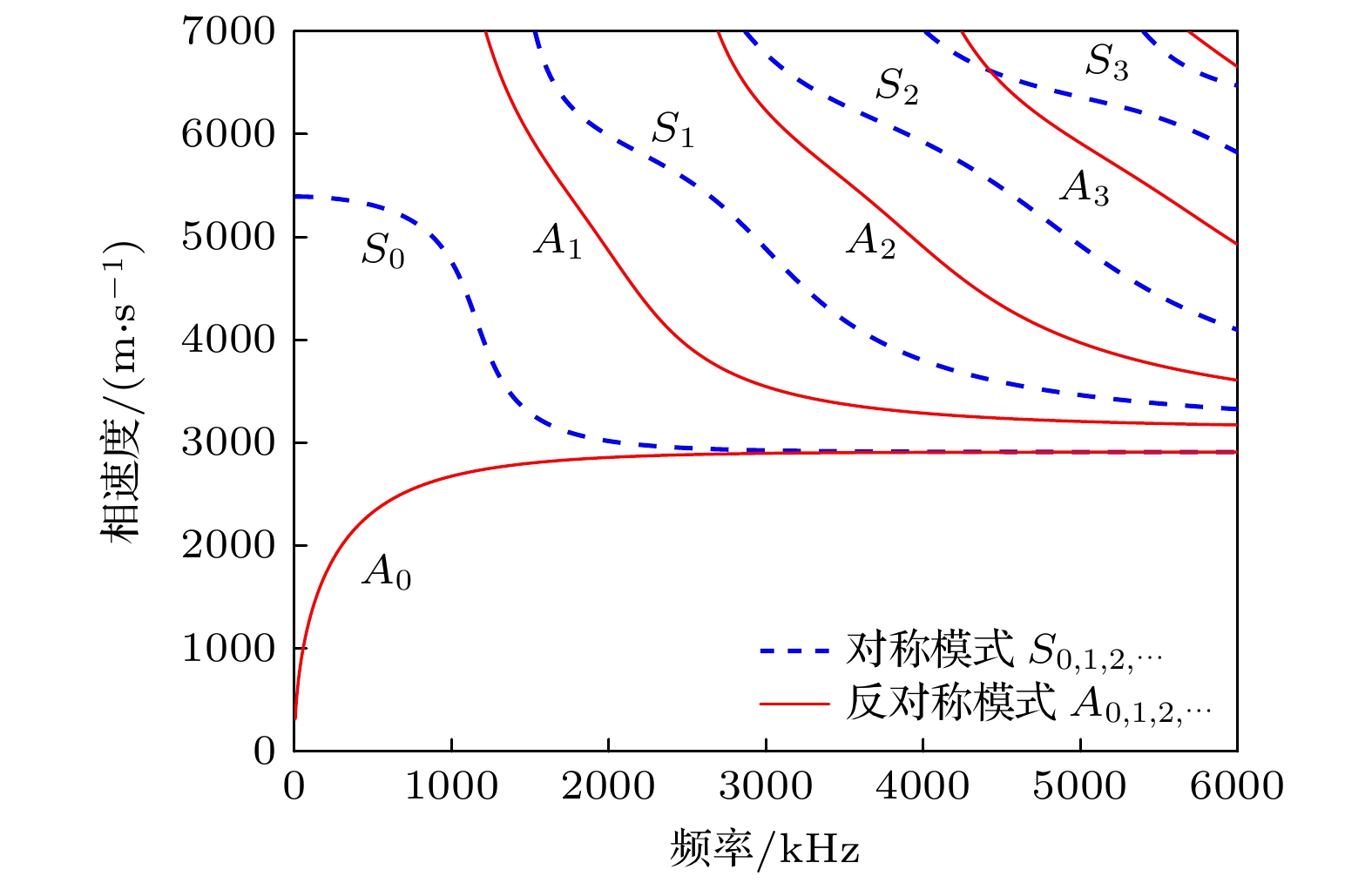
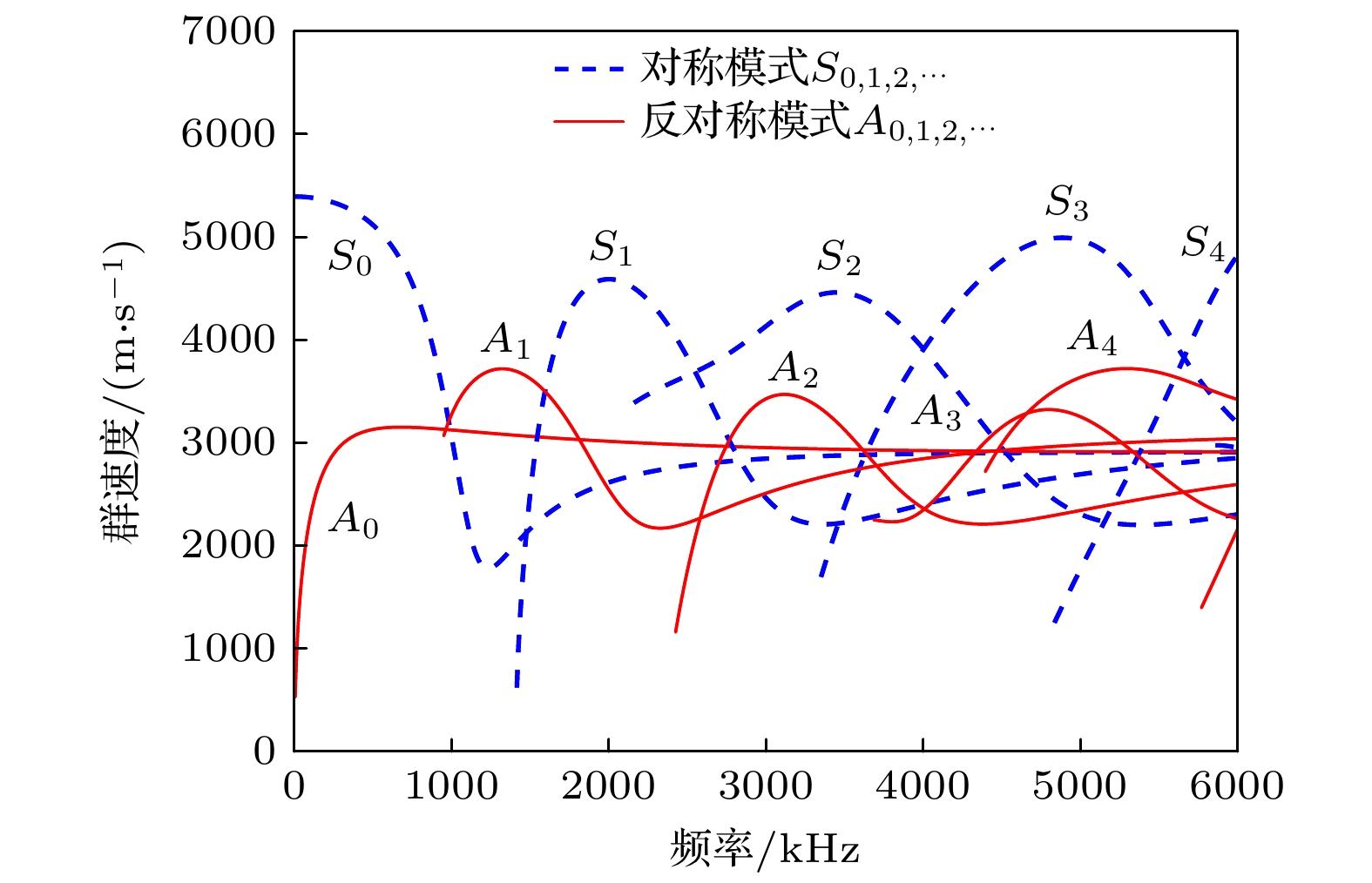
利用COMSOL Multiphysics构建三维模型, 一块尺寸为500 mm (长)×500 mm (宽)×2 mm (厚)的铝板, 材料参数见表1. 根据材料属性, 计算此铝板中传播的兰姆波相速度和群速度频散曲线, 如图3和图4所示.
由频散曲线可以看出, 当激励信号中心频率较低时, 板中传播的兰姆波仅有
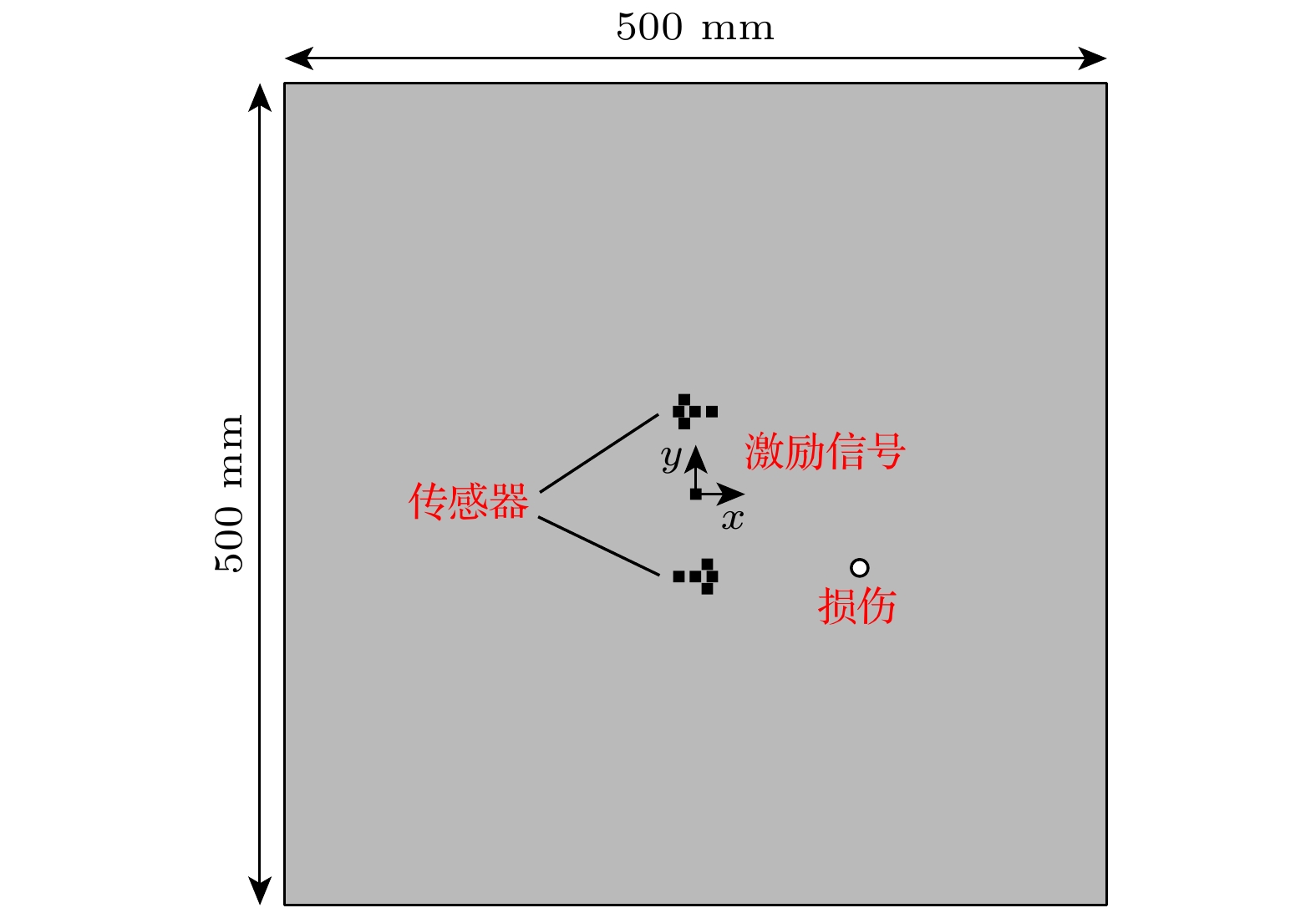
$ {{{A}}}_{0} $ 与$ {{{S}}}_{0} $ 两个模态; 频率较高时, 板中传播的兰姆波存在多个高阶模态. 由于A0模态的波长比S0小, 使得A0模态波对损伤更加敏感, 并且在传播过程中遇到损伤时, A0模态波仅产生散射的$ {{{A}}}_{0} $ 模态. 因此, 为了避免其他模态波对检测结果产生影响, 使用$ {{{A}}}_{0} $ 模态开展检测工作. 在激发频率的选取上, 为了使$ {{{A}}}_{0} $ 模态波响应大, 避免其他模态波的影响, 参考工程上对薄板进行检测时, 一般采用中心频率为150 kHz的谐振式传感器, 将激励频率最终设置为150 kHz. 考虑到检测效果与数据处理的便捷性, 应选择脉冲式窄带信号来模拟声发射源信号, 激励信号最终设置为 Hanning窗调制的3周期正弦信号, 表达式如下:在板中心处放置一点载荷用作激发激励信号, 距离此点载荷上、下方各50 mm处, 分别放置一组扇形传感器簇, 传感器的间距设置为10 mm, 传感器处的应力信息被记录为接收信号. 激励声源的坐标为(0.00, 0.00) mm, 传感器的位置坐标见表2. 模型的几何形状以及传感器的位置如图5所示. 使用自由四面体划分网格, 为满足收敛克朗条件 (Courant-Friedrichs-Lewy condition), 网格尺寸设置为2 mm, 求解总时间为180 μs, 固定步长为0.1 μs.
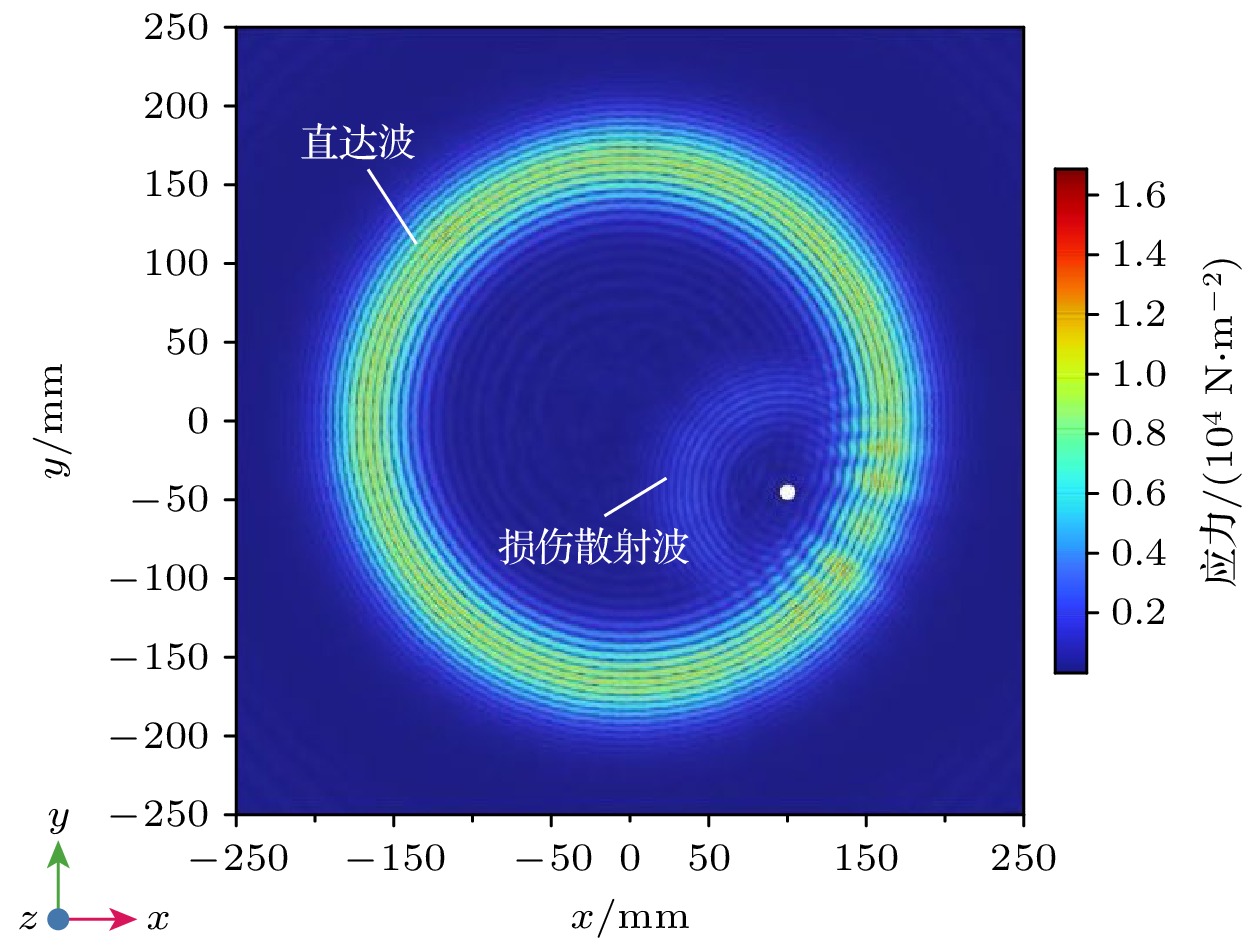
为了验证此方法的稳定性, 共选取了8个不同位置的损伤, 损伤的中心位置如表3所列, 同时为使损伤散射信号易于观察, 使用直径为10 mm的通孔模拟损伤. 当损伤位于(100, –45)时, 第70 μs的波场快照如图6所示, 可以看出, 弹性波以圆形波前传播, 损伤附近可见激励信号与损伤相互作用产生的损伤散射波.
此时, 下方扇形传感器簇的S1所接收到的有损信号与无损时的基线信号对比如图7所示. 图7(a)中, 黑线表示有损伤时接收到的信号, 红线为基线信号. 有损伤时, 接收到的信号可见3个明显波包, 第1个波包为S1接收到的激励信号, 第2个波包为激励信号与损伤相互作用产生的散射信号, 第3个波包为边界反射波. 借助受损结构中接收到的信号和无损结构中接收到的基线信号进行时域相干相减处理得到差值信号, 即可实现损伤散射波的有效分离, 如图7(b)所示. 同理, 其他传感器的损伤散射信号也利用此方法得到, 后续对损伤散射信号进行处理.
-
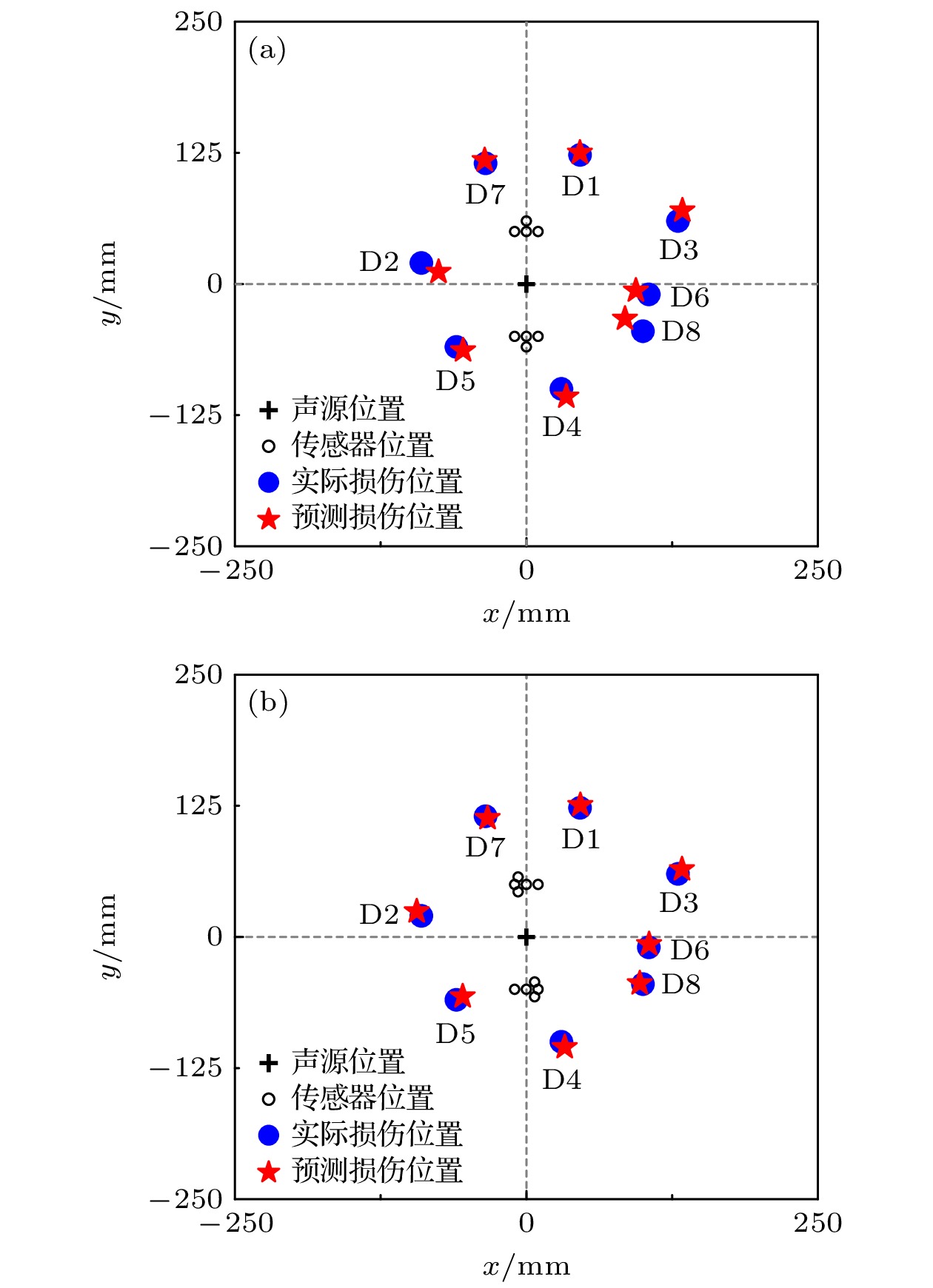
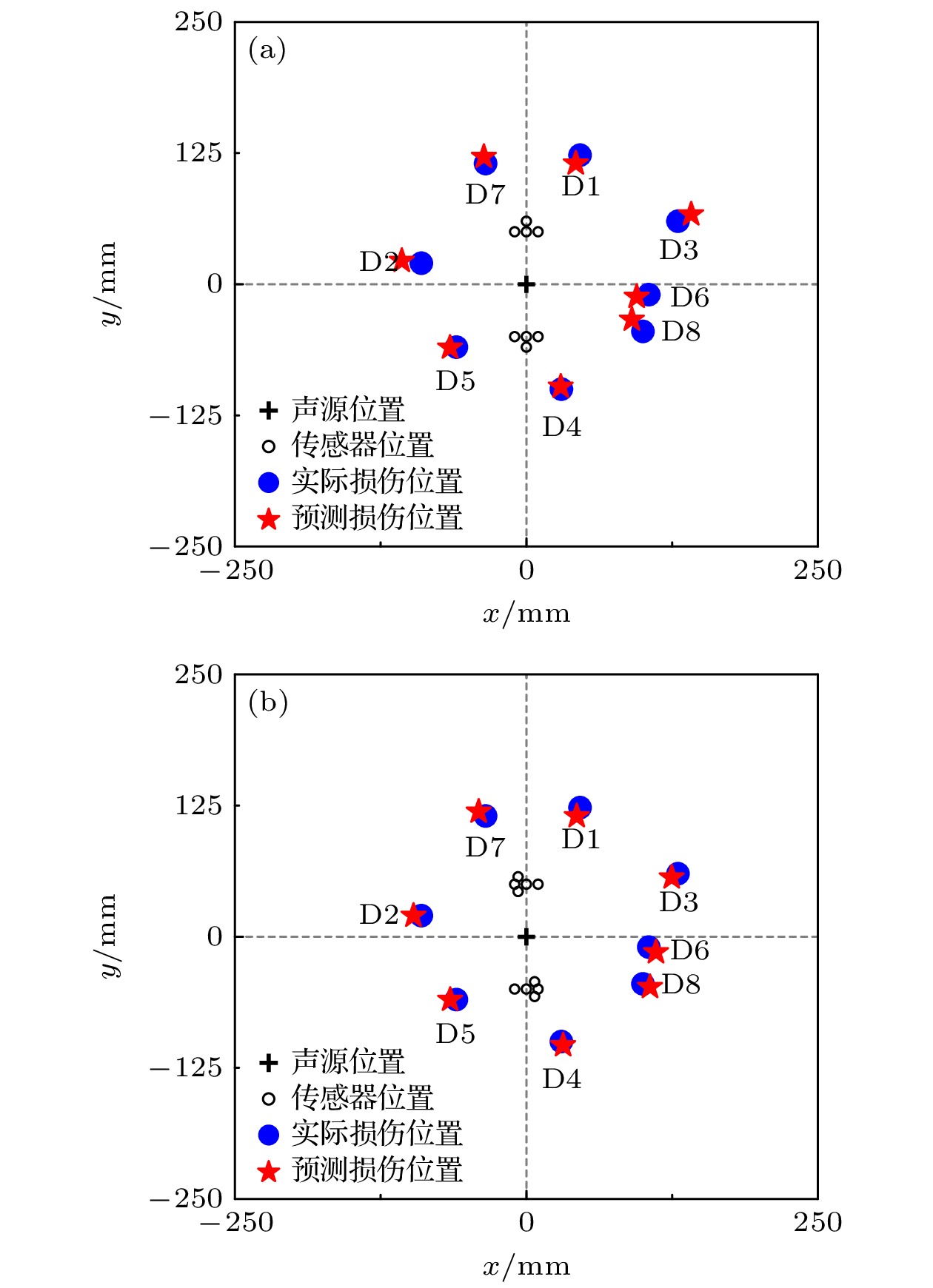
对接收到的损伤散射信号利用扇形传感器簇损伤定位方法进行处理, 可以得到预测的损伤位置, 预测结果与误差展示在表3和图8(b)中. 为了进行对比, 将T形传感器簇摆放在相同位置, 并使用T形传感器簇定位方法同样对这8个损伤位置开展仿真研究, 预测结果与误差展示在表3和图8(a)中.
仿真结果表明, 扇形传感器簇损伤定位方法可以准确检测出位于传感器阵列水平方向附近的损伤. 而使用T形传感器簇检测损伤时, 存在一定的损伤定位盲区. 例如, 对于在线性阵列水平方向较近的损伤D2, D3, D5, D8, 使用T形传感器簇进行检测时, 误差较大; 而使用扇形传感器簇的检测结果误差较小. 对于其他方向上的损伤, 使用扇形传感器簇也可以准确检测出来.
扇形传感器簇定位方法有效地改善了检测盲区问题, 并且在以上损伤例子中, 最大预测误差不超过6.37 mm, 仿真结果证明了此方法的可行性.
-
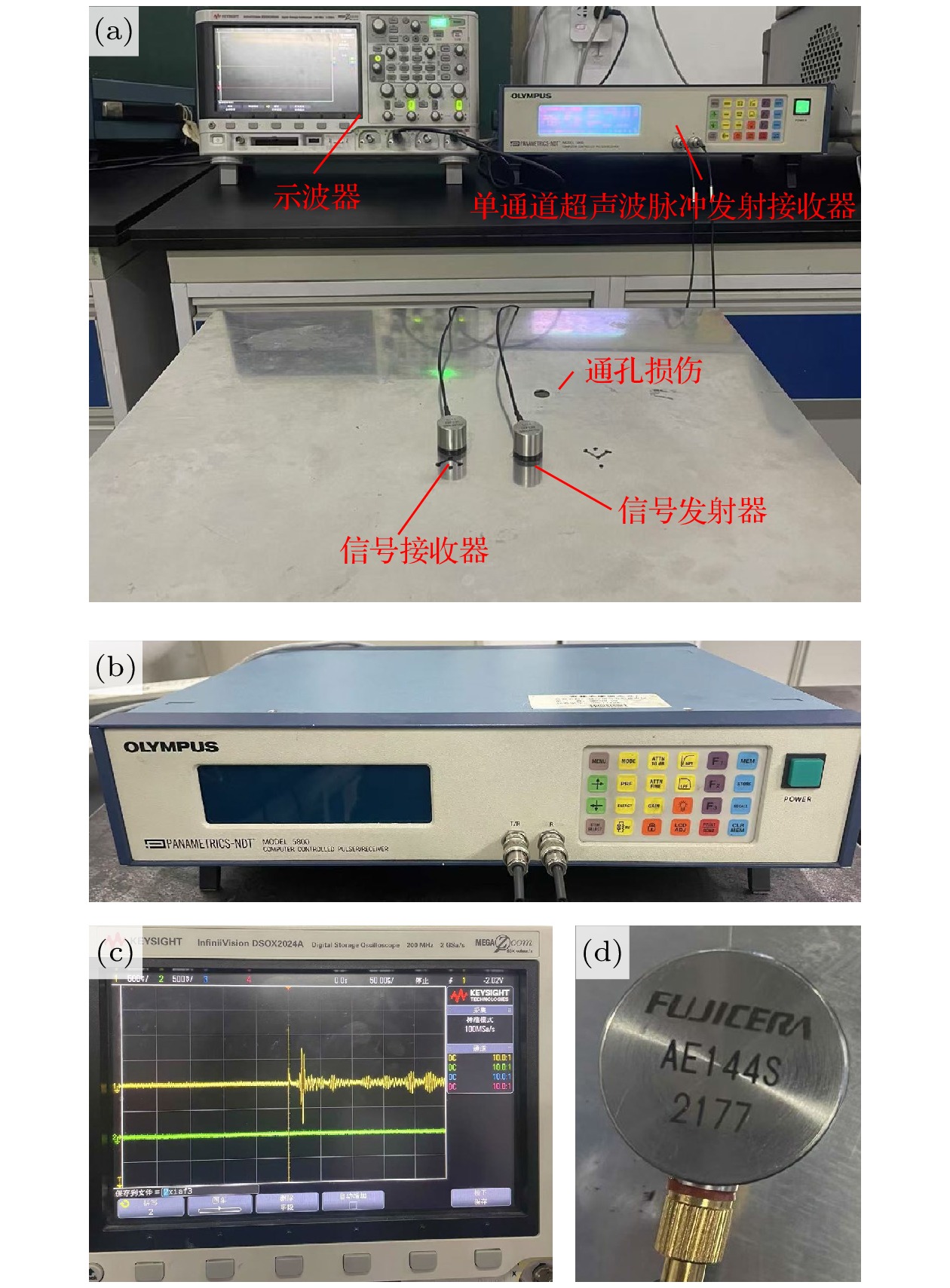
为了进一步验证扇形传感器簇损伤定位方法的有效性, 在实验室条件下, 利用铝板上开展了物理实验研究. 实验中使用两块材质相同且尺寸均为500 mm(长)×500 mm(宽)×2 mm(厚)的铝板, 其中一块板上人为加工了一直径约为10 mm的通孔用于模拟损伤, 另一块无损伤铝板用于接收健康基线信号. 采用OLYMPUS 5800脉冲信号发射器、示波器和谐振频率为150 kHz的AE144S传感器组成实验装置, 如图9所示. 采样频率为10 MHz.
传感器排列方式与仿真中相同, 实验中通过转动有损铝板, 更改损伤与激励源的相对位置, 来模拟不同位置的损伤. 共选取了8个不同位置的损伤, 损伤中心坐标与仿真中相同, 坐标如表4所列. 当损伤位于(105, –10)时, 传感器S1接收到的有损信号与基线信号如图10(a)所示, 借助有损伤时传感器接收到的信号与基线信号作差值可以得到损伤散射信号, 如图10(b)所示. 同理, 其他传感器接收到的损伤信号也利用此方法获得, 对损伤散射信号进行数据处理.
使用扇形传感器簇的检测结果以及误差展示在表4与图11(b)中, 同样为了进行对比, 实验中也使用了T形传感器簇对相同位置的损伤进行预测, 预测结果及误差展示在表4与图11(a)中.
与前述仿真结论相同, 实验结果同样表明, 扇形传感器簇可以准确地检测出板上的损伤, 并且与T形传感器簇相比, 在检测靠近传感器阵列水平方向的损伤时, 扇形传感器簇有着更高的预测精度. 例如, 对于在线性阵列水平方向较近的损伤D2, D3, D5, D8, 使用T形传感器簇进行检测时, 误差较大; 而使用扇形传感器簇的检测结果误差较小. 对于其他方向上的损伤, 使用扇形传感器簇也可以准确检测出来.
扇形传感器簇定位方法有效地改善了盲区问题, 并且在以上损伤例子中, 最大预测误差不超过8.64 mm, 实验结果证明了此方法的可行性.
-
本文工作针对线性阵列及LSSC定位方法中存在的损伤定位盲区问题, 兼顾波束成形与LSSC定位方法的优势, 创新性地设计了一种扇形传感器簇结构, 有效解决了损伤定位盲区问题. 通过将5个传感器排列成扇形结构, 利用这种几何结构, 可以有效减少损伤定位盲区. 使用两组扇形传感器簇以及一个激发信号的声发射源组成检测系统, 可以准确检测出板中损伤位置. 为了验证此方法的有效性, 采用铝板进行仿真与实验验证, 并将预测结果与使用T形传感器簇的预测结果进行对比. 仿真与实验结果均证明扇形传感器簇损伤定位方法可以有效减少水平方向上的损伤定位盲区, 提高损伤定位精度.
本文所提出的扇形传感器簇定位方法具有无损伤定位盲区的优点. 扇形传感器簇有效减少了损伤定位盲区. 与T形传感器簇相比, 扇形传感器簇可以准确定位出在阵列水平方向附近的损伤, 具有更高的损伤定位精度. 并且此方法操作简便, 由于没有损伤定位盲区, 扇形传感器簇可以随意摆放. 进行数据处理时, 无需求解复杂的非线性方程. 基于扇形传感器簇的板结构损伤定位方法为损伤定位提供了新的理论方法, 对于板材的兰姆波的损伤检测方法研究具有重要的意义.
基于扇形传感器簇的板结构损伤定位方法
A damage detection method of plate structure using fan-shaped sensor clusters
-
摘要: 利用波束成形或L形传感器簇定位方法对板类结构上的损伤进行定位时存在盲区. 本文结合波束成形与L形传感器簇定位方法, 通过将5个传感器排列成扇形的方式, 提出了一种扇形传感器簇损伤定位方法, 可以有效减少损伤定位盲区. 使用两组扇形传感器簇以及一个用于发射激励信号的传感器即可准确检测出板中损伤的位置. 通过仿真和实验验证了扇形传感器簇损伤定位方法的可行性, 并与采用T形传感器簇时的预测结果进行比较, 结果表明扇形传感器簇损伤定位方法可以更准确地识别不同位置的损伤. 仿真和实验结果表明, 扇形传感器簇损伤定位方法可以减少损伤定位盲区, 提高损伤定位的精度.Abstract:
Plate structures are widely used in large-scale engineering fields such as aerospace, hull manufacturing, and construction. However, the plate structure is easily damaged during long-term service or when it is impacted by foreign objects. Such a damage may lead to serious safety accidents. Beamforming and L-shaped sensor cluster (LSSC) localization method can be used to locate the damage on the plate. However, when using beamforming method or LSSC localization method to locate the damages on plate-like structures, there exists blind area. In this paper, by combining the beamforming method and LSSC localization method, a fan-shaped sensor cluster localization method is proposed through arranging five sensors in a fan shape, which can effectively reduce the blind areas. The positions of damages in the plate can be accurately detected by using two groups of fan-shaped sensor clusters and one sensor for transmitting the excitation signal. The feasibility of the fan-shaped sensor cluster localization method is verified through numerical simulations and experiments, and the results are compared with those obtained by using the T-shaped sensor cluster. The results show that the fan-shaped sensor cluster localization method can more accurately identify the damages at different positions. Both simulation and experimental results indicate that the fan-shaped sensor cluster localization method can reduce the blind area and improve the accuracy of damage location. -
Key words:
- damage localization /
- fan-shaped sensor clusters /
- T-shaped sensor cluster /
- beamforming .
-
-
图 2 初步预测结果图 (a)实际角度为80°的预测结果; (b)实际角度为5°时的预测结果
Figure 2. Schematic diagram of initial forecast results: (a) Prediction of an actual DOA of 80°; (b) the prediction of an actual DOA of 5°.
图 3 2 mm厚铝板相速度频散曲线
Figure 3. Phase velocity dispersion curves of an aluminum plate with a thickness of 2 mm.
图 4 2 mm厚铝板的群速度频散曲线
Figure 4. Group velocity dispersion curves of an aluminum plate with a thickness of 2 mm.
图 6 t = 70 μs的波场快照(损伤位于(100, –45))
Figure 6. Wavefield snapshot at t = 70 μs (the damage is located at (100, –45)).
图 7 (a)损伤位于(100, –45)时, 传感器S1接收到的损伤信号与无损时的基线信号对比; (b)利用传感器S1接收到的有损信号减去基线信号得到的差值信号
Figure 7. (a) Damaged signal and the healthy signal received by the S1 when the damage is located at (100, –45); (b) the differential signal obtained by subtracting the healthy signal from the damaged signal received by the sensor S1.
图 8 仿真定位结果示意图 (a) T形传感器簇定位结果; (b)扇形传感器簇定位结果
Figure 8. Schematic diagram of simulation localization results: (a) Localization results of T-shaped sensor cluster; (b) localization results of fan-shaped sensor cluster.
图 9 (a)实验装置示意图; (b) OLYMPUS 5800脉冲信号发射器; (c)实验中使用示波器接收到的信号; (d) AE144S传感器
Figure 9. (a) Photo of the experimental setup; (b) OLYMPUS 5800 pulse signal transmitter; (c) the signal received by the oscilloscope in the experiment; (d) AE144S sensor.
图 10 (a)损伤位于(105, –10)时, 下方扇形传感器簇中的S3接收到的损伤信号与无损时的基线信号对比; (b)经过滤波后, 利用传感器S3接收到的有损信号减去基线信号得到的差值信号
Figure 10. (a) Damaged aluminum signal and the healthy aluminum signal received by the S3 of the fan-shaped sensor cluster on the lower side when the damage is located at (105, –10); (b) the differential signal obtained by subtracting the healthy signal from the damaged signal received by the sensor S3 after filtering.
图 11 实验定位结果示意图 (a) T形传感器簇定位结果; (b)扇形传感器簇定位结果
Figure 11. Schematic diagram of experimental localization results: (a) Localization results of T-shaped sensor cluster; (b) localization results of fan-shaped sensor cluster.
表 1 铝板材料属性
Table 1. Material parameters of aluminum plate.
材料属性 数值 密度 $\rho $ /(kg·m–3)2700 泊松比 $\sigma $ 0.33 杨氏模量 E/GPa 70 
下载: 导出CSV
表 2 传感器的位置坐标
Table 2. Coordinates of sensors.
传感器标记 坐标/mm 传感器标记 坐标/mm S1 (–10.00, –50.00) S6 (–10.00, 50.00) S2 (0.00, –50.00) S7 (0.00, 50.00) S3 (10.00, –50.00) S8 (10.00, 50.00) S4 (7.07, –42.93) S9 (–7.07, 57.07) S5 (7.07, –57.07) S10 (–7.07, 42.93)
下载: 导出CSV
表 3 仿真定位结果与误差
Table 3. Simulation localization results and errors.
编号 实际损伤坐标/mm T形传感器簇 扇形传感器簇 预测损伤坐标/mm 误差/mm 预测损伤坐标/mm 误差/mm D1 (46.00, 123.00) (45.93, 125.16) 2.16 (46.29, 125.73) 2.75 D2 (–90.00, 20.00) (–75.34, 11.45) 16.97 (–94.02, 24.28) 5.87 D3 (130.00, 60.00) (133.83, 70.07) 10.77 (133.48, 64.39) 5.61 D4 (30.00, –100.00) (34.30, –107.32) 8.49 (32.96, –105.08) 5.88 D5 (–60.00, –60.00) (–54.31, –63.35) 9.27 (–54.58, –56.65) 6.37 D6 (105.00, –10.00) (93.94, –6.28) 11.67 (105.19, –6.87) 3.14 D7 (–35.00, 115.00) (–35.72, 118.03) 3.11 (–33.22, 113.27) 2.48 D8 (100.00, –45.00) (84.55, –33.09) 19.51 (97.29, –44.28) 2.80
下载: 导出CSV
表 4 实验定位结果与误差
Table 4. Experimental localization results and errors.
编号 实际损伤坐标/mm T形传感器簇 扇形传感器簇 预测损伤坐标/mm 误差/mm 预测损伤坐标/mm 误差/mm D1 (46.00, 123.00) (42.39, 115.11) 8.68 (43.22, 114.82) 8.64 D2 (–90.00, 20.00) (–106.88, 22.25) 17.03 (–96.76, 20.04) 6.76 D3 (130.00, 60.00) (141.36, 66.56) 13.12 (124.69, 56.48) 6.37 D4 (30.00, –100.00) (29.52, –97.61) 2.44 (31.51, –103.49) 3.80 D5 (–60.00, –60.00) (–65.45, –60.33) 5.46 (–65.40, –60.12) 5.40 D6 (105.00, –10.00) (94.63, –12.02) 10.56 (111.13, –14.78) 7.77 D7 (–35.00, 115.00) (–36.40, 121.49) 6.64 (–40.94, 119.23) 7.29 D8 (100.00, –45.00) (90.54, –33.69) 14.74 (106.07, –47.88) 6.72
下载: 导出CSV
-
[1] 胡海峰 2011 博士学位论文 (长沙: 国防科学技术大学) Hu H F 2011 Ph. D. Dissertation (Changsha: National University of Defense Technology [2] 冉启芳 1999 无损检测 21 75 Ran Q F 1999 Nondestr. Test 21 75 [3] 邬冠华, 熊鸿建 2016 仪器仪表学报 37 1683 doi: 10.3969/j.issn.0254-3087.2016.08.001 Wu G H, Xiong H J 2016 Chin. J. Sci. Instrum. 37 1683 doi: 10.3969/j.issn.0254-3087.2016.08.001 [4] 马国, 贾华东, 卢长煜, 陈理想, 张贵芝, 张立平, 杨超 2019 无损检测 41 62 doi: 10.11973/wsjc201904013 Ma G, Jia H D, Lu C Y, Chen L X, Zhang G Z, Zhang L P, Yang C 2019 Nondestr. Test 41 62 doi: 10.11973/wsjc201904013 [5] 赵金玲 2017 博士学位论文 (南京: 南京航空航天大学) Zhao J L 2017 Ph. D. Dissertation (Nanjing: Nanjing University of Aeronautics and Astronautics [6] 孙明健, 刘婷, 程星振, 陈德应, 闫锋刚, 冯乃章 2016 物理学报 65 167802 doi: 10.7498/aps.65.167802 Sun M J, Liu T, Cheng X Z, Chen D Y, Yan F G, Feng N Z 2016 Acta Phys. Sin. 65 167802 doi: 10.7498/aps.65.167802 [7] Humeida Y, Wilcox P D, Todd M D 2014 NDT E Int. 68 43 doi: 10.1016/j.ndteint.2014.07.007 [8] Luo K, Liu Y J, Liang W 2024 NDT & E Int. 143 103047 doi: 10.1016/j.ndteint.2024.103047 [9] Chen S J, Zhou S P, Li Y, Xiang Y X, Qi M X 2017 Chin. Phys. Lett. 34 044301 doi: 10.1088/0256-307X/34/4/044301 [10] 王强, 袁慎芳 2008 航空学报 29 1061 doi: 10.3321/j.issn:1000-6893.2008.04.048 Wang Q, Yuan S F 2008 Acta Aeronaut. Astronaut. Sin. 29 1061 doi: 10.3321/j.issn:1000-6893.2008.04.048 [11] 刘增华, 徐营赞, 何存富, 吴斌 2014 工程力学 31 232 doi: 10.6052/j.issn.1000-4750.2013.07.0645 Liu Z H, Xu Y Z, He C F, Wu B 2014 Eng. Mech. 31 232 doi: 10.6052/j.issn.1000-4750.2013.07.0645 [12] 张海燕, 孙修立, 曹亚萍, 陈先华, 于建波 2010 物理学报 59 7111 doi: 10.7498/aps.59.7111 Zhang H Y, Sun X L, Cao Y P, Chen X H, Yu J B 2010 Acta Phys. Sin. 59 7111 doi: 10.7498/aps.59.7111 [13] Zhang G D, Kundu T, Deymier P A, Runge K 2025 Ultrasonics 145 107492 doi: 10.1016/j.ultras.2024.107492 [14] Xu C B, Wang Q, Gao Q J, Deng M X 2025 Mech. Syst. Signal Proc. 223 11926 doi: /10.1016/j.ymssp.2024.111926 [15] 张海燕, 杨杰, 范国鹏, 朱文发, 柴晓冬 2017 物理学报 66 214301 doi: 10.7498/aps.66.214301 Zhang H Y, Yang J, Fan G P, Zhu W F, Chai X D 2017 Acta Phys. Sin. 66 214301 doi: 10.7498/aps.66.214301 [16] Ambrozinski L, Stepinski T, Uhl T, Ochonski J, Klepka A 2012 Key Eng. Mater. 518 87 doi: 10.4028/www.scientific.net/KEM.518.87 [17] 杨益新, 孙超, 鄢社锋, 马远良, 肖国有 2003 声学学报 28 504 doi: 10.3321/j.issn:0371-0025.2003.06.004 Yang Y X, Sun C, Yan S F, Ma Y L, Xiao G Y 2003 Acta Acust. 28 504 doi: 10.3321/j.issn:0371-0025.2003.06.004 [18] McLaskey G C, Glaser S D, Grosse C U 2010 J. Sound Vib. 329 2384 doi: 10.1016/j.jsv.2009.08.037 [19] Wang W Q, Shao H Z 2014 IEEE J. Sel. Top. Signal Process. 8 106 doi: 10.1109/JSTSP.2013.2285528 [20] Cantero C S, Aranguren G, Malik M K, Etxaniz J, Martín de la Escalera F 2020 Sensors 20 1445 doi: 10.3390/s20051445 [21] He T, Pan Q, Liu Y G, Liu X D, Hu D Y 2012 Ultrasonics 52 587 doi: 10.1016/j.ultras.2011.12.003 [22] Li L, Yang K, Bian X Y, Liu Q H, Yang Y Z, Ma F Y 2019 Sensors 19 3152 doi: 10.3390/s19143152 [23] Zhang Z H, Zhong Y T, Xiang J W, Jiang Y Y, Wang Z L 2020 IEEE Sens J. 20 14932 doi: 10.1109/JSEN.2020.3009981 [24] Jung H K, Zhou S J, Park G 2019 J. Intell. Mater. Syst. Struct. 30 351 doi: 10.1177/1045389X18810804 [25] Wang Z L, Yuan S F, Qiu L, Liu B 2015 J. Vibroeng. 17 2338 [26] Zhong Y T, Xiang J W 2019 Smart. Struct. Syst. 24 173 doi: 10.12989/sss.2019.24.2.173 [27] Yu L, Giurgiutiu V 2008 Ultrasonics 48 117 doi: 10.1016/j.ultras.2007.10.008 [28] Kundu T 2012 European Workshop on Structural Health Monitoring Dresden, Germany, July 3–6, 2012 p2 [29] Kundu T, Nakatani H, Takeda N 2012 Ultrasonics 52 740 doi: 10.1016/j.ultras.2012.01.017 [30] Ma C N, Zhou Z X, Liu J X, Cui Z W, Kundu T 2023 Ultrasonics 132 107020 doi: 10.1016/j.ultras.2023.107020 [31] Yin S X, Cui Z W, Kundu T 2018 Ultrasonics 84 34 doi: 10.1016/j.ultras.2017.10.007 [32] Yin S X, Xiao H P, Xu C B, Wang J S, Deng M X, Kundu T 2022 Ultrasonics 124 106770 doi: 10.1016/j.ultras.2022.106770 [33] Sen N, Gawroński M, Packo P, Uhl T, Kundu T 2021 Mech. Syst. Signal Proc. 153 107489 doi: 10.1016/j.ymssp.2020.107489 [34] Zhou Z X, Cui Z W, Liu J X, Kundu T 2023 Eng. Fract. Mech. 277 108995 doi: 10.1016/j.engfracmech.2022.108995 [35] Gao Q, Jeon J Y, Park G, Kong Y, Shen Y D, Xiang J W 2021 J. Intell. Mater. Syst. Struct. 33 1028 doi: 10.1177/1045389X211039558 [36] Gao Q, Jeon J Y, Park G, Shen Y D, Xiang J W 2021 Struct. Health. Monit. 21 451 doi: 10.1177/14759217211004236 [37] Gao Q, Jeon J Y, Xiang J W, Park G 2023 IEEE Sens. J. 23 2970 doi: 10.1109/JSEN.2022.3231875 [38] Xue C R, Xu G, Wang X K, Gao J C, Gao D J 2021 Ultrasonics 115 106438 doi: 10.1016/j.ultras.2021.106438 -
计量
- 文章访问数: 55
- HTML全文浏览数: 55
- PDF下载数: 1
- 施引文献: 0