在核反应系统中, 原子核内核子的动量是一个至关重要的考虑因素. 通过分析核子的动量分布及其他动力学参数, 能够更深入地理解核子内部的运动模式, 并揭示它们之间的相互作用. 对原子核内核子动量分布的研究, 为核反应机制及核衰变过程的理解提供了重要的见解. 假设核内核子的运动不能超越费米面, 因此单个核子的动量无法超过费米动量. 然而, 后续的高能电子散射实验在轻质量系统中发现, 核内约20%的核子会成对出现并表现出关联效应^[1]. 随后, 在2014年, Hen等^[2]对重质量系统进行了高能电子散射实验, 发现类似核子关联效应也存在于丰中子核中. 在这些系统中, 核子对主要以质子-中子关联模式形成. 这种关联影响了核内的动量分布, 使得关联核子通常具有高于传统费米气体模型预测的费米动量的动量. 因此, 核内核子的动量分布呈现出高动量尾巴, 即高动量分布, 在丰中子核中, 由于中子数量多于质子, 质子更有可能获得高动量. 通过对不同系统高能电子散射的实验数据中, 高动量核子在核内的存在得到证实. Hen等^[3]为这些高动量核子的出现提供了解释, 将其归因于核子间张量力引起的短程关联. 中子与质子间的张量力不同于两个质子或两个中子间的张量力, 并且在此基础上给出短程关联导致的高动量尾大致遵循$1/k^4 $分布.

核子间的短程关联结构及由此产生的核子内高动量分布, 对核物理研究的多个方面产生了显著影响. 例如, 在研究核的对称能时, 考虑核结构中的短程关联显著降低了对称能的动能项, 有时甚至使其变为负值^[4–6]. 在具有短程关联的量子多体系统中, 动量大于费米动量的核子影响了费米子系统的纠缠熵^[7,8]. 在核天体物理和中子星研究中, 核子间的短程关联结构影响了中子星的状态方程(EOS)和耦合参数^[9–11]. 当高能μ子穿过核时, 核内的结构函数与自由核子中的不同, 这种现象被称为EMC效应. 研究表明, 这些差异与核内核子间的短程关联之间存在特定的线性关系, 这可能是EMC效应背后的关键因素^[12,13]. 短程关联效应对强子模型中暗物质的研究也有部分影响^[14,15]. 在中子星冷却的Urca过程中, 短程关联通过修正质子谱函数的宽度, 导致中子星的Urca过程冷却速率在低质子分数下呈现平滑变化, 取代了传统费米液体理论中质子分数达到一定阈值时才启动的快速冷却模式, 从而改变了中子星冷却的预期行为^[16–18]. 因此, 在核物理研究中, 考虑核子间的短程关联及由此产生的核子高动量分布具有重要的意义.

重离子碰撞的过程是一个相当复杂的过程, 首先准备阶段要对进行碰撞的炮核以及靶核进行初始化操作. 对弹核与靶核的初始化操作考虑到原子核内部核子的密度分布, 采用Monte-Carlo方法给出原子核内部每个核子的坐标分布以及动量分布, 且动量分布满足费米气体模型. 在符合核结构模型的结合能与均方根半径情况下生成原子核, 观察时间演化下结合能以及均方根半径浮动均在合理范围后选做初始化原子核.

费米气体模型将原子核内的核子视为独立运动的费米子, 受平均场约束. 核子遵循泡利不相容原理, 从低到高能填充, 填满的最高能为费米能级, 核子的分布完全在费米面内部, 核子的动量分布在费米面内均匀分布. 质子与中子的费米动量表示为

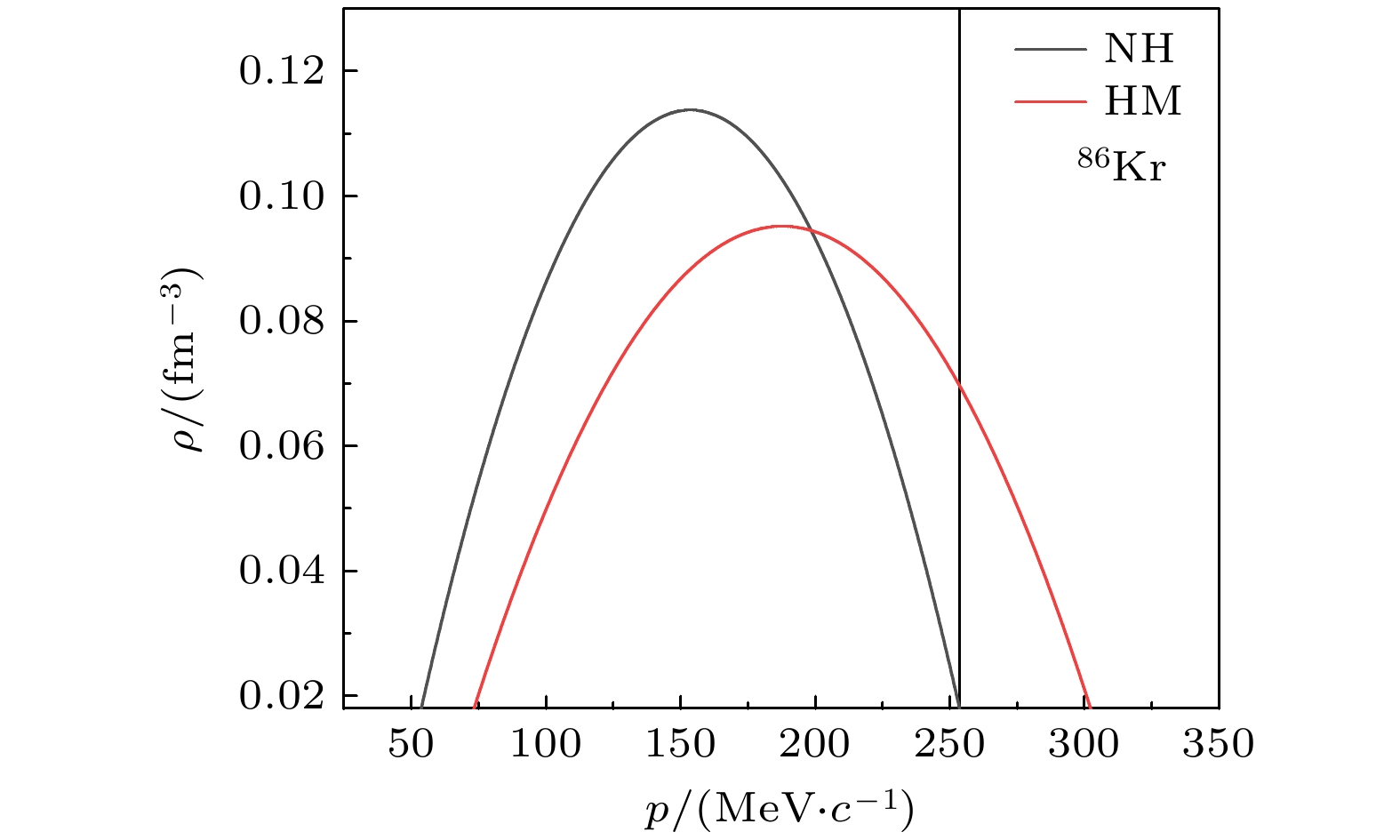
其中$ {\rho _{\text{p}}} $和$ {\rho _{\text{n}}} $代表质子和中子的密度; $ \delta $为同位旋不对称度; $ \rho $为总的核子密度. 质子与中子的动量分布为

其中C为归一化参数, 对整个动量空间积分后为1. 研究重点关注短程关联诱导的核内高动量分布特征, 文中暂未涉及短程关联的微观结构解析及其关联势的具体形式讨论, 相关理论模型的深化阐释将留待后续工作展开. 本文在符合动量守恒的情况下考虑高动量核子为20%, 根据Monte-Carlo方法各抽取10%的中子与质子, 让抽取的核子符合高动量核子的特性, 随后降低剩余核子动量以达到能量守恒, 将核静止放置500 fm/c后, 核的结合能与均方根半径仍在合理范围内作为初始化的高动量原子核. ⁸⁶Kr核内动量分布如图1所示.

对于重离子碰撞的研究, 采用半经典的量子分子动力学模型(QMD)^[19–21], 在QMD模型中每个核子都存在于相空间的双高斯相干态表示为

其中$ {\boldsymbol{r}}_i $与$ {{\boldsymbol p_i}} $为第i个核子的坐标与动量空间的波包中心; L为波包宽度(L = 3.8 fm); 并给出N个核子体系的总波函数表示为

通过欧拉-拉格朗日方程导出核子的时间演化方程为

在QMD模型中单核子势表示为

其中$ {U}^{{\mathrm{S}}{\mathrm{k}}{\mathrm{y}}} $表示密度依赖的Skyrme势, $ {U}^{{\mathrm{Y}}{\mathrm{u}}{\mathrm{k}}} $表示Yukawa势, $ {U}^{{\mathrm{C}}{\mathrm{o}}{\mathrm{u}}{\mathrm{l}}} $表示库仑势, $ {U}^{{\mathrm{M}}{\mathrm{D}}{\mathrm{I}}} $表示动量依赖相互作用势, $ {U}^{{\mathrm{P}}{\mathrm{a}}{\mathrm{u}}{\mathrm{l}}{\mathrm{i}}} $表示泡利势, $ {U}^{{\mathrm{s}}{\mathrm{y}}{\mathrm{m}}} $对称势^[22,23].

在重离子碰撞的过程中, 核子-核子间碰撞截面的差异表示为同位旋效应, 当考虑同位旋相关核子-核子截面的差异时则存在:

当不考虑同位旋相关核子-核子截面的差异时存在:

核内韧致辐射在能量为200 MeV内的重离子碰撞中应用较多, 核内韧致辐射分为质子-中子碰撞以及质子-质子核内碰撞, 研究发现中能重离子碰撞过程中, 质子-中子碰撞占主导地位, 产生的韧致辐射光子可作为高动量分布(短程关联)以及密度依赖对称能的敏感观测指针^[24–26]. 核内产生γ光子的机制很多, 诸如巨共振衰变γ、统计衰变γ和介子衰变γ等, 不同类型的γ光子主要是从能量角度区分, 本文主要参考韧致辐射γ光子.

在核物理研究中, 光子作为一种敏感的观测量. 相比于π介子和各种重子, 光子具有更高的产生率, 并且更容易被探测到. 同时, 光子不会对正在进行的核反应过程产生影响. 光子一旦产生, 就会在核内电磁场的作用下迅速发射出去. 因此, 本文选取核反应中产生的光子作为探针, 来研究核内核子的高动量分布.

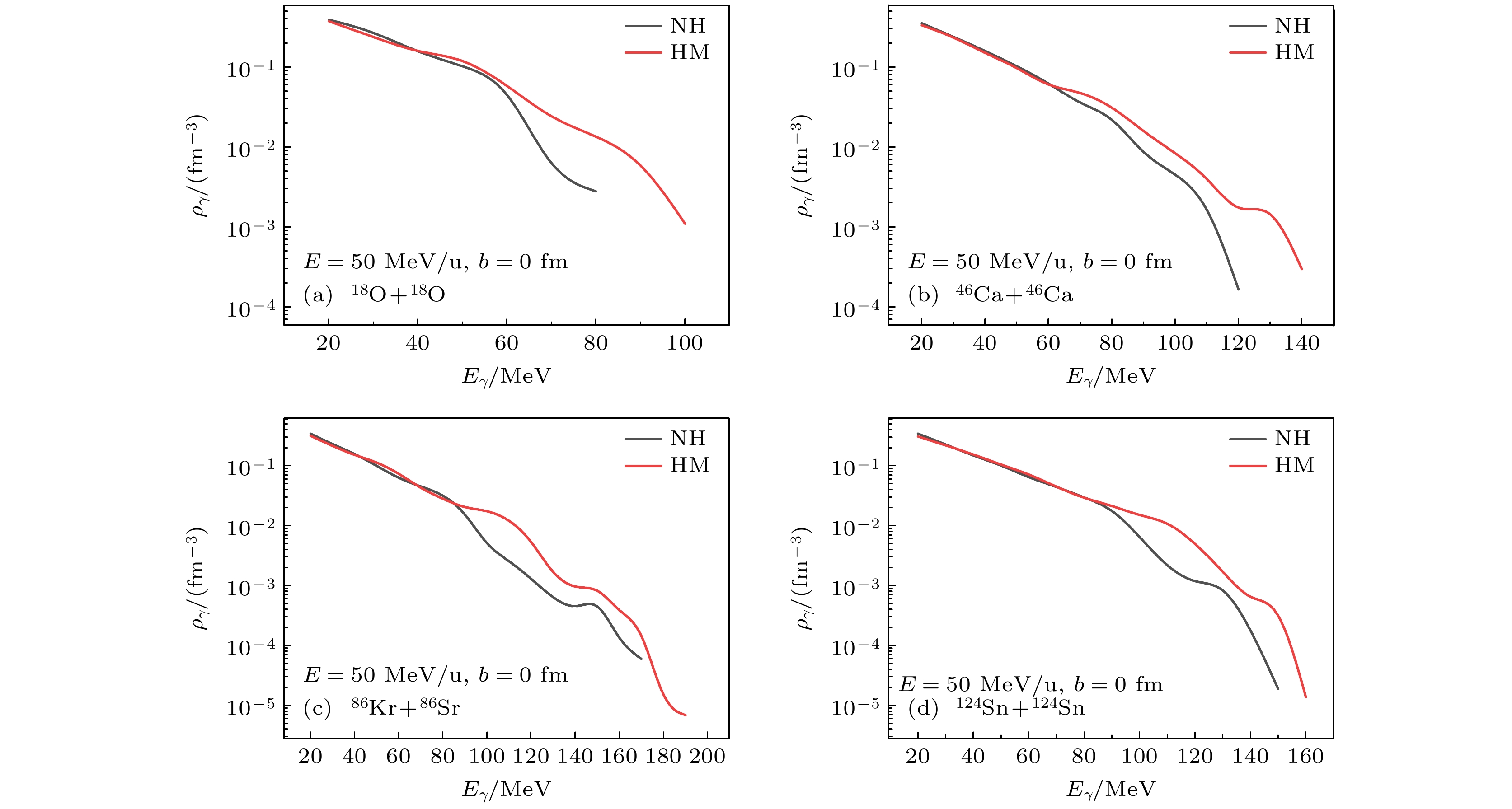
图2展示了入射能量为50 MeV/u、碰撞参数b为0 fm的核反应系统中光子密度与光子能量的关系. 图2(a)为轻质量核反应系统(¹⁸O+¹⁸O), 图2(b)为较轻质量核反应系统(⁴⁶Ca+⁴⁶Ca), 图2(c)为中等质量核反应系统(⁸⁶Kr+⁸⁶Sr), 图2(d)为重质量核反应系统(¹²⁴Sn+¹²⁴Sn). 其中, 红线表示考虑高动量分布的情况, 黑线表示不考虑高动量分布的情况. 如图2所示, 对于较轻、中等、重质量核系统, 光子能量分布在90 MeV左右开始出现差异, 而轻质量核反应系统也在60 MeV左右开始出现差异, 考虑高动量分布的系统在高光子能量处的光子密度高于不考虑高动量分布的系统. 此外, 考虑高动量分布时, 碰撞产生的光子最大能量更大. 这是因为考虑高动量分布后, 系统产生的光子总数减少, 且主要减少的是低能区的光子. 在不考虑高动量分布时, 低能区光子所携带的能量被转移到了高能光子区. 因此, 在低能区两种情况下光子密度没有明显差异, 而在高能区光子密度的差异则较为明显. 其原因可能是高动量核子在反应过程中生成的高能光子的概率相较于其他核子概率更高.

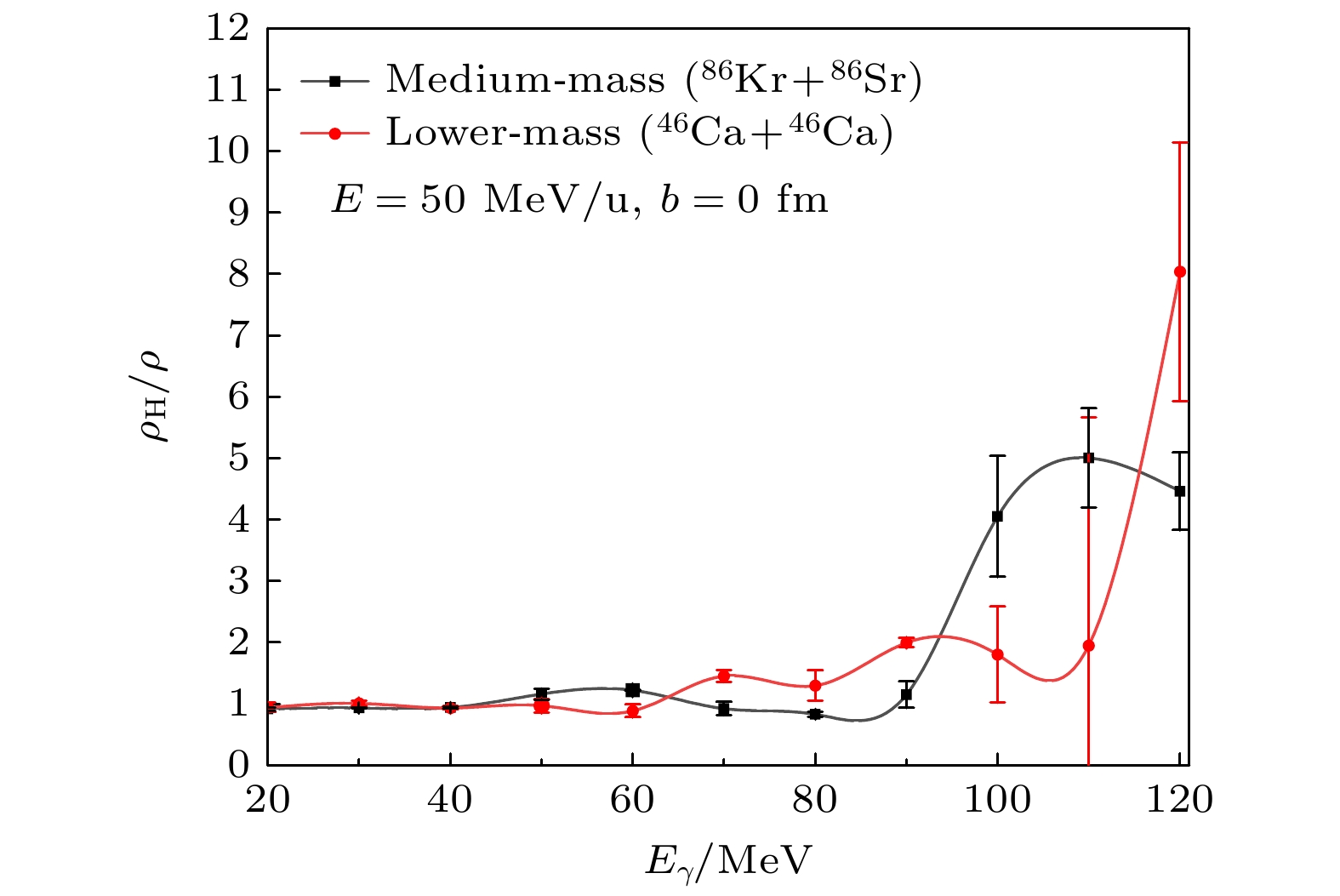
为了更清晰地展示高动量分布引起的光谱变化, 我们做了进一步处理. 图3展示了较轻质量核系统和中等质量核系统中高动量分布系统与常规系统的光子密度比与光子能量的关系. 从图3可以看出, 在低光子能量区, 光子密度比在1附近波动. 然而, 当光子能量进入一定范围后, 光子密度比始终大于1, 并在特定区间内呈现爆发式增长. 这一现象适用于较轻质量核系统(⁴⁶Ca+⁴⁶Ca)和中等质量核系统(⁸⁶Kr+⁸⁶Sr).

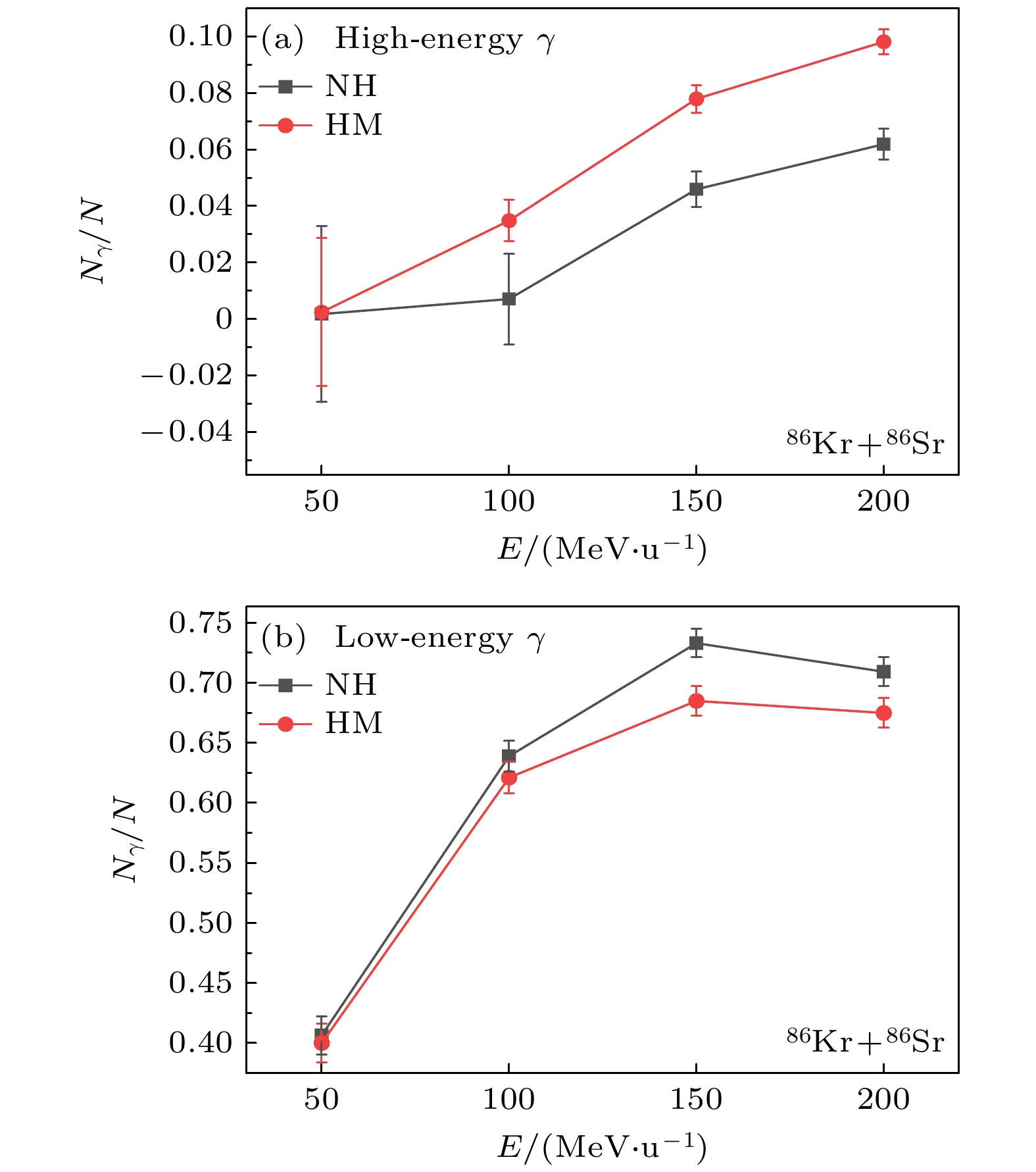
同时在一定入射能量范围内, 本文探讨了不同入射能量下光子相对数与入射能量的关系. 图4展示了碰撞参数b为0 fm时, 中等质量核反应系统⁸⁶Kr+⁸⁶Sr产生的光子相对数量与入射能量E的关系. 图4(a)描绘了光子能量在150 MeV附近的情况, 图4(b)描绘了光子能量在50 MeV附近的情况. 其中, 黑线表示不考虑高动量分布的情况, 红线表示考虑高动量分布的情况. 从图4(a)中可以看出, 对于能量在150 MeV附近的高能光子, 在入射能量为50—200 MeV/u的范围内, 考虑高动量分布的系统产生的高能光子相对数量始终高于不考虑高动量分布的系统, 并且随着入射能量的增加, 这种差异更加明显. 从图4(b)中可以看出, 随着入射能量的增加, 反应过程中产生的能量在50 MeV附近的光子相对数量显著增加. 在入射能量为50—200 MeV/u的范围内, 无论入射能量如何, 考虑高动量分布的系统产生的低能光子相对数量始终低于不考虑高动量分布的系统. 这是因为当考虑高动量分布时, 核内部分核子的动量高于传统核子. 这些高动量核子碰撞产生的光子能量高于传统核子碰撞产生的光子能量. 因此, 在低能区, 考虑高动量分布的系统碰撞产生的光子相对数量低于不考虑高动量分布的系统. 这种差异在入射能量较低时并不十分明显, 但随着入射能量的增加, 差异变得更加显著.

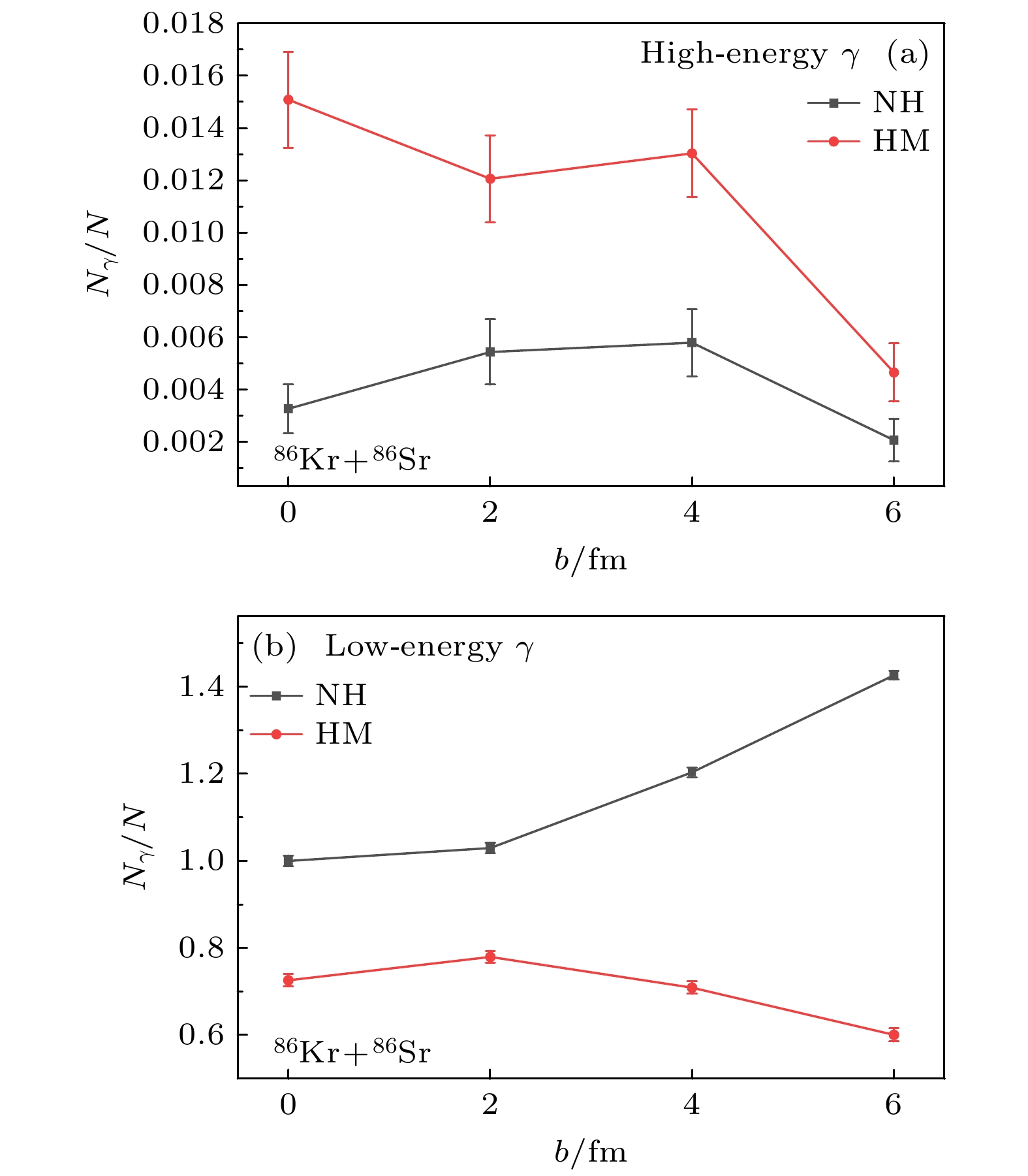
图5展示了入射能量E = 50 MeV/u时, ⁸⁶Kr+⁸⁶Sr系统产生的光子相对数量与碰撞参数b的关系. 图5(a)展示了能量在120 MeV附近的光子相对数量, 图5(b)展示了能量在30 MeV附近的光子相对数量. 其中, 红线表示考虑高动量分布的情况, 黑线表示不考虑高动量分布的情况. 从图5(a)中可以看出, 在碰撞参数b为0—6 fm的范围内, 考虑高动量分布的系统产生的高能光子相对数量普遍高于不考虑高动量分布的系统. 图5(b)显示, 在碰撞参数b为0—6 fm的范围内, 考虑高动量分布的系统产生的低能光子相对数量普遍低于不考虑高动量分布的系统. 这表明当考虑高动量分布时, 低能光子向高能光子转变的现象与碰撞参数无关, 是一种普遍现象.

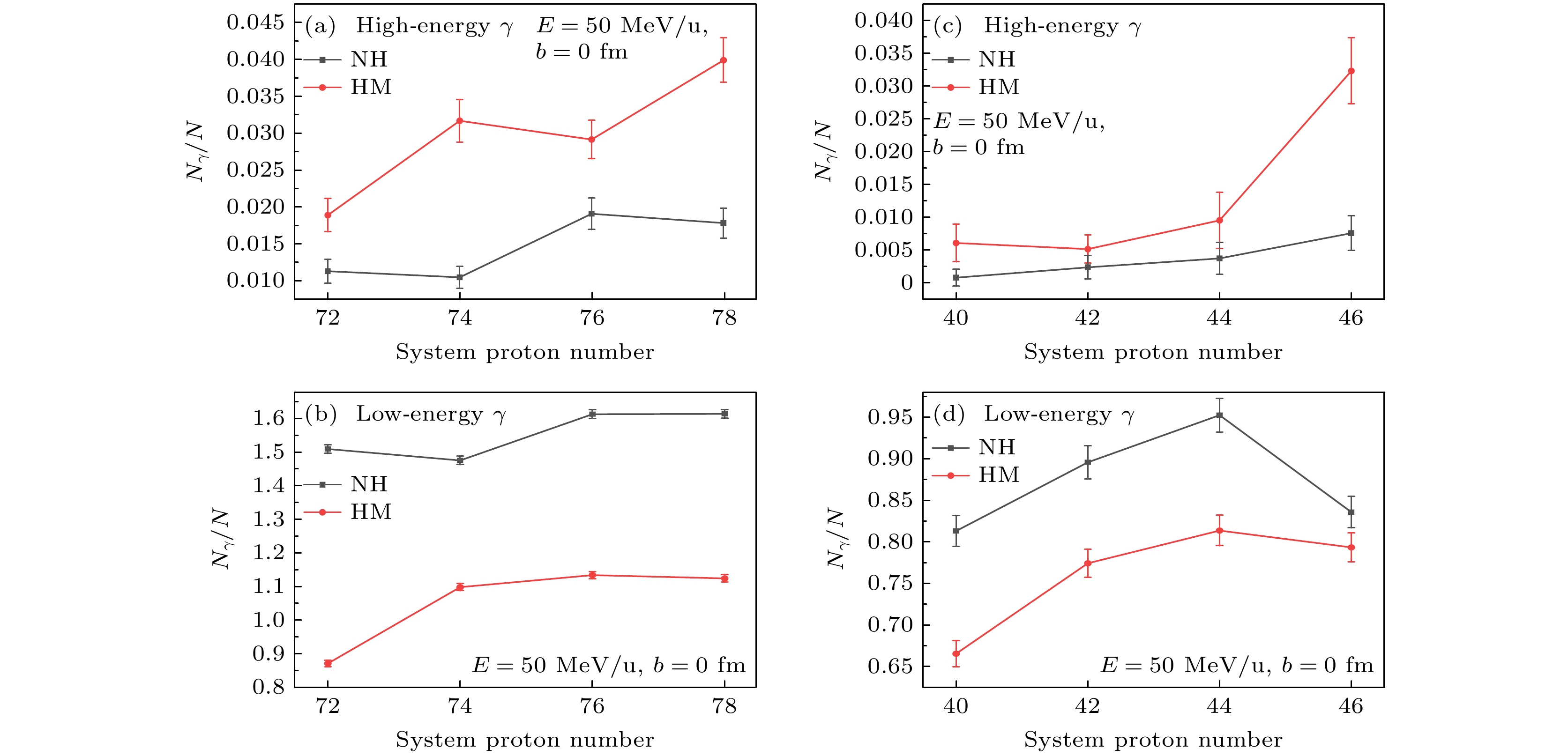
为了确保结论的普适性, 图6展示了入射能量为50 MeV/u时, 不同中等质量核系统(⁸⁶Kr+⁸⁶Kr, ⁸⁶Kr+⁸⁶Sr, ⁸⁶Kr+⁸⁶Zr, ⁸⁶Kr+⁸⁶Mo)和不同较轻质量核系统(⁴⁶Ca+⁴⁶Ca, ⁴⁴Ca+⁴⁸Ti, ⁴⁶Ti+⁴⁶Ti, ⁴⁶V+⁴⁶V)在对心碰撞中产生的低能和高能光子相对数量的关系. 横轴表示系统的总质子数, 纵轴表示光子相对数量. 图6(a)和图6(b)为中等质量核系统, 图6(c)和图6(d)为较轻质量核系统. 图6中表明, 无论何种核系统, 对于低能光子, 考虑高动量分布时碰撞产生的光子相对数量始终低于不考虑高动量分布的情况; 而对于高能光子, 考虑高动量分布时碰撞产生的光子相对数量始终高于不考虑高动量分布的情况. 这表明, 低能光子向高能光子的能量转移是不同系统中的普遍现象, 与之前的结论一致.

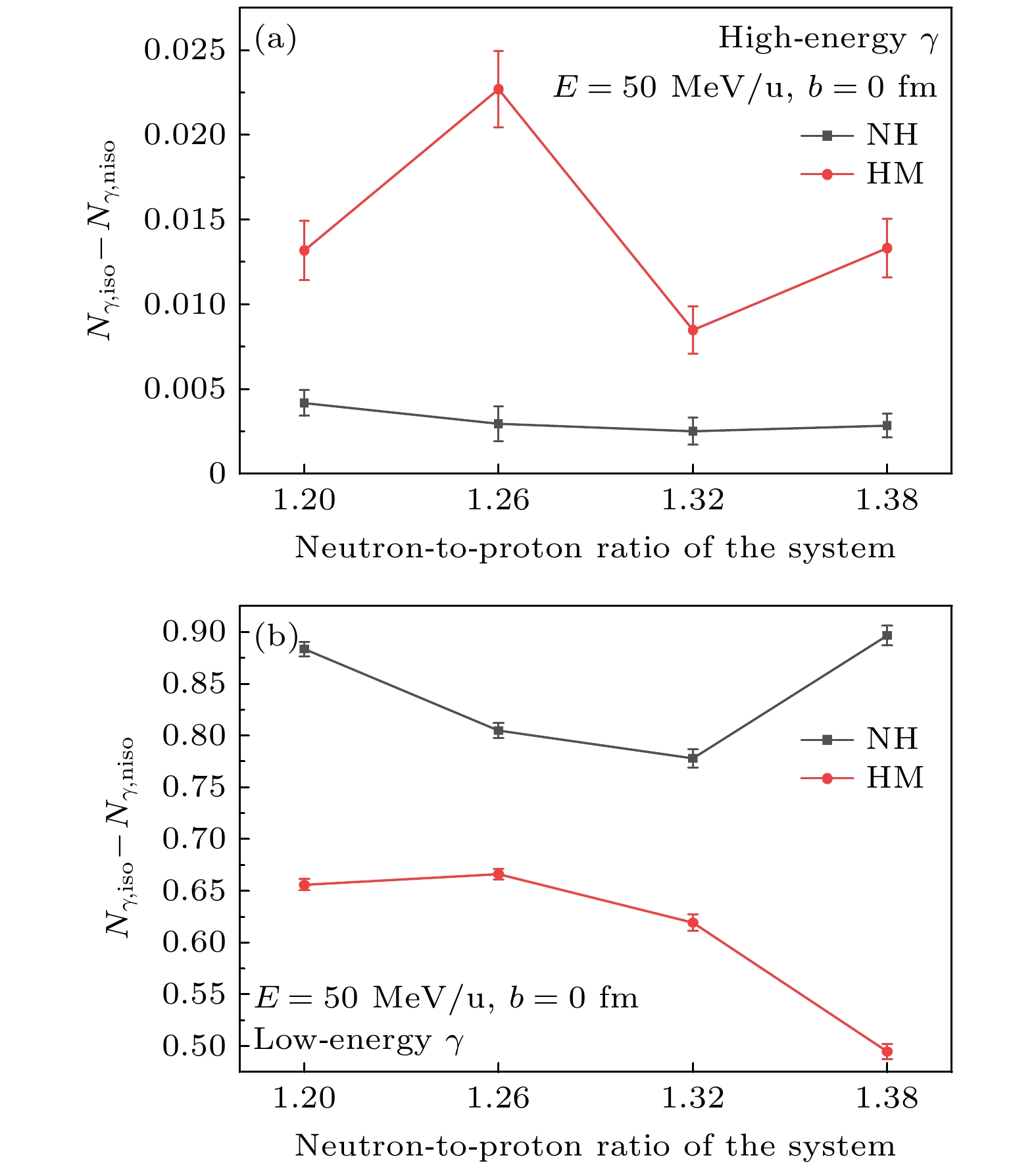
在重离子碰撞中, 同位旋效应与高动量核子分布的关系也能为理解核物理状态提供重大帮助, 图7以E = 50 MeV/u、对心碰撞条件为基础, 对比了四组系统(⁸⁶Kr+⁸⁶Kr, ⁸⁶Kr+⁸⁶Sr, ⁸⁶Kr+⁸⁶Zr, ⁸⁶Kr+⁸⁶Mo)在是否考虑高动量分布时的光子产额差异, 横轴为系统的中质比. 结果显示: 红线(含高动量分布)与黑线(无高动量分布)在图7(a) 120 MeV高能光子区间的相对差异显著小于图7(b) 25 MeV低能区间的差异. 同位旋效应通过调节质子-中子碰撞概率显著改变光子产额. 引入同位旋的系统无论是否含高动量分布, 其光子产额均高于未引入的同位素系统. 值得注意的是, 低能光子区(25 MeV)中, 无同位旋修正的系统因高动量分布产生的产额差异更显著; 而在高能区(120 MeV), 含同位旋的系统反而表现出更大的高动量分布造成的光子产额差异. 这一现象与高动量核子的关联特性密切相关: 中子-质子对中的中子可能优先参与碰撞, 而关联张量力会驱动其配对的质子发射高能光子. 同位旋效应不仅影响核子碰撞概率, 还通过调控关联核子对的贡献, 导致低能光子区的光子产额差异较小, 而高能光子区的光子产额差异较大.

本文研究了不同质量核系统的高动量分布与核反应过程中发射的光子之间的关系, 涉及入射能量、碰撞参数以及同位旋截止截面引起的相对光子产额. 研究表明, 对于所考虑的系统, 包含高动量分布会导致低能范围内的光子密度与传统费米气体系统相当, 但在高能范围内存在显著差异. 此外, 碰撞后产生的最大光子能量超过了传统费米气体系统. 值得注意的是, 在碰撞参数b = 0 fm时, 入射能量的增加加剧了高动量分布引起的能量转移现象, 在E = 150 MeV/u时达到峰值, 随后随着能量的进一步增加而减弱. 高动量分布引起的能量转移现象随着碰撞参数b的变化而持续存在, 在b = 6 fm时达到顶峰. 此外, 在高动量分布条件下, 考虑同位旋截止截面发现, 具有高动量分布的核粒子倾向于以相关对的形式出现, 主要是中子-质子对, 导致碰撞概率的重新调整. 因此很明显, 高动量分布与碰撞能量、碰撞参数和同位旋相关核子-核子碰撞截面密切相关.