利用随时间变化的驱动场来操控量子系统或人工量子系统的动力学行为, 以实现量子态的相干布居数转移, 近年来受到广泛关注. 相关应用涵盖了原子分子干涉仪^[1,2]、化学反应^[3]、原子和二聚物分子转化系统^[4]、超冷原子量子模拟^[5]、原子分子碰撞^[6,7]和量子信息处理^[8,9]等多个研究领域. 为了实现相干量子调控, 需要精确设计脉冲的强度、频率、相位及其与量子系统相互作用的时间. 例如, 受激拉曼绝热通道方案(STIRAP) 利用部分重叠的斯托克斯脉冲和泵浦脉冲与三能级系统相互作用, 使系统沿着特定的路径演化, 从而在两个具有相同宇称的能级之间实现高保真度的布居数转移. STIRAP基于绝热演化, 对外场的控制参数具有鲁棒性. 在演化过程中, 由于没有中间态被占据, 不会因中间态的自发辐射导致保真度降低, 这使其成为实现量子态相干布居数转移的一种有效方法. 然而, STIRAP需要较长的演化时间, 容易受到环境诱导的耗散和退相干的影响.

研究者将超绝热方案^[10,11]或绝热捷径方案^[12,13]应用于三能级系统中, 以加速STIRAP过程. 通过在原有的哈密顿量中引入微波场与两个较低能级的耦合项, 消除非绝热效应, 使系统严格沿着原哈密顿量的本征态演化. 但其局限性在于, 由于电偶极禁闭的存在, 微波场与两个较低量子态之间的耦合在实际应用中可能并不可行. 除此之外, 考虑到斯托克斯脉冲和泵浦脉冲驱动下三能级系统具有的特定李代数结构, 研究者们提出了一系列的非绝热方案. 例如, 基于在单光子共振条件下的含时三能级系统具有$ SU(2) $对称性, Chen和Muga^[14]利用$ SU(2) $李代数生成元表示的不变量算子设计脉冲, Huang等^[15]则利用$ SU(2) $变换反向设计了哈密顿量. 在双光子共振情况下, 考虑到三能级系统具有部分的$ SU(3) $对称性, Li等^[16]提出利用$ SU(3) $李代数变换方法, 逆向设计三能级系统的 哈密顿量. 然而, 这些方案在调控三能级系统的动力学过程中采用了旋转波近似处理. 当涉及到半 导体量子系统^[17]、超导量子系统^[18,19]、光机械系 统^[20]、氮空位色中心量子系统^[21] 等的超快调控或者脉冲与系统的强耦合相互作用时, 旋转波近似并不适用. 事实上, 无旋转波近似的量子信息处理 过程更能准确反映真实的量子调控. 基于此, 研究者们提出了一些在无旋转波近似下的量子调控方案. 2015年, Chen等^[22]提出了在无旋转波近似下的量子绝热捷径方案, 能够实现对两能级和三能级量子系统精确的量子调控, 但未能有效降低系统演化过程中的Rabi振荡, 也不能避免脉冲的奇点. Kang等^[23]则基于由预设的含时参数确定的不变量算子, 设计了系统的哈密顿量, 通过调控参数实现了两个较低能级之间的布居数转移. 尽管在哈密顿量中不需要引入与微波场相关的辅助项, 就能实现高保真度的量子调控, 并有效避免演化过程中的奇异性, 但缺点是需要引入多组脉冲且仍然存在Rabi振荡. 这些方案驱使我们寻找新的量子调控方法, 以实现以下目标: 1)在不需要引入微波场与两个较低能级之间的耦合相互作用, 就能实现高保真度的布居数转移; 2)系统的动力学过程可以严格解析求解; 3)只需要少量几组斯托克斯脉冲和泵浦脉冲即可完成相应的量子调控任务; 4)在整个布居数转移的过程中, 不会出现Rabi振荡或奇异点.

本文将采用基于SU(3)李代数变换的逆向设计方案, 构造在无旋转波近似下可严格求解的三 能级量子系统的哈密顿量. 通过求解含时薛定谔方程, 得到哈密顿量中含时控制参数的限制条件, 从而在理想情况下实现系统的完整布居数转移. 我们发现, 在演化过程中, 脉冲的强度和相位均不会 出现奇异性. 此外, 基于本方案, 通过两个具体模型演示了仅需三组脉冲即可驱动系统实现高保 真度布居数转移, 且演化过程中不会出现Rabi振荡. 最后, 讨论了中间态衰变对布居数转移过程的影响.

考虑一个具有Λ位型的三能级系统, 其基态$ |1\rangle $和亚稳态$ |3\rangle $分别通过泵浦脉冲和斯托克斯脉冲与激发态$ |2\rangle $耦合. 泵浦脉冲和斯托克斯脉冲分别表示为

在选取了一组正交归一化基矢$ \{|1\rangle, |2\rangle, |3\rangle\} $后, 薛定谔表象下系统的哈密顿量可以写作:

其中, 自由项$ H_{0} $和相互作用项$ H_{{\mathrm{I}}}(t) $分别为(取$ \hbar = 1 $)

式中, $ \varOmega_{{\mathrm{p}}}(t) = {\boldsymbol{d}}_{12}\cdot{\boldsymbol{E}}_{{\mathrm{p}}0}(t) $和$ \varOmega_{{\mathrm{s}}}(t) = {\boldsymbol{d}}_{32}\cdot{\boldsymbol{E}}_{{\mathrm{s}}0}(t) $分别表示泵浦脉冲和斯托克斯脉冲的拉比频率, $ {\boldsymbol{d}}_{12} $和$ {\boldsymbol{d}}_{32} $分别用来描述对应于电偶极跃迁$ |1\rangle \rightarrow |2\rangle $和$ |3\rangle \rightarrow |2\rangle $的电偶极矩. 为了计算和讨论的方便, 将薛定谔表象变换到以脉冲频率$ \omega_{{\mathrm{p}}}(t) $和$ \omega_{{\mathrm{s}}}(t) $旋转的表象中(将其定义为转动表象), 相应的转动变换矩阵可以取作:

在转动表象中系统的哈密顿量可以表示为

将方程(2)和方程(3)代入方程(4), 并略去与动力学演化过程无关的$ \omega_{2}I $项(由于此项仅在系统演化过程中引入一个全局相位因子, 而全局相位不会影响物理观测结果), 可以得到在无旋转波近似下哈密顿量的矩阵形式:

其中, $ \tilde{\varOmega}_{{\mathrm{p}}}(t) = \varOmega_{{\mathrm{p}}}(t) \exp\left[{\mathrm{i}}\displaystyle\int_{t_0}^{t} \omega_{{\mathrm{p}}}(t'){\mathrm{d}} t'\right] $和$ \tilde{\varOmega}_{{\mathrm{s}}}(t) = \varOmega_{{\mathrm{s}}}(t)\exp\left[{\mathrm{i}}\displaystyle\int_{t_0}^{t} \omega_{{\mathrm{s}}}(t'){\mathrm{d}} t'\right] $分别对应于泵浦脉冲和斯托克斯脉冲的复拉比频率, $ \varDelta_{{\mathrm{p}}}(t) = \omega_{2}-\omega_{1}-\omega_{{\mathrm{p}}}(t) $和$ \varDelta_{{\mathrm{s}}}(t) = \omega_{2}-\omega_{3}-\omega_{{\mathrm{{\mathrm{s}}}}}(t) $用于描述泵浦脉冲和斯托克斯脉冲相对于各自相关跃迁的失谐量. 接下来, 将利用$ SU(3) $李代数变换方法, 逆向设计出由(5)式给出的哈密顿量, 以便对系统的动力学过程进行解析求解.

在本文中, 仅考虑泵浦脉冲和斯托克斯脉冲具有相同的频率$ \omega_{{\mathrm{p}}}(t) = \omega_{{\mathrm{s}}}(t) = \omega(t) $, 以及双光子共振$ \varDelta_{{\mathrm{p}}}(t) = \varDelta_{{\mathrm{s}}}(t) = \varDelta(t) $的情况. 为了方便计算, 令$ \displaystyle\int_{t_0}^{t} \omega(t'){\mathrm{d}} t' = \theta(t) $. 考虑到任意的三能级系统具有完全或部分的$ SU(3) $对称性^[16], 可以通过引入$ SU(3) $李代数的生成元^[24]:

和不属于$ SU(3) $李代数生成元的对角算符:

将哈密顿量(5)式改写为

其中$ \varOmega_{{\mathrm{p}}}^{1}(t) $和$ \varOmega_{{\mathrm{p}}}^{2}(t) $分别对应于复泵浦脉冲$ \tilde{\varOmega}_{{\mathrm{p}}}(t) $的实部和虚部, $ \varOmega_{{\mathrm{s}}}^{1}(t) $和$ \varOmega_{{\mathrm{s}}}^{2}(t) $分别表示复斯托克斯脉冲$ \tilde{\varOmega}_{{\mathrm{s}}}(t) $的实部和虚部.

为了逆向设计用方程(8)描述的三能级系统的哈密顿量, 使支配系统沿着非绝热通道演化的薛定谔方程(9)能够被解析求解,

一种可行的方案^[16]是通过引入与时间有关的$ SU(3) $李代数的正则变换:

将原表象变换到正则表象. 在正则表象中的波函数$ |\psi_{{\mathrm{g}}}(t)\rangle $满足一个新的薛定谔方程:

其中哈密顿量$ H_{{\mathrm{g}}}(t) $应该仅含有对角算符$ E_{3} $, 以及$ SU(3) $李代数的卡当算子$ \lambda_{3} $和$ \lambda_{8} $:

使薛定谔方程(11)容易求解, 进而通过方程(10)得到薛定谔表象中波函数的解析表达式. 这里各算子的系数$ f_{3, 8, E}(t) $是与时间相关的实函数. 相应地, 原表象中的哈密顿量$ H(t) $可通过$ H_{{\mathrm{g}}}(t) $和$ {\boldsymbol{G}}(t) $表示为

有趣的是, 上述$ SU(3) $变换方法也暗示系统拥有不变量算子^[25]:

其中$ {\boldsymbol{I}}_{0} = \mathrm{diag}(1, 0, -1) $为一个三阶对角矩阵. 容易验证, 算符$ I(t) $满足方程:

现在通过选取适当的正则变换矩阵$ {\boldsymbol{G}}(t) $和有效哈密顿量$ H_{{\mathrm{g}}}(t) $中的实函数$ f_{3, 8, E}(t) $, 得到由方程(8)给出的哈密顿量中各算子系数的解析表达式. 一般而言, $ {\boldsymbol{G}}(t) $的选择并不是唯一的, 但通常应包含尽可能少的生成元, 以便哈密顿量$ H(t) $具有简洁的表达式. 为此, 这里选取:

相应地将方程(12)和方程(16)代入方程(13), 并与方程(8)进行比较, 容易得到:

可以看出, 斯托克斯脉冲和泵浦脉冲的强度与相位仅与随时间变化的控制参数$ \beta(t) $有关, 因此系统的演化完全可以由$ \beta(t) $来调控. 接下来, 通过求解薛定谔方程(9)并给出参数$ \beta(t) $在边界处的限制条件, 研究系统的非绝热动力学行为, 以实现系统从初态$ |1\rangle $到末态$ |3\rangle $的快速且高保真度的布居数转移.

本节通过解析求解薛定谔方程(9), 研究由方程(8)和方程(17)描述的三能级系统的动力学行为. 考虑到在方程(10)中, 原表象中的波函数$ |\psi(t)\rangle $和正则表象中的波函数$ |\psi_{{\mathrm{g}}}(t)\rangle $通过幺正算符$ {\boldsymbol{G}}(t) $相联系. 这意味着两个表象下的时间演化算子满足以下关系:

根据方程(11)和方程(12), 可以得到正则表象中的时间演化算子:

其中与时间有关的实函数$ f_{3, 8, E}(t) $的表达式已经通过方程(16)给出. 相应地薛定谔方程(9)的3个特解, 亦即系统的非绝热动力学基矢, 可以通过$ |\psi_{m}(t)\rangle = U(t, t_0)|m\rangle(m = 1, 2, 3) $给出. 直接计算后得到:

其中量子态:

为方程(14)式中不变量算子$ I(t) $对应于本征值$ 1 $, $ 0 $, $ -1 $的本征态. 方程(20)中各相位因子的表达式如下:

考虑系统在时间间隔$ t\in[t_0, t_{\mathrm{f}}] $内的演化, 给定$ \beta(t) $在边界处的第一个限制条件:

可以验证: 如果系统在初始时刻$ t = t_0 $处于态$ |1\rangle $时, 系统将沿着非绝热通道$ |\psi_{1}(t)\rangle $演化, 在末时刻$ t = t_{\mathrm{f}} $到达目标态$ |3\rangle $. 类似地, 当系统初始时刻处在态$ |3\rangle $, 系统将沿着非绝热通道$ |\psi_{3}(t)\rangle $演化, 并最终处于态$ |1\rangle $. 因此, 系统的非绝热动力学将实现量子态$ |1\rangle\leftrightarrow|3\rangle $快速且完整的布居数转移. 此外, 要设计出如方程(17)所描述的斯托克斯脉冲和泵浦脉冲, 还需要加上限制条件:

总之, 通过给定具有任意初等函数形式且满足上述两个限定条件的控制参数$ \beta(t) $, 可以设计出所需的脉冲, 驱动三能级系统实现量子态的相干布居数转移. 更重要的是, 只要$ \beta(t) $是连续, $ \dot{\beta(t)} $有界且连续或仅有有限个间断点, 就能保证在演化过程中无论是相位因子(22)式还是脉冲(17)式, 都不会出现奇异点.

以上方案提供了精确设计脉冲, 来实现量子态$ |1\rangle $和$ |3\rangle $之间相干布居数转移的具体思路. 接下来, 将介绍几个典型的例子.

为了描述方便, 首先定义分段函数:

模型1中的脉冲具有如下函数形式:

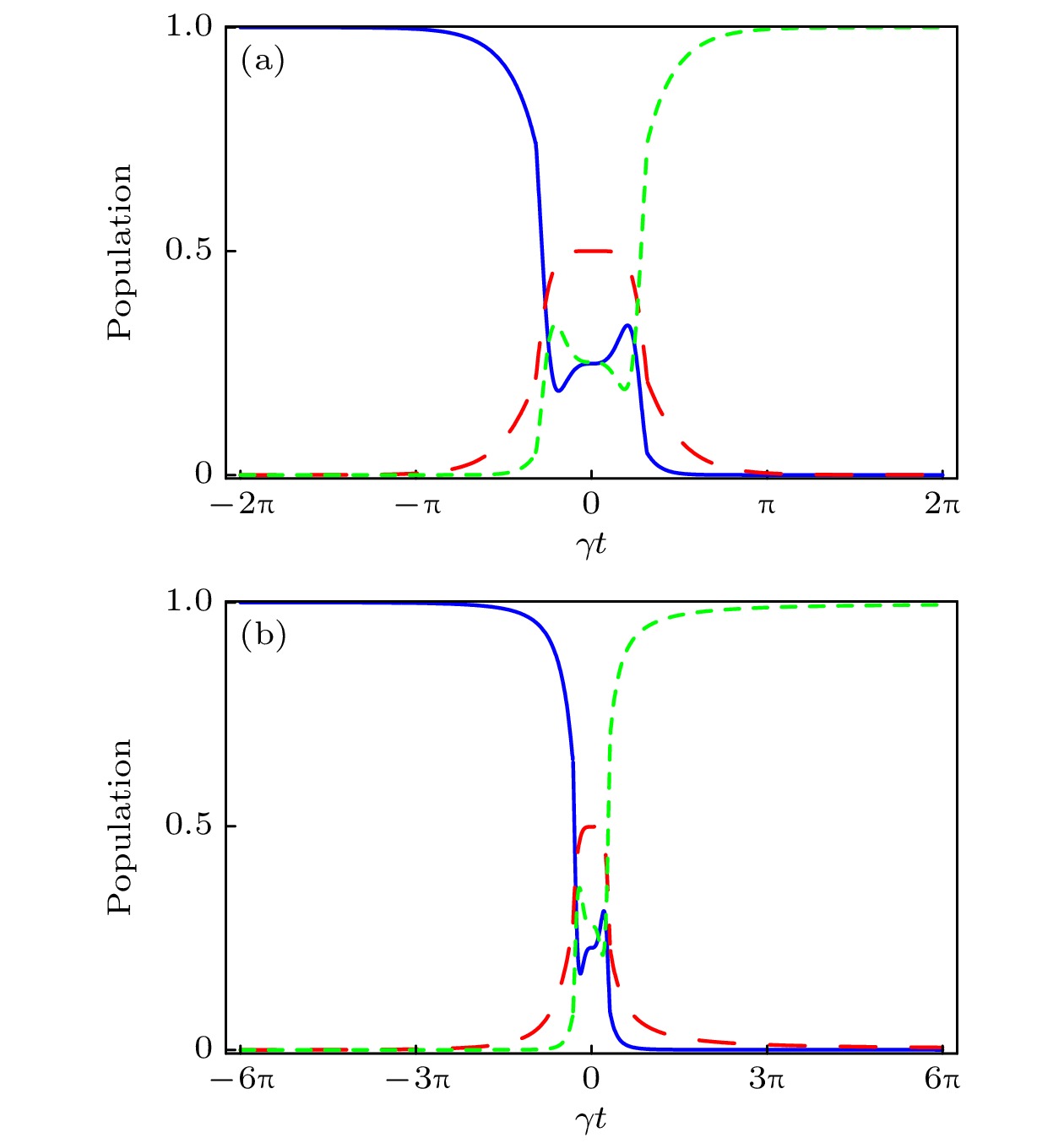
其中$ \gamma t\in(-\infty, +\infty) $. 可以看到, 系统在整个的演化过程中, 虽然脉冲强度有限, 但持续时间趋于无限大. 因此, 基于实际量子调控的需要, 对演化时间进行截断是不可避免的, 这里选取$ \gamma t\in[-2{{\pi}}, 2{{\pi}}] $. 为了进一步刻画系统在非绝热演化过程中的多通道跃迁, 引入物理量:

相应的布居数转移过程如图1(a)所示.

模型2中的脉冲通过如下函数来描述

此脉冲可通过选取$ \beta(t) = {\pi}/{2} + A(t)\arctan(\gamma t) $得到, 其中$ \gamma t\in(-\infty, +\infty) $确保含时参数$ \gamma t\in (0, \pi) $. 同样的, 基于实际演化的需要, 取截断时间$ \gamma t\in [-6\pi, 6\pi] $, 以确保系统沿着实际的量子态$ |\psi_{1}(t)\rangle $演化到末态$ |3\rangle $的概率超过$ 0.998 $. 相应的布局数转移过程如图1(b)所示.

需要强调的是, 与文献[23]方案相比, 通过上述两个模型描述的系统的动力学过程没有出现Rabi振荡, 且仅需引入最多三组脉冲即可实现布居数转移. 原则上, 本方案可设计无限多的解析模型, 且其动力学过程与这两个模型类似.

在实际的量子调控过程中, 诸如原子之间的碰撞、自发辐射等因素会导致激发态$ |2\rangle $的衰变, 影响布居数转移的效率. 假设脉冲与系统的相互作用时间远小于系统的弛豫时间, 使单个原子的激发态$ |2\rangle $向其基态$ |1\rangle $和亚稳态$ |3\rangle $的自发辐射效应可以忽略. 在这种情况下, 仅考虑量子态$ |2\rangle $以与时间无关的衰变率Γ从原子衰变到环境中. 此时系统的哈密顿量可以唯象的表示为

其满足刘维尔方程:

可以看到, 系统的动力学行为可以完全由密度算符$ \rho(t) $来描述. 然而, 由于衰变项的存在, 密度算符$ \tilde{\rho}(t) $不再满足保迹性. 为此, 引入归一化的密度算符$\rho(t) $以确保$ \mathrm{tr}\rho(t) = 1 $:

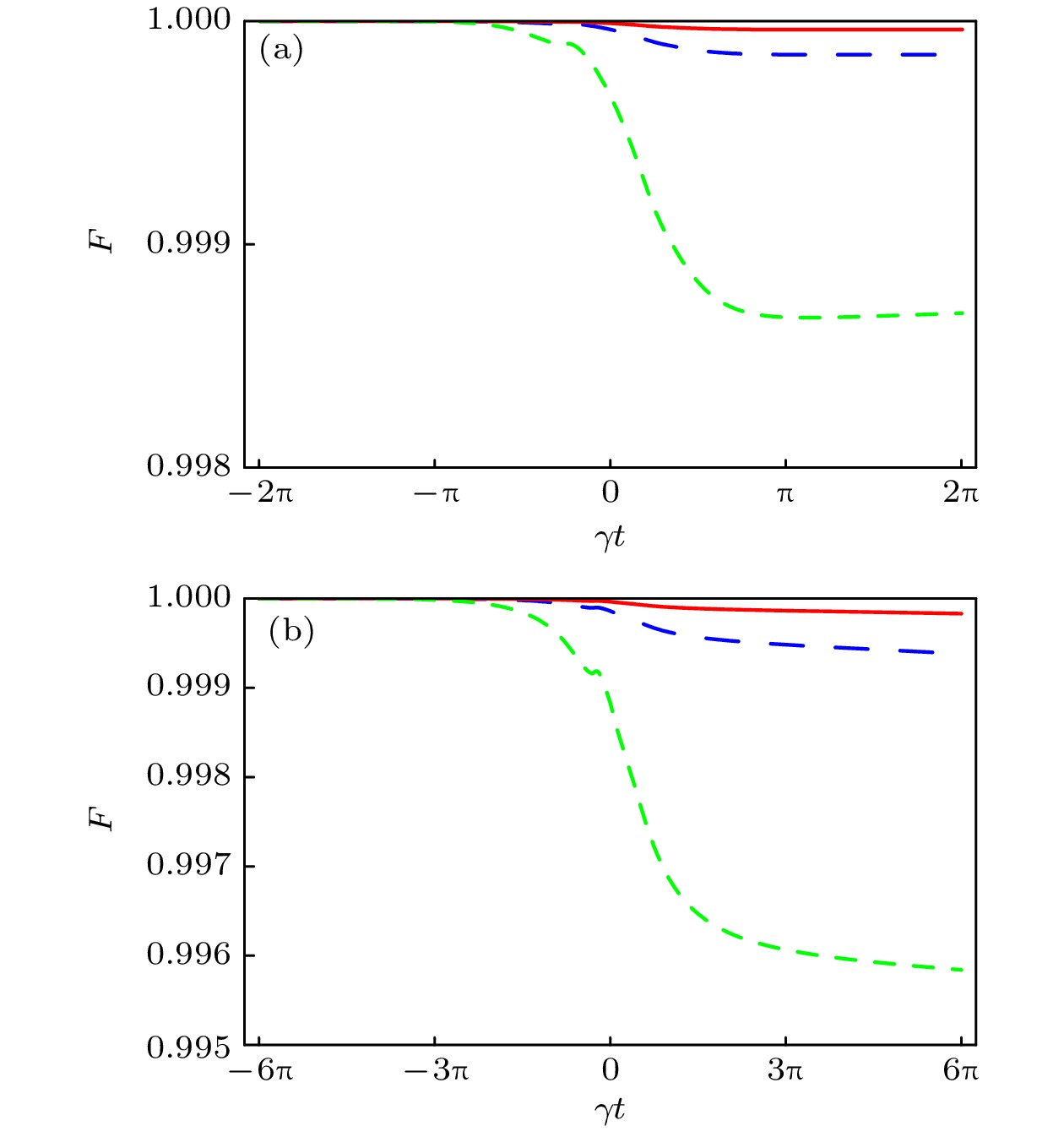
为了进一步分析激发态$ |2\rangle $的衰变对量子态相干布居数转移的影响, 引入保真度$ F = |\langle\psi_{1}(t)|\times \rho(t)|\psi_{1}(t)\rangle| $, 其中非绝热基矢$ |\psi_{1}(t)\rangle $的具体表达式见方程(20). 给定初始状态$ \tilde{\rho}(t_0) = |1\rangle\langle1 | $, 我们数值计算了方程(30), 其中的哈密顿量分别由方程(26)和(28)给出. 这两个模型中保真度随时间的关系如图2所示. 这里已经采用了如下的实验参数: 中性原子的衰减速率$ \varGamma = 3\pi\times10^{6} \ {\rm{Hz}}$^[26]; 扫描频率为$ \gamma = 6\pi\times10^{8}\ {\rm{Hz}} $; 模型1和模型2中的脉冲持续时间分别为$ \Delta t_{1} = 3.3\ {\rm{ns}} $和$ \Delta t_{2} = 10\ {\rm{ns}} $. 结果表明, 在末时刻模型1和模型2的保真度可以分别达到$ F(\gamma t_{1}) = 99.996\% $和$ F(\gamma t_{2}) = 99.983\% $.

本文采用$ SU(3) $李代数的逆向设计方案, 构造了在无旋转波近似下可以严格求解的含时三能级系统的哈密顿量, 并讨论了系统的非绝热动力学行为. 研究结果表明, 无论是在理想情况下, 还是基于脉冲截断和中间态衰变的实际演化中, 都可以实现高保真度的非绝热布居数转移. 与以往在无旋转波近似下的三能级系统非绝热量子调控方案相比, 本方案成功克服了演化过程中可能出现的Rabi振荡和脉冲奇异性的问题, 这为在无旋转波近似下电磁诱导透明、激光无翻转放大等进一步研究提供了一个可以借鉴的思路.