定向凝固技术借助人为手段调控固液界面的传播速率, 促使金属微观结构依循预期方向演变. 在此过程中, 固液界面会产生复杂多样的微观结构, 其中胞晶与枝晶属于界面形成过程中的典型微观结构, 这种微观结构对最终材料的品质和性能有着直接的影响. 因此, 定向凝固系统中界面结构的形成及其稳定性, 一直以来都是材料科学、凝聚态物理学和非线性科学等领域的重要研究课题.

诸多学者对晶体生长进行了研究, Mullins和Sekerka^[1,2]建立了平界面形态线性稳定性理论, 称为M-S理论, 这一理论已经成为研究固液界面形态特征的重要依据. 王自东等^[3,4]基于M-S理论, 考虑了界面曲率非线性和界面成分以及界面温度非线性对固液界面形态的影响, 建立了固液界面前沿扰动振幅随时间变化的非线性方程, 并推导非线性方程的解. Pelcé和Pumir^[5]发现了定向凝固过程中胞晶生长与Hele-Shaw粘指生长的内在相似性. Pocheau和Georgelin^[6–8], Georgelin等^[9]研究了Hele-Shaw生长室中胞晶形成的动力学, 发现胞晶形态的选择依赖于它的生长历史. Xu^[10–12]提出了界面波(IFW)理论, 利用摄动方法推导出了自由枝晶稳定性生长的理论模型, 研究了定向凝固中深胞晶界面斑图的形成演化, 并发现了胞晶深度取决于量子化条件. Chen和Xu^[13,14]利用Saffmen-Taylor^[15]曲线坐标得到了深胞晶形态的近似解析解, 发现了深胞晶生长的稳定性机制. 在此基础上, 蒋晗等^[16]与Sun和Jiang^[17]深入地研究了各向异性表面张力和各向异性界面动力学分别对深胞晶界面形态稳定性的影响, 但这些研究均忽略了流场对深胞晶的影响.

在流场的作用下, 范海龙等^[18]通过渐近分析发现流动会使柱状晶体的上游生长加快、下游生长减慢, 并且柱状晶的偏转角度也受到远场流动的 影响. 曹斌等^[19]发现远场来流会使球晶迎流面的稳定性降低, 并且随流速增大会降低球晶的临界稳定半径. 李向明等^[20]利用渐近分析方法发现了远场来流的强弱显著影响枝晶生长的Peclet数、尖端半径与生长速度. 王建元等^[21]发现切向流动使得胞晶阵列发生顺流偏转, 胞晶迎流侧容易产生分枝. 王贤斌等^[22]发现在液相对流作用下, 其对流流速越大, 胞晶尖端分岔越明显. Pandit等^[23]考察了由横截面变化引发的对流对胞晶与枝晶界面的影响, 并且这种对流似乎抑制了胞晶的形成. Trived等^[24]研究发现, 在存在流体流动的情况下, 平面状到胞状的转变受到了抑制, 并且流动速度会使胞晶到枝晶转变的临界速度略有提高. 曾红波等^[25]研究发现强迫对流显著影响定向凝固枝晶的生长方向, 导致上游方向的枝晶更粗大且生长更快, 并随流速增加而增强. Zheng和Chen^[26]应用多尺度方法研究了振荡流对定向凝固中柱状晶生长的影响, 研究发现振荡流交替加速和减缓柱状晶体的生长. Chen等^[27]利用渐近分析法探讨了剪切流对过冷熔体柱状晶体生长的影响, 剪切流显著地改变了柱状晶体的界面形态. 这些研究均表明, 流场对于晶体的生长和界面稳定性有着重要影响.

基于远场来流的流动不受局部扰动的强烈影响, 具有相对稳定和均匀的特性. 本文将建立一个综合温度场和浓度场以及远场来流的数学模型, 采用多重变量法和匹配渐近法. 研究远场来流作用下定向凝固中深胞晶生长的稳定性, 并揭示远场来流对不稳定区域大小的影响.

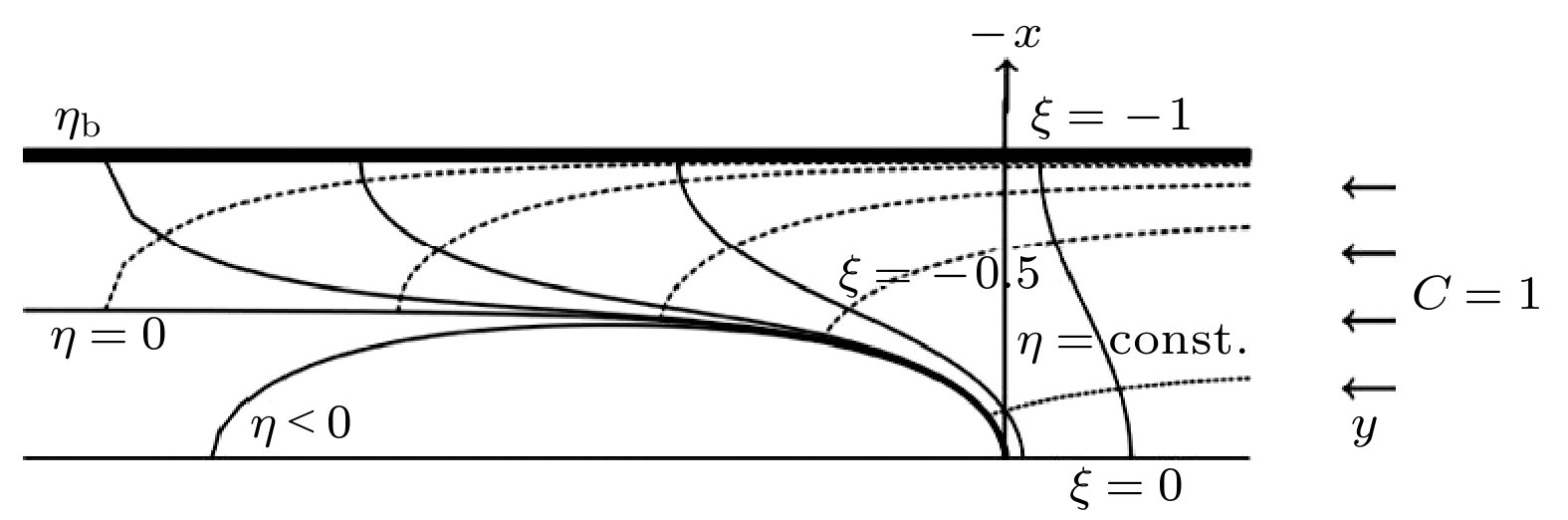
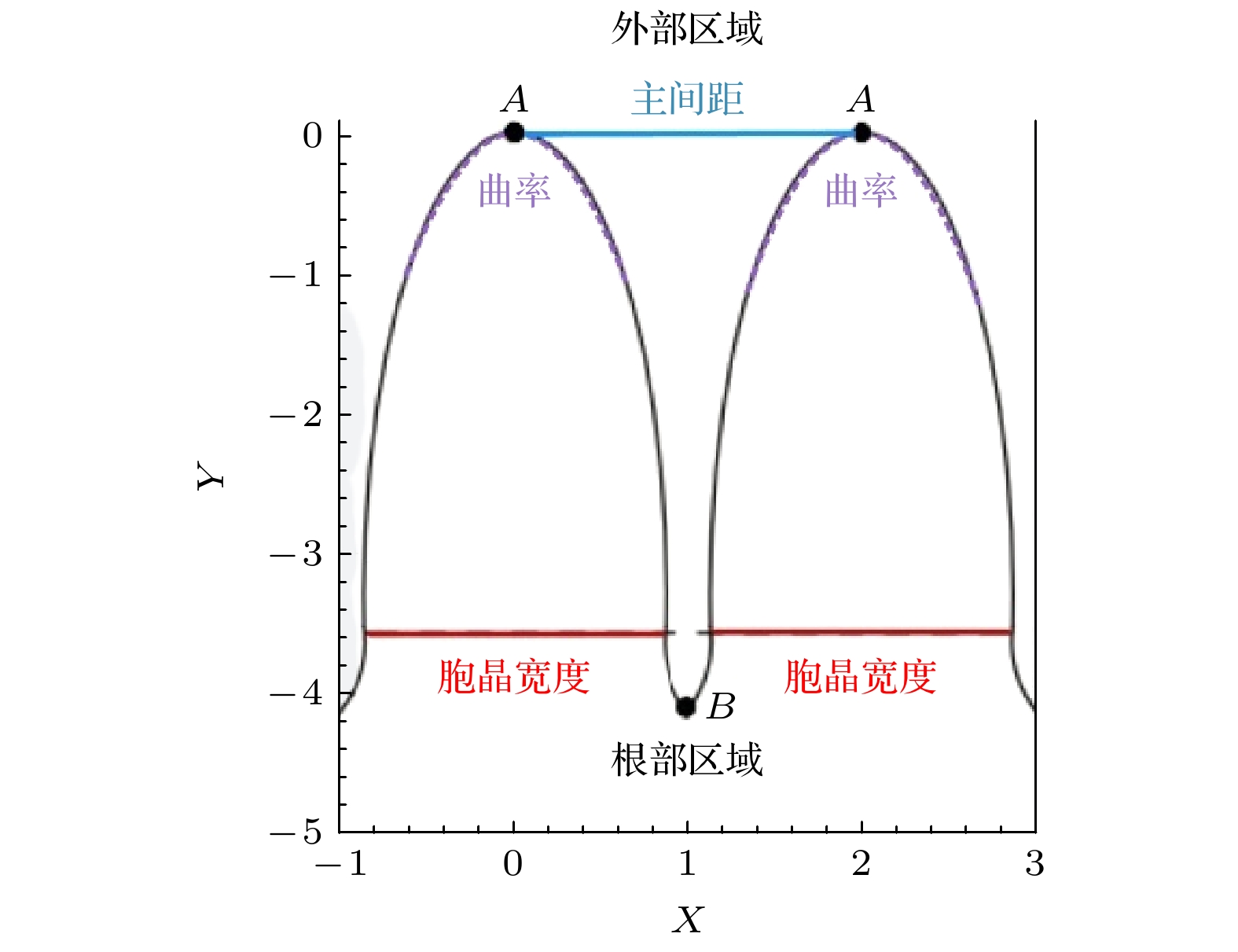
本文将使用二元合金熔体作为实验中的样本材料, 并将样本放置于细长的Hele-Shaw 生长室中, 那么凝固过程可以进行二维处理. 二元混合系统中次组元看作稀释的杂质, 忽略溶质在固相中的扩散, 界面上均为各向同性的表面能, 固相和液相中除扩散系数外其余热力学性质均相同. 现假定系统的温度梯度为${G_{\text{T}}}$, 浓度为$C$, 远场浓度为${C_\infty }$, 且${C_\infty }$为浓度尺度; 胞晶列的周期为${l_{\text{w}}}$, 深胞晶尖端半径为${l_{\text{t}}}$, 且${l_{\text{t}}}$为长度尺度, 胞晶相对宽度为${\lambda _0}$, 其中${\lambda _0}$与主间距参数$W$有关; 单位体积熔体凝固产生的潜热为$\Delta H$, 固相与液相达到热力学平衡时的温度为${T_{\text{M}}}$, 溶质扩散系数为${k_{\text{D}}}$, 表面张力系数为$\gamma $, 熔体密度为$\rho $, 液相比热容为${c_{\text{P}}}$. 在平面直角坐标系中, 界面以均匀速度$V$沿$y$轴拉动, 且$V$为速度尺度, 其方向为上液相方向, 在远场处有一小的来流${U_\infty }$, 且沿着$x$轴的方向扰动, 其中流场流速为$U$. 现定义溶质扩散长度为${l_{\text{D}}} = {k_{\text{D}}}/V$, 毛细长度为${l_{\text{c}}} = \gamma \rho {c_{\text{p}}}{T_{\text{M}}}/{\left( {\Delta H} \right)^2}$, 其中$ {l_{\text{t}}}/V $为时间尺度, $\Delta H/\left( {{c_{\text{P}}}\rho } \right)$为温度尺度; 无量纲化的温度梯度为$ G = \dfrac {{c_{\text{p}}}\rho {G_{\text{T}}}{l_{\text{D}}}}{\Delta H} $, 形态学参数为$ M = - \dfrac{m\rho {c_{\text{p}}}{C_\infty }}{ \Delta H} $, 其中$m < 0$为相图中液相线的斜率, 主间距参数为$W = \dfrac{l_{\text{W}}}{l_{\text{t}}}$, 参数${\lambda _{\text{G}}} = \dfrac{l_{\text{D}}}{l_{\text{G}}} = \dfrac{G}{M}$, 其中${l_{\text{G}}} = - m \dfrac{C_\infty }{G_{\text{T}}}$. 现假定其溶质扩散长度远远大于单个深胞晶尖端半径, 即${l_{\text{t}}} = {l_{\text{D}}}$, 选取小参数$ \varepsilon = (l_{\text{c}}/l_{\text{t}})^{1/2} $进行渐近分析, 其中$ \varepsilon = 1 $, Péclet数也可以写为$ Pe = \varepsilon \hat Pe = {l_{\text{t}}}/{l_{\text{D}}} $, 其中$ \hat Pe = O\left( 1 \right) $. 图1给出了胞晶列的界面图, 其中蓝色线段表示主间距, 红色线段表示胞晶宽度, 紫色虚线表示曲率.

由于受流场影响下的深胞晶生长需满足溶质扩散方程、界面方程和热传导方程以及 Navier-Stokes 方程和连续性方程, 同时也需满足热平衡条件、界面分离条件和Gibbs-Thomson条件以及质量守恒条件. 在此假设二元合金熔体为不可压缩牛顿流体, 现在利用Saffmen-Taylor解构造曲线坐标系$\left( {\xi , \eta } \right)$^[13], 如图2所示, 那么曲线坐标系$\left( {\xi , \eta } \right)$与平面直角坐标系$\left( {x, y} \right)$的转化关系为

其中,

基于胞晶列的周期性, 现假设每个胞晶宽度都为$W$, 那么只需要考虑单个区间即可, 从而此模型就等价于在讨论固定侧壁$x = \pm W$的通道中单个胞晶的生长模型. 根据Navier-Stokes 方程和连续性方程以及界面光滑条件和远场条件, 求得流场速度$U$在直角坐标系$\left( {x, y} \right)$下的渐近解为: $ U ={U_0} + \varepsilon {U_{1}}{+} \cdots $, 其中$ {U_{0}} = - Guj $, $ {U_1}{\text{ = i}}{U_\infty } \left( {1 - {{\mathrm{e}}^{ - y/Sc}}} \right) $, 其中$Gu$表示流动强度^[28], $Sc$表示施密特准数.

在$ \left( {\xi , \eta } \right) $曲线坐标系下, 非稳定态的胞晶生长服从下面的控制方程:

且边界条件为

(i) 远场区域内: 当$ \eta \to \infty $时, 有$ C \to 1; $

(ii) 侧壁上: 当$ \xi = \pm 1 $时, 有$ \partial C{\text{/}}\partial \xi = 0; $

(iii) 界面上: $ \eta = {\eta _{\mathrm{S}}}\left( {\xi , t, \varepsilon } \right) $, 有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

其中${y_*} = \varepsilon \hat Pe{\lambda _G}{y_0}$, $ K\left\{ {{\eta _{\text{S}}}} \right\} $是两倍平均曲率算子, $ \kappa $是分离系数.

现将胞晶生长的定常解作为基态, 则当$ \varepsilon \to 0 $时, 在界面条件为$ \eta = O\left( 1 \right) $的子区域附近, 整体的定常解可简化为^[29]

其中,

假设非稳定态胞晶生长的解可以表示为

其中$ {C_{\text{B}}}\left( {\xi , \eta , \varepsilon } \right) $表示为基态解, $ \tilde C\left( {\xi , \eta , t, \varepsilon } \right) $表示为扰动态解. 现将(7)式代入(2)式—(4)式中, 可以得到线性扰动系统满足的控制方程:

且边界条件为:

(i) 在远场区域内: 当$ \eta \to \infty $时, 有$ \tilde C \to 0; $

(ii) 在侧壁上: 当$ \xi = \pm 1 $时, 有$ \partial \tilde C/\partial \xi = 0; $

(iii) 在界面$ \eta = {\eta _{\text{B}}} $上, 将界面条件以基态解的界面做Taylor展开, 可得扰动态的界面条件如下:

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

其中,

现定义快变量^[14], 并利用多重变量渐近展开法来求解扰动态的渐近解. 即

其中$ {\xi _0} $待定, $ \beta = {\varepsilon ^{1/2}} $, $ - 1 < \xi < 0,\; - \infty < {\xi _ + } < 0,\;0 \leqslant \eta < \infty ,\; 0 \leqslant {\eta _ + } < \infty $.

现假定$ \left( {\phi , \varphi } \right) $这对函数服从Cauchy-Riemann条件, 那么$ g\left( {\xi , \eta } \right) = - {\varphi _\xi } = {\phi _\eta }, $$ k\left( {\xi , \eta } \right) = {\varphi _\eta } = {\phi _\xi }, $ 其中$ g\left( {\xi , 0} \right) = g\left( {{\xi _0}, \eta } \right) = 0, $$ \phi \left( {{\xi _0},\; \eta ,\; \varepsilon } \right) = 0, $$ \varphi \left( \xi , 0, \varepsilon \right) =0. $ 因此有, ${g_\xi } = {k_\eta }, \; - {k_\xi } = {g_\eta }. $

可以推出当独立变量$ \left( {\xi , \eta } \right) $转变成$ \left( {{\xi _ + }, {\eta _ + }} \right) $的情况下, Laplace方程的形式不会改变. 为了将单重变量转化为多重变量形式, 由定义的快变量(11)式可知, 可以采用以下求导替换:

将(11)式代入(8)式中, 可得到转化后的多重变量控制方程:

并且当$ \xi = {\xi _ + } = 0 $时, 在胞晶的尖端处, 有$ {\tilde \eta _{\text{S}}} = 0 $, $ \partial {\tilde \eta _{\text{S}}}/\partial \xi + {\beta ^{ - 1}}k\partial {\tilde \eta _{\text{S}}}/\partial {\xi _ + } = 0 $. 同时对在界面$ \eta ={\eta _+} = 0 $上的扰动态解$ \left( {\tilde C, {{\tilde \eta }_{\mathrm{S}}}} \right) $作Taylor展开, 则有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

其中$ \overline k = k\left( {\xi , 0} \right) $, $ {G_0} = G\left( {\xi , 0} \right) = \left( \lambda _0^2 +{{\left( {1 - {\lambda _0}} \right)}^2} {{\tan }^2}\left( {\pi \xi /2} \right) \right)^{1/2} $.

现按照多重变量$ \left( {\xi , \eta , {\xi _ + }, {\eta _ + }, {t_ + }} \right) $, 那么非稳定态胞晶生长的解可以表示为

由控制方程(8)式以及远场条件、侧壁条件、界面条件(9)式、 (10)式构成的系统, 若将此系统转化为多重变量系统, 那么有如下形式的渐近展开解:

若将(16)式代入(12)式—(14)式中, 那么可以得到多重变量系统的控制方程以及边界条件.

在零级近似中, 由于扰动项相乘为高阶小项, 可以忽略, 即可得零级近似系统的控制方程:

边界条件为:

(i) 在远场区域内: 当$ {\eta _{+}} \to {+}\infty $时, 有$ {\tilde C_0} \to 0$; (ii) 在侧壁上: 当$ \xi = \pm 1 $时, 有$ \partial {\tilde C_0}/\partial {\xi _ + } = 0$; (iii) 在界面$ \eta = {\eta _ + } = 0 $上, 有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

其中$ {\overline k_0} = {k_0}\left( {\xi , 0} \right) $.

(iv) 在胞晶尖端: 当$ \xi = {\xi _ + } = 0 $时, 有$ \partial {\tilde h_0}/ \partial {\xi _ + } ={\tilde h_0} = 0 $.

现考虑零级近似方程(17)式的一般模式解:

其中$ {D_0} $为一个任意的复常数.

现将(20)式代入界面条件(18)式、(19)式中, 则

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

其中$ {\overline \varOmega _0}\left( \xi \right) = {\varOmega _0}\left( {\xi , 0} \right). $

根据(21)式和(22)式可以求得色散公式为

其中,

由(23)式可知, 色散公式是关于$ {\overline k_0} $的三次多项式, 对给定的复参数$ {\sigma _0} $, 可以得到三个复波数即: $ \left\{ {\overline k_0^{(1)}\left( {\xi , 0} \right), \overline k_0^{(2)}\left( {\xi , 0} \right), \overline k_0^{(3)}\left( {\xi , 0} \right)} \right\} $. 色散公式展示了胞晶列生长系统内扰动态的界面波特征, 为了进一步分析色散公式, 现利用变量替换, 再次引用新的变量$ \rho $来替代$ \xi $, 即

且当$ \xi \to {1^ - } $时, $ \rho \to \infty $, 则有$ {G_0} = {\lambda _0}S\left( \rho \right) $, 另外, 对(24)式求关于$ \xi $导数, 则有

其中$ S\left( \rho \right) = {\left( {1 + {\rho ^2}} \right)^{1/2}} $, $ a = \left( {1 - {\lambda _0}} \right)/{\lambda _0} $.

现应用新变量$ \rho $来表示扰动态的解:

其中$ {\tilde k_{0}}\left( {\rho , 0} \right) = {\overline k_{0}}\left( {\xi , 0} \right)/G\left( \rho \right) $, $ {\rho _0} = \rho \left( {{\xi _0}} \right) $.

若将(24)式—(26)式代入色散公式(23)式中, 那么色散公式就可以用新变量$ \rho $表示为如下形式:

若令$ {k_{\text{e}}}(\rho) = G(\rho){\tilde k_0} (\rho)/(\lambda _0^2{B_1})^{1/2} $, $ {\sigma _{\text{e}}} = {\sigma _0}{B_0}/B_1^{1/2} $, 则有

对于给定的复数$ {\sigma _0} $, 那么(28)式就存在3个根, 分别为

其中,

若要使浓度场$ {\tilde C_0} $满足远场条件$ {\tilde C_0} \to 0 $, 那么必须满足$ \text{Re} \left[ {{{\overline k}_0}\left( {\xi , 0} \right)} \right] > 0 $, 由于$ \text{Re} \left[ {\overline k_0^{(2)}\left( {\xi , 0} \right)} \right] < 0 $, 因此波函数$ k_{\text{e}}^{{\text{(2)}}}\left( \rho \right) $的解$ {H_2}\left( \rho \right) $给出的扰动态的远场条件不能满足, 需舍掉. 只有波函数$ k_{\text{e}}^{{\text{(1)}}}\left( \rho \right) $和$ k_{\text{e}}^{{\text{(3)}}}\left( \rho \right) $的解$ {H_1}\left( \rho \right) $和$ {H_3}\left( \rho \right) $才满足条件, 其中$ {H_3}\left( \rho \right) $是长界面波, $ {H_1}\left( \rho \right) $是短界面波. 那么外部区域的通解可用两个基本界面行波的组合表示: $ {\tilde h_0} \left( \rho \right) = {D_1}{H_1} \left( \rho \right) + {D_3}{H_1}\left( \rho \right) $, 其中$ {D_1} $和$ {D_3} $为待定常数, 且

一级近似系统的控制方程为

将(20)式中$ {\tilde C_0} $代入一级近似的控制方程(29) 式中, 则

为了消除长期项, 则有$ \partial {\varOmega _0}/\partial \eta - \text{i}\partial {\varOmega _0}/\partial \xi = 0. $

那么由上面的结论, 可以将一级近似的控制方程表示为

且在界面$ \eta = {\eta _ + } = 0 $上, 有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

以上一级近似系统是非齐次的, 现考虑一级近似方程(30)式有以下形式的标准模式解:

将(33)式代入界面条件(31)式和(32)式中, 可得

(a) Gibbs-Thomson条件:

其中, $ {\overline \varOmega _1}\left( \xi \right) = {\varOmega _1}\left( {\xi , 0} \right) $,

(b) 质量守恒条件:

其中,

若(34)式和(35)式构成的非齐次线性系统的系数矩阵的行列式为零, 那么$ \left\{ {{\varOmega _1}, {D_1}} \right\} $有非平凡解的相容性条件为

现将$ {I_1} $和$ {I_2} $代入(36)式, 可以得到:

其中,

由(37)式可以看出, 一级近似解$ {\overline k_1}\left( \xi \right) $在函数$ F\left( \xi \right) $的解处有奇异性, 它位于$ \xi $的扩展复平面$ \varsigma = \xi + {\text{i}}{\xi _{\text{I}}} $内. 为了说明多重变量渐近展开(MVE)解的奇异性, 需要将$ F\left( \xi \right) $, $ {\overline k_0}\left( {\xi , 0} \right) $, $ {Y_\xi }\left( {\xi , 0} \right) $, $ {G_0}\left( \xi \right) $等函数解析扩展到复平面$ \varsigma = \xi + {\text{i}}{\xi _{\text{I}}} $内, 那么与之对应的函数分别为$ F\left( \varsigma \right) $, $ {\overline k_0}\left( {\varsigma , 0} \right) $, $ {Y_\varsigma }\left( {\varsigma , 0} \right) $, $ {G_0}\left( \varsigma \right) $等. 同时, 函数$ {\overline k_0}\left( {\rho , 0} \right) $解析延拓为复平面$ \rho =\rho + {\text{i}}{\rho _{\text{I}}} $内的复函数$ {\tilde k_0}(\rho , 0) $.

波数函数$ {\overline k_0}\left( {\varsigma , 0} \right) = \big\{ \overline k_0^{(1)}( {\varsigma , 0} ), \overline k_0^{(2)} ( {\varsigma , 0} ),\overline k_0^{({3})} ( {\varsigma , 0} ) \big\} $服从扩展后的色散公式:

那么在奇异点$ F\left( {{\varsigma _{\text{c}}}} \right) = 0 $处, 有$ \dfrac{\partial {\sigma _0}}{\partial {\overline k_0}} = \dfrac{\partial \displaystyle\sum {( {{{\overline k}_0}, {\varsigma _{\text{c}}}} )} }{\partial {\overline k_0}} = 0, $ 则

解析函数$ {\tilde k_0}\left( {\rho , 0} \right) = \big\{ \tilde k_0^{(1)}\left( {\rho , 0} \right),\tilde k_0^{(2)}\left( {\rho , 0} \right),\tilde k_0^{({3})} \left( {\rho , 0} \right) \big\} $服从扩展后的色散公式:

其中奇异点$ \rho = {\rho _{\text{C}}} $也在复平面$ \rho $内, 并且满足$ \partial {\sigma _0}/\partial {\tilde k_0} = \partial \displaystyle\sum {({{\tilde k}_0}, {\rho _{\text{C}}})} /\partial {\tilde k_0} = 0 $, 则

由(42)式可以得到三个复奇异点, 其中$ {\sigma _0} $为复数, $0 \leqslant {{\mathrm{Re}}} \left\{ {{\sigma _0}} \right\} \ll 1$, 当$ {\sigma _0} \to 0 $时, 奇异点$ {\rho _{\text{C}}} \to - {\text{i}} $.

现在对$ {\sigma _0} $进行固定, 并对(39)式两端求关于$ \varsigma $的偏导数和全导数, 由此可得$ {\overline k_0}\left( \varsigma \right){\varLambda _0}\left( \varsigma \right) = {\overline k'_0}\left( \varsigma \right)F\left( \varsigma \right) $, 其中,

当$ \varsigma = {\varsigma _{\text{c}}} $时, 有$ F'\left( {{\varsigma _{\text{c}}}} \right)F\left( {{\varsigma _{\text{c}}}} \right) = O\left( 1 \right) $, 故(37)式$ {\overline k_1}\left( \xi \right) $可以表示为

其中,

从(43)式可得, 解有一个孤立奇点$ {\varsigma _{\mathrm{c}}} $, 当$ \varsigma \to {\varsigma _{\text{c}}} $时, 有

其中$ {m_1}, {m_2} = O\left( 1 \right) $.

由于函数$ {\overline k_1}\left( \varsigma \right) $在平面$ \varsigma $内, 并且还是具有孤立奇异点的解析函数, 那么它在奇异点$ {\varsigma _{\text{c}}} $附近可展开为Laurent级数. 根据(44)式中暗含着$ {\varLambda _1}\left( {{\varsigma _{\text{c}}}} \right) = 0 $, 并且$ \varsigma = {\varsigma _{\text{c}}} $是函数$ {\overline k_1}\left( \varsigma \right) $在复平面$ \varsigma $内的单极点, 则可以得到$ {\sigma _1} $的表达式为

根据(45)式不难发现, 若$ {\sigma _0} $已知, 则$ {\sigma _1} $随之确定, 然而$ {\sigma _0} $仍为自由参数. 接下来将对解在奇异点$ {\varsigma _{\text{c}}} $附近进行分析, 并在$ \left( {\varsigma , \eta } \right) $平面内推导函数$ {\sigma _0} $的表达式.

由于MVE解在扩展平面内$ \left( {{\varsigma _{\text{c}}}, 0} \right) $处无效, 则解在$ \left| {\varsigma - {\varsigma _{\text{c}}}} \right| \ll 1, {\text{ }}\left| \eta \right| \ll 1 $邻域内不再有多个长度尺度. 因此, 为了求点$ \left( {{\varsigma _{\text{c}}}, 0} \right) $附近的内解, 需要对齐次系统展开分析, 即线性扰动系统(8)式以及界面条件(9)式和(10)式. 现引入内变量^[14]:

其中指数$ \alpha $待定.

使用上述内变量以后, 那么杂质浓度和界面形状函数表示为

现将(46)式和(47)式代入(8)式—(10)式中, 那么内解系统的控制方程为:

其中在界面上, 当$ {\eta _{\text{*}}} = 0 $时, 有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

现将内解进行渐近展开, 则

将(51)式代入(48)式—(50)式中, 由此可得到内解系统的零级近似控制方程, 即

其中在界面上, 当$ {\eta _{\text{*}}} = 0 $时, 有

(a) Gibbs-Thomson条件:

(b) 质量守恒条件:

现定义内变量$ {\rho _*} = \left( {\rho - {\rho _{\text{c}}}} \right)/{\varepsilon ^\alpha } $, 那么由控制方程(52)式以及解的解析性, 可得$ \partial {\tilde C_{*_0}}/\partial {\eta _*} = {{\mathrm{i}}} \partial {\tilde C_{*_0}}/\partial {\varsigma _*} $, 则(54)式可以用变量$ \rho $与内变量$ {\rho _*} $表示为

为了求解三阶常微分方程(55)式, 可以对在不同区域的解应用变换. 对外部区域的解应用变换:

对内部区域的解应用变换:

这里$ {\tilde k_{\text{c}}}\left( \rho \right) $为待定的参照波数函数, 并且参照波数函数$ {\tilde k_{\text{c}}}\left( \rho \right) $需要满足不等式$ \text{Re} \left[ {\tilde k_0^{(3)}} \right] <\text{Re}\left[ {{{\tilde k}_{\text{c}}}} \right] < \text{Re} \left[ {\tilde k_0^{(1)}} \right] $. 通过变换可以发现, 外部区域的解$ {\tilde h_0}\left( \rho \right) $可以看作是两个$ W $波的组合, 其解可以写为$ {\tilde W_0}\left( \rho \right) = {D_1}\tilde W_0^{( + )}\left( \rho \right) + {D_3}\tilde W_0^{( - )}\left( \rho \right) $, 其中

此处, 与短$ H $波$ {H_1}\left( \rho \right) $相对应的$ \tilde W_0^{( + )}\left( \rho \right) $现在是$ W $外行波; 与长$ H $波$ {H_3}\left( \rho \right) $相对应的$ \tilde W_0^{( - )}\left( \rho \right) $现在是$ W $内行波.

根据(57)式可以将(55)式重写为关于函数$ {\tilde W_{*0}}\left( {{\rho _*}} \right) $形式的控制方程, 即

其中,

现在选取适当的$ {\tilde k_{\text{c}}} $, 使得$ {\varDelta _1}(\rho ) = 0 $, 那么就有$ {\varDelta _0}\left( \rho \right) = \dfrac{2}{{\sqrt {27} }}\dfrac{{\sqrt {{B_1}} }}{{{B_0}}}{\left[ {\dfrac{{1 - \text{i}\rho }}{{S\left( \rho \right)}}} \right]^{3/2}} $和$ {\varDelta _2}\left( \rho \right) = \text{i}{\lambda _0}{G^2}\left( \rho \right) \times {\left[ {3\left( {1 - \text{i}\rho } \right){B_1}S\left( \rho \right)} \right]^{1/2}} $. 因此(58)式可以重新表示为

由(59)式可以发现, 此方程有孤立奇点和转向点: $ \rho = \pm {\text{i}} $, $ \rho = \pm {\text{i}}\alpha $, $ \rho = {\rho _{\text{c}}} $. 其中$ {\rho _{\text{c}}} $是方程在复平面$ \rho $内的一个简单转向点, $ \rho = \pm {\text{i}} $, $ \rho = \pm {\text{i}}\alpha $分别是函数$ S\left( \rho \right) $和$ G\left( \rho \right) $的零点. 由于

现要研究转向点$ {\rho _{\text{c}}} $附近的内解, 从而得出一致有效的渐近解, 那么需要从以下两种不同的情况进行分析: (i) $ \left| {{\sigma _0}} \right| = O\left( {1} \right) $, (ii) $ \left| {{\sigma _0}} \right| \ll 1 $.

现定义新变量$ {\hat \rho _*} = A{\rho _*} $, $ A = O\left( {1} \right) $, 分别考虑这两种情况, 在远场处内解的零级近似具有的形式: $ {\tilde W_{*_0}}\left( {{{\hat \rho }_*}} \right) = {D_*}\hat \rho _*^{1/2}H_v^{(2)}\left( z \right) $, 其中$ z = 2 v\hat \rho _*^{1/2 v} $, $ v = 1/\left( {{p_0} + 2} \right) $.

对于情况(i) $ \left| {{\sigma _0}} \right| = O\left( {1} \right) $有: $ {\hat \rho _*} = {A^{1/3}}{\rho _*} $, $ A = O\left( {1} \right) $, $ {p_0} = 1 $, $ {\theta _{\text{L}}} = 2{\pi}/3 $, $ \alpha = 1/3 $, $ v = 1/3 $; 对于情况(ii) $ \left| {{\sigma _0}} \right| \ll 1 $有: $ {\hat \rho _*} = A_*^{4/15}{\rho _*} $, $ {A_*} = O\left( {1} \right) $, $ {p_0} = 7/4 $, $ {\theta _{\text{L}}} = 8{\pi}/15 $, $ \alpha = 2/7 $, $ v = 4/15 $; 其中参数$ {\theta _{\text{L}}} $表示两条Stokes线之间的开角.

通过匹配内解与外解, 最终可以得到两种情况下的连接条件的统一形式:

在此基础上, 应用尖端光滑条件后, 特征值$ {\sigma _0} $将会确定为稳定性参数$ \varepsilon $和流动强度$ Gu $等其他物理参数的函数.

首先考虑情况(i), 假设$ {\sigma _0}{=}{\sigma _R} - {\text{i}}\omega $$ \left( {\omega > 0} \right) $, 现只对生长速度很小的模式进行稳定性分析, 然而此模式频率的数量级可以为$ \omega = O\left( {1} \right) $. 在外部区域内, 使用复特征值$ {\sigma _0} $表示物理解为:$ \text{Re} \big\{ {{{\tilde h}_0} ( {\rho , t} )} \big\} = \text{Re} \left\{ {H \left( \rho \right){{\text{e}}^{{\sigma _0}t/\beta }}} \right\} $, 其中$ H\left( \rho \right) ={D_1}{H_1} + {D_3}{H_3} $, $ {D_1} $与$ {D_{3}} $是$ H $波的系数. 现假设$ {d_1} = {D_1} {{\text{e}}^{ - {\text{i}}{\chi _1}}} $, $ {d_3} = {D_3}{{\text{e}}^{ - {\text{i}}{\chi _3}}} $, $ {\chi _1} = {\beta ^{ - 1}} \displaystyle\int_0^{{\rho _{\text{c}}}} {\tilde k_0^{(1)}} {\mathrm{d}}\rho $, $ {\chi _3} = {\beta ^{ - 1}} \displaystyle\int_0^{{\rho _{\text{c}}}} {\tilde k_0^{(3)}} {\mathrm{d}}\rho $.

现将$ v = 1/3 $代入(61)式有: $ {D_1}/{D_3} = - {\text{i}} $, 再令$ \chi = {\chi _1} - {\chi _3} $, 则有

为了满足尖端光滑性条件, 系数$ {d_1} $和$ {d_3} $必服从:

(i) 对称S-模式:

(ii) 反对称A-模式:

现定义$ \hat k_0^{(i)} ( \rho ) = \dfrac{\tilde k_0^{(i)}( \rho )}{( {\lambda _0^2{B_1}} )^{1/2}} $, $ {\varepsilon _v} = \dfrac{\beta }{ {\lambda _0}{B_1}^{1/2}} $, 则由(63)式—(65)式可以得到其量子化条件:

其中S-模式和A-模式分别为

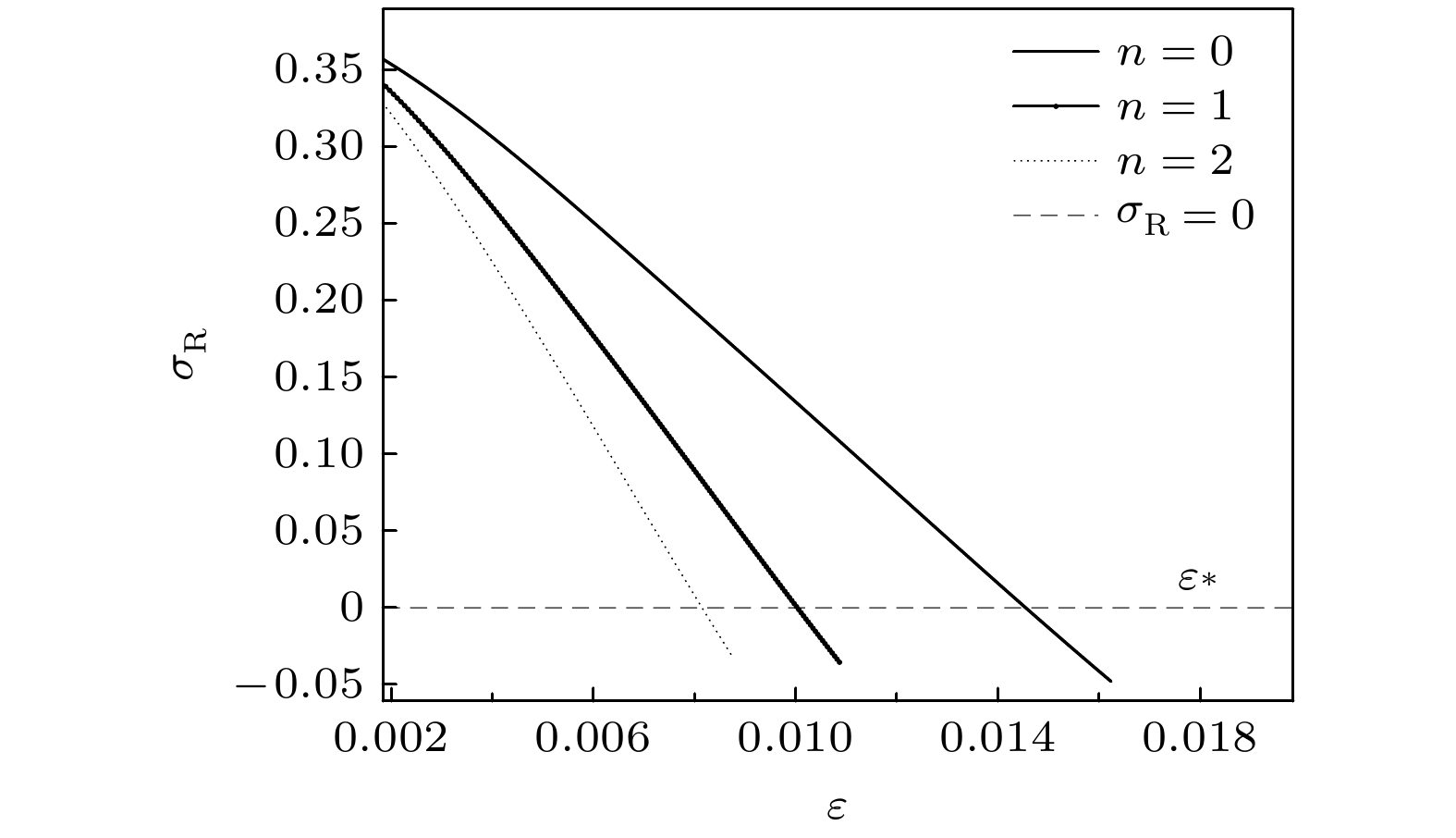
量子化条件(66)式确定了情况(i)复特征值$ {\sigma _0} $的频谱: $ \left\{ {{\sigma _{{0}, n}}} \right\} $, 其中$ n = 0, 1, \cdots $, 此复特征值的频谱产生两个离散的本征模式列: 对称S-模式和反对称A-模式. 图3给出了量子化条件下特征值实部随稳定性参数$ \varepsilon $的变化曲线, 在给定物理参数后, 系统允许一组中性稳定模式$ {\sigma _{\text{R}}} = 0 $, 此时$ \varepsilon = {\varepsilon _{ * , n}} $, 其中$ n = 0, 1, \cdots $且$ {\varepsilon _ * } = {\varepsilon _{ * , 0}} > {\varepsilon _{ * , 1}} > {\varepsilon _{ * , 2}} > \cdots $, 其中$ {\varepsilon _*} $为临界稳定性参数. 在零级近似中, 可以应用$ \text{Re} \left\{ {{\sigma _0}} \right\} = 0 $来求解$ {\varepsilon _*} $的值; 在一级近似中, 可以应用$ \text{Re} \left\{ {{\sigma _0} + \varepsilon {\sigma _1}} \right\} = 0 $来求解$ {\varepsilon _ * } $的值. 这些模式表现为沿着界面传播的行波, 也称此整体振荡不稳定机制为 GTW机制.

为了单独检测每个操作条件对特征值的影 响以及计算方便, 现使用新的操作参数:$ {\varepsilon _{\text{c}}} = {\left( {{l_{\text{c}}}V/{k_{\text{D}}}} \right)^{1/2}} $, 其中$ {\varepsilon _{\text{c}}} $是一个测定拉动速度$ V $的新参数. 此外, 还有$ {\lambda _{\text{G}}} = {G_{\text{c}}}/\varepsilon _{\text{c}}^{2} $, 其中$ {G_{\text{c}}} = {l_{\text{c}}}/{l_{\text{G}}} $, 它是一个测定温度梯度的新参数. 同时$ {B_1} $也可表示为$ {B_1} = \hat Pe{\hat B_1} $, 其中

用来计算胞晶生长的数据源于Pocheau^[8]等应用的纯SCN系统.

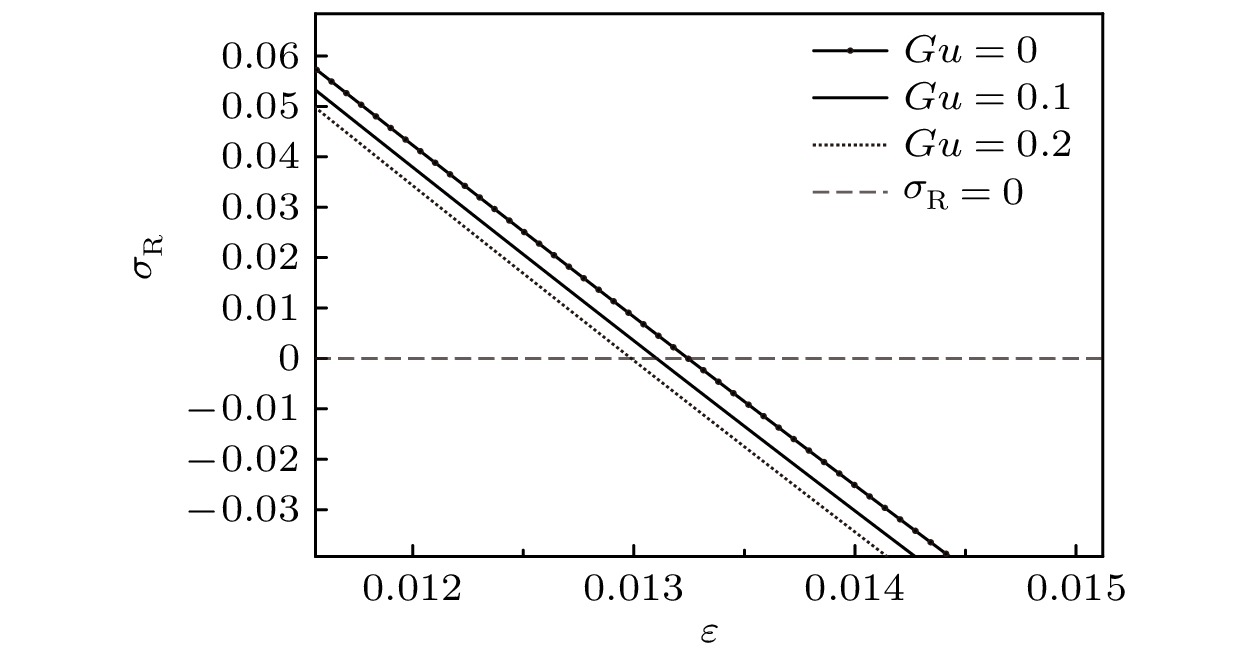
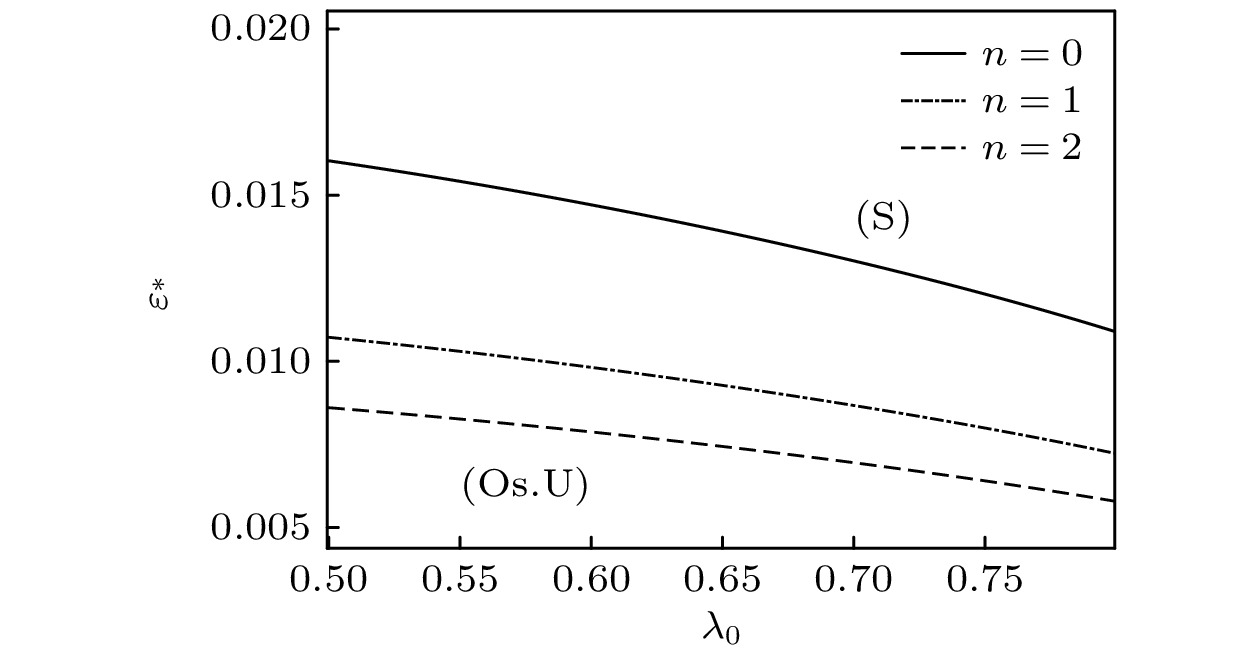
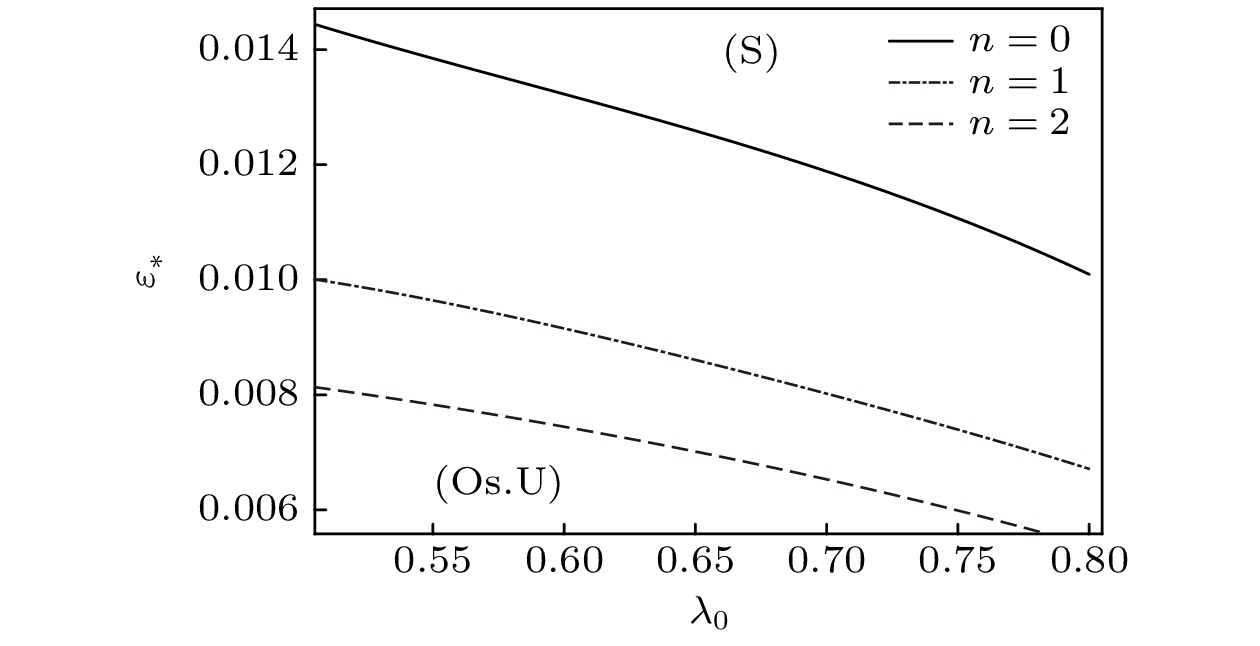
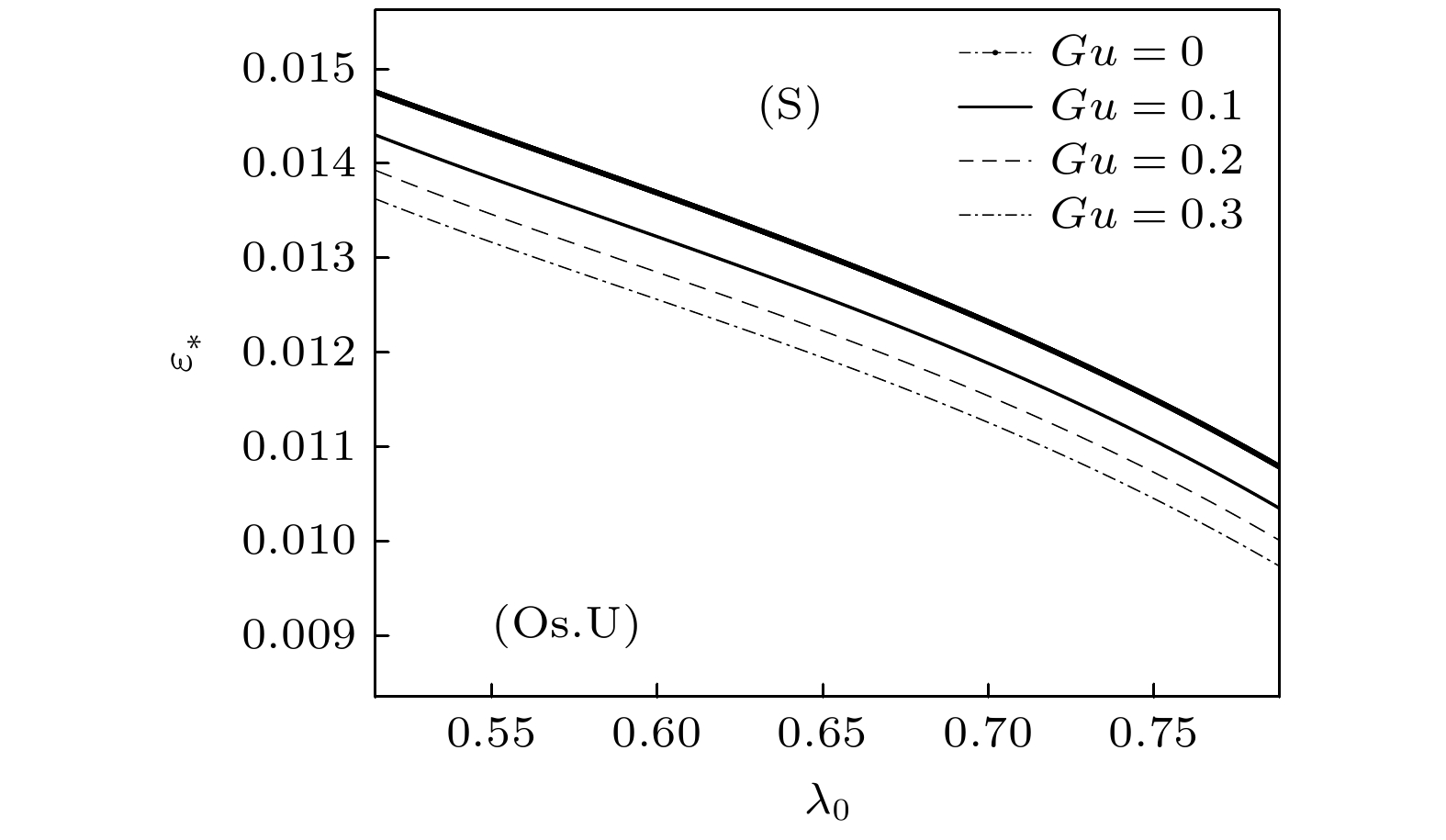
通过计算S-模式和A-模式的量子化条件发现, 对于同一指标$ n $, 其中GTW-S模式的增长率远比GTW-A式的增长率大, 针对此种情况称GTW-S模式比GTW-A更加危险. 此外还可以得到稳定性判断依据, 若稳定性参数大于临界稳定性参数, 则深胞晶的生长是稳定的; 若稳定性参数小于临界稳定性参数, 则深胞晶的生长是不稳定的. 图4展示了在$ n = 0 $的S-模式中, 随着流动强度$ Gu $增强, 临界稳定性参数变小. 图5和图6分别展示了在远场来流影响时, 零级近似与一级近似GTW-S中性模式的曲线, 通过对比发现, 一级近似下的临界稳定性参数小于零级近似下的临界稳定性参数, 并且都是在$ n = 0 $时最危险. 图7展示了$ n = 0 $时一级近似GTW-S中性模式的曲线, 随着流动强度$ Gu $的增强, 中性模式产生强振荡的枝晶结构的整体振荡不稳定性的稳定区域变大. 这里与Wang等^[22]和Pandit 等^[23]得到的实验结果相同, 加入流场后会抑制胞晶的形成, 使得胞晶尖端出现分叉.

根据以上的分析, GTW-S 中性模式的曲线将参数平面$ \left( {\varepsilon , {\lambda _{0}}} \right) $分成了$ S $区域和$ {\text{Os}}{\text{.U}} $区域, 即为稳定区域和不稳定区域. 由此可以得出系统的基态振荡稳定性判断依据: 若$ \left( {\varepsilon , {\lambda _{0}}} \right) \in S $, 则振荡稳定, 若$ \left( {\varepsilon , {\lambda _{0}}} \right) \in {\text{Os}}{\text{.U}} $, 则振荡不稳定. 整体GTW中性态描述了一个完美的周期性排列的以无穷小量级振幅振荡的枝晶列, 它有一个固定的相对宽度$ {\lambda _0} $和选定的$ \varepsilon = {\varepsilon _ * }, $ 从而有固定的主间距和尖端位置. 然而, 它有一个振荡的尖端半径和枝晶界面形状, 故称GTW的中性曲线为枝晶分枝, 称GTW模式波为枝晶模式. LF-S中性模式曲线可称为胞晶分枝, 由于对应的相对宽度的取值范围是$ 0.5 <{\lambda _0} < 1, $ 而且其光滑的界面形状像Saffman-Taylor解的指状, 故LF-S模式可称为胞晶模式^[14].

针对情况(ii)实特征值的频谱, 其系统也允许两种类型的整体低频(LF)模式. 但情况(ii)在推导过程中需要处理更高阶的非线性方程, 这使得理论分析和数值计算的难度大幅增加, 后续将继续开展对低频模式的研究.

本文基于界面波理论深入探讨了定向凝固过程中远场来流对深胞晶界面形态稳定性的影响. 以胞晶生长的定常解作为基态, 应用匹配渐近展开法和多重变量渐近展开法, 有效解决了远场来流情况下线性扰动态的特征值问题. 在此基础上, 进一步导出了胞晶界面扰动振幅变化率的色散关系, 并据此得出了整体模式解及其特征值的量子化条件, 建立了用于判断深胞晶生长临界稳定性的依据. 研究结果表明, 在远场来流影响下的系统中有两种主要不稳定性机制: 整体振荡(GTW)不稳定性与低频(LF)不稳定性, 并且系统允许对称模式和反对称模式. 若深胞晶的界面稳定性参数大于临界稳定性参数, 则深胞晶的生长稳定; 若小于, 则深胞晶的生长不稳定. 在远场来流的影响下, 对称的GTW-S模式比反对称的GTW-A更加危险, 并且 GTW-S模式中$ n = 0 $的情况是最危险的振荡模式, 其不稳定区域也是最大的. 此外, 随着流动强度$ Gu $的增强, 临界稳定性参数变小, 中性模式产生强振荡的枝晶结构的整体振荡不稳定性的稳定区域也会变大.