高级搜索

基于简正波强度匹配的浅海水平阵目标深度估计方法

,  ,  ,  , 

downloadPDF

上一篇

下一篇

殷敬伟, 尹家瑞, 曹然, 黄春龙, 李理. 基于简正波强度匹配的浅海水平阵目标深度估计方法[J]. 物理学报, 2025, 74(14): 144301-1. doi: 10.7498/aps.74.20250419
引用本文: 殷敬伟, 尹家瑞, 曹然, 黄春龙, 李理. 基于简正波强度匹配的浅海水平阵目标深度估计方法[J]. 物理学报, 2025, 74(14): 144301-1. doi: 10.7498/aps.74.20250419
shu
Jingwei YIN, Jiarui YIN, Ran CAO, Chunlong HUANG, Li LI. A target depth estimation method in shallow water based on matched normal mode intensity[J]. Acta Physica Sinica, 2025, 74(14): 144301-1. doi: 10.7498/aps.74.20250419
Citation: Jingwei YIN, Jiarui YIN, Ran CAO, Chunlong HUANG, Li LI. A target depth estimation method in shallow water based on matched normal mode intensity[J]. Acta Physica Sinica, 2025, 74(14): 144301-1. doi: 10.7498/aps.74.20250419
shu

基于简正波强度匹配的浅海水平阵目标深度估计方法

  • 1.

    哈尔滨工程大学, 水声技术全国重点实验室, 哈尔滨　150001

  • 2.

    极地海洋声学与技术应用教育部重点实验室 (哈尔滨工程大学), 哈尔滨　150001

  • 3.

    哈尔滨工程大学水声工程学院, 哈尔滨　150001

    • 作者简介: 殷敬伟. E-mail: yinjingwei@hrbeu.edu.cn .
    通讯作者: E-mail: cran@hrbeu.edu.cn.; 

  • 中图分类号: 43.20.+g, 43.30.+m, 43.60.+d

A target depth estimation method in shallow water based on matched normal mode intensity

  • 1.

    National Key Laboratory of Underwater Acoustic Technology, Harbin Engineering University, Harbin 150001, China

  • 2.

    Key Laboratory for Polar Acoustics and Application of Ministry of Education (Harbin Engineering University), Harbin 150001, China

  • 3.

    College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China

    • Corresponding author: E-mail: cran@hrbeu.edu.cn.; 

  • MSC: 43.20.+g, 43.30.+m, 43.60.+d

  • 摘要: 针对浅海波导中存在的底质参数失配造成水平阵难以正确获取目标深度的问题, 在未知底质参数条件下, 提出了一种基于简正波强度匹配的目标深度估计方法. 通过波数域波束形成技术估计波导中各阶简正波的水平波数和强度, 在简正波模态函数特征方程的基础上利用有限差分法对简正波模态函数进行反演, 计算估计和反演简正波强度之间的匹配度, 最终实现目标深度估计. 基于水平均匀线列阵的仿真结果表明, 所提的算法无需底质参数即可实现对浅海目标深度较为准确的估计. 同时分析了算法在不同的底质参数、阵列孔径、声源频率、信噪比和声速失配条件下的深度估计性能. 结果表明, 所提方法不受底质参数失配的影响, 同时对声速失配较为稳健, 在阵元数不少于128, 频带范围为50—150 Hz, 阵元信噪比大于–10 dB的条件下可对全海深目标深度进行有效估计. 最终利用南海浅海的海试数据对所提方法的可行性进行了验证.
    Abstract: A novel target depth estimation method based on normal mode intensity match is proposed for shallow water environment by using horizontal array to overcome the performance degradation observed in traditional approaches under the condition that seabed parameters are not matched. Firstly, horizontal wavenumbers and normal mode intensities are estimated through wavenumber domain beamforming. Secondly, modal function of normal mode inversion is performed by solving the modal function characteristic equation by using the finite difference method. Thirdly, the match degree between inverted and estimated normal mode intensities is evaluated to estimate target depth. The numerical simulation results show that the proposed method can accurately estimate the target depth in shallow water scenarios without knowing the seabed parameters. Furthermore, the performance of the method is analyzed under different conditions including different seabed parameters, array apertures and source frequencies. The results reveal three conclusions: 1) the mismatch of seabed parameters has no influence on the method; 2) the effective performance of full depth source estimation requires no less than 128 array elements, a frequency band range of 50–150 Hz, and the signal-to-noise radio of the element on a horizontal line array exceeding –10 dB; 3) the method has robust performance against sound speed profile mismatch. Finally, the feasibility of the proposed method is validated by the experimental data received by a horizontally towing 77-element array during the shallow-water sea trial in the South China Sea.
  • 加载中

  • 图 1  浅海水平分层波导模型

    Figure 1.  Model of shallow water horizontal layered waveguide.

    下载: 全尺寸图片 幻灯片

    图 2  有限差分网格

    Figure 2.  Finite difference grids.

    下载: 全尺寸图片 幻灯片

    图 3  仿真使用的浅海波导模型

    Figure 3.  Model of shallow water waveguide used in simulation.

    下载: 全尺寸图片 幻灯片

    图 4  20 m声源深度下简正波水平波数与强度仿真结果　(a) 理论与估计水平波数; (b) 低阶简正波理论与估计水平波数; (c) 理论与估计简正波强度

    Figure 4.  Simulation results of normal mode wavenumbers and intensities at 20 m source depth: (a) Theoretical and estimated horizontal wavenumbers; (b) theoretical and estimated horizontal wavenumbers of low order normal modes; (c) theoretical and estimated normal mode intensities.

    下载: 全尺寸图片 幻灯片

    图 5  70 Hz处反演简正波模态函数

    Figure 5.  Modal functions of normal mode in 70 Hz by inverting.

    下载: 全尺寸图片 幻灯片

    图 6  目标深度估计结果　(a) 目标深度$1 — 99{\text{ m}}$; (b) 目标深度$52{\text{ m}}$

    Figure 6.  Results of depth estimation: (a) Source depth of $1 - 99{\text{ m}}$; (b) source depth of $52{\text{ m}}$.

    下载: 全尺寸图片 幻灯片

    图 7  不同阵列孔径下深度估计结果　(a) 水平阵阵元数64; (b) 水平阵阵元数128; (c) 声源深度$52$ m与$69{\text{ m}}$

    Figure 7.  Results of depth estimation in different array aperture: (a) Number of horizontal array sensors is 64; (b) number of horizontal array sensors is 128; (c) source depth of $52$m and $69{\text{ m}}$.

    下载: 全尺寸图片 幻灯片

    图 8  不同波导深度下$\delta $与$N$的关系

    Figure 8.  Relationship between number of sensor and $\delta $in different waveguide depth.

    下载: 全尺寸图片 幻灯片

    图 9  $\delta $与$\Delta B$的关系

    Figure 9.  Relationship between $\delta $and bandwidth $\Delta B$.

    下载: 全尺寸图片 幻灯片

    图 10  不同频率下深度估计结果　(a) 频率30 Hz; (b) 频率100 Hz; (c) 频率 200 Hz

    Figure 10.  Results of depth estimation in different frequency: (a) Frequency is 30 Hz; (b) frequency is 100 Hz; (c) frequency is 200 Hz.

    下载: 全尺寸图片 幻灯片

    图 11  30 m声源深度下简正波水平波数与强度仿真结果　(a) 理论与估计水平波数; (b) 低阶简正波理论与估计水平波数; (c) 理论与估计简正波强度

    Figure 11.  Simulation results of normal mode wavenumbers and intensities at 30 m source depth: (a) Theoretical and estimated horizontal wavenumbers; (b) theoretical and estimated horizontal wavenumbers of low order normal modes; (c) theoretical and estimated normal mode intensities.

    下载: 全尺寸图片 幻灯片

    图 12  不同底质参数下深度估计结果　(a) MFP (无失配); (b) 波数域匹配方法(无失配); (c) 本文所提方法(无失配); (d) MFP(失配); (e) 波数域匹配方法(失配); (f) 本文所提方法(失配)

    Figure 12.  Results of depth estimation in different seabed parameters: (a) MFP (without mismatch); (b) wavenumber domain match method (without mismatch); (c) proposed method (without mismatch); (d) MFP (mismatch); (e) wavenumber domain match method (mismatch); (f) proposed method (mismatch).

    下载: 全尺寸图片 幻灯片

    图 13  不同信噪比下深度估计结果　(a) MFP (${\text{SNR}} = - 15{\text{ dB}}$); (b) 波数域匹配 (${\text{SNR}} = - 15{\text{ dB}}$); (c) 本文方法 (${\text{SNR}} = $$ - 15{\text{ dB}}$); (d) MFP (${\text{SNR}} = - 10{\text{ dB}}$); (e) 波数域匹配 (${\text{SNR}} = - 10{\text{ dB}}$); (f) 本文方法 (${\text{SNR}} = - 10{\text{ dB}}$); (g) MFP (${\text{SNR}} = $$ - 5{\text{ dB}}$); (h) 波数域匹配; (${\text{SNR}} = - 5{\text{ dB}}$); (i) 本文方法 (${\text{SNR}} = - 5{\text{ dB}}$)

    Figure 13.  Results of depth estimation in different SNR: (a) MFP (${\text{SNR}} = - 15{\text{ dB}}$); (b) wavenumber domain match method (${\text{SNR}} = - 15{\text{ dB}}$); (c) proposed method (${\text{SNR}} = - 15{\text{ dB}}$); (d) MFP (${\text{SNR}} = - 10{\text{ dB}}$); (e) wavenumber domain match method (${\text{SNR}} = - 10{\text{ dB}}$); (f) proposed method (${\text{SNR}} = - 10{\text{ dB}}$); (g) MFP (${\text{SNR}} = - 5{\text{ dB}}$); (h) wavenumber domain match method (${\text{SNR}} = - 5{\text{ dB}}$); (i) proposed method (${\text{SNR}} = - 5{\text{ dB}}$).

    下载: 全尺寸图片 幻灯片

    图 14  不同$\delta $下深度估计结果　(a) MFP ($\delta = 5{\text{ m/s}}$); (b) 波数域匹配 ($\delta = 5{\text{ m/s}}$); (c) 本文方法 ($\delta = 5{\text{ m/s}}$); (d) MFP ($\delta = $$ 10{\text{ m/s}}$); (e) 波数域匹配 ($\delta = 10{\text{ m/s}}$); (f) 本文方法 ($\delta = 10{\text{ m/s}}$); (g) MFP ($\delta = 15{\text{ m/s}}$); (h) 波数域匹配; ($\delta = 15{\text{ m/s}}$); (i) 本文方法 ($\delta = 15{\text{ m/s}}$)

    Figure 14.  Results of depth estimation in different $\delta $: (a) MFP ($\delta = 5{\text{ m/s}}$); (b) wavenumber domain match method ($\delta = 5{\text{ m/s}}$); (c) proposed method ($\delta = 5{\text{ m/s}}$); (d) MFP ($\delta = 10{\text{ m/s}}$); (e) wavenumber domain match method ($\delta = 10{\text{ m/s}}$); (f) proposed method ($\delta = 10{\text{ m/s}}$); (g) MFP ($\delta = 15{\text{ m/s}}$); (h) wavenumber domain match method ($\delta = 15{\text{ m/s}}$); (i) proposed method ($\delta = 15{\text{ m/s}}$).

    下载: 全尺寸图片 幻灯片

    图 15  试验态势

    Figure 15.  Experimental situation.

    下载: 全尺寸图片 幻灯片

    图 16  海试数据处理结果　(a) 估计水平波数; (b) 波数域波束形成; (c) 160 Hz处反演简正波模态函数; (d) 估计目标深度; (e) 1—5 m内估计目标深度

    Figure 16.  Results of experiment data processing: (a) Estimated horizontal wavenumbers; (b) wavenumber domain beamforming; (c) modal functions of normal mode at 160 Hz by inverting; (d) estimated target depth; (e) estimated target depth between 1 and 5 m.

    下载: 全尺寸图片 幻灯片
  • [1] Bucker H P 1976 J. Acoust. Soc. Am. 59 368 doi: 10.1121/1.380872
    [2] Baggeroer A B, Kuperman W A, Mikhalevsky P N 1993 IEEE J. Oceanic Eng. 18 401 doi: 10.1109/48.262292
    [3] Krolik J L 1992 J. Acoust. Soc. Am. 92 1408 doi: 10.1121/1.403935
    [4] Schmidt H, Kuperman W A, Scheer E K 1990 J. Acoust. Soc. Am. 88 1851 doi: 10.1121/1.400208
    [5] 李建龙, 潘翔 2008 声学学报 33 205 doi: 10.3321/j.issn:0371-0025.2008.03.003 Li J L, Pan X 2008 Acta Acustica 33 205 doi: 10.3321/j.issn:0371-0025.2008.03.003
    [6] 杨坤德, 马远良, 邹士新, 雷波 2006 声学学报 31 496 doi: 10.3321/j.issn:0371-0025.2006.06.004 Yang K D, Ma Y L, Zou S X, Lei B 2006 Acta Acustica 31 496 doi: 10.3321/j.issn:0371-0025.2006.06.004
    [7] 王奇, 王英民, 魏志强 2020 声学学报 45 475 doi: 10.15949/j.cnki.0371-0025.2020.04.004 Wang Q, Wang Y M, Wei Z Q 2020 Acta Acustica 45 475 doi: 10.15949/j.cnki.0371-0025.2020.04.004
    [8] Hursky P, Hodgkiss W S, Kuperman W A 2001 J. Acoust. Soc. Am. 109 1355 doi: 10.1121/1.1353592
    [9] Dosso S E, Wilmut M J 2008 J. Acoust. Soc. Am. 124 82 doi: 10.1121/1.2918244
    [10] Dosso S E, Wilmut M J 2013 JASA Express Lett. 133 274 doi: 10.1121/1.4794931
    [11] Li X L, Xu Y J, Gao W, Wang H Z, Wang L 2024 Remote Sens. 16 2227 doi: 10.3390/rs16122227
    [12] Akins F H, Kuperman W A 2022 JASA Express Lett. 2 074802 doi: 10.1121/10.0012041
    [13] Yang T C 2014 J. Acoust. Soc. Am. 135 1218 doi: 10.1121/1.4863270
    [14] Yang T C 2019 J. Acoust. Soc. Am. 146 4740 doi: 10.1121/1.5138595
    [15] 周玉媛, 孙超, 谢磊, 刘宗伟 2023 物理学报 72 084302 doi: 10.7498/aps.72.20222361 Zhou Y Y, Sun C, Xie L, Liu Z W 2023 Acta Phys. Sin. 72 084302 doi: 10.7498/aps.72.20222361
    [16] 孟瑞洁, 周士弘, 李风华, 戚聿波 2019 物理学报 68 134304 doi: 10.7498/aps.68.20190221 Meng R J, Zhou S H, Li F H, Qi Y B 2019 Acta Phys. Sin. 68 134304 doi: 10.7498/aps.68.20190221
    [17] 王宣, 孙超, 李明杨, 张少东 2022 物理学报 71 084304 doi: 10.7498/aps.71.20211742 Wang X, Sun C, Li M Y, Zhang S D 2022 Acta Phys. Sin. 71 084304 doi: 10.7498/aps.71.20211742
    [18] Bogart C W, Yang T C 1994 J. Acoust. Soc. Am. 96 1677 doi: 10.1121/1.410247
    [19] Nicolas B, Mars J, Lacoume J 2006 EURASIP J. Adv. Signal Process 65901 1 doi: 10.1155/ASP/2006/65901
    [20] Zhang Y K, Yang Q L, Yang K D 2023 Ocean Eng. 286 115502 doi: 10.1016/j.oceaneng.2023.115502
    [21] Liang G L, Zhang Y F, Zou N, Wang J J 2018 Math. Prob. Eng. 7824671 7824671 doi: 10.1155/2018/7824671
    [22] Premus V E, Helfrick M N 2013 J. Acoust. Soc. Am. 133 4019 doi: 10.1121/1.4804317
    [23] 李天宇, 李宇, 黄海宁, 杨习山 2021 声学学报 46 497 doi: 10.15949/j.cnki.0371-0025.2021.04.002 Li T Y, Li Y, Huang H N, Yang X S 2021 Acta Acustica 46 497 doi: 10.15949/j.cnki.0371-0025.2021.04.002
    [24] 李鹏, 章新华, 付留芳, 曾祥旭 2017 物理学报 66 084301 doi: 10.7498/aps.66.084301 Li P, Zhang X H, Fu L F, Zeng X X 2017 Acta Phys. Sin. 66 084301 doi: 10.7498/aps.66.084301
    [25] Zhang H C, Zhou S H, Liu C P, Qi Y B 2024 J. Acoust. Soc. Am. 156 1148 doi: 10.1121/10.0028229
    [26] Du Z Y, Hao Y, Qiu L H, Li C M, Liang G L 2024 J. Acoust. Soc. Am. 156 2989 doi: 10.1121/10.0034240
    [27] 汪德昭, 尚尔昌 2013 水声学 (第二版) (北京: 科学出版社) 第74页 Wang D Z, Shang E C 2013 Hydroacoustics (2nd Ed.) (Beijing: Science Press) p74
    [28] 芬恩 B 延森, 威廉 A 库珀曼, 亨利克 施米特著 (周利生, 王鲁军, 杜栓平 译) 2017 计算海洋声学(北京: 国防工业出版社)第286—287页 Jensen F B, Kuperman W A, Porter M B, Schimit H(translated by Zhou L S, Wang L J, Du S P)2017 Computational Ocean Acoustics (Beijing: National Defense Industry Press) pp286–287
    [29] Li X L, Wang P Y 2021 JASA Express Lett. 1 126002 doi: 10.1121/10.0006960
    [30] Porter M B 1991 The KRAKEN Normal Mode Program (La Spezia: SACLANT Undersea Research Centre) p1
    [31] 国家标准化管理委员会 2024 GB/T 44042-2024(北京: 国家标准化管理委员会)第三部分 Standardization Administration of the People’s Republic of China 2024 GB/T 44042-2024 (Beijing: Standardization Administration of the People’s Republic of China) Part3
  • 加载中
图( 16)
计量
  • 文章访问数:  18
  • HTML全文浏览数:  18
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-04-01
  • 刊出日期:  2025-07-20

基于简正波强度匹配的浅海水平阵目标深度估计方法

    通讯作者: E-mail: cran@hrbeu.edu.cn.; 
    作者简介: 殷敬伟. E-mail: yinjingwei@hrbeu.edu.cn
  • 1. 哈尔滨工程大学, 水声技术全国重点实验室, 哈尔滨　150001
  • 2. 极地海洋声学与技术应用教育部重点实验室 (哈尔滨工程大学), 哈尔滨　150001
  • 3. 哈尔滨工程大学水声工程学院, 哈尔滨　150001
  • 收稿日期:  2025-04-01

摘要: 针对浅海波导中存在的底质参数失配造成水平阵难以正确获取目标深度的问题, 在未知底质参数条件下, 提出了一种基于简正波强度匹配的目标深度估计方法. 通过波数域波束形成技术估计波导中各阶简正波的水平波数和强度, 在简正波模态函数特征方程的基础上利用有限差分法对简正波模态函数进行反演, 计算估计和反演简正波强度之间的匹配度, 最终实现目标深度估计. 基于水平均匀线列阵的仿真结果表明, 所提的算法无需底质参数即可实现对浅海目标深度较为准确的估计. 同时分析了算法在不同的底质参数、阵列孔径、声源频率、信噪比和声速失配条件下的深度估计性能. 结果表明, 所提方法不受底质参数失配的影响, 同时对声速失配较为稳健, 在阵元数不少于128, 频带范围为50—150 Hz, 阵元信噪比大于–10 dB的条件下可对全海深目标深度进行有效估计. 最终利用南海浅海的海试数据对所提方法的可行性进行了验证.

English Abstract

    全文HTML

    1.   引　言

    • 目标深度估计是水声被动定位的重要环节, 也是水声被动定位的难点, 对识别目标类型、目标跟踪等实际应用场景具有重要意义. 由于目标深度信息蕴含在接收信号的水声物理场结构中, 所以通常需要根据环境先验信息确定声场结构, 进而提取目标深度. 然而, 准确的环境先验信息获取非常困难, 而不准确的环境信息常导致深度估计产生较大误差, 因此减少对先验信息的依赖, 对于目标深度估计研究具有重要意义.

      匹配场处理方法(matched field processing, MFP)[1,2]是常用的目标深度估计方法, MFP充分利用了信号在水声波导中的传播特性, 将阵列接收信号与声学模型计算得到的拷贝场向量进行匹配以实现目标深度估计. 但准确的海洋环境信息通常难以获取, 因此拷贝场向量常与真实值存在较大差别, 致使MFP失配而产生性能退化. 为减少环境失配对MFP的影响, 国内外学者进行了大量研究, 主要提出了两类方法. 第一类方法通过增强MFP对于环境失配的宽容性, 以减少环境失配时性能的下降. Krolik[3]通过人工扰动声速剖面产生的声压场对最小方差匹配场波束形成器施加线性约束, 提高了MFP在声速失配下的稳健性. Schmit等[4]对最大似然方法施加多个线性约束, 提出了一种邻域位置约束的匹配场方法, 提高了MFP对于环境失配的宽容性. 李建龙和潘翔[5]基于概率方法, 将环境参数建模为随机变量, 利用贝叶斯推断在失配情况下实现了目标深度的准确估计. 杨坤德等[6]将环境扰动时拷贝场协方差矩阵的特征向量引入到匹配场处理器中, 增强了MFP的宽容性. 王奇等[7]分析了环境扰动情况下的声场成分构成, 结合声场扰动模型与稀疏贝叶斯学习方法, 提高了MFP的宽容性和精度. 然而, 此类方法虽然提高了MFP在失配场景下的性能, 但存在一定的宽容性限度, 当环境失配程度较高时, 算法性能依然会急剧下降. 第二类方法为数据驱动的匹配场处理方法, 与传统匹配场方法不同, 此类方法无需某些环境参数(如底质参数)的先验信息, 而是从数据中估计环境参数或反演简正波模态函数, 因此理论上消除了某些环境参数失配产生的性能下降问题. Hursky等[8]通过打靶法计算波导中可能传播的所有简正波的模态函数, 并与垂直阵接收数据进行匹配, 消除了匹配场深度估计时对于底质参数的需要. Dosso和Wilmut[9,10]结合贝叶斯方法, 利用垂直阵接收数据反演声速剖面和底质参数, 无需环境先验即可对目标深度进行估计. Li等[11]研究了单水听器场景下的目标深度估计方法, 方法要求声源运动且辐射信号为两个不同频率的简谐信号, 通过有限差分公式关联简正波模态函数与水平波数, 利用浅海波导中运动目标的声场特征构造代价函数, 最后经由最小化代价函数确定波导中的简正波模态函数, 该方法无需底质参数即可估计目标深度. Akins和Kuperman[12]将MUSIC算法引入模态匹配中, 消除了短垂直阵进行目标深度估计时对于底质参数的依赖. Yang[13,14]通过目标相对垂直阵运动形成的水平孔径, 在无环境先验的情况下反演波导中简正波的模态函数及其水平波数, 实现了目标深度估计, 但是对目标初始距离较为敏感. 周玉媛等[15]在Yang[13,14]的基础上提出一种基于波束-波数域非相干匹配的浅海运动声源深度估计方法, 相比于后者, 该方法不依赖目标初始距离, 无需先验信息即可利用垂直阵准确估计目标深度. 由于数据驱动的匹配场处理方法无需某些环境参数, 因此相比于宽容性的匹配场方法, 在环境参数失配显著时深度估计性能不会受到影响. 垂直阵对水声物理场的深度方向进行采样, 可直接获得声场中的简正波模态函数, 因此上述深度估计方法大多基于垂直阵提出, 无法直接用于水平阵目标深度估计. 相比于垂直阵, 水平阵不受海深对于阵列孔径的限制, 且布放灵活, 隐蔽性高, 但是没有垂直孔径, 故深度估计难度较大, 研究水平阵深度估计方法是当前目标深度估计研究的重点.

      由于水平阵可以直接对水声物理场的水平方向进行采样, 所以相比垂直阵更容易进行简正波分离, 并以此完成目标检测[16]、测距[17]等任务. 利用水平阵分离简正波, 从其水平波数中提取目标的深度信息是当前浅海目标深度估计的主要思路. Bogart和Yang[18]对水平阵模态匹配方法的目标深度估计性能进行了分析. Nicolas[19]等通过水平阵估计接收信号的频率-波数曲线, 并与拷贝场曲线进行匹配, 成功实现了目标深度的估计. Zhang等[20]将不同深度下各阶简正波强度变化作为特征, 利用海底水平阵完成了目标深度判决. Liang等[21]结合改进AR回归模型和Hankel变换, 在运动目标场景下利用水平阵得到了简正波的水平波数和强度, 并通过与拷贝场匹配的方式估计目标深度. Premus和Helfrick[22]在已知目标距离的情况下分离接收信号中的简正波, 并利用子空间投影构造了目标深度判决问题. 李天宇等[23]对小孔径水平阵目标深度估计问题进行了研究, 通过合成孔径技术提高了简正波分离的精度, 并利用Camberra距离度量估计与理论简正波强度, 有效对目标深度进行了估计. 李鹏等[24]提出了一种波数域匹配深度估计方法, 通过将水平阵波数域波束形成的结果与声学模型计算的理论结果进行匹配, 实现了目标深度的估计. 尽管上述方法均可以实现基于水平阵的目标深度估计, 但需要较为准确的环境信息计算拷贝场向量, 当产生环境失配时, 上述方法可能失效, 无法准确估计目标深度.

      针对上述问题, 本文将数据驱动匹配场方法的思想引入到波数域匹配深度估计方法中, 提出了一种基于简正波强度匹配的浅海水平阵目标深度估计方法, 在已知声速剖面的情况下, 通过波数域波束形成估计波导中简正波的水平波数及强度, 并基于简正波模态函数的特征方程, 结合有限差分法数值反演波导中的简正波模态函数. 之后, 计算反演简正波强度并与估计值进行匹配, 实现目标深度估计. 由于通过波束形成测得的水平波数构造特征方程反演简正波模态函数, 因此本文方法无需波导的底质参数信息.

      本文结构如下: 第2节首先建立浅海水平分层波导简正波模型, 然后以该模型为基础, 给出了波数域波束形成的输出表达式, 说明了简正波模态函数反演原理及简正波强度匹配的深度估计方法; 第3节仿真检验了基于简正波强度匹配的浅海水平阵目标深度估计方法的性能, 讨论了阵列孔径、频率对测深性能的影响, 并与MFP, 波数域匹配方法, 在不同底质参数、信噪比和声速失配下进行了对比; 第4节利用南海海试数据验证了提出方法的有效性; 第5节给出相关结论.

    2.   基于简正波强度匹配的浅海水平阵目标深度估计方法原理

      2.1.   简正波模型

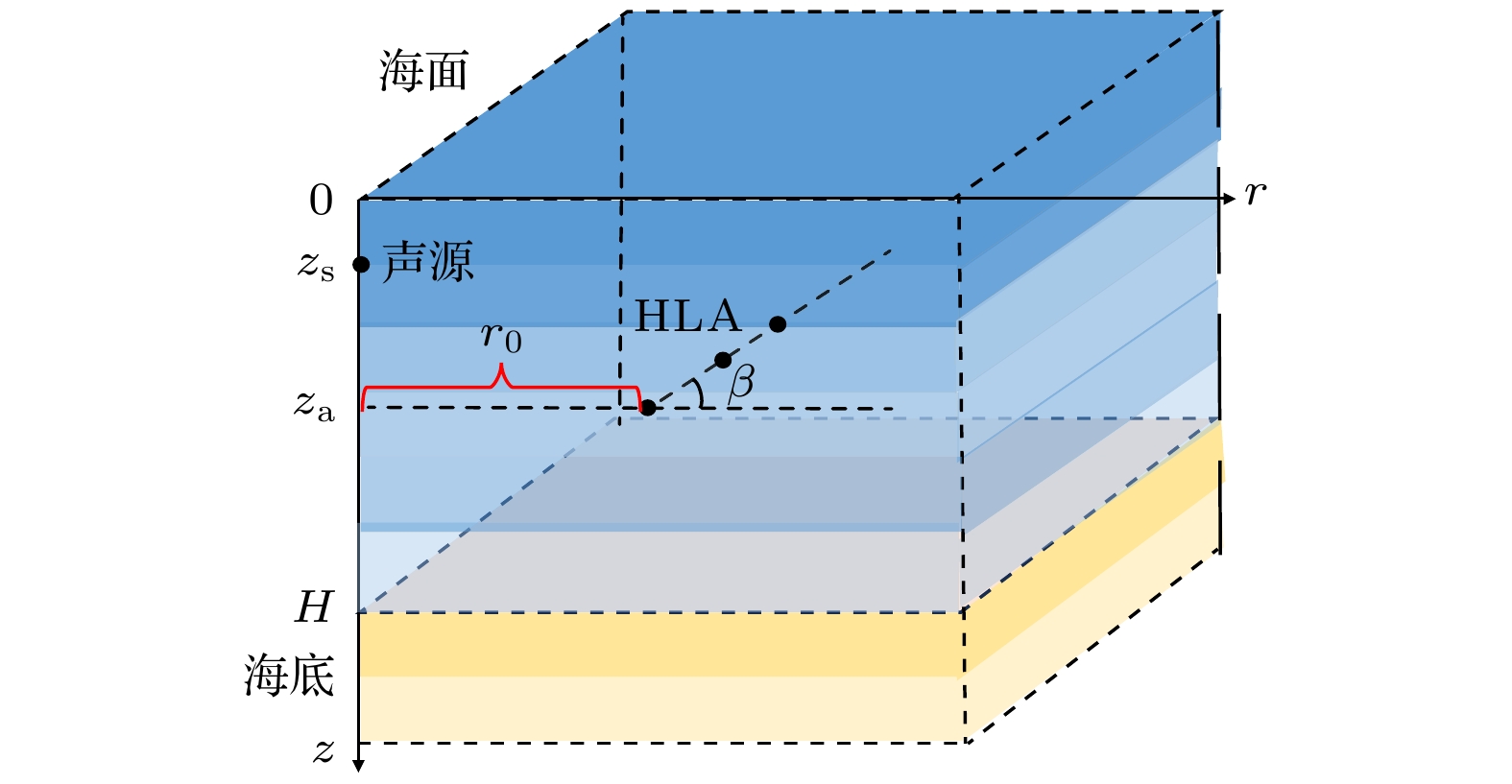
    • 假设水平分层波导深度为$H$, 水体声速为$c(z)$, 密度为$\rho (z)$. 阵元数$N$, 阵元间隔$d$的均匀水平线阵位于深度${z_{\text{a}}}$, 参考阵元与深度为${z_{\text{s}}}$的声源水平距离为${r_0}$. 假设接收阵列位于声源远场, 根据简正波理论, 第$n$个阵元上接收的频域声压信号可以写为[25]

      式中, $n = 0, 1, \cdots , N - 1$代表阵元序号; $f$表示声源频率; $M$为波导中传播简正波的最高阶数; ${\varPsi _m}(z)$表示波导中第$m$阶简正波模态函数; ${k_{{\text{r}}m}}$为第$m$阶简正波的水平波数; $\beta $为声源相对阵列的水平方位角, 可以通过角度域波束形成得到. 需要说明的是, 为方便表述, 本文中使用“简正波模态函数”指代“简正波的模态深度函数”, 例如第$m$阶简正波模态函数指第$m$阶简正波的模态深度函数${\varPsi _m}(z)$.

      • 2.2.   波数域波束形成

    • 为估计波导中传播简正波的水平波数, 利用水平阵对接收声压信号进行波数域波束形成, 假设${r_0} \gg (N - 1)d$, 可以得到波束输出为

      式中, ${\varphi _m}(kr) = \dfrac{{(N - 1)d({k_{\text{r}}} - {k_{{\text{r}}m}})\cos \beta }}{2}$; $\varepsilon $是其他简正波进行波束形成时产生的泄漏. 当阵列孔径较大时, 由于偏离中心时波束衰减迅速, 因此$\varepsilon $可以忽略不计[26].

      分别定义第$m$阶简正波强度${B_m}(f, {z_{\text{s}}}, {z_{\text{a}}})$和频率为$f$时的简正波强度$B(f, {z_{\text{s}}}, {z_{\text{a}}})$为

      通过波束输出结果$Y(f, {k_{\text{r}}})$可以估计波导中各阶简正波的水平波数${k_{{\text{r}}m}}$及强度${B_m}(f, {z_{\text{s}}}, {z_{\text{a}}})$, 估计所得的简正波强度${B_m}(f, {z_{\text{s}}}, {z_{\text{a}}})$相比(3)式中定义含有乘项$ {{\sqrt {2{\pi}} }}/[{{\rho ({z_{\text{s}}})\sqrt {{r_0}\cos \beta } }}] $, 由于各阶简正波强度均含有相同乘项, 所以并不影响后续信号处理. 当缺少底质信息时, 无法计算各阶简正波的理论水平波数, 因此无法确定估计水平波数的阶数$m$. 按照大小对估计所得的水平波数进行排序:

      式中, $D$代表估计得到的水平波数个数, 为方便后续表示, 仍然保留下标$m$, 但此时下标$m$的意义为排序后的水平波数序号而非简正波阶数.

      由上述分析可以看出, 利用水平阵进行波数域波束形成可以得到波导中简正波的水平波数和强度, 这些信息通过描述波导的声学方程与目标相联系, 从中可以提取目标的深度信息.

      • 2.3.   利用估计水平波数反演简正波模态函数

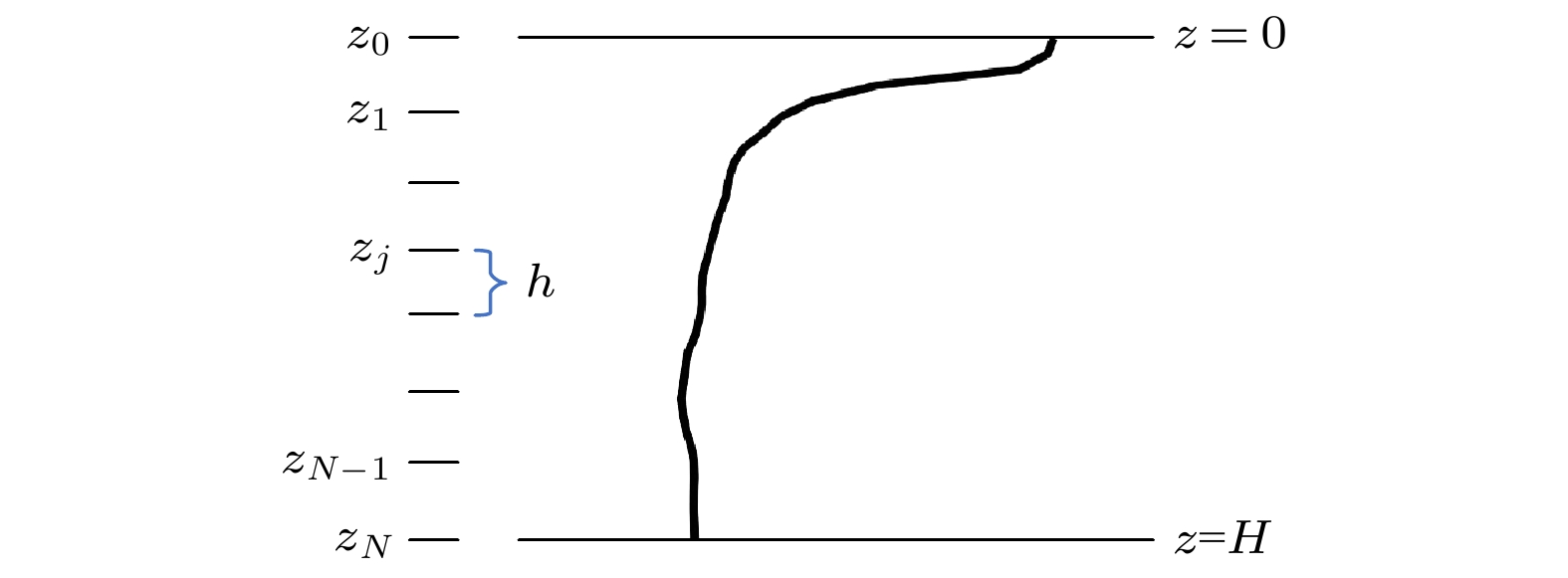
    • 由于目标的深度信息蕴含在波导中的简正波模态函数中, 所以在进行目标深度估计时, 需要得到波导中的简正波模态函数. 当声速剖面和海面边界条件已知时, 作为波动方程的海底边界条件, 海底底质参数决定了波导中的简正波模态函数. 当简正波水平波数由波数域波束形成得到时, 无需底质参数即可确定波导中的简正波模态函数. 首先按照图1所示方式建立柱坐标系, 此时波动方程可以写为

      对波动方程进行Fourier变换, 可以将波动方程简化为Helmholtz方程[27]:

      对Helmholtz方程进行Hankel变换, 得到第$m$阶简正波模态函数满足的特征方程:

      式中, $k(z)$为深度$z$处的声波波数. 当通过波数域波束形成得到某阶简正波的水平波数${k_{{\text{r}}m}}$后, 可以通过数值方法求解上述微分方程进而反演简正波模态函数$ {\varPsi _m}(z) $.

      本文中, 使用有限差分法[28]进行特征方程的求解, 如图2所示, 将深度区间分为$N$个等间隔区间, 每个区间的宽度为$h$, 为保证对简正波模态函数的充分采样, 通常将$h$选为波长的1/10. 根据Li和Wang[29]的研究结果, 可利用差分近似导数, 分别得到$ {\varPsi '_m}({z_j}) $的前向和后向差分近似式:

      结合(9)式与(10)式, 可以得到二阶导数的中心差分近似式:

      将(9)式—(11)式中的差分近似式代入到(8)式中, 得到有限差分法的数值迭代公式:

      迭代公式的初始条件为

      其中$\omega $表示声源角频率; $a$代表非0的任意常数, 一般取为1.

      通过下式对计算所得的简正波模态函数$ {\varPsi _m}(z) $进行归一化以与(1)式中的简正波定义相符合:

      通过上述步骤, 可在没有底质信息的情况下反演波导中的简正波模态函数.

      • 2.4.   简正波强度匹配估计目标深度

    • 由于目标的深度信息蕴含在波导中的简正波模态函数中, 所以可以通过反演得到的简正波模态函数估计目标深度. 利用反演简正波模态函数$ {\varPsi _m}(z) $, 根据(3)式的定义, 可以计算声源位于不同搜索深度${z_{{\text{ref}}}}$时, 水平阵深度处反演简正波强度${\tilde B_m}(f, {z_{{\text{ref}}}}, {z_{\text{a}}})$. 当${z_{{\text{ref}}}}$发生变化时, $\tilde B(f, {z_{{\text{ref}}}}, {z_{\text{a}}})$随之变化. 利用这一特性, 在深度区间上划分网格, 将声源在不同网格点深度上产生的反演简正波强度$\tilde B(f, {z_{{\text{ref}}}}, {z_{\text{a}}})$与估计简正波强度$B(f, {z_{\text{s}}}, {z_{\text{a}}})$进行匹配, 匹配度最高的搜索深度${z_{{\text{ref}}}}$即为估计声源深度$ {\tilde z_{\text{s}}} $.

      为通过简正波强度匹配估计声源深度, Li等[24]将估计简正波强度和声学软件计算的理论简正波强度之间的相关系数作为匹配度的度量, 本文使用了相似的匹配度定义, 定义频率为$f$, 声源深度为${z_{\text{s}}}$, 搜索深度为${z_{{\text{ref}}}}$时估计与反演简正波强度的匹配度为

      式中, ${\text{Cov}}[ \cdot ]$表示协方差; $d[ \cdot ]$表示方差.

      由于单频点情况下, 阵列获取目标深度信息的能力有限, 所以对${N_f}$个频率上获得的相关系数$ R(f, {z_{\text{s}}}, {z_{{\text{ref}}}}) $进行算术平均以获得宽带匹配度$ {R_{{\text{WB}}}}({f_1}, {f_{{N_f}}}, {z_{\text{s}}}, {z_{{\text{ref}}}}) $:

      式中, ${f_1}$为处理频带频率下限; ${f_{{N_f}}}$为处理频带频率上限. 对搜索声源深度${z_{{\text{ref}}}}$进行遍历时, $ {R_{{\text{WB}}}}({f_1}, {f_{{N_f}}}, {z_{\text{s}}}, {z_{{\text{ref}}}}) $最大值对应的深度${z_{{\text{ref}}}}$即为估计声源深度${\tilde z_{\text{s}}}$.

    3.   仿真与性能分析

    • 本节首先给出水平分层浅海波导仿真环境及参数设置, 对本文提出的基于简正波强度匹配的水平阵目标深度估计方法进行仿真验证. 再对阵列孔径、声源频率对本文方法性能的影响进行讨论, 最后对比分析MFP、波数域匹配和本文方法在不同底质参数、信噪比和声速失配条件下的性能.

      • 3.1.   仿真环境

    • 本节采用图3所示的浅海波导进行算法仿真和性能分析, 仿真环境参数设置如下: 波导深度为100 m, 沉积层厚度为2.5 m, 纵波声速为1620 m/s, 密度为1.76 g/cm3, 纵波衰减系数为0.2 dB/λ; 基岩层纵波声速为1760 m/s, 密度为2.0 g/cm3, 纵波衰减系数为0.2 dB/λ. 阵列为布置于海底, 阵元数128, 阵元间距8 m的均匀水平线列阵. 声源位于阵列端射方向, 且与阵列相距5 km.

      • 3.2.   不同声源深度的估计结果

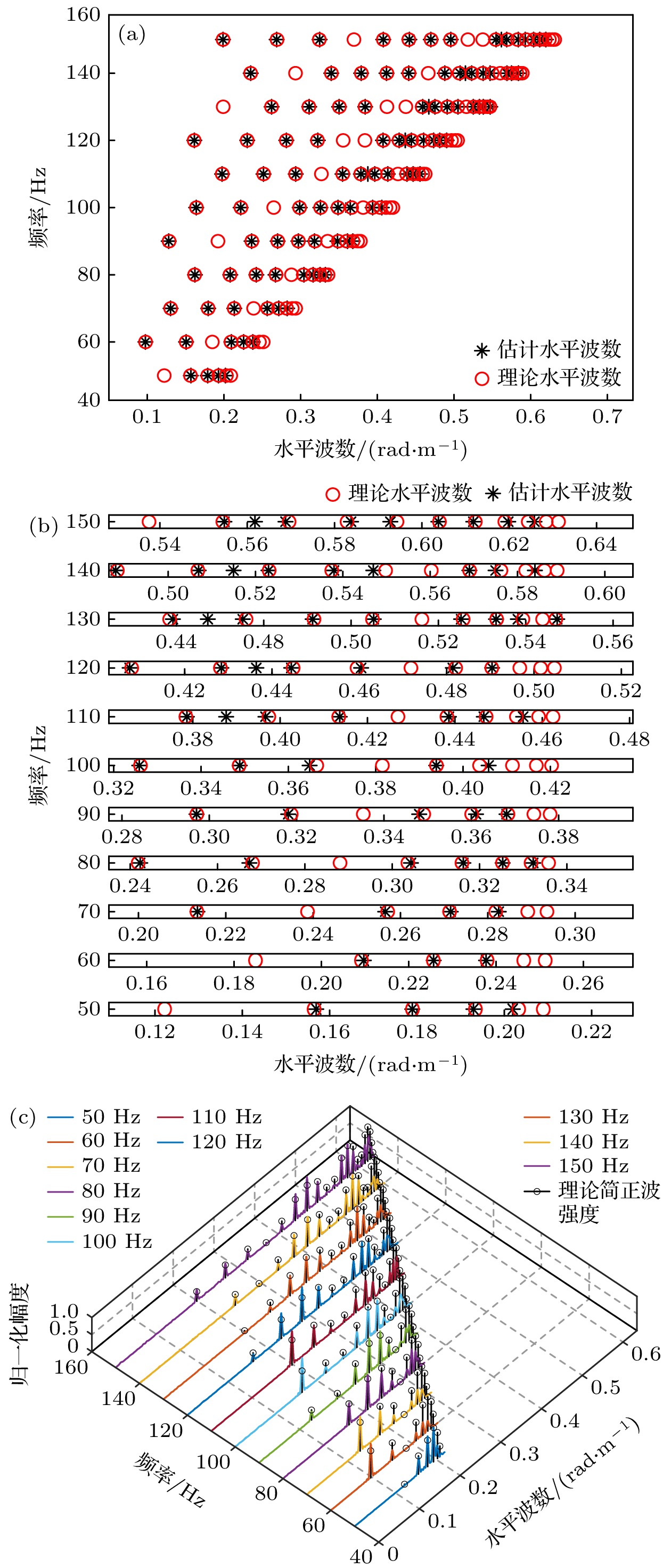
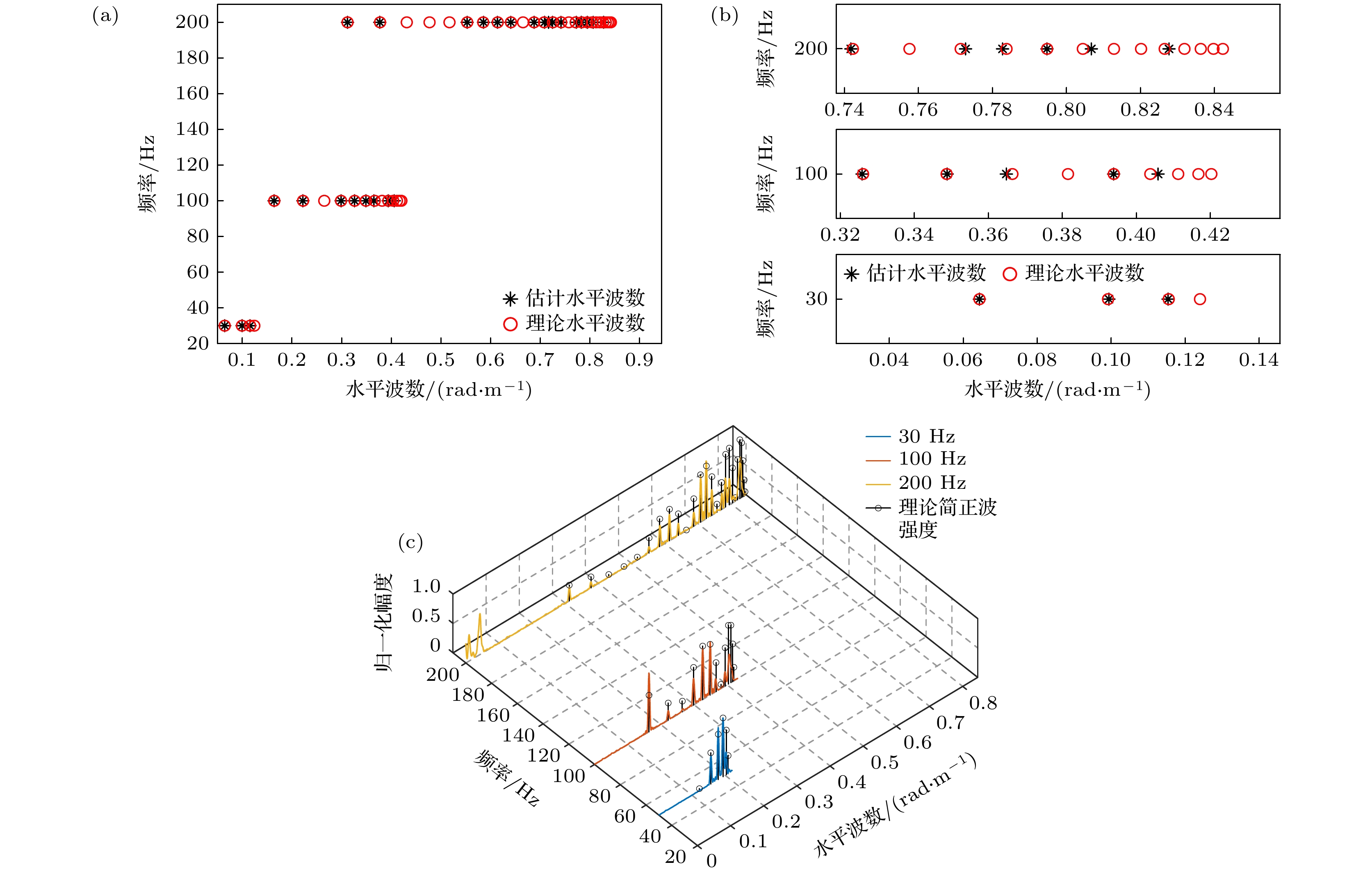
    • 为验证本文方法的可行性, 在图3的仿真环境下进行声源深度估计, 仿真阵列接收数据由Kraken简正波模型[30]生成, 阵列接收噪声为服从分布${\text{CN}}(0, {\sigma ^2}I)$的空间高斯白噪声, 信噪比定义为${\text{SNR}} = 10{\log _{10}}({{\sigma _{\text{s}}^{2}}}/{{{\sigma ^2}}})$, 其中$\sigma _s^2$为水平阵各阵元接收信号功率的均值. 文中的理论简正波模态函数与理论水平波数也均由Kraken简正波模型计算得到. 仿真中处理声源频段为50到150 Hz, 每隔10 Hz取一频点进行处理, 信噪比为10 dB, 设置声源深度由1到99m进行变化, 变化步长为1 m, 利用本文所提方法对目标深度进行估计. 20 m声源深度下的简正波水平波数与强度仿真结果如图4所示.

      观察图4的结果, 可以发现在仿真频点上, 波数域波束形成可以分离出大部分简正波, 但由于阵列孔径的限制, 难以准确分离低阶简正波. 同时, 存在一些强度较小的简正波, 这些简正波易被噪声和波束旁瓣淹没从而难以准确分离.

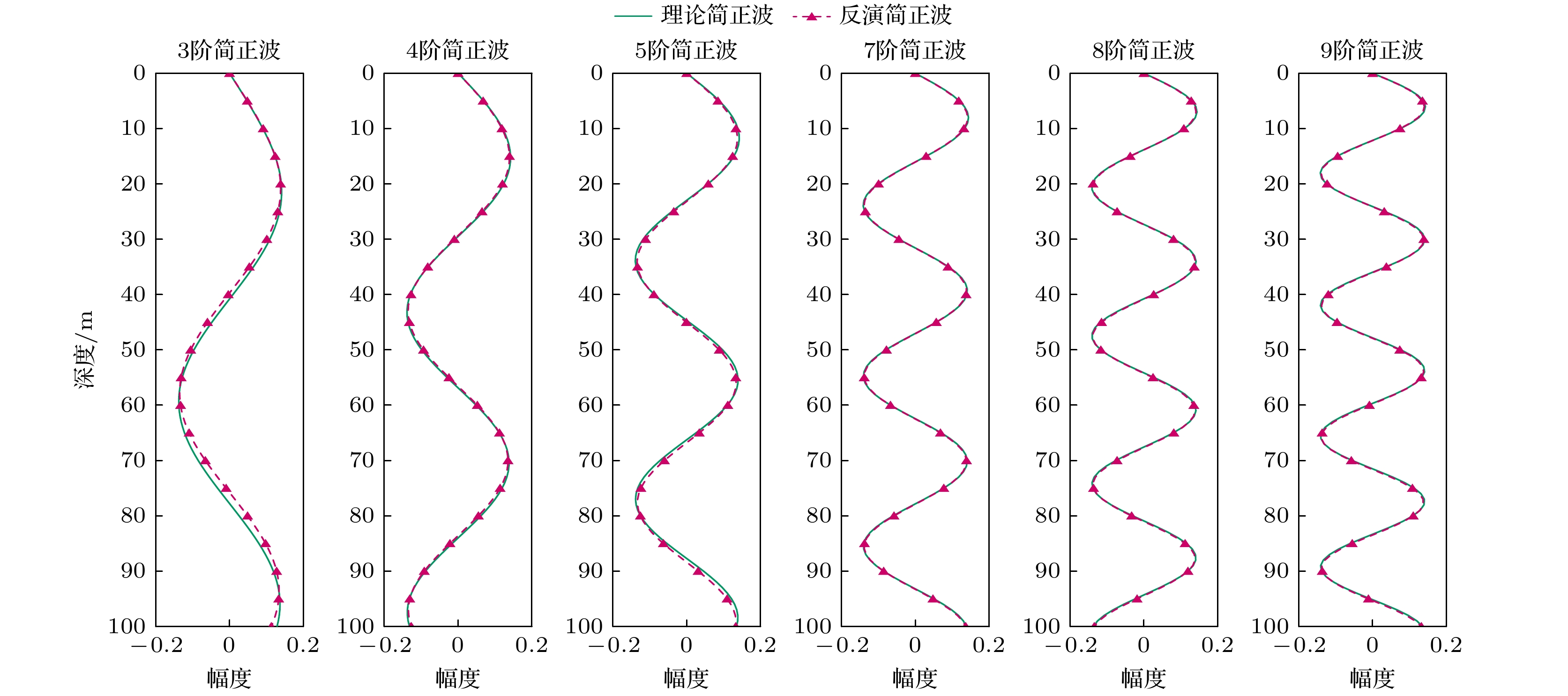
      利用波束形成得到的水平波数, 通过(12)式中的迭代方程反演波导中的简正波模态函数. 图5中给出了70 Hz处反演简正波和理论简正波模态函数的波形图, 可以看出, 3阶简正波模态函数存在较大误差, 误差原因可以通过相邻简正波水平波数差与水平阵列主瓣宽度的大小关系进行解释. 对于$n$阶简正波和$n + 1$阶简正波, 水平波数${k_{{\text{r}}n}}$和${k_{{\text{r}}(n + 1)}}$之差可通过下式近似[28]:

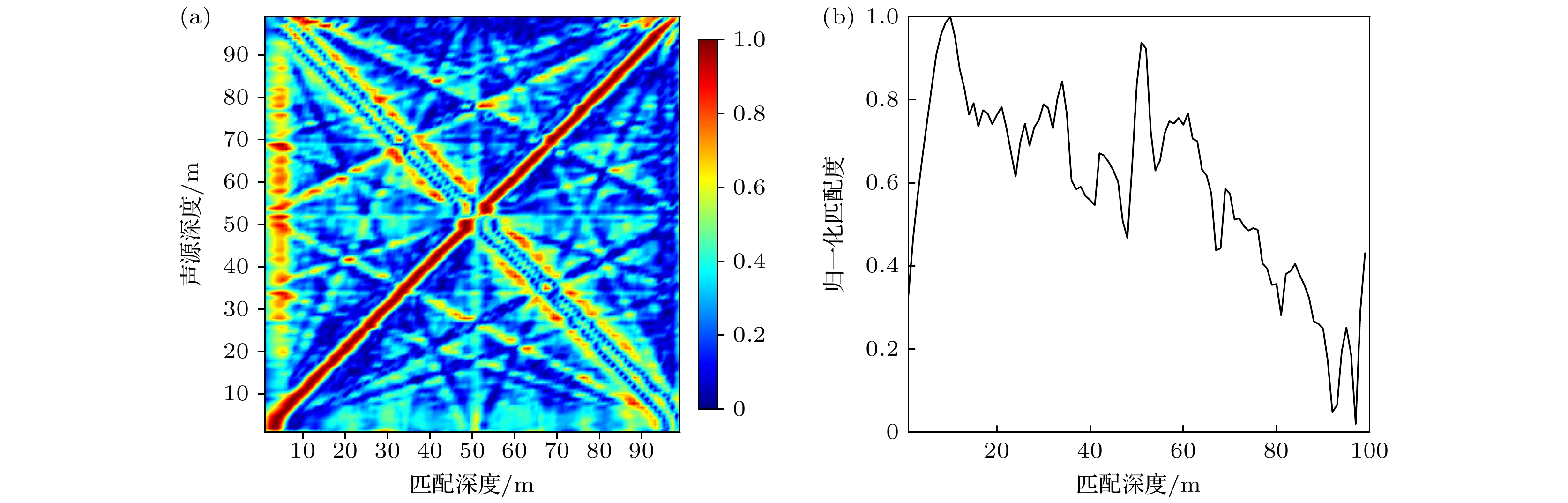
      式中, ${L_n}$为$n$阶简正波的水平跨度, 随简正波阶数的降低而增大. 因此伴随简正波阶数的降低, 相邻简正波的水平波数差逐渐减少, 当水平波数差小于水平阵主瓣宽度时, 无法对其进行分离. 由于水平阵主瓣宽度与阵列孔径成反比, 而仿真所用的阵列孔径较小, 阵列主瓣宽度大于2, 3阶简正波的水平波数差, 致使水平波数混叠, 难以准确反演3阶简正波模态函数.

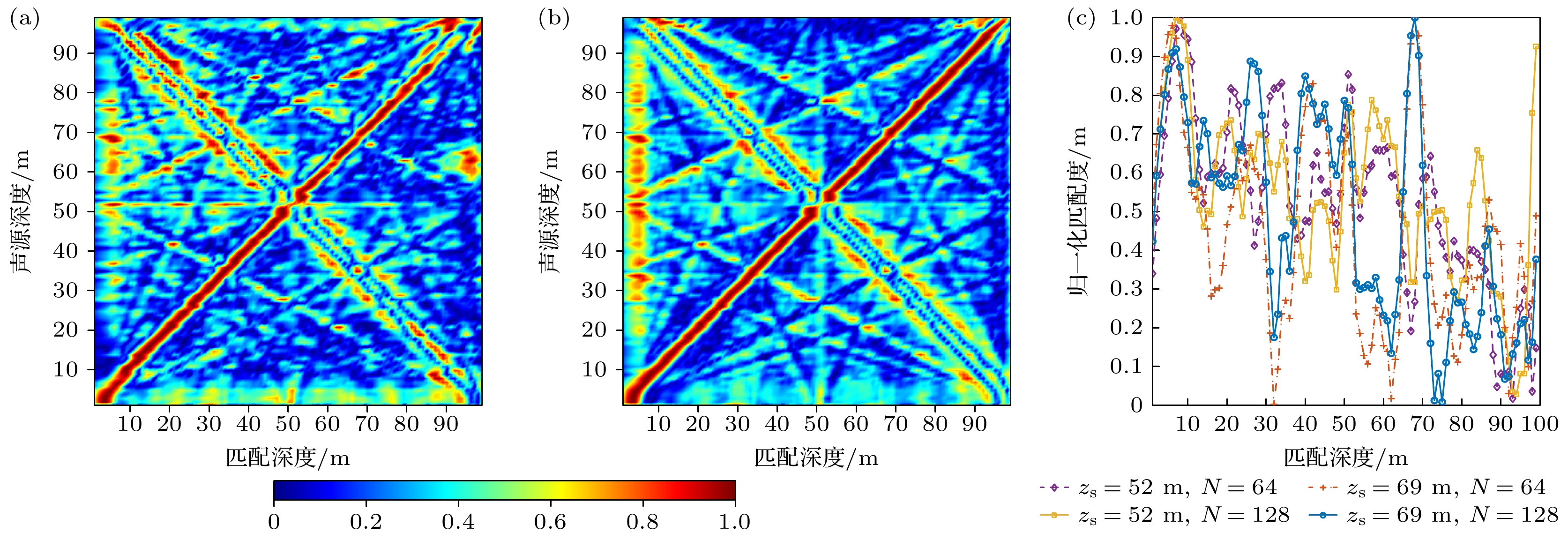
      在各声源深度上, 利用波数域波束形成估计简正波水平波数与强度, 通过特征方程反演简正波模态函数, 并按照(16)式计算匹配度, 匹配搜索的深度区间为1—99 m, 搜索网格为1 m. 图6(a)展示了不同声源深度下的匹配结果. 从图6(a)中可以看出, 在仿真条件下, 本文所提方法在无底质参数时可达到近乎全海深声源的深度估计能力. 注意到声源深度在$52{\text{ m}}$时, 匹配度峰值出现在$10{\text{ m}}$, 如图6(b)所示, 深度估计算法失效, 这是由于在仿真波导条件下, 声源激发的简正波强度相似度较高, 只有分离出波导中的所有简正波, 才能够消除测深的模糊性. 然而由于仿真所用阵列孔径的限制, 无法充分分离低阶简正波, 因此在声源深度$52{\text{ m}}$时出现了伪峰.

      • 3.3.   阵列孔径的影响

    • 阵列孔径决定了阵列的简正波分离能力, 大孔径阵列可以分离出在波数域上更加接近的简正波, 正确分离更多的简正波有利于减少目标深度估计的模糊性, 进而提高测深算法的性能. 此外, 目标相对阵列的水平方位变化可以等效为阵列孔径的变化, 当目标与阵列的水平方位角为$\beta $, 阵列孔径为$R$时, 等效的阵列孔径为$R\cos \beta $, 因此本节对阵列孔径对于算法性能的影响进行研究. 在图3的环境条件下, 分别设置阵元个数为64, 128. 声源以$1{\text{ m}}$为步长从深度$1{\text{ m}}$到深度$99{\text{ m}}$变化, 利用本文所提方法进行声源深度估计, 结果分别显示在图7(a)与图7(b)中.

      从图7(a)中可以看出, 当阵元数为64时, 由于阵列孔径较小, 无法准确分离低阶简正波, 使得声源位于某些深度时, 存在某些简正波强度相似度较高的深度, 因此测深结果中会出现较高的旁瓣. 当声源深度大于$85{\text{ m}}$时, 匹配结果中出现伪峰, 深度估计算法失效. 当阵元数增加到128时, 由于阵列孔径的增大, 阵列对低阶简正波的分离能力增强, 匹配时产生的模糊性随之降低, 此时对于深度大于$85{\text{ m}}$的目标, 也可以准确实现深度估计. 此外, 存在一些声源深度, 测深时会产生伪峰和较高的旁瓣, 且随着阵列孔径的增大, 二者变化较小, 如图7(c)所示, 这可能是因为波导中简正波模态函数的形状使得当声源存在于这些深度时, 产生的简正波强度与伪峰或旁瓣深度处简正波强度具有较高的相似度, 当阵列孔径较小, 无法分离出波导中的所有简正波时, 仅使用部分简正波进行匹配造成了伪峰和高旁瓣的产生.

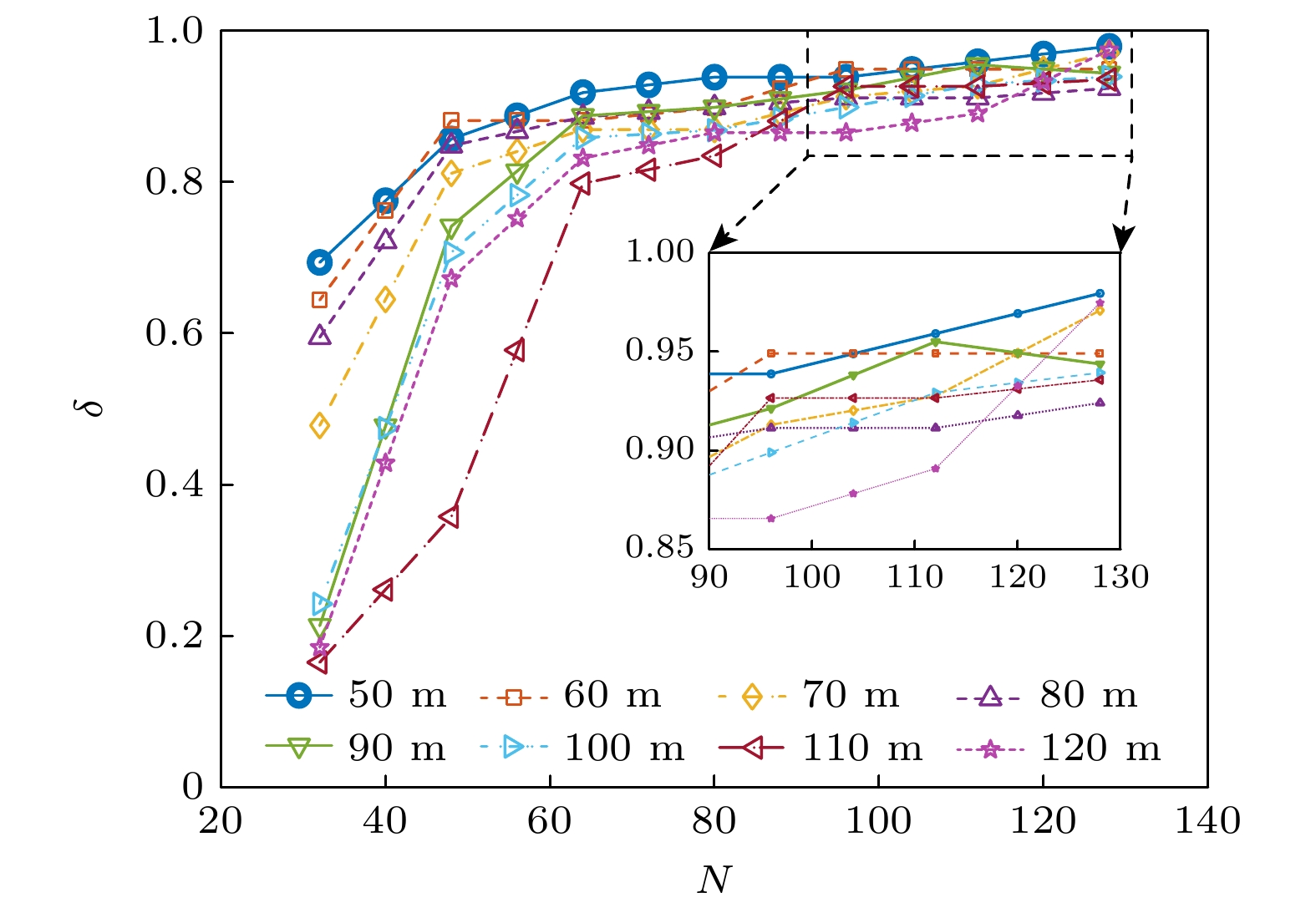
      为进一步研究阵列孔径的影响, 定义测深成功比例$\delta $为测深成功的声源深度数量与设置声源深度数量之比, 当估计深度与实际深度之差在$2{\text{ m}}$以内时即认为测深成功. 例如, 令声源深度由$1$到$99{\text{ m}}$以步长$1{\text{ m}}$变化, 其中在20, 60, 30 m三个深度上算法测深成功, 此时测深成功比例为$\delta = {3}/{{99}}$. 在不同波导深度下研究$\delta $随阵列孔径的变化, 当波导深度小于100 m时, 截取图3中的声速剖面, 当波导深度大于100 m时, 在图3声速剖面的基础上进行线性外推. 仿真中阵元间隔为8 m, 处理声源频段为50到$150{\text{ Hz}}$, 每隔$10{\text{ Hz}}$取一频点进行处理, 信噪比为$10{\text{ dB}}$, 设置声源深度由$1{\text{ m}}$到$(H - 1){\text{ m}}$进行变化, 其中$H$为波导深度, 变化步长为$1{\text{ m}}$. 在不同波导深度与阵元数$N$下得到的$\delta $值如图8所示.

      观察图8可以发现, 在所有波导深度下$\delta $均与$N$成正比, 且变化曲线先陡峭后平缓. 这是由于在阵元数较少时, 阵列孔径较小, 使得能够分离的简正波数量较少, 因此测深模糊程度较高; 当阵元数增加时, 能够分离的简正波数目迅速增加, $\delta $也随之快速增加; 当阵列孔径增加到某一长度时, 已能够分离波导中的大部分简正波, 未分离简正波数量较少, 继续增大阵列孔径分离这些简正波对测深性能的提升有限, 此时$\delta $随阵元的增加而缓慢增加. Bogart和Yang[18]给出了一种低频声源条件下关于水平阵列孔径选取的经验准则:

      其中$L$为水平阵列孔径, 当满足此准则时, 水平阵列可以实现与全海深垂直阵相近的定位能力. 从图8中可以看出, 在不同波导深度下, 满足(18)式准则的阵列孔径均可以使得$\delta \gt 0.9$. 因此(18)式可用来粗略估计本文方法测深时应选择的阵列孔径量级.

      • 3.4.   频率的影响

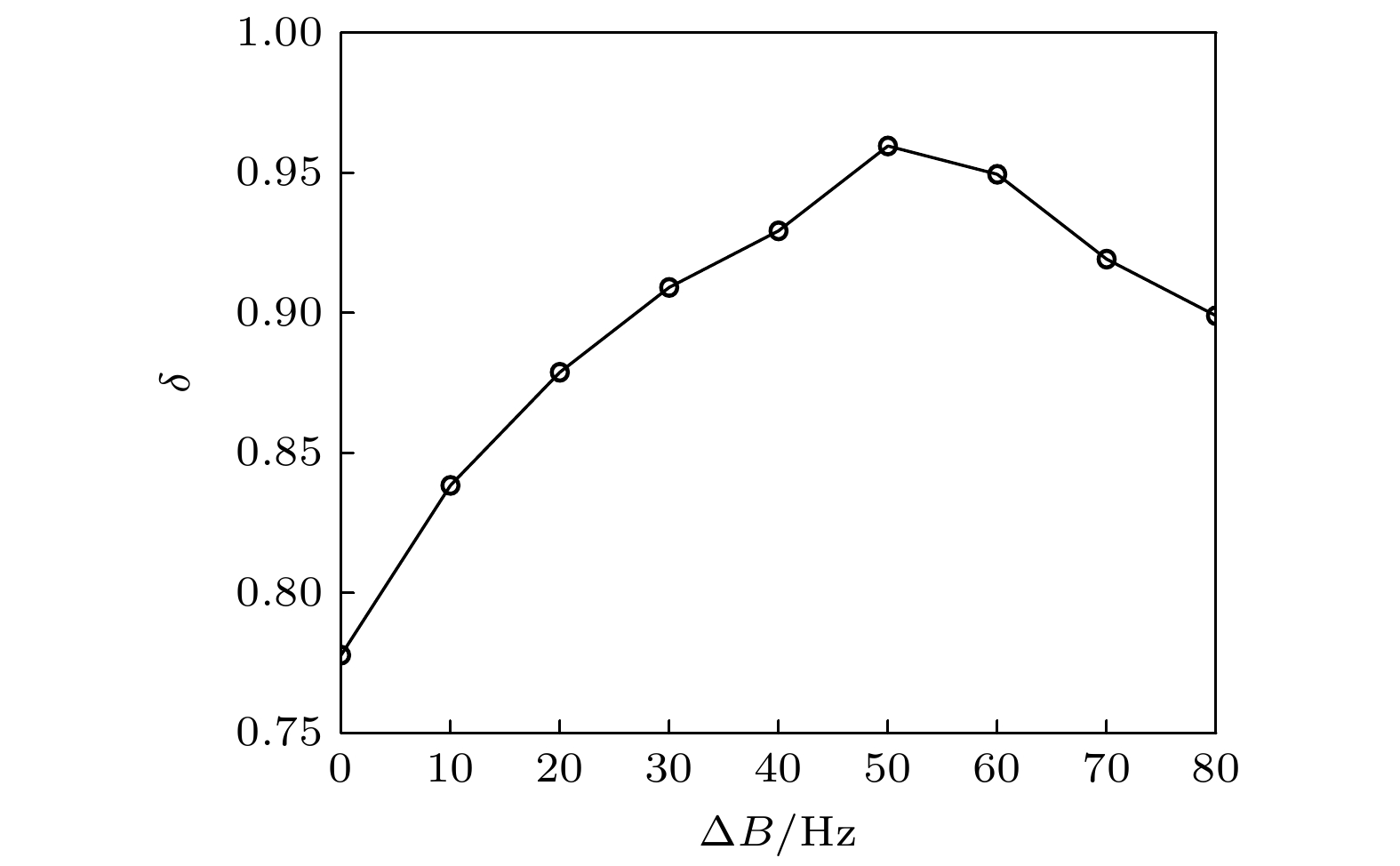
    • 波导中的简正波数量和水平波数间距与声源频率息息相关, 为研究频率对于算法深度估计性能的影响, 对不同带宽条件下的$\delta $值进行仿真. 仿真环境与图3相同, 阵列阵元数为128, 阵元间隔为$8{\text{ m}}$. 处理的中心频率为$100{\text{ Hz}}$, 处理频段为$f \in [100 - \Delta B, 100 + \Delta B]$, 每隔$10{\text{ Hz}}$选取一频点进行处理, 仿真结果如图9所示.

      从图9中可以看出, 随着$\Delta B$的增加$\delta $的值先增大后减小, 在$\Delta B = 50{\text{ Hz}}$时取到最大值, 因此频段$50—150{\text{ Hz}}$可以作为仿真条件下的最优频段. 当$\Delta B \leqslant 50{\text{ Hz}}$时, 增加$\Delta B$可以使算法处理的频点增加因而获得更多声场信息, 减少深度估计的模糊性, 因此$\delta $随之增大. 而当$\Delta B \gt 50{\text{ Hz}}$时, 继续增加$\Delta B$, 此时增加的频点上测深结果模糊性较大, 反而使得$\delta $随带宽增加而减小.

      上述$\delta $随$\Delta B$的增加而减小的现象可以通过分析方法的单频性能进行解释. 在单频情况下对测深算法进行仿真, 在图3的环境条件下, 分别设置声源频率与阵列处理频率为$30{\text{ Hz}}$, $100{\text{ Hz}}$和$200{\text{ Hz}}$, 令声源以$1{\text{ m}}$的步长由深度$1{\text{ m}}$到深度$99{\text{ m}}$变化, 对声源的深度进行估计, 深度估计结果如图10所示. 观察图10中展示的结果, 注意到当频率为$30{\text{ Hz}}$时, 测深结果中存在较多的伪峰, 难以估计声源深度; 当频率为$100{\text{ Hz}}$时, 虽然在某些深度上依然存在一些伪峰, 但是在大多数深度上, 均可有效估计目标深度; 而当频率增加到$200{\text{ Hz}}$时, 算法性能再次退化, 只有少数几个深度上可以较为准确地估计目标深度.

      图11给出了声源深度为30 m时, 频率为30, 100, 200 Hz时简正波水平波数与强度的仿真 结果.

      从图11中可以看出, 当频率为$30{\text{ Hz}}$时, 波导中存在的简正波数量较少, 因此每一阶简正波均对测深性能具有较大影响, 而由于阵列孔径的限制, 难以完全分离低阶简正波, 导致深度估计时出现了较多的伪峰. 当频率为$200{\text{ Hz}}$时, 声源激发出大量简正波, 其中一些强度较小, 极易被噪声和波束旁瓣所淹没, 因此难以分离. 此外随着频率的提高, 低阶简正波数量随之增加, 使得分离难度进一步增加, 故在高频情况下, 相比于简正波总数, 只有少数简正波能够被分离, 难以消除测深时的模糊性, 使得此时算法的深度估计性能退化严重. 当频率为$100{\text{ Hz}}$时, 可以分离得到大部分的简正波, 这些简正波足以在大部分深度上消除深度估计的模糊性. 通过以上分析可知, 本文所提算法在单频条件下深度估计性能有限, 需使用宽带信号消除深度估计时的模糊性. 然而宽带信号的带宽$\Delta B$并非越大越好, 当$\Delta B$增加到某个值时, 继续增加$\Delta B$反而会使得算法深度估计性能下降.

      • 3.5.   底质参数的影响

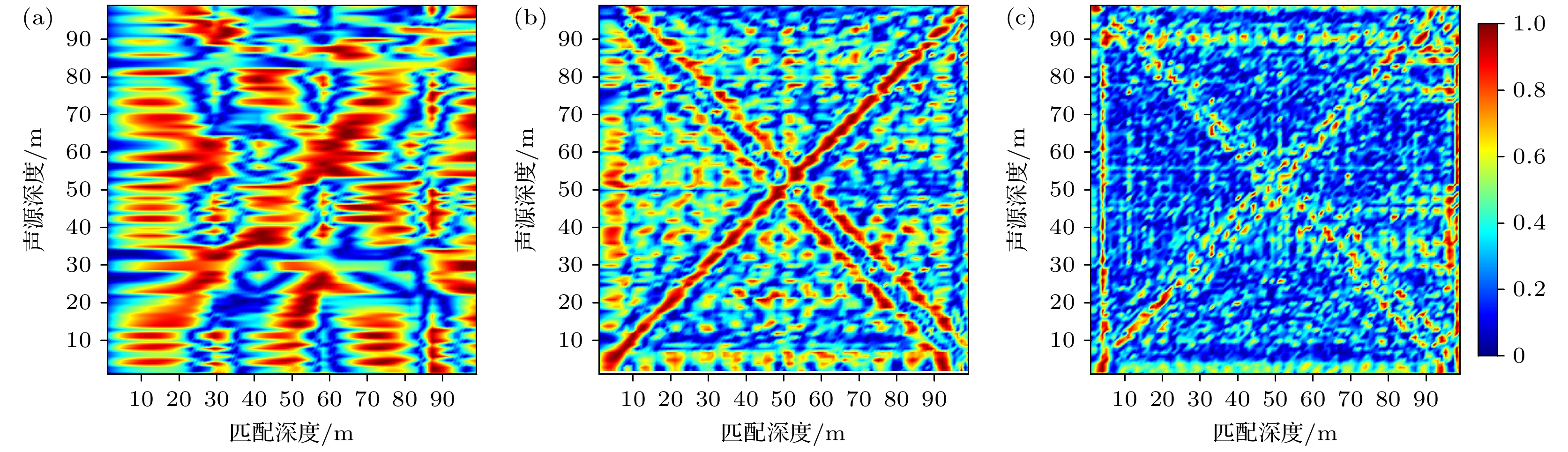
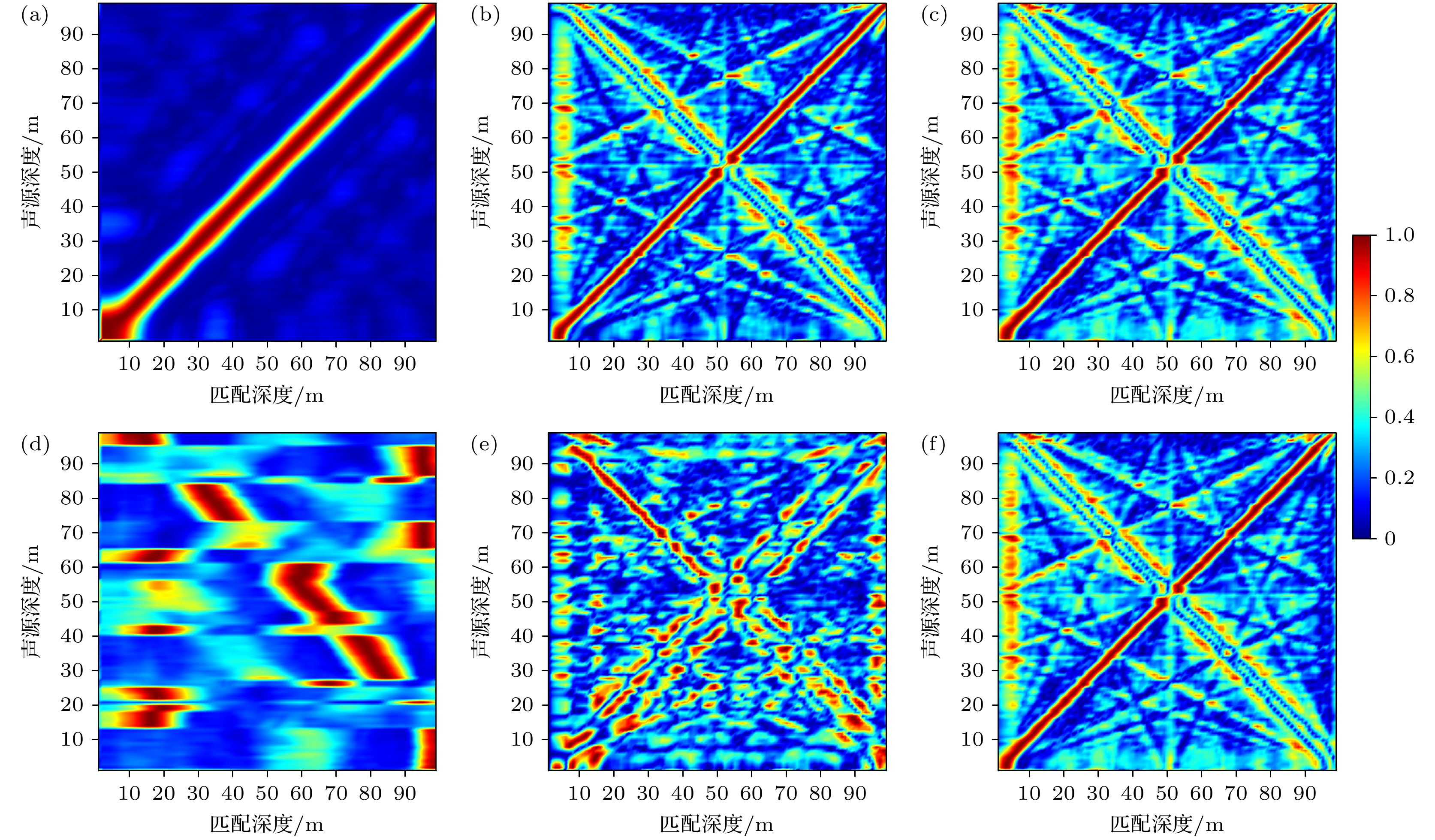
    • 在实际场景中, 海底特性十分复杂且难以准确获取, 在进行目标深度估计时常出现底质参数失配. 由于本文方法无需利用海底底质参数确定波导中简正波的水平波数, 因此在理论上不受底质参数失配的影响. 为了研究底质参数对于目标深度估计的影响, 分别在底质参数无失配和失配场景下仿真MFP, 波数域匹配方法和本文方法, 仿真环境与参数设置与3.2节一致. 三种方法的目标深度估计结果如图12(a), (b), (c)所示. 可以看出, 无底质参数失配时三种方法均可准确估计目标深度, 相比于本文方法, MFP和波数域匹配方法具有较低的旁瓣, 其中, MFP由于充分利用了声场信息, 因此具有最低的旁瓣. 而本文方法利用反演简正波模态函数估计目标深度, 由于估计水平波数值存在误差且阵列孔径限制下难以完全分离简正波, 因此能够利用的声场信息并不完备, 在三种方法中旁瓣最高.

      为研究底质参数失配对于算法性能的影响, 保持仿真环境条件不变, 在底质参数失配条件下进行目标深度估计, 失配底质参数设置如下: 沉积层厚度为$5{\text{ m}}$, 纵波声速为$ 1570{\text{ m/s}} $, 密度为${1}{\text{.6 g/c}}{{\text{m}}^{3}}$, 纵波衰减系数为$0.2{\text{ dB/}}\lambda $; 基岩层纵波声速为$1680{\text{ m/s}}$, 密度为$1.6{\text{ g/c}}{{\text{m}}^{3}}$, 纵波衰减系数为$0.2{\text{ dB/}}\lambda $. 利用上述三种方法进行目标深度估计, 结果如图12(d), (e), (f)所示. 可看出, 由于存在底质参数失配, MFP方法和波数域匹配方法性能均发生了严重退化. 而本文方法通过接收数据反演简正波模态函数, 因此不需要波导的底质信息, 目标深度估计性能不受底质参数失配的影响.

      • 3.6.   信噪比与声速失配的影响

    • 在实际水声探测中, 复杂的海洋环境使得目标信噪比在不同场景下差异显著. 当信噪比较低时, 波束形成器估计水平波数可能存在较大偏差, 进而影响深度估计性能. 其次, 海水声速剖面受温度、盐度和压力等多物理场耦合作用呈现显著时变特性, 制约了海洋声速剖面的实时获取, 而海底水平阵受限于水平结构更加难以获取准确的声速剖面, 这势必会制约依赖声速剖面反演简正波模态函数的本文方法的性能. 针对上述问题, 本节分别对信噪比与声速失配对于算法性能的影响进行分析.

      • 3.6.1.   信噪比的影响

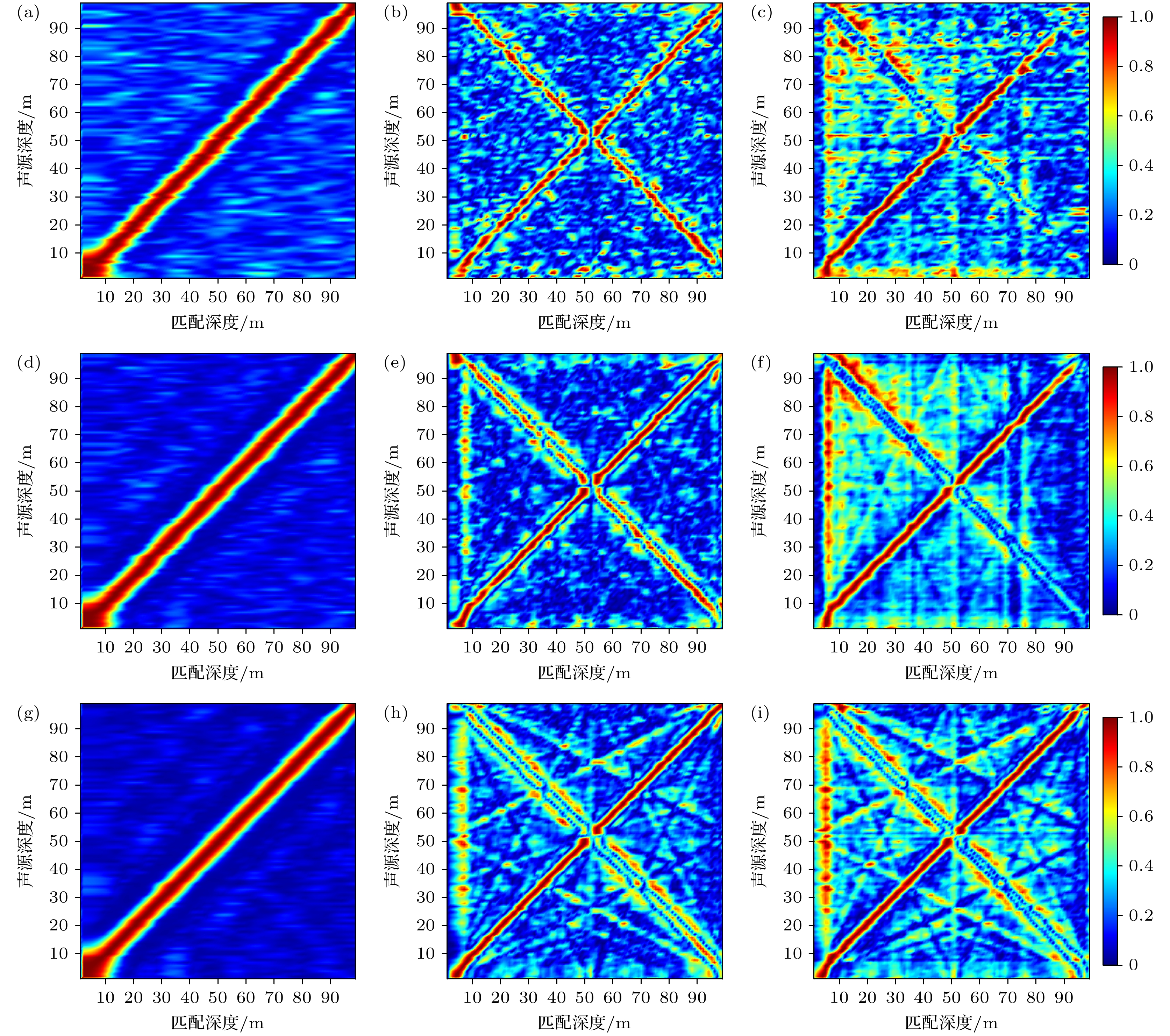
    • 为研究信噪比对于算法测深性能的影响, 在图3的环境条件下, 设置阵元数为128, 处理声源频段为50到$150{\text{ Hz}}$, 每隔$10{\text{ Hz}}$取一频点进行处理, 设置声源深度由$1{\text{ m}}$到$99{\text{ m}}$进行变化, 变化步长为$1{\text{ m}}$. 在信噪比为$ - 15 $, $ - 10$, $ - 5{\text{ dB}}$的条件下分别使用MFP, 波数域匹配方法, 本文所提方法估计声源深度, 仿真时MFP和波数域匹配方法无失配, 结果如图13所示.

      分析图13中的结果可知, 仿真的三种方法中, MFP对信噪比敏感性最低, 在仿真选择的信噪比上均可较为准确估计声源深度. 相比于MFP, 波数域匹配方法和本文所提方法对信噪比较为敏感, 当信噪比为$ - 15{\text{ dB}}$时, 深度估计性能较差; 当信噪比为$ - 10{\text{ dB}}$时, 波数域匹配方法对仿真所设的所有声源深度几乎均可准确估计, 而本文所提方法在声源深度小于$90{\text{ m}}$时与波数域匹配方法性能相近, 声源深度大于$90{\text{ m}}$时失效; 当信噪比增加到$ - 5{\text{ dB}}$时, 本文方法对声源深度大于$90{\text{ m}}$的目标也可实现准确深度估计.

      • 3.6.2.   声速失配的影响

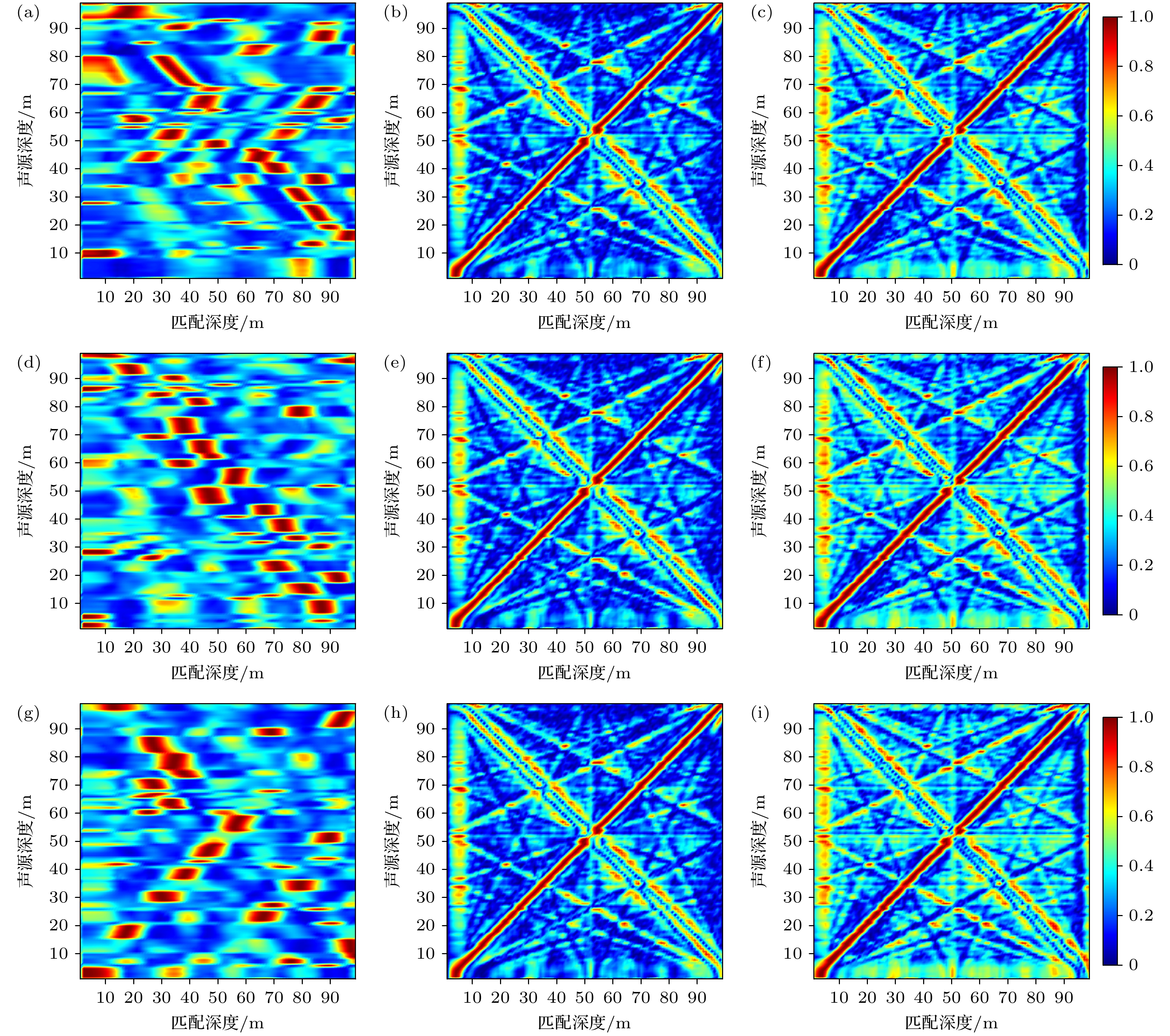
    • 假设实际声速剖面为$\Delta c(z) \sim U( - \delta , \delta )$, 先验声速剖面为$\Delta c(z) \sim U( - \delta , \delta )$, 其中声速扰动$\Delta c(z) \sim U( - \delta , \delta )$为先验声速剖面与实际声速剖面之差. 假设$\Delta c(z) \sim U( - \delta , \delta )$服从均匀分布, 即$\Delta c(z) \sim U( - \delta , \delta )$, 令$\delta $分别为$ 5 $, $ 10 $, $ 15{\text{ m/s}} $, 信噪比为$10{\text{ dB}}$, 其他仿真参数与3.6.1节相同, 分别使用MFP, 波数域匹配方法和本文所提方法估计声源深度, 结果如图14所示.

      观察图14中的结果, 可知MFP对于声速扰动极为敏感, 当$\delta $为$5{\text{ m/s}}$时, 算法即失效, 无法估计声源深度. 而波数域匹配方法和本文所提方法对于声速扰动具有较高的稳健性, 当$\delta $由$5{\text{ m/s}}$增加到$15{\text{ m/s}}$时, 两种方法均可对声源深度进行准确估计.

    4.   海试数据处理

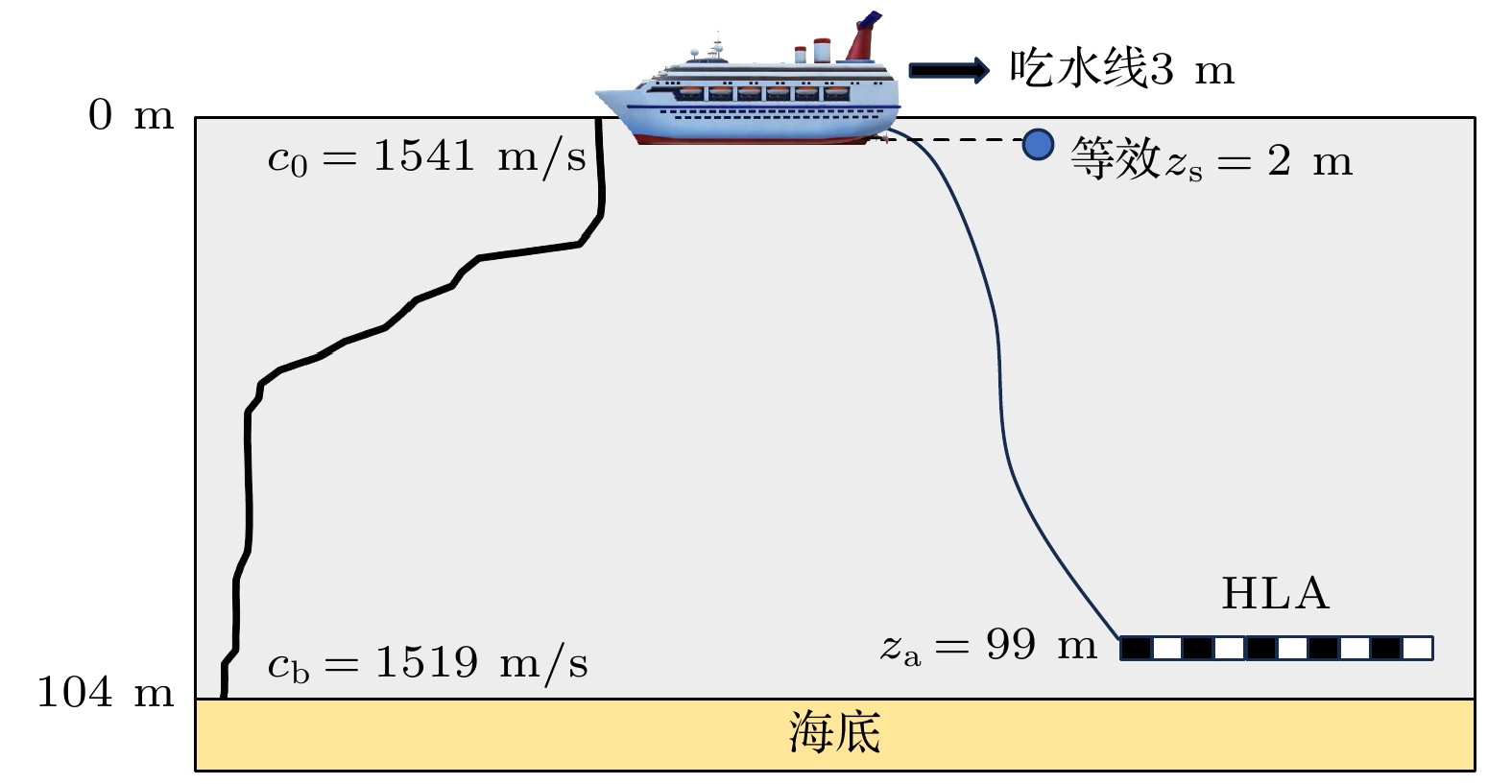
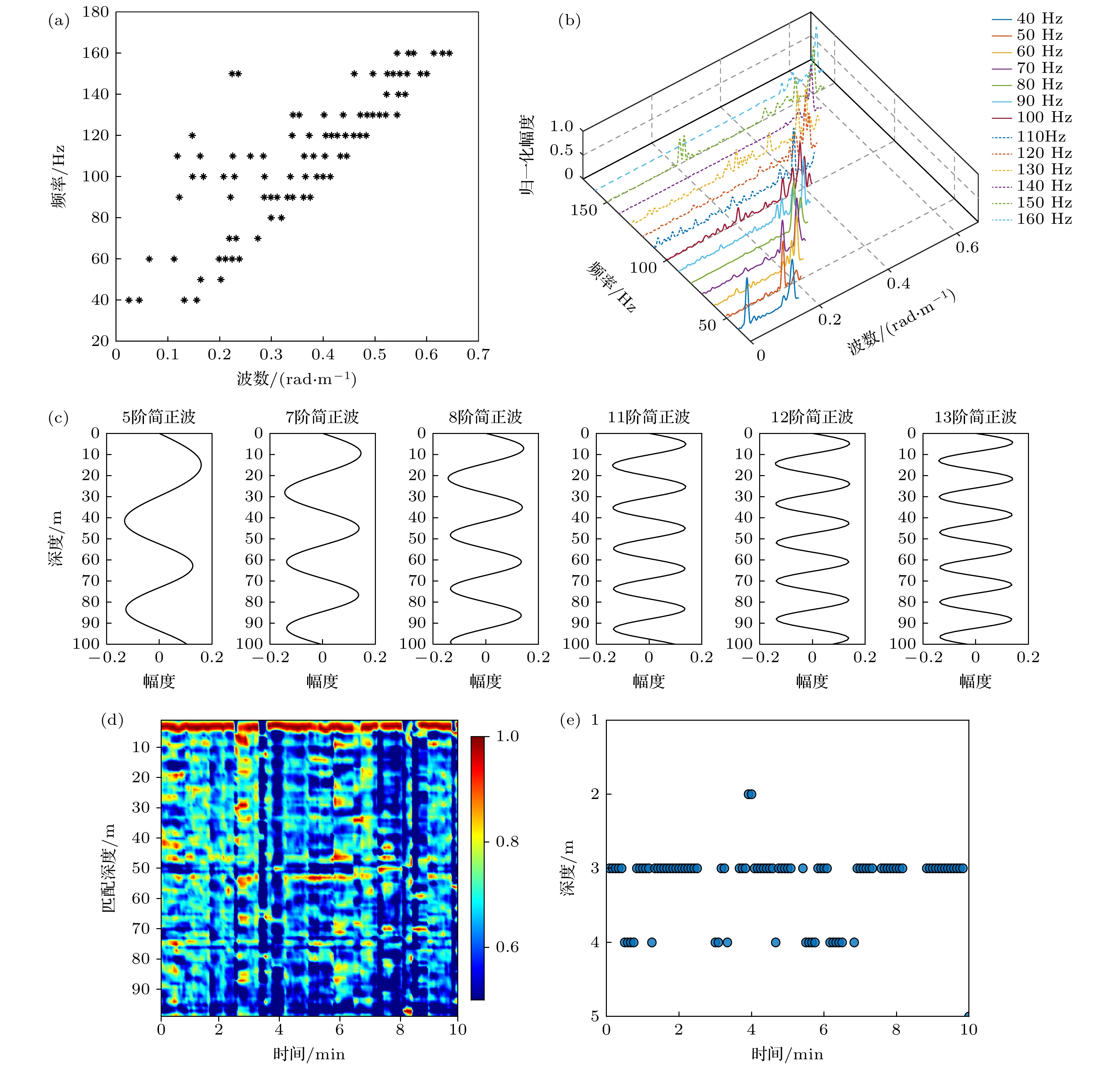
    • 通过对海试中水下拖曳直线阵列接收到的声源信号进行处理, 分析和验证所提出的基于简正波强度匹配的浅海水平阵目标深度估计方法的可行性. 海试数据为2021年7月南海浅海区域水平阵被动探测试验数据. 试验海区水深约$104{\text{ m}}$, 海底地形平坦, 图15展示了试验态势与测量的声速剖面, 水下$3 —10{\text{ m}}$之间存在一个等温层, 水下$10 — 56{\text{ m}}$之间存在一个温跃层, 为典型的夏季浅海水文条件, 试验过程中未对海底底质信息进行测量. 试验中, 声源为拖曳母船, 船舶吃水深度为$3{\text{ m}}$, 根据标准[31], 可以等效为一深度为$2{\text{ m}}$的近水面声源. 阵列为采样频率$8{\text{ kHz}}$, 阵元数77, 相邻阵元间距$8{\text{ m}}$, 阵列深度$99{\text{ m}}$的均匀线列阵, 拖缆长度$500{\text{ m}}$, 拖曳速度6节. 处理数据长度为10 min, 数据处理的频率范围为$40 — 160{\text{ Hz}}$, 每隔$10{\text{ Hz}}$取一个频点进行处理, 共13个频点, 每10 s进行一次频域采样, 数据重叠率为50%.

      使用本文方法对目标深度进行估计, 通过波数域波束形成估计波导中简正波水平波数, 波数域搜索间隔为$ 0.001{\text{ rad/m}} $, 利用估计所得的水平波数反演简正波模态函数, 并通过强度匹配进行深度估计, 匹配搜索区间为1到$103{\text{ m}}$, 搜索步长为$1{\text{ m}}$, 数据处理结果展示在图16中.

      分析图16中的结果, 可以发现大多数时刻深度估计结果为$3{\text{ m}}$, 与目标的理论深度$2{\text{ m}}$较为接近, 这说明了本文提出的深度估计方法可在缺少底质参数的情况下较为准确地估计目标的深度. 深度估计结果中与目标理论深度之间存在$1$—$2{\text{ m}}$的误差, 造成这种现象的原因可能有多种, 首先试验所用的阵列孔径有限, 难以完全分离波导中的简正波; 其次阵列实际深度可能与理论布放深度存在偏差; 此外, 阵列为柔性拖曳阵, 拖曳过程中存在形变, 在波束形成中引入了误差.

    5.   结　论

    • 所提出的基于简正波强度匹配的浅海水平阵目标深度估计算法可以在无需波导底质参数的情况下实现良好的浅海目标深度估计性能, 且对声速失配具有较高的稳健性, 在信噪比大于$ - 10{\text{ dB}}$时能够达到较高的深度估计性能. 该方法利用水平线阵进行波数域波束形成, 估计波导中简正波的水平波数和强度, 并通过有限差分法数值计算特征方程反演简正波模态函数, 将反演与估计简正波强度进行匹配从而确定目标的深度. 仿真分析和海试数据处理结果都验证了所提方法在无底质参数情况下进行目标深度估计的可行性. 由于所提方法需要较大孔径的阵列来对简正波进行分离, 因此当阵列孔径较小时, 性能会出现一定程度的下降. 其次, 为消除目标深度估计的模糊性, 还需处理信号具有较宽频带. 文中假设的波导为水平分层波导, 这是一种较为理想的水声波导, 在实际海洋环境中, 海底和海面并不是理想的平面, 而是会产生一定的起伏, 声速剖面也会随着水平距离的变化而变化, 这些因素会对简正波分离产生较大的影响. 因此, 减少对于大孔径阵列和宽带信号的依赖, 提高算法在非理想波导条件下的适用性是下一步的研究重点.

    参考文献 (31)

目录

/

返回文章
返回