血栓性疾病是心脑血管栓塞事件的主要诱因^[1,2], 传统介入疗法(如药物溶栓、手术取栓)因其高出血风险^[3]、靶向性不足及术后复发等问题在临床的普遍使用上受到制约. 超声溶栓技术凭借非侵入性治疗特性^[4], 通过空化气泡溃灭产生的瞬态冲击实现血栓机械破碎^[5], 展现出独特的安全-效益平衡优势. 然而, 临床转化中暴露出空化能量传递效率低与损伤可控性差的双重瓶颈^[6], 其核心科学问题在于多气泡协同空蚀机制及其与血栓动态力学响应的耦合规律尚未明晰.

在单气泡动力学领域, 大量研究指出气泡动力学在很大程度上受附近边界类型的控制. 刚性边界附近, Bußmann等^[7]在气泡近壁区域重现了低距离的快速针状式射流, 远离壁的常规射流, 以及介于两者之间的混合式射流3种喷射机制. 在Iga和Sasaki^[8]的研究中发现附着在壁上的环形气泡反弹有可能在材料内部造成更深的损坏. Bokman等^[9]采用高速X射线相差成像技术, 将测得的气泡形状与数值模拟结果进行比较, 有助于确认和阐明飞溅现象. 对于弹性边界条件, 不同材料的能量耗散特性显著改变溃灭模式. Li等^[10]观察到弹性边界附近气泡的反向射流现象, 提出边界变形导致的局部高压将液体射流从边界驱离. Reese等^[11]通过探测弹性表面上的切向应力, 表明断裂可能从弹性材料内部开始. Ren等^[12]实验发现气泡与液滴间的4种典型相互作用, 即油滴破裂、水滴截留、油滴大变形和油滴轻微变形. Turangan等^[13]研究表明, 气泡与弹性膜间的相互作用会加强气泡收缩, 并可能导致蘑菇形、气泡伸长和气泡分裂. 复杂几何边界通过流场约束效应产生独特的动力学特征. Brujan等^[14]在矩形通道中的实验表明, 气泡的喷射行为在单射流和指向通道每个壁的3个液体射流之间变化. Andrews等^[15]发现多孔边界的不对称性降低, 导致气泡坍塌产生的射流效果降低. Li等^[16]提出了气泡-球体相互作用的分类, 即“弱”、“中等”和“强”相互作用, 在最大体积时刻采用3种不同的气泡形状来标识.

实际液体系统中的空化气泡通常以气泡云形式存在, 由于气泡之间的相互作用, 导致空化动力学更加复杂. 现有多气泡动力学行为研究主要聚焦两大方向. 一方面是多气泡振荡耦合效应, 研究表明气泡之间的相互作用会显著减少较小气泡的径向振荡^[17–19]. 当气泡彼此非常接近时, 它们可能会聚结(两个大小几乎相等的同相气泡的结合)^[20,21], 或者其中一个会坍缩到另一个气泡中(对于异相气泡或相对大小不同的气泡)^[22]. Zhang和Yao^[23]指出由于多个气泡之间的凹陷效应, 气泡周期随着气泡中心距离的减小而增大. 徐珂等^[24]研究指出泡群中泡的位置距离泡群中心越远, 泡的膨胀半径越大; 随着泡群中泡的数目增加, 泡的振幅减小. Qin等^[25]发现随着超声振幅增加或频率降低, 泡间相互作用会显著增大, 增大表面张力和液体黏度可以减小泡间相互作用对声空化特性的影响. 许龙等^[26]构建了超声空化双泡耦合模型, 结果显示相比于单泡, 耦合双气泡呈现最大半径减小、膨胀时间缩短, 收缩开始时间提前、持续时间延长的特征. Wang等^[27]探讨了双气泡系统中气泡的脉动和平移, 结果表明, 对于两个相同的气泡, 降低超声频率或增大振幅可以增强脉动并提高气泡的平移速度.

多气泡动力学行为研究的另一方面则侧重于多气泡坍塌耦合效应. 张凌新等^[28]发现在多泡流场中, 中心气泡的溃灭过程存在先延迟后加速现象, 随着周围气泡数的增多或气泡间距的减小, 中心气泡的溃灭时间增长、压力峰值增大. Terasaki等^[29]研究了在不同时间延迟下引入另一个气泡对气泡中射流行为的影响, 并提供了状态图, 其显示了射流方向的转变, 作为时间延迟和气泡之间距离的函数. 在Hong等^[30]的研究报告中, 演示了超声场中可变形单元附近的气泡相互作用, 他们发现, 与单个气泡坍塌相比, 两个坍塌的气泡会产生强烈的液体射流, 导致细胞发生显著变形. Sankin等^[31]研究了激光产生的串联微泡与单个细胞的相互作用, 研究指出, 单个气泡积累的势能是有限的, 其坍塌不足以刺穿组织, 通过串联微气泡相互作用传递和聚焦能量可以帮助实现这一目标. Lauer等^[32]数值研究了冲击波引起的空腔阵列在水中的坍塌行为, 对于3个气泡, 最上游气泡坍塌引起的压力低于单个气泡的压力, 当气泡之间的距离较小时, 第二和第三气泡引起的压力变高. Chahine和Hsiao ^[33]以及Ochiai和Ishimoto ^[34,35]讨论了多个气泡的相互作用对气泡坍塌行为和气泡坍塌引起的脉冲压力的影响, 结果表明壁面压力在一定的气泡尺寸以及气泡间距下达到最大值.

尽管上述研究深化了气泡动力学认知, 但现有成果多关注于流体域中的泡间耦合效应, 缺乏对血栓黏弹性介质中的多气泡协同空蚀效应的系统研究: 即未考虑血栓率相关本构特性(渐增硬化、应力松弛、应变率强化效应)对固体内部射流冲击叠加的调制作用; 缺乏气泡群参数与血栓内应力累积的定量映射模型. 本文构建了考虑血栓运动的气-液-固多物理场耦合模型, 引入结构阻尼项表征血栓运动过程中能量耗散, 量化分析了血栓附近空化气泡溃灭动力学特性. 在此基础上结合血栓率本构模型分析了多气泡射流在血栓内部的协同空蚀效应, 重点揭示多气泡冲击序列匹配与血栓动态力学响应的协同机制, 建立了气泡群初始半径分布与应力累积的定量映射关系, 并给出协同空蚀效应预测方程, 为超声溶栓能量的定向投射技术提供理论支撑.

血栓附近的超声空化过程涉及气-液-固三相耦合作用, 气泡动力学行为(包括生长、收缩与溃灭)不仅受血液流动影响, 还与血栓壁面的动态响应密切相关, 该过程的数学模型由以下控制方程描述.

气液两相流采用Navier-Stokes方程组表征, 包括质量守恒方程、动量守恒方程和能量守恒方程:

式中, $\rho $为混合相密度, ${\boldsymbol{u}}$为速度矢量, $p$为压力, $\mu $为混合相黏度, I为单位矩阵, ${{\boldsymbol{F}}_\sigma }$为表面张力项, $E$为总能量, $\lambda $为传热系数, $T$为温度. 动量方程的右边部分给出了压力梯度、黏度和表面张力的影响.

采用VOF(volume of fluid)模型捕捉气液界面演化, 液相体积分数的输运方程为

其中, ${\alpha _{\text{l}}}$为液相的体积分数(在液相, ${\alpha _{\text{l}}}$ = 1; 气相, ${\alpha _{\text{l}}}$ = 0; 在气液交界面处, $0 \lt {\alpha _{\text{l}}} \lt 1$). 混合相物性参数通过体积分数加权计算:

下标l和g分别代表液相(血液)和气相(空化泡内气体). 气相压缩性由理想气体状态方程描述:

式中, Q为摩尔气体常数. 而血液的压缩性在高压冲击下不可忽略, 其密度-压力关系通过Tait状态方程表征:

其中, ${\rho _0}$与${K_0}$分别为参考压力${p_0}$下的血液密度与体积模量, $\Delta p = p - {p_0}$, n为密度指数.

由于气泡给予固体的作用力主要在垂直方向上, 因此假设血栓仅在Y方向发生弹性振动. 为表征血栓运动过程中能量耗散的特性, 考虑由于材料内摩擦引起的结构阻尼, 引入复弹性模量$ \tilde E = E\left( {1 + {\text{i}}\tilde \eta } \right) $, 因此, 对于存在阻尼的单轴线弹性, 应力-应变关系可以写为

式中$ \tilde \sigma $是复应力, $ \tilde \varepsilon $是复应变, i是虚数单位, $\tilde \eta $为损耗因子. 则血栓的运动由以下方程控制:

方程中m为等效质量, k为刚度系数, $y$为位移, $\dot y$为速度, $\ddot y$为加速度, $ f\left( t \right) $为流体的作用力.

此外, 在流固耦合界面上须满足位移和应力连续条件:

其中${\boldsymbol{\sigma}} $为应力张量, ${\boldsymbol{n}}$为耦合边界上的外法线方向矢量, 下标f和s分别表示流体域和固体域.

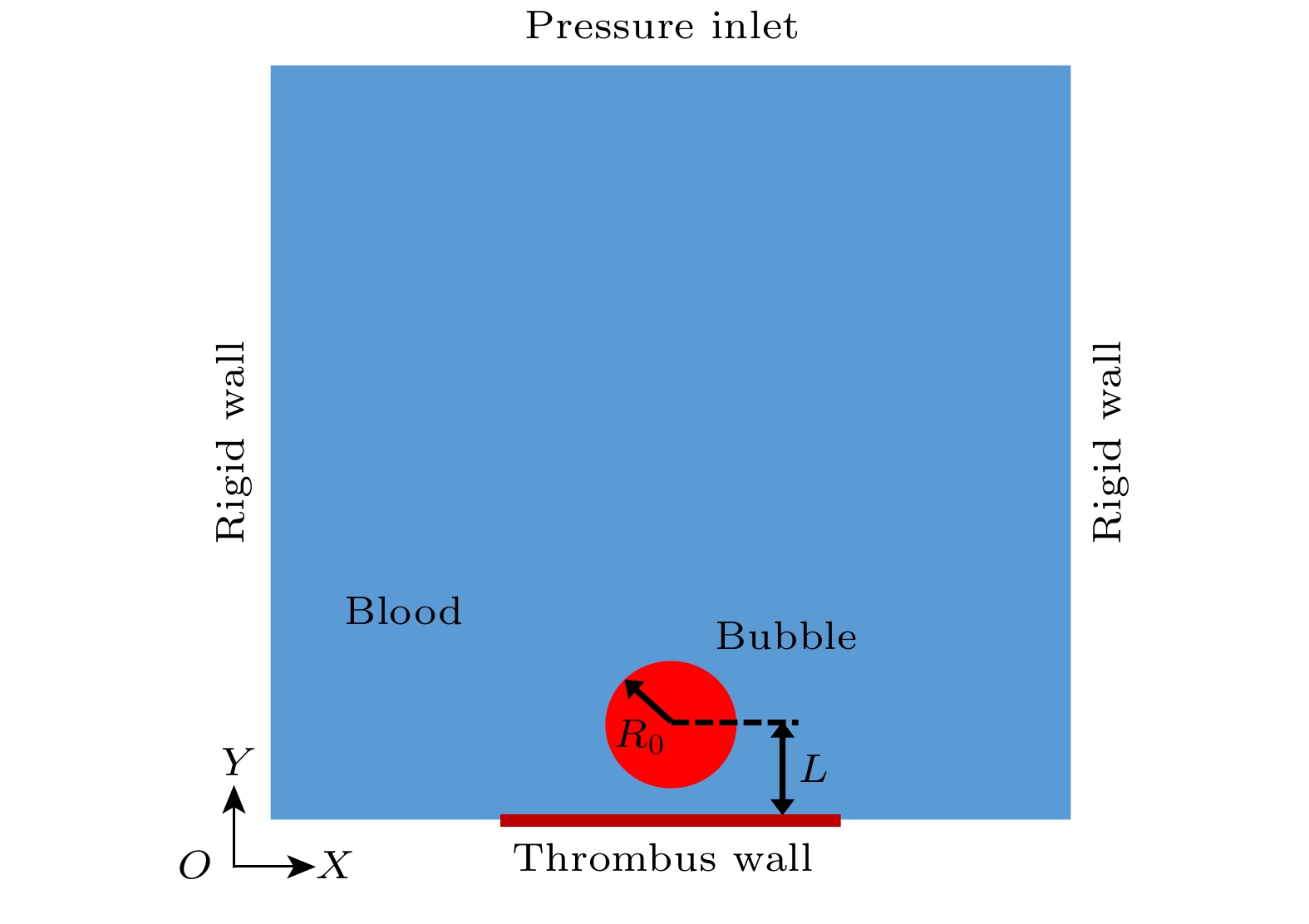
计算域初始几何构型如图1所示, 尺寸为1 mm × 1 mm, 空化气泡初始半径R₀ = 40 μm, 计算域横向边界距气泡中心足够远, 可忽略壁面效应对气泡动力学的影响. 气泡置于底部壁面附近, 定义无量纲距离参数$\gamma = L/{R_0}$表征气泡与下壁面的相对位置, 其中L为气泡中心至壁面的垂直距离.

左、右边界设为无滑移刚性壁面. 上边界通过用户自定义函数(UDF)写入表征超声的压力边界条件$P = {P_{\mathrm{A}}}{\text{sin}}\left( {2{\pi}ft} \right)$, 其中${P_{\mathrm{A}}}$表示超声振幅, f 代表超声频率. 下边界中心区域(长度0.4 mm)采用动网格技术模拟血栓运动, 用UDF编写振动方程并实现流固耦合数据传递. 泡内初始压力遵循公式${p_{{\text{g0}}}} = {p_0} + 2\sigma /{R_0}$, 其中$\sigma $为表面张力系数. 计算过程使用Fluent完成, 控制方程采用有限体积法离散, 采用PISO算法迭代求解. 梯度项用最小二乘法格式, 动量项、密度项和能量项均选用二阶迎风格式, 时间项则用一阶隐式格式. 仿真参数^[36,37]列于表1, 时间步长取Δt = 1×10^–7 s (对应20 kHz超声周期分辨率).

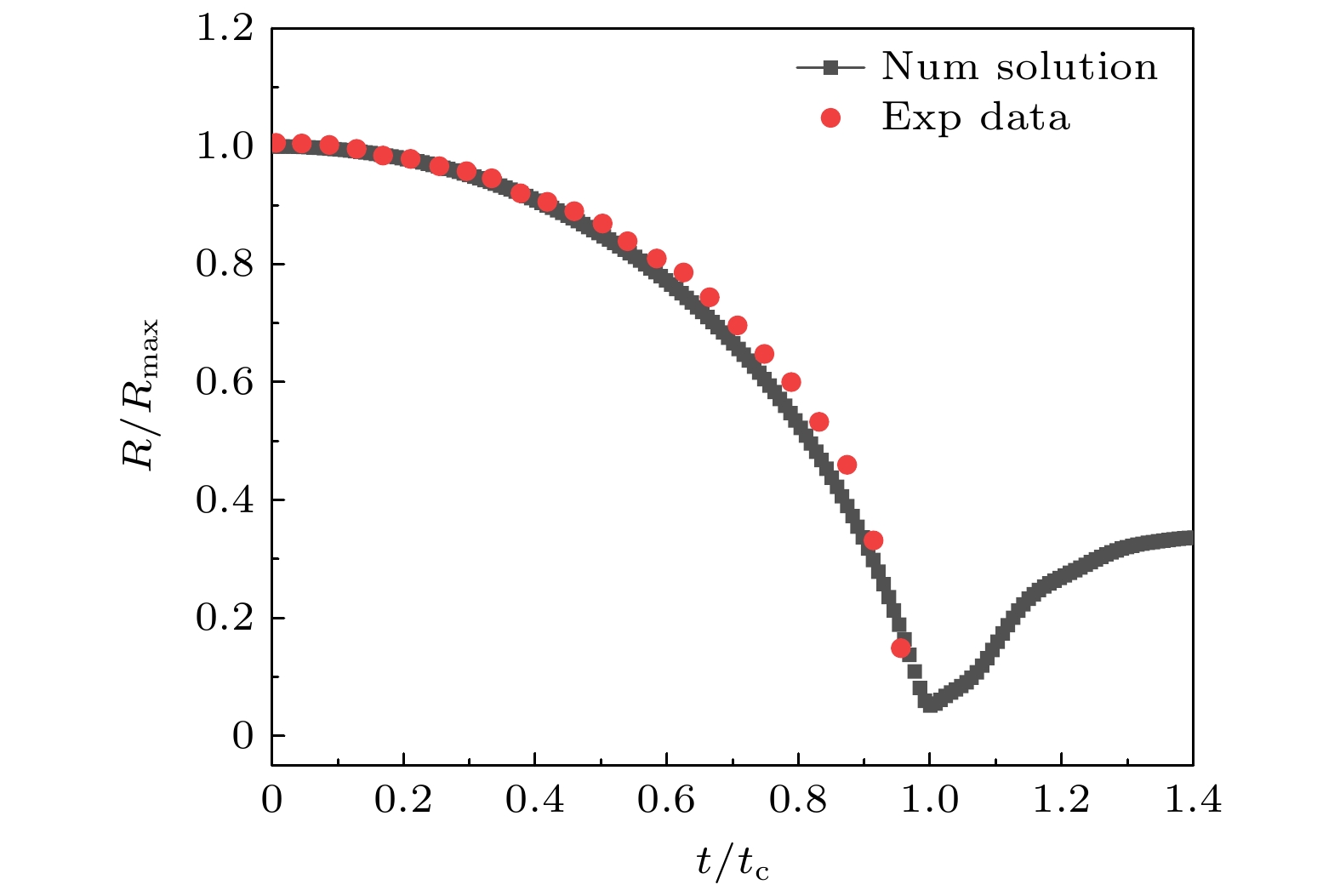
为消除尺度效应, 定义无量纲半径R/R_max和无量纲坍塌时间t/t_c, 其中R_max为气泡最大半径, t_c为气泡坍塌阶段时间. 将仿真计算结果与文 献[39]中弹性边界附近气泡坍塌实验数据进行对比, 如图2所示, 可以看出气泡半径的时间演变几乎相同, 数值结果与实验数据符合较好, 表明本文所建立数值模型在预测近壁气泡动力学行为方面的可靠性.

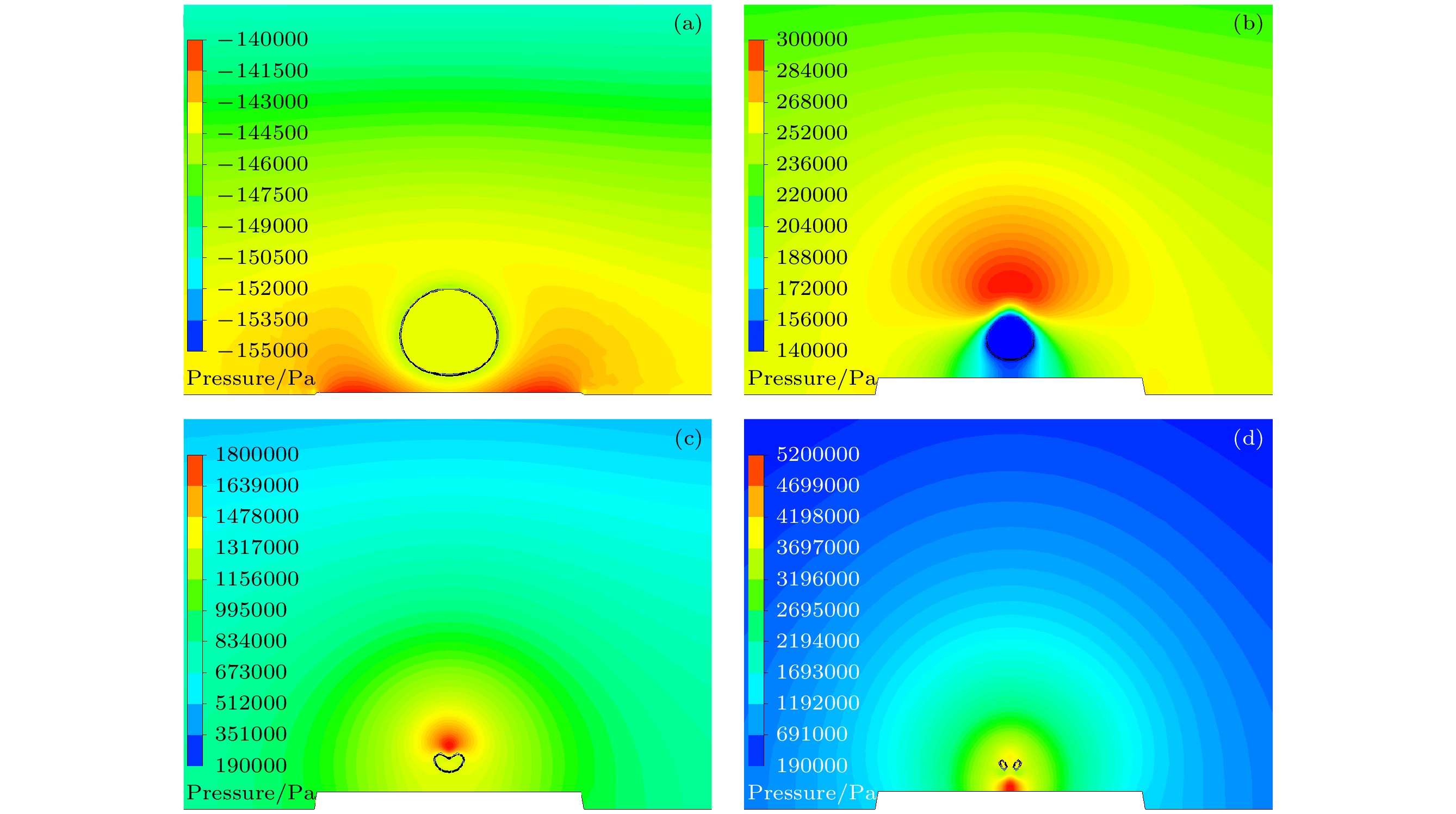
在超声激励(f = 20 kHz, P_A = 200 kPa, m = 1 g, R₀ = 40 μm, γ = 1.8)下, 血栓附近空化气泡演化过程如图3所示. 膨胀阶段, 气泡在超声负压相的驱动下开始膨胀, 与此同时, 超声负压相的作用使血栓壁面向气泡移动, 在气泡底部形成局部高压区, 如图3(a)所示. 收缩阶段, 在超声正压相的驱动下气泡剧烈收缩, 受壁面边界效应影响, 气泡远离壁面端产生了更大的压力梯度, 而壁面上移产生的高压区沿气泡表面向上扩展, 导致压力梯度分布发生重构, 促使气泡顶端维持尖锐几何形态, 如图3(b)所示. 射流冲击阶段, 超声能量在气泡远离壁面端持续积累, 诱发气泡尖端产生指向壁面的内凹射流结构, 如图3(c)所示. 在t = 40.7 μs时, 射流穿透气泡并冲击壁面, 在壁面中心区域形成5.2 MPa的瞬态压力峰值, 如图3(d)所示.

结果表明, 壁面冲击压力源于气泡非球形溃灭诱导的微射流, 并且血栓运动会显著影响气泡溃灭形态. 在本文研究背景下, 关键可控参数包括血栓质量m、无量纲距离γ、超声频率f、超声振幅P_A以及气泡初始半径R₀, 弄清其定量影响规律可为超声溶栓中的空蚀预测提供理论依据.

1)超声参数(超声振幅P_A, 超声频率f)影响

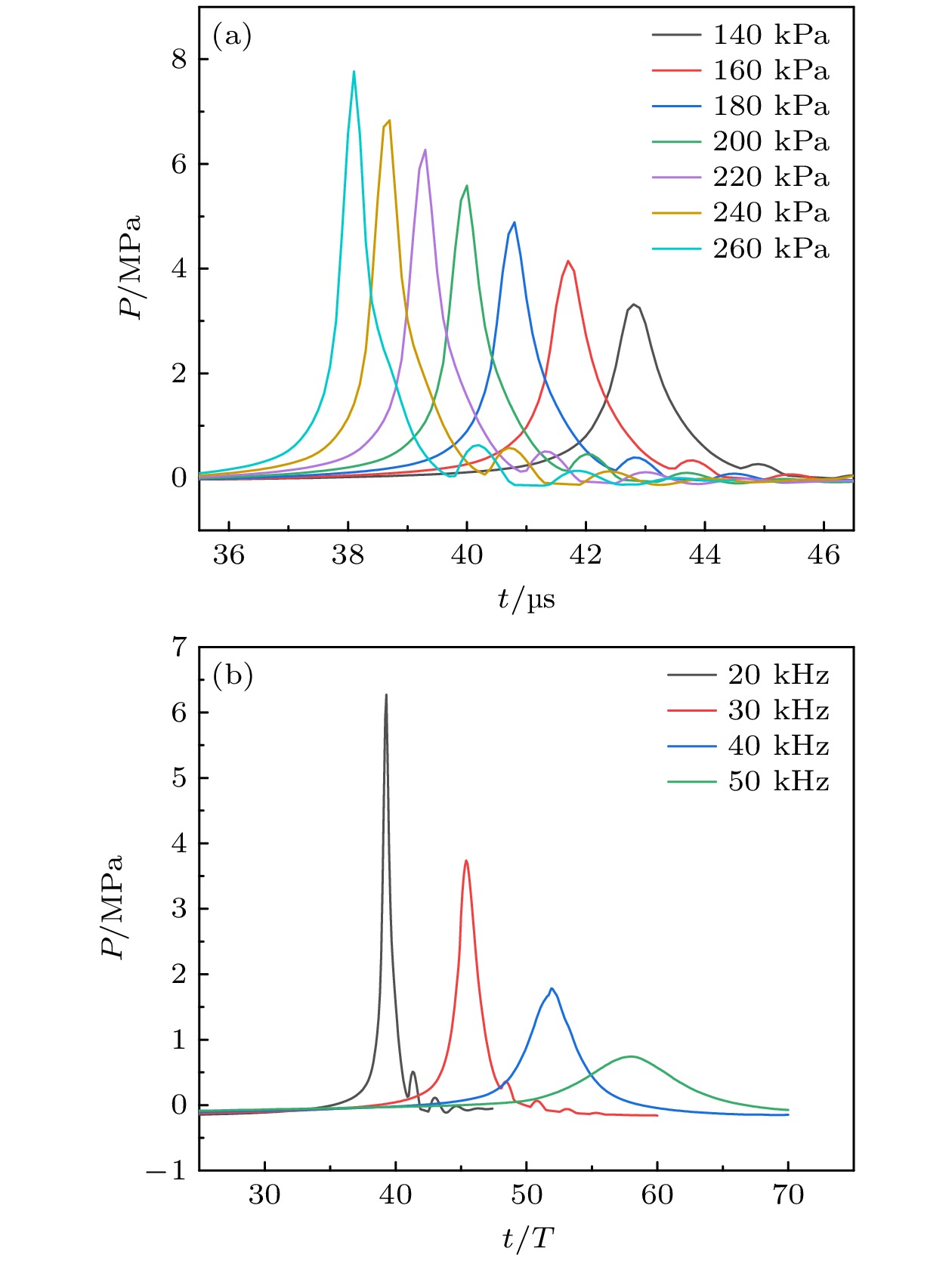
图4(a)所示为固定f = 20 kHz, m = 1 g, R₀ = 40 μm, γ = 1.4情况下, 超声振幅P_A = 140—260 kPa时壁面中心压力的时间历程: 随着P_A增大, 射流冲击到达时间由0.856T提前至0.762T (T为超声周期), 压力峰值从3.3 MPa增至7.8 MPa, 增长了136.4%. 此现象归因于高振幅超声促使气泡能量吸收增强及溃灭速度加快, 从而强化空化效应.

图4(b)所示为固定P_A = 220 kPa, m = 1 g, R₀ = 40 μm, γ = 1.4情况下, 超声频率 f = 20—50 kHz时壁面中心压力的时程曲线, 定义无量纲时间${t^*} = t/T$. 可以看到随着 f 增大, 射流冲击压力峰值从6.3 MPa减至0.7 MPa, 降低了88.9%, 冲击到达时间${t^*}$从0.786T推迟至1.16T. 该现象源于高频激励缩短了空化气泡的能量积累时间, 导致空化效应显著减弱.

2)血栓质量、无量纲距离、气泡初始半径影响

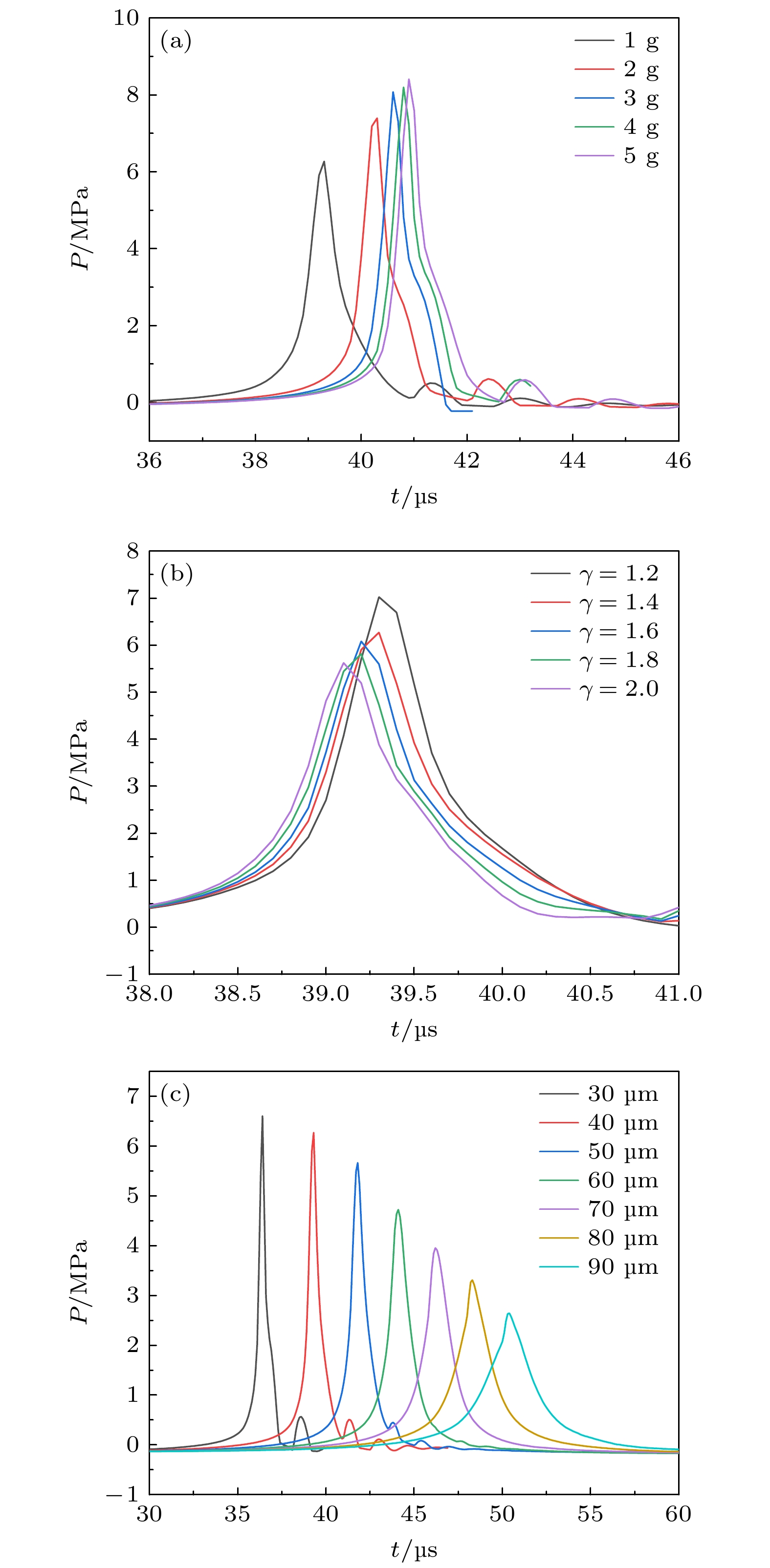
图5(a)为固定f = 20 kHz, P_A = 220 kPa, R₀ = 40 μm, γ = 1.4情况下, 血栓质量m = 1—5 g时壁面中心压力的时程曲线: 随着m增大, 射流冲击到达时间从0.786T延迟至0.818T, 同时压力峰值由6.3 MPa增至8.4 MPa, 增长33.3%. 该现象源于较小血栓质量引发较大壁面位移, 导致气泡提前溃灭从而降低冲击强度.

图5(b)为固定f = 20 kHz, P_A = 220 kPa, m = 1 g, R₀ = 40 μm情况下, 无量纲距离γ =1.2—2.0范围内壁面中心压力的时间历程, 随着γ增大, 射流冲击到达时间由0.786T提前至0.782T, 压力峰值从7.0 MPa降至5.6 MPa, 降低20.0%. 这归因于射流能量随传播距离增大而衰减.

图5(c)为固定f = 20 kHz, P_A = 220 kPa, m = 1 g, γ = 1.4情况下, 气泡初始半径R₀ = 30—90 μm时壁面中心压力的时间历程, 随着R₀的增大, 射流冲击到达时间由0.728T 延迟至1.008T, 压力峰值从6.6 MPa减至2.6 MPa, 降低了60.6%. 该现象归因于大初始半径气泡在膨胀阶段形成更大体积, 导致压缩溃灭过程时间延长, 削弱空化强度.

综上所述, 在所模拟的参数条件下, 射流冲击强度对各参数的敏感性从大到小排序为: 超声振幅、超声频率、气泡初始半径、血栓质量、无量纲距离.

通过组合单气泡溃灭冲击压力时程, 施加于血栓模型上边界中心区域, 以血栓内部最大应力的增幅来定量表征多气泡协同作用下应力的累积效应. 气泡间的相互作用会增强壁面冲击压力已得到相当的关注^[32,34,35], 但已有研究的重点在于泡间耦合效应和壁面压力的增强效应, 而血栓应力累积效果还取决于血栓的本构特性. 这里忽略了流体域中的泡间动力学耦合效应, 研究的关键是准确合理地给出血栓黏弹性响应的率相关本构模型.

本文结合超弹性Ogden模型与黏弹性Prony级数表征血栓的渐增硬化与应力松弛行为, Ogden模型对应的应变势能函数表达式为

式中, N为模型的阶数, ${\mu _i}$和${\alpha _i}$为材料参数, 分别表示材料的剪切模量和渐增硬化指数, ${\lambda _1}, {\lambda _2}, {\lambda _3}$为主伸长率.

Prony级数描述剪切松弛模量随时间演化规律:

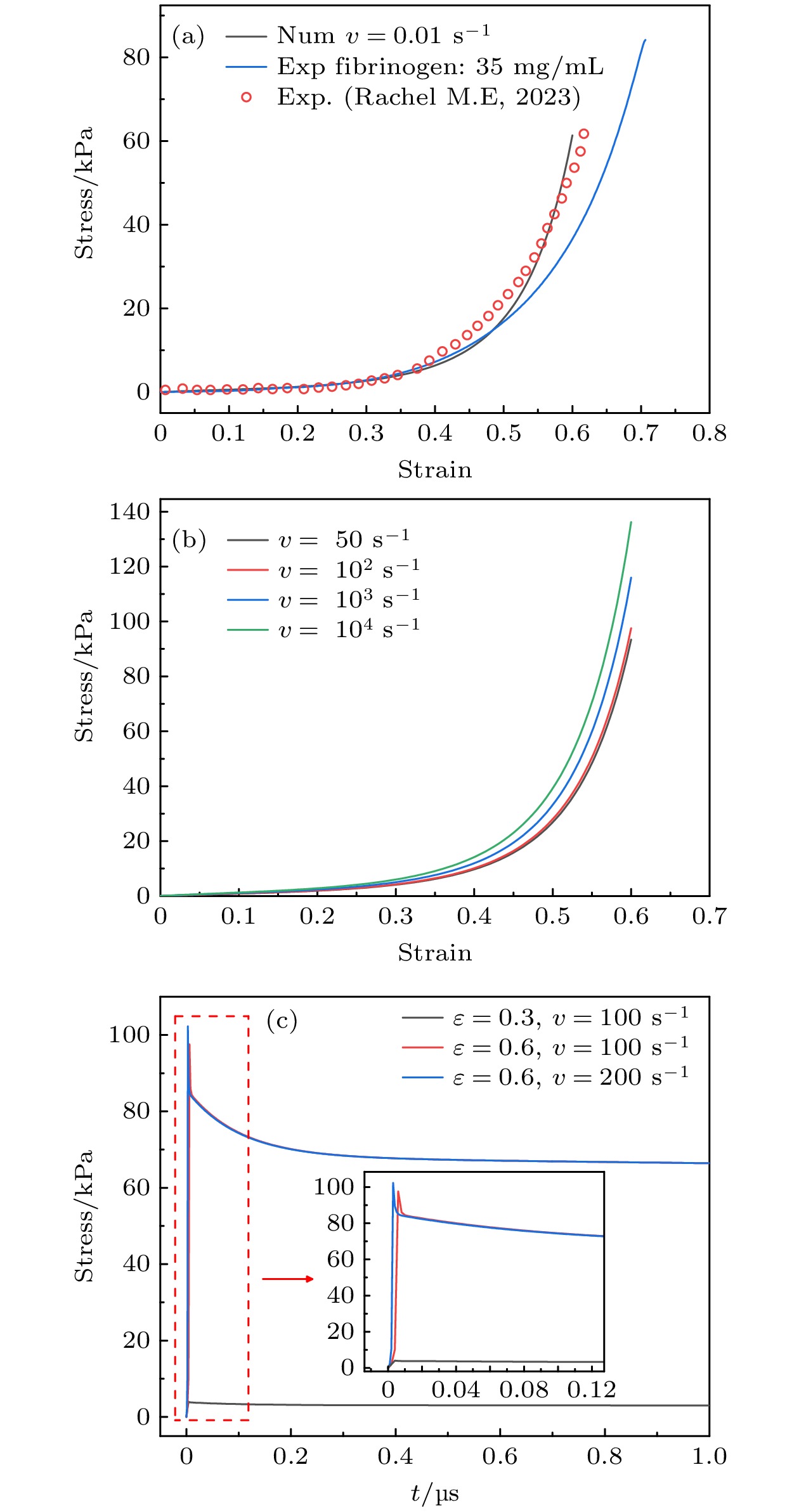
其中${G_0}$为初始剪切模量, ${g_i} = {G_i}/{G_0}$, 表示第i个Prony项的归一化松弛模量($0 \lt {g_i} \lt 1$), ${\tau _i}$为第i个Prony项的松弛时间. 血栓模型简化为1 cm × 1 cm的二维平面正方形, 模型下边界固定${u_y} = 0$, 在应变水平为0.6的条件下, 设置上边界加载速率v分别为0.01, 50, 10², 10³, 10⁴ s^–1. 计算过程使用Abaqus完成, 血栓密度ρ = 1059 kg/m³, 时间增量Δt = 1×10^–8 s.

图6(a)展示了准静态条件(v = 0.01 s^–1)下血栓本构模型仿真结果与文献[40]中血凝块单轴压缩实验数据以及纤维蛋白原浓度为35 mg/mL的凝块单轴压缩实验的对比, 验证了模型的渐增硬化特性. 图6(b)所示为血栓在不同加载速率下的力学响应特征, 加载速率v = 50 s^–1时应力缓慢上升, 加载速率$v \geqslant {10^3}{\text{ }}{{\text{s}}^{{{ - 1}}}}$时弹性模量提升, 应力应变曲线斜率显著增大, 动态硬化效应显著. 图6(c)所示为血栓在不同应变-加载速率下的应力时程曲线, 呈现典型的应力松弛特征. 结果表明, 所建立的Ogden-Prony本构模型能够有效表征血栓的率相关力学行为, 满足超声空化冲击场景下的仿真需求.

需要说明的是, 本文研究重点关注在射流冲击序列下血栓内的应力累积效应, 这种累积效应是利用了血栓这种生物材料特有的渐增硬化本构特性(变形增大时, 应力持续增长, 且增长幅度增大), 因此在冲击作用下表征血栓的应变率相关本构行为是问题的关键.

泡群同步发生空化时, 多气泡产生的射流冲击序列通过血栓本构模型的渐增硬化与应变率强化效应共同引发应力累积, 即多气泡协同空蚀效应. 在此过程中射流冲击序列的时序差异(Δt_jet)与压力峰值梯度(Δp_max)会显著影响应力累积效果, 其中Δt_jet表示射流冲击之间的时间间隔, Δp_max代表射流冲击压力峰值之差.

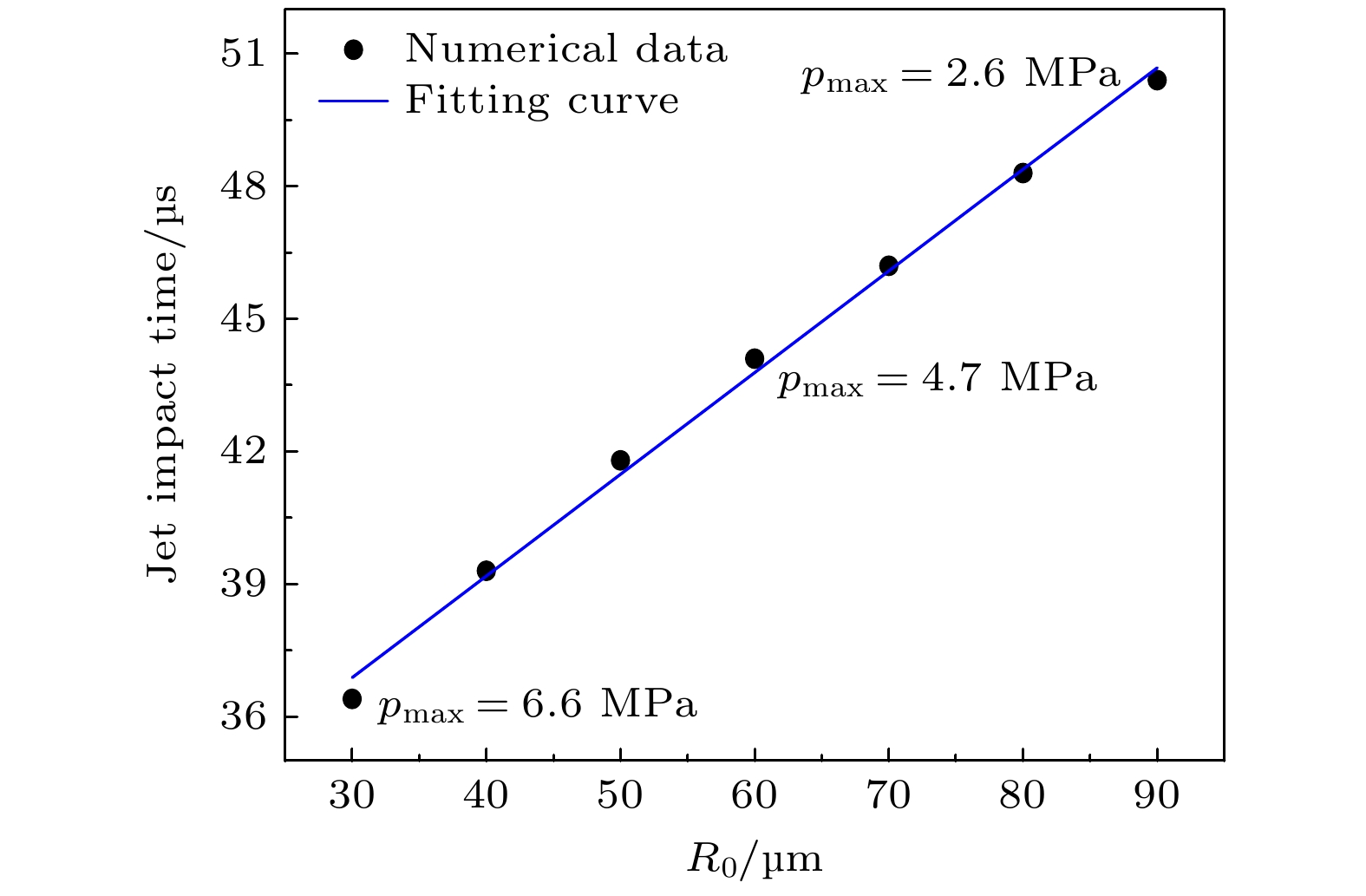
在超声参数(f = 20 kHz, P_A = 220 kPa)及血栓质量(m = 1 g)恒定的条件下, 无量纲距离γ 对射流冲击序列时空特性的影响相较于气泡初始半径R₀的影响可忽略(见第2.3.2节讨论), 因此这里只讨论由气泡初始半径分布主导的射流冲击序列的差异性. 在进一步固定γ = 1.4的条件下, 由单气泡初始半径R₀与冲击到达时间t_jet关系可见(如图7所示), 随着R₀增大, 射流冲击到达时间t_jet 延迟, 射流压力峰值p_max不断衰减. 由此可以推断, 对于多气泡在忽略耦合效应情况下, 初始半径分布的差异性设计是实现应力累积的关键.

分析表明, 在忽略泡间耦合效应的前提下, 泡群中初始半径最小(R_min)和最大(R_max)的两个气泡产生的射流冲击间隔时间最长, 产生的叠加效果最弱, 代表着泡群协同空蚀效应的下限, 由此将多气泡问题的讨论简化为双气泡进行, 双气泡分布与血栓表面平行. 同时由单气泡空化压力云图(图3), 可以发现壁面所受冲击呈区域分布, 射流冲击序列通过在一定区域内连续作用实现应力累积. 因此, 取泡群中这两个极端半径气泡来研究不同初始半径分布范围(ΔR/R_c)对应力累积效应的影响, 其中$\Delta R = \left( {{R_{\max }} - {R_{\min }}} \right)/2$, R_c指单个气泡外轮廓对应的半径, 定义为${R_{\text{c}}} = \left( {{R_{\max }} + {R_{\min }}} \right)/2$, 代表泡群中气泡初始半径的中间尺寸, 即泡群中气泡的中心半径.

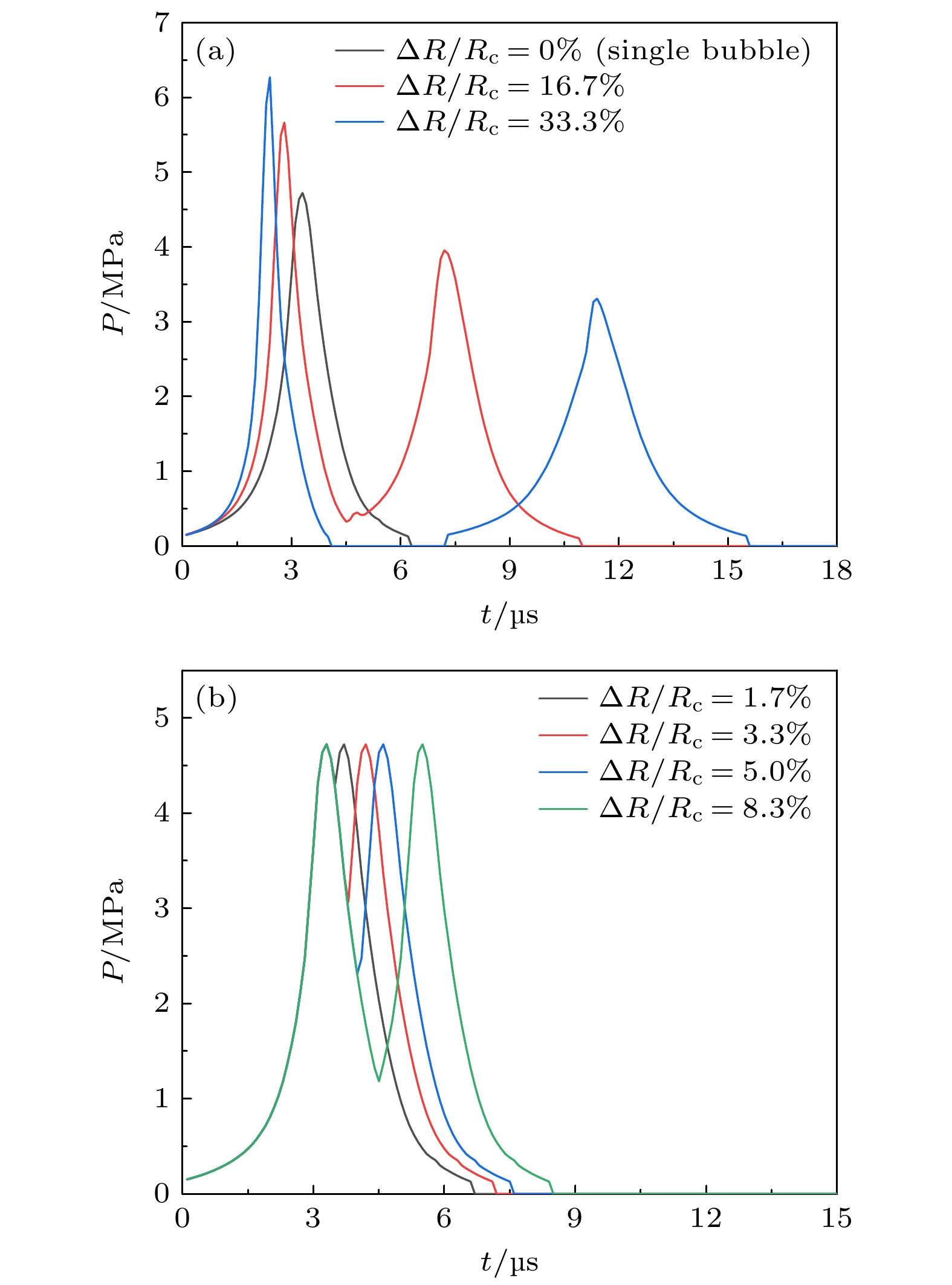
Kim等^[41]在实验中通过高速相机观察到超声产生的大量空化气泡半径分布可达16—164 μm, 同样在Vyas等^[42]的超声空化实验中, 观察到超声产生的空化气泡最大半径范围在40—80 μm. 因此, 在综合考虑实际声空化情况与数值计算精度的条件下, 假定泡群的中心半径为R_c = 60 μm, 泡群初始半径分布设计如表2所示, 两个极端半径气泡的射流时序差由拟合方程${t_{\rm jet}} = 0.23{R_0} + 29.98$计算得到, 其中R₀单位为μm, t_jet单位为μs.

泡群初始半径分布范围ΔR/R_c > 8.3%时, 双气泡冲击载荷序列基于数值模拟获得的射流冲击压力峰进行组合构建, 如图8(a)所示; 泡群初始半径分布范围ΔR/R_c ≤ 8.3%时, 近似以中心半径60 μm的射流冲击压力峰为基准, 通过表2中射流时序差生成时序偏移载荷进行组合构建双气泡冲击载荷序列, 如图8(b)所示.

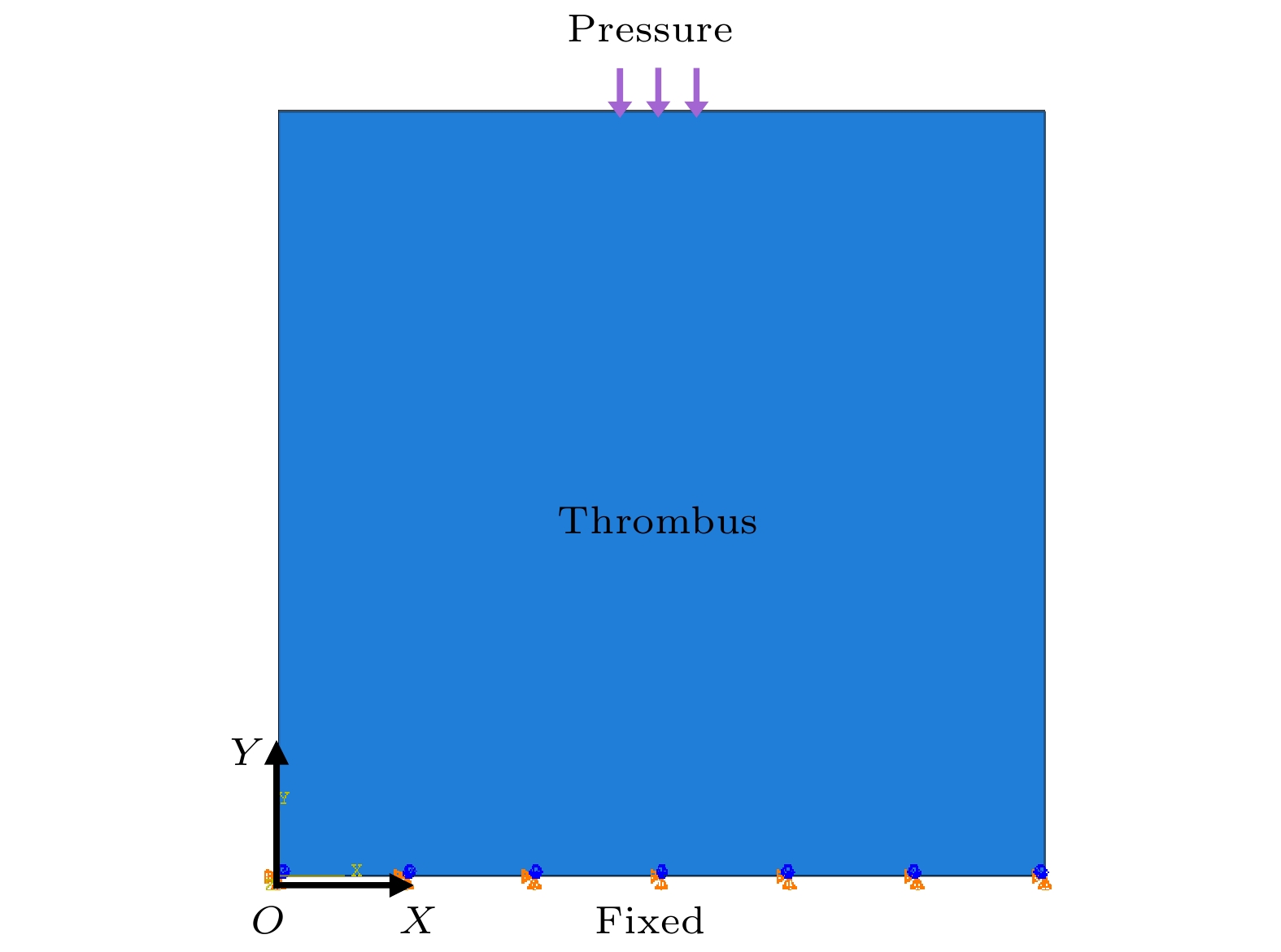
上述动态载荷均施加于血栓模型上边界中心区域(长度1 mm), 如图9所示. 血栓模型简化为1 cm × 1 cm的二维平面正方形, 模型下边界固定, 计算过程使用Abaqus完成, 材料参数与3.1节中Ogden-Prony本构模型所设参数一致, 时间增量Δt = 1×10^–8 s, 以确保冲击载荷求解稳定性.

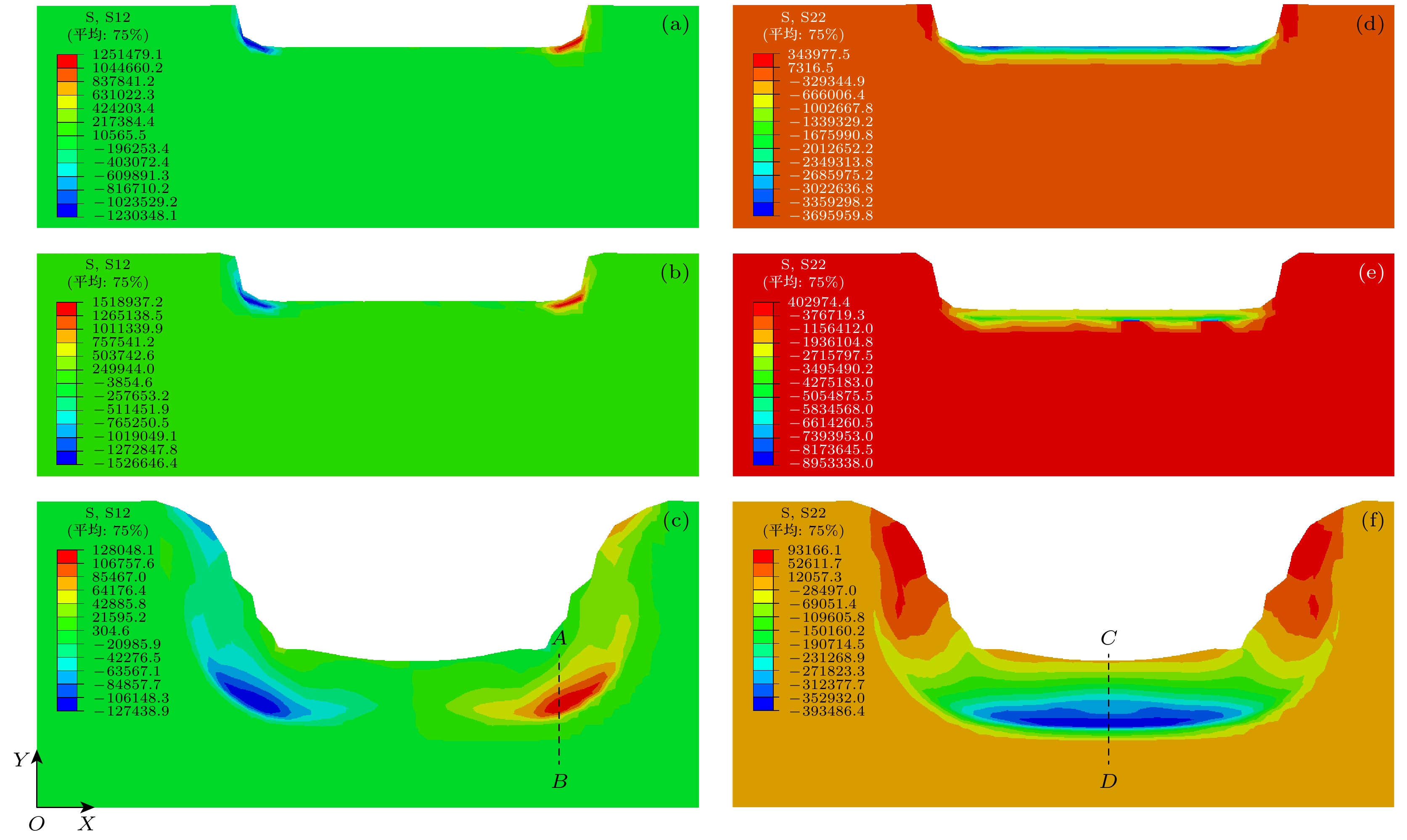
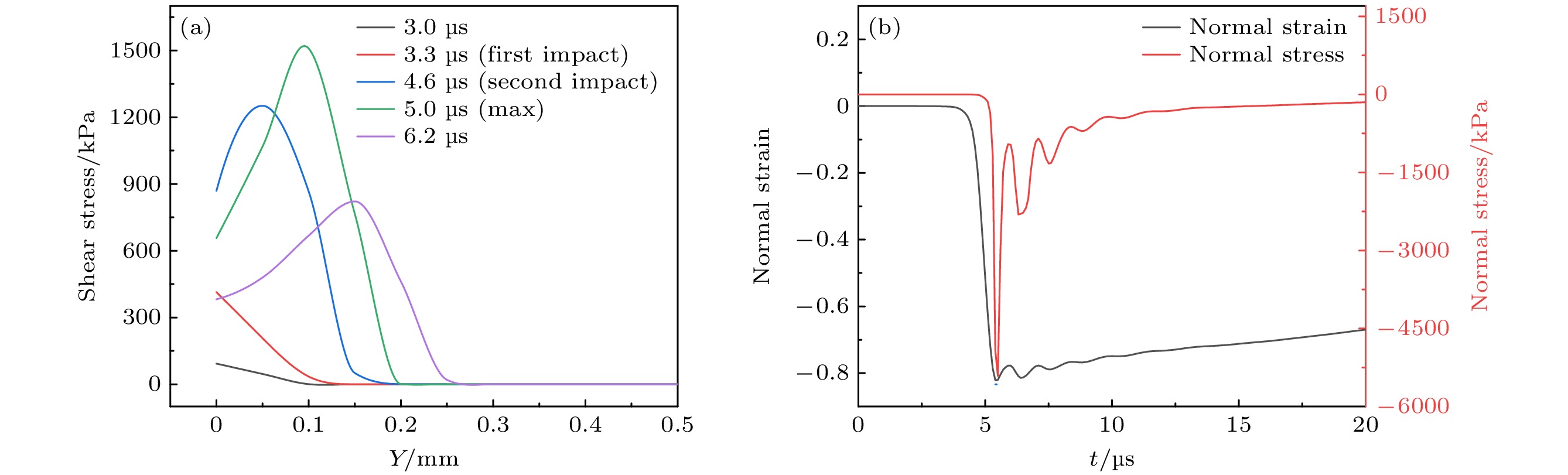
图10所示为血栓在双气泡(ΔR/R_c = 5.0%)冲击载荷下的剪应力${\tau _{xy}}$与正应力${\sigma _y}$分布云图, 坐标原点位于血栓模型左下角顶点处(如图9所示), 可见血栓在气泡空化产生的射流冲击作用下发生明显变形, 相应冲击载荷压力峰值为4.7 MPa. 同时, 可以发现最大剪应力出现在血栓凹陷侧, 如图10(c)所示, 最大正应力出现在模型轴线附近, 如图10(f)所示. 应力分布仅在冲击位置周围变化显著, 这是由于在气泡空化冲击的瞬态场景下, 冲击载荷作用时间非常短暂(20 μs内), 导致远离冲击位置处的血栓变形微小, 从而应力分布变化不明显.

在血栓凹陷侧取截线AB, 提取t = 3.0 μs, 3.3 μs(首次冲击到达)、4.6 μs(二次冲击到达)、5.0 μs(最大剪应力出现)、6.2 μs等特征时刻的剪应力沿截线分布曲线, 如图11(a)所示, 同时提取轴线上距壁面0.2 mm位置处的正应力应变响应曲线, 如图11(b)所示. 可以看到, 最大应力皆出现在两次冲击之后, 体现了由血栓本构模型特性引发的应力累积效应.

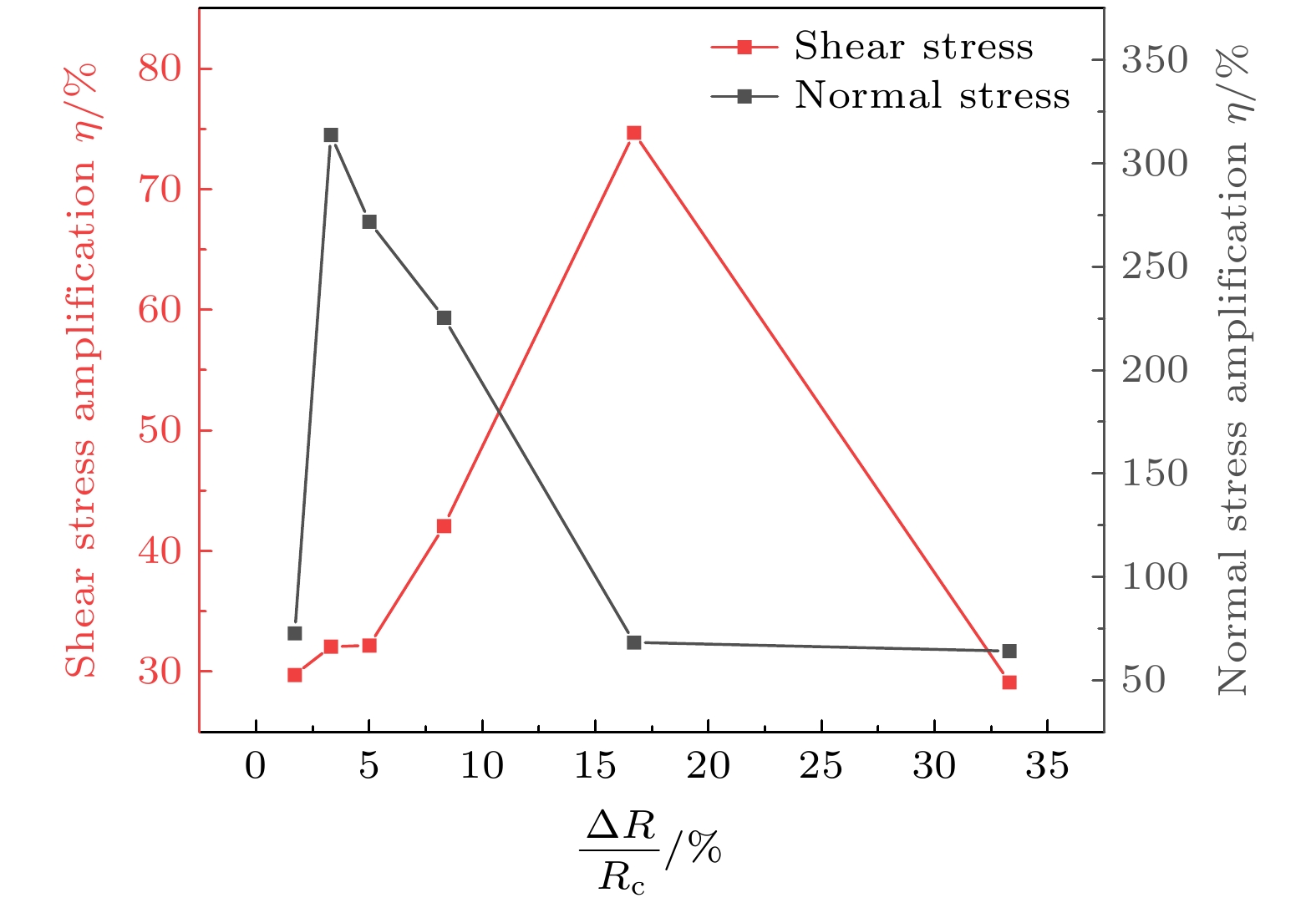
以血栓内部最大应力(剪应力取图10(c)中截线AB上最大值, 正应力取图10(f)中截线CD上最大值)的增幅η为评价指标, 由此得到的相对应力增幅表征多气泡应力累积效应的理论下限:

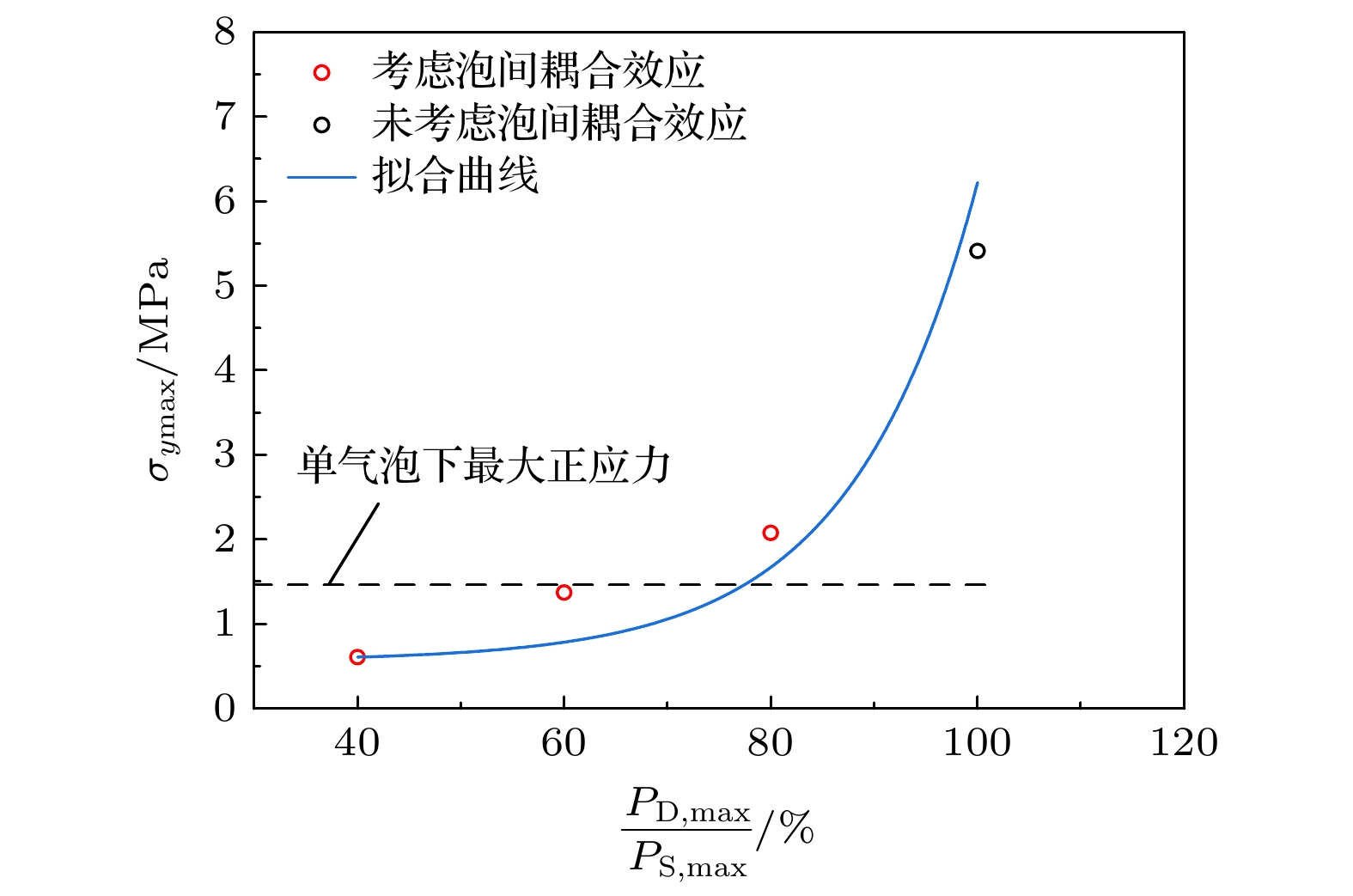
式中, ${\sigma _{\rm two}}$为极端半径双气泡(R_min, R_max)协同冲击下的最大应力, $ {\sigma _{{\mathrm{single}}}} $为中心半径单气泡(R_c)冲击下的最大应力. 图12所示为不同ΔR/R_c下的剪应力与正应力增幅η变化, 在模拟范围内最大剪应力增幅为74.7%, 当ΔR/R_c = 15.5%—18.4%时, 剪应力增幅η > 70%; 最大正应力增幅为313.9%, 当ΔR/R_c = 2.9%—6.5%时, 正应力增幅η > 250%.

值得注意的是, 单气泡冲击载荷下, 血栓内最大正应力为1.45 MPa, 双气泡冲击载荷下, 最大正应力达6.02 MPa, 同时现有研究指出血栓最大抗拉强度为2.39 MPa^[43], 纤维蛋白纤维(构成血栓的重要组分)的拉伸强度为6—21 MPa^[44], 表明单气泡冲击可能无法对血栓造成破坏, 而多气泡冲击序列下的应力累积效应是导致血栓破碎的根本原因.

计算结果表明, 双气泡射流冲击会在血栓内部产生相较于单气泡增强的应力, 这与文献[32,34,35]中提到的泡间相互作用增强壁面冲击压力相似, 都揭示了泡间相互作用的协同增强效果. 但现有研究的关注重点在于流体域内的泡间耦合效应, 本文则基于血栓率本构模型分析了多气泡射流在血栓内部的协同效应对应力累积的影响, 从另一视角展现了多气泡的协同空蚀效应, 为超声溶栓能量的定向投射技术提供了理论支撑.

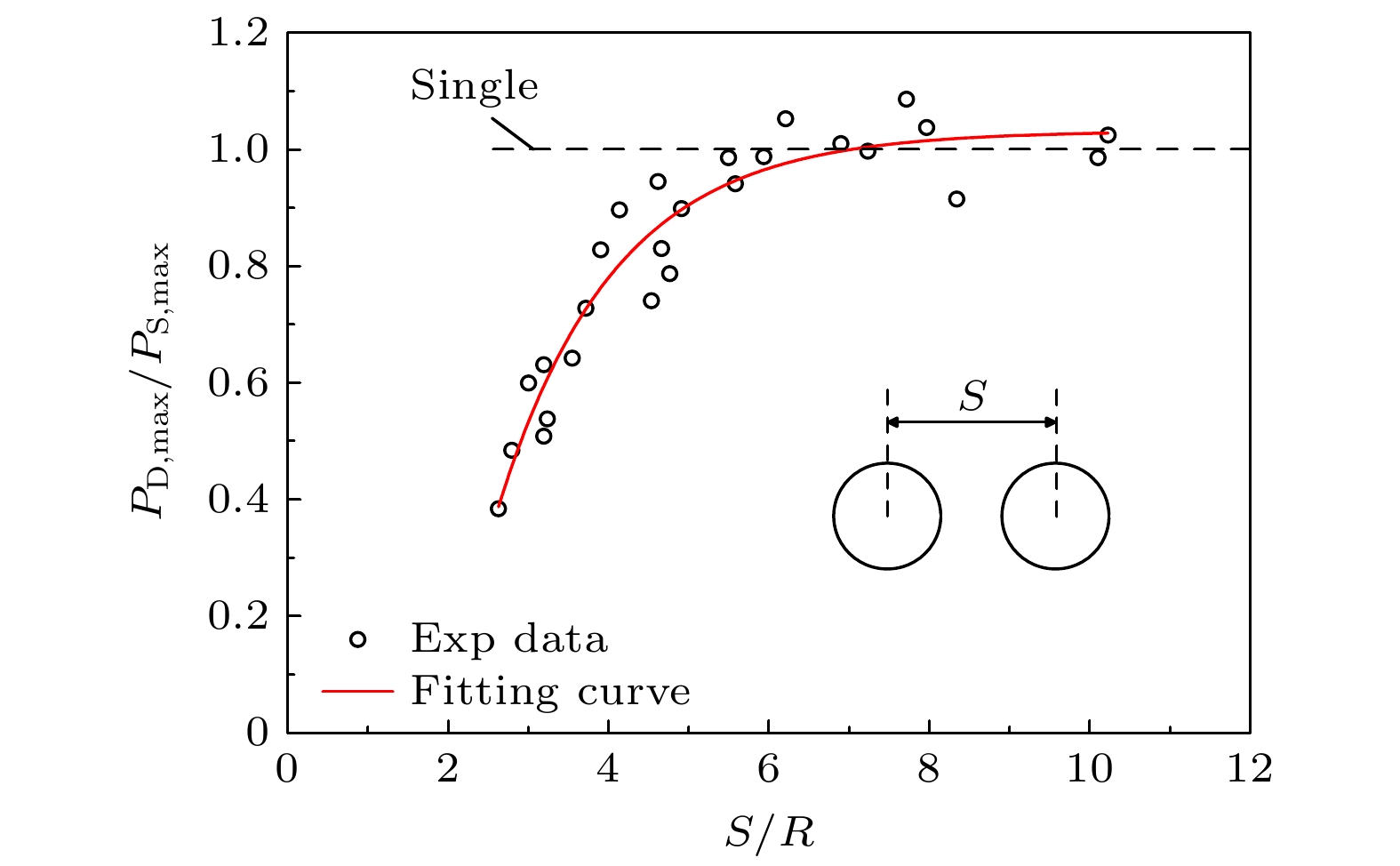
根据Tomita等^[45]实验给出的双气泡间距离与气泡对壁面冲击压力间的关系(如图13所示), 可以发现, 当S/R在2—10之间变化时, 双气泡工况下冲击压力相较单气泡时衰减40%—100%(无影响), 其中S为两个气泡中心的间距, R为气泡半径.

为考察泡间耦合效应对应力累积的影响, 将双气泡(ΔR/R_c = 5.0%)冲击压力峰值依次降低40%, 60%, 80%, 分别计算冲击衰减后血栓内的应力累积效果. 图14所示为冲击压力峰值衰减与未衰减(100%)时血栓内最大正应力变化, 可以看到考虑泡间耦合效应使冲击压力峰值衰减60%时, 血栓内最大正应力与单气泡工况在同一水平, 此时两个气泡壁之间的距离约为一个气泡半径; 气泡壁之间的距离持续增大时, 泡间耦合效应对冲击压力峰值的衰减效果削弱, 当该距离大于两个气泡直径时, 泡间耦合效应几乎消失, 此时双气泡冲击序列引发的应力累积可达单气泡的3.7倍.

需要指出的是, 双气泡工况下计算得到的应力增幅是代表多气泡应力累积效应的下限, 当气泡增多时, 基于血栓渐增硬化的本构特性, 射流序列的冲击会使血栓内应力持续增长, 造成相较单气泡冲击下更大的破坏, 即血栓力学特性引发的射流冲击序列下血栓内应力的持续累积.

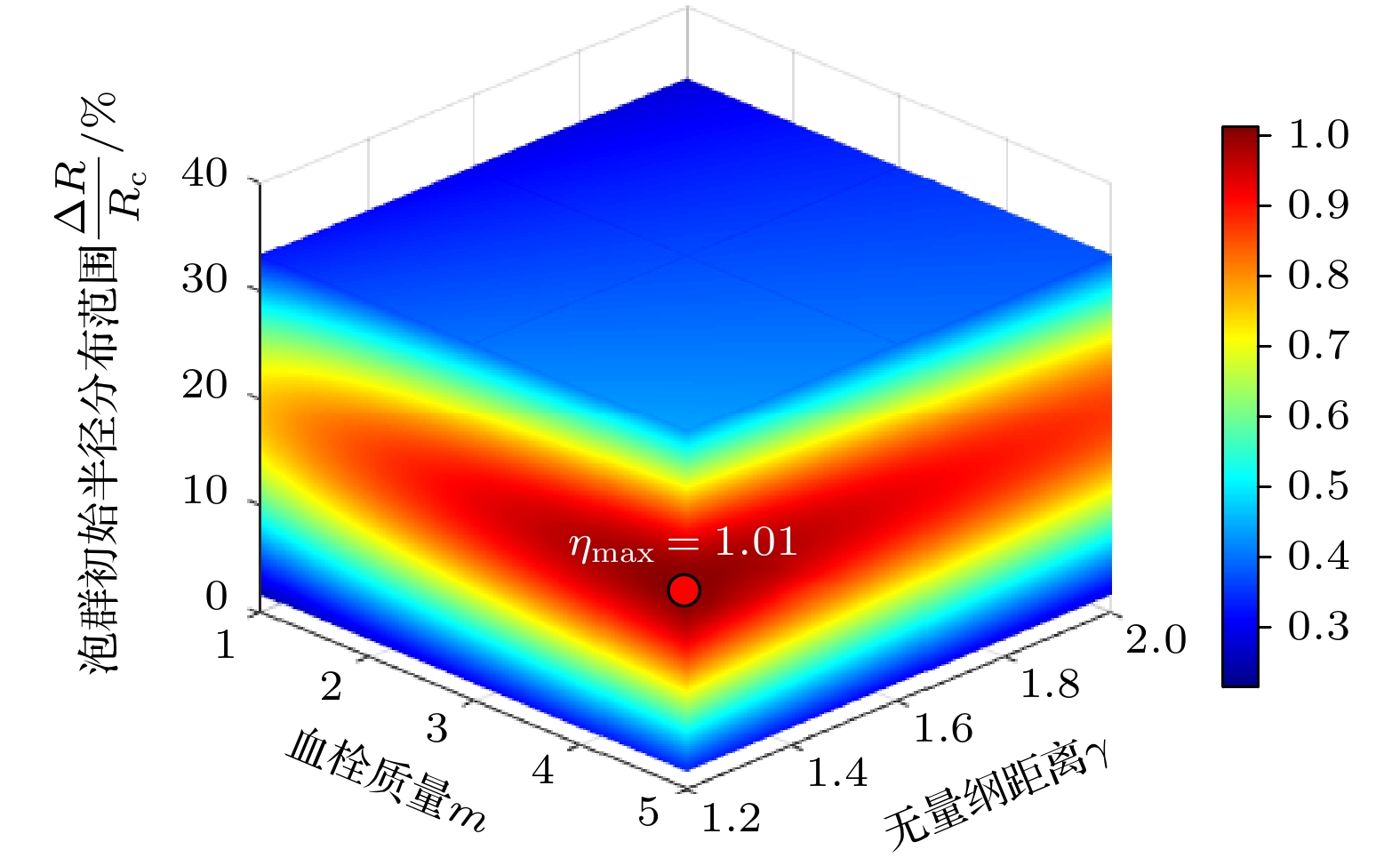
基于单气泡参数敏感性分析与泡群初始半径分布对剪应力累积效应的影响, 建立了以血栓质量m、无量纲距离γ、泡群初始半径分布范围ΔR/R_c为变量的剪应力增幅η预测方程:

式中${m_0} = 1{\text{ g}}$, 等号右边三项分别为泡群分布协同项, 经验系数${a_1} = 0.725, {a_2} = - 0.185, {a_3} = 0.159$通过图12中ΔR/R_c-η关系拟合得到; 距离衰减修正项(近壁距离偏离1.4时的能量衰减修正), 经验系数${a_4} = 0.3$通过图5(b)中γ-p_max关系拟合得到; 质量增益修正项(血栓质量增加对压力峰值的提升修正), 经验系数${a_5} = 0.18$通过图5(a)中m-p_max关系拟合得到.

图15为m = 1—5 g, γ = 1.2—2.0, ΔR/R_c = 1.7%—33.3%时, 根据剪应力增幅预测方程得到的η变化情况, 图中3个坐标轴分别代表m, γ和ΔR/R_c, 颜色表示η大小, 可以看到在所设参数范围内η最大值为101%.

本文针对超声溶栓中多气泡冲击序列协同效应的调控问题, 构建了考虑血栓运动的气-液-固多物理场耦合模型, 引入结构阻尼项表征血栓运动过程中能量耗散, 量化分析了血栓附近空化气泡溃灭动力学特性. 在此基础上结合血栓率本构模型讨论了射流序列的调控, 以及射流冲击序列引发的应力累积效应, 并以血栓内部最大应力增幅来量化冲击序列的协同效果, 给出了协同空蚀效应预测方程.

数值结果表明, 壁面冲击压力源于气泡非球形溃灭诱导的微射流, 并且血栓运动会显著影响气泡溃灭形态. 在本文模拟参数范围内, 射流冲击强度与血栓质量、超声振幅呈正相关, 与无量纲距离、超声频率、气泡初始半径呈负相关. Ogden-Prony率相关本构模型在宽应变率范围内有效表征了血栓的渐增硬化、应变率强化与应力松弛行为, 满足空化冲击瞬态载荷的仿真需求. 多气泡产生的射流冲击序列通过血栓本构模型的渐增硬化及应变率强化效应引发应力累积, 且应力累积效果受气泡初始半径分布范围ΔR/R_c显著影响. 多气泡协同效应存在相对优化的半径分布范围, 通过射流序列匹配可使血栓内部正应力或剪应力获得较高增幅. 本文从血栓力学特性的角度出发, 从另一视角展现了多气泡的协同空蚀效应, 为超声溶栓能量的定向投射技术提供了理论支撑.