-
近年来, 随着信息技术的发展, 光操纵和光处理技术越来越受到人们的关注. 其中, 光子在实空间中的局域化在基础研究和应用领域都具有重要意义. 从波动方程可以很容易理解波的传播, 但波的局域化(束缚态的产生)则更为复杂. 通常, 只有不存在合适的出射波或由于对称不匹配而被禁止时, 才能实现波的局域化. 对于电磁波, 这通常是用金属镜、全反射或高度无序介质[1]实现的; 对于电子波, 这通常是通过构建势垒来实现的. 1929年, 冯·诺伊曼和维格纳提出了第1个反例[2], 他们设计了一个量子势来捕获一个电子, 这个电子的能量通常允许与发射波耦合. 此后, 在光子[3–5]、量子系统[6,7]、声子[8]、水波[9]等各种波系统中观测到了类似现象.
光子晶体的出现为光学操控提供了新的机制. 光子晶体(photonic crystals, PCs)是一种在一维、二维或三维空间具有周期介质分布的光学结构[10]. 由于光在周期光子结构中的布拉格散射, PCs具有光子能带结构, 它决定了光子晶体的光学特性. 当光的频率位于带隙内时, 其不能在PCs中传播[11]. 2013年, Hsu等[12]实验证实, 即使在周围的介质中允许出射波, 光也可以被完美地限制在图案化的电介质板光子晶体中, 即连续域束缚态(bound states in a continuum, BICs). 理想的BICs可在实空间中实现完美的光子局域化, 并且理论上它们的寿命是无限长的, 品质因子(quality factors)Q无穷大[13–15]. 在引入扰动后, 理想的具有无穷大Q值的BICs会转变为具有有限Q值的准BICs, 由于BICs具备超强的频率选择性和超低的损耗性, 它可以大幅提高光电器件效率, 因此其已被用于增强各种应用, 如激光器[16–19]和天线[20,21]. 在过去的二十年里, BICs受到了广泛的关注与研究, 除了光子晶体[22]之外, 近年来研究人员同样在超表面[23–25]、亚波长光栅[26–28]中发现了BICs.
为进一步优化光子晶体的设计, 在实验上对其动量空间进行表征和调控是十分必要的. 本工作设计并实验制备了可见光波段的光子晶体, 利用自主搭建的角分辨光路对其动量空间进行表征, 实验测得的能带结构与使用时域有限差分法(finite difference time domain, FDTD)仿真结果一致, 并通过调整光子晶体几何参数实现了对其动量空间的有效调控. 通过设计两个周期不同的光子晶体横向异质结构, 利用两者带隙错位实现了高品质因子Q低模式体积V的微腔, 实现了对光子的有效局域化. 本研究为BICs的设计和优化提供了一定的指导, 同时高质量微腔对于提高光与物质相互作用具有重要意义.
-
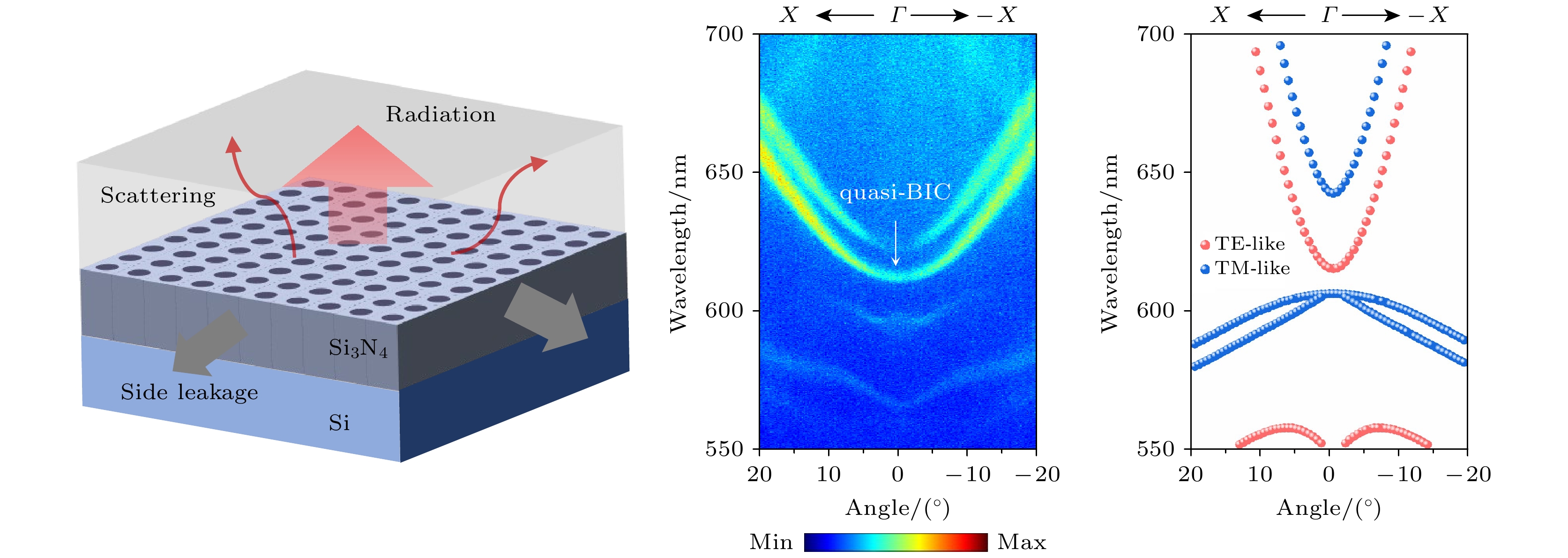
分析发现造成光子晶体能量损耗的因素有辐射、侧向能量泄漏以及由于制造缺陷引起的散射损耗等, 这些因素限制了光子晶体的品质因子Q. 首先考虑垂直(厚度)方向的局域化. 本文设计的光子晶体示意图如图1(a)所示, 光子晶体是由圆柱形孔按照四方晶格结构排列组成. 周期性几何结构产生光子能带结构, 其方式类似于固体中的周期性电势可以产生电子能带结构[29,30]. 具有C4对称性的四方晶格光子晶体, 在动量空间Γ点的高对称性导致光子晶体内部模式与外部传播模式(辐射连续体)之间的对称失配, 从而在光线上方出现了具有无限寿命的束缚态, 实现垂直(厚度)方向的局域化[31]. 使用FDTD计算得到的光子晶体能带结构如图1(b)所示, 图中红色圆点代表TE模式, 蓝色圆点代表TM模式. 通过仿真计算得出本结构的TE1能带具有更高的Q值, 因此本研究聚焦于TE1能带.
氮化硅(Si3N4)在可见光波段具有较高的折射率, 因此采用沉积365 nm厚度Si3N4薄膜的硅(Si)基平板制备光子晶体, 使用椭偏仪测得Si3N4在600 nm的折射率为2.23. 使用电子束光刻 (electronic beam lithography, EBL)与电感耦合等离子体(capacitively coupled plasma, ICP)刻蚀技术相结合, 在Si基Si3N4薄层加工出设计的周期性圆形空气孔结构, 制备的光子晶体样品扫描电子显微镜(scanning electron microscope, SEM)正视图和侧视图分别如图1(c), (d)所示. 光子晶体的高度h为365 nm, 周期a为326 nm, 圆形空气孔直径d为223 nm. 为保证光子晶体垂直(厚度)方向介电环境的对称性, 使用质量分数为50%的氢氧化钾(KOH)溶液浸泡样品, 湿法刻蚀清除结构下方的Si衬底, 使光子晶体悬空.
-
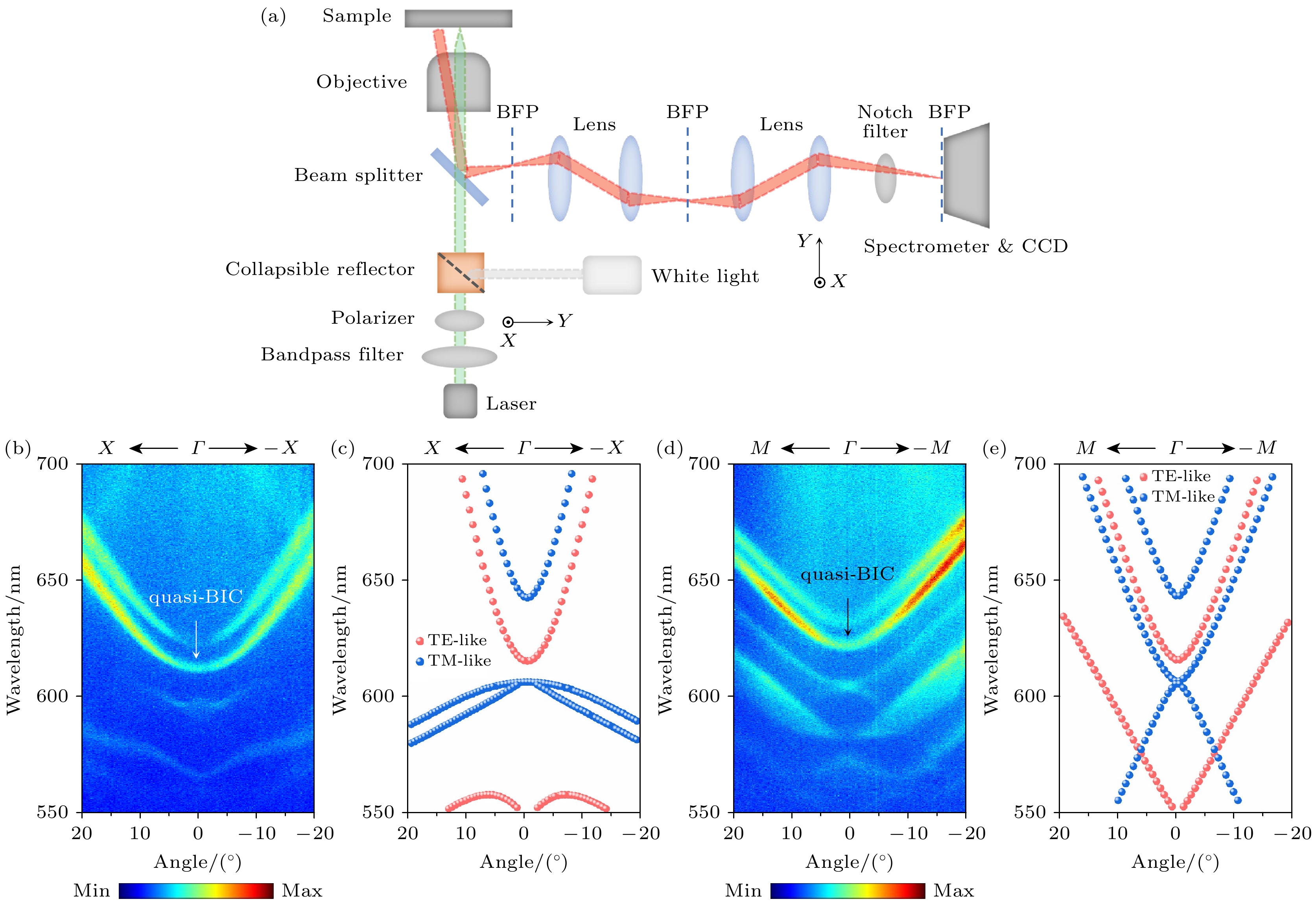
通过自主搭建的角分辨光路测量光子晶体的角分辨光致发光(photoluminescence, PL)光谱. 角分辨光路示意图如图2(a)所示, 将样品放置在物镜(40×, NA 0.6)的像平面上, 使用波长532 nm的线偏振连续激光激发, 样品的PL信号通过物镜收集. 通过一系列透镜将物镜的后焦平面(back focal plane, BFP)成像到光谱仪(Andor SR-303i)的入射狭缝上. 通过狭缝后的光被300行/mm的光栅散射, 产生角度和波长分辨的PL光谱, 由2D EMCCD相机(Andor Newton 971)拍摄. 利用Si3N4衬底微弱的光致发光, 与光子晶体模式耦合可以测得光子晶体能带.
入射光偏振方向沿图中Y方向并调整样品摆放角度, 使光子晶体动量空间平面与光谱仪狭缝成0°夹角, 得到沿Γ-X方向的角分辨PL光谱如图2(b)所示. 可以看出, TE1能带Γ点两侧波长在625 nm处的PL强度较其他能带强度更强, 但该能带在Γ点附近的强度较偏离Γ点位置处的强度明显减弱, 形成较暗的缺陷. 根据前文的理论分析, Γ点的高对称性导致的对称失配将会产生无限寿命的束缚态, 使得此处辐射消失, 表现为无PL光强. 实验结果中尽管强度明显减弱, 但并未完全消失, 这表明能带该位置处的一部分光子未被完全束缚, 而是出现了辐射泄漏, 形成了准BIC. 其中既有位于Γ点, 与对称性相关的准BIC, 又有偏离Γ点, 由几何参数引起的干涉相消导致的偶然准BIC. 相较于BIC而言, 除了材料的吸收和有限尺寸之外, 加工误差和缺陷引起的散射损耗是准BIC中向外辐射泄漏通道得到抑制但并未完全消除的主要因素, 从而可以在Γ点测得部分信号. 为了验证这一猜想, 我们使用FDTD对光子晶体的Q值进行仿真计算, 对于理想的圆柱形空气孔结构, 其Q值为5500左右, 而对于圆柱底部有部分加工残余的非理想结构, 其Q值将会降低至2000左右. 这一仿真结果表明加工误差与缺陷将会破坏结构的对称性, 导致光子晶体的Q值迅速退化, BIC向准BIC演化. 图2(c)是使用FDTD仿真得到的光子晶体能带结构, TE模式能带位置与实验结果相吻合, TM模式能带位置略有偏离, 但形状保持一致. 调整样品摆放角度, 使光子晶体动量空间平面与光谱仪狭缝成45°夹角, 得到沿Γ-M方向的角分辨PL光谱如图2(d)所示, 与之对应的能带仿真结果如图2(e)所示. TE1能带同样呈现出Γ点附近的强度弱而两侧强的特点.
-
准BIC模式在Γ点附近可以实现垂直(厚度)方向的局域化, 但在水平方向上是非局域化的, 纵然准BIC模式具有较高的Q值可以在光子晶体中局域较高的能量, 但非局域化的模式体积使得
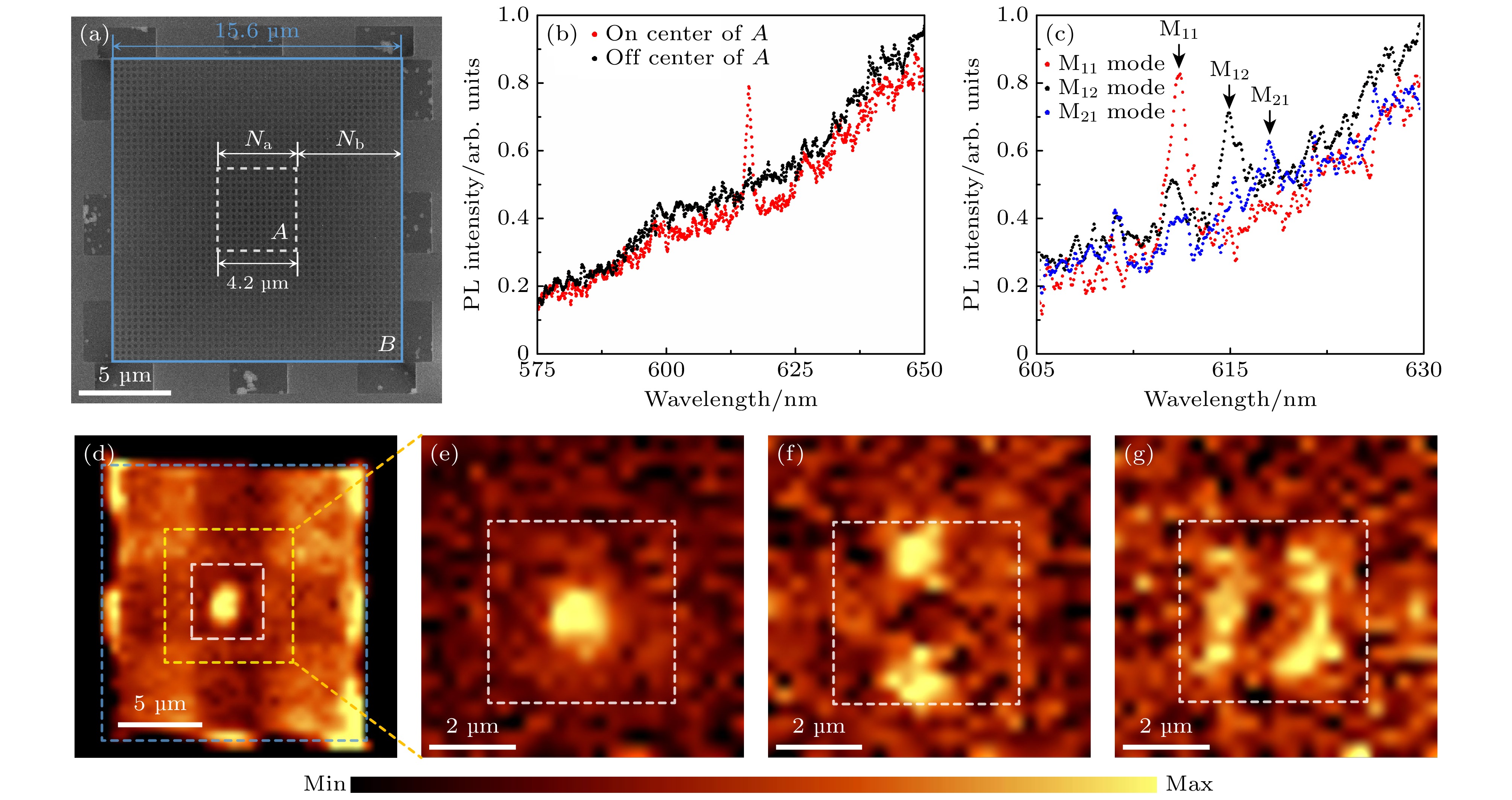
$ Q/V $ 的比值较低, 这限制了其在增强与局域发射体的光-物质相互作用[32–34]、量子光学[35]、非线性光学[36,37]等方面的应用. 通过设计不同周期光子晶体横向异质结构来实现水平方向的局域化. 通过能带设计将A区域光子晶体的能带置于B区域光子晶体带隙范围, 同时离散化的共振能量可以与偏离Γ点的偶然准BIC相匹配[38]. 如图3(a)所示, A区域光子晶体的周期a为325 nm, B区域光子晶体周期b为335 nm, 两个区域的光子晶体高度h和孔洞结构直径d分别为365 nm和214 nm, 两区域之间的间隔g为330 nm.通过光致荧光光谱对微腔进行表征. 使用波长532 nm线偏振连续激光分别激发A区域的中心位置和非中心位置, 得到的PL谱线如图3(b)所示. A区域中心位置处PL谱线在616 nm附近有很高的尖峰, 激发点位偏离A区域中心位置则尖峰消失. 通过尖峰半高宽估算微腔的Q约为600. 使用激发光对光子晶体区域逐点扫描得到的PL扫描图像如图3(d)所示. 由图3(d)可知, 光子晶体横向异质结构可以将模式很好地局域在A区域, 实现光子晶体模式在水平方向上的局域化. 通过光子晶体模式分布估算, 光子晶体的模式体积V为
$1\; \text{μm}^{3} $ , 品质因子与模式体积比值达到6 × 1014 cm–3.对A区域(扫描区域如图3(d)黄色虚线所示)进行更高分辨率PL扫描以表征光子晶体的模式分布. 图3(e)是峰位位于616 nm(图3(c)红色曲线)的PL扫描图像, 该图像呈现光子晶体M11模式的单极热点分布特点. 图3(f), (g)呈现双极型热点分布, 这是光子晶体的M12模式和M21模式, 这两个模式的峰位分别位于620 nm和623 nm, 峰位偏差3 nm. 这是由于加工误差轻微破坏了光子晶体的C4对称性, 导致光子晶体M12和M21模式能量出现略微差异.
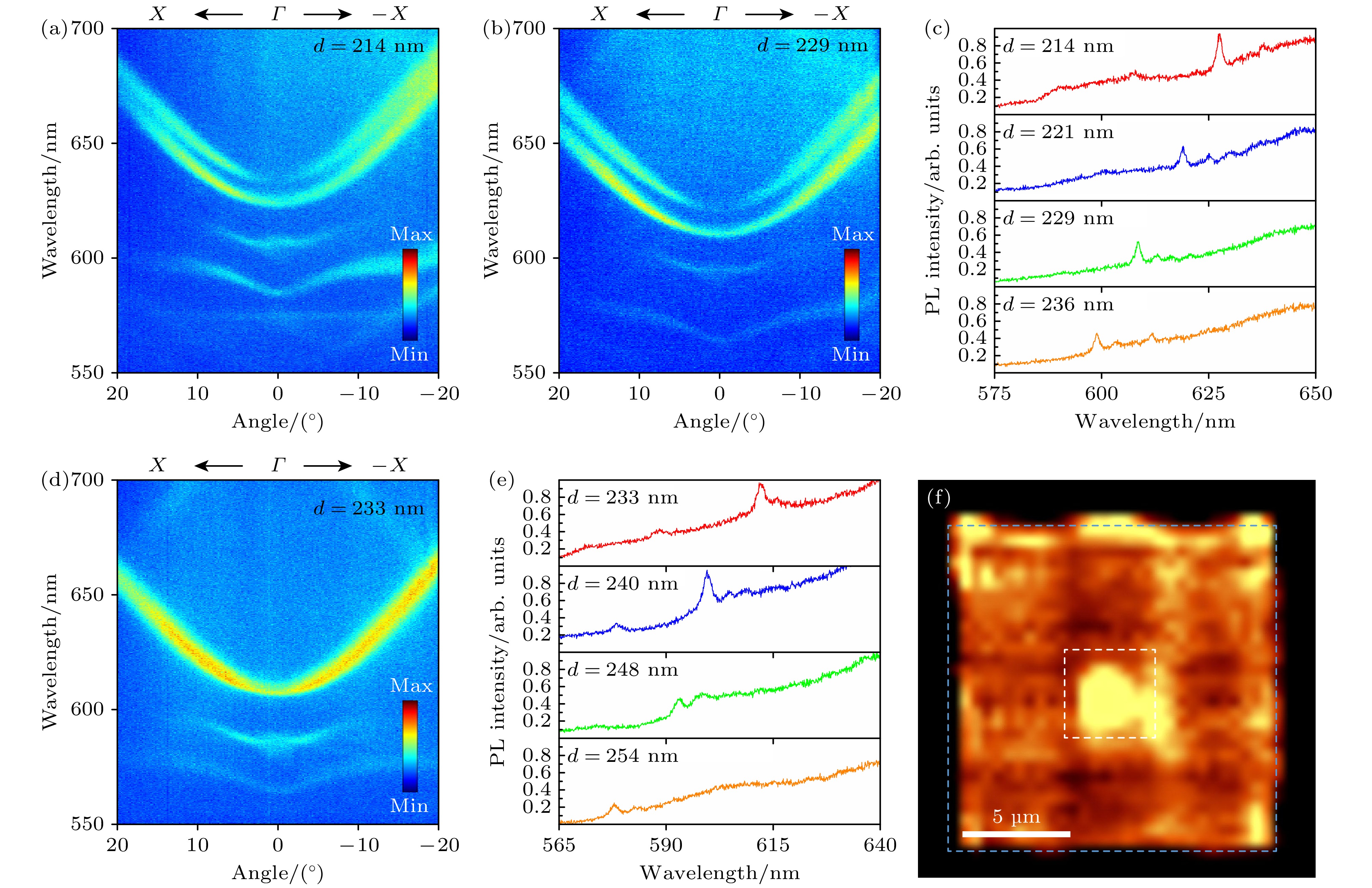
为研究光子晶体微腔的性质与参数的关系, 通过改变光子晶体的孔洞直径d和高度h研究参数变化对能带、品质因子和模式分布等特征的影响. 首先只改变光子晶体的孔洞直径d, 光子晶体的高度为365 nm, 其他参数与图3(a)保持一致. 图4(a), (b)分别是孔洞直径d为214 nm和229 nm的光子晶体角分辨PL光谱, 对比两幅图得出, 改变光子晶体的孔洞直径d会使得光子晶体能带沿波长整体移动. 不同孔洞直径的光子晶体PL光谱如图4(c)所示. 光子晶体的共振波长随着孔洞直径d的增大发生蓝移. 分析尖峰半高宽发现, 通过改变波长获得的最高Q为600.
接下来研究改变光子晶体的高度h对光子晶体微腔特性的影响. 图4(d)是高度h为330 nm, 孔洞直径d为233 nm的光子晶体角分辨PL光谱, 该光谱显示Γ-X方向TE1能带在Γ点附近的信号没有明显缺陷. 分析高度h为330 nm不同孔洞直径的光子晶体PL光谱(图4(e))得到最高Q为300, 随d的改变整体在250附近波动. 相较高度365 nm的光子晶体显著下降. A区域的模式分布(图4(f))直观表明光子晶体对光子的局域性降低. 通过以上分析得出, h降低30 nm使得非对称点处限制z方向光子泄漏的偶然准BIC消失, 会严重影响光子晶体微腔Q值.
-
本工作研究了可见光波段Si3N4光子晶体中的BIC, 通过动量空间实验观测到准BIC, 从而在垂直方向实现了对光子的有效局域化. 在实现垂直方向局域化的基础上, 设计不同周期光子晶体的横向异质结构, 利用两者的能带套嵌实现了对光子水平方向上的局域化, 实现了品质因子与模式体积之比达到6 × 1014 cm–3的高品质微腔. 通过调整光子晶体的结构参数实现了对其动量空间的有效调控. 本研究对光子晶体动量空间的表征和调控对光子晶体的优化设计具有重要指导意义. 同时, 高品质光子晶体微腔对于增强与局域发射体的光-物质相互作用、非线性光学、量子光学等方面具有巨大的应用前景.
感谢北京大学物理学院朱振东副研究员和国家纳米科学中心胡海峰副研究员对样品加工的帮助, 北京大学物理学院成星博士对光致荧光测量的帮助以及北京大学电子学院彭超教授与郑昭博士的讨论对课题的启发.
Si3N4光子晶体连续域准束缚态表征及调控
Characterization and control of quasi-bound states in the continuous in Si3N4 photonic crystals
-
摘要: 实空间中光子的局域化在基础研究和技术应用领域具有重要意义. 连续域束缚态(bound states in the continuum, BICs)为光子的局域化提供了新的机制, 其中最重要的方案之一是光子晶体. 然而光子晶体在制备过程中会不可避免地引入误差和缺陷, 动量空间表征可以分析加工误差和缺陷对于光子晶体能带特性的影响, 进而指导光子晶体器件的设计和制备. 本文设计了可见光波段的光子晶体, 通过动量空间表征观测到了连续域准束缚态(quasi-BIC), 从而在垂直方向上实现了对光子的高度局域化, 并通过调整结构参数, 实现了对光子晶体动量空间的特征调控. 进一步设计不同周期光子晶体的横向异质结构, 利用两者的能带套嵌实现了对光子水平方向上的局域化, 以此制备了品质因子与模式体积之比达到6 × 1014 cm–3的高品质光学微腔. 本研究对于光子晶体的设计以及增强光与物质相互作用具有重要意义.Abstract: Photon localization is of great significance in both basic research and technical applications. Bound states in the continuum (BICs) in photonic crystal provide a new mechanism for effective photon localization. However, the imperfections and defects are inevitable in the process of fabricating photonic crystals. Momentum-space characterization is used as a powerful tool to analyze how such processing variations affect the photonic band structure, providing information for designing and fabricating photonic crystal devices. In this work, a photonic crystal in the visible light band is designed and its band structure is analyzed through FDTD simulation. The high symmetry at the point in momentum space Γ leads to a symmetry mismatch between the internal mode of the photonic crystal and the external propagation mode (radiation continuum), so that bound states with infinite lifetime appear above the light, thereby achieving the localization of photons in the vertical direction. At the same time, the angle-resolved photoluminescence (PL) spectrum of the photonic crystal is measured through the self-built angle-resolved optical path. The weak photoluminescence of the Si3N4 substrate is coupled with the photonic crystal mode for measuring the photonic crystal band. It can be observed that the band structure is consistent with the simulation results. At the same time, the intensity of the TE1 band near the Γ point is significantly weakened compared with the intensity at the position away from the Γ point, but it is not completely eliminated. This shows that errors and defects caused in fabrication process will destroy the symmetry of the structure, causing the BIC to evolve into the quasi-BIC. The quasi-BIC mode achieves effective localization of photons in the vertical direction near the Γ point. Furthermore, a heterostructure of photonic crystals with different periods is designed to achieve lateral photon localization by utilizing the band nesting between the photonic ctystals with different periods. Through this approach, this study ultimately develops a high-quality microcavity with a ratio of impressive quality factor to mode volume of $ 6\times {10}^{14} $ cm–3, and achieves characteristic regulation of the momentum space of photonic crystals by adjusting the structural parameters. This research is of great significance for designing photonic crystals and studying the interaction between light and matter.
-
Key words:
- photonic crystals /
- bound states in the continuum /
- momentum space /
- visible wavelengths .
-

-
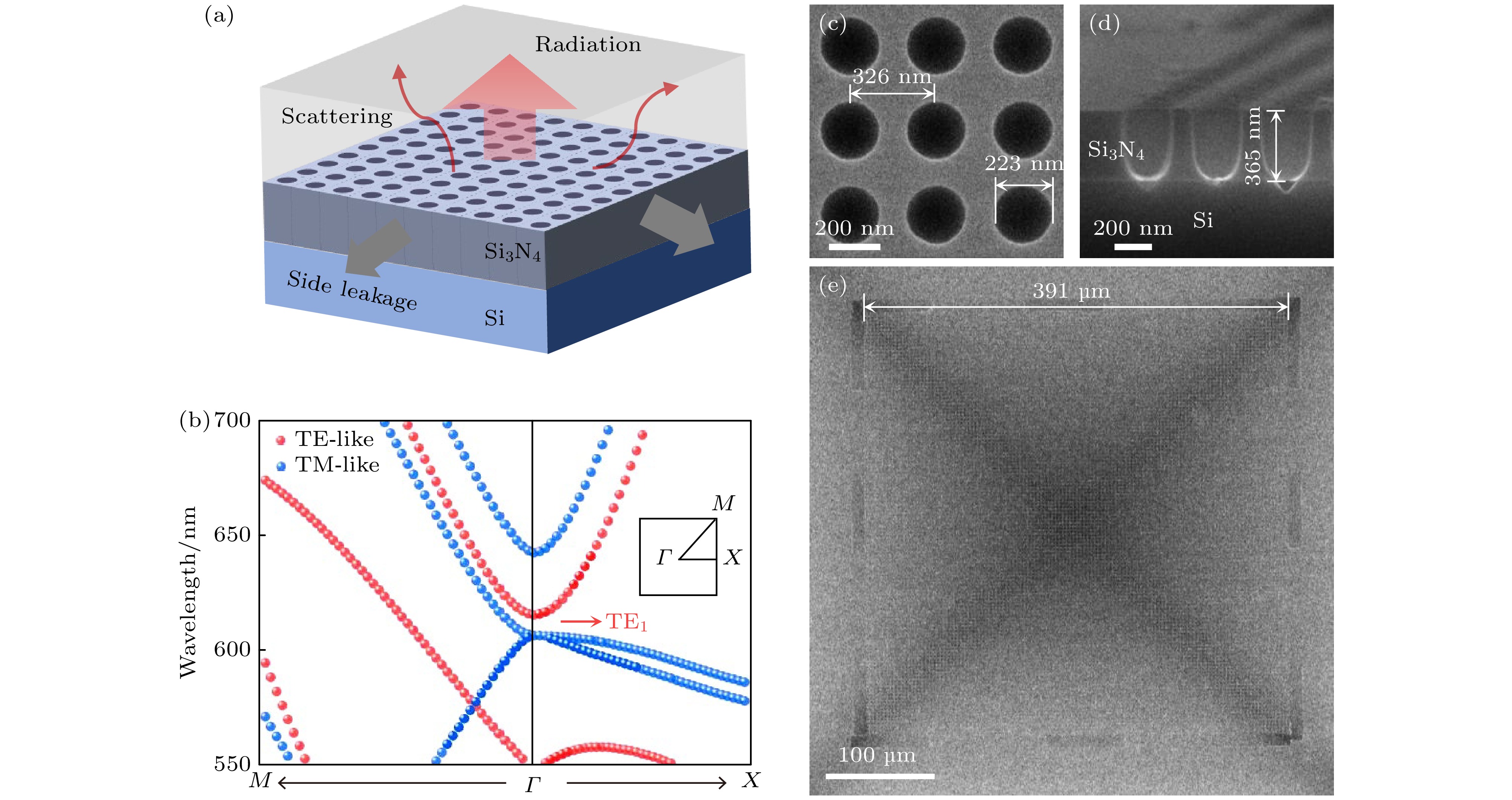
图 1 光子晶体的设计和制备 (a) 光子晶体及导致其损耗因素的示意图; (b) 模拟的能带结构, 其中红色圆点代表TE模式, 蓝色圆点代表TM模式, 插图为第一个布里渊区; (c) 制备的光子晶体局部的扫描电子显微镜俯视图, 周期为326 nm, 孔洞结构直径为223 nm; (d) 制备的光子晶体扫描电子显微镜侧视图, 其中孔洞结构的高度为365 nm; (e) 光子晶体的扫描电子显微镜图像
Figure 1. Design and fabrication of photonic crystal: (a) Schematic of a photonic crystal and the factors contributing to loss. (b) Simulated band structure. The TE band is marked with red dots and the TM band is marked with blue dots. Inset: the first Brillouin zone. (c) Scanning electron microscope images of the fabricated photonic crystal from top views. The period is 326 nm and the diameter of the cylindrical holes is 223 nm. (d) Scanning electron microscope images of the fabricated photonic crystal from side views. The height of the cylindrical holes is 365 nm. (e) Scanning electron microscope images of the fabricated photonic crystal.
图 2 光子晶体动量空间表征 (a) 角分辨光路原理示意图, 其中绿色线代表激发光, 浅红色线代表样品光致荧光信号, “BFP”表示后焦面; (b) 沿Γ-X方向和(d)沿Γ-M方向的角分辨光致荧光光谱; (c) 沿Γ-X方向和(e)沿Γ-M方向能带仿真. 光子晶体结构参数如图1(c), (d)所示
Figure 2. Characterization of momentum in photonic crystal: (a) Schematic of angle-resolved optical path. The green lines represent the incident light. The light red region denotes photoluminescence signal. BFP, back focal plane. (b), (d) Measured angle-resolved photoluminescence (PL) spectra along Γ-X (b) and Γ-M (d) directions. (c), (e) Calculated band structure along Γ-X (c) and Γ-M (e) directions. The structure parameters of photonic crystal are shown in Fig. 1(c) and Fig. 1(d).
图 3 微腔的模式表征 (a) 微腔SEM图像, A区域光子晶体(周期 a = 325 nm, 直径d = 214 nm, 孔洞数目
$ {N}_{a} $ = 13)由不同周期的B区域光子晶体(周期b = 335 nm, 直径d = 214 nm, 孔洞数目$ {N}_{b} $ = 17)包围, 两区域之间的间隔为330 nm; (b) 光子晶体PL光谱; (c) 光子晶体的模式热点位置处的PL光谱; (d) 光子晶体的PL扫描图像; (e) M11模式、(f) M12模式和(g) M21模式的远场模式分布; 白色虚线和蓝色虚线分别表示A区域和B区域光子晶体边界; 黄色虚线表示模式表征的扫描区域Figure 3. Characterization of micro-cavity modes: (a) SEM image of micro-cavity. Region A photonic crystal (period a = 325 nm, diameter d = 214 nm, the number of holes
$ {N}_{\mathrm{a}} $ = 13) are surrounded by region B photonic crystal (period b = 335 nm, diameter d = 214 nm, the number of holes$ {N}_{\mathrm{b}} $ = 17) with different periods, and the interval between the two regions is 330 nm. (b) PL spectral of photonic crystal. (c) PL spectral of mode hot spot in photonic crystal. (d) PL mapping image of photonic crystal. The far-field distribution of (e) M11, (f) M12 and (g) M21 modes. The white dashed and blue dashed represent the photonic crystal boundaries of region A and region B, respectively. The yellow dashed represents the scan area of the mode characterization.图 4 微腔的参数调控 (a), (b) 孔洞直径d为(a) 214 nm和(b) 229 nm的光子晶体角分辨PL光谱; (c) 不同孔洞直径的微腔光子晶体A区域PL光谱; (d) 高度h为330 nm, 孔洞直径d为233 nm的光子晶体角分辨PL光谱; (e) 高度h为330 nm, 不同孔洞直径的微腔光子晶体A区域PL光谱; (f) 高度h为330 nm, 孔洞直径d为233 nm的光子晶体PL扫描图像, 白色虚线和蓝色虚线分别表示A区域和B区域光子晶体边界; 图4样品的其他结构参数均与图3(a)相同
Figure 4. Parameters tuning of micro-cavity: (a), (b) Measured angle-resolved PL spectra of photonic crystals with hole diameter d of (a) 214 nm and (b) 229 nm; (c) PL spectra of region A of microcavity photonic crystals with different hole diameters; (d) measured angle-resolved PL spectra of photonic crystals with height h of 330 nm and hole diameter d of 233 nm; (e) PL spectra of region A of microcavity photonic crystals with different hole diameters and a height h of 330 nm; (f) PL mapping image of photonic crystals with height h of 330 nm and hole diameter d of 233 nm. The white dashed and blue dashed represent the photonic crystal boundaries of region A and region B respectively. Other structural parameters of the sample in Fig. 4 are the same as those in Fig. 3(a).
-
[1] Genack A Z, Garcia N 1991 Phys. Rev. Lett. 66 2064 doi: 10.1103/PhysRevLett.66.2064 [2] von Neumann J, Wigner E P 1929 Phys. Z. 30 465 [3] Fan S, Joannopoulos J D 2002 Phys. Rev. B 65 235112 doi: 10.1103/PhysRevB.65.235112 [4] Gomis-Bresco J, Artigas D, Torner L 2017 Nat. Photonics 11 232 doi: 10.1038/nphoton.2017.31 [5] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901 doi: 10.1103/PhysRevLett.107.183901 [6] Friedrich H, Wintgen D 1985 Phys. Rev. A 32 3231 doi: 10.1103/PhysRevA.32.3231 [7] Zhang J M, Braak D, Kollar M 2012 Phys. Rev. Lett. 109 116405 doi: 10.1103/PhysRevLett.109.116405 [8] Lim T C, Farnell G W 1969 J. Acoust. Soc. Am. 45 845 doi: 10.1121/1.1911556 [9] Porter R, Evans D V 2005 Wave Motion 43 29 doi: 10.1016/j.wavemoti.2005.05.005 [10] Joannopoulos J D, Villeneuve P R, Fan S 1997 Nature 386 143 doi: 10.1038/386143a0 [11] Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photonics Rev. 16 2100300 doi: 10.1002/lpor.202100300 [12] Hsu C W, Zhen B, Lee J, Chua S L, Johnson S G, Joannopoulos J D, Soljačić M 2013 Nature 499 188 doi: 10.1038/nature12289 [13] Jin J, Yin X, Ni L, Soljačić M, Zhen B, Peng C 2019 Nature 574 501 doi: 10.1038/s41586-019-1664-7 [14] Marinica D C, Borisov A G, Shabanov S V 2008 Phys. Rev. Lett. 100 183902 doi: 10.1103/PhysRevLett.100.183902 [15] Molina M I, Miroshnichenko A E, Kivshar Y S 2012 Phys. Rev. Lett. 108 070401 doi: 10.1103/PhysRevLett.108.070401 [16] Hirose K, Liang Y, Kurosaka Y, Watanabe A, Sugiyama T, Noda S 2014 Nat. Photonics 8 406 doi: 10.1038/nphoton.2014.75 [17] Kodigala A, Lepetit T, Gu Q, Bahari B, Fainman Y, Kanté B 2017 Nature 541 196 doi: 10.1038/nature20799 [18] Hwang M S, Lee H C, Kim K H, Jeong K Y, Kwon S H, Koshelev K, Kivshar Y, Park H G 2021 Nat. Commun. 12 4135 doi: 10.1038/s41467-021-24502-0 [19] 闫梦, 孙珂, 宁廷银, 赵丽娜, 任莹莹, 霍燕燕 2023 物理学报 72 044202 doi: 10.7498/aps.72.20221894 Yan M, Sun K, Ning T Y, Zhao L N, Ren Y Y, Huo Y Y 2023 Acta Phys. Sin. 72 044202 doi: 10.7498/aps.72.20221894 [20] Iwahashi S, Kurosaka Y, Sakai K, Kitamura K, Takayama N, Noda S 2011 Opt. Express 19 11963 doi: 10.1364/OE.19.011963 [21] Kitamura K, Sakai K, Takayama N, Nishimoto M, Noda S 2012 Opt. Lett. 37 2421 doi: 10.1364/OL.37.002421 [22] Yang J L, Shi A Q, Peng Y C, Peng P, Liu J J 2024 Chin. Phys. B 33 084206 doi: 10.1088/1674-1056/ad4630 [23] Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903 doi: 10.1103/PhysRevLett.121.193903 [24] Wang D, Xiong A Y, Zhang J Q, She Z D, Kang X F, Zhu Y, Ghosh S, Xiong Q H 2024 Chin. Phys. B 33 128103 doi: 10.1088/1674-1056/ad8db5 [25] 夏兆生, 刘宇行, 包正, 王丽华, 吴博, 王刚, 王辉, 任信钢, 黄志祥 2024 物理学报 73 178102 doi: 10.7498/aps.73.20240834 Xiao Z S, Liu Y X, Bao Z, Wang L H, Wu B, Wang G, Wang H, Ren X G, Huang Z X 2024 Acta Phys. Sin. 73 178102 doi: 10.7498/aps.73.20240834 [26] Wu F, Wu J, Guo Z, Jiang H, Sun Y, Li Y, Ren J, Chen H, 2019 Phys. Rev. Appl. 12 014028 doi: 10.1103/PhysRevApplied.12.014028 [27] Wu F, Qi X, Qin M, Luo M, Long Y, Wu J, Sun Y, Jiang H, Liu T, Xiao S, Chen H 2024 Phys. Rev. B 109 085436 doi: 10.1103/PhysRevB.109.085436 [28] Wei M, Long Y, Wu F, Liu G G, Zhang B 2025 Sci. Bull. 70 882 doi: 10.1016/j.scib.2025.01.006 [29] Zhen B, Hsu C W, Lu L, Stone A D, Soljačić M 2014 Phys. Rev. Lett. 113 257401 doi: 10.1103/PhysRevLett.113.257401 [30] Men H, Lee K Y K, Freund R M, Peraire J, Johnson S G 2014 Opt. Express 22 22632 doi: 10.1364/OE.22.022632 [31] Lee J, Zhen B, Chua S L, Qiu W, Joannopoulos J D, Soljačić M, Shapira O 2012 Phys. Rev. Lett. 109 067401 doi: 10.1103/PhysRevLett.109.067401 [32] Perczel J, Borregaard J, Chang D E, Yelin S F, Lukin M D 2020 Phys. Rev. Lett. 124 083603 doi: 10.1103/PhysRevLett.124.083603 [33] Ge X, Minkov M, Fan S, Li X, Zhou W 2019 npj 2D Mater. Appl. 3 16 doi: 10.1038/s41699-019-0099-1 [34] Wu M, Ding L, Sabatini R P, Sagar L K, Bappi G, Paniagua-Domínguez R, Sargent E H, Kuznetsov A I 2021 Nano Lett. 21 9754 doi: 10.1021/acs.nanolett.1c03696 [35] Sun S, Kim H, Luo Z, Solomon G S, Waks E 2018 Science 361 57 doi: 10.1126/science.aat3581 [36] Carletti L, Koshelev K, De Angelis C, Kivshar Y 2018 Phys. Rev. Lett. 121 033903 doi: 10.1103/PhysRevLett.121.033903 [37] Bernhardt N, Koshelev K, White S J U, Meng K W C, Fröch J E, Kim S, Tran T T, Choi D Y, Kivshar Y, Solntsev A S 2020 Nano Lett. 20 5309 doi: 10.1021/acs.nanolett.0c01603 [38] Chen Z H, Yin X F, Jin J C, Zheng Z, Zhang Z X, Wang F F, He L, Zhen B, Peng C 2022 Sci. Bull. 67 359 doi: 10.1016/j.scib.2021.10.020 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: