首页
登录
注册
下载:
-
近年来, 超声无损检测技术因其非侵入性、采集速度快和安全性高等优势, 在工业检测领域中占据重要地位[1–3]. 在传统超声成像方法中, 全聚焦成像方法(total focusing method, TFM)因其成像精度、分辨率高, 被视为超声成像的“黄金标准”[4–6]. 然而, 该方法具有明显的空间依赖性, 当目标缺陷位于相控阵换能器的声轴中心区域时, 该方法能够实现较好的缺陷定位精度与成像效果. 当缺陷偏离声轴中心即检测角度逐渐增大时, 成像质量呈现显著的退化趋势, 严重制约了缺陷的识别能力[7–9]. 针对此方法局限, 众多学者提出了基于二维相控阵的解决方案. Yu和Giurgiutiu [10]通过二维阵列结构实现了铝板损伤的精确识别. Stepinski等[11]系统分析了二维对称阵列的波束方向性, 为大角度检测的波束控制提供了理论依据. 尽管二维相控阵在成像性能上具有优势, 然而相较于一维阵列, 二维阵列的阵元数量和排布复杂度大幅提高, 不仅提高了系统成本, 而且数据采集量的大幅增长导致成像时间长, 检测效率明显下降.
因此, 为了保持一维阵列优势的同时有效检测偏离声轴中心的缺陷, 研究者引入了平面波成像技术[12–14]. 平面波成像(plane wave imaging, PWI)通过一次发射形成近似平面的宽波前, 可在短时间内覆盖较大成像区域, 实现高效的数据采集[15]. 然而, 平面波由于不具备发射聚焦特性, 其波前能量分布均匀, 导致不同成像点的后向散射信号易发生混叠, 从而影响成像质量[16,17]. 为提高平面波成像质量, Montaldo等[18]提出多角度复合平面波成像方法(coherent plane wave compounding, CPWC), 该方法通过多个角度的平面波信号进行相干叠加, 在保持高速数据采集优势的同时提高了图像质量. Afrakhteh和Behnam[19]对角度选择策略进行优化, 进一步增强了CPWC在复杂结构检测中的适应性. 由于不同区域对角度复合的敏感性存在差异, 会导致图像整体质量分布不均. 在实际应用中, CPWC成像结果仍易受到旁瓣引起的背景杂波干扰, 从而影响成像对比度和缺陷边缘的识别[20].
为进一步提升复合平面波图像质量, 国内外学者在CPWC基础上提出了多种图像增强方法. 首先, 最小方差(minimum variance, MV)方法是被广泛研究的自适应波束形成算法. 该方法通过凸优化求取最优权重, 在保持目标信号功率不变的前提下最小化输出能量, 能够在一定程度上提高成像分辨率, 但对比度提升效果有限[21]. Xu等[22]将最小方差波束形成与相干系数结合, 虽然改善了图像对比度和分辨率, 但相干系数会显著降低背景区域亮度, 增大噪声方差, 导致对比噪声比下降. 张芸芸等[23]应用相位迁移的方法实现平面波图像在多层结构的准确、快速重建, 从而获取高质量图像. Yang等[24]提出使用复合平面波成像结合相干因子的方法, 该方法比传统CPWC在对比度CR和广义信噪比上分别提高了197%和20%, 尽管成像效果显著改善, 但复合平面波的多次发射增加了数据采集时间, 降低了成像效率. Dolmatov等[25]基于相位迁移理论与Stolt变换, 实现了复杂形状物体缺陷的精确成像, 但该方法的计算复杂度较高, 且对物体几何形状的先验知识依赖性强. Chen等[26]提出一种修正符号相干因子, 使该因子适用于超声平面波成像的频域波束形成, 实现了更高质量的成像, 但该方法在处理强散射体时容易出现过度抑制现象, 可能导致弱缺陷信号的丢失. 以上这些方法虽然在不同程度上提升了图像分辨率、对比度和成像稳定性, 但大多依赖于复杂的权重函数构建、相位信息处理或频域变换, 增加了算法的复杂度.
近年来, 延迟乘和(delay multiply and sum, DMAS)已成为一种新兴的波束形成技术. Lim等[27]通过对延迟后的信号进行乘法运算提升了聚焦效果, 随后被引入到超声领域, 展现出良好的图像增强能力[28–30]. Chen等[31]基于TFM方法提出一种引入加窗因子的DMAS波束形成方式, 通过增强信号的空间相干性并抑制旁瓣干扰, 实现混凝土结构中深部缺陷的高分辨率成像. Esmailian等[32]将滤波后的DMAS引入医学成像领域, 实现了对囊肿的精准定位, 获得了对比度高、散斑信噪比高的图像. 现有DMAS相关研究多基于点式激励或全矩阵数据, 在快速检测场景下的应用研究相对匮乏.
鉴于此, 本文提出一种基于复合平面波延迟乘和的成像方法. 该方法将多角度平面波技术与延迟乘和算法相结合, 通过阵元在多个角度回波下接收的信号进行交叉相乘, 用延迟乘和策略替代传统的直接延迟叠加方法, 有效提高了缺陷成像的分辨率、对比度和信噪比, 为复杂结构件的无损检测提供了新的技术途径.
-
全矩阵捕获(full matrix capture, FMC)技术是超声相控阵检测中广泛应用的数据采集方式. 其基本思想是: 设线性阵列共有
$ N $ 个阵元, 在检测过程中, 依次以每个阵元作为发射源, 所有阵元同时作为接收通道进行采集回波信号. 经过$ N $ 次发射-接收操作后, 最终可获得一个包含$ N \times N $ 组时域回波数据的全矩阵信号. 该全矩阵数据包含了被检测区域中完整的声波散射信息, 是后续图像重建的重要基础.全聚焦成像方法基于时域信号的延迟叠加原理, 通过对FMC数据进行后处理实现成像, 其成像原理如图1所示. 首先, 将成像区域离散为网格点, 然后计算每个网格点到各发射-接收阵元对之间的声波传播路径. 根据(1)式计算得到的声传播时间, 在原始信号中提取对应时刻的回波幅值. 随后根据(2)式, 将该网格点
$ p $ 位置的所有发射-接收对应的信号幅值进行叠加, 得到其像素值$ {Y_{{\text{TFM}}}}\left( p \right) $ .其中,
$ {t_{i, j}}\left( p \right) $ 为声波从第$ i $ 个阵元传播至像素点$ p $ 点, 再从$ p $ 点反射至接收阵元$ j $ 的总传播时间;$ {x_i} $ 与$ {x_j} $ 分别表示发射与接收阵元的位置;$ z $ 表示像素点的纵向位置;$ c $ 为声波在介质中的速度;$ {S_{i, j}}\left( t \right) $ 表示第$ i $ 个阵元发射、第$ j $ 个阵元接收的回波信号. -
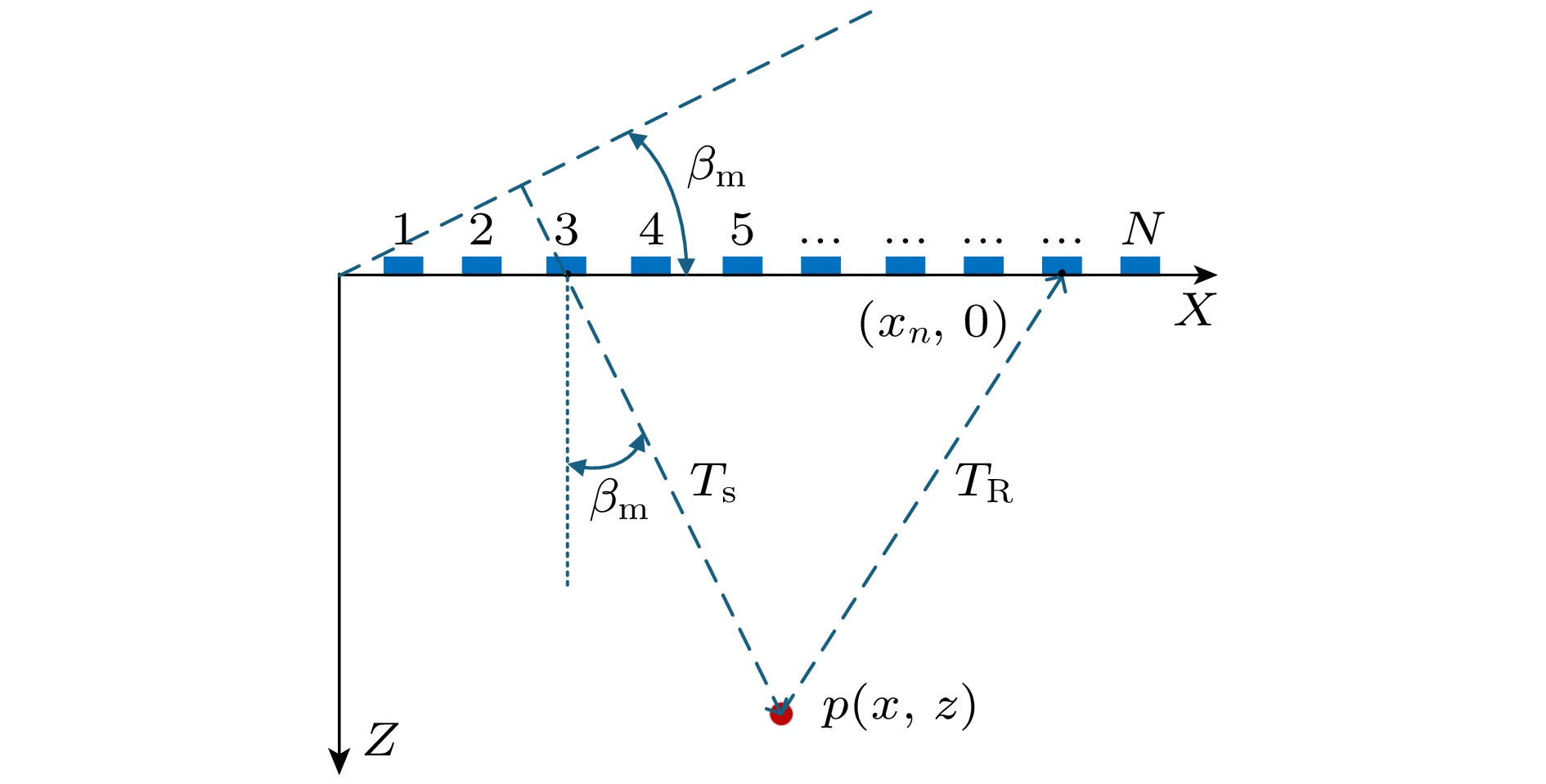
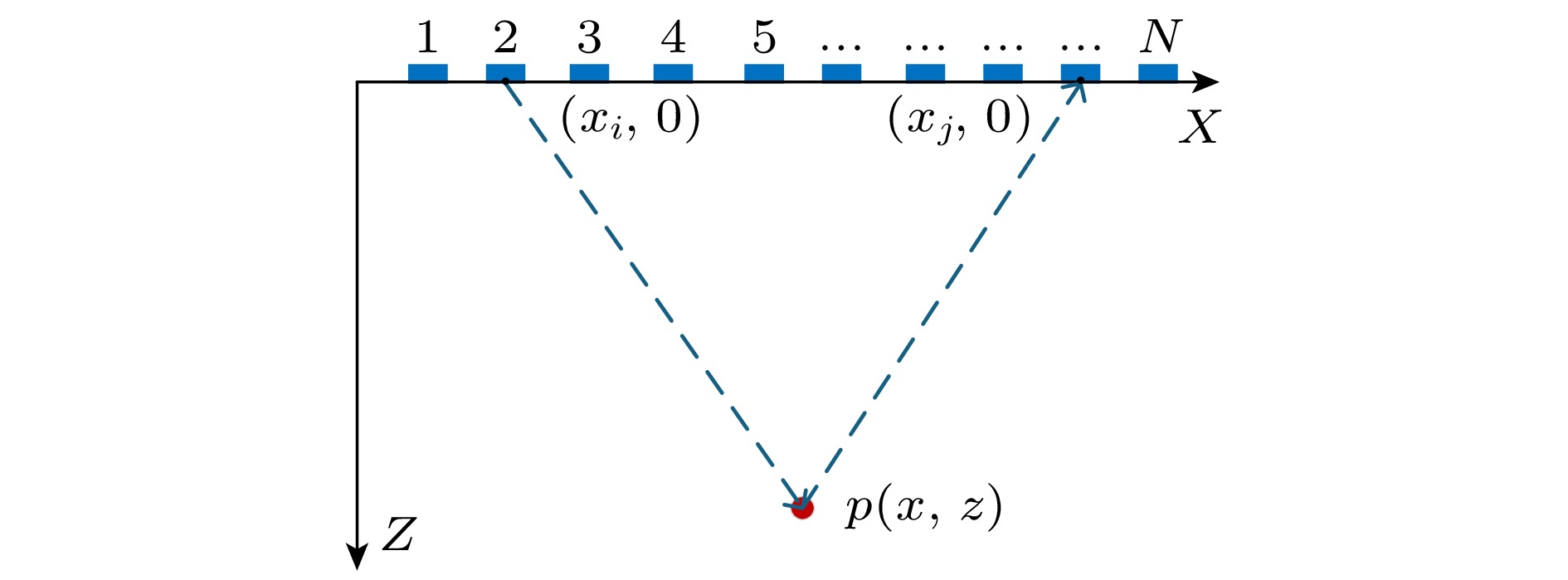
复合平面波成像是一种在超声成像中广泛应用的成像方法. 该方法通过从多个角度发射平面波并进行图像叠加, 实现空间聚焦的效果, 有效改善传统平面波成像中分辨率低和图像模糊的问题. 如图2所示, 设线性阵列包含
$ N $ 个阵元, 位于介质的上方.$ X $ 轴沿阵列方向,$ Z $ 轴为深度方向, 成像区域内某像素点$ p $ 的坐标为$ \left( {x, z} \right) $ .为实现平面波的偏转, 在成像区域内发射角度为
$ {\beta _{\text{m}}} $ 的平面波, 需要对阵列中各个阵元的激发时刻施加相应的延迟时间$ {\sigma _n} $ :其中,
$ {x_n} $ 是第$ n $ 个阵元的位置.对于偏转角为
$ {\beta _{\text{m}}} $ 的平面波, 其传播至像素点$ p $ 的传输时间记为$ {T_{\text{S}}} $ , 从像素点$ p $ 传播至第$ i $ 个接收阵元的传输时间记为$ {T_{\text{R}}} $ ,$ {T_{\text{S}}} $ 和$ {T_{\text{R}}} $ 的计算表达式为由此可得该角度下的平面波总传输时间
$ T(p) $ , 即根据计算出的聚焦延迟时间, 求得复合平面波在
$ p $ 点的像素值:其中,
$ M $ 为平面波角度的个数,$ {S_{m, i}} $ 表示以第$ m $ 个角度偏转发射的平面波在阵元$ i $ 处接收的回波信号.通过对回波信号施加相应的延迟时间
$ T(p) $ 后, 可获得用于成像的延迟对齐信号, 根据聚焦延迟时间, 对$ M $ 个角度下$ N $ 个阵元的回波数据进行相干叠加, 以获得该像素点处的像素值, 其复杂度为$ O\left( {MN} \right) $ . 对成像区域网格中的所有像素点重复以上操作, 从而得到目标区域的成像图像.CPWC算法通过多角度平面波相干叠加实现复合成像, 从而有效提升成像质量. 相比传统的TFM算法, CPWC能够提供更丰富的视角信息, 使得超声波在结构中的检测区域更加多样, 增强了成像区域的全方位覆盖能力, 特别是在目标边缘等情况下表现出更优的成像效果.
TFM和CPWC方法均是通过对接收到的回波信号进行延迟对齐后直接叠加, 以实现能量聚焦. 尽管该类延迟叠加策略实现方式简单、复杂度低、计算效率较高, 但在多缺陷或强散射环境中, 易受到非相干信号的干扰, 导致阵元接收信号之间的相位一致性降低, 进而引起能量叠加失真. 这种信号间相位失配不仅会产生较多的伪像, 还会让图像的分辨率和对比度显著降低, 最终影响缺陷识别的准确性. 而延迟乘和算法通过所有发射-接收通道的延迟对齐信号进行两两乘积运算, 有效强化了信号的空间相干性. 该空间相干性表现为同一散射源在不同阵元处产生的回波信号具有相位一致性, 乘积处理增强了有效信号在成像中的响应, 同时抑制了相位不一致的噪声和旁瓣信号, 从而提高了图像的质量与抗噪能力.
在此基础上, 将延迟乘和算法引入复合平面波成像, 构建CPWC-DMAS成像算法, 可进一步提升波束形成性能与成像质量. DMAS算法需要对
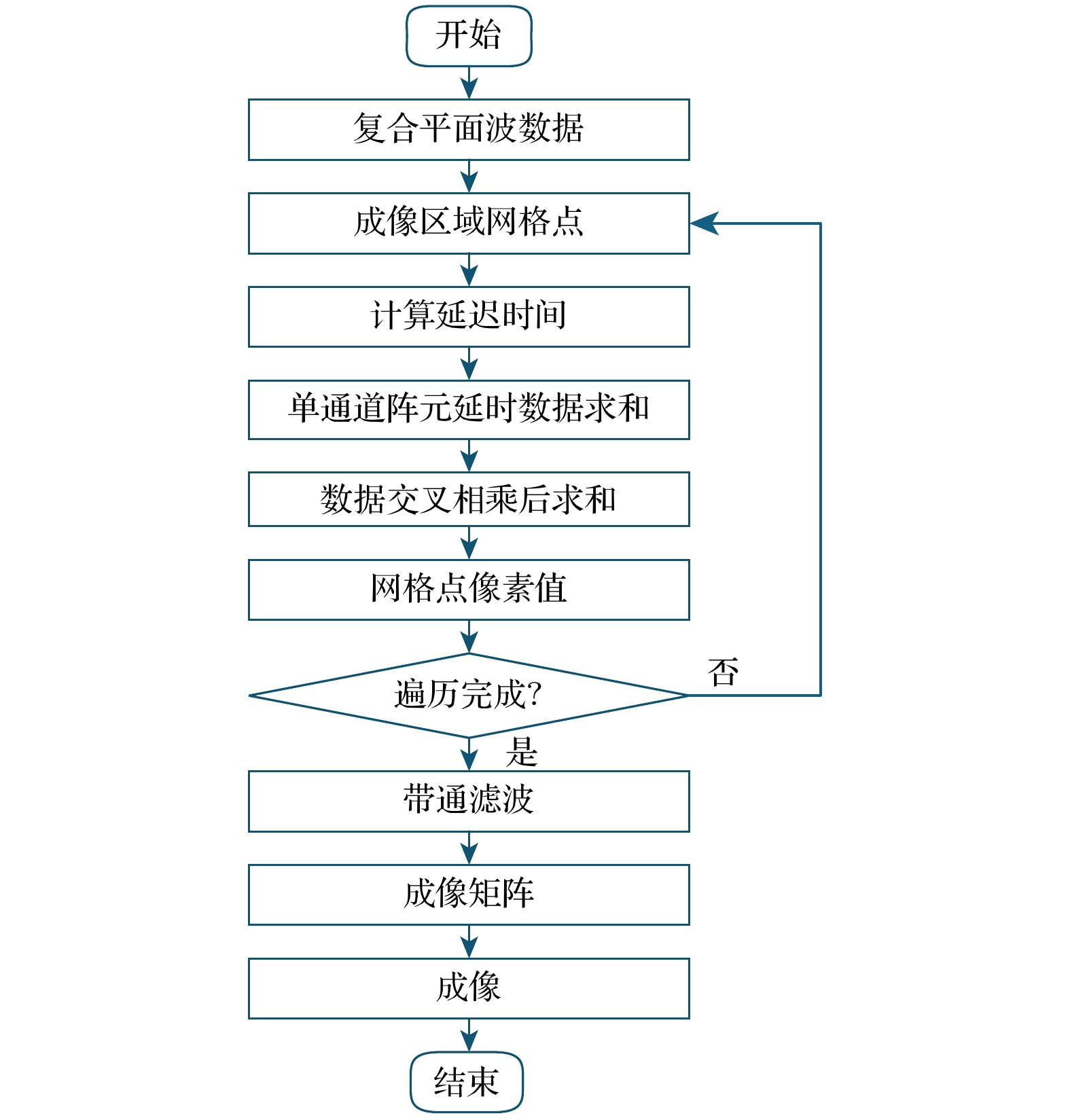
$ M $ 个发射角度, 所有阵元接收的延迟校正信号进行两两相乘运算, 其复杂度为$ O\left( {{M^2}{N^2}} \right) $ , 该算法中包含的大量耦合乘法操作虽提升了成像效果, 但也增加了计算复杂度. 为保证检测效率, 对其进行简化, CPWC-DMAS算法通过对每个阵元在所有角度的平面波回波信号进行复合((8)式); 对所有复合信号进行交叉相乘后求和, 从而得到对应像素点的像素值$ {Y_{{\text{CPWC-DMAS}}}}\left( p \right) $ ((9)式):该过程计算复杂度为
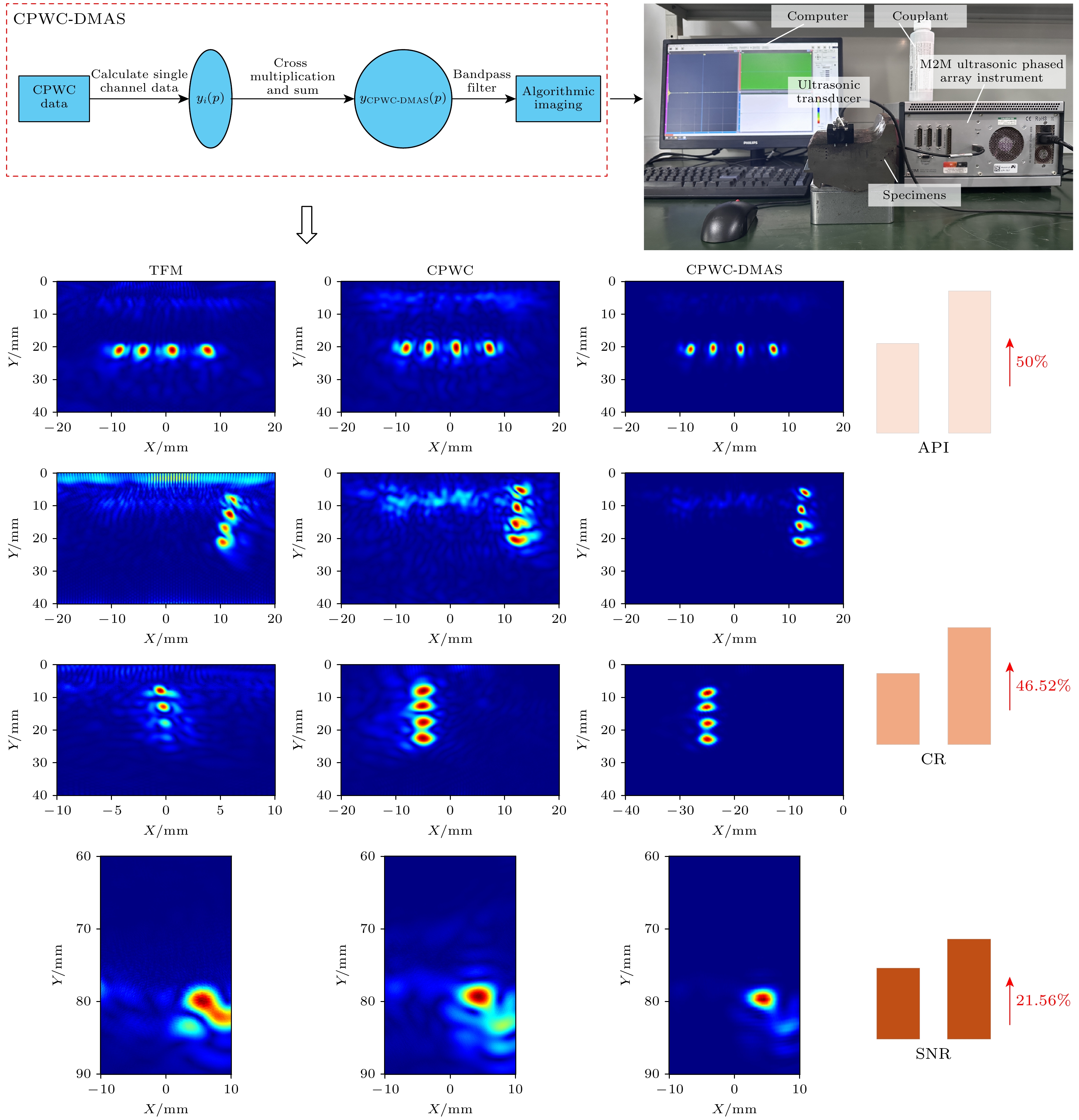
$ O\left( {MN + {N^2}} \right) $ , 其中$ O\left( {MN} \right) $ 为各阵元在所有$ M $ 个角度上进行平面波回波数据复合的复杂度,$ O\left( {{N^2}} \right) $ 为复合信号间交叉相乘求和的复杂度. (9)式中$ {y_i}\left( p \right) $ 是第$ i $ 个阵元在所有角度的平面波回波信号的复合.由于(9)式中的信号交叉相乘, 输出的信号被乘法调制为两个频率的新信号, 一个集中在零频附近, 另一个集中在二倍频附近. 系统通过二倍频带通滤波器对输出信号进行处理, 选择性地提取二倍频分量并抑制零频成分. 该带通滤波器的中心频率设置为5 MHz, 即原始载波频率的两倍, 通带和阻带均以5 MHz对称的频率选择. 提取的二倍频分量是原始信号频率的两倍, 根据波束形成理论, 声束宽度与波的频率呈反比关系, 频率加倍将使得声束宽度显著减小, 从而形成更窄、更集中的声束. 这种变化使声波能量聚集在更小的区域内, 有效减少了相邻散射体信号之间的重叠现象. 因此, 随着频率的提高, 成像分辨率得到显著改善. CPWC-DMAS算法的整体流程图如图3所示.
-
本文所构建的实验系统主要由M2M超声相控阵、线性阵列换能器、计算机平台、耦合剂以及含典型人工缺陷的钢轨与车轮试样组成, 换能器参数分别为: 中心频率2.5 MHz, 阵元数量32, 阵元宽度0.9 mm, 阵元中心间距1 mm. 本文采用的钢轨和车轮试样虽同为金属, 但几何形状存在显著差异, 钢轨为工字形截面的长条形结构, 车轮为旋转对称体的曲面结构, 通过这两种试样可以验证算法在不同材料特性、几何形状以及缺陷分布条件下的有效性. 在钢轨试样中预设轨头位置的横向、纵向两类典型缺陷, 如图4(a), (b)所示. 在车轮试样中预设轮辋位置的纵向、底部两类典型缺陷, 如图4(c)所示. 缺陷直径均为2 mm. A, B, D三个区域的缺陷主要位于声轴中心附近, 在–25°—25°范围内发射的平面波可以覆盖整个缺陷, 步进为1°, 共采集51个角度的数据. C区缺陷为纵向分布且靠近边缘区域, 在左侧0°—80°范围内发射的平面波不仅可以覆盖整个缺陷, 还可以突出平面波在偏离声轴区域缺陷检测上的效果, 步进同为1°, 共采集81组角度的数据.
-
为了对比不同成像算法的性能, 本文采用阵列性能指标(array performance index, API)、对比度(contrast ratio, CR)以及信噪比(signal-to-noise ratio, SNR)作为评估标准.
API为超声图像中幅值高于主峰值–6 dB的像素点所围成的区域面积, 并进一步归一化为以波长的平方为单位的无量纲面积, 定义为
其中,
${A_{{-6} {\text{ dB}}}}$ 表示超声图像中幅值高于主峰值–6 dB的像素点所围成的区域面积,$\lambda $ 表示波长. API越低, 图像分辨率越高.CR为超声图像中缺陷区域与背景区域之间信号强度的对比度, 定义为
其中,
${\mu _{{\text{flaw}}}}$ 和$ {\mu _{{\text{bck}}}} $ 分别表示缺陷区域和背景区域信号的平均强度. CR越高, 图像缺陷与背景的区分能力越强, 对比度越高.SNR为超声图像中缺陷的信号与噪声的比值, 定义为
其中,
${\sigma _{{\text{bck}}}}$ 代表背景区域信号的标准差. SNR越高则表明图像抗噪能力越强, 信噪比越高. -
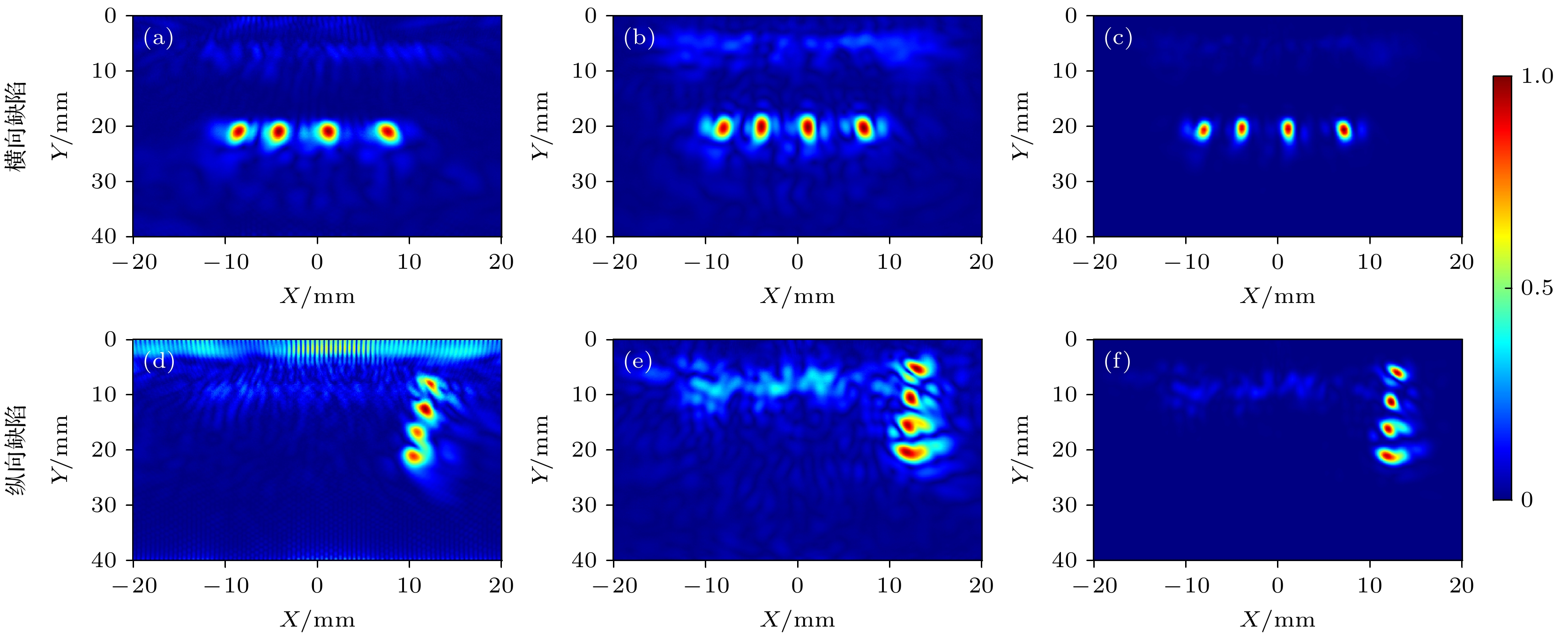
钢轨中横向缺陷和纵向缺陷结果如图5所示. 从成像结果可以看出, 对于横向缺陷见图5(a)—(c), TFM与CPWC算法均能够在成像中较清晰地重构缺陷轮廓, 且缺陷幅值基本一致, 说明CPWC在成像质量上可达到与TFM相当的效果. 然而, 两者均存在一定程度的背景噪声与伪像干扰, 尤其在缺陷周围区域较为明显, 对缺陷识别造成干扰. 相比之下, CPWC-DMAS算法通过将不同阵元在多个角度的平面波数据进行交叉相乘并求和, 引入复合平面波信号的空间相干性, 并结合二倍频成像, 有效抑制背景噪声, 显著提升成像清晰度和分辨率, 缺陷边界更锐利, 伪像显著减少. 对于纵向缺陷见图5(d)—(f), TFM成像中部分缺陷(B1, B3, B4)的反射幅值较弱, 且存在一定的成像位置偏差, 表现出对纵向缺陷识别能力的不足. CPWC算法凭借平面波的角度覆盖优势, 能够更准确地成像纵向缺陷, 且位置和形态均较为真实, 但仍存在一定程度的伪像干扰. 而CPWC-DMAS算法利用二倍频成像在图像中展现出最优的成像效果, 不仅抑制了背景噪声干扰, 且增强了缺陷的图像分辨率、对比度和边缘清晰度.
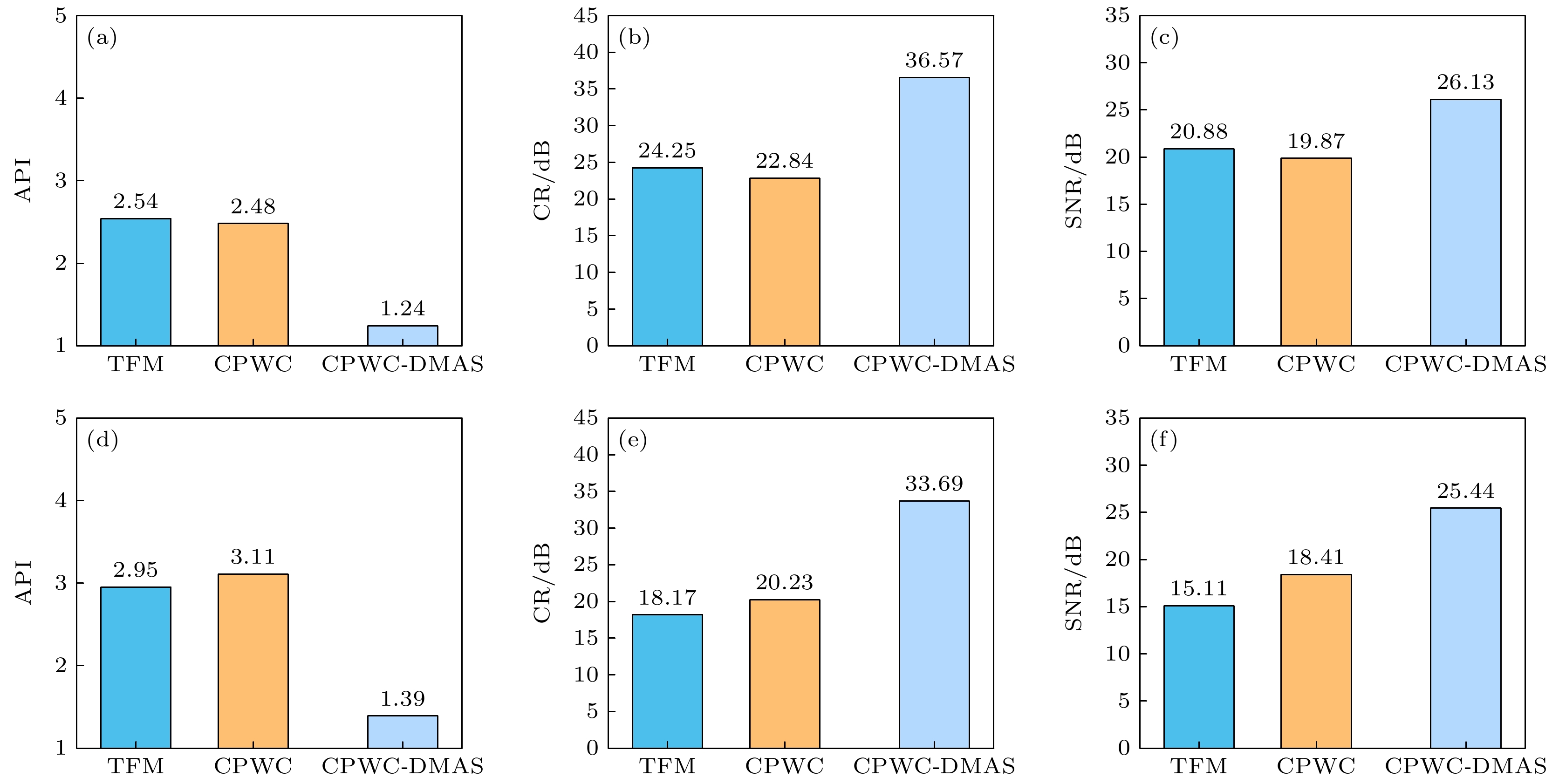
为了进一步对比几种成像算法之间的性能, 分别计算成像性能指标API, CR以及SNR. 对于钢轨中A区横向缺陷: 图6(a)为不同算法的成像结果API值, TFM, CPWC以及CPWC-DMAS三种算法成像结果API值分别为2.54, 2.48和1.24, CPWC-DMAS算法相比TFM和CPWC分别提高了51.18%, 50%. 图6(b)为不同算法成像结果对比度, TFM, CPWC和CPWC-DMAS三种算法成 像结果对比度分别为24.25 dB, 22.84 dB和36.57 dB, CPWC-DMAS算法相比TFM和CPWC分别提高了12.23 dB, 13.73 dB. 图6(c)为不同算法成像结果信噪比, TFM, CPWC和CPWC-DMAS三种算法成像结果信噪比分别为20.88 dB, 19.87 dB和26.13 dB, CPWC-DMAS算法相比于TFM和CPWC分别提高了5.25 dB, 6.26 dB. 对于钢轨中B区纵向缺陷: 图6(d)为不同算法的成像结果API值, TFM, CPWC以及CPWC-DMAS三种算法成像结果API值分别为2.95, 3.11和1.39, CPWC-DMAS算法相比TFM和CPWC分别提高了52.88%, 55.31%. 图6(e)为不同算法成像结果对比度, TFM, CPWC和CPWC-DMAS三种算法成像结果对比度分别为18.17 dB, 20.23 dB, 33.69 dB, CPWC-DMAS算法相比TFM和CPWC分别提高了15.52 dB, 13.46 dB. 图6(f)为不同算法成像结果信噪比, TFM, CPWC和CPWC-DMAS三种算法成像结果信噪比分别为15.11 dB, 18.41 dB和26.13 dB, CPWC-DMAS算法相比TFM和CPWC分别提高了10.33 dB, 7.03 dB. 由此可知, CPWC-DMAS算法在钢轨缺陷检测中表现出显著优势, 在抑制背景噪声和伪像方面提升效果明显.
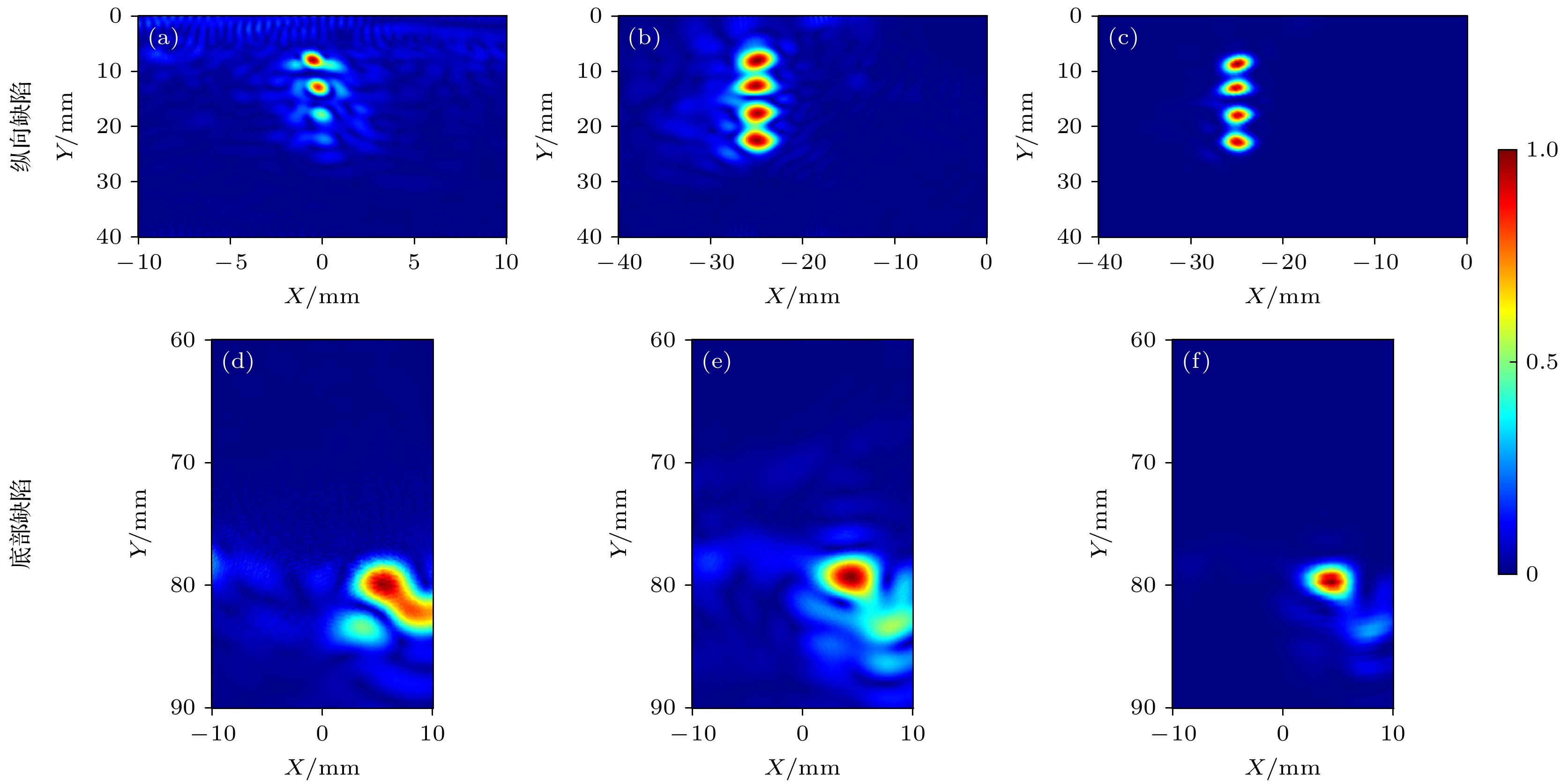
车轮中纵向缺陷与底部缺陷的成像结果如图7所示. 从成像结果可以看出, 对于纵向缺陷(图7(a)—(c)), TFM算法仅能有效成像第一个缺陷, 其余缺陷反射幅值较弱, 甚至难以辨识, 存在明显的识别遗漏现象, 且成像位置存在一定偏差. CPWC算法凭借平面波的偏转特性, 能够较清晰地重构多个纵向缺陷的轮廓, 但缺陷之间存在粘连现象, 且图像中仍伴随较多背景噪声与伪像, 对缺陷识别带来一定干扰. 而CPWC-DMAS算法利用二倍频成像, 抑制了背景噪声干扰, 有效分离了各个纵向缺陷, 缺陷边缘清晰, 图像分辨率、对比度明显提升. 对于底部缺陷(图7(d)—(f)), TFM成像中缺陷与车轮底部边界之间的伪像粘连严重, 难以准确区分真实缺陷与结构反射, 成像质量最差. CPWC算法基于多角度平面波发射策略, 有效增强了相控阵轴心区的覆盖能力, 同时相对弱化了两侧边界回波的影响, 在一定程度上解决了缺陷与底部边界的粘连现象, 提升了成像清晰度, 但背景中仍存在大量伪像干扰. CPWC-DMAS算法在此类缺陷的成像中同样表现最优, 该方法利用二倍频成像的高分辨率优势, 有效抑制了背景噪声和伪像干扰, 不仅能够有效区分底部缺陷与边界回波, 避免了信号混叠, 同时显著提升了缺陷的成像对比度和边界清晰度, 增强了缺陷的识别能力.
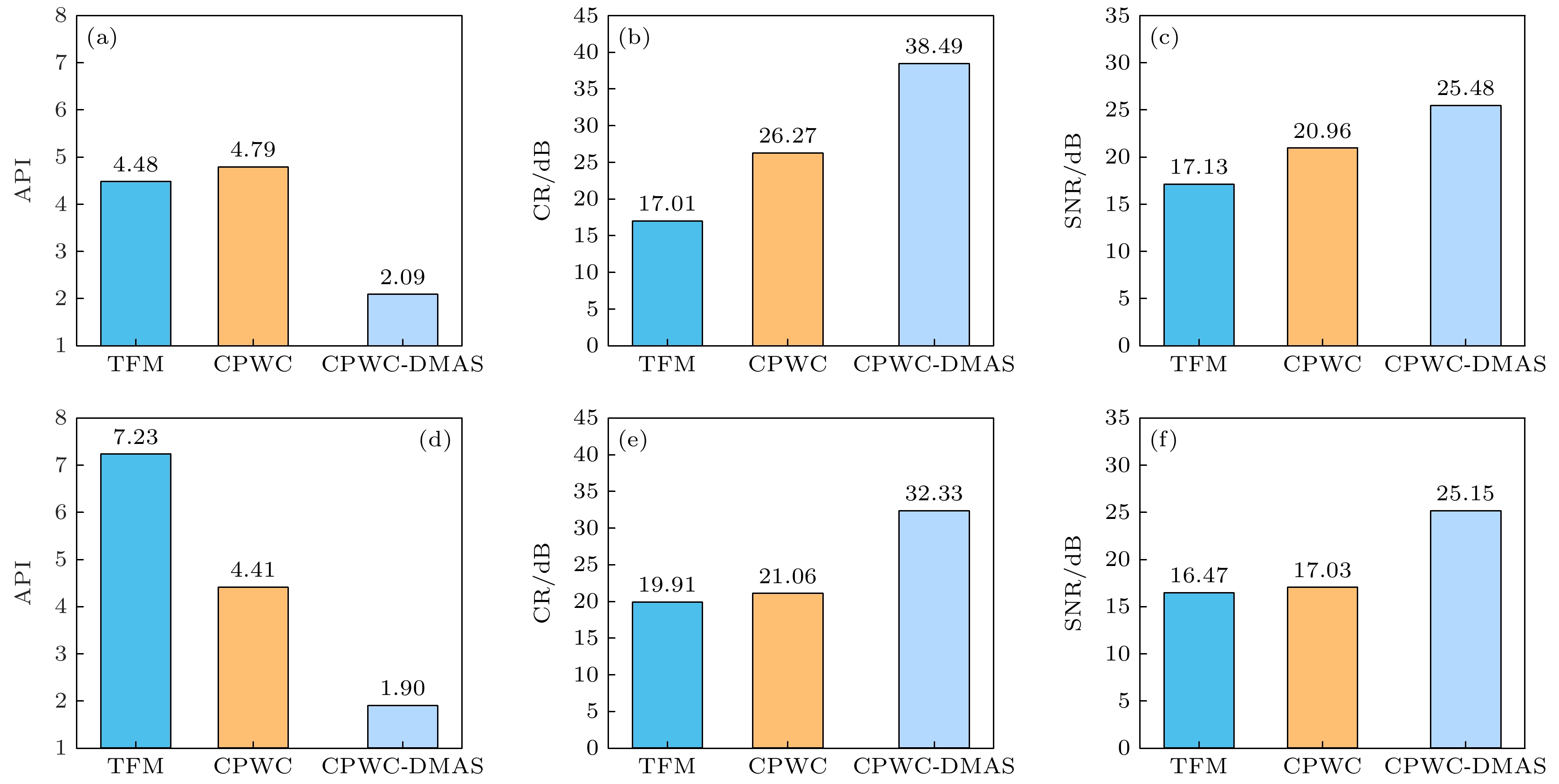
接下来分别计算成像性能指标API, CR和SNR. 对于C区车轮纵向缺陷: 图8(a)为不同算法的成像结果API值, TFM, CPWC以及CPWC-DMAS三种算法成像结果API值分别为4.48, 4.79和2.09, CPWC-DMAS算法相比TFM和CPWC分别提高了53.35%, 56.37%. 图8(b)为不同算法成像结果对比度, TFM, CPWC和CPWC-DMAS三种算法成像结果对比度分别为17.01 dB, 26.27 dB和38.49 dB, CPWC-DMAS算法相比于TFM和CPWC分别提高了21.48 dB, 12.22 dB. 图8(c)为不同算法成像结果信噪比, TFM, CPWC和CPWC-DMAS三种算法成像结果信噪比分别为17.13 dB, 20.96 dB和25.48 dB, CPWC-DMAS算法相比TFM和CPWC分别提高了8.35 dB, 4.52 dB. 对于D区车轮底部缺陷: 图8(d)为不同算法的成像结果API值, TFM, CPWC以及CPWC-DMAS三种算法成像结果API值分别为7.23, 4.41和2.09, CPWC-DMAS算法相比TFM和CPWC分别提高了73.72%, 56.92%. 图8(e)为不同算法成像结果对比度, TFM, CPWC和CPWC-DMAS三种算法成像结果对比度分别为19.91 dB, 21.06 dB, 32.33 dB, CPWC-DMAS算法相比TFM和CPWC分别提高了12.42 dB, 11.27 dB. 图8(f)为不同算法成像结果信噪比, TFM, CPWC和CPWC-DMAS三种算法成像结果信噪比分别为16.47 dB, 17.03 dB和25.15 dB, CPWC-DMAS算法相比于TFM和CPWC分别提高了8.68 dB, 8.12 dB. 由此可知, CPWC-DMAS算法在车轮缺陷检测中表现出显著优势, 有效抑制了背景噪声和伪像, 在分辨率、对比度和信噪比方面提升效果显著.
综上所述, 相较于TFM与CPWC, CPWC-DMAS在成像质量和API, CR, SNR性能指标上均有显著提升. 在钢轨和车轮的纵向缺陷检测中, CPWC-DMAS展现出了更强的缺陷识别能力, 在车轮底部复杂区域能够有效区分缺陷信号与几何边界回波, 特别是在处理缺陷边界模糊和相邻缺陷粘连等复杂情况时显示出更高的准确性.
-
针对传统超声成像方法在成像分辨率低、偏离声轴区域成像质量低及伪像多的问题, 本文提出了复合平面波延迟乘和成像方法. 该方法融合复合平面波成像与延迟乘和波束形成策略, 有效提升了图像分辨率、对比度及信噪比. 为验证该方法的有效性, 本文搭建了超声实验平台, 并在钢轨与车轮构件上进行实验. 具体结论如下:
1)将延迟乘和与复合平面波成像结合, 进一步提高了成像分辨率. 相比传统TFM和CPWC算法, CPWC-DMAS对于与声波传播方向平行的缺陷回波具有更高的响应灵敏度, 从而提高了成像质量和缺陷分辨能力.
2)本文提出的CPWC-DMAS算法通过将多角度平面波回波数据进行交叉相乘后求和, 引入信号的空间相干性, 并进行二倍频成像, 增强了信噪比, 抑制了伪像, 提高了分辨率.
3)通过实验验证了CPWC-DMAS算法的正确性与有效性. 实验结果表明: CPWC-DMAS算法与TFM与CPWC算法相比, 在API性能方面提升了51.18%, 50%, 在CR方面提升了50.8%, 46.52%, 在SNR方面提升了25.14%, 21.56%.
本文提出一种基于复合平面波延迟乘和成像方法, 实现多角度复合平面波的高质量成像, 但在实际应用中存在结构尺寸差异较大、声波传播路径复杂、角度复合数据量大等问题, 后续将对平面波发射角度, 波束形成方法进行深入研究, 以提高成像质量和检测效率.
基于复合平面波延迟乘和的超声成像方法
Ultrasonic imaging method based on coherent plane wave compounding with delay multiplication and sum
-
摘要: 平面波成像因其数据采集速度快, 系统结构简单, 在无损检测中得到广泛应用. 但由于其采用非聚焦发射方式, 声能分布分散, 成像质量较差. 为改善成像质量, 复合平面波成像方法通过多角度平面波的相干叠加来提升成像效果, 但在图像分辨率、对比度以及伪像抑制方面仍存在不足. 为了提高平面波成像质量, 本文提出一种基于复合平面波延迟乘和成像方法(coherent plane wave compounding-delay multiply and sum, CPWC-DMAS). 首先对多个角度的平面波信号进行相干叠加, 实现多角度信息融合. 然后在图像输出中引入空间相干性来提高图像质量, 实现多角度复合平面波的高质量成像. 最后, 对钢轨与车轮构件进行实验验证, 结果表明: CPWC-DMAS算法与全聚焦和复合平面波算法相比, 在阵列性能指标方面提升了51.18%和50%, 在对比度方面提升了50.8%和46.52%, 在信噪比方面提升了25.14%和21.56%, 提高了成像质量和分辨能力.Abstract: Plane wave imaging has widespread applications in non-destructive testing due to its fast data acquisition speed and simple system architecture. However, traditional plane wave imaging employs an unfocused transmission scheme. This results in dispersed acoustic energy distribution, low imaging resolution, and poor image quality. Although coherent plane wave compounding (CPWC) improves imaging performance through multi-angle coherent summation, it still has shortcomings in image resolution, contrast, and artifact suppression when detecting defects far from the acoustic axis center. To break through these limitations, this paper proposes a coherent plane wave compounding with delay multiplication and sum (CPWC-DMAS) method in which multi-angle plane wave is combined with DMAS beamforming technology to enhance imaging quality and resolution capability. First, coherent summation of multi-angle plane wave signals is performed to achieve comprehensive angular information fusion, ensuring effective coverage of the detection region. Subsequently, the DMAS method is used to perform cross-multiplication and summation of signals acquired from all angles by different array elements, utilizing the spatial coherence between received signals from different array elements to effectively enhance the target echo signals, while suppressing incoherent noise and reducing artifacts. Finally, to validate the correctness and effectiveness of the proposed method, experimental verification is conducted on defects embedded in steel rail and wheel components. The results indicate that compared with the total focusing method and CPWC algorithms, the proposed CPWC-DMAS algorithm achieves significant improvements of 51.18% and 50% in array performance index, 50.8% and 46.52% in contrast ratio, and 25.14% and 21.56% in signal-to-noise ratio, respectively. In summary, the proposed CPWC-DMAS algorithm demonstrates significant advantages over traditional methods in resolution enhancement, contrast improvement, and artifact suppression, achieving high-quality imaging for multi-angle coherent plane wave compounding. This method provides a novel approach for detecting defects both near and away from the center of acoustic axis, offering new insights into defect detection in complex structures with broad engineering applications.
-
Key words:
- ultrasound imaging /
- coherent plane wave compounding /
- delay multiply and sum /
- defect detection .
-
-
图 2 平面波算法示意图
Figure 2. Schematic diagram of the coherent plane wave compounding algorithm.
图 4 钢轨与车轮试样缺陷分布 (a) A区钢轨横向缺陷; (b) B区钢轨纵向缺陷; (c) C区车轮纵向缺陷, D区车轮底部缺陷
Figure 4. Distribution of defects in rail and wheel specimens: (a) Transverse defects in Region A of the rail; (b) longitudinal defects in Region B of the rail; (c) longitudinal defects in Region C of the wheel, bottom defect in Region D of the wheel.
图 5 钢轨缺陷成像结果 (a), (d) TFM; (b), (e) CPWC; (c), (f) CPWC-DMAS
Figure 5. Imaging results of rail defects: (a), (d) TFM; (b), (e) CPWC; (c), (f) CPWC-DMAS.
图 6 钢轨缺陷成像指标 (a)—(c)横向缺陷的API, CR, SNR; (d)—(f)纵向缺陷的API, CR, SNR
Figure 6. Rail defect imaging metrics: (a)—(c) API, CR, SNR for transverse defects; (d)—(f) API, CR, SNR for longitudinal defects.
图 7 车轮缺陷成像结果 (a), (d) TFM; (b), (e) CPWC; (c), (f) CPWC-DMAS
Figure 7. Imaging results of wheel defects: (a), (d) TFM; (b), (e) CPWC; (c), (f) CPWC-DMAS.
图 8 车轮缺陷成像指标 (a)—(c) 纵向缺陷的API, CR, SNR; (d)—(f) 底部缺陷的API, CR, SNR
Figure 8. Wheel defect imaging metrics: (a)–(c) API, CR, SNR for longitudinal defects; (d)–(f) API, CR, SNR for bottom defects.
-
[1] Gupta M, Khan M A, Butola R, Singari R M 2022 Adv. Mater. Process. Te. 8 2286 doi: 10.1080/2374068x.2021.1909332 [2] Shi H, Ebrahimi M, Zhou P, Shao K, Li J 2023 J. Process Mech. Eng. 237 511 doi: 10.1177/09544089221114253 [3] 朱琦, 许多, 张元军, 李玉娟, 王文, 张海燕 2022 物理学报 71 244301 doi: 10.7498/aps.71.20221504 Zhu Q, Xu D, Zhang Y J, Li Y J, Wang W, Zhang H Y 2022 Acta Phys. Sin. 71 244301 doi: 10.7498/aps.71.20221504 [4] Zhu W F, Wei Z B, Fan G P, Li Z W, Xu J C, Qi W W, Mei Y H, Zhao C Y 2025 Nondestruct. Test. Eva DOI: 10.1080/10589759.2025.2495355 [5] He H B, Sun K H, Sun C M, He J G, Liang E F, Liu Q 2023 Photoacoustics 31 100490 doi: 10.1016/j.pacs.2023.100490 [6] Xu Q, Wang H T, Yao Y Z, Li X 2021 Proceedings of the IEEE Far East NDT New Technology & Application Forum Kunming, China, December 14–17, 2021, p309 [7] Yang J J, Fan G P, Xiang Y X, Zhang H Y, Zhu W F, Zhang H, Li Z W 2024 Constr. Build. Mater. 425 135948 doi: 10.1016/j.conbuildmat.2024.135948 [8] Gao C X, Zhu W F, Xiang Y X, Zhang H Y, Fan G P, Zhang H 2024 J. Nondestruct. Eval. 43 26 doi: 10.1007/s10921-023-01040-x [9] Li C J, Zhang H, Qi Y, Hou C L, Zhu W F, Zhou X, Chai X D, Qi W W, Fan G P, Xu J C, Zhang H Y 2025 Appl. Acoust. 231 110493 doi: 10.1016/j.apacoust.2024.110493 [10] Yu L Y, Giurgiutiu V 2008 Ultrasonics 48 117 doi: 10.1016/j.ultras.2007.10.008 [11] Stepinski T, Ambrozinski L, Uhl T 2013 Proceedings of the Structural Health Monitoring Dresden, Germany, September 3–6, 2013, p2210 [12] Hendriks G A, Weijers G, Chen C, Hertel M, Lee C Y, Dueppenbecker P M, Radicke M, Milkowski A, Hansen H H, De Korte C L 2022 IEEE. T. Ultrason. Ferr. 69 2039 doi: 10.1109/TUFFC.2022.3165632 [13] Jensen J A 2007 Prog. Biophys. Mol. Bio. 93 153 doi: 10.1016/j.pbiomolbio.2006.07.025 [14] Bazulin E G, Evseev I V 2021 Russ. J. Nondestruct. Test. 57 423 doi: 10.1134/S1061830921060048 [15] Luo L, Tan Y H, Li J L, Zhang Y, Gao X R 2022 NDT E Int. 127 102601 doi: 10.1016/j.ndteint.2021.102601 [16] Zhang X, Liu J, He Q, Zhang H Y, Luo J W 2018 Proceedings of the IEEE International Ultrasonics Symposium Kobe, Japan, October 22–25, 2018 p1 [17] Tan Y H, Luo L, Li J L, Zhang Y, Gao X R, Peng J P 2022 J. Nondestruct. Eval. 41 33 doi: 10.1007/s10921-022-00863-4 [18] Montaldo G, Tanter M, Bercoff J, Benech N, Fink M 2009 IEEE. T. Ultrason. Ferr. 56 489 doi: 10.1109/TUFFC.2009.1067 [19] Afrakhteh S, Behnam H 2021 IEEE. T. Ultrason. Ferr. 68 3094 doi: 10.1109/TUFFC.2021.3087504 [20] Zhang X W, Wang Q 2023 Ultrasonics 132 106972 doi: 10.1016/j.ultras.2023.106972 [21] Synnevag J F, Austeng A, Holm S 2009 IEEE. T. Ultrason. Ferr. 56 1868 doi: 10.1109/TUFFC.2009.1263 [22] Xu M, Chen Y, Ding M, Ming Y 2012 Proceedings of Medical Imaging 2012: Ultrasonic Imaging, Tomography, and Therapy San Diego, USA, February 4–9, 2012 p122 [23] 张芸芸, 李义方, 石勤振, 许乐修, 戴菲, 邢文宇, 他得安 2023 物理学报 72 154303 doi: 10.7498/aps.72.20230581 Zhang Y Y, Li Y F, Shi Q Z, Xu L X, Dai F, Xing W Y, Ta D A 2023 Acta Phys. Sin. 72 154303 doi: 10.7498/aps.72.20230581 [24] Yang C, Jiao Y, Jiang T Y, Xu Y W, Cui Y Y 2020 Appl. Sci. 10 2250 doi: 10.3390/app10072250 [25] Dolmatov D, Sednev D, Pinchuk R 2018 Key Eng. Mater. 769 262 doi: 10.4028/www.scientific.net/KEM.769.262 [26] Chen Y, Kong Q R, Xiong Z H, Mao Q Q, Chen M, Lu C 2023 Ultrasound Med. Biol. 49 802 doi: 10.1016/j.ultrasmedbio.2022.11.008 [27] Lim H B, Nhung N T T, Li E P, Thang N D 2008 IEEE. T. Biomed. Eng. 55 1697 doi: 10.1109/TBME.2008.919716 [28] Matrone G, Savoia A S, Caliano G, Magenes G 2015 Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society Milan, Italy, August 25–29, 2015, p137 [29] Matrone G, Savoia A S, Caliano G, Magenes G 2016 Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society Orlando, FL, USA, August 16–20, 2016, p3223 [30] Yan X, Qi Y X, Wang Y M, Wang Y Y 2021 IEEE. T. Ultrason. Ferr. 69 580 doi: 10.1109/TUFFC.2021.312787 [31] Chen Y Q, Rong L F, Song Y, Yang X Y 2025 KSCE. J. Civ. Eng. 29 100235 doi: 10.1016/j.kscej.2025.100235 [32] Esmailian K, Asl B M 2022 Comput. Meth. Prog. Bio. 226 107171 doi: 10.1016/j.cmpb.2022.107171 -
图( 9)
计量
- 文章访问数: 26
- HTML全文浏览数: 26
- PDF下载数: 3
- 施引文献: 0