高级搜索

高压下二维材料结构和光电性能研究进展

,  , 

downloadPDF

上一篇

下一篇

程龄莹, 张华芳, 毛艳丽. 高压下二维材料结构和光电性能研究进展[J]. 物理学报, 2025, 74(20): 200701-1. doi: 10.7498/aps.74.20251034
引用本文: 程龄莹, 张华芳, 毛艳丽. 高压下二维材料结构和光电性能研究进展[J]. 物理学报, 2025, 74(20): 200701-1. doi: 10.7498/aps.74.20251034
shu
Lingying CHENG, Huafang ZHANG, Yanli MAO. Recent progress of structures and photoelectric properties of two-dimensional materials under high pressure[J]. Acta Physica Sinica, 2025, 74(20): 200701-1. doi: 10.7498/aps.74.20251034
Citation: Lingying CHENG, Huafang ZHANG, Yanli MAO. Recent progress of structures and photoelectric properties of two-dimensional materials under high pressure[J]. Acta Physica Sinica, 2025, 74(20): 200701-1. doi: 10.7498/aps.74.20251034
shu

高压下二维材料结构和光电性能研究进展

  • 河南大学物理与电子学院, 开封　475004

    • 通讯作者: E-mail: ylmao@henu.edu.cn.

  • 中图分类号: 07.35.+k, 87.15.Zg

Recent progress of structures and photoelectric properties of two-dimensional materials under high pressure

  • School of Physics and Electronics, Henan University, Kaifeng 475004, China

    • Corresponding author: E-mail: ylmao@henu.edu.cn.

  • MSC: 07.35.+k, 87.15.Zg

  • 摘要: 二维材料因其优异的光电性能在基础科学探索与光电子学、能源存储和转换器件等未来技术应用中展现出巨大的潜力, 成为凝聚态物理和材料科学领域的前沿热点. 二维材料独特的层状结构使其物理性能极易受外场的影响. 高压技术作为一种高效、连续且清洁的调控手段, 可以通过压缩原子间距、增强层间耦合, 甚至诱导结构相变, 进而实现对二维材料结构的精准调控以及光电性能的优化提升. 本文以石墨烯、过渡金属二硫族化合物、二维金属卤化物钙钛矿等为例, 结合金刚石对顶砧高压装置以及原位高压表征技术, 重点探讨了它们在高压下的结构演化规律与光电性能调控机制, 并指出了这一新兴研究领域所面临的挑战和机遇, 以期为新型高性能功能材料的开发和实际应用有所启发.
    Abstract: Two-dimensional (2D) materials, due to their outstanding photoelectric properties, have demonstrated significant potential in both fundamental scientific research and future technological applications, including optoelectronics, energy storage, and conversion devices, establishing them as a cutting-edge research field in condensed matter physics and materials science. The distinctive layered structure of 2D materials renders their physical properties highly sensitive to external stimuli. High-pressure technology, serving as an efficient, continuous, and clean tuning tool, enables precise structural control and optimization of the photoelectric properties of 2D materials by compressing atomic distances, strengthening interlayer coupling, and even inducing structural phase transitions. This article focuses on prototypical two-dimensional materials, including graphene, transition metal dichalcogenides (TMDs), and two-dimensional metal halide perovskites. Employing the diamond anvil cell combined with multimodal in situ high-pressure characterization techniques such as X-ray diffraction, Raman spectroscopy, photoluminescence, and electrical transport measurements, we systematically elucidate the effects of high pressure on the structural and photoelectric properties of these materials. The key findings indicate that high pressure can induce the graphene to transition from a semimetal state to a semiconducting state, even a superconducting state, triggering off structural phase transitions and semiconductor-to-metal transitions in TMDs such as MoS2 and WTe2, and leading to a pressure-dependent bandgap narrowing and significant enhancement of luminescence intensity in two-dimensional perovskites. This work highlights the utility of high-pressure techniques in revealing the intrinsic correlations between the microstructure and macroscopic properties of two-dimensional materials. Furthermore, it discusses the key challenges and opportunities in this emerging research area, providing insights into the development and practical application of novel functional materials.
  • 加载中

  • 图 1  (a) 在DAC中压缩薄层石墨烯的XRD图谱; (b) 加压至52 GPa(左)和卸压(右)时石墨烯样品的拉曼光谱; (c) 卸压后与初始的石墨烯样品拉曼光谱对比[12]; (d) 三层、六层及多层石墨烯吸光度随压力的变化关系; (e) 三层、六层、十二层及多层石墨烯在2.0 eV光子能量处的吸光度压力依赖关系[13]

    Figure 1.  (a) XRD patterns of few-layer graphene compressed in a DAC; (b) Raman spectra of the present graphene sample obtained as the pressure increases to 52 GPa (left) and then decreases to ambient (right); (c) comparison of Raman spectra between depressurized and initial graphene samples[12]; (d) optical absorbance of tri-, hexa-, and multilayer graphene as a function of pressure; (e) pressure dependence of the absorbance of tri-, hexa-, 12-, and multilayer graphene at a photon energy of 2.0 eV[13].

    下载: 全尺寸图片 幻灯片

    图 2  (a) 在室温下测量的三层石墨烯的电阻-压力曲线, 黑色虚线表示电阻量子, h/4e2 ~ 6.45 kΩ, 超过此值, 无序导体在低温下会由于安德森局域化而表现为绝缘体; (b) 压缩下三层石墨烯的光学吸收谱图; (c) 加压和卸压过程中, 光子能量为1.5 eV时的吸收率演化[16]; VC-石墨烯在400—800 nm可见光范围和800—2000 nm红外沿着(d) [010]和(e) [001]方向的电磁波吸收系数; (f) VC-石墨烯在2—12 μm红外范围沿着[010]方向的电磁波吸收系数; (g) 理论计算的VC-石墨烯能带结构; (h)不同压力下石墨烯超材料的带隙工程[17]

    Figure 2.  (a) Resistance-pressure curves of trilayer graphene measured at room temperature. The black dashed line denotes the resistance quantum, h/4e2 ~ 6.45 kΩ, above which, a disordered conductor would behave as an insulator at low temperatures due to Anderson localization; (b) the optical absorbance patterns of trilayer graphene under compression; (c) evolution of absorbance at a photon energy of 1.5 eV during compression and decompression[16]; electromagnetic wave absorption coefficient of VC-graphene in the visible range of 400–800 nm and infrared range of 800–2000 nm along (d) [010] and (e) [001] directions; (f) the electromagnetic wave absorption coefficient along [010] direction of VC-graphene in the infrared range of 2–12 μm; (g) band structure of VC-graphene calculated; (h) bandgap engineering of graphene metamaterials under different pressures[17].

    下载: 全尺寸图片 幻灯片

    图 3  (a) 块材MoS2的晶胞示意图(左), 单层 MoS2的俯视图(右)[22]; (b) 不同压力下块体、多层、双层和单层MoS2样品的拉曼光谱[24]; (c) WTe2在加压(标记为c)和卸压(标记为d)过程中的同步辐射XRD图谱, 图中数字表示以GPa为单位的压力值[31]; (d) 单层MoS2在不同静水压下的PL光谱; (e) 单层MoS2的PL峰能量随压力的演化; (f) 单层MoS2的PL峰积分强度随压力的演化[34]; (g) ReX2 (X = S, Se)以及MoX2和WX2 第一直接光学跃迁的压力系数对比[36]

    Figure 3.  (a) The unit cell of bulk MoS2 (left) top view of the MoS2 monolayer(right)[22]; (b) Raman spectra of bulk, multilayer, bilayer, and monolayer MoS2 samples under different pressures[24]; (c) synchrotron XRD patterns of WTe2 during the compression (denoted by c) and decompression (by d), numbers represent pressures in unit of GPa[31]; (d) PL spectra of monolayer MoS2 for various pressures; (e) the evolution of energy of the predominant PL peak versus pressure; (f) integrated intensities of PL peak under various pressures[34]; (g) histogram showing the pressure coefficient of the first direct optical transitions of ReX2 (X = S, Se), MoX2 and WX2 [36].

    下载: 全尺寸图片 幻灯片

    图 4  (a) MoS2的电阻率对压力的依赖关系可划分为3个区域, 即半导体相(SC)、中间相(IS)和金属相(M), 插图为理论计算的电阻率-压力依赖关系; MoS2的电阻率对压力的依赖关系可划分为半导体相(SC)、中间相(IS)和金属相(M)三个区域, 插图为理论计算的电阻率随压力的变化趋势; (b) 金属态下MoS2的电阻率随温度的变化, 插图为实验观测的半导体态MoS2的电阻率-温度行为[30]; (c)—(e) 不同压力ReS2面内电阻的温度依赖关系; (f) 102.0 GPa压力下ReS2电阻下降特征的磁场依赖性, 插图显示了102.0 GPa时上临界场μ0Hc2 的温度依赖性[32]

    Figure 4.  (a) Pressure-dependent electrical resistivity of MoS2, three characteristic regions have been identified: semiconducting (SC), intermediate state (IS) and metallic regions. Inset: theoretically calculated pressure-dependent electrical resistivity; (b) temperature-dependent resistivity of MoS2 in the metallic state, the inset shows the experimental temperature-dependent semiconducting behavior of MoS2. The solid lines serve as visual guides[30]; (c)–(e) the temperature dependence of the in-plane electric resistance of ReS2 at different pressures; (f) magnetic field dependence of the resistance drop in ReS2 at 102.0 GPa, the inset shows the temperature dependence of the upper critical field μ0Hc2 at 102.0 GPa[32].

    下载: 全尺寸图片 幻灯片

    图 5  (PEA)2PbI4在压力下的结构演变与强各向异性压缩　(a) 二维钙钛矿在压力下的同步辐射XRD光谱; (b) 晶胞体积随压力的变化; (c) Pb─I键长随压力的变化, 面内方向($\langle{\text{Pb─I}}\rangle_{{\mathrm{equatorial}}} $)与面外方向($\langle{\text{Pb─I}}\rangle_{{\mathrm{axial}}} $)的键长变化略有不同; (d) 晶胞参数a, b和c随压力的变化; (e) 第一性原理计算证实了a, b和c参数随压力变化的相同趋势, 这强化了对各向异性压缩现象的观测[45]

    Figure 5.  Structural evolution and strongly anisotropic compression of (PEA)2PbI4 under pressure: (a) Synchrotron radiation XRD spectra of 2D perovskite under pressure; (b) pressure dependence of unit cell volume; (c) pressure dependence of the Pb─I bond length, which is slightly different in in-plane ($ \langle{\text{Pb─I}}\rangle_{{\mathrm{equatorial}}}$) and out-of-plane ($\langle{\text{Pb─I}}\rangle_{{\mathrm{axial}}} $) directions; (d) pressure dependence of unit cell parameters: a, b, and c; (e) identical pressure dependence of a, b, and c is confirmed by first-principles calculation, which enhances the observation of anisotropic compression[45].

    下载: 全尺寸图片 幻灯片

    图 6  (a) (BA)2PbI4的高压原位XRD测量; (b), (c) 第一次和第二次相变的详细变化; (d) 第一次相变前后(BA)2PbI4的晶体结构示意图; (e) (BA)2PbI4的原位高压吸收光谱; (f) 选定压力下 (BA)2PbI4的光学图像; (g) (BA)2PbI4的带隙随压力的变化; (h) 常压条件下(BA)2PbI4的吸收光谱; (i) 2.2 GPa以下(BA)2PbI4带隙的变化[52]

    Figure 6.  (a) In situ XRD measurements of (BA)2PbI4 under high pressures; (b), (c) detailed variations of the first and second transition; (d) schematic crystal structures of (BA)2 PbI4 before and after the first phase transition; (e) in situ high-pressure absorption spectra of (BA)2PbI4; (f) optical images of (BA)2PbI4 at selected pressures; (g) variations of the (BA)2PbI4 band gap as a function of pressure; (h) the absorption spectrum of (BA)2PbI4 at ambient conditions; (i) variations of the of (BA)2PbI4 band gap below 2.2 GPa[52].

    下载: 全尺寸图片 幻灯片

    图 7  (BA)2(MA)Pb2I7的原位高压光吸收测试　(a) 压力依赖的光学吸光度谱的彩色图, (b) 压力依赖的(αdhν)2随光子能量变化的彩色图; (c) 各种杂化钙钛矿带隙的压力依赖性总结; (d) (BA)2(MA)Pb2I7的高压同步辐射XRD图谱; (e) 晶面间距的压力依赖性, 插图显示了平均晶格常数(dave)的压力依赖性; (f) XRD展宽证明的压力诱导原子畸变; (g) 压缩过程中带隙演化的结构起源[54]

    Figure 7.  In situ high-pressure optical absorption measurements of (BA)2(MA)Pb2I7: (a) color plots of pressure-dependent optical absorbance spectra, (b) color plots of pressure-dependent (αdhν)2 versus photon energy; (c) summary of the pressure dependence of the bandgap for various hybrid perovskites (d)–(f) in situ high-pressure structural characterizations on (BA)2(MA)Pb2I7: (d) high-pressure synchrotron XRD patterns at various 2 theta ranges, (e) pressure dependence of the d-spacing, the inset shows the pressure dependence of dave, (f) pressure-induced atomic distortions evidenced by broadened XRD; (g) structural origin of bandgap evolution in compression[54].

    下载: 全尺寸图片 幻灯片

    图 8  (a) (3AMP)(MA)n–1PbnI3n+1 (n = 1, 2, 4)的归一化晶面间距随压力的演化; (b) 不同晶面的FWHM随压力的演化; (3AMP)(MA)n–1PbnI3n+1在压力条件下的光吸收特性, n = 1 (c), n = 2 (d)和n = 4 (e)的光吸收等高线图; (f) (3AMP)(MA)n–1PbnI3n+1(n = 1, 2, 4)的带隙演化总结[56]

    Figure 8.  (a) Evolution of normalized lattice spacing of (3AMP)(MA)n–1PbnI3n+1(n = 1, 2, 4); (b) FWHM as a function of pressure for different lattice planes; contour plots of optical absorbance of n = 1 (c), n = 2 (d) n = 4 (e); (f) summary of bandgap evolutions of (3AMP)(MA)n–1PbnI3n+1(n = 1, 2, 4) [56].

    下载: 全尺寸图片 幻灯片

    图 9  (a), (b) 多种杂化钙钛矿的带隙演化对比, 虚线代表Shockley–Queisser 最优带隙值(≈1.33 eV), (a), (b)分别使用线性和对数标度, 其中后者显示了低压区域的更多细节; (c) 二维和三维钙钛矿的带隙可调性随无机层厚度/晶胞纵向总长度的变化关系; (d) 高压下杂化钙钛矿的通用压力驱动行为示意图[57]

    Figure 9.  (a), (b) Comparison of pressure-driven bandgap evolution between various hybrid perovskites, the dashed line represents the Shockley–Queisser optimal magnitude (≈1.33 eV), for pressure axis, (a), (b) use linear and log scale, respectively, where the latter shows more details in low-pressure region; (c) bandgap tunability of 2D and 3D perovskites as a function of inorganic layer thickness/total unit cell length along the longitudinal direction; (d) a schematic diagram and illustration for hybrid perovskites under high pressures[57].

    下载: 全尺寸图片 幻灯片

    图 10  (a)—(c) (2meptH2)PbCl4的高压PL测量 (a) (2meptH2)PbCl4 的发射光谱随压力的演化; (b) 在355 nm 紫外光照射下, 选定压力点的光学图像; (c) 发射的色度坐标随压力的变化关系. (d) (2meptH2)PbCl4 晶体在常压条件和 5.0 GPa 下自陷激子发射演化的示意图[60]. (e)—(g) (CMA)2PbI4的高压PL测量 (e) 在360 nm 紫外光照射下, 选定压力点的光学图像; (f) 360 nm 激发下的PL光谱随压力的演化; (g) PL峰位置的压力依赖性, 并与 DFT 计算的带隙能量值作为参考进行比较[68]. (h)—(k) (HA)2(GA)Pb2I7 单晶的高压原位光学特性 (h) (HA)2(GA)Pb2I7在405 nm激发下发射光谱随压力的演化; (i) 选定压力下 PL光谱的拟合曲线; (j) 俘获态发射贡献度和 PL强度随压力的变化关系; (k) 带隙演化随压力的变化关系及相应的光学图像[69]

    Figure 10.  (a)–(c) PL measurements of (2meptH2)PbCl4 at high pressure: (a) Pressure-induced evolution of emission spectra of (2meptH2)PbCl4 upon compression; (b) optical images at selected pressures under UV irradiation of 355 nm; (c) chromaticity coordinates of the emissions as a function of pressure. (d) illustration of the evolution of self-trapped exciton emission of the (2 meptH2)PbCl4 crystal at ambient conditions and 5.0 GPa[60]. (e)–(g) PL measurements of (CMA)2PbI4 at high pressure: (e) Optical image of the sample chamber at selected pressures with a 360 nm UV laser as the excitation source; (f) PL spectra excited by a 360 nm UV laser upon compression at selected pressures; (g) pressure dependence of PL peak positions compared with DFT computed bandgap energies as reference[68]. (h)–(k) in situ optical properties of (HA)2(GA)Pb2I7 single crystals under high pressures: (h) PL spectra excited by 405 nm laser during compression; (i) the fitting curves of the PL spectra under selected pressures; (j) contribution of trapped states emission and the PL intensity as a function of pressure; (k) bandgap evolution as a function of pressure and the corresponding optical images[69].

    下载: 全尺寸图片 幻灯片

    图 11  (a) (3AMP)PbI4(n = 1)在1 atm—9.7 GPa 压力范围内的 PL 光谱; (b) (3AMP)(MA)3Pb4I13(n = 4)在 1 atm—4.0 GPa 压力范围内的 PL 光谱; (c) D-J 型钙钛矿(3AMP)PbI4和(3AMP)(MA)3Pb4I13, R-P型钙钛矿(GA)(MA)2Pb2I7, (MA) (BA)2Pb2I7的归一化 PL 峰值强度总结[56]

    Figure 11.  (a) PL spectra of (3AMP)PbI4 (n = 1) from 1 atm to 9.7 GPa; (b) PL spectra of (3AMP)(MA)3Pb4I13 (n = 4) from 1 atm to 4.0 GPa; (c) summary of normalized PL peak intensities of D-J perovskites (3AMP)PbI4 and (3AMP)(MA)3Pb4I13, alternating-cation R-P perovskite (GA)(MA)2Pb2I7 and R-P perovskite (MA)(BA)2Pb2I7[56].

    下载: 全尺寸图片 幻灯片

    图 12  (a) (BA)4AgBiBr8在高压下的PL光谱; (b) (BA)4AgBiBr8光致发光显微照片随压力增大的变化图像; (c) 2.5 GPa下(BA)4AgBiBr8的吸收和发射图谱; (d) (BA)4AgBiBr8的PL峰位和归一化 PL 强度作为压力的函数; (e) 在环境条件(左)下和压缩时(右)与自陷激子相关的发射机制图示[74]

    Figure 12.  (a) PL spectra of (BA)4AgBiBr8 at high pressure; (b) PL micrographs showing PL intensity changes with increasing pressure; (c) absorption and emission spectra for (BA)4AgBiBr8 at 2.5 GPa; (d) the PL location of (BA)4AgBiBr8 as a function of pressure and normalized PL intensity as a function of pressure; (e) illustrations of PIE mechanism associated with exciton self-trapping at ambient conditions (left) and upon compression (right)[74].

    下载: 全尺寸图片 幻灯片

    图 13  (BA)2PbI4在环境条件(a)和3.1 GPa (b)下的阻抗数据; (c)(BA)2PbI4的电阻随压力的变化关系[52]; (d) (BA)2(FA)Sn2I7 在405, 980, 1532 nm激光照射下的I-T曲线[80]; (e)加压过程中Cs2PbI2Cl2的光电流变化; (f)压力诱导的Cs2PbI2Cl2光电导率演化, 插图展示了金刚石对顶砧中铂电极与晶体的显微图像; (g)压力促进激子解离的机理示意图[82]

    Figure 13.  Impedance data of (BA)2PbI4 at ambient conditions (a) and 3.1 GPa (b)[52]; (c) pressure dependence of the resistance of (BA)2PbI4; (d) the I-T curves of (BA)2(FA)Sn2I7 samples under different pressures under 405, 980, and 1532 nm laser irradiation[80]; (e) photocurrents upon compression of Cs2PbI2Cl2 in phase I; (f) pressure-induced evolution of photoconductivity of Cs2PbI2Cl2, the inset displays a microphotograph of the crystal with platinum probes in the DAC; (g) schematic diagram of the pressure-promoted exciton dissociation[82].

    下载: 全尺寸图片 幻灯片

    图 14  (a) 所选压力下Ti3C2Tx的代表性XRPD图谱和(b) 相应的放大(002)峰; (c) 晶格参数(a, c, V)随压力的变化; (d) 压缩过程中(0.5 GPa)和压力完全释放后(0.3 GPa)的(002)峰图谱[87]

    Figure 14.  (a) Representative XRPD patterns of Ti3C2Tx at selected pressures and (b) corresponding magnified (002) peak; (c) lattice parameters (a, c, and V) as functions of pressure; (d) patterns of the (002) peak at 0.5 GPa during compression and 0.3 GPa after pressure being fully released[87].

    下载: 全尺寸图片 幻灯片

    图 15  (a) Ti3C2Tx在循环压力下电阻R随压力的变化, 插图是约0.69 GPa 以上的放大图; (b) 压缩前后的变温电阻[87]

    Figure 15.  (a) Pressure-dependent resistance (R) of Ti3C2Tx under cyclic pressures, inset is the enlarged part above ~0.69 GPa; (b) variable-temperature resistance before and after compression[87].

    下载: 全尺寸图片 幻灯片

    图 16  (a) FL-CN 的 PL 发射颜色和样品颜色变化的示意图; (b) 选定压力下 FL-CN 的归一化 PL 光谱; (c) 发射的压力依赖性色度坐标; (d) 选定压力下 PL 能量(在 3 GPa 后由于 PL 光谱展宽特征, 需拟合为一个峰而非3个峰)的压力依赖性[95]

    Figure 16.  (a) A sketch map for the PL emission color and sample color change of FL-CN; (b) The normalized PL spectra of FL-CN at selected pressures; (c) the pressure-dependent chromaticity coordinates of the emissions; (d) the dependence of PL energy at selected pressures (one peak instead of three is necessary to fit the experimental data for the broad features of PL spectra after 3 GPa)[95]

    下载: 全尺寸图片 幻灯片

    图 17  (a) 不同压力下 FL-CN 的代表性同步辐射XRD图谱; (b) 选定压力下 FL-CN、石墨和少层石墨烯的c/c0; (c) (100)衍射的压力依赖性[95]

    Figure 17.  (a) Representative synchrotron XRD patterns of FL-CN at different pressures; (b) the c/c0 of FL-CN, graphite, and few-layer graphene at selected pressures; (c) pressure dependence of the (100) diffraction peak[95].

    下载: 全尺寸图片 幻灯片

    图 18  (a) 在发生 h-BN向w-BN 转变的压力范围内, 加压测量中记录的 BN 样品在几个压力下的红外透射光谱; (b) 在相变发生的压力范围内, 另一个 BN 样品在几个压力下的反射光谱[105]; (c), (d) 两条不同缺陷发射线的压力依赖性; (e) 在0.5—3.5 GPa压力范围内, 9个典型缺陷的发射线PL峰值能量随压力的函数关系, 右列中的数字代表相应的压力系数; (f) 压力系数负值绝对值低于2 meV/GPa的缺陷发射线随压力的变化[106]

    Figure 18.  (a) IR transmission spectra of a BN sample recorded in the upstroke measurement at several pressures over the range where the h-BN to w-BN transition takes place; (b) reflectance spectra of a different BN sample at several pressures over the pressure range where the phase transition occurs[105]; (c), (d) pressure-dependence of PL spectra for two defect emission lines; (e) PL peak energy as a function of pressure for the emission lines from 9 typical defects between 0.5 and 3.5 GPa; (f) pressure evolution of defect emission lines whose pressure coefficients exhibit negative values with absolute magnitudes less than 2 meV/GPa[106].

    下载: 全尺寸图片 幻灯片
  • [1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 doi: 10.1126/science.1102896
    [2] Huang X, Zeng Z Y, Fan Z X, Liu J Q, Zhang H 2013 Chem. Soc. Rev. 44 1934 doi: 10.1039/C2CS35387C
    [3] Kannan P K, Late D J, Morgan H, Rout C S 2015 Nanoscale 7 13293 doi: 10.1039/C5NR03633J
    [4] Sun Y F, Gao S, Lei F C, Xie Y 2014 Chem. Soc. Rev. 44 623 doi: 10.1039/C4CS00236A
    [5] Novoselov K S, Mishchenko A, Carvalho A, Neto A H C 2016 Science 353 aac9439 doi: 10.1126/science.aac9439
    [6] Chow W L, Yu P, Liu F C, Hong J H, Wang X L, Zeng Q S, Hsu C, Zhu C, Zhou J D, Wang X W, Xia J, Yan J X, Chen Y, Wu D, Yu T, Zheng Z X, Lin H, Jin C H, Tay B K, Liu Z 2017 Adv. Mater. 29 1602969 doi: 10.1002/adma.201602969
    [7] Mao H K, Chen B, Chen J, Li K, Lin J F, Yang W G, Zheng H 2016 Matter Radiat. Extrems 1 59 doi: 10.1016/j.mre.2016.01.005
    [8] Mao H K, Xu J, Bell P M 1986 J. Geophys. Res. Atmos. 91 4673 doi: 10.1029/JB091iB05p04673
    [9] 郑海飞 2015 金刚石压腔高温高压实验技术及其应用 (北京: 科学出版社) 第78—88页 Zheng H F 2015 Diamond Anvil Cell High-Pressure and High-Temperature Experimental Techniques and Their Applications (Beijing: Science Press) pp78–88
    [10] Zheng J, Zhang H, Dong S H, Liu Y P, Nai C T, Shin H S, Jeong H Y, Liu B, Loh K P 2014 Nat. Commun. 5 2995 doi: 10.1038/ncomms3995
    [11] Gu L, Liu S, Zhao H C, Yu H B 2015 ACS Appl. Mater. Interfaces 7 17641 doi: 10.1021/acsami.5b05531
    [12] Clark S M, Jeon K J, Chen J Y, Yoo C S 2012 Solid State Commun. 154 15 doi: 10.1016/j.ssc.2012.10.002
    [13] Ke F, Zhang L K, Chen Y B, Yin K T, Wang C X, Tzeng Y K, Lin Y, Dong H L, Liu Z X, Tse J S, Mao W L, Wu J Q, Chen B 2020 Nano Lett. 20 5916 doi: 10.1021/acs.nanolett.0c01872
    [14] Mak K F, Shan J, Heinz T F 2011 Phys. Rev. Lett. 106 046401 doi: 10.1103/PhysRevLett.106.046401
    [15] Carr S, Fang S, Jarillo-Herrero P, Kaxiras E 2018 Phys. Rev. B 98 085144 doi: 10.1103/PhysRevB.98.085144
    [16] Ke F, Chen Y B, Yin K T, Yan J J, Zhang H Z, Liu Z X, Tse J S, Wu J Q, Mao H K, Chen B 2019 Proc. Natl. Acad. Sci. USA. 116 9186 doi: 10.1073/pnas.1820890116
    [17] Luo B C, Wu L W, Li D, Zhang Z L, Yu X C, Li G W, Song H Z 2022 Carbon 196 146 doi: 10.1016/j.carbon.2022.04.065
    [18] Akinwande D, Huyghebaert C, Wang C H, Serna M I, Goossens S, Li L J, Wong H S P, Koppens F H L 2019 Nature 573 507 doi: 10.1038/s41586-019-1573-9
    [19] Novoselov K S, Jiang D, Schedin F, Booth T J, Khotkevich V V, Morozov S V, Geim A K 2005 Proc. Natl. Acad. Sci. USA. 102 10451 doi: 10.1073/pnas.0502848102
    [20] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805 doi: 10.1103/PhysRevLett.105.136805
    [21] Splendiani A, Sun L, Zhang Y, Li T, Kim J, Chim C Y, Galli G, Wang F 2010 Nano Lett. 10 1271 doi: 10.1021/nl903868w
    [22] Xiao D, Liu G B, Feng W X, Xu X D, Yao W 2012 Phys. Rev. Lett. 108 196802 doi: 10.1103/PhysRevLett.108.196802
    [23] Tanwar S, Arya A, Gaur A, Sharma A L 2021 J. Phys. Condens. Matter 33 303002 doi: 10.1088/1361-648X/abfb3c
    [24] Cheng X R, Li Y Y, Shang J M, Hu C S, Ren Y F, Liu M, Qi Z M 2017 Nano Res. 11 855 doi: 10.1007/s12274-017-1696-y
    [25] Chi Z H, Zhao X M, Zhang H, Goncharov A F, Lobanov S S, Kagayama T, Sakata M, Chen X J 2014 Phys. Rev. Lett. 113 036802 doi: 10.1103/PhysRevLett.113.036802
    [26] Tosatti E, Hromadova L, Martoňák R 2013 Bull. Am. Phys. Soc. 87 144105 doi: 10.1103/PhysRevB.87.144105
    [27] Fan X F, Singh D J, Jiang Q, Zheng W T 2016 Phys. Chem. Chem. Phys. 18 12080 doi: 10.1039/C6CP00715E
    [28] Wang S M, Zhang J Z, He D W, Zhang Y, Wang L P, Xu H W, Wen X D, Ge H, Zhao Y S 2013 J. Phys. Chem. Solids 75 100 doi: 10.1016/j.jpcs.2013.09.001
    [29] Bhattacharyya S, Singh A K 2012 Phys. Rev. B 86 075454 doi: 10.1103/PhysRevB.86.075454
    [30] Nayak A P, Pandey T, Voiry D, Liu J, Moran S T, Sharma A, Tan C, Chen C H, Li L J, Chhowalla M, Lin J F, Singh A K, Akinwande D 2014 Nano Lett. 15 346 doi: 10.1021/nl5036397
    [31] Zhou Y H, Chen X L, Li N N, Zhang R R, Wang X F, An C, Zhou Y, Pan X C, Song F Q, Wang B G, Yang W G, Yang Z R, Zhang Y H 2016 AIP Adv. 6 075008 doi: 10.1063/1.4959026
    [32] Zhou D W, Zhou Y H, Pu C Y, Chen X L, Lu P C, Wang X F, An C, Zhou Y, Miao F, Ho C H, Sun J, Yang Z R, Xing D Y 2017 NPJ Quantum Mater. 2 19 doi: 10.1038/s41535-017-0023-x
    [33] Yan Y L, Jin C L, Wang J, Qin T R, Li F F, Wang K, Han Y H, Gao C X 2017 J. Phys. Chem. Lett. 8 3648 doi: 10.1021/acs.jpclett.7b01031
    [34] Fu L, Wan Y, Tang N, Ding Y M, Gao J, Yu J C, Guan H M, Zhang K, Wang W Y, Zhang C F, Shi J J, Wu X, Shi S F, Ge W K, Dai L, Shen B 2017 Sci. Adv. 3 e1700162 doi: 10.1126/sciadv.1700162
    [35] Gong Y, Zhou Q, Huang X, Han B, Fu X, Gao H, Li F, Cui T 2017 Chem. NanoMat. 3 238 (in Chinese) doi: 10.1002/cnma.201600346
    [36] Oliva R, Laurien M, Dybala F, Kopaczek J, Qin Y, Tongay S, Rubel O, Kudrawiec R 2019 NPJ 2D Mater. Appl. 3 20 doi: 10.1038/s41699-019-0102-x
    [37] Lorchat E, Froehlicher G, Berciaud S 2016 ACS Nano 10 2752 doi: 10.1021/acsnano.5b07844
    [38] Hou D B, Ma Y Z, Du J G, Yan J Y, Ji C, Zhu H Y 2010 J. Phys. Chem. Solids 71 1571 doi: 10.1016/j.jpcs.2010.08.002
    [39] Kao Y C, Huang T, Lin D Y, Huang Y S, Tiong K K, Lee H Y, Lin J M, Sheu H S, Lin C M 2012 J. Chem. Phys. 137 024509 doi: 10.1063/1.4733985
    [40] Nayak A P, Bhattacharyya S, Zhu J, Liu J, Wu X, Pandey T, Jin C, Singh A K, Akinwande D, Lin J F 2014 Nat. Commun. 5 3731 doi: 10.1038/ncomms4731
    [41] Jiang F Y, Yang D W, Jiang Y Y, Liu T F, Zhao X G, Ming Y, Luo B W, Qin F, Fan J C, Han H W, Zhang L J, Zhou Y H 2017 J. Am. Chem. Soc. 140 1019 doi: 10.1021/jacs.7b10739
    [42] Zhang F, Zhang H Y, Zhu L J, Qin L, Wang Y G, Hu Y F, Lou Z D, Hou Y B, Teng F 2019 J. Mater. Chem. C 7 4004 doi: 10.1039/C8TC06249H
    [43] Li L N, Sun Z H, Wang P, Hu W D, Wang S S, Ji C M, Hong M C, Luo J H 2017 Angew. Chem. Int. Ed. 56 12150 doi: 10.1002/anie.201705836
    [44] Xu Y K, Wang M, Lei Y T, Ci Z P, Jin Z W 2020 Adv. Energy Mater. 10 2002558 doi: 10.1002/aenm.202002558
    [45] Liu G, Gong J, Kong L P, Schaller R D, Hu Q Y, Liu Z X, Yan S, Yang W G, Stoumpos C C, Kanatzidis M G, Mao H K, Xu T 2018 Proc. Natl. Acad. Sci. USA. 115 8076 doi: 10.1073/pnas.1809167115
    [46] Capitani F, Marini C, Caramazza S, Postorino P, Garbarino G, Hanfland M, Pisanu A, Quadrelli P, Malavasi L 2016 J. Appl. Phys. 119 185901 doi: 10.1063/1.4948577
    [47] Liu G, Kong L P, Gong J, Yang W G, Mao H K, Hu Q Y, Liu Z X, Schaller R D, Zhang D Z, Xu T 2016 Adv. Funct. Mater. 27 1604208 doi: 10.1002/adfm.201604208
    [48] Ou T, Yan J, Xiao C, Shen W, Liu C, Liu X, Han Y, Ma Y, Gao C 2016 Nanoscale 8 11426 doi: 10.1039/C5NR07842C
    [49] Jaffe A, Lin Y, Mao W L, Karunadasa H I 2017 J. Am. Chem. Soc. 139 4330 doi: 10.1021/jacs.7b01162
    [50] Yu P Y, Welber B 1978 Solid State Commun. 25 209 doi: 10.1016/0038-1098(78)90214-4
    [51] Mujica A, Rubio A, Muñoz A, Needs R J 2003 Rev. Mod. Phys. 75 863 doi: 10.1103/RevModPhys.75.863
    [52] Yuan Y, Liu X, Ma X, Wang X, Li X, Xiao J, Li X, Zhang H, Wang L 2019 Adv. Sci. 6 1900240 doi: 10.1002/advs.201900240
    [53] Jaffe A, Lin Y, Mao W L, Karunadasa H I 2015 J. Am. Chem. Soc. 137 1673 doi: 10.1021/ja512396m
    [54] Liu G, Kong L P, Guo P J, Stoumpos C C, Hu Q Y, Liu Z X, Cai Z H, Gosztola D J, Mao H K, Kanatzidis M G, Schaller R D 2017 ACS Energy Lett. 2 2518 doi: 10.1021/acsenergylett.7b00807
    [55] Kong L P, Liu G, Gong J, Hu Q Y, Schaller R D, Dera P, Zhang D Z, Liu Z X, Yang W G, Zhu K, Tang Y Z, Wang C Y, Wei S H, Xu T, Mao H K 2016 Proc. Natl. Acad. Sci. USA. 113 8910 doi: 10.1073/pnas.1609030113
    [56] Kong L P, Liu G, Gong J, Mao L L, Chen M T, Hu Q Y, Lü X J, Yang W G, Kanatzidis M G, Mao H K 2020 Proc. Natl. Acad. Sci. USA. 117 16121 doi: 10.1073/pnas.2003561117
    [57] Kong L P, Gong J, Spanopoulos I, Yan S, Li Z Y, Zhu Z K, Liu X Y, Zhu Y N, Dong H L, Shu H Y, Hu Q Y, Yang W G, Mao H K, Kanatzidis M G, Liu G 2024 Adv. Funct. Mater. 34 2414437 doi: 10.1002/adfm.202414437
    [58] Kong L P, Gong J, Hu Q Y, Capitani F, Celeste A, Hattori T, Sano-Furukawa A, Li N N, Yang W G, Liu G, Mao H K 2020 Adv. Funct. Mater. 31 2009131 doi: 10.1002/adfm.202009131
    [59] Yin T T, Liu B, Yan J X, Fang Y N, Chen M H, Chong W K, Jiang S J, Kuo J L, Fang J Y, Liang P, Wei S H, Loh K P, Sum T C, White T J, Shen Z X 2018 J. Am. Chem. Soc. 141 1235 doi: 10.1021/jacs.8b07765
    [60] Fang Y, Wang J, Zhang L, Niu G, Sui L, Wu G, Yuan K, Wang K, Zou B 2023 Chem. Sci. 14 2652 doi: 10.1039/D2SC06982B
    [61] Li X F, Wang S S, Zhao S G, Li L N, Li Y Q, Zhao B Q, Shen Y G, Wu Z Y, Shan P, Luo J H 2018 Chem. Eur. J. 24 9243 doi: 10.1002/chem.201802056
    [62] Duan D W, Ge C Y, Rahaman M Z, Lin C H, Shi Y M, Lin H R, Hu H L, Wu T 2023 NPG Asia Mater. 15 8 doi: 10.1038/s41427-023-00465-0
    [63] Wang Y Q, Guo S H, Luo H, Zhou C K, Lin H R, Ma X D, Hu Q Y, Du M H, Ma B W, Yang W G, Lü X J 2020 J. Am. Chem. Soc. 142 16001 doi: 10.1021/jacs.0c07166
    [64] Wang S S, Yao Y P, Wu Z Y, Peng Y, Li L N, Luo J H 2018 J. Mater. Chem. C 6 12267 doi: 10.1039/C8TC03167C
    [65] Cheng X W, Xie Z, Zheng W, Li R F, Deng Z H, Tu D T, Shang X Y, Xu J, Gong Z L, Li X J, Chen X Y 2022 Adv. Sci. 9 2103724 doi: 10.1002/advs.202103724
    [66] Meng X, Ji S J, Wang Q J, Wang X C, Bai T X, Zhang R L, Yang B, Li Y M, Shao Z P, Jiang J K, Han K L, Liu F 2022 Adv. Sci. 9 2203596 doi: 10.1002/advs.202203596
    [67] Luo H, Guo S H, Zhang Y B, Bu K J, Lin H R, Wang Y G, Yin Y F, Zhang D Z, Jin S Y, Zhang W Q, Yang W G, Ma B W, Lü X J 2021 Adv. Sci. 8 2100786 doi: 10.1002/advs.202100786
    [68] Ratté J, Macintosh M F, DiLoreto L, Liu J, Mihalyi-Koch W, Hautzinger M P, Guzei I A, Dong Z, Jin S, Song Y 2023 J. Phys. Chem. Lett. 14 403 doi: 10.1021/acs.jpclett.2c03555
    [69] Guo S H, Zhao Y S, Bu K J, Fu Y P, Luo H, Chen M T, Hautzinger M P, Wang Y G, Jin S, Yang W G, Lü X J 2020 Angew. Chem. Int. Ed. 59 17533 doi: 10.1002/anie.202001635
    [70] Ma Z W, Liu Z, Lu S Y, Wang L R, Feng X L, Yang D W, Wang K, Xiao G J, Zhang L J, Redfern S A T, Zou B 2018 Nat. Commun. 9 4506 doi: 10.1038/s41467-018-06840-8
    [71] Liu S, Sun S S, Gan C K, Del Águila A G, Fang Y N, Xing J, Ha T T DO, White T J, Li H G, Huang W, Xiong Q 2019 Sci. Adv. 5 eaav9445 doi: 10.1126/sciadv.aav9445
    [72] Zhang L, Liu C M, Wang L R, Liu C L, Wang K, Zou B 2018 Angew. Chem. Int. Ed. 57 11213 doi: 10.1002/anie.201804310
    [73] Li M, Liu T B, Wang Y G, Yang W G, Lü X J 2020 Matter Radiat. Extrems 5 018201 doi: 10.1063/1.5133653
    [74] Fang Y Y, Zhang L, Wu L W, Yan J J, Lin Y, Wang K, Mao W L, Zou B 2019 Angew. Chem. Int. Ed. 58 15249 doi: 10.1002/anie.201906311
    [75] Mao L L, Wu Y L, Stoumpos C C, Wasielewski M R, Kanatzidis M G 2017 J. Am. Chem. Soc. 139 5210 doi: 10.1021/jacs.7b01312
    [76] Szafrański M, Katrusiak A 2016 J. Phys. Chem. Lett. 7 3458 doi: 10.1021/acs.jpclett.6b01648
    [77] Wang Y G, Lü X J, Yang W G, Wen T, Yang L X, Ren X T, Wang L, Lin Z S, Zhao Y S 2015 J. Am. Chem. Soc. 137 11144 doi: 10.1021/jacs.5b06346
    [78] Lü X J, Wang Y G, Stoumpos C C, Hu Q, Guo X, Chen H, Yang L, Smith J S, Yang W, Zhao Y, Xu H, Kanatzidis M G, Jia Q 2016 Adv. Mater. 28 8663 doi: 10.1002/adma.201600771
    [79] Li Q, Wang Y G, Pan W C, Yang W G, Zou B, Tang J, Quan Z W 2017 Angew. Chem. Int. Ed. 56 15969 doi: 10.1002/anie.201708684
    [80] Cui H, Zhang H F, Xu S, Cheng L Y, Tao H H, Wang L R, Pan G C, You W W, Mao Y L 2025 Appl. Phys. Lett. 126 173101 doi: 10.1063/5.0266788
    [81] Chen Y P, Fu R J, Wang L R, Ma Z W, Xiao G J, Wang K, Zou B 2019 J. Mater. Chem. A 7 6357 doi: 10.1039/C8TA11992A
    [82] Guo S H, Bu K J, Li J W, Hu Q Y, Luo H, He Y H, Wu Y H, Zhang DZ, Zhao Y S, Yang W G, Kanatzidis M G, Lü X J 2021 J. Am. Chem. Soc. 143 2545 doi: 10.1021/jacs.0c11730
    [83] Miyata A, Mitioglu A, Plochocka P, Portugall O, Wang J T W, Stranks S D, Snaith H J, Nicholas R J 2015 Nat. Phys. 11 582 doi: 10.1038/nphys3357
    [84] Li S R, Luo J J, Liu J, Tang J 2019 J. Phys. Chem. Lett. 10 1999 doi: 10.1021/acs.jpclett.8b03604
    [85] Yuan M J, Quan L N, Comin R, Walters G, Sabatini R, Voznyy O, Hoogland S, Zhao Y, Beauregard E M, Kanjanaboos P, Lu Z, Kim D H, Sargent E H 2016 Nat. Nanotechnol. 11 872 doi: 10.1038/nnano.2016.110
    [86] Anasori B, Lukatskaya M R, Gogotsi Y 2017 Nat. Rev. Mater. 2 16098 doi: 10.1038/natrevmats.2016.98
    [87] Lv J C, Jia H S, Chen G B, Wang Y X, Liu M, Ning Y Y, Wang Y J, Yuan L, Lu M, Zhang J K 2022 ACS Appl. Mater. Interfaces 14 46056 doi: 10.1021/acsami.2c13220
    [88] Zhang J K, Zhang Y L, Wu X X, Ma Y Z, Chien S Y, Guan R Q, Zhang D Z, Yang B, Yan B M, Yang J H 2018 ACS Appl. Mater. Interfaces 10 42856 doi: 10.1021/acsami.8b15259
    [89] Wang Y F, Xu Y H, Hu M L, Ling H, Zhu X 2020 Nanophotonics 9 1601 doi: 10.1515/nanoph-2019-0556
    [90] Li X H, Li S S, Cui H L, Zhang R Z 2020 ACS Omega 5 22248 doi: 10.1021/acsomega.0c02435
    [91] Shivani V, Sriram S 2025 Diamond Relat. Mater. 154 112192 doi: 10.1016/j.diamond.2025.112192
    [92] Ye C Q, Liu M Z 2022 J. Mol. Model. 28 40 doi: 10.1007/s00894-021-05024-4
    [93] Yang J H, Wu X T, Li X F, Liu Y, Gao M, Liu X Y, Kong L N, Yang S Y 2011 Appl. Phys. A 105 161 doi: 10.1007/s00339-011-6471-4
    [94] Li Y A, Zhang J, Wang Q S, Jin Y X, Huang D H, Cui Q L, Zou G T 2010 J. Phys. Chem. B 114 9429 doi: 10.1021/jp103729c
    [95] Hu K, Yao M G, Yang Z X, Xiao G J, Zhu L Y, Zhang H, Liu R, Zou B, Liu B B 2020 Nanoscale 12 12300 doi: 10.1039/D0NR01542C
    [96] Ruan L W, Zhu Y J, Qiu L G, Yuan Y P, Lu Y X 2014 Comput. Mater. Sci. 91 258 doi: 10.1016/j.commatsci.2014.04.058
    [97] Zhou J Z, Zhu M Y, Han Y, Zhou X F, Wang S M, Chen J Z, Wu H, Hou Y, Lu Y 2024 J. Appl. Phys. 135 224301 doi: 10.1063/5.0209443
    [98] Wickramaratne D, Weston L, Van De Walle C G 2018 J. Phys. Chem. C 122 25524 doi: 10.1021/acs.jpcc.8b09087
    [99] Cai Q, Scullion D, Gan W, Falin A, Zhang S, Watanabe K, Taniguchi T, Chen Y, Santos E J G, Li L H 2019 Sci. Adv. 5 eaav0129 doi: 10.1126/sciadv.aav0129
    [100] Yeol K MA, Zhang L, Jin S, Wang Y, Yoon S I, Hwang H, Oh J, Jeong D S, Wang M, Chatterjee S, Kim G, Jang A R, Yang J, Ryu S, Jeong H Y, Ruoff R S, Chhowalla M, Ding F, Shin H S 2022 Nature 606 88 doi: 10.1038/s41586-022-04745-7
    [101] Chang H Y, Yang S, Lee J, Tao L, Hwang W S, Jena D, Lu N, Akinwande D 2013 ACS Nano 7 5446 doi: 10.1021/nn401429w
    [102] Lee G H, Cui X, Kim Y D, Arefe G, Zhang X, Lee C H, Ye F, Watanabe K, Taniguchi T, Kim P, Hone J 2015 ACS Nano 9 7019 doi: 10.1021/acsnano.5b01341
    [103] Britnell L, Gorbachev R V, Geim A K, Ponomarenko L A, Mishchenko A, Greenaway M T, Fromhold T M, Novoselov K S, Eaves L 2013 Nat. Commun. 4 1794 doi: 10.1038/ncomms2817
    [104] Britnell L, Gorbachev R V, Jalil R, Belle B D, Schedin F, Katsnelson M I, Eaves L, Morozov S V, Mayorov A S, Peres N M R, Neto A H C, Leist J, Geim A K, Ponomarenko L A, Novoselov K S 2012 Nano Lett. 12 1707 doi: 10.1021/nl3002205
    [105] Segura A, Cuscó R, Taniguchi T, Watanabe K, Cassabois G, Gil B, Artús L 2019 J. Phys. Chem. C 123 20167 doi: 10.1021/acs.jpcc.9b06163
    [106] Xue Y Z, Wang H, Tan Q H, Zhang J, Yu T J, Ding K, Jiang D S, Dou X M, Shi J J, Sun B Q 2018 ACS Nano 12 7127 doi: 10.1021/acsnano.8b02970
    [107] Akamaru H, Onodera A, Endo T, Mishima O 2002 J. Phys. Chem. Solids 63 887 doi: 10.1016/S0022-3697(01)00244-X
  • 加载中
图( 18)
计量
  • 文章访问数:  58
  • HTML全文浏览数:  58
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-08-02
  • 刊出日期:  2025-10-20

高压下二维材料结构和光电性能研究进展

    通讯作者: E-mail: ylmao@henu.edu.cn.
  • 河南大学物理与电子学院, 开封　475004
  • 收稿日期:  2025-08-02

摘要: 二维材料因其优异的光电性能在基础科学探索与光电子学、能源存储和转换器件等未来技术应用中展现出巨大的潜力, 成为凝聚态物理和材料科学领域的前沿热点. 二维材料独特的层状结构使其物理性能极易受外场的影响. 高压技术作为一种高效、连续且清洁的调控手段, 可以通过压缩原子间距、增强层间耦合, 甚至诱导结构相变, 进而实现对二维材料结构的精准调控以及光电性能的优化提升. 本文以石墨烯、过渡金属二硫族化合物、二维金属卤化物钙钛矿等为例, 结合金刚石对顶砧高压装置以及原位高压表征技术, 重点探讨了它们在高压下的结构演化规律与光电性能调控机制, 并指出了这一新兴研究领域所面临的挑战和机遇, 以期为新型高性能功能材料的开发和实际应用有所启发.

English Abstract

    全文HTML

    1.   引　言

    • 2004 年, 英国物理学家 Novoselov等[1]利用机械剥离方法制备出了原子级厚度的石墨烯, 从此开启了探索二维材料的新纪元, 无论是在基础物性研究领域, 还是在电子设备、太阳能电池、光电探测器、传感器等产业化应用领域, 二维材料都得到了广泛关注和快速发展[2,3].

      二维材料是指由单层或少层原子、分子构成的晶体材料, 其特点是电子在垂直于平面方向上的运动受到强烈限制, 导致量子限域效应显著, 从而表现出与三维材料截然不同的电子结构和物理性质[4–6]. 二维材料层内原子是通过共价键或者离子键连接, 而层间则由范德瓦耳斯力结合而成, 这种独特的层状结构使其物理性质与层间电子相互作用密切相关. 此外, 在含有重元素的二维材料中, 自旋轨道耦合效应较为显著, 是调控其电子能带结构和自旋性质的关键因素. 因此, 对二维材料的结构和性能之间的关系进行深入研究, 实现二维材料结构与物性的可控调控, 对开发其潜在的商业化用途具有重要意义.

      在多样化的外场调控方法中, 压力工程是一种强有力的手段, 其能在不引入杂质或额外变量的前提下, 通过压缩原子间距、增强轨道重叠, 有效诱导材料的结构相变. 此外, 得益于过去数十年高压装置与高压原位探测技术的协同发展, 高压研究领域取得了显著进展. 众多同步辐射技术向高压研究的迁移应用, 对基础物理、化学、地球及材料科学产生了深远影响, 极大地拓展了人类探索量子物态和材料功能的前沿, 例如高压成功诱导了二维MoS2从半导体态到金属态的相变, 以及高压对层状黑磷能带结构和激子行为的精确调控[7]. 因此, 将高压实验技术与二维材料结合, 可以有效调控二维材料层间距及层内原子排列, 实现对二维材料光电性能的有效调制.

      本文总结了近年来利用压力工程对石墨烯、二维过渡金属二硫族化合物(transition metal dichalcogenides, TMDs)及二维金属卤化物钙钛矿等材料的结构和光电性能调控的最新研究进展, 深入分析关键科学问题, 并对未来发展进行展望, 以期为相关领域的研究者提供有益参考.

    2.   高压实验技术

    • 高压装置与高压测试手段的发展推动高压科学的发展. 在20世纪初, 高压技术刚刚起步, 英国物理学家Percy Williams Bridgman (高压物理学的先驱之一)设计了第一个对顶压砧, 该装置利用悬臂将两个由碳化钨制成的砧面压在一起. 20世纪50年代, 美国国家标准局的Alvin Van Valkenburg首次将已知最硬的材料—金刚石引入对顶砧装置中, 设计了原始的金刚石对顶砧(diamond anvil cell, DAC). 这种装置通过削平金刚石尖端并采用虎钳状设计, 能够将压力集中在样品上, 从而在微小的尺寸上产生极高的压力. 此后, 科学家们逐步改进了DAC的设计, DAC现在可以产生的压力已达到百 GPa 量级.

      随着DAC的问世与发展, 科学家们也逐步掌握和完善了压力测量技术、传压介质技术和金属垫片技术.

      压力测量—红宝石荧光法是一种广泛用于测量高压的技术, 尤其是在DAC中. 该方法依赖于微小的红宝石晶体发射的荧光波长随压力的偏移[8], 具有便捷且精度和灵敏度高、可测压力高的特点. 金刚石拉曼法是另一种用于测量压力的技术. 金刚石声子模式的拉曼位移随压力变化, 通常用于测量30 GPa至数百GPa的压力. 此外, 在使用红外光谱进行高压下物质的原位研究时, 可以用物质的红外光谱吸收峰进行压力的标定. 利用同步辐射X射线衍射, 通过测量样品的晶格常数变化(如金、铂等标定物质的状态方程), 可直接计算压力.

      传压介质—传压介质的作用是将施加的压力传递到样品上去. 实际研究中可以选用固态、液态或气态物质作为传压介质. 实验室通常采用较软的固态物质如 NaCl, KBr作为传压介质, 可以使样品达到近于静水压环境. 当实验需要良好的静水压条件时, 必须采用液态或气态物质作为传压介质. 例如采用甲醇-乙醇(4∶1)混合溶液作为传压介质, 其可以实现的最高静水压环境可达10 GPa. 若有条件进行气态物质的装样, 可以采用He, Ne, Ar等物质作为传压介质. 这些气体物质在数百GPa的压力下仍然具有较好的准静水压性质[9].

      金属垫片—金属垫片不仅可以密封样品, 还可以保护金刚石表面, 提高实验的安全性和稳定性. 用于金刚石压腔高温高压实验的垫片有许多种金属材料, 目前常用作为垫片的金属有301或304不锈钢片、铼片、铑片、铜片、钛片、铍铜片等. 垫片材料的选择需要考虑以下两个因素: 1) 垫片的金属, 进行极高压的实验时, 一般需要选用具有大弹性模量的金属作为垫片, 例如铼片、锇片等; 2) 实验研究的对象, 对于无水体系的高压实验, 可以采用不锈钢片作为垫片, 但若进行含水体系和温度高于250 ℃的实验时, 则需要选用硬度大的铼片.

      实验室通常运用金刚石对顶砧操作的过程如下: 采用DAC给置于两个砧面中间的密封垫片施压, 垫片会在金刚石周围形成环形隆起, 之后利用手工打孔或激光打孔技术在垫片压痕的中心处钻取圆孔作为样品腔, 然后将样品、传压介质以及红宝石装入样品腔中并将上金刚石砧面装配上, 即可进行原位高压检测. 虽然天然金刚石是一种超硬材料, 但由于其脆性极易发生断裂, 因此在使用DAC装置前应检查两个金刚石砧面的对准与垫片的正确安装, 并且在进行加压卸压的实验过程中, 均应缓慢进行, 避免砧面的损毁.

    3.   高压下二维材料的结构演化与性能调控

      3.1.   二维材料石墨烯在高压下的研究

    • 石墨烯是第一种已知的二维材料, 由单层碳原子以sp2杂化轨道组成, 呈六角形蜂巢晶格结构. 它是目前已知最薄材料之一, 其厚度比一根头发的直径小100万倍. 自石墨烯材料发现以来, 由于其引人注目的电学、力学、光学和化学性质, 它们已广泛应用于从电子学到医学的几乎所有领域, 为世界带来革命性的变化[10,11]. 近年来, 石墨烯在高压条件下的研究已成为材料科学和凝聚态物理领域的热点之一, 不仅深化了对二维材料基本物理化学性质的理解, 还为其在能源、电子、催化和复合材料等领域的应用提供了新的思路.

      • 3.1.1.   石墨烯在高压下的结构相变

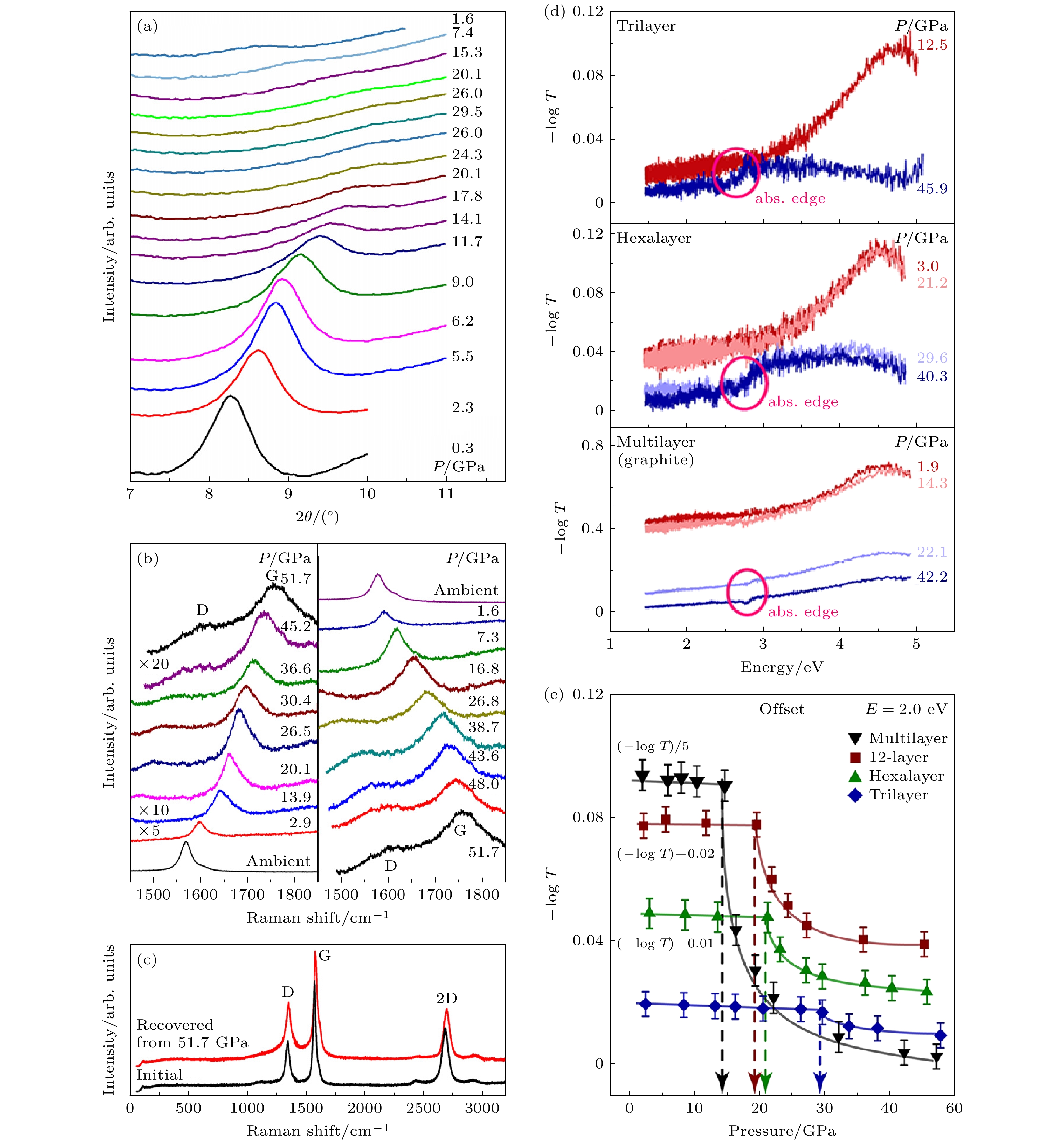
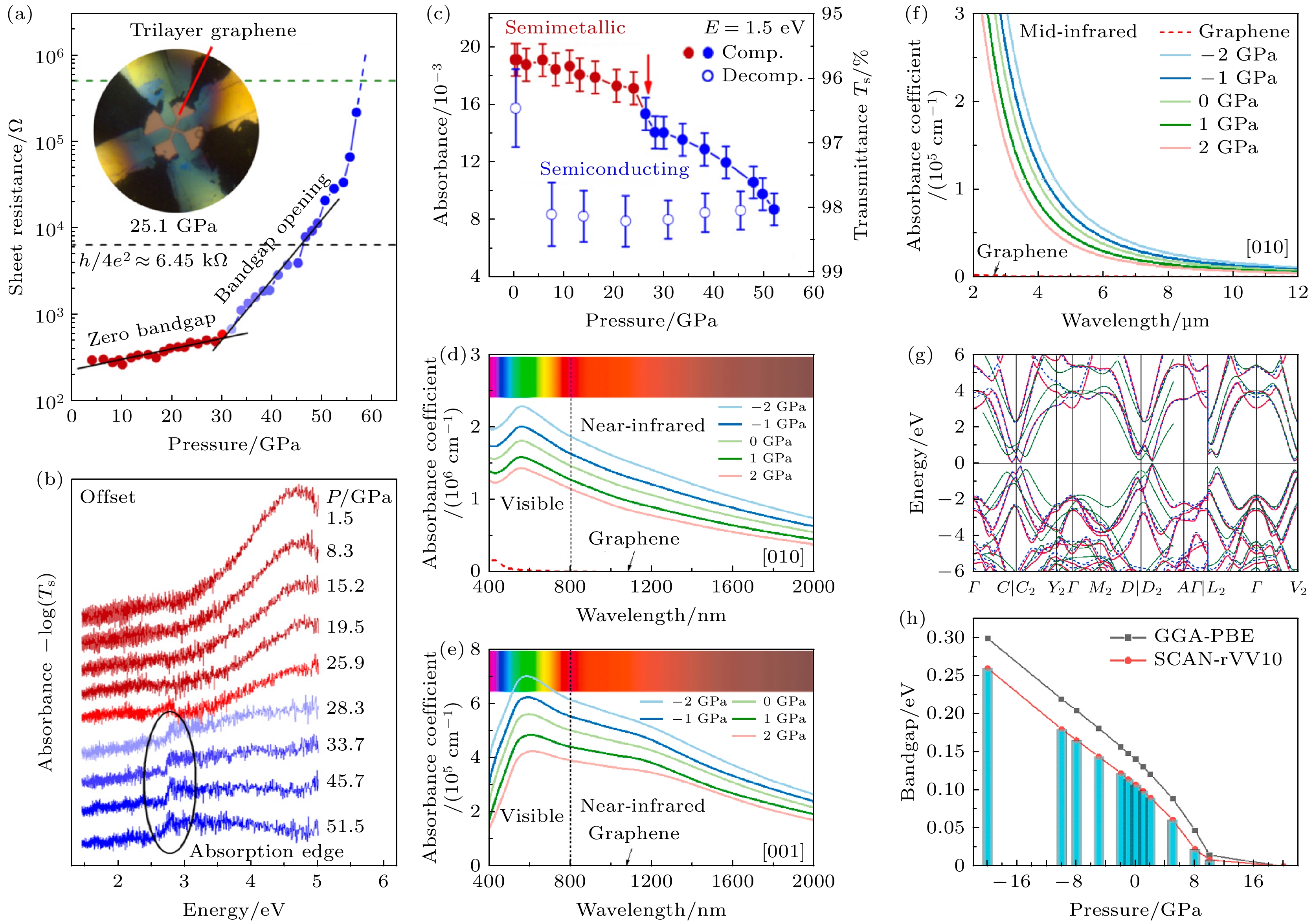
    • 在高压条件下, 石墨烯的碳原子层间距会发生变化, 进而引发其相关物理特性的转变. Clark等[12]利用X射线衍射(X-ray diffraction, XRD)和拉曼光谱技术研究了压力对薄层(约7层)石墨烯结构的影响. 如图1(a)所示, 随着压力的增大, 衍射峰逐渐向更高角度方向移动, 表明其晶格间距在逐渐减小. 图1(b)显示了薄层石墨烯的拉曼光谱, 由最强的G带、D带以及二次谐波2D带3个谱带组成. 石墨烯的主要拉曼活性模式是位于1582 cm–1的G带, 其源于具有$ {{{\mathrm{E}}}}_{2{{\mathrm{g}}}} $对称性的面内振动的sp2碳原子, 表征碳原子间的光学声子模. 当石墨烯层发生弯曲时, G模会软化, 因此, G带的光谱特征对应力状态、应变及晶格无序性高度敏感. D带则与结构无序性相关, 光谱中较弱的D带表明样品质量良好. 在高压实验中, 由于来自金刚石压砧的拉曼信号强烈重叠, 很难观察到D波段和2D波段在压力下的变化, 因此, 研究人员主要关注石墨烯纳米板G带的演变. 在压缩至52 GPa的过程中, D带、G带均向高波数方向移动, 这一现象表明压力增大使得石墨烯的电子能带结构发生变化. 此外, 图1(c)对比了原始样品和卸压后样品的拉曼光谱, 显示了石墨烯在压缩循环过程中的高度可逆性和稳定性.

      Ke等[13]利用红外(0.2—1.0 eV)和可见光-紫外(1.4—4.9 eV)吸收光谱研究了机械剥离的三层及更厚石墨烯中压力诱导的sp2-sp3金刚石化所需要的压强. 从图1(d)可观察到, 所有三至十二层石墨烯样品的吸光度在起始压力以上均呈现显著转变. 在环境条件下相变前, 所有石墨烯样品在4.6 eV光子能量处均观测到显著的非对称吸收峰, 该特征峰源于石墨烯带间跃迁的激子共振[14]. 此峰及其吸收光谱对压力不敏感, 直至金刚石化过程发生. 相变后, 所有样品在0.2—1.0 eV和1.4—2.5 eV能区的吸光度骤降并随压力增大逐渐趋近于零. 所有少层石墨烯样品在约2.8 eV处均出现弱吸收边, 随后在更高光子能量下吸收持续增强. 如图1(e)所示, 三、六及十二层石墨烯的金刚石化压力分别为在28.3, 20.6和19.4 GPa附近, 即对于三层及以上的石墨烯, 层数越多, 所需要的转变压强越小. 光学显微镜观测证实三层及以上石墨烯在相变压力以上透明度显著增大. 卸压过程中高压相可稳定保持至1.0 GPa. 光吸收测量表明, 机械剥离的三层、四层、六层、十二层及多层石墨烯在压缩下均经历系统的sp2-sp3金刚石化转变, 且高压相具有相似的电子结构.

      理论研究表明, 外场压力对魔角双层石墨烯(twisted bilayer graphene, tBLG)的电子结构具有显著调控作用. Carr等[15]通过第一性原理计算系统考察了高压条件下石墨烯中扭转角度与层间相互作用的演化规律. 基于层间距依赖的耦合理论框架, 研究人员精确计算了弛豫体系的能带结构, 发现原子弛豫效应对理解tBLG低能物理特性至关重要. 研究结果显示, 压力调控可有效诱导关联电子态的形成, 其典型特征是平带出现的临界扭转角随压力增大而单调递增. 理论分析表明, 增大扭转角会减小莫尔超晶格的特征尺寸, 这种几何约束效应可能通过强化层间耦合强度来促进关联电子行为, 包括超导转变温度(Tc)的提升. 尽管当前对关联机制的理解仍不完善, 难以实现定量预测, 但该研究提出了逆向研究思路: 通过系统测量压力依赖的关联行为, 有望为揭示tBLG及其衍生体系中非常规超导的微观机制提供新的研究途径.

      实验观测与理论计算均表明, 外部压力作为一种高效且可控的调控手段, 不仅可调节石墨烯层间耦合强度、显著改变其能带结构特征, 更能诱导关联电子行为, 甚至在特定临界条件下引发结构相变. 这些独特的压力效应使得石墨烯体系成为研究维度约束下量子现象的理想平台, 也为新型功能材料的理性设计提供了重要参考.

      • 3.1.2.   石墨烯在高压下光电性能的调控

    • 由于压力的调控, 材料可以缩短层间距, 并进一步形成共价键, 而非范德瓦耳斯相互作用. 对于典型的二维材料石墨烯, Ke等[16]在环境温度下研究了三层石墨烯电阻的压力响应(见图2(a)). 在30.1 GPa以下, 三层石墨烯的电阻随压力平稳变化. 当压力达到约33.0 GPa时, 电阻突然增大. 随着进一步压缩至59.0 GPa, 电阻急剧增大了超过3个数量级. 这一观察结果清晰地证实了带隙的打开. 为了精确追踪带隙的演化, 在1.4—4.9 eV的能量范围内测量了加压下三层石墨烯的可见-紫外透射光谱: 在28.3 GPa以下, 吸收光谱随压力增大未发生显著变化, 主要特征表现为在约4.6 eV处的激子吸收峰随压力增大出现小幅蓝移. 在28.3 GPa时, 通过1.5 eV辐射能量可检测到吸收率的显著变化, 如图2(b), (c)所示, 三层石墨烯的吸收率在初始阶段随压力平稳变化, 直至25.9 GPa. 在28.3 GPa时观察到吸收率的突然下降, 随后随着进一步压缩至51.5 GPa, 吸收率持续降低. 实验结果表明, 三层石墨烯中存在较大的本征带隙, 需要较宽的压力范围才能使半金属态的三层石墨烯完全转变为半导体态, 且高压能够将石墨烯的禁带打开至(2.5±0.3) eV. 在卸压过程中, 半导体相在压力降至几GPa时保持不变, 但在完全卸压后几乎恢复到原始状态, 即高压下石墨烯半金属-半导体的转变是可逆过程.

      Luo等[17]提出了一种新型原子级石墨烯超材料—垂直交叉石墨烯纳米片(VC-石墨烯), 与原始石墨烯的零带隙相比, VC-石墨烯表现出107 meV的带隙, 并利用压力工程, 获得了0—260 meV范围内的可调带隙, 使VC-石墨烯在基于半导体的现代电子器件中具有巨大潜力. 单层石墨烯用于光子和光电子应用的一个基本挑战是其单原子层对可见光和红外光的电磁波吸收有限. 计算得到的不同压力下VC-石墨烯与单层石墨烯的吸收系数对比. 如图2(d)—(f)所示, 与单层石墨烯相比, 在VC-石墨烯中观察到了对可见光和红外光的超高吸收系数, 且其宽吸收带宽覆盖了现有任何单一商用光电探测器或成像传感器的响应范围[18].

      VC-石墨烯的电子特性如图2(g), (h)所示. 图2(g)中VC-石墨烯的能带结构显示两个狄拉克锥穿过费米能级. 与零带隙的石墨烯相比, VC-石墨烯呈现出一个打开的带隙. 在零压力下, 使用常规GGA-PBE泛函计算带隙为140 meV. 考虑范德瓦耳斯相互作用后, 使用元GGA SCAN-rvv10计算得到的带隙为107 meV. 该结果通过了DFTB+计算的100 meV和范数守恒方法计算的110 meV进一步验证. 通过压力工程, 可实现对VC-石墨烯0—260 meV的可调带隙(图2(h)), 使VC-石墨烯成为一个极具前景的半导体平台, 有望用于开发具有宽带宽和增强光学响应度的现代光子与光电子器件. 高压实验技术和理论模拟方法的不断进步, 将推动石墨烯高压研究不断取得重要突破, 引领材料科学和凝聚态物理的前沿发展.

      • 3.2.   二维材料TMDs在高压下的研究

    • 2005年, 继石墨烯机械剥离法的突破性发现之后, Novoselov等[19]利用同样的剥离技术得到了TMDs中的代表性材料—二硫化钼(MoS2)单层. 2010 年, Mak等[20,21]证明了MoS2单层具有直接带隙和强的光致发光(photoluminescence, PL)现象, 自此TMDs 的研究热潮正式开启.

      TMDs 的晶胞结构通常具有六边形或菱形对称性, 其中金属原子呈现八面体或三角棱柱配位[22]. 其化学式为MX2, M代表过渡金属元素, X代表硫族元素. TMDs家族中的一些材料在红外和可见光谱区域具有直接带隙, 并表现出较强的光与物质相互作用, 非常适用于光学和光电子学中的各种应用[23]. 研究高压对TMDs结构和物理特性的调控作用, 对深入理解这类材料在极端条件下的力学行为以及开发新型功能器件具有重要的科学意义和应用价值.

      • 3.2.1.   二维材料TMDs在高压下的结构相变

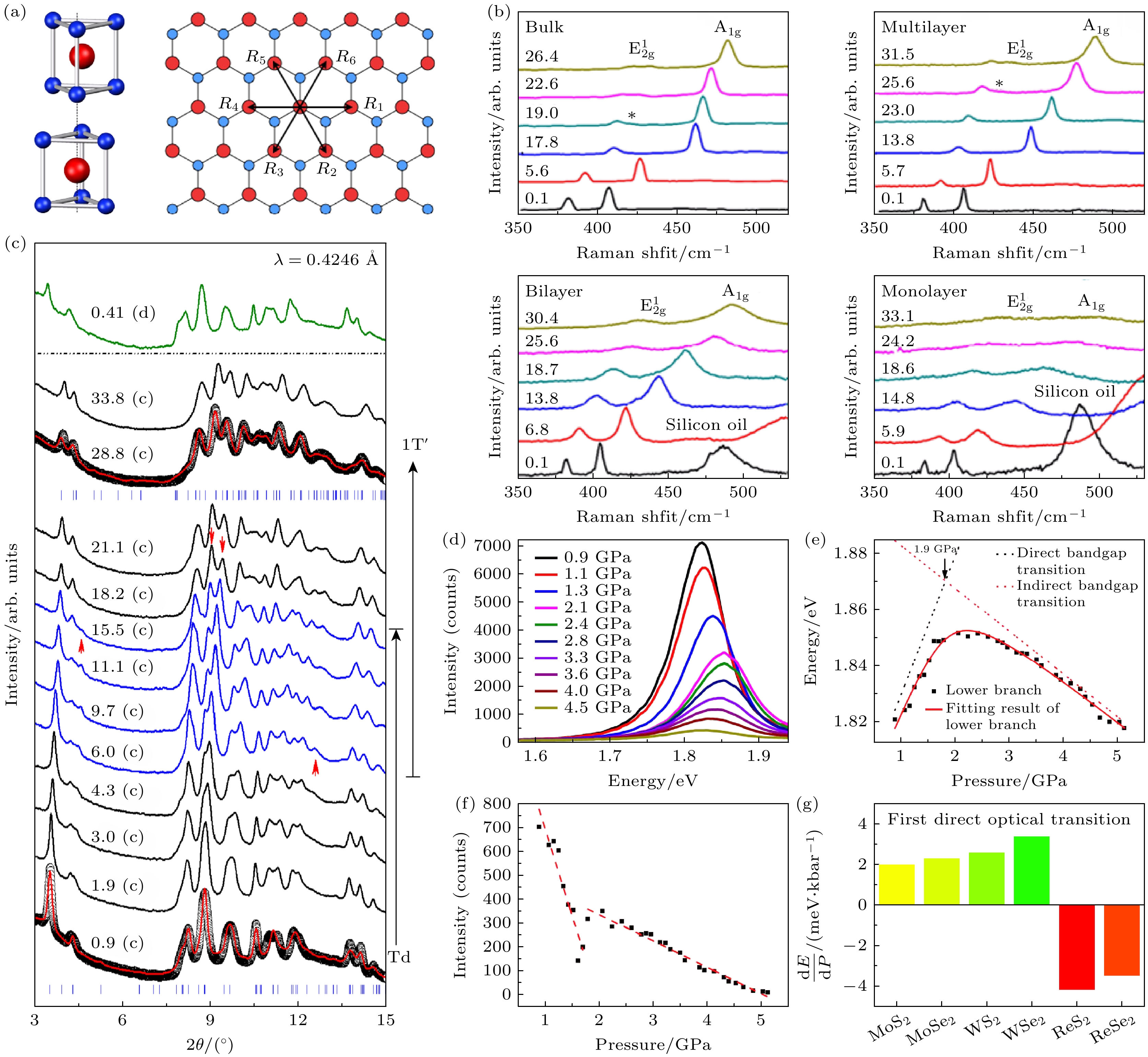
    • Cheng等[24]报道了层状MoS2的结构相变压力具有厚度依赖性的规律. 图3(b)分别展示了室温条件下单层、双层、多层(约200层)及块体MoS2的压力依赖性拉曼光谱. 在块体MoS2中, 随着压力增至17.8 GPa, 拉曼光谱始终保持双峰构型, 但由于静水压下原子间相互作用增强, $ {\mathrm{A}}_{1\mathrm{g}} $和$ {\mathrm{E}}_{2\mathrm{g}}^{1} $模式均向高频方向移动. 当压力继续升高, $ {\mathrm{E}}_{2\mathrm{g}}^{1} $会劈裂为双峰并在419 cm–1处出现新峰, 这标志着2Hc相到2Ha相的多晶型结构相变[25–28]. MoS2具有各向异性压缩特性: 静水压下层间距缩减幅 度显著大于层内间距, 其初始压缩主要沿层间法向进行. 进一步压缩会引发2Hc相到2Ha相变以适应层间距减小, 同时伴随类似半导体-金属转变 的带隙闭合[25,29]. 多层MoS2(约200层)虽呈现与 块体相似的相变趋势, 但需达到更高转变压力(约25.6 GPa)才出现$ {\mathrm{E}}_{2\mathrm{g}}^{1} $模式的劈裂. 双层MoS2在加压过程中虽展现相同的峰位移动趋势, 但在所测量的最高压力30.4 GPa下仍未出现新峰或峰劈裂, 表明其转变压力更高, 理论预测双层体系相变压力约36.0 GPa[30]. 而单层MoS2在30 GPa以下无相变发生, 故在30.4 GPa高压下也未观察到新峰或峰劈裂.

      本实验表明薄层材料中层间耦合强度减弱, 其相变激活压力由受压下的层间相互作用决定. 一般而言, 纳米材料表面能高于块体材料, 且材料中的尺寸效应会显著提升相变势垒, 改变相变压力. 此外, 二维纳米体系中尺寸效应还会调控层间相互作用强度, 因此2Hc到2Ha的相变压力具有显著厚度依赖性, 并且可以通过操纵膜厚度来调制层间排斥的程度.

      Zhou等[31]报道了与MoS2结构类似的二碲化钨(WTe2)在高压下的结构演化. 环境条件下, WTe2结晶为正交晶系, 空间群为Pnm21. 钨原子在八面体配位环境中与碲原子成键. 其晶胞包含两层Te-W-Te片层结构, 其中一层相对于另一层旋转180°, 这种堆垛构型被称为Td-WTe2. 图3(c)中原位高压XRD图谱所示, 随着压力增大, 所有衍射峰均向高角度方向移动, 表明Td-WTe2晶格发生收缩. 当压力达到6.0 GPa时, 在约12.5°处出现新的衍射峰. 至18.2 GPa时, 除约4.6°处的衍射峰完全消失外, 部分衍射峰的相对强度也发生了显著变化. 进一步研究发现, 低压相与高压相可分别用单一Td相和1T' 相(空间群P21/m)精确拟合. 在6.0—15.5 GPa压力区间, XRD图谱呈现高低压两相共存特征. 当压力降至0.41 GPa时, XRD图谱恢复至初始结构, 证实该压力驱动相变具有可逆性.

      在TMDs家族中, 二硫化铼(ReS2)因其在常压下形成的独特低对称性畸变晶体结构而占据特殊地位. 该材料层间相互作用较弱, 因此其体相性质与单层相似. Zhou等[32]采用第一性原理计算, 系统研究了单层ReS2的高压相变行为, 并预测出两种新型高压相: 在较低的压强下, ReS2会从1T相转变为1T' 相, 在90 GPa时转变为具有I41/amd对称性的超导相. Yan等[33]结合高压拉曼光谱测量和第一性原理计算探究了多层ReS2的高压结构相变, 揭示了多层ReS2在压缩条件下的晶格演化, 并识别出两个关键的结构相变阶段: 在1.1—8.0 GPa范围内, 压力主要诱导ReS2层内发生晶格畸变, 改变Re—S键合方式; 8.0 GPa后, 层间耦合增强, 伴随晶格对称性的改变, 相变开始; 在19.6 GPa时相变完成, 体系进入稳定的高压相, 并维持至33.7 GPa. ReS2在高压下优先发生层内结构相变而非层间结构相变的特殊现象, 与其独特的层间相互作用机制和耦合强度密切相关. 综上所述, 二维过渡金属二硫族化合物在高压下的结构相变行为表现出显著的厚度依赖性和材料特异性, 其相变机制主要受层间相互作用、晶格对称性和电子结构调控的影响.

      • 3.2.2.   高压对TMDs的能带调控

    • 在高压条件下, 二维TMDs材料的晶格常数和层间耦合作用会发生显著变化, 从而对其电子能带结构产生显著的调控作用. Fu等[34]通过研究单层MoS2的PL光谱在高压下的演化, 发现了MoS2由直接带隙向间接带隙的转变过程. 已知单层MoS2的能带结构在K(K')点处具有直接带隙, 而次低导带极小值位于Λ点—该点可能与K点的价带顶发生相互作用, 从而形成间接光学带隙跃迁. Fu等[34]对单层MoS2进行了室温下的原位高压PL光谱的测量, 实验数据如图3(d)—(f)所示, 清晰地观测到了直接-间接带隙的转变过程. 随着压力增大, 直接跃迁发光峰以49.4 meV/GPa的速率移动, 而间接跃迁发光峰则以–15.3 meV/GPa的速率移动. 实验在1.9 GPa压力下观测到临界转变点, 该结果与第一性原理计算结果吻合, 证实了该转变源于导带中K-Λ点的能带交叉现象. 研究表明, 单层WSe2在高压条件下同样存在直接带隙向间接带隙的转变特征. Gong等[35]系统研究了单层二硒化钨(WSe2)在压力作用下的电子能带结构演变. 随着压力增大, 直接带隙Κ→K' 带间跃迁能量持续增大, 而间接带隙Λ→Κ带间跃迁能量逐渐减小, 导致材料在3.8 GPa时发生显著的直接-间接带隙转变.

      ReX2体系(X = S, Se)因其降低的晶体对称性导致了复杂的电子能带结构, 从而展现出不同于其他TMDs材料的独特性质. Oliva等[36]通过实验与理论相结合的方法, 系统研究了高压静水压下ReS2和ReSe2的电子能带结构. 图3(g)实验观测表明, ReX2的首个直接光学跃迁表现出显著的负压力系数, 这与MoS2, WS2等传统TMDs的正压力系数形成鲜明对比. 深入分析表明, ReX2的特殊行为源于两个关键因素: 1)晶体结构的各向异性导致层间耦合减弱, 高压XRD和低频拉曼谱证实其范德瓦耳斯相互作用强度显著低于MoS2[37–39]; 2)铼的d电子构型差异, Re相比第6族金属多一个价电子, 使得Re-$ {{\mathrm{d}}}_{{z}^{2}} $轨道在带边态中占据主导地位. 轨道分析表明, 面外取向的Re-$ {{\mathrm{d}}}_{{z}^{2}} $和X-pz轨道对价带顶的能级演化具有决定性影响.

      综上, 高压条件下TMDs的电子能带结构演化不仅受晶格压缩和层间耦合作用的调控, 还与材料的晶体对称性、轨道成分及电子构型密切相关. 这些研究为理解TMDs的能带工程及高压物性调控提供了重要理论基础, 同时也为新型光电器件和量子材料的设计开辟了新思路.

      • 3.2.3.   高压对TMDs电学性能的调控

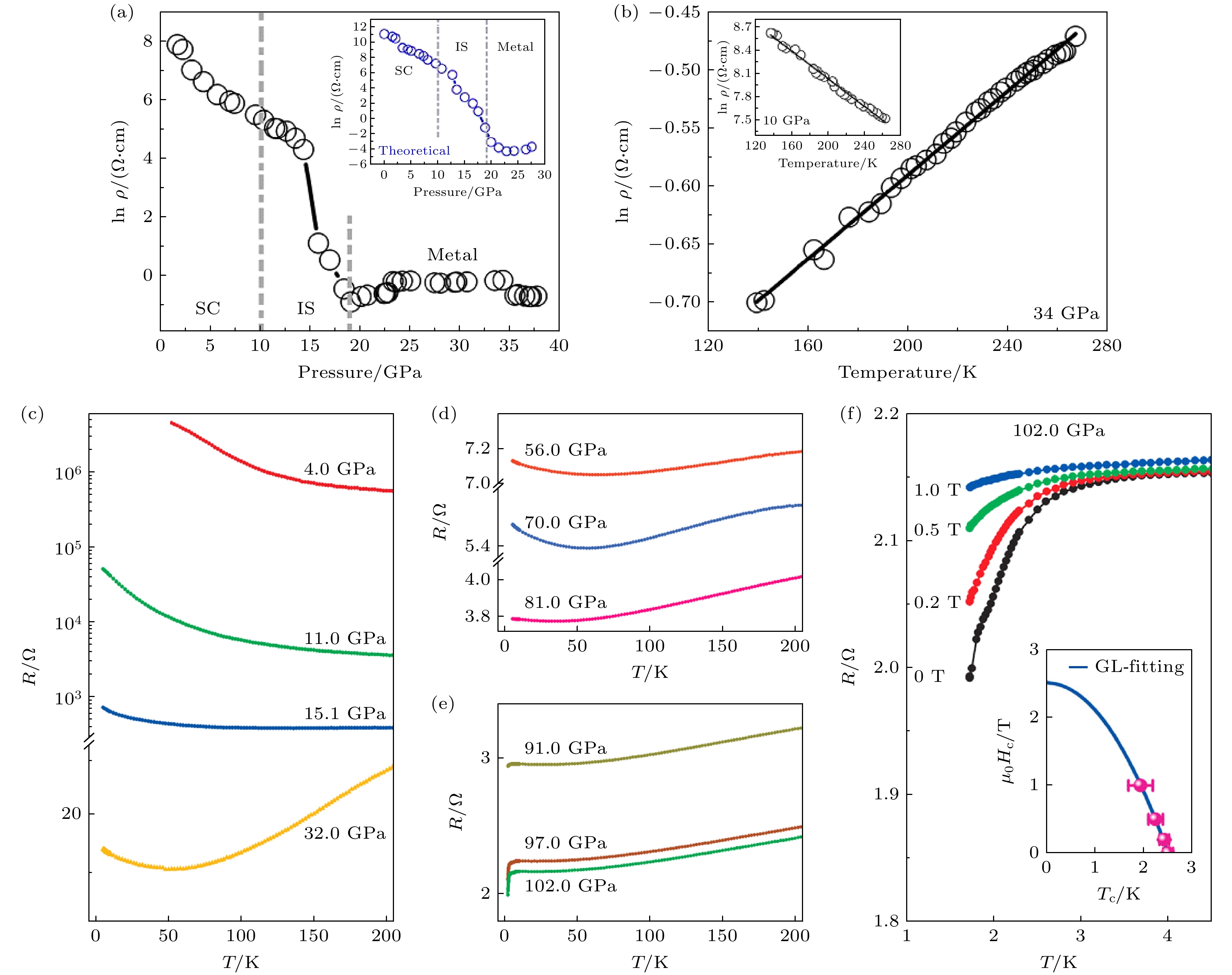
    • 在高压条件下, TMDs材料会经历显著的层间距离压缩和晶格结构重构, 这些结构变化会影响其电子能带结构, 进而诱导出金属化转变和超导等新颖量子现象. Nayak等[40]通过实验测试与理论计算相结合的方法证明了MoS2在高压下会发生金属化转变. 实验观测表明, 在室温条件下, MoS2的电阻率(ρ)随静水压力的增大(最高至10 GPa)呈现逐渐降低的趋势. 这一现象可通过压力激活载流子输运模型予以解释, 且理论预测与实验数据高度吻合. 在10—19 GPa的压力区间内, 电阻率骤降约3个数量级(图4(a)), 表明材料可能经历显著的电子结构转变. 进一步的第一性原理计算证实, 多层MoS2在约20 GPa附近发生半导体-金属相变(图4(a)插图), 其本质归因于压力诱导的能隙闭合, 从而导致电子态的重构.

      为深入理解相变前后的电学行为, 研究人员进行了原位变温电阻率测量. 根据经典固体物理理论, 半导体因热激活载流子导致电阻率随温度(T)升高而降低, 而金属导体因电子-声子散射增强呈现相反趋势. 实验数据与这一理论预期高度一致: 在10 GPa下, MoS2的电阻率呈现负温度系数 (图4(b)插图), 而在34 GPa下则表现出正温度系数(图4(b)). 此外, 电阻率-温度依赖关系在10 GPa下符合指数衰减规律, 而在34 GPa下则遵循线性关系, 分别对应半导体和金属的典型特征. 该实验结果得到了玻尔兹曼输运理论(BTT)计算的进一步支持, 这不仅验证了实验观测的可靠性, 更为理解MoS2在高压条件下的电子态演化机制提供了坚实的理论支撑.

      Zhou等[32]通过系统的高压输运测量, 揭示了ReS2从半导体到金属态再到超导态的连续相变过程, 如图4(c)—(e)所示. 在低压区间(<11.0 GPa), 材料保持着典型的半导体特性, 其电阻行为与常压状态基本一致. 随着压力增至11.0—15.1 GPa区间, 电阻骤降两个数量级, 并在15.1 GPa时于100 K以上温区出现显著的非半导体行为, 这一现象被归因于压力诱导的晶格结构重构. 值得注意的是, 在32.0—70.0 GPa的压力区域, 材料表现出独特的电子态分离特征: 高温区呈现金属导电行为, 而低温区仍维持半导体特性, 这种双稳态行为暗示了ReS2电子结构的复杂演化机制. 理论计算与实验观测共同证实, 当压力超过81.0 GPa时, 半导体特征被完全抑制, 标志着金属化转变完成. 在高压区间(>90 GPa), 电阻曲线在2.5 K附近呈现明显的下降趋势, 且该特征随压力增至102.0 GPa持续增强. 外加磁场的电阻测量(图4(f))证实了其超导转变: 在102.0 GPa下, c轴磁场导致超导转变温度随磁场增强向低温移动且幅度减弱. Ginzburg-Landau理论分析得出了2.509 T的上临界磁场值(图4(f)插图), 确证了压力诱导超导态. 虽然非静水压条件导致的压力梯度阻碍了零电阻观测, 但卸压实验显示超导态可保持至55.0 GPa, 展现出优异的压力记忆效应, 为压力调控超导研究提供了新方向.

      高压通过压缩晶格间距和增强层间耦合, 可有效调控TMDs的电子能带结构, 诱导半导体-金属甚至超导态的转变, 这种调控不依赖化学掺杂, 避免了杂质引入对材料性能的影响, 为研究本征电子输运机制提供了理想平台.

      • 3.3.   二维金属卤化物钙钛矿在高压下的研究

    • 近年来, 二维(2D)金属卤化物钙钛矿作为一类新兴的半导体材料, 因其独特的晶体结构和优越的物理性质, 在太阳能电池[41]、发光二极管[42]、光电探测器[43]等领域引起了广泛关注. 与传统的三维(3D)钙钛矿相比, 二维钙钛矿通过引入有机阳离子层, 形成了无机八面体层与有机层交替排列的结构, 不仅显著提高了材料的环境稳定性, 还赋予了其丰富的量子限域效应和可设计的电子性质. 为充分发挥二维钙钛矿在光伏领域的潜力, 对其结构与性能之间的关系进行深入研究显得尤为重要. 高压技术可以通过调控材料的晶格结构, 揭示其内在物理机制, 并为开发新型功能材料提供指导.

      • 3.3.1.   二维钙钛矿的结构

    • 二维钙钛矿常见的结构有R-P(Ruddleseden-Popper)型和D-J(Dion-Jacobson)型[44]. R-P相的结构通式为$ {\text{A}}_{2}{\text{A}}_{n-1}^{\prime}{\text{B}}_{n}{\text{X}}_{3 n+1} $(n = 1, 2, 3, …), 其中A是大的单价有机阳离子, 例如: 丁基胺(BA+)、苯甲胺(PEA+)等, A' 通常为甲基胺(MA+)或甲酰胺(FA+)等单价阳离子, B位是二价金属阳离子, 例如Pb2+或Sn2+. 在R-P相的结构中, 相邻的无机层之间由A位有机阳离子的尾部通过范德瓦耳斯力进行连接, 每个阳离子只能和一个无机层形成化学键, 无机层之间交错排列.

      D-J相的结构通式是$ {\text{PA}}_{n-1}^{\prime}{\text{P}}_{n}{\text{X}}_{3 n+1} $ (n = 1, 2, 3, …), 与R-P相不同的是P为二价的有机阳离 子, 例如1, 4丁二胺(BDA2+). 在D-J相的结构中, 每个二价的有机阳离子可以同时连接两个相 邻的无机层, 从而能够使相邻的无机层能够精确 地垂直排列. 这种连接方法有效地增强了相互作用力并且减少相邻无机层之间的距离, 并促进层间电荷传输.

      在以上介绍的两种二维钙钛矿中, 无机层数n = 1的结构被称为纯二维钙钛矿, n = 2—5的结构被称为准二维钙钛矿, n = ∞则表示三维钙钛矿. 二维钙钛矿中无机层和有机层交替排列, 形成天然的多重量子阱结构. 无机层作为量子阱, 具有较窄的带隙, 而有机层作为势垒, 具有较宽的带隙. 这种周期性结构导致载流子在垂直于层状结构的方向上受到强烈的量子限域效应, 从而表现出独特的电子和光学性质.

      • 3.3.2.   二维钙钛矿在高压下的结构演化与带隙调控

    • 二维钙钛矿材料因其独特的多重量子阱结构, 展现出显著的二维晶体特性以及面外的量子和介电限制效应, 这种结构特性使其在外部压力调控下能够实现能带结构、晶格对称性以及光学性质的显著变化, 从而为探索压力诱导的新型物理现象和功能特性提供了一个极具潜力的研究平台. Liu等[45]通过实验和理论计算相结合的方法研究了二维钙钛矿(PEA)2PbI4 (PEA = 苯乙胺)在高压下的系列性质, 证明了长链PEA分子和2D构型在调制晶格和能带结构中起到关键作用. 该材料在 0—3.5 GPa下显示出320 meV的带隙可调谐性以及恒定的量子产率, 这比传统的半导体材料具有更大的优势.

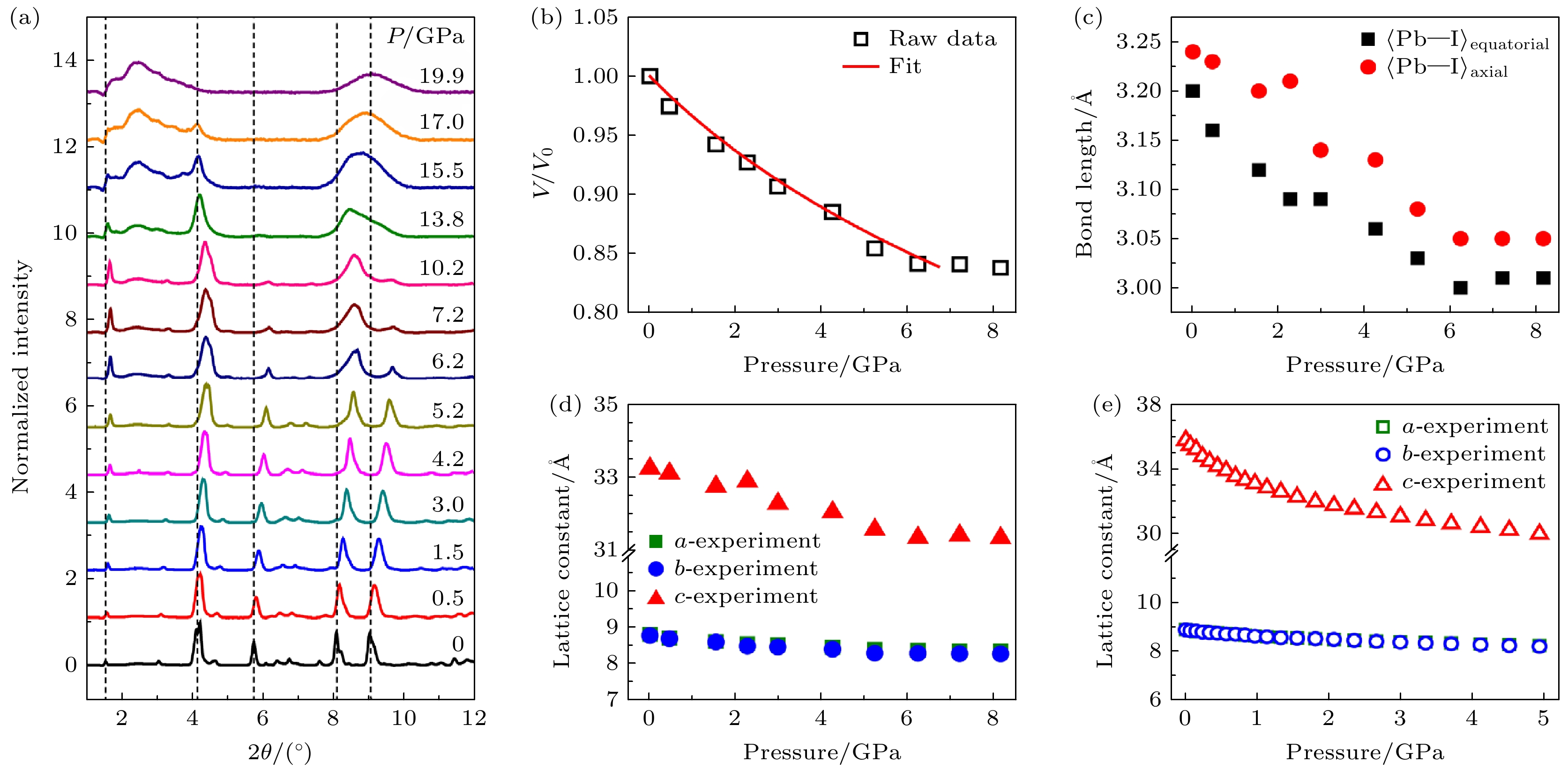
      通过图5(a)所示(PEA)2PbI4同步辐射XRD图像观察到, 在0—20 GPa静水压力作用下, XRD峰的衍射角2θ随着压力的增大而增大, 这是晶体压缩的标志. 在10.2 GPa之后, 衍射峰均明显变宽, 表明在高压下晶格结构变得无序, 图5(b)显示出了以V/V0的形式减小的晶胞体积, 依据Birch-Murnaghan方程拟合, 获得(PEA)2PbI4的体积模量B0约为26.8 GPa. 三维材料MAPbI3和FAPbI3也经历了类似的体积减小, (PEA)2PbI4的体积模量明显大于MAPbI3的13.6 GPa[46]和FAPbI3的11.0 GPa[47,48], 材料的可压缩性与其体积模量成 反比, 即(PEA)2PbI4的可压缩性比3D钙钛矿的可压缩性小得多, 2D 钙钛矿 (PEA)2PbI4更硬且更耐压缩, 这种刚性行为源于(PEA)2PbI4材料中[PbI6]4–八面体独特的晶格变化. 高压下(PEA)2PbI4的晶体结构变化具有高度各向异性, 主要表现为沿c 轴(垂直于[PbI6]4–八面体层)的压缩, 而a轴和b轴的压缩较小(图5(d), (e)). 这种各向异性压缩使得晶体在高压下保持结构稳定, 避免了相变和[PbI6]4–八面体的扭曲. 此外, 有机层在高压下起到类似“弹簧层”的作用, 吸收大部分压缩能量, 保护无机[PbI6]4–八面体层不受扭曲和旋转的影响, 从而保持了Pb—I键的稳定性.

      高压下二维钙钛矿(PEA)2PbI4独特的各向异性使其在调控其带隙时具有恒定的光学性能. 众所周知, 化学键的扭曲和弯曲严重破坏了半导体中原始晶体场, 扰乱了原子之间的波函数重叠, 抑制了带边跃迁的效率[49–51]. 然而, (PEA)2PbI4完美地保留了[PbI6]4–八面体的几何形状从而保持 Pb─I键的稳定性和质量. 因此, 在压缩过程中, 可以最大程度地保持带边跃迁的效率. 在0—4 GPa的压力范围内, (PEA)2PbI4在高压下的光学性能表现出可逆性, 带隙红移可达320 meV, 这主要源于量子限制效应的减弱: 有机层厚度快速减小导致势垒降低, 电子(空穴)波函数更容易穿透势垒. Pb的p轨道和I的s轨道的特殊能带排列也导致了与常规半导体不同的带隙红移行为. 这种在高压下的结构稳定性和光学性能的可逆性使其在高压光电应用中具有潜在优势.

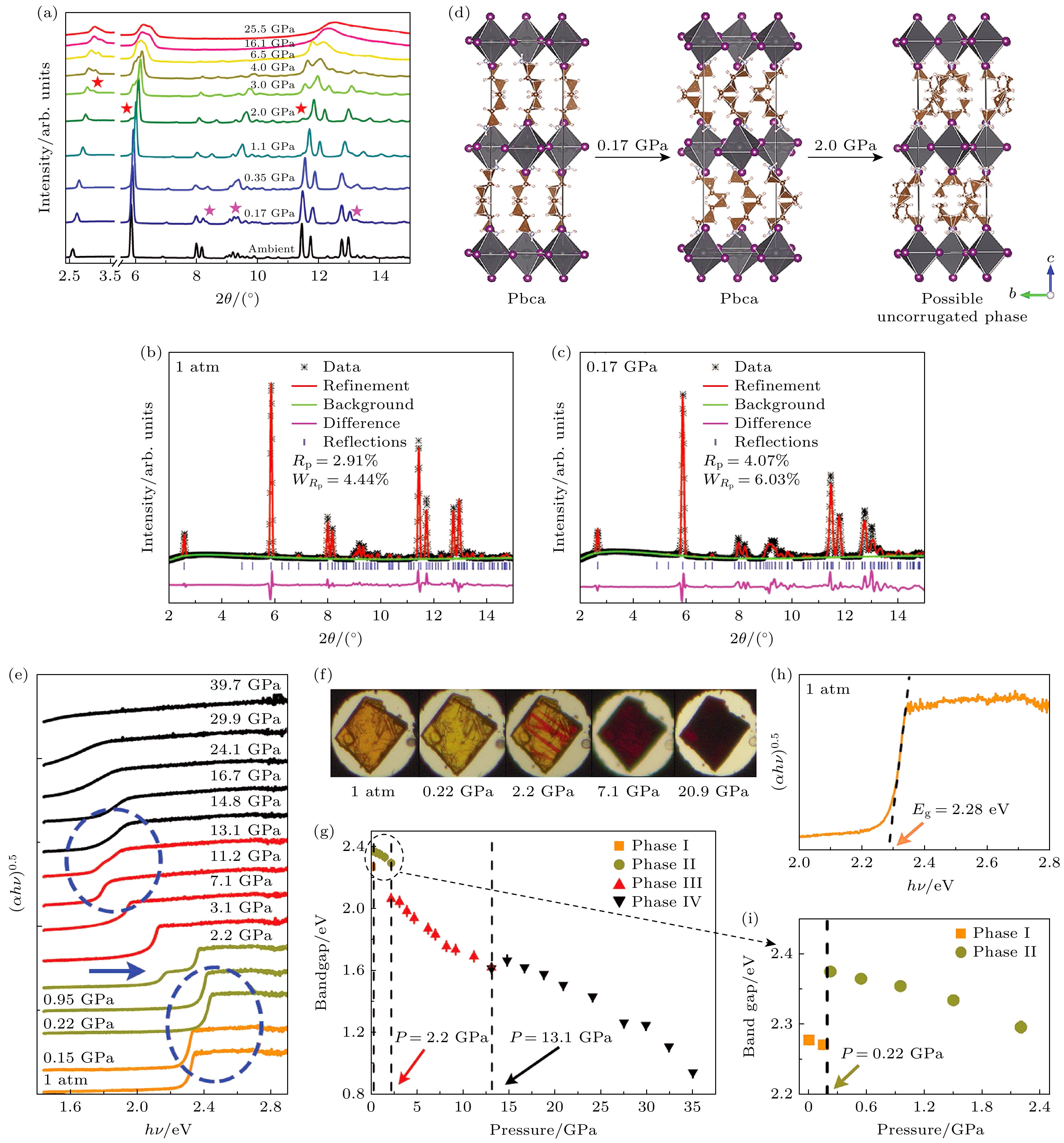
      对于不同的二维钙钛矿, 因存在不同长度和构型的有机配体, 这也会影响高压下的结构和电子演变. Yuan等[52]发现高压下(BA)2PbI4 (BA = 丁基胺)表现出显著带隙减小、载流子寿命延长的效应, 这一现象归因于高压引起的晶格压缩和电子结构变化, 导致能带结构的重新排列和载流子动力学的改善. 该团队在压缩至25.5 GPa的过程中对(BA)2PbI4进行了XRD测量如图6(a)—(d)所示. 在常压条件下, (BA)2PbI4呈现K2NiF4型结构, [PbI6] 基团形成波纹状的无机层, 两层交错的BA+嵌入无机层之间. 有机层与无机层通过c方向的N—H···I氢键相互作用. 在0.17 GPa时, 观察到若干新的衍射环, 并推断该压力下发生同构相变, 新相对应于常压下的低温Pbca相. 首次相变后, [PbI6] 基团沿a方向旋转, 使得无机层更加交错排列. 有机阳离子保持其初始构型但在相变后重新排列, 这种重排导致层间距减小. 第二次相变发生在2 GPa附近, 出现3个新的衍射峰, 部分样品在2.0 GPa后发生变化, 推测(BA)2PbI4转变为P21/a相. 与类似材料(C2H5NH3)2CuCl4的比较表明[53], (BA)2PbI4在2 GPa时转变为P21/a相是合理的, 但是实验结果与吸收测量结果存在冲突, 表明(BA)2PbI4在2.0 GPa附近可能转变为倾斜较小的相. 在6.5 GPa以上衍射环变弱且变宽, 部分弱峰消失, 表明有机层无序度增大. 在更高压力下, 仅剩5个宽峰, 表明(BA)2PbI4发生非晶化.

      压力诱导的晶体结构变化通常会导致电子结构的改变, 进而影响材料的带隙. 在常压下, (BA)2 PbI4带隙为2.28 eV, 远大于Shockle-Queisser极限(≈1.33 eV). Yuan等[52]对(BA)2PbI4进行了如 图6(e)所示从环境条件到大约40 GPa的紫外-可见吸收测量, 以探究结构变化对带隙的影响. 在0.22 GPa时, 带隙突然跃升至2.37 eV, 这源自于[PbI6]4–八面体倾斜增大. 在2.2 GPa时, 出现新的吸收边, 对应带隙为2.06 eV, 在XRD中发现该压力下[PbI6]4–八面体倾斜减小, 样品发生了第二次相变, 带隙急剧减小. 在13.1 GPa后, 压力导致的Pb-I键长缩短, 带隙继续随压力增大而减小. 在27.5 GPa时, 带隙降至1.25 eV, 接近Shockle-Queisser理论中的理想带隙, 表明此时(BA)2PbI4可能表现出优异的光伏性能.

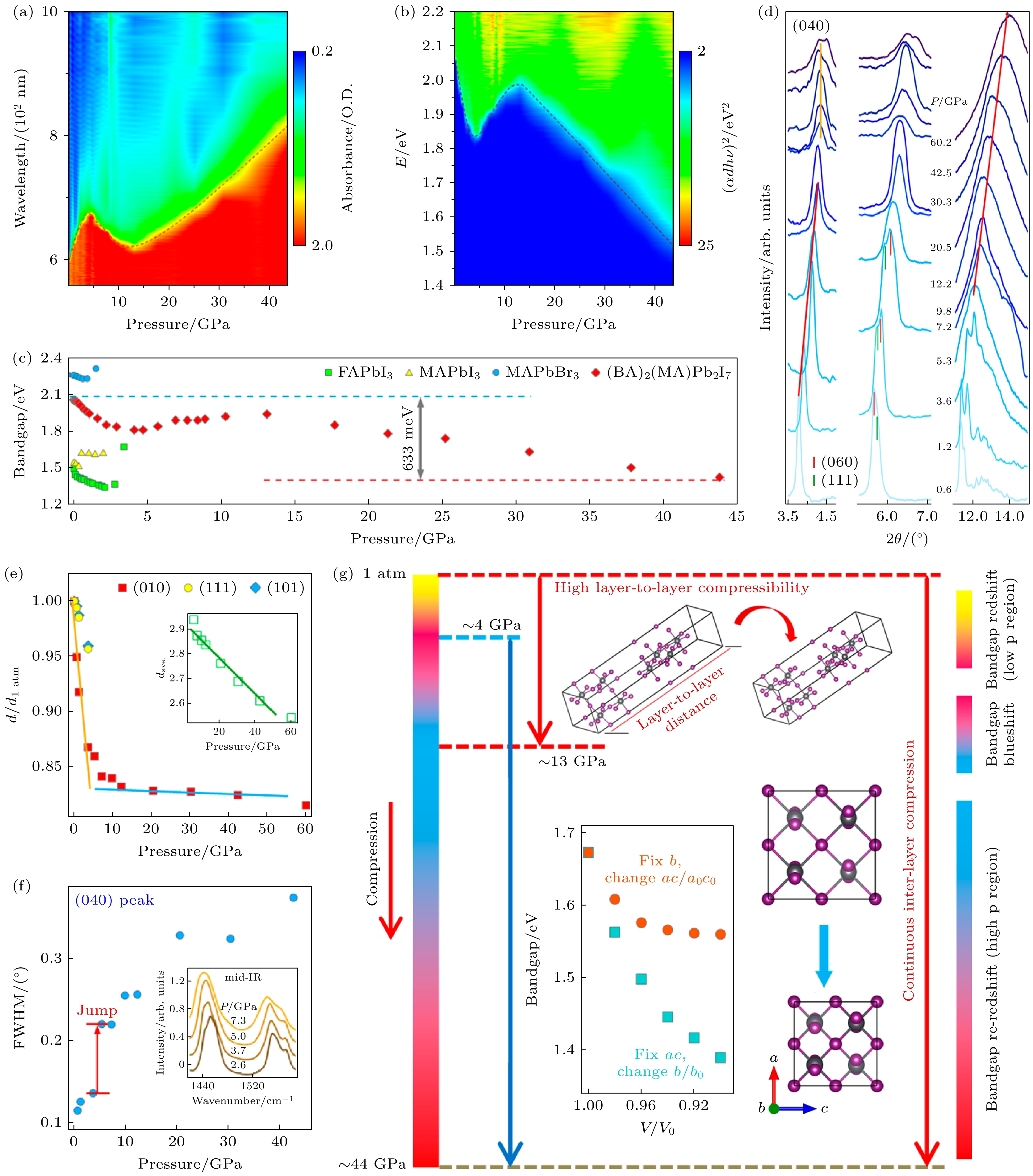
      Liu等[54]报道了R-P型的准二维钙钛矿(BA)2 (MA)Pb2I7 (n = 2)在高压下的结构和光电性质变化, 发现该材料在压缩过程中表现出独特的双层压缩和层间压缩两阶段行为, 并伴随着原子畸变. 如图7(a), (b)所示, 在4 GPa以下(BA)2(MA)Pb2I7带隙呈现红移, 4—13 GPa区间转为蓝移. 这种低压区“蓝移-红移”转变现象普遍存在于杂化钙钛矿中, 其物理根源在于原子畸变[47,55]. 值得注意的是, (BA)2(MA)Pb2I7在13 GPa处观测到三维钙钛矿中未曾出现的二次不连续性(图7(c)), 该突变触发高压区“再次红移”, 对太阳光谱吸收优化具有重要意义.

      为探究(BA)2(MA)Pb2I7带隙“再红移“的结构起源, 同步辐射高压XRD实验拓展至60 GPa(图7(d)). XRD图谱中(040)/(111)布拉格峰表明, (BA)2(MA)Pb2I7的晶面间距演变呈现显著各向异性压缩: 12.2 GPa前体积塌缩主要由b轴缩短主导, 具体表现为(040)衍射峰晶面间距的减小(图7(e)), 对应有机阳离子占据的层间距减小, 此后b轴抗压性显著增强, 该现象表明高压区体积塌缩主要源于层内压缩. 同时, (040)衍射峰的半峰宽(full width at half maximum, FWHM)在3.6—5.3 GPa间出现跃变式展宽(图7(f)), 证实了压力诱导的原子畸变.

      (BA)2(MA)Pb2I7在低压下, 层间压缩占据主导地位, 而在高压下, 层内压缩占主导. 这种结构演化可以从以下事实理解: 层间插入的有机部分较软, 而无机亚晶格较难压缩, 并且与带隙变化密切相关. 随着压力增大, Pb的s轨道和I的p轨道的耦合增强, 推高了价带顶部, 同时导带底部主要由Pb p轨道的非键局域态主导, 对键长或压力不敏感, 从而导致带隙变窄. 因此, 4 GPa以下的带隙红移和13 GPa后的再次红移可以分别理解为层间和层内压缩的结果. 4—13 GPa之间的蓝移可以解释为原子畸变降低了晶格对称性, 减少了Pb的s和I的p轨道的耦合.

      此外, 该项研究还发现材料在卸压后仍能部分保留高压诱导的改性特性: 与初始时刻相比, 具有更窄的带隙(1.93 eV), 光致发光增强了150%, 并且具有良好的环境稳定性. 这些发现表明压力工程可以作为一种有效的手段来调控二维钙钛矿的光电性质, 为开发高性能太阳能吸收材料提供了新的思路.

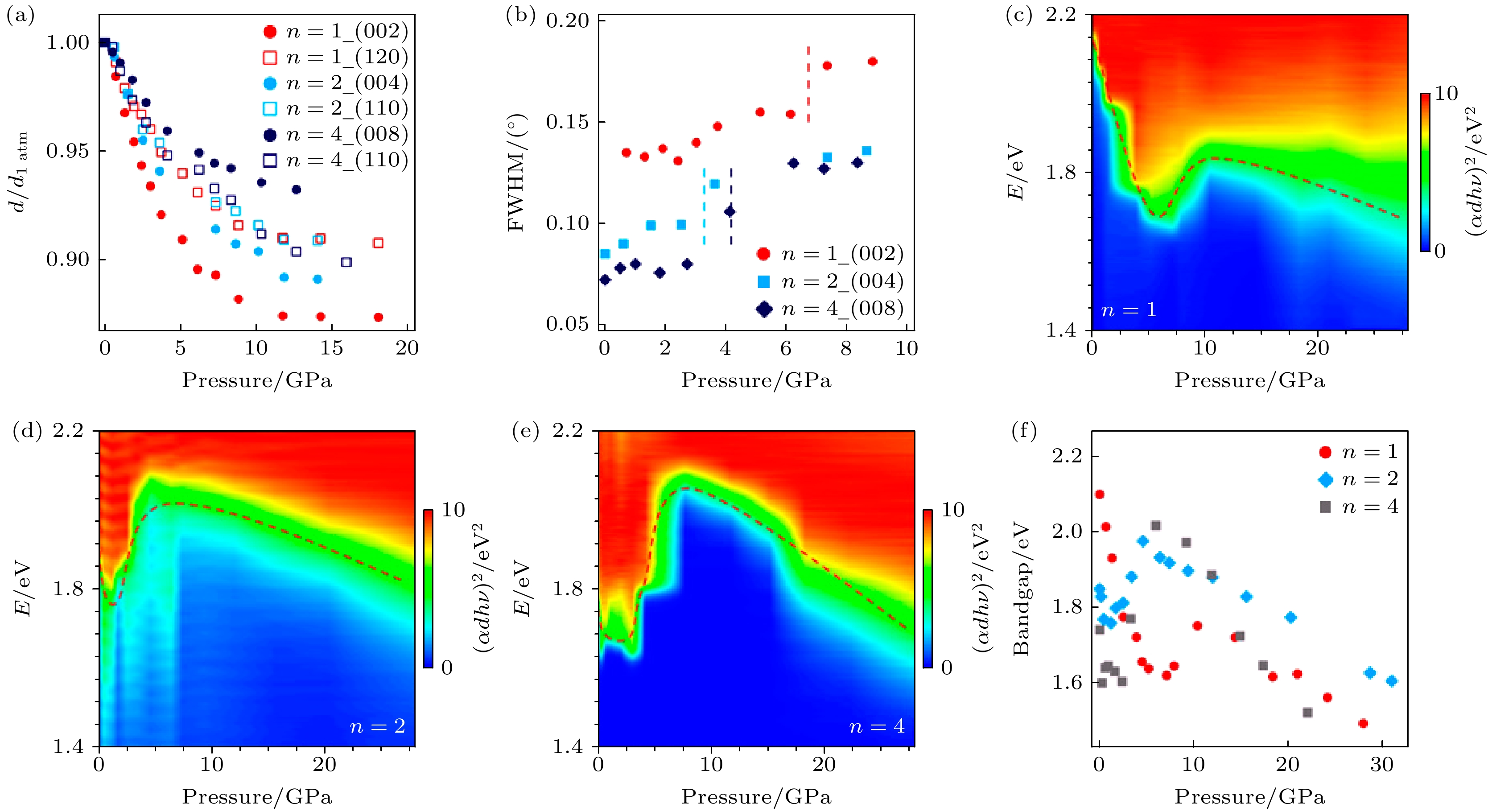
      Kong等[56]报道了系列二维D-J型钙钛矿(3AMP)(MA)n–1PbnI3n+1 (3AMP = 3-(氨基甲基)哌啶鎓)在高压下结构及光学性能变化. 研究发现层间压缩性在低n值材料中占主导地位, 而在高n值材料中层内压缩性更为显著, 带隙的变化与原子畸变密切相关. 在原位高压XRD实验中观察到, 随着压力增大, (3AMP) PbI4, (3AMP)(MA)Pb2I7, (3AMP)(MA)3Pb4I13三种钙钛矿的布拉格衍射峰均向更大角度移动, 表明晶格间距减小. 当压力达到较高值时, 这3种材料开始发生非晶化. 值得注意的是, 二维D-J型钙钛矿的压力驱动非晶化并非突然转变, 而是一个渐进过程. 此外, Kong等[56]还研究了D-J钙钛矿的各向异性压缩行为(图8(a)), 结果显示(3AMP) PbI4在垂直于层方向(002)的压缩性远大于面内方向(120), 表明层间压缩在该材料中占主导地位. 类似的现象也出现在(3AMP)(MA)Pb2I7中, 但其层间与层内压缩性的差异小于(3AMP) PbI4. 对于(3AMP)(MA)3Pb4I13, 层内压缩比层间压缩更容易. 这些结果表明, 随着n值的增大, 有机成分减少, 层间压缩性减弱.

      通过分析图8(c)—(e)的原位高压吸收光谱, 发现3种D-J钙钛矿材料(3AMP) PbI4, (3AMP)(MA)Pb2I7, (3AMP)(MA)3Pb4I13在压力下的带隙变化均呈现红移-蓝移-红移的模式(图8(f)). 通过分析(00l)晶面的FWHM随压力的变化(图8(b)), 对比发现FWHM急剧上升的拐点压力与带隙红移-蓝移的转折点高度一致, 进一步证实了D-J钙钛矿带隙蓝移的根源与原子畸变有关. 对于(3AMP) PbI4, 尽管层间压缩是主要机制, 但由于(00l)方向不存在Pb—I键, 其带隙红移主要由面内压缩引起的键长缩短导致. 类似地, (3AMP)(MA)Pb2I7的带隙红移也部分归因于面内Pb—I键距缩短. 而对于(3AMP)(MA)3Pb4I13, 这种压缩在Pb—I键长和键角之间产生了显著的竞争效应, 导致带隙在1—2.4 GPa压力范围内波动. 压力超过10.4 GPa, 4.6 GPa和6.0 GPa时, 3种材料的带隙开始持续红移, 最终可能在70 GPa以上实现金属化.

      当压力从高压状态释放后, (3 AMP)PbI4的光学带隙从2.10 eV增加至2.50 eV, 而(3 AMP)(MA)3Pb4I13的带隙从1.74 eV缩小到1.58 eV, 接近于三维MAPbI3的带隙, 表明高压处理可以有效改变材料的光学性质.

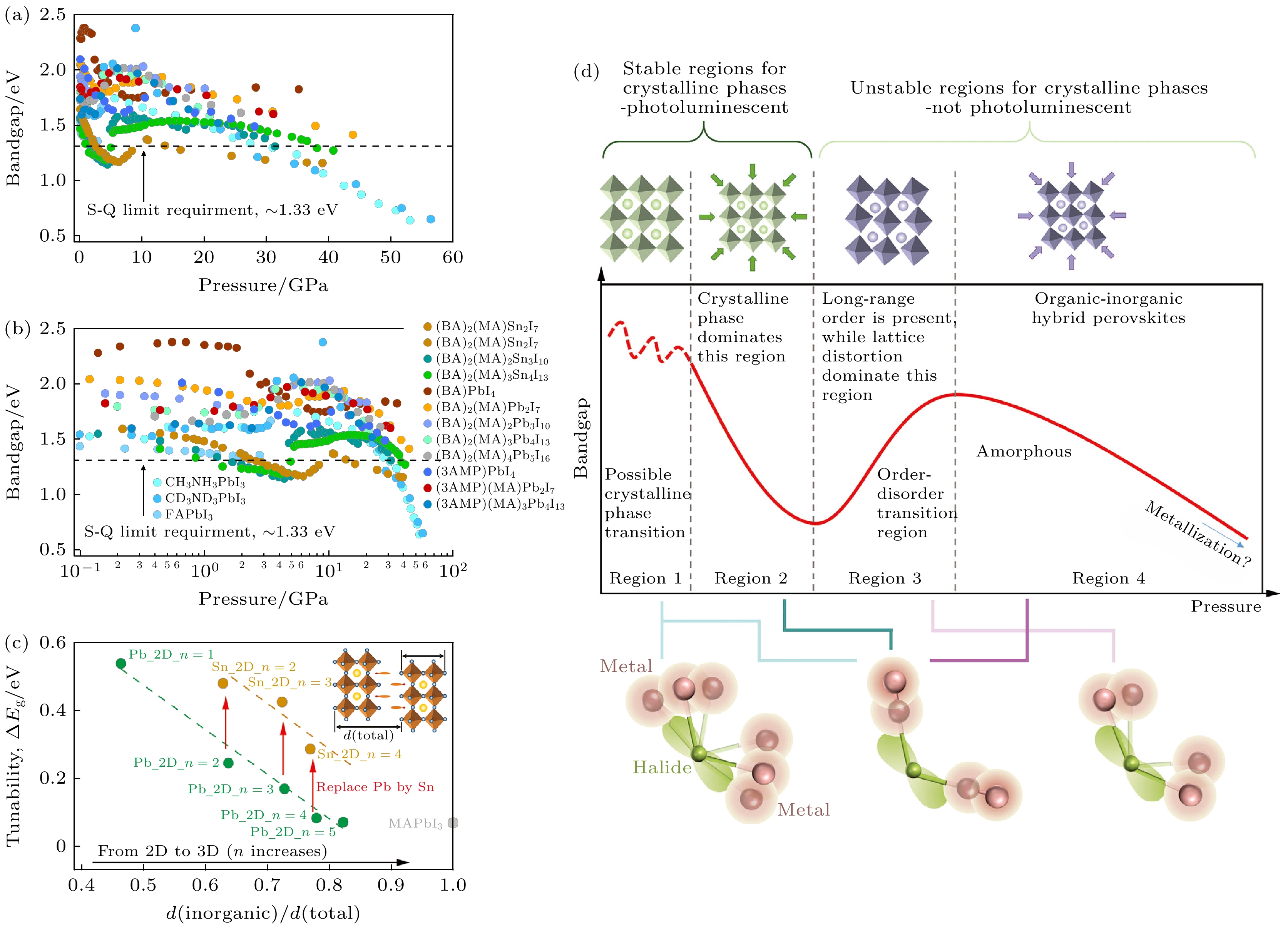
      Kong等[57]对比了三维、二维R-P型和D-J型的有机无机杂化钙钛矿的带隙随压力的变化(图9(a), (b)). 研究发现, 所有化合物均呈现相似的带隙演化规律: 初始变化后出现显著红移, 随后蓝移, 最终发生“再红移”, 带隙再次减小[45,49,55,56,58,59], 这一行为与A位有机阳离子、B位金属阳离子及钙钛矿维度无关, 表明杂化钙钛矿的结构与光学性质之间存在普适关联. 带隙的变化本质上源于电子波函数的重叠程度, 其压力依赖性可归因于金属-卤化物化学键在压力下的转变, 具体包括键角减小、增大以及键长缩短, 这些转变对应于图9(d)中展示的4个不同区域.

      在低压至中等压力范围内(区域1和区域2), 杂化钙钛矿中保持着长程有序. 在区域1中, 可能会发生晶相转变, 导致结构和带隙的变化更加复杂. 通常钙钛矿材料中的带隙变化依赖于金属(Pb或Sn)和卤素原子的电子轨道重叠, 而键长和键角的变化会引起轨道重叠的改变, 从而影响带隙. 在区域1中, 可能会出现轻微的带隙蓝移和红移, 蓝移源于卤素原子周围键角减小导致的轨道重叠降低, 红移则来自键长压缩引起的波函数重叠增强. 在区域2中, 键长的减小占据主导, 抵消了区域1中可能的蓝移, 从而使带隙变窄. 随着压力持续增大, 晶格畸变加剧, 结构趋于无序. 在区域3中, 原子发生畸变导致许多金属-卤化物-金属键错位、键角变窄, 从而减少了电子波函数的重叠, 带隙显著拓宽. 继续压缩至区域4, 系统达到高度无序和高密度的非晶态. 此时, 键角的灵活性受到限制, 键长的缩短再次在带隙演化中起决定性作用, 引发第二次红移甚至压力诱导的金属化.

      值得注意的是: 杂化钙钛矿的有机和无机晶格并不是孤立的结构部分, 而是密切相关的组成部分. 由于二维钙钛矿晶体结构的各向异性, 在中低压力范围内, 层间距离显著减小以抵抗外部压力, 从而导致带隙出现红移. 在更高压力范围内, 有机层达到其吸收压力的极限, 导致无机层发生畸变, 进而引起带隙蓝移. 此外, 对于铅基和锡基钙钛矿, 带隙可调性随着钙钛矿组成中n值的减小而增大, 这与每种化合物中无机层厚度的系统性变化一致(图9(c)). 由于无机层之间的有机层填充的空间具有高度可压缩性, 有机层在初始压缩时吸收了大量的能量, 并“保护”了无机亚晶格免受无序影响, 从而推迟了从区域3开始的带隙蓝移, 并提供了更大的带隙可调性, 特别是对于低n值的化合物.

      综上, 二维钙钛矿材料在高压下的结构演化研究表明, 无论是R-P型还是D-J型结构, 压力均优先作用于有机间隔阳离子层, 引发层间距的显著减小. 相较于D-J型结构, R-P型结构通常表现出更高的初始压缩率, 这一结构差异直接影响其在高压下的光学与电学等物性演化路径; 有机阳离子对二维钙钛矿的电子性质无直接影响, 带隙变化主要与[BX6]4–八面体的结构变化有关; 应力诱导的晶格结构畸变会导致材料能带结构的重构, 从而引起带隙能量的改变.

      • 3.3.3.   二维钙钛矿在高压下的发光调控

    • 二维钙钛矿材料的发光性能受其晶体结构、组分、缺陷态等因素的影响, 而高压作为一种有效的外部调控手段, 可以通过改变材料的晶格常数、电子结构等, 调控其光学性能.

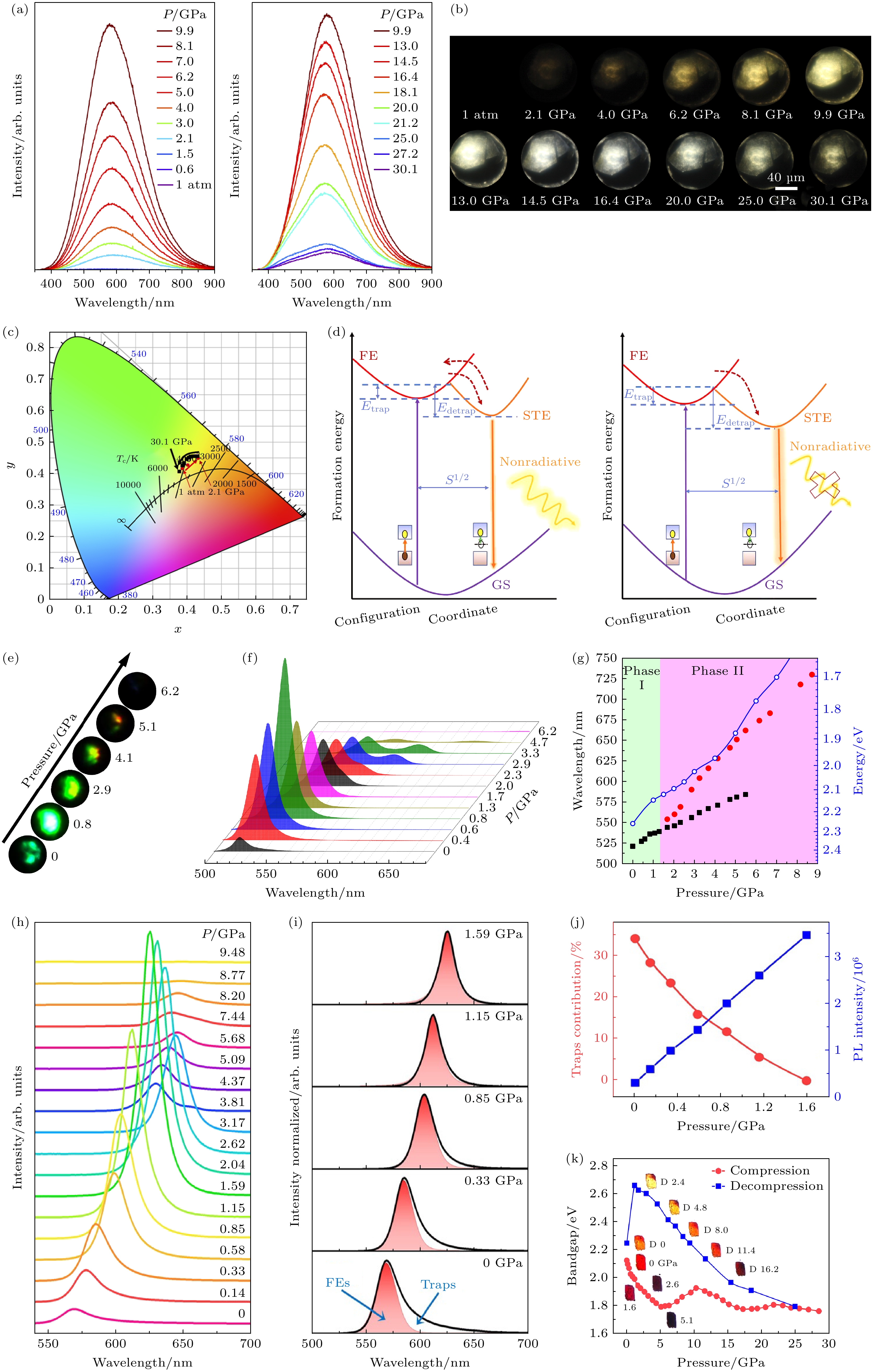
      Fang等[60]通过压力调控在二维钙钛矿(2meptH2)PbCl4 (2 mept = 2-甲基-1, 5-二氨基戊烷)中实现了暖白光发射的增强. 在环境条件下, 该材料在355 nm紫外光激发下表现出极弱的PL强度, 量子产率仅为1.05%, 最大发射峰位于580 nm, 呈现宽带发射特征. 234 nm的斯托克斯位移表明其PL源于自陷态发射. 图10(a)的原位高压PL测试显示, 样品的PL强度在1.5 GPa前保持不变. 在2.1 GPa时PL强度急剧增大8倍, 并在9.9 GPa时达到最大值. 然而, 当压力继续增大至30.1 GPa时, 样品的发射强度逐渐减弱, 但即使在30.1 GPa时, PL强度仍显著高于环境条件下的强度. 图10(b)显微照片清晰地展示了加压过程中PL亮度与颜色的变化, 在压力区间内始终保持暖白光发射, 相关色温约4000 K, 显色指数大于80 (图10(c)). 这种高性能的单组分暖白光发射在低维钙钛矿研究中极为罕见[61,62].

      (2meptH2)PbCl4在高压下的光致发光增强 机制如图10(d)所示. 由于无机骨架受到大尺寸有机阳离子的保护, 导致晶体结构变形程度较小, 电子-声子耦合能较弱. 因此, 自由激子态与自陷激子态之间的能量差有限, 自陷激子的去捕获能力 增强, 如图10(d)中向上的红色箭头所示, 因此2.1 GPa以下样品的PL较弱[63]. 随着进一步压缩, 晶体结构的畸变程度在2.1 GPa时显著增大, 这有利于自陷激子的形成并增强了自陷激子的电子-声子耦合[64,65]. 因此, PL强度的显著增大可归因于2.1 GPa时自陷激子的去捕获能力减弱所促进的辐射复合. 此外, 自陷激子的声子辅助非辐射复合过程被极大抑制, 导致(2meptH2)PbCl4晶体的PL进一步增强, 直至9.9 GPa[66,67]. 在9.9 GPa以上的压力下, 样品的畸变加剧并进入无序阶段, 从而抑制了辐射复合并促进了非辐射跃迁, 此时PL开始减弱. 此外, PL光谱的形状始终保持明显的对称性, 表明具有宽发射的多个自陷激子态在平衡中很好地共存. 同时, 样品的宽带发射始终覆盖整个可见光谱范围, 这为样品始终保持暖白光发射提供了支持.

      Jesse等[68]报道了(CMA)2PbI4 (CMA = 环己基甲基铵)的PL随压力的变化. 光谱如图10(f)所示, 在常压下, PL峰位在521 nm附近且发射轮廓不对称. 在加压过程中, PL的强度逐渐增大, 至0.8 GPa其强度约为常压下的10倍, 这表明压力显著增强了PL效率. 同时, PL发射峰在加压下变得更加对称, 这表明结构向更规则的[PbI6]4–八面体转变. 进一步加压后, PL强度显著下降, 直至在约9 GPa时完全淬灭. 在整个压力范围内PL峰不断红移, 这与压力诱导的带隙变窄一致. 当样品被压缩到1.3 GPa以上时, PL轮廓表现出明显的分裂(图10(g)), 并在进一步加压时显著分解为两个PL峰, 且具有非常明显的压力依赖红移速率. 这一观察表明在1.3 GPa附近可能存在相变, 其中1.3 GPa以上的高压相(标记为Phase II)可能具有相对于低压相新的激子结构.

      Guo等[69]通过压力的手段在(HA)2(GA)Pb2I7(HA = 正己基铵, GA = 胍)中实现了12倍的发射增强. 在环境条件下, (HA)2(GA)Pb2I7表现出相对较弱的发光, 中心波长约为570 nm, 具有不对称的峰形, 其中低能侧的发光主要归因于俘获载流子的辐射复合. 通过拟合PL光谱估算了每个压力下自由激子和俘获态对发光的贡献, 如图10(i)所示. 在环境压力下, (HA)2(GA)Pb2I7的PL光谱中俘获态的贡献显著, 这可能导致其较弱的PL强度. 随着压缩的进行, 俘获态的发光贡献逐渐减小, 随后俘获态发光在1.59 GPa时完全消失, 此时PL强度达到环境条件下的12倍. 图10(j)展示了俘获态发光的贡献和总PL强度随压力的变化, 证实了载流子俘获的抑制与PL强度增大之间的强相关性. 据报道, 自由激子和俘获态之间的能垒降低会导致载流子俘获的减少. (HA)2(GA)Pb2I7的能垒变化可能是由于压力对Pb-I无机亚晶格的调制和调控, 使其畸变减小, 从而显著影响激子-声子相互作用.

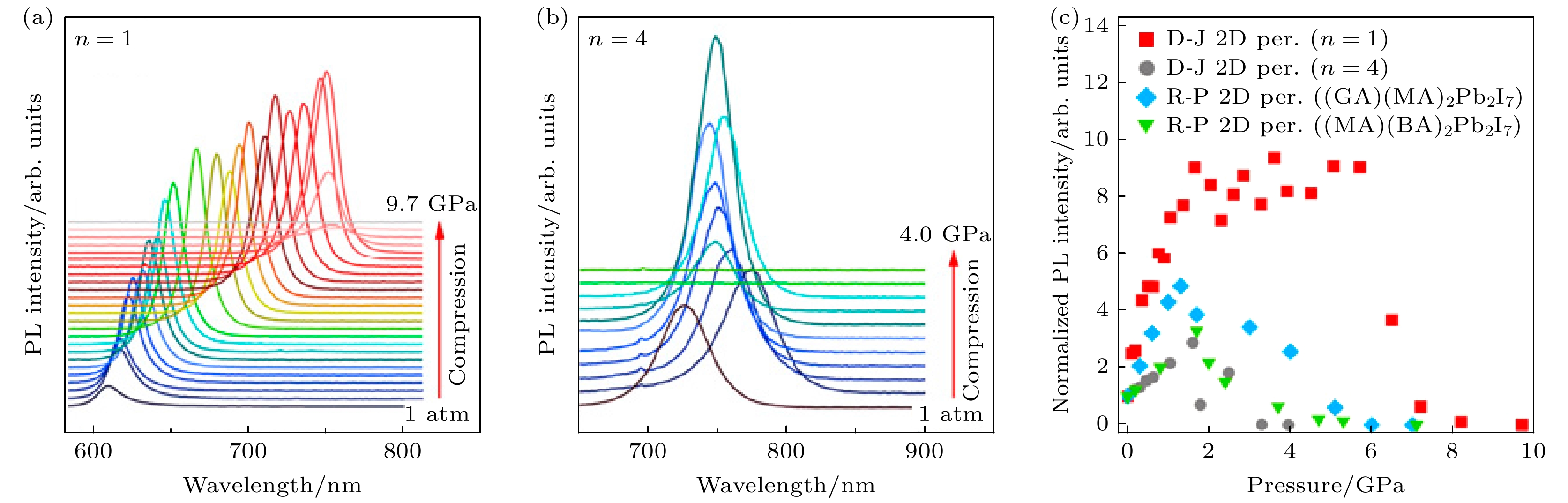
      Kong等[56]在二维D-J型钙钛矿的研究中发现, 不同n值的材料发光特性有所差异. 图11(a), (b)为(3AMP)PbI4 (n = 1)和(3AMP)(MA)3Pb4I13(n = 4)的原位高压PL测试. 随着压力从环境压力(1 atm =1.01325 × 105 Pa)逐渐增至9.7 GPa, (3AMP)PbI4的PL发射峰表现出连续红移的现象, 从初始的561 nm显著移动至7.1 GPa下的735 nm, 红移幅度达到174 nm. 相比之下, (3AMP)(MA)3Pb4I13的PL光谱随压力的变化呈现出更为复杂的演化行为. 在低压区域(1 atm—1 GPa), PL发射峰从721 nm红移至774 nm, 随后在1 GPa附近发生蓝移, 峰位移动至745 nm. 在1.0—2.5 GPa的中等压力范围内, PL峰位在745—755 nm之间表现出轻微的波动.

      PL波长变化的差异归因于(3AMP)PbI4和(3AMP)(MA)3Pb4I13的不同晶格结构. (3AMP)PbI4的单层结构仅允许层内Pb—I键长的压缩, 从而导致PL的单调变化. 对于(3AMP)(MA)3Pb4I13, 压缩不仅促进了多层无机层板内的键长缩短效应, 还减小了层板之间的距离, 从而引起电子结构的复杂变化, 并导致带隙的改变. 此外, 如图11(c)所示, (3AMP)PbI4在加压至中等压力2—6 GPa时, 其发光强度相对于环境压力下的发光强度增强了近1个数量级, 这可能是由于结构畸变引起的激子结合能增大或自陷激子发射增强所致[70–72]. (3AMP)PbI4的PL发光增强效应远强于(3AMP)(MA)3Pb4I13, 后者在环境压力至1.7 GPa范围内的发光强度最大增强了3倍. 然而, 当压力进一步增至约6 GPa和1.75 GPa时, (3AMP)PbI4和(3AMP)(MA)3Pb4I13的PL强度均出现下降, 这与其晶格部分非晶化有关[73].

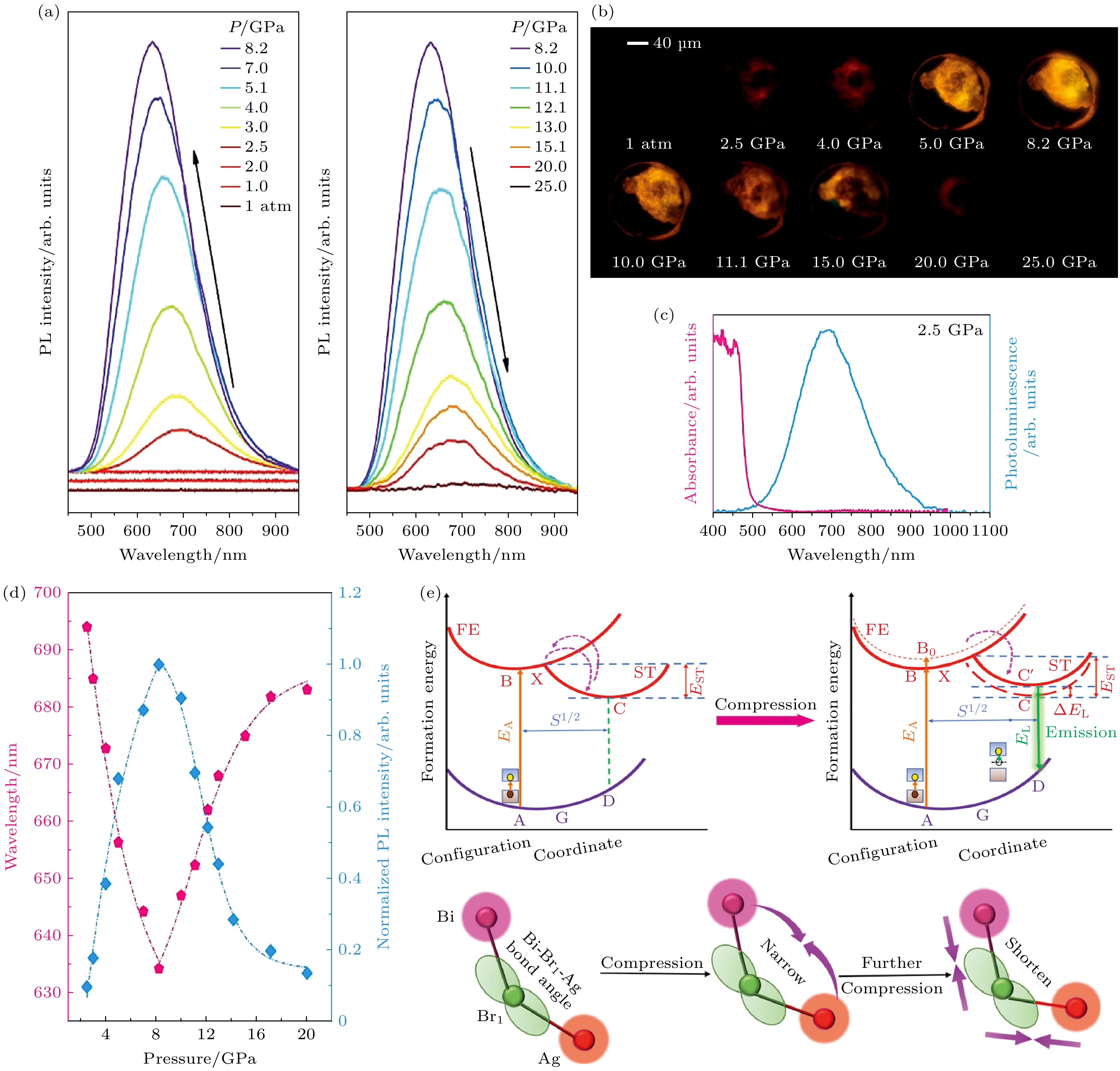
      压致发光现象是高压科学领域中一项重要发现—某些在常压下不具备发光特性的材料, 在高压环境中会因晶体结构的显著变化, 引发能带结构的重新排列或缺陷态的形成, 从而激发出可见光或近可见光范围的发光. 这一发现不仅揭示了材料在极端条件下独特的光学行为, 还为深入探究材料的结构相变、电子态演化以及应力-光学耦合机制提供了全新的研究视角. Fang等[74]在二维卤化物钙钛矿(BA)4AgBiBr8中观察到2.5 GPa处的压力诱导发射现象. 图12(a)展示了PL光谱随压力增大的演变过程. 在常压条件下, 样品并不发光, 当压力增大至2.5 GPa时, 出现了一个半峰宽约为180 nm的宽发射带, 表现出219 nm的斯托克斯位移(图12(c)), 这源于自陷激子的发射[75]. 随着进一步加压, (BA)4AgBiBr8的PL强度逐渐增大. 在8.2 GPa时, PL强度达到最大值, 且PL峰位出现蓝移. 进一步加压PL强度开始减弱且峰位发生红移(图12(d)). 当压力达到25.0 GPa时, PL发生猝灭.

      图12(e)展示了(BA)4AgBiBr8的发射机制随压力增大的演变过程. 在常压条件下, 原始的单斜相结构的弱电子-声子耦合能量导致束缚激子容易通过热激活从自陷态脱离回到束缚激子态, 从而阻碍了发光. 在2.5 GPa以上, 结构转变和相关的晶格畸变促进了更强的电子-声子耦合强度, 从而形成了稳定的自陷激子, 自陷激子被有效地阻止重新转化为束缚激子, 这增加了辐射复合的可能性, 与大斯托克斯位移和宽带PL的出现相一致. 如图12(e)所示, 激发跃迁从A→B, STEs的辐射发射源自C→D. 随着压力增大到8.2 GPa, MBr6八面体进一步压缩, Ag—Br1和Bi—Br1键强度增强, 这降低了晶格弛豫能, 从而进一步提高了辐射复合的可能性, PL强度增强. 同时, ST态向更高能量移动, 使得STEs的光致发光能量增加. 因此, 随着压力的增大, PL强度显著且持续增强, PL峰位蓝移. 随着进一步压缩, 逐渐降低的结晶度导致更多的非辐射复合, 这可能使A→B→C→X路径成为可能, 所以在更高压力下PL强度减弱且峰位红移.

      综上所述, 高压作为一种外部调控手段, 能够显著改变二维钙钛矿材料的光学性能: 1)在多个研究中表明, 自陷激子的形成和辐射复合被认为是高压下PL增强的主要原因; 2)高压可以抑制载流子的俘获, 减少非辐射复合, 从而提高PL效率; 3)高压通常会导致材料的带隙变窄, 从而引起PL峰的红移; 4)压力在超过一定限度后, 材料的PL强度会减弱甚至完全淬灭, 这通常与材料的晶格非晶化或结构无序化有关.

      • 3.3.4.   二维钙钛矿在高压下的电学性能调控

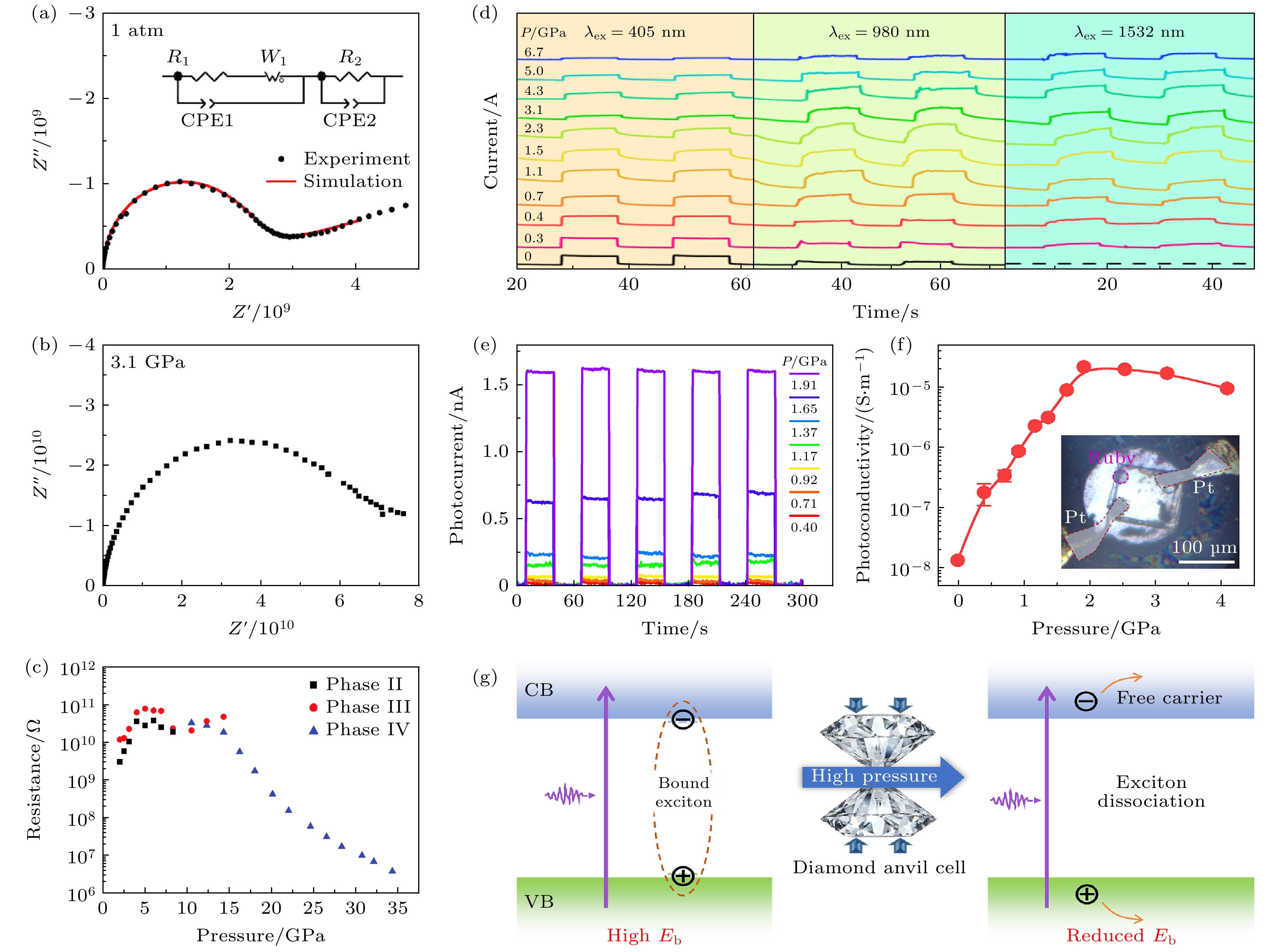
    • 压力诱导的带隙调控机制在三维钙钛矿材料中已被广泛证实, 并成为一种有效调控材料电学性能的重要手段[49,76–78]. 对于二维钙钛矿, Yuan等[52]研究了 (BA)2PbI4在高压下的电输运行为. 图13(a), (b)的高压阻抗测量结果显示, 在环境条件下, 高频区出现半圆, 低频区出现向上倾斜的直尾, 表明 (BA)2PbI4表现出离子输运行为. 值得注意的是, 在3.1 GPa时, 向上倾斜的直线开始向Z′轴弯曲, 表明压力诱导了从离子输运行为向电输运行为的转变. 如图13(c)所示, (BA)2PbI4的电阻在常压至6 GPa范围内随压力增大而增大. 超过6 GPa后, 随着有机层无序度的增大, 电阻开始下降. 在第三次相变后, [PbI6]4–八面体畸变导致结构非晶化, 同时电阻随压力增大急剧下降. Jaffe等[49,79]曾报道, 类似的结构非晶化在高压下会导致带隙持续变窄. Jaffe等[49,79]推断, Pb─I键压缩的增大以及局域尺度上的结构变化在带隙和电导率变化中起重要作用. Li等[79]尝试在不考虑非晶化的情况下模拟压缩下的带隙演化, 但实验与计算结果之间的巨大差异使他们推测结构非晶化是维持带隙变窄的潜在机制. (BA)2PbI4与其类似, 故推断结构非晶化导致了带隙持续变窄和电阻下降. 电阻的快速下降伴随着局域尺度上的结构变化, 在约34 GPa时, 电阻降低了近10000倍, 证明(BA)2PbI4在高压下具有更优异的电学性能.

      Cui等[80]研究了准二维钙钛矿(BA)2(FA)Sn2I7在压力下的光电响应, 测量了样品于不同压力下在405, 980 和 1532 nm激光照射下的光响应I-T曲线. 从图13(d)可以看出, 405 nm照射下, 样品在常压即表现出显著光响应, 随压力增至1.1 GPa时开关比达到峰值1.12, 较常压提升1.51倍, 其后响应衰减. 980 nm光照在常压响应微弱, 但压力诱导下呈现相似的增强规律, 最大开关比达1.18. (BA)2(FA)Sn2I7样品中存在压力诱导荧光增强的现象, 这表明在适当的压力下产生了更多的光生电子-空穴对. 电子-空穴对在外部偏压下有效分离, 从而改善了样品的光电响应[81]. 值得注意的是, 样品在常压下对1532 nm激光没有响应, 但压力超过0.3 GPa后产生可检测光电流, 1.1 GPa时开关比达1.07, 表明压力将光谱响应拓展至近红外Ⅱ区. 在环境压力下, 样品是直接带隙材料, 入射光子的能量小于带隙能量, 因此在1532 nm激光照射下无法产生光生载流子. 当压力超过0.3 GPa时, 可以检测到光电流, 表明吸收阈值高于1532 nm. 因为压力引发的结构相变可能导致深能级缺陷态形成, 使低于带隙能量的光子激发载流子跃迁成为可能. 本研究证明了通过施加压力可以增强样品在近红外光下的光响应, 这一发现为设计具有可调控宽带响应的新型光电探测器提供了新策略.

      Guo等[82]发现全无机二维钙钛矿Cs2PbI2Cl2单晶在高压下呈现显著光电流增强效应. Cs2PbI2Cl2的光电流表现出快速的开关响应, 并在压力达到2 GPa时迅速增强(图13(e)). 相应的光电导率在1.91 GPa时显著增大了超过3个数量级, 达到2.2×10–5 S/m, (图13(f)). Cs2PbI2Cl2中光响应演化的机制如图13(g)所示. 激子可以稳定存在或解离成自由载流子, 具体取决于结合能 Eb, 这使得Eb成为光电材料的关键参数之一[83–85]. 在环境条件下, Cs2PbI2Cl2相对较高的Eb值稳定了激子. 压力作用下, Eb减小, 这意味着激子更有可能解离为自由载流子. 此外, 压力诱导的更高迁移率使得这些自由载流子更容易向电流收集器迁移. 因此, 通过压力降低激子特征, Cs2PbI2Cl2的光响应得到了显著增强.

      综上所述, 压力调控通过诱导相变、非晶化和带隙变窄, 显著影响了钙钛矿材料的电学性能. 这为材料性能的优化提供了新的途径.

      • 3.4.   其他二维材料

      3.4.1.   二维过渡金属碳化物和氮化物在高压下的结构和性能研究

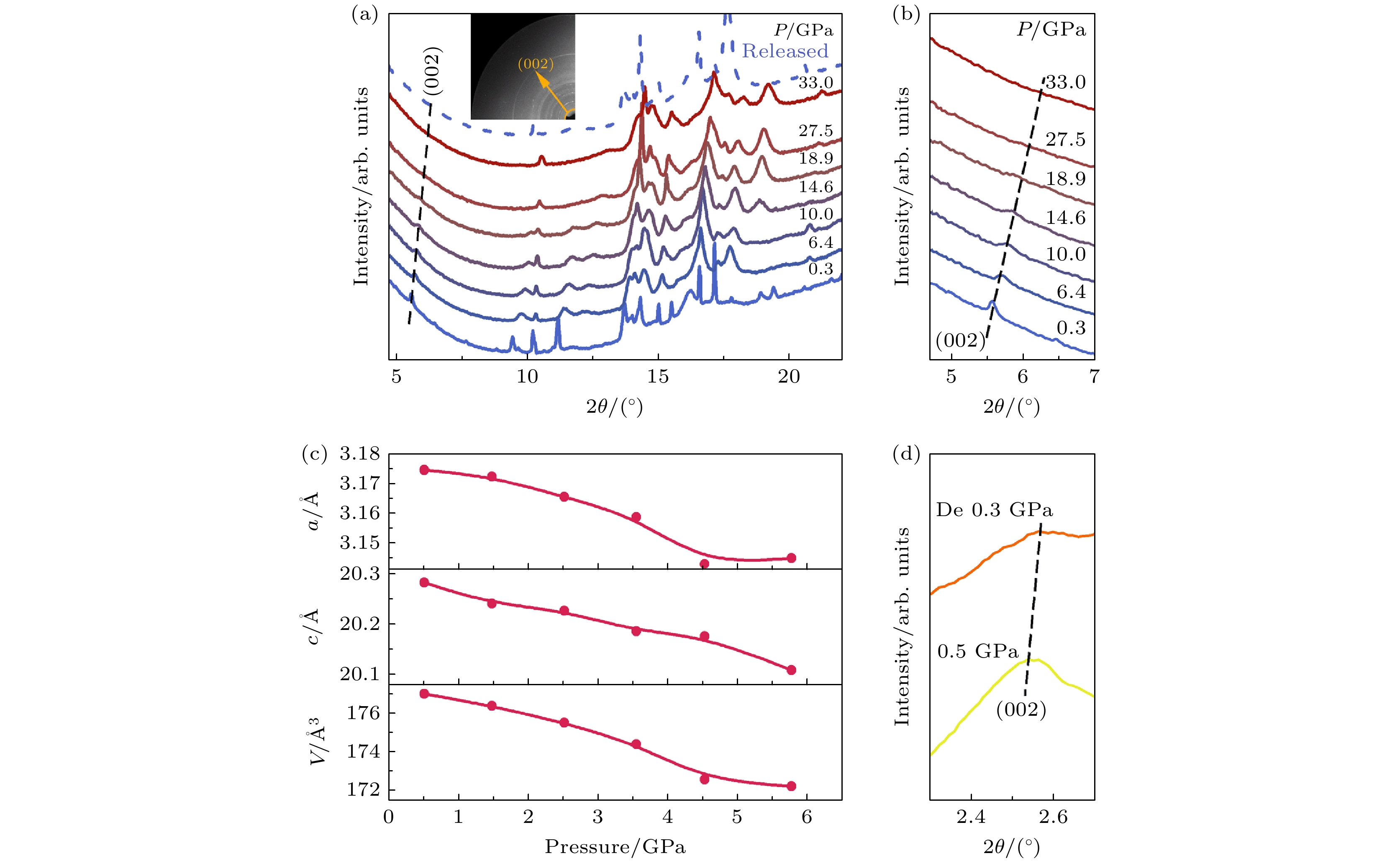
    • 二维过渡金属碳化物和氮化物(MXene)是一类新兴二维无机化合物材料, 因其具有独特的层状结构、高导电性和丰富的表面化学性质, 在超级电容器和电池的电极材料领域引起了广泛关注[86]. Lv等[87]利用高压原位同步辐射、阻抗谱等实验测试研究了高压下MXene材料Ti3C2Tx的结构-功能关系. 如图14(a)所示, 原位X射线粉末衍射(XRPD)图谱表明, 在33 GPa压力范围内未出现新衍射峰, 证实材料未发生相变. 图14(b)所示为(002)衍射峰随压力增大持续向高角度偏移, 表明晶格沿c轴方向发生显著压缩(图14(c)), 这与MXene层状结构的各向异性密切相关. 值得注意的是, 在卸压至常压后(0.3 GPa), (002)峰位偏移仍部分保留(图14(d)), 揭示了压力诱导晶格收缩的不可逆性.

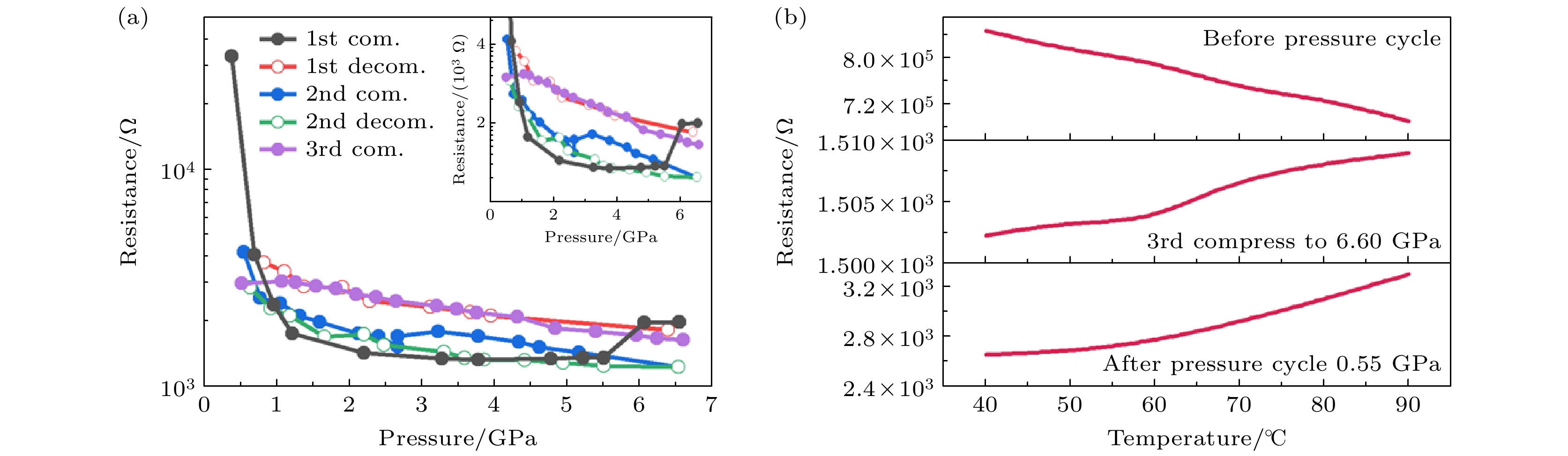
      压力引起的连续晶格收缩必然会影响 Ti3C2Tx的电荷载流子传输[88]. Lv等[89]通过对Ti3C2Tx样品进行高压原位阻抗谱测试, 发现电阻(R)随压力呈阶段性变化(图15(a)): 在0.4—2.2 GPa区间, R从3.3×104 Ω急剧降低至1.4×103 Ω(降幅>90%); 当压力增大到2.2 GPa以上时, R缓慢下降. 在第1次卸压过程中, 样品的电阻随着压力降低而逐渐增大, 当压力降至0.5 GPa时, R恢复至4.2×103 Ω, 仍较初始值低1个数量级, 这表明压力对样品的导电性具有显著且不可逆的影响. 先前研究表明Ti3C2Tx是一种窄带隙碳化物, 在常压下具有半导体或金属特性, 图15(b)的变温电阻测试进一步揭示, 在DAC中压缩之前, 样品电阻随温度逐渐降低, 显示出半导体特性, 而6.6 GPa高压下电阻开始随温度升高, 显示出金属特性, 并在卸压至0.55 GPa后维持金属态. 该半导体-金属转变源于压力诱导的窄带隙闭合, 促使自由载流子浓度显著增大.

      Li等[90]通过密度泛函理论计算系统研究了表面氧功能化的Ti2C MXene (Ti2CO2)在压力调控下的电子结构与光学性质演变. 研究结果表明, Ti2CO2在0—7 GPa压力范围内保持结构稳定性, 并在7 GPa时发生半导体-金属相变, 其金属化主要源于Ti-3d态电子贡献. 能带结构计算进一步揭示, 随着压力增大, Ti-d轨道与C-p/O-p轨道间的杂化作用显著增强, 导致材料带隙逐渐减小直至闭合. 此外, 在光学性质方面, 压力诱导使得材料在可见光区域(约2.5 eV)的介电函数虚部峰强度明显提升, 同时光吸收能力显著增强, 这一现象源于Ti-d与C-p 态, 以及 Ti-d与O-p态之间的电荷转移加剧. 该研究为理解压力对MXene材料电子能带结构和光电性能的调控机制提供了理论依据.

      研究表明, 压力作用能够显著改善MXene材料的电子输运特性, 同时可精准调控其光响应性能. 这些发现可为开发新一代可调谐电子器件和光电器件提供重要的理论指导和实验依据.

      • 3.4.2.   石墨相氮化碳在高压下的结构和性能研究

    • 石墨相氮化碳(g-C3N4)是一种典型的有机聚合物半导体, 其结构特征表现为碳氮元素构成的类石墨烯二维层状框架[91], 层内通过sp2杂化的C—N共价键形成三均三嗪(tri-s-triazine)单元网络[92], 层间则依赖范德瓦耳斯力堆叠, 其中石墨相在室温条件下展现最优热力学稳定性[93,94]. 该材料体系因制备工艺简易、原料成本低廉、可见光响应特性、卓越的化学稳定性及无金属组分等优势, 在光电催化领域备受瞩目. Hu等[95]针对少层 g-C3N4 (FL-CN)的高压研究证明, 压力诱导的层间相互作用增强影响了光生载流子的电荷分离, 从而导致PL增强. 如图16(a)所示, 在0—16 GPa压力区间内, FL-CN样品的颜色经历了从初始白色到黄色最终为橙色的转变. 值得注意的是, 在极低压力下观察到PL强度增强, 之后随着压力进一步增加, PL强度单调衰减. 此外, 随着施加压力的增大, FL-CN 的 PL 峰发生红移, 从初始的436 nm到16 GPa 时达到555 nm(图16(b)), 此现象在图16(c) 中表现为从蓝色到黄色的轨迹变化. 通过对 FL-CN 样品的 PL光谱拟合, 识别出3个PL分量(即(σ*-LP(P1), π*-LP(P2) and π*-π(P3)), 并将获得的PL能量作为压力的函数绘制在图16(d)中. 当压力小于3 GPa时, 各发射峰能量以约0.025 eV/GPa的系数线性降低, 该趋势与第一性原理计算结果吻合[96]. 在3 GPa以上, PL谱带显著展宽, 3组分拟合会产生大的离散和不确定性, 此时需采用主峰位置追踪演化行为.

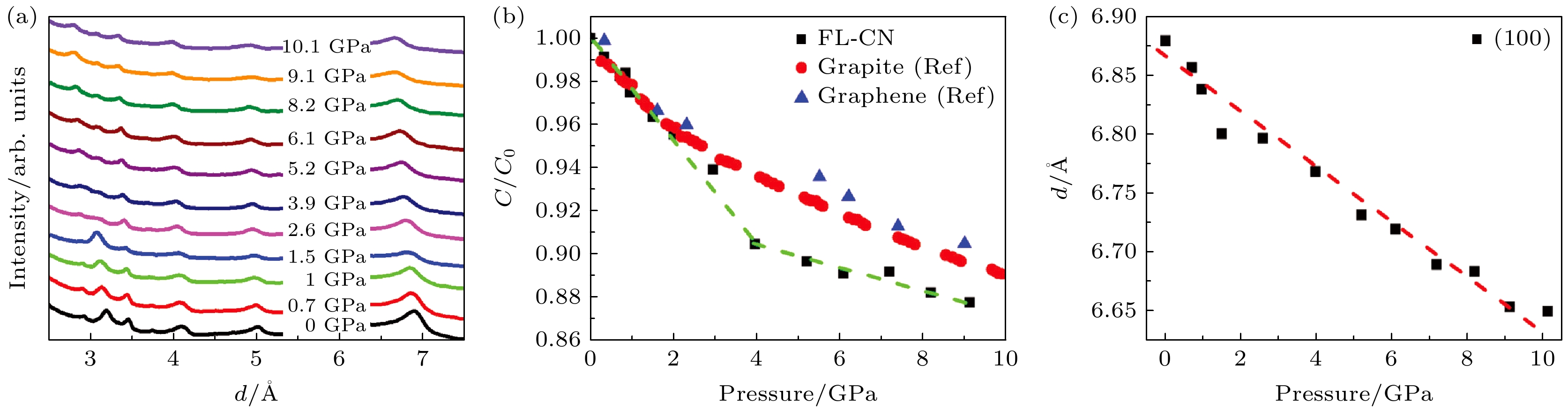
      为理解 PL 行为中这些异常转变的潜在机制, Hu等[95]对图17(a)所示的 FL-CN 样品进行了高压 XRD 研究. 结果表明, 在高压下样品没有发生结构相变, 而在图17(b)中观察到(002)峰位置作为压力函数的曲线斜率在约3 GPa处发生明显变化. 在此转变之后, 对应于层间距的(002)衍射峰强度显著降低且压缩性降低, 表明层间堆垛有序度降低而层间相互作用增强. 相比之下, 来自层内衍射的 (100) 晶面的d间距随着压力增大线性减小(图17(c)). 对AA (对齐式)与AB (错位式)堆叠g-C3N4的压缩行为研究表明, 两者在3 GPa以下的层间压缩行为相似, 但随着压力升高, AB堆叠材料沿c轴的压缩性明显低于AA堆叠. 因此g-C3N4层间压缩性变化的现象是源于压力驱动的层间滑移转变: 三均三嗪单元滑移至相邻层孔隙位点, 形成了能态更稳定的AB堆垛构型. 该重构过程导致层间体积坍缩, 并增强氮孤对电子密集区域的轨道杂化. 此电子结构重组直接影响与氮孤对电子相关的PL发射, 表现为少层 g-C3N4 转变为压缩性较低的状态时, PL强度显著降低, 并且PL峰合并为一个宽谱带, 其中与氮孤对电子相关的 P1和P2 PL峰似乎比P3对压力更敏感, 并且在压力下强度下降更显著. 该机制完美关联了结构转变与光学响应的对应关系, 确立层间相互作用为调控g-C3N4光电性能的核心物理参量.

      • 3.4.3.   六方氮化硼在高压下的结构和性能研究

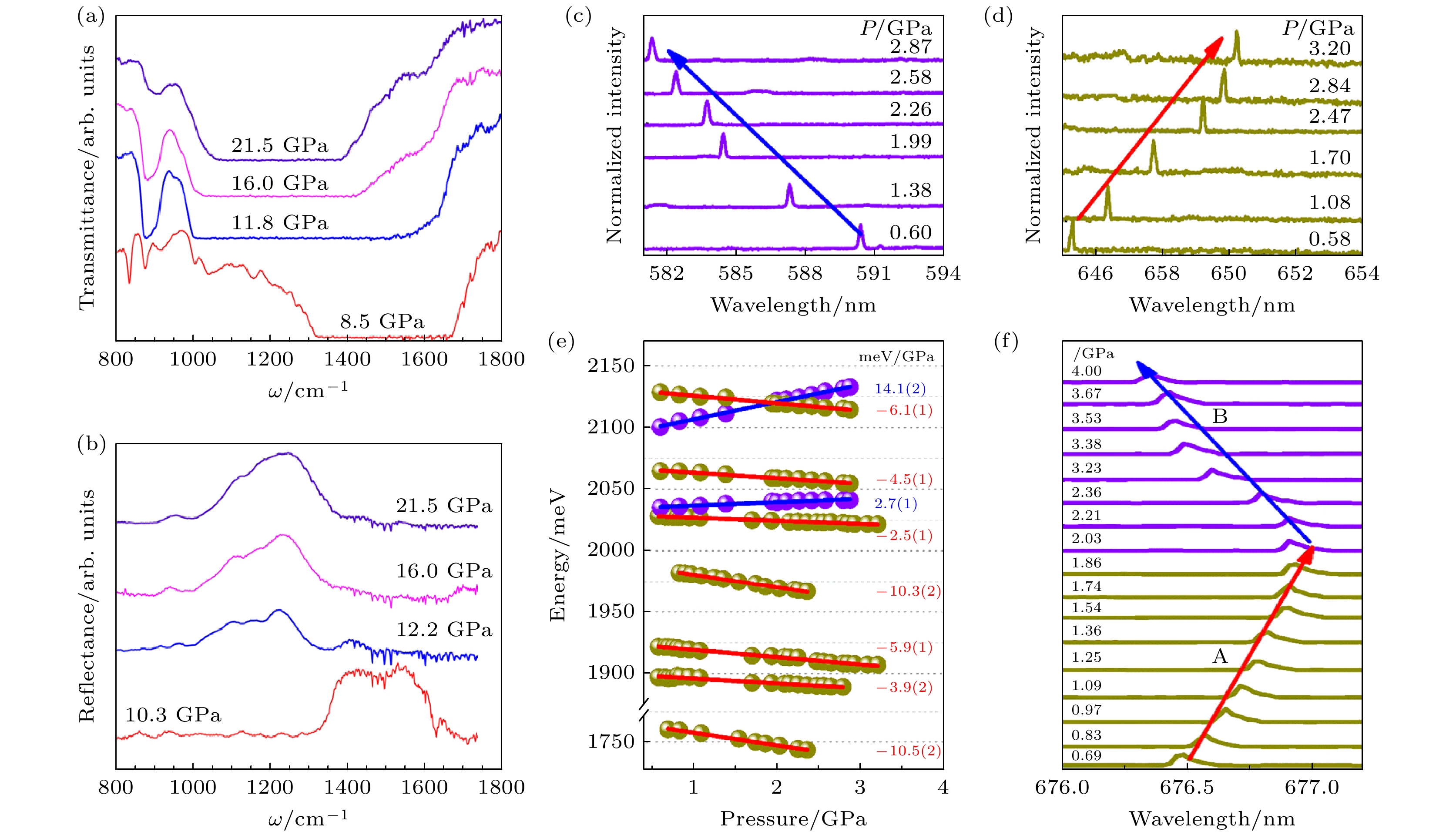
    • 二维材料六方氮化硼(h-BN)因其蜂窝晶格中硼原子和氮原子的交替排列被称为“白色石墨烯”[97], 这种材料因独特的电子传导和热传导特性引起了广泛的研究兴趣, 其无缺陷、超平整特性及5.9 eV以上的大带隙[98–100]使其被深入研究作为栅极电介质[101]、电子封装材料[102]和隧道结[103,104]. 与石墨烯类似, 加压过程中层间距缩短可引发相变和能带调制. Segura等[105]利用高压原位红外反射、透射光谱, 研究了氮化硼在13 GPa左右的压强下发生从h-BN到纤锌矿氮化硼(w-BN)的不可逆相变. 在环境压力条件下, h-BN在正入射(电场方向垂直于c轴, E⊥c)的红外反射光谱中, 于1360—1630 cm–1波数范围内观测到一个特征性的剩余射线带. 该谱带对应于h-BN六方层状晶体结构中E1 u的横向光学(TO)模与纵向光学(LO)模. 随着压力升高, h-BN开始向w-BN相转变. 此相变过程在光谱上表现为: h-BN特征剩余射线带的消失, 同时在更低频率处新出现一个剩余射线带, 该新谱带对应于w-BN晶体的TO模和LO模. 图18(b)展示了h-BN样品在相变压力范围内的加压过程所测得的红外反射光谱, 直观反映了上述变化. 与此一致, 图18(a)所示的透射光谱也呈现同步演变. 在8.5 GPa压力下, 透射光谱在1320—1670 cm–1区间内呈现接近零透射率的区域, 这对应于h-BN高反射率的剩余射线带, 表明样品仍保持其层状六方结构. 当压力增至约12 GPa时, 接近零透射率的区域向低频方向展宽, 标志着样品开始发生由h-BN向w-BN结构的逐步相变. 压力进一步增大导致该区域再次变窄, 但其中心位置持续向低频移动. 至21.5 GPa时, 近零透射区已迁移至1050—1380 cm–1光谱范围, 此特征与w-BN的剩余射线带完全吻合, 表明相变过程已完成.

      Xue等[106]将高压实验技术与第一性原理计算相结合, 揭示了h-BN中缺陷发光的反常压力依赖性是源于层内和层间的相互作用竞争. 图18(c), (d)显示了高压实验下观测到的PL光谱, 其发光峰分别呈现蓝移和红移, 对应的压力系数分别为(+14.1 ±0.2) meV/GPa和(–5.9±0.1) meV/GPa. 图18(e)描绘了该样品中9条典型PL发射线峰值能量随压力的变化关系, 所得压力系数的绝对值均小于15 meV/GPa, 且大部分低于6 meV/GPa. 值得注意的是, h-BN 带隙的压力依赖性约为 –36 meV/GPa[107]. 其绝对值显著大于源自点缺陷的 PL 发射线的压力系数. 这一对比表明, h-BN 中的单光子发射(SPE)源于深能级中心, 其相关电子态局域于带隙深处. 此外, 在小于 4 GPa 的低压区域, 观察到压力系数负值绝对值低于2 meV/GPa的PL发射线存在压力诱导的压力系数符号反转现象(图18(f)). 结合第一性原理计算研究进一步阐明: 对于单层 h-BN, 所有原子共面, 压力仅诱导面内应变. 当压力作用于层内的共价键时, 缺陷能级间距增大, PL峰持续蓝移. 对于双层或多层 h-BN, 压力同时诱导面内应变和面外应变, 此时, 层内相互作用和层间相互作用的竞争共同决定了能量位移特性. 随着压力增大, 最初占主导的层间相互作用PL峰诱导红移, 随后, 不断增强的层内相互作用逐渐占据主导, 最终诱导峰值蓝移. 以上研究进一步表明, 高压可有效调控二维材料的层间相互作用及相关光电性能.

    4.   总结与展望

    • 二维材料因其丰富的材料种类及多样可调的物理特性而引发了广泛科研人员的研究兴趣, 高压技术作为一种高效、连续且可控的手段, 在其光电性能调控中展现了巨大的研究潜力. 本文重点探讨了高压下石墨烯、二维过渡金属二硫族化合物和二维钙钛矿材料的结构演化以及光电性能调控: 高压下石墨烯表现出从半金属到半导体甚至超导态的转变, 层间耦合强度的调控为研究其电子能带结构和关联效应提供了重要途径; 二维TMDs中MoS2, WTe2等材料在高压下发生结构相变和半导体-金属转变, 厚度依赖的相变行为揭示了层间相互作用的关键性; 在二维钙钛矿中表现出压力诱导的带隙窄化和发光增强等现象. 这些研究表明, 高压不仅是一种极端条件模拟手段, 更是调控材料性能的有效工具, 为新型功能材料的设计和优化提供了重要参考.

      尽管高压调控二维材料研究已取得显著进展, 但该领域仍存在诸多亟待解决的科学与技术难题: 实现均匀可控的高压环境是二维材料研究面临的首要挑战, 与传统三维材料不同, 二维材料对压力梯度极为敏感, 微小的压力分布不均即可导致样品不同区域出现较大的性能差异性, 这严重影响了实验结果的可靠性和重复性; 环境稳定性问题也不容忽视. 许多高压诱导的新相在常压下会迅速退化, 如何通过界面工程、表面钝化或应变工程等方法稳定这些亚稳相, 是材料设计和器件集成的核心问题; 此外, 将高压调控的二维材料转化为实际可用的功能器件面临多重障碍, 例如, 虽然高压能显著增强某些二维材料的超导转变温度, 但维持器件长期工作在高压环境下的能耗和成本问题尚未解决.

      未来高压科学的发展可能集中在以下几个方面: 1)高压装置的进一步优化, 目前DAC技术已能实现数百GPa的压力, 但在更高压力下金刚石的机械稳定性和传压介质的静水压性能仍需改进; 2)原位表征技术的集成, 高压下的原位测量技术, 如X射线衍射、拉曼光谱、光学吸收谱等已较为成熟, 但如何实现更高时空分辨率的动态观测仍需突破; 3)高压与多场耦合调控, 单一压力调控已展现出丰富物理现象, 而结合电场、磁场等多物理场调控, 有望揭示更复杂的量子行为. 例如, 高压下二维材料的谷极化、自旋-轨道耦合效应可能为自旋电子学提供新机遇; 4)高压技术在能源与信息领域的应用, 高压可优化太阳能电池等能源材料的性能. 例如, 二维钙钛矿在高压下的带隙窄化和载流子寿命延长为高效光伏器件设计提供了新思路; 而高压诱导的非晶化、相变等行为可用于开发新型存储材料; 此外, 高压敏感材料在传感器领域也有潜在应用.

      总之, 高压实验技术作为一门跨学科的研究手段, 将继续推动材料科学、凝聚态物理和化学等领域的前沿发展. 通过技术创新和多学科交叉, 高压科学有望在未来揭示更多未知的物理现象, 并为解决能源、信息、环境等重大挑战提供新思路.

    参考文献 (107)

目录

/

返回文章
返回