全文HTML
-
7Li和7Be在宇宙原初核合成(primordial nucleosynthesis)中扮演着重要角色,其直接或间接参与由H,He等元素进一步合成C,O等更重元素的过程[1]。目前,大爆炸核合成(big bang nucleosynthesis, BBN)理论已经能够对宇宙中2H和4He 的原初丰度给出较好的预测,然而,根据BBN计算所得的Li元素原初丰度却高于观测值约3倍[2]。进一步了解7Li和7Be的能级结构,尤其是高激发态能谱及其波函数相关性质,有助于探索潜在的涉及7Li和7Be在宇宙早期产生和湮灭的相关反应,进而为解决宇宙学Li问题提供思路。作为七核子系统,7Li和7Be原子核中能够形成丰富的团簇结构[3−5],包括α+t (3He),6He (6Li)+p,5He (5Li)+d以及一些三体或四体团簇结构等。基于原子核中的团簇结构,人们发展出各种微观团簇模型[6−7],这些理论模型对于描述团簇结构明显的轻核十分有效。因此,有必要基于团簇模型对7Li和7Be的能级结构,尤其是高激发态能级进行研究。
微观模型(microscopic models)采用对核子空间坐标完全反对称化的波函数,通过求解本征方程,得到系统的本征能量和本征波函数,能够在不依赖参数的情况下较为准确地描述轻核的一些重要性质。本文通过生成坐标法(generator coordinate method, GCM)[8]求解7Li和7Be的能谱和波函数。GCM首先假定系统中一些团簇的存在,并为其赋予生成坐标(generator coordinates),通过叠加 一系列具有不同生成坐标的基矢波函数并代入本征方程解得叠加系数,即得到系统的波函数。通过在系统中假定团簇的存在以缩小基矢函数的位形空间,GCM能够在不破坏系统波函数物理意义的情况下,大幅缩减计算量,因此被广泛应用于对原子核系统的束缚态以及散射问题的研究中。
1970年代以来,人们利用微观团簇模型对7Li和7Be进行了大量理论研究[9−12],但受早期计算设备限制,其中大多数工作仅考虑α+t (3He)两体团簇模型。由于泡利不相容原理,α是最为稳定的原子核团簇,具有较高的结合能,一般情况下,原子核中的α团簇很难被破坏,因此,在较低的能量范围内处理原子核问题时假定α团簇的存在是合理的。但3H或3He结合能相对较低,远不如α稳定,因此在原子核中不一定会形成很好的团簇结构。另一方面,近来有实验显示,在7Li,7Be以及其他一些轻核中还可能存在较为明显的6Li+n和6He+p等壳结构[13−15]。这些结构的形成,是简单的α+t (3He)两体团簇模型所无法描述的,因此,我们采用
$ \alpha+{\mathrm{n}}+{\mathrm{n}}\,({\mathrm{p}})+{\mathrm{p}} $ 四体团簇模型对7Li和7Be进行GCM计算,并对其基态和激发态能谱进行分析。 -
在微观模型中,原子核的波函数可以写为对每个核子的空间运动学坐标进行反对称化的Brink波函数[16]:
其中单粒子波函数为
其空间部分取以生成坐标
$ {\boldsymbol{R}}_j $ 为中心、$ b $ 为宽度的高斯波包,$ \chi_k $ 和$ \tau_k $ 分别为其自旋与同位旋部分。在式(1)中,$ {\boldsymbol{R}}_1 $ ,$ {\boldsymbol{R}}_2 $ ,$ {\boldsymbol{R}}_3 $ 和$ {\boldsymbol{R}}_4 $ 分别为α粒子和其他三个单核子团簇的生成坐标。利用角动量和宇称投影算符可以将内禀Brink波函数(1)投影到特定的角动量和宇称本征态上。然而,Brink波函数中每个核子的波函数都被限制在特定的生成坐标附近,这显然与实际的原子核系统不符。为了得到更接近实际情况的原子核波函数,需要以角动量和宇称投影的Brink波函数为基矢,对一系列不同的生成坐标进行叠加
其中
$ \{c_{i,K}\} $ 为叠加系数。将波函数(5)代入到薛定谔方程,可得到Hill-Wheeler方程通过矩阵对角化求解此式即得到系统波函数(5)中Brink基矢波函数的叠加系数
$\{c_{i,\,K}\}$ 和本征能量$ E $ 。 -
根据上述理论模型,我们对7Li和7Be原子核进行了两体、三体和四体GCM计算。其中,两体GCM计算中7Li和7Be的Brink基矢波函数分别取为α+t和α+3He结构,三体计算中取为
$ \alpha+{\mathrm{d}}+{\mathrm{n}} $ 和$ \alpha+{\mathrm{d}}+{\mathrm{p}} $ 结构,而四体计算中则取$ \alpha+{\mathrm{n}}+{\mathrm{n}}+{\mathrm{p}} $ 和$ \alpha+{\mathrm{n}}+{\mathrm{p}}+{\mathrm{p}} $ 结构,谐振子参数取为$b = {1.46}\;{\rm fm}$ 。在计算中,哈密顿量包含动能项、核子-核子中心势、自旋-轨道耦合势和库仑相互作用项:其中
$ T_{\rm{{c.m.}}} $ 为质心动能。核子-核子中心势采用Volkov No.2形式[17]:其中:
$ a_1={1.01}\;{\rm fm} $ ,$ a_2={1.8}\;{\rm fm} $ ,$ v_1={61.14}\;{\rm MeV} $ ,$ v_2= - {60.65}\;{\rm MeV} $ ,$ W=1-M $ ,$ M=0.6 $ ,$ B=H=0.08 $ 。自旋-轨道势取为G3RS势[18−19]其中:
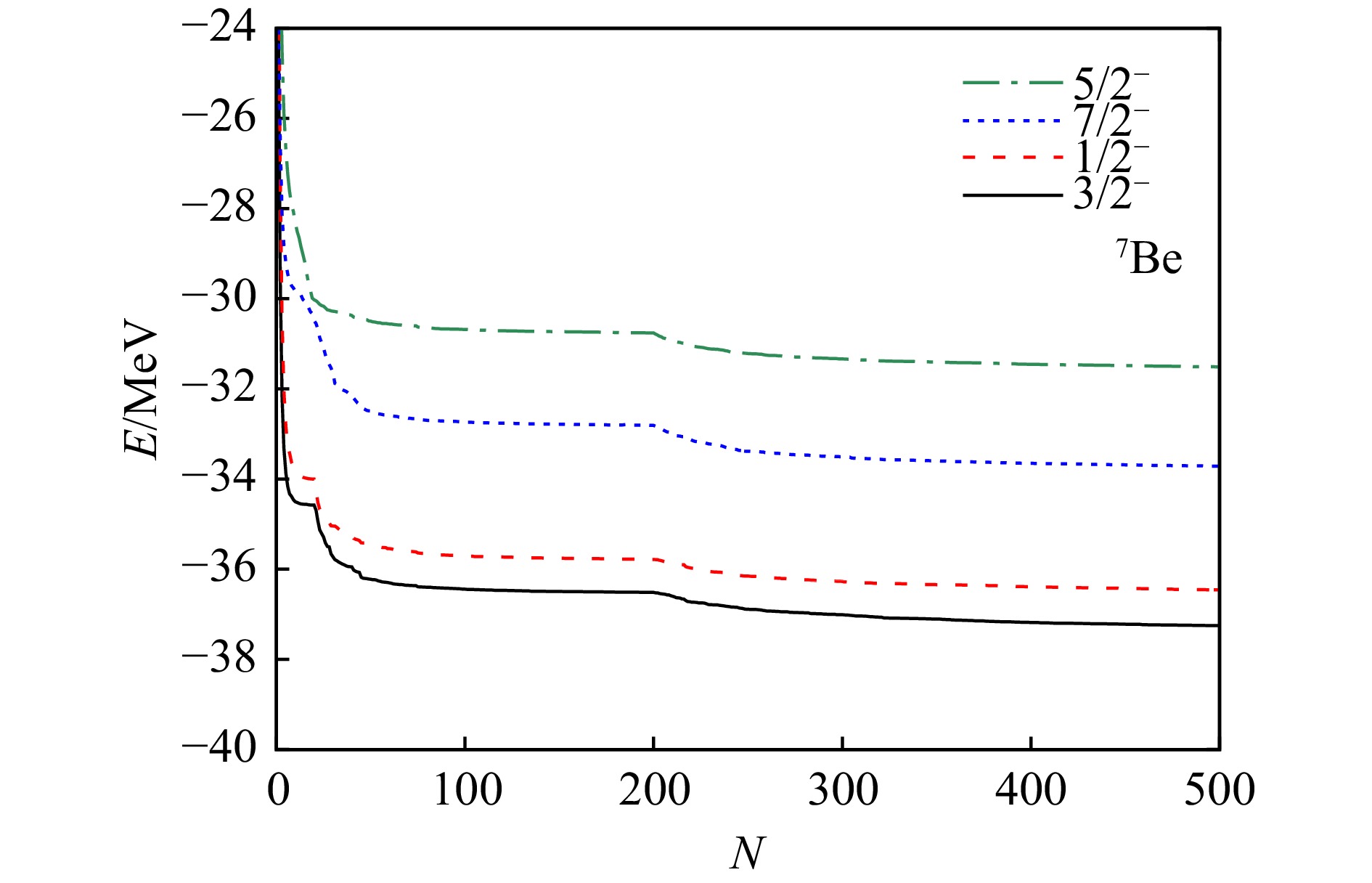
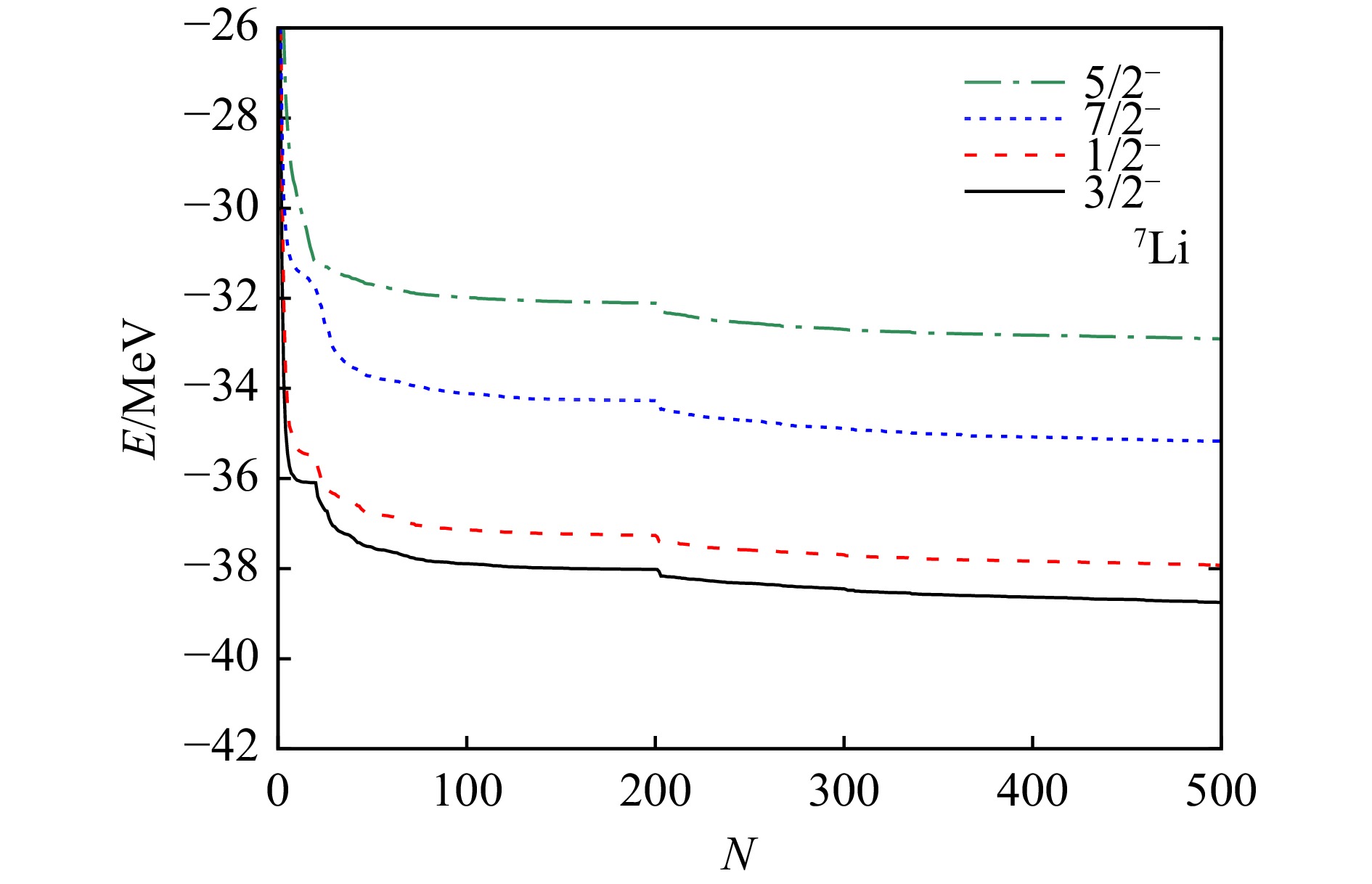
$v_0={2\;000}\;{\rm MeV}$ ,$ d_1 $ 和$ d_2 $ 分别取为 5.0 fm−2 和 2.778 fm−2。上述参数的改变会对能谱产生一定的影响,但本文目的在于讨论包含不同团簇结构的关联对计算结果的影响,因此,不失一般性,我们皆采取微观团簇理论中的常用取值。图1 和图2 分别为7Li和7Be的GCM计算所得基态
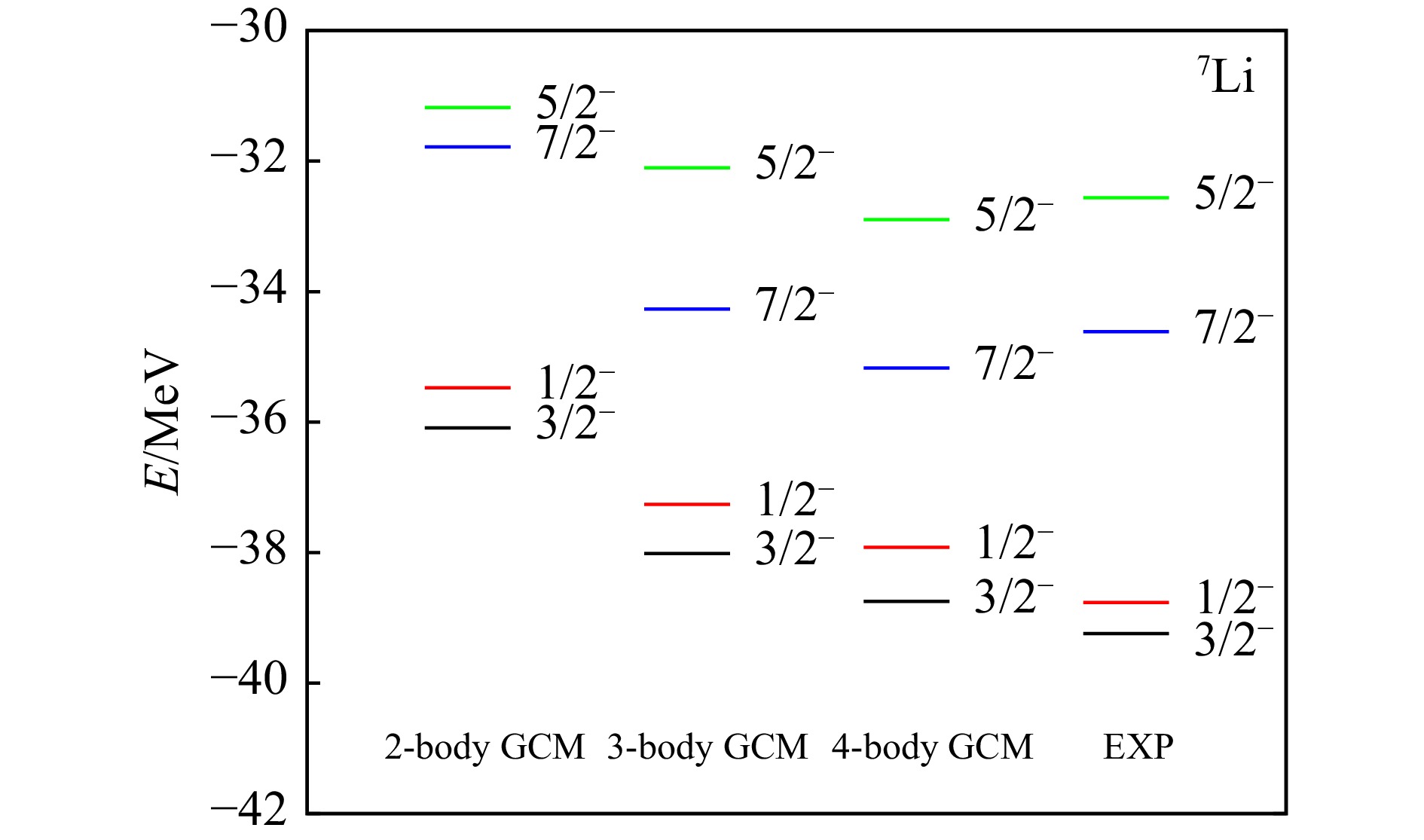
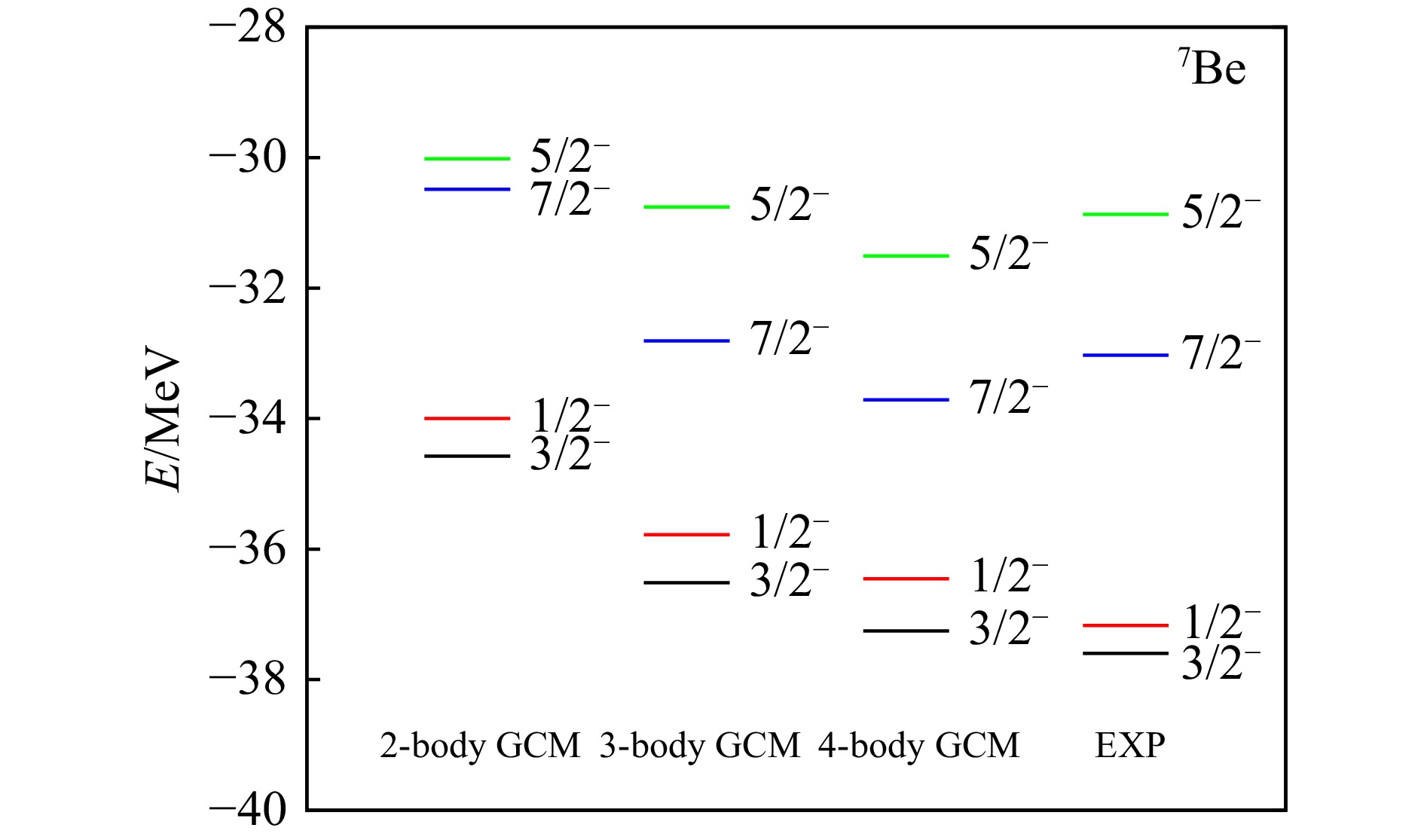
$ 3/2^- $ ,和三个激发态$ 1/2^- $ ,$ 7/2^- $ 和$ 5/2^- $ 的本征能量随基矢数目N的变化。由于7Li和7Be具有相似的结构,其能量变化的趋势类似。单个Brink波函数计算所得的能量较高,与实验值偏离较大,这是由于原子核内的团簇被固定在生成坐标处,不符合真实量子系统的情况。随着不同生成坐标构型基矢的加入,求解方程(6)得到的本征能量逐渐降低,图中基矢数目$ N=20 $ 和$ N=200 $ 分别为开始加入三体基矢和四体基矢处,该处能量下降较快,因此在GCM计算中扩大基矢空间对能量 值影响较为明显。最终,随着基矢数目的不断增加,各能级能量变化趋于平缓,说明我们计算中所取的基矢数目足够得到收敛的能量值。GCM计算得到的7Li和7Be的能谱和实验数据如图3 和图4 所示,作为一组镜像核,7Li和7Be能谱性质十分接近。我们列出了在GCM中分别取两体、三体和四体团簇结构的计算结果,其中,三组计算下7Li基态能量分别为−36.09 MeV,−38.02 MeV和−38.75 MeV,7Be的基态能量分别为−34.58 MeV,−36.52 MeV和−37.25 MeV。计算结果表明,两体的GCM计算可以得到正确的能级顺序,但能级之间的间距与实验有较大偏差。其中激发能较高的
$ 7/2^- $ 和$ 5/2^- $ 两个能级,实验上两能级相差2.05 MeV,而两体GCM计算 所得的两能级仅相差0.61 MeV。此外,两体GCM计算得到的基态能量高于实验值约3 MeV,而三体和四体GCM计算得到的基态能量与 实验值的偏差均不高于2 MeV。由此可见,仅通过两体α+t (3He)团簇模型无法较好地描述7Li (7Be)的能谱,这暗示了在7Li (7Be)的基态 和激发态中存在更为丰富的团簇结构。随着三体和四体团簇基矢的引入,GCM计算所得能谱更加接近实验能谱。其中,三体GCM计算已经能够得到正确的能级间隔,
$ 7/2^- $ 和$ 5/2^- $ 两能级相差2.16 MeV,接近实验值。加入四体团簇基矢则进一步使能谱整体降低。其中,基态$ 3/2^- $ 和第一激发态$ 1/2^- $ 的能量相比三体计算均降低了约0.7 MeV,更加接近实验值。而随着能谱整体降低,$ 7/2^- $ 和$ 5/2^- $ 的能量开始低于实验值,较三体计算所得结果更加偏离实验数 据。这是由于GCM仅适用于处理束缚态问题,而实验上的$ 7/2^- $ 和$ 5/2^- $ 态是激发能较高的共振态,GCM计算只能近似给出其能级和波函数。因此,通过增大GCM的基矢空间并不能更好地描述$ 7/2^- $ 和$ 5/2^- $ 两个共振态,而需要更有效的共振态处理方法。利用GCM计算所得的各能级波函数,我们计算了7Li和7Be的原子核半径,见表1和2,其中四体GCM计算所得7Li基态的核半径接近实验值(2.42 fm)[21]。通过对比不同组GCM计算结果,我们发现对于7Li和7Be,
$ 3/2^- $ 和$ 1/2^- $ 态的核半径随基矢空间的扩大变化较小,说明两体团簇模型在一定程度上能够得到其正确的波函数。而$ 7/2^- $ 和$ 5/2^- $ 态在仅考虑两体结构的情况下计算得到的核半径与最终四体计算的结果差距较大,这可能是由于在计算能量高于α+t (3He)阈值的激发态时,两体团簇模型引入了本不应该存在于束缚态波函数中的连续态成分,而只有通过在计算中引入三体甚至四体团簇成分,才能得到更加接近实际情况的束缚态波函数。 -
我们基于四体微观团簇模型开展了7Li和7Be的GCM计算,并与两体和三体计算结果对比。结果发现,虽然两体GCM计算能够得到正确的能级顺序,但其能谱的一些重要性质如基态能量和能级间距等与实验能谱差别较大。通过在GCM计算中加入三体和四体团簇结构,得到了更加符合实验数据的能谱,说明在7Li和7Be的基态和激发态中不止存在单一的α+t (3He)团簇结构,而是存在较为丰富的团簇结构组分。此外,两体团簇模型计算得到的波函数也无法准确得到一些较高激发态的核半径。因此,为了更好地描述7Li和7Be原子核的基态和激发态性质,在计算中加入三体及四体结构是必要的。基于我们得到的更加精准的基态和激发态波函数,有望进一步研究7Li和7Be的相关核反应性质。

 首页
首页 登录
登录 注册
注册




 下载:
下载: