全文HTML
-
2017年,人类首次通过引力波观测到双中子星并合,该事件即标志着人类步入了多信使天文学时代的GW170817事件[1]。中子星的独特性质为我们提供了极端条件场景下的物理规律检验平台,包括强场下的引力理论检验、低温下的高密核物质性质以及支撑恒星演化的高能天体物理现象[2]。随着未来LIGO-Virgo-KAGRA的运行,还有诸如Einstein Telescope[3]、Cosmic Explorer[4]的投入使用,我们将会获得更多关于中子星的精确观测数据,为认识中子星的性质以及高密核物质的物态提供天文观测支持。
另一方面,目前对于暗物质的了解还不够深入。1933年,Zwicky发现后发座星系团中所有恒星的质量仅提供了防止星系逃脱星系团引力所需质量的1%,这表明后发座星系团中有大量不可观测但具有质量的物质,即暗物质[5−6]。VERA进一步研究发现,在距银心大于8.5 kpc的区域,恒星旋转曲线变平,这与牛顿平方反比定律所预言的下降趋势不符,这进一步支持了暗物质存在的猜想[7−8]。在过去的几十年,天体物理学家和实验物理学家们试图通过不同途径找到暗物质存在的证据,但目前也仅有间接性的证明[9−14]。关于暗物质的形成及性质,有许多文献对其进行了总结[15−19]。近年来,许多研究将暗物质与中子星结合起来,希望利用中子星这一天然极端环境对暗物质进行更好的限制[20−33]。对于含暗物质中子星的结构,目前主流观点认为具有三种可能。第一种结构是拥有一个核物质核和一个暗物质壳(或暗物质晕);第二种结构是拥有一个暗物质核和核物质壳;在第三种结构中,含暗物质中子星有一个混合核(即核物质和暗物质同时存在)和一个暗物质壳或一个核物质壳[34]。除此之外,中子星对暗物质的吸积或暗物质星与中子星间的双星合并也被广泛研究。研究人员对中子星与暗物质的捕获作用进行了一系列计算[35−37],Hippert等[38]通过对镜像中子星与普通中子星进行双星合并数值模拟后发现,合并产物也可能是一颗质量介于1.2~1.6
$ { {M}}_\odot $ 的含暗物质中子星,这为含有较高暗物质质量比例中子星的形成提供了新的依据。由于中子星的许多性质直接取决于物态方程的选择,而目前对于中子星内核的高密度核物质的物态方程的认识还存在很大的不确定性,这意味着通过高密核物质的物态方程和相对论框架下的流体静力学平衡方程计算给出的中子星性质参量也具有很大的不确定性,因此人们期望寻找和建立物理量间不依赖于物态方程的关联,即普适性关系。近十年来,人们建立了大量的普适性关系,如著名的I-LOVE-Q关系,即转动惯量I,潮汐洛夫数λ以及归一化四极矩Q之间的关系[39],不同准振荡模式之间的关系[40−41]。另外,Jiang等[42]基于引力结合能建立了致密星之间的普适性关系;Sun等[43]建立了对于快速旋转中子星的准普适关系;Chen等[44]将普适关系进行了补充,建立了快转夸克星的振荡模式与其他性质量之间的关系。对于部分难以观测的物理量,普适性关系的研究提供了一个对其进行预测的途径。例如,如果对I-Love-Q关系中的某两个量进行了测量,那么剩下的那个量就可以通过该关系预测,而不必考虑物态方程的选择。而对于部分仍存在很大不确定性的物理量如半径R,潮汐形变Λ等,普适性关系可以进一步减小其不确定度。如Yang等[45]基于对称能斜率L = (54±8) MeV的前提,利用普适关系得到R1.4 = 12.00~12.58 km,Λ1.4 = 321.7~561.3。Cai等[46−47]基于无量纲TOV方程,基于级数展开的方法得到中子星质量半径与核心区高密物态的关系,极大的降低了中子星核心区域物态的不确定性,并对其声速进行了进一步约束。对于普适性关系的成因,Yagi等[48]认为一种可能的解释是,普适性关系如I-Love-Q关系与NS的壳层性质联系更为紧密,而壳层物质恰恰对应着我们所熟知的低密核物质,其核物理不确定性是最低的。在这种机制下的壳层性质具有相似性,因此具有一定的普适性。
本文我们利用线性相关分析方法,对暗物质中子星的各种性质参量进行分析。线性相关分析是研究两个量之间相关性质的有效方法。它的系数r反映了两个量之间线性相关的强弱,可以表示为
其中:X、Y表示研究的对象;Cov(X, Y)为协方差;D(X)、D(Y)分别表示X、Y的方差。相关系数r的绝对值越接近于1,说明两个量之间的相关强度越大,越接近线性;反之,若越接近于0,两个量之间的关联度越小。通过比较含暗物质中子星与普通中子星的普适性关系结果,我们将对普适性关系的成因有进一步的理解,进而加深对于核物质的性质理解。另外,两者普适性关系间的可区分效应将为对于暗物质的天文观测提供新的思路,并给出理论支持。
本文第一部分将对文章所使用的核物质与暗物质物态方程进行介绍,并简要说明含暗物质中子星所使用的二流体TOV方程。第二部分给出不同物理量之间的关联度分析结果,并据此进行普适性关系的研究。最后一部分将给出结论并进行总结。
-
物态方程描述了物质密度、压强等参量之间的函数关系。目前人们通过核物理理论和地面核物理实验对于核物质低密度端的物态方程的认识相对比较清楚,但对于高密度段,特别是两倍饱和核密度以上的核物质物态方程的认识还具有很大的不确定性。近年来,关于中子星的天文观测取得了较大的突破,例如LIGO等对双中子星并合的引力辐射观测,NICER对中子星质量半径的同时观测等,从而开辟了通过天文观测反向约束核物质的状态方程的新途径。
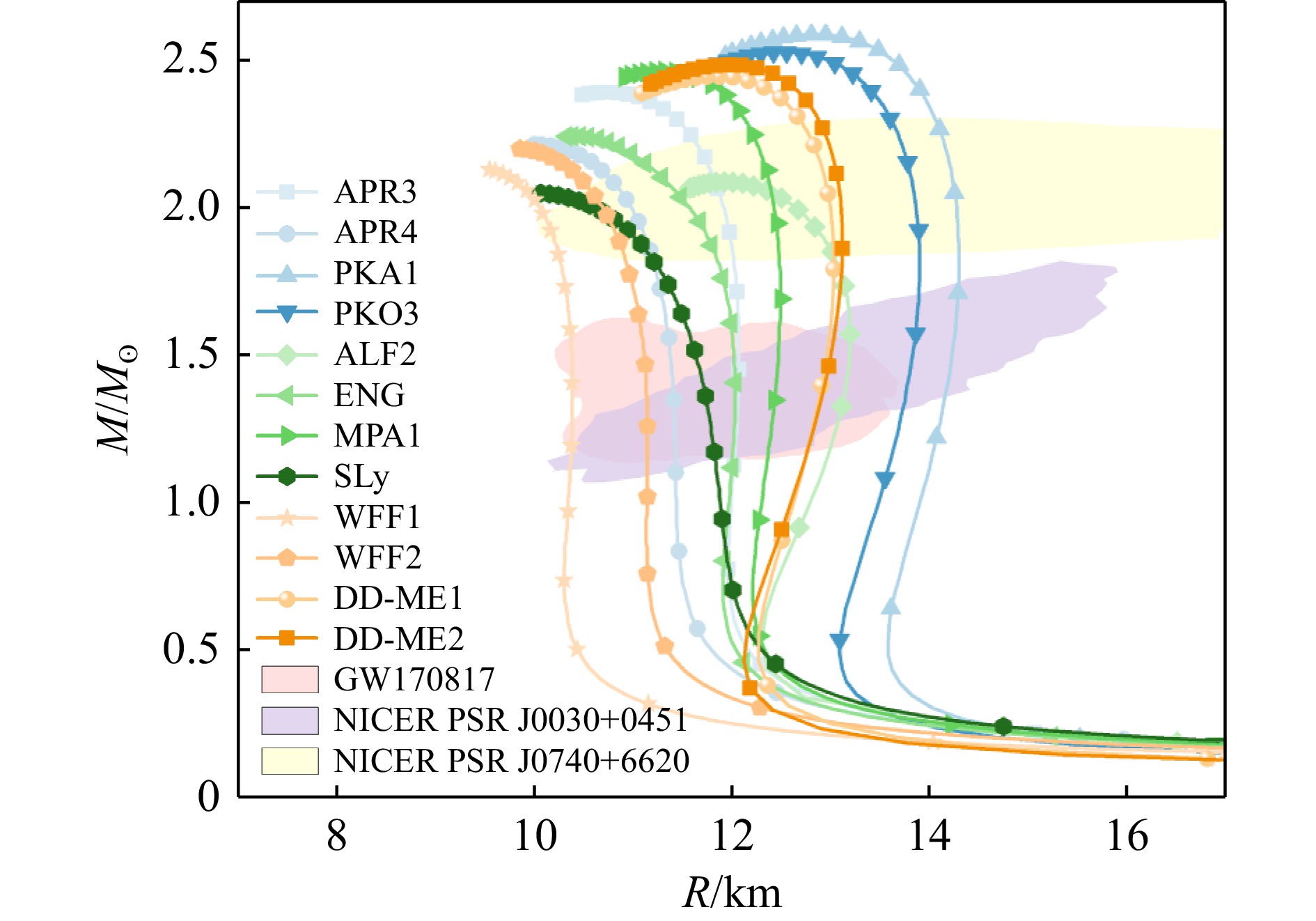
本文所使用的物态方程如下:ALF2[49],APR3[50],APR4[50],ENG[51],MPA1[52],SLy[53],WFF1[54],WFF2[54],DD-ME1[55],DD-ME2[56],PKA1[57],PKO3[58]。图1给出了所使用物态的M-R关系曲线。
而由于暗物质的性质尚未确定,这里我们考虑费米粒子暗物质,并且只用简单的模型来表示暗物质的物态方程。我们使用的物态是零温理想费米气体。在一定的范围内,该物态也可以用多方物态来近似。零温理想费米气体的状态方程如下[61]:
其中
μ为粒子质量,而n是暗物质粒子的数密度。
-
对于含暗物质中子星,假设暗物质和核物质之间只存在引力相互作用,此时不同组分的密度和压强可以分开计算获得。对于内部具有两种仅通过引力互相作用的流体的静态中子星,我们使用二流体TOV方程[62]:
其中下标B和D分别代表了核物质和暗物质。εi(r)(i = B, D, 下同), Pi(r),Mi(r)分别代表半径r处对应组分的能量密度、压强以及半径r内的质量,不带下标的表示两组分之和(如P(r) = PB(r)+PD(r));c和G为光速和万有引力常数。积分从r = 0,M(r) = 0开始,给定核物质和暗物质的初始能量密度和压强,代入二流体TOV方程计算得到不同组分压强为0时对应的半径,数值较大者则为含暗物质中子星总半径R。
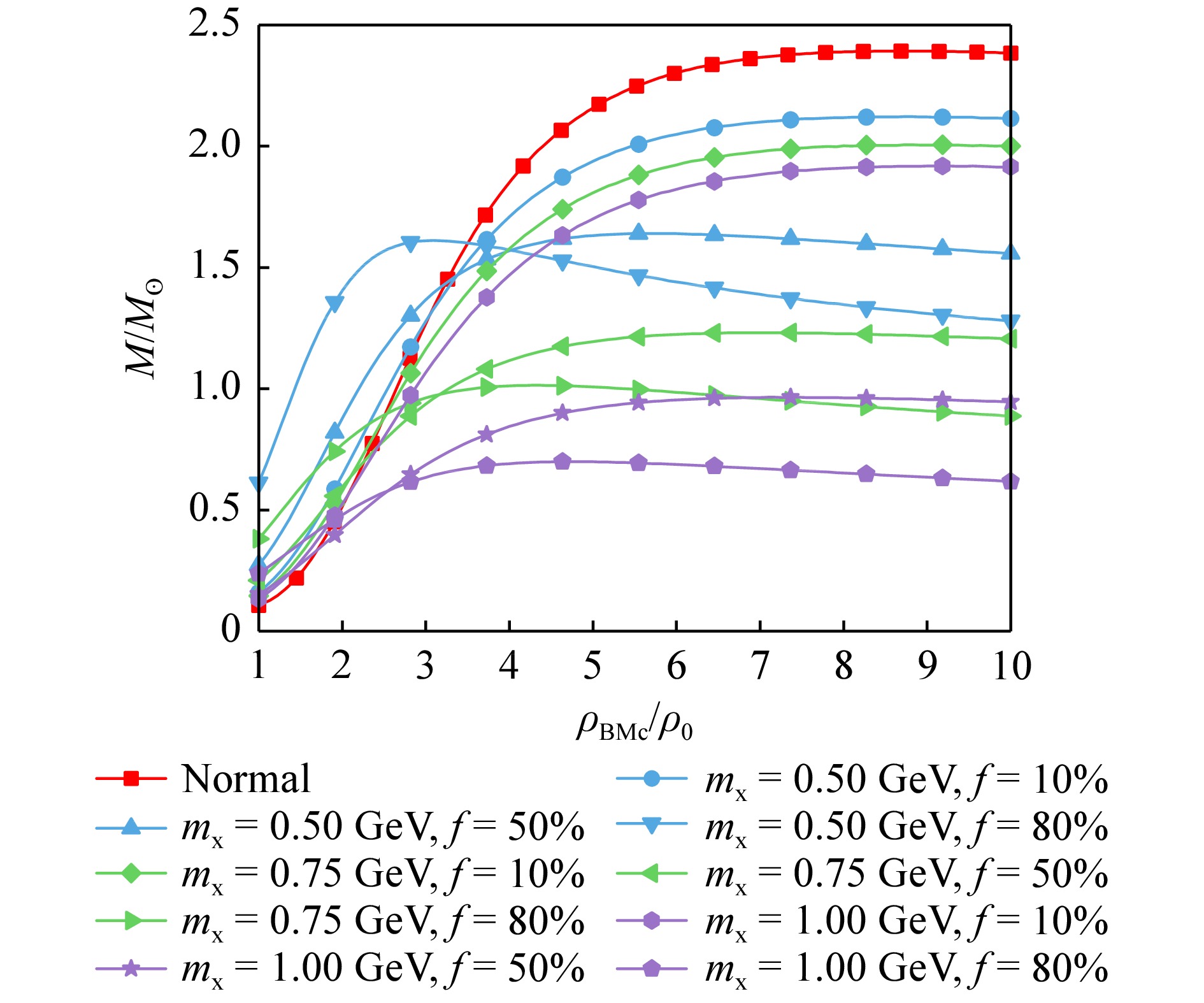
图2给出了核物质物态为APR3时的含暗物质中子星M-ρBMc关系(ρBMc指核物质中心密度,ρ0为饱和核密度,下同)。从图中可以看到,暗物质的存在减小了中子星的最大质量,且暗物质粒子质量越大,质量比例越高,最大质量的减小程度越明显。另外,随着含暗物质质量比例增大,最大质量点对应的核物质中心密度减小。
-
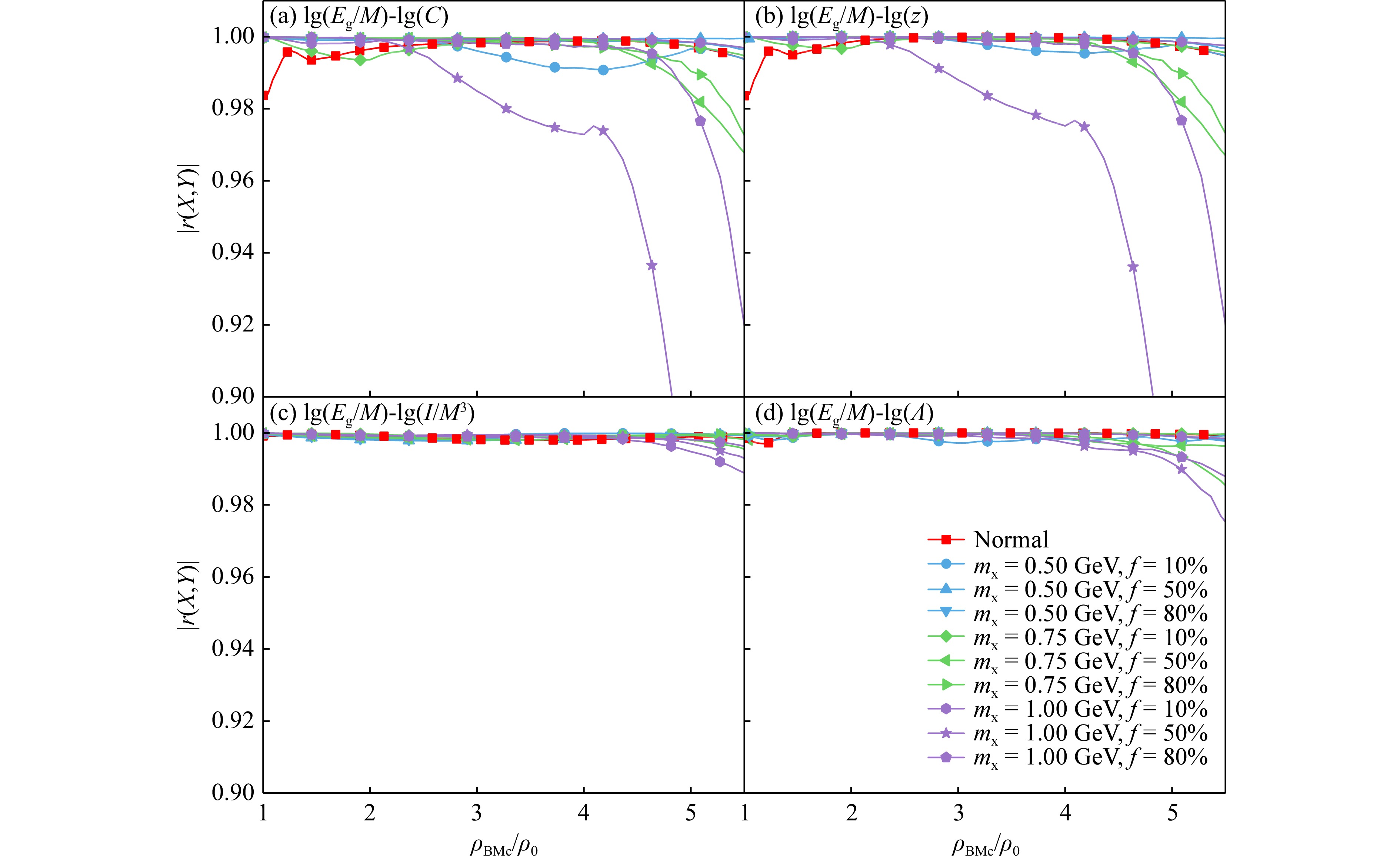
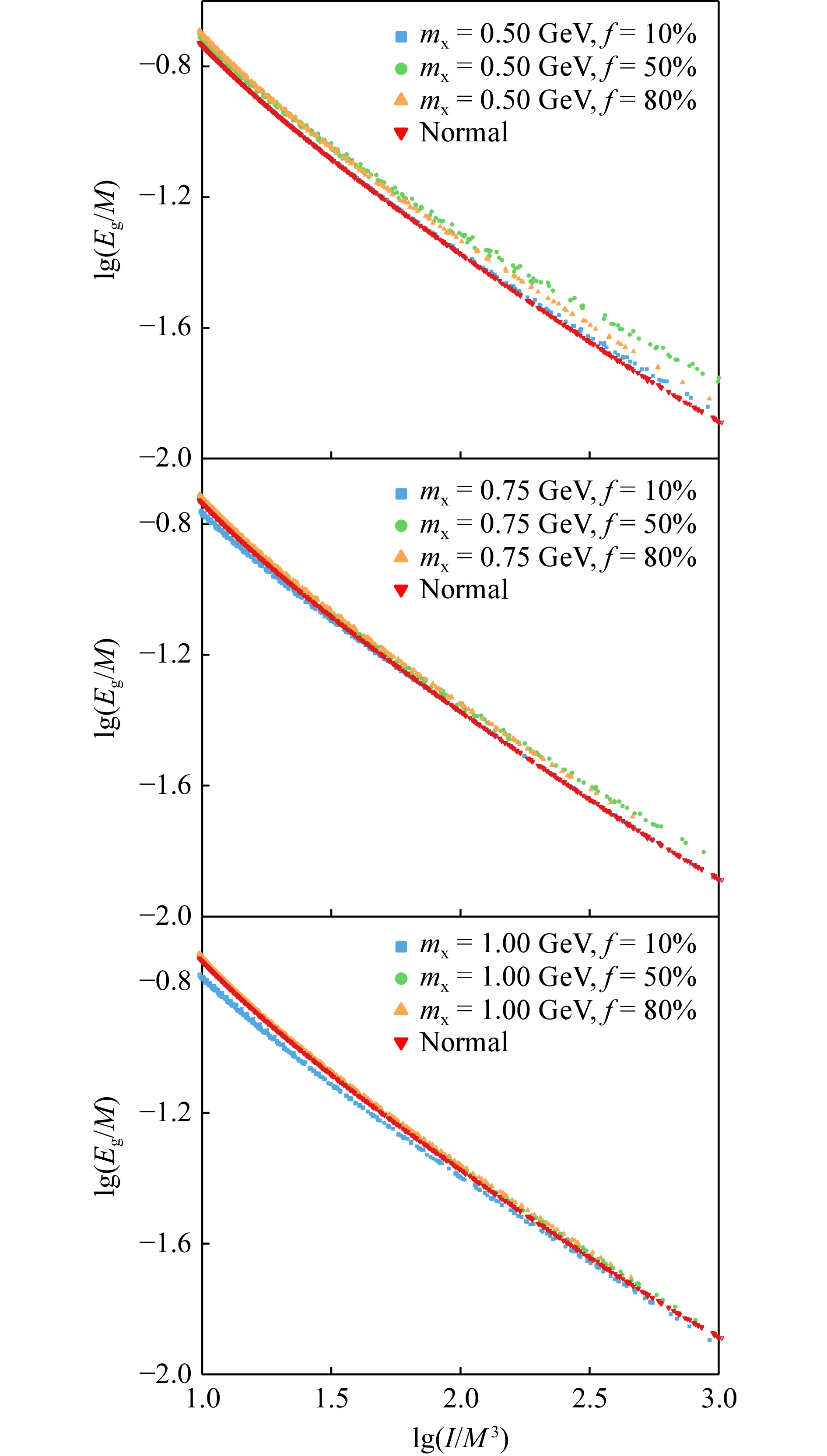
在普适性关系研究中,我们可以首先利用线性相关分析筛选出具有良好关联度的性质参量,然后再进行具体分析。在图3中我们分别给出无量纲引力结合能Eg/M与致密度C、表面引力红移z、无量纲转动惯量I/M3、潮汐形变Λ的关联度(各量均取对数形式,下同)。
首先可以明显看到,图3所示的四组关系在核物质中心密度介于1~5ρ0时均保持着良好的关联度。进一步观察可以发现,lg(Eg/M)与lg(C)和lg(Eg/M)与lg(z)关系在mx = 1.00 GeV,f = 50%时,在核物质中心密度增大的情况下出现了关联度明显降低的情况。而对于lg(Eg/M)与lg(Λ)和lg(Eg/M)lg(I/M3)关系,关联度受核物质中心密度增大的影响并不明显,两组关系的关联度均在强关联区间进行窄幅波动,这表明对应性质参量在暗物质存在的情况下仍具有良好的关联度,暗示着可能存在普适关系。
我们还可以看到,lg(Eg/M)与lg(C)和lg(Eg/M)与lg(z)的关联度曲线具有相似性,这是由于表面引力红移z与致密度C之间存在函数关系,导致两者的关联度表现出了类似的变化趋势。另外,在四组普适性关系中,关联度变化最为剧烈的均为mx = 1.00 GeV的情况,这是由于与另外两种粒子质量的暗物质相比,此时的暗物质物态软化最明显,进而影响了中子星的全局性质。
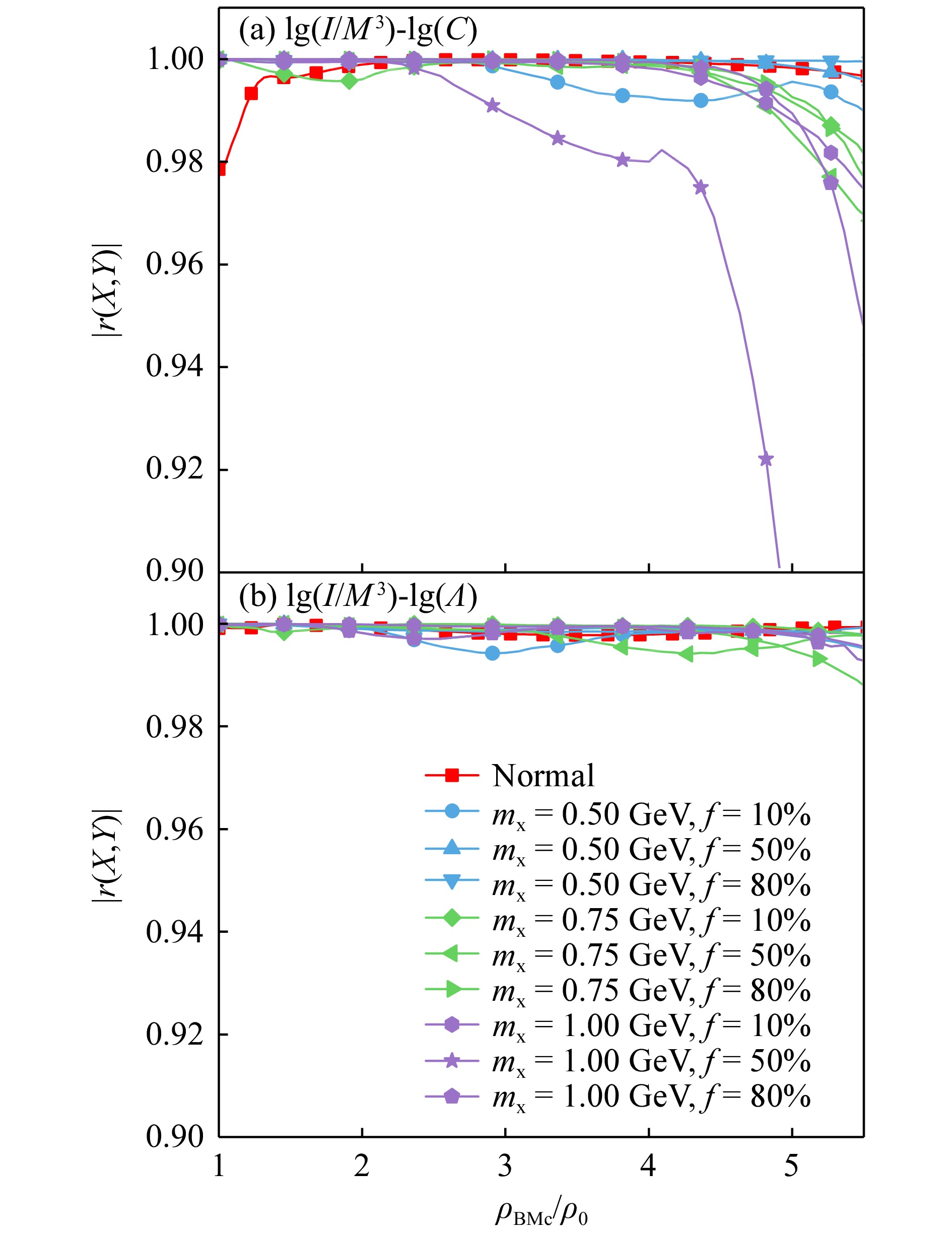
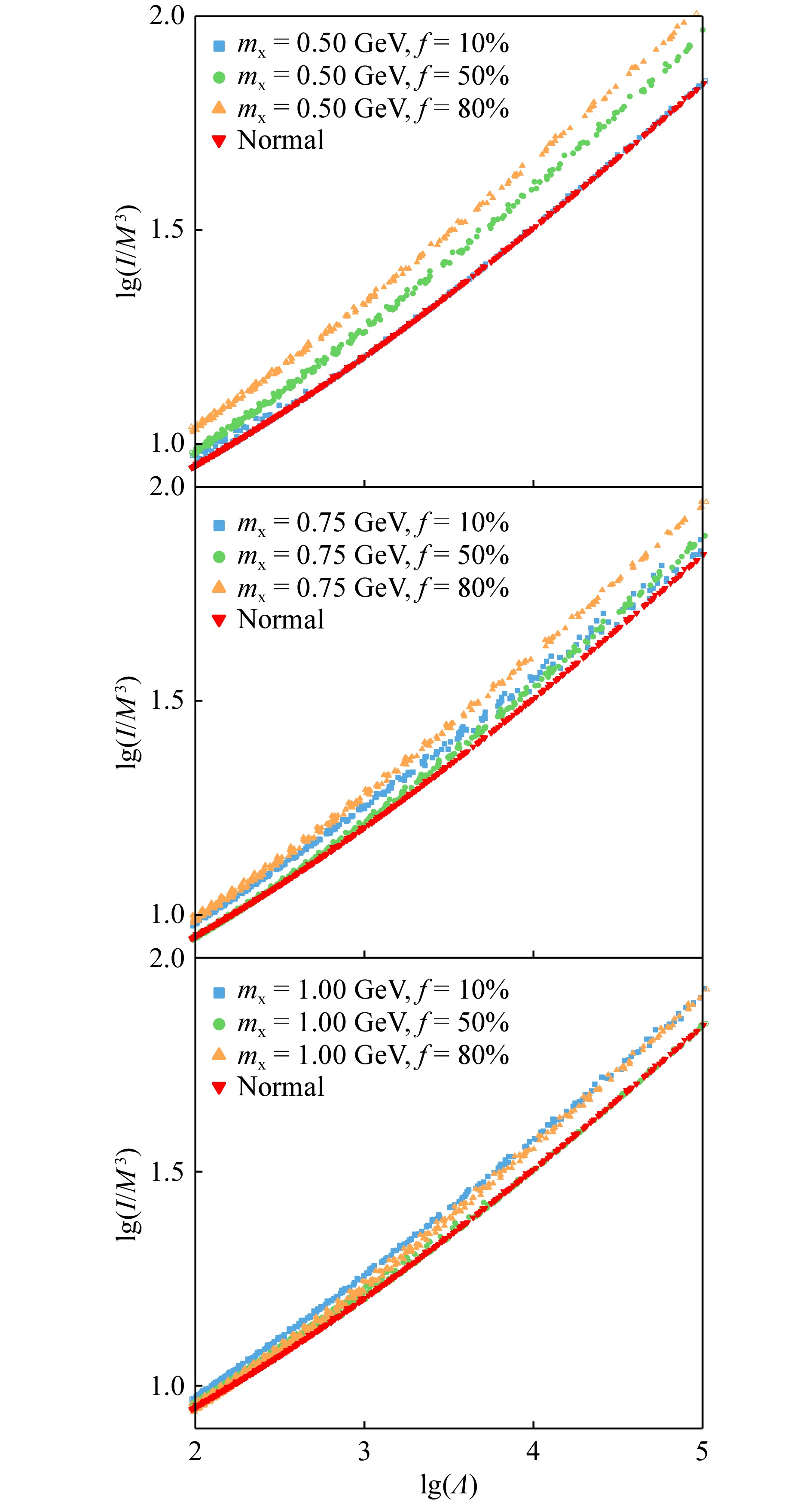
在图4中,我们给出了无量纲转动惯量I/M3与致密度C和潮汐形变Λ的关联度。同图3的结果类似,对于lg(I/M3)与lg(C),其关联度在mx = 1.00 GeV,f = 50%时也出现了关联度明显降低的情况;而对于lg(I/M3)与lg(Λ),其关联度一直保持在强关联区间,这代表暗物质的存在不会影响对应性质参量之间的关联度,同样暗示了可能存在的普适关系。
需要注意的是,虽然许多性质参量在暗物质存在时仍能保持良好关联度,但由于不同暗物质粒子质量和质量比例可能会使得含暗物质中子星与普通中子星的普适性关系产生区分效应,因此对于上述拥有良好关联度的性质参量,我们还需要具体研究暗物质带来的差异。
综合上述关联度的结果,我们在随后的内容中将对Eg/M与Λ,Eg/M与I/M3,以及I/M3与Λ三组保持较好关联性的关系进行普适关系研究。
-
Lattimer等[63]曾提出中子星结合能与致密度之间具有普适性关系,换句话说,中子星结合能隐含了中子星致密度的信息[63]。然而,中子星总结合能包括核结合能和引力结合能,而只有后者具有质量分布信息。因此,Jiang等[42]认为引力结合能是研究中子星普适关系的良好性质参量。
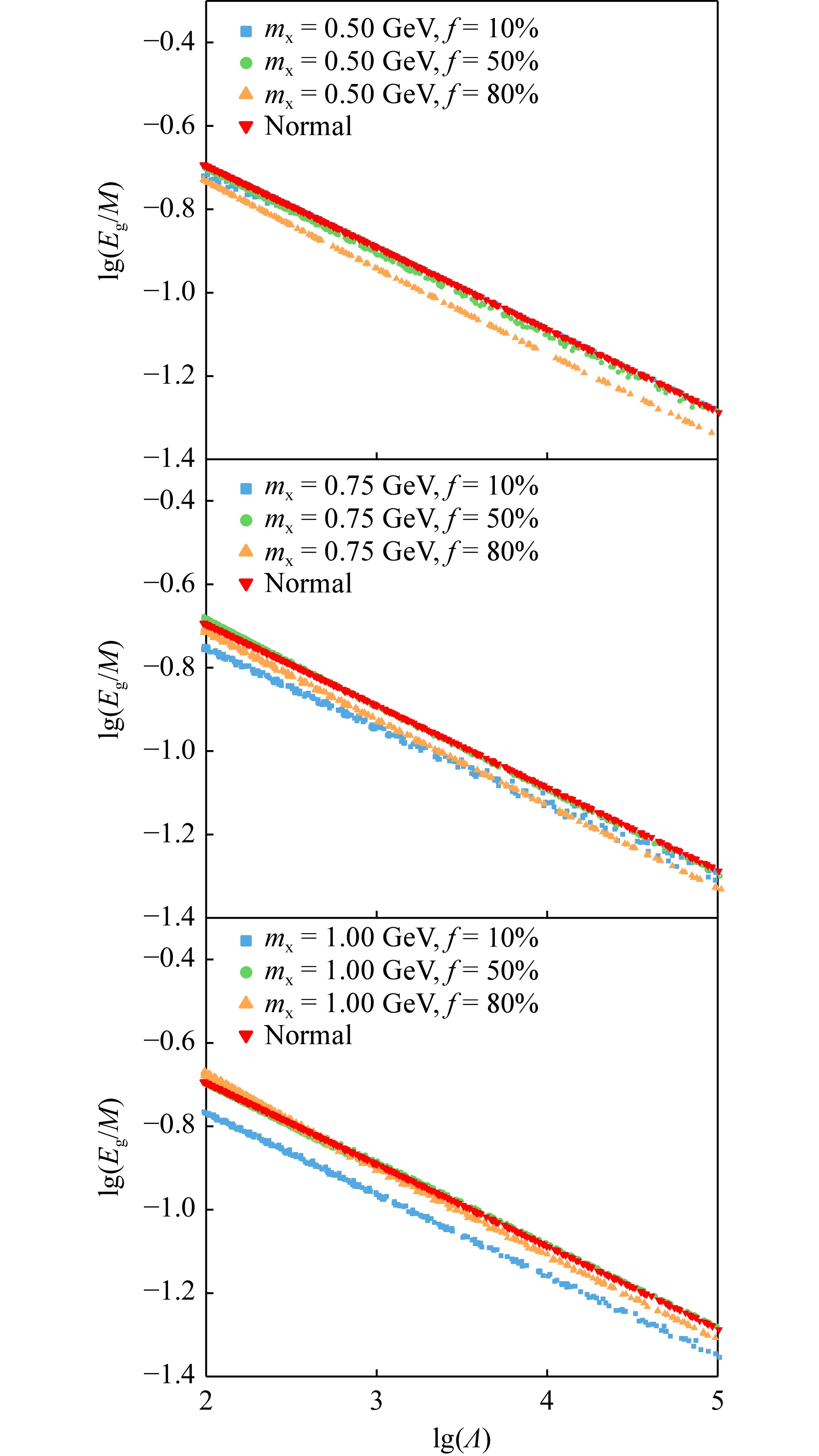
图5给出了lg(Eg/M)-lg(Λ)的普适关系曲线,两者之间存在明显的负相关关系,且与普通中子星的结果相比,暗物质的存在并没有扭转其相关性。负相关关系的成因是由于质量越大的中子星一般刚度也越大,即响应外场时所发生的四极形变越小,潮汐形变越小(即图像左侧区域对应的中子星质量较大);而无量纲引力结合能通常正比于中子星的质量,因此引力结合能与潮汐形变存在着负相关关系。
从图5我们可以看到,改变暗物质粒子质量和含暗物质质量比例对于普适关系的曲线的影响十分明显。例如,对于含相同暗物质质量比例的中子星,当质量比例f = 10%时,粒子质量的提高使得含暗物质中子星的引力结合能有所降低,但小质量含暗物质中子星的减小程度更为明显。质量比例f = 50%时,粒子质量的提高增加了大质量含暗物质中子星的引力结合能。质量比例f = 80%时,粒子质量的提高使得含暗物质中子星的引力结合能有所增加,但大质量含暗物质中子星的增加程度更明显。正是由于暗物质粒子质量和质量比例的改变给引力结合能带来的不同影响,普适关系曲线产生了观测上的可区分效应。该关系中,区分效应最明显的是暗物质粒子质量mx = 0.75和1.00 GeV时,质量比例f = 10%的普适关系曲线,粒子质量mx = 0.50 GeV且质量比例f = 80%时可区分效应次之。当观测上获得更多相关性质参量的数据,该关系中的可区分效应将可以作为判断暗物质存在的初步依据。
-
图6给出了lg(Eg/M)-lg(I/M3)的普适关系曲线,两者之间同样存在明显的负相关关系。但要注意到的是,这里我们使用了转动惯量的无量纲形式,对于小质量中子星,无量纲转动惯量的值应该更大,因而图6左侧对应着质量较大的中子星,右侧对应着质量较小的中子星。而从前文我们可以得知,无量纲引力结合能正比于中子星质量。因此,lg(Eg/M)与lg(I/M3)之间存在负相关关系。
同样地,暗物质的存在并没有扭转该关系的相关性,且对比起lg(Eg/M)-lg(Λ)关系,除了mx = 0.50 GeV时,在含暗物质中子星质量较小时出现了稍微明显的区分效应,其他粒子质量下暗物质的存在并未使普适性关系产生显著的区分效应。由于引力结合能和转动惯量都包含了中子星质量分布的信息,通过该关系我们可以发现,理想费米气体作为暗物质的存在对于中子星质量分布的影响并不明显,使得不同暗物质粒子质量和含不同暗物质质量比例下的中子星仍能保持与普通中子星相似的质量分布情况。这进一步说明,对于中子星普适关系的研究,无量纲转动惯量I/M3是一个良好性质的参量。
而虽然该关系并未产生观测上的可区分效应,其在普通中子星和含暗物质中子星的间高度一致性将帮助我们更深刻地认识普适性关系的成因,并对中子星结构有更多的了解。
-
图7给出了lg(I/M3)-lg(Λ)的普适关系曲线,两者之间存在着正相关关系。两者存在正相关的原因是显而易见的,从数学关系来看,lg(Eg/M)与lg(I/M3)、lg(Λ)都存在负相关关系,则lg(I/M3)与lg(Λ)理应存在正相关关系。而对中子星的性质进行分析我们发现,小质量中子星有着更大的潮汐形变以及更大的无量纲转动惯量值,这再一次解释了lg(I/M3)-lg(Λ)正相关关系的成因。
与lg(Eg/M)-lg(Λ)的普适关系曲线不同,该关系中区分效应最明显的是暗物质粒子质量mx = 0.50 GeV时,含暗物质质量比例f = 80%的情况,质量比例f = 50%的时候次之。且随着粒子质量的增加,含暗物质质量比例f = 80%的普适关系曲线与普通中子星的可区分效应减弱,而质量比例f = 10%的普适关系曲线与普通中子星的可区分效应增强。
-
对于线性关系较强的普适性关系,最常用的拟合方法是多项式展开,即将一物理量由另一物理量的不同幂次形式之和来表示。在式(13)中,X和Y分别对应着关系中的具体性质参量,“lg”代表取以10为底的对数,“i”表示拟合公式的保留项最高幂数,而高阶项则略去:
在这里,我们仅以lg(I/M3)-lg(Λ)关系为例,探讨通过普适性关系判断暗物质存在的可能性。对于该关系,良好的线性关联度使得我们可以以较少的项数取得较高的拟合精度,则式(13)变成如下形式:
其拟合系数及相关统计学误差由表1给出。对于拟合公式,残差平方和(RSS)代表着拟合公式的误差,决定系数(R2)表示因变量的变化中有多少百分比可以由自变量的变化来解释(越接近于1则解释能力越强)。从表1可以看出,对于不同暗物质粒子质量和含不同暗物质质量比例的中子星,lg(I/M3)-lg(Λ)关系的RSS相较于普通中子星的RSS均有所降低,其R2值则与普通中子星的结果相近,均保持在十分接近于1的水平。而在关系的拟合误差方面,其最大拟合误差均保持在2%~5%的范围内,体现出该关系良好的普适性。
另一方面,转动惯量的测量有望在最近数年内通过利用PSR J0737-3039这一独特的双脉冲星系统实现,该系统中的一颗脉冲星PSR J0737-3039A质量为 M = 1.338 1±0.000 7
$ { {M}}_\odot $ [64−65]。假设PSR J0737-3039A与GW170817中的双星具有相近的潮汐形变能力,即$ \varLambda _{1.3381}^{} = 190_{-120}^{+390} $ [1],我们可以通过结合表1预测其转动惯量范围为${\mathrm{I}} = 1.128 9_{-0.0018}^{+0.0017} \times 10^{38}\; {\mathrm{kg}} \boldsymbol\cdot {\mathrm{m}}^2$ ,该结果处于Landry和Kumar[66]预测得到的$1.36_{-0.26}^{+0.12} \times 10^{38}\; {\mathrm{kg}} \boldsymbol\cdot {\mathrm{m}}^2$ 和Lim等[67]预测得到的$1.15_{-0.24}^{+0.38}\times 10^{38}\; {\mathrm{kg}} \boldsymbol\cdot {\mathrm{m}}^2$ 区间下沿,而略低于Silva等[68]预测得到的$1.64_{-0.37}^{+0.52}\times 10^{38}\; {\mathrm{kg}} \boldsymbol\cdot {\mathrm{m}}^2$ 和$1.68_{-0.48}^{+0.53} \times 10^{38}\; {\mathrm{kg}} \boldsymbol\cdot {\mathrm{m}}^2$ 。利用含暗物质中子星普适关系预测得到的结果如表2所列。从其中可以看到,对于一颗质量为1.338 1±0.000 7
$ { {M}}_\odot $ 的中子星,在含暗物质粒子质量mx = 0.50 GeV且质量比例f = 50%和80%的时候普适关系所预测的转动惯量与普通中子星所预测的结果区别较为明显,两者之间的差距分别在10.02%和22.07%,这使得我们有机会判断质量相近的中子星是否含暗物质。另外从图7我们可以看到,对于具有较大潮汐形变的中子星(亦即质量较小),普通中子星普适关系曲线与含暗物质中子星普适关系曲线区别较为明显,而在目前观测到的潮汐形变区间内,只有暗物质粒子质量较小且中子星含暗物质质量比例较高时才会有明显区别,这也是表2中mx = 1.00 GeV预测误差较小的原因。 -
对于含暗物质中子星性质参量的普适关系研究,我们主要关注两个方面,一是不同暗物质粒子质量或者质量比例对于普适性关系的影响,能否起到辨识中子星是否含暗物质的作用;二是观测是否存在可靠的普适性关系,即无论是否含暗物质,对于结果的影响都不明显,此时该性质参量是普适性关系研究的良好物理量。
通过将不同暗物质粒子质量和含不同暗物质质量比例的含暗物质中子星与普通中子星的普适关系曲线进行对比,我们可以发现暗物质的引入并不会改变性质参量间存在的关系形式(在本文中即其指数关系),但将使含暗物质中子星与普通中子星的普适关系曲线产生观测上的可区分效应。例如,对于lg(I/M3)与lg(Λ)关系,由于显著可区分效应的存在,使其可以成为利用观测数据判断暗物质存在的依据。在暗物质粒子质量mx = 0.50 GeV且质量比例f = 50%和80%的时候含暗物质中子星的转动惯量与普通中子星的区别较为明显,两者之间的差距分别在10.02%和22.07%。随着未来获得更多关于质量和潮汐形变的高精度观测结果,以及在不久将来可能实现的转动惯量的观测,普适关系将能使我们更好地判断中子星是否含暗物质。
本文所使用的暗物质物态只是许多暗物质模型中的一个,但是不同类型的暗物质对于中子星整体性质的影响可能截然不同的,在后面的工作中,我们将对更多含不同类型暗物质的中子星进行检验,以期能对中子星和暗物质有更进一步的理解。

 首页
首页 登录
登录 注册
注册




 下载:
下载: