宇宙中铁到铀元素的起源是21世纪物理学最重要的前沿课题之一。太阳系内元素丰度的研究表明，绝大多数重核素都是通过两种不同类型的中子俘获过程形成：慢速中子俘获过程(s-process)和快速中子俘获过程(r-process)^[1]。前者的反应路径主要在稳定线附近，后者则更倾向于远离稳定线。这两个过程都是通过吸收中子和β衰变来合成重元素。s过程在分支点附近，如⁹⁵Zr，¹⁴⁷Nd，¹⁶⁹Nd，¹⁸⁵W，¹⁸⁶Re，¹⁹¹Os等非稳定核可以继续俘获更多中子而不进行β衰变^[2]，其过程尚待深入研究。r过程被认为主要发生在极端富中子环境下的天体内部，如超新星爆发(Supernovae)^[3−4]和双中子星合并^[5]。近年来通过将天文观测与引力波探测结合起来，确认了中子星合并为r过程的主要发生场所^[6−7]。这两种过程中涉及到寿命比较短的非稳定的丰中子核素，其(n, γ)反应难以用实验直接测量。

奥斯陆方法(Oslo Method)^[8]是一种用于间接测量中子俘获截面的实验技术。通过测定高激发态原子核至基态的连续γ衰变过程，它能够准确地提取核能级密度(Nuclear Level Density, NLD)和γ射线强度函数(γ Strength Function, γSF)，这两者是原子核在准连续能级区域最基本的性质。在原子核的激发能量较高且能级间距过小以至无法分辨各个能级的情况下，NLD取代了离散的能级，成为了核物理实验可以确定的原子核的性质。相较于在低激发能区域的实验研究，针对放射性核素NLD测量的实验研究相对有限。γSF用于描述特定光子能量下的平均衰变或吸收概率，其中包含了原子核矮共振、巨电偶极子共振和剪刀共振等的信息^[9]。

在Hauser-Feshbach反应模型框架内，以γSF、NLD以及中子与核的光学模型势(Optical Model Potential)等信息为输入参数，能准确地求得中子俘获截面^[10−12]。β-奥斯陆(β−Oslo)方法^[13−17]是一种新发展的Oslo方法，其可以通过放射性母核自发β衰变产生高能态的核。这个方法可用于低流强核素的实验研究，间接推算远离稳定线原子核的中子俘获截面和反应率。精确测量中子俘获截面不仅在核结构和核天体物理学研究上具备重要意义，对新型核技术也同样重要，如宇宙计数器$ {\mathrm{Re}}/{\mathrm{Os}} $时钟的研究^[18]、新型核反应堆的设计^[19−21]以及核废料的处理^[22−23]等。

Oslo方法主要包括4个步骤：利用探测器的γ射线响应函数，展开源自高激发态原子核的连续γ射线谱^[24]；提取γ衰变谱的初代γ射线谱，去除其它级联的γ射线^[25]；利用归一化的初代γ谱，同时获取NLD和γSF这两个函数^[26]；利用已知的实验数据确定最终的NLD和γSF^[26]。

本文探讨了在β−Oslo实验中，去除衰变电子对γ谱解谱影响的方法。第1节介绍了衰变电子影响γ探测的情况；第2节分别为新方法的基本原理，γ射线和电子对探测器的响应矩阵，以及解谱计算；第3节为总结。

我们使用一套接近全立体角的BGO探测器^[27−28]来进行β−Oslo类型的实验，实验计划在中国科学院近代物理研究所重离子加速器的放射性束流终端^[29]进行。该探测器由八块横截面为梯形的柱状晶体构成，按中心轴成对称分布，可以测量γ的全吸收谱。实验中将放射性核素停阻在探测器中心的薄硅中，测量其发生β衰变之后，高激发态子核发生的级联γ衰变谱。实验将得到单块BGO晶体的γ谱，和所有BGO探测器的γ能量加和谱，这两种谱对β−Oslo实验非常重要。

测量中γ射线与BGO晶体之间会发生诸多相互作用，如光电效应、康普顿散射和正反电子对效应等，所以有一定的概率只有部分光子能量沉积至探测器中。因此，作为Oslo方法的第一步，要将γ射线在探测器中沉积的能量展开成真实的γ入射能量(即全能峰γ光谱)，我们在之前的研究中已经详细介绍了这种方法^[30]。但是，在β−Oslo实验中，β衰变产生的电子也会与级联的γ射线一同打入BGO探测器中，产生不小的能量沉积，两者在时间上无法分开。所以我们要在展开的γ谱的同时，将电子的影响去除。单块BGO测量得到的γ谱和整套探测器测量得到的BGO阵列的能量加和谱，都需要去除电子的影响。同时，如果我们从一种γ测量谱中提取了电子的能量分布，就可以推知并扣除电子对另一种γ谱的影响。为简化计算，本文假设的γ衰变的多重性为1，只讨论单块BGO测量谱的解法。

β−Oslo实验中的电子能量沉积不可忽略，对γ谱的解谱有较大的影响。但在目前的已发表的β−Oslo实验研究中并没有明确提及该问题^[15]。因此这里我们基于已有的Oslo解谱方法提出一个新的在γ谱中去除β电子影响的方法。我们以⁶¹Mn衰变测量实验为例，⁶¹Mn发生β衰变产生⁶¹Fe，同时释放出电子和反中微子，紧随其后处于激发态的⁶¹Fe会退激产生γ。

实验中，⁶¹Mn发生β衰变及⁶¹Fe退激产生的γ有如下的能量关系：

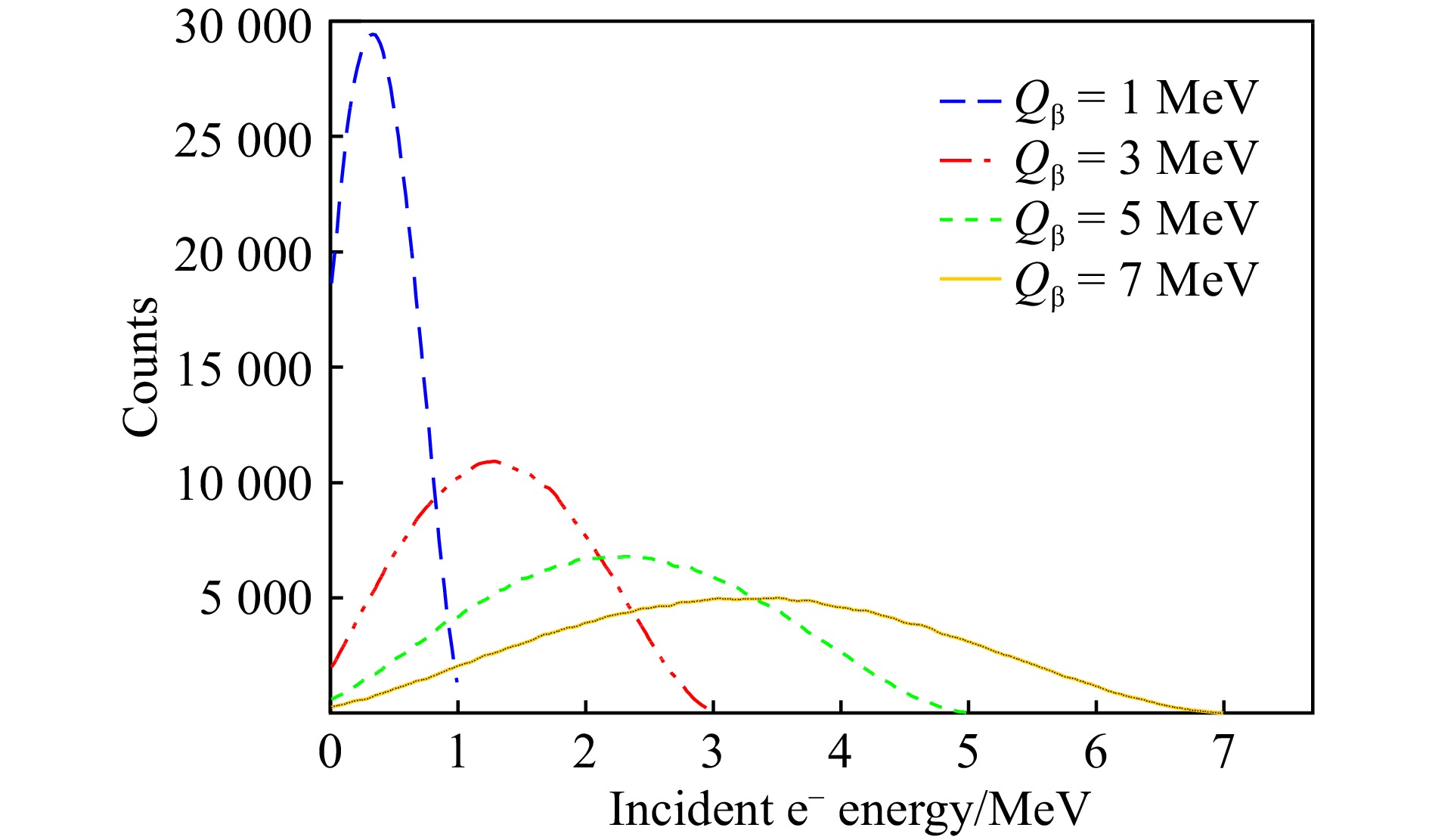
其中：Q为⁶¹Mn基态与⁶¹Fe基态的能级差值，$ Q_{\beta} $为β衰变能，他包含了衰变电子的能量$ E_{{\mathrm{e}}} $及反中微子带走的能量，$ E_{\gamma} $为γ射线的总能量。通过Geant4^[31]模拟，我们可以得到在不同的衰变能的前提下，电子的能量分布，如图1中的一些示例。在这里，我们假设所有的β衰变为容许跃迁，并且不考虑子核退激发过程中内转换电子的影响。

理论上，我们可以分别构建探测器的γ响应矩阵$ R_{\gamma}(E,\,E_{\gamma}) $和电子响应矩阵$ R_{\rm e}(E,\,Q_{\beta}) $。其中，$ E_{\gamma} $和$ Q_{\beta} $分别为γ的入射能量和β衰变能，E则为γ或电子在探测器里沉积的能量。

粒子入射到探测器中，发生各种相互作用，在探测器中沉积能量并被收集生成能谱。探测器得到的实验观测谱(折叠谱)与真实入射谱(展开谱)之间存在以下关系：

其中：f为实验观测谱；R为探测器响应函数矩阵；u为入射谱。对于本实验，有两种粒子入射到BGO探测器内，所以有以下关系：

其中：$ f_{{\mathrm{total}}} $为γ射线和电子总的沉积能量谱；$u_{\gamma},\; u_{Q_{\beta}}$分别为γ的入射谱和β衰变能分布谱。原则上基于以上公式，我们可以构造γ响应函数矩阵和关于β衰变能的电子响应函数矩阵，通过实验观测谱，解出入射γ谱。

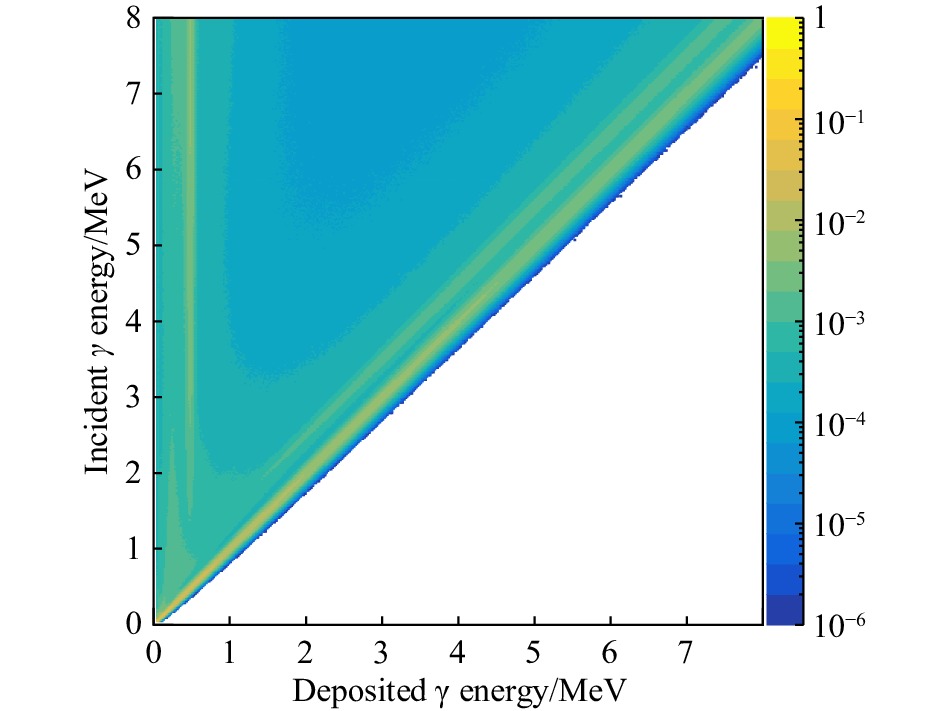
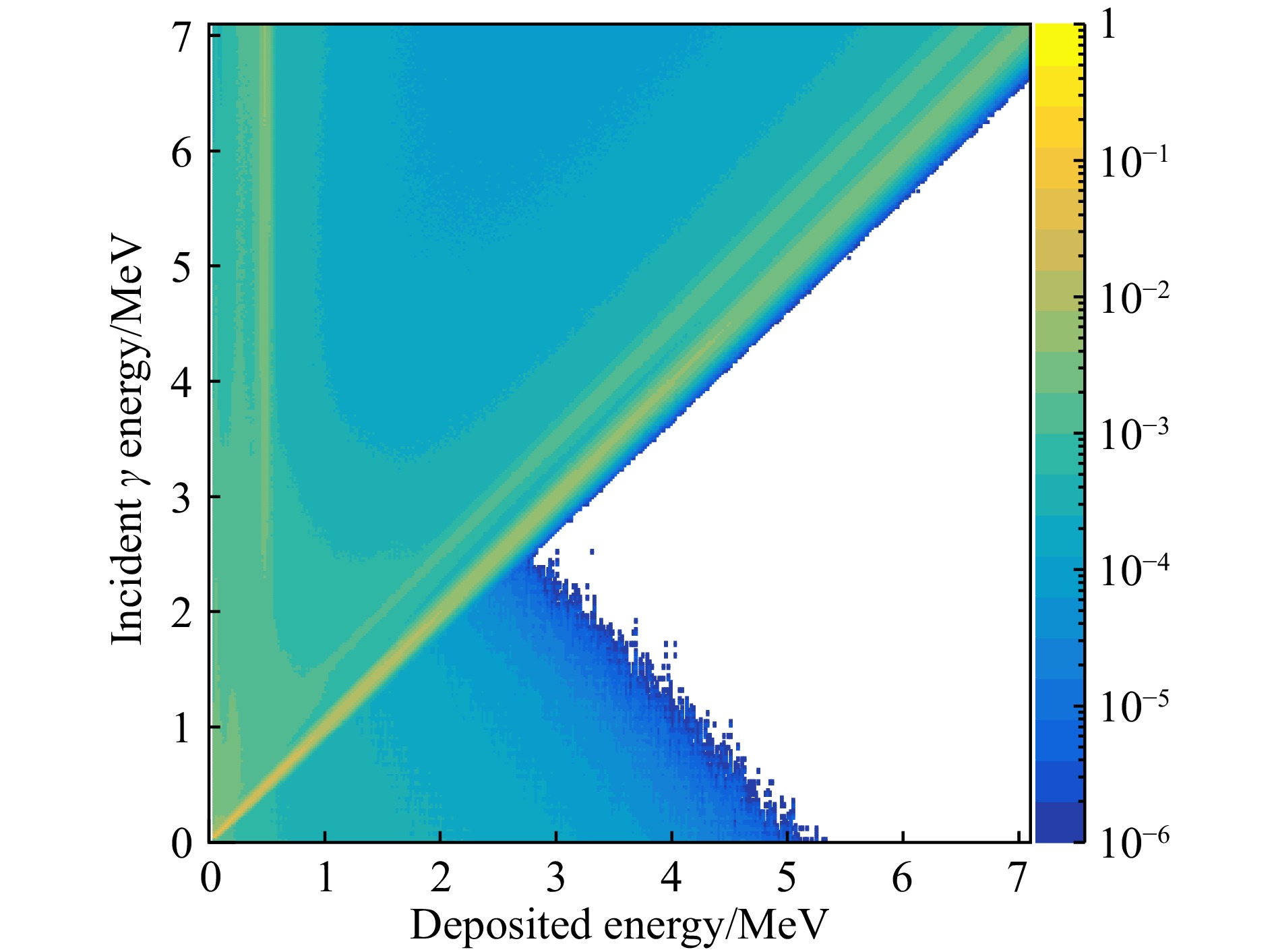
探测器对γ射线响应函数矩阵的建立，之前的文章中已有详细的论述^[30]。该矩阵是通过Geant4模拟不同能量的γ射线，入射到BGO探测器阵列中的能量沉积得到的。我们也用²⁴¹Am，¹³⁷Cs，⁶⁰Co，¹³³Ba，²⁰⁷Bi等一系列的放射源，对BGO探测器阵列进行了刻度和效率修正。如图2所示，单块BGO探测器的响应矩阵$ R_{\gamma}(E,\,E_{\gamma}) $，矩阵为400×400阶，图中纵轴为入射γ的真实能量，横轴为探测器测得的γ能量，图中彩色数值为相应像素点对应的探测效率密度，图中每一行的效率密度加和最大值为1。该矩阵在实际进行解谱运算时需要旋转到正确的方向。

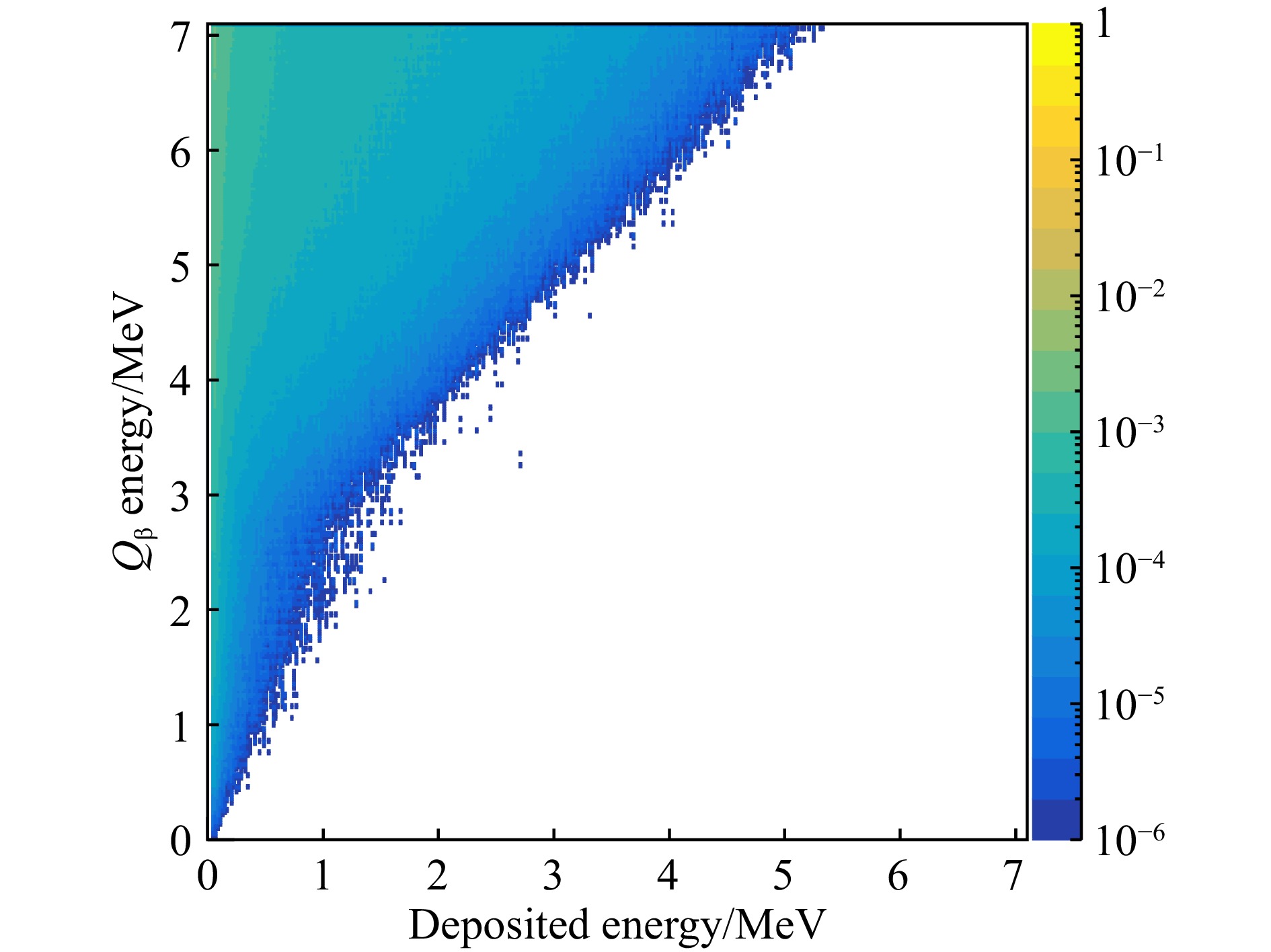
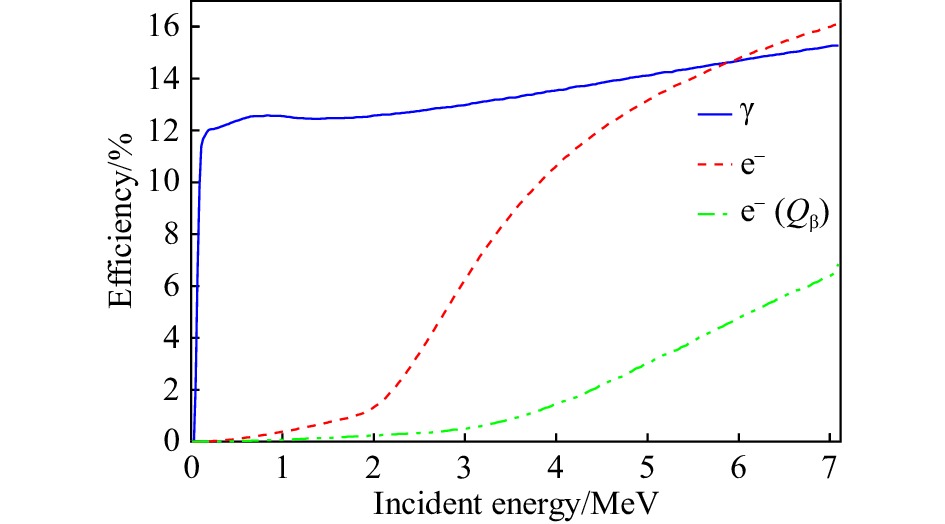
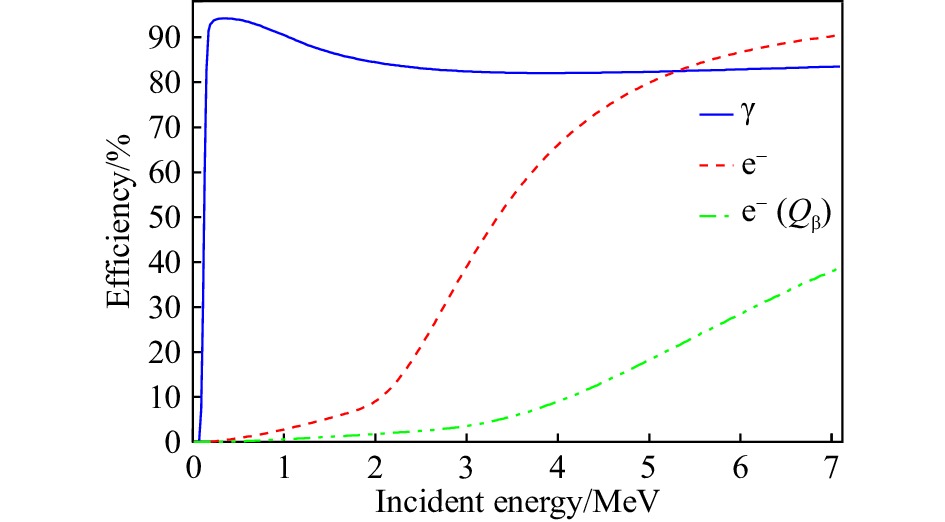
对于基于衰变能的电子的响应矩阵$ R_{{\mathrm{e}}}(E,\,Q_{\beta}) $的构建，可以通过Geant4中模拟β衰变过程来实现。对于给定的衰变能，通过模拟可以分别得到放出的电子和反中微子的能量，因为中微子几乎不与其他粒子发生作用，所以取出其中的电子的能量，模拟入射到探测器中，得到电子的探测器沉积能量，分别对$ 1,\,2,\,3,\, \cdots ,\, 8\; {\mathrm{MeV}} $的$ Q_{\beta} $能量进行模拟，得到该能量下电子沉积能量谱，然后通过插值法得到各能量下的电子沉积能量谱，并对各衰变能的模拟总数进行归一化，从而构造出基于衰变能的电子响应矩阵，如图3所示，纵轴为衰变能，横轴为衰变电子在探测器中的响应能量，彩色数值为探测效率。

同时，我们也可以得到探测器阵列对γ射线和衰变电子的探测效率。图4为单块BGO的探测效率，图5为整套BGO(能量加和谱)的探测效率。两图中的蓝色实线为探测器测量γ射线的效率；红色虚线为探测器测量衰变电子的效率，此时的横轴代表着电子的入射能量；绿色虚实线也是探测器测量衰变电子的效率，但此时的横轴代表着β衰变能。

然后，为简化矩阵计算，我们将$ R_{\gamma}(E,\,E_{\gamma}) $和$ R_{\rm e}(E,\,Q_{\beta}) $进行变换和合并，由式(1)可知，γ入射能量$ E_{\gamma} $与$ Q-Q_{\beta} $对应，因此可将$ R_{\rm e}(E,\,Q_{\beta}) $在入射能量(纵轴)方向进行倒置，并与$ R_{\gamma}(E,\,E_{\gamma}) $矩阵依据相同的入射能量道进行合并，构造出探测器总的响应矩阵$ R_{{\mathrm{total}}} $，合并结果如图6所示。可以看到，纵轴为γ入射能量，横轴为沉积能量。若γ 入射能量为$ E_{\gamma} $，则由总响应矩阵$ R_{{\mathrm{total}}} $可以得到γ和电子的总响应，其在数值上等于能量为$ E_{\gamma} $的γ在探测器中的响应加上β衰变能为$ Q-(E_{\gamma}) $时，衰变电子在探测器中的响应。此时式 (3)演变为

此方程中，只存在一一对应的一个γ入射谱$ u_{\gamma} $，响应矩阵$ R_{{\mathrm{total}}} $和探测器观测谱$ f_{{\mathrm{total}}} $。

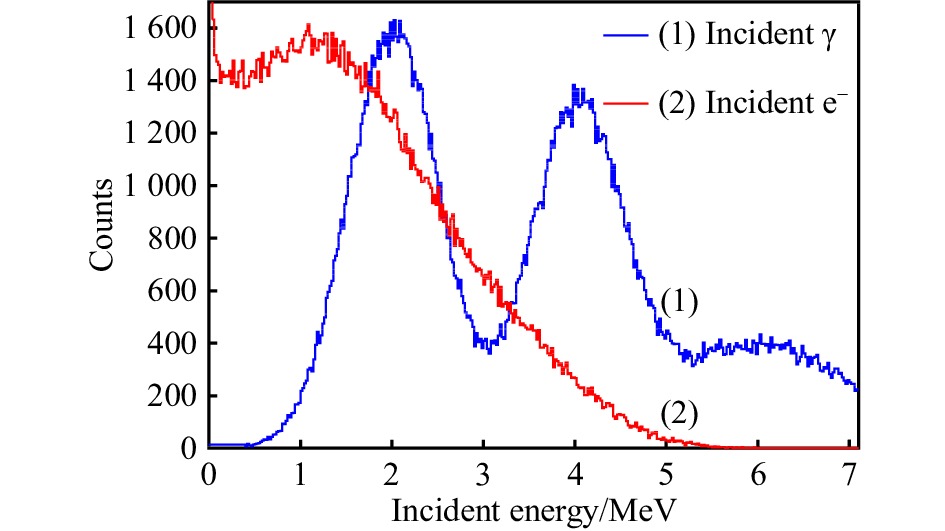
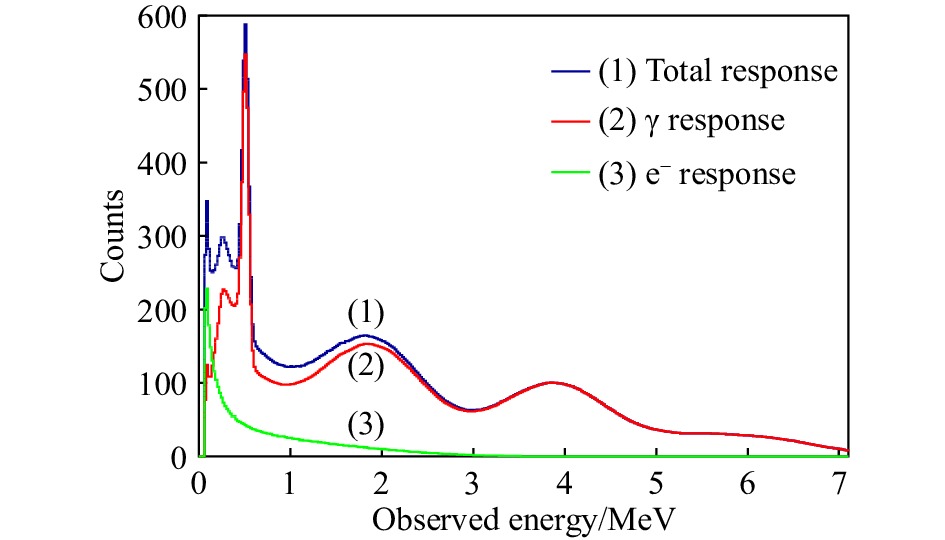
我们模拟一个β衰变和γ入射谱打入BGO探测器中，得到单块BGO探测的观测谱。然后利用总响应函数矩阵反解这个观测谱，来验证本方法是否可以去除衰变电子的影响，解出真实的γ入射谱。图7为我们模拟构造的入射谱，蓝色线(1)为γ入射谱$ u_{\gamma} $，红色线(2)为与之相应的电子入射谱$ u_{{\mathrm{e}}} $。

图8为单块BGO探测器测量到的能量谱，也称为折叠谱。其中红色线(2)为γ在探测器中沉积的能量分布，绿色线(3)为相应的衰变电子在探测器中沉积的能量分布，蓝色线(1)为探测器测量到的总能量分布。实际上，我们在实验时只能观测到总的能量分布，无法观测到电子和γ射线各自的分布。

接下来我们要利用式 (4)，通过模拟实验得到的观测谱$ f_{{\mathrm{total}}} $及已知的探测器总响应函数矩阵$ R_{{\mathrm{total}}} $，来反解出真实的γ入射谱(展开谱)$ u^*_{\gamma} $，并与原始的$ u_{\gamma} $对比，来验证去除电子影响及展开γ入射谱是否成功。反解不能通过简单地求出$ R_{{\mathrm{total}}} $的逆矩阵来进行^[24]，必须另寻巧妙的数学方法。

因为$ R_{{\mathrm{total}}} $为n阶的方形矩阵，所以由式(4)可以得出$ f_{{\mathrm{total}}} $关于$ u_{\gamma} $的n元线性方程组

其中：$ A_{ij},\, x_{ij},\, y_{ij} (i,\,j:1,\,2,\,3 \cdots n) $分别为$ R_{{\mathrm{total}}} $的矩阵元，要反解的$ u_{\gamma} $各元素值和$ f_{{\mathrm{total}}} $各元素值。经过研究发现，若使用迭代法求解，此线性方程组迭代矩阵的谱半径$ ||D||>1 $，无法保证迭代收敛，因此无法使用之前研究中使用的矩阵泰勒展开及Jacobi、Gauss–Seidel等迭代法^[30]。这里我们使用了列主元消去法来求解此线性方程组，它是高斯消去法的改进方法，主要步骤为：将线性方程组表示为增广矩阵的形式；选择第一列中绝对值最大的元素作为主元素，并将该主元素所在的行与第一行交换；使用主元所在行的倍数，将除主元素外的其他元素消为零，得到第一行的消元结果；重复上述步骤，依次选择第二列、第三列等的主元素，并进行行交换和消元操作，直到得到上三角矩阵或者方阵的对角线元素是非零元素或很接近零的元素；使用回代法求解得到方程组的解。其通过减小数值误差的传播，提高计算的稳定性，同时相对于普通的高斯消去法，可以得到更精确的解。

这里还有一个问题，在使用列主元消去法反解时，第一次反解得到的γ展开谱，其与原始模拟值相比会有非常大的振荡，仅在能量最高的部分(区间宽度约0.6 MeV)符合得较好，这就需要叠加新的方法来解谱。

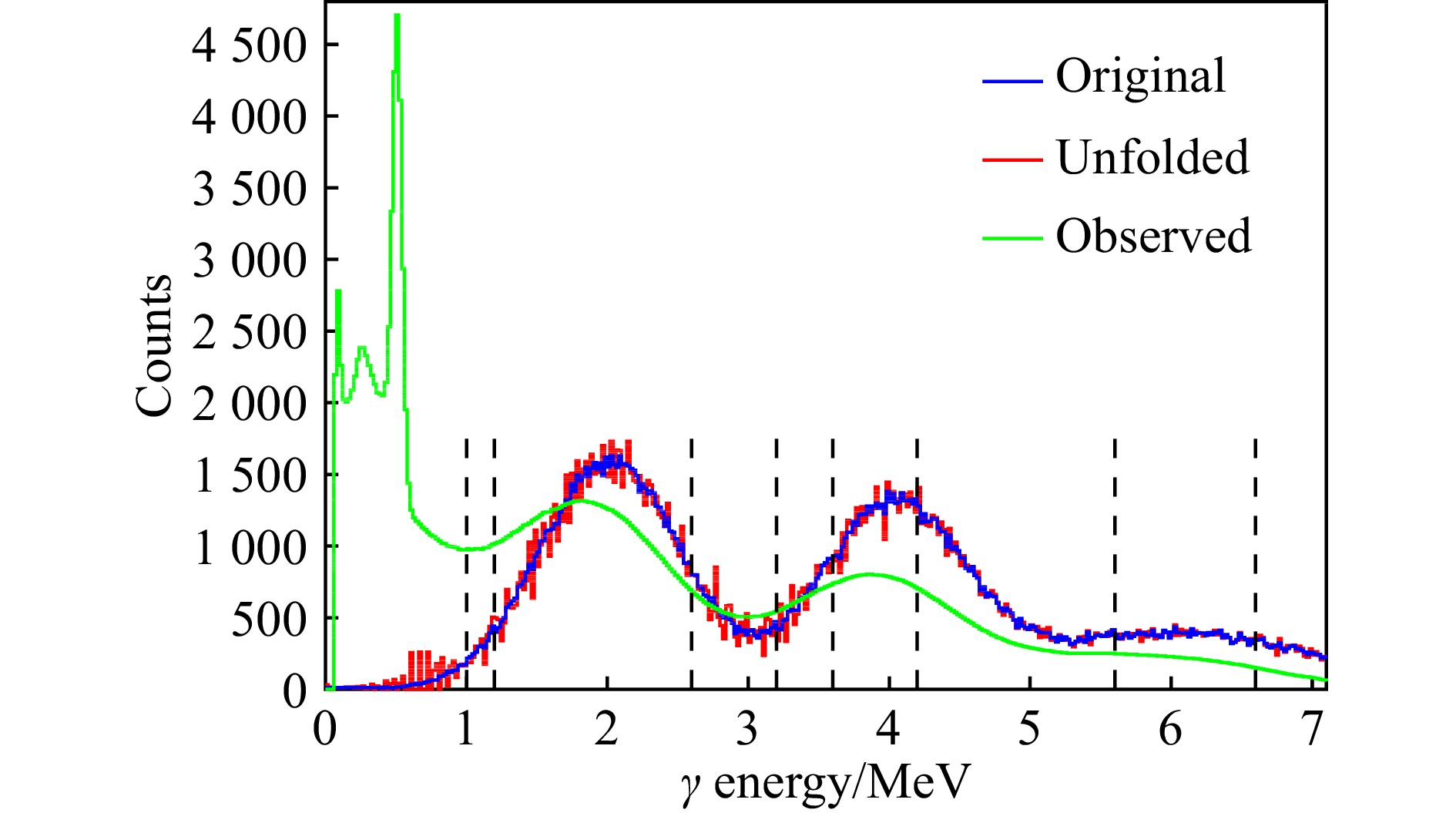
因为高能的γ射线会产生低能的γ观测谱，而低能的γ射线不会产生高能的γ能量沉积。而对应的衰变电子在高能方向上的干扰也较少。所以我们从无振荡的高能段开始，往低能方向分段反解。如图9所示，首先在解出的展开谱中选取最右边的无振荡的能量区间，记为$ u^*_{0} $，用总响应矩阵乘以这部分得到其对应观测谱$R_{{\mathrm{total}}}\boldsymbol\cdot u^*_{0}$，再用总观测谱减去这部分，记为$ f_{0} $。将$ f_{0} $代入列主元消去法，得到展开谱，并从中去除$ u^*_{0} $部分，这时候就会产生一段次高能的不振荡的区间部分，记为$ u^*_{1} $。重复上述步骤，不断向低能级逼近，可以将所有的展开谱$ u^*_{f} $解出来。图9中的黑色虚线展示了本次分段求解划分的9个区间，图中蓝线为γ入射的原始模拟值$ u_{f} $，红色部分为计算展开谱$ u^*_{f} $，可以看出两者符合得较好，验证了在γ探测谱去除衰变电子影响的方法的可靠性。图中绿线为单块BGO探测器观测谱$ f_{{\mathrm{total}}} $乘以8倍的结果，以用于比较。

本文提出了一种新的解谱方法，在β衰变和子核的γ探测实验中，可以去除衰变电子对γ探测器的影响，正确地展开γ探测谱。此方法改进了β−Oslo实验技术，通过建立合并γ射线和电子的总探测器响应函数矩阵，结合列主元消去法和逐段迭代反解法，来求出γ展开谱。本文通过模拟计算解谱，验证了新方法的可靠性。