首页
登录
注册
-
相对于使用常规螺纹连接管杆柱而言，连续管能够大幅度节省作业时间和作业成本，已成为油气田开采装备中非常重要的组成部分，被广泛应用于钻井、完井、测井、修井等作业中，因此被誉为“万能作业设备”[1-3]。
连续管在井下钻磨桥塞等作业时，承受动力钻具反扭矩和内压载荷，在每次起升下放作业中都要经历6次拉直-弯曲塑性变形，承受弯曲、扭矩和内压载荷[4-6]。内压、弯曲载荷、扭矩载荷耦合作用易引起连续管疲劳并产生微裂纹，微裂纹发生扩展至穿透管壁，使连续管失效。因此，非常有必要开展连续管在内压、弯扭耦合载荷下的疲劳寿命研究，正确有效地预测连续管的疲劳寿命情况。
目前，我国对连续管累积损伤量还没有十分有效的理论计算模型和无损检测方法。国内外学者对连续管疲劳失效进行研究，例如：Newman等[7-8]根据疲劳损伤的Miner线性累积理论建立了寿命估计模型；Avakov等[9]以等效应变为主应变的失效准则建立了疲劳寿命预测模型；王优强[10]、何春生[11]和李子丰[12]等通过理论或实验，对疲劳寿命进行研究。研究工作主要集中在内压和弯曲载荷两种载荷对疲劳性能的影响，而且大多针对应力、应变与载荷的关系，很少涉及循环次数与载荷的关系。本研究主要探讨内压、弯曲载荷和扭矩载荷3种载荷耦合作用对连续管疲劳寿命的影响。
-
采用修正的Brown-Miller疲劳寿命理论模型[14-15]。设最大剪应变
${\gamma _{\max }} = {\varepsilon _1} - {\varepsilon _3}$ ，最大正应变${\varepsilon _{\rm{n}}}{\rm{ = }}\left( {{\varepsilon _1}{\rm{ + }}{\varepsilon _3}} \right)/2$ ，单轴平面应变中，${\varepsilon _2}{{ = - v}}{\varepsilon _1}$ ，${\varepsilon _3}{{ = - v}}{\varepsilon _1}$ ，则式中：
${{v}}$ 为泊松比，${\varepsilon _1}$ 、${\varepsilon _2}$ 和${\varepsilon _3}$ 分别为第1、第2和第3主应变。Brown-Miller应变-寿命方程为
考虑平均应力的影响，利用Morrow平均应力准则进行修正，修正后应变-寿命公式为
式中：
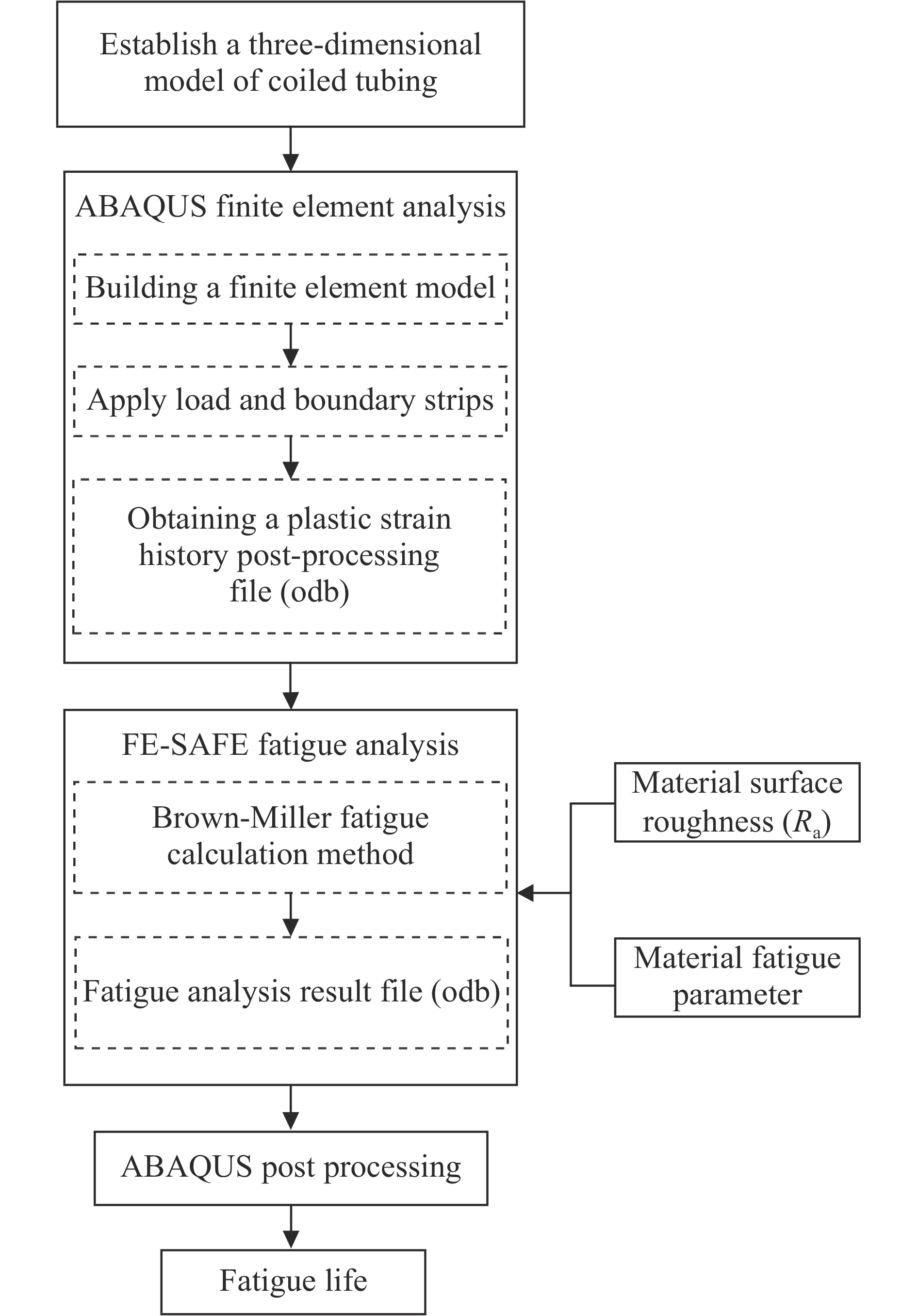
${\gamma _{\max }}$ 和${\varepsilon _{\rm{n}}}$ 为剪应变和正应变，${\sigma '_{\rm{f}}}$ 为疲劳强度系数，${\varepsilon '_{\rm{f}}}$ 为疲劳延性系数，b为疲劳强度指数，f为疲劳延性指数，${\sigma _{\rm{m}}}$ 为平均应力，E为弹性模量。基于上述疲劳分析理论，采用FE-SAFE疲劳分析软件对耦合载荷下连续管疲劳寿命进行研究，疲劳寿命分析流程如图2所示。
-
以外径60.325 mm连续管为研究对象，连续管长度为1.2 m，壁厚为4.775 mm，建立带压作业时连续管的循环弯曲和扭转三维有限元模型，研究弯曲载荷、内压载荷和扭矩载荷耦合作用对疲劳寿命的影响。连续管材料参数如表1所示[16-17]。
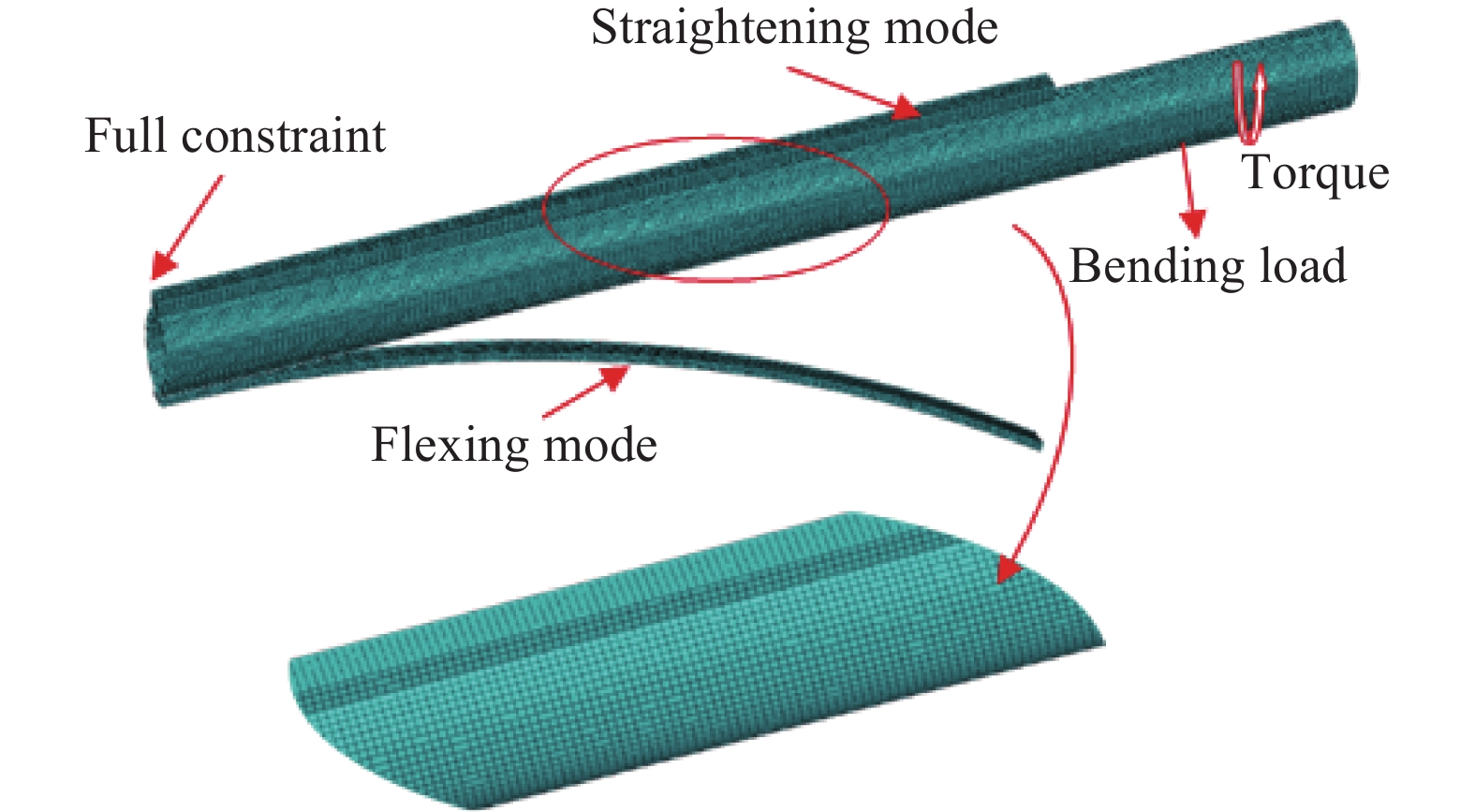
利用ABAQUS软件建立连续管低周疲劳有限元模型，如图3所示，该模型包括挠曲模、矫直模、连续管。连续管一端固定，另一端施加扭矩和弯曲载荷，弯曲通过位移加载实现，连续管在挠曲模和矫直模之间进行弯直循环。挠曲模和矫直模材料为普通结构钢，并将两个模施加固定约束。连续管与两个模板的接触选择实体的面面接触，接触类型为无摩擦接触，求解方程选择纯罚函数法。采用C3D8R单元划分网格，网格数目为186250。
将ABAQUS计算结果导入FE-SAFE疲劳分析软件，在该软件定义载荷历程，表面粗糙度设置为0.25，材料属性如表1所示，选用修正的Brown-Miller疲劳寿命模型。通过材料属性参数自动生成材料
$\varepsilon {{ - N}}$ 曲线，然后将ABAQUS的结果文件与$\varepsilon {{ - N}}$ 曲线进行对比，从而得出疲劳循环次数。如图4所示，连续管疲劳循环次数为198，疲劳敏感区出现在连续管弯直过程受拉面和受压面，与现场连续管易疲劳位置相吻合，证实了数值模型的可行性。 -
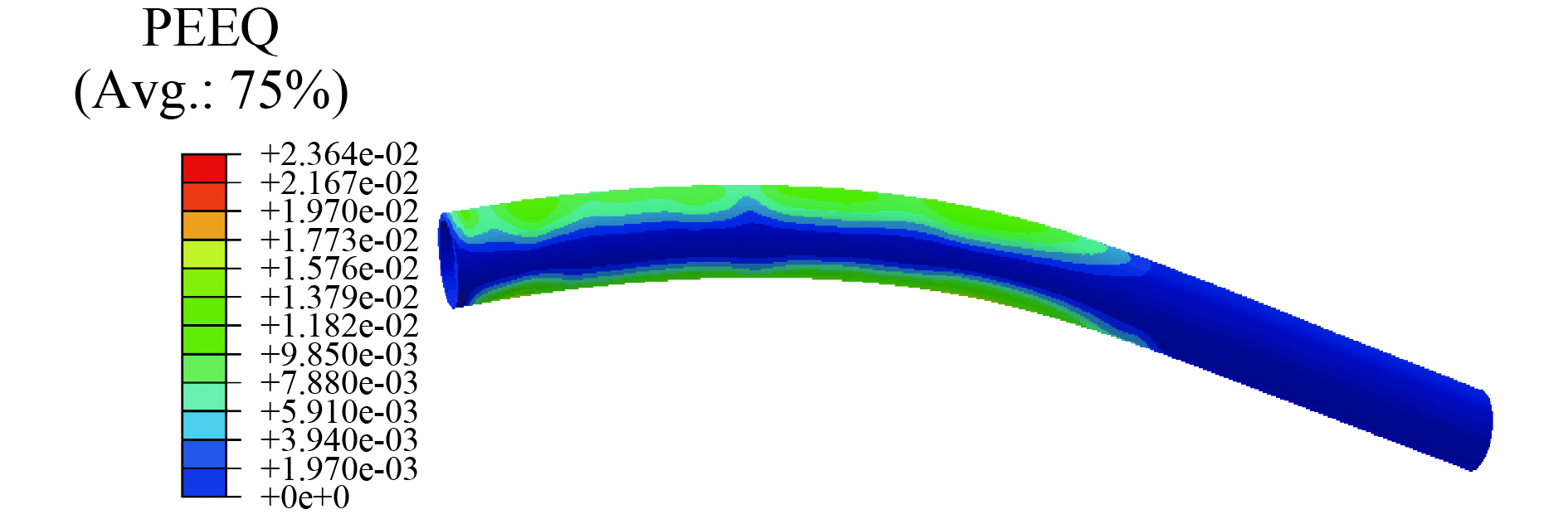
连续管在每次起下作业中都要承受6次弯直和内压载荷，本研究采用有限元方法研究连续管在内压和循环弯曲复合载荷作用下的疲劳寿命。通过对连续管在不同内压下的循环弯曲的分析，可以得出带压循环弯曲时，连续管的Mises应力-应变云图和疲劳寿命云图。内压为30 MPa、弯曲半径为2108 mm时的等效塑性应变云图如图5所示，疲劳循环次数云图如图6所示。
分析不同内压下连续管塑性应变云图和疲劳寿命云图，得出如下结果：连续管在整个循环弯曲过程中，最大塑性应变出现在因弯曲引起的轴向拉伸面和压缩面，而两侧面产生的塑性应变相对较小，所以弯曲引起的轴向拉伸面和压缩面最先失效，且最大应力应变区域在连续管固定端开始约2/3连续管位置，与疲劳寿命结果云图一致。
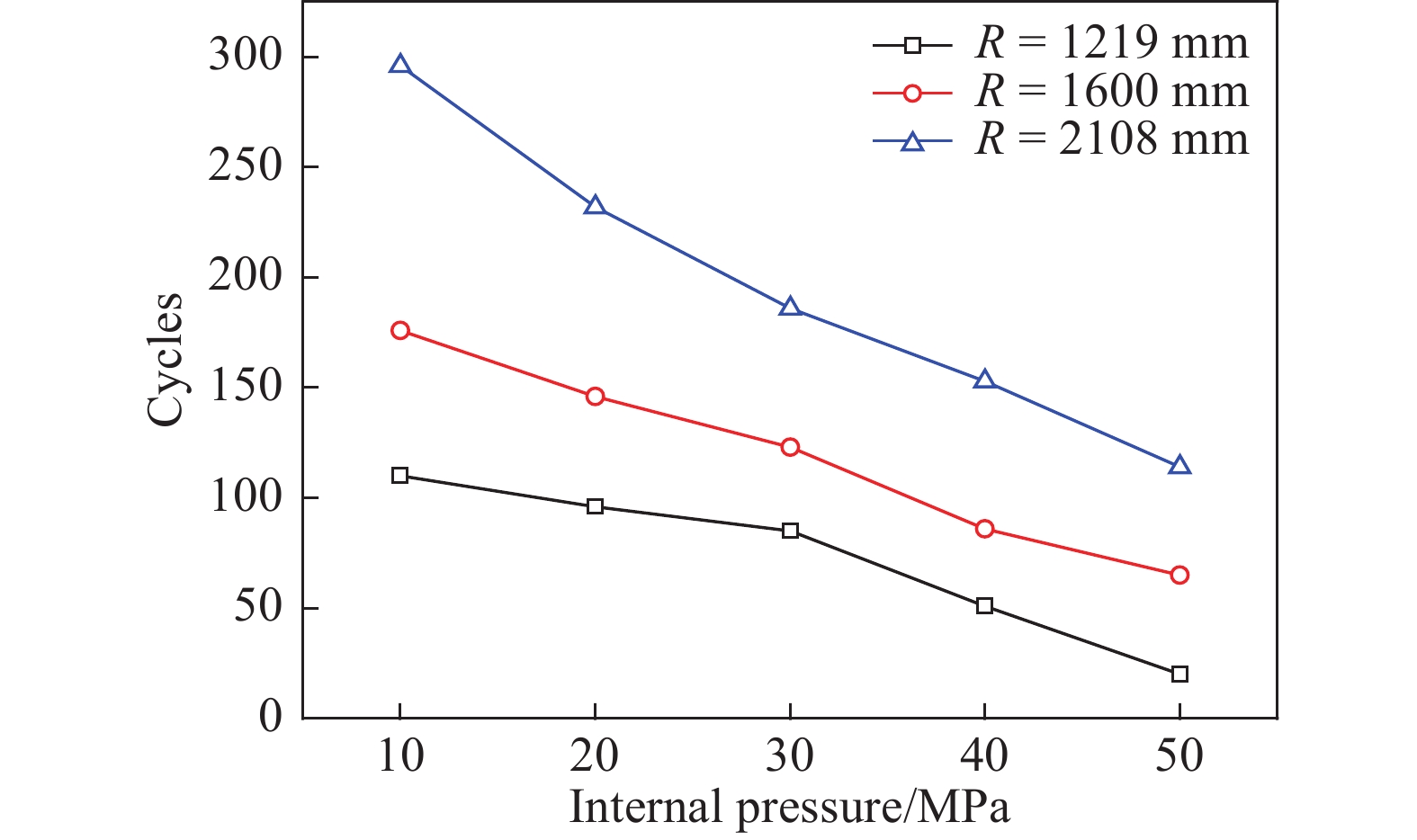
图6为循环次数随着内压变化曲线图，在不同的滚筒半径R下，随着连续管内压的增加，连续管弯曲疲劳循环次数近似线性降低，滚筒半径为2108 mm时，内压为10 MPa时连续管疲劳循环次数约为300，而内压为50 MPa时连续管疲劳循环次数降为125，疲劳寿命降低了约58.3%，由此得出内压加速了连续管的疲劳失效。从图6也可以看出，滚筒半径对连续管疲劳寿命的影响较大，所以建议在允许的情况下，选用较大直径的滚筒。
-
目前，国内的连续管疲劳试验机只能进行带压弯曲疲劳实验，暂时较难开展内压、弯扭耦合载荷下的连续管疲劳实验，所以进行了内压影响下连续管疲劳寿命研究，以期对有限元分析结果进行定性的验证。
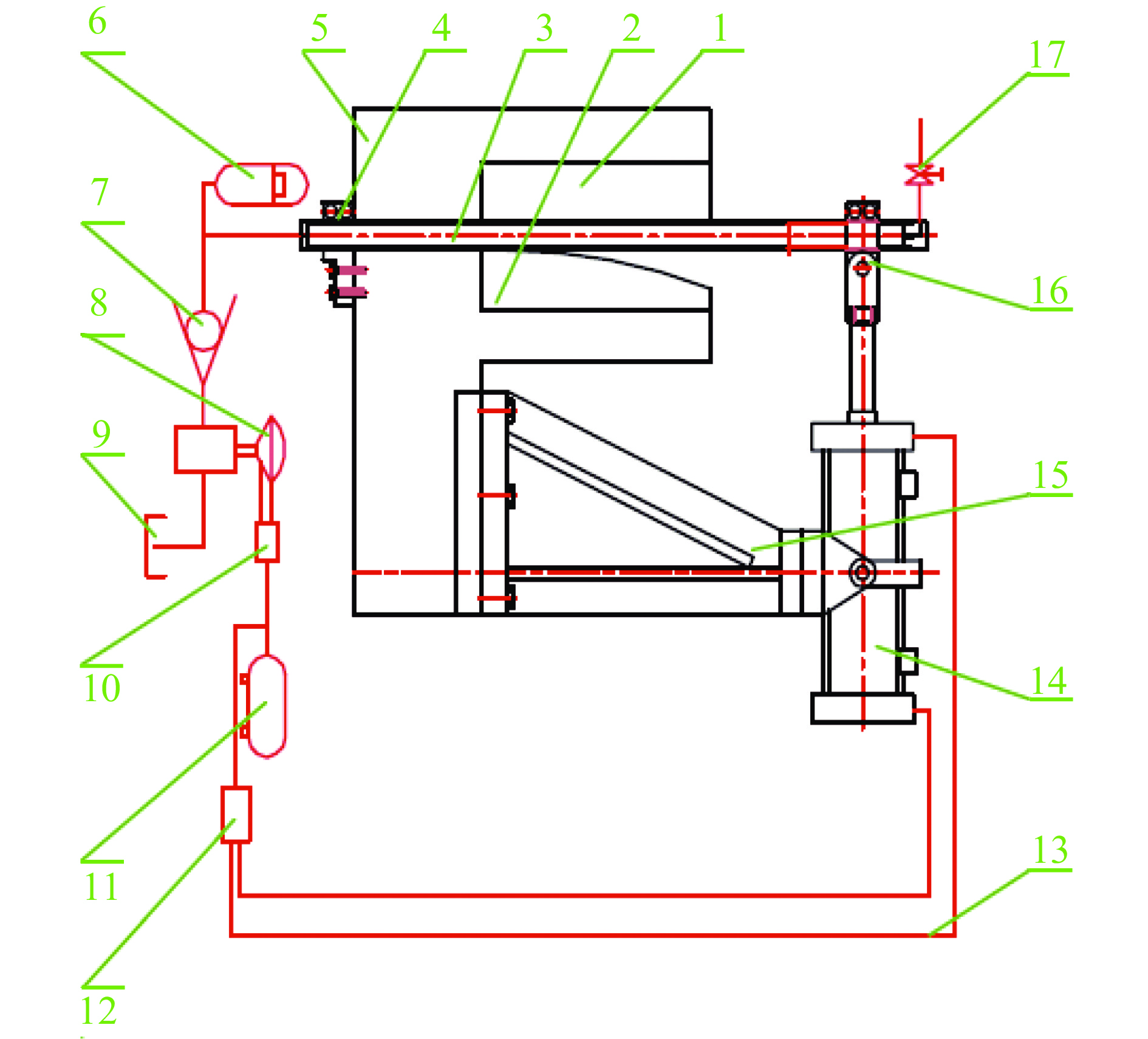
利用外径为60.325 mm的连续管进行实验研究，实验用连续管的长度约为1.4 m。如图7所示，挠曲模半径为1219 mm，实验试样一端密封，另一端与增压设备连接。两端密封的连续管试样被安装在疲劳实验机上。实验过程如下：增压器向管子里面注水，当管子里注满水后，泄压阀被打开，随后增压器开始对试样打压直到压力达到预定值。打压后液压缸驱动连续管可动端在挠曲模和直模间做往复运动直到连续管试样疲劳失效，LCD显示器自动地记录和显示连续管弯曲循环次数。
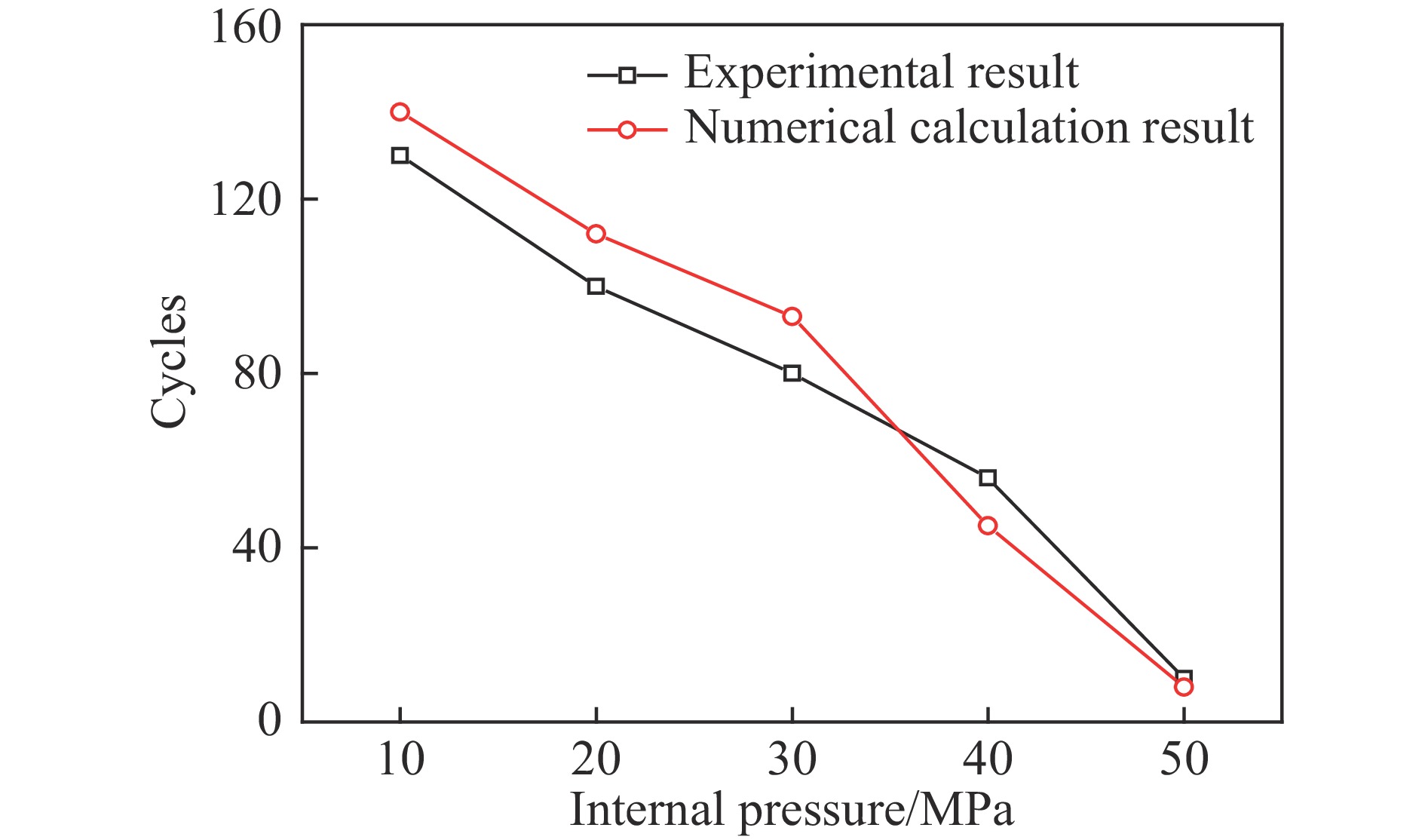
连续管内压在0～50 MPa时，分别测试了连续管试样的疲劳寿命。实验结果如图8所示，实验结果与数值计算结果趋势是相吻合的，实验结果证实了有限元计算结果是可行性的。对比结果得出，最小相对误差为7%，最大相对误差为25%，此误差在工程中是可以被接受的。
-
为了验证连续管低周疲劳寿命有限元模型的正确性，以文献[18]中的实验模型为研究对象，模型参数为：管长1200 mm，弯曲半径为2108 mm，直径为60.325 mm，壁厚为4.775 mm。以文献[18]中的实验结果验证数值计算结果，表2为有限元值与实验值对比。由对比结果可知，最大相对误差为13%，该误差在工程中是可以被接受的，由此证实该模型是可行的。
-
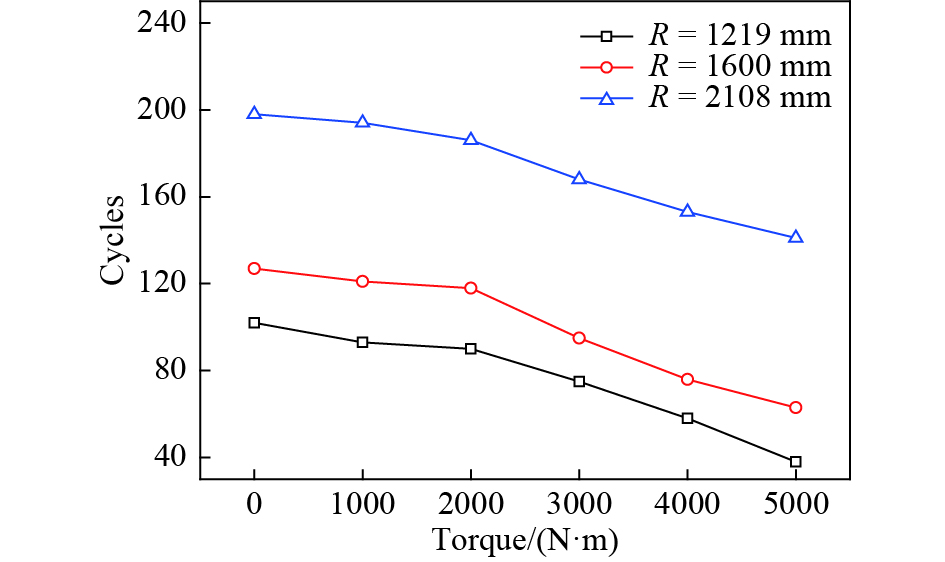
内压为30 MPa时，不同弯曲半径下，扭矩对连续管疲劳循环次数的影响如图9所示。在内压和弯扭载荷耦合作用下，连续管疲劳循环次数随着扭矩的增加依次减小。扭矩为0～2000 N·m时，连续管疲劳循环次数受扭矩变化的影响相对较小。扭矩在2000～5000 N·m时，疲劳循环次数受扭矩的影响相对较大。滚筒半径为1219 mm时：扭矩为零时连续管疲劳循环次数约为100，而扭矩为5000 N·m时连续管疲劳循环次数降为40，疲劳寿命降低了约60%。从图9也可看出，弯曲半径越小，扭矩对连续管疲劳寿命的影响越明显。
-
连续管在钻井或钻磨桥塞时，动力钻具顶部产生的反扭矩易引起连续管疲劳失效，甚至扭断。内压和扭矩耦合作用时，连续管的疲劳循环次数如表3所示。由表3可知，扭矩在理论安全标准范围内，扭矩对连续管的疲劳寿命影响较小。无内压时，循环次数下降的临界值大约在6400～6800 N·m；内压为30～60 MPa时，循环次数下降的临界值大约在5800～6000 N·m。数值计算结果均小于《连续管工程技术手册》给出的屈服扭矩（6839 N·m）[19-20]，进一步证实该临界值是相对准确的。内压大于30 MPa会急剧加速连续管疲劳失效。扭矩超过临界扭矩时，循环次数随着扭矩的小幅增大急剧下降。由此得出，连续管在小于临界扭矩的工况下使用是安全可行的。
-
（1）连续管最大塑性应变和疲劳敏感区出现在轴向拉伸面和压缩面，与现场连续管失效情况是一致的，且实验结果证实了有限元计算结果是可行的。在弯曲载荷与内压耦合加载下，随着内压的增加，连续管疲劳寿命相应的降低。
（2）在内压、弯扭耦合加载下，现有实验结果证实数值计算模型是可行的，扭矩增大时，连续管疲劳寿命降低较快。通过计算得到了连续管安全服役的临界扭矩值。
内压、弯扭耦合载荷下连续管疲劳寿命评估
Fatigue Life Evaluation of Coiled Tube under Coupled Load of Internal Pressure, Bending and Torsion
-
摘要: 针对连续管在作业中易出现疲劳失效等问题，进行了连续管在内压、弯扭耦合加载下疲劳寿命评估。首先分析了耦合加载下连续管低周疲劳失效机理，基于Brown-Miller疲劳寿命模型建立了连续管疲劳寿命数值计算模型，开展了内压和弯曲加载下连续管疲劳实验，实验结果证实该数值模型是可行的。计算了内压和弯曲耦合加载下连续管低周疲劳寿命，以及内压和弯扭耦合加载下连续管低周疲劳寿命。计算结果表明，连续管最大塑性应变和疲劳敏感区出现在轴向拉伸面和压缩面，与现场连续管失效情况是一致的。通过计算得到了连续管安全服役的临界扭矩值和内压值。Abstract: It is necessary to evaluate the fatigue life of coiled tube (CT) under the coupled load of internal pressure, bending load and torsion. First, the failure mechanism of low cycle fatigue of CT under coupling loading is analyzed. Based on Brown-Miller fatigue life model, a numerical calculation model of CT fatigue life is established. The low cycle fatigue life of CT under the coupling load of internal pressure and bending load is calculated. And also the low cycle fatigue life of CT under the load of internal pressure, bending load and torsion is calculated. The calculation results show that the maximum plastic strain and fatigue sensitive areas of CT appear on the axial tensile surface and compression surface, which is consistent with the failure of CT on oil field. The critical torque value and internal pressure of CT are obtained by calculation for CT safety service.
-
Key words:
- coiled tube /
- torsion /
- plastic deformation /
- fatigue life /
- coupling load .
-
-
图 5 连续管低周疲劳塑性应变云图
Figure 5. Low-cycle fatigue plastic strain distribution map on coiled tube
图 8 实验结果与数值计算结果对比
Figure 8. Comparison of experimental results with numerical simulation results
图 9 弯扭内压耦合载荷下扭矩对疲劳循环次数的影响
Figure 9. Effect of torque on fatigue cycle number under the coupled load of moment, torque and internal pressure
Material type Outer diameter/mm Wall thickness/mm Elastic modulus/MPa Poisson’s ratio CT-800 60.325 4.775 210 000 0.3 Yield stress/MPa Cyclic strain hardening
coefficient/MPaCyclic strain
hardening indexSection shrinkage/% 552 785 0.1 58.18 
下载: 导出CSV
表 2 有限元模拟值与实验值对比
Table 2. Comparison of finite element simulation results and experimental results
Internal pressure/MPa Experimental value/N Finite element value/N Error/% 65 50 45 10 65 49 45 8 65 52 45 13
下载: 导出CSV
表 3 内压、扭矩对连续管疲劳寿命的影响
Table 3. Influence of internal pressure and torque on fatigue life of coiled tube
Torque/（N·m） Fatigue life Torque/（N·m） Fatigue life 0 MPa 30 MPa 60 MPa 0 MPa 30 MPa 60 MPa 1000 >107 >107 >107 7300 8650 352 4000 >107 >107 >107 7400 2090 280 5500 >107 >107 >107 7420 745 234 5800 >107 ≥107 ≥107 7450 349 196 6000 >107 1331 111 7480 238 145 6200 >107 856 38 7500 179 122 6400 ≥107 623 1 7700 18 6800 36 890 408
下载: 导出CSV
-
[1] GHOBADI M, MUZYCHKA Y S. Pressure drop in mini-scale coiled tubing [J]. Experimental Thermal and Fluid Science, 2014, 57: 57–64. doi: 10.1016/j.expthermflusci.2014.04.011 [2] 袁发勇, 马卫国. 连续管水平井工程技术 [M]. 北京: 科学出版社, 2018: 1–19. YUAN F Y, MA W G. Coiled tubing engineering technology in horizontal wells [M]. Beijing: Science Press, 2018: 1–19. [3] ISHAK J. Numerical evaluation of cyclic strains in physically small defects in coiled tubing [D]. Tulsa, OK: The University of Tulsa, 2016: 1–9. [4] OYEDOKUN O, SCHUBERT J. Extending the reach of coiled tubing in directional wells with downhole motors [C]//SPE/ICoTA Coiled Tubing and Well Intervention Conference & Exhibition. Woodlands, TX, 2014. [5] TIPTON S M, CARLSON G H, SOREM J R. Fatigue integrity analysis of rotating coiled tubing [C]//SPE/ICoTA Coiled Tubing and Well Intervention Conference and Exhibition. Woodlands, TX, 2006. [6] 毕宗岳, 张晓峰, 张万鹏. 连续管疲劳寿命试验研究 [J]. 焊管, 2012, 35(6): 5–8. doi: 10.3969/j.issn.1001-3938.2012.06.001 BI Z Y, ZHANG X F, ZHANG W P. Research on fatigue life test of coiled tubing [J]. Welded Pipe, 2012, 35(6): 5–8. doi: 10.3969/j.issn.1001-3938.2012.06.001 [7] NEWMAN K R, NEWBURN D A. Coiled-tubing-life modeling: SPE22820 [R]. Richardson, TX: Society of Petroleum Engineers , 1991. [8] NEWMAN K R. Determining the working life of a coiled tubing string [J]. Offshore Incorporating Oilman, 1991, 51(12): 31–36. [9] AVAKOV V A, MARTIN J. Large coiled tubing fatigue life [C]//SPE/ICoTA North American Coiled Tubing Roundtable. Richardson, TX: Society of Petroleum Engineers, 1997. [10] 王优强, 张嗣伟, 方爱国. 连续管的失效形式与原因概述 [J]. 石油矿场械, 1999, 28(4): 15–l8. WANG Y Q, ZHANG S W, FANG A G. Overview of failure modes and causes of coiled tubing [J]. Oil Field Equipment, 1999, 28(4): 15–l8. [11] 何春生. 连续油管低周疲劳寿命预测及屈曲分析方法研究[D]. 大庆: 东北石油大学, 2014: 17–47. HE C S. The prediction of low cycle fatigue life and study of buckling analysis method for coiled tubing [D]. Daqing: Northeast Petroleum University, 2014: 17–47. [12] 李子丰, 李雪娇, 王鹏. 预弯曲连续油管及其疲劳寿命预测 [J]. 石油学报, 2012, 33(4): 706–710. LI Z F, LI X J, WANG P. Pre-bending coiled tubing and its fatigue life prediction [J]. Acta Petrolei Sinica, 2012, 33(4): 706–710. [13] LIU S H, XIAO H, GUAN F, et al. Coiled tubing failure analysis and ultimate bearing capacity under multi-group load [J]. Engineering Failure Analysis, 2017, 79(9): 803–811. [14] 尚德广, 王德俊. 多轴疲劳强度 [M]. 北京:科学出版社, 2007: 118–128. SHANG D G, WANG D J. Multiaxial fatigue strength [M]. Beijing: Science Press, 2007: 118–128. [15] 林腾蛟, 沈亮, 赵俊渝. 风电增速箱输出级齿轮副疲劳寿命有限元分析 [J]. 重庆大学学报, 2012, 35(1): 1–6. LIN T J, SHEN L, ZHAO J Y. Fatigue life finite element analysis of output gear pair of wind turbine speed-increase gearbox [J]. Journal of Chongqing University, 2012, 35(1): 1–6. [16] JIANG Y, SEHIITOGLU H. Modeling of cyclic ratcheting plasticity [J]. Journal of Applied Mechanics, 1996, 63(3): 726–733. doi: 10.1115/1.2823356 [17] AMITKUMAR C. Local strain approach for fatigue life prediction of coiled tubing with surface defects [D]. Tulsa, OK: The University of Tulsa, 2010. [18] PEROZO N, PAZ C A, TEODORIU C, et al. A novel testing facility for coiled tubing fatigue valuation under deep drilling conditions [C]//SPE Western Regional Meeting. Anchorage, AK, 2016. [19] 周永霞. 先进技术提高了连续油管钻井能力 [J]. 国外石油机械, 1996, 7(3): 14–16. ZHOU Y X. Advanced technology improves the ability of coiled tubing drilling [J]. Foreign Petroleum Machinery, 1996, 7(3): 14–16. [20] 赵章明. 连续油管工程技术手册 [M]. 北京:石油工业出版社, 2011: 39–49. ZHAO Z M. Coiled tubing engineering technical manual [M]. Beijing: Petroleum Industry Press, 2011: 39–49. -
图( 9) 表( 3)
计量
- 文章访问数: 3605
- HTML全文浏览数: 3605
- PDF下载数: 42
- 施引文献: 0