高级搜索

SPH方法在宽速域岩石侵彻问题中的应用

,  ,  , 

downloadPDF

上一篇

下一篇

强洪夫, 张国星, 王广, 黄拳章. SPH方法在宽速域岩石侵彻问题中的应用[J]. 高压物理学报, 2019, 33(5): 055105-1. doi: 10.11858/gywlxb.20180621
引用本文: 强洪夫, 张国星, 王广, 黄拳章. SPH方法在宽速域岩石侵彻问题中的应用[J]. 高压物理学报, 2019, 33(5): 055105-1. doi: 10.11858/gywlxb.20180621
shu
Hongfu QIANG, Guoxing ZHANG, Guang WANG, Quanzhang HUANG. Application of SPH Method for Problem of Rock Penetration within the Wide-Ranged Velocity[J]. gaoyawli, 2019, 33(5): 055105-1. doi: 10.11858/gywlxb.20180621
Citation: Hongfu QIANG, Guoxing ZHANG, Guang WANG, Quanzhang HUANG. Application of SPH Method for Problem of Rock Penetration within the Wide-Ranged Velocity[J]. gaoyawli, 2019, 33(5): 055105-1. doi: 10.11858/gywlxb.20180621
shu

SPH方法在宽速域岩石侵彻问题中的应用

  • 火箭军工程大学，陕西 西安　710025

    • 作者简介: 强洪夫（1963－），男，博士，教授，博士生导师，主要从事材料与结构失效行为与高性能数值模拟研究. E-mail：qiang@263.net .
    通讯作者: 张国星（1994－），男，硕士研究生，主要从事计算力学研究. E-mail：1428071753@qq.com; 

  • 中图分类号: O313.4

Application of SPH Method for Problem of Rock Penetration within the Wide-Ranged Velocity

  • Rocket Force University of Engineering, Xi’an 710025, China

    • Corresponding author: Guoxing ZHANG, 1428071753@qq.com ; 

  • MSC: O313.4

  • 摘要: 采用光滑粒子流体动力学（SPH）方法对花岗岩靶板受碰撞侵彻的大应变、高应变率变形问题进行了数值模拟。为了描述弹目材料的非线性变形及破坏特性，对花岗岩靶板引入了Holmquist-Johnson-Cook（HJC）本构模型及损伤模型，对弹体引入含损伤的Johnson-Cook（J-C）本构方程和Grüneisen状态方程，靶板与弹体均离散成拉格朗日粒子。通过自编程序仿真计算0～4 m/s的着靶速度下花岗岩靶板的三维侵彻过程，对比分析了钢珠在不同弹体条件下的侵彻结果，在固体侵彻、半流体侵彻和流体侵彻的区域内拟合了侵彻深度随着靶速度的变化曲线。数值计算结果显示，侵彻深度随着靶速度的增加在固体侵彻区间（$ {v_0} \lt 1421\;{\rm{m}}/{\rm{s}}$）呈现递增趋势，在半流体侵彻区间（$ 1421\; {\rm{m}}/{\rm{s}} \leqslant {v_0}\leqslant1700 \;{\rm{m}}/{\rm{s}}$）呈现递减趋势，在流体侵彻区间（${v_0} \gt 1700\;{\rm{m}}/{\rm{s}} $）呈现递增趋势并逐渐趋于平滑，达到峰值。
    Abstract: The smoothed particle hydrodynamics (SPH) method is used to simulate the deformation of penetration of granite at large strain and high strain rates. In order to describe the nonlinear deformation and failure characteristics of the projectile and target, the Holmquist-Johnson-Cook (HJC) constitutive model, damage model, Johnson-Cook (J-C) constitutive model and Grüneisen equation of state for granite are introduced, in which the projectile and the fortifications are discretized into Lagrangian particles. In simulation of three-dimensional penetration process of granite targets by self-made program at the speed from 0 m/s to 4000 m/s, we compare and analyzes the penetration results of steel balls under different projectile conditions. The curve of the penetration depth with the penetration velocity is fitted in solid penetration, semi-fluid penetration and fluid invasion. The numerical results show that the penetration depth increases with the increase of the penetration velocity in the solid penetration interval ($ {v_0} \lt 1421\;\,{\rm{m}}/{\rm{s}} $). A decreasing trend is shown in the semi-fluid penetration interval ($ 1421\;{\rm{m}}/{\rm{s}} \leqslant {v_0} \leqslant 1700\;{\rm{m}}/{\rm{s}} $), while an increasing trend is shown in the fluid penetration interval ($ 1421\;{\rm{m}}/{\rm{s}} \lt {v_0} \lt 1700\;{\rm{m}}/{\rm{s}} $) and gradually tended to reach the peak.
  • 加载中

  • 图 1  三维SPH粒子

    Figure 1.  Three-dimensional SPH particle

    下载: 全尺寸图片 幻灯片

    图 2  侵彻速度与侵彻深度的关系

    Figure 2.  Penetration depth vs. penetration velocity

    下载: 全尺寸图片 幻灯片

    图 3  不同速度下SPH数值模拟的成坑结果

    Figure 3.  Results of the pit at diferent penetration velocities by SPH

    下载: 全尺寸图片 幻灯片

    图 4  LS-DYNA软件模拟成坑结果[1]

    Figure 4.  Result of the pit by LS-DYNA[1]

    下载: 全尺寸图片 幻灯片

    图 5  花岗岩受撞击成坑的实验结果[1]

    Figure 5.  Experimental mesoscopic results of granite impacted pits[1]

    下载: 全尺寸图片 幻灯片

    图 6  侵彻深度随着着靶速度的变化曲线

    Figure 6.  Penetration depth vs. penetration velocity

    下载: 全尺寸图片 幻灯片

    图 7  侵彻深度与侵彻马赫数的关系曲线[4]

    Figure 7.  Penetration depth vs. Mach number Ma[4]

    下载: 全尺寸图片 幻灯片

    图 8  不同侵彻速度下岩石靶板成坑结果

    Figure 8.  Size of the pit at different penetration velocities

    下载: 全尺寸图片 幻灯片

    图 9  侵彻过程中弹目的压力变化图

    Figure 9.  Pressure change of the penetrating process

    下载: 全尺寸图片 幻灯片

    图 10  0～4000 m/s速度范围内弹体分段作为刚体和非刚体的侵彻深度随着靶速度的变化

    Figure 10.  Value of the penetration depth and the penetration velocity from 0 to 4000 m/s

    下载: 全尺寸图片 幻灯片

    图 11  0～800 m/s的初速度范围内刚体弹和非刚体弹体的侵彻深度随着靶速度的变化

    Figure 11.  Penetration depth vs. penetration velocity from 0 to 800 m/s

    下载: 全尺寸图片 幻灯片

    图 12  0～4000 m/s的初速度范围内非刚体弹侵彻深度随着靶速度的变化关系

    Figure 12.  Penetration depth vs. penetration velocity from 0 to 4000 m/s

    下载: 全尺寸图片 幻灯片

    图 13  1000～1600 m/s的着靶速度范围内非刚体弹侵彻深度随着靶速度的变化

    Figure 13.  Penetration depth vs. penetration velocity from 1000 to 1600 m/s

    下载: 全尺寸图片 幻灯片

    表 1  花岗岩靶板的HJC强度模型参数

    Table 1.  Strength model parameters for the granite

    G/GPaρ/(kg∙m−3)A/MPaB/MPaN${\dot \varepsilon _0}/{s^{ - 1}}$Cfc′/MPaSmaxD1D2εf
    14.19280095016000.791.00.008126.5700.0341.00.01
    下载: 导出CSV

    表 2  花岗岩靶板的HJC状态方程参数

    Table 2.  Equation of state parameters for the granite

    pc/MPaμcpl/MPaμlT/MPaK1/GPaK2/GPaK3/GPa
    42.20.0032790.028.78685–171208
    下载: 导出CSV

    表 3  钢珠的材料参数

    Table 3.  Strength model parameters for the projectile

    G/GPaρ/(kg∙m−3)σy/GPaB/GPaNC1/(m∙s−1)CTmelt/KS1γ0M
    81.878000.2350.31.0335740.2616001.921.690.014
    下载: 导出CSV

    表 4  SPH数值模拟的侵彻深度结果

    Table 4.  Depth of pit formed by numerical simulation of SPH

    v0/(m∙s−1)h/mmv0/(m∙s−1)h/mm
    973.012024.20
    1093.292514.72
    1713.962694.91
    1753.97
    下载: 导出CSV
  • [1] KUANG Y C, LIN W, XU X F, et al. Study on the fragmentation of granite due to the impact of single particle and double particles [J]. Petroleum, 2016, 2(3): 267–272. doi: 10.1016/j.petlm.2016.04.001
    [2] TOBIAS H, FRANK S, KLAUS T, et al. Hypervelocity impacts on dry and wet sandstone: observations of ejecta dynamics and crater growth [J]. Meteoritics & Planetary Science, 2013, 48(1): 23–32.
    [3] 李争, 刘元雪, 胡明, 等. “上帝之杖”天基动能武器毁伤效应评估 [J]. 振动与冲击, 2016, 35(18): 159–180. LI Z, LIU Y X, HU M, et al. Damage effect evaluation of god stick space-based kinetic energy weapons [J]. Journal of Vibration and Shock, 2016, 35(18): 159–180.
    [4] 王明洋, 邱艳宇, 李杰, 等. 超高速长杆弹对岩石侵彻、地冲击效应理论与实验研究 [J]. 岩石力学与工程学报, 2018, 37(3): 564–572. WANG M Y, QIU Y Y, LI J, et al. Theoretical and experimental study on rock penetration and ground impact effects of hypervelocity long rod projectiles [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(3): 564–572.
    [5] 强洪夫, 范树佳, 陈福振, 等. 基于SPH方法的聚能射流侵彻混凝土靶板数值模拟 [J]. 爆炸与冲击, 2016, 36(4): 516–524. doi: 10.11883/1001-1455(2016)04-0516-09 QIANG H F, FAN S J, CHEN F Z, et al. Numerical simulation on penetration of concrete target by shaped charge jet with SPH method [J]. Explosion and Shock Waves, 2016, 36(4): 516–524. doi: 10.11883/1001-1455(2016)04-0516-09
    [6] LUCY L B. A numerical approach to the testing of the fission hypothesis [J]. Astronomical Journal, 1977, 8(12): 1013–1024.
    [7] MONAGHAN J J. Smoothed particle hydrodynamics [J]. Annual Review of Astronomy and Astrophysics, 1992, 30: 543–574. doi: 10.1146/annurev.aa.30.090192.002551
    [8] LIU G R, LIU M B. 光滑粒子流体动力学——一种无网格粒子法[M]. 韩旭, 杨刚, 强洪夫, 译. 长沙: 湖南大学出版社, 2005. LIU G R, LIU M B. Smoothed particle hydrodynamics: a meshfree particle method [M]. Translated by HAN X, YANG G, QIANG H F. Changsha: Hunan University Press, 2005.
    [9] 强洪夫. 光滑粒子流体动力学新方法及应用 [M]. 第2版. 北京: 科学出版社, 2017: 258–262. QIANG H F. The new method and application of smoothed particle hydrodynamics [M]. 2nd ed. Beijing: Science Press, 2017: 258–262.
    [10] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures [C]//7th International Symposium on Ballistics. The Hague, Netherlands, 1983.
    [11] 肖云凯, 方秦, 吴昊, 等. Johnson-Cook本构模型参数敏感度分析 [J]. 应用数学和力学, 2015, 36(Suppl): 21–28. XIAO Y K, FANG Q, WU H, et al. Analysis of parameter sensitivity for the Johnson-Cook constitutive model [J]. Applied Mathematics and Mechanics, 2015, 36(Suppl): 21–28.
    [12] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjective to large strain, high strain rates, and high pressure [C]//14th International Symposium on Ballistics. Québec, Canada, 1993: 591–600.
    [13] 李争, 刘元雪, 谭仪忠, 等. 钨合金动能弹超高速侵彻钢靶的破坏特性 [J]. 后勤工程学院学报, 2016, 32(1): 7–12. doi: 10.3969/j.issn.1672-7843.2016.01.002 LI Z, LIU Y X, TAN Y Z, et al. Damage property of tungsten alloy kinetic energy projectile hypervelocity penetrating into steal target [J]. Journal of Logistical Engineering University, 2016, 32(1): 7–12. doi: 10.3969/j.issn.1672-7843.2016.01.002
    [14] 何翔, 徐翔云, 孙桂娟, 等. 弹体高速侵彻混凝土的效应实验 [J]. 爆炸与冲击, 2010, 30(1): 1–6. doi: 10.11883/1001-1455(2010)01-0001-06 HE X, XU X Y, SUN G J, et al. Experimental investigation on projectiles’ high-velocity penetration into concrete targets [J]. Explosion and Shock Waves, 2010, 30(1): 1–6. doi: 10.11883/1001-1455(2010)01-0001-06
    [15] YOUNG C W. Penetration equation: SAND 97-2426 [R]. Albuquerque, NM: Sandia National Laboratories, 1997.
  • 加载中
图( 13) 表( 4)
计量
  • 文章访问数:  1814
  • HTML全文浏览数:  1814
  • PDF下载数:  12
  • 施引文献:  0
出版历程
  • 收稿日期:  2018-08-27
  • 刊出日期:  2019-10-05

SPH方法在宽速域岩石侵彻问题中的应用

    通讯作者: 张国星（1994－），男，硕士研究生，主要从事计算力学研究. E-mail：1428071753@qq.com; 
    作者简介: 强洪夫（1963－），男，博士，教授，博士生导师，主要从事材料与结构失效行为与高性能数值模拟研究. E-mail：qiang@263.net
  • 火箭军工程大学，陕西 西安　710025
  • 收稿日期:  2018-08-27

摘要: 采用光滑粒子流体动力学（SPH）方法对花岗岩靶板受碰撞侵彻的大应变、高应变率变形问题进行了数值模拟。为了描述弹目材料的非线性变形及破坏特性，对花岗岩靶板引入了Holmquist-Johnson-Cook（HJC）本构模型及损伤模型，对弹体引入含损伤的Johnson-Cook（J-C）本构方程和Grüneisen状态方程，靶板与弹体均离散成拉格朗日粒子。通过自编程序仿真计算0～4 m/s的着靶速度下花岗岩靶板的三维侵彻过程，对比分析了钢珠在不同弹体条件下的侵彻结果，在固体侵彻、半流体侵彻和流体侵彻的区域内拟合了侵彻深度随着靶速度的变化曲线。数值计算结果显示，侵彻深度随着靶速度的增加在固体侵彻区间（$ {v_0} \lt 1421\;{\rm{m}}/{\rm{s}}$）呈现递增趋势，在半流体侵彻区间（$ 1421\; {\rm{m}}/{\rm{s}} \leqslant {v_0}\leqslant1700 \;{\rm{m}}/{\rm{s}}$）呈现递减趋势，在流体侵彻区间（${v_0} \gt 1700\;{\rm{m}}/{\rm{s}} $）呈现递增趋势并逐渐趋于平滑，达到峰值。

English Abstract

    全文HTML

  • 长期以来，碰撞侵彻问题的研究主要集中在低速和中高速领域[1]，但近些年高速和超高速侵彻研究得到了越来越广泛的关注[2]，特别是超高速动能武器的出现，如“上帝之杖”天基武器[3]、“破浪骑士”高速动能钻地武器等，其对地打击速度均能达到3000 m/s，甚至更高。随着着靶速度的不断提高，实验研究的成本和难度也在不断增加，因而国内外对高速和超高速侵彻的实验研究较少，相关研究主要集中在理论研究和数值仿真上。其中，对于理论研究而言，侵彻理论需要随着着靶速度的提高进行修正。王明洋等[4]将侵彻理论研究区间随着靶速度的不同划分为固体侵彻区间和（半）流体侵彻区间，但该理论运用于仿真计算时，需要根据着靶速度的变化采用不同的侵彻理论，仿真计算较为复杂，所以如何运用统一的方法成了解决仿真计算宽速度域碰撞问题的重点之一。基于流体动力学方程的SPH (Smoothed Particle Hydrodynamics)方法已经在高速和超高速碰撞领域得到了广泛的运用[5]，本研究将弹目材料的本构方程和状态方程有效地引入算法中，使该方法能够适用于具有材料强度的低速和中高速的固体侵彻问题，由此便可用统一的SPH方法解决宽速域碰撞侵彻的仿真问题。

    对此，本研究以流体动力学方程为基础的SPH新方法拓展运用到低速碰撞领域，以四川地区花岗岩为对象开展不同着靶速度下碰撞侵彻问题研究，并与试验法和Lagrange网格法的开坑结果进行对比，同时在低速、中高速、高速和超高速的着靶速度区间对钢珠作为非刚体的侵彻过程进行仿真分析，给出开坑深度随着着靶速度的变化规律。

1.   适用于侵彻碰撞问题的SPH新方法

  • 相比较于成功应用于计算流体动力学问题的SPH方法，适用于碰撞侵彻问题的SPH新方法也基于流体动力学基本方程，其基本方程Navier-Stokes（N-S）方程的质量守恒方程、动量守恒方程、能量守恒方程和运动方程在固体介质中表达式为

    式中：$\rho $为密度，${v^\alpha }$为速度分量，$e$为单位质量的内能，${\sigma ^{\alpha \beta }}$为总应力张量分量，空间坐标${x^\alpha }$和时间$t$为独立变量。（1）式中的重复上标符合Einstein求和约定。

    适用于碰撞侵彻问题的SPH新方法需要将弹目材料的本构方程和状态方程引入其中，使得SPH算法能够描述材料强度[6-9]。为此，自编了SPH侵彻仿真程序，其中：对金属材料引入Johnson-Cook（J-C）本构模型[10]和Grüneisen状态方程[11]；对岩石靶板材料引入了考虑压缩强度的压力相关性、应变率效应和损伤软化效应的HJC本构模型和状态方程[12]；同时为了消除由于数值不稳定造成的粒子间的非物理穿透，引入了Monaghan型[7]的人工黏性；并且为了防止在一些特殊情况下产生过热现象，引入了Monaghan导出的适用于SPH方法的人工热流项[7]，以减小内能等物理量的计算误差。

    综上，在考虑人工黏性和人工热量的影响下，流体动力学基本方程（Navier-Stokes方程）的质量守恒方程、动量守恒方程、能量守恒方程和运动方程的SPH离散表达式为

    式中：$\overline {\dot \varepsilon } _i^{\alpha \beta } = {\dot \varepsilon ^{\alpha \beta }} - {{\text{δ}}^{\alpha \beta }}{\dot \varepsilon ^{\gamma \gamma }}/3$，$p$为压强，${{g}}$为单位质量体积力，${{\tau}} $为偏应力张量。

2.   对低速和中高速侵彻问题的数值模拟

  • 弹体侵彻岩石时，主要以速度区分侵彻类型，即分为低速（0～500 m/s）、中高速（500～1300 m/s）、高速（1300～3000 m/s）和超高速（大于3000 m/s）[13]侵彻。在低速和中高速领域以固体侵彻类型为主，弹体的初始动能主要消耗在侵彻过程中侵彻阻抗的消耗做功，其中当弹体初速度${v_0} \leqslant 800\;{\rm{m}}/{\rm{s}}$时弹体几乎不发生形变和质量磨蚀，可以假设为刚体处理[14]，不考虑形变变化，则靶板目标的体积压缩呈线性变化。

    如果将弹体假设为刚体处理，则弹体垂直侵彻的运动方程和初始条件为

    式中：${M_0}$为弹体初始质量，F为弹体阻抗，$h$为侵彻深度。

    将侵彻深度和侵彻阻抗无量纲化，即

    式中：$\overline h $为无量纲侵彻深度，$\overline F $为无量纲侵彻阻抗，$D$为弹体直径，${\tau \rm_s}$为靶板材料的动态强度。对（4）式积分处理得

    式中：$I$为冲击因子。由（5）式可知，弹体侵彻深度是冲击不变量因子的函数。对于低速和中高速的刚体弹体碰撞问题，国内外经验公式[15]均体现了侵彻深度与侵彻速度的线性关系。

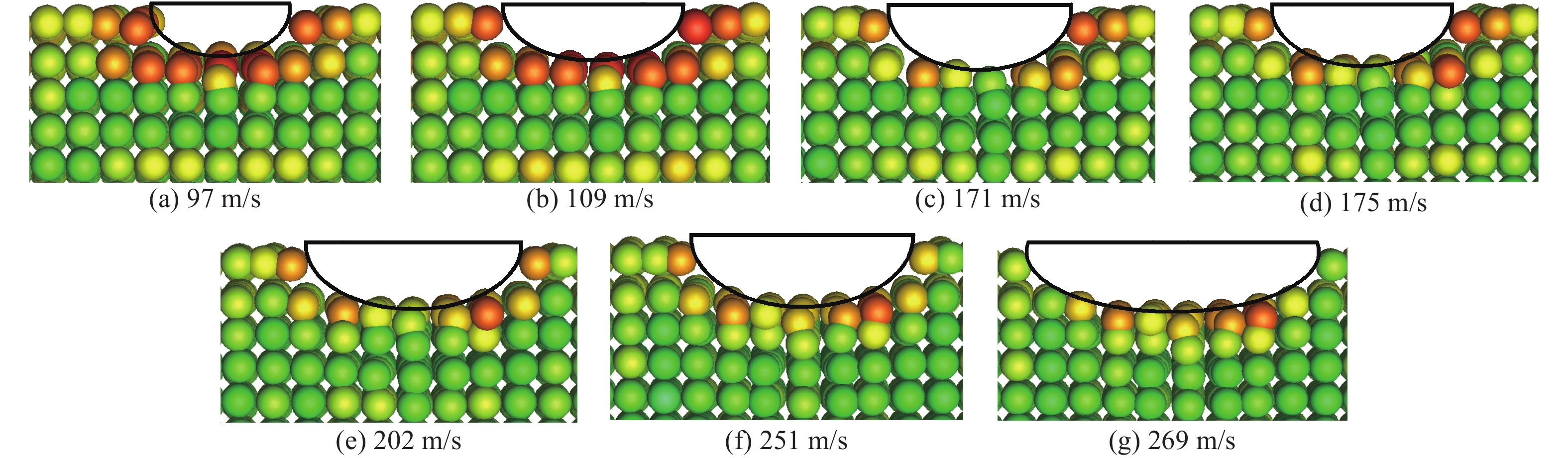
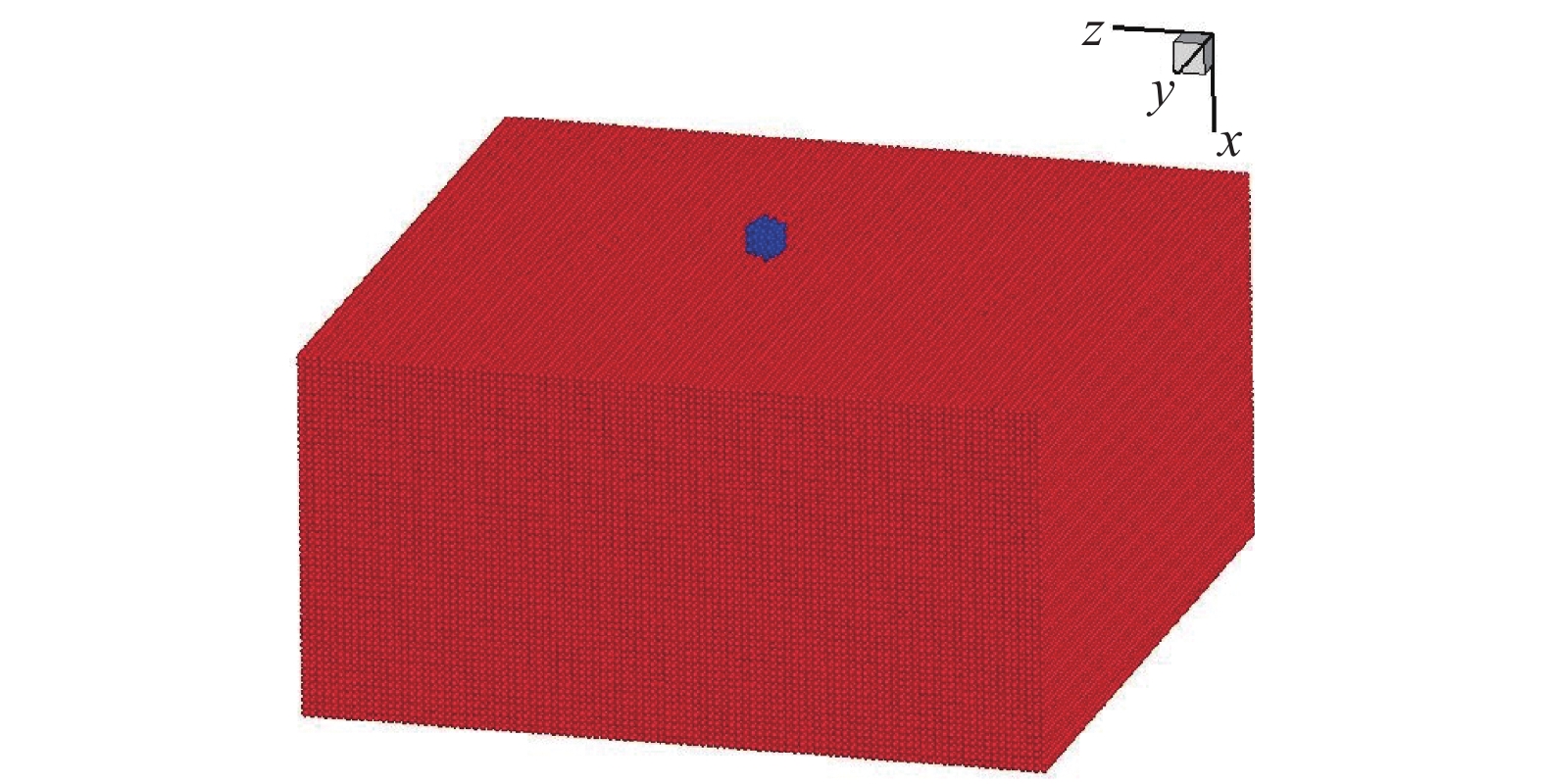
    本研究将SPH方法拓展运用于弹体作为刚体的低速和中高速碰撞，仿真计算了Kuang等[1]的实验算例。该算例采用$9.5\;{\rm{mm}}$直径的钢珠撞击四川地区的花岗岩（声速$c \approx 1030\;{\rm{m}}/{\rm{s}}$）。图1为三维SPH粒子图。在计算仿真中，花岗岩靶板和钢珠的材料参数[1]如表1、表2和表3所示。对于花岗岩靶板的材料参数，根据Young[15]提出的经验公式，靶板目标的可侵彻性参数$S = 12{\left( {{f'_{\rm c}}{{ Q}}} \right)^{ - 0.3}}$，其中${{Q}}$表征材料受节理、裂隙、裂缝和层面影响的大小。对于本研究算例，花岗岩靶板的尺寸相较于钢珠足够大，同时在仿真计算中认为花岗岩靶板层在受侵彻前不含损伤，因而该花岗岩材料属于Young定义材料${{Q}}$级别中的“Massive”级和“Rock Quality Very Good/Excellent”级，取Q=0.9。通过公式计算得到$S = 2.9$，与Young给出的岩石$S$取2.5~3.5相符合，据此，本研究所采用的花岗岩的材料参数是科学适用的。

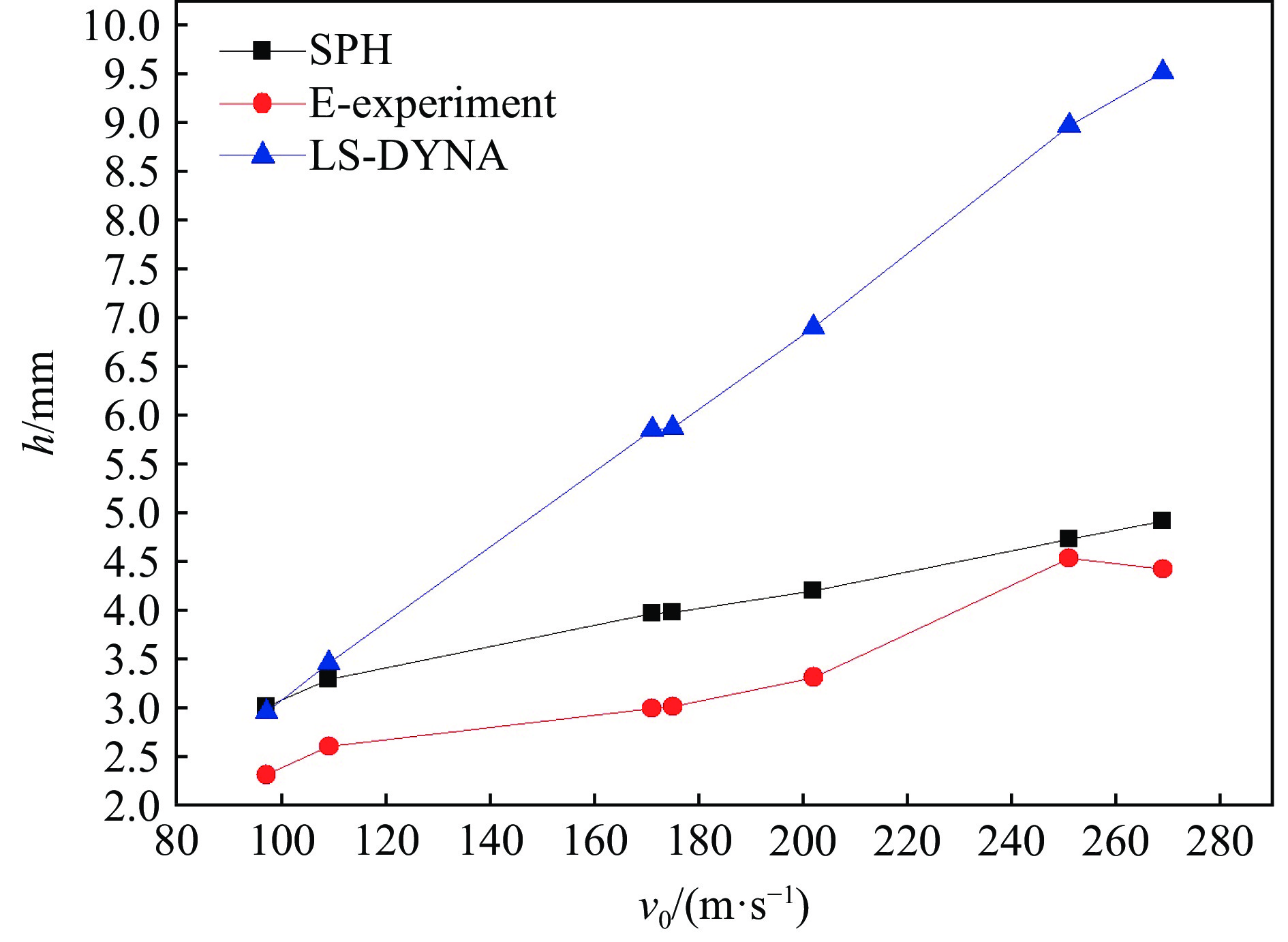
    参照对比算例，以97、109、171、175、202、251、$269\;{\rm{m}}/{\rm{s}}$的着靶速度进行SPH数值模拟，仿真成坑深度结果见表4。将SPH数值模拟结果与文献[1]中基于LS-DYNA仿真软件的Lagrange网格法结果和实验结果进行对比。从侵彻深度随着着靶速度的变化曲线来看（见图2），SPH方法的模拟结果更加接近实验值。

    从成坑形状来看：图3中SPH方法模拟的成坑形状为长条椭圆形，成坑是通过弹体碰撞挤压靶板形成的，在该速度区间未造成粒子失效即破碎；图4中Lagrange网格法的成坑形状为近似圆形，成坑是通过靶板网格受弹体网格碰撞后失效消失形成的；图5中实验结果的成坑形状为长条近似椭圆形，成坑是由碰撞挤压形成的，未造成靶板材料的破坏。对比发现，SPH数值模拟结果在成坑形状上更加接近实验结果；Lagrange网格法的结果存在网格消除，即存在质量不守恒的问题，相比较而言，SPH方法只存在粒子位移，不存在粒子消除，所以可以保证质量守恒。综上，基于流体动力学方程的SPH方法适用于弹体假设为刚体的固体侵彻类型，并较Lagrange网格法更加有效。

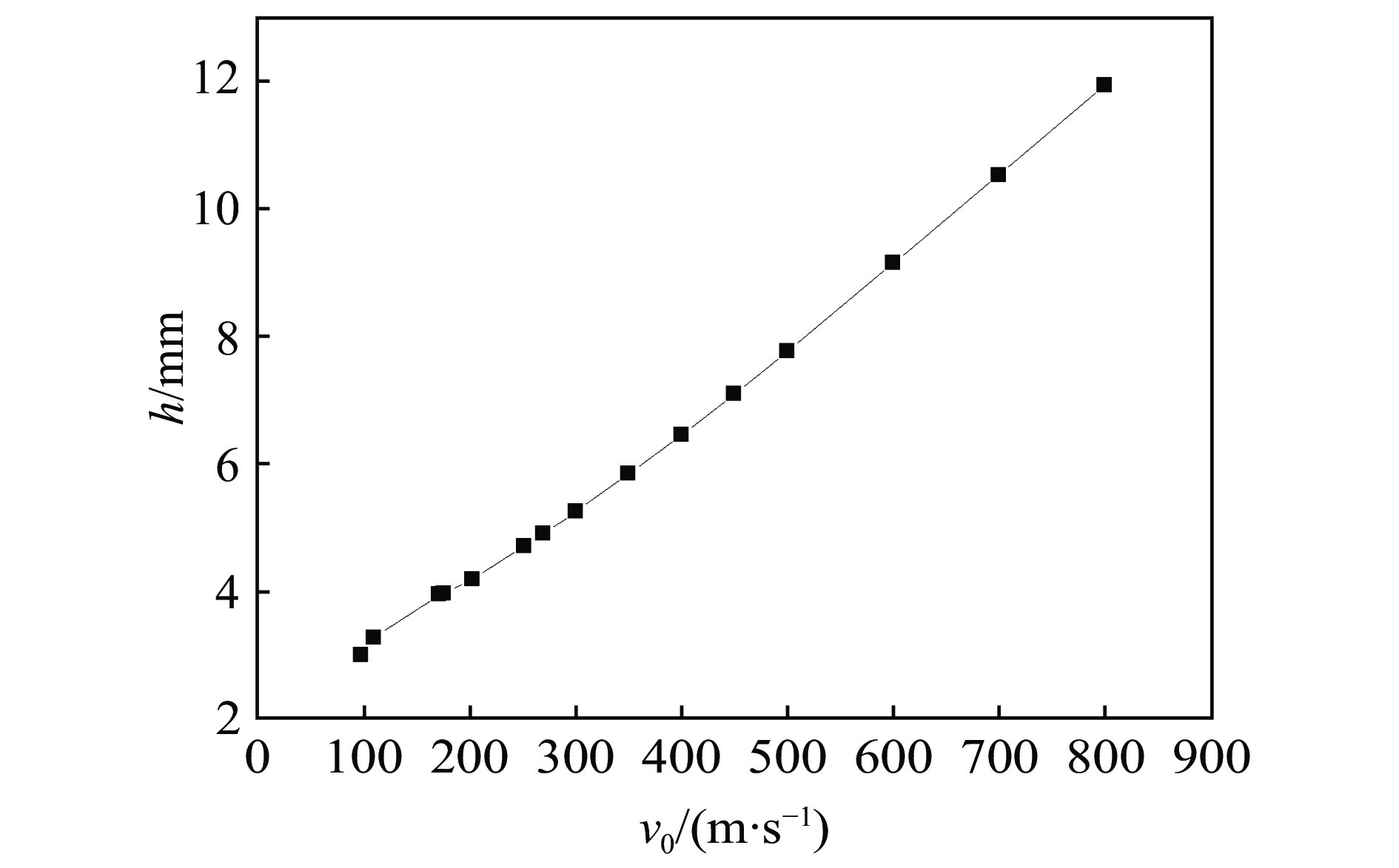
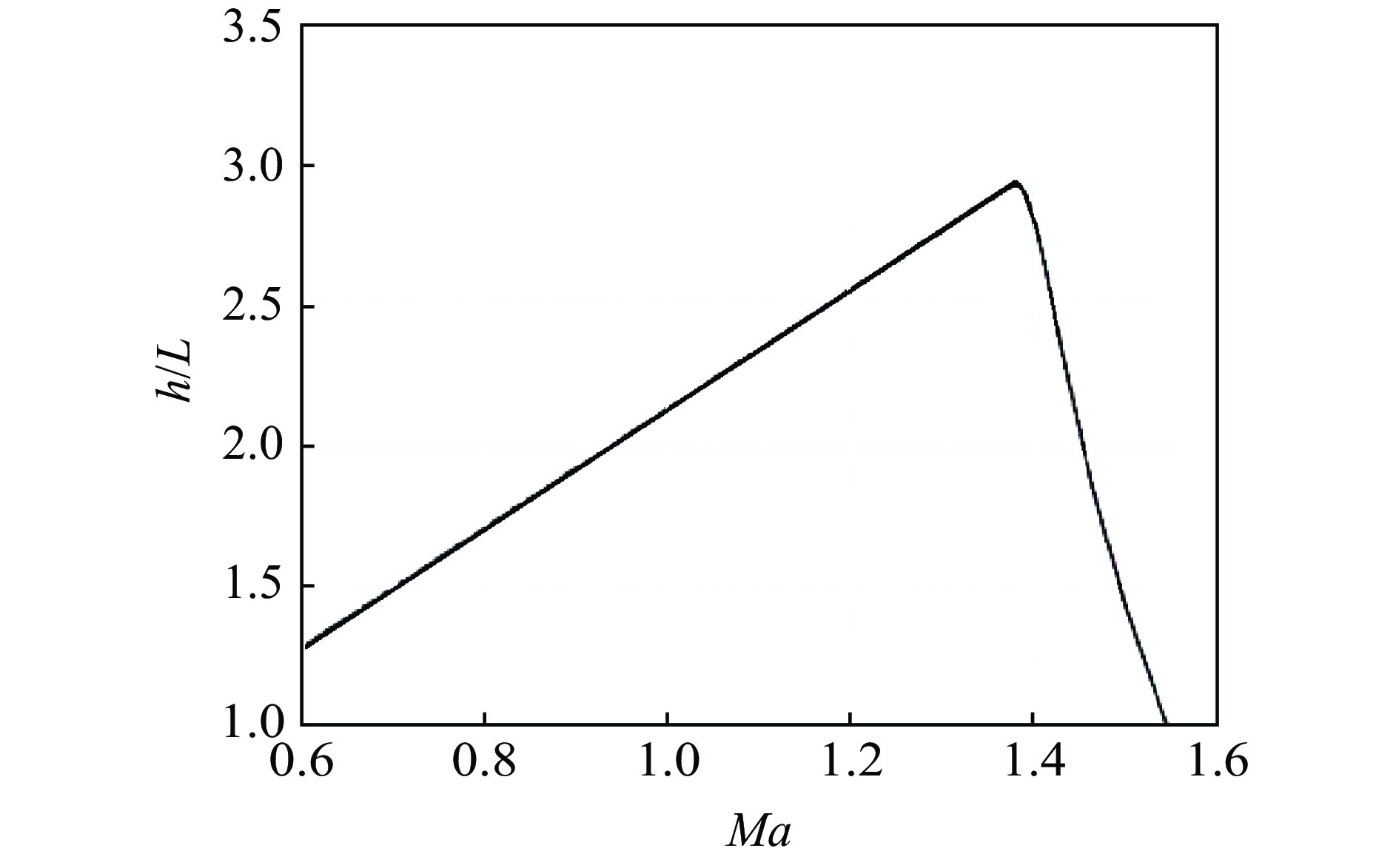
    根据文献可知，侵彻速度${v_0} \leqslant 800\;{\rm{m}}/{\rm{s}}$时，弹体均可假设为刚体，所以针对上述实验算例，将着靶速度提升为300、350、400、450、500、600、700、$800\;{\rm{m}}/{\rm{s}}$，拟合出着靶速度${v_0}$在0～800 m/s范围内的侵彻深度随着靶速度的变化曲线，如图6所示。

    根据王明洋等[4]的固体侵彻理论中侵彻深度随着着靶速度的变化关系（见图7），该数值关系符合Young的经验公式。当马赫数${Ma} < 1.4$时，因不考虑弹体侵蚀和形变，所以射流长度$L$保持不变，则侵彻深度随着着靶速度呈正比例的线性关系，其中，$h/L = \lambda $，$h$为侵彻深度，$L$为射流长度。在弹丸碰撞花岗岩靶板的问题中，根据固体侵彻理论[4]，${v_0} < 1421\;{\rm{m}}/{\rm{s}}$（即${Ma} < 1.38$）时符合线性递增关系。图6中，弹体在0～800 m/s的速度范围内，即马赫数Ma 在0～0.78之间，侵彻深度与侵彻速度基本呈线性递增关系，与固体侵彻理论[4]相符合。

3.   SPH新方法在宽速域内的运用

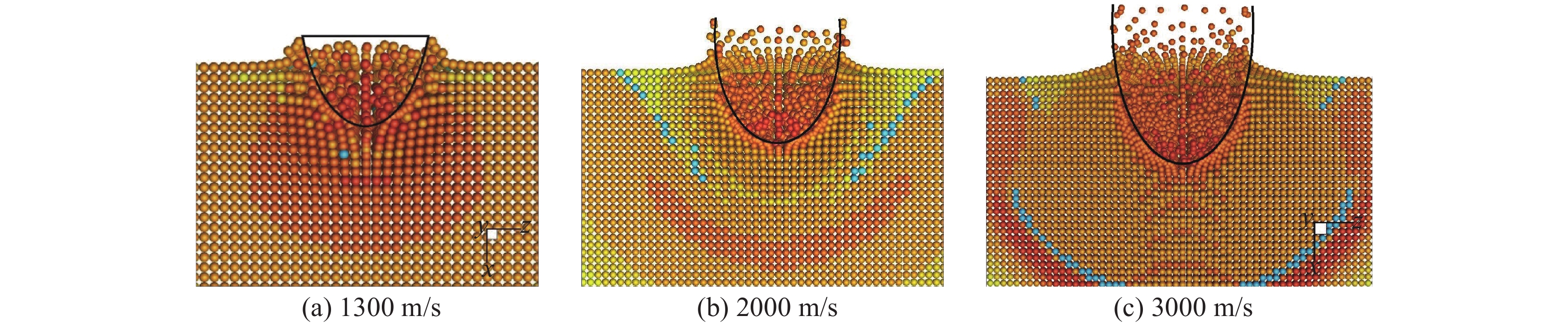
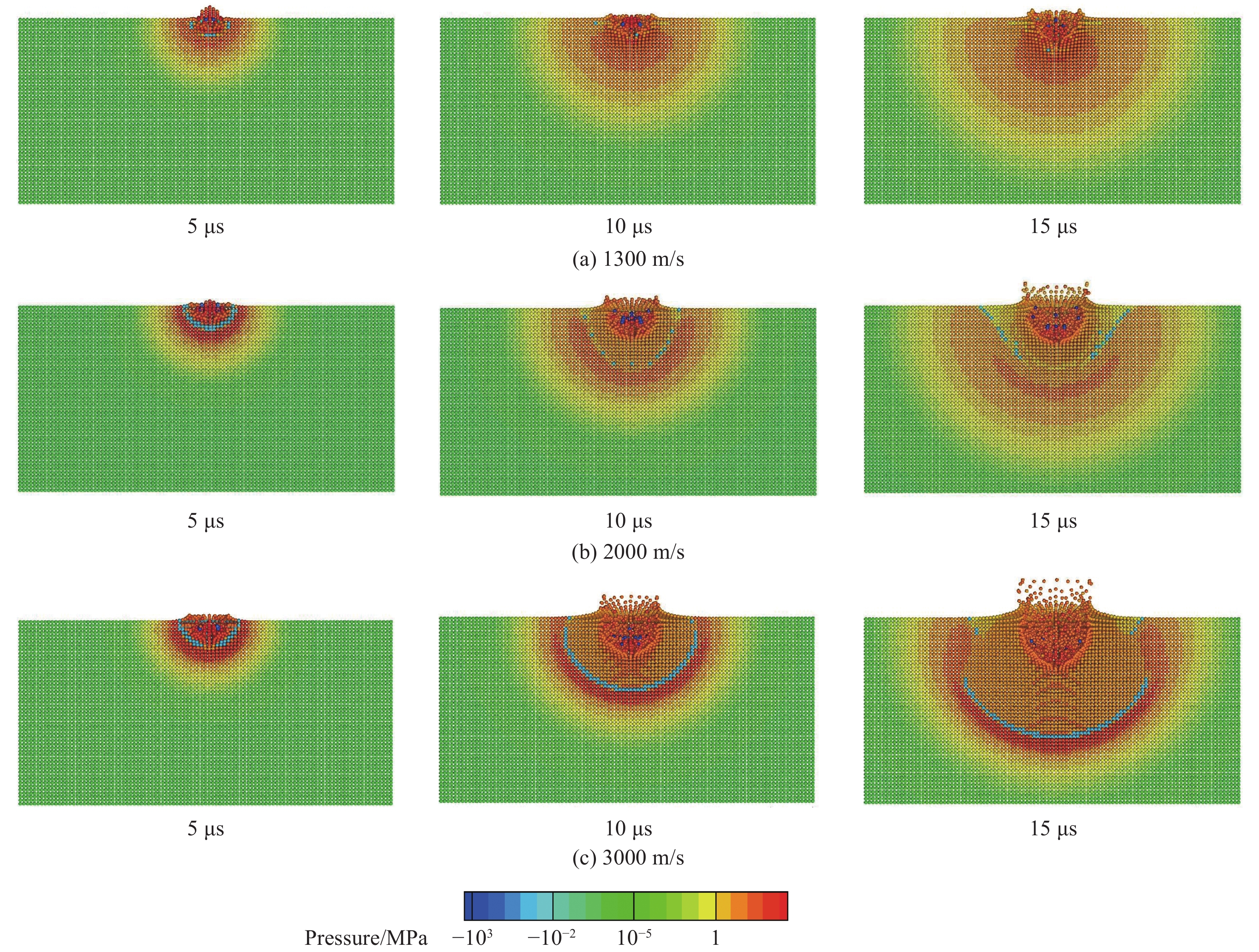
  • 当${v_0} > 800\;{\rm{m}}/{\rm{s}}$时，弹体不可作为刚体处理。其中，当$800\;{\rm{m/s}}< {v_0}< 1300\;{\rm{m/s}}$时，弹体侵彻仍属于中高速侵彻范畴，仍能采用SPH新方法对侵彻过程进行仿真计算；当${v_0} > 1300\;{\rm{m}}/{\rm{s}}$时，弹体侵彻为高速和超高速侵彻，属于（半）流体侵彻范畴。因自编程序基于采用流体动力学方程的SPH方法，该方法已经较为成熟地运用于处于流体侵彻领域的高速和超高速碰撞领域[5]。前面对于直径为$9.5\;{\rm{mm}}$的钢珠在弹体可以假设为刚体的条件下撞击岩石靶板的问题进行了讨论，为探究在0～4000 m/s宽速度域内侵彻深度随着靶速度的变化关系，本研究继续对着靶速度为800～4000 m/s的侵彻过程进行仿真，得到了不同速度条件下花岗岩靶板的成坑过程。因为在该速度域内弹体不作为刚体处理，需要考虑形变和粒子的失效（即质量损失），所以对钢材料弹体引入含损伤J-C本构模型（J-C Damage本构）和Grüneisen状态方程。其中，1300、2000和3000 m/s的着靶速度下的最终成坑结果如图8所示，靶板开坑过程和压力变化过程如图9所示。

    图9给出了3种侵彻速度下不同时刻靶板材料应力波传播的情况。根据应力波传播速度的基本理论，在理想情况下，应力波速公式为

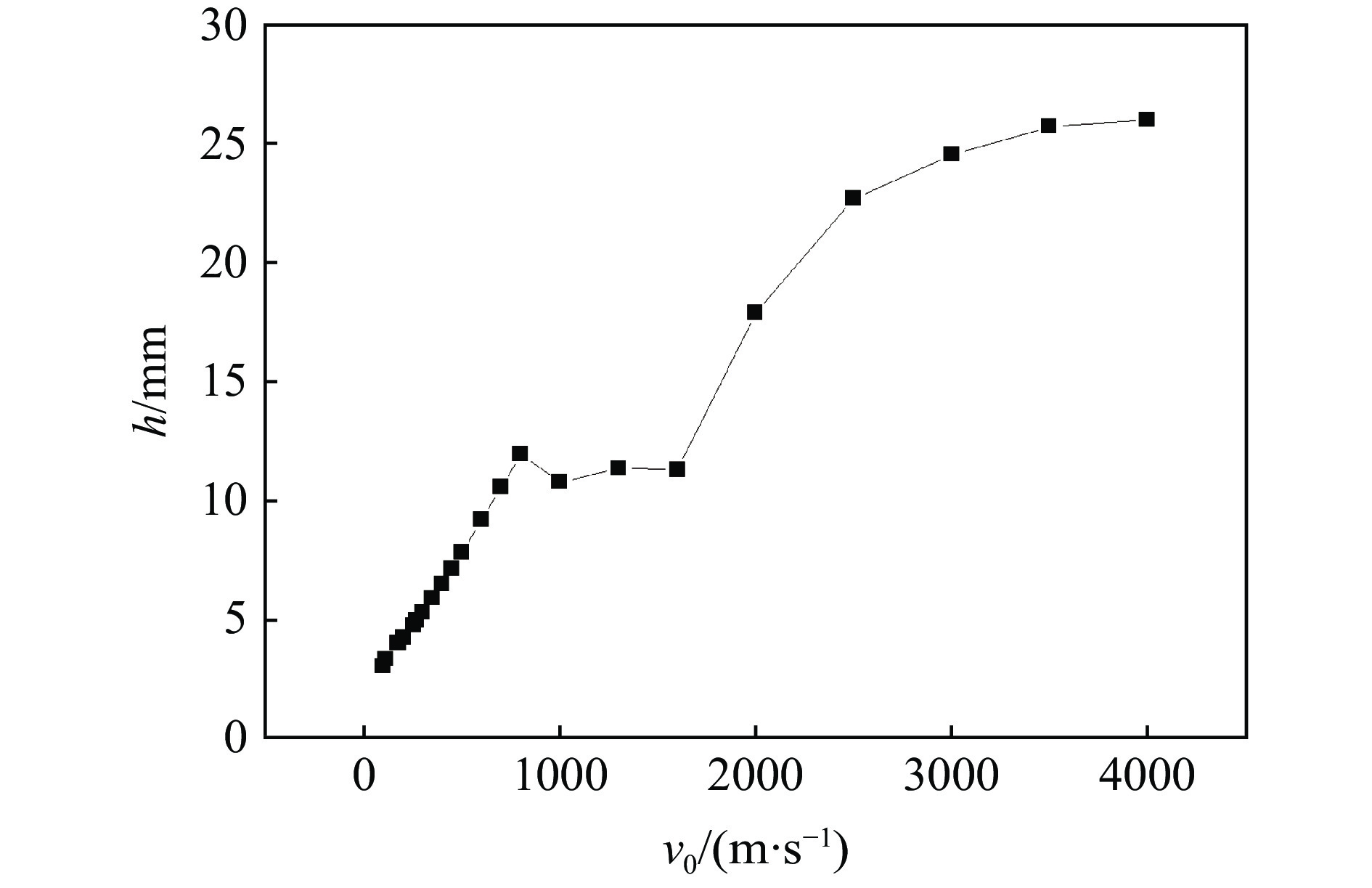
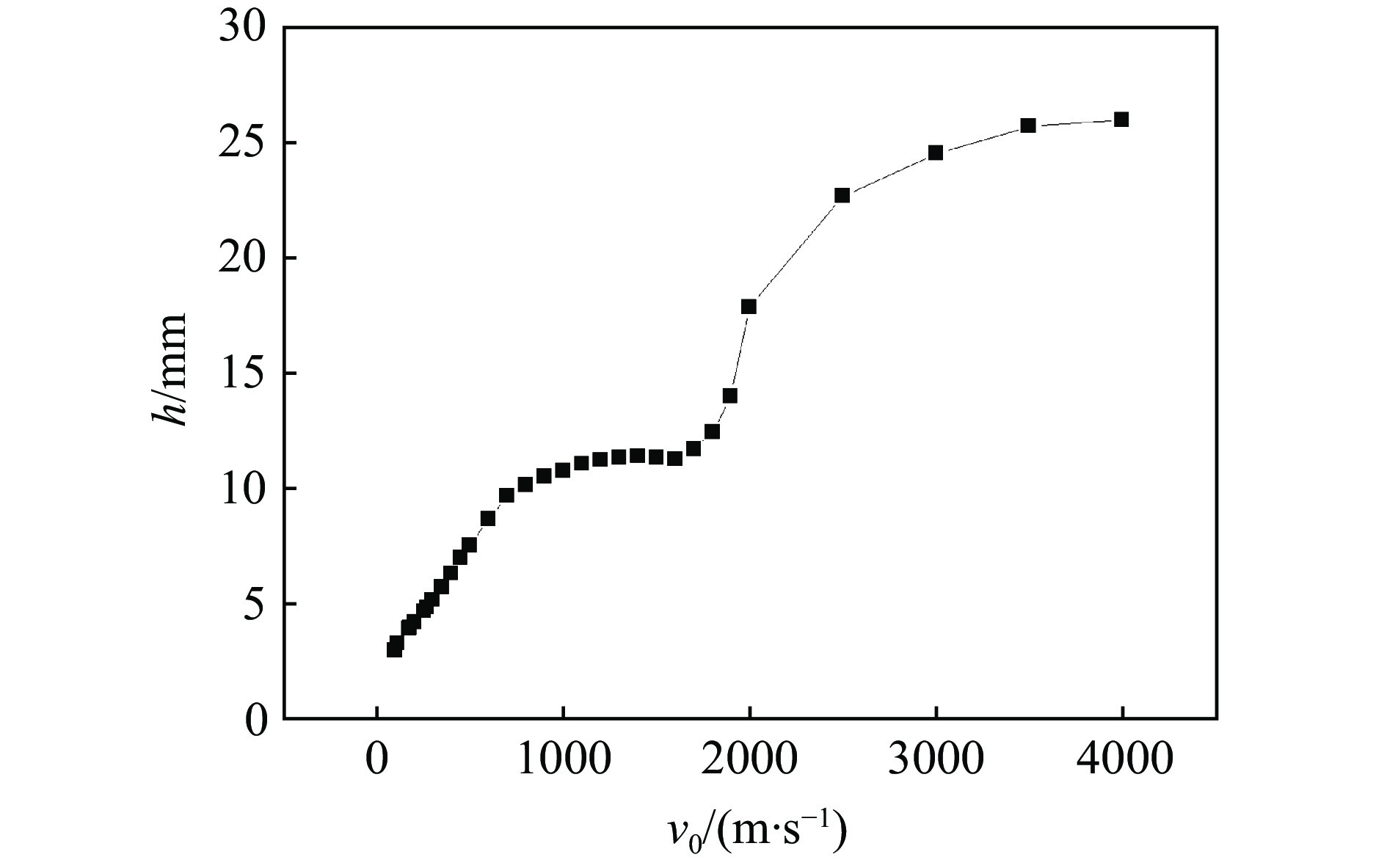
    式中：$E$为材料的杨氏模量，$\rho $为应力波传输介质的密度。对此根据仿真对象的材料参数，计算得到理论上的应力波波速为$3630\;{\rm{m}}/{\rm{s}}$；仿真计算中3种不同侵彻速度下应力波波速均为$3712\;{\rm{m}}/{\rm{s}}$，波速不受侵彻速度的影响，与理论波速值较为一致。

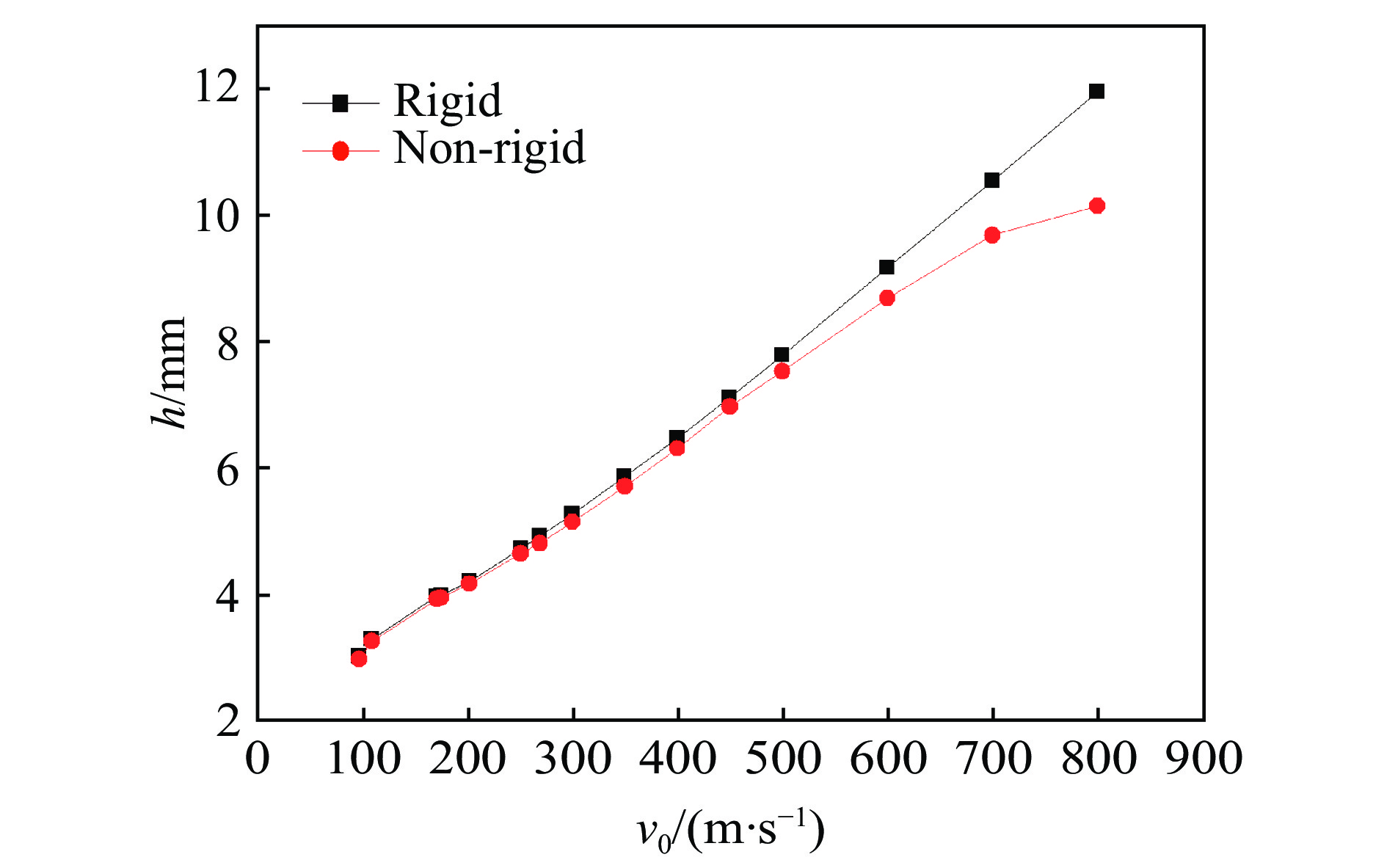
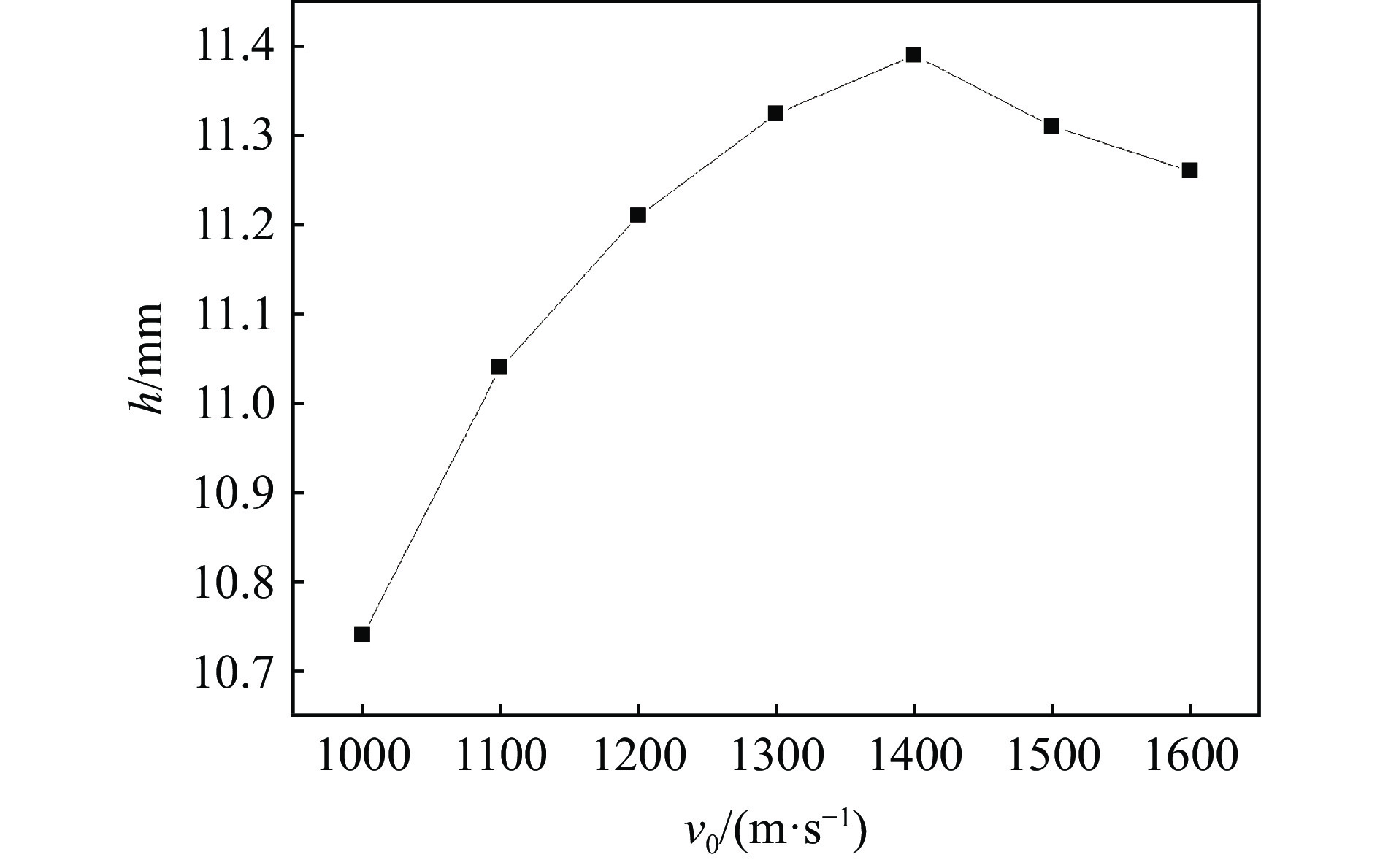
    图10为仿真拟合的0～4000 m/s速度区间内侵彻深度随着靶速度的变化曲线图。在$0 \leqslant {v_0} \leqslant 800\;{\rm{m/s}}$（Ma为0～0.78）的范围内，侵彻类型是假设弹体为刚体的固体侵彻类型，在该区间内侵彻深度随着靶速度的增大线性递增；但当v0 = 1000 m/s时，侵彻深度h = 10.74 mm，明显小于v0 = 800 m/s时的侵彻深度，考虑到前后钢珠的弹体条件不一样，可能会对结果存在影响，因而本研究在0～800 m/s的着靶速度范围内将弹体也考虑为非刚体进行仿真计算。同时从图10中还可以观察到，在800～2000 m/s的速度范围内，关系曲线没有明显的规律，因而本研究在该区域继续取多个速度点进行仿真计算，以考察侵彻深度随着靶速度的变化关系，仿真结果如图11、图12和图13所示。

    从图11中可以观察到，当考虑钢珠形变后，侵彻深度均小于相同着靶速度下刚体弹体的侵彻深度，两者的差值随着着靶速度的增加而增加，仿真结果显示弹体在0～800 m/s的着靶速度范围内存在变形，形变量随着着靶速度的增加而增加。图12为在0～4000 m/s的范围内均考虑弹体形变后，拟合的侵彻深度与着靶速度的数值关系曲线，在800～2000 m/s的速度范围内以100 m/s的速度间隔取速度点进行仿真计算。其中，当800 m/s < v0 < 1421 m/s时，侵彻仍处固体侵彻的区间，侵彻深度随着靶速度的增加逐渐递增，但侵彻类型已经由中高速侵彻向高速侵彻转变，递增的幅度明显变小；当$1421\;{\rm{m}}/{\rm{s}} \leqslant {v_0} \leqslant 1700\;{\rm{m}}/{\rm{s}}$时，侵彻处于半流体侵彻区域，是固体侵彻向流体侵彻转化的区域，随着侵彻速度的增加，弹体形变趋势增大，阻力增大幅度变大，因而在该区域内侵彻深度随着着靶速度的增加而递减，如图13所示；当${v_0} > 1700\;{\rm{m}}/{\rm{s}}$时，侵彻近区介质动应力处于流体状态，属于流体侵彻的范畴，在该区域内弹体的形变时间很短，弹体的形变对侵彻深度的影响较小，出现了侵彻深度随着靶速度的增加呈现非线性递增的趋势，递增趋势变缓，随着着靶速度增加，开坑深度趋近于峰值。

4.   结　论

  • 针对不同着靶速度范围内的碰撞侵彻过程进行了讨论和分析，主要从探索侵彻深度随着着靶速度的变化规律出发，将基于流体动力学基本方程的SPH数值模拟方法运用于低速、中高速、高速和超高速的碰撞侵彻领域，并在0～4000 m/s的速度范围内，拟合出了侵彻深度与着靶速度的数值关系曲线，结合数值模拟结果，总结如下。

    (1)基于流体动力学基本方程的SPH方法适用于假设弹体为刚体的固体侵彻类型。仿真结果显示，在0～800 m/s的着靶速度范围内，刚体弹丸的侵彻深度随着靶速度呈线性递增的趋势，成坑结果相比于Lagrange网格法的模拟结果更加贴近实验结果。但在该区域内，考虑弹体形变时，侵彻深度略小于刚体弹结果，两者的差值随着靶速度的增加而增加。

    (2)对于非刚体钢珠侵彻中国四川地区花岗岩的问题，在着靶速度为0～4000 m/s的区间内，钢珠的侵彻经历了固体侵彻和（半）流体侵彻，其中：在${v_0} < 1421\;{\rm{m}}/{\rm{s}}$范围内，随着靶速度${v_0}$的增加，侵彻深度$h$不断增大，但弹体形变的加大导致侵彻深度$h$的增长幅度降低；在$1421\;{\rm{m}}/{\rm{s}} \leqslant {v_0} \leqslant 1700\;{\rm{m}}/{\rm{s}}$范围内，侵彻处于固体侵彻向流体侵彻的过渡区，在该区域随着着靶速度的增加，侵彻深度$h$有明显的下降；在${v_0} > 1700\;{\rm{m}}/{\rm{s}}$范围内，侵彻处于完全的流体侵彻，侵彻深度随侵彻速度非线性递增；当${v_0} > 3000\;{\rm{m}}/{\rm{s}}$时，递增趋势变缓，随着着靶速度增加，侵彻深度趋近于峰值。

参考文献 (15)

目录

/

返回文章
返回