-
近年来,以降低车辆自身重量为目标,采用高强度、低厚度的钢板材料逐渐成为车辆制造业的发展方向之一[1-3]。与此同时,在满足车辆整体设计轻量化的基础上,还要求车辆结构具有较强的刚度并在碰撞时具有较高的吸能效率。帽型薄壁梁结构可通过自身结构的塑性变形实现被动吸能,从而作为主要承载和碰撞吸能部件(如车架前纵梁等)被广泛应用于汽车与航空等领域。因此,研究帽型薄壁梁结构在冲击载荷作用下的变形模式和吸能特性具有重要意义。
20世纪60年代,Alexander[4]率先通过实验和运动学可变形理论相结合研究圆形薄壁梁轴向压溃并给出了理论模型,为后续薄壁结构受轴向冲击耐撞性研究打下基础。Wierzbicki等[5]在此基础上系统研究了方形帽型梁结构,简化折叠单元的模型,应用宏单元法提出超折叠单元理论,分析矩形薄壁梁受冲击载荷时的压溃行为,为研究轴向冲击薄壁梁理论提供基础。White等[6-7]利用超折叠单元理论对低碳钢帽型和双帽型梁准静态轴向加载和动态轴向加载下的平均碰撞载荷进行了理论分析和准确预测。Tarigopula等[8]对DP800双相钢方形截面和帽型截面薄壁梁进行轴向压溃实验,并通过仿真实验验证了超折叠理论。顾纪超等[9]结合超折叠单元理论,准确预测了不同材料、不同厚度帽型薄壁梁在轴向压溃时的平均碰撞力,提出了通用帽型梁结构轴向压溃理论,并通过实验和数值模拟对理论的正确性进行验证。王特捷等[10]进行了不同壁厚帽型梁试件的落锤冲击实验,分析其能量吸收特性,发现随着壁厚变薄,试件会发生弯曲失稳,厚度为1.0 mm的试件较厚度为1.2 mm和0.8 mm的试件具有更高的能量吸收效率。李亚等[11]分析了DP600双相钢的烘烤特性对碰撞实验的影响,并验证了修正的Johnson-Cook模型对DP600双相钢动态力学性能描述的准确性。田泽等[12]对DP980双相钢帽型梁进行了落锤实验和模拟计算,得到其压溃模式和最大变形量,并通过计算模拟研究截面参数改变对DP980双相钢帽型梁整体碰撞吸能效果的影响。
前期研究中帽型梁材质单一且实验冲击载荷能量较低,本研究在此基础上针对DP980和DP780两种不同材质的帽型梁试件开展了高初始能量落锤轴向冲击实验,分别从变形模式、最大形变量、峰值载荷和整体能量吸收能力,对两种异材帽型梁结构在几何参数、加工工艺、加载条件相同情况下的抗冲击性能进行对比,为汽车设计和制造行业的选材提供依据。
-
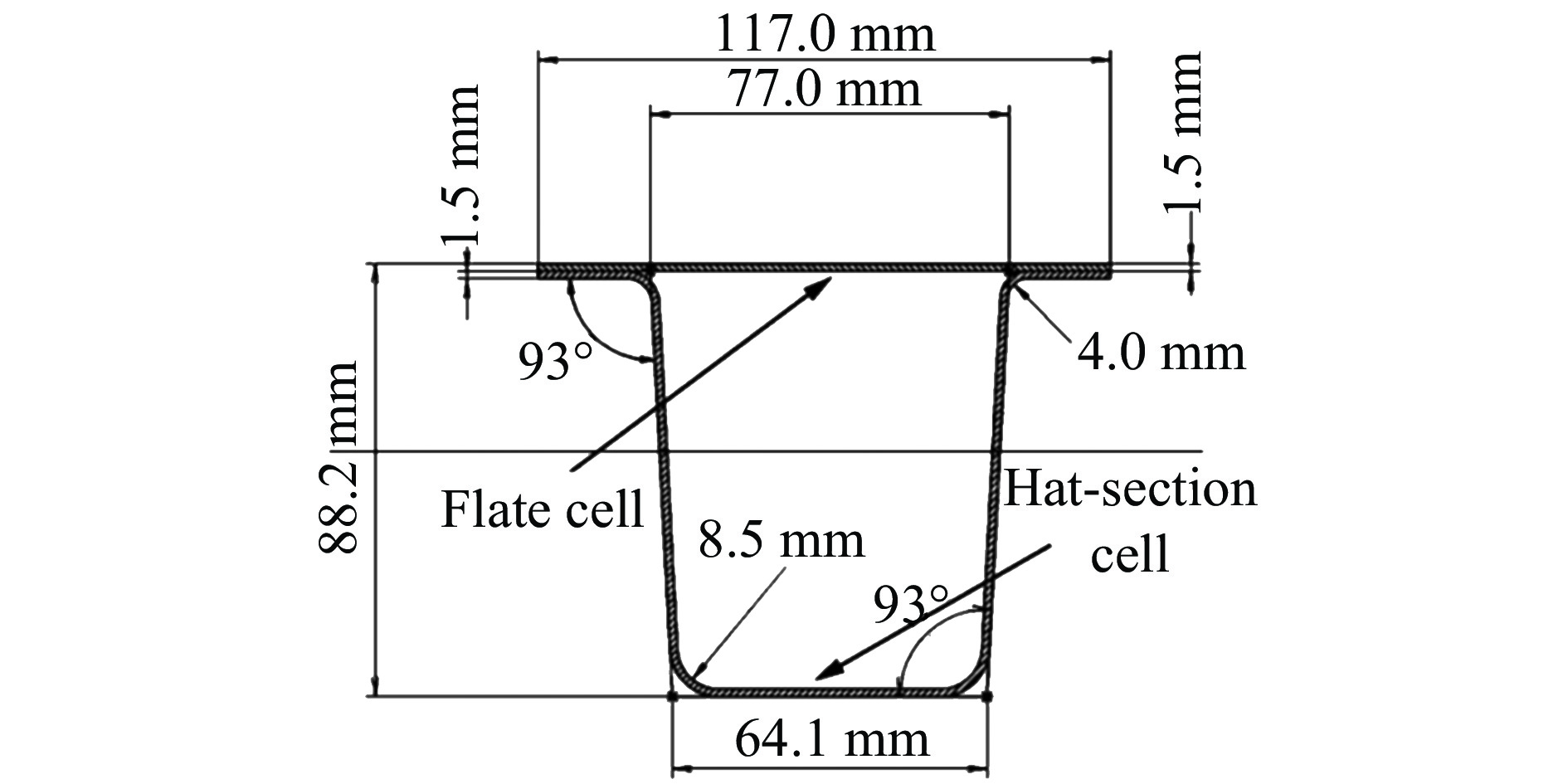
如图1(a)所示,实验试样为含倒角的帽型梁结构。该试样由帽型结构和上、下两块盖板组成,其中帽型结构又包括帽型单元和平板单元。为研究帽型单元材料对帽型梁动态响应的影响,轴向冲击实验采用两组实验试件,每组6个试样,如图1(b)所示。其中,A组帽型单元(Hat-Section Cell)材质为DP980双相钢,B组帽型单元材质为DP780双相钢;试件其余部件所用材料相同,上下盖板(Cover Plate)材质均为DC01钢,平板单元(Flate Cell)材质为CR380LA钢。帽型结构主体采用厚度为1.5 mm、长度为400 mm的钢板;盖板尺寸为140 mm×120 mm×3 mm的钢板;在上下盖板中心处各开一个直径为40 mm的圆孔。帽型梁截面尺寸如图2所示,可以看出帽型单元存在呈轴对称分布的四处弯折以及倒角,其中弯折角度为93°,倒角半径分别为4.0 mm和8.5 mm。同时在试件盖板上添加尺寸为260 mm×200 mm×8 mm的高强度钢板作为垫板,以保证实验过程中试件受到均匀的冲击载荷。
此外,由于双相钢存在很大的冷作硬化效应,常温加工过程中表面层金属硬度增加,需较大应力使其发生塑性变形,为达到实验要求的尺寸精度,特制造配套模具用于加工帽型单元。帽型梁的帽型单元和平板单元通过点焊形式焊接,焊点距离结构侧边缘10 mm,距上、下边缘8 mm,焊点间距32 mm。焊点满足工程要求
$d \geqslant 1.5\sqrt t $ (t为焊接板的厚度,d为焊点直径)。上下盖板通过电弧焊接与帽型结构连接。本实验所用两组试件的几何尺寸、加工工艺、焊接工艺完全相同。为方便记录实验数据,对实验试件进行编号:第1组DP980帽型梁试件记为A1~A6,第2组DP780帽型梁试件记为B1~B6。 -
轴向冲击实验在太原理工大学DHR940落锤上进行。落锤主体结构分为加载装置和固定装置,最大下落高度为13 m,锤头及配重的最大质量为270 kg。实验中所用落锤的整体质量为241 kg,下落高度设置为7.55 m,初始冲击速度为12.16 m/s。在实验过程中,试件将承受巨大的冲击载荷,从实验准确性和安全性双重因素考虑,为防止试件受冲击后发生飞溅和滑移等情况,采用两块C型板通过压盖试件边缘进行固定,实验试件的装配如图3所示。
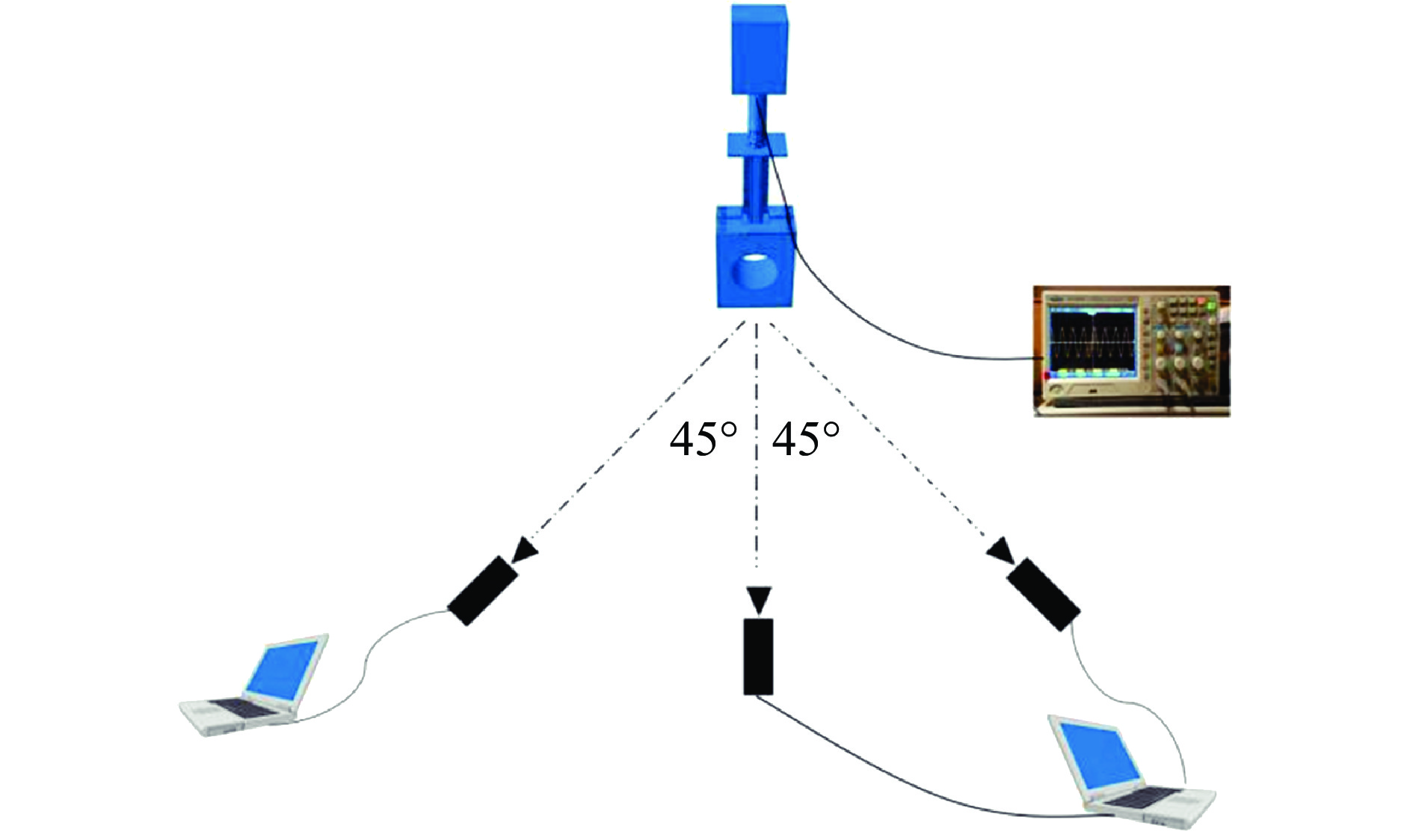
实验测试装置如图4所示,通过量程为2 MN的FXY-2000应变式力传感器记录实验过程中试件所受的冲击载荷。采用SHS型MTI-3D测试设备,应用数字图像相关法(Digital Image Correlation, DIC),在锤头表面制备人工散斑,通过捕捉散斑移动信息获取锤头的位移时程曲线,同时记录试件在轴向冲击载荷作用下的变形过程[13]。实验测试采用3台I-speed 716型高速摄像机(104帧/秒,分辨率为1280×1024像素),其中试件正前方相机拍摄的图像用于DIC数据处理,另外两台相机与试件成45°夹角,以便多角度观察试件的变形模式。
-
图5为高速摄影拍摄A组DP980帽型梁结构典型试件A5的冲击变形全过程。
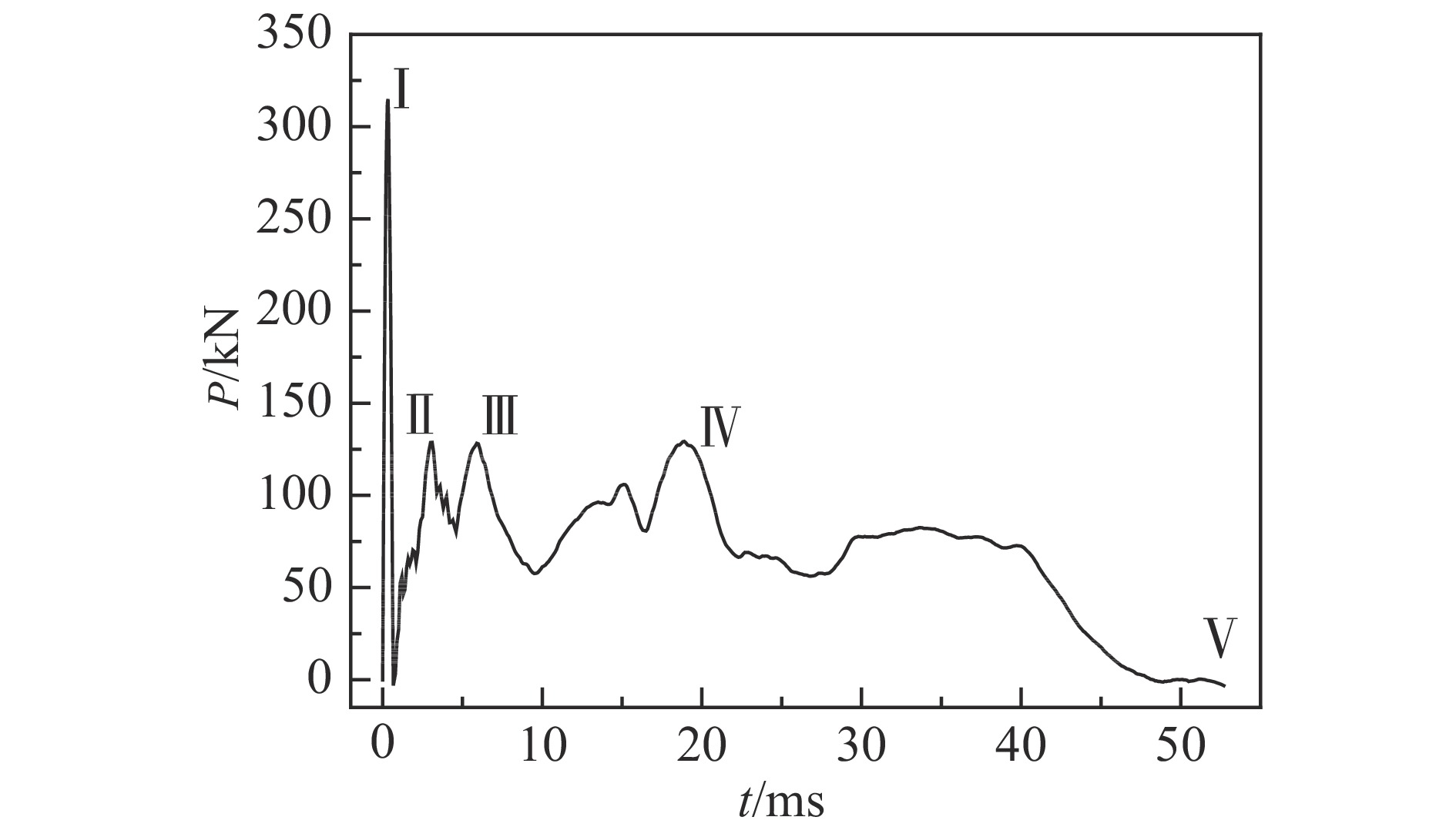
从图5可以看出:该帽型梁受冲击载荷时发生屈曲变形,在试件上端共产生3个褶皱,试件下部未产生明显变形;试件所有焊点未发生开裂等破坏现象;A组试件在实验中的重复性良好,变形模式基本相同,可视为紧凑型。冲击变形过程可分为3个阶段:溃缩变形、回弹和二次撞击阶段。如图6所示,将变形模式与实验冲击力(P)时程曲线结合,曲线上标注的各点分别对应图5中的冲击变形模式:冲击开始时,锤头下落接触上方垫板,载荷迅速增加,曲线形成第1个峰值,对应状态I;继而试件进入临界状态,冲击力增大,试件发生塑性屈曲,形成第1个褶皱,冲击力急剧下落,即曲线第2个峰值状态II;随着锤头持续下落,产生第2、3个褶皱,即曲线峰值状态III;试件发生压溃,对应状态IV;随后进入回弹阶段,锤头与垫板发生分离,并出现轻微二次撞击,对应曲线状态V,为试件最终变形形态。
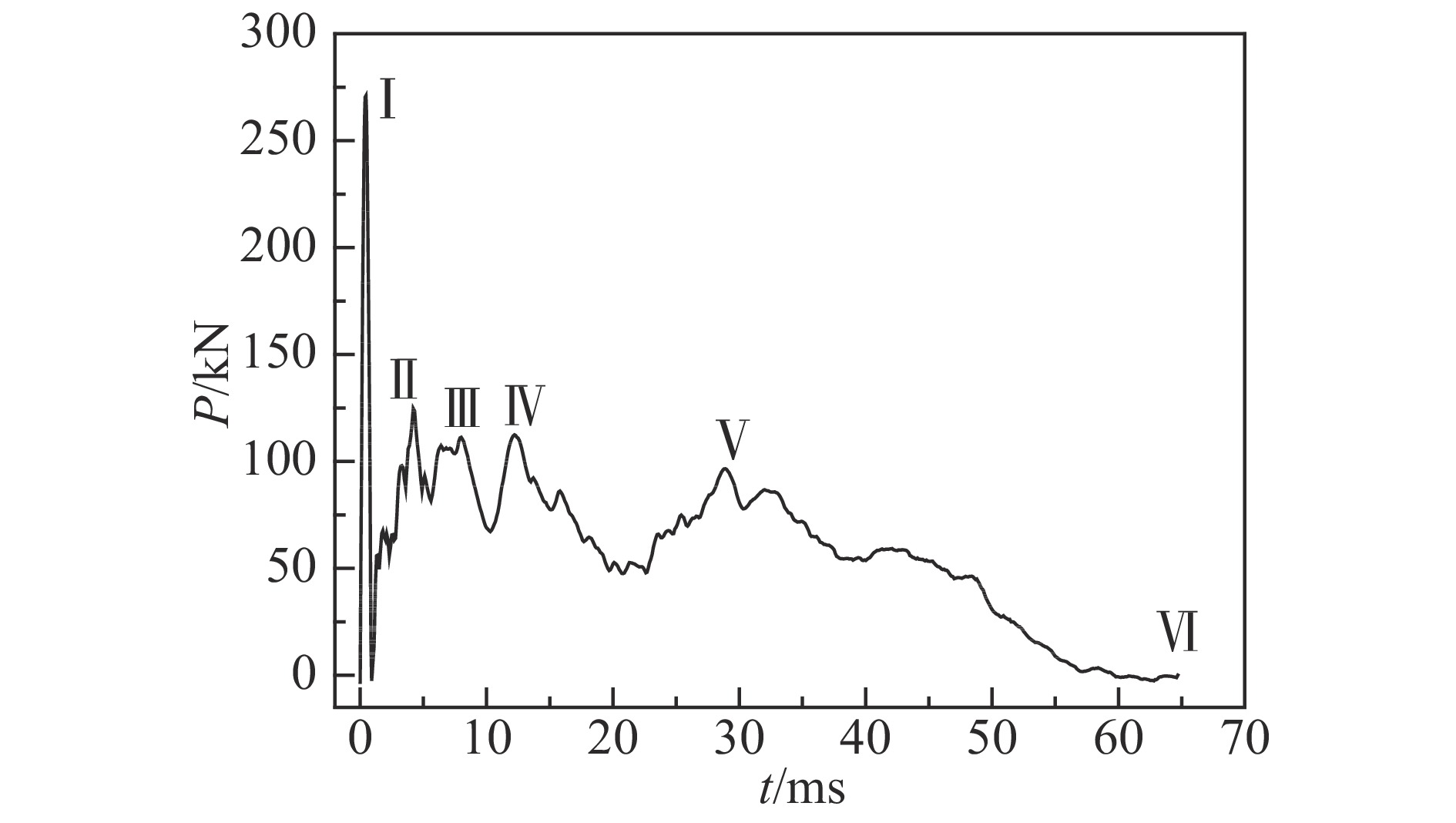
图7为高速摄影拍摄的B组DP780帽型梁结构典型试件B2的冲击变形全过程。从拍摄图像可以看出:该帽型梁受冲击载荷时发生屈曲变形,试件上端共产生了4个褶皱,试件下部未产生明显变形;试件所有焊点未发生开裂等破坏现象;B组试件在实验中的重复性良好,变形模式基本相同,可视为紧凑型。冲击变形过程同样可分为3个阶段,即溃缩变形、回弹和二次撞击阶段。将变形模式结合实验冲击力时程曲线进行分析,图8中曲线上标注的各点分别对应图7中各个冲击变形模式。可以看出:冲击开始时,锤头下落接触上方垫板,载荷迅速增加,曲线形成峰值,对应曲线状态I;继而试件进入临界状态,冲击力增大,试件发生塑性屈曲,形成第2个褶皱,导致冲击力急剧下落,对应曲线状态II;随着锤头持续下落,因同样原因产生第3、4、5个褶皱,试件发生压溃,分别对应曲线状态III、状态IV和状态V;随后试件进入回弹阶段,锤头与垫板发生分离,并出现轻微二次撞击,即曲线状态VI,为试件最终变形形态。
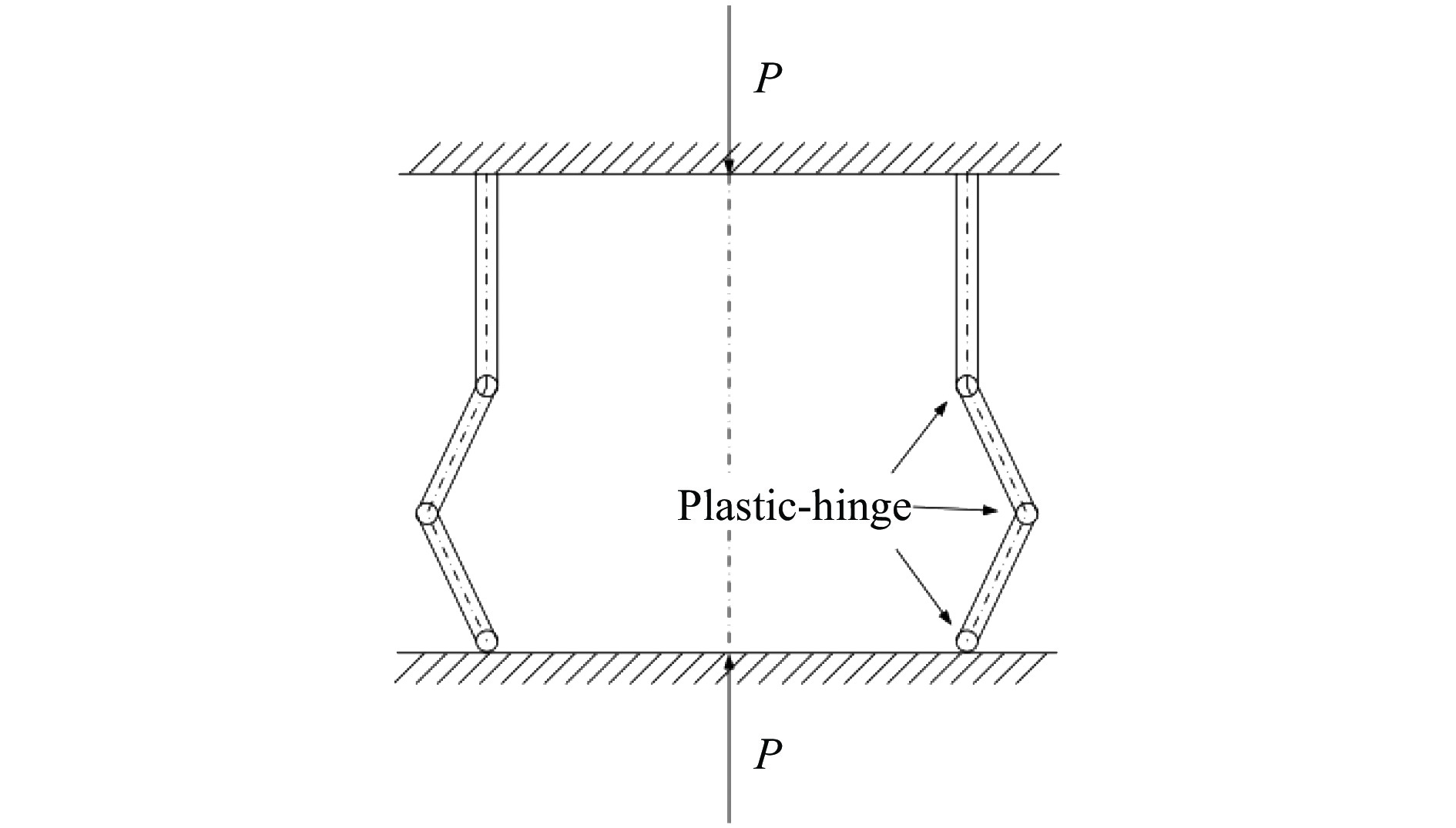
通过上述实验结果可以看出:两组实验的褶皱均出现在试件结构的上部,塑性屈曲变形均为从上至下传播且试件下端无明显变形,而造成试件产生屈曲和褶皱的所有塑性变形都发生在图9所示的局部化塑性铰上。在变形过程中,4个平面板以刚体形式运动,屈曲弯折变形产生的圆柱面以塑性铰线为界,且铰线向相反方向运动形成更宽的塑性区域,以此产生变形褶皱。两组实验的变形模式均为紧凑型,此模式有利于提高结构在冲击载荷下的能量吸收率,同时不易出现失稳状况。在完成冲击碰撞后,两组试样的焊点均未发生破坏,说明变形模式改变与焊点无关。此外,DP780帽型梁结构受冲击载荷形成的褶皱为4个,比DP980帽型梁结构多1个。
-
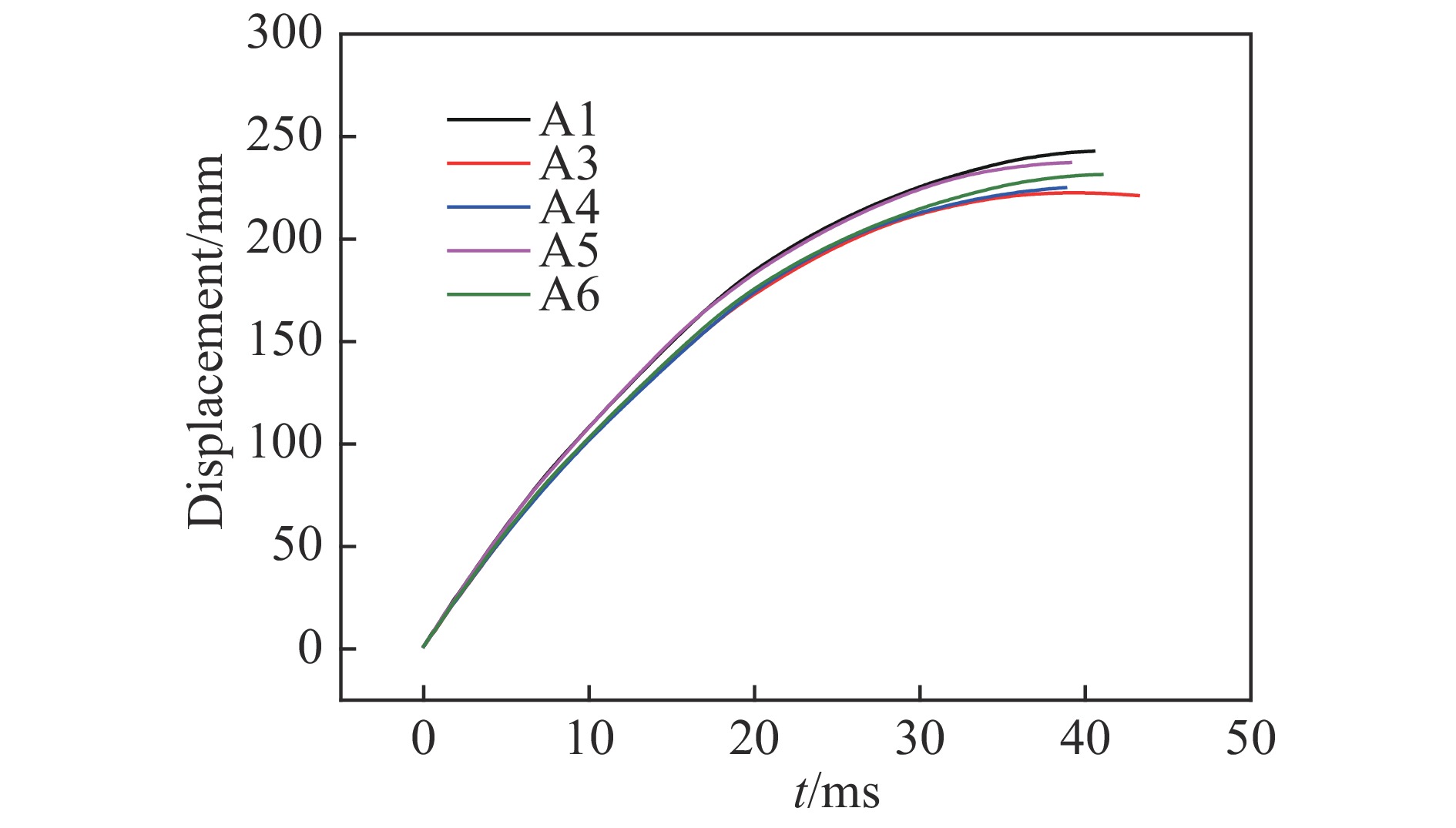
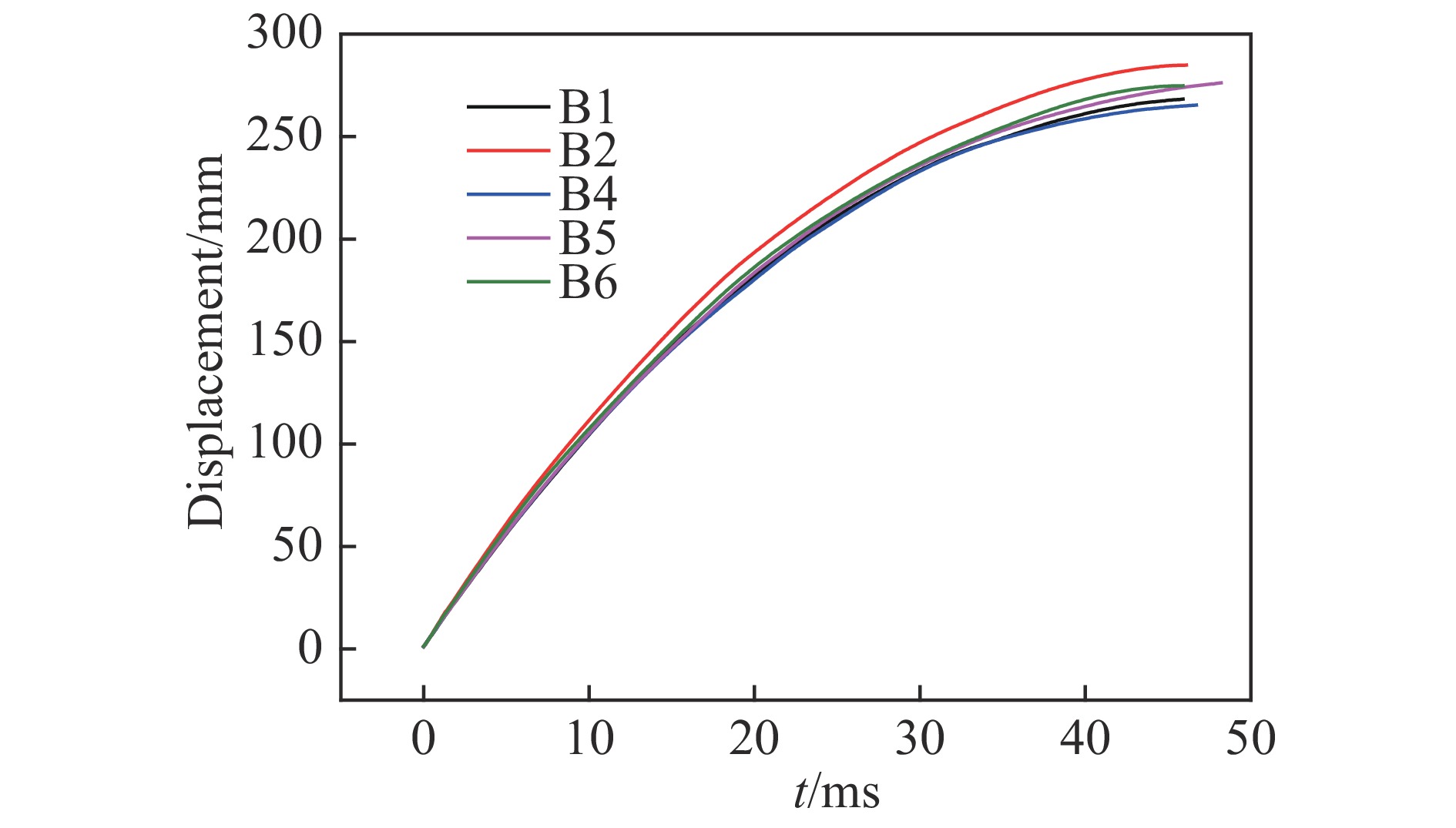
通过DIC数据处理软件分别得到两组实验锤头的位移-时间曲线。图10、图11分别为A组和B组采集的试件冲击至最大位移处的位移曲线。从图10中可以看出,A组试件从冲击开始至39~43.1 ms时间范围内位移达到峰值,位移区间为221.3~242.9 mm。从图11中可以看出,B组试件从冲击开始至45.9~48.2 ms时间范围内位移达到峰值,位移区间为265.4~284.9 mm。冲击实验过程中B组DP780试件的冲击载荷作用时间更长,位移峰值更大。
表1总结了DP980和DP780帽型梁结构轴向冲击实验的最终变形参数,其中h表示试件的残余高度,t表示载荷作用时间。通过表1可以看出:两组试件的实验数据一致性均较好,B组DP780试件受冲击载荷后的残余高度比A组降低约50 mm,实验冲击载荷作用时间比A组增加约10 ms。上述差异是由于两组帽型梁选用材料不同导致的。
-
采用如下指标评估帽型梁结构在冲击载荷下的动态力学性能:总吸收能量(EA)、峰值载荷(Fmax)、平均碰撞载荷(Favg)和碰撞力效率(Crash Force Efficiency,η)[14]。
总吸收能量为结构在碰撞时吸收的能量总和,可以表示为[15]
式中:δ为变形位移,F(t)为冲击载荷。总吸能量在数值上等于载荷-位移曲线下方所围的面积。
平均碰撞载荷为总吸能量与变形位移的比值,即
平均碰撞载荷是对结构吸能能力的整体表征,吸收相同能量时,变形位移越大,平均碰撞载荷越小。
碰撞力效率为平均碰撞载荷与峰值载荷的比值,即
在冲击过程中,减小峰值载荷,可以提高平均载荷占比,从而有利于结构的能量吸收。
冲击过程中试件的实际冲击载荷、加速度和速度可根据(4)式~(6)式求出
式中:P(t)为t时刻传感器测得的冲击载荷,F(t)为t时刻试件受到的实际冲击载荷,g为重力加速度,a(t)为t时刻的加速度,vi为t=0时刻的速度,v(t)为t时刻的速度。
整理有效实验数据得到表2。通过(4)式和DIC位移曲线,可以计算试件受冲击吸收的总能量,B组DP780帽型梁试件吸收的总能量与A组DP980帽型梁试件吸收的总能量相近且略高于A组,这是由于DP780双相钢屈服强度低、延伸率高,在同等冲击条件下能够产生更大的变形位移,在本实验中比A组多产生一个压溃褶皱,因此吸收了更多的能量。
通过应变式力传感器测得冲击过程中两组试件所受冲击载荷,根据表2可以得出:A组DP980试件的峰值载荷区间为301.67~327.64 kN,B组DP780试件的峰值载荷区间为260.60~273.48 kN,两组实验试样在加工过程中产生焊接变形,存在微小的个体差异,因此每组实验的峰值载荷均为区间段,并非某个固定值;与B组相比,A组试件的峰值载荷提高了40~50 kN,冲击过程中下方垫块受到的冲击力更大,其原因在于A组试件所采用的DP980双相钢的屈服强度高于B组DP780双相钢,在受到相同冲击条件下更难发生屈曲变形,所以具有更高的峰值载荷。
考虑平均碰撞载荷,实验结果表明:A组DP980帽型梁试件的平均碰撞载荷水平高于B组试件,同时实验结果也反映出两组试件的冲击载荷碰撞力效率相差不大。对比上述吸能指标可以得出,DP980和DP780双相钢帽型梁受冲击载荷时的能量吸收性能相近。
-
(1)在本研究的实验条件下,异材同厚的两组帽型梁试件在受到轴向冲击时,由冲击端产生塑性屈曲变形,固定端无明显变化。试件主要通过塑性变形产生褶皱来吸收能量,同时变形模式均表现为紧凑型,这不仅有利于提高结构对冲击能量的吸收,而且相较于非紧凑型变形模式更稳定,不易发生整体失稳。
(2)帽型梁结构中帽型单元的材料属性对其在冲击载荷作用下的变形模式有着显著的影响,对其碰撞能量吸收性能影响很小。
(3)与DP780双相钢帽型梁相比,DP980双相钢帽型梁受冲击载荷时的变形位移更小,可有效防止后方物体受到冲击,更宜作为抗冲击变形防护结构。
(4)与DP980双相钢帽型梁相比,DP780双相钢帽型梁受冲击载荷时的峰值载荷更小,对后方被防护结构传递的冲击力更小,更宜作为抗冲击载荷防护结构。
DP980与DP780双相钢帽型梁轴向冲击实验对比
Comparisons between DP780 and DP980 Duplex Steel Beams with Hat-Section under Axial Impact
-
摘要: 作为汽车及航空工业中主要承载和碰撞吸能部件,帽型薄壁梁可通过自身结构塑性变形实现被动吸能。因此,研究帽型薄壁梁结构在冲击载荷作用下的变形模式和吸能特性对其被动安全设计具有重要的意义。分别对DP980和DP780双相钢帽型薄壁梁结构开展了落锤轴向冲击实验,并对其变形位移、峰值载荷、变形模态和能量吸收能力进行分析。研究结果表明:无论是DP980还是DP780帽型梁试件,在受到冲击载荷作用时,均从试件上部发生塑性屈曲变形并形成褶皱,其下部则无明显变形;DP980帽型梁冲击变形更小,残余高度更高,宜作为抗冲击变形防护结构;DP780帽型梁最终屈曲变形产生褶皱更多,冲击载荷作用时间增加,峰值载荷更低,宜作为抗冲击载荷防护结构。综合考虑吸能效果,DP980帽型梁的能量吸收能力与DP780帽型梁相近,研究结果为冲击防护结构的选材提供依据。Abstract: As the main energy absorbing component of bearing and collision in the automobile and aviation industry, the hat-section beam structure absorbs energy through plastic deformation of its own structure, which is the main criteria for previous safety design. Therefore, it is of great significance to study the deformation characteristics and energy absorption characteristics of the hat-section and thin-walled beam structure under impact load. In this paper, the axial dropping impact tests of DP780 and DP980 duplex steel with hat-section thin-walled beam structures are carried out with a dropping hammer designed by ourselves, and the maximum displacement, peak load, deformation modes and energy absorption are obtained. The results show that the plastic buckling of the upper part of the specimen is formed and the deformation of the lower part is unobvious for DP980 and DP780 hat-section beams under impact loads. The DP980 hat-section beam has less impact deformation and higher residual height, which can be used as the protection structure of anti-impact deformation. The DP780 hat-section beam has more wrinkles produced by final buckling deformation, and its impact time increases and the peak load is much lower, which can be used as the protection structure of anti-impact load. The energy absorption capacity of the DP980 hat-section beam is similar to that of the DP780 hat-section beam. The results provide the basis for the selection of anti-impact performance with thin-walled structure.
-
Key words:
- hat-section beam /
- duplex steel /
- axial impact /
- deformation modes /
- energy absorption capacity .
-

-
表 1 实验变形参数
Table 1. Deformation parameters from experiments
Specimen h/mm t/ms Specimen h/mm t/ms A1 200 48.2 B1 147 58.7 A2 198 48.6 B2 150 59.7 A3 198 48.8 B3 150 59.2 A4 198 48.4 B4 151 59.6 A5 193 49.3 B5 140 63.6 A6 192 49.9 B6 151 60.1 表 2 试件冲击实验结果
Table 2. Impact test results of the specimens
Specimen EA/kJ Fmax/kN Favg/kN η Specimen EA/kJ Fmax/kN Favg/kN η A1 16.9 327.64 84.50 0.2579 B1 17.5 269.27 69.16 0.2568 A3 17.1 315.52 84.65 0.2682 B2 17.6 268.58 70.40 0.2560 A4 17.1 301.67 84.75 0.2809 B4 17.7 271.19 71.08 0.2621 A5 17.2 312.59 83.09 0.2658 B5 17.6 273.48 67.69 0.2475 A6 17.3 306.69 83.17 0.2711 B6 17.2 260.60 69.07 0.2650 -
[1] ABRAMOWICZ W. Thin-walled structures as impact energy absorbers [J]. Thin-Walled Structures, 2003, 41(2): 91–107. [2] ABEDRABBO N, MAYER R, THOMPSON A, et al. Crash response of advanced high-strength steel tubes: experiment and model [J]. International Journal of Impact Engineering, 2009, 36(8): 1044–1057. doi: 10.1016/j.ijimpeng.2009.02.006 [3] ZHANG X W, SU H, YU T X. Energy absorption of an axially crushed square tube with a buckling initiator [J]. International Journal of Impact Engineering, 2009, 36(3): 402–417. doi: 10.1016/j.ijimpeng.2008.02.002 [4] ALEXANDER J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading [J]. Quarterly Journal of Mechanics & Applied Mathematics, 1960, 13(1): 10–15. [5] WIERZBICKI T, ABRAMOWICZ W. On the crushing mechanics of thin-walled structures [J]. Journal of Applied Mechanics, 1983, 50(4): 727–734. [6] WHITE M D, JONES N, ABRAMOWICZ W. A theoretical analysis for the quasi-static axial crushing of top-hat and double-hat thin-walled sections [J]. International Journal of Mechanical Sciences, 1999, 41(2): 209–233. doi: 10.1016/S0020-7403(98)00048-4 [7] WHITE M D, JONES N. A theoretical analysis for the dynamic axial crushing of top-hat and double-hat thin-walled sections [J]. Proceedings of the Institution of Mechanical, 1999, 213(4): 307–325. [8] TARIGOPULA V, LANGSETH M, HOPPERSTAD O S, et al. Axial crushing of thin-walled high-strength steel sections [J]. International Journal of Impact Engineering, 2006, 32(5): 847–882. doi: 10.1016/j.ijimpeng.2005.07.010 [9] 顾纪超, 樊涛, 段利斌, 等. 异材异厚帽型梁结构轴向压溃理论研究 [J]. 汽车工程学报, 2016, 6(4): 252–259. doi: 10.3969/j.issn.2095-1469.2016.04.03 GU J C, FAN T, DUAN L B, et al. Research on axial crushing theory of hat-section beam with different materials and thickness [J]. Chinese Journal of Automotive Engineering, 2016, 6(4): 252–259. doi: 10.3969/j.issn.2095-1469.2016.04.03 [10] 王特捷, 付应乾, 俞鑫炉, 等. 帽型梁落锤轴向冲击实验及有限元分析 [J]. 现代应用物理, 2014(1): 59–62. doi: 10.3969/j.issn.2095-6223.2014.01.011 WANG T J, FU Y Q, YU X L, et al. Experiment and the finite element analysis for hat-beam structure under axial crash of dropping hammer [J]. Modern Applie Physics, 2014(1): 59–62. doi: 10.3969/j.issn.2095-6223.2014.01.011 [11] 李亚, 陈新平, 连昌伟. 双相钢DP600帽型梁碰撞实验与数值模拟 [J]. 精密成形工程, 2017, 9(6): 87–92. doi: 10.3969/j.issn.1674-6457.2017.06.017 LI Y, CHEN X P, LIAN C W. Collision experiment and numerical simulation on hat-shape beam by dual phase steel DP600 [J]. Journal of Netshape Forming Engineering, 2017, 9(6): 87–92. doi: 10.3969/j.issn.1674-6457.2017.06.017 [12] 田泽, 韩阳, 尹晓文, 等. 截面几何参数对帽型梁轴向冲击响应的影响 [J]. 高压物理学报, 2018, 32(5): 94–101. doi: 10.11858/gywlxb.20180521 TIAN Z, HAN Y, YIN X W, et al. Effect of sectional geometrical parameters of hat-section beam on its axial impact responses [J]. Chinese Journal of High Pressure Physics, 2018, 32(5): 94–101. doi: 10.11858/gywlxb.20180521 [13] 朱飞鹏, 龚琰, 白鹏翔, 等. 基于二维DIC的脆性材料拉伸应力-应变曲线测定 [J]. 实验力学, 2018, 33(3): 333–342. doi: 10.7520/1001-4888-17-023 ZHU F P, GONG Y, BAI P X, et al. Determination of tensile stress-strain curve of brittle materials based on two-dimensional digital image correlation [J]. Journal of Experimental Mechanics, 2018, 33(3): 333–342. doi: 10.7520/1001-4888-17-023 [14] 江志勇.基于轿车薄壁构件碰撞的变形及吸能特性的仿真与分析 [D]. 武汉: 武汉理工大学, 2009: 41–43. [15] TANG T, ZHANG W, YIN H, et al. Crushing analysis of thin-walled beams with various section geometries under lateral impact [J]. Thin-Walled Structures, 2016, 102: 43–57. doi: 10.1016/j.tws.2016.01.017 -


 首页
首页 登录
登录 注册
注册




 下载:
下载: