实验选用甲基乙烯基硅橡胶，其代号为MVQ，是日本信越化工公司生产的KE951型号硅橡胶生胶经由190 ℃高温硫化得到的厚度为3 mm的黑色板材。

硅橡胶在准静态加载下的单向拉伸测试在Instron-E3000材料试验机上进行。试样形状为等宽长条形，长度为140 mm，除夹持段外为70 mm，试样宽度为14 mm。橡胶类材料不可采用夹式引伸仪测量实验过程中的变形信息，因而采用自动网格法^[15]这一非接触式光学测量方法进行位移测量。相较于全息干涉法、云纹法等其他非接触式光测方法，自动网格法对操作环境无特殊的防震要求，且只需要白光光源，光路简单易操作。该方法通过CCD实时记录实验过程中布置在试件表面的网格点阵的运动，通过数字图像相关技术自动识别和比较变形前后的点阵图像，最终获得不同时刻试件中的变形场信息。该方法主要包含3个步骤：试件表面网格点阵的制作、网格点阵的拍摄以及数字图像的后处理。

中应变率单向拉伸测试在液压伺服的中应变率材料试验机上进行，试样形状亦为等宽长条形，为了和试验机夹持端匹配，试样宽度设置为12 mm，试样夹持段长度为25 mm。

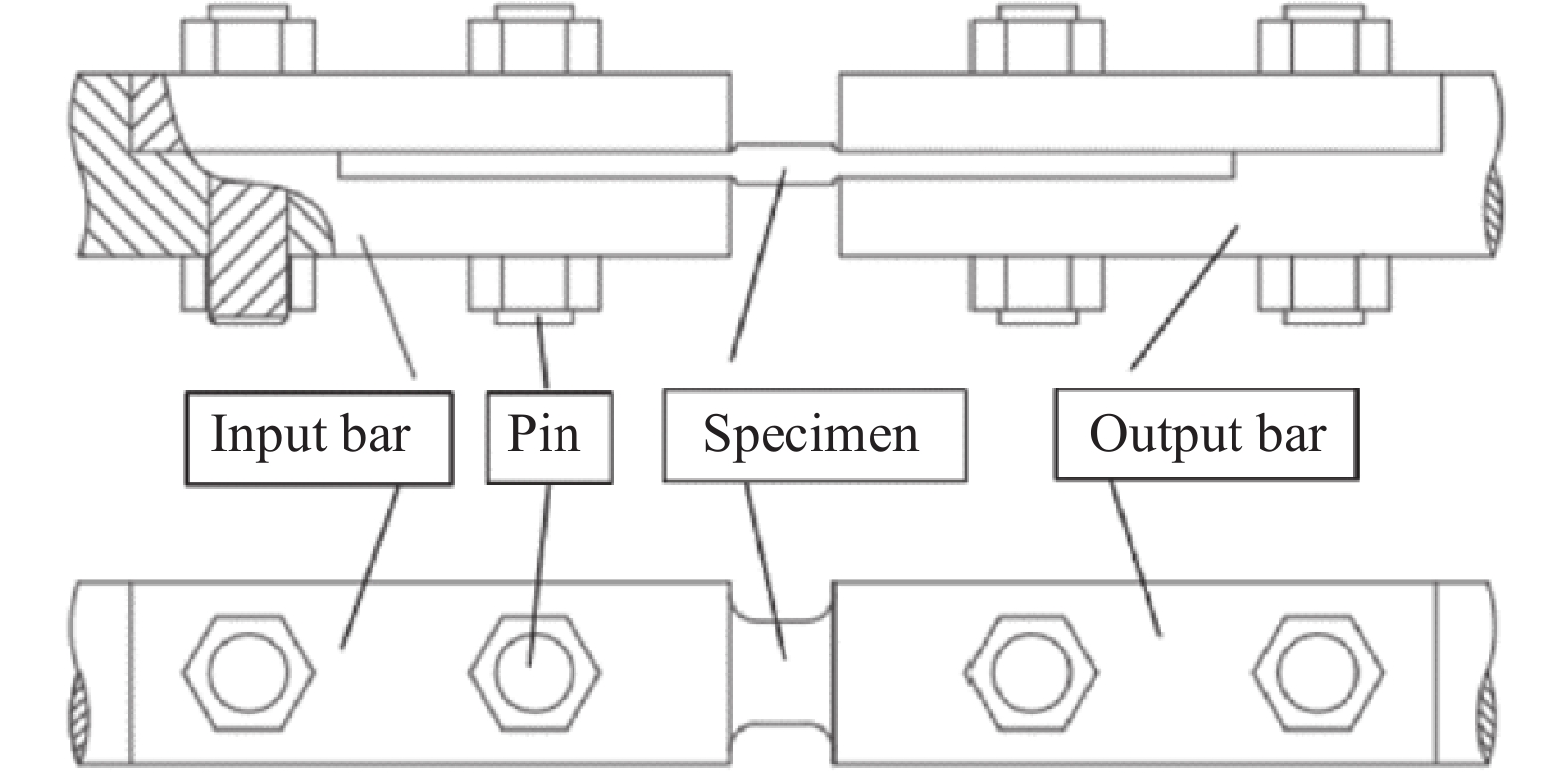
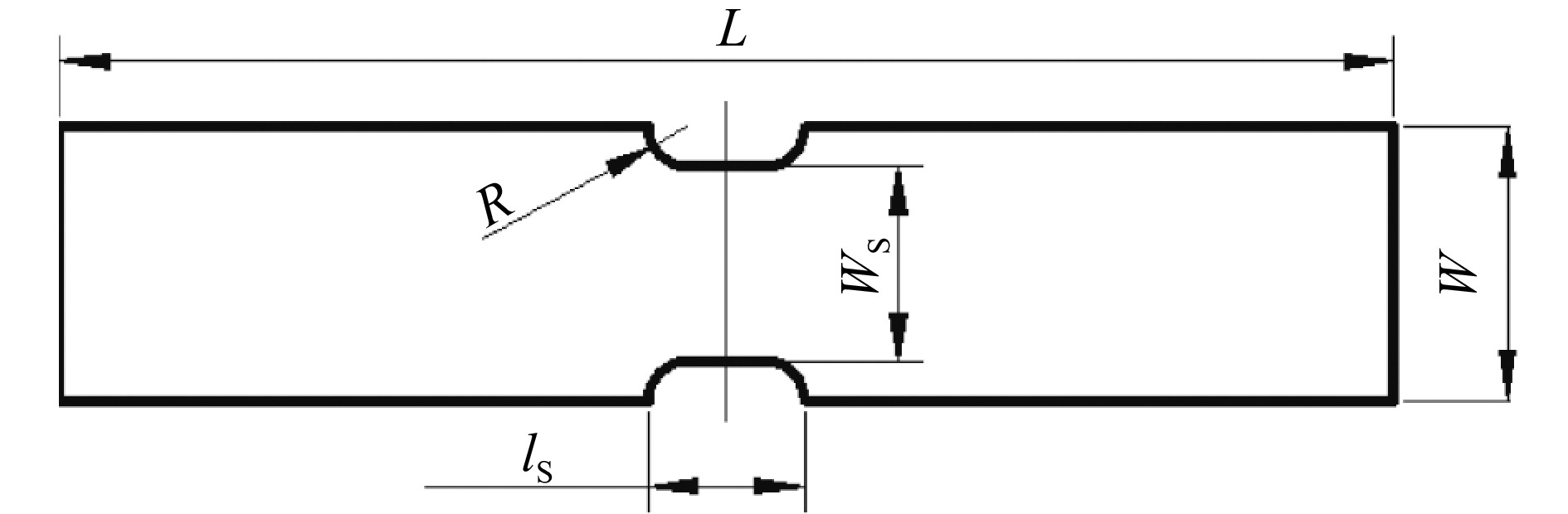
高应变率单向拉伸测试在旋转盘式间接杆杆型SHTB上进行，试样形状为平板哑铃型（如图1所示），试样由橡胶裁刀配合冲片机冲压制得。鉴于硅橡胶低模量、低波阻抗的特性，本课题组发展了针对橡胶类材料的高应变率拉伸测试技术^[16]。该技术利用前置金属短杆解决了实验过程中加载脉冲形状控制以及恒应变率加载的问题；采用半导体应变片（灵敏度系数约为120）代替普通应变片（灵敏度系数约为2），有效提升了透射信号的信噪比，同时结合铝透射杆，有效解决了透射波信号弱的问题。

硅橡胶材料“软”的特征导致其不能采用螺纹连接的方式，又由于其表面活性基团少、表面能小，难以找到快速有效的胶粘连接方式，故发展了一种机械连接方式（如图2所示），用于实现硅橡胶和实验杆的有效连接。为了确保在拉伸加载过程中试样不会从夹持段中滑出，需要将试件沿厚度方向由3 mm夹紧至2 mm，这将在试件连接段（即夹持段）端部到试验段产生一个厚度从2 mm到3 mm的过渡段。该段内的变形情况是非均匀的，且处于复杂应力状态（称之为端部效应），因此实验过程中不能简单地按照两个夹持段端部（即入射杆右端和透射杆左端）之间的标距计算试件的工程应变，即实验中基于入射/透射杆端的相对位移获得的工程应力-工程应变曲线并非试件材料真实的本构响应。为此建立了应变修正关系对实测的应变信息进行修正。准静态测试时，利用自动网格法测得的结果是材料的真实响应，通过建立高应变率实验中采用短试件（长细比小）获得的应力-应变测试曲线与准静态实验中长试件（长细比大）的应力-应变测试结果之间的转换关系，对高应变率实验结果进行标定。本研究中假设端部效应的影响与应变率无关，利用Instron E3000材料试验机对准静态试样和高应变率试样（采用和高应变率实验时相同的连接方式）进行应变率为0.001 s^–1的单向拉伸测试，其中准静态试样的应变信息由自动网格法测量，而高应变率试样的应变信息由夹头位移计算得到。对比二者的实验结果，得到高应变率试样的应变标定关系为$ {\varepsilon _{{\rm{calibrated}}}} = 1.08{\varepsilon _{{\rm{measured}}}}$，即伸长比满足$ {\lambda _{{\rm{calibrated}}}} - 1 = 1.08\left( {{\lambda _{{\rm{measured}}}} - 1} \right)$。

通过实验探索和简单的数值模拟，最终确定了动态试样的尺寸为：试验段宽度W_s=8 mm、长度l_s=8 mm、倒角R=2 mm，试样夹持段和实验杆相匹配，宽度为14 mm，试样总长度为68 mm。经验证，该尺寸设计可以很好地满足SHTB的一维测试原理。试样中的平均工程应力、平均工程应变和平均工程应变率可根据入射/透射杆上的应变信息计算得到，其计算公式如下

式中：E和A分别为入射/透射杆的弹性模量和横截面积，A_s为试件的横截面积，C₀为杆中的应力波波速，$ {\varepsilon _{\rm i}}\left( t \right)$和$ {\varepsilon _{\rm r}}\left( t \right)$分别为入射波和反射波经过时入射杆上的应变历史，$ {\varepsilon _{\rm t}}\left( t \right)$为透射波经过时透射杆上的应变历史。

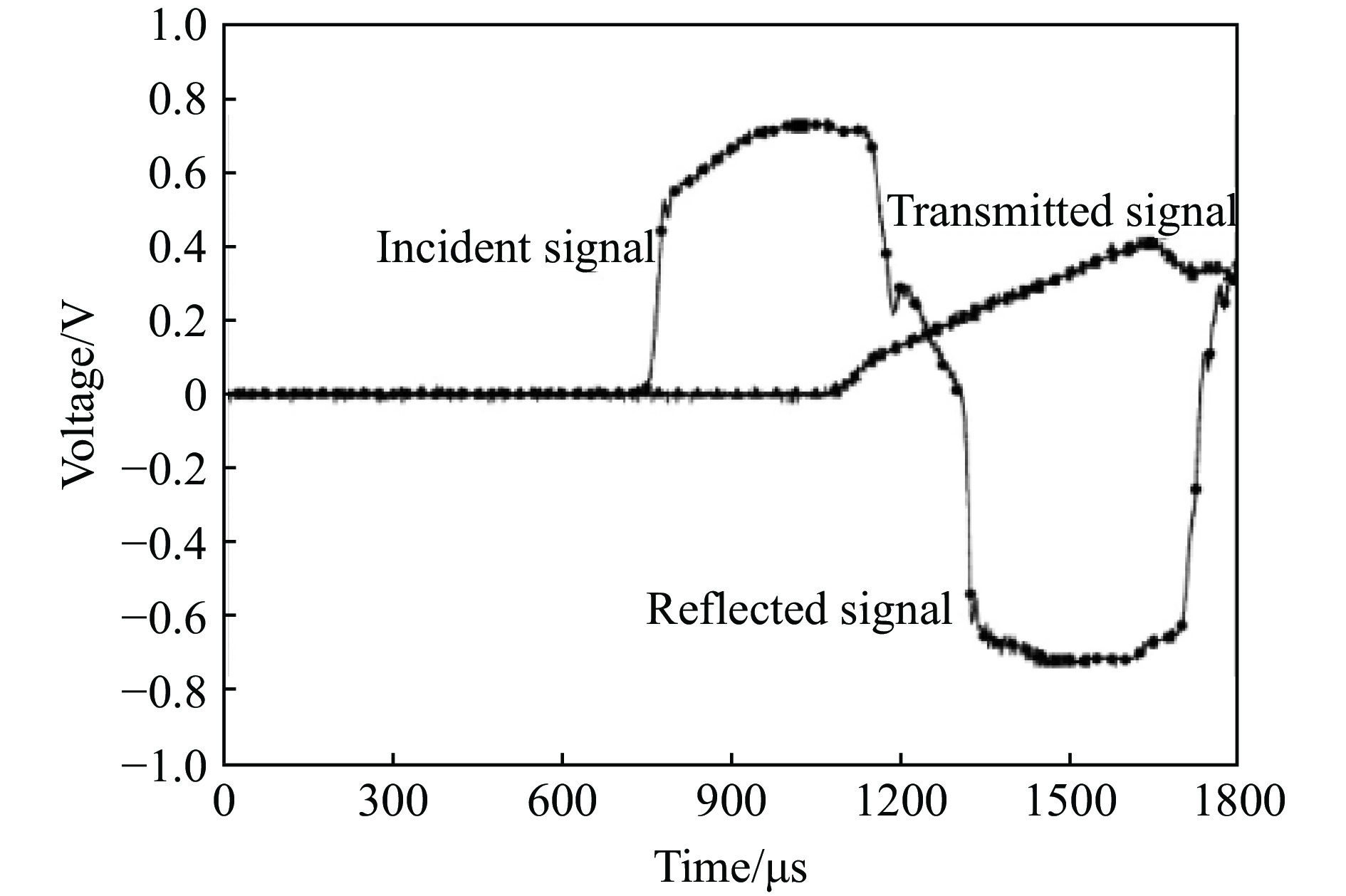
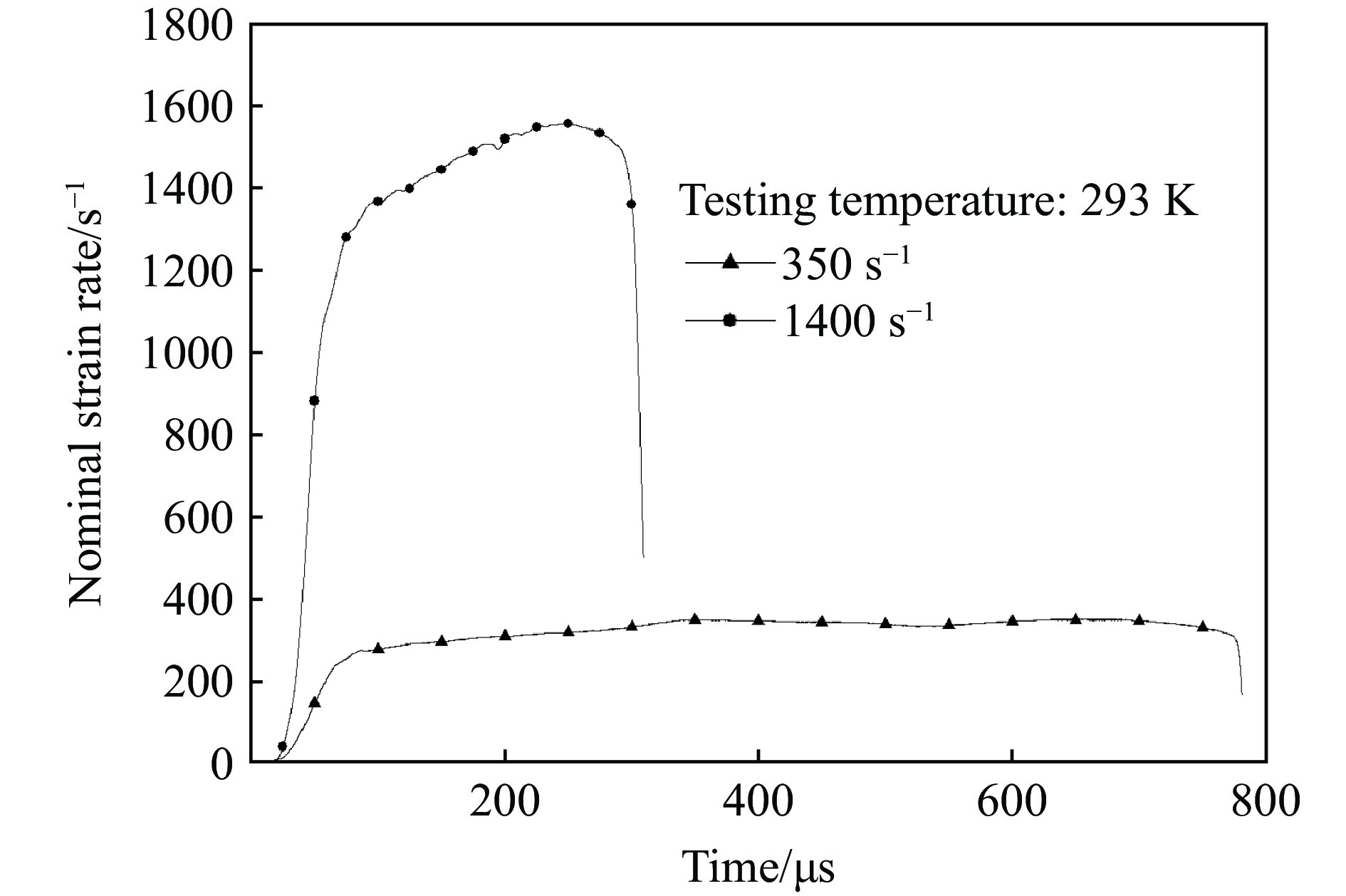
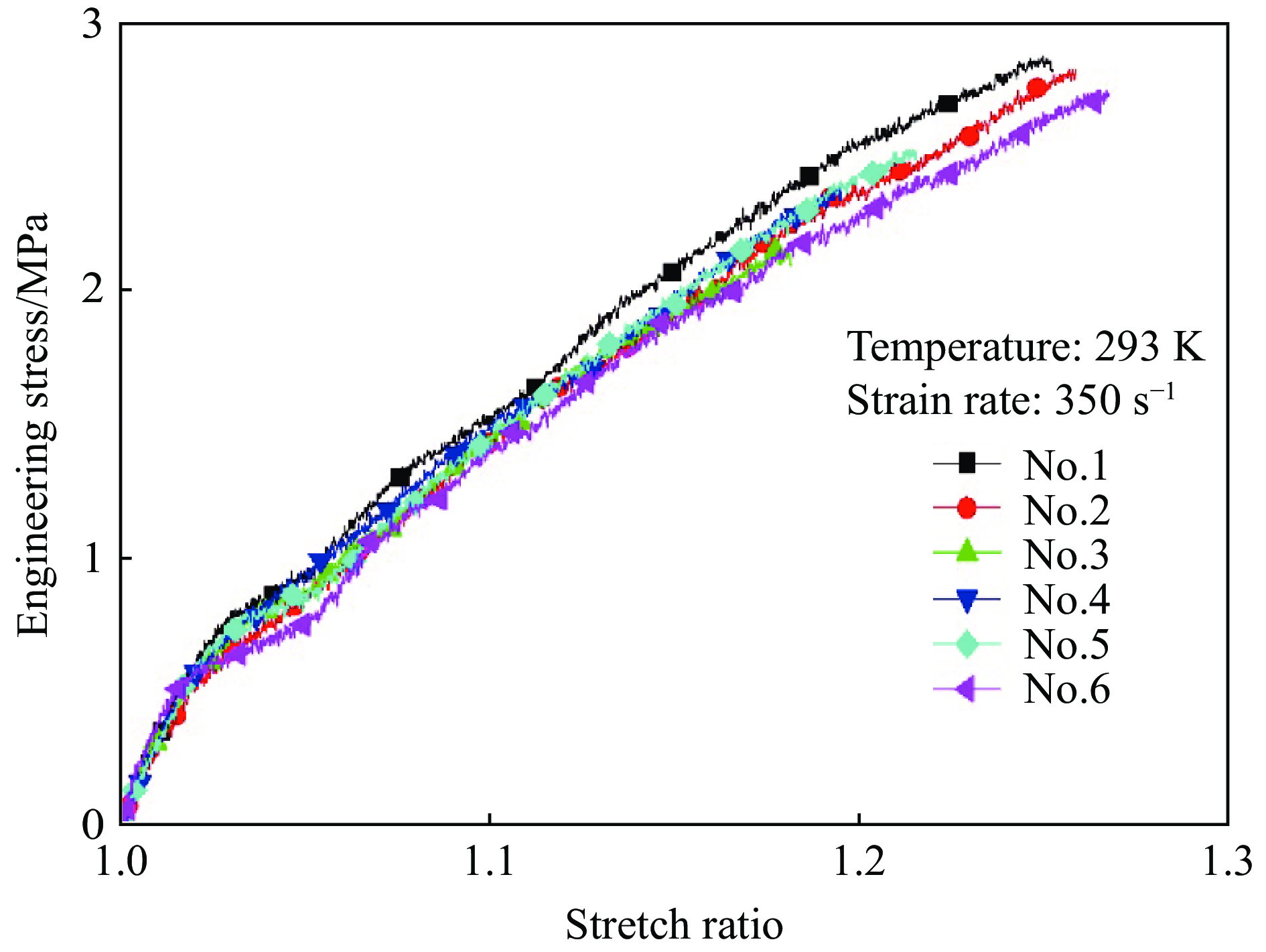
基于前述的橡胶类材料高应变率拉伸测试技术，对硅橡胶进行了应变率分别为350 s^–1和1400 s^–1的单向拉伸测试。图3所示为入射杆和透射杆上应变片实测得到的入射波、反射波以及透射波信号，可以看到入射脉冲平稳光滑，透射波信噪比满足测试精度要求。图4为应变率-时间曲线，可见基本实现了恒应变率加载。图5给出了应变率为350 s^–1工况下的重复性曲线。硅橡胶的高应变率单向拉伸测试结果和金属材料相比表现出较差的重复性，为此，每个工况至少进行了5次有效实验，并选取其中一条作为该工况下的代表性曲线。

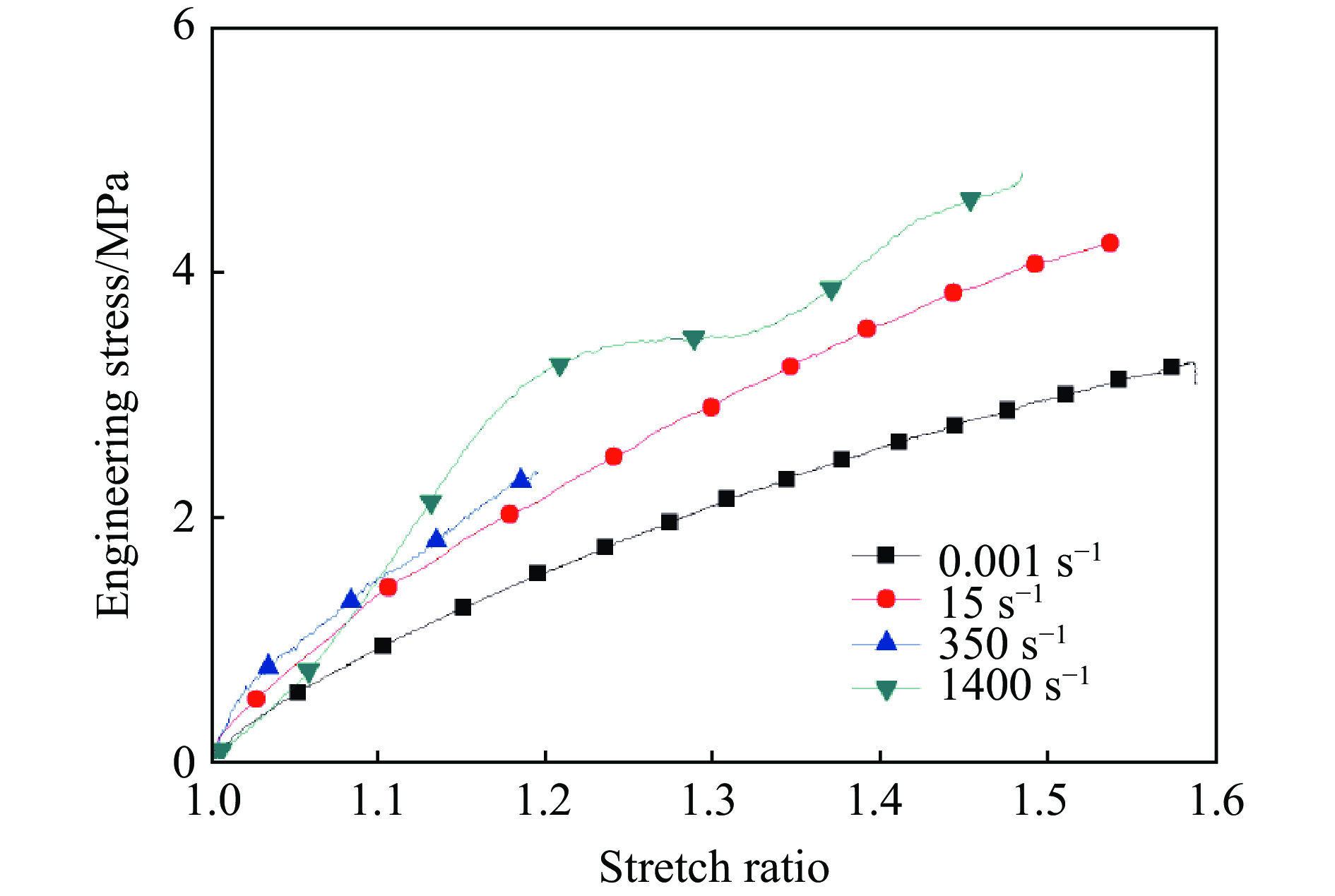
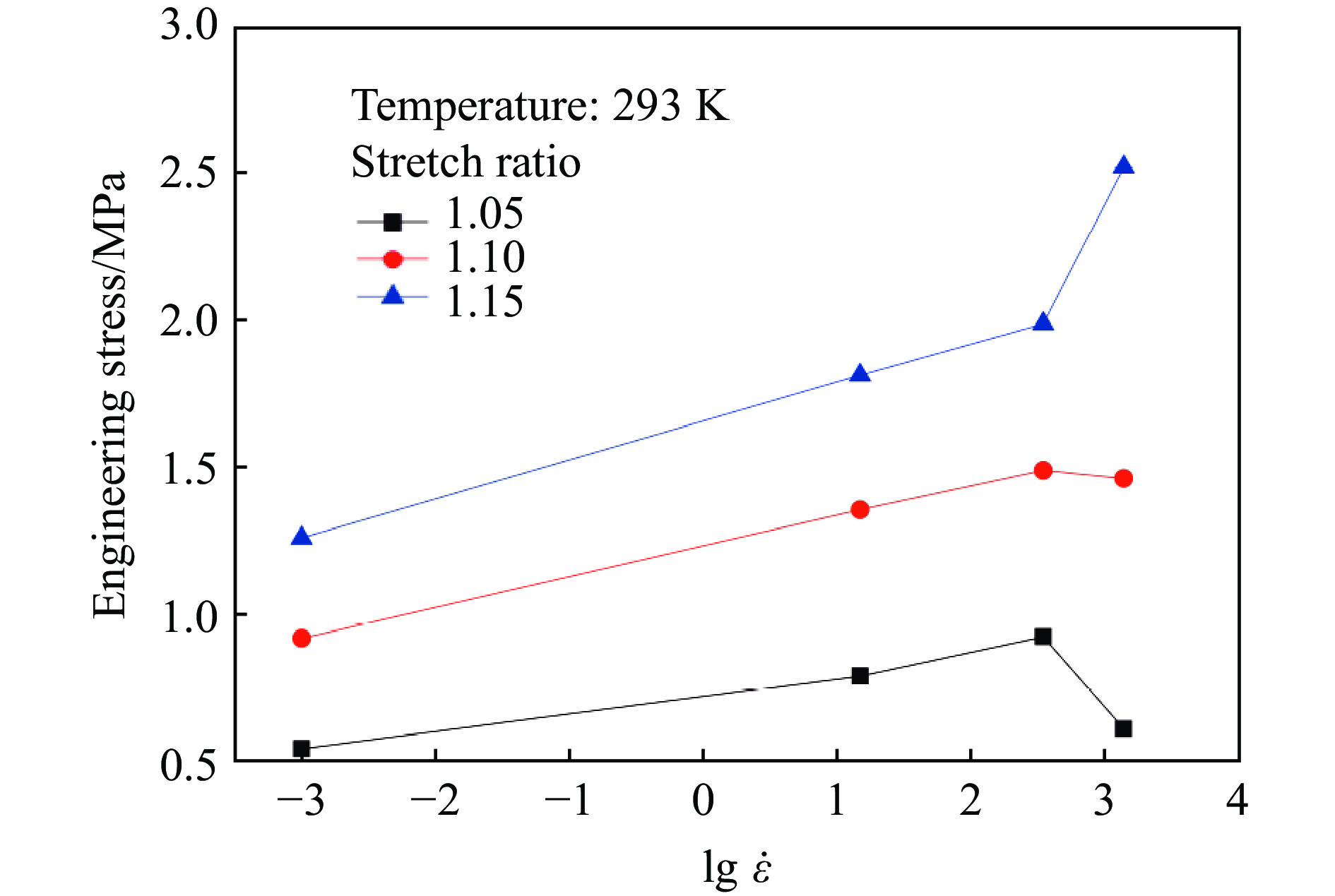
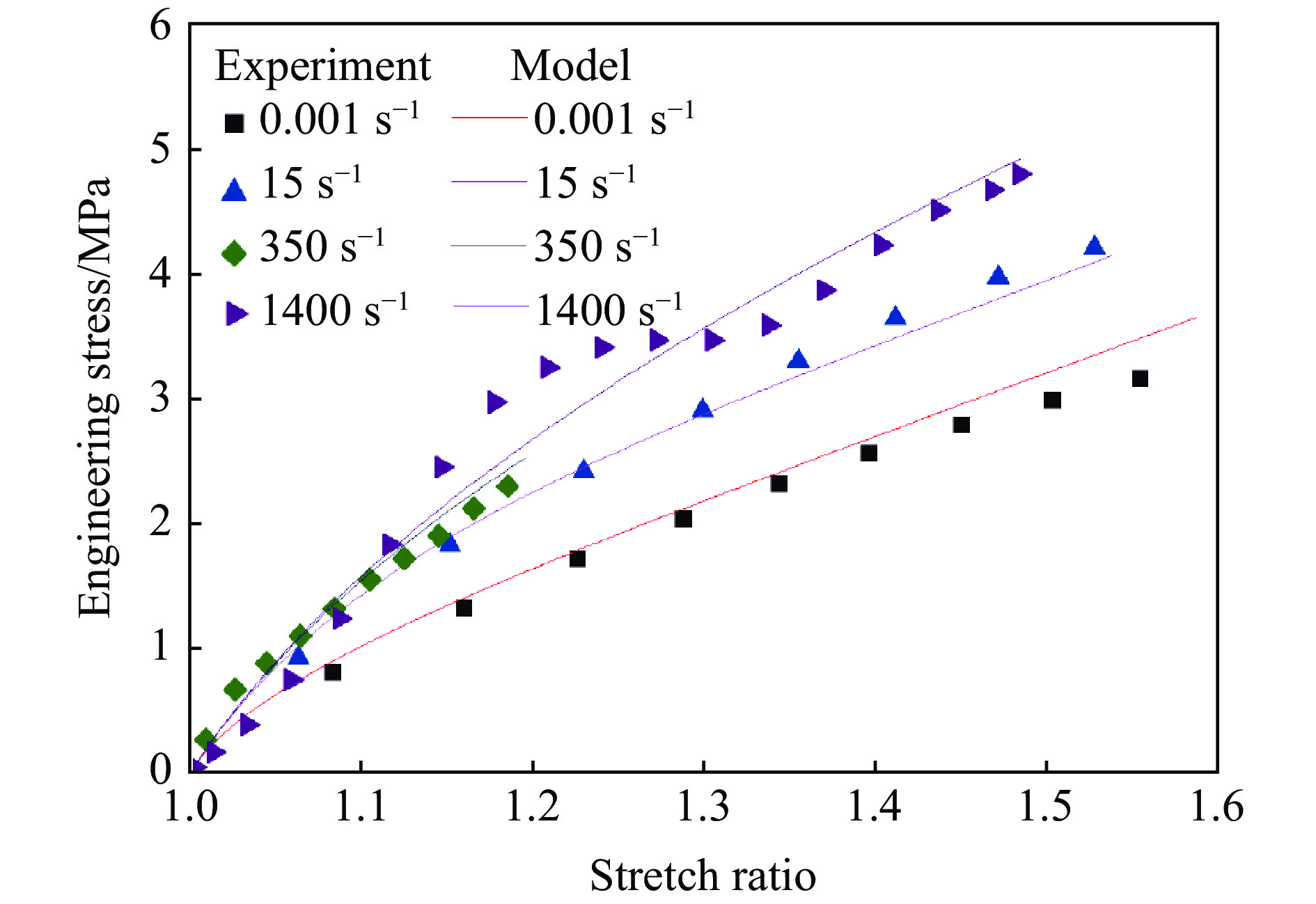
硅橡胶在低-中-高应变率单向拉伸加载下的工程应力-伸长比曲线如图6所示。为了更直观地考察硅橡胶拉伸力学行为的应变率相关性，图7中给出了给定应变下应力随应变率变化曲线。从图6中可以看到：曲线的切线模量随着应变的增大呈现下降的趋势，试样卸载后的残余变形极小，硅橡胶的拉伸力学响应呈现典型的非线性弹性；随着应变率的升高，模量和定伸长应力均上升，表现出应变率硬化的特征。

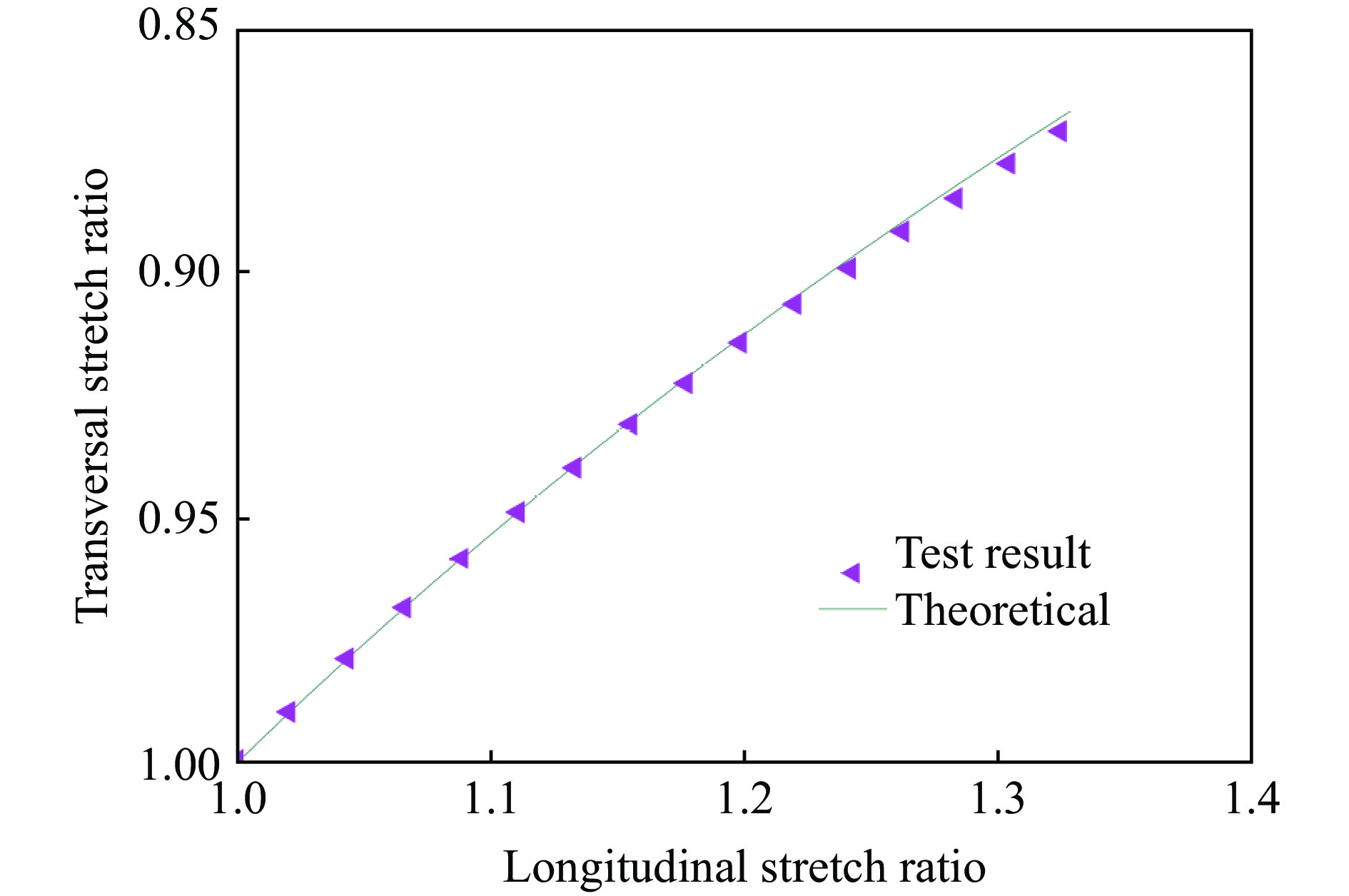
运用自动网格法可以同时测量纵、横两个方向的变形信息这一优势，考察了硅橡胶的泊松效应。对于理想不可压缩材料，在各项同性假设前提下，试样中的体积变化与主伸长比满足$ {{{\rm{\Delta }}V}}/{{{V_0}}} = {\lambda _1}{\lambda _2}{\lambda _3} - 1 = {\lambda _1}\lambda _2^2 - 1 = 0$，可得$ {\lambda _2} = 1/\sqrt {{\lambda _1}} $。利用自动网格法测得准静态下的横向-纵向伸长比结果，并与理论结果对比（如图8所示），结果显示硅橡胶在实验所测的变形范围内可近似为不可压缩材料。

根据理论基础的不同，超弹性本构模型可分为分子网络模型和唯象模型两大类。由于唯象模型相较于分子网络模型具有形式简单、参数少的优势，因此采用唯象超弹性模型对硅橡胶非线性弹性响应进行表征。最具代表性的唯象本构模型是Rilvin提出的多项式模型^[12]，其应变能密度函数表达式为

式中：I₁、I₂分别为应变张量的第一和第二不变量，C_ij为材料参数。众多学者在此基础上分别取不同的低阶项得到了一系列简化模型，如取N=1，则可得到经典的Moony-Rivlin（MR）模型。本研究最终采用修正MR模型对硅橡胶的非线性弹性行为进行表征，该模型将MR模型中I₂–3的一次项变更为指数形式

式中：C、a、b为模型参数。相应地，不可压缩假设下单轴拉伸加载时工程应力（$ {\sigma _{\rm n}}$）-伸长比（$ \lambda $）的表达式为

线性黏弹性模型由于形式简单而得到广泛的应用。以最常用的Maxwell模型为例，其在恒应变率加载下的应力-应变关系可以表达为

式中：E₀为Maxwell体中弹簧的模量；$ \theta $为松弛时间，表示Maxwell体在外力卸载以后恢复到原始状态所需要的时间。通过对$ \theta $作用机理的研究发现，一个固定松弛时间的Maxwell体能有效描述应变率跨度在两个数量级之内的黏弹性应力-应变响应，在此跨度区间之外描述能力较差。经典的三元件模型（采用一个Maxwell体模型和一个弹簧并联的形式）运用广泛，然而由于只采用了一个固定松弛时间的Maxwell体，所以仅能描述材料在应变率跨度为两个数量级范围内的黏弹性力学响应。ZWT模型^[14]将两个Maxwell体并联，分别表征高聚物材料在准静态和高应变率下的黏弹性力学响应，可以有效地描述材料在准静态和高应变率加载下的黏弹性力学响应。对于本研究所涉及的加载应变率范围（10^–3～10³ s^–1），则必须引入3个Maxwell体，这会导致模型形式过于复杂、模型参数过多，给模型参数的准确确定带来困难。

采用一个率相关的Maxwell体模型描述硅橡胶拉伸力学行为的黏弹性特征，其松弛时间表达为应变率的函数

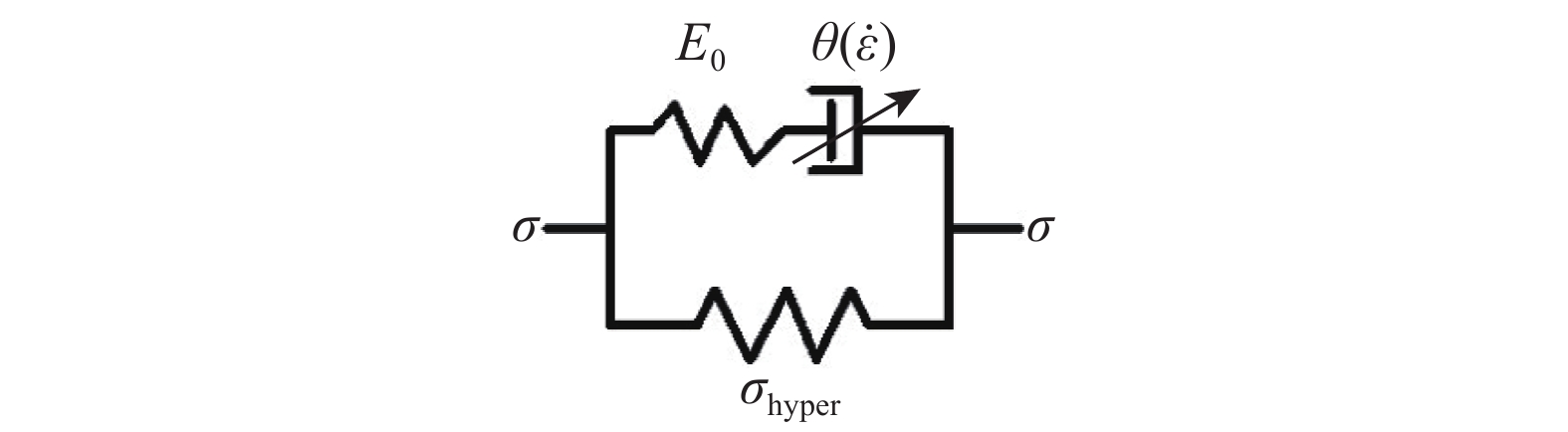
最终得到一个唯象黏超弹性模型，其一维流变学形式如图9所示，即一个超弹性的弹簧和一个松弛时间率相关的Maxwell体的并联，分别对应硅橡胶单向拉伸力学行为的非线性弹性响应和黏弹性响应，其中超弹性模型使用修正MR模型。超弹性模型和率相关Maxwell体以及黏超弹性模型的表达式分别为

为方便计，统一表达为伸长比$ \lambda \left( { \lambda = 1 + \varepsilon } \right)$的函数，则有

为简单计，（8）式中特征应变率$ {\dot \varepsilon _0}$取为0.001 s^–1，采用非线性最小二乘法对硅橡胶在不同应变率下的工程应力-伸长比曲线进行拟合，得到拟合结果与实验结果的对比如图10所示，相应的模型参数值见表1。由图10可见，模型结果和实验结果具有较好的重合性，对于1400 s^–1应变率的实验结果，模型结果亦能很好地体现实验曲线的变化趋势，说明本研究提出的以率相关的Maxwell体并联修正MR模型得到的唯象黏超弹性模型能很好地描述硅橡胶材料在大应变率跨度内的黏超弹性变形特征。

（1）通过改进的SHTB测试技术，可以准确地获得硅橡胶在高应变率加载下的拉伸力学响应，对比硅橡胶在低-中-高应变率下的单向拉伸测试结果可知：硅橡胶的拉伸力学行为具有显著的非线性特征和明显的应变率敏感性。

（2）将超弹性弹簧和松弛时间率相关的Maxwell体并联构建了一个唯象黏超弹性模型，二者分别对应于材料率无关的超弹性响应和率相关的黏弹性响应，模型拟合结果和实验结果的对比显示该唯象模型能很好地表征硅橡胶在大应变率范围内拉伸力学行为的非线性和应变率相关性特征。