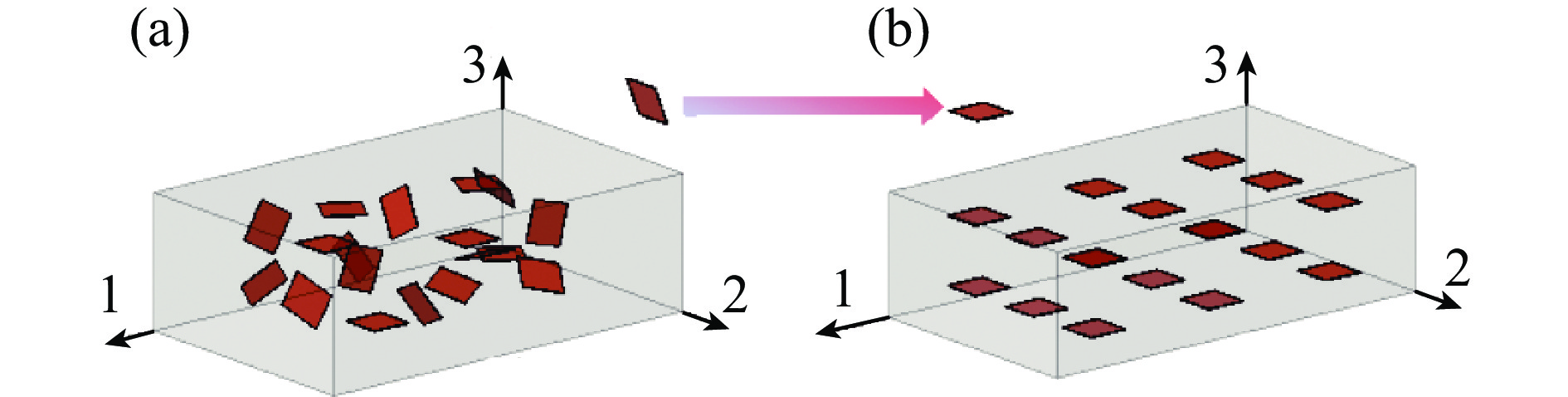
石墨烯纳米片在基体中主要存在两种排列模式：随机排列和定向排列，如图1所示。本研究将石墨烯纳米片随机排列状态下的梁称为R-梁，定向排列状态下的梁称为W-梁（梁在坐标系1-2面内振动）和L-梁（梁在坐标系1-3面内振动）。

Halpin-Tsai模型^[17]被广泛用于预测石墨烯纳米片单向或随机排列状态下复合材料的模量参数，其微观力学模型如下。

（1）随机排列模式

其中参数${\eta _{\rm{M}}}{\text{、}}\!\!{\eta _{\rm{N}}}$分别为

（2）定向排列模式

其中参数${\eta _{\rm{E}}}{\text{、}}\!\!{\eta _{\rm{G}}}$分别为

式中：下标R、W、L分别表示R-梁、W-梁、L-梁，下标G、M分别表示石墨烯纳米片和基体材料；${L_{\rm{G}}}$、${T_{\rm{G}}}$和${V_{\rm{G}}}$分别表示石墨烯纳米片的平均长度、厚度以及其在基体中的体积分数；E、G分别表示材料的杨氏模量和剪切模量；$\zeta $表示增强因子，其数值大小由表1给出^[18]。特别说明的是，石墨烯纳米片定向排列时，复合材料为横观各向同性，因此L-梁和W-梁的弹性模量相同，而剪切模量需要分别讨论。

复合材料的密度ρ_C和泊松比${\nu _{\rm{C}}}$可由混合定律估算

由冯卡门非线性应变-位移关系得

式中：u、$\phi $和w分别代表梁的轴向位移、横截面转角和横向位移。则梁的动能K、外激励做功Θ和应变能U可以表示为

式中：l、h分别为梁的长度和高度，T为梁端中性面上的均布轴向力。

由哈密顿原理，即 ${\text{δ}}\displaystyle\int_{{t_1}}^{{t_2}} {\left( {K - U + {\textit{Θ}} } \right){\rm{d}}t} = 0$，可以得到

刚度和惯性的相关参数分别为

梁的轴力、弯矩和剪力分别为

则边界条件可以表示为

对于含有初值条件的偏微分方程，因其解析解通常无法由理论推导获得，所以一种有效的半解析数值方法—微分求积(DQ)法^[16]被广泛应用于工程计算领域。它的基本思想是将函数在某点处的偏导数用全域内所有节点函数值的加权和来表示，具有数学原理简单、精度高、收敛快等特点。先采用DQ法将控制方程离散处理，之后通过简单的数学变换，发现可以将控制方程转变成特征值问题进行求解，故而大幅度地降低了计算难度，简化了问题求解。

利用切比雪夫公式对梁的轴线进行离散

由微分求积法有

式中：${l_j}$为拉格朗日插值多项式，$H_{ij}^{(k)}$为加权系数

则控制方程组(13)式可离散为

边界条件可类似地离散，此处略去该过程。将(24)式的解写成静态和动态两部分

式中：下标s表示梁的静态屈曲解，下标 ${\text{Γ}} $ 表示梁在屈曲附近的振动解。

对于静态屈曲问题，其控制方程可以表示为

根据(26)式及边界条件，采用权系数矩阵修正法^[19]处理刚度矩阵，可建立如下特征值问题

式中：${{ d}_{\rm s}} = {\left\{ {{{\left\{ {{u_{{\rm s}j}}} \right\}}^{\rm{T}}},{{\left\{ {{w_{{\rm s}j}}} \right\}}^{\rm{T}}},{{\left\{ {{\phi _{{\rm s}j}}} \right\}}^{\rm{T}}}} \right\}^{\rm{T}}}$，${{ K}_{{\rm{L}}1}}$和${{ K}_{{\rm{L2}}}}$为常系数刚度矩阵，${{ K}_{{\rm{NL}}1}}$和${{ K}_{{\rm{NL2}}}}$为非线性矩阵，其中元素分别为${{ d}_{\rm s}}$的一次和二次函数。

去掉(27)式的非线性项，可以得到系统的标准特征值方程

求解(28)式，即可得到系统的临界屈曲荷载${T_{{\rm{cr}}}}$和屈曲模态${{ d}_{\rm s}}$。

对于动态振动问题，考虑微幅振动，假设系统的解为

式中：$\omega $为固有频率。需要指出的是，当轴向力T小于临界屈曲力${T_{{\rm{cr}}}}$，${\bar { d}_{\rm s}}$取${ 0}$，轴向力T大于临界屈曲力${T_{{\rm{cr}}}}$，${\bar { d}_{\rm s}}$取系统屈曲后的新平衡解，其值可由非线性特征方程(27)式通过迭代法求解得到。则含动态解的控制方程可以表示为

(30)式忽略了动态位移非线性项。结合(30)式及边界条件，采用权系数矩阵修正法，可以得到如下方程

式中：${{ K}_{\rm T}}$为含轴向力的变刚度矩阵，${ M}$为质量矩阵。求解(31)式的特征值${\omega ^2}$和特征向量${{\bar { d}}_{{\text{Γ}}} }$，即可得到石墨烯纳米复合材料梁在屈曲前后的固有频率和振型。

以石墨烯-环氧树脂基复合材料为例，分析石墨烯纳米片的排列方式、几何尺寸及体积分数对环氧树脂基复合材料梁的临界屈曲力及屈曲附近振动的影响。两种材料的物性参数如表2所示。如不特别说明，石墨烯纳米片的长度和厚度分别取$1\;{\text{μ}}{\rm{m}}$和0.8 nm，体积分数取1.8%，梁的截面尺寸为$5\;{\rm{cm}} \times 5\;{\rm{cm}}$，长度为1 m。需要特别说明的是，作为一种二维材料，石墨烯纳米片只存在面内剪切模量，即${G_{{\rm G}\left( {13} \right)}} = {G_{{\rm G}\left( {23} \right)}} = 0$^[20]。

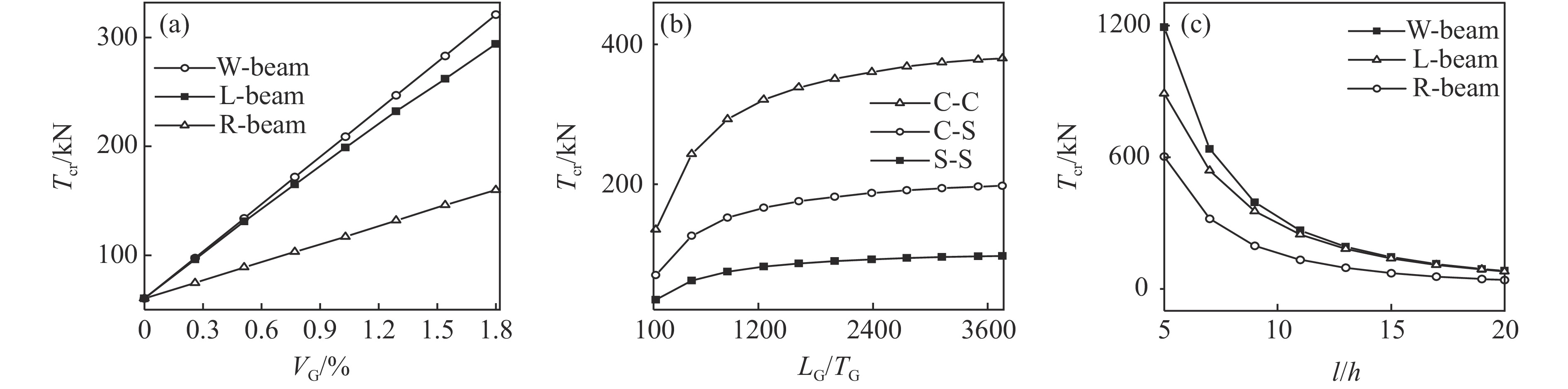
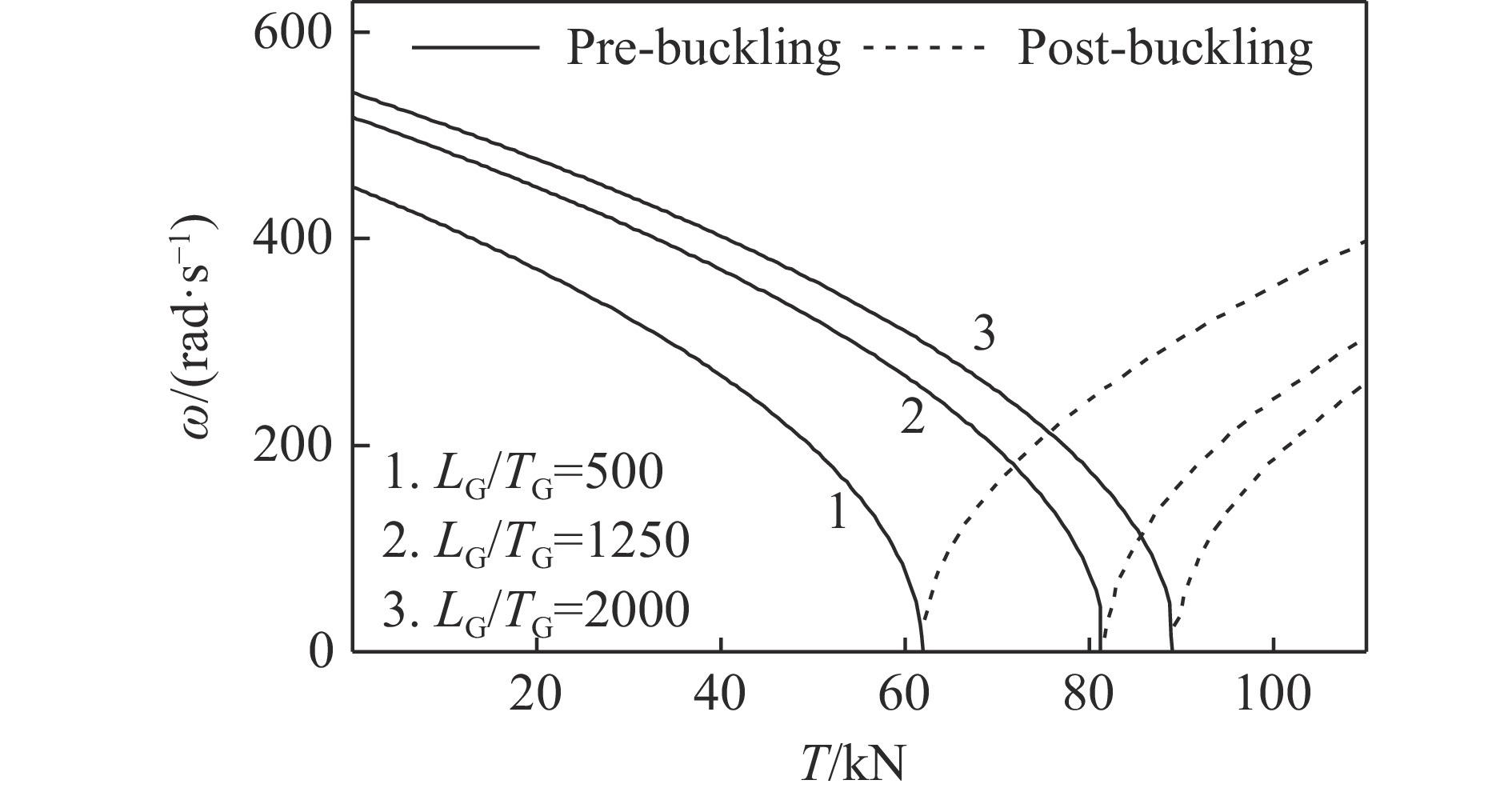
不同约束方式下，3种梁的第1阶临界屈曲荷载如表3所示。通过与欧拉梁临界屈曲载荷表达式${T_{{\rm{cr}}}} = {{{n^2}{{\text{π}}^2}EI} / {{{\left( {\mu l} \right)}^2}}}$($\mu $为长度因数)计算的结果进行对比，发现微分求积法求解的数值解具有良好的精度。值得注意的是，因欧拉伯努利梁忽略了截面剪切力的影响，故采用上述解析表达式算得的R-梁和L-梁的临界屈曲载荷没有区别。这同时也说明，研究石墨烯纳米片定向排列情况时，必须考虑剪切力的影响，需采用一阶或高阶剪切梁理论。从表3还可以看出，在相同的约束条件下，W-梁与L-梁具有比R-梁更高的临界荷载，说明石墨烯纳米片定向排列模式下的复合材料梁的结构稳定性优于石墨烯纳米片随机排列的情况。同时，两端固支约束（C-C）下，石墨烯纳米复合材料梁的屈曲荷载最大，一端固支一端简支（C-S）约束下次之，两端简支（S-S）约束下最小，与预期结果吻合。

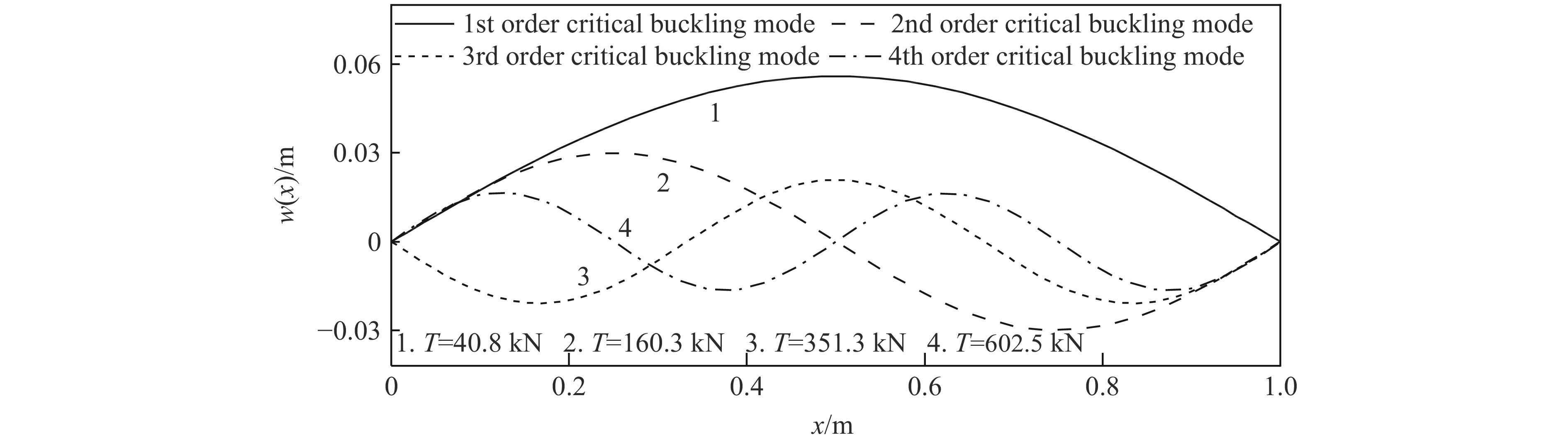
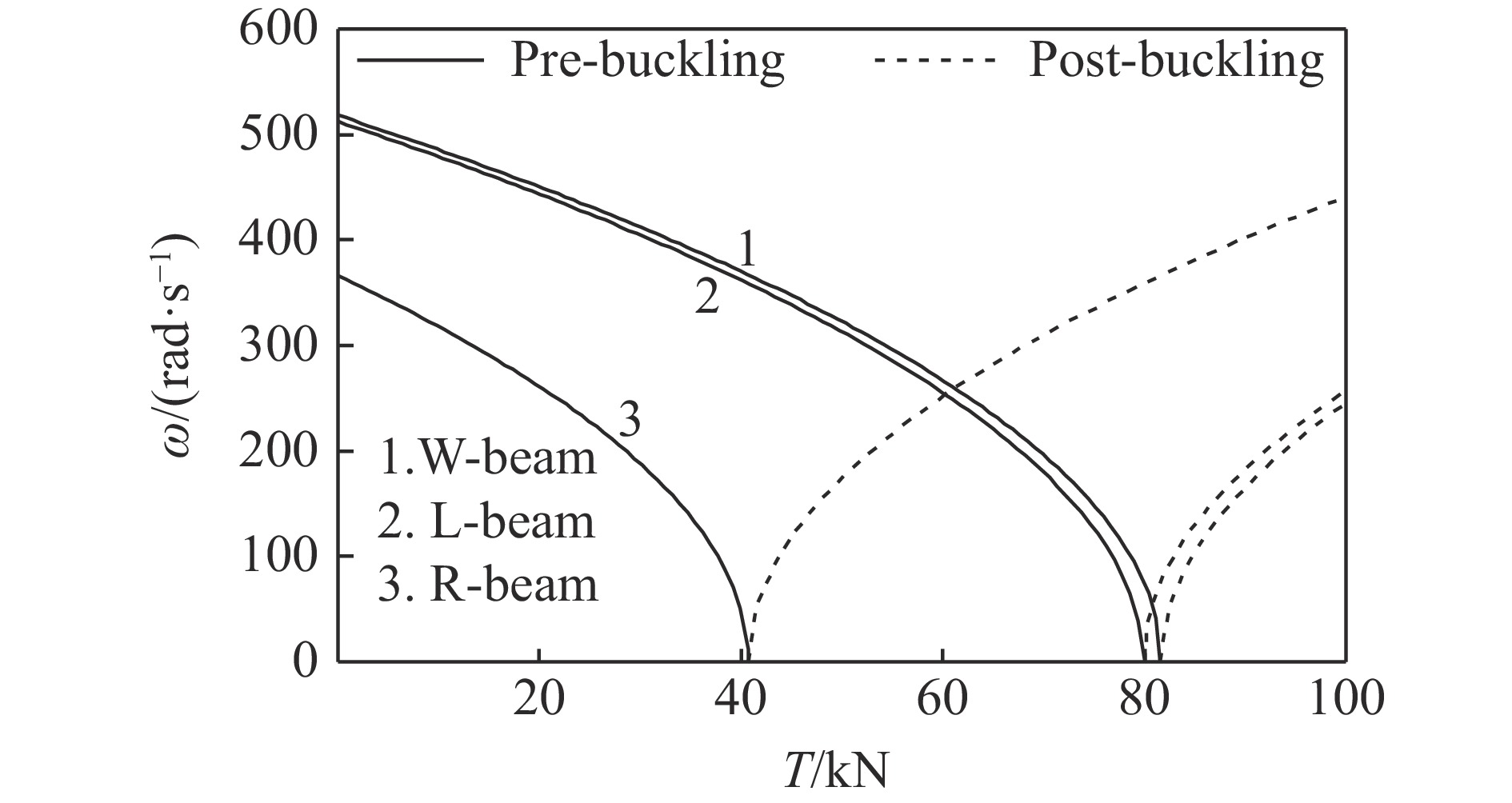
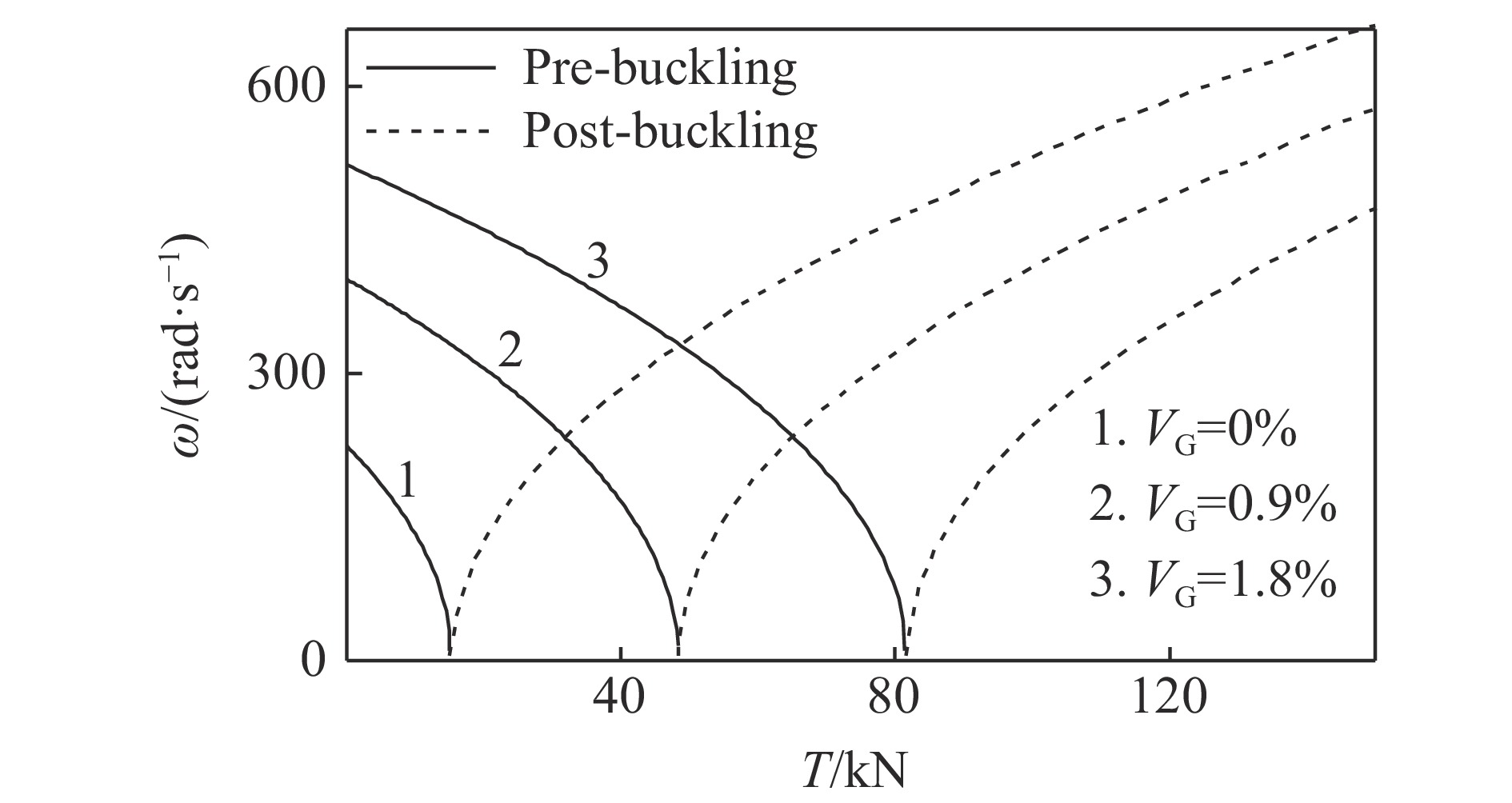
图2显示了不同参数对石墨烯纳米复合材料梁第1阶临界屈曲载荷的影响。以两端固支约束为例，分析了石墨烯纳米片在基体中的体积分数对梁的第1阶临界屈曲荷载的影响，结果如图2(a)所示。可以看出，石墨烯纳米复合材料梁的临界屈曲力受石墨烯浓度的影响很大，例如，石墨烯体积分数为1.8%的W-梁，其第1阶临界屈曲荷载约为纯环氧树脂梁的6倍。以W-梁为例，研究了石墨烯纳米片的长厚比对梁的第1阶临界屈曲荷载的影响，结果如图2（b）所示。可以看出：当长厚比${{{L_{\rm G}}} / {{T_{\rm G}}}}$低于2000时，W-梁的临界屈曲力受其影响较大；超过2000时，则影响不明显。其原因是石墨烯纳米片过大的比表面积引起了团聚现象^[24]。图2(c)显示了两端简支石墨烯纳米复合材料梁的长细比对梁的临界屈曲载荷的影响。可以看出，随着长细比的增加，3种梁的临界屈曲载荷皆逐渐减小，与预期相符。图3简单介绍了S-S约束下R-梁的前4阶临界屈曲模态。从图3中发现，轴向力取各阶临界屈曲荷载时，梁表现出相应阶的屈曲模态，这种现象符合系统的稳定性理论，即低阶模态会逐渐向高阶模态跃迁。

以两端简支梁为例，研究了轴向力作用下梁在第1阶屈曲附近的基频随参数的变化规律，结果如图4～图7所示。可以发现，梁在轴力等于临界屈曲载荷时具有零基频现象。图4给出了石墨烯排列模式对梁屈曲前后基频的影响规律。可以看出：在屈曲发生前，R-梁、W-梁以及L-梁的基频都随着轴向力的增大而降低，同时W-梁和L-梁的基频显著高于R-梁，即定向排列的情况比随机排列情况能更好地提高梁的刚度。其原因是石墨烯纳米片定向排列时片层与基体材料间的界面作用力更大，能有效抑制聚合物链的滑移，故而显著提高了纳米复合材料的力学性能^[14]，同时在所考虑的两种定向排列情况下，W-梁比L-梁的基频稍高。然而发生屈曲后，情况正好相反，即随机排列模式下梁的基频反而大大高于定向排列模式，同时L-梁的基频比W-梁稍高。图5显示了石墨烯体积分数对梁屈曲前后基频的影响。可以看出，石墨烯浓度越大，屈曲前梁的基频越大，屈曲后梁的基频反而越小。图6给出了石墨烯纳米片长厚比对梁屈曲前后基频的影响。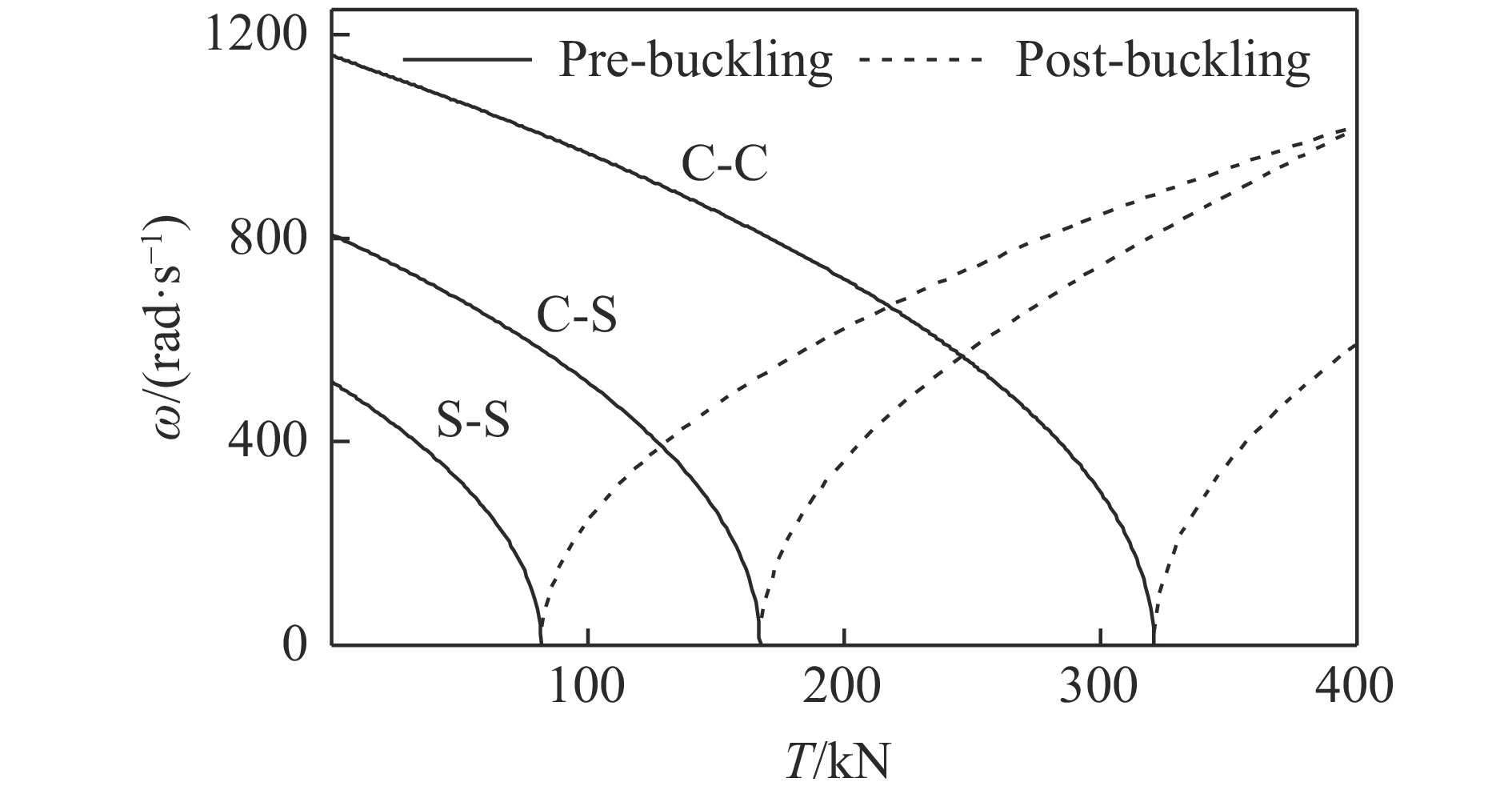可以看出，发生屈曲之前，${{{L_{\rm G}}} / {{T_{\rm G}}}}$增大会提高梁的基频；发生屈曲后，${{{L_{\rm G}}} / {{T_{\rm G}}}}$增大反而会降低梁的基频。图7比较了不同边界条件对梁屈曲前后基频的影响。可以看出：屈曲前两端固支梁具有最高基频，一端固支一端简支梁次之，两端简支梁基频最低；屈曲后，现象正好相反。

分析了石墨烯纳米复合材料梁的临界屈曲荷载及屈曲附近的自由振动特性。考虑石墨烯纳米片不同的排列模式，采用一阶剪切梁理论建立梁的控制方程，并应用微分求积法进行数值求解，得到如下主要结果：

（1）掺杂少量的石墨烯纳米片或石墨烯纳米片以定向的模式排列时，梁的临界屈曲载荷可以得到大幅提高。当石墨烯纳米片在同样浓度及排列模式下，宽厚比取2000左右时，梁的临界屈曲载荷达到最优。

（2）石墨烯纳米片定向排列模式下的梁，其抗屈曲能力优于随机排列的情况。这是因为石墨烯纳米片定向排列时片层与基体材料间的界面作用力更大，可以有效提高界面荷载的传递能力。同时在两种定向排列模式中，W-梁比L-梁具有更好的结构稳定性。

（3）屈曲发生前，轴向压力的增大会降低石墨烯纳米复合材料梁的固有频率。而屈曲发生后，现象正好相反。