高级搜索

旋转对卵形弹侵彻钢板影响的FEM-SPH耦合模拟

,  ,  ,  , 

downloadPDF

上一篇

下一篇

肖毅华, 吴和成, 朱爱华, 董晃晃, 平学成. 旋转对卵形弹侵彻钢板影响的FEM-SPH耦合模拟[J]. 高压物理学报, 2019, 33(5): 055103-1. doi: 10.11858/gywlxb.20180675
引用本文: 肖毅华, 吴和成, 朱爱华, 董晃晃, 平学成. 旋转对卵形弹侵彻钢板影响的FEM-SPH耦合模拟[J]. 高压物理学报, 2019, 33(5): 055103-1. doi: 10.11858/gywlxb.20180675
shu
Yihua XIAO, Hecheng WU, Aihua ZHU, Huanghuang DONG, Xuecheng PING. Effect of Rotation on Penetration of Steel Plate by Ogival Projectile Using Coupled FEM-SPH Simulation[J]. gaoyawli, 2019, 33(5): 055103-1. doi: 10.11858/gywlxb.20180675
Citation: Yihua XIAO, Hecheng WU, Aihua ZHU, Huanghuang DONG, Xuecheng PING. Effect of Rotation on Penetration of Steel Plate by Ogival Projectile Using Coupled FEM-SPH Simulation[J]. gaoyawli, 2019, 33(5): 055103-1. doi: 10.11858/gywlxb.20180675
shu

旋转对卵形弹侵彻钢板影响的FEM-SPH耦合模拟

  • 1.

    华东交通大学机电与车辆工程学院，江西 南昌　330013

  • 2.

    杭叉集团股份有限公司，浙江 杭州　310000

  • 3.

    天津科技大学机械工程学院，天津　300457

    • 作者简介: 肖毅华（1984—），男，博士，副教授. 主要从事防护材料/结构设计与分析、机械结构强度与破坏研究. E-mail：xiaoyihua@ecjtu.edu.cn .

  • 中图分类号: O385

Effect of Rotation on Penetration of Steel Plate by Ogival Projectile Using Coupled FEM-SPH Simulation

  • 1.

    School of Mechatronics and Vehicle Engineering, East China Jiaotong University, Nanchang 330013, China

  • 2.

    Hangcha Group Co., Ltd, Hangzhou 310000, China

  • 3.

    College of Mechanical Engineering, Tianjin University of Science and Technology, Tianjin 300457, China

  • MSC: O385

  • 摘要: 建立了卵形弹侵彻钢板的FEM-SPH耦合计算模型，研究了弹靶间摩擦系数对弹体剩余速度计算结果的影响，根据实验结果确定了合理的摩擦系数，使耦合计算模型能准确地预测弹体剩余速度和靶板弹道极限。以该模型为基础，在两种不同着靶速度下，研究了弹体的旋转对其正侵彻和以不同入射角斜侵彻钢板时剩余速度和弹道偏转的影响。正侵彻下：旋转对弹体剩余速度的影响大，而对弹道偏转的影响很小；随着转速的增加，剩余速度增大，弹体侵彻能力提高。斜侵彻下：旋转对弹体的剩余速度和弹道偏转都有明显影响，但弹体转速的增大并不总使其侵彻能力提高，与入射角和着靶速度有关；同时旋转使弹体沿入射面外发生偏转，其偏转方向与弹体的旋转方向相关。
    Abstract: A coupled FEM-SPH model for an ogival-nosed projectile penetrating into a steel plate was established. The influence of friction coefficient between projectile and plate on residual velocity estimation for projectile was analyzed. Based on the experimental data, a suitable friction coefficient was determined such that the model can accurately predict residual velocities of projectile and ballistic limit of target. Based on the model, effects of projectile rotation on its residual velocity and ballistic deflection were studied for normal and oblique penetration with two different incident velocities and different incident angles. For normal penetration, rotation has a significant influence on residual velocity of projectile while few effects on ballistic deflection. The residual velocity and penetration capability of projectile increase with the growth of rotation speed. For oblique penetration, rotation has obvious effects on both residual velocity and ballistic deflection of projectile. The penetration capability of projectile does not monotonically increase with the growth of rotation speed and is dependent on incident angle and velocity. Deflections out of incident plane are induced by projectile rotation, and the deflection direction is related to the rotation direction of projectile.
  • 加载中

  • 图 1  FEM-SPH耦合计算模型

    Figure 1.  Coupled FEM-SPH model

    下载: 全尺寸图片 幻灯片

    图 2  不同摩擦系数下的剩余速度总体相对误差

    Figure 2.  Overall relative error of residual velocity for different friction coefficients

    下载: 全尺寸图片 幻灯片

    图 3  数值模拟和实验[10]获得的弹靶变形情况对比

    Figure 3.  Comparison of deformations of projectile and target obtained by numerical simulation and experiment[10]

    下载: 全尺寸图片 幻灯片

    图 4  剩余速度随转速的变化曲线

    Figure 4.  Residual velocity-rotation speed curves

    下载: 全尺寸图片 幻灯片

    图 5  着靶速度为298.2 m/s时不同转速下弹体侵彻钢板过程中的变形

    Figure 5.  Penetration deformations of steel plate with different rotation speeds of projectile at an incident velocity of 298.2 m/s

    下载: 全尺寸图片 幻灯片

    图 6  着靶速度为365.0 m/s时不同转速下弹体侵彻钢板过程中的变形

    Figure 6.  Penetration deformations of steel plate with different rotation speeds of projectile at an incident velocity of 365.0 m/s

    下载: 全尺寸图片 幻灯片

    图 7  靶板中观测粒子在xz平面内的运动轨迹（着靶速度298.2 m/s）

    Figure 7.  Trajectories in xz plane of the observed particles in the target (Incident velocity: 298.2 m/s)

    下载: 全尺寸图片 幻灯片

    图 8  转速随时间的变化曲线

    Figure 8.  Curves of rotation speed time history

    下载: 全尺寸图片 幻灯片

    图 9  不同着靶速度时剩余速度随转速的变化曲线

    Figure 9.  Residual velocity-rotation speed curves for different incident velocities

    下载: 全尺寸图片 幻灯片

    图 10  着靶速度365.0 m/s、入射角45°和转速5×105 r/min时的变形

    Figure 10.  Deformations for incident velocity 365.0 m/s, incident angle 45° and rotation speed 5×105 r/min

    下载: 全尺寸图片 幻灯片

    图 11  侵彻过程中任意时刻的弹体偏转角示意图

    Figure 11.  Schematic for deflection angles of projectile at an arbitrary time of penetration process

    下载: 全尺寸图片 幻灯片

    图 12  着靶速度298.2 m/s时弹体偏转角$\Delta {\alpha _1}$的变化曲线

    Figure 12.  Changes of projectile deflection angle $\Delta {\alpha _1}$ for incident velocity of 298.2 m/s

    下载: 全尺寸图片 幻灯片

    图 13  着靶速度298.2 m/s时弹体偏转角$\Delta {\alpha _2}$的变化曲线

    Figure 13.  Changes of projectile deflection angle $\Delta {\alpha _2}$ for incident velocity of 298.2 m/s

    下载: 全尺寸图片 幻灯片

    图 14  着靶速度365.0 m/s时弹体偏转角$\Delta {\alpha _1}$的变化曲线

    Figure 14.  Changes of projectile deflection angle $\Delta {\alpha _1}$ for incident velocity of 365.0 m/s

    下载: 全尺寸图片 幻灯片

    图 15  着靶速度为365.0 m/s时弹体偏转角$\Delta {\alpha _2}$的变化曲线

    Figure 15.  Changes of projectile deflection angle $\Delta {\alpha _2}$ for incident velocity of 365.0 m/s

    下载: 全尺寸图片 幻灯片

    图 16  弹体沿相反方向旋转时弹体姿态的对比

    Figure 16.  Comparison of projectile attitudes for projectile rotating in opposite directions

    下载: 全尺寸图片 幻灯片

    图 17  弹体沿相反方向旋转时弹体偏转角的对比

    Figure 17.  Comparison of projectile deflection angles for projectile rotating in opposite directions

    下载: 全尺寸图片 幻灯片

    表 1  钢板的材料参数[11]

    Table 1.  Material parameters for steel plate[11]

    Mass density/
    (kg·m–3)    		Young’s modulus/GPaPoisson’s ratioTaylor-Quinney coefficient $\chi $Specific heat Cp/(J·kg–1·K–1)Thermal expansion coefficient $\alpha $/K–1Damage coupling parameter $\beta $
    78502100.330.94521.2×10–50
    Johnson-Cook (JC) strength model parameters
    A/MPaB/MPanC${\dot \varepsilon _0}$/s–1mTr/K
    4993820.4580.00795×10–40.893293
    JC strength model parametersJC damage model parameters
    Tm/KT0/KD1D2D3D4D5
    18002930.6361.936–2.969–0.0141.014
    JC damage model parametersVoce hardening parametersCritical temperature parameter Tc/K
    DcpdQ1C1Q2C2
    1000001800
    下载: 导出CSV

    表 2  弹体材料参数[11]

    Table 2.  Material parameters for projectile[11]

    Mass density/(kg·m–3)Young’s modulus/GPaPoisson’s ratio Yield stress ${\sigma _{\rm{y}}}$/MPaTangent modulus ETAN/GPa
    78502040.33190015
    下载: 导出CSV

    表 3  剩余速度和弹道极限的数值模拟结果与实验结果对比

    Table 3.  Comparison of residual velocity and ballistic limit obtained by numerical simulation and experiment

    MethodResidual velocity/(m·s–1)Ballistic limit/(m·s–1)
    vi = 298.2 m·s–1vi = 324.6 m·s–1vi = 346.6 m·s–1vi = 365.0 m·s–1
    Experiment[10]91.2160.3193.3239.9295.9
    Simulation95.3158.7197.6226.2284.0
    Relative error/% 4.5 1.0 2.2 5.7 4.0
    下载: 导出CSV
  • [1] 李晓杰, 姜力, 赵铮, 等. 高速旋转弹头侵彻运动金属薄板的数值模拟 [J]. 爆炸与冲击, 2008, 28(1): 57–61. doi: 10.3321/j.issn:1001-1455.2008.01.010 LI X J, JIANG L, ZHAO Z, et al. Numerical study on penetration of a high-speed-rotating bullet into the moving sheet-metal plate [J]. Explosion and Shock Waves, 2008, 28(1): 57–61. doi: 10.3321/j.issn:1001-1455.2008.01.010
    [2] 李勇, 于海龙, 芮筱亭. 旋转弹侵彻钢板的数值模拟 [J]. 火力与指挥控制, 2014(12): 31–35. LI Y, YU H L, RUI X T. Numerical study on penetration of rotating projectile into steel plate [J]. Fire Control & Command Control, 2014(12): 31–35.
    [3] 赵海龙, 王华. 旋转战斗部侵彻多层间隔靶的终点弹道的数值模拟 [J]. 中北大学学报(自然科学版), 2017, 38(3): 295–301. doi: 10.3969/j.issn.1673-3193.2017.03.009 ZHAO H L, WANG H. Numerical simulation of terminal ballistic of rotating warhead penetrating into multi-layer spaced target [J]. Journal of North University of China (Natural Science Edition), 2017, 38(3): 295–301. doi: 10.3969/j.issn.1673-3193.2017.03.009
    [4] 庞春旭, 何勇, 沈晓军, 等. 刻槽弹体旋转侵彻铝靶试验与数值模拟 [J]. 弹道学报, 2015, 27(1): 70–75. doi: 10.3969/j.issn.1004-499X.2015.01.014 PANG C X, HE Y, SHEN X J, et al. Experimental investigation and numerical simulation on grooved projectile rotationally penetrating into aluminum target [J]. Journal of Ballistics, 2015, 27(1): 70–75. doi: 10.3969/j.issn.1004-499X.2015.01.014
    [5] 庞春旭, 何勇, 沈晓军, 等. 刻槽弹体旋转侵彻混凝土效应试验研究 [J]. 兵工学报, 2015, 36(1): 46–52. doi: 10.3969/j.issn.1000-1093.2015.01.007 PANG C X, HE Y, SHEN X J, et al. Experimental investigation on penetration of grooved projectiles into concrete targets [J]. Acta Armamentarii, 2015, 36(1): 46–52. doi: 10.3969/j.issn.1000-1093.2015.01.007
    [6] 潘绪超, 何勇, 何源, 等. 旋转助推钻地弹侵彻混凝土靶试验研究 [J]. 固体火箭技术, 2011, 34(2): 146–149. doi: 10.3969/j.issn.1006-2793.2011.02.003 PAN X C, HE Y, HE Y, et al. Experimental study of penetrating concrete target with a spin-boosted earth penetrating weapon [J]. Journal of Solid Rocket Technology, 2011, 34(2): 146–149. doi: 10.3969/j.issn.1006-2793.2011.02.003
    [7] 赵子龙, 张瑾瑾, 黄晓琼. 长杆弹侵彻半无限厚土的旋转效应分析 [J]. 振动与冲击, 2010, 29(4): 9–11. doi: 10.3969/j.issn.1000-3835.2010.04.003 ZHAO Z L, ZHANG J J, HUANG X Q. Revolution effect analysis of a long rod penetrating into soil [J]. Journal of Vibration & Shock, 2010, 29(4): 9–11. doi: 10.3969/j.issn.1000-3835.2010.04.003
    [8] GUPTA N K, MADHU V. Normal and oblique impact of a kinetic energy projectile on mild steel plates [J]. International Journal of Impact Engineering, 1992, 12(3): 333–343. doi: 10.1016/0734-743X(92)90101-X
    [9] MADHU V, RAMANJANEYULU K, BHAT T B, et al. An experimental study of penetration resistance of ceramic armour subjected to projectile impact [J]. International Journal of Impact Engineering, 2005, 32(1): 337–350.
    [10] DEY S, BØRVIK T, HOPPERSTAD O S, et al. The effect of target strength on the perforation of steel plates using three different projectile nose shapes [J]. International Journal of Impact Engineering, 2004, 30(8): 1005–1038.
    [11] BØRVIK T, HOPPERSTAD O S, BERSTAD T, et al. A computational model of viscoplasticity and ductile damage for impact and penetration [J]. European Journal of Mechanics-A/Solids, 2001, 20(5): 685–712. doi: 10.1016/S0997-7538(01)01157-3
    [12] ROSENBERG Z, DEKEL E. 终点弹道学[M]. 钟方平, 译. 北京: 国防工业出版社, 2014: 85–86.
    [13] BØRVIK T, HOPPERSTAD O S, BERSTAD T, et al. Perforation of 12 mm thick steel plates by 20 mm diameter projectiles with flat, hemispherical and conical noses: part Ⅱ: numerical simulations [J]. International Journal of Impact Engineering, 2002, 27(1): 37–64. doi: 10.1016/S0734-743X(01)00035-5
  • 加载中
图( 17) 表( 3)
计量
  • 文章访问数:  1878
  • HTML全文浏览数:  1878
  • PDF下载数:  13
  • 施引文献:  0
出版历程
  • 收稿日期:  2018-11-07
  • 刊出日期:  2019-10-05

旋转对卵形弹侵彻钢板影响的FEM-SPH耦合模拟

    作者简介: 肖毅华（1984—），男，博士，副教授. 主要从事防护材料/结构设计与分析、机械结构强度与破坏研究. E-mail：xiaoyihua@ecjtu.edu.cn
  • 1. 华东交通大学机电与车辆工程学院，江西 南昌　330013
  • 2. 杭叉集团股份有限公司，浙江 杭州　310000
  • 3. 天津科技大学机械工程学院，天津　300457
  • 收稿日期:  2018-11-07

摘要: 建立了卵形弹侵彻钢板的FEM-SPH耦合计算模型，研究了弹靶间摩擦系数对弹体剩余速度计算结果的影响，根据实验结果确定了合理的摩擦系数，使耦合计算模型能准确地预测弹体剩余速度和靶板弹道极限。以该模型为基础，在两种不同着靶速度下，研究了弹体的旋转对其正侵彻和以不同入射角斜侵彻钢板时剩余速度和弹道偏转的影响。正侵彻下：旋转对弹体剩余速度的影响大，而对弹道偏转的影响很小；随着转速的增加，剩余速度增大，弹体侵彻能力提高。斜侵彻下：旋转对弹体的剩余速度和弹道偏转都有明显影响，但弹体转速的增大并不总使其侵彻能力提高，与入射角和着靶速度有关；同时旋转使弹体沿入射面外发生偏转，其偏转方向与弹体的旋转方向相关。

English Abstract

    全文HTML

  • 钢板在各类防护结构中具有广泛的应用，常用于构造轻型装甲车、坦克等军用车辆的基体装甲或复合装甲。目前虽有很多研究分析了弹体侵彻钢板过程，但较少考虑弹体旋转对侵彻过程的影响。实际中，许多弹体是高速旋转的，依靠陀螺效应保持在空中飞行的稳定性，弹体的旋转速度可高达十万以上转每分钟。因此，研究旋转对弹体侵彻过程的影响具有重要的实际意义。国内一些研究者开展了相关的研究。李晓杰等[1]模拟了高速旋转弹侵彻运动金属薄板，研究了弹体转速和薄板运动速度对弹体最终速度和翻转角度以及弹道偏移的影响。李勇等[2]采用LS-DYNA对旋转弹侵彻钢板进行了模拟，研究了转速对垂直侵彻和斜侵彻下弹体速度、加速度以及弹体质量损失的影响。赵海龙和王华[3]通过数值模拟研究了旋转战斗部侵彻多层间隔靶过程，分析了旋转速度等因素对战斗部剩余速度、弹道偏移角等的影响。庞春旭等[4]采用试验和数值模拟研究了旋转刻槽弹侵彻铝靶过程，发现旋转能有效地提高弹体的侵深。庞春旭等[5]还研究了旋转刻槽弹对混凝土靶的侵彻。潘绪超等[6]通过试验研究了旋转助推钻地弹侵彻混凝土靶，建立了侵彻速度与弹体转速及火箭发动机推力间的关系。赵子龙等[7]建立了考虑旋转效应的长杆弹侵彻土壤介质的动力学方程，通过数值求解得到了撞击力和侵入位移。在国外，一些研究者[8-9]也报道了钢、陶瓷等靶板在弹体侵彻下的性能，但公开文献中很少见关于弹体旋转影响的详细研究。现有的研究大部分考虑正侵彻条件下弹体旋转的影响，对不同入射角斜侵彻情况下弹体旋转的影响仍缺乏系统的研究。同时，现有研究主要采用试验方法和有限元方法（Finite Element Method，FEM）模拟。试验方法的成本非常高，单一的试验平台通常只能对应特定的转速。而FEM在侵彻模拟方面存在一定困难，精度不高。

    本研究考虑卵形弹侵彻12 mm厚Weldox 460 E钢板，讨论弹体旋转对其侵彻过程的影响。采用FEM-SPH耦合模拟技术，利用光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）模拟靶板大变形和破坏的优势，同时方便处理弹靶间的接触界面。先根据无旋转弹体侵彻钢板的实验数据确定合理的摩擦系数，对FEM-SPH耦合模型进行验证。然后考虑弹体具有不同转速的情况，通过数值模拟研究旋转和不旋转弹体以不同着靶速度正、斜侵彻钢板过程，分析旋转对弹体剩余速度和弹道偏转角的影响。

1.   卵形弹侵彻钢板的FEM-SPH耦合计算模型

  • 基于LS-DYNA建立了如图1所示的卵形钢弹侵彻钢板的FEM-SPH耦合计算模型。弹体的直径为20 mm，总长度为95 mm，CRH（Caliber Radius Head）为3，总质量为0.197 kg，材料为Arne工具钢。钢板的厚度为12 mm，周边被夹持，中心留有直径500 mm的圆形自由变形区，材料为Weldox 460 E钢。上述模型设置与Dey等[10]开展的侵彻实验相同，其实验结果为模型验证提供参考。由于弹体强度远高于靶板强度，实验发现弹体在侵彻过程中变形很小。因此，采用FEM将弹体离散，而采用SPH粒子将钢板离散，从而有效地模拟钢板在弹体冲击下的大变形和破坏。为了约束钢板的周边，其边缘部分的上、下方都布置了额外的固定粒子。这些粒子与靶板粒子的材料性能相同，参与靶板粒子的SPH近似计算，同时对其各方向的位移施加约束，实现对靶板的夹持。弹体与钢板间的接触通过*CONTACT_NODES_TO_SURFACES定义。钢板和弹体的材料模型分别采用*MAT_MODIFIED_JOHNSON_COOK和*MAT_PLASTIC_KINEMATIC模型。弹体和钢板材料的本构参数采用Børvik等[11]的研究结果，具体的材料参数见表1和表2。

2.   摩擦系数的确定

  • 摩擦是侵彻过程中的不确定性因素。目前，关于弹靶间摩擦作用的研究还不够透彻，通常假设摩擦作用很小，甚至忽略摩擦[12]。Børvik等[13]指出：对于平头弹侵彻钢板，摩擦可忽略不计；而对于锥形弹和半球形弹，则需要考虑摩擦。这主要由于平头弹侵彻导致靶板发生冲塞失效，弹体头部与靶板间的相对滑移较小；而尖形弹体侵彻主要导致靶板发生塑性扩孔失效，弹体头部在侵彻过程中向周围挤压靶板材料，弹靶间相对滑移较大。

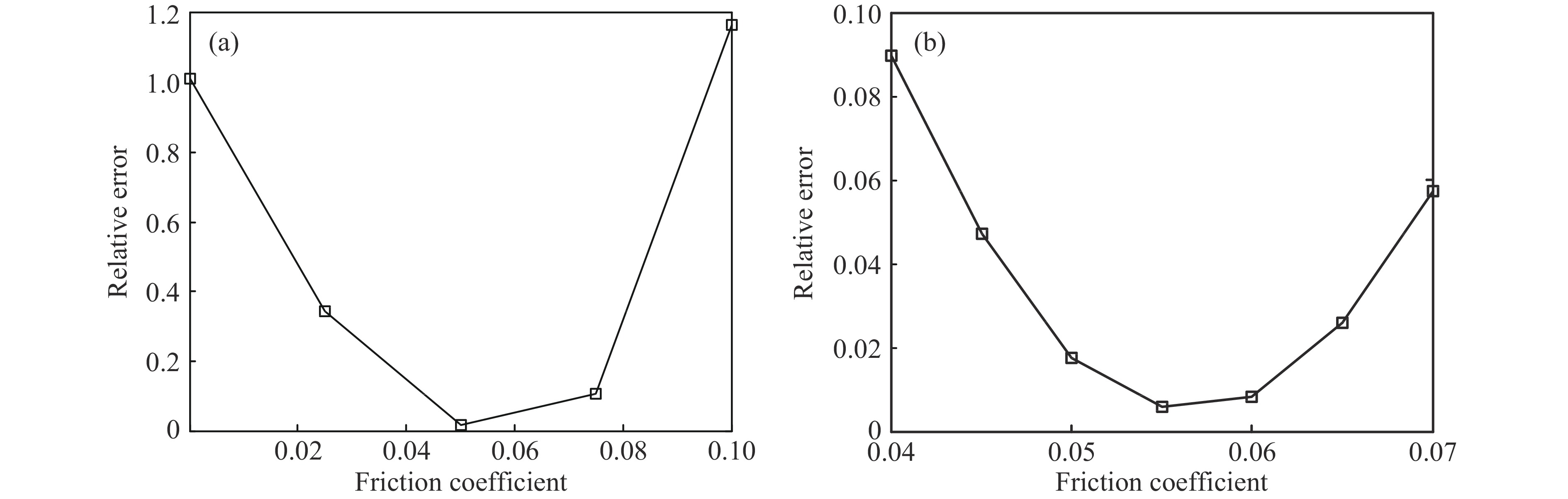
    为了得到合理的摩擦系数，先在较大的区间[0, 0.1]内对摩擦系数进行敏感性分析，然后通过局部加密取样点对摩擦系数取值进行优化。在敏感性分析中，取0、0.025、0.050、0.075和0.100共5种不同摩擦系数。针对每个摩擦系数，计算弹体着靶速度为298.2、324.6、346.6和365.0 m/s共4种工况。定义任意摩擦系数下弹体剩余速度的计算结果与实验结果[10]的总体相对误差为

    式中：$v_{i{\rm{r}}}^{\rm{c}}$和$v_{i{\rm{r}}}^{\rm{e}}$分别表示第$i$种着靶速度下计算和实验得到的剩余速度。弹体的剩余速度取其穿透靶板后的刚体速度，其分量大小等于弹体总动量除以弹体总质量，通过在LS-PrePost中后处理时选取Resultant Rigid Body Velocity得到。图2(a)给出了不同摩擦系数下的剩余速度总体相对误差。可见，总体相对误差随摩擦系数变化明显，说明剩余速度计算结果对摩擦系数敏感，摩擦作用不可忽略。摩擦系数为0.05时，剩余速度的总体相对误差最小，该值与Børvik等[13]所采用的一致。考虑到在前述摩擦系数范围内相对误差变化较大，为了进一步优化摩擦系数取值，在0.05的邻域范围[0.04, 0.07]区间内加密摩擦系数取样，每隔0.005进行取样。图2(b)给出了在这些摩擦系数下计算得到的剩余速度总体相对误差。当摩擦系数为0.055时，总体相对误差最小。表3给出了该摩擦系数下计算的剩余速度和弹道极限。其中，弹道极限由剩余速度结果按以下解析模型拟合得到。

    式中：${v_{\rm{i}} }$为着靶速度，${v_{\rm{r}}}$为剩余速度；$a$、$p$和${v_{{\rm{bl}}}}$为模型常数，通过拟合得到，${v_{{\rm{bl}}}}$即为弹道极限。由表3可见，剩余速度的最大相对误差为5.7%，弹道极限的相对误差为4.0%，计算模型能很好地预测剩余速度和弹道极限。图3给出了着靶速度为298.2 m/s时两个典型时刻的弹靶变形情况。模拟结果与实验中的高速摄像结果[10]也符合得较好。因此，在后续研究中，摩擦系数采用0.055。

3.   旋转对正侵彻和斜侵彻过程的影响

  • 以第2节所述模型为基础，通过在模型中给弹体设定不同的转速，分析弹体正侵彻和斜侵彻钢板时其转速对剩余速度和弹道偏转的影响。

    • 3.1.   旋转对正侵彻的影响

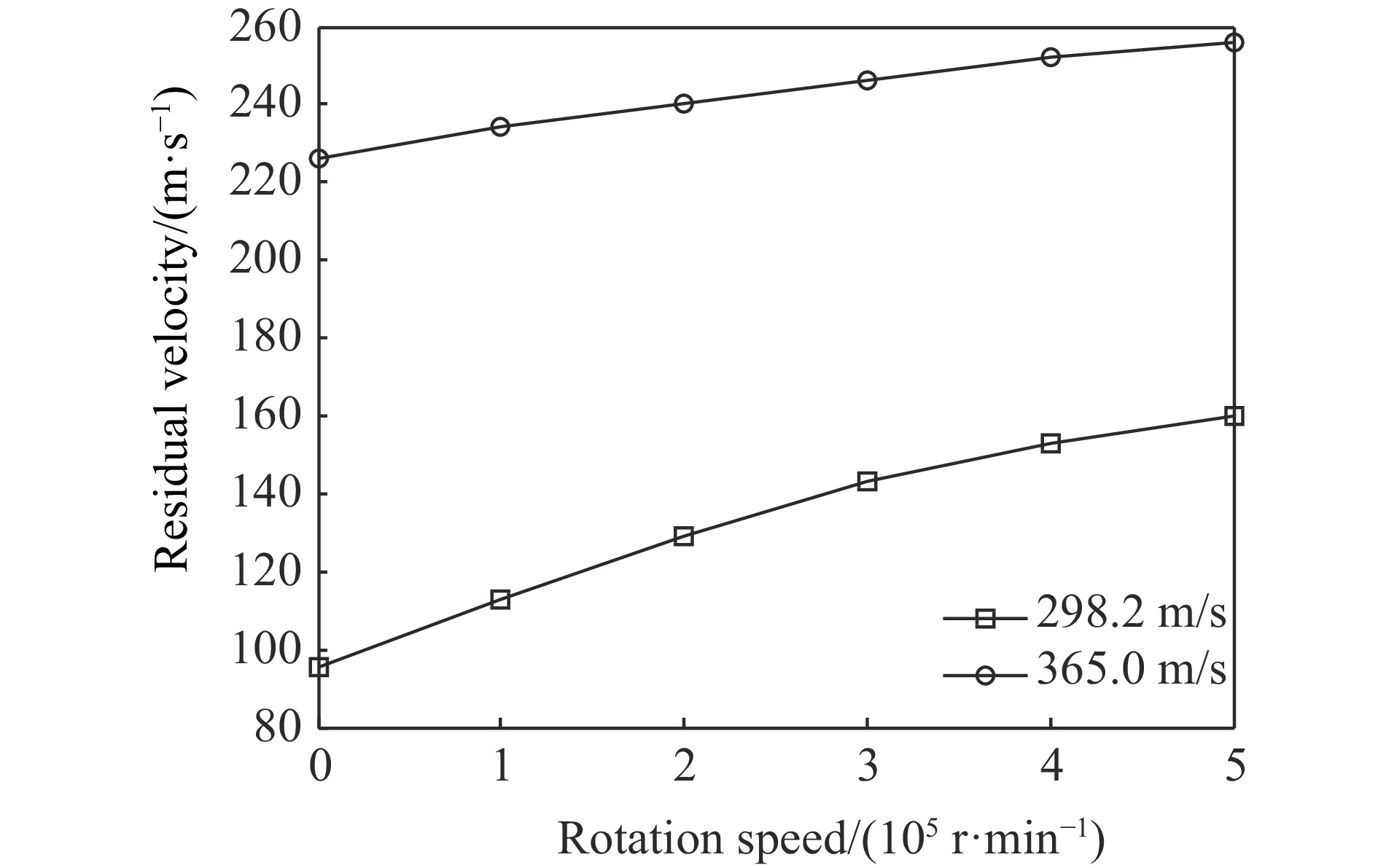
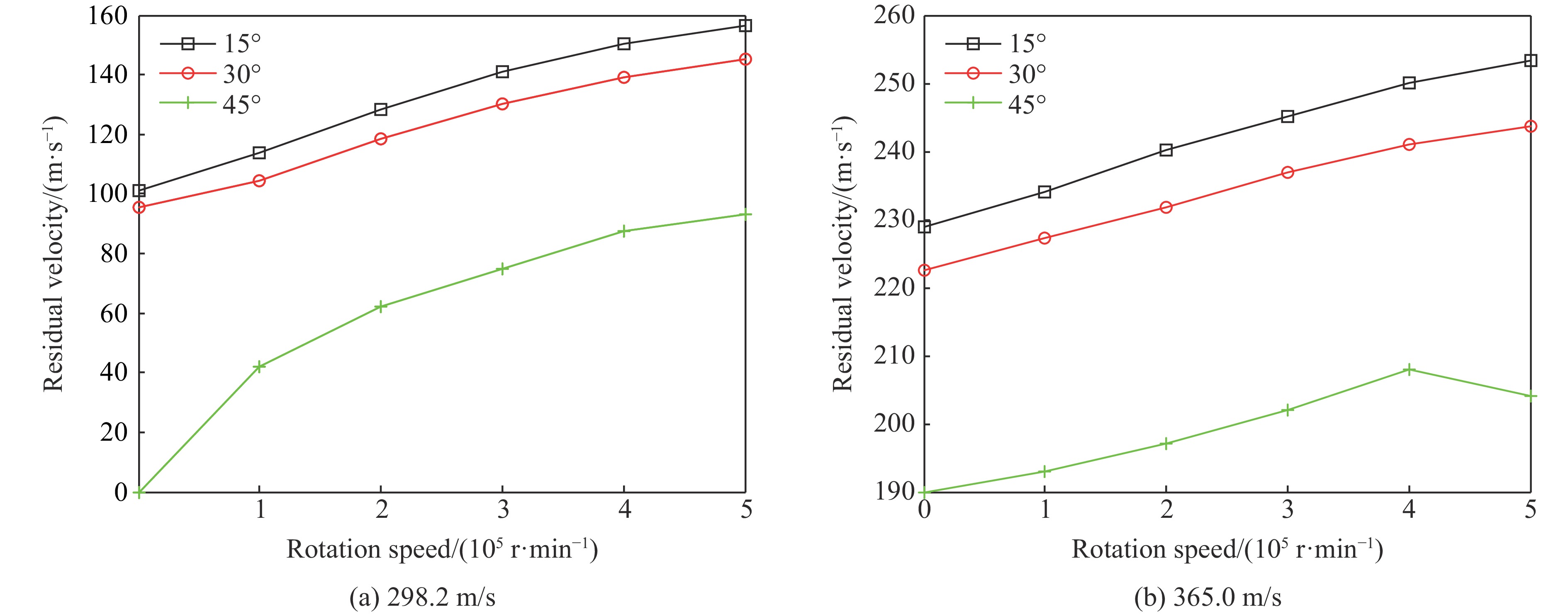
  • 针对弹体正侵彻钢板，考虑弹体转速为0、1×105、2×105、3×105、4×105和5×105 r/min 6种情况，分析着靶速度为298.2和365.0 m/s时转速对弹体侵彻钢板过程的影响。图4给出了不同着靶速度下弹体剩余速度随转速的变化曲线。可见，旋转对弹体的剩余速度有较大影响。弹体的剩余速度随转速的增大而增大。着靶速度为298.2 m/s的剩余速度曲线斜率大于着靶速度为365.0 m/s的曲线斜率，说明着靶速度较小时转速对弹体的剩余速度影响较大。图5和图6分别给出了着靶速度为298.2 m/s和365.0 m/s时不同转速下弹体侵彻钢板的变形图。可见，对于正侵彻，由于弹体受力较均衡、受到的偏转力矩很小，因此在不同旋转速度下弹道都没有发生明显的偏转。

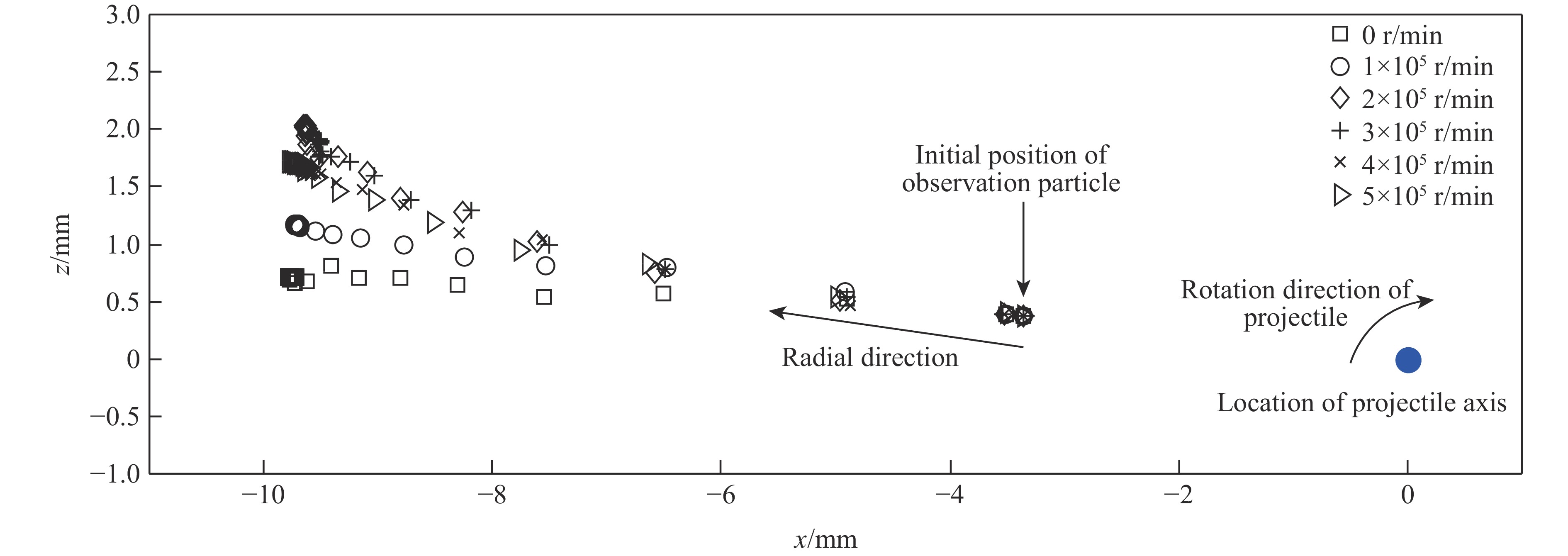
    图7为靶板中1个观察粒子在xz平面内的运动轨迹。该粒子在靶板上表面，距弹体轴线约3.4 mm。可见，粒子在弹体对靶板的挤压作用下沿径向运动。当弹体头部全部侵入靶板时，粒子被挤到弹体边缘（离弹体轴线约10 mm）处，粒子停止径向运动，主要随弹体沿侵彻方向（y方向）运动。对比弹体旋转和不旋转的情况可见，在弹体旋转的情况下，由于弹靶间的摩擦力作用，粒子沿径向运动的同时有明显的沿弹体表面切向的运动。上述结果说明在旋转弹侵彻作用下靶板材料不仅因挤压而发生径向流动，而且受剪切作用沿弹体切向流动，这使靶板材料更容易破坏、失去承载能力，因而弹体的轴向阻力变小，剩余速度变大。

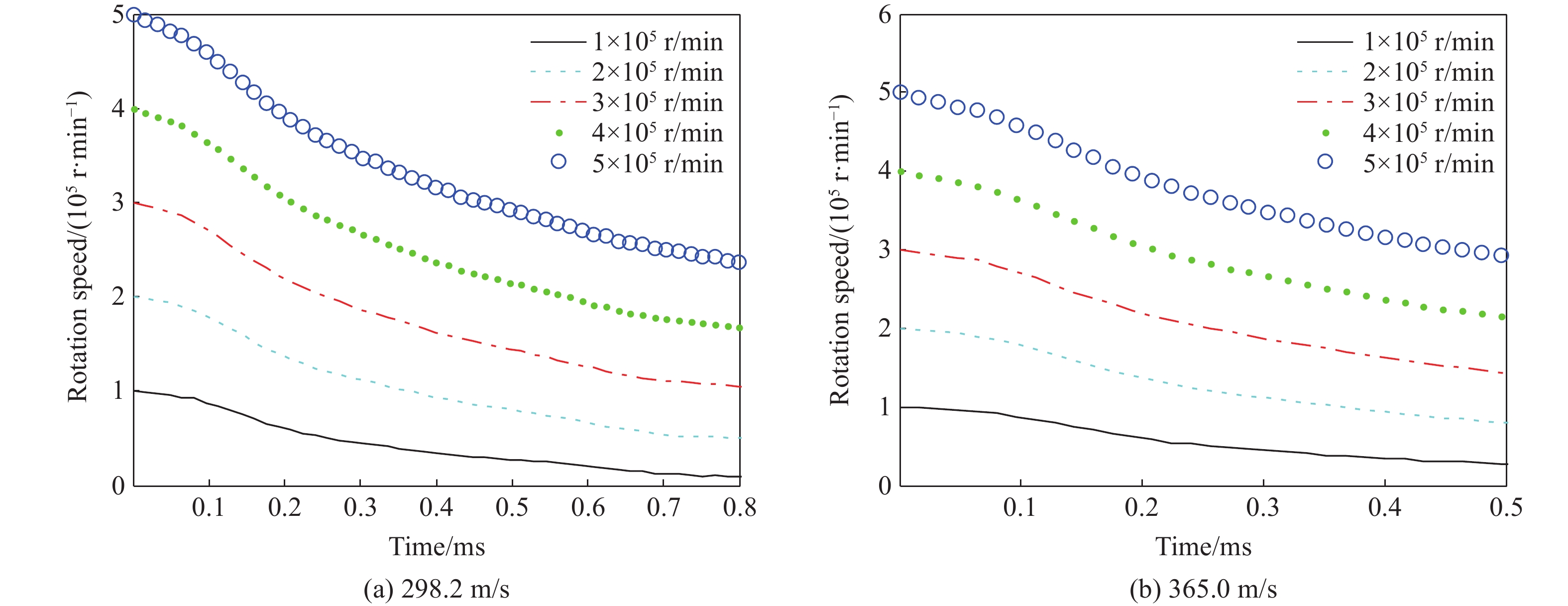
    图8给出了着靶速度为298.2和365.0 m/s时侵彻过程中弹体转速的变化曲线。弹体转速取为弹尾圆周上4个均布粒子绕弹轴线的转速的平均值。可见：弹体的初始转速越高，侵彻过程中弹体转速下降得越明显，说明越多的弹体转动动能转化为靶板的内能和动能；相同转速情况下，弹体的着靶速度较高时，侵彻过程中弹体转速的下降要小些。

    • 3.2.   旋转对斜侵彻的影响

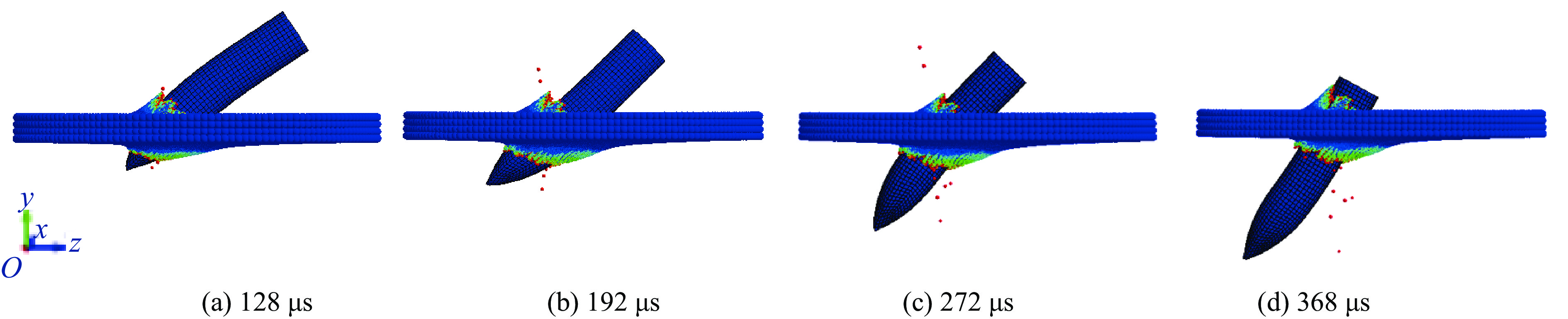
  • 针对弹体斜侵彻钢板，考虑弹体入射角为15°、30°和45° 3种情况，并仍取前述两种弹体着靶速度和6种不同转速，对各工况进行了数值模拟。图9(a)给出了着靶速度为298.2 m/s时弹体剩余速度随转速的变化：当入射角度为45°、转速为零时，弹体不能穿透钢板，剩余速度记为零；其余工况下弹体都能穿透钢板。由图9(a)可见，弹体剩余速度随转速增加而单调上升，说明在该着靶速度下弹体旋转始终使其侵彻能力加强。图9(b)给出了着靶速度为365.0 m/s时弹体剩余速度随转速的变化：所有工况下弹体都能穿透钢板；当入射角相对较小(15°和30°)时，弹体剩余速度随转速增加而单调上升；但当入射角增大到45°时，弹体剩余速度在转速为4×105 r/min时达到最大，之后随弹体转速增加反而出现下降。图10给出了入射角45°、转速5×105 r/min时侵彻过程中典型时刻的变形图。在该工况下，弹体产生了明显的垂直于轴线方向的横向弯曲，导致弹体在穿透靶板过程中与侵彻通道周边靶板材料的接触碰撞增加，受到的阻力增大，因而该工况下的剩余速度反而低于低转速情况下的剩余速度。上述结果表明弹体转速的增高并不总使其侵彻能力加强，而与着靶速度和入射角间有一定的匹配关系。

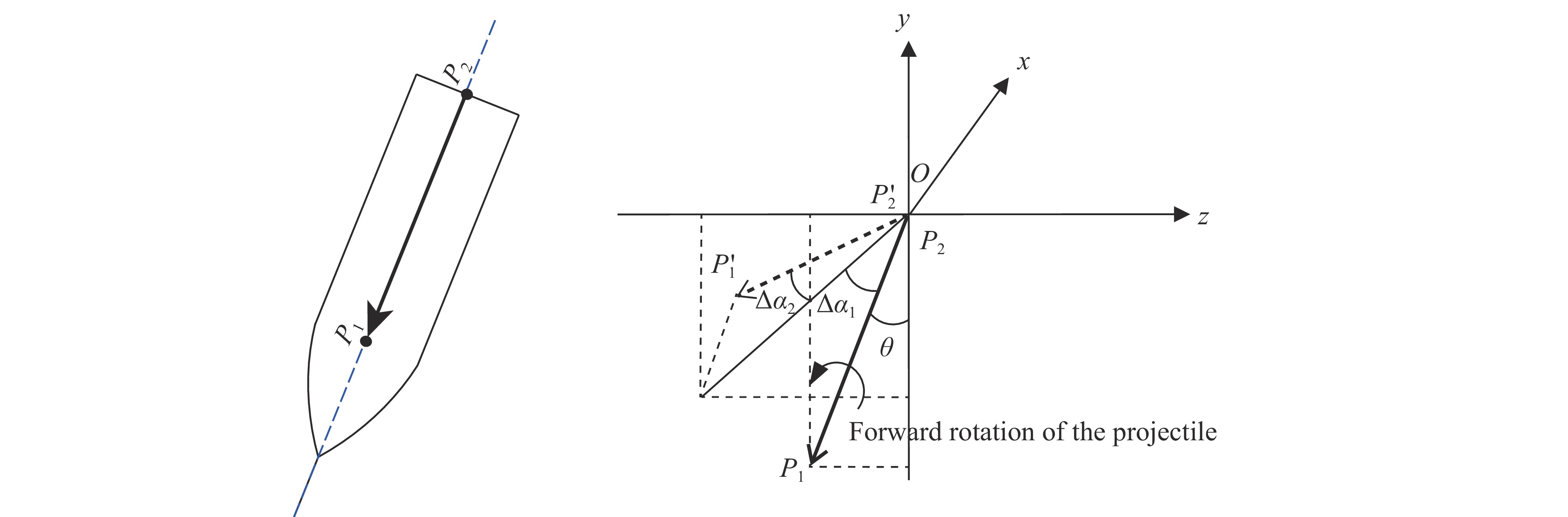
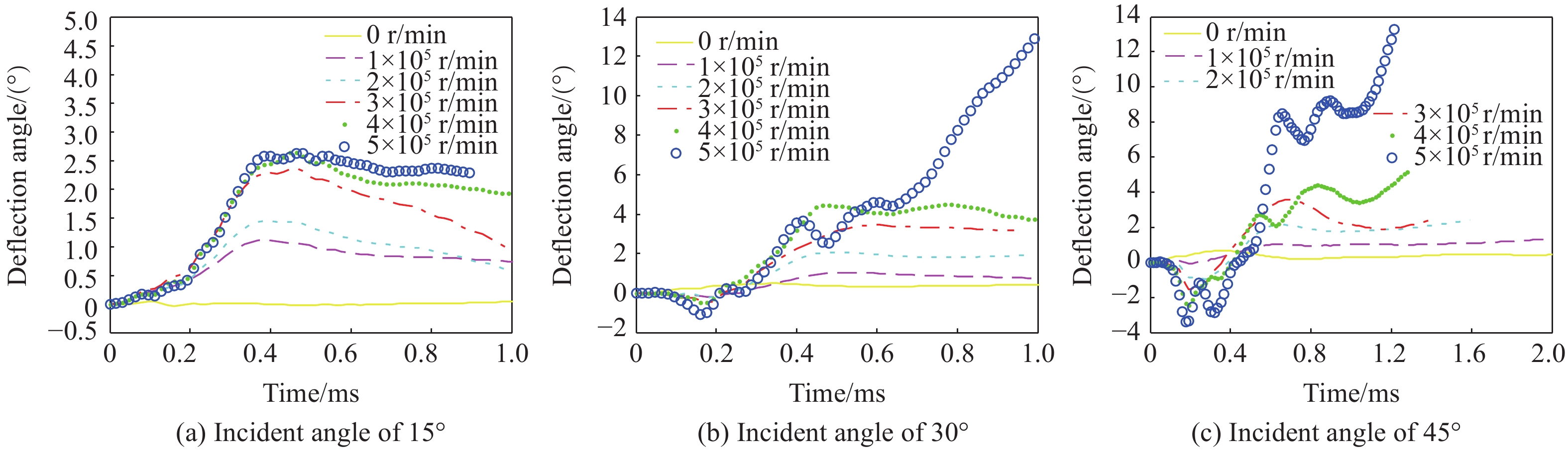
    弹体在斜侵彻过程中受力非对称，发生明显的弹道偏转。为描述侵彻过程中某时刻弹体偏转的程度，取图11所示弹身首末两端中心点连线向量${{{P}_2}{{P}_1}} $的方向变化进行度量。${{{P}_2}{{P}_1}}$（即弹体轴线）在初始时刻位于yz平面（入射面）内，其相对于y轴负向的夹角$\theta $即为弹体入射角。在侵彻过程中，${{{P}_2}{{P}_1}}$偏转到${{{P}_2'}{{ P}_1'}}$，相对于初始时刻产生图11所示的yz面内的偏转角$\Delta {\alpha _1}$和沿yz面外的偏转角$\Delta {\alpha _2}$。图示情况下$\Delta {\alpha _1}$和$\Delta {\alpha _2}$为正值，反之为负。为叙述方便，同时定义图11所示的弹体转向为正，反之为负。

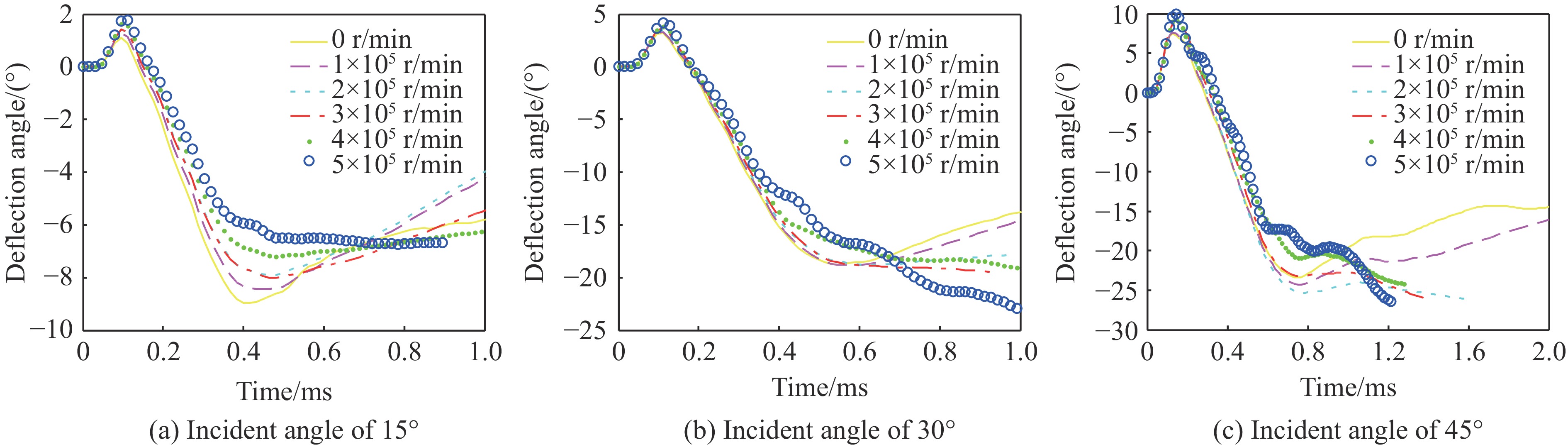
    图12给出了着靶速度为298.2 m/s时弹体偏转角$\Delta {\alpha _1}$的变化曲线。可见，在yz面内的弹体偏转角$\Delta {\alpha _1}$都呈先增大再减小、减小到零后接着反向增大的趋势。最初偏转角增大的过程为弹体头部侵入过程，此时与弹体头部上方作用的靶板材料少，而与其下方作用的靶板材料多，受力不平衡，受到偏转力矩，因而发生正向偏转。当弹体尖端开始穿出靶板背面时，与弹体头部上方作用的靶板材料多，与其下方作用的靶板材料少，所受偏转力矩方向与侵入时恰好相反，因而弹体沿相反方向转动，偏转角$\Delta {\alpha _1}$反向增大。在弹体尖端穿出靶板背面到整个弹体头部穿出靶板背面的过程中，各工况下的偏转角$\Delta {\alpha _1}$都近似线性地增大。在弹体头部全部穿出靶板背面后，弹身与靶板中形成的侵彻通道周边的材料发生摩擦和碰撞作用，各工况下偏转角$\Delta {\alpha _1} $的变化出现很大的差异。由图12(a)～图12(c)可见，随着入射角的增大，侵入过程中弹体在yz面内产生的偏转量也增大。在相同入射角下，随着转速的增加，弹体在yz面内正向偏转过程中的偏转量略有增大，而在反向偏转过程中（弹体头部全部穿出之前）的偏转量有减小趋势。当入射角较大（如30°和45°）、转速高（5×105 r/min）时，弹体容易出现类似图10所示的较明显的横向弯曲，因而弹体偏转角$\Delta {\alpha _1}$以及后述的偏转角$\Delta {\alpha _2}$都出现了波浪形变化。

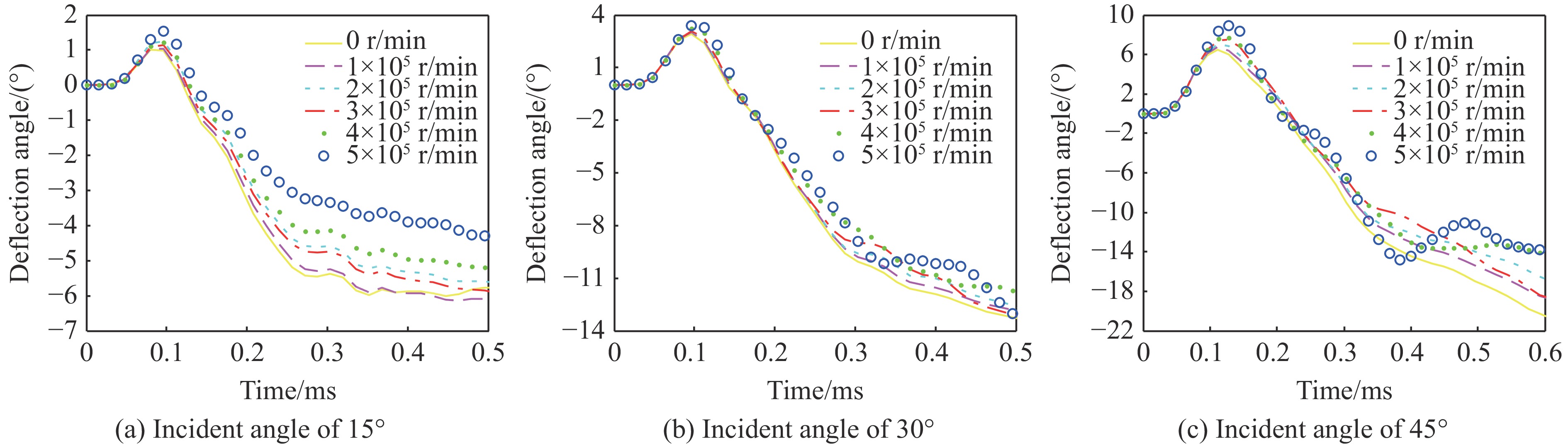
    图13给出了着靶速度为298.2 m/s时弹体偏转角$\Delta {\alpha _2}$的变化曲线。当转速为零时，弹体基本不产生沿yz面外的偏转。当弹体存在转动时，会出现一定的沿yz面外的偏转。在入射角较小（15°）时，随着转速的增加，沿yz面外的偏转量呈增大趋势。当入射角增大到30°时，沿yz面外的偏转量先随转速的增加呈增大趋势，而当转速较高时，弹体出现明显的横向弯曲，弹体沿面外的偏转量呈现出波浪形变化。入射角为45°时的情况与入射角为30°时的情况类似，但在较高转速下弹体沿面外的偏转量的波动更加剧烈。当弹体正向转动时，弹体沿yz面外的偏转角最终都为正，弹体头部相对尾部往x轴正向偏转。

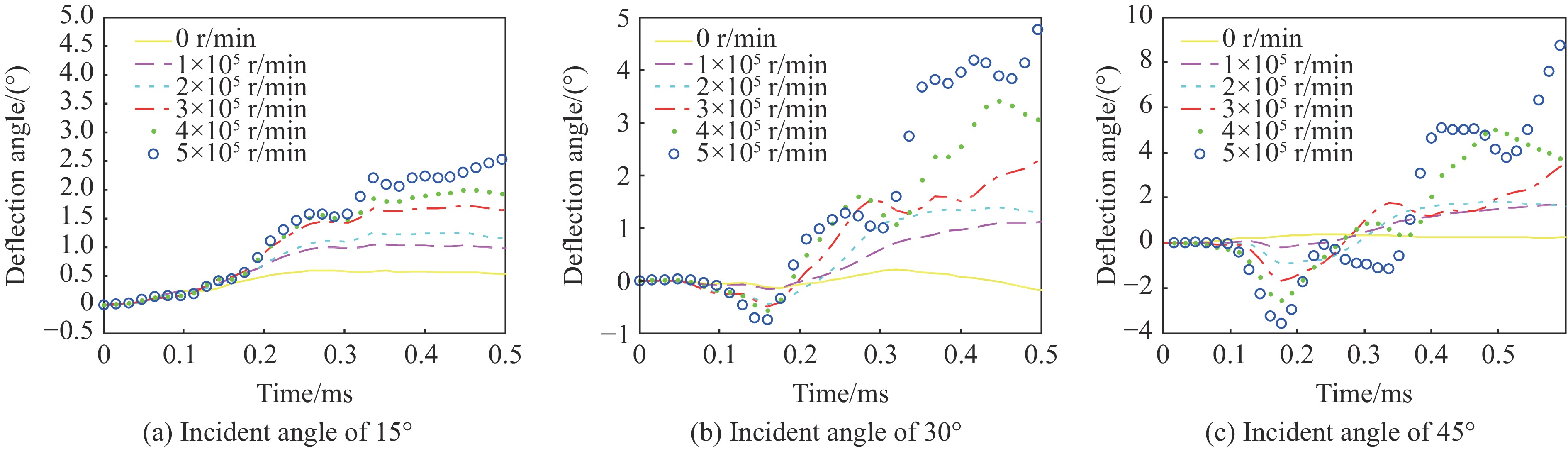
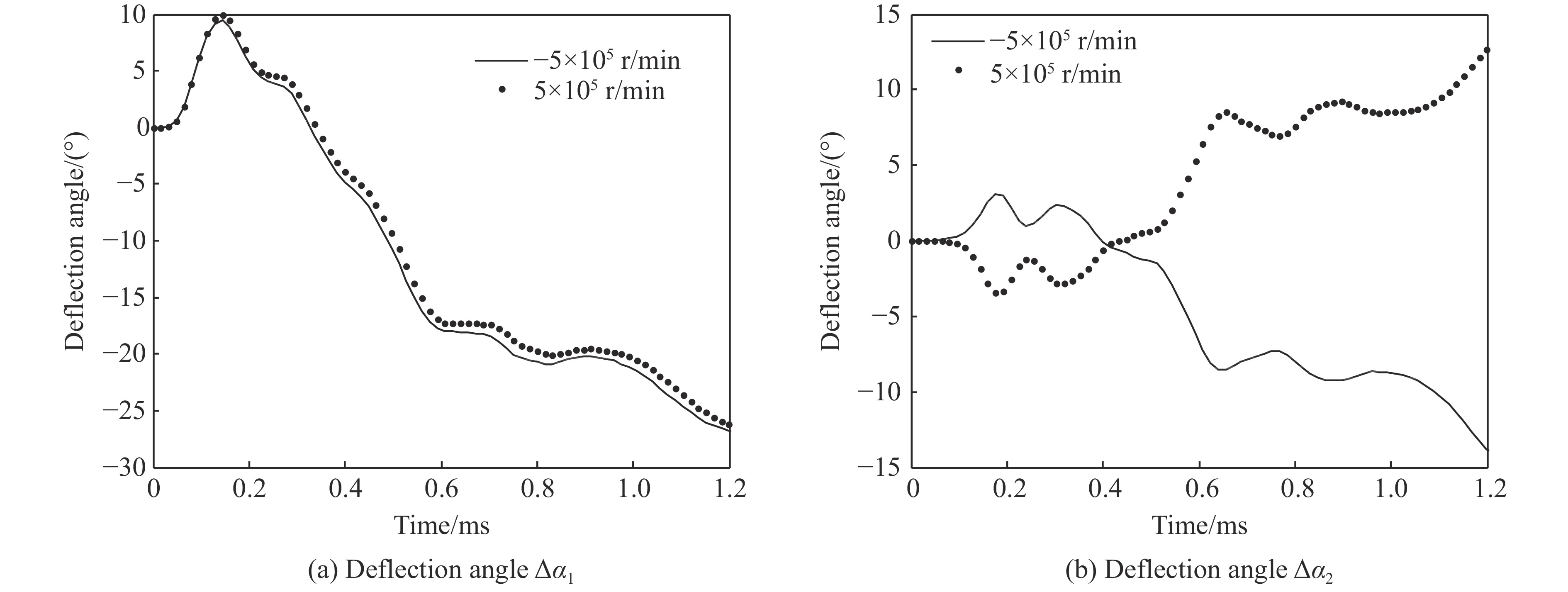
    图14和图15分别给出了着靶速度为365.0 m/s时弹体偏转角$\Delta {\alpha _1}$和$\Delta {\alpha _2}$的变化曲线。弹体的偏转角变化规律基本与着靶速度为298.2 m/s时相同。

    为了研究旋转方向对弹体沿面外偏转的影响，在相同入射角和着靶速度的情况下，设定弹体转速分别为5×105和–5×105 r/min两种工况进行计算。图16给出两种情况下相同时刻的弹体姿态。可见，弹体旋转方向反向时，弹体沿yz面外的偏转方向相应地也反向。图17对比了这两种工况下偏转角$\Delta {\alpha _1}$和$\Delta {\alpha _2}$的变化曲线。可见，在yz面内的偏转角$\Delta {\alpha _1}$的变化大致一样；沿yz面外的偏转角$\Delta {\alpha _2}$的大小相近，但方向恰好相反。这种面外偏转方向变化的主要原因是：弹体在旋入靶板和旋出靶板时两侧所受的载荷不同，因而沿yz面外出现偏转；而当弹体旋向改变时，旋入侧和旋出侧正好相反，因而面外偏转方向变得相反。

4.   结　论

  • 对卵形弹正侵彻钢板的FEM-SPH耦合模型的摩擦系数进行了优化，优化后的模型准确地预测了弹体的剩余速度。基于该模型，引入弹体旋转，开展了旋转卵形弹正侵彻和斜侵彻钢板的数值模拟，分析了旋转对弹体剩余速度和弹道偏转的影响，得到如下主要结论。

    （1）对于正侵彻，旋转对弹体的剩余速度影响较大，随着转速的增大，弹体的剩余速度增大，侵彻能力增强，但旋转不会引起明显的弹道偏转。

    （2）对于斜侵彻，旋转对弹体的剩余速度有明显的影响，但旋转并不总使弹体的剩余速度增加、侵彻能力增强。当侵彻速度较低、入射角较小时，弹体剩余速度随转速增加而单调增加；当侵彻速度较高、入射角较大时，弹体在高转速下容易出现横向弯曲，弹体剩余速度可能出现随转速增加反而减小的情况。

    （3）对于斜侵彻，旋转对弹道偏转也有较明显的影响。旋转会引起弹体沿入射面外发生偏转，偏转程度随转速增加变得更剧烈；而且，当入射角较大、转速较高时，弹体会出现横向弯曲，沿入射面外偏转量呈现波浪形变化，并且弹体沿入射面外的偏转方向取决于弹体的转向。

参考文献 (13)

目录

/

返回文章
返回