基于一维应力波理论，试样的应力$\sigma \left( t \right)$、应变$\varepsilon \left( t \right)$和应变率$\dot \varepsilon\left( t \right)$可描述为

式中：A₀、C₀和E₀分别为压杆横截面面积、体积声速和弹性模量；A_s、L_s分别为试样横截面面积和长度，$ {\varepsilon _{\rm{i}}}$、$ {\varepsilon _{\rm{r}}}$、$ {\varepsilon _{\rm{t}}}$分别为入射、反射和透射应变。

动态压缩实验样品采用热压烧结成型的AD95陶瓷，密度$ \rho $=3869 kg/m³。由于陶瓷强度高、破坏应变小，设计试样时需兼顾端面应力集中和屈曲破坏的影响。Wang等^[10]提出陶瓷的高应变率加载需满足长径比为2的要求。为此，本研究选用尺寸为$\varnothing$5.5 mm×11.0 mm的圆柱形试样。通过准静态加载实验，获得了材料的弹性模量E=290 GPa，通过查阅文献得到AD95陶瓷的泊松比为0.23^[11]。根据应力波理论，可计算得到材料的纵波波速为9594 m/s，横波波速为5661 m/s。

图1为改进的分离式霍普金森压杆（SHPB）装置示意图。压杆为高强度钢杆，直径为14.5 mm，撞击杆长度为250 mm，入射杆和透射杆的长度为1300 mm。采用添加WC垫块的方法避免试样对加载平台的破坏，考虑材料阻抗匹配，垫块尺寸取$\varnothing $10.3 mm×5 mm。为了有效收集实验后的陶瓷碎片，在样品外侧沿压杆设计了一个套筒装置。波形整形器选用塑性较好的紫铜，尺寸为$ \varnothing $6 mm×2 mm，以提高入射波加载时间，并减小波的弥散效应。

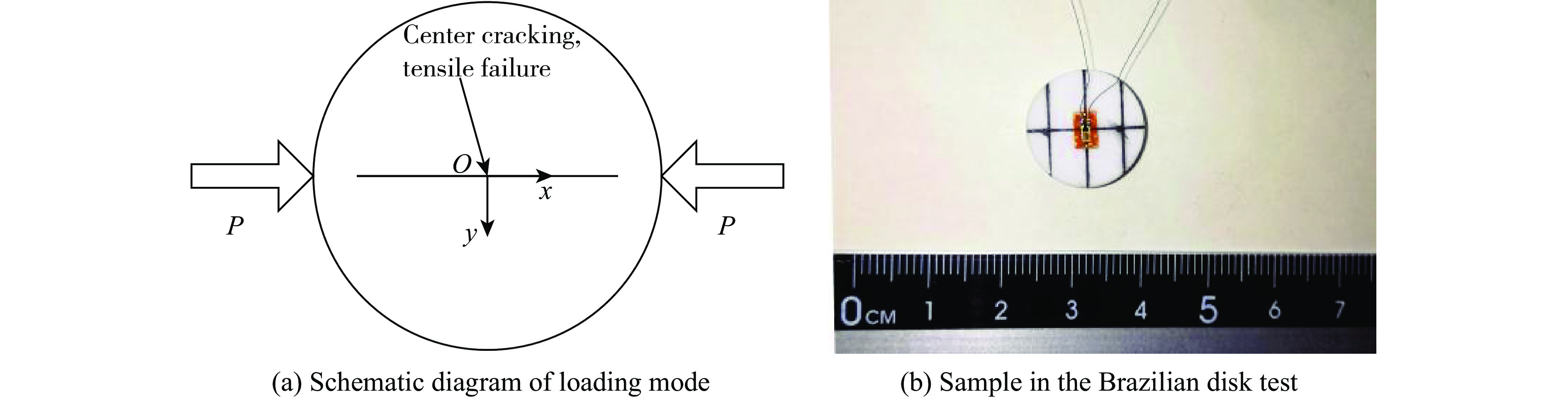
巴西圆盘实验是针对脆性材料的间接拉伸实验，在圆盘状试样的侧面沿径向施加力，则在试样内垂直加载方向产生拉伸效应。当拉应力大于材料的抗拉强度时，试样将沿径向发生劈裂破坏，如图2（a）所示。弹性力学对圆盘中心位置的环向应力${\sigma _\theta }$和径向应力${\sigma _r}$给出了解析解

式中：P为作用于圆盘两端的径向加载力，P_c为圆盘周围受到的环向压力，D、d分别为圆盘的直径和厚度，r为圆盘中心测量点与平面参考点之间的距离。

动态巴西圆盘实验的加载装置（见图2）包括压杆、垫块、波形整形器等。试样尺寸为$\varnothing$16.11 mm×6.60 mm，试样表面平行度和平面度分别为0.001 mm和0.01 mm。由于陶瓷试样的破坏应变较小，需要在圆盘试样的中心点位置粘贴小尺寸应变片，以直接测量实时应变，如图2（b）所示。为避免试样与加载杆端面摩擦效应的影响，在两者之间添加适量的二硫化钼润滑剂。

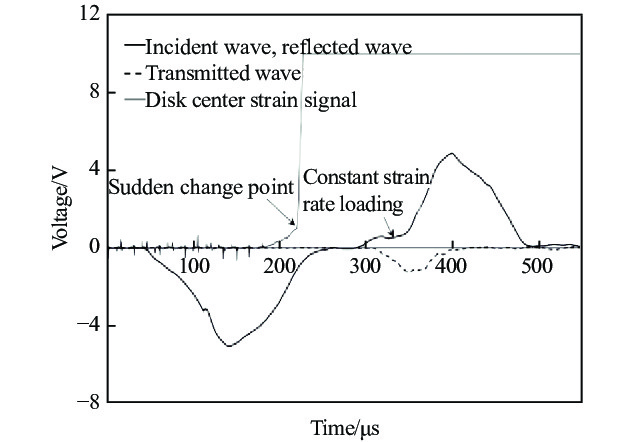
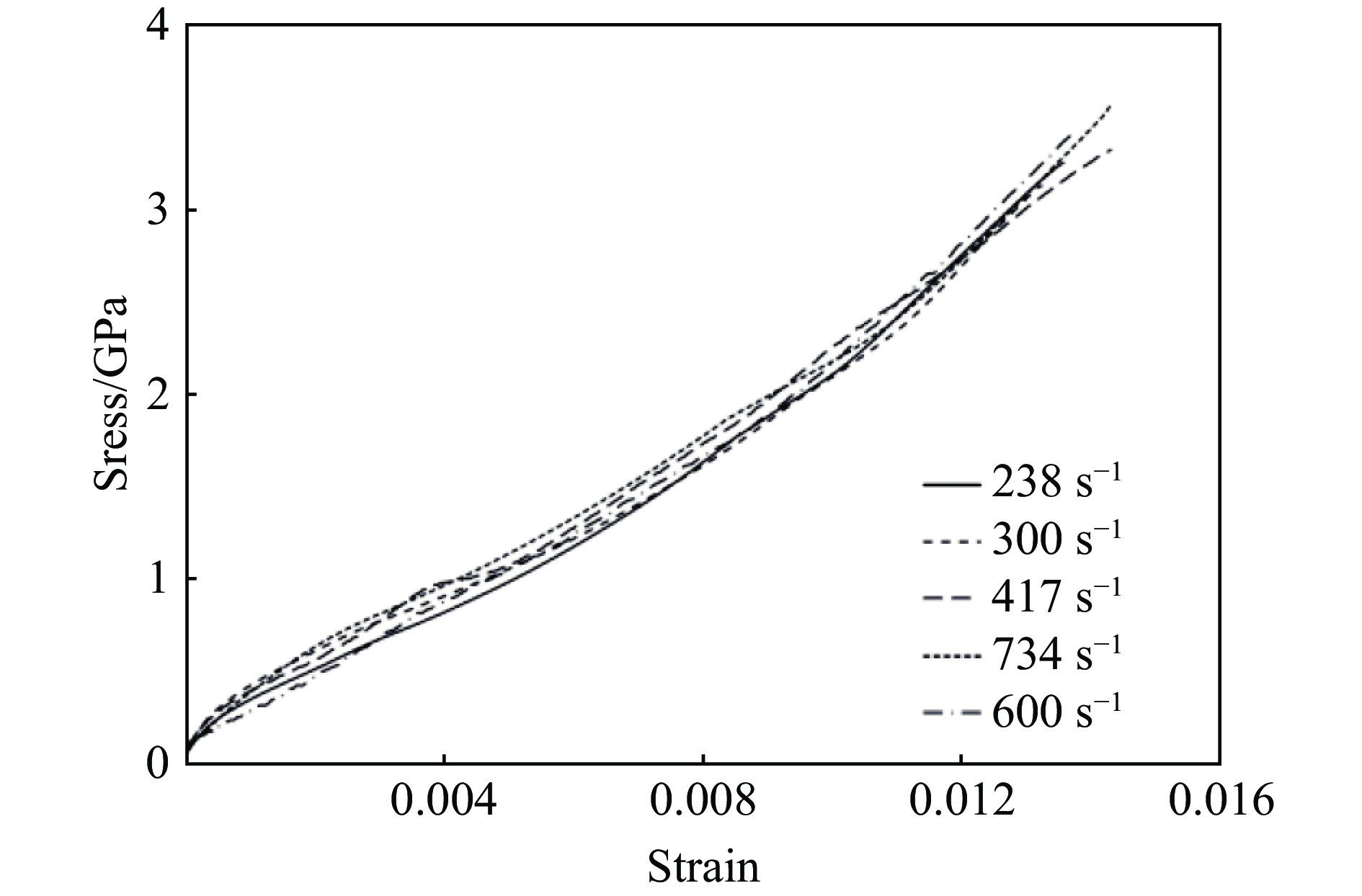
脆性陶瓷的破坏应变较小，一维应力波加载时间对试样内部应力均匀性的影响较大，短时间加载的矩形脉冲伴随波的弥散会导致陶瓷发生局部破坏。图3为动态压缩加载下的典型信号。由图3可知，入射波为理想的三角波，入射波的脉宽约为$ 200 \;{\text{μ}}{\rm s}$。由反射波信号可知，试样经历恒应变率加载平台段后，信号出现一个突跃，表明此时材料的波阻抗迅速降低，压缩波全部返回入射杆，材料表现出明显的脆性特征。

图4为不同应变率下陶瓷材料的动态应力-应变曲线。由图4可知，应力-应变曲线近似呈直线，符合Al₂O₃陶瓷典型的弹脆性特征，且陶瓷的动态压缩强度随着应变率的增加而增加，说明材料具有明显的应变率正相关性。动态加载下Al₂O₃的弹性模量约为290 GPa，受实验条件限制，动态失效应变的测量并不准确，但从中仍可发现材料弹性模量的应变率敏感性并不明显。

一维应力波加载下圆柱陶瓷的破坏分为劈开破坏和粉碎性破坏，而劈开破坏形式并不代表材料的真实压缩强度^[12]。杨震琦等^[13]对Al₂O₃陶瓷进行了一维应力波加载实验，试件尺寸为$\varnothing$10 mm×8 mm，实验收集到的陶瓷碎片如图5（a）和图5（b）所示，其破坏形式为典型的劈开破坏。研究表明，劈开破坏的原因多为试样端面的局部应力集中。本研究采用尺寸为$\varnothing$5.5 mm×11.0 mm的圆柱试样，收集到的陶瓷破坏形态为颗粒状，如图5（c）和图5（d）所示。可见，在一维应力冲击加载下，回收的颗粒尺寸大小不一，说明粉碎破坏模式下陶瓷仍存在局部应力集中现象，大颗粒陶瓷由圆柱试样外侧破坏形成，而应力均匀加载产生了小颗粒状陶瓷。

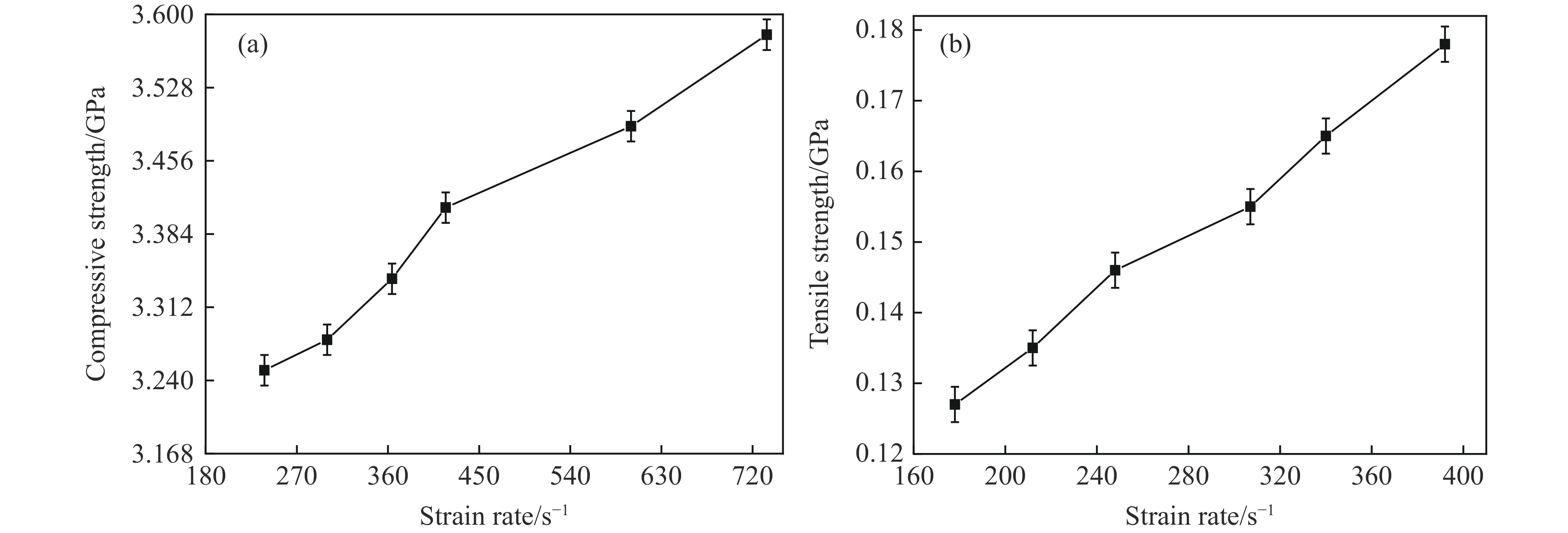
在6种不同的应变率下进行动态抗压/拉实验，每个应变率下做4次重复性试验，利用最小二乘法对平均抗拉/压数值进行统计。从图6可以看出，在一维应力波动态加载下Al₂O₃陶瓷的抗拉/压强度与应变率呈正相关性。随着应力的逐步提高，试样内部承载能力最弱处先发生裂纹的成核扩展；随着应变率的提高，由于应力波加载的作用时间很短，而裂纹成核扩展需要一定时间，因此在裂纹成核扩展过程中，应力波仍在对试样加载，试样中的应力水平提高，比该处承载能力更强的地方相继达到裂纹成核扩展条件，裂纹沿多条路径同时扩展，试样中的裂纹越来越密集，此时可看作一维应力下的轴向压缩，最终导致试样失稳破坏^[14]。因此，Al₂O₃陶瓷的强度对应变率有较强的依赖性。另外，Al₂O₃陶瓷的抗压强度约为抗拉强度的20倍，这是因为陶瓷晶体中可动位错少，而位错运动又很困难，故一旦达到屈服强度，陶瓷晶体就断裂了，在拉伸时当裂纹达到临界尺寸就失稳扩展而断裂，而压缩时裂纹或者闭合或者呈稳态缓慢扩展，并转向平行于压缩轴^[15]。

如图7所示，收集的动态巴西圆盘试样主要为两个半圆，主裂纹沿加载方向，且满足巴西圆盘实验的中心开裂要求。破碎的圆盘主要呈“川”字型，试样与加载端的接触区域破碎严重，说明两者的点接触使得试样存在局部应力集中；然而圆盘中心区域裂纹基本呈直线状，说明满足应力均匀性，且试样在此处的受力主要是沿径向的拉伸作用。

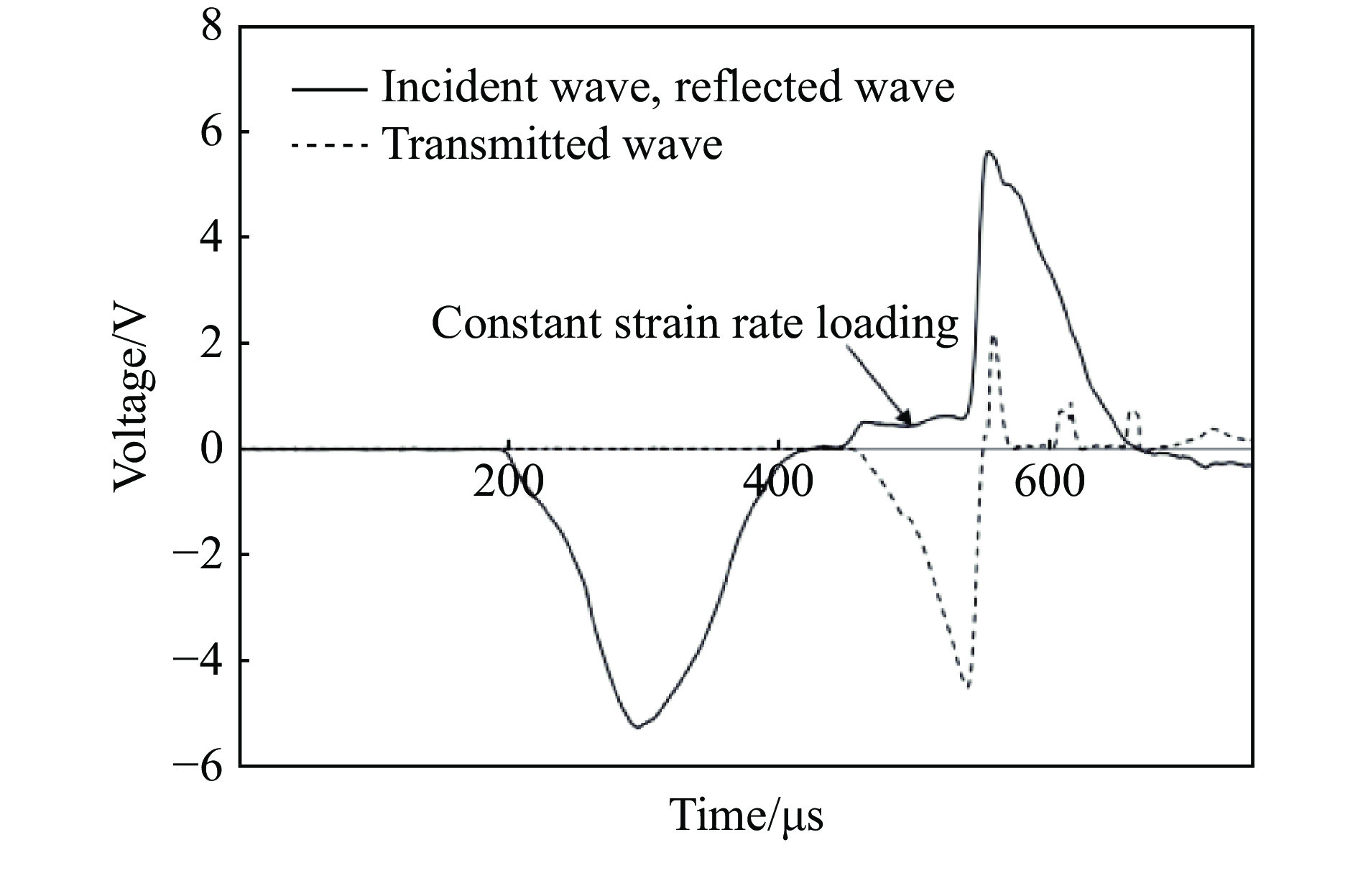
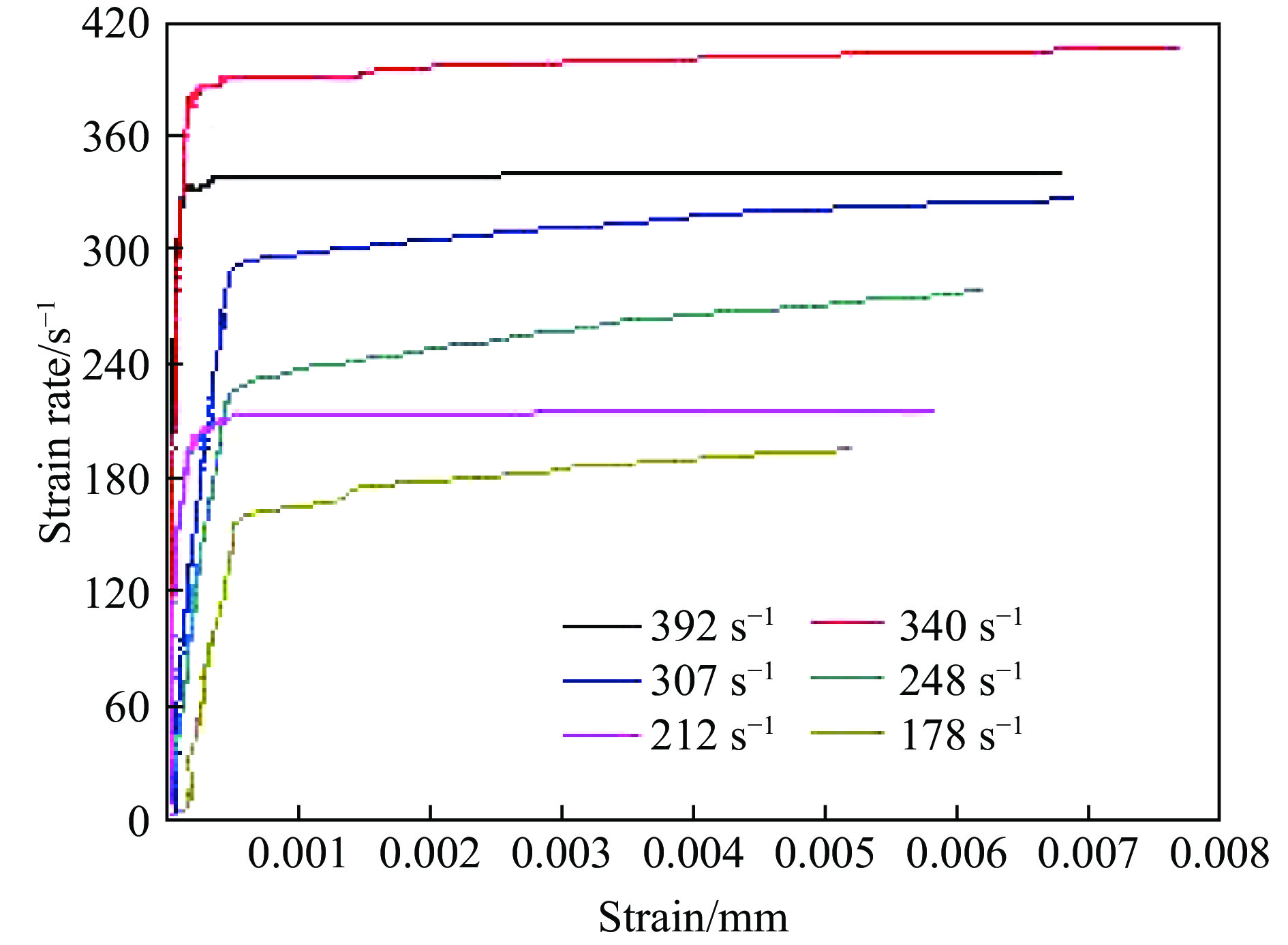
图8给出了动态巴西圆盘实验典型信号。通过紫铜整形后，入射波仍为典型的三角波，并且坡度更加缓和；$ 310{\text{～}}350 \;{\text{μ}}{\rm s}$之间为信号平台段，实现了对试样的恒应变率加载；随后，信号出现突跃，表明此时材料的波阻抗迅速降低，压缩波全部返回入射杆；圆盘试样中心位置粘贴的应变片测量的信号存在一个突跃点，材料在此时瞬间破坏，说明材料在动态拉伸状态下也表现出明显的脆性特征。

图9显示了Al₂O₃陶瓷在不同恒应变率动态加载下的应变率-应变曲线。通过分析可以看出：Al₂O₃陶瓷在破坏前的变形主要是弹性变形，在弹性范围内就会发生脆性断裂破坏；在斜波加载过程中，应变率的大小与斜加载波的坡度成正比，坡度越大，应变率越大，陶瓷作为脆性材料的破坏应变很小，且应变随着应变率的增大而增大，陶瓷的抗拉强度与应变率也呈正相关。

Grady等^[16]从破坏机理上对碎裂现象进行了理论分析，基于能量守恒提出了关于碎片尺度的计算公式

式中：s为碎片尺寸，G_c为断裂能，$ \rho $为材料密度。

Glenn等^[17]对能量守恒方程进行了修正，在能量守恒方程中加入了一个应变能项，并假设破碎后储存的应变能和局部动能耗散为断裂能，有

式中：$ \phi = {\left( {{\rm{sin}}\, h} \right)^{ - 1}} {\beta {{\left( {\dfrac{3}{\alpha }} \right)}^{3/2}}} $ ，$\alpha = \dfrac{{3\sigma _{\rm c}^2}}{{\rho E\varepsilon }}$ ，$\beta = \dfrac{3}{2}\dfrac{{{G_{\rm c}}}}{{\rho {{\dot \varepsilon }^2}}}$，E为弹性模量，$ {\sigma _{\rm{c}}}$为抗压强度，h为陶瓷试样高度。

(6)式和(7)式直接源于能量守恒关系。Zhou^[18]考虑到材料的动态碎裂是一个涉及裂纹成核、扩展以及相互作用等动态机制的复杂过程，建立了脆性材料破碎的动力学模型（DID），得到

式中：c为弹性波速，$c = \sqrt {E/\rho } $；t_f为断裂能。扩展过程中，裂纹对邻近介质产生卸载。被卸载区域的单向长度为ct_f，称为动态孤立裂纹扩展过程的影响尺度^[19]。

对(6)式、(7)式和(8)式进行无量纲化处理，可简化为

式中：${\varepsilon _0} = \dfrac{{c\sigma _{\rm t}^3}}{{{E^2}{G_{\rm c}}}}$，${s_0} = \dfrac{{E{G_{\rm c}}}}{{\sigma _{\rm c}^2}}$，$\dot \varepsilon = \dfrac{{c{\sigma _{\rm c}}}}{{Eh}}$，$\overline {\dot \varepsilon } = \dfrac{{\dot \varepsilon }}{{{{\dot \varepsilon }_0}}}$，$ {\sigma _{\rm{t}}}$为抗压强度。

对一维应力波加载下Al₂O₃陶瓷压缩试样进行软回收，采用初步筛分法和超声波振动仪分离颗粒，然后采用JX-2000显微图像分析仪对陶瓷颗粒图像进行二值化处理，得到颗粒粒径分布特征，最后对不同尺寸颗粒进行整理，获得颗粒陶瓷的个数累积。

试样破碎后产生碎片的大小及形状是试样加载过程中裂纹演化及能量释放等微观过程的真实反映。图10为回收的陶瓷颗粒分类，可见Al₂O₃陶瓷试样在一维应力波作用下的破碎颗粒尺寸差异较大。根据颗粒形状判断，部分大尺寸陶瓷颗粒主要为试样的边缘或者表面损伤后形成的碎片，这部分试样受应力集中作用明显。将试验中获得的陶瓷颗粒尺寸进行分类：极小尺寸颗粒（小于$ 300 \;{\text{μ}}{\rm m}$）、小尺寸颗粒（$ 300 {\text{～}}500 \;{\text{μ}}{\rm m}$）、中等尺寸颗粒（$ 500{\text{～}}1000 \;{\text{μ}}{\rm m}$）、大尺寸颗粒（$ 1000{\text{～}}1500 \;{\text{μ}}{\rm m}$）和超大尺寸颗粒（大于$ 1500 \;{\text{μ}}{\rm m}$）。

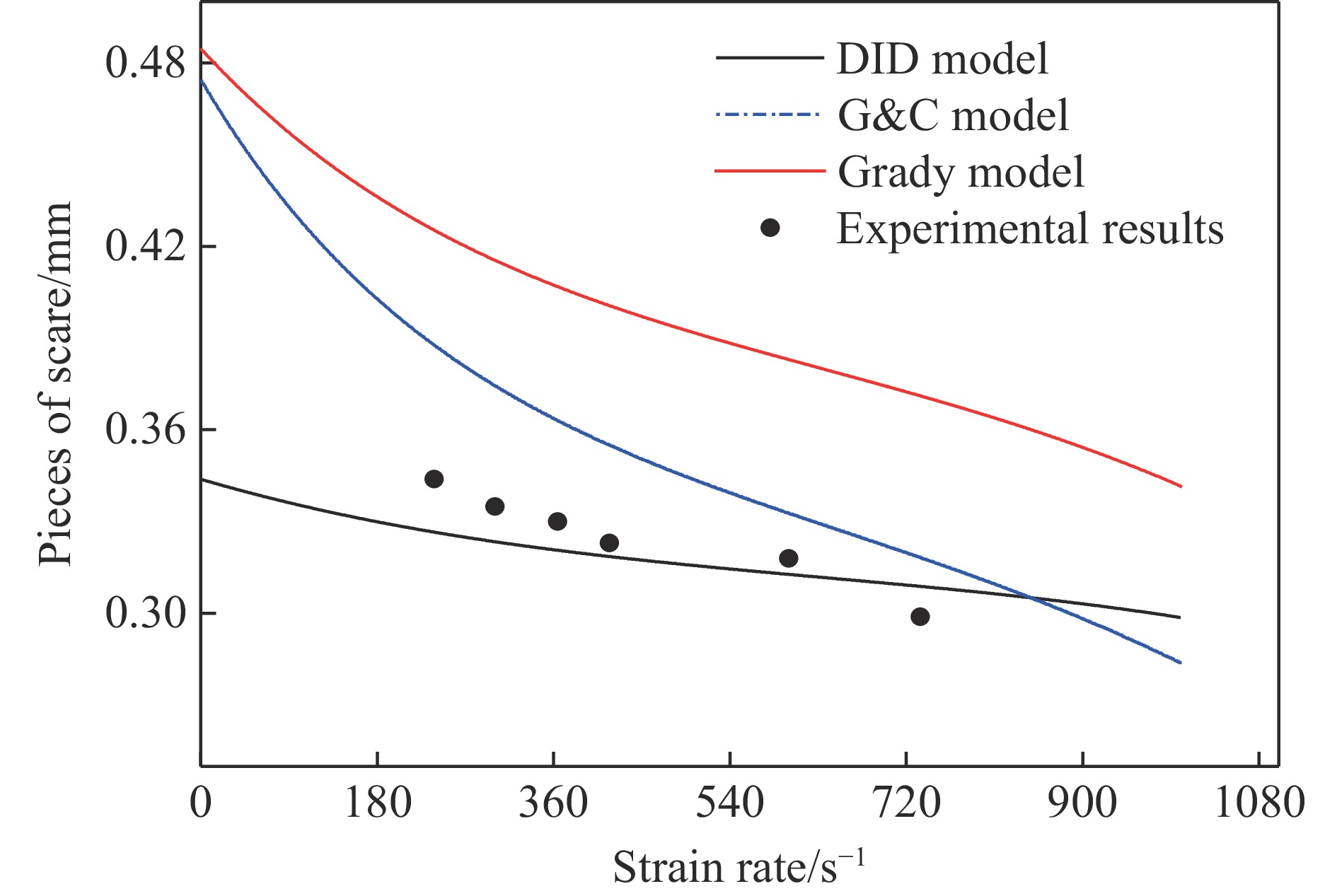
将分类后的颗粒粒径进行统计分析，计算颗粒体积当量的等效直径，其中$ 300 \;{\text{μ}}{\rm m}$以上较大尺寸颗粒采用BC-1600 电子显微镜统计，$ 300 \;{\text{μ}}{\rm m}$以下的颗粒使用JX-2000图像显微仪分析，分析和统计结果如表1所示。由表1可知：随着应变率的增加，尺寸小于$ 300 \;{\text{μ}}{\rm m}$和$ 500 {\text{～}} 1000 \;{\text{μ}}{\rm m}$颗粒数量逐渐增大，300～$500 \;{\text{μ}}{\rm m}$以及大于$ 1000 \;{\text{μ}}{\rm m}$的颗粒数量逐渐减小，颗粒总数增大，颗粒平均粒径逐渐减小，破坏所需的能量增大，符合能量守恒定律。同时，应力集中的影响随着加载应变率的增加而逐渐减弱。对于一些超大颗粒，则是由于应力集中造成的，圆角根部的应力集中系数越高，其边缘越容易发生脆性破碎。此外，还能够得出脆性陶瓷材料的颗粒破碎程度与应变率呈正相关。

将实验获得的Al₂O₃陶瓷参数（见表2和表3）带入(9)式、(10)式和(11)式中，获得了无量纲化的Grady、G&C和DID陶瓷破碎尺寸模型，如图11所示。目前，Glenn等^[17]给出的高应变率下G&C标度关系在相当大范围内被验证是准确的，但模型中碎裂过程的能量转换假设一直存在争议。近年来一些数值模拟和理论分析表明，Grady公式显著高估了碎片尺寸，而且完全忽略了微裂纹的扩张、颈缩等机制，碎裂的物理过程被过分简化。由图11可知：DID模型比较吻合脆性材料的碎片尺度特性；而Grady模型由于源于将韧性材料模型推广到脆性材料中，与本实验结果的偏差较大。同时，相比于理论破碎颗粒尺度，材料在真实破坏条件下的颗粒尺寸更大，这是由于陶瓷内部分布着大量微裂纹和微气孔，在冲击作用下微孔洞会产生应力集中现象，从而形成部分尺寸较大的颗粒。

为了分析Al₂O₃陶瓷在冲击载荷下的失效和破碎特性，对设计的试样开展了霍普金森杆动态拉伸/压缩实验，获得了动态加载下Al₂O₃陶瓷的率敏感性以及应力集中特点；对回收的颗粒陶瓷进行粒度分析，得到了陶瓷在一维应力波作用下的破碎特性，得到以下主要结论。

（1）一维应力波加载下，Al₂O₃陶瓷的动态抗拉和抗压强度均表现出随应变率的正相关性，材料的抗压强度约为抗拉强度的20倍。

（2）Al₂O₃陶瓷试样在一维应力波作用下的破碎颗粒尺寸差异较大，部分大尺寸颗粒主要来自试样边缘或表面。破碎的陶瓷颗粒总数随加载应变率的增加而增大，颗粒的平均粒径逐渐减小。应力集中的影响随加载应变率的增加而逐渐减弱，脆性陶瓷材料的颗粒破碎程度与应变率成正相关。

（3）G&C模型得到的破碎尺寸在低应变率下比实际破碎尺寸大，说明材料的裂纹成核和扩展对于陶瓷破碎有着不可忽视的影响；Grady模型证明不可将韧性材料模型推广到脆性材料中；DID模型考虑了材料的初始缺陷，计算结果与脆性材料的实际破碎尺寸比较吻合。对于材料在真实破坏条件下的颗粒破碎尺寸，应力集中这一因素不可忽视。