-
本文所述的微喷射是指冲击波从金属等材料表面反射时产生的物质喷射。据报道,这一现象最早由Walsh等[1]在实验中发现。一般情况下,喷射物的质量很小, 主要来源于(近)表面微米及亚微米尺度缺陷[2–4],因此这种物质喷射常被简称为微喷射。由于其在冲击压缩科学与技术领域中的重要性[5–6],微喷射现象自被发现以来便受到国内外研究学者的广泛关注与重视。早期的微喷射研究以实验手段为主[7–28],多年来微喷射实验技术已取得长足进展,发展了Asay膜[2, 14]、压电探针[15–16]、X射线成像[17–18]、全息成像[19–20]、高速摄影[21]、质子照相[22–23]、光子多普勒测速[24–25]以及回收[26–28]等诸多测试技术。大量实验研究[9, 11]表明,微喷射是一种典型的多机制、多影响因素的复杂动力学现象,图1和图2分别给出了喷射物形成机制示意图与实验观测结果。需要说明,金属表面喷射物质量一般在每平方厘米100 mg以内,喷射颗粒直径大多在10 μm以内,而最大喷射速度可达每秒数公里,这些现象特征为微喷射的精细测量带来极大困难。如何获得更直接、更精确的喷射数据仍然是当前实验研究领域的热点问题。
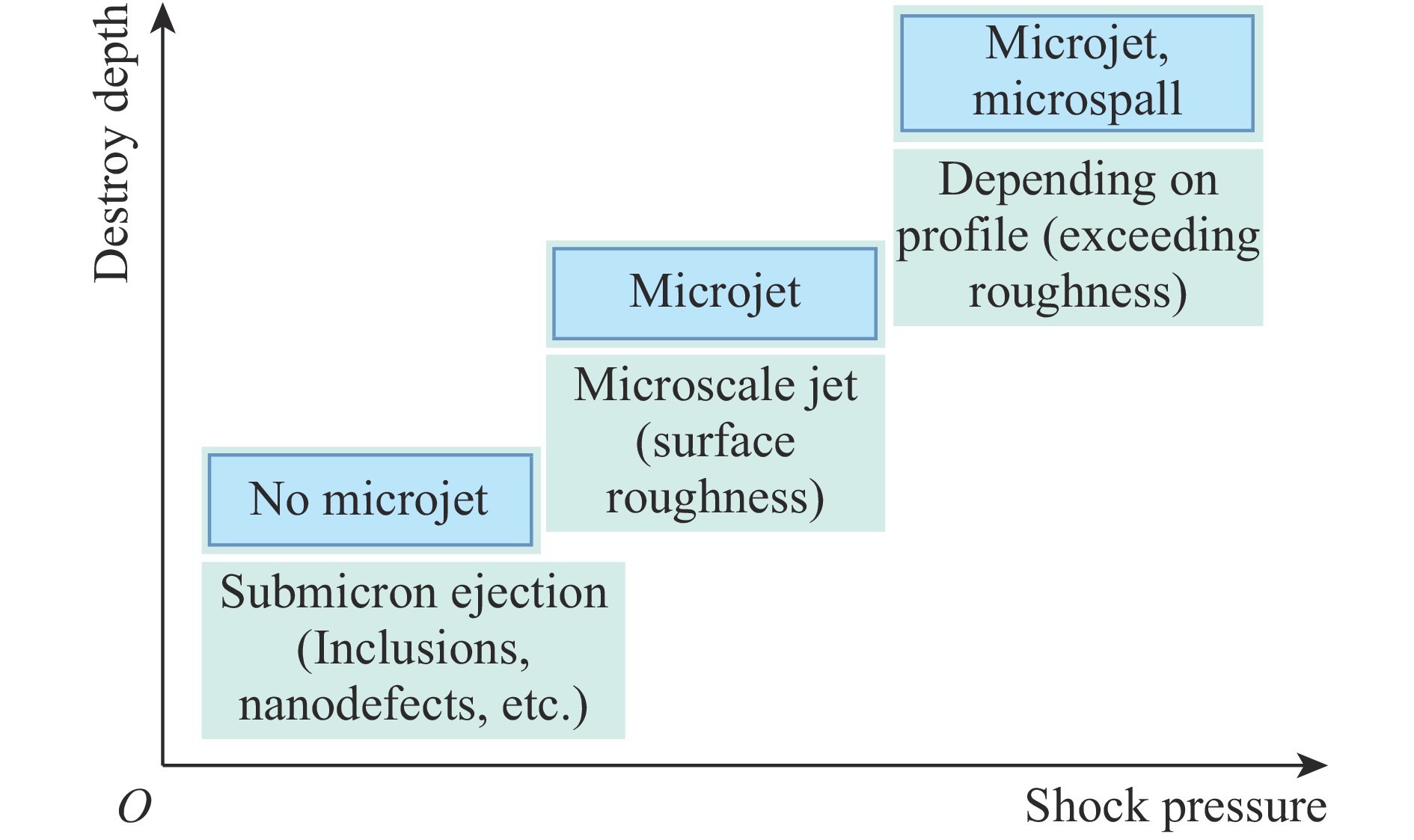
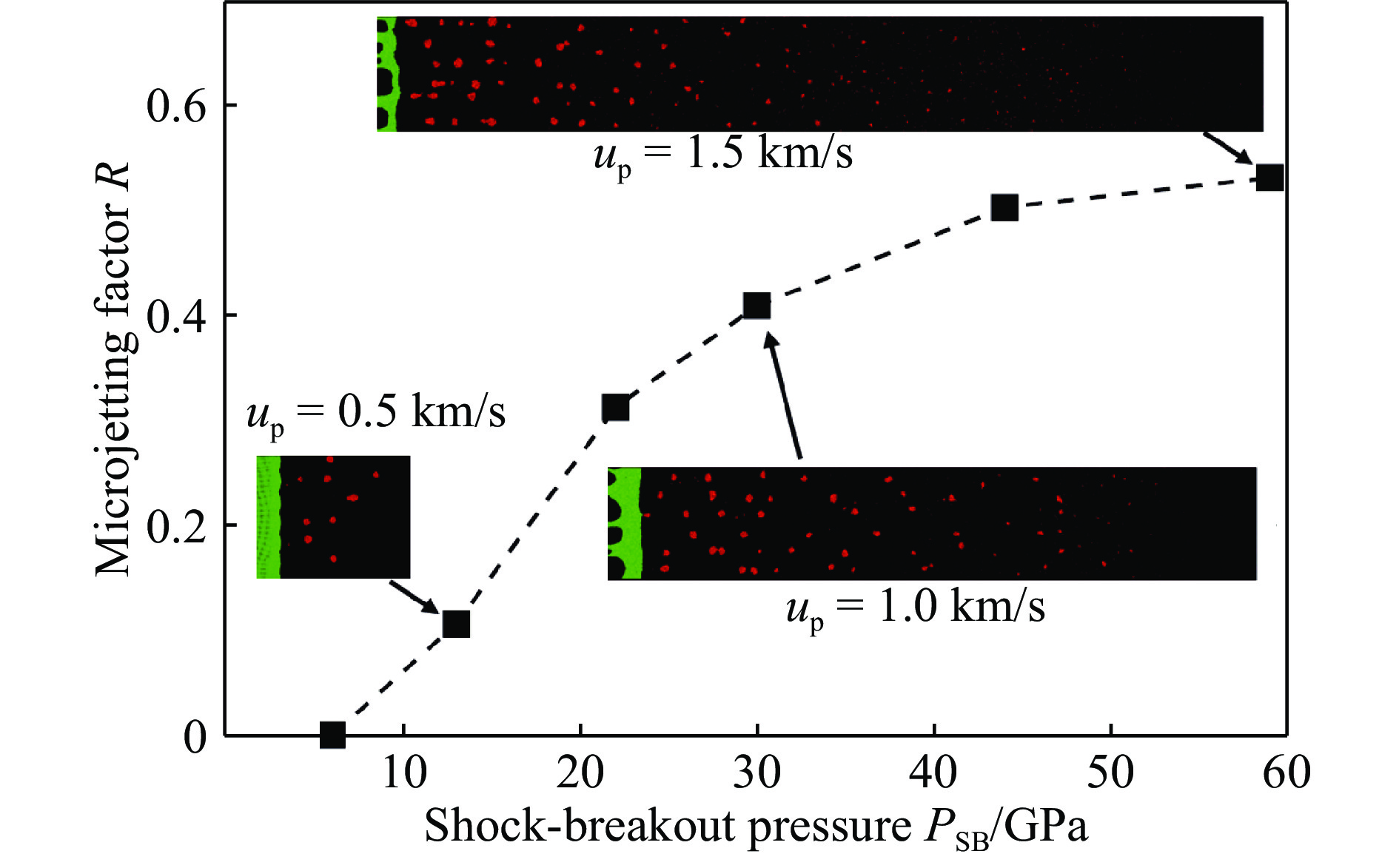
喷射物的产生不仅与表面缺陷相关,还显著地依赖于冲击压力、波形、材料强度与熔化等因素。随着冲击压力的升高,微喷射物理机制会发生转变,微喷射质量相应出现阶段性变化,如图3所示。实际中,微射流和微层裂是最主要的两种物质喷射机制。前者主要与表面缺陷相关,因聚能效应产生较高速度喷射物;后者是指材料近表面的动态拉伸破坏,主要取决于加载波形以及材料是否熔化。对于爆轰或激光等加载方式,冲击波一般为非持续的,此时微射流与微层裂都会发生。总的来说,微喷射过程涵盖了近表面区域的大变形、熔化与损伤断裂等一系列复杂物理问题。
2017年,Buttler等[29]对微喷射现象的研究历史按年代作了简要回顾,指出微喷射物理是一个年轻的研究领域,但近年来已取得巨大进步,喷射物产生的物理机制至今已完全探明。最近,王裴等[30]总结了其课题组近年来在微喷射及喷射混合方面的理论研究进展。本文分别从微观分子动力学(Molecular Dynamics, MD)和宏观连续介质力学(Continuum Mechanics, CM)层次,回顾微喷射现象国内外数值模拟研究进展及相关建模工作,归纳了当前微喷射数值模拟研究仍存在的一些难点问题。
全文HTML
-
MD是基于材料微观结构建模的确定性模拟方法,分子或原子的运动服从牛顿定律。有关MD原理与方法已有大量参考资料,这里不再赘述。随着近年来计算机性能的飞速发展,MD模拟已成为微喷射物理机制研究的一种主要技术手段。
1993年,张景琳等[31]率先开展了微喷射现象的MD研究。受当时计算条件限制,该模拟采用二维计算模型和较简单的Morse两体势,给出了冲击压力和沟槽角度因素的定性分析,得到的喷射速度与自由面速度的比值在1~3之间。虽然未能给出喷射质量的变化规律,但已显示出MD方法的独特优势。2002年,陈军等[32]结合类紧束缚杂化多体势模拟了金属铜的微喷射现象, 基于模拟结果分析了沟槽表面的波系传播以及负压区和正压区的形成, 由此解释了沟槽产生微射流的动力学过程。2005年,陈其峰等[33]采用大规模MD模拟对喷射质量进行了统计分析,见图4,其中α为喷射系数,α=NE/Ng,NE和Ng分别为喷射粒子数和沟槽缺失粒子数。结果显示,熔化温度之下纳米沟槽射流的最大喷射系数约等于1,熔化温度之上喷射系数会大幅度增加。与此同时,美国Los Alamos实验室Germann等开展了更大规模的微喷射MD模拟,但至今未见详细报道,仅在文献[34]中展示了部分微射流形成及断裂的模拟图像。
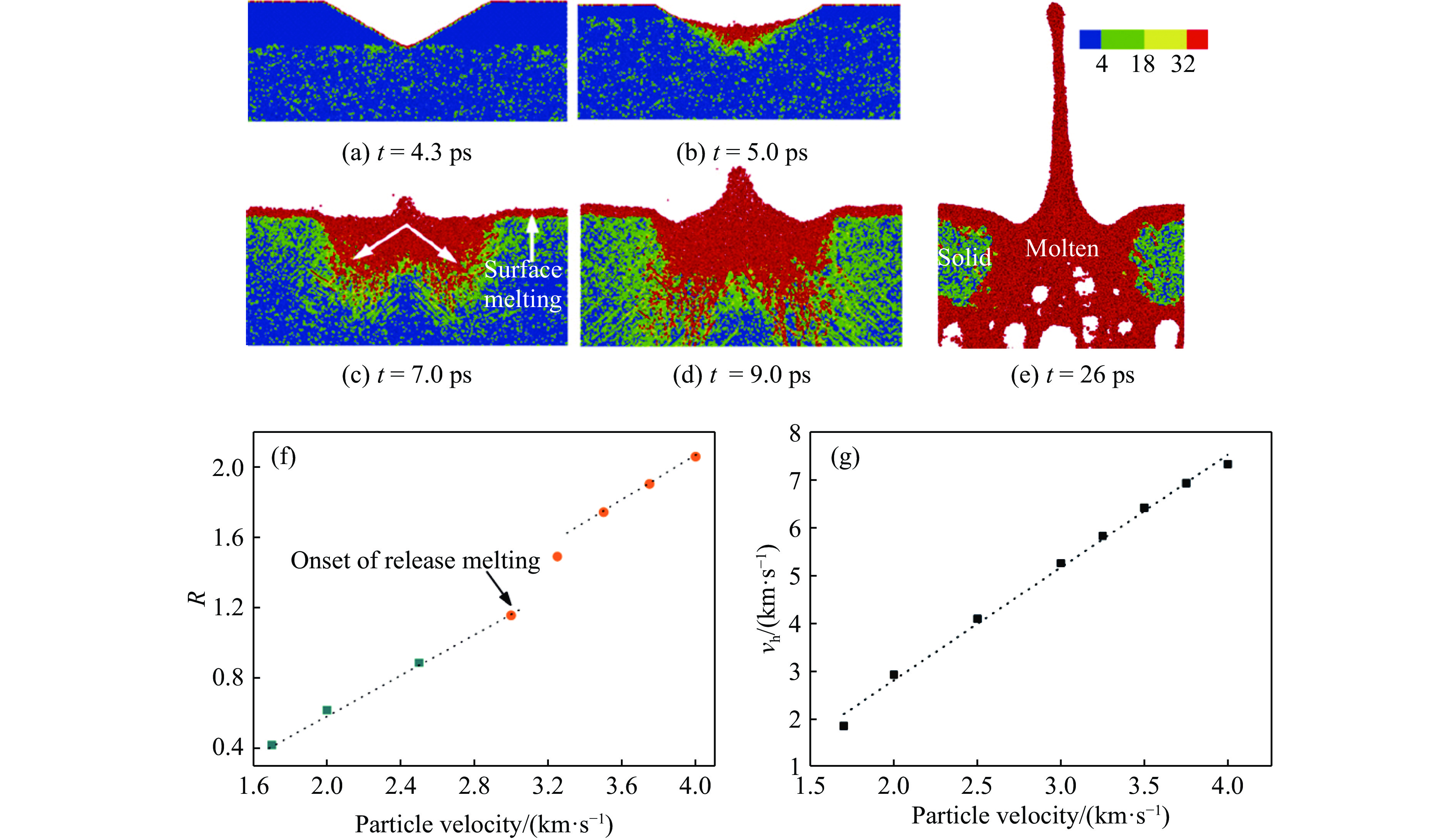
如前文所说,微喷射质量并不总是对应缺陷质量。对此问题,邵建立等[35]基于铝的势函数模型,模拟分析了不同冲击压力下的微射流形成过程,重点探讨了材料熔化的影响机制。模拟结果反映了缺陷塌缩局部熔化、卸载和冲击熔化等物理过程。例如,图5给出了典型卸载熔化(红色区域)时的射流喷射图像,图中颜色对应原子中心对称参数值。由此可解释熔化导致喷射质量显著增加的部分原因。此外,模拟结果还显示,最大喷射速度对材料是否熔化并不敏感,这与后来的实验结果[36]是一致的。其原因在于,头部喷射物源于沟槽底部区域,这些物质从早期塌缩便处于熔化状态,卸载熔化则主要影响射流根部物质的流动。
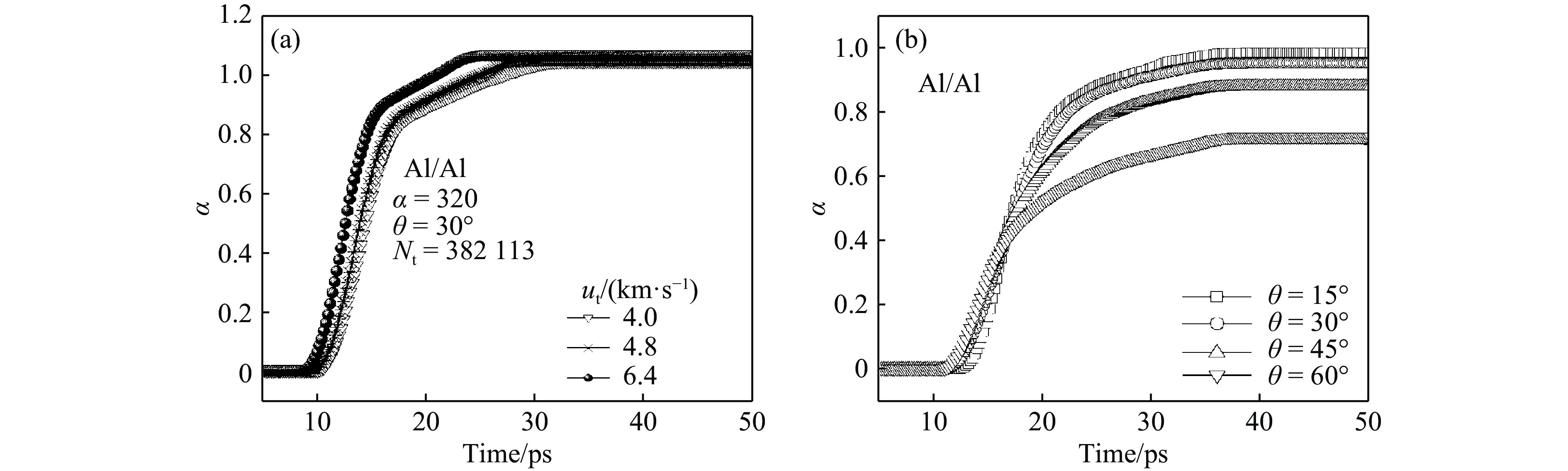
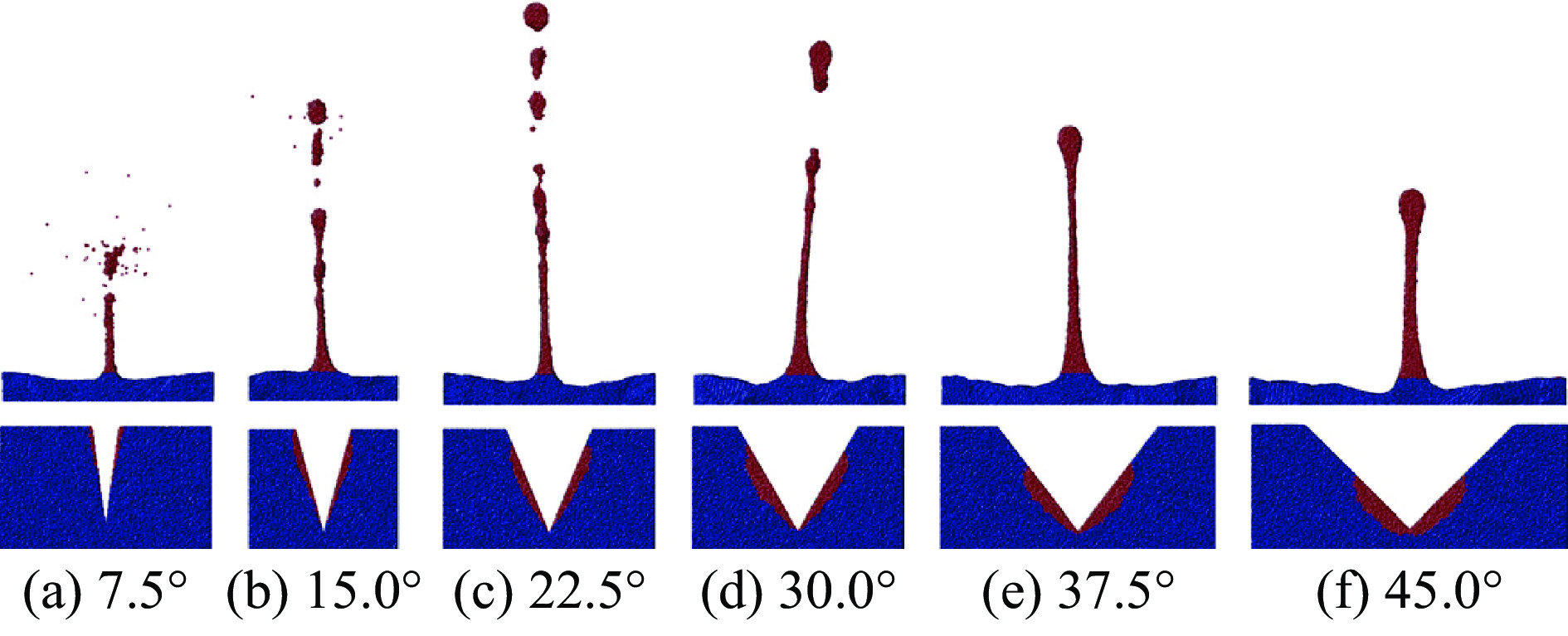
除冲击压力以外,材料表面形貌是影响微射流发展的另一重要因素。叶建军等[37]基于金属铜的MD模拟,定性比较了楔形、圆形和方形沟槽产生的射流,结果表明,楔形缺陷更容易发生微喷射,且喷射速度随着楔形角的增大而减小。2014年,李博等[38]对沟槽角度及缺陷形状进行了序列化MD模拟分析。结果显示,最大喷射速度与自由面速度之比随着半角增加呈线性减小,且不同材料和不同尺度具有相似比值,但喷射系数则在某个中间角度达到最大值。图6为2 km/s 碰撞速度下不同沟槽角度的喷射图像及其物质来源比较。此外,模拟结果还显示,晶体结构或缺陷形状的不对称性可引起射流方向的较大改变。
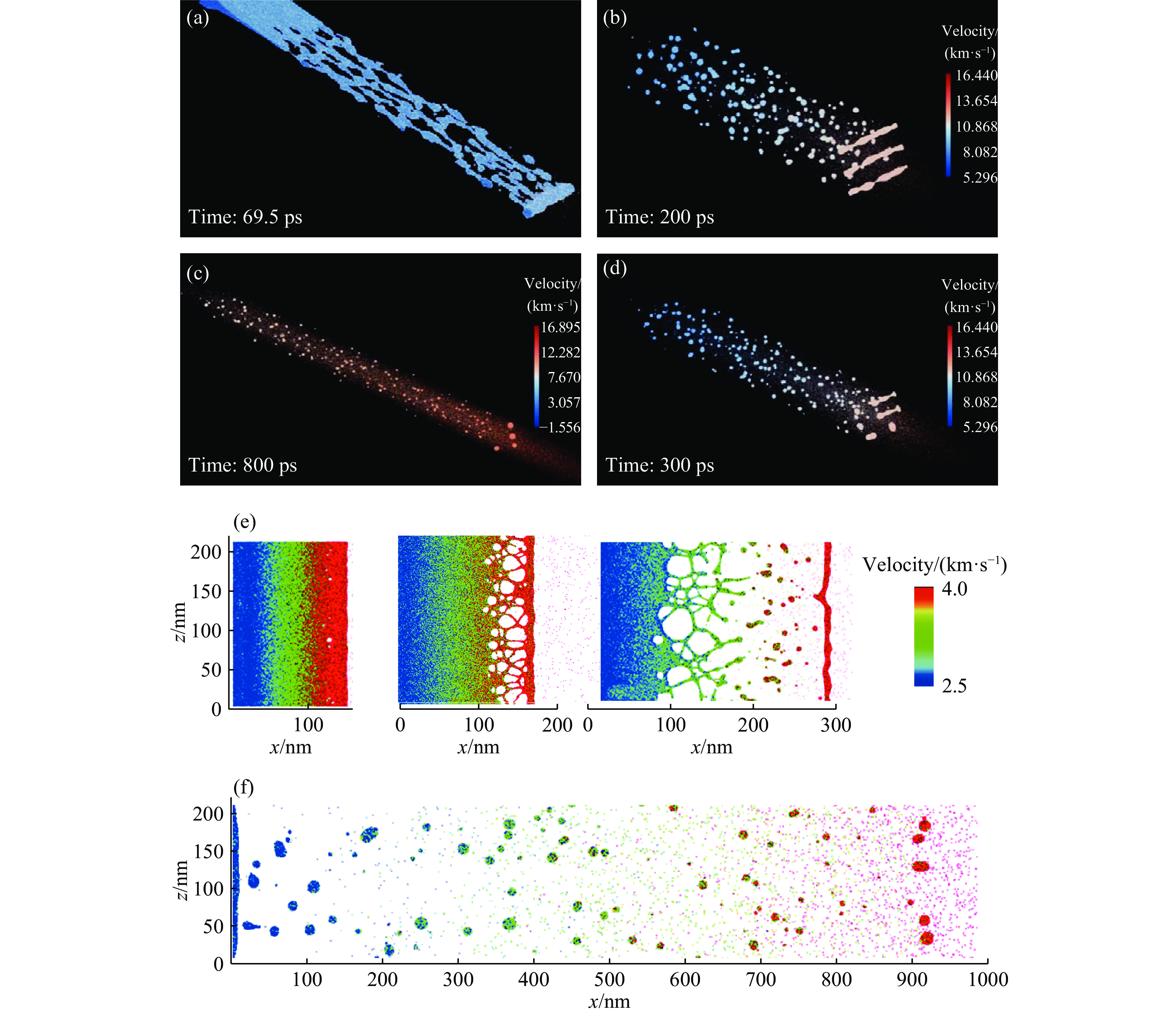
在速度梯度作用下,微射流最终将断裂成一定的颗粒分布状态。Durand等[39]基于金属铜的长时演化模拟研究了微射流断裂颗粒尺度分布,其结果显示喷射颗粒最终会保持球形,尺寸分布呈幂律关系,这与碎片化过程的大多数测量非常一致。之后,通过进一步对金属铜和锡不同表面扰动幅值下微射流破碎[40]模拟发现,小尺寸极限服从幂律分布,而大尺寸极限服从指数分布。与此同时,何安民等[41–43]开展了冲击强度与沟槽尺寸等因素的系列模拟分析,详细阐述了喷射颗粒存在的不同分布形式。结果表明,较小尺度颗粒服从包含不同特征常数的幂律分布,而较大尺度颗粒则更满足双指数分布。图7给出了金属铜微射流破碎过程的MD模拟图像,颜色表示粒子速度[39, 43]。近期,吴凤超等[44]模拟研究了气体环境下喷射颗粒的形成和演化过程,因涉及物质混合过程,此处不再更多介绍。
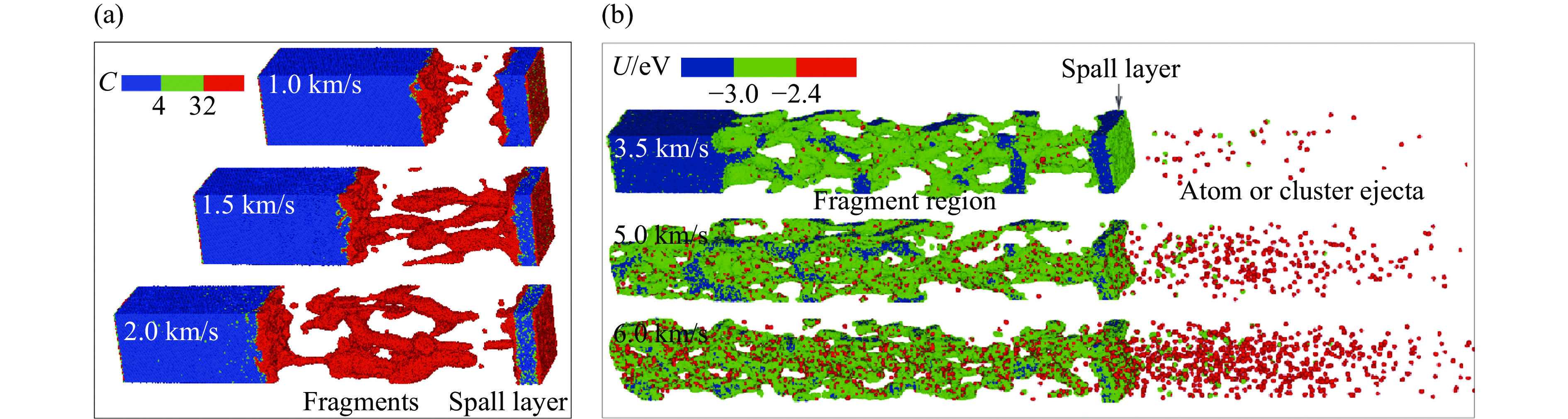
当加载波为衰减冲击波时,冲击前沿后的衰减波形不仅影响微射流机制,还会诱发微层裂机制的发生。任国武等[45]通过控制活塞推动时间模拟了衰减冲击波作用下金属铅的喷射性质。这种控制方法与薄飞片撞击靶板最终形成的衰减冲击波是等同的。模拟结果显示,卸载或冲击熔化条件下喷射体的密度分布曲线因颗粒细小而变得光滑。值得关注的是,小角度周期性表面对应的喷射系数较小(小于0.6),见图8,这与前文关于角度效应的模拟分析是一致的。与此同时,邵建立等[46]模拟了持续和衰减冲击加载下铝的喷射状态,结果显示:在较低的冲击压力下,衰减冲击导致射流质量略有增加;而在较高的冲击压力下,衰减冲击导致微射流质量明显减少。
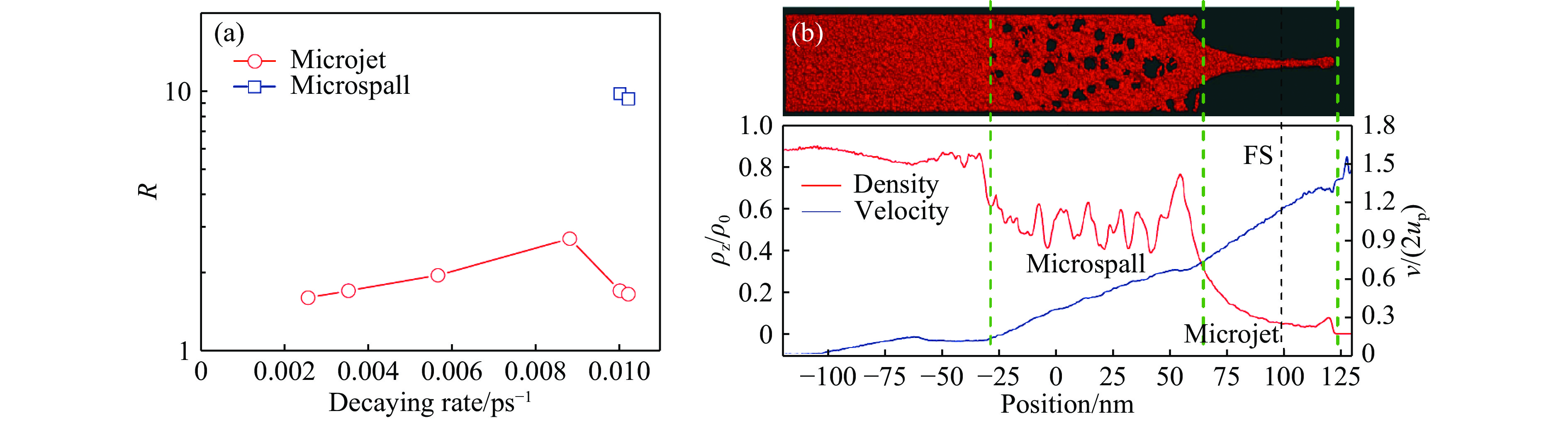
为进一步理解衰减波形对微射流的影响规律,邵建立等[47]通过活塞速度历史模拟了不同冲击波形加载情况。结果表明,随着衰减速率的增加,微射流质量呈现先增加后减小的趋势,这一变化正是由于衰减冲击下微层裂的发生,见图9。图9(b)中左侧纵坐标
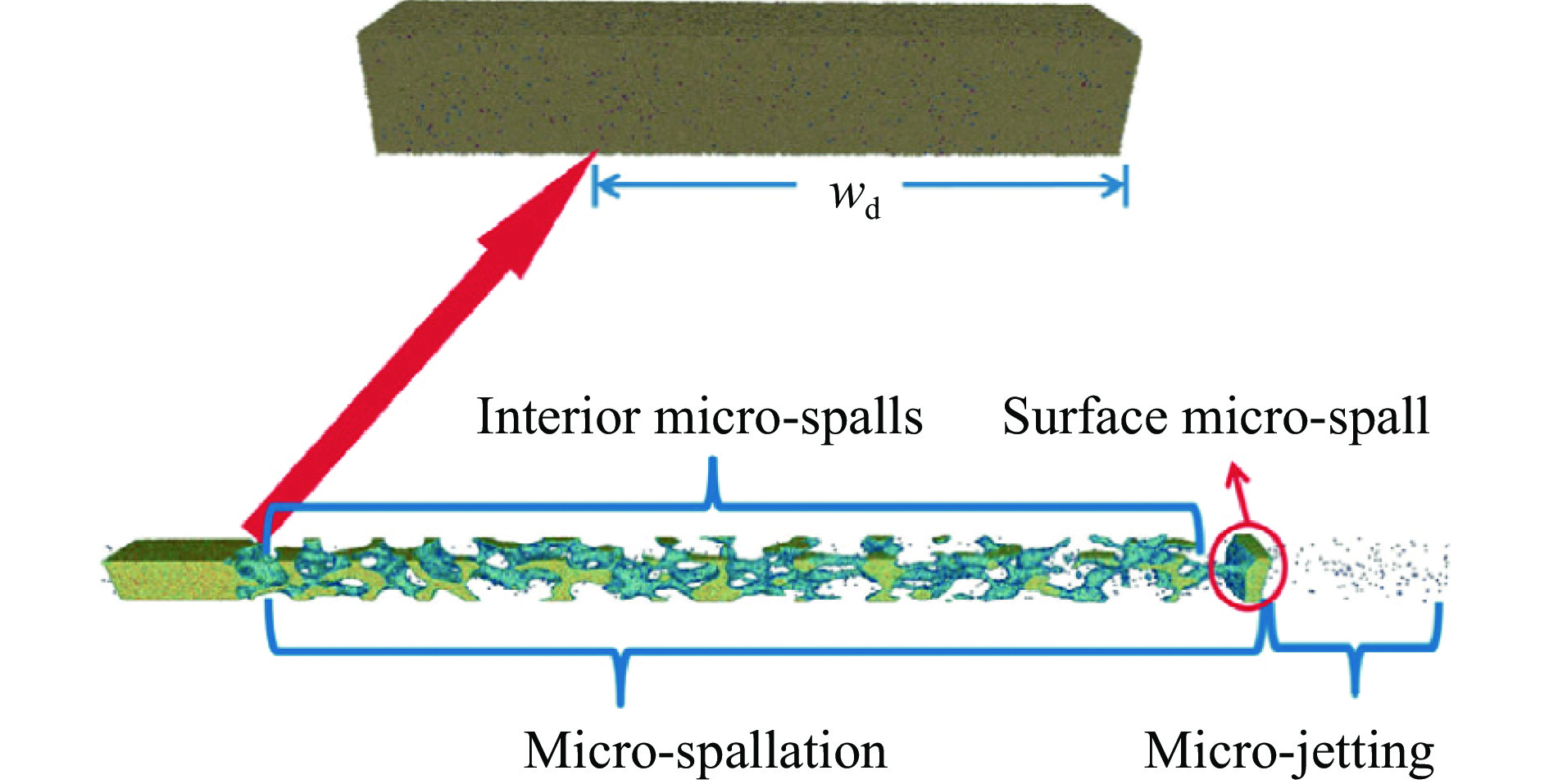
${\rho _{\rm{z}}}/{\rho _0}$ 为当前密度与初始密度之比,右侧纵坐标为粒子速度与2倍活塞速度之比。当衰减速度较低时,主要表现为对界面的回拉及形状改变,微射流因此被拉长;而当衰减速率较高时,缺陷区域获得的冲击波能量迅速减小,微射流机制明显减弱。微射流和微层裂速度在空间上呈线性分布,微射流具有更高的速度梯度。最近,伍鲍等[48]通过对低熔点金属锡在持续和非持续冲击下喷射状态模拟和对比分析,进一步论述了加载波形因素的作用规律。显然,伴随微层裂机制的出现,微喷射状态已发生本质变化。2008年,Soulard[49]便模拟了表面无缺陷金属铜的微层裂过程。结果显示,冲击熔化和卸载熔化两种状态均可得到连续的损伤演化至破碎过程,且微层裂区的拉伸强度可以忽略;但是当熔化速度足够慢时,便可观察到表面固体层裂片的形成。后来,向美珍等[50]对金属铅的微层裂过程进行了MD模拟,着重分析了经典层裂和微层裂空穴形核数量和空间分布的差异及应力演化差异,并通过不同位置的热力学路径分析解读了表面和内部微层裂的差异,见图10。此外,廖异等[51]进一步对低熔点金属锡的微层裂过程进行了模拟,给出了锡材料中孔洞成核及破坏过程的分析。邵建立等[52–53]基于不同碰撞速度下微层裂过程的模拟,分析了熔化前后的破坏形态差异(见图11)及破坏深度的变化,并通过对冲击压力峰值和衰减波形的系列模拟,给出了一般三角形波作用下层裂片厚度和损伤深度的估算方法。
-
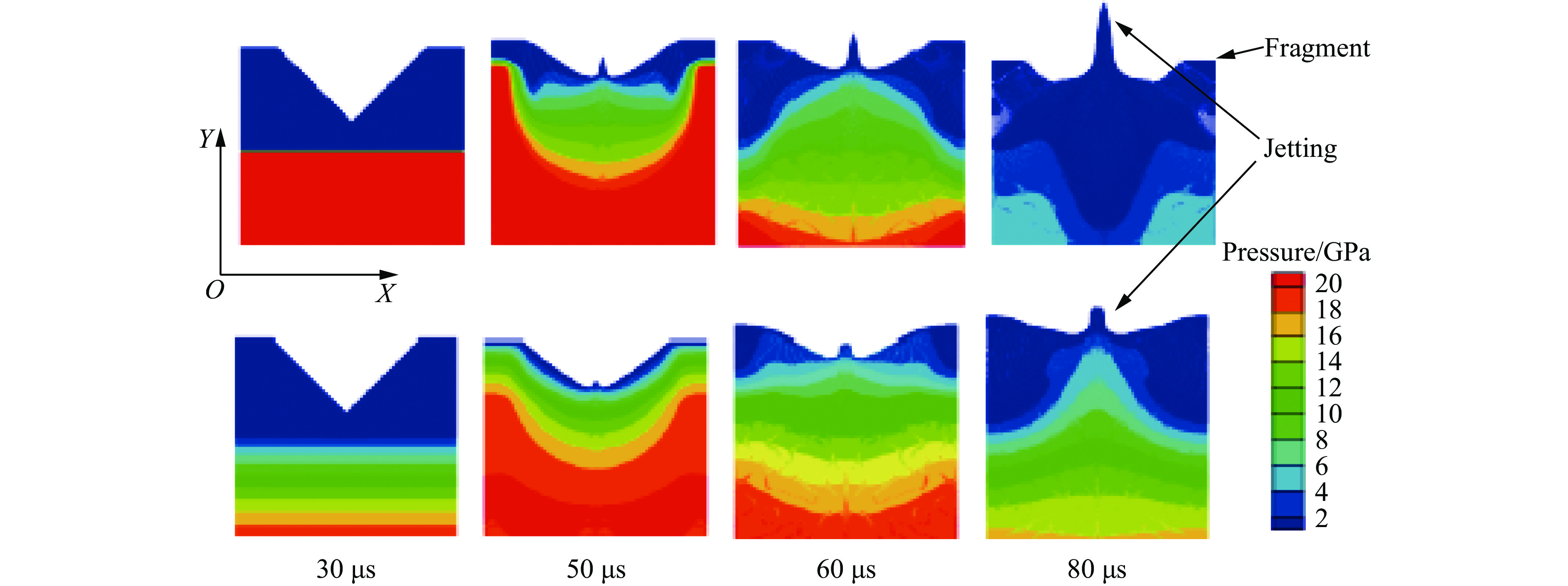
光滑粒子流体动力学(Smoothed Particle Hydrodynamics,SPH)方法是一种无网格的拉氏计算方法,易于处理大变形问题;欧拉数值方法把网格固定在空间上,允许物质的大变形和流动。至今,微喷射现象的CM模拟研究主要采用这两类方法。2004年,王裴等[54]采用SPH方法模拟了冲击加载下金属表面沟槽的射流现象,分析了喷射物的总质量、最大速度和质量-速度曲线,模拟结果与实验结果基本符合,表明SPH方法是模拟微射流的一种有效手段。图12为冲击加载(上)和具有一定加载波前沿宽度加载(下)的微射流形成过程。
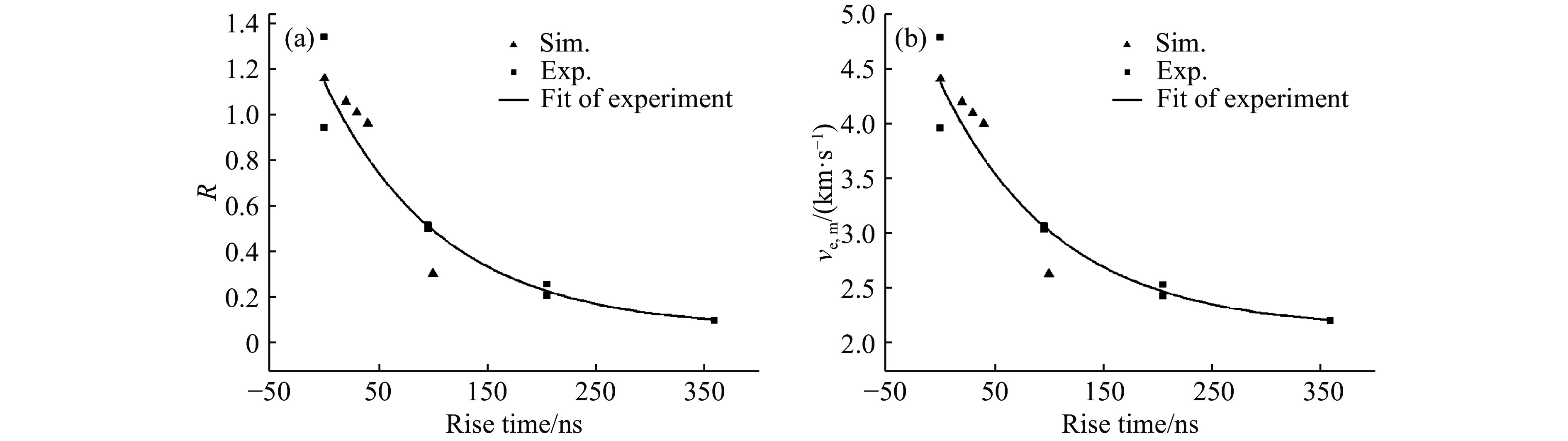
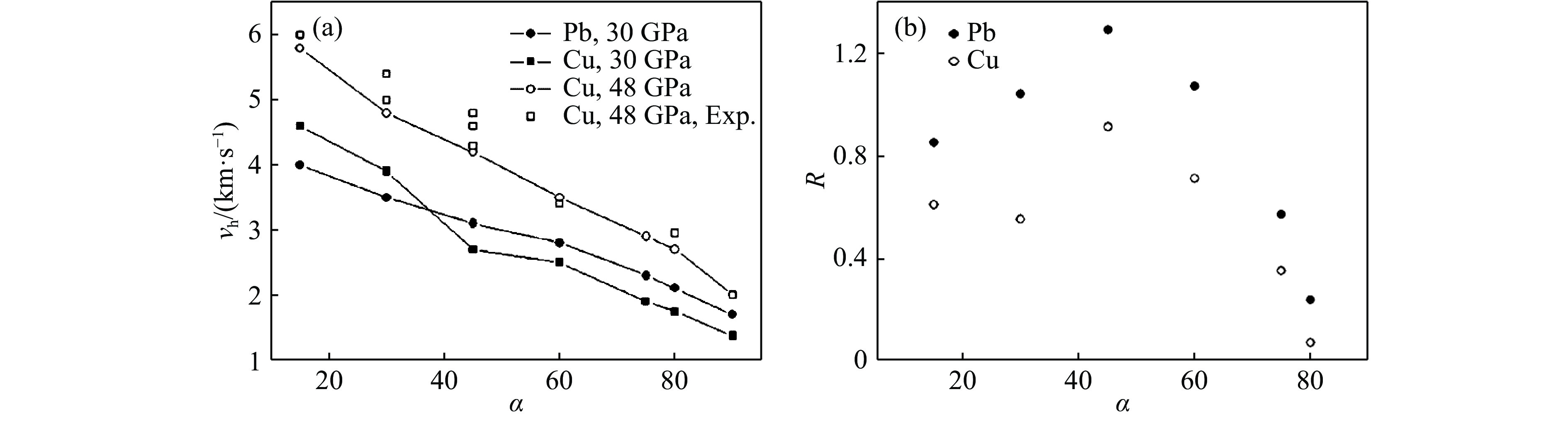
随后,王裴等[56]基于SPH模拟结果分析了加载波前沿上升时间对微射流的影响规律。结果表明,随着加载波前沿宽度增加,微射流质量和头部速度都会减小,同时低速喷射物所占比例增大,这是由于沟槽斜面粒子的碰撞速度降低,碰撞角度增大,导致部分粒子达到射流强度封锁条件而不再形成射流,见图13。通过金属铅和铜表面沟槽冲击微射流过程模拟[57],进一步给出了头部速度和喷射系数随沟槽夹角的变化。结果显示,喷射系数在沟槽半角为45°时达到最大值,随着角度的增加或减小,喷射系数均会减小;而最大喷射速度随沟槽角度的增加近似成线性减小,见图14。此外,通过追踪粒子运动轨迹分析了微射流物质来源,发现随着沟槽夹角增加,射流物质来源由沟槽两侧逐步向沟槽底部过渡。
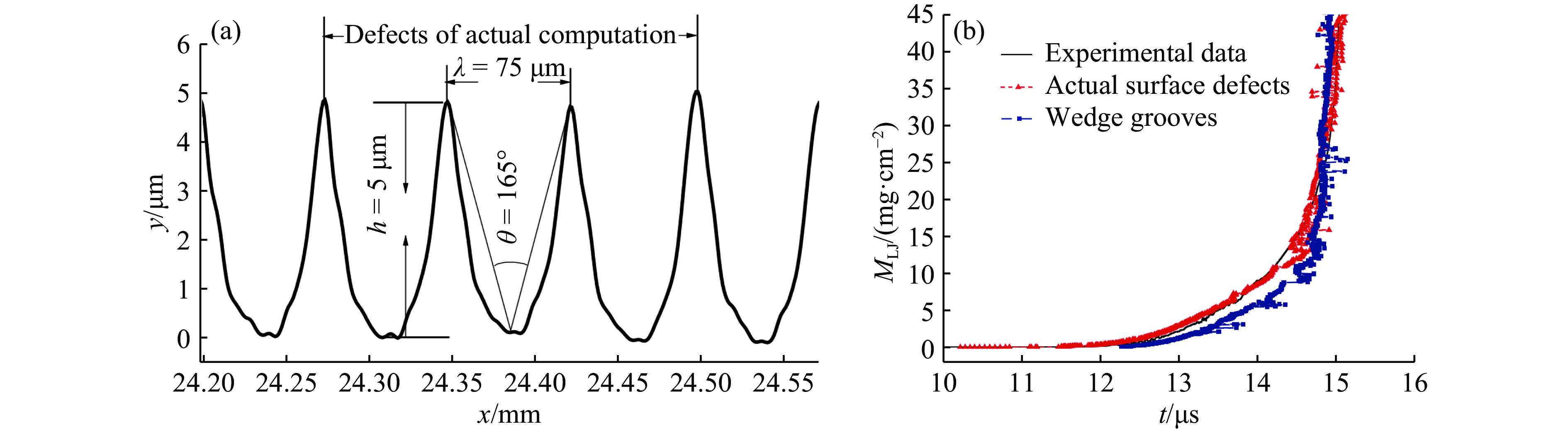
此前,大多数值模拟都采用了楔形槽等简化模型,为细致考察表面形貌这一变化因素,赵信文等[58]根据样品表面形貌的实测结果进行了SPH建模和模拟。结果表明,基于实测样品缺陷建模的计算结果与实验结果更加符合,见图15。分析发现,在实测样品缺陷诱导微喷射过程中存在“二次汇聚喷射”机制,与单次喷射相比,该机制可产生更高速度的喷射物,并影响微喷物的空间密度分布。这再次表明表面微细结构对微喷射现象的影响是显著的。
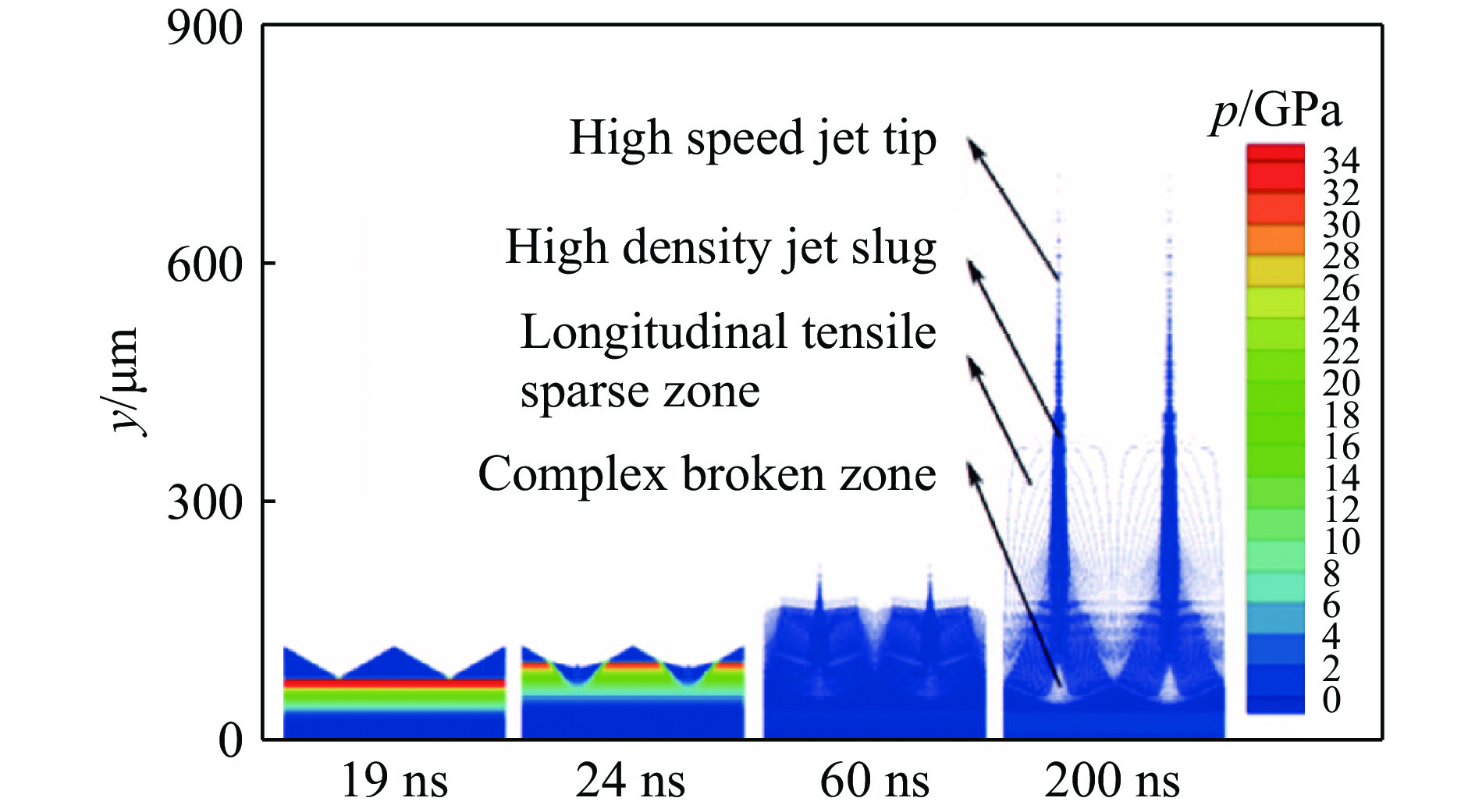
上述CM模拟主要关注了持续冲击下微射流形成及质量累计过程。为从CM角度理解衰减冲击下近表面破坏模式与复杂喷射状态,刘文斌等[59]采用SPH方法模拟了三角波加载下微喷射现象。根据模拟结果,可将三角波加载下喷射物的空间分布分为高速颗粒、射流杆体、纵向散碎和复杂断裂等多个区域,显然这与持续冲击下的尖钉-气泡结构有本质不同。统计结果显示,在相同的冲击压力峰值下,三角波加载产生的高速喷射物明显减少,但会产生更多的低速喷射物,因此总的喷射质量明显增加。换句话说,此时衰减波形是决定喷射总量的主要因素,表面缺陷主要决定喷射物的分布状态,见图16。此前,Rességuier等[60]曾利用SPH模拟结果解读了其激光加载微射流实验。
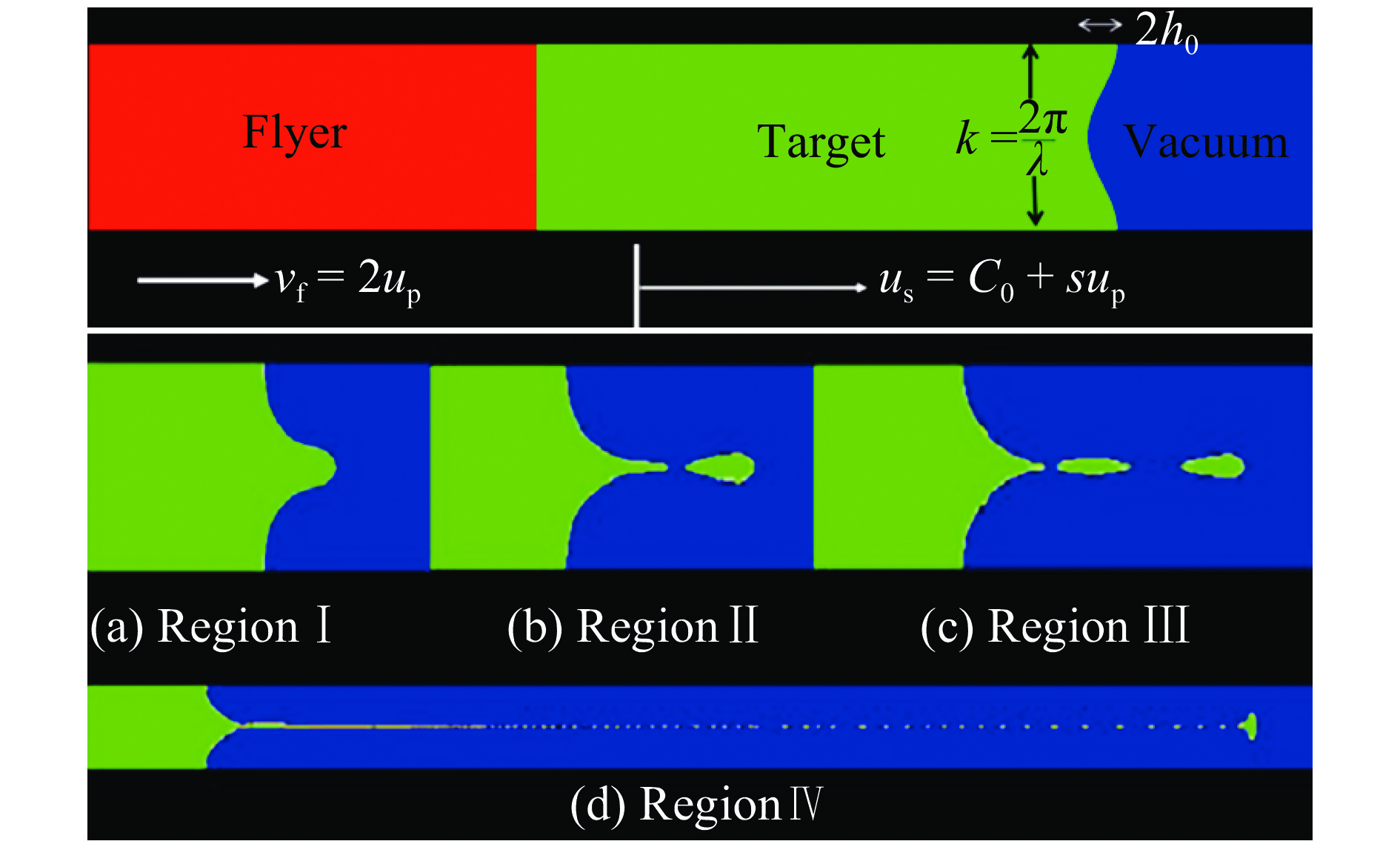
利用Los Alamos国家实验室开发的欧拉有限差分程序PAGOSA,Kullback等[61]模拟研究了不同扰动幅值、波数和几何形状情况下的微射流过程。图17给出了几种典型喷射状态,该模拟中采用了Mie-Grüniesen状态方程和弹性理想塑性强度模型。结果表明,总的微喷射质量取决于初始扰动幅值和波数的乘积。微喷射质量随该乘积呈现阶段性变化,且当该乘积超过某阈值时,喷射质量便呈现出单调增加趋势。此外,刘超等[62–63]采用二维弹塑性流体力学欧拉程序MEPH,模拟分析了不同形状、不同角度沟槽缺陷的最大喷射速度及喷射系数的变化规律,并进一步讨论了不同缺陷形状对喷射速度和喷射系数的影响。相关结论与前文SPH模拟和实验基本吻合。
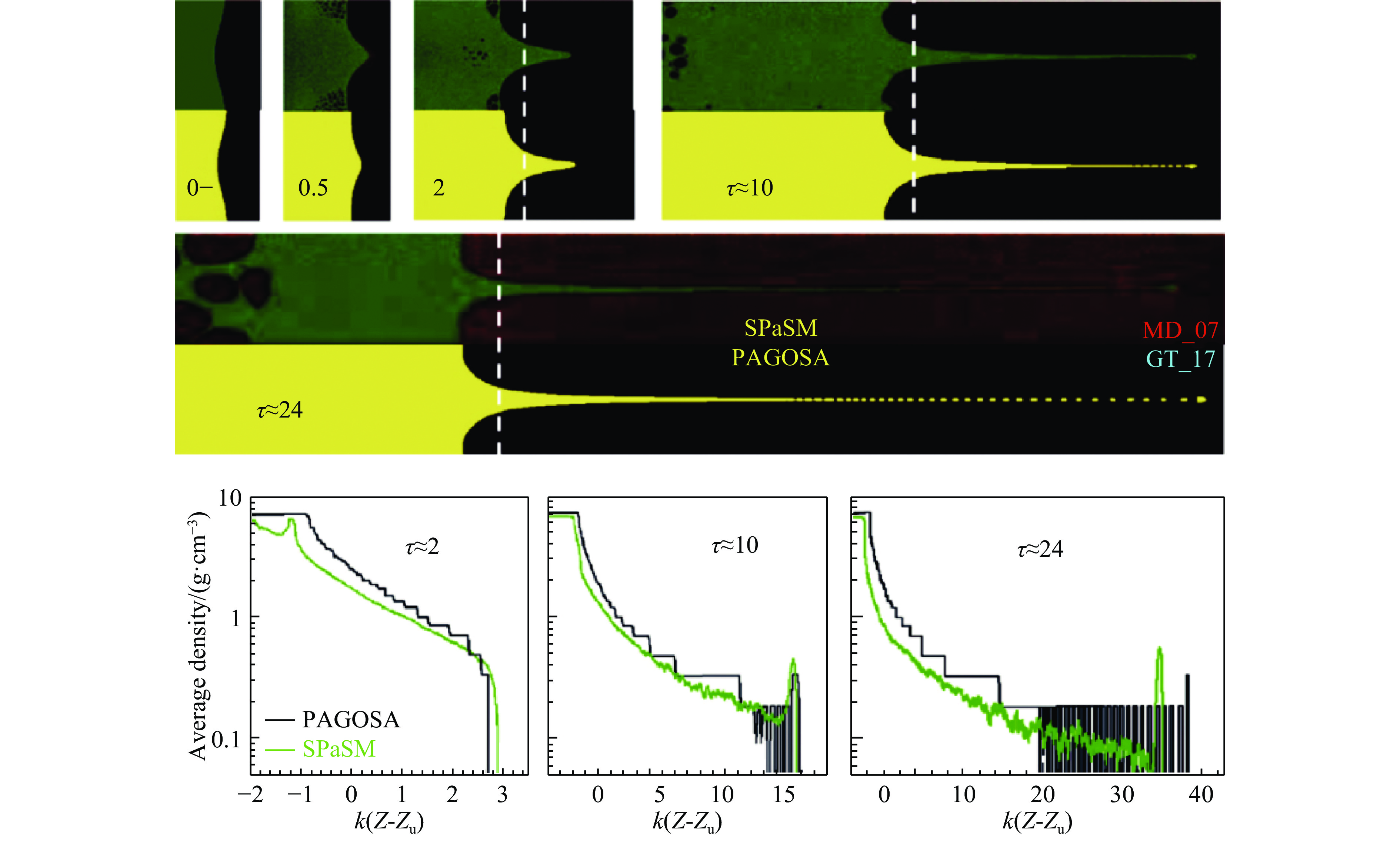
通过对MD和CM(PAGOSA程序)模拟结果的综合分析,见图18(图中时间τ和位置k(Z-Zu)均以沟槽尺寸进行了缩比),Dimonte等[64]提出了一个简单的微喷射代数模型,该模型中微喷射面密度是由冲击后的金属密度和饱和的气泡幅值决定的,该模型与MD和CM模拟结果一致,并已被实验验证。Cherne 等[65]同样基于MD(SPaSM程序)和CM(FLASH程序)模拟,对多种材料的不同表面形貌进行了一系列数值分析。由此将上述喷射质量公式拓展至多种表面形状。
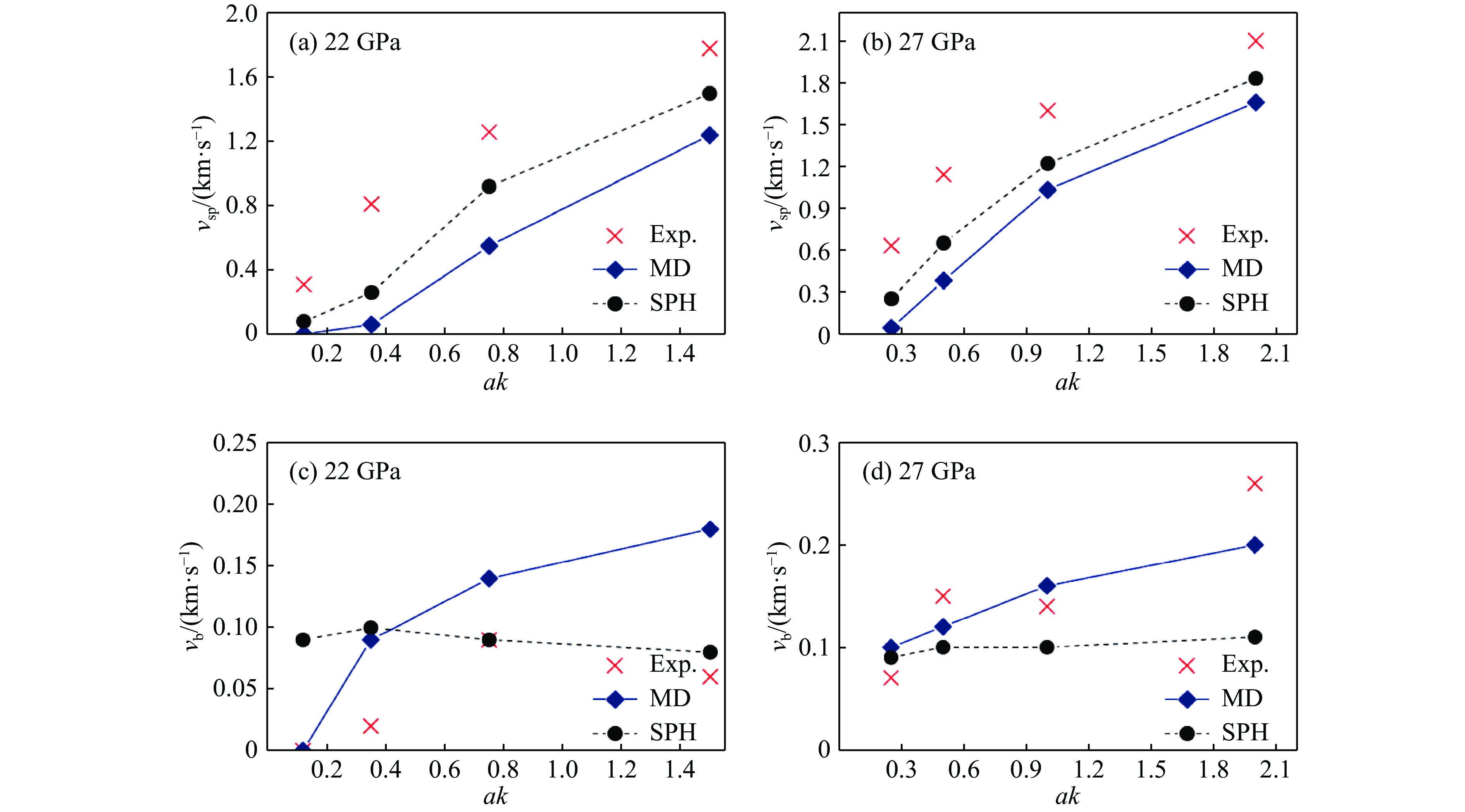
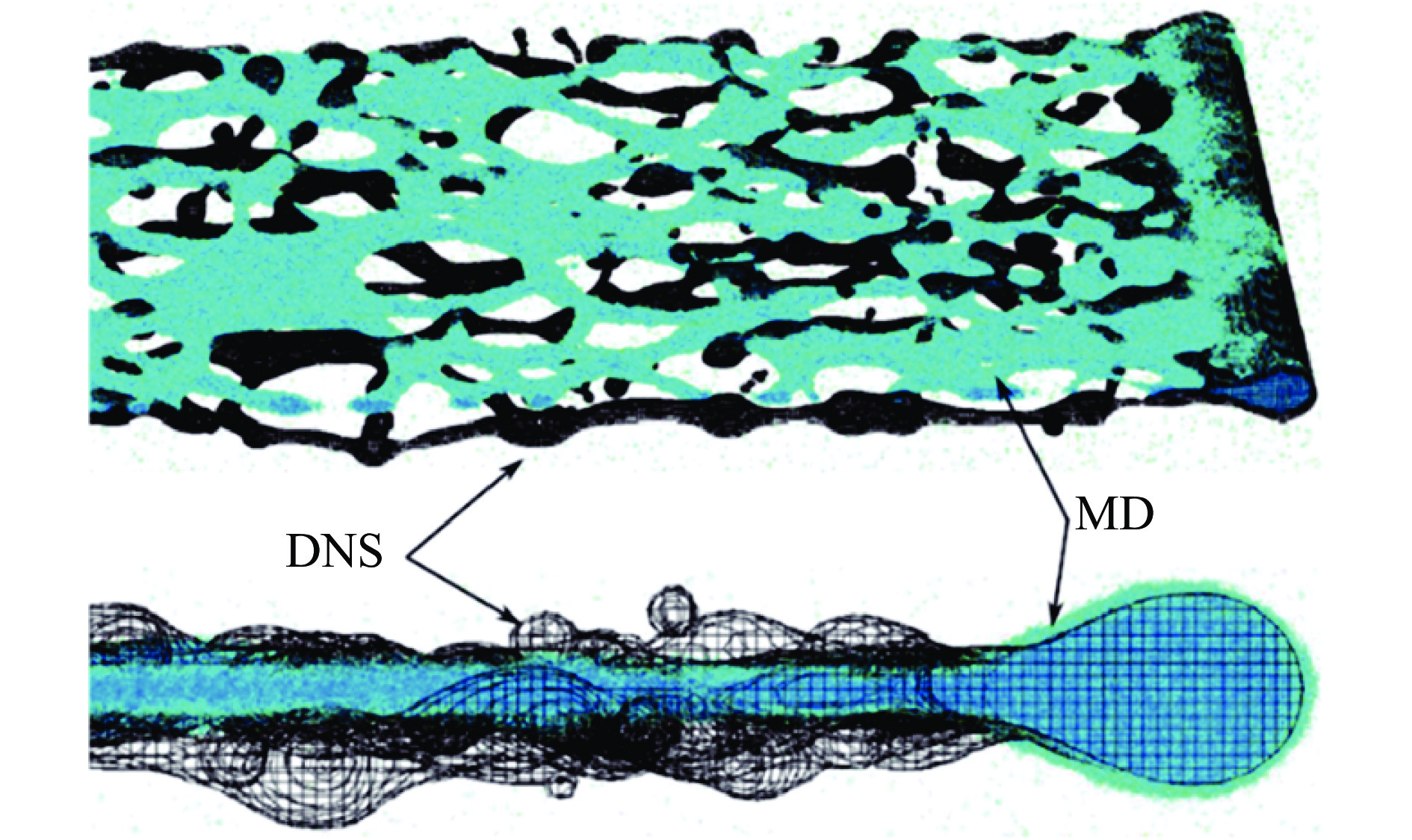
与此同时,其他更多工作也采用了MD和CM模拟的联合分析[66–67]。其中,Dyachko等[66]对锡样品进行了MD和SPH对比模拟,见图19,图中vsp和vb分别为尖钉和气泡的速度,ak表示扰动幅值。SPH模拟采用真实的实验尺寸,MD则采用比例缩放的样品尺寸。结果表明,MD和SPH模拟的射流速度和质量分布基本一致,表面张力对小尺度样品喷射射流的深刻影响可以部分解释MD和实验中观察到的峰值速度差异。此外,Durand等[67]采用大规模MD和CM模拟开展了相近尺寸的数值模拟。CM方法采用基于自适应网格细化的欧拉流体动力学方法,其状态方程由MD模拟得到。模拟结果表明,CM模拟得到的射流轮廓、质量和速度与MD方法所得结果一致,见图20,并指出材料的黏性和表面张力对CM模拟结果有很大影响,是CM建模中值得关注的问题。
-
通过对微喷射现象的数值模拟研究,希望建立包含材料性质、表面状态及动力学条件等因素的喷射物质总量、质量-速度及颗粒尺度分布模型,以应用于工程力学问题的量化模拟中[6]。在早期研究中,Asay等[4]基于实验规律提出了一个由表面缺陷质量估算喷射总量的模型。韩长生[68]从经典射流理论出发,基于“等效金属罩质量”假设,推导了定常流动下冲击波与楔形槽表面正规与非正规反射条件下微射流质量的半经验公式。这些模型可以大致描述部分实验结果,然而由于模型过于简化,无法描述更宽范围的实验数据及其变化规律,比如,喷射物总量与缺陷深度、沟槽角度或波长的关系,更为严重的是无法反映熔化前后材料喷射状态的显著差异。
随着数值模拟研究的不断深入,建模工作也取得可喜进展。2011年,Georgievskaya等[69]基于不可压流体和小扰动假设,根据Richtmyer-Meshkov(RM)不稳定性理论给出了喷射质量随时间演化的近似方程,并通过数值计算验证其估算的正确性。之后,Dimonte等[64]假设微射流总量由RM气泡饱和振幅决定,建立了与表面初始扰动相关的微射流总量模型。2015年,Cherne等[65]对上述模型进一步修正,引入抛物型气泡形状的假设,以及初始扰动相位反转的时间修正因子,最终构建了描述微射流总量以及最大速度随材料性质、表面扰动状态以及加载动力学条件变化的理论模型,并将其推广至不同形貌表面缺陷微射流喷射状态的描述。
式中:
$m(t)$ 为$t$ 时刻的喷射面密度”,${m_0}$ 为初始缺陷面密度,$\Delta t$ 为扰动反转特征时间,$\beta $ 为时间尺度因子,$\tau $ 为约化时间,${\dot \eta ^{\rm s}}$ 为尖钉渐近增长速度,${\dot \eta _0}^{\rm {b,s}}$ 为气泡或尖钉的线性增长阶段的最大速度,${F_{\rm l}}$ 为线性冲击压缩因子,$F_{\rm nl}^{\rm b,s}$ 为非线性关联因子,$k$ 为初始扰动波数,${h_0}$ 为初始扰动振幅,$\Delta u$ 为表面速度。该模型可以较好地描述熔化状态下金属微射流总量与最大速度的不同尺度(包括MD和CM)数值模拟结果以及相关实验数据,是微喷射理论建模研究的重要进展。根据强度介质不稳定性理论,未熔化材料仍可发生界面塑性流动失稳。在此情况下,虽然强度效应会抑制界面不稳定性的发展,但在特定状态下RM尖钉会持续增长,最终断裂破碎而形成物质喷射。为进一步发展强度介质微喷射模型,何安民等[70]基于弹塑性欧拉数值模拟获得的强度介质扰动增长与物质喷射之间的内在联系,结合理想弹塑性固体界面RM不稳定理论,构建了强度介质微喷射总量模型,即
式中:
$\sigma _{{\rm{ej}}}^{\max }$ 为强度介质最大喷射质量,$\alpha $ 取为0 ~1之间小数,${\rho _{\rm{0}}}$ 为材料初始密度,$\eta _{\rm{b}}^{{\rm{max}}}$ 为气泡饱和振幅,${\eta _{\rm{0}}}$ 为初始扰动振幅,k为初始扰动波数,Y为材料的等效屈服强度。综合上述强度介质和纯流体微喷射模型,可以给出平面冲击下宽压力区间的喷射总量和最大速度的一般描述。然而对于更复杂的加载条件,则必须考虑实际波形等因素。对于爆轰、激光等加载波形条件,借助经验模型或判据条件,已进行部分数值模拟分析[71–73]。其中,张凤国等[74]基于应力波传播理论,采用应力瞬时断裂判据和损伤累积判据,分析了简单三角波强加载下延性金属的多次层裂破坏问题,给出了层裂片厚度对冲击波宽度与强度的比值的变化,在强冲击加载条件下,破坏深度约为冲击波宽度的一半。最近,邵建立等[53]基于MD模拟分析了不同衰减冲击波下金属铅的破坏形态和深度变化,结合模拟得到的样品内部拉应力和密度变化,给出了表面层裂片厚度和样品破坏深度的近似公式,即
式中:Ts为层裂片厚度,
$\lambda $ 为三角波宽度,${\rho _{\rm{s}}}$ 和${\rho _{\rm d}}$ 分别为层裂片和破坏区的平均密度,${\rho _0}$ 为材料初始密度,${\sigma _{\rm s}}$ 和${\sigma _{\rm b}}$ 分别为层裂应力和冲击应力峰值。关于喷射物颗粒尺度的信息,可以采用幂律关系和指数关系来描述其终态分布,但其中主要参数的取值还很难从理论上确定。实际上,MD方法可以直接模拟出颗粒化全过程,但还局限于纳米尺度和极端应变率条件,与实际情况下的断裂颗粒还相差很大。而从CM角度,采用射流失稳断裂[73]、能量破碎等理论[74]可以对颗粒尺度进行估算,但这依然包含较多经验判据或参数,对实际状态下颗粒度的定量化分析仍然具有较高难度。
-
至今,微喷射现象研究已有60余年的历史,微喷射现象的主要特征及喷射物产生机制已被充分阐明,该领域研究正在蓬勃发展[29]。目前微喷射现象数值模拟主要包括微观尺度MD和宏观尺度CM两类方法,前者侧重于物理机理揭示,后者侧重于动力学分析。不同物理尺度模拟的对比分析受到越来越多的关注。根据研究现状,微喷射数值模拟仍存在以下几方面难点问题。
(1)微喷射现象的多物理尺度模拟。微喷射是典型的多尺度演化问题,现有模拟手段还局限于微观或宏观尺度,为发展更具物理基础的建模,需要特别关注不同物理尺度的耦合建模与模拟方法,从材料结构和动力学两方面深化对微喷射现象的量化规律认识。
(2)强冲击加卸载下表面区域的材料模型。实际上,表面物质与内部质点经历的力学途径存在明显差异,当我们重点关注表面物质演化时,需要考虑材料模型及参数的适用性,比如,Dimonte等[75]便利用不稳定性增长来反推材料表面区域的等效屈服强度。
(3)表面几何形貌和加载波形的复杂相互作用。冲击波与粗糙表面的相互作用实际上是一个三维或者准二维问题,在衰减冲击条件下可出现复杂的表面拉应力区,这会影响甚至改变近表面物质的破坏模式。这对于理解微喷射全局状态,尤其是低速喷射物的分布十分重要。
希望本文能为后续微喷射及相关领域的数值模拟与建模研究提供有益参考。

 首页
首页 登录
登录 注册
注册





 下载:
下载: