-
钢筋混凝土结构自问世以来便得到了广泛应用,对混凝土设计理论的研究也不断深入。混凝土结构在使用过程中可能受到各种冲击荷载作用,导致构件失效,甚至造成结构的连续性倒塌。由于结构发生倒塌的后果十分严重,而目前对冲击荷载作用下结构的连续性倒塌响应的研究尚不够充分,因此,有必要对冲击荷载作用下钢筋混凝土结构的连续性倒塌性能开展更深入的研究。
迄今为止,国内外学者对钢筋混凝土结构的动力响应及连续性倒塌性能开展的研究表明,钢筋混凝土结构由于材料的率敏感性[1-2]和惯性作用,其动力响应与静力响应明显不同。Do等[3]用数值模拟方法对桥柱在车辆撞击作用下的动力响应和失效模式进行了研究;刘飞等[4]对有轴力的钢筋混凝土柱进行了数值模拟,分析了其破坏模式及转换机理;史先达[5]、宿华祥等[6]利用LS-DYNA软件中同样的材料模型,分别对钢筋混凝土梁、板和墙的冲击试验进行了验证,模拟结果与试验结果吻合良好,说明所采用的材料模型是适用和准确的;美国世界贸易中心受到飞机撞击倒塌后,陆新征等[7]利用LS-DYNA软件对其受撞击倒塌过程进行了数值模拟和参数讨论;何庆锋[8]对一榀钢筋混凝土框架进行了拟静力倒塌试验,分析了结构失效过程中所经历的弹性、塑性和悬索作用阶段,对结构受力机制的转换过程进行了探讨;Hou等[9]提出了简化计算梁柱子结构荷载-位移曲线的方法,并开展了试验验证,基于能量原理,对结构的抗连续性倒塌能力进行预估;李凤武[10]利用钢筋混凝土框架结构开展了倒塌试验,通过瞬时拆除中柱来研究结构的动力响应,并对动力参数进行了分析,发现单个构件的破坏失效不一定会引起结构的倒塌;Vaughan等[11]利用一栋4层缩尺框架结构开展了倒塌试验,发现移除几个连续构件时结构只发生局部倒塌,表明框架结构自身具有一定的抗连续性倒塌能力;罗维刚等[12]通过ABAQUS软件研究了考虑楼板影响时钢筋混凝土结构的连续性倒塌响应,同时分析了拆柱时间的影响,结果表明,考虑楼板作用后结构的动力响应明显减小,并且当拆柱时间短于剩余结构自振周期的1/4时,时间越短,结构动力响应越明显;Kang等[13]利用LS-DYNA软件模拟了汽车撞击钢框架的底层柱,分析了撞击过后结构的连续性倒塌过程;Sasani等[14-15]对两栋钢筋混凝土结构分别进行的爆破试验研究表明,拆除部分柱后结构未发生倒塌,破坏柱所受轴力会传递给相邻的钢筋混凝土柱。
本研究采用LS-DYNA显示动力学有限元软件,对钢筋混凝土框架在冲击荷载作用下的响应进行数值分析,通过钢筋混凝土框架在锤击作用下的有限元模拟,分析钢筋混凝土框架的抗冲击和抗连续性倒塌性能,在此基础上分析加密底层柱箍筋密度对框架抗连续性倒塌性能的影响。
全文HTML
-
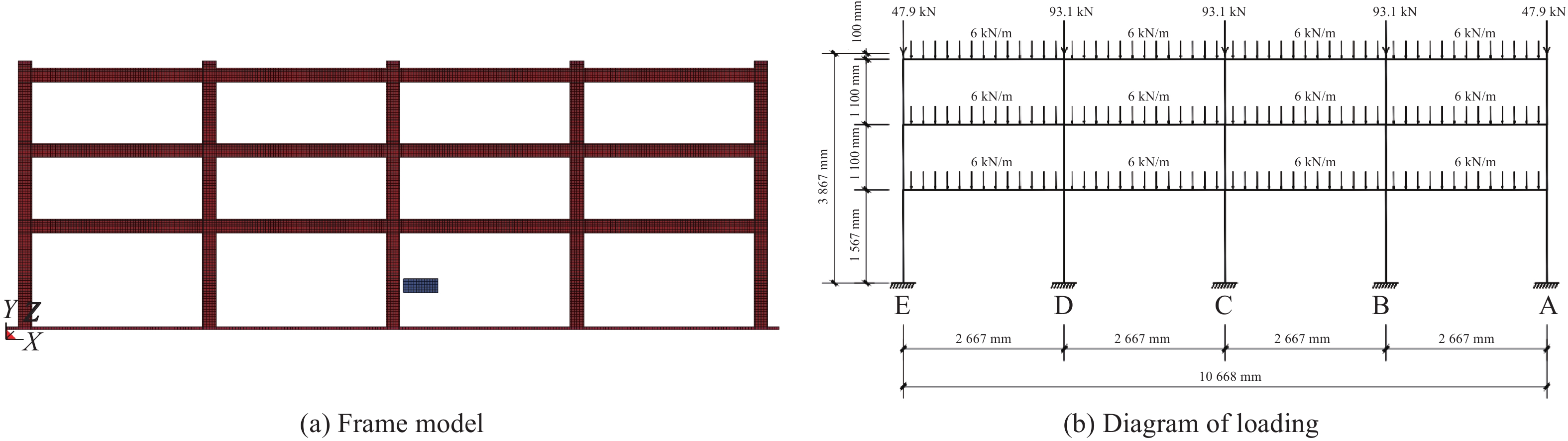
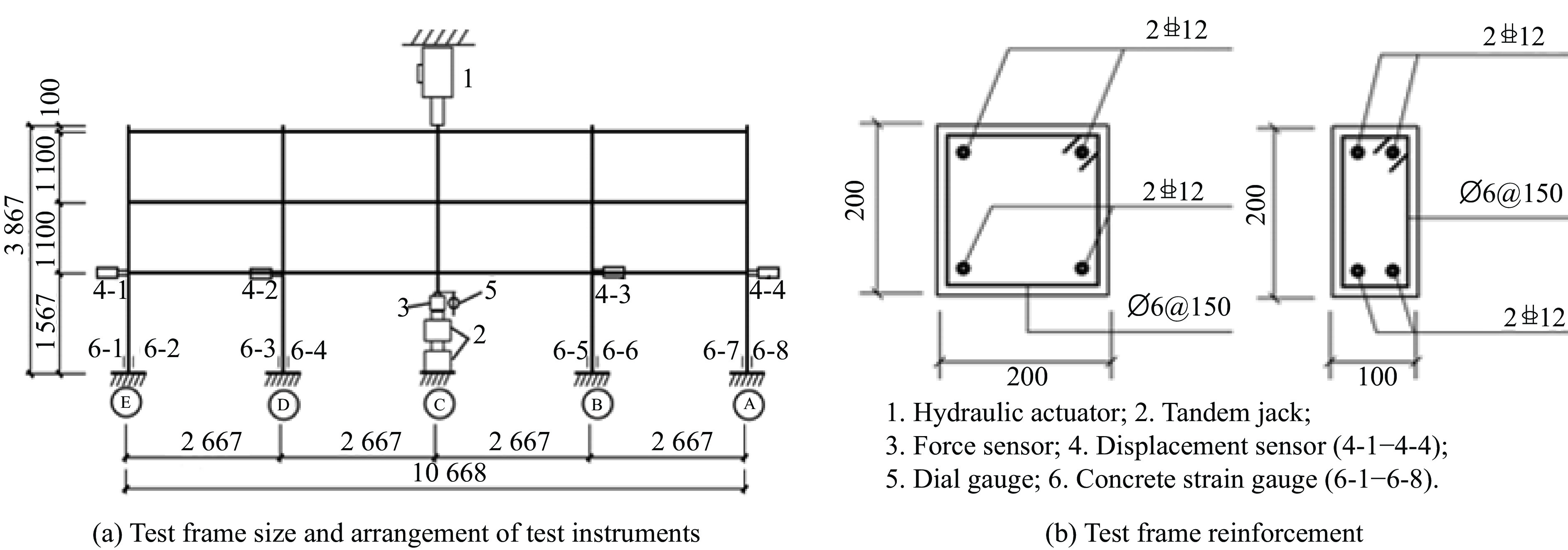
根据参考文献[8]中的试验框架建立模型,框架尺寸及配筋如图1所示。通过中柱顶部上端加载千斤顶和下部两个卸载千斤顶控制中柱轴力,记录不同中柱位移时钢筋和混凝土的应变,并对中柱竖向位移和各层框架柱顶的水平位移进行记录。通过试验数据和试验现象,对框架的受力过程进行分析,并对此钢筋混凝土平面框架受力机制的转换过程进行探讨。
该模型的原型为一栋8层钢筋混凝土框架结构的图书馆,原型抽取中柱后结构并不会发生连续性倒塌,本研究采用的单榀框架并未考虑结构空间作用的有利影响。此外,模拟中也没有考虑楼板的作用,实际结构中楼板的加入能够提高结构抗连续性倒塌的能力。
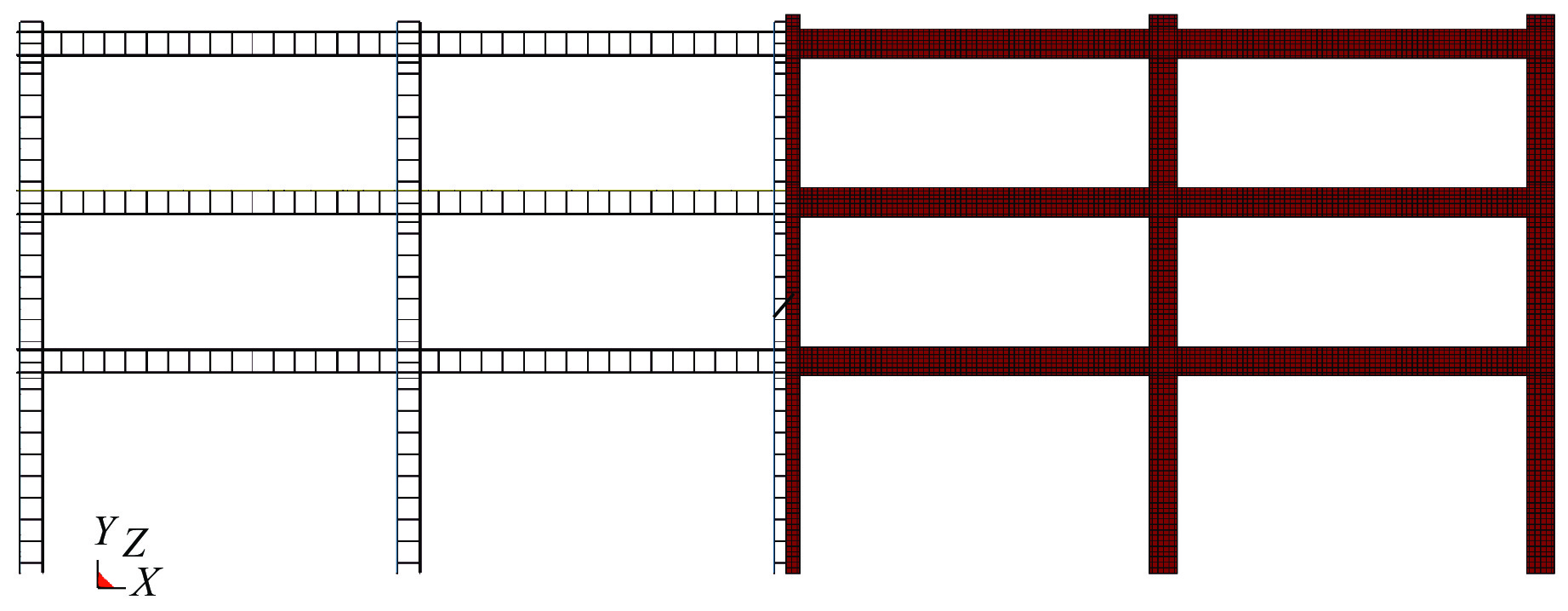
钢筋混凝土框架的有限元模型如图2所示。考虑到框架结构的对称性,采用1/2建模的方式加快计算速度,模型基于XY平面对称,且在对称面上施加对称约束;钢筋混凝土柱顶为50 mm厚的钢垫板,避免在集中荷载作用下柱顶混凝土发生局部破坏。钢筋和混凝土之间采用分离式共节点的方式建模,添加关键字*LOAD_BODY_Y对模型整体施加重力加速度。
-
LS-DYNA软件中的CSCM模型可兼顾材料的硬化、损伤及率相关性,能够很好地模拟混凝土结构在低速冲击作用下的响应[16]。本研究中采用的混凝土材料模型为MAT_CSCM(MAT159),混凝土材料的侵蚀应变设为0.1,即混凝土应变达到0.1后单元被删除并退出计算;钢筋采用考虑应变率效应的MAT_PLASTIC_KINEMATIC(MAT3)模型。
模型中的材料参数取值参考文献[8],材料本构模型及相关参数见表1。其中,ρ为密度,E为弹性模量,ν为泊松比,fc为混凝土抗压强度,d为粗骨料最大粒径,fy为钢筋屈服强度,fu为钢筋极限强度。
1.1. 有限元模型
1.2. 材料模型
-
为了保证所采用的有限元模型的正确性,对文献[17]中梁的冲击试验结果和文献[8]中框架的倒塌过程进行了数值模拟。由于本研究中数值模拟采用的材料模型与文献[17]一致,故在钢筋混凝土梁试验的有限元模拟中不再赘述,仅给出模拟和试验的对比结果。
-
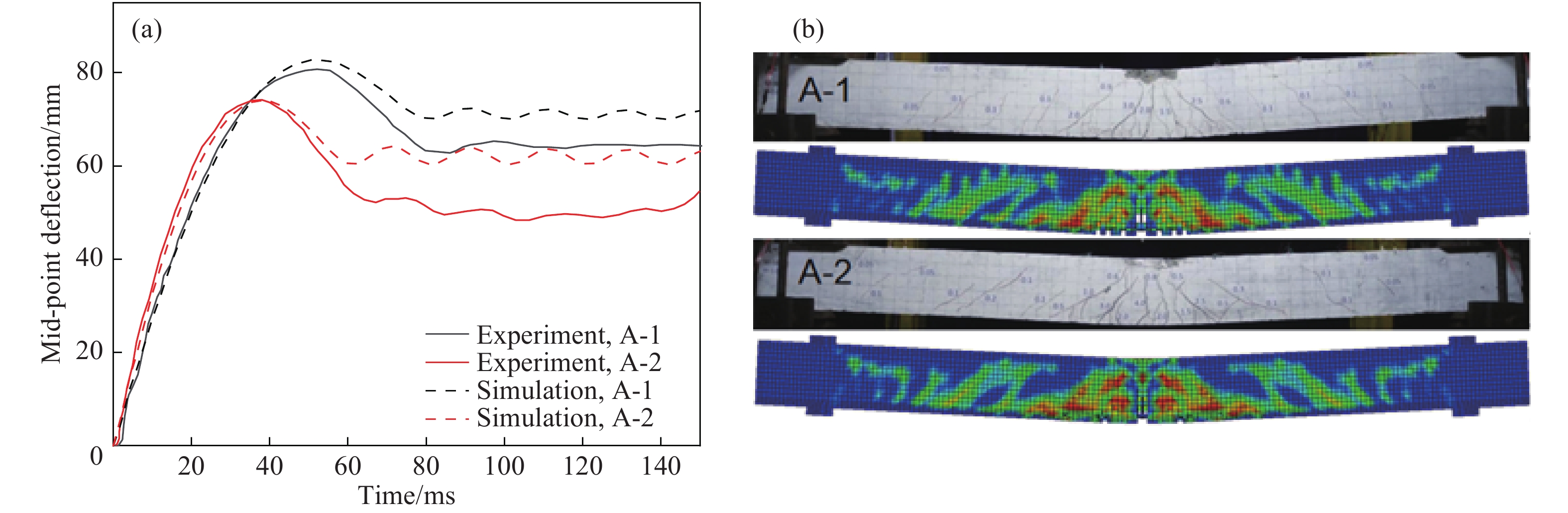
根据文献[17]中的试验梁进行建模,在支座中心处施加竖向线约束来模拟试验中梁体的边界条件,采用1/4建模,并在对称面上施加对称边界条件。所有构件最大位移的试验值和模拟值列于表2。梁A-1和梁A-2的跨中位移时程曲线和梁体损伤的对比如图3所示。由图3的对比结果可知,试验值和模拟值较接近。
-
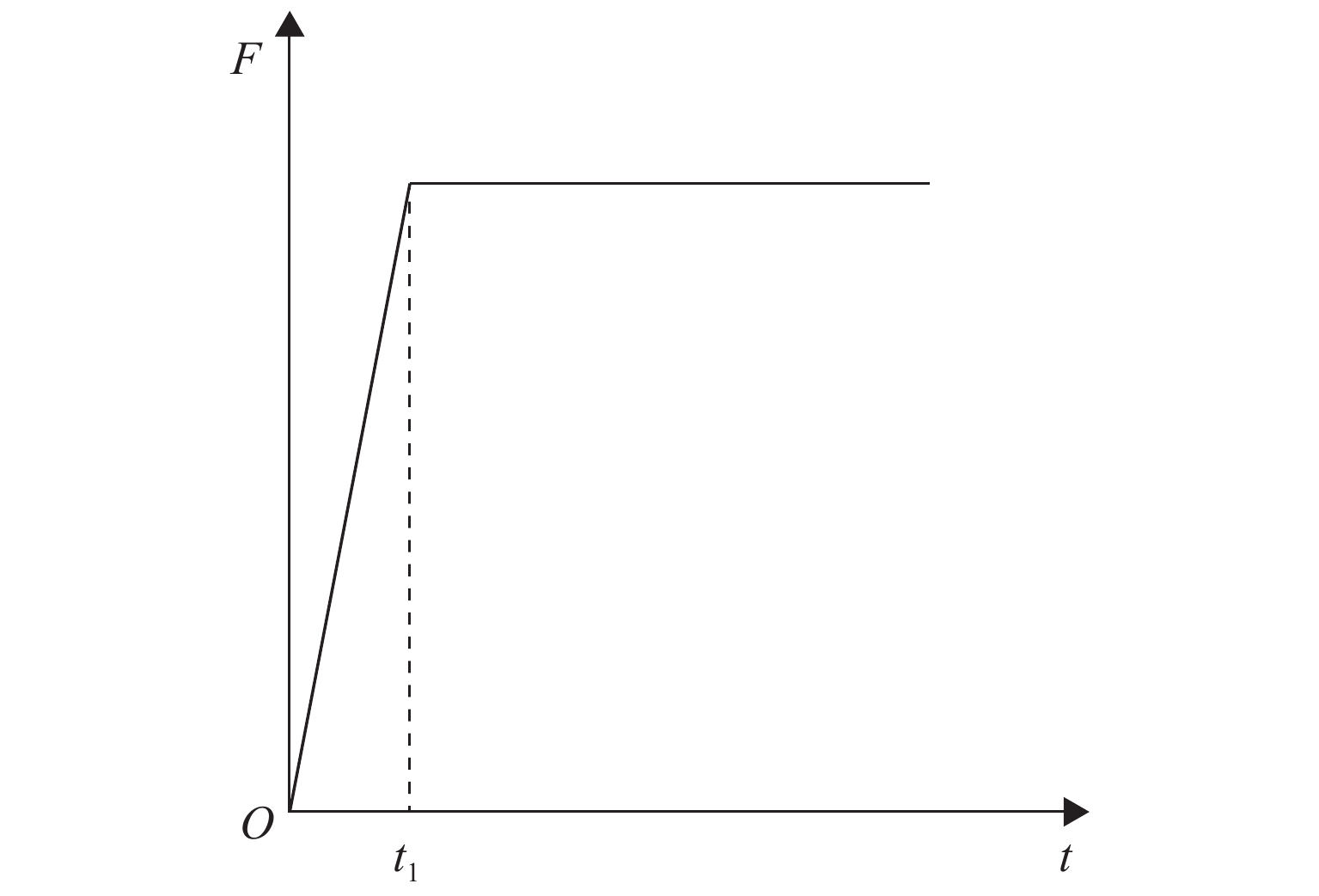
采用直接在中柱柱顶施加荷载作用的方式,对试验框架进行非线性模拟分析,如图4所示。文献[8]对图4所示的冲击荷载作用时的动力系数进行了分析,计算结果表明,动力系数仅与结构的自振频率和冲击上升阶段的作用时间有关。试验框架的自振频率为0.061 s,文献[8]中计算的动力系数μ与失效时间t1的关系如表3所示,本研究在进行倒塌过程验证时,失效时间t1取为0.061 s。
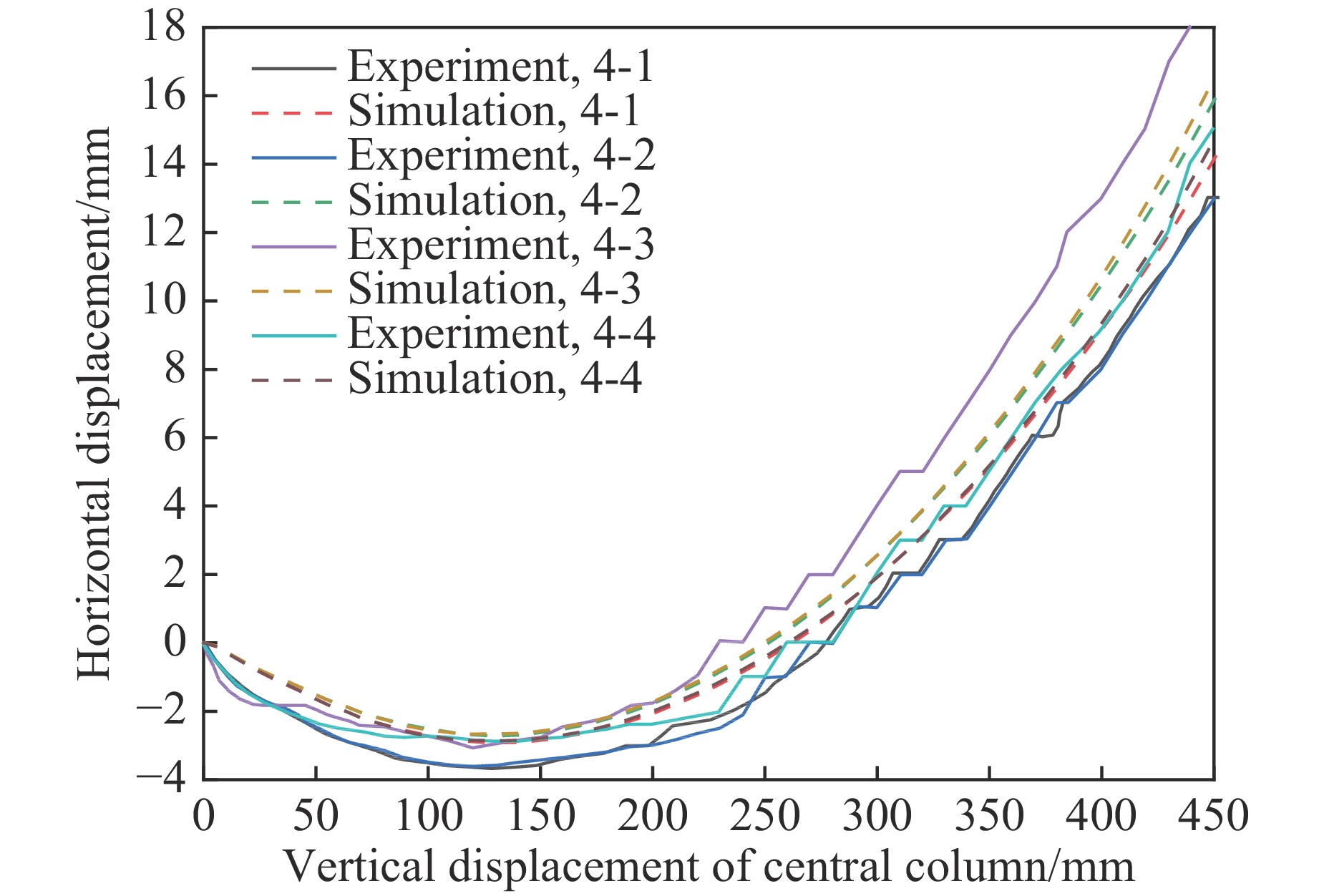
图5给出了框架失去中柱后一层柱顶水平位移与中柱竖向位移的关系对比。由图5可知,试验和数值模拟结果均反映出结构受力机制的转换,即柱顶位移先向外移动,当中柱位移达到140 mm左右时,柱顶位移开始向内移动。另外,从图5可以看出,模拟曲线和试验曲线有较高的吻合度,能够反映框架在失去中柱后结构的倒塌过程。
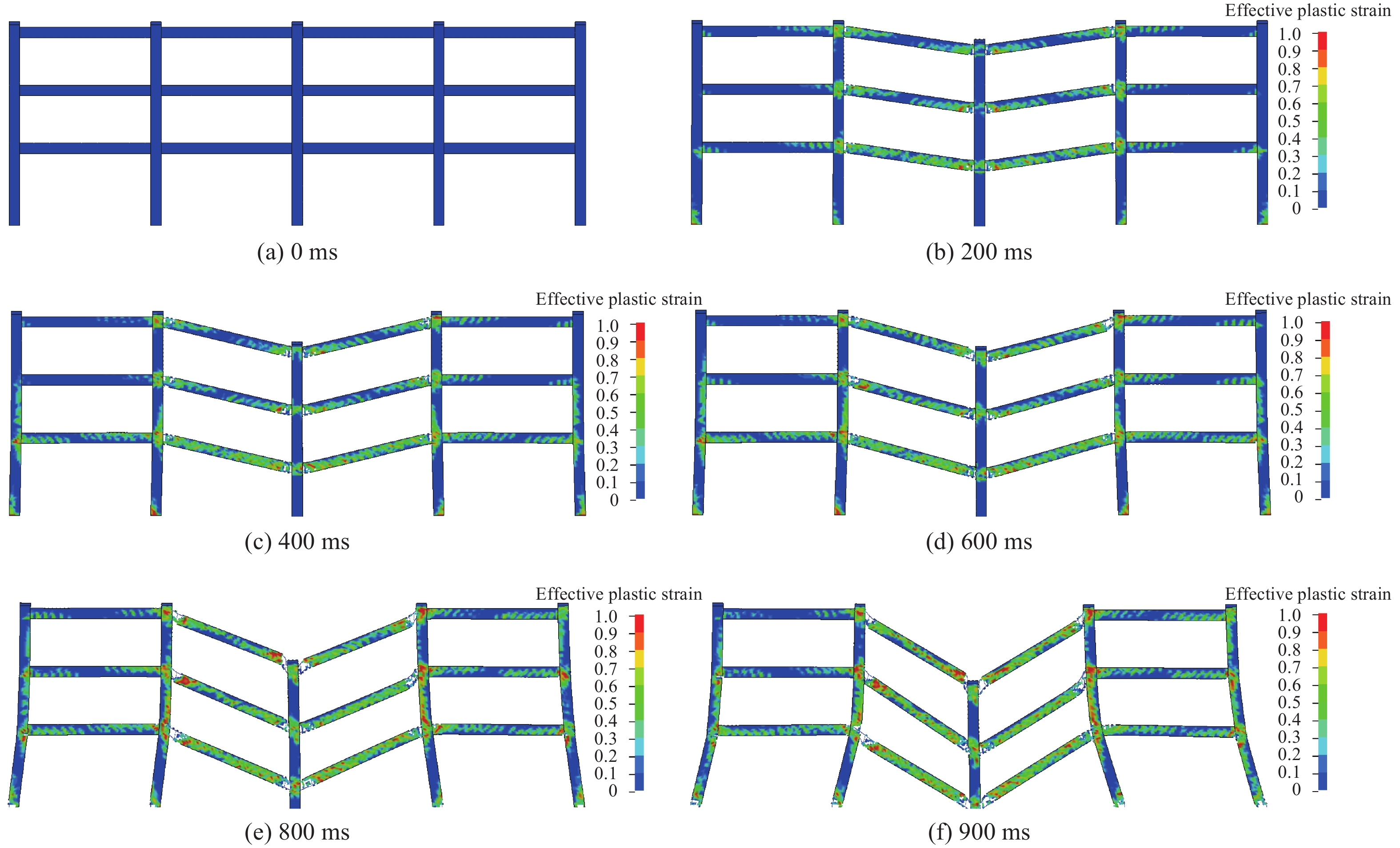
图6给出了框架倒塌过程中中柱竖向位移为0、200、400、600、800、900 ms时的损伤变形,在模型中通过释放中柱底部的固定约束模拟抽柱试验。
由图6可知:当中柱底部的固定约束释放后,中柱在柱顶力作用下向下移动,与其相连的6根钢筋混凝土梁先出现损伤破坏;随着中柱向下移动,边框梁柱相继出现损伤,最终发生整体连续性倒塌。结合柱顶水平位移和中柱竖向位移的关系曲线,本研究能够较真实地模拟结构抽柱倒塌破坏过程。
2.1. 钢筋混凝土梁试验的有限元模拟
2.2. 钢筋混凝土框架倒塌过程模拟
-
冲击荷载作用下框架的有限元模型如图7所示,其中图7(a)为框架和锤体的示意图,图7(b)为框架所受荷载作用,即取3层框架时的实际受荷。锤体质量为1 000 kg,冲击速度为4 m/s,在此冲击作用下得出的结果能够较好地反映框架动力效应的差别。
-
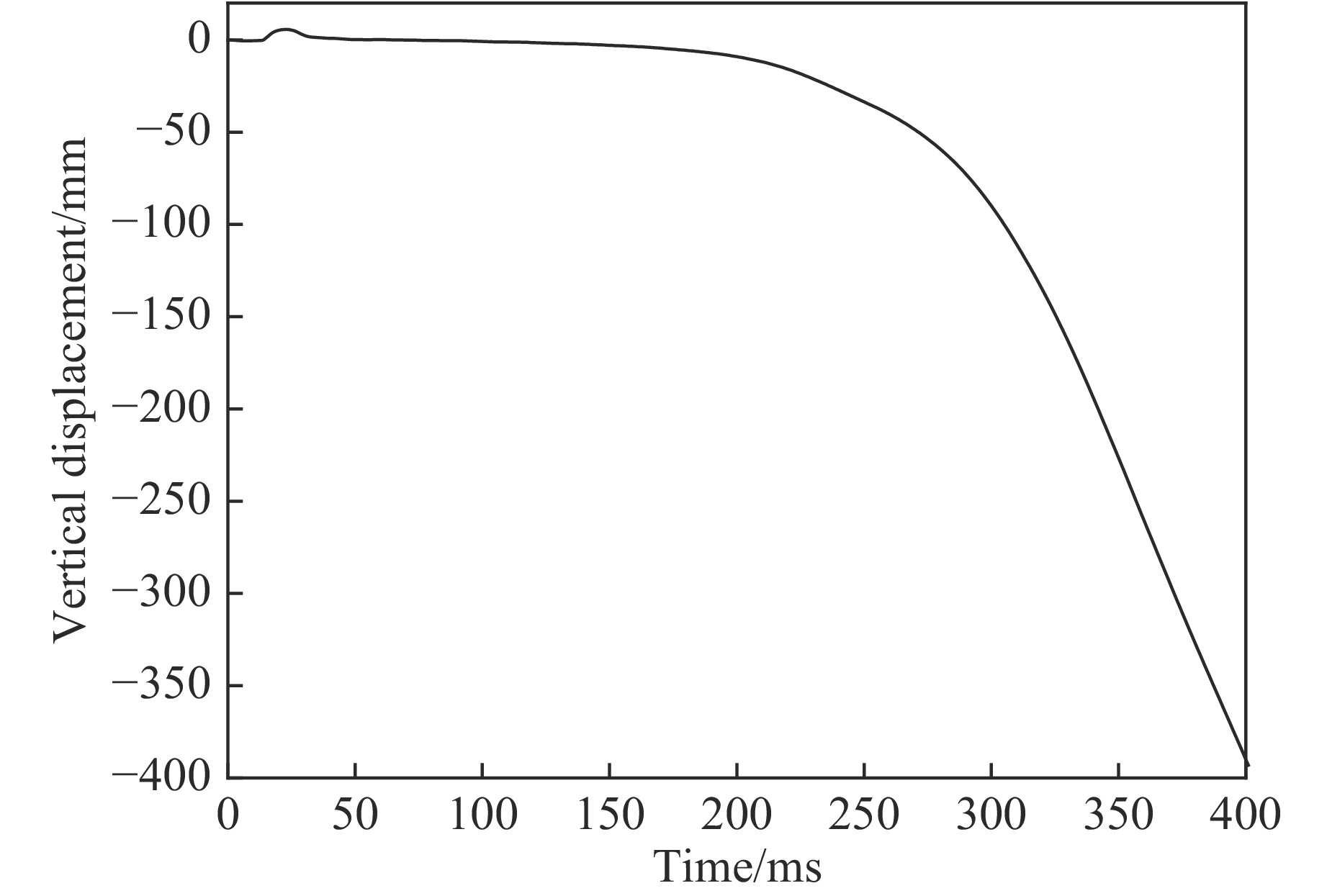
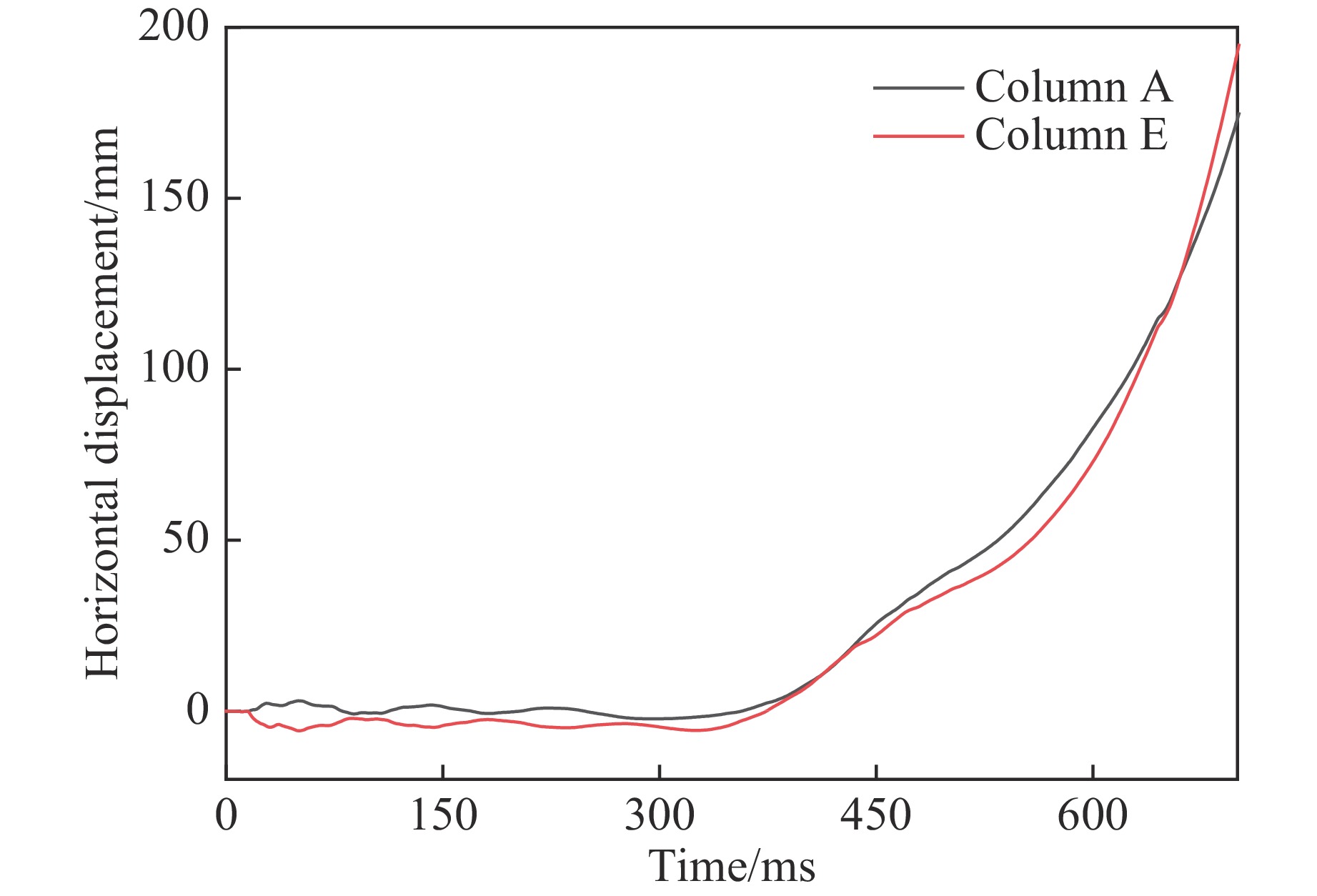
对钢筋混凝土框架底层中柱受到锤击作用后的整体倒塌过程进行模拟分析。前250 ms中柱柱顶的竖向位移时程曲线(正值代表向上,负值代表向下)如图8所示,A柱和E柱柱顶水平位移时程曲线(正值代表向内,负值代表向外)如图9所示。
由图8可知,冲击伊始,中柱柱顶出现向上的位移,峰值为5.72 mm,与静力试验和抽柱模拟中中柱的竖向位移没有向上位移不同。此处向上的竖向位移是由“拱作用”机制导致的,与试验框架柱顶有向外的位移及文献[6]中钢筋混凝土剪力墙在冲击作用下先有向上位移一致;中柱竖向位移刚开始下降时速度较慢,随着时间增加,下降速度增大,这是由于钢筋混凝土柱在受到冲击作用后虽然已不能抵抗结构上的竖向力,但是仍有一定的残余承载力。由图9可知:冲击伊始,A柱向内、E柱向外移动,即两者均向冲击方向移动,此时冲击作用对水平位移起主导作用;作用持续一段时间后,A柱和E柱均向外移动;最终框架向内移动,直至结构倒塌。
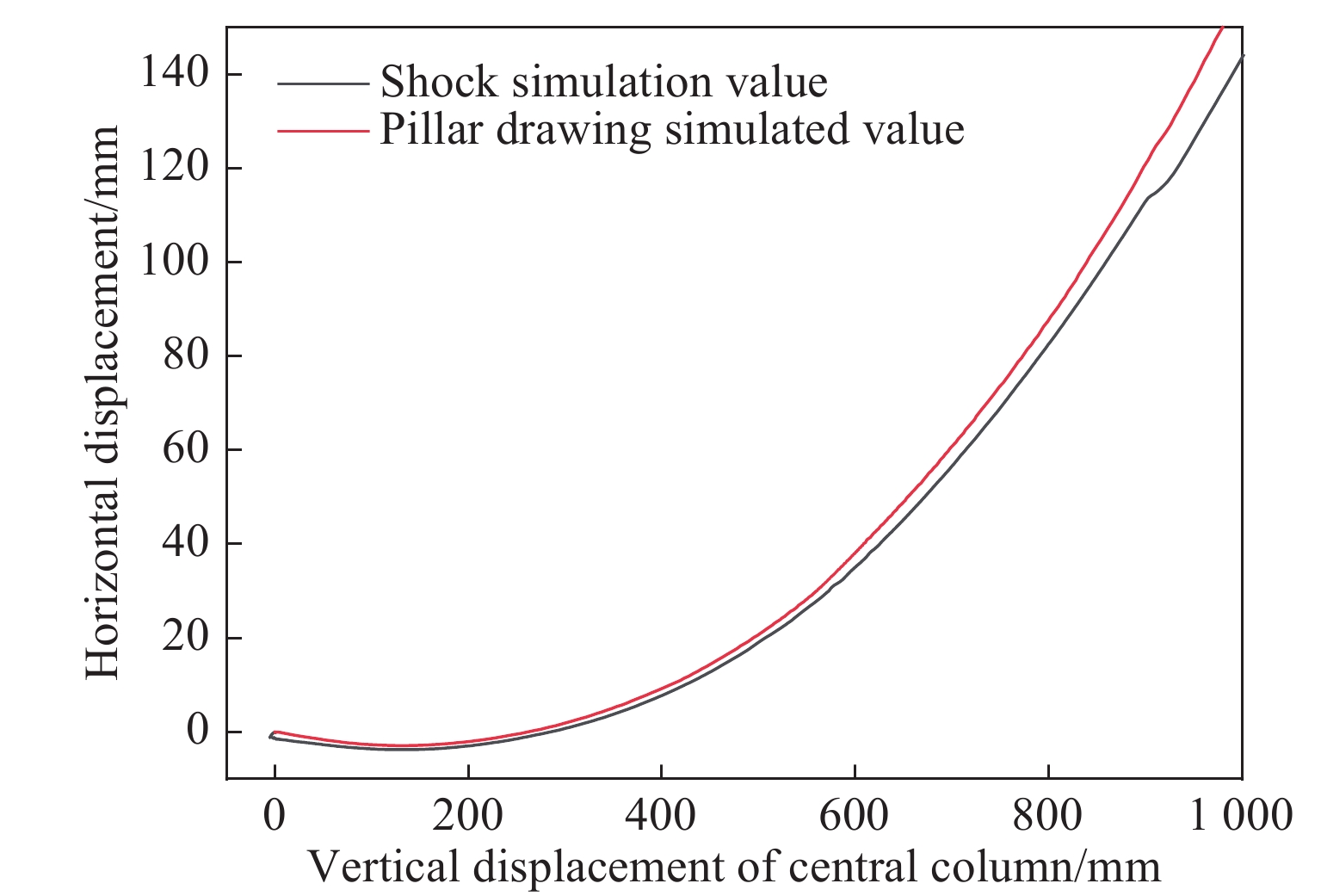
图10给出了A柱和E柱一层柱顶水平位移平均值的时程曲线。由图10可知,一层柱顶先向外后向内移动,说明中柱受到冲击作用直至框架倒塌的过程中仍有“拱作用”。图11中的水平位移为一层A柱和E柱柱顶水平位移的平均值(向内为正,向外为负)。从图11可以看出,两条曲线的变化趋势基本一致,随着中柱竖向位移的增大,柱顶先向外后向内移动,框架向外移动是由于出现了“拱作用”。不同之处在于,抽柱模拟中中柱向下的竖向位移持续增大,冲击作用后中柱柱顶的位移先向上后持续向下移动。冲击作用下得出的曲线在抽柱模拟曲线的下方,但两者差别不大。由此可知,采用静力试验模拟得出的试验结果与冲击作用的结果基本一致,仅在冲击作用初始阶段不同,采用静力试验能够模拟冲击作用下结构的倒塌过程。当然,由于柱体在冲击作用后仍有一定承载力,不同的冲击作用下柱体完全失去承载力所需要的时间不同。
-
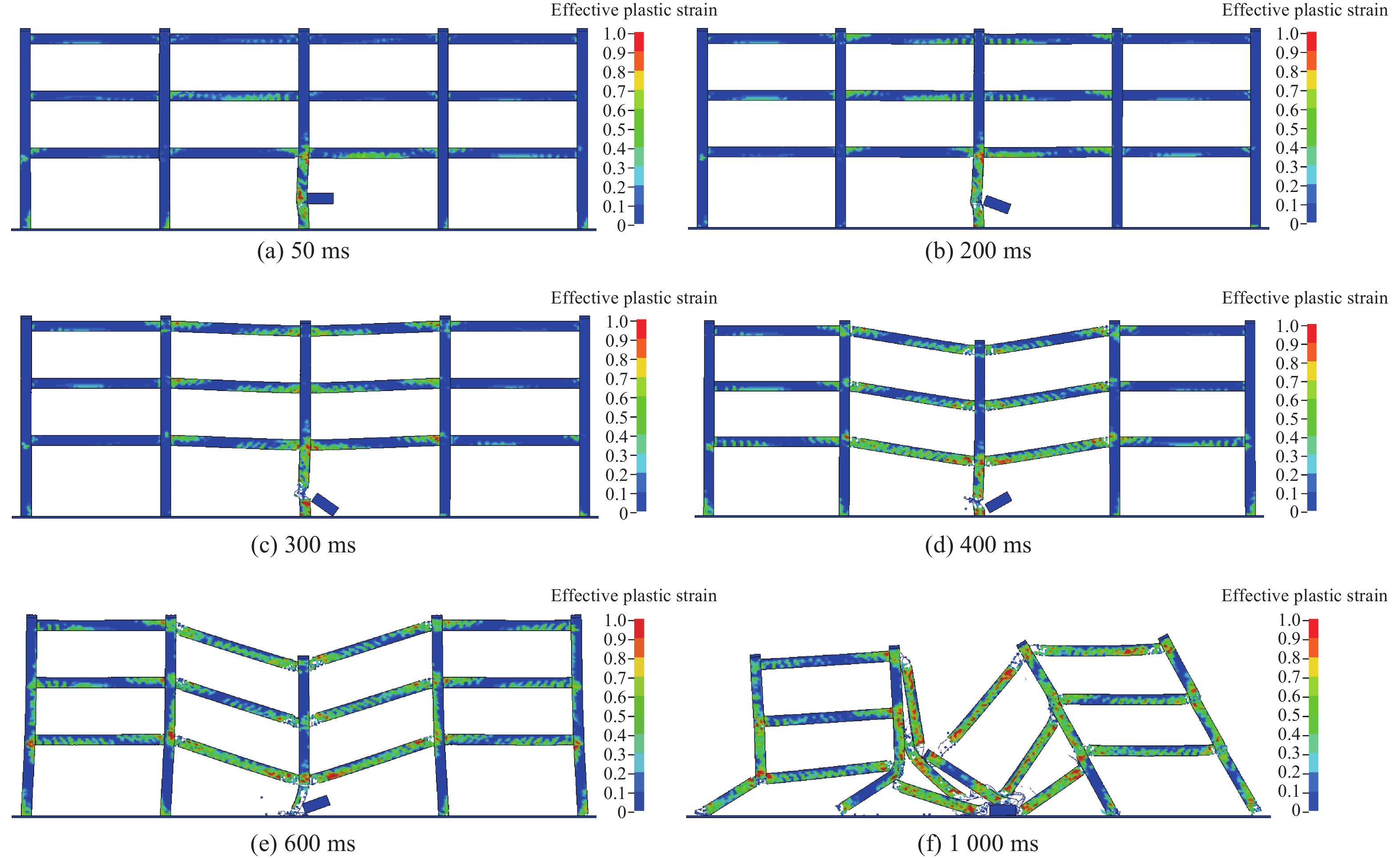
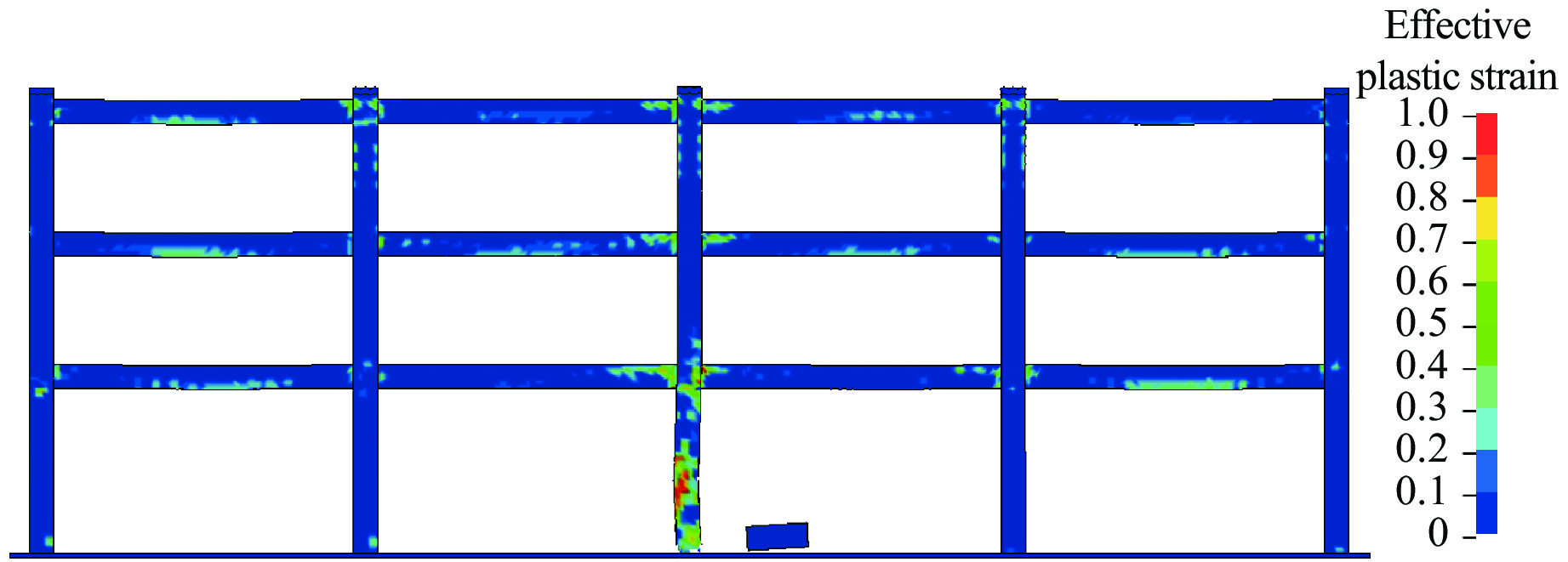
图12为钢筋混凝土框架受到冲击作用50、200、300、400、600、1 000 ms时的倒塌过程。
由图12可知:框架一层中柱受到冲击作用后,冲击作用点附近先发生破坏,50 ms时,冲击作用尚未结束,此时结构整体产生向左的位移,柱底右侧的塑性应变较大;200 ms时,底层中柱部分混凝土单元破坏失效,中间两跨的梁体破坏加重;300 ms以后,随着中柱不断下沉,边框在中间跨梁拉力和梁柱上竖向力的作用下不断发生破坏;1 000 ms时,结构整体破坏倒塌。
-
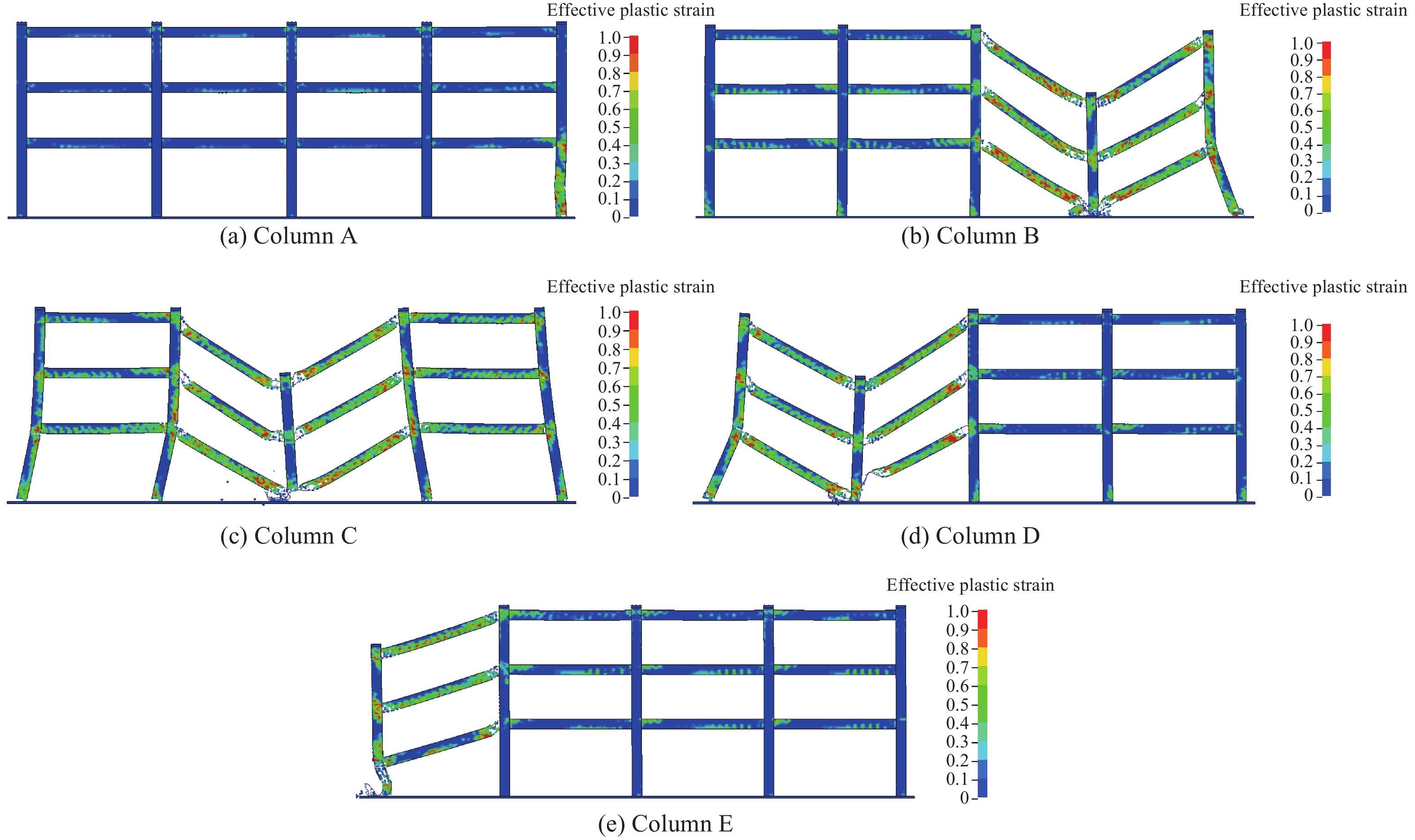
对一层A、B、C、D、E柱分别进行冲击模拟,冲击高度、冲击方向和冲击作用区域均一致,模拟冲击质量为1 000 kg,冲击速度为4 m/s,总冲击时间为2 s。图13给出了一层各柱在受到冲击作用后整个框架的损伤情况,其中图13(a)、图13(e)分别为A、E柱受到冲击作用2 s时的损伤情况,图13(b)、图13(c)、图13(d)分别为B、C、D柱破坏后柱子下沉高度为一层框架高度时的损伤破坏情况。
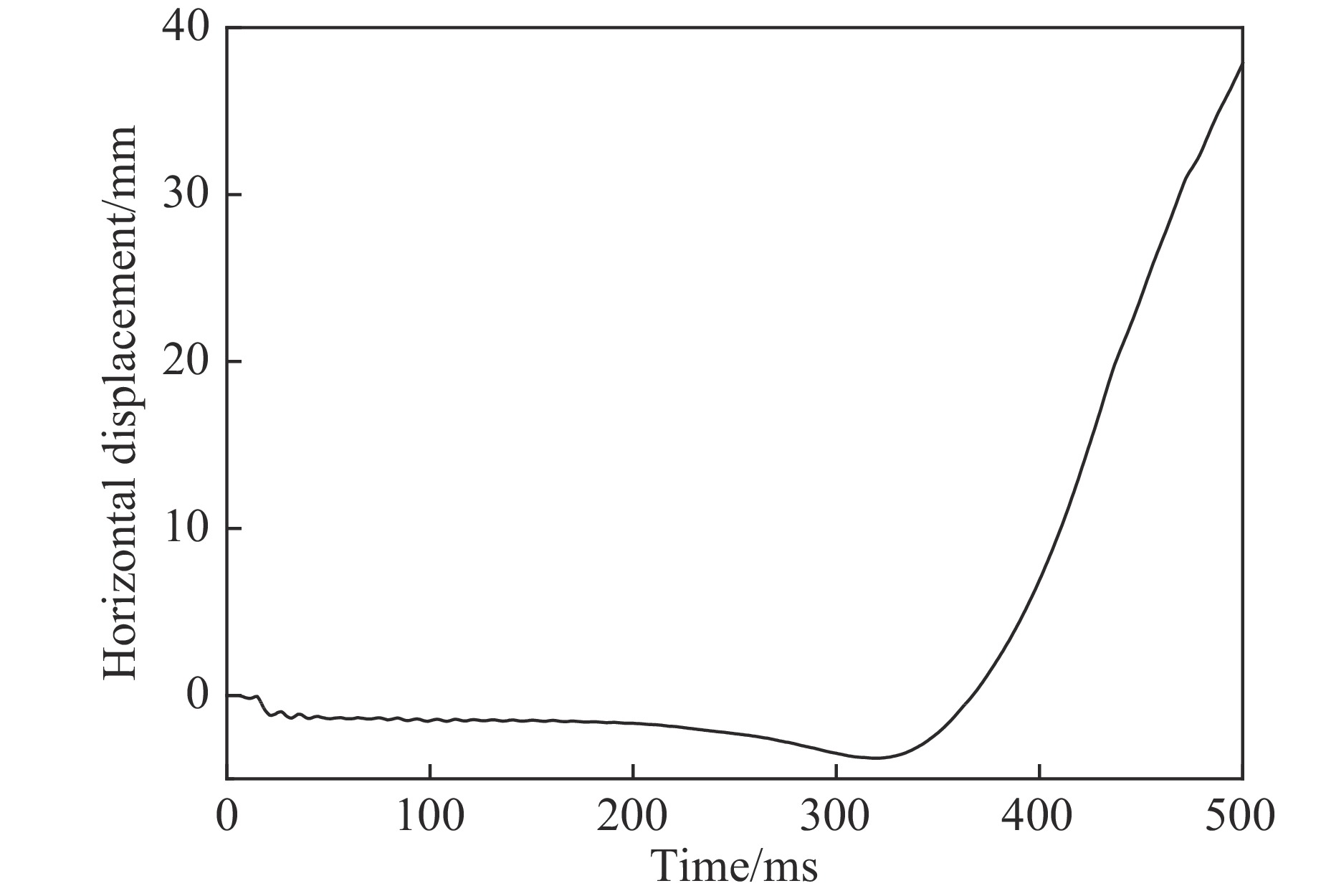
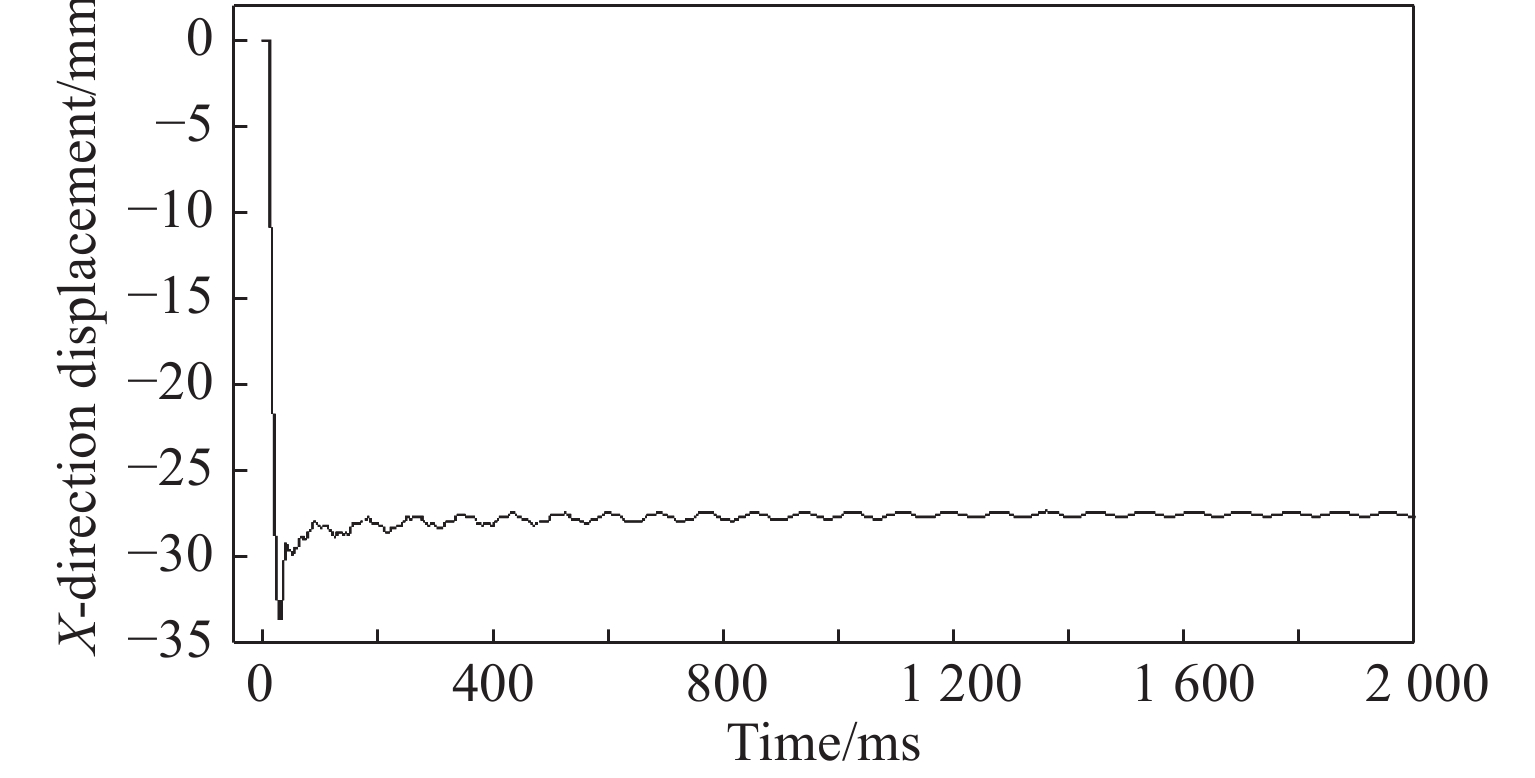
表4给出了在受到冲击作用2 s时框架结构倒塌的范围。由表4数据可知:中柱受冲击作用后整体框架发生倒塌,B、D柱受到冲击作用后有两跨框架发生倒塌,E柱受到冲击作用后仅有边跨发生倒塌,A柱受到冲击作用后并未发生倒塌。提取A柱冲击作用点处的水平位移时程曲线,如图14所示。由图14可知,A柱受到冲击作用后的水平位移为逐渐衰减的正弦曲线,结构不会发生倒塌。在同样的冲击作用下,中间柱的破坏会导致结构的倒塌,E柱受到冲击作用后虽导致边跨倒塌,但延迟了倒塌的过程,而A柱在受到冲击作用后并未发生倒塌。由图7(b)可知,中间3根柱的轴力约为边柱轴力的2倍,验证了文献[6]的结论,即随着轴力的增加,钢筋混凝土柱(墙)破坏失效所需要的冲击能减小。
在本节的框架结构中边柱与中间柱受力的不同之处在于边柱受偏心轴向压力的作用,偏心轴压对A柱有利,对E柱不利,因此冲击A柱时没有发生倒塌,而冲击E柱时发生倒塌。
-
结构的抗连续性倒塌设计方法主要有:概念设计法、关键构件法、拆除构件法和拉结强度法。关键构件法是通过对结构中的关键构件进行加强来增强构件的抗冲击性能,从而降低结构发生连续性倒塌的可能性。本节在前面研究的基础之上,对构件进行加强,并对加强后的结构重新进行计算分析。
受冲击作用后中柱失效导致整榀框架倒塌。把底层中柱视为关键构件进行箍筋加密,试验框架结构的中柱箍筋间距为150 mm,加密后箍筋间距为75 mm。在有限元建模过程中,可以通过对中间柱水平切分加密,再挑选出加密箍筋所在位置的线并赋予钢筋属性。钢筋混凝土柱箍筋加密后,环箍效应增强,使得冲击作用后混凝土裂缝的发展得到抑制,混凝土损伤减少,冲击后柱的残余承载力更大,从而延缓甚至避免框架倒塌。对底层中柱箍筋加密之后,施加同样的冲击作用进行计算分析,结果见图15和图16。
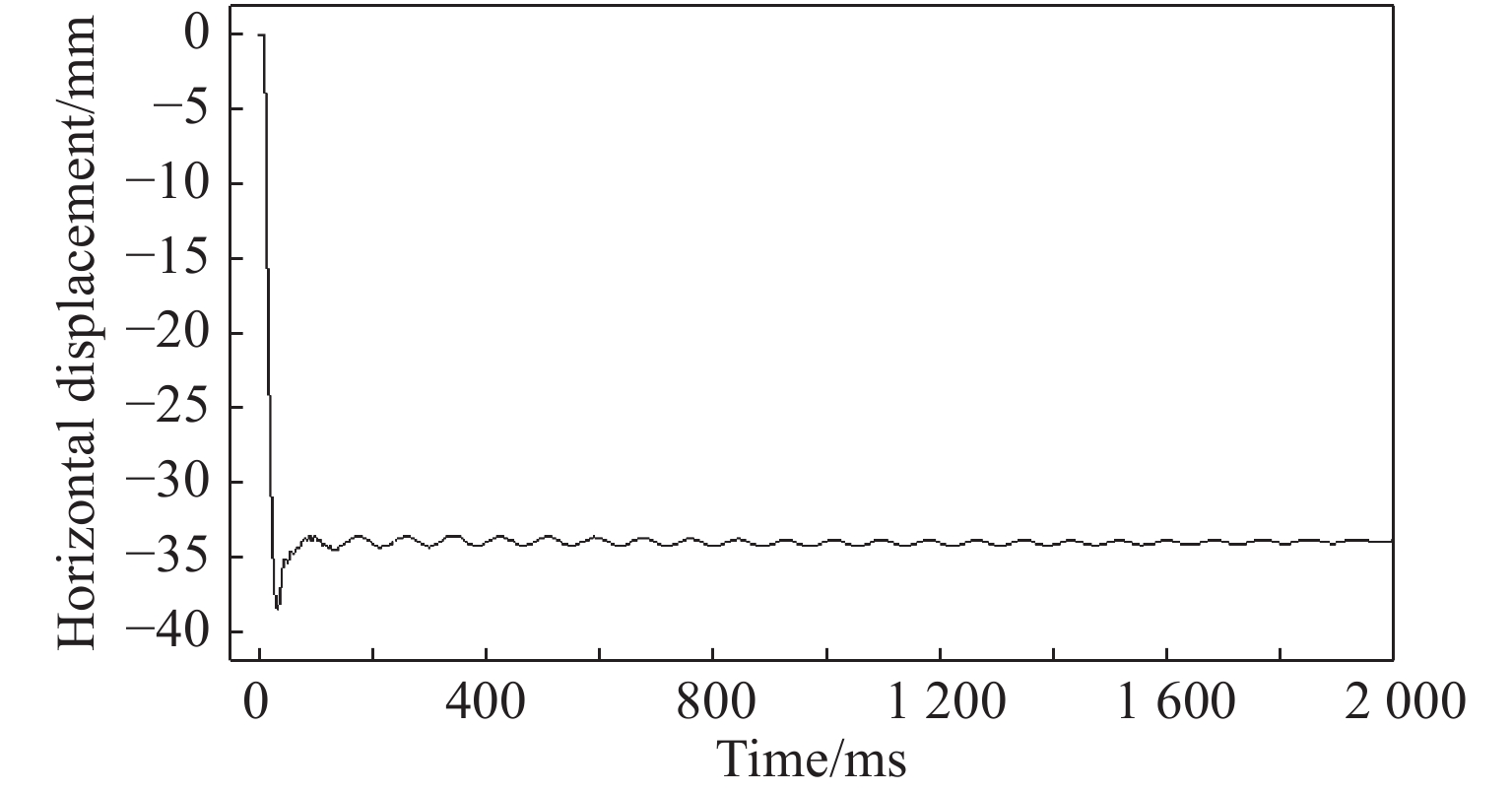
由图15可以看出,加密箍筋之后,在同样的冲击作用下,框架未发生倒塌。一层中柱在冲击作用下损伤最严重,但仍有承载能力;其余梁柱虽有一定损伤,但结构整体未发生较大破坏。图16为一层中柱加密箍筋后冲击作用点处X方向位移时程曲线。由图16可知,冲击作用点在X方向的位移最终在27.5 mm上下衰减振荡。
由此可见,对框架柱进行箍筋加密后,可以显著地增强框架柱的抗冲击能力,并可有效地延缓和避免结构发生倒塌。因此,在实际的框架结构中,可以通过对关键柱加密箍筋来提高钢筋混凝土柱的抗冲击能力及框架的抗倒塌能力。
3.1. 有限元模型
3.2. 框架位移分析
3.3. 框架倒塌过程分析
3.4. 冲击不同位置柱时框架的整体响应
3.5. 箍筋对框架抗连续性倒塌的影响
-
以单榀钢筋混凝土框架的试验模型为研究对象,采用数值模拟方法,对冲击荷载作用下该框架的抗倒塌性能进行了研究,得出如下主要结论。
(1)采用ANSYS/LS-DYNA建立钢筋混凝土框架的有限元模型进行抽柱模拟,能够真实反映实际框架结构的倒塌过程,结合对单个钢筋混凝土构件试验结果开展的数值模拟验证,保证了数值模拟分析的有效性。
(2)底层中柱受到冲击作用后的响应与试验不同,在“拱作用”影响下,中柱柱顶会先出现向上的位移,当中柱失去承载力后框架发生整体连续性倒塌,倒塌过程与试验以及抽柱模拟的倒塌过程一致。
(3)冲击中柱结构倒塌过程中存在“拱作用”向“悬索作用”转换的机制,柱顶先向外移动再向内移动。虽然在冲击初始阶段,柱顶均向冲击方向移动,但总体仍向外移动。
(4)对底层各根钢筋混凝土柱施加同样的冲击作用,冲击中柱时会发生整体倒塌破坏,冲击其他柱时破坏范围较小,冲击边柱A时框架未发生倒塌。其原因有二:一是边柱轴力比中间柱轴力小,使柱破坏失去承载力所需的冲击能增大;二是边柱承受偏心压力的作用,A柱的偏心压力起有利作用。
(5)加密柱箍筋能够增强钢筋混凝土柱的抗冲击能力,延缓甚至避免钢筋混凝土框架结构的连续性倒塌。

 首页
首页 登录
登录 注册
注册




 下载:
下载: