首页
登录
注册
-
当低密度流体在惯性力作用下加速高密度流体时，界面上的预制初始扰动会增长，这种现象称为Rayleigh-Taylor（RT）不稳定性[1-2]。同样，在金属材料界面也会发生RT不稳定性，产生与流体界面不稳定性类似的尖钉和气泡结构，但是与流体界面不稳定性的最大不同之处在于金属材料具有强度效应，而研究表明金属材料强度能够抑制扰动增长[3-6]。并且，金属的强度效应也会使金属界面不稳定性问题比流体界面不稳定性更复杂，需要考虑的因素更多，比如金属材料的本构方程、损伤断裂、相变、熔化、微结构特征等。金属界面不稳定性的发生常常预示着材料经历高温、高压、高应变率等极端环境，因而常存在于惯性约束聚变[7-9]、超新星爆炸[10]、小行星撞击[11-12]、地球内核运动和板块构造[13-14]以及爆炸焊接等领域，因此具有重要的研究意义。
目前，金属材料界面不稳定性的理论研究主要利用能量平衡[15-17]或力平衡[18-20]原理，推导扰动增长所满足的色散关系，即线性分析；由于这些线性分析方法均采用理想塑性本构关系，因此预测扰动增长受到较大的限制。Bai等[21]基于能量平衡原理，采用Steinberg-Guinan（SG）和Johnson-Cook（JC）本构模型及变压力的准等熵加载历程，针对有限厚度金属平板问题，推导了相应的扰动增长方程，对线性分析方法进行了拓展，使其能够用于平面几何中金属材料不稳定性线性至非线性段增长的预测，并对爆轰驱动和等离子体驱动的金属界面不稳定性实验[6, 20, 22-23]进行了分析，结果和实验吻合较好，但是这种线性分析方法仍然存在较大的局限性，如目前还无法考虑加载过程等。
金属材料RT不稳定性的实验研究始于20世纪70年代，首次由Barnes等[22, 24]通过炸药爆轰准等熵驱动铝平板实现，并利用高能X射线照相观察界面扰动增长。之后的平面爆轰驱动金属材料RT不稳定性实验[25-27]均采用相似的装置。美国和俄罗斯开展了大量有关金属材料界面不稳定性的研究工作，包括界面扰动增长规律及影响因素等。Olson等[28]通过爆轰驱动实验，研究了铜材料的微结构和机加工对RT不稳定性增长的影响，发现单晶晶向和材料加工导致的应变硬化会影响扰动增长，而多晶材料的晶粒尺寸和晶界强化在所研究的加载条件下对扰动增长无影响。Wang等[27]通过爆轰驱动实验和数值模拟，研究了纯铝的RT不稳定性增长规律和强度因素（基于SG本构模型的初始剪切模量和初始屈服强度）对扰动增长的影响。何长江等[29]通过数值模拟研究了初始扰动波长对平面爆轰驱动铝RT不稳定性增长的影响。郝鹏程等[30]和刘军等[31]通过对内爆加载金属钢壳的数值模拟，研究了材料强度（剪切模量和基于理想弹塑性本构的屈服强度以及是否考虑弹塑性）和初始波长对界面扰动增长的影响。平面爆轰准等熵加载的压力一般在30 GPa左右，为了提高加载压力，Frahan等[26]采用两级炸药爆轰驱动技术，即第一级炸药驱动铁飞片撞击起爆第二级炸药，再加载样品，使加载压力提高到50 GPa，由此研究了该加载压力下铍的RT不稳定性问题，并结合数值模拟对材料不同本构模型的适用性进行了检验。为了研究极端加载压力和应变率条件下的金属界面不稳定性及材料混合行为，人们又发展了电磁加载[32-33]和激光加载技术[5-6, 23]，并开展了大量研究工作，如Park等[5-6, 34]利用Omega激光器，结合数值模拟，研究了钒和钽分别在100 GPa和350 GPa的准等熵加载压力下的扰动增长行为。目前，美国国家点火装置NIF已经能够实现超过1 TPa的准等熵加载[35]。
由于材料强度对金属界面不稳定性发展有抑制作用，所以近年来人们又将其作为一种手段来研究金属材料的强度—扰动增长法[4, 25, 36]。Lorenz等[23]利用基于激光准等熵加载技术的RT扰动增长法研究了峰值压力为20 GPa时6061-T6铝的屈服强度，结果显示该条件下6061-T6铝的屈服强度比正常条件下高出3.6倍。Park等[5-6]利用激光准等熵加载实验和数值模拟研究发现了钒在100 GPa加载条件下具有一种新的RT不稳定性致稳机制—声子拖曳导致有效晶格黏性增大，进而导致钒的强度增大，对RT不稳定性的致稳作用增强；而且研究显示钒的强度增大了3.5倍，而350 GPa加载压力下钽的强度增大了13倍[34]。Belof等[37]通过爆轰驱动铁的RT不稳定性实验和数值模拟，确认了铁在经历
$\alpha \to \varepsilon \to \alpha '$ 相变过程中强度大大提高。本研究利用自研的爆轰与冲击动力学欧拉计算程序和SG本构模型，针对爆轰驱动金属锡RT不稳定性增长对两类模型初始参数的敏感性进行数值模拟分析，一类是样品的初始参数，包括初始扰动振幅、初始扰动波长和样品初始厚度，另一类是SG本构模型的初始参数。
-
对于考虑爆轰和材料弹塑性行为的多物质、大变形及强冲击波物理问题，发展了高保真度的爆轰与冲击动力学欧拉有限体积计算程序，其守恒型控制方程组为
式中：下标i、j分别代表x、y、z 3个方向，遵循张量运算法则，V为控制体体积，S为控制体表面积，ni为外法向单位矢量，ρ、uk (k = i, j)、p、E分别为密度、速度、压强和单位质量总能量，sij为偏应力张量分量。
采用维数分裂技术，将式(1)描述的物理问题分解为多个一维问题。对于每个一维问题，采用PPM（Piecewise parabolic method）方法对单元内物理量的分布进行插值和重构，然后通过欧拉型两步算法进行计算，即物理量的Lagrange推进求解，再将拉氏网格上的物理量映射到静止的欧拉网格上。材料强度效应、炸药爆轰过程和人工黏性在Lagrange步中实现。多物质界面采用体积分数方法进行捕捉。
数值模拟中，炸药和金属材料分别采用JWL和Mie-Grüneisen状态方程（EOS）描述
式中：v = ρ0/ρ为相对比容，T为温度，α、σ、R1、R2、ω为常数，
$\bar E$ 为单位体积内能。式中：
$\mu = \dfrac{\rho }{{{\rho _0}}} - 1$ 为相对压缩度，ρ0为初始密度，c为零压声速，γ0为Grüneisen系数，$\alpha $ 、S1、S2、S3为常数。金属材料采用SG本构模型描述。SG本构模型是在弹塑性本构方程中引入压力、温度和应变率项，并且压力与应变率对流动应力的耦合效应具有可分离变量特性。因为SG本构模型中流动应力依赖于压力，所以材料的本构方程与状态方程之间存在某种耦合关系。这一耦合关系反映了高压下金属材料的压力硬化特性。SG本构模型给出的动态屈服强度YSG和剪切模量G分别为
式中：Y0和G0分别为初始屈服强度和剪切模量，β和n分别为材料应变硬化系数和硬化指数，A为压力硬化系数，η = ρ/ρ0为材料压缩比，B为热软化系数。
-
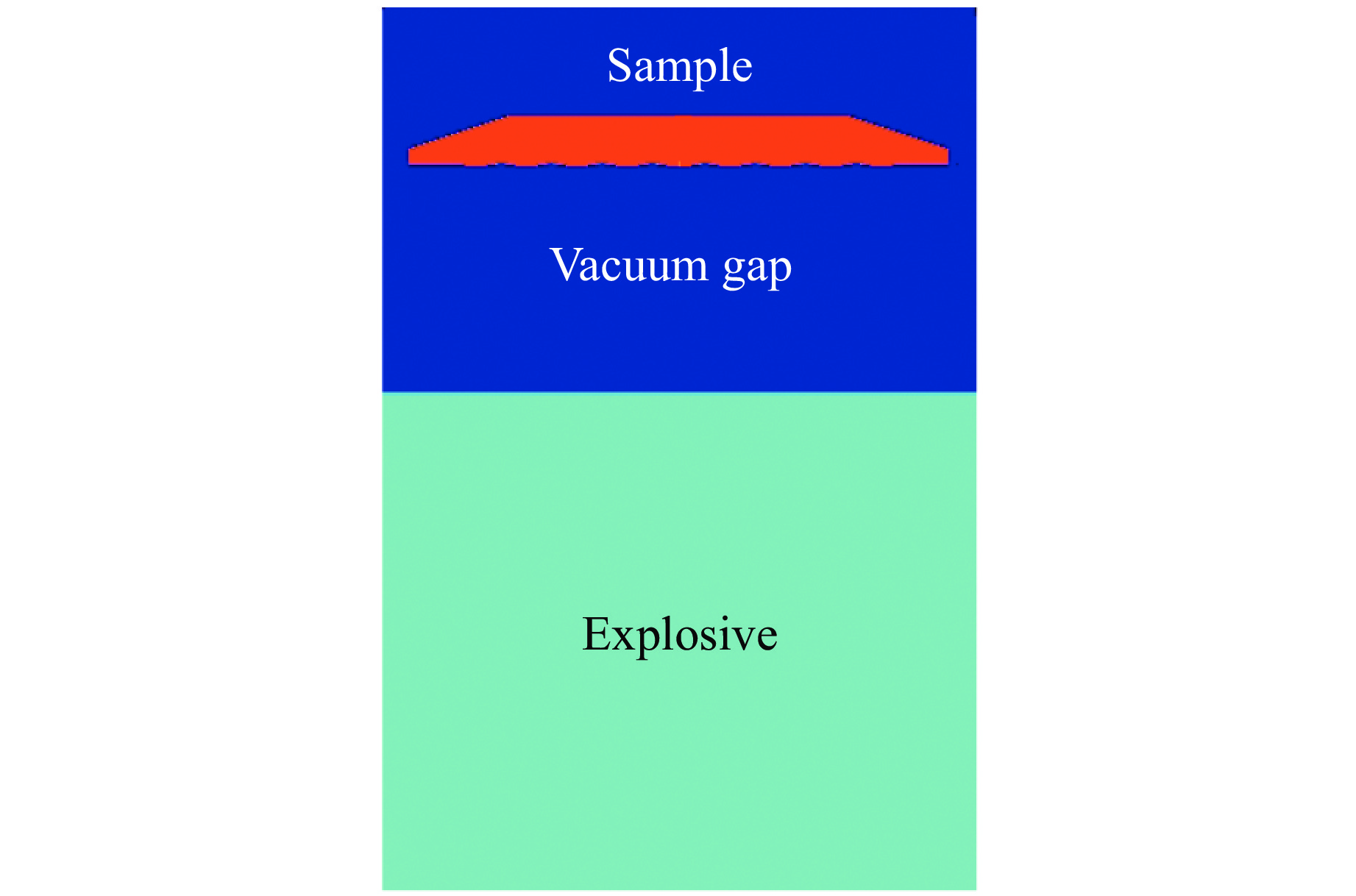
简化的二维计算模型见图1，炸药为JO-9159，样品为金属锡。炸药高度为30 mm；样品直径为32 mm，厚度3 mm，样品面向炸药一侧的界面上预置了初始振幅a0 = 0.1 mm、初始波长λ0 = 3 mm的正弦形式初始扰动。炸药和样品之间的真空间隙尺寸为10 mm。该真空间隙保证了爆轰产物经过真空间隙加载样品的过程中压力连续增大，形成轻介质对重介质的准等熵加载，进而诱发RT不稳定性；它的另一个作用是确保在高压下样品温度依然低于熔化温度[23]。
JO-9159炸药的JWL状态方程参数见表1，锡的Mie-Grüneisen状态方程参数和SG本构模型标准参数见表2和表3。其中：pCJ和DCJ分别为炸药的爆压和爆速，Ymax为材料最大屈服强度。
-
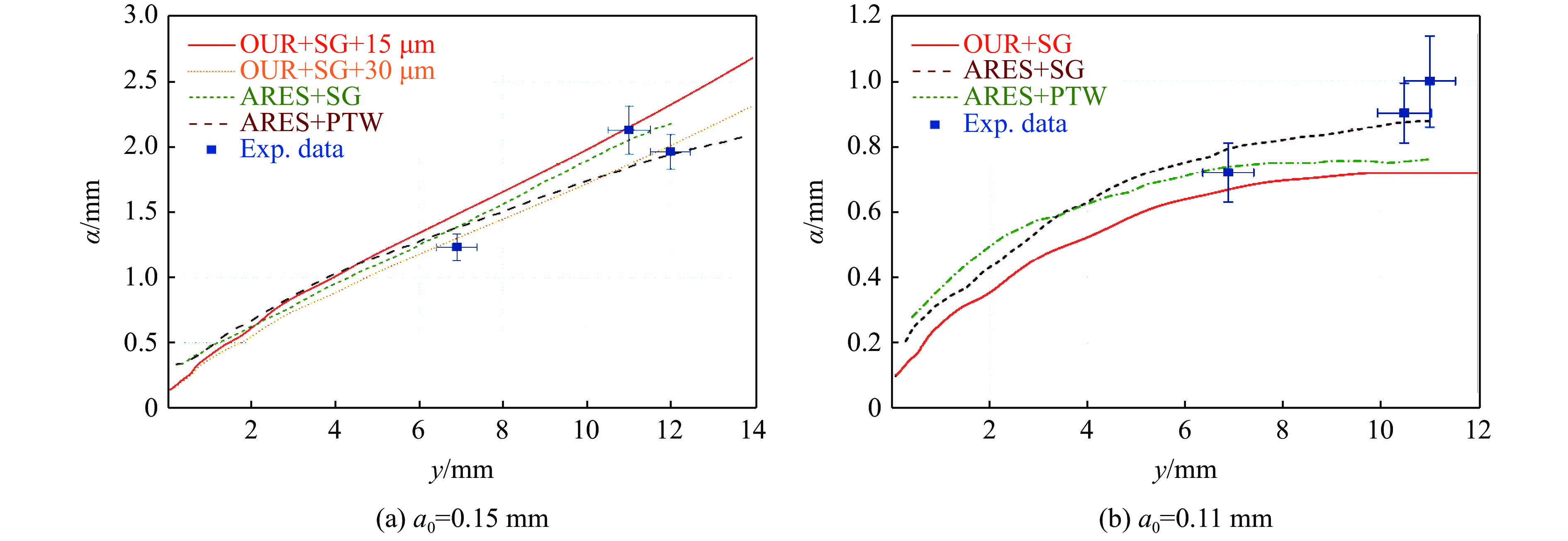
在开展金属锡RT不稳定性数值模拟研究之前，先通过对Lindquist等[38]的爆轰驱动T-6061铝的RT不稳定性实验进行模拟，确认本计算程序的可靠性。该实验采用HMX炸药爆轰加载1.5 mm厚的铝样品，加载压力峰值为30 GPa。初始扰动波长λ0 = 2 mm，初始扰动振幅a0 = 0.15 mm, 0.11 mm。图2给出了本研究通过自研欧拉程序计算得到的扰动振幅a和文献中采用ARES程序计算的结果，及其与实验结果的比较（横轴y为自由面运动位移）。可以看出，吻合度较好，表明自研的欧拉程序模拟这类爆轰驱动金属材料界面不稳定性是准确的。
-
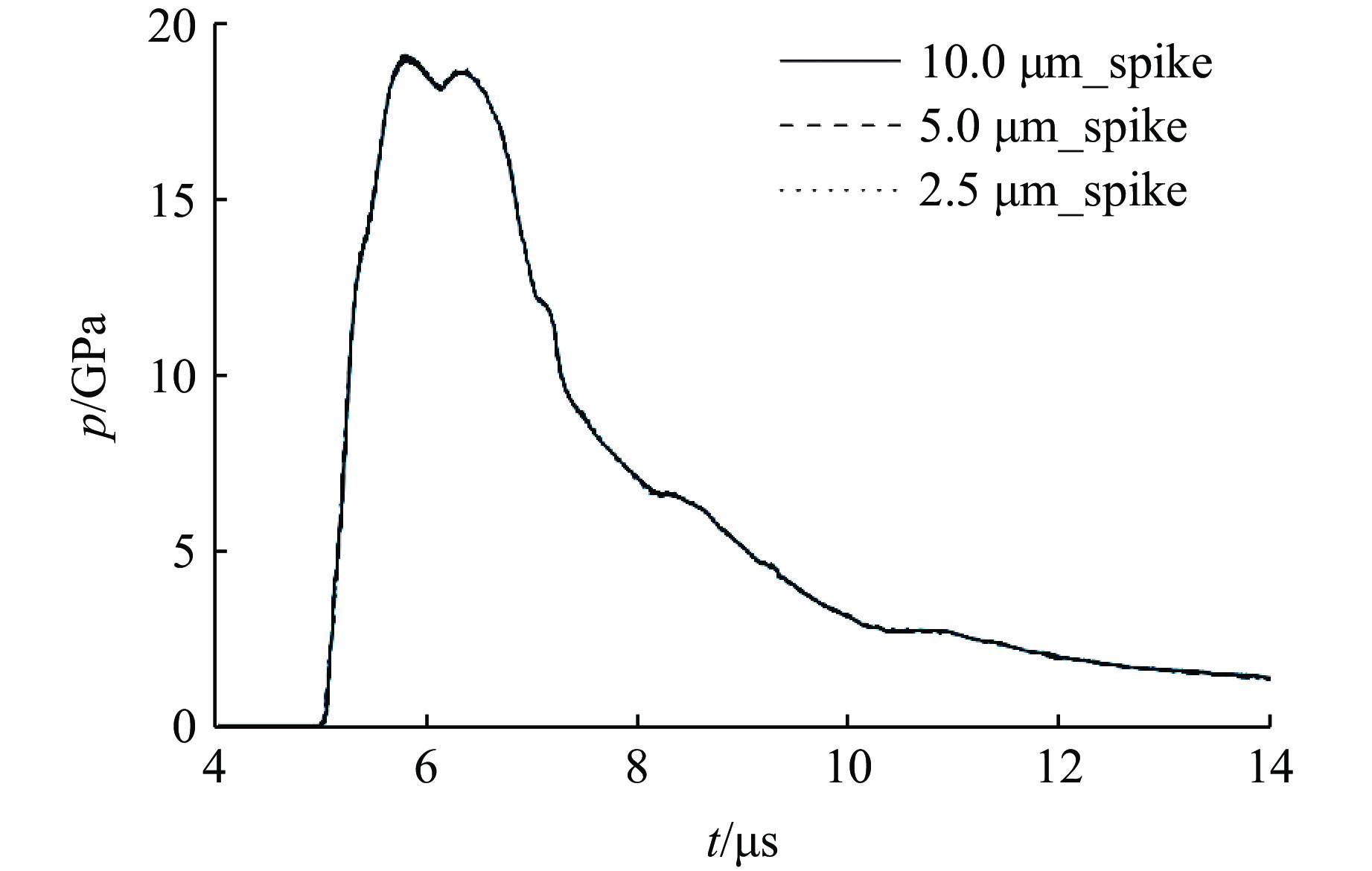
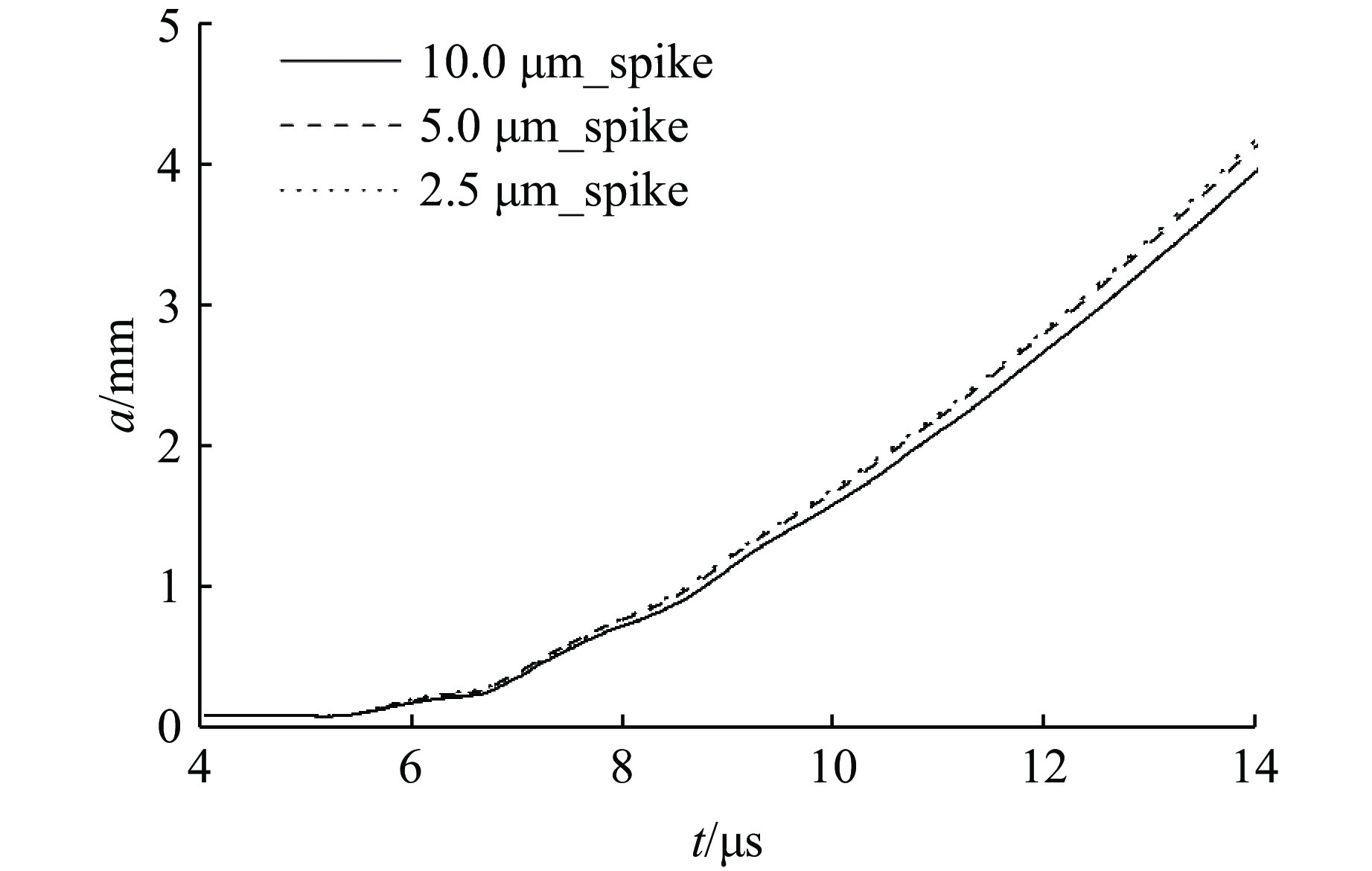
首先，考察模拟结果对计算网格的收敛性问题。图3和图4分别给出了网格尺寸为10.0、5.0和2.5
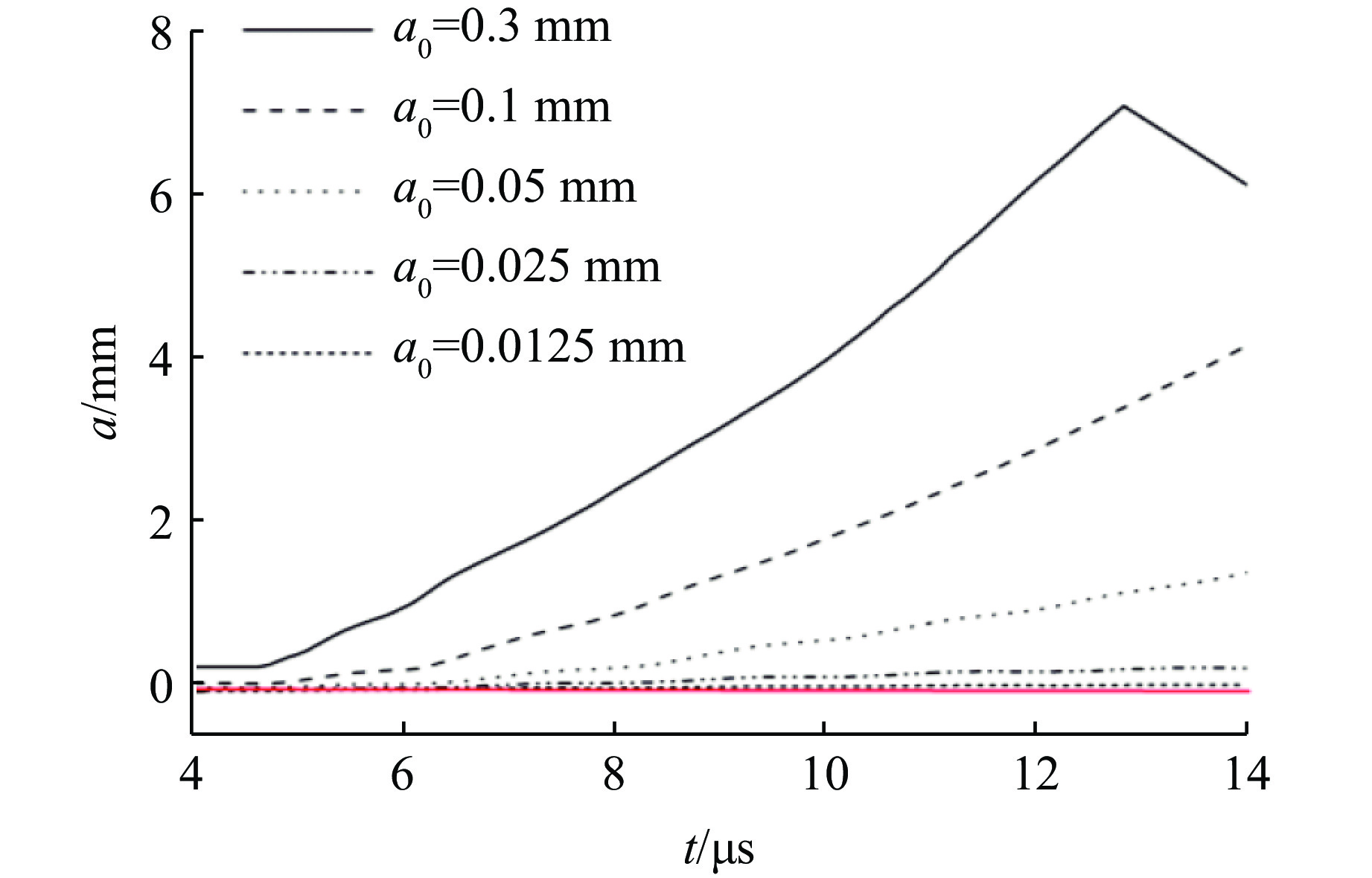
${\text{μ}}{\rm{m}}$ 时加载压力剖面和扰动振幅增长曲线。可以看出，2.5${\text{μ}}{\rm{m}}$ 时模拟结果已经达到收敛，所以后续的所有计算均采用2.5${\text{μ}}{\rm{m}}$ 的计算网格。从图3还可以看出：加载压力p是连续光滑增大的，近似形成对界面的准等熵加载；之后由于爆轰产物膨胀压力持续减小及由自由面多次反射的稀疏波抵达扰动界面形成持续的卸载作用，加载压力逐渐减小。接下来，通过数值模拟研究金属锡样品初始参数，包括初始扰动振幅、初始扰动波长、样品初始厚度对爆轰驱动金属锡RT不稳定性增长的影响。在研究初始振幅的影响时，保持初始波长λ0为3 mm，样品初始厚度h为3 mm，初始振幅a0分别取0.3、0.1、0.05、0.025和0.012 5 mm。图5显示了不同初始振幅时的扰动振幅增长曲线。可以看出：随着初始振幅的减小，扰动振幅增长也减弱；当初始振幅减小到一定值后，扰动振幅不再增长，即爆轰驱动金属锡RT不稳定性增长存在一个截止初始振幅。
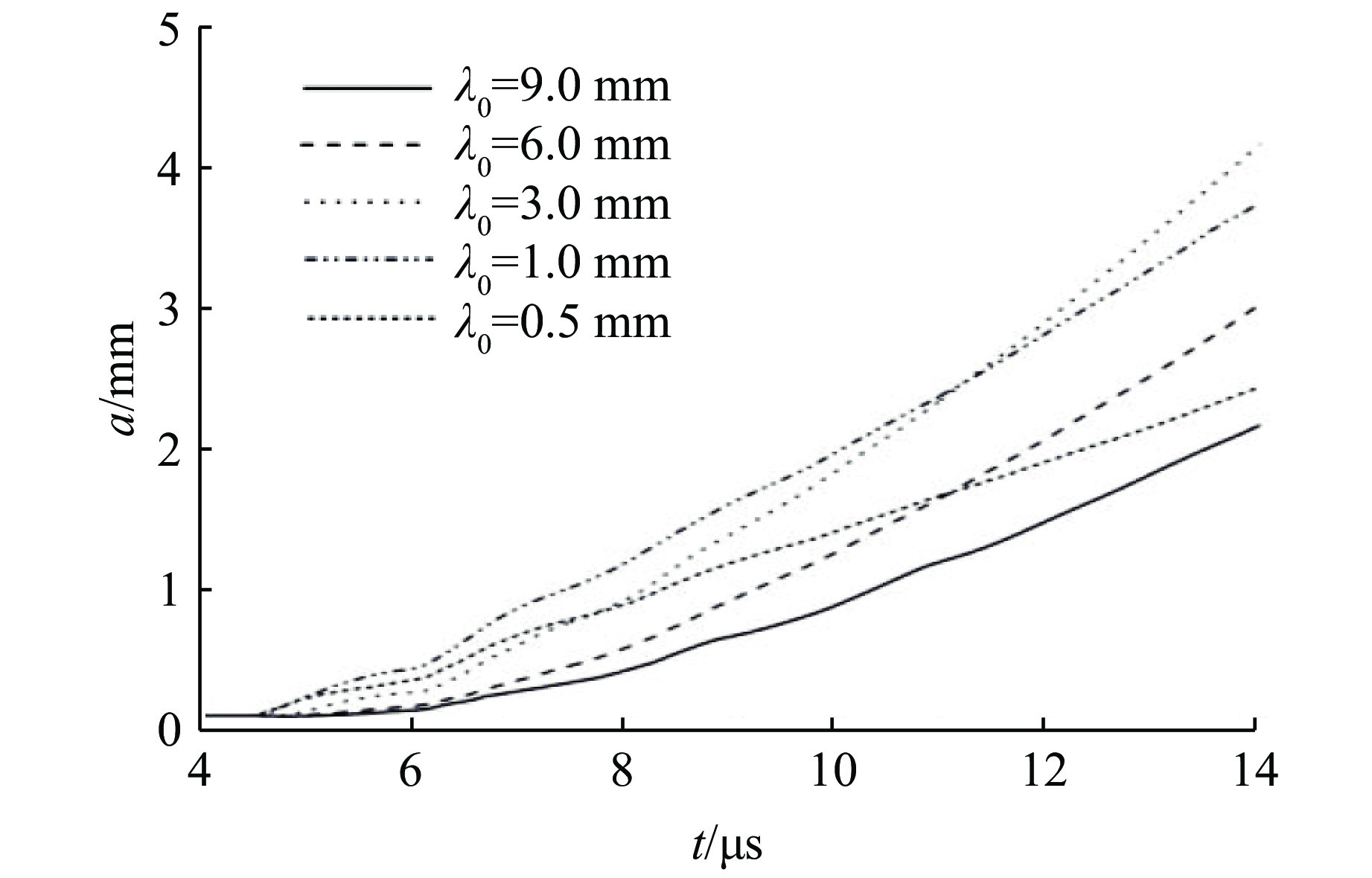
在研究初始波长的影响时，保持初始振幅为0.1 mm，样品初始厚度为3 mm，而初始波长λ0分别取9、6、3、1和0.5 mm。图6给出了不同初始波长时的扰动振幅增长曲线。从初始波长为9 mm开始，随着初始波长的减小，扰动振幅逐渐增大；但是，当初始波长减小到一定程度后，扰动振幅增长又随着初始波长的减小而减小。所以爆轰驱动金属锡RT不稳定性增长存在一个最不稳定的波长，或者增长速度最快的模态。
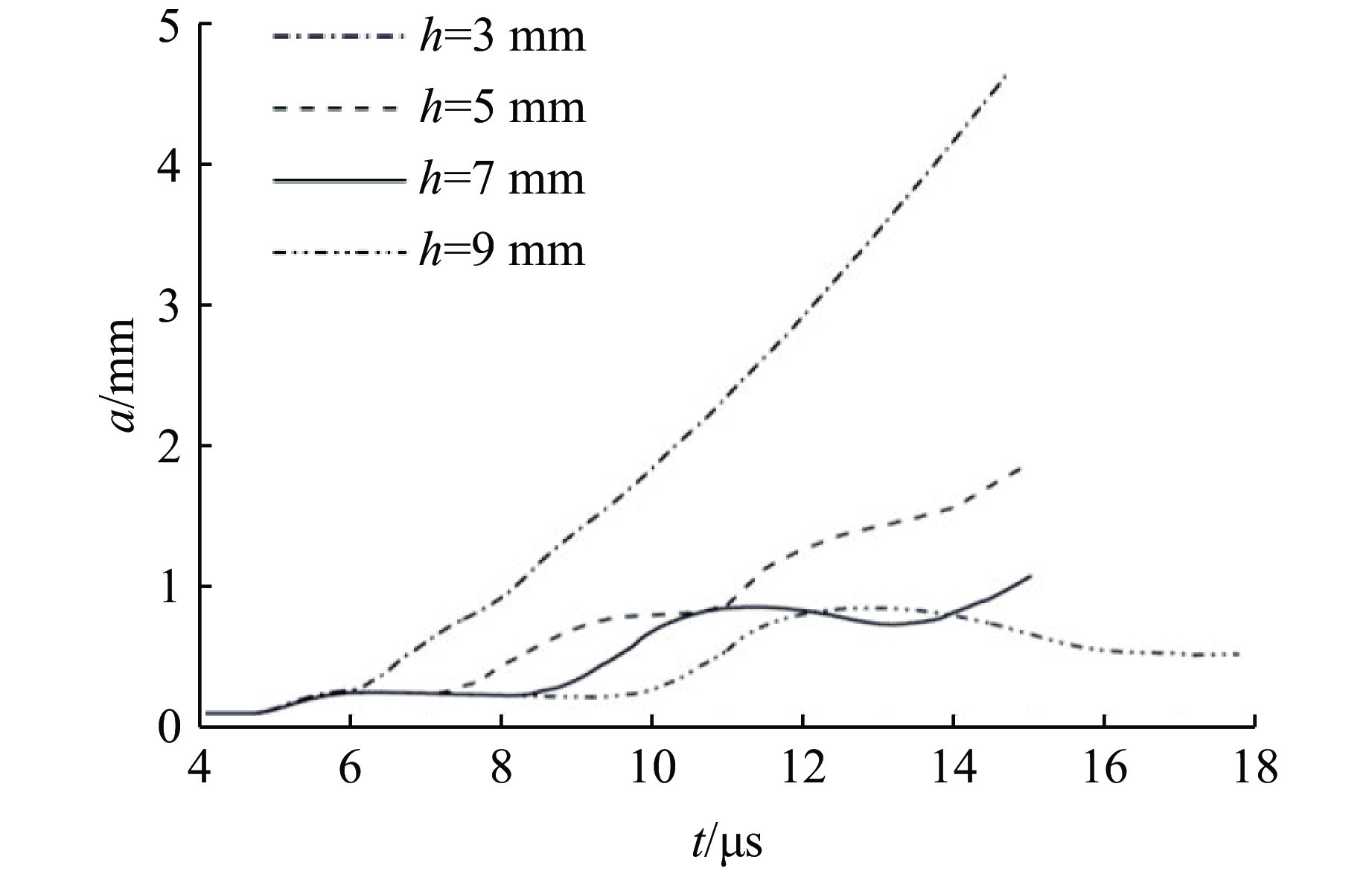
在研究样品初始厚度的影响时，保持初始振幅为0.1 mm，初始波长为3 mm，而样品初始厚度h分别取3、5、7和9 mm。图7显示了样品初始厚度不同时的扰动振幅增长曲线。随着样品初始厚度的增大，扰动增长减弱，表明样品厚度增大可以抑制扰动增长；而且当样品厚度增大到一定程度时，扰动增长停止，即爆轰驱动金属锡RT不稳定性增长存在一个样品截止厚度。
-
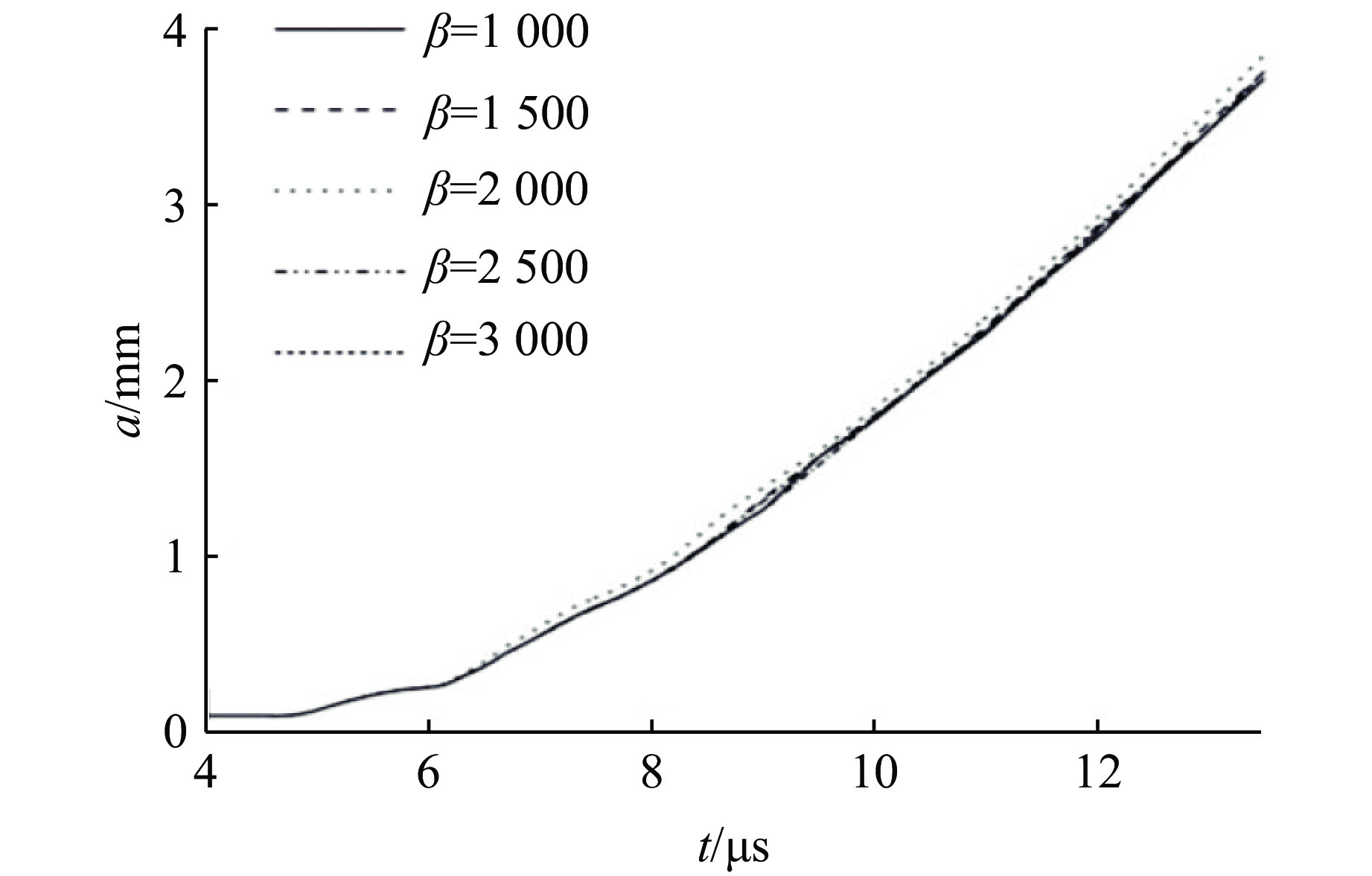
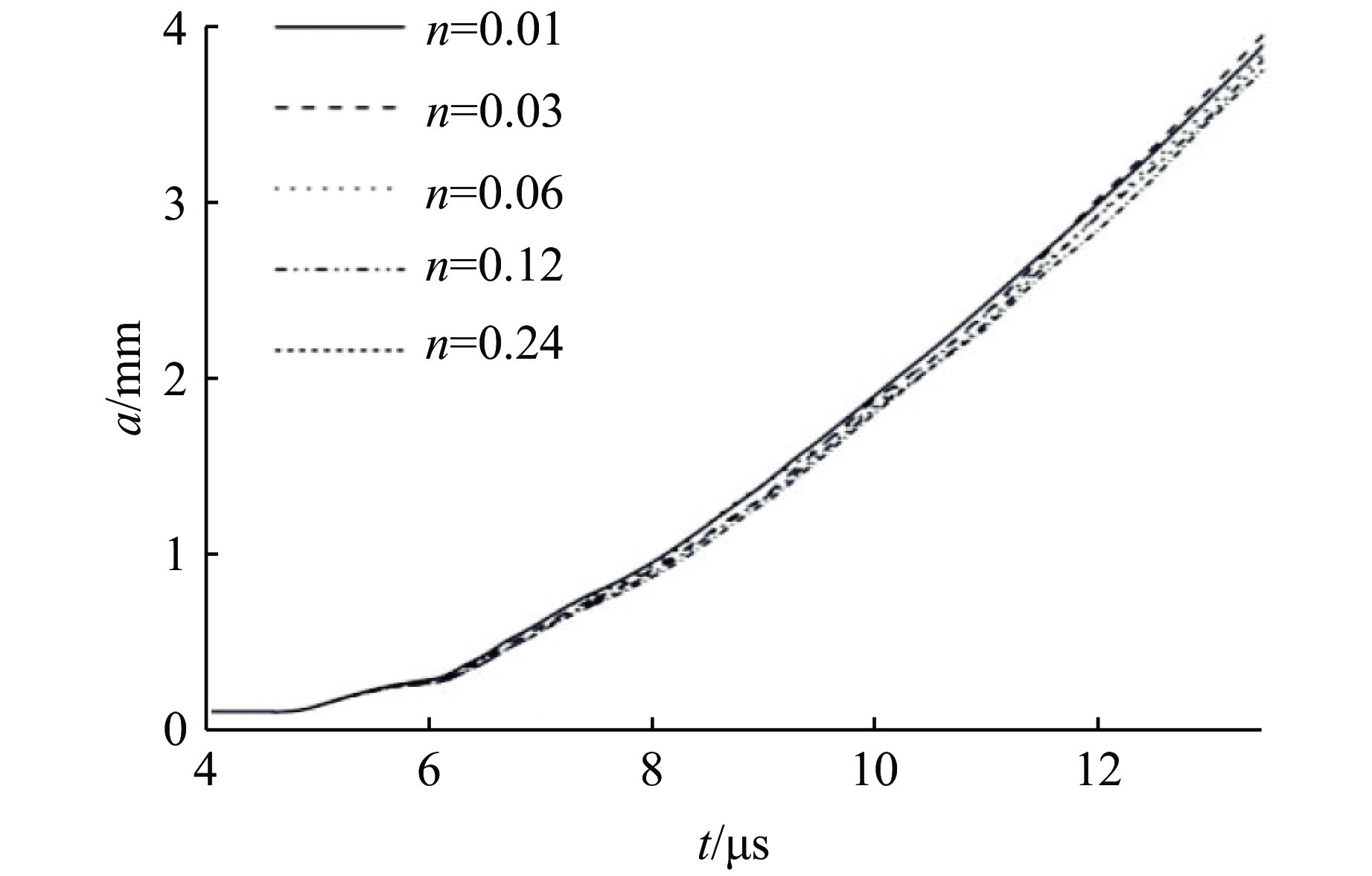
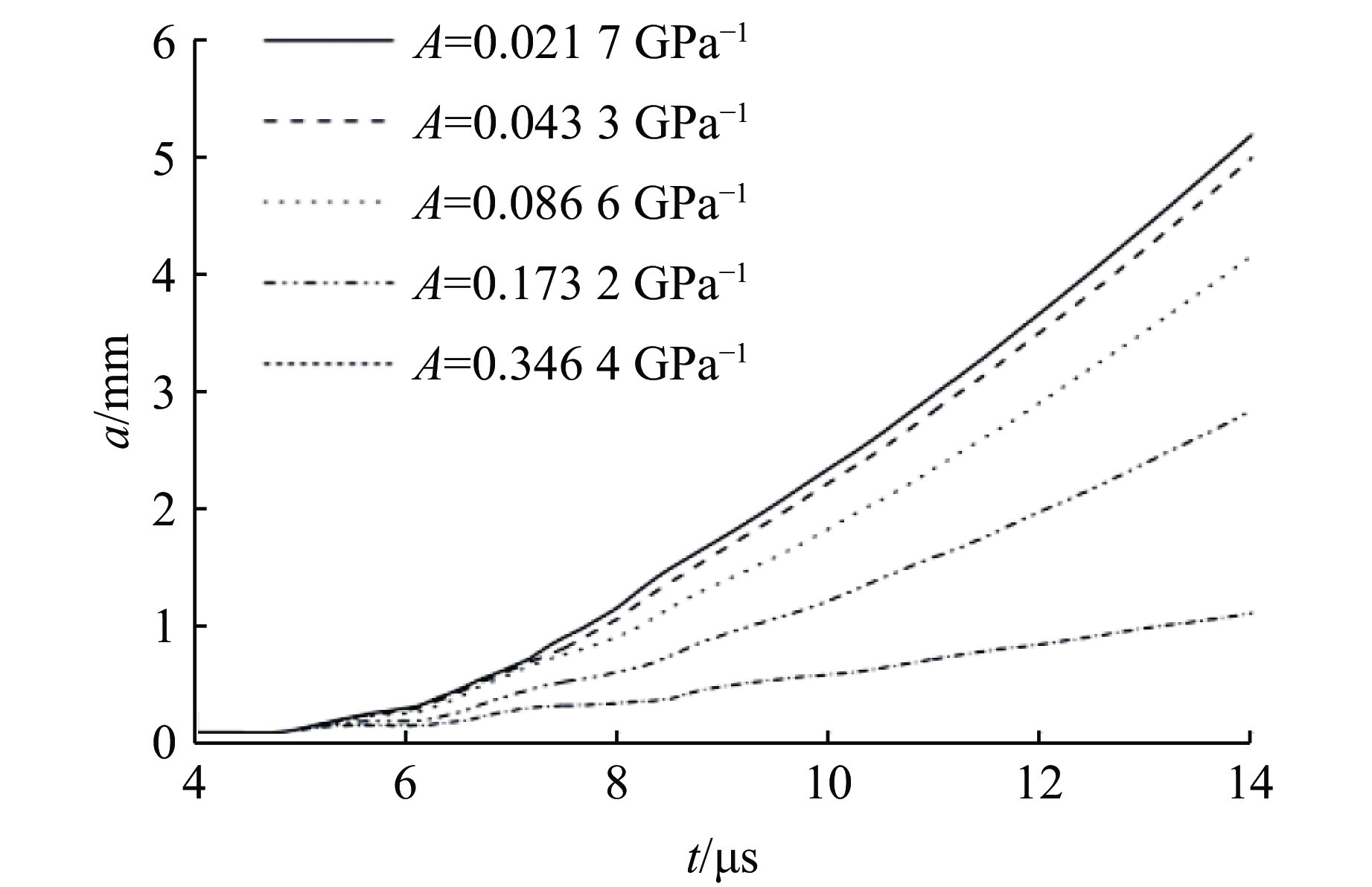
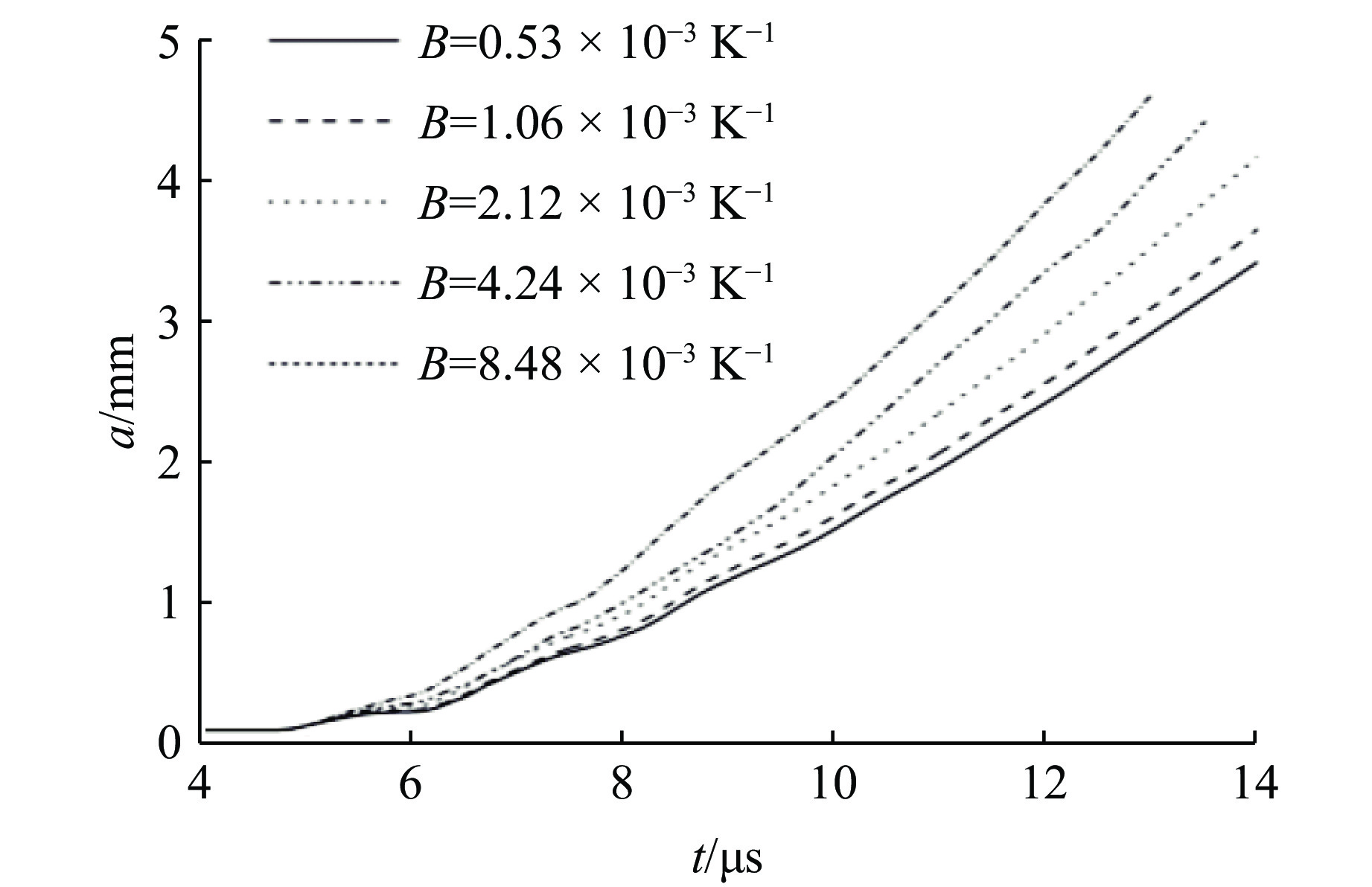
研究金属锡RT不稳定性增长对SG本构模型参数的敏感性时，计算模型的初始厚度取3 mm，初始振幅取0.1 mm，初始波长取3 mm。SG本构模型的可调参数包括应变硬化系数β、应变硬化指数n、压力硬化系数A和热软化系数B，对于锡材料，它们的标准值分别为2 000、0.06、0.086 6 GPa–1、2 120 K–1（见表3）。在研究其中一个参数的影响时，其余参数均取标准值。材料应变硬化系数β依次取1 000、1 500、2 000、2 500、3 000；应变硬化指数n依次取0.01、0.03、0.06、0.12、0.24；压力硬化系数A依次取0.021 7、0.043 3、0.086 6、0.173 2、0.346 4 GPa–1；热软化系数B依次取0.53×10−3、1.06×10−3、2. 12×10−3、4.24×10−3、8.48×10−3 K–1。
图8～图11分别给出了改变锡SG本构模型的应变硬化系数β、应变硬化指数n、压力硬化系数A和热软化系数B时的扰动振幅增长曲线。可以看出：在爆轰准等熵驱动下金属材料发生复杂流动，此时材料应变硬化系数和应变硬化指数的变化对扰动振幅增长的影响很小，即这两个SG本构模型参数的改变对材料屈服强度的影响较小；而压力硬化系数和热软化系数的变化对扰动增长的影响显著，随着压力硬化系数的增大，扰动增长受到的抑制作用越显著，而随着热软化系数的减小，扰动增长受到抑制效果的变化却逐渐减小，即热软化系数小到一定程度时其变化将很难改变材料屈服强度。根据文献分析可知，高压高应变率加载条件下，金属材料的强度一般都会增大，而标准参数的本构模型一般都低估了材料强度。因此基于SG本构模型，采用扰动增长法预估高压高应变率下锡的材料强度，修正压力硬化系数以获得合理的强度是一条合理的途径。
-
开展了爆轰驱动金属锡RT不稳定性增长对样品初始参数和SG本构模型初始参数敏感性的数值模拟分析，得出以下结论。
（1）样品初始参数（初始振幅、初始波长、样品初始厚度）对爆轰驱动锡RT不稳定性增长有重要影响。RT不稳定性增长随着初始振幅的减小而减小，且存在一个截止初始振幅；存在一个最不稳定的模态（波长），当初始波长大于该波长时，RT不稳定性增长随着初始波长的减小而增大，反之，RT不稳定性增长随着初始波长的减小而减小；样品厚度的增大可以抑制RT不稳定性增长，而且存在一个样品截止厚度。
（2）金属锡的RT不稳定性增长对其SG本构模型应变硬化系数和应变硬化指数的变化不敏感，而对压力硬化系数和热软化系数比较敏感，但是从采用扰动增长法预估材料强度的角度来说，修正压力硬化系数以获得合理的锡材料强度是合理的途径。
金属锡Rayleigh-Taylor不稳定性对模型参数敏感性的数值分析
Numerical Analysis of Sensitivity of Tin Rayleigh-Taylor Instability to Model Parameters
-
摘要: 利用自研的爆轰与冲击动力学欧拉计算程序和Steinberg-Guinan（SG）本构模型，数值模拟分析了样品初始参数（初始振幅、初始波长、样品初始厚度）和SG本构模型初始参数对爆轰驱动锡Rayleigh-Taylor（RT）不稳定性增长的影响。结果表明金属锡样品的初始参数对其RT不稳定性增长有很大的影响。RT不稳定性增长随着初始振幅的减小而减小，且存在一个截止初始振幅；存在一个最不稳定的模态（波长），当初始波长大于该波长时，RT不稳定性增长随着初始波长的减小而增大，反之，RT不稳定性增长随着初始波长的减小而减小；样品厚度的增大可以抑制RT不稳定性增长，而且存在一个样品截止厚度。金属锡的RT不稳定性增长对其SG本构模型应变硬化系数和应变硬化指数的变化不敏感，而对压力硬化系数和热软化系数比较敏感。从采用扰动增长法预估材料强度的角度来说，修正压力硬化系数以获得锡合理的材料强度是合理的途径。
-
关键词:
- Rayleigh-Taylor不稳定性 /
- 材料强度 /
- 本构模型
Abstract: The sensitivity of Rayleigh-Taylor instability of tin driven by explosion to the initial parameters of sample (initial amplitude, wavelength and thickness of sample) and the initial parameters of SG constitutive model are numerical investigated by using an in-house Eulerian detonation and shock wave code. It concludes that the initial parameters of sample have a significant effect on the RT instability of Sn. The Sn RT instability grows more slowly with the initial amplitude decreasing, and a cutoff initial amplitude exists. A most unstable mode (wavelength) exists, when the initial wavelength is larger than this value, the RT instability grows faster as the initial wavelength diminishes; on the contrary, the RT instability grows slower as the initial wavelength decreases. The larger thickness of sample can restrain the growth of RT instability greatly, and a cutoff thickness of sample also exists. The Sn RT instability growth is not sensitive to the strain hardening coefficient and exponent, and it is greatly sensitive to the pressure hardening coefficient and thermal softening coefficient. But it should be a practical path to estimate the material strength of Sn through modifying the pressure hardening coefficient of SG model.-
Key words:
- Rayleigh-Taylor instability /
- material strength /
- constitutive model .
-
-
图 2 Lindquist等爆轰驱动铝实验的扰动振幅比较
Figure 2. Comparison of perturbation amplitudes of Lindquist et al.’s experiments driven by explosion
图 5 不同初始振幅时的扰动振幅增长曲线
Figure 5. Perturbation amplitude growth for different initial amplitude
图 6 不同初始波长时的扰动振幅增长曲线
Figure 6. Perturbation amplitude growth for different initial wavelength
图 7 不同样品初始厚度时的扰动振幅增长曲线
Figure 7. Perturbation amplitude growth for different initial thickness of sample
图 8 应变硬化系数不同时的扰动振幅增长曲线
Figure 8. Perturbation amplitude growth for different strain hardening coefficient
图 9 应变硬化指数不同时的扰动振幅增长曲线
Figure 9. Perturbation amplitude growth for different strain hardening exponent
图 10 压力硬化系数不同时的扰动振幅增长曲线
Figure 10. Perturbation amplitude growth for different pressure hardening coefficient
图 11 热软化系数不同时的扰动振幅增长曲线
Figure 11. Perturbation amplitude growth for different thermal softening coefficient
表 1 JO-9159炸药JWL状态方程参数
Table 1. EOS parameters of JO-9159 explosive
ρ0/(g·cm–3) pCJ/GPa DCJ/(km·s–1) α/GPa σ/GPa R1 R2 ω 1.86 36 8.862 934.8 12.7 4.6 1.1 0.37 
下载: 导出CSV
表 2 锡的Mie-Grüneisen状态方程参数
Table 2. Mie-Grüneisen EOS parameters of Sn
ρ0/(g·cm–3) c/(km·s–1) γ0 $\alpha $ 
S1 S2 S3 7.287 2.61 2.18 0.47 1.51 0 0
下载: 导出CSV
表 3 锡的SG本构模型参数
Table 3. SG constitutive model parameters of Sn
Y0/GPa Ymax/GPa G0/GPa β n A/GPa–1 B/K–1 0.16 0.22 17.9 2 000.0 0.06 0.086 6 2.12×10–3
下载: 导出CSV
-
[1] TAYLOR G I. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I [J]. Proceedings of the Royal Society of London Series A, 1950, 201(1065): 192–196. [2] RICHTMYER R D. Taylor instability in shock acceleration of compressible fluids [J]. Communications on Pure and Applied Mathematics, 1960, 13(2): 297–319. doi: 10.1002/cpa.3160130207 [3] CAMPBELL E M, HUNT J T, BLISS E S, et al. Nova experimental facility [J]. Review of Scientific Instruments, 1986, 57(8): 2101–2106. doi: 10.1063/1.1138755 [4] DIMONTE G, TERRONES G, CHERNE F J, et al. Use of the Richtmyer-Meshkov instability to infer yield stress at high-energy densities [J]. Physical Review Letters, 2011, 107(26): 264502. doi: 10.1103/PhysRevLett.107.264502 [5] PARK H S, LORENZ K T, CAVALLO R M, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate [J]. Physical Review Letters, 2010, 104(13): 135504. doi: 10.1103/PhysRevLett.104.135504 [6] PARK H S, REMINGTON B A, BECKER R C, et al. Strong stabilization of the Rayleigh-Taylor instability by material strength at megabar pressures [J]. Physics of Plasmas, 2010, 17(5): 056314. doi: 10.1063/1.3363170 [7] NUCKOLLS J, WOOD L, THIESSEN A, et al. Laser compression of matter to super-high densities: thermonuclear (CTR) applications [J]. Nature, 1972, 239(5368): 139–142. doi: 10.1038/239139a0 [8] MCCRORY R L, MONTIERTH L, MORSE R L, et al. Nonlinear evolution of ablation-driven Rayleigh-Taylor instability [J]. Physical Review Letters, 1981, 46(5): 336–339. doi: 10.1103/PhysRevLett.46.336 [9] LINDL J D, MEAD W C. Two-dimensional simulation of fluid instability in laser-fusion pellets [J]. Physical Review Letters, 1975, 34(20): 1273–1276. doi: 10.1103/PhysRevLett.34.1273 [10] KIFONIDIS K, PLEWA T, SCHECK L, et al. Non-spherical core collapse supernovae-II. the late-time evolution of globally anisotropic neutrino-driven explosions and their implications for SN 1987 A [J]. Astronomy & Astrophysics, 2006, 453(2): 661–678. [11] MAC LOW M M, ZAHNLE K. Explosion of comet Shoemaker-Levy 9 on entry into the Jovian atmosphere [J]. The Astrophysical Journal, 1994, 434: L33–L36. doi: 10.1086/187565 [12] SHUVALOV V V, ARTEMIEVA N A. Numerical modeling of Tunguska-like impacts [J]. Planetary and Space Science, 2002, 50(2): 181–192. doi: 10.1016/S0032-0633(01)00079-4 [13] KAUS B J P, PODLADCHIKOV Y Y. Forward and reverse modeling of the three-dimensional viscous Rayleigh-Taylor instability [J]. Geophysical Research Letters, 2001, 28(6): 1095–1098. doi: 10.1029/2000GL011789 [14] MOLNAR P, HOUSEMAN G A, CONRAD C P. Rayleigh-Taylor instability and convective thinning of mechanically thickened lithosphere: effects of non-linear viscosity decreasing exponentially with depth and of horizontal shortening of the layer [J]. Geophysical Journal International, 1998, 133(3): 568–584. doi: 10.1046/j.1365-246X.1998.00510.x [15] MILES J W. Taylor instability of a flat plate, General atomic division of general dynamics: GAMD-7335 [R]. 1966. [16] WHITE G N. A one degree of freedom model for the Tayloy instability of an ideally plastic metal plate: LA-5225-MS [R]. Los Alamos, NM: Los Alamos National Laboratory, 1973. [17] ROBINSON A C, SWEGLE J W. Acceleration instability in elastic-plastic solids. II. analytical techniques [J]. Journal of Applied Physics, 1989, 66(7): 2859–2872. doi: 10.1063/1.344191 [18] PIRIZ A R, CELA J J L, CORTAZAR O D, et al. Rayleigh-Taylor instability in elastic solids [J]. Physical Review E, 2005, 72(5): 056313. doi: 10.1103/PhysRevE.72.056313 [19] PIRIZ A R, LÓPEZ CELA J J, TAHIR N A. Rayleigh-Taylor instability in elastic-plastic solids [J]. Journal of Applied Physics, 2009, 105(11): 116101. doi: 10.1063/1.3139267 [20] PIRIZ A R, CELA J J L, TAHIR N A. Linear analysis of incompressible Rayleigh-Taylor instability in solids [J]. Physical Review E, 2009, 80(4): 046305. doi: 10.1103/PhysRevE.80.046305 [21] BAI X B, WANG T, ZHU Y X, et al. Expansion of linear analysis of Rayleigh-Taylor interface instability of metal materials [J]. World Journal of Mechanics, 2018, 8(4): 94–106. doi: 10.4236/wjm.2018.84008 [22] BARNES J F, BLEWETT P J, MCQUEEN R G, et al. Taylor instability in solids [J]. Journal of Applied Physics, 1974, 45(2): 727–732. doi: 10.1063/1.1663310 [23] LORENZ K T, EDWARDS M J, GLENDINNING S G, et al. Accessing ultrahigh-pressure, quasi-isentropic states of matter [J]. Physics of Plasmas, 2005, 12(5): 056309. doi: 10.1063/1.1873812 [24] BARNES J F, JANNEY D H, LONDON R K, et al. Further experimentation on Taylor instability in solids [J]. Journal of Applied Physics, 1980, 51(9): 4678–4679. doi: 10.1063/1.328339 [25] LINDQUIST M J, CAVALLO R M, LORENZ K T, et al. Aluminum Rayleigh Taylor strength measurements and calculations [R]. Livermore, CA: Lawrence Livermore National Laboratory, 2007. [26] DE FRAHAN M T H, BELOF J L, CAVALLO R M, et al. Experimental and numerical investigations of beryllium strength models using the Rayleigh-Taylor instability [J]. Journal of Applied Physics, 2015, 117(22): 225901. doi: 10.1063/1.4922336 [27] WANG T, BAI J S, CAO R Y, et al. Numerical investigations of perturbation growth in aluminum flyer driven by explosion [J]. Chinese Journal of High Pressure Physics, 2018, 32(3): 032301. [28] OLSON R T, CERRETA E K, MORRIS C, et al. The effect of microstructure on Rayleigh-Taylor instability growth in solids [J]. Journal of Physics: Conference Series, 2014, 500(11): 112048. doi: 10.1088/1742-6596/500/11/112048 [29] 何长江, 周海兵, 杭义洪. 爆轰驱动金属铝界面不稳定性的数值分析 [J]. 中国科学G辑, 2009, 39(9): 1170–1173. HE C J, ZHOU H B, HANG Y H. Numerical study on the instability of metal Al driven by detonation [J]. Science in China (Series G), 2009, 39(9): 1170–1173. [30] 郝鹏程, 冯其京, 胡晓棉. 内爆加载金属界面不稳定性的数值分析 [J]. 爆炸与冲击, 2016, 36(6): 739–744. doi: 10.11883/1001-1455(2016)06-0739-06 HAO P C, FENG Q J, HU X M. A numerical study of the instability of the metal shell in the implosion [J]. Explosion and Shock Waves, 2016, 36(6): 739–744. doi: 10.11883/1001-1455(2016)06-0739-06 [31] 刘军, 冯其京, 周海兵. 柱面内爆驱动金属界面不稳定性的数值模拟研究 [J]. 物理学报, 2014, 63(15): 155201. doi: 10.7498/aps.63.155201 LIU J, FENG Q J, ZHOU H B. Simulation study of interface instability in metals driven by cylindrical implosion [J]. Acta Physica Sinica, 2014, 63(15): 155201. doi: 10.7498/aps.63.155201 [32] SLUTZ S A, HERRMANN M C, VESEY R A, et al. Pulsed-power-driven cylindrical liner implosions of laser preheated fuel magnetized with an axial field [J]. Physics of Plasmas, 2010, 17(5): 056303. doi: 10.1063/1.3333505 [33] MCBRIDE R D, SLUTZ S A, JENNINGS C A, et al. Penetrating radiography of imploding and stagnating beryllium liners on the Z accelerator [J]. Physical Review Letters, 2012, 109(13): 135004. doi: 10.1103/PhysRevLett.109.135004 [34] PARK H S, ARSENLIS A, BARTON N R. Stabilization of the Rayleigh-Taylor instability by material strength at high pressure and high strain rates [C]//16th International Workshop on the Physics of Compressible Turbulent Mixing. Marseilles, France, 2018. [35] REMINGTON B A, PARK H S, PRISBREY S T, et al. Progress towards materials science above 1 000 GPa (10 Mbar) on the NIF laser: LLNL-CONF-411555 [R]. Livermore, CA: Lawrence Livermore National Laboratory, 2009. [36] JENSEN B J, CHERNE F J, PRIME M B, et al. Jet formation in cerium metal to examine material strength [J]. Journal of Applied Physics, 2015, 118(19): 195903. doi: 10.1063/1.4935879 [37] BELOF J L, CAVALLO R M, OLSON R T, et al. Rayleigh-Taylor strength experiments of the pressure-induced α→ε→α′ phase transition in iron [C]//AIP Conference Proceedings. American Institute of Physics, 2012, 1426(1): 1521–1524. [38] LINDQUIST M J, CAVALLO R M, LORENZ K T, et al. Aluminum Rayleigh Taylor strength measurements and calculations [C]//LEGRAND M, VANDENBOOMGAERDE M. 10th International Workshop on Physics of Compressible Turbulent Mixing. Paris, France, 2006. -
图( 11) 表( 3)
计量
- 文章访问数: 1468
- HTML全文浏览数: 1468
- PDF下载数: 8
- 施引文献: 0