-
钝感高能炸药(Insensitive high explosive, IHE)具有突出的安全性能[1],是目前最具影响力的高能材料,在国防工业和工程爆破中有着广泛应用,其冲击起爆特征受到广泛关注。深入了解炸药冲击起爆过程,对研究可靠起爆炸药、避免炸药在意外冲击下发生爆炸具有重要意义。
隔层对冲击波具有明显的衰减效果,隔板起爆实验是研究炸药冲击起爆特性的有效方法之一[2],其中金属材料隔层广泛应用于冲击起爆实验。陈朗等[3]利用隔板实验对固体炸药的冲击起爆过程进行研究,得到了JO-9159炸药的起爆压力阈值和爆轰成长距离。胡湘渝等[4]运用DYNA2D程序对隔板实验过程进行了数值模拟,并与实验结果进行对比,较好地拟合了实验结果。郑波等[5]利用隔板实验对比探究了验证板对固体推进剂的冲击起爆影响。向梅等[6]通过数值模拟比较了铝、有机玻璃、钢隔层和未反应JB-9014炸药的爆轰反应边界值,发现有机玻璃对冲击波的衰减和铝近似,钢隔层对冲击波的衰减较快。以上研究均把隔层作为一种实验工具,没有针对隔层对冲击起爆的具体影响开展研究。
在冲击起爆过程中,空气间隙是一个重要的干扰因素。空气间隙与隔层有较大差异,传爆药和隔层间的空气间隙不仅会使冲击波衰减,而且会使本来的冲击压缩过程转变成准等熵压缩[7]和冲击压缩两个过程。因此,探究空气间隙和金属隔层对冲击起爆的影响,对于研究炸药的冲击起爆特性具有重要意义。
本研究以炸药驱动金属隔层和金属隔层冲击起爆B型炸药两个实验为基础,在实验中加入了空气间隙,通过对测得的金属隔层后界面速度和B型炸药的粒子速度进行分析,得到金属隔层和空气间隙对冲击起爆的影响。
全文HTML
-
在火炮加载平台上对金属隔层和B型炸药进行冲击实验,采用光子多普勒测速仪[8-10](Photonic Doppler velocimetry, PDV)测量金属隔层和B型炸药样品的粒子速度。样品和PDV光纤探头粘贴于样品架,位置关系如图1所示。
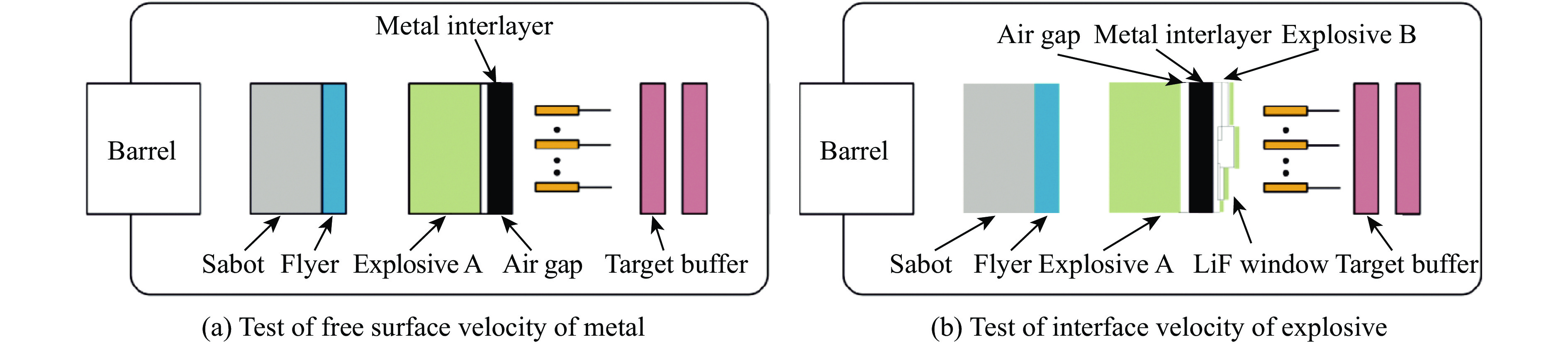
实验分为3个过程,装置如图2所示。首先,测量金属隔层自由界面速度,如图2(a)所示,用飞片撞击尺寸为
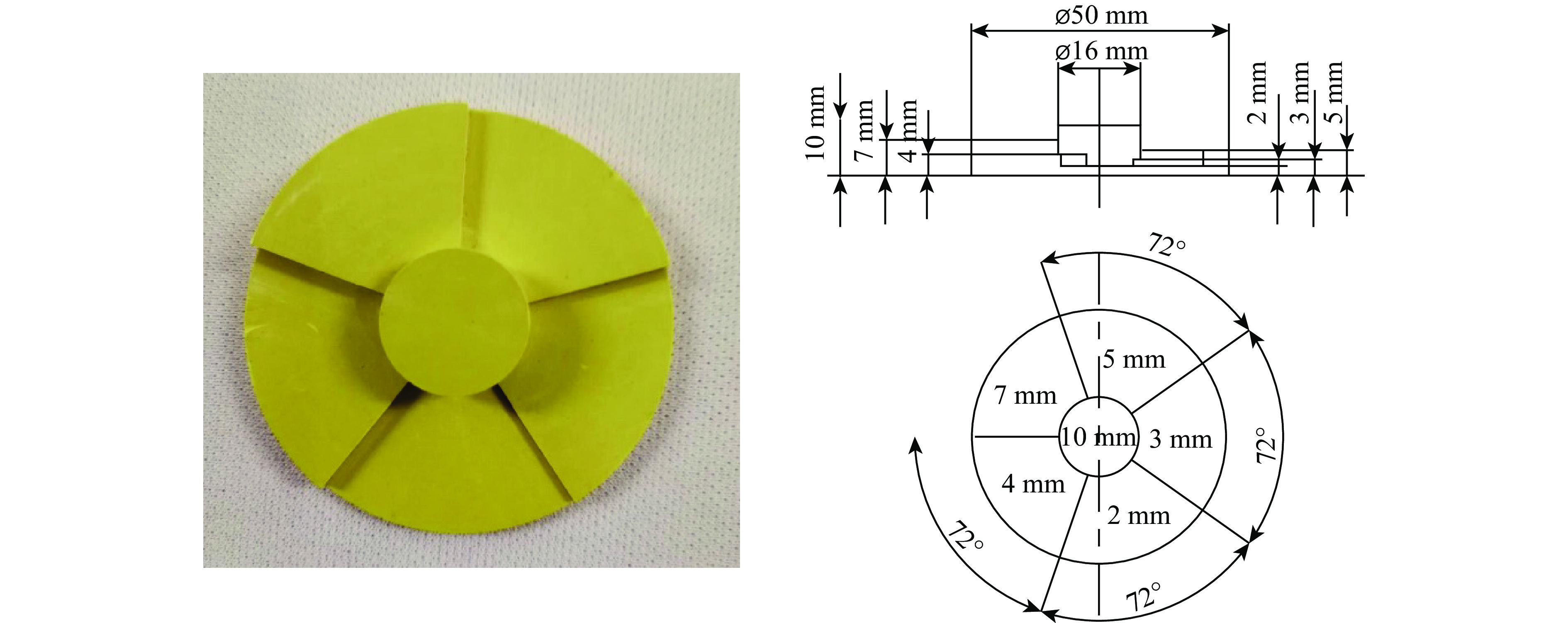
$\varnothing $ 50 mm × 30 mm的 A型炸药,使其达到爆轰状态,爆轰波通过厚度为0.3 mm的空气间隙到达金属隔层,用PDV测量金属隔层自由界面速度,金属隔层自由界面速度的变化可以反映传爆药和金属隔层间的空气间隙对冲击波的影响,通过界面速度计算出透射压力,再根据入射压力得到金属隔层的冲击波透射率。其次,如图2(b)所示,在金属隔层后贴合如图3所示的台阶型B型炸药,台阶厚度分别为2、3、4、5、7和10 mm,每个台阶面粘贴尺寸为$\varnothing $ 15 mm × 11 mm 的LiF窗口,通过PDV测速系统测量每个台阶样品和LiF窗口的界面速度,根据速度的变化,判断炸药的反应情况,得到传爆药和金属隔层间的空气间隙对冲击起爆的影响。最后,在金属隔层和B型炸药样品间增加一个0.22 mm厚的空气间隙,与上一过程中PDV测速系统测量得到的界面速度进行对比,得出金属隔层和B型炸药样品间的空气间隙对冲击起爆的影响。实验条件如表1所示。
-
通过解析解预先估算金属隔层的速度,根据声学近似理论[11],用等熵线方程描述爆轰产物,金属视为刚体,得到金属自由界面速度u
式中:Dj为A型炸药的爆轰速度;θ和η为过程量,
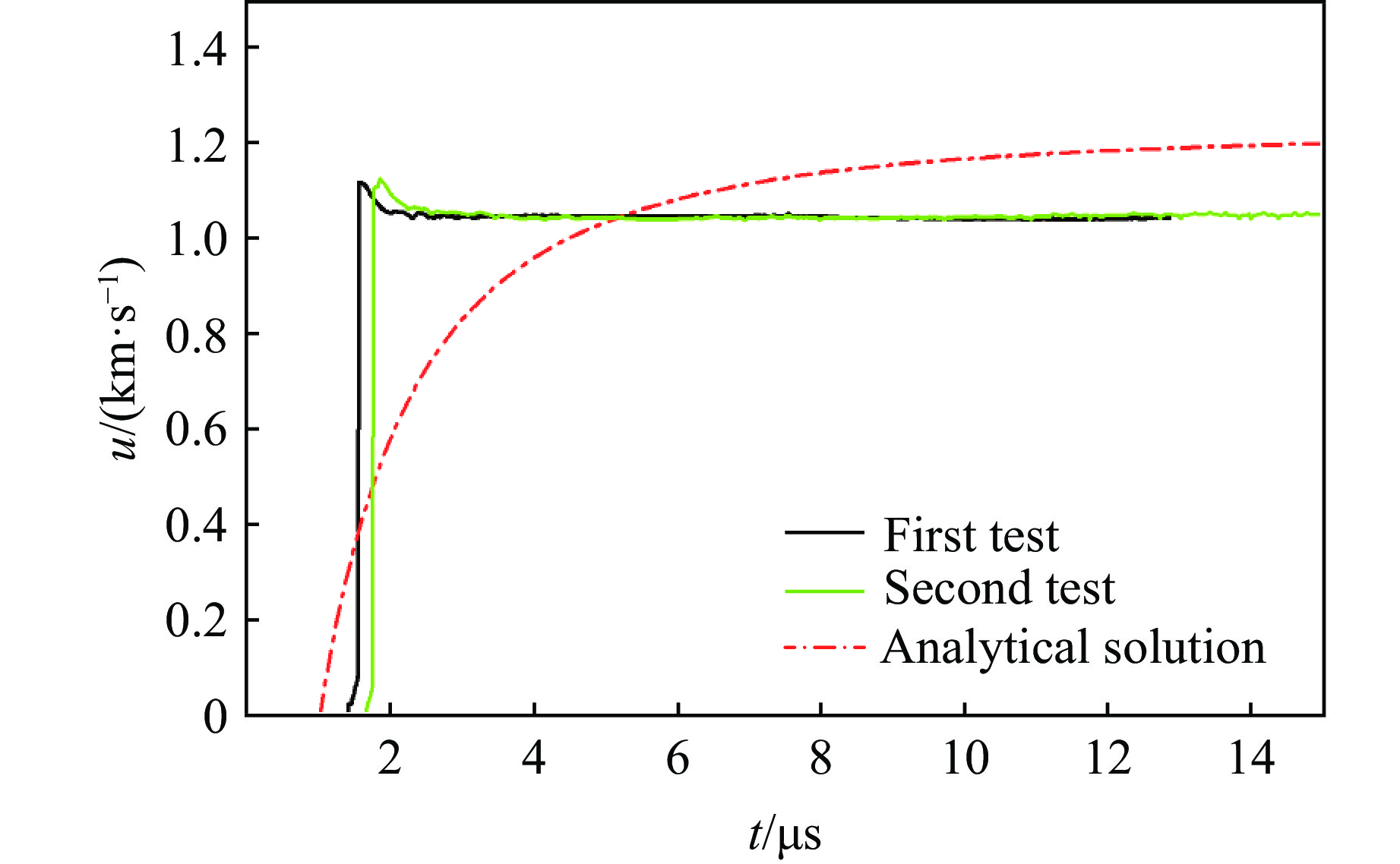
$\theta = {\left[ {1 + 2\eta \left({1 - l/{D_{\rm j}}t} \right)} \right]^{ - 1/2}}$ ,$\eta =m{\left( {k + 1} \right)^{k - 1}}/$ $M{k^k} $ ;l 为装药长度;m为A型炸药的质量;M为金属片的质量;k为爆轰产物的多方气体指数;t为炸药起爆的零点时间。本研究中取Dj = 8.87 km/s,k = 3,l = 31.09 mm,m = 113.525 g,M = 179.47 g。把Dj、k、m、M和l的值代入式(1),得到u关于t的函数,根据该函数得出的金属隔层速度曲线解析解和由Shot 01、Shot 02测量得到的金属隔层自由界面中心点速度曲线如图4所示。
由图4可知,测量得到的金属自由界面速度与理论计算得到的速度解析解相比有一定偏差,这是因为理论计算需要满足3个前提条件:(1)金属隔层为刚体;(2)爆轰波冲击绝热刚壁,反射冲击波的熵增极小,冲击波可视为波阵面上有间断的简单压缩波,爆轰产物的熵视为常数;(3)气体产物和被抛射物体都处于管内运动。上述条件与实际情况是不符合的。首先,金属并不是刚体,反应过程中有形变,其熵是减小的;其次,炸药的爆轰波存在尖峰,不是简单的压缩波;最后,本实验并非处于管内运动,实验空间是开放的,炸药质量应为有效部分质量ma,ma小于炸药质量m。因此,解析解并不能反映爆炸的实际反应情况,只能用来估算最终的理论速度,且实际速度相较于理论值偏小。金属自由界面速度没有持续加速,只有一次起跳,是因为实验中使用的金属材料阻抗较大,且相对较厚,由后界面反射的冲击波在到达前界面的过程中,在金属隔层中衰减,冲击波到达自由界面时,比自由界面压力低,不能使自由界面速度加速。在爆轰产物的推动作用下,金属隔层保持匀速飞行。
PDV测速系统测得的是金属后界面速度,根据应力波理论[12],冲击波后的粒子速度为后界面速度的1/2。由冲击波后粒子速度可以得到后界面的透射压力p2out
式中:ρ2为金属隔层密度,Dt为金属隔层冲击波速度,c2和λ2为线性Hugoniot关系式中的常系数,u2为金属后界面速度。
为了得到金属隔层的冲击波透射率,需要首先得到金属隔层的入射压强。可由A型炸药与金属隔层阻抗匹配[13]得出
式中:pj为A型炸药的爆轰压力,ρ1为A型炸药密度,ut为金属隔层前界面粒子速度。
pj数值见表2,其中,uj为炸药爆轰时的粒子速度,cj为炸药爆轰时的内部声速。把pj代入式(3),求得金属隔层前界面粒子速度ut。金属隔层的入射压力p2in可描述为
根据图4,u2取图中速度起跳的最高点,把u2代入式(2),计算得出透射压力p2out,由式(4)计算得出入射压力p2in,结果列于表3。
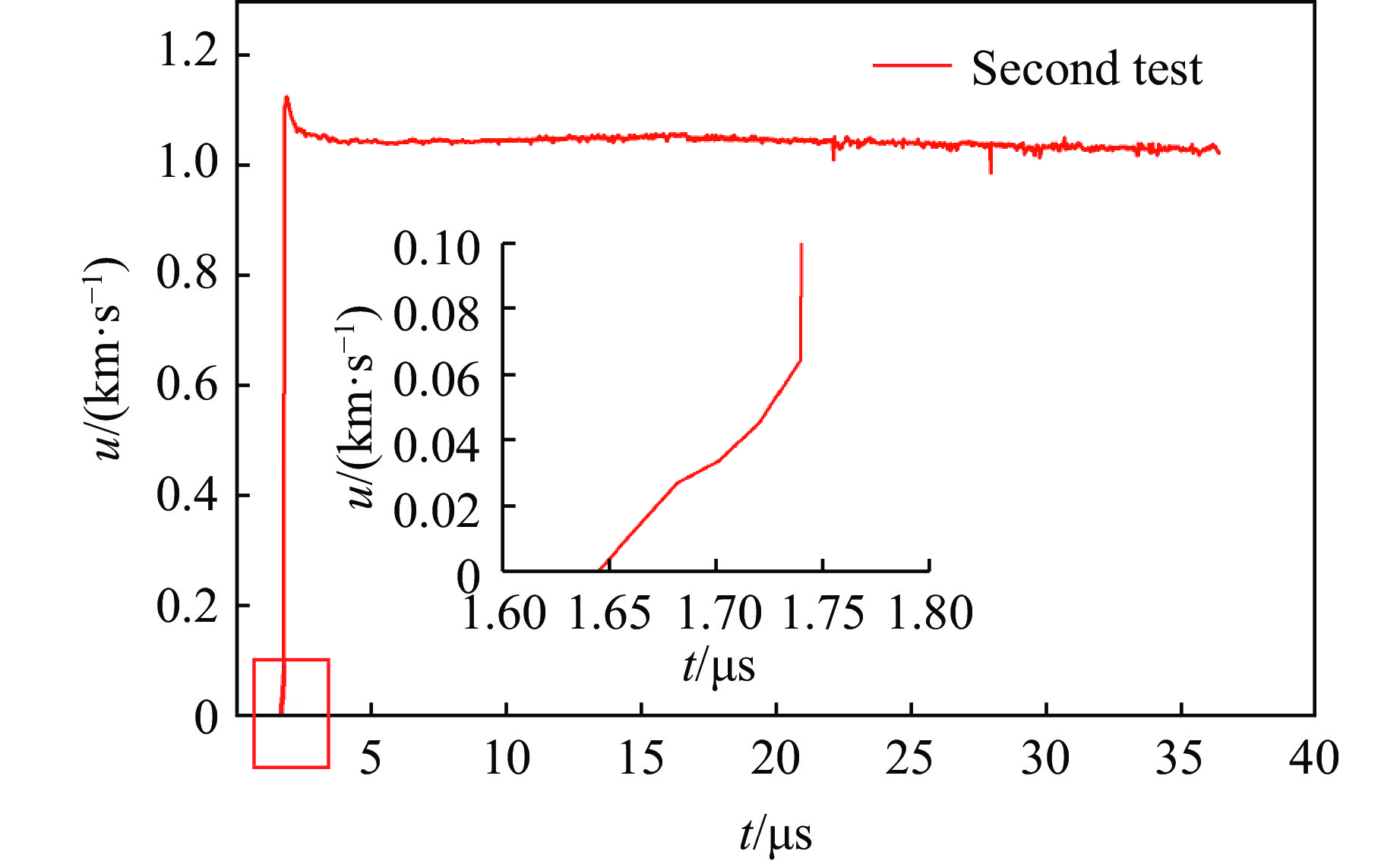
图5为图4中第3个点的速度开始增长时前面部分的放大图像。由图5可知,金属自由界面粒子速度刚开始增长的时候,并不是直接跳跃至最高点,而是经过一段平滑的曲线增长。这是由于在金属隔层和传爆药之间存在厚度为0.3 mm的空气间隙,当冲击波通过空气间隙时,对空气进行压缩,金属隔层压力的增加是连续的,可以把这个过程看作是对金属隔层进行准等熵压缩。
同时,空气间隙也会使冲击波的幅值衰减,从冲击波传入空气间隙到传出这段时间,爆轰产物在空气间隙中膨胀,将其近似地视为等熵膨胀,在此期间压强的改变量
$ {\text{Δ}}p$ 为式中:
$ {\text{Δ}} \overline v$ 为空气间隙的厚度和装药厚度的比值。p由A型炸药的爆轰产物JWL状态方程表示式中:A、B、R1、R2、
$\overline \omega $ 为经验系数,$\overline v $ 为爆轰产物的相对比容,e0为单位初始体积的比内能。对压强求相对体积的偏导可得A型炸药的JWL状态方程参数如表2所示。
把
$ {\text{Δ}}\overline v$ 和JWL状态方程参数代入式(5)和式(7),得到爆轰产物在空气间隙中做等熵膨胀时减少的压强$ {\text{Δ}}p$ :$ {\text{Δ}}p$ = –119.819 1 × 0.013 38 GPa = –1.598 2 GPa。将炸药和金属阻抗匹配后的入射压力近似地处理为p2in与$ {\text{Δ}}p$ 之和,得到金属隔层厚度为5 mm时各个测量点的透射率η1,结果如表4所示。由表4可知,金属隔层厚度为5 mm时,冲击波透射率范围为58.83%~76.82%,平均透射率为70.46%。考虑到侧向稀疏波影响,选择两次测试中心点的透射率,分别为72.10%和72.59%,取其平均值72.35%。
-
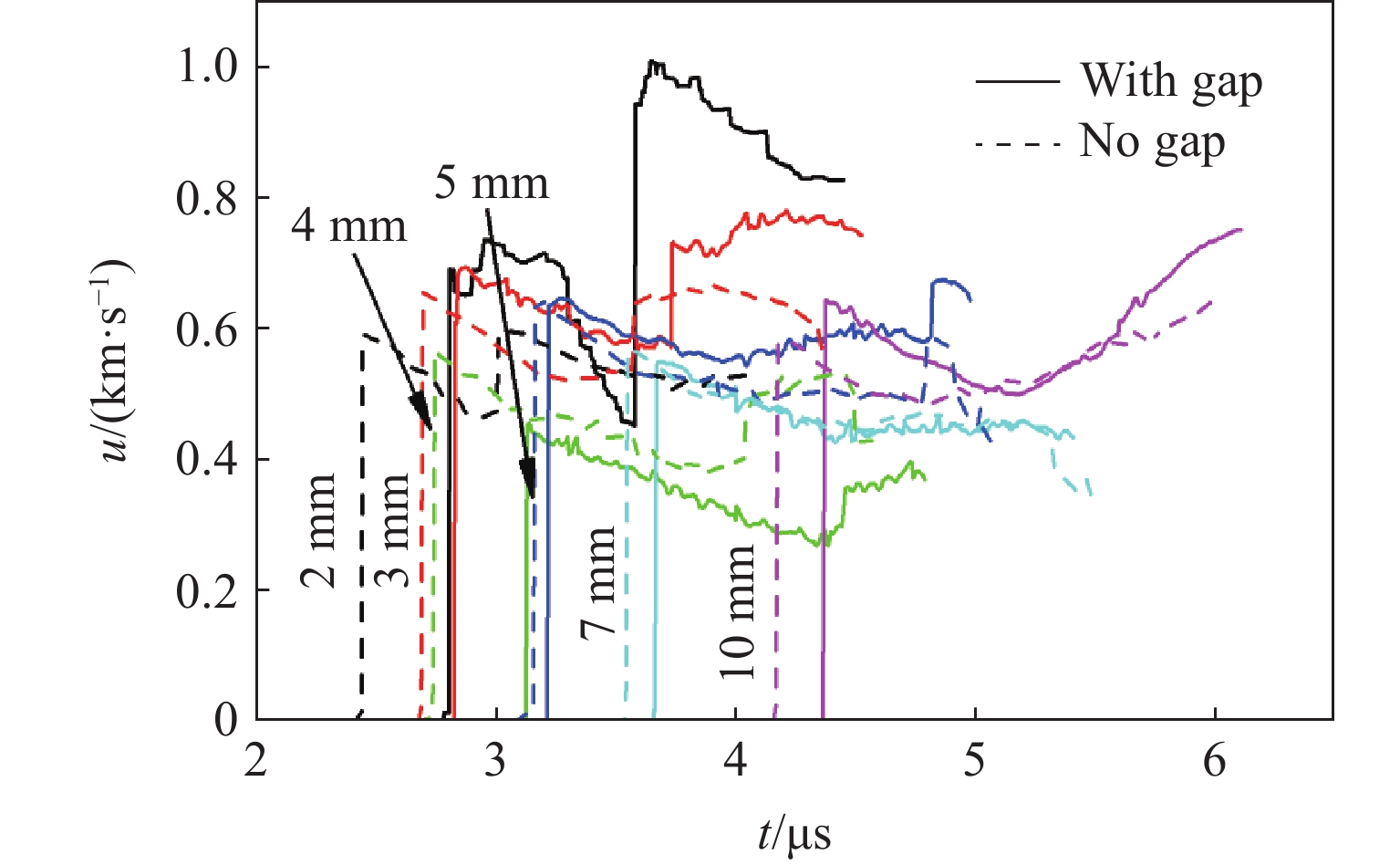
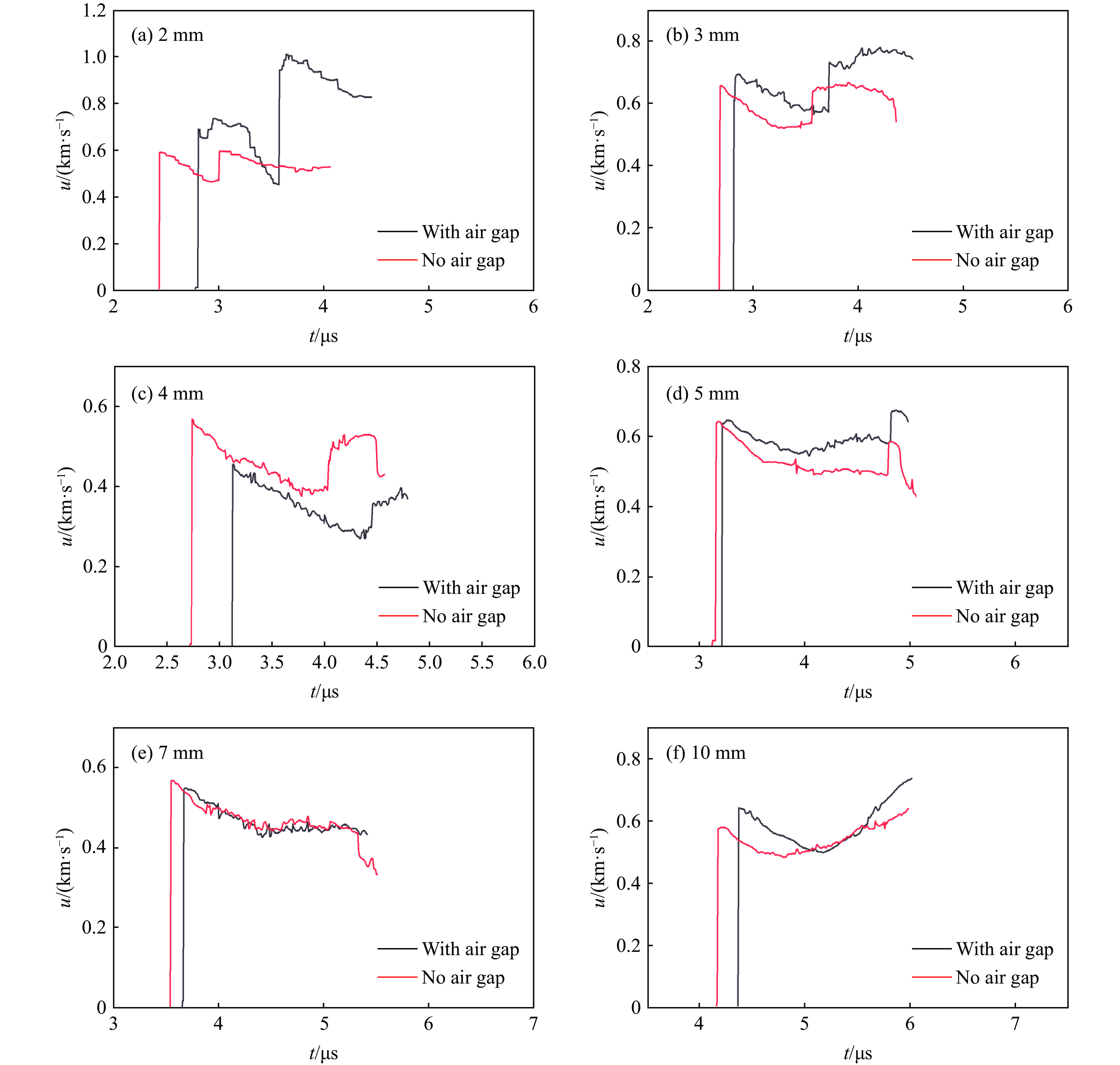
分别测得金属隔层与台阶型样品炸药之间存在和不存在空气间隙情况下样品的后界面速度,如图6和图7所示。
当金属隔层和B型炸药紧密贴合时,对样品炸药产生作用的是A型炸药爆轰后通过金属隔层传播的冲击波,图像显示为三角波。当金属隔层和B型炸药之间存在空气间隙时,金属隔层撞击B型炸药会产生一个持续的压力,输入的应是方波,由于本实验中空气间隙过小,仅为0.22 mm,因此未能形成方波。图7为不同厚度台阶面测试位置的速度对比图像。由图7可知,B型炸药厚度为2、3、5和10 mm时,当金属隔层和B型炸药之间有空气间隙时,第一次起跳的速度高于没有空气间隙,这是由于金属隔层在通过空气间隙时产生了加速。
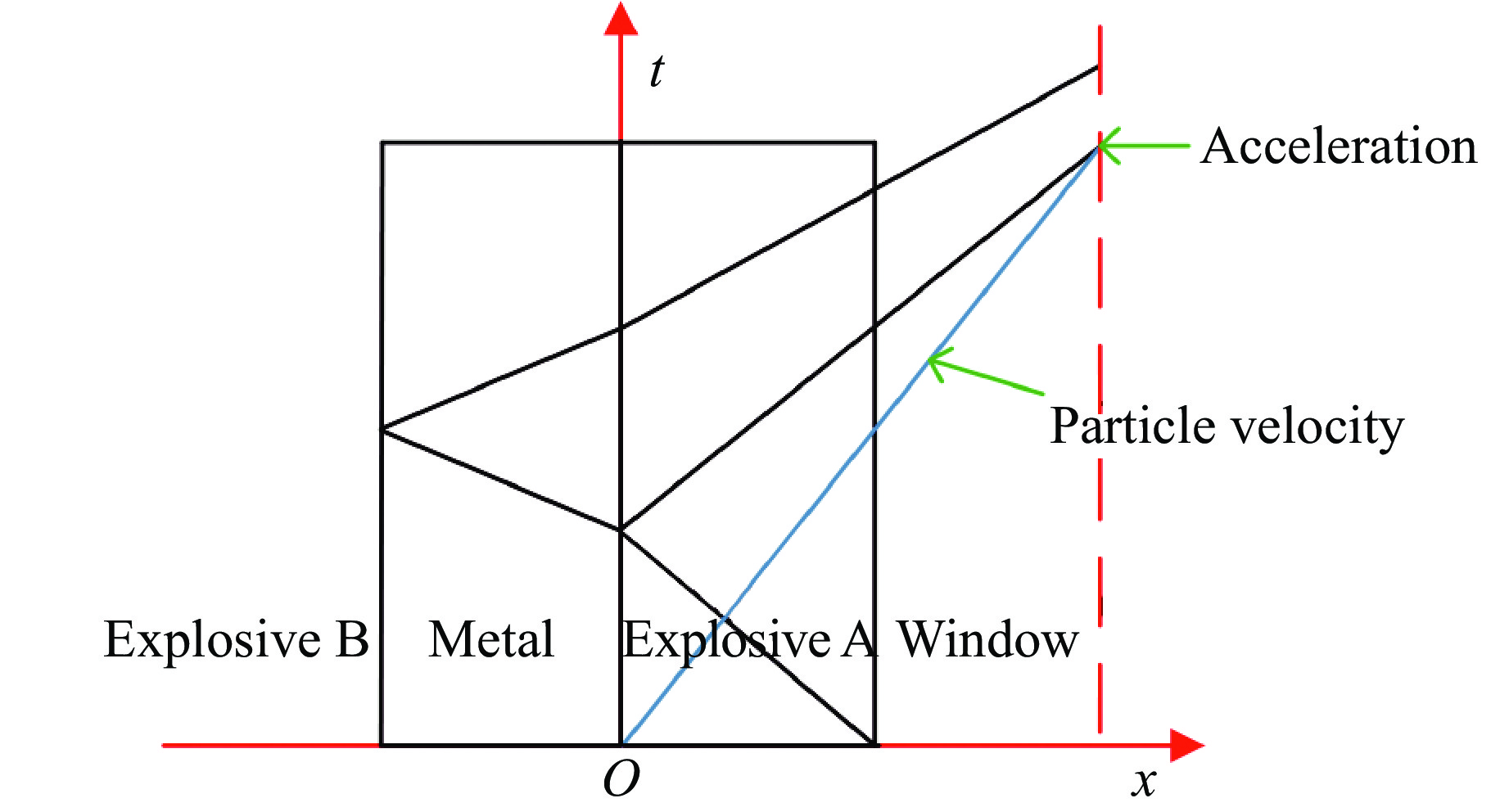
由图6可知,厚度小于7 mm的样品后界面速度都出现了二次起跳,波系图如图8所示。因为LiF窗口和金属隔层的阻抗比A型炸药的阻抗高,均会对冲击波产生反射;B型炸药处于高温高压的爆轰状态时,在金属前界面也会反射冲击波。利用式(8)、式(9)、式(10)可以估算金属隔层后界面反射的冲击波二次起跳的间隔时间
$ {\text{Δ}}t$ 。取没有空气间隙、样品厚度为3 mm的后界面粒子速度692.48 m/s,代入式(8)、式(9)、式(10),得到冲击二次起跳间隔时间为0.94$ {\text{μ}}{\rm{s}}$ ,如果是金属隔层前界面反射的冲击波,二次起跳间隔时间还会增加1$ {\text{μ}}{\rm{s}}$ 左右。表5列出了从图像得到的二次起跳的间隔时间,和理论计算基本一致,所以二次起跳是由金属隔层后界面反射的冲击波引起的。式中:t3为冲击波从金属隔层后界面到达LiF窗口的时间,h为样品台阶厚度,D3为样品冲击波速度,
$ {\text{Δ}}t_1$ 为冲击波从LiF窗口到达金属后界面的时间,$ {\text{Δ}}t_2$ 为冲击波从金属后界面反射后追到样品粒子的时间。由表5可知,台阶样品厚度从2 mm增加到5 mm时,二次起跳的时间间隔逐渐增加,这是由于随着台阶厚度的增加,冲击波反射时间变长。在台阶样品厚度为7 mm和10 mm时,没有观察到二次起跳现象,这是因为相较于前面的台阶,7 mm和10 mm台阶相对较厚,冲击波追赶粒子所需的时间更长,所以在光纤探头能够测量的时间范围内冲击波未能追到后界面的粒子。
由于这4次实验都是利用飞片起爆A型炸药,然后通过空气间隙和金属隔层,所以Shot 01、Shot 02和Shot 03、Shot 04实验中金属隔层的速度相同。根据金属后界面自由速度对台阶型B型炸药进行阻抗匹配,将B型炸药参数(ρ = 1.893 g/cm3, c = 2.418 77 km/s, λ = 2.139 61)[15]代入式(3),得到B型炸药的前界面粒子速度u3为0.980 km/s,冲击波速度D3为4.515 km/s,入射压强p3为8.389 GPa。 如图6所示,仅台阶厚度为10 mm的B型炸药样品的后界面速度有上升趋势,说明当入射压力为8.389 GPa时,反应发生在样品厚度为7~10 mm之间的某个位置。
2.1. 金属隔层和空气间隙对透射压力的影响
2.2. 金属隔层对钝感炸药冲击起爆的影响
-
在火炮平台上进行了一系列一维平面冲击实验。采用PDV测速系统对金属隔层自由界面速度和B型炸药后界面速度进行了测量,得到了速度随时间变化曲线,由此分析得出以下结论。
(1)运用阻抗匹配方法,根据金属隔层后界面速度和A型炸药爆轰粒子速度,得到了金属隔层的透射压力和入射压力,进而计算得到金属隔层厚度为5 mm时冲击波的透射率为72.35%;
(2)传爆药和金属隔层之间的空气间隙使原本的冲击压缩过程转变为准等熵压缩和冲击压缩两个过程,同时使冲击波的幅值减小;
(3)金属隔层和B型炸药间存在较小空气间隙时,会使金属隔层产生加速,炸药更加容易反应;
(4)当金属隔层厚度为5 mm,并且存在空气间隙时,A型炸药不能使厚度为10 mm的B型炸药达到爆轰状态。

 首页
首页 登录
登录 注册
注册








 下载:
下载: