首页
登录
注册
-
多孔结构[1–3]由于具有高比强度、低相对密度、高韧性和优异的吸能特性，被广泛应用于生物医学、航空航天、电子通讯、建筑等领域。多孔结构一般具有复杂的几何特征，通过传统方法加工往往会受到限制，而利用增材制造技术[4]几乎可以制造任意复杂形状的多孔结构。许多科研工作者通过实验对多孔结构进行了大量研究，包括裂纹扩展[5–6]、化学腐蚀[7]等。由于多孔结构的机械性能显著依赖于其结构单元的变形机制，因此对加载过程中多孔结构的变形模式和吸能特性的研究至关重要。
李振等[8]从变形模式、平台应力和吸能性能3方面讨论了并联梯度蜂窝结构的梯度系数对其面内特性的影响，研究表明，并联梯度蜂窝呈现“X”形塑性坍塌带，并联梯度并未对变形模式产生影响。Ma等[9]研究了准静态压缩下可重入蜂窝圆柱壳的变形行为和不同冲击速度下的能量吸收，结果表明，双层复合比单层可重入蜂窝圆柱壳具有更好的吸能能力，且其在低速冲击下的能量吸收能力更强。Li等[10]分析了聚乳酸（polylactic acid，PLA）材料蜂窝薄壁管在动态压缩下的变形模式和吸能特性，发现压缩速度越高，吸能越多，且开裂沿着纤维层展开。另外，负泊松比蜂窝结构的变形模式和吸能特性被广泛研究，如手性结构[11–12]、内凹蜂窝结构[13–14]、星型结构[15–16]、3D双箭头结构[17]。田新宇等[18]通过实验研究了多孔工字梁的吸能特性，发现与内凹胞元、圆胞元和方胞元相比，蜂窝胞元工字梁的吸能性能最好，负泊松比胞元会使薄壁工字梁失稳变形模式发生明显改变。Kagome蜂窝是由正六边形和正三角形组合成的结构，王博等[19]模拟了低速冲击下蜂窝结构的坍塌行为和能量吸收性能，结果表明，Kagome蜂窝结构在压缩变形时产生了特有的局部蜂窝旋转变形，且其吸能特性优于正三角形和菱形蜂窝。目前，对多孔结构变形模式和吸能特性的研究仍集中于各种一体式多孔结构，很少涉及模块化多孔结构。模块化多孔结构可以根据结构的防护要求灵活装配组合，且模块化可以改善一体化中试件两单元间总是发生塑性铰破坏的问题，使其有更大的变形空间，从而具备更强的能量吸收性能。
本研究将利用增材制造技术制备具有正、负泊松比效应单元填充的8种模块化多孔结构，通过准静态压缩实验获得其力-位移曲线，并利用高速相机记录其变形过程，采用ABAQUS有限元软件进行数值模拟，并与实验对比，进一步分析模块化多孔结构的变形模式和吸能特性，以期为多孔结构在工程中的应用提供新思路。
-
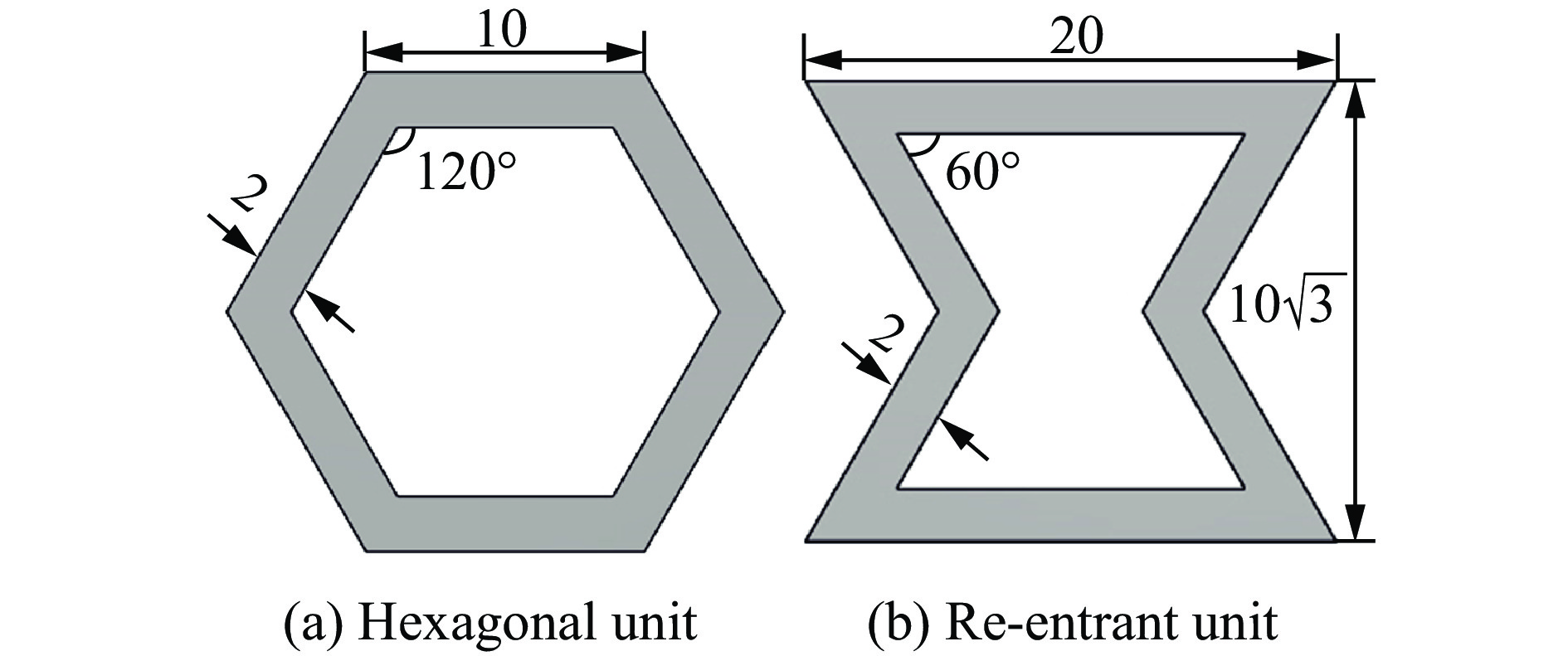
如图1所示，本研究选择具有正、负泊松比效应的正六边形和内凹形2种典型填充单元。正六边形和内凹形单元的水平肋杆长度分别为10和20 mm，斜肋杆倾斜角分别为120°和60°，壁厚均为2 mm，内凹形单元的高度为
$ 10\sqrt 3 $ mm。 -
为了研究模块化多孔结构在不同填充方式下的变形模式和吸能特性，将正六边形单元和内凹形单元交替横纵排列组合填充2层和3层，共得到8种多孔结构：正六边形结构（H）、内凹形结构（R）、正六边形/内凹形结构（H/R）和内凹形/正六边形结构（R/H），其内部填充形貌见表1。2层和3层正六边形、内凹形交替填充的多孔结构如图2所示。
-
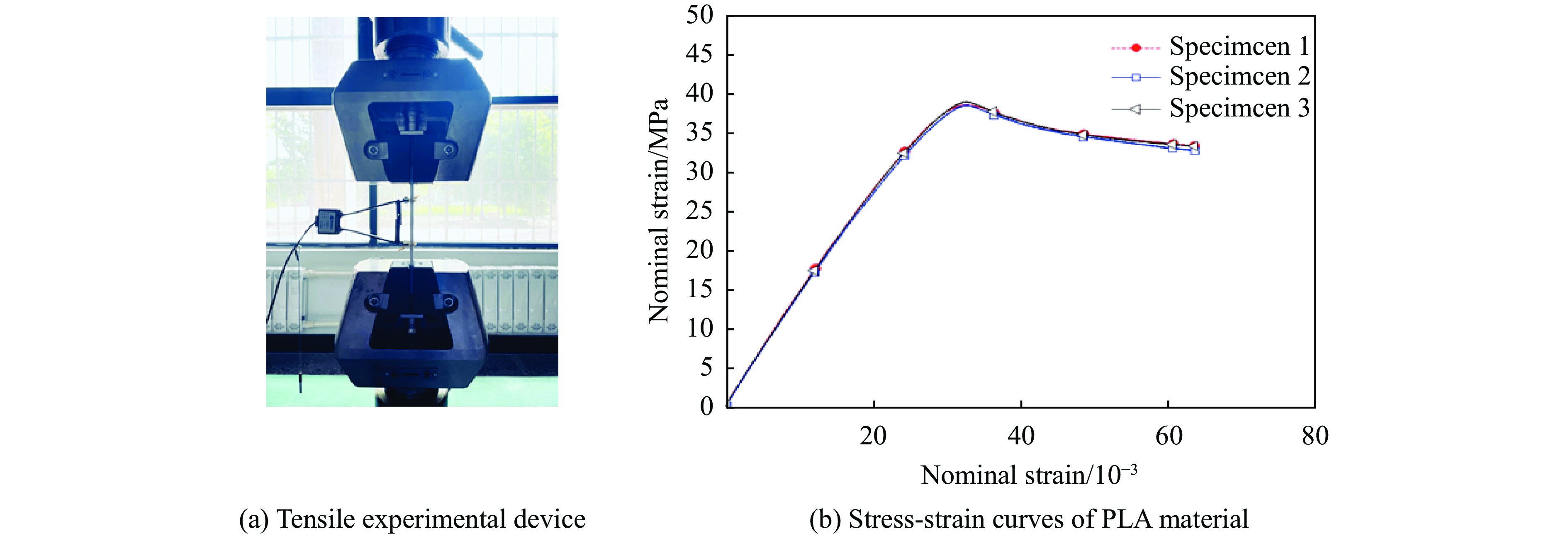
使用3D打印机制备实验标准试件，选用生物降解塑料PLA作为模块化多孔结构的原材料。首先，根据ISO 527-1塑料拉伸性能的测定标准制备“狗骨头”试件，试件标距50 mm；然后，通过微机控制电子万能试验机完成3组标准试件的准静态拉伸实验，获得力学参数，加载速率为10 mm/min。准静态拉伸实验装置及应力-应变曲线如图3所示。测得弹性模量E=
2808.85 MPa，屈服应力$ \sigma $ ys=39.18 MPa，泊松比$ \mu $ =0.3。 -
通过SOLIDWORKS软件设计并建立结构的三维模型，导出STL格式。使用3D打印机分别打印填充单元和框架，得到模块化多孔结构，如图4所示。采用JGcreat软件切片，设定最优参数：打印层高0.1 mm，打印温度210 ℃，打印速度30 mm/s，打印平台温度50 ℃。
-
使用微机控制电子万能试验机（CMT-5305）开展模块化多孔结构的室温准静态压缩实验，研究其变形模式和吸能特性。执行GB/T 1041—2008塑料压缩性能的测定标准，设置加载速度为1 mm/min，通过位移控制加载方式，压头下压至模块化多孔结构的压缩应变为0.57。采用计算机记录压缩试验的力-位移曲线，每隔0.5 mm位移高速相机拍摄一次照片捕捉试件的变形过程，实验装置如图5所示。
-
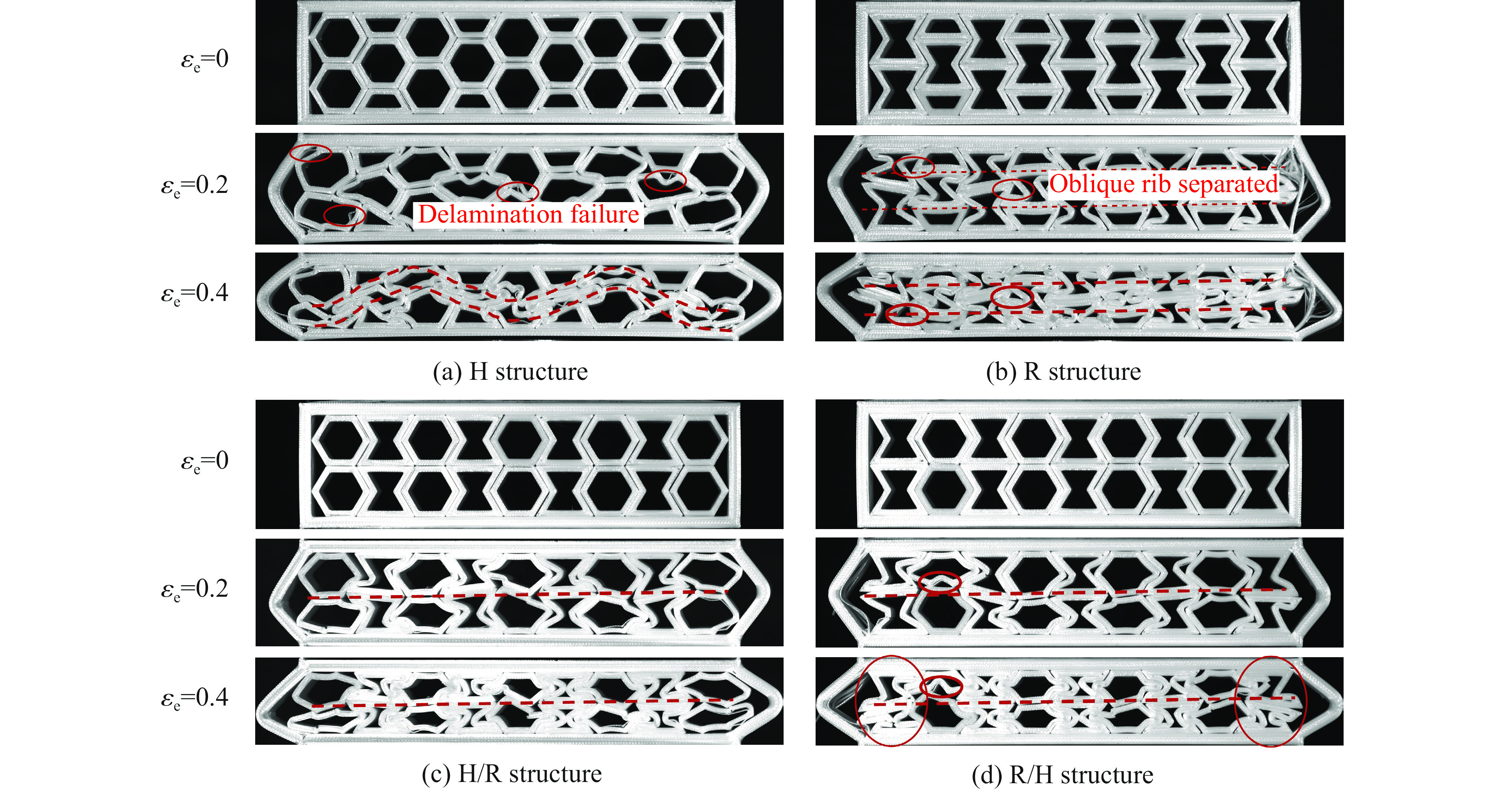
为了研究模块化多孔结构的变形模式和吸能特性，对8种模块化多孔结构进行了准静态压缩实验，压缩应变εe分别为0、0.2和0.4，8种多孔结构表现出了不同的变形和破坏模式，如图6和图7所示。从图6(a)可以看出，正六边形填充的多孔结构中，由于每个填充单元均具有正泊松比效应[20–21]，因此，在整个变形进程中，结构发生竖向压缩、横向膨胀，导致原有紧密接触的单元斜肋的接触更加紧密，产生了严重的挤压变形，水平肋出现多处明显的分层破坏和弯曲破坏。随着应变增大，剪切破坏情况愈发严重。压缩应变为0.4时，出现明显的剪切破坏条带，填充单元中部层明显坍塌，整个结构无法保持原本的形状，斜肋发生弯曲和屈曲大变形。如图6(b)所示，内凹形填充的多孔结构中，由于每个填充单元均具有负泊松比效应[22–25]，承受竖向压缩时，其横向均向内收缩，导致原有紧密接触的单元斜肋逐渐分离，但水平肋仍然能够保持在同一水平位置，继续压缩斜肋发生弯曲和屈曲大变形直至完全致密化，水平肋依旧保持在同一水平线上。如图6(c)～图6(d)所示，由于填充单元分别具有正泊松比效应和负泊松比效应，交替填充多孔结构在承受竖向压缩时，正六边形单元横向向外膨胀，同时内凹形单元横向向内收缩，横向收缩与膨胀相互配合，使得原有紧密接触的单元斜肋配合良好。水平肋在整个压缩过程中大多能保持在同一水平线上，仅少量正六边形单元发生剪切变形，导致水平肋未能继续保持水平，斜肋发生弯曲和屈曲大变形，整个结构仍然可以较好地保持原本的形状直至完全致密化。
如图7(a)所示，3层正六边形填充多孔结构在压缩应变为0.2时出现了剪切破坏条带；随着压缩应变增大，其剪切破坏更加明显，特别是中部层发生了大量剪切破坏导致结构坍塌，大量填充单元被挤压破坏，整个结构无法保持原有形状。如图7(b)所示，在压缩应变为0.2时，内凹形填充多孔结构中部层也存在45°方向明显的剪切变形；随着压缩应变的增大，内凹形单元横向收缩，导致结构大量变形，单元孔隙减小。在压缩应变为0.4时，单元结合较密实，发生大量剪切变形，剪切破坏更加明显。如图7(c)～图7(d)所示，交替填充多孔结构的斜肋配合良好，水平肋在整个压缩过程中大多能保持在同一水平线上。相对于2层结构而言，3层交替填充结构的中部层存在轻微的剪切变形，其水平肋小幅度倾斜。当内凹形与正六边形交替填充时，明显观察到最外侧内凹形单元由于挤压导致变形减小。8种填充结构单元连接处均存在塑性断裂。
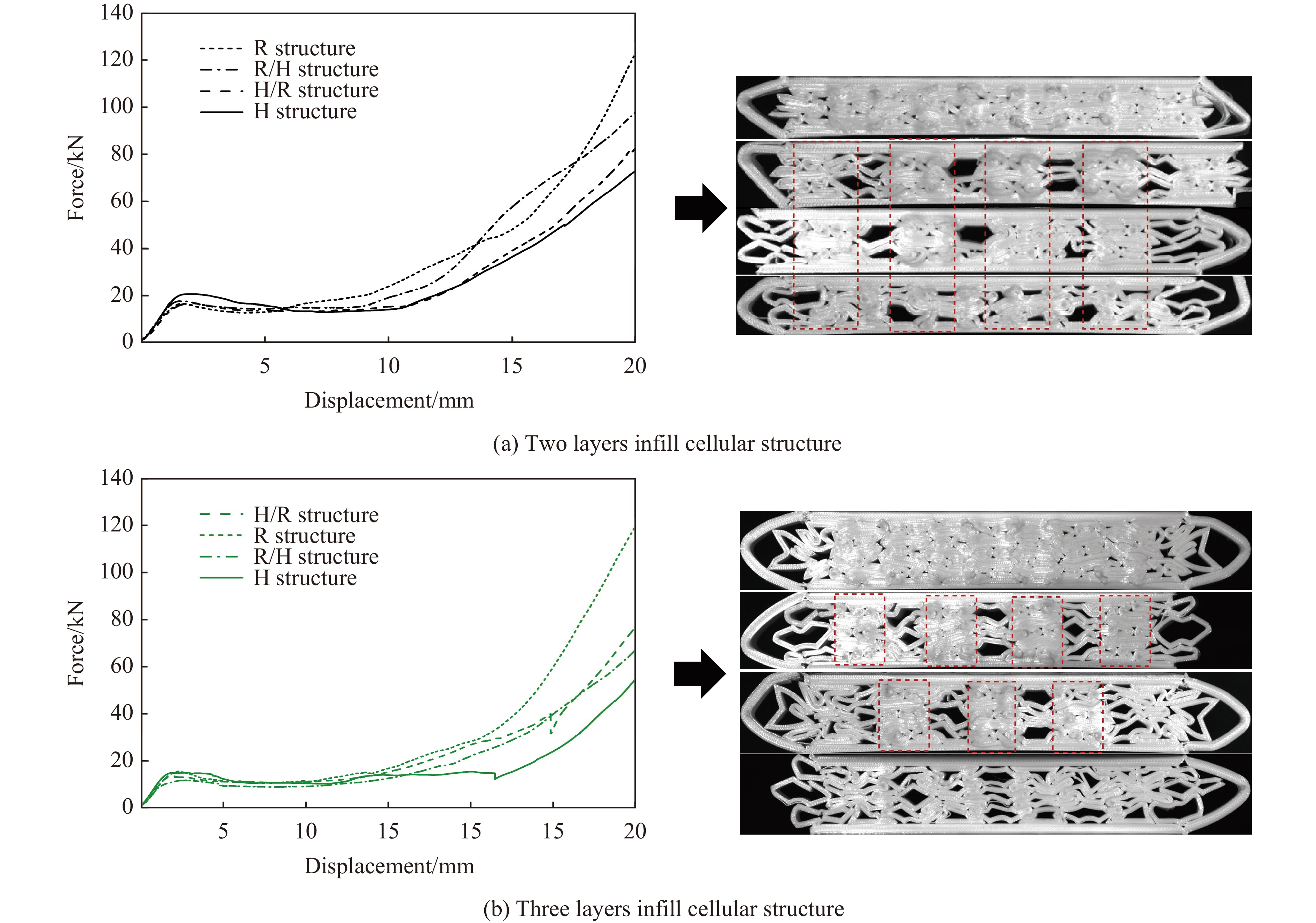
图8展示了8种模型多孔结构的压力-位移曲线。如图8(a)所示，下压至原高度的57%时，2层多孔结构的承载力由大到小依次为R结构、R/H结构、H/R结构和H结构，承载力分别为123、98、83和73 kN。如图8(b)所示，3层多孔结构的承载力由大到小依次为R结构、H/R结构、R/H结构和H结构，承载力分别为119、76、67和56 kN。3层填充多孔结构的承载力均小于对应的2层结构。内凹形结构独特的负泊松比效应使其性能表现得更好，包括更高的抗断裂性能、吸能性能，压力-位移曲线更为平缓。变形量是承载力大小的重要判断依据，填充内凹形单元的数量会直接影响其变形量。观察图8中的变形结构可知，2层填充多孔结构主要承载区的变形量明显高于3层多孔结构，且内凹形填充多孔结构的变形量均最大。在2层填充多孔结构中，变形量的大小与填充内凹形结构的数量一致；而在3层填充结构中，内凹形与正六边形交替填充最外侧的内凹形边缘，边缘挤压时未发生大量变形，导致其承载力的大小排序与2层结构存在区别。单元破坏包括连接处塑性断裂破坏、弯曲破坏、屈曲破坏、剪切破坏和分层破坏，如图9所示。
-
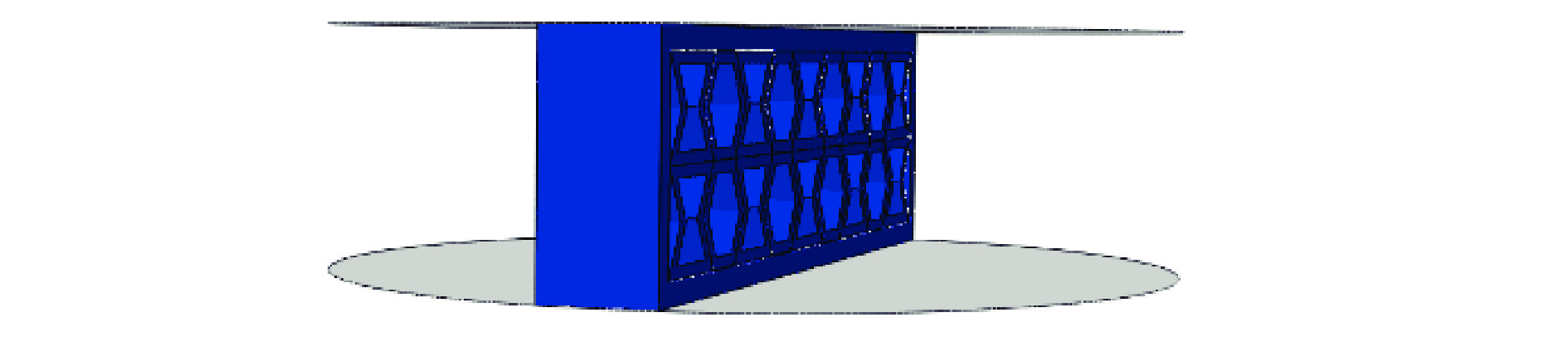
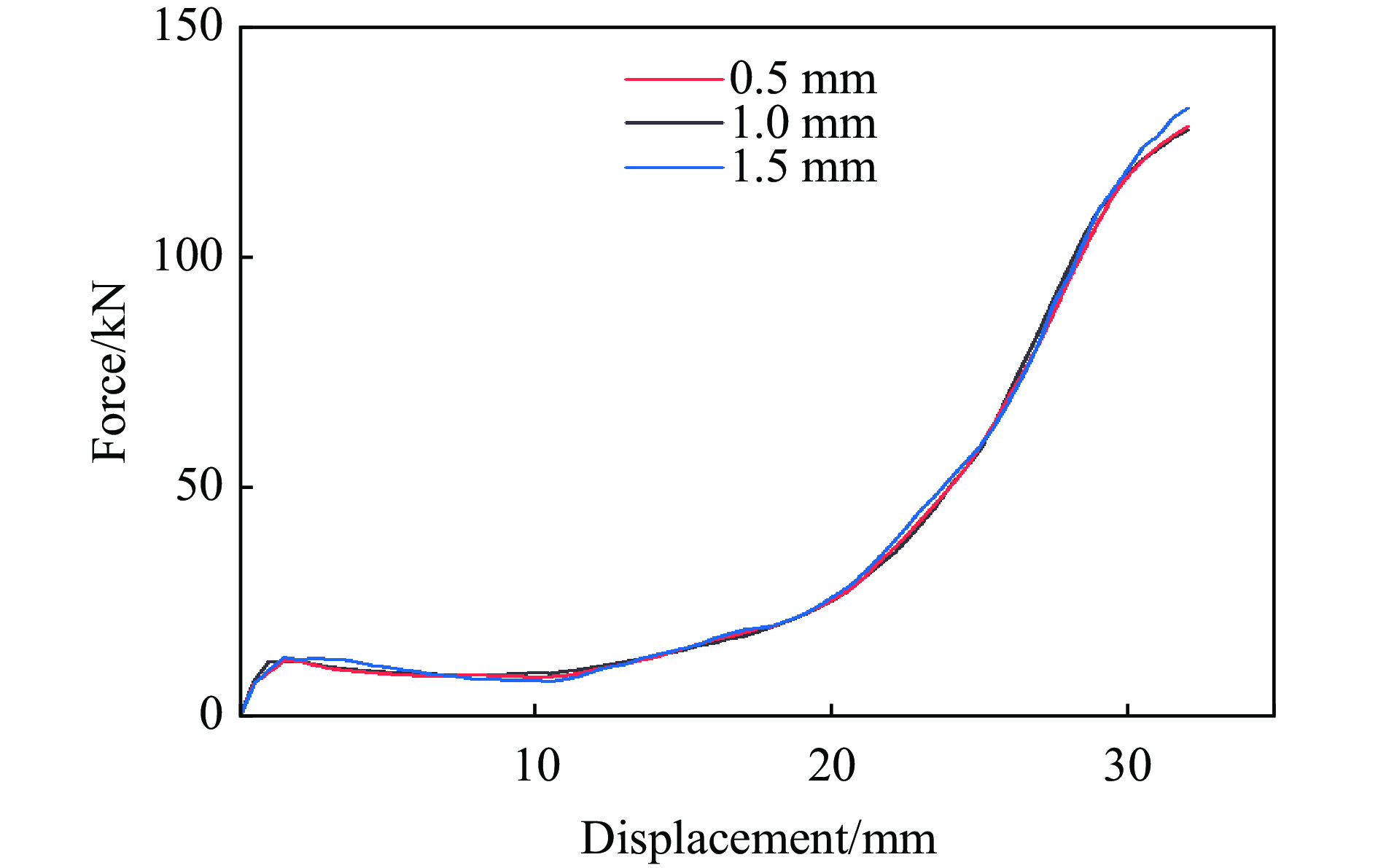
采用ABAQUS/Explicit软件对模块化多孔结构的准静态单轴压缩实验过程进行模拟。如图10所示，建立的有限元模型与实验几何参数相同，将试件放置在支撑板与加载板之间，支撑板和加载板均为离散刚体，各模块化组件之间均为通用接触。将PLA材料属性赋予模块化多孔结构模型，设置接触面摩擦因数为0.3，采用六面体网格划分，并进行网格无关性验证，如图11所示，单元网格尺寸分别为0.5、1.0、1.5 mm。为了保证模拟结果的精确性和计算的高效性，划分单元尺寸为1.0 mm×1.0 mm，单元属性为C3D8R，加载板以1 mm/min的速度向下压缩，压缩至原高度的57%时停止。
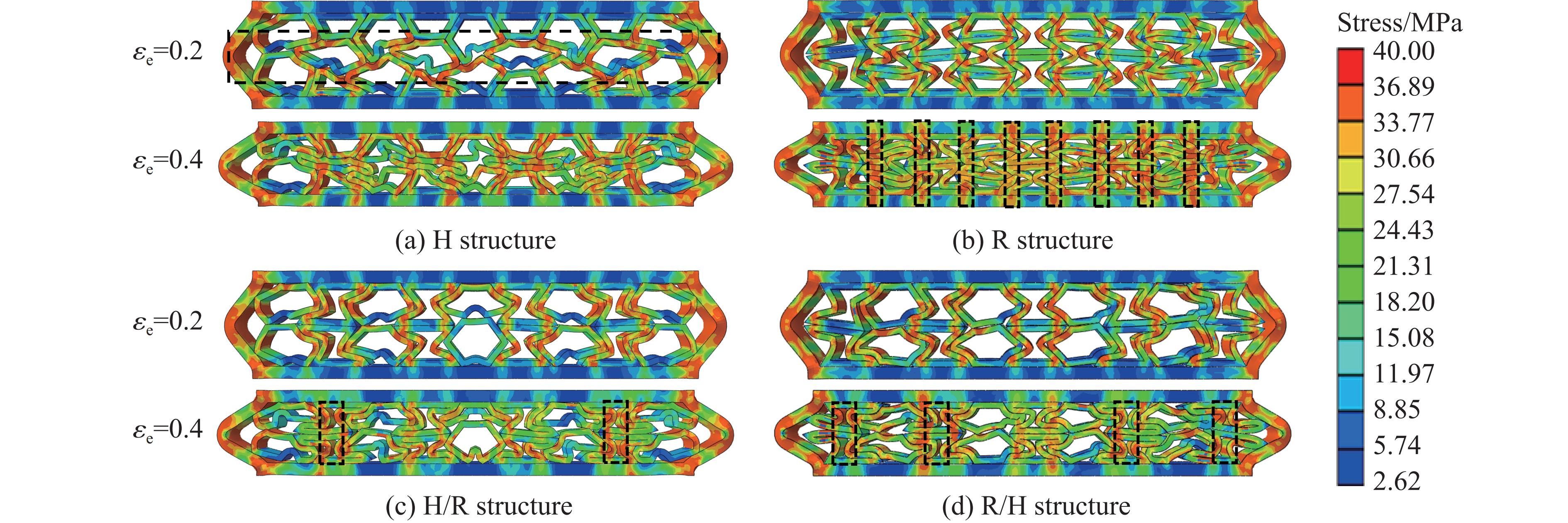
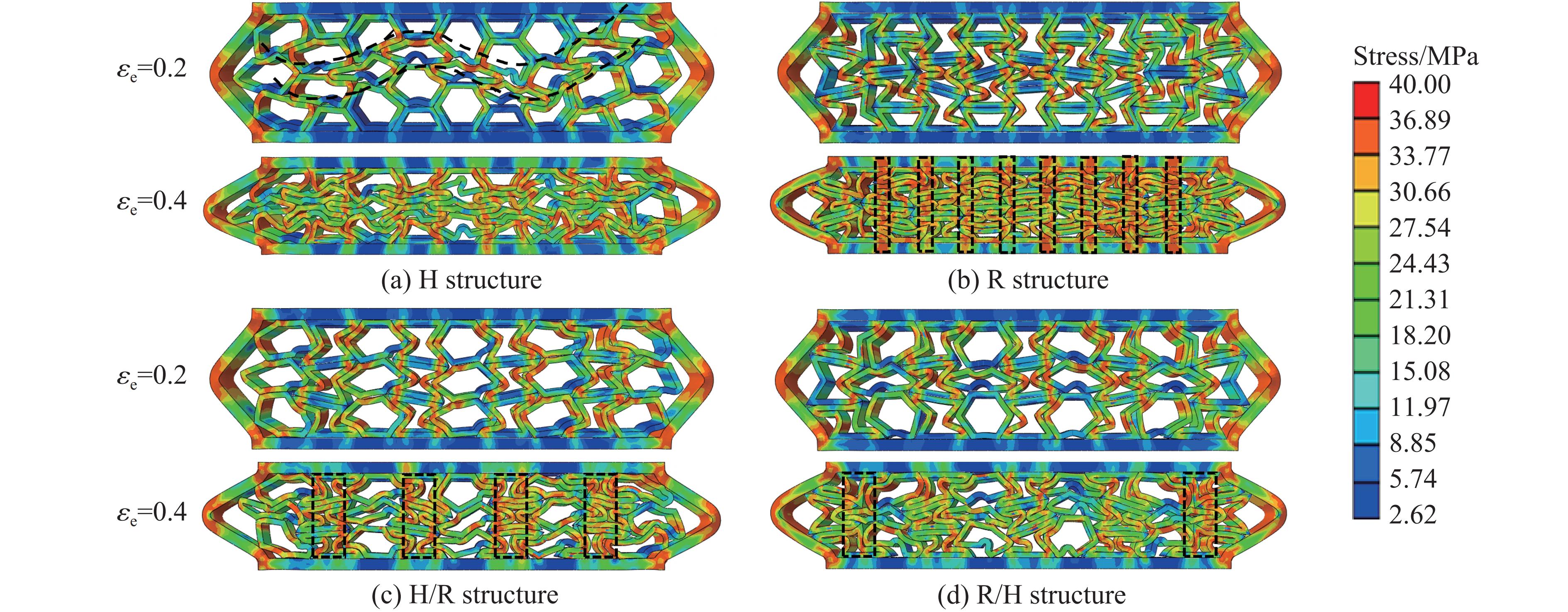
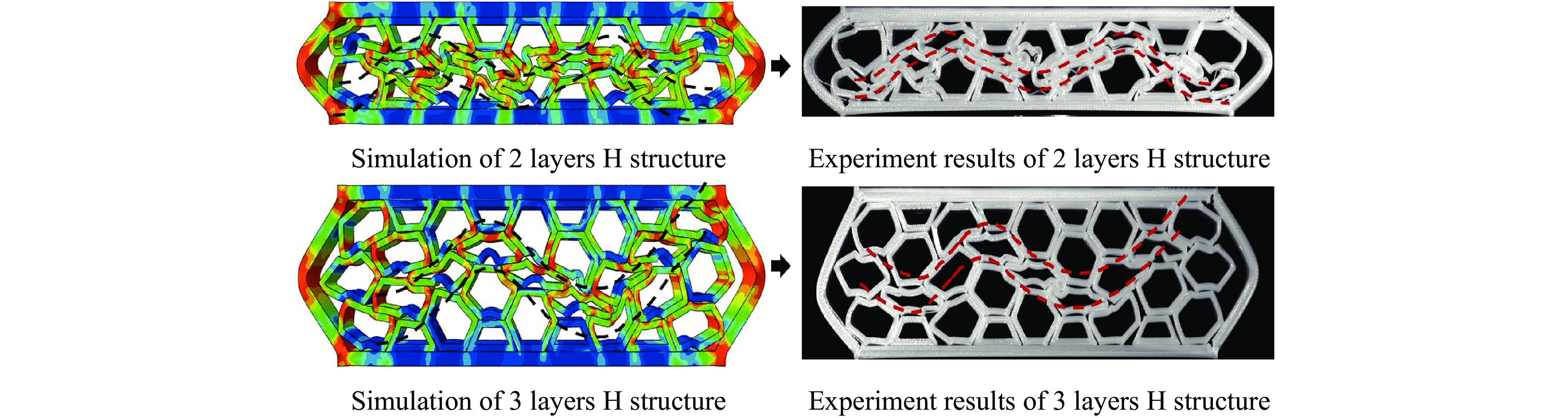
图12和图13分别为2层、3层填充多孔结构的应力云图。2层、3层填充多孔结构左右两侧边框及边框连接处应力均保持最大，为40 MPa，与实验过程中边框处易发生断裂的结果吻合。当压缩应变较小时，模块化多孔结构的应力集中区为单元斜肋的尖端，随着应变增大，应力集中区向斜肋和水平肋扩展。
如图12(a)和图12(b)所示，当压缩应变为0.2时，虚线框内的正六边形单元斜肋杆尖端的应力较大，承受主要荷载，是正六边形填充多孔结构中部层首先坍塌的原因，此时内凹形填充多孔结构的应力集中在全部内凹形斜肋的尖端。压缩应变增大至0.4时，应力集中区扩展至整条斜肋和部分水平肋，且内凹形填充多孔结构的应力扩展到边框，形成明显、均匀的应力集中条带。如图12(c)和图12(d)所示，当压缩应变为0.2时，交替填充多孔结构的应力集中区为2类单元斜肋的尖端；当压缩应变增大至0.4时，应力集中区向斜肋扩展，且内凹形单元承受的应力明显大于正六边形单元，存在几个应力明显较大区域，且H/R结构的应力较大区域多于R/H结构。
如图13(a)和图13(b)所示，当压缩应变为0.2时，3层正六边形填充多孔结构表现出明显的剪切应力条带；当压缩应变为0.4时，内凹形填充结构的应力扩展到边框，且表现出明显、均匀的应力条带，与2层内凹形填充结构一致。如图13(c)～图13(d)所示，当压缩应变为0.4时，交替填充多孔结构存在几个明显应力较大区域，且H/R结构的应力较大区域多于R/H结构，与2层交替填充结构不同。
-
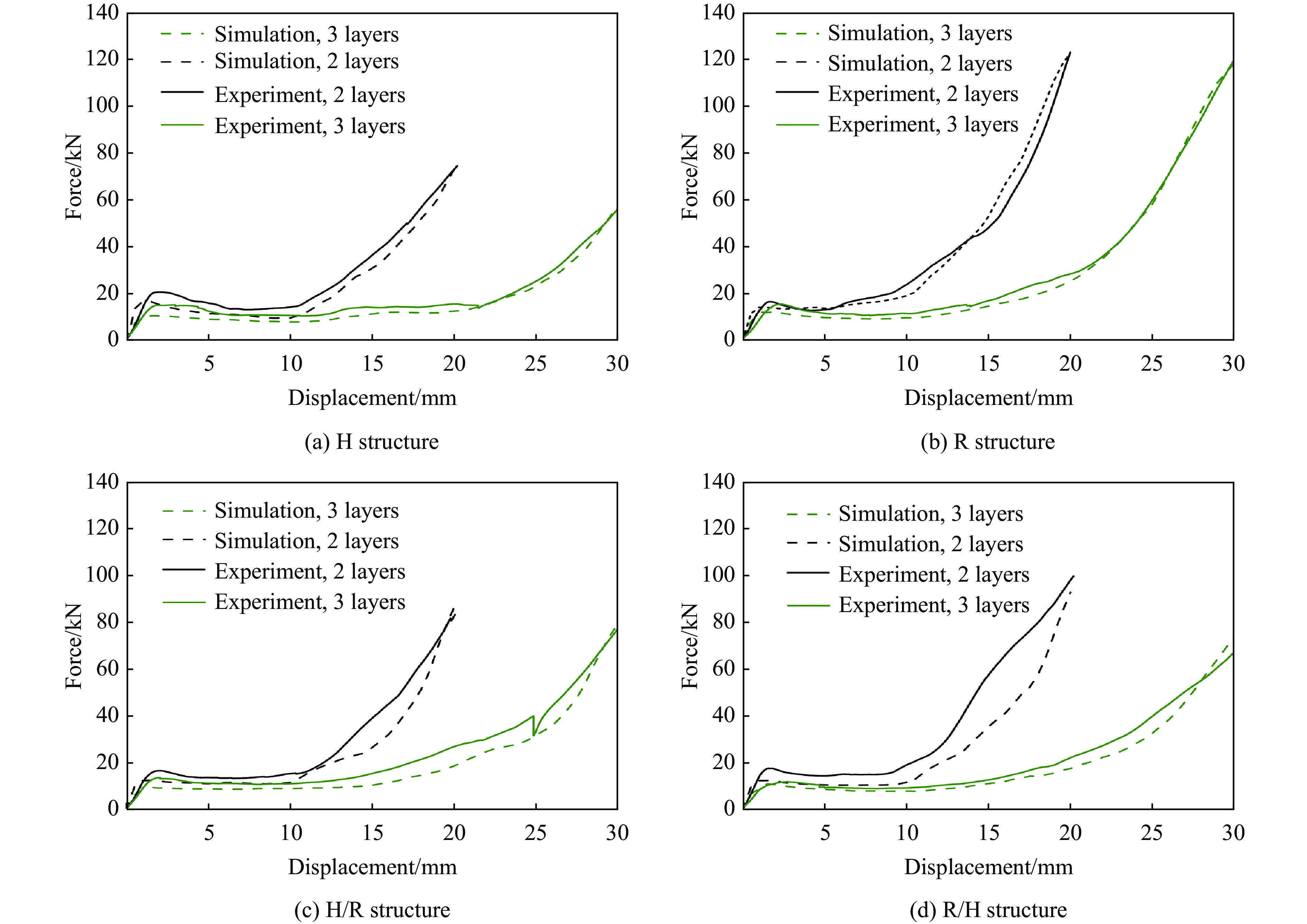
图14给出了准静态压缩实验和有限元模拟得到的正六边形、内凹形、交替填充多孔结构试件的力-位移曲线。实验测试和数值模拟计算的变形模式基本保持一致，力-位移曲线包含3个阶段：第1阶段为线弹性变形阶段，承载力的局部最大值分别为20.676、15.236、16.635、15.576、16.774、13.764、17.780、11.957 kN；在第2阶段中，结构单元的斜肋发生弯曲与屈曲变形，导致承载力降低，产生应力平台区，引发单元结构坍塌；第3阶段为致密化阶段，力-位移曲线急速上升。模块化多孔结构准静态压缩实验和模拟有限元的力-位移曲线吻合较好。图15为正六边形填充多孔结构的剪切破坏条带，应力分布能够准确反映其剪切破坏条带。
-
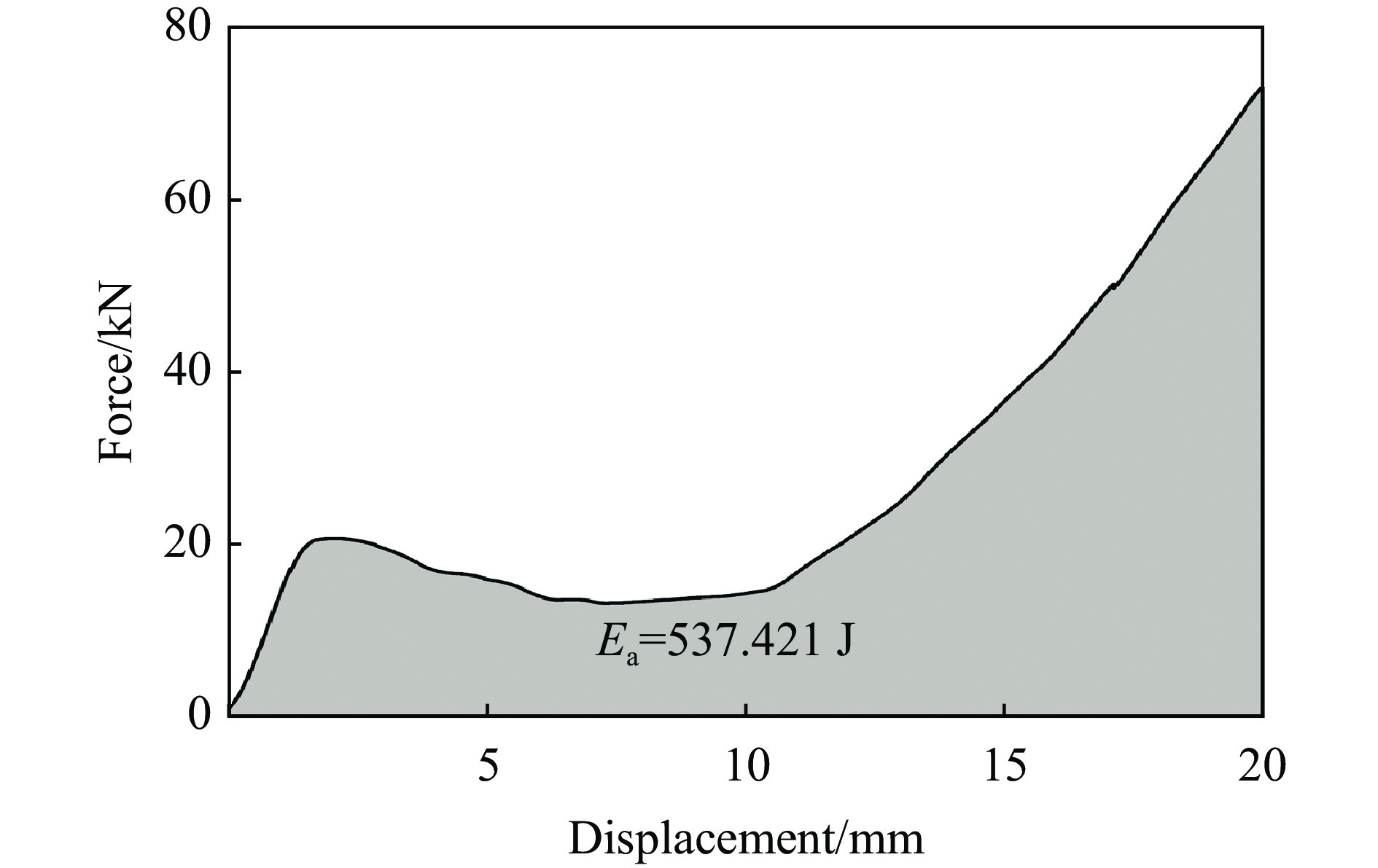
能量吸收是评估结构抵抗压缩性能的主要依据。对比结构吸收的总能量、比吸能、峰值压缩力和平均压缩力，研究模块化多孔结构的吸能差异。图16给出了2层正六边形填充多孔结构的力-位移曲线。其中，Ea为试件压缩至原高度57%的过程中吸收的总能量，即图16中力-位移曲线中的阴影面积，是评价试件吸能性能的主要指标
式中：L为试件压缩行程，s为位移，F(s)为试件压缩过程中的荷载。
比吸能Esa是研究结构吸能特性的重要指标，即试件单位质量在压缩过程中吸收的能量
式中：M为试件的总质量。
Fp为结构在压缩密实之前的压缩力峰值，通常出现在荷载的初始阶段。平均压缩力为
不同填充多孔结构的总吸能Ea、比吸能Esa、峰值压缩力Fp、平均压缩力Fa见表2。从表2可以看出，2层填充多孔结构的峰值压缩力均大于3层填充，且比吸能大于其对应的3层填充。由于内凹形单元具有负泊松比效应，在承受竖向荷载时的横向收缩使多孔结构的密实化程度更高，因此吸能效果更显著。内凹形填充单元的变形量越大，结构越密实，吸收的能量越大。内凹形填充多孔结构的总吸能和平均压缩力在4种填充方式中总是最大，且比吸能可以维持在较高且稳定的水平；正六边形填充多孔结构的总吸能、平均压缩力和比吸能总是最小。除内凹形与正六边形交替填充多孔结构外，3层填充多孔结构的总吸能大于相同结构构型的2层填充多孔结构，其原因是3层内凹形与正六边形交替填充多孔结构边缘的内凹形由于挤压使得受力减小，导致其能量吸收减少。2层内凹形与正六边形交替填充结构的总吸能小于内凹形填充结构，但比吸能最大，为7.853 J/g。单个正六边形结构的质量小于内凹形，在2层内凹形填充中加入正六边形单元组成交替填充结构有利于提高其比吸能。3层正六边形填充结构的总吸能小，且比吸能最小，为4.728 J/g，与压缩原高度57%时最小的变形量吻合。
-
为了研究模块化多孔结构的变形模式和吸能特性，设计了8种结构进行准静态压缩实验，利用ABAQUS有限元仿真软件对其在准静态压缩下的行为进行了数值模拟，分析其变形模式和吸能特性，得出以下结论。
(1) 不同填充方式下的多孔结构在准静态压缩下表现出不同的变形模式，正六边形填充结构中会出现明显的剪切破坏条带，导致中部层坍塌。3层内凹形填充结构中大量内凹形结构单元表现出45°方向的剪切变形；2层内凹形结构及交替填充结构单元的水平肋仍能够保持在水平方向上。
(2) 不同填充方式下的多孔结构在准静态压缩下表现出不同的破坏模式，正六边形填充出现明显的水平肋分层破坏和斜肋挤压屈曲破坏，内凹形填充结构出现明显的斜肋分离现象和屈曲破坏，交替填充仍能保持原有形状。
(3) 2层填充多孔结构的峰值压缩力和比吸能均大于3层填充结构。正六边形填充结构的总吸能、平均压缩力和比吸能在4种填充方式中总是最小的；内凹形填充结构的总吸能和平均压缩力总是最大的，且比吸能保持在稳定、较高的水平。
模块化多孔结构的变形模式及吸能特性
Deformation Mode and Energy Absorption of Modularized Cellular Structures
-
摘要: 模块化多孔结构相较于传统一体式结构能够更加灵活地满足装配需求，研究其变形模式和吸能特性，可为多孔结构在工程中的应用提供新思路。选用具有正泊松比效应的正六边形和具有负泊松比效应的内凹形作为模块化多孔结构的填充单元，共设计了8种结构，并进行了准静态压缩实验。实验结果与有限元模拟计算结果吻合良好。研究发现：不同填充方式的结构具有不同的变形模式，其中正六边形填充表现出明显的剪切破坏带，交替填充能较好地保持单元的初始形状；2层填充多孔结构的压缩力峰值均大于3层填充结构，2层结构的比吸能也大于对应的3层填充结构；正六边形填充结构的总吸能、平均压缩力和比吸能在4种填充方式中均最小；内凹形填充结构的总吸能和平均压缩力均最大，且其比吸能保持在稳定且较高的水平。Abstract: Compared with the traditional integrated structures, modularized cellular structures can meet the assembly requirements more flexibly. The deformation modes and energy absorption were studied to provide new ideas for the application of cellular structures in engineering, the regular hexagon with positive Poisson’s ratio effect and the re-entrant hexagon with negative Poisson’s ratio effect were selected as the infill units of the modularized cellular structures in this paper, and eight kinds of structures were designed for quasi-static compression experiments. The experimental results were in good agreement with the simulation results. The cellular structures with different infill approaches had different deformation modes under the compression experiments, in which the regular hexagon infill units showed obvious shear failure bands, and the alternate infill approaches can maintain the original units shape. The peak force of the two-layer infill cellular structures were greater than the three-layer infill structures, and the specific absorption energy were greater than the corresponding three-layer infill structures. The total absorption energy, average compression force and specific absorption energy of the hexagon infill structures were always the smallest among the four infill approaches, while the total absorption energy and average compression force of the re-entrant hexagon infill structures were always the largest and the specific absorption energy was kept at a stable and high level.
-
-
图 1 2种典型填充单元的基本尺寸（单位：mm）
Figure 1. Two typical infill units and their basic dimensions (Unit: mm)
图 2 2层和3层正六边形、内凹形交替填充的多孔结构（单位：mm）
Figure 2. Infill cellular structures of two and three layers hexagon alternating with re-entrant (Unit: mm)
图 6 2层填充多孔结构的变形模式
Figure 6. Deformation modes of two layers infill cellular structures
图 7 3层填充多孔结构的变形模式
Figure 7. Deformation modes of three layers infill cellular structures
图 8 2层和3层多孔结构的压力-位移曲线
Figure 8. Force-displacement curves of two and three layers cellular structures
图 12 2层填充多孔结构的应力云图
Figure 12. Stress diagrams of two layers infill cellular structures
图 13 3层填充多孔结构的应力云图
Figure 13. Stress diagrams of three layers infill cellular structures
图 14 填充多孔结构的力-位移实验与数值模拟曲线
Figure 14. Force-displacement experimental and simulation curves of infill cellular structures
图 15 正六边形填充多孔结构的剪切破坏条带
Figure 15. Shear failure strips of hexagon infill cellular structures
图 16 2层正六边形填充多孔结构的力-位移曲线及总能量吸收
Figure 16. Force-displacement curve and total energy absorption of two layers hexagon infilled cellular structure
表 1 8种多孔结构的内部填充
Table 1. Internal infill of eight cellular structures
Layer number Structural style H R H/R R/H 2 
3 
下载: 导出CSV
表 2 8种多孔结构的吸能指标
Table 2. Energy absorption index of eight cellular structures
Structure Layer Ea/J Esa/(J·g−1) Fp/kN Fa/kN H 2 537.421 6.796 20.676 26.871 R 730.291 7.373 16.635 36.515 H/R 550.843 6.445 16.774 27.542 R/H 693.729 7.853 17.780 34.687 H 3 540.071 4.728 15.236 18.002 R 948.612 7.263 15.576 31.620 H/R 719.230 6.164 13.764 23.974 R/H 647.934 5.396 11.957 21.598
下载: 导出CSV
-
[1] BABAEI M, KIARASI F, ASEMI K, et al. Functionally graded saturated porous structures: a review [J]. Journal of Computational Applied Mechanics, 2022, 53(2): 297–308. doi: 10.22059/jcamech.2022.342710.719 [2] YANG B S, CHEN W H, XIN R L, et al. Pomelo peel-inspired 3D-printed porous structure for efficient absorption of compressive strain energy [J]. Journal of Bionic Engineering, 2022, 19(2): 448–457. doi: 10.1007/s42235-021-00145-1 [3] AJAJ R M, PARANCHEERIVILAKKATHIL M S, AMOOZGAR M, et al. Recent developments in the aeroelasticity of morphing aircraft [J]. Progress in Aerospace Sciences, 2021, 120: 100682. doi: 10.1016/j.paerosci.2020.100682 [4] CHOWDHURY S, YADAIAH N, PRAKASH C, et al. Laser powder bed fusion: a state-of-the-art review of the technology, materials, properties & defects, and numerical modelling [J]. Journal of Materials Research and Technology, 2022, 20: 2109–2172. doi: 10.1016/j.jmrt.2022.07.121 [5] 张欣茹, 邓庆田, 李新波, 等. 预制裂纹参数及相对密度对平面多孔结构裂纹扩展的影响 [J]. 实验力学, 2023, 38(1): 68–80. doi: 10.7520/1001-4888-22-057 ZHANG X R, DENG Q T, LI X B, et al. Influences of prefabricated crack parameters and relative density on crack propagation in planar cellular structures [J]. Journal of Experimental Mechanics, 2023, 38(1): 68–80. doi: 10.7520/1001-4888-22-057 [6] ZHANG X R, DENG Q T, LI X B. Effects of damage mode on crack propagation pattern in additively manufactured honeycomb cellular panel [J]. Journal of Failure Analysis and Prevention, 2023, 23(5): 2090–2104. doi: 10.1007/s11668-023-01749-x [7] SHIVARAM M J, ARYA S B, NAYAK J, et al. Role of porosity on electrochemical corrosion behavior of porous Ti-20Nb-5Ag alloy in simulated body fluid [J]. Materials Today: Proceedings, 2020, 33: 5257–5261. doi: 10.1016/j.matpr.2020.02.952 [8] 李振, 丁洋, 王陶, 等. 新型并联梯度蜂窝结构的面内力学性能 [J]. 复合材料学报, 2020, 37(1): 155–163. doi: 10.13801/j.cnki.fhclxb.20190417.003 LI Z, DING Y, WANG T, et al. In-plane crushing behaviors of honeycombs with a novel parallel graded design [J]. Acta Materiae Compositae Sinica, 2020, 37(1): 155–163. doi: 10.13801/j.cnki.fhclxb.20190417.003 [9] MA N F, DENG Q T, LI X B. Deformation behaviors and energy absorption of composite re-entrant honeycomb cylindrical shells under axial load [J]. Materials, 2021, 14(23): 7129. doi: 10.3390/ma14237129 [10] LI T, DENG Q T, LI X B. Energy absorption and deformation modes of several thin-walled tubes under dynamic compression [J]. Structures, 2023, 54: 890–897. doi: 10.1016/j.istruc.2023.05.099 [11] 王雪松, 刘卫东, 刘典. 新型反四手性蜂窝结构的面内拉伸弹性 [J]. 复合材料学报, 2023, 40(8): 4849–4861. doi: 10.13801/j.cnki.fhclxb.20221107.003 WANG X S, LIU W D, LIU D. In-plane tensile elasticity of a novel anti-tetrachiral cellular structure [J]. Acta Materiae Compositae Sinica, 2023, 40(8): 4849–4861. doi: 10.13801/j.cnki.fhclxb.20221107.003 [12] JIAO C X, YAN G. Design and elastic mechanical response of a novel 3D-printed hexa-chiral helical structure with negative Poisson’s ratio [J]. Materials & Design, 2021, 212: 110219. doi: 10.1016/j.matdes.2021.110219 [13] ZHOU H Y, JIA K C, WANG X J, et al. Experimental and numerical investigation of low velocity impact response of foam concrete filled auxetic honeycombs [J]. Thin-Walled Structures, 2020, 154: 106898. doi: 10.1016/j.tws.2020.106898 [14] 尤泽华, 肖俊华, 王美芬. 弧边内凹蜂窝负泊松比结构的力学性能 [J]. 复合材料学报, 2022, 39(7): 3570–3580. doi: 10.13801/j.cnki.fhclxb.20210729.003 YOU Z H, XIAO J H, WANG M F. Mechanical properties of arc concave honeycomb structure with negative Poisson’s ratio [J]. Acta Materiae Compositae Sinica, 2022, 39(7): 3570–3580. doi: 10.13801/j.cnki.fhclxb.20210729.003 [15] 卢子兴, 王欢, 杨振宇, 等. 星型-箭头蜂窝结构的面内动态压溃行为 [J]. 复合材料学报, 2019, 36(8): 1893–1900. doi: 10.13801/j.cnki.fhclxb.20180908.001 LU Z X, WANG H, YANG Z Y, et al. In-plane dynamic crushing of star-arrowhead honeycomb structure [J]. Acta Materiae Compositae Sinica, 2019, 36(8): 1893–1900. doi: 10.13801/j.cnki.fhclxb.20180908.001 [16] 杨泽水, 薛玉祥, 刘爱荣. 三维负泊松比星型结构冲击动力学研究 [J]. 工程力学, 2022, 39(Suppl 1): 356–363. doi: 10.6052/j.issn.1000-4750.2021.05.S057 YANG Z S, XUE Y X, LIU A R. Study on the impact dynamics of three-dimensional star-shaped structure with negative Poisson’s ratio [J]. Engineering Mechanics, 2022, 39(Suppl 1): 356–363. doi: 10.6052/j.issn.1000-4750.2021.05.S057 [17] GUO M F, YANG H, ZHOU Y M, et al. Mechanical properties of 3D hybrid double arrow-head structure with tunable Poisson’s ratio [J]. Aerospace Science and Technology, 2021, 119: 107177. doi: 10.1016/j.ast.2021.107177 [18] 田新宇, 邓庆田, 李新波, 等. 多孔工字梁的准静态压缩稳定性及能量吸收性能 [J]. 高压物理学报, 2023, 37(4): 044103. doi: 10.11858/gywlxb.20230657 TIAN X Y, DENG Q T, LI X B, et al. Quasi-static compression stability and energy absorption performance of cellular I-beam [J]. Chinese Journal of High Pressure Physics, 2023, 37(4): 044103. doi: 10.11858/gywlxb.20230657 [19] 王博, 张雄, 徐胜利. 2D周期蜂窝结构面内静动态压缩力学行为研究 [J]. 力学学报, 2009, 41(2): 274–281. doi: 10.6052/0459-1879-2009-2-2007-400 WANG B, ZHANG X, XU S L. Mechanical behavior of 2D periodic honeycombs under in-plane uniaxial compression [J]. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 274–281. doi: 10.6052/0459-1879-2009-2-2007-400 [20] 龙凯, 谷先广, 韩丹. 考虑泊松效应的材料/结构一体化设计方法 [J]. 复合材料学报, 2017, 34(6): 1252–1260. doi: 10.13801/j.cnki.fhclxb.20161024.001 LONG K, GU X G, HAN D. A concurrent design method for microstructures of materials and macrostructures by considering the Poisson effect [J]. Acta Materiae Compositae Sinica, 2017, 34(6): 1252–1260. doi: 10.13801/j.cnki.fhclxb.20161024.001 [21] BATES S R G, FARROW I R, TRASK R S. 3D printed polyurethane honeycombs for repeated tailored energy absorption [J]. Materials & Design, 2016, 112: 172–183. doi: 10.1016/j.matdes.2016.08.062 [22] ZHOU J, LIU H B, DEAR J P, et al. Comparison of different quasi-static loading conditions of additively manufactured composite hexagonal and auxetic cellular structures [J]. International Journal of Mechanical Sciences, 2023, 244: 108054. doi: 10.1016/j.ijmecsci.2022.108054 [23] LI Y, CHEN Z H, XIAO D B, et al. The dynamic response of shallow sandwich arch with auxetic metallic honeycomb core under localized impulsive loading [J]. International Journal of Impact Engineering, 2020, 137: 103442. doi: 10.1016/j.ijimpeng.2019.103442 [24] LUO H C, REN X, ZHANG Y, et al. Mechanical properties of foam-filled hexagonal and re-entrant honeycombs under uniaxial compression [J]. Composite Structures, 2022, 280: 114922. doi: 10.1016/j.compstruct.2021.114922 [25] OH J H, KIM J S, NGUYEN V H, et al. Auxetic graphene oxide-porous foam for acoustic wave and shock energy dissipation [J]. Composites Part B: Engineering, 2020, 186: 107817. doi: 10.1016/j.compositesb.2020.107817 -
计量
- 文章访问数: 96
- HTML全文浏览数: 96
- PDF下载数: 4
- 施引文献: 0