根据水平集法，采用2种隐式函数近似描述典型TPMS单胞结构Gyroid与IWP^[9]

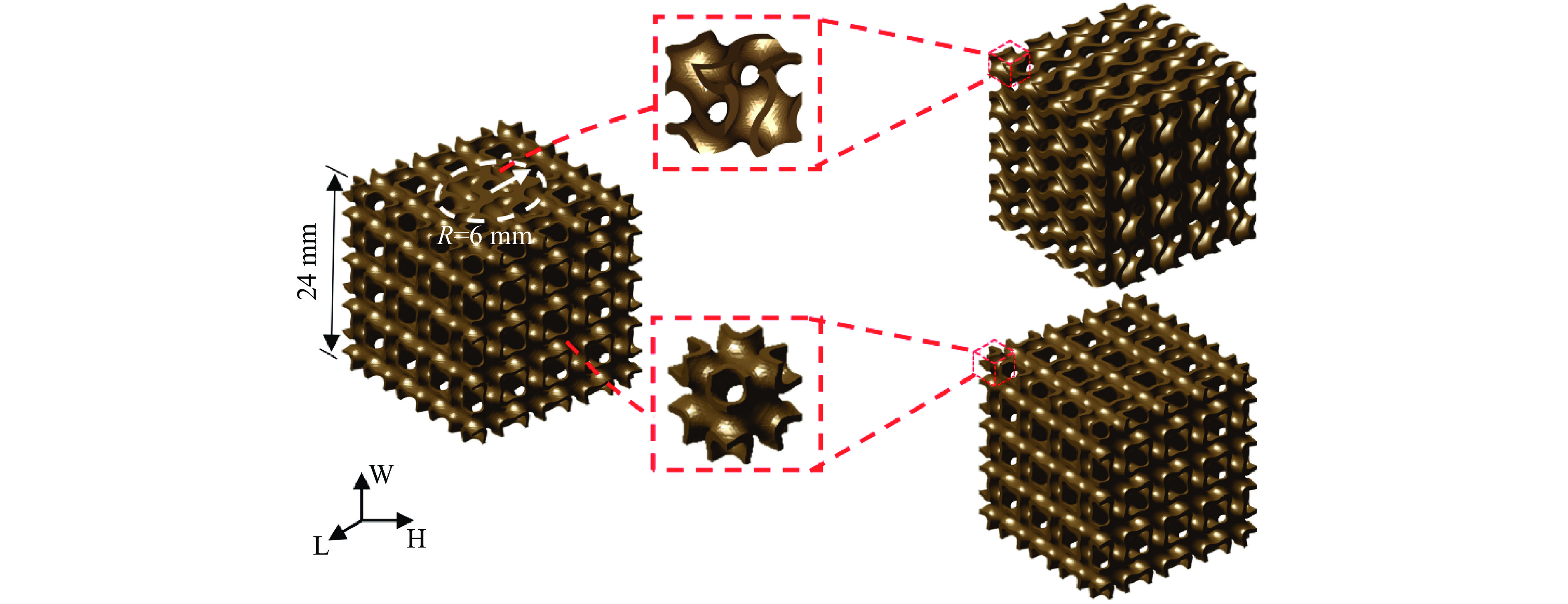
式中：$X = 2\text{π} x/L$，$Y = 2\text{π} y/L$，$Z = 2\text{π} \textit{z}/L$，L为单胞尺寸，x、y、z为3个互相垂直的笛卡尔坐标值^[17]，C为水平集常数。2种TPMS的基本单胞构型如图1所示。

本研究中的密度${\rho ^*}$为结构的相对密度，可以表示为

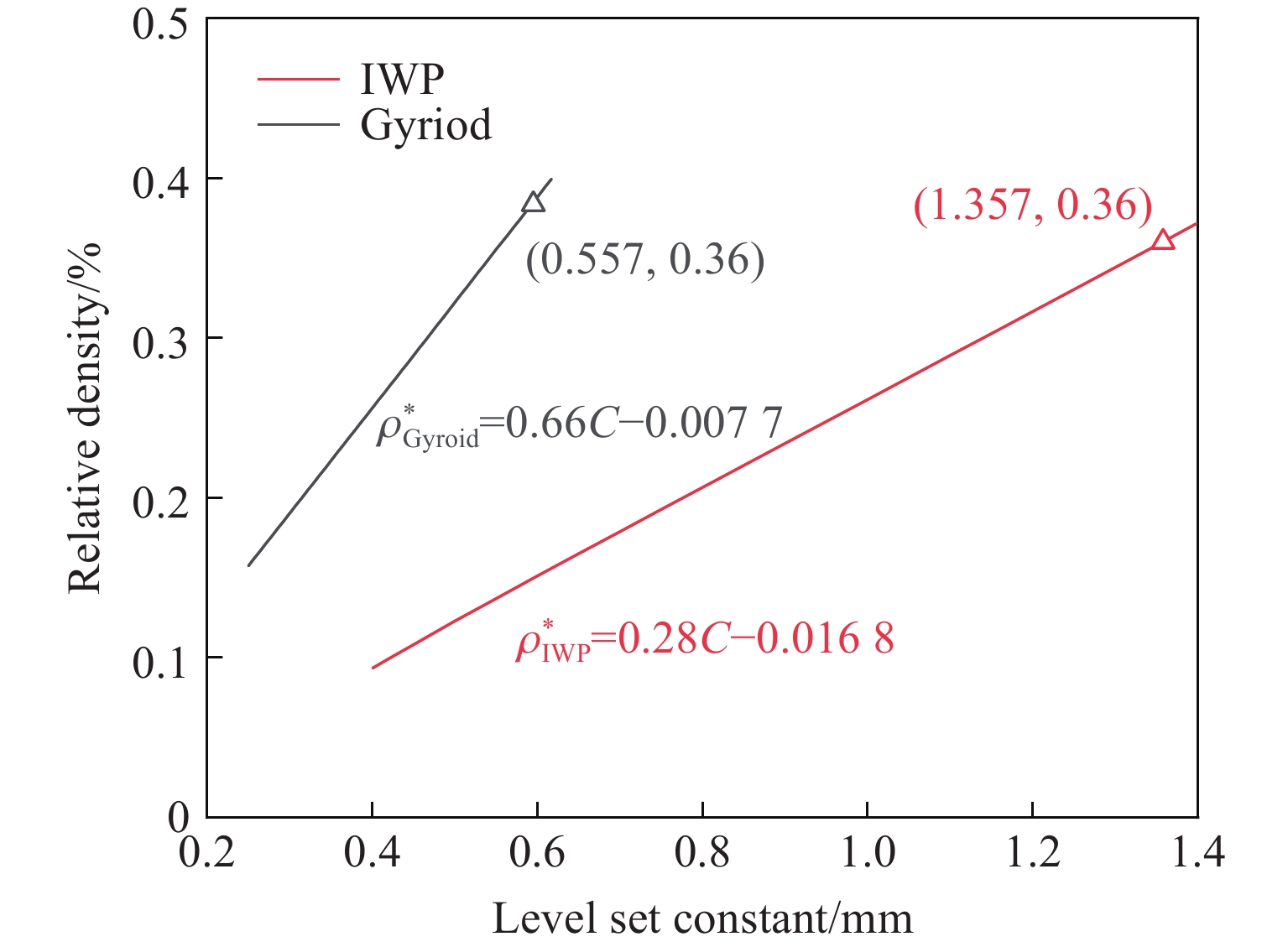
式中：m为结构的质量，V为结构的体积，${\rho _{\rm{s}}}$为基体材料的密度。

水平集常数与相对密度的关系如图2所示。其中，${\rho ^*_{\rm{Gyroid}}} $和${\rho ^*_{\rm{IWP}}} $分别为Gyroid和IWP结构的相对密度。从图2可以看出，水平集常数C是构成TPMS结构的重要参数，通过改变C的大小可以实现曲面的偏移，从而进一步控制TPMS结构的孔隙大小，并且相对密度${\rho ^*}$与C呈线性关系。例如，相对密度为36%时，Gyroid和IWP结构的水平集常数分别为0.557和1.357。在相同的相对密度下，Gyroid结构相对于IWP结构有着更高的曲面面积。

图3给出了GIP混合结构的设计方法，将Gyroid结构作为内层结构镶嵌在IWP结构内部混合半径R=6 mm的范围内。通过设置内外相同的水平集常数，使IWP与Gyroid结构的质量比约为3∶2，混合结构的相对密度为36%，从而实现在相同相对密度下超材料结构的多功能集成。混合结构GIP的设计表达式可以表示为

式中：$A\left( {x,y,\textit{z}} \right)$为在0～1之间变化的空间过渡函数，用来连接Gyroid和IWP结构。本研究采用Sigmoid函数^[18]来设计平滑圆柱形过渡边界，Sigmoid函数可以表示为

式中：k为描述不同拓扑形式点阵之间过渡宽度的参数。在不同的Sigmoid函数下，k值越小，过渡区域越宽，过渡越光滑。本工作对k=1的情况进行研究。为实现内、外的径向混合效果，将$G(x,y,\textit{z})$定义为圆心函数，用于控制2个TPMS子结构相交的边界。

本研究中晶格结构的单胞尺寸为6 mm×6 mm×6 mm，受多孔结构边界效应的影响，结构单胞数量可能会影响结构的整体力学性能。根据数值模拟结果^[19–20]并综合考虑力学性能和计算效率，选取4×4×4的单胞个数对TPMS结构进行力学性能研究，几何模型如图3所示。

利用金属3D打印机制作了3种构型的TPMS结构（Gyroid结构、IWP结构和GIP混合结构），将冲击方向与圆柱形过渡层轴线方向相同的结构记为GIP-1，冲击方向与圆柱形过渡层轴线方向垂直的结构记为GIP-2。选择316L不锈钢作为3D打印成型材料，SLM工艺参数如下：激光功率为270 W，扫描速度为950 mm/s，光斑直径为70 μm，不锈钢粉末颗粒直径为15～53 μm，单层铺粉厚度为50 μm。对固化后的试样进行吹粉和喷砂处理，以克服材料在加工过程中的一些缺陷。打印试样采用的晶格数量为4×4×4单元格，立方体边长为24 mm，相对密度为36%。打印的3种TPMS结构试件如图4所示。

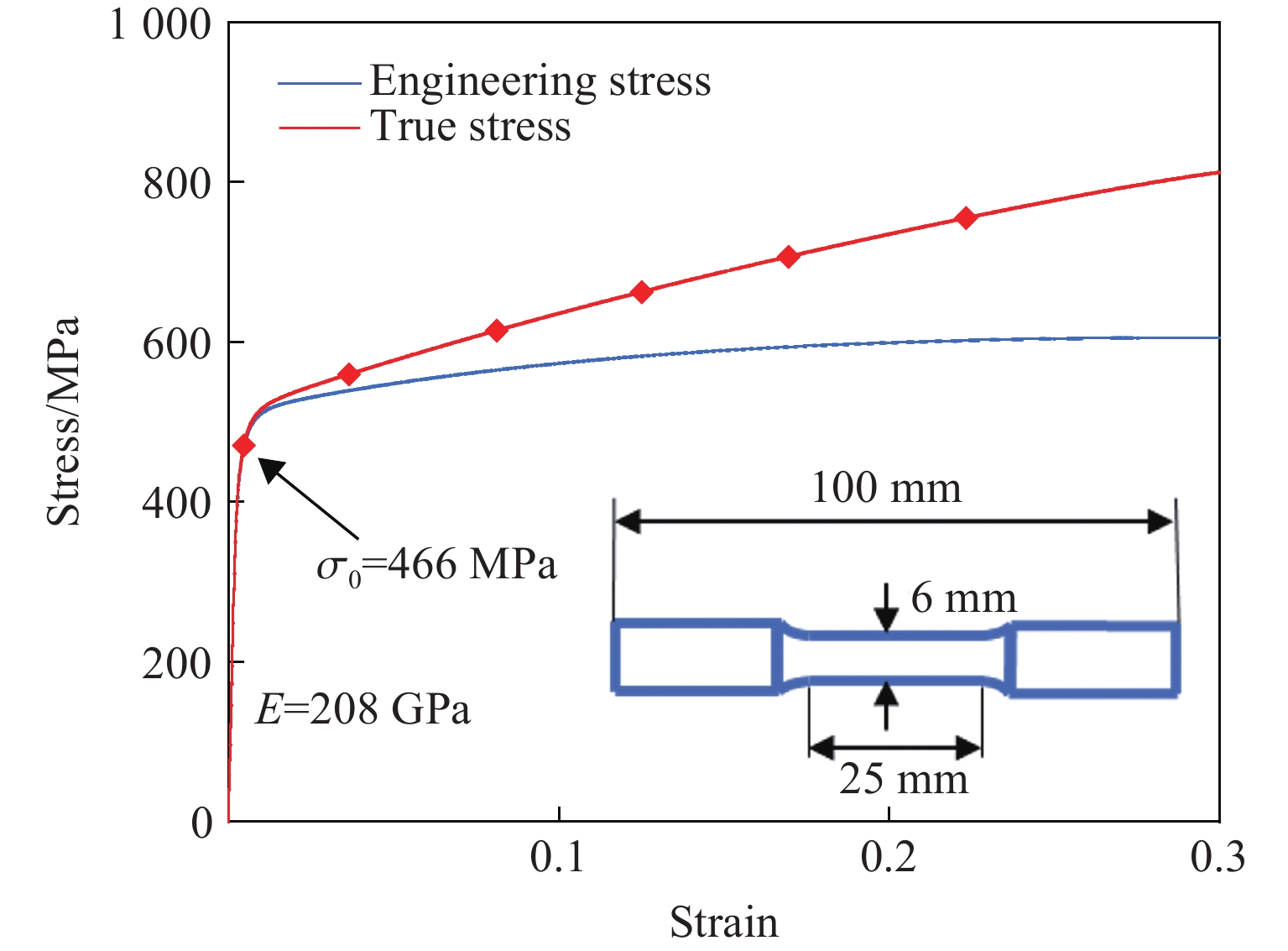
为了获得316L不锈钢材料的真实参数，通过SLM技术制备了标准拉伸试样（ASTME8/E8M标准），并对其进行了准静态拉伸实验。3D打印制备的拉伸试样尺寸参数和实验曲线如图5所示。316L不锈钢材料的应力-应变曲线表现出明显的双线性特征，具体的力学参数如下：密度为7 830 kg/m³，杨氏模量E=208 GPa，泊松比μ=0.3，初始屈服应力σ₀=466 MPa。

为了确定打印试样的打印精度，对试样质量进行测量，每种试样均测量3次，并取3次测量结果的平均值，结果如表1所示。

从表1可以看出，测量得到的打印试样的平均质量为40.37 g，平均相对密度为37.29%，测量误差均在5%以内。

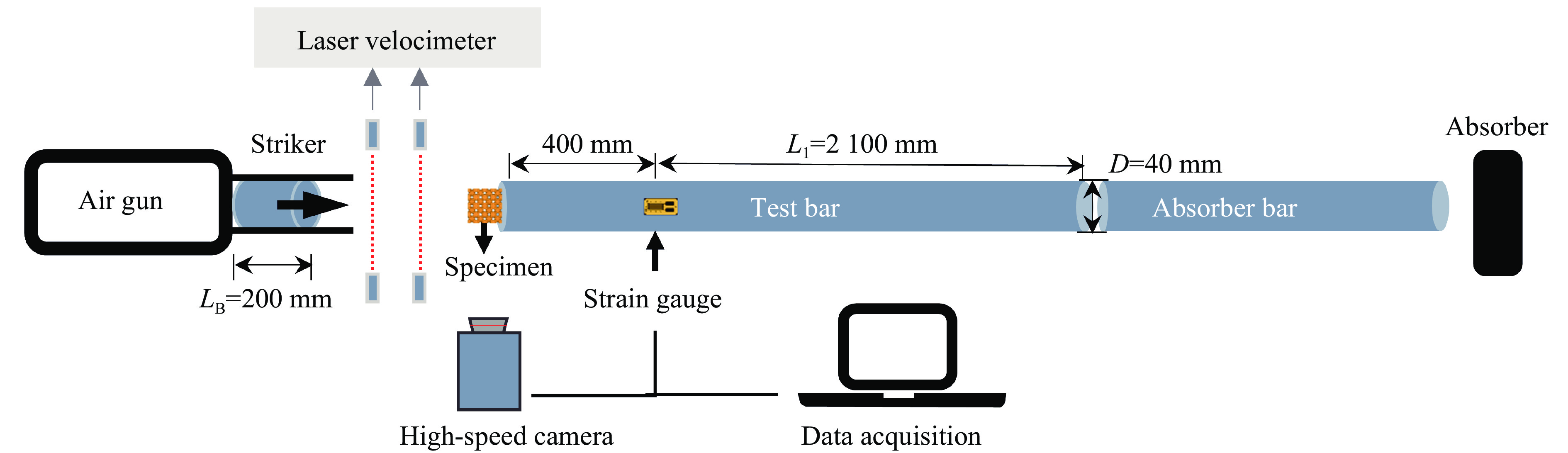
采用直撞式霍普金森杆装置对试件进行中速动态冲击实验，将试样粘贴在测试杆的端部，并使用空气动力气枪加速撞击杆对试样施加直接冲击，实验装置如图6所示。

测试杆和撞击杆均由GCr15钢制成，材料的杨氏模量为210 GPa，密度为7 850 kg/m³，杆的直径D均为40 mm，测试杆长度L=2 500 mm，撞击杆长度L_B=200 mm，应力波在杆中传播的波速C₀为4 499 m/s，试件的长度L_s=24 mm。使用一对应变计（对臂半桥）采集传输到测试杆的电信号，应变片粘贴在距离测试杆远端L₁=2 100 mm处，如图6所示。使用高速摄像机拍摄图像，像素为320×128，帧率为1×10⁵ s⁻¹。加载速度由红外测速仪确定。

直撞式霍普金森杆技术是研究材料在高应变率下的动态力学性能的方法之一，尤其适用于晶格超结构的动态表征^[21]。该装置由传统霍普金森杆实验装置改进而成，撞击杆直接撞击的加载方式可以使试件产生更高的冲击应变，并能够将动能从撞击器直接传递到试件。实验时，当应力波传播到撞击杆与试件的界面时，由于撞击杆与试件之间的波阻抗不匹配，一部分冲击脉冲透过试件进入测试杆形成透射脉冲，另一部分则反射回撞击杆形成反射脉冲，通过分析连接在测试杆上的应变片数据确定试样与测试杆接触面处的应力。从测试杆远端反射的信号到达应变片之前的时间间隔$\Delta t = $ $ 2{L_1}/{C_0} = 0.93\;{\rm{ms}}$，而入射波脉冲持续时间（脉冲宽度）${t_{\rm{i}}} = 2{L_{\rm{B}}}/{C_0} = 0.089\;{\rm{ms}}$，因此，反射波不会对记录信号产生影响。采用如下推导方法，从记录中提取单个波的相关数据，计算试件的应力-应变关系

式中：${E_0}$为压杆的杨氏模量，${A_0} = {{\text{π} {D^2}}}/{4}$为压杆的横截面积，A_s为试件的横截面积，v_B和M_B分别为撞击杆的速度和质量，$\varepsilon _{\rm{t}}^*(t)$为安装在测试杆上的应变片记录的试件作用引起的右行应力波。

TPMS结构均由MS Lattice^[18]创建，采用Hypermesh软件对结构进行网格重划分，综合考虑计算精度和计算效率，设置网格尺寸为0.3 mm，网格类型为八节点六面体实体单元。材料模型使用PIECEWISE_LINEAR_PLASTICITY（MAT_24）模型，将实验曲线作为材料参数直接输入，同时考虑基体材料的应变率效应，采用Cowper-Symonds模型

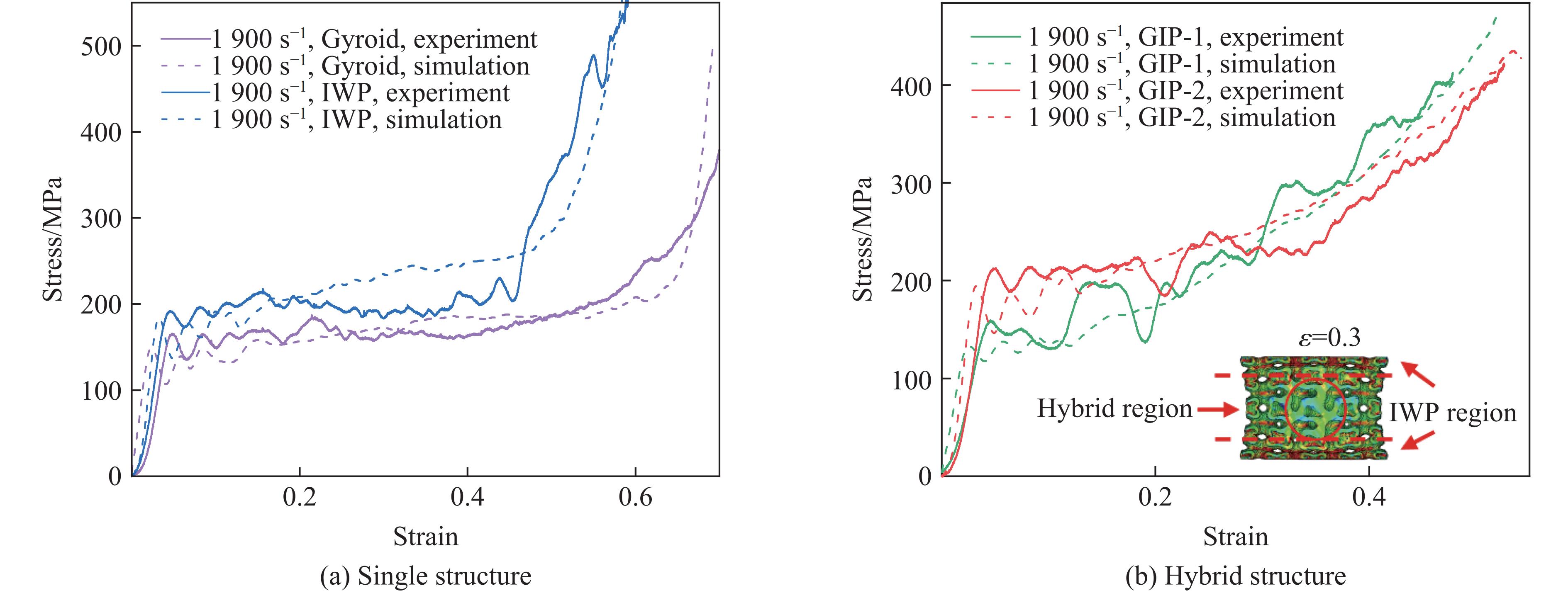
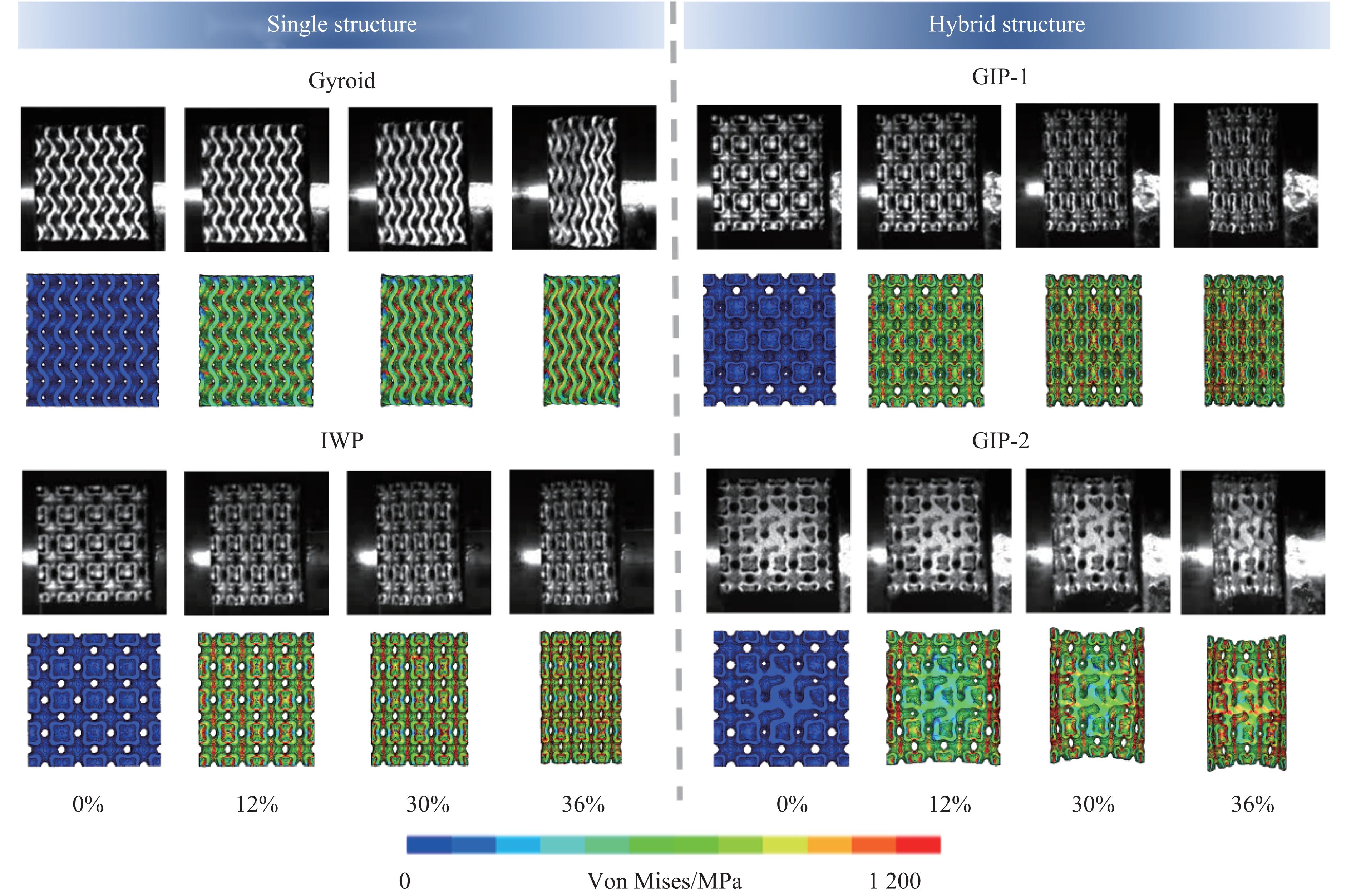
式中：${\sigma _{\rm{d}}}$为动态屈服应力，${\sigma _{\rm{y}}}$为静态屈服应力，C和P为应力放大因子。根据参考文献[12, 22]，分别设置C和P为1 704.5 s⁻¹和5.2。杆与试件之间选用AUTOMATIC_GENERAL的接触方式，静态和动态的摩擦系数分别设置为0.3和0.2^[23]。通过创建撞击杆来施加压缩载荷，并设置相应的初始速度。通过实验观测到结构在变形过程中未出现破坏失效，因此，在有限元模拟中不考虑失效。

将单一结构和混合结构在直撞式霍普金森杆冲击下的有限元模拟结果与实验结果进行比较。应力-应变曲线和变形演化过程如图7和图8所示，可以看出，数值模拟结果与实验结果吻合良好。表明该有限元建模方法能够较好地模拟TPMS结构的动态行为。

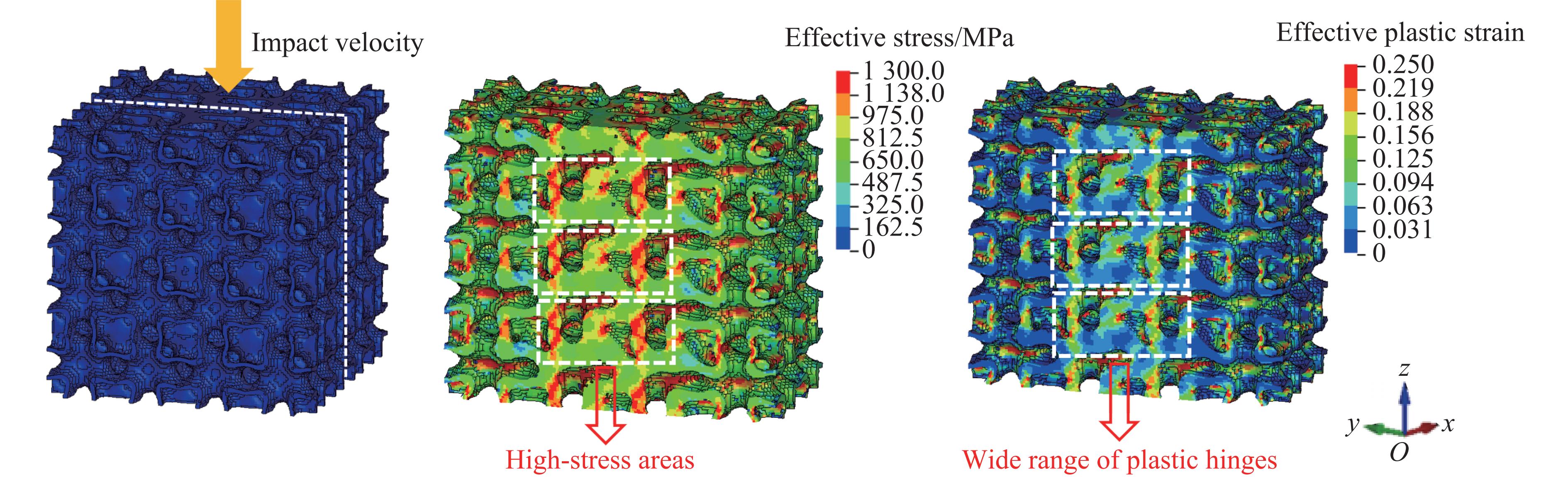
图8给出了实验和数值模拟得到的单一结构和混合结构在应变率为1 900 s⁻¹（冲击速度为50 m/s）的动态冲击下的变形演化过程。从图8中可以看出，Gyroid和IWP结构均呈现出均匀的压缩变形模式。在受到冲击载荷时，混合结构GIP-1从变形初期直至密实化都呈现均匀压溃的变形模式。相较于单一结构，混合结构GIP-1展现出了独特的优势，其Gyroid子域和IWP子域并非孤立存在，而是协同工作，共同有效地承受外部载荷。这种协同作用不仅增强了结构的整体稳定性，还使得混合结构GIP-1在承受冲击时能够展现出更加优异的性能。图9给出了在50 m/s冲击载荷下混合结构GIP-1的1/2有限元模型剖面。可以看出，在混合结构GIP-1的内部，圆柱形区域经过特殊设计，形成了大范围的塑性铰。这些塑性铰的存在使得结构在受到外力作用时能够发生塑性变形，从而吸收大量的冲击能量。这种设计不仅显著提高了混合结构GIP-1的刚度和强度，还进一步增强了其能量吸收能力，使其在防护和能量吸收领域具有广阔的应用前景。

防护结构的设计需要具备多级能量吸收能力，为了实现这一目标，第一平台的设计显得尤为重要。它不仅需要具有较小的初始峰值应力，以减轻碰撞时产生的冲击力，还需要具备良好的缓冲能力，以有效地吸收和分散冲击能量。然而，当结构压缩到一定程度时，承载力需要加强并提供高的能量吸收效率。实验结果显示，混合结构GIP-2具有明显的多级平台承载和变形能力。在动态载荷作用下，混合结构GIP-2的变形首先集中在模型两端的IWP子域，此时IWP结构内部的相互作用增强，吸能迅速增大。随着压缩位移的继续增加，混合结构GIP-2由两端向中间混合层方向对称逐层变形直至达到密实化。图7(b)中绿色区域块标记了应力-应变曲线的2个能量吸收阶段。可以看出，第1阶段显示出较大的应力波动，波动中波峰和波谷交替出现，其中波谷对应于每层单胞的屈曲，波峰对应于每层单胞密实化后结构的高变形阻力。第2阶段的能量吸收在应变达到0.3时开始，此时靠近杆两端的IWP子域首先出现变形，并逐渐达到局部密实状态。这一变化标志着第1阶段能量吸收结束和第2阶段能量吸收开始。随着两端IWP子域的密实化，中间的混合基元层开始发挥主导作用，应力水平较高，该平台阶段有一定程度的应变硬化，在混合结构GIP-2的抗冲击过程中扮演着重要角色。这一阶段的能量吸收主要通过混合层的变形来实现，其幅度远大于第1阶段。因此，混合结构GIP-2通过两级能量吸收机制实现了大幅度的能量吸收。首先，通过IWP子域的局部密实化吸收一部分能量；然后，中间混合层的主导作用进一步增强了结构的能量吸收能力，使其在抗冲击过程中表现出色。这种设计思路为开发高性能的能量吸收结构提供了新的途径。

以初始峰值应力${\sigma _{\rm{peak}}}$、平台应力${\sigma _{\rm{pl}}}$和比吸能（specific energy absorption，SEA）作为评价指标来评估TPMS结构的耐撞性能。平台应力${\sigma _{\rm{pl}}}$^[12]表示为

式中：$\varepsilon _{\rm{i}}$为屈服应力点对应的应变，$\varepsilon _{\rm{d}}$为结构的密实化应变。密实化应变${\varepsilon _{\rm{d}}}$可由能量吸收效率曲线$\eta (\varepsilon )$确定^[24]

$\eta (\varepsilon )$曲线的峰值点对应的应变为密实化应变${\varepsilon _{\rm{d}}}$。

TPMS结构吸收的总能量（W）可以表示为^[25]

比吸能E_SA的表达式为

式中：$\rho $为晶格结构的密度。

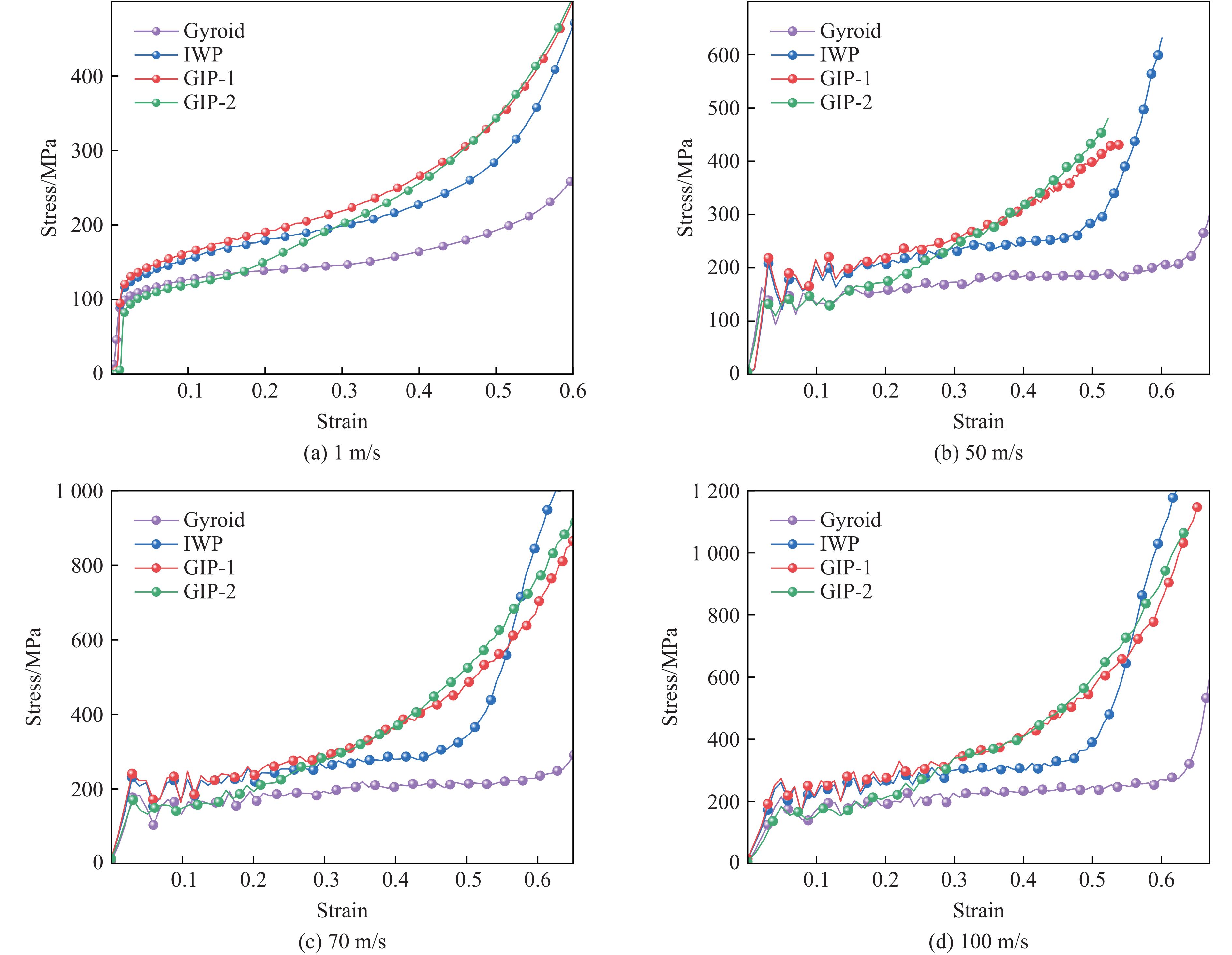
图10给出了不同冲击速度下TPMS各胞元的应力-应变曲线。从图10可以看出，不同冲击速度下各结构的应力-应变曲线具有3个阶段，即线弹性阶段、强化阶段和密实化阶段，曲线整体没有出现明显的应力波动，表明TPMS结构在受到冲击时能够保持稳定的性能，避免了因应力波动而导致的结构失效或性能下降。如图10(a)所示，当冲击速度为1 m/s时，在初始短暂的线弹性阶段后，结构出现塑性变形，应力-应变曲线出现一个较长的强化阶段。随着结构被进一步压缩，胞元之间的相互作用增强，应力迅速上升，进入密实化阶段。如图10(b)所示，由于载荷的作用时间较短，在50 m/s的冲击速度下，单一TPMS结构（Gyroid和IWP）均达到了密实化，其中Gyroid结构的强化效果并不明显，表现出较长的平台阶段。混合结构在强化阶段变形结束，具有较好的抗冲击承载能力，GIP-1结构表现出较高的初始峰值应力，而GIP-2结构的初始峰值应力较低，但其强化效果更加明显。如图10(c)和图10(d)所示，当冲击速度高于50 m/s时，所有结构均进入密实化阶段，初始峰值应力有明显提高。

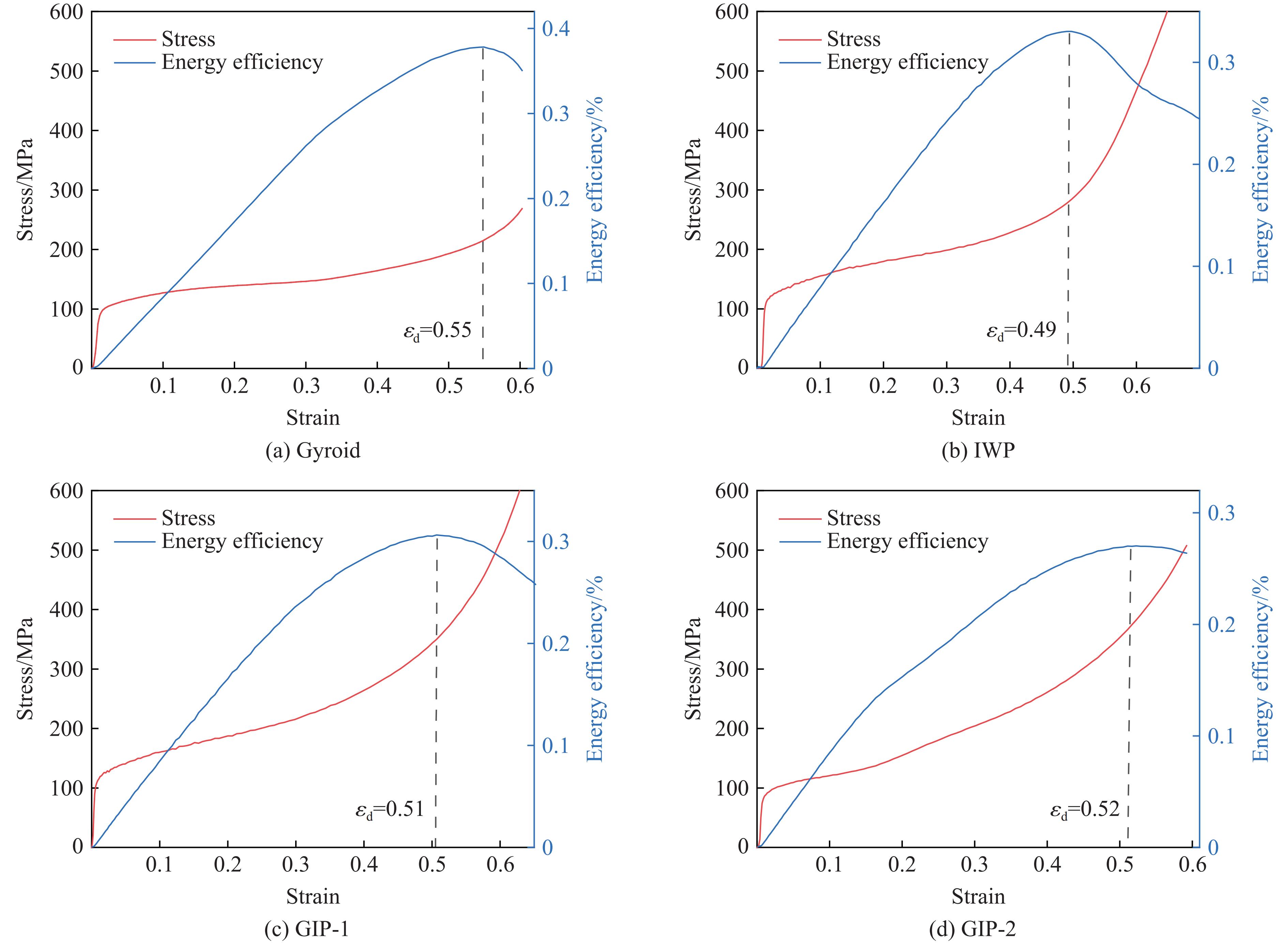
图11给出了单一结构和混合结构的能量吸收效率和密实化应变曲线。从图11可以看出，Gyroid和IWP结构的密实化应变分别为0.55和0.49；对于混合结构GIP，当沿圆柱形过渡层轴线方向冲击时（GIP-1），密实化应变为0.51，垂直于圆柱形过渡层轴线方向冲击时（GIP-2），密实化应变为0.52。由此可以看出，混合结构GIP的密实化应变介于单一结构Gyroid和IWP的密实化应变之间。

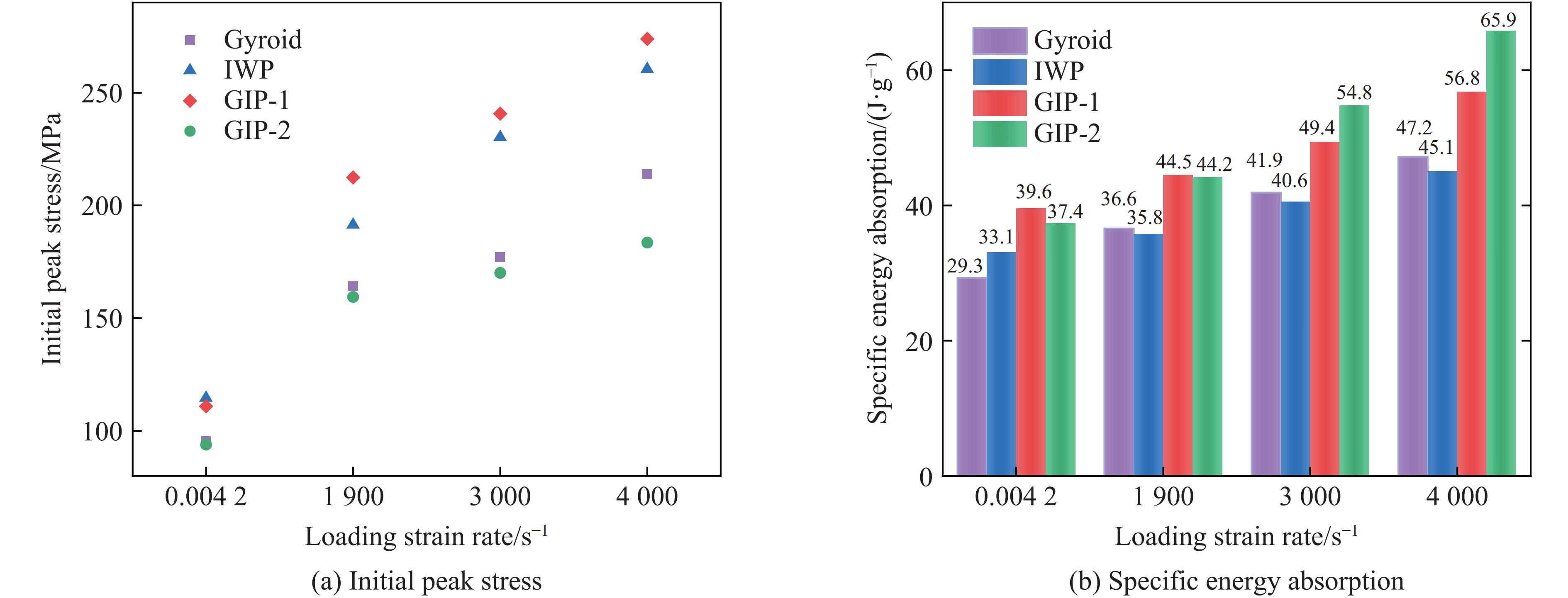
图12给出了不同结构的初始峰值应力和比吸能对比，从图12中可以看出，与单一结构Gyroid和IWP相比，混合结构GIP在能量吸收方面有明显提高，在不同加载条件下，GIP-2结构总是具有最小的初始峰值应力。在1 m/s冲击速度下，GIP-1的比吸能大于GIP-2，但是随着冲击速度的提升，GIP-2结构的吸能效果不断增强。在50 m/s的冲击速度下，GIP-1与GIP-2结构的比吸能趋于相同。在70 m/s的冲击速度下，GIP-1结构的比吸能相较于单一的Gyroid结构和IWP结构分别提升了17.95%和22.11%；而GIP-2结构在这一冲击速度下显示出最高的比吸能，与Gyroid结构和IWP结构相比，GIP-2结构的比吸能分别高出了43.65%和35.25%。吸能性能的显著提升主要归功于GIP-2结构设计的独特性。这种混合设计不仅结合了Gyroid结构和IWP结构的优点，还在结构内部形成了大范围的塑性铰，从而实现了高效的能量吸收。此外，GIP-2结构在冲击过程中的多级能量吸收机制也为其优异的力学性能提供了有力支撑。

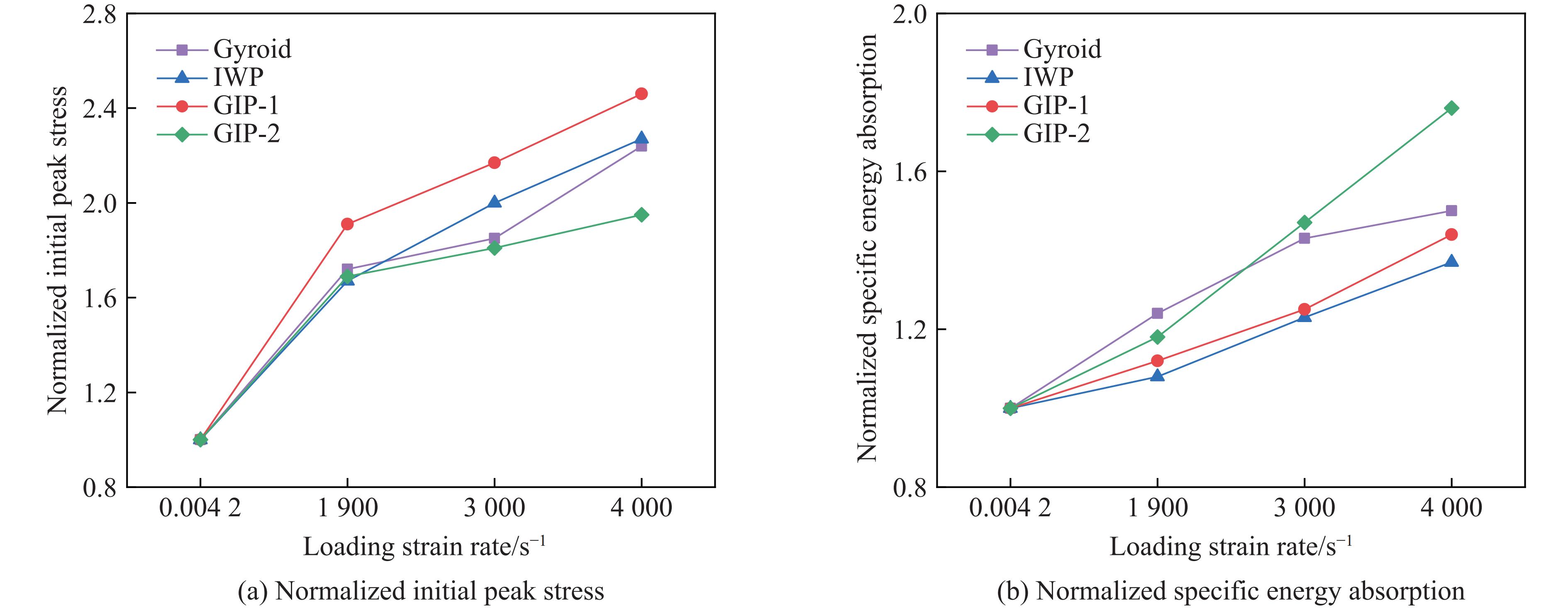
图13给出了不同加载条件下的初始峰值应力和比吸能的应变率敏感性。所有加载条件下的结果均通过准静态下的计算结果归一化来描述结构的应变率敏感性^[12]。可以看出，所有结构的初始峰值应力和比吸能均表现出明显正相关的应变率效应。GIP-1结构的初始峰值应力对应变率变化敏感，而GIP-2结构的初始峰值应力对应变率变化比较敏感，表现出更好的稳定性。GIP-2结构的比吸能受应变率影响最显著，当应变率高于3 000 s⁻¹（冲击速度为70 m/s）时具有最好的能量吸收能力。由此可以看出，混合结构GIP在垂直于圆柱形过渡层轴线方向冲击时（GIP-2），能够更好地发挥Gyroid和IWP基元结构的冲击吸能效果。

对单一TPMS结构（Gyroid和IWP）和混合结构GIP在直撞式霍普金森杆冲击加载下的动态力学响应进行了实验及有限元模拟，分析了不同加载条件下拓扑构型和冲击速度对结构动态力学性能的影响，得到以下主要结论。

(1) TPMS晶格超结构的应力-应变曲线表现出典型的3个阶段：线弹性阶段、强化阶段以及密实化阶段，并显示出一定程度的应变硬化；混合结构GIP的应力-应变曲线相比单一TPMS结构具有更强的硬化效果。

(2) 混合TPMS结构设计使得结构的能量吸收能力大幅度提升。在70 m/s的冲击速度下，GIP-1结构的比吸能相较于单一的Gyroid结构和IWP结构分别提升了17.95%和22.11%。GIP-2结构在不同加载条件下始终具有最低的初始峰值应力，并保持了混合设计带来的增大比吸能的优势，与IWP结构相比，GIP-2结构的初始峰值应力至少降低了16.68%。GIP-2结构能够更有效地将冲击能量转化为结构的变形能，是最佳的抗冲击结构设计。

(3) 所有结构均显示出不同程度的应变率敏感性。结构的初始峰值应力和比吸能均随应变率的增加而增大，其中初始峰值应力受应变率的影响更大。在更高的冲击应变率下，相较于其他结构，GIP-2结构低初始峰值应力和高比吸能的优点更为突出。