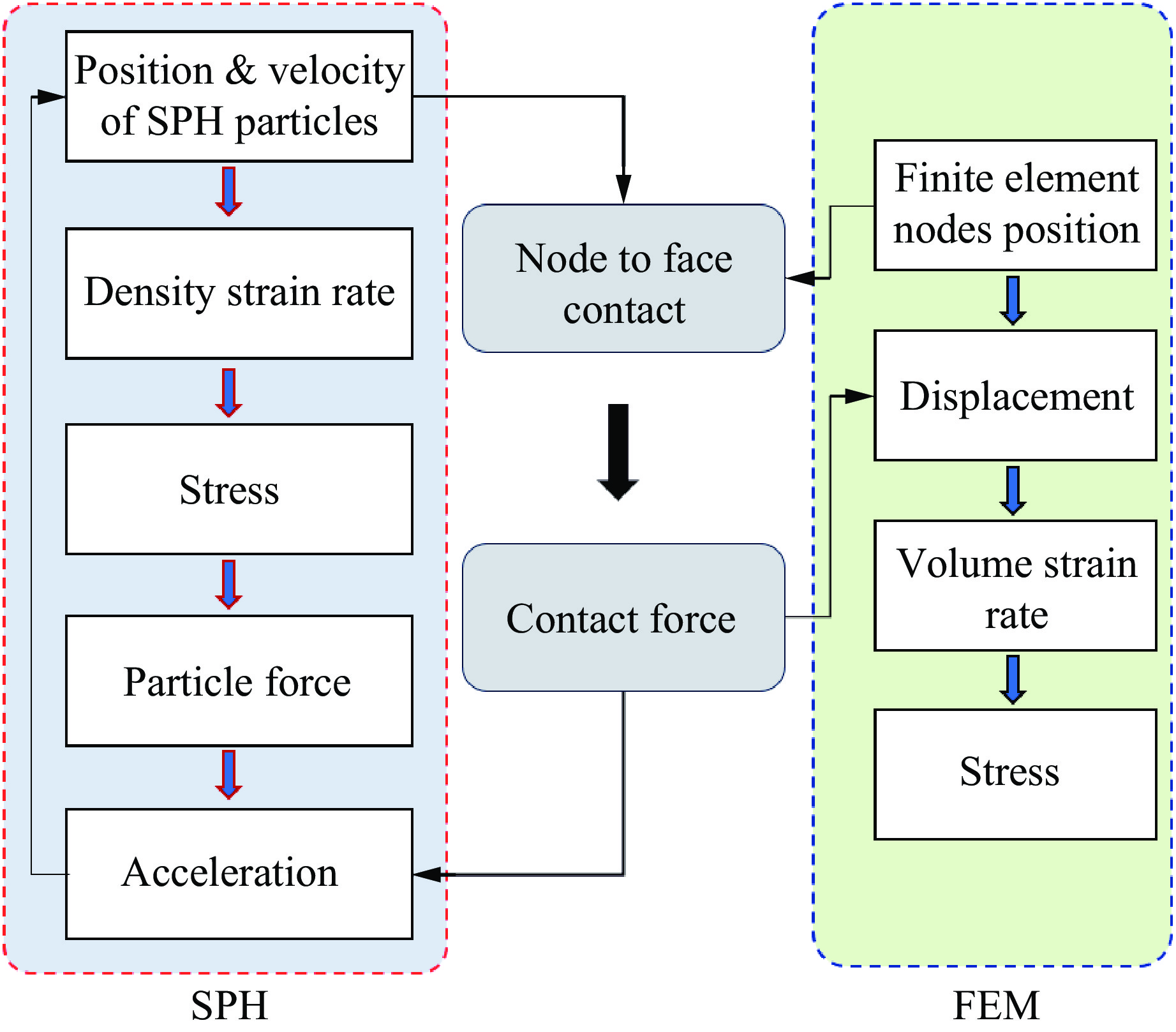
SPH-FEM耦合理论结合了SPH和FEM的优势，能很好地解决流-固耦合中的冲击大变形问题，如水射流冲击煤岩的情况^[17–19]。单一的FEM方法虽然在计算效率以及连续材料变形计算的准确性上很高，但是经常会因为网格畸变终止计算或导致计算错误；SPH方法虽然计算效率相对较低^[20–21]，但具有自适应性强的特点，可以有效解决网格畸形引起的计算错误。因此，本研究采用SPH方法对水射流建模，同时，采用FEM方法描述煤岩的力学性能，以获得相对准确的煤岩损伤特征，并提升计算效率。此外，采用点-面算法定义水射流与煤岩之间的相互作用，其中，水射流作为从属部分，煤岩作为主要部分，水射流与煤岩接触界面满足速度相等的滑动条件^[22–23]。耦合算法的计算原理如图1所示。图1左侧部分显示了SPH方法的计算过程，右侧部分显示了FEM方法的计算过程。

现有水射流破岩的数值模拟研究通常是将水射流设置为二维矩形或者三维圆柱形水柱，并对射流赋予恒定的或随时间变化的冲击速度，如李洪盛^[24]、周维^[25]通过采用LS-DYNA与Excel的接口赋予射流随时间正弦变化的周期性脉冲速度。然而，上述射流速度的赋值方法存在一定的局限性。在水射流冲击煤岩的实践应用中，射流从喷嘴喷出后，在空气等介质中的运动速度及方向会发生改变。此外，当射流撞击煤岩时，射流速度将降低，并且，射流粒子的运动方向发生改变。因此，射流在撞击煤岩时并未保持原有的正弦变化速度。针对上述问题，考虑到高压水射流是柱塞泵活塞的挤压作用形成的，本研究通过对柱塞施加正弦变换速度来实现超高压自激脉冲水射流脉动速度的赋值。

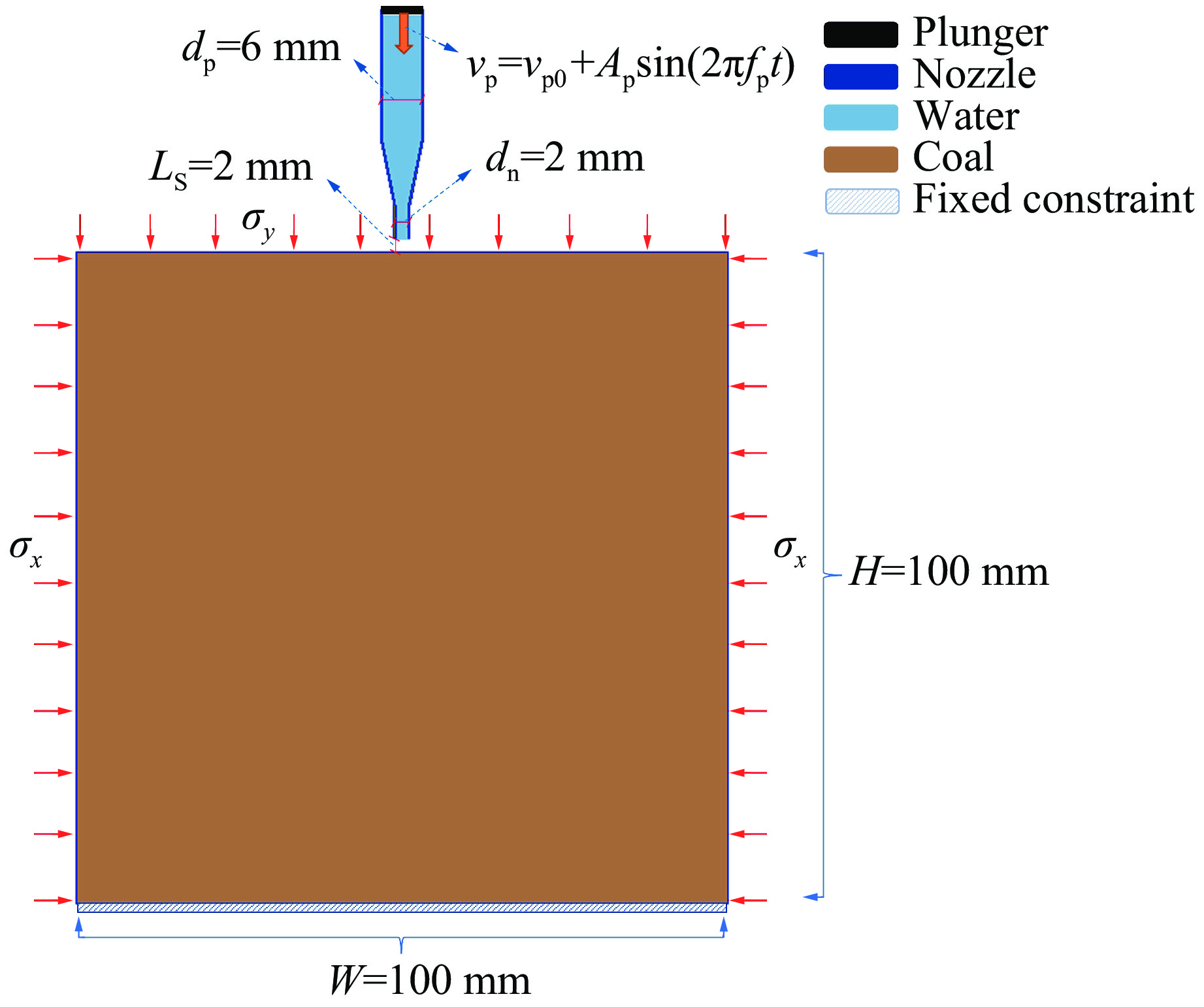
在水射流破除煤岩的工程实践中（如煤矿井下水力割缝、水力冲孔等），煤岩往往处于应力加载环境。为研究应力环境下高压脉冲射流冲击下煤岩的破碎机理和破碎效率，采用SPH-FEM耦合方法，建立了应力加载条件下高压脉冲水射流冲击煤岩的数值计算模型。模型主要包括水射流和受载煤岩2部分。水流受到柱塞挤压，形成高速射流从喷嘴喷出^[26]。通过调整柱塞的挤压速度，可改变水射流的参数，如射流速度、脉动幅度、脉动频率等。通过对煤岩施加不同方向和大小的应力获得不同的应力赋存环境^[17]。在数值计算模型中，喷嘴和柱塞通过FEM有限元方法定义为刚性单元，煤岩同样通过FEM算法定义，喷嘴内的水通过光滑粒子流SPH算法定义。将煤岩设置为长（W）和宽（H）均为100 mm的矩形区域，在煤岩的水平和垂直方向上分别施加不同大小的应力σ_x和σ_y，即应力赋存环境为（σ_x，σ_y）。对无应力（σ_x=σ_y=0 MPa）加载工况和二维等应力（σ_x=σ_y=10 MPa）加载工况开展研究。根据埋深与地应力的统计关系^[16]，10 MPa二维应力对应300 m的埋深。柱塞直径d_p为6 mm，喷嘴为锥形收敛喷嘴，收敛角为30°，喷嘴的出口直径d_n为2 mm，靶距L_S为2 mm。柱塞按以下运动速度压缩喷嘴内的水粒子

式中：v_p和v_p0分别为柱塞的挤压速度和平均速度，单位为m/s；A_p和f_p分别为柱塞挤压速度的振幅和频率，单位分别为m/s和Hz；t为时间，单位为s。高压脉冲射流冲击受载煤岩的数值计算模型如图2所示。

网格尺寸直接决定数值计算的耦合效果，甚至影响煤岩损伤分布的精确性以及裂纹的衍生情况。为精确模拟超高压脉冲水射流冲击下煤岩的破碎特征，分析煤岩在超高压脉冲水射流冲击作用下的损伤分布特征以及裂纹衍生形态，参照文献[17, 19]，根据前期不同网格尺寸模型的试算结果，将FEM网格单元尺寸设定为0.2 mm。此外，考虑实际工况中待破碎煤岩的面积较大，为消除模拟中的边界反射影响，模型两侧设置为非反射边界，底部施加固定约束。

当大量光滑粒子冲击煤岩时，粒子会迅速积累，导致计算时间显著增加和错误概率增加，为解决上述问题，采用箱约束方法以确保仅箱内的粒子参与计算。通过施加此限制，可以有效限制SPH方法的粒子搜索范围，提高计算精度，降低错误概率。

NULL材料模型通常用于描述不具备弹性或塑性行为的材料，如水等流体。Grüneisen状态方程则是一种常用的流体状态方程，用于描述流体的压缩性质和声速等物理特性。因此，数值计算中SPH方法采用NULL材料模型和Grüneisen状态方程。该方法可以有效地描述水射流的运动行为和物理特性，从而实现水射流冲击煤岩等复杂问题的数值模拟。Grüneisen状态方程为

式中：E为单位体积内能，J；ρ₀为水射流密度，g/cm³；μ为黏性系数；C为冲击波波速（v_S）-粒子速度（v_P）曲线的截距，m/s；S₁、S₂、S₃为v_S-v_P曲线的斜率；γ₀为Grüneisen常数；α为Grüneisen系数与体积关系的修正系数。水射流的本构模型参数如表1^{[17, 19]}所示。

目前，常用于岩石的损伤本构模型主要有3种：HJC（Holmquist-Johnson-Cook）模型、RHT（Riedel-Hiermaier-Thoma）模型和JC（Johnson-Cook）系列模型。与其他模型相比，RHT模型可以捕捉煤岩在动态载荷下的拉伸和压缩损伤演化，因为岩石类材料具有应变率效应，在动态加载下其强度增加，RHT模型通过引入动态应变率增强因子可以描述材料在压缩和拉伸作用下的应变率效应。因此，本研究将RHT模型作为煤岩的本构模型，模型具体参数见表2^[17]。其中，ρ_r为岩石密度，G和f_c分别为剪切模量和抗压强度，α₀为初始孔隙率，$ F_{\text{t}}^* $为相对抗拉强度，p_crush为压缩压力，D₁和D₂为损伤系数。损伤变量D是累积等效塑性应变增量$\Delta{\varepsilon} _{\rm{p}} $与最终失效等效塑性应变的比值

式中：$ \varepsilon _{\text{p}}^{\text{f}} $为塑性应变。

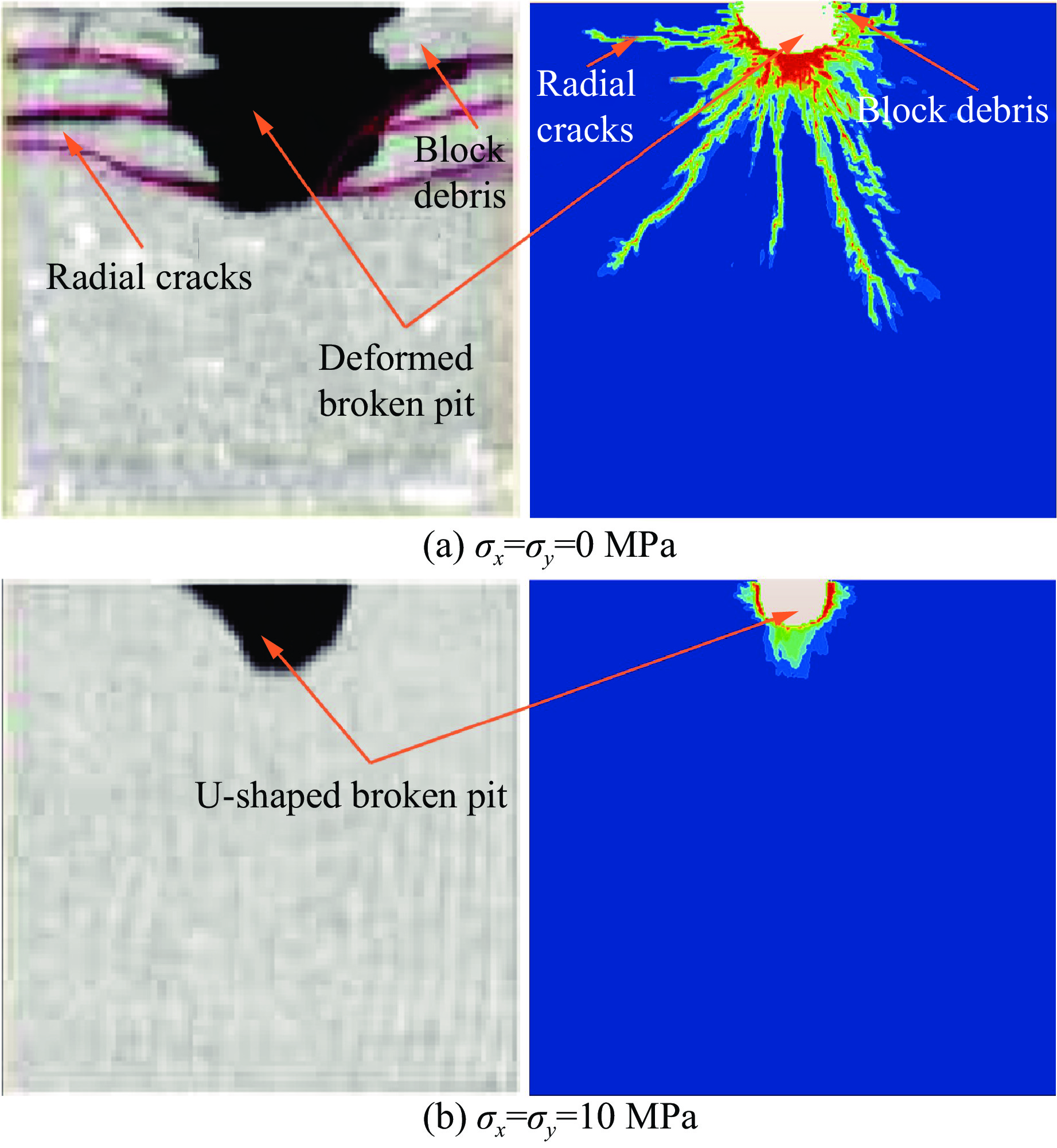
为验证数值模拟方法与计算结果的正确性，将煤岩在无、有应力加载下的计算结果与曹世荣^[16]的高压水射流破碎煤岩的试验结果进行对比，如图3所示。由图3(a)可知：在无应力（σ_x=σ_y=0 MPa）加载下，煤岩破碎坑形态不规则，呈现畸形，破碎坑周围产生了众多主裂纹（如水平分布的径向裂纹）。此外，在破碎坑表面易产生块状剥落体。由图3(b)可知：在二维应力（σ_x=σ_y=10 MPa）加载下，煤岩破碎坑范围更小，呈现U形状态，破碎坑周围无明显裂纹。综上所述，数值模拟结果与试验现象具有高度的相似性，表明本研究采用的数值模拟方法可行，获得的模拟结果可信。

通过提取水射流粒子的速度演化规律以及分析不同位置处水射流粒子喷出喷嘴后的初速度，揭示不同射流形式下水粒子速度的演化规律。

喷嘴结构包括管路直线段、收敛段和出口直线段。喷嘴结构以及特征粒子的位置分布如图4所示。

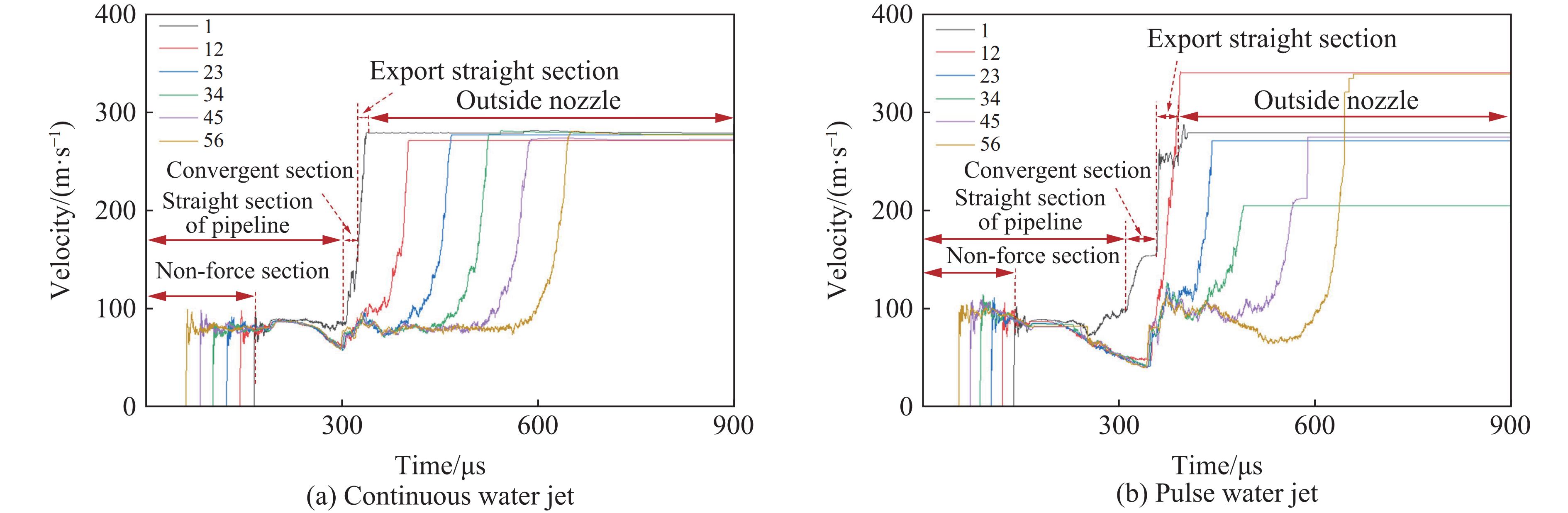
喷嘴内部存在大量水粒子，水粒子在加速过程中存在相互碰撞。为更好地获得水粒子速度随时间加速的全过程，选取喷嘴管路轴心线上6个水粒子（即特征粒子1、12、23、34、45和56），如图4所示。射流轴线上水粒子在不同时刻的速度结果如图5所示。图5(a)中柱塞运动速度恒定为80 m/s，即连续射流；图5(b)中柱塞运动速度满足v_p=80+20sin(2π×3000t)，即脉冲射流。

由图5可知，2种射流形式下水粒子的运动速度随时间的变化特征极为相似，其演化规律为：水粒子进入喷嘴收敛段前，柱塞的挤压力并未传递至特征粒子，特征粒子未受力，因而出现零速度段；当粒子间的挤压作用传递到特征粒子时，特征粒子速度突增，随后，粒子速度在管路直线段内波动。当水粒子进入收敛段后，在流量一定的情况下，由于过流断面面积逐渐减小，水粒子速度增大。进入直线段后，由于收敛段积聚的压能持续释放，水粒子速度继续增大，但增量有限，并在直线段末端趋于稳定。在离开喷嘴后的短距离内，不考虑喷嘴外空气阻力的影响，水流的速度小幅增加，并迅速稳定，主要是因为喷嘴中的水介质在瞬间高压下存在微量的体积压缩，离开喷嘴后能量得到释放^[26]。值得关注的是，当柱塞以恒定速度挤压时，不同位置处的水粒子喷出喷嘴的速度基本一致，大约为274 m/s；当柱塞以符合正弦函数变化的速度挤压时，不同位置处水粒子的喷出速度相差较大，6个特征粒子的喷出速度分别为279.62、340.85、271.52、205.57、275.03和339.68 m/s，具有明显的脉动特性。因此，为揭示柱塞运动形式对喷嘴内水粒子喷出速度的影响，有必要对喷嘴内不同位置处水粒子的喷出速度进行研究。

为减少水粒子间的相互碰撞对其喷出速度的影响，在喷嘴轴心线上选取特征水粒子1～61，相邻粒子间距离均为$\Delta$x=0.6 mm，粒子的具体分布见图4。

图6显示了2种射流形式下特征水粒子1～61的喷出初速度。从图6(a)可以发现，特征水粒子的喷出速度几乎相同，约为274 m/s；从图6(b)可以发现，不同位置处的水粒子喷出后的初速度具有正弦函数的周期性变化特征，平均速度约为265 m/s，较连续射流的喷出速度降低了3.3%，差异较小。此外，数值模拟中水射流的喷出速度比理论计算的速度略大，主要原因是喷嘴内水粒子间存在间隙，柱塞的挤压作用会使水粒子不断加速，从而大于水粒子在无压缩且充满喷嘴的理想状态下的射流速度。值得关注的是，当柱塞具有正弦变化的速度时，特征水粒子喷出喷嘴后的初速度也较好地符合正弦变化，其峰值速度约为343 m/s，脉冲幅值约为78 m/s。

综上所述，本研究提出的对柱塞施加脉动速度的方法能较好地模拟自激脉冲水射流速度的周期性脉动变化，为进一步开展真实工况下高压脉冲水射流冲击煤岩研究奠定了基础。

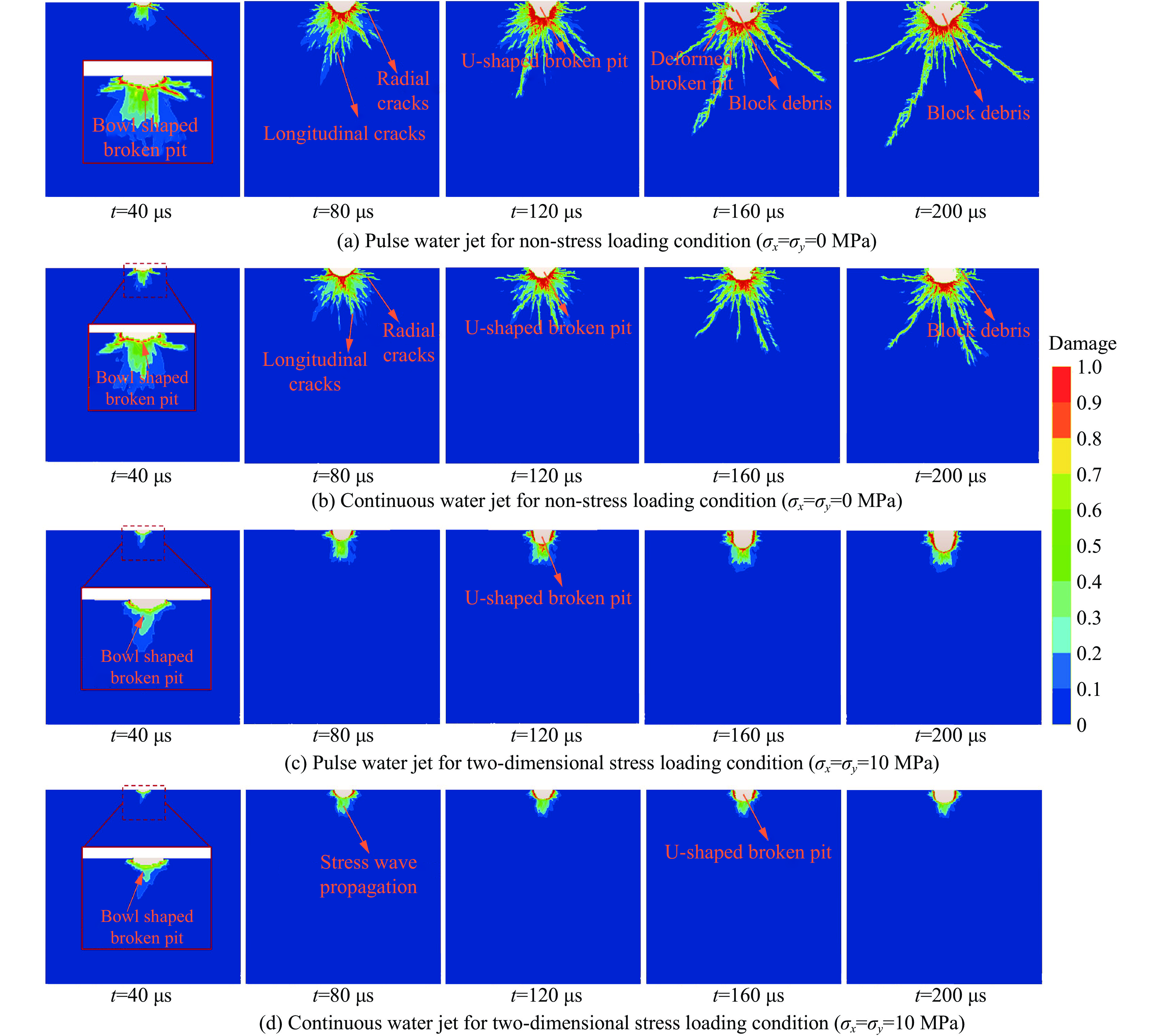
为分析脉冲水射流冲击下受载煤岩损伤破坏效率随时间的变化关系，提取了无、有应力加载条件下脉冲射流和连续射流冲击下不同时刻煤岩的损伤破坏云图，如图7所示。

在无应力加载工况下（σ_x=σ_y=0 MPa）高压脉冲水射流冲击时，煤岩破坏坑的形状、尺寸以及裂纹形态均随冲击时间的变化而发生明显的变化，如图7(a)所示。在水射流的初始冲击阶段，即t=40 μs时，破坏坑形状近似为碗状，破碎坑周侧产生了明显损伤破坏区，径向裂纹开始萌生，应力波以冲击点为中心向煤岩深部传播，且应力波能量向煤岩内部传播的过程中呈现逐层递减的趋势。当t=80 μs时，破坏坑的深度和宽度逐渐增大，已形成较为密集的径向裂纹和纵向裂纹（图7(a)）。随着射流的持续冲击，破碎坑的形状逐渐演变为U形，且裂纹进一步扩展和衍生。当脉冲射流的持续作用超过160 μs后，破碎坑内壁出现了块状剥落体，这主要是由于射流回流对破碎坑内壁产生了自下而上的冲击，使上内壁在水楔作用下块状剥落，这也使得破碎坑的形状呈畸形发展。在无应力加载工况下，高压连续水射流破碎煤岩的效果如图7(b)所示。高压连续水射流产生的煤岩破碎坑的形态及尺寸大小、裂纹分布形态等演化规律与脉冲射流产生的结果类似，但破碎坑范围更小，其周围的重点损伤区域范围更小，主裂纹的长度更长，说明脉冲射流具有更高的破煤岩效率。

相较于无应力加载条件，二维应力加载条件下(σ_x=σ_y=10 MPa)高压脉冲水射流和连续水射流的破岩效率都显著降低，如图7(c)和图7(d)所示。二维应力加载条件下，煤岩的强度增大，因此，无论是脉冲射流还是连续射流的破岩能力减弱，破岩范围缩小。在射流冲击受载煤岩初期（如t=40 μs），脉冲射流和连续射流冲击形成的破坏坑形貌也呈现碗状，但破碎坑深度和宽度较无应力加载情况下小，并且在破碎坑底部出现了一定范围的纵向损伤区。随着射流冲击的持续，破碎坑形貌开始向U形演化，脉冲射流冲击下煤岩破碎坑形状更早地演变成U形。脉冲射流冲击下和连续射流冲击下，U形破碎坑的形成时间分别为120和160 μs，表明脉冲射流对受载煤岩的破碎效率比连续射流更高。此外，煤岩在分别受到上述2种射流作用的200 μs后，均未产生宏观裂缝。由此可知，二维应力的加载对煤岩内部裂纹的衍生以及传播演化具有明显的抑制作用。此外，尽管煤岩在连续射流和脉冲射流冲击下的破坏坑形状相似，但其尺寸略有差异，在相同冲击时间下，脉冲射流形成的破坏坑深度比连续射流更深，例如在t=160 μs和t=200 μs时，脉冲射流形成的破坏坑深度分别为9.25和11.00 mm，较连续射流的破坏坑深度分别增加了54.17%和62.96%，再次表明脉冲射流具有更高的破岩效率。

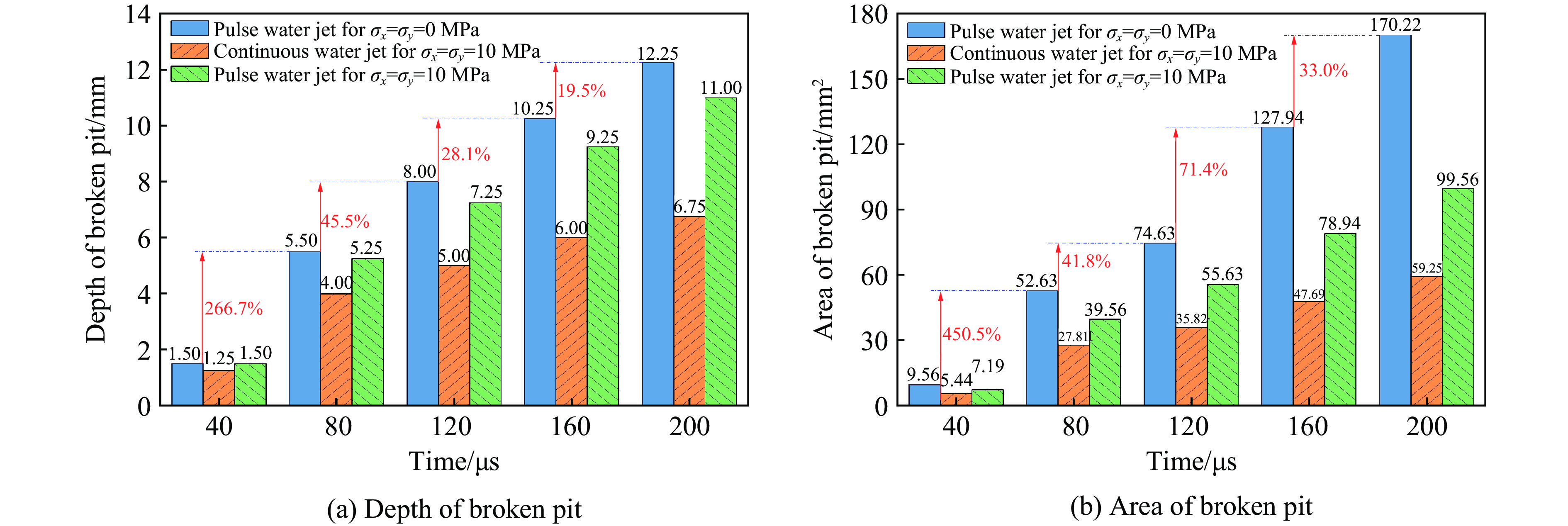
为定量分析不同工况下受载煤岩的时序特性，提取了不同时刻高压水射流冲击作用下受载煤岩的破碎坑深度和面积。

图8(a)显示了破碎坑深度随冲击时间的变化关系。在无应力加载条件下，破碎坑的深度明显大于二维应力加载条件下的破碎坑深度。t=200 μs时，二维应力加载工况下连续射流和脉冲射流产生的破碎坑深度分别为6.75和11.00 mm，低于无应力加载条件下的12.25 mm。此外，破碎坑深度随冲击时间的增加呈明显增长趋势，但其增长幅度均逐渐减小。例如，脉冲射流冲击下无应力加载的煤岩破碎坑深度的增幅在40～80 μs、80～120 μs、120～160 μs和160～200 μs 4个时间段内分别为266.7%、45.5%、28.1%和19.5%。此外，在相同冲击时间下，脉冲射流冲击下无应力加载的煤岩的破碎坑深度最大，脉冲射流冲击下二维应力加载的煤岩的破碎坑深度次之，连续射流冲击下二维应力加载的煤岩的破碎坑深度最小，再次表明二维应力的存在阻碍了射流破碎煤岩，同时，脉冲射流对受载煤岩的破碎效果较连续射流更好。

图8(b)显示了破碎坑面积随冲击时间的变化趋势，可以看出，破碎坑面积随冲击时间的增加呈明显的增长趋势，且增长幅度呈现波动状态。例如，在脉冲射流冲击作用下，无应力加载煤岩的破碎坑面积的增长率在0～80 μs、80～120 μs、120～160 μs和160～200 μs 4个时间段内分别为450.5%、41.8%、71.4%和33.0%。在相同的冲击时间下，破碎坑面积的变化规律与破碎坑深度的变化规律类似，即脉冲射流破碎无应力加载煤岩的效果优于脉冲射流破碎二维应力加载煤岩的效果，脉冲射流破碎二维应力加载煤岩的效果优于连续射流破碎二维应力加载煤岩。这主要是因为脉冲射流冲击下无应力加载的煤岩会产生较多裂缝，裂缝的产生对后续煤岩的破碎起一定的促进作用，但在应力加载工况下裂纹不易产生。随着冲击时间的持续增加，上述3种工况下煤岩破碎坑的面积差异也在增加，因为冲击时间越长，由滞止压力产生的水垫效应越明显，削弱了水射流的破碎效果。对于脉冲射流来说，由于冲击速度不断变化，水垫效应阻碍煤岩破碎的能力比连续射流弱，使得脉冲射流具有更好的破岩效果，并且，脉冲射流较少受到冲击时间的影响。

为揭示关键脉冲参数对煤岩破坏效果的影响，以下将探讨柱塞的平均速度、脉冲幅值、脉冲频率对脉冲射流冲击下受载煤岩损伤破坏特征的影响。

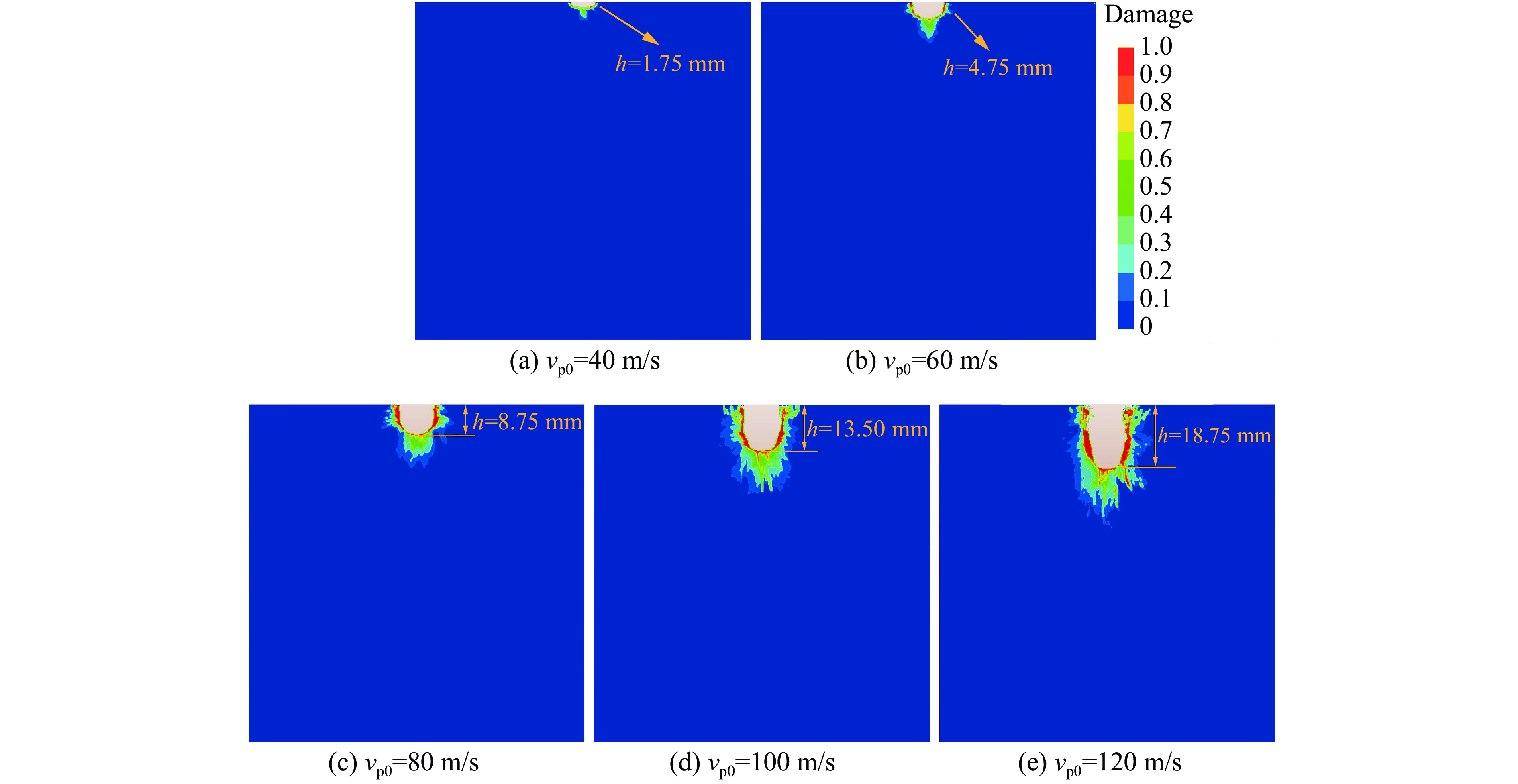
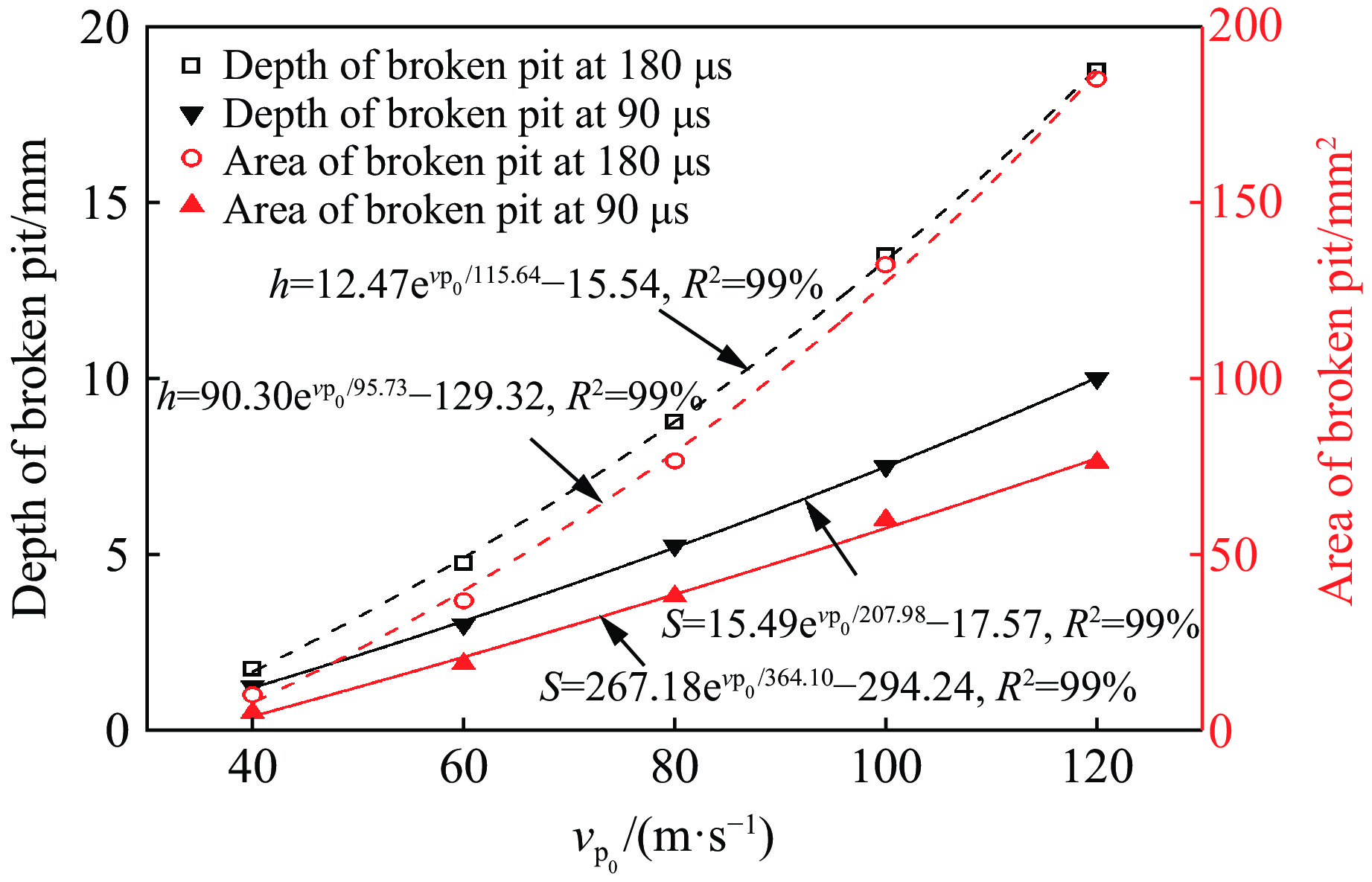
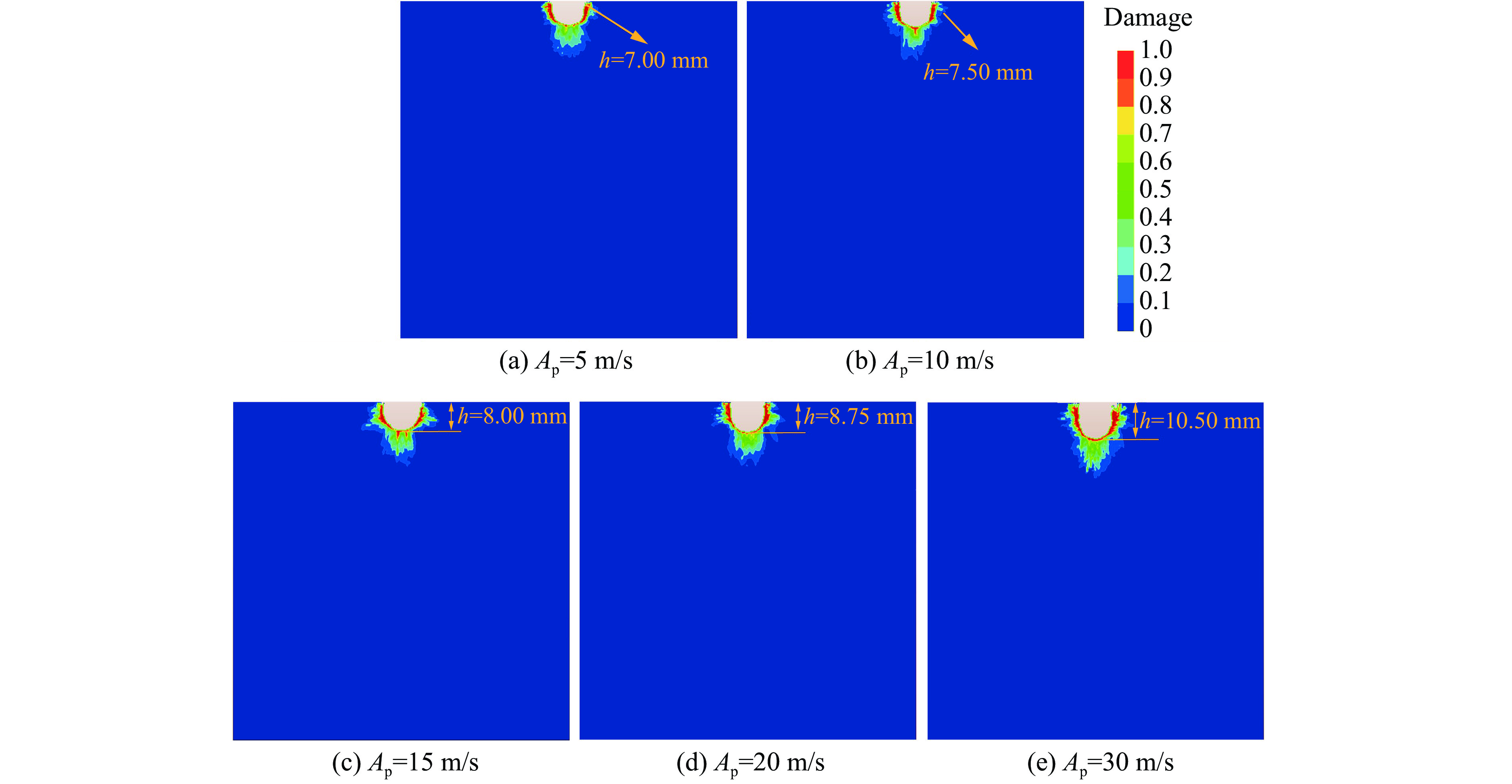
为研究柱塞的平均速度对高压脉冲水射流冲击下受载煤岩破坏效果的影响，将柱塞脉冲幅值和脉冲频率分别设为20 m/s和3000 Hz。图9显示了180 μs时不同柱塞平均速度下受载煤岩(σ_x=σ_y=10 MPa)的损伤破坏云图，可以发现，受载煤岩的损伤破坏范围随柱塞平均速度的增大呈明显增大趋势，具体表现为煤岩破碎坑宽度、深度h以及面积S的增大。当柱塞的平均速度为40 m/s时，脉冲射流对煤岩造成的损伤破坏很小，破碎坑形状为碗状，深度仅为1.75 mm，且应力波向煤岩内部传播的距离较小。当柱塞平均速度达到60 m/s甚至更高时，煤岩破碎坑的形状均呈U形，但其深度明显不同。

t=90 μs和t=180 μs时脉冲射流冲击下二维应力加载煤岩的破碎坑深度h和面积S如图10所示。当柱塞平均速度较小时，如v_p0=40 m/s、t=90 μs时，煤岩破碎坑的深度和面积仅为1.25 mm和5.03 mm²，远低于v_p0=120 m/s时的10.00 mm和76.16 mm²；v_p0=40 m/s、t=180 μs时，煤岩破碎坑的深度和面积仅为1.75 mm和10.00 mm²，远低于v_p0=120 m/s时的18.75 mm和185.13 mm²。此外，破碎坑的深度和面积均随柱塞的平均速度的增加呈指数增加，其增长速率逐渐增大，主要是由于柱塞的平均速度对射流的整体速度以及射流能量的影响非常大。射流的冲击动能与射流速度的三次方成正比^[27]

式中：E_f为射流的冲击动能，ρ_w为射流的密度，d为射流的直径，v为射流的速度。当射流速度增加时，射流对煤岩的冲击能量也显著增加，从而具有更好的破坏效果。因此，柱塞的平均速度对受载煤岩的作用效果较大。此外，脉冲射流不断变化的撞击速度大幅减小了水垫效应对煤岩破碎的阻碍。

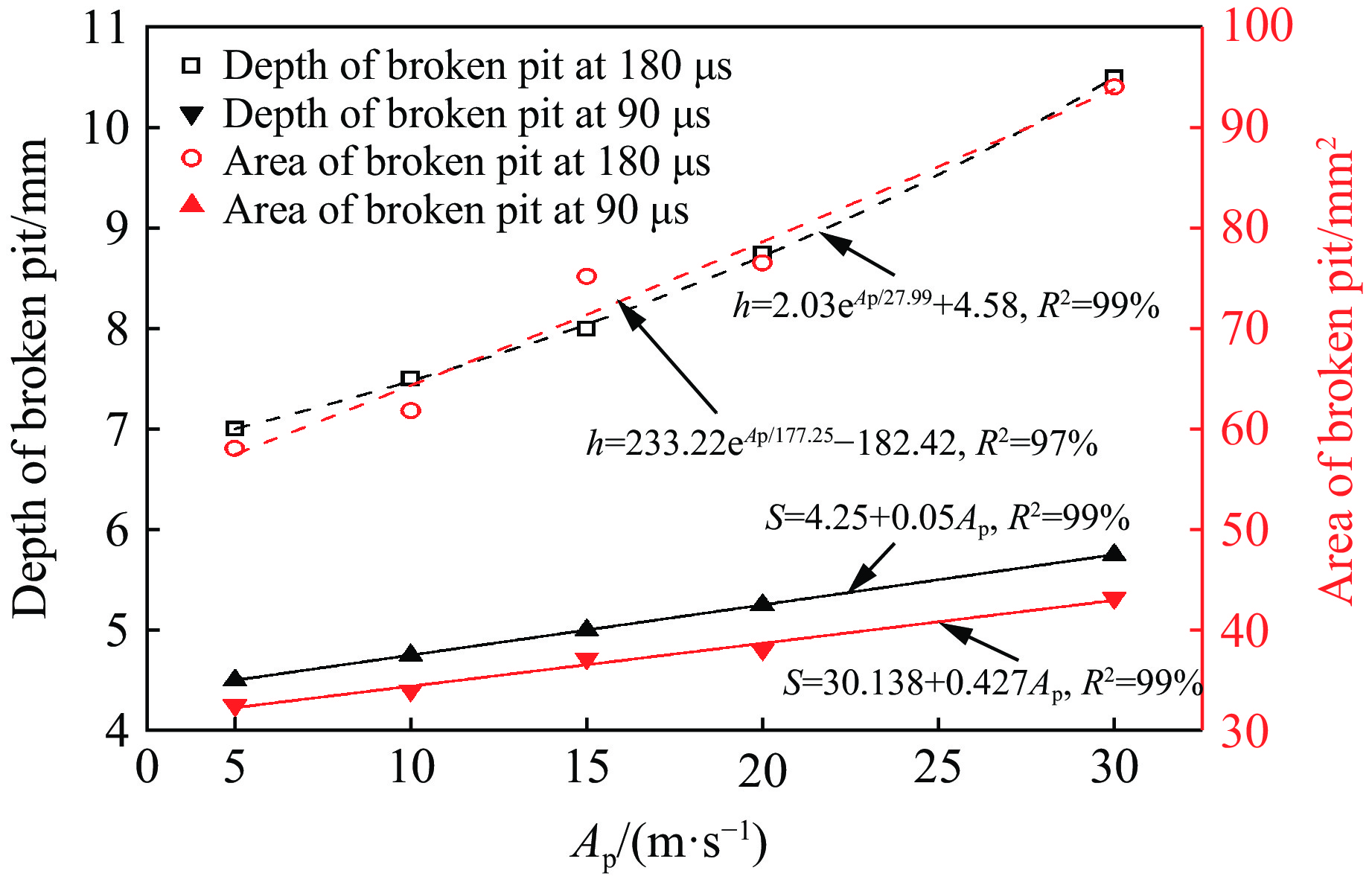
将柱塞的平均速度和脉冲频率分别设为80 m/s和3000 Hz，t=180 μs时不同柱塞脉冲幅值下脉冲射流冲击受载煤岩的损伤破坏云图如图11所示。受载煤岩的破碎坑均呈U形，破碎坑内壁两侧均产生了重度损伤区域（红橙色），应力波能量主要从破碎坑底部传播至煤岩内部。这主要是因为二维应力加载的煤岩强度更高，射流返流对破碎坑两侧并没有产生有效的冲击，但破碎坑底部一直受到脉冲射流的持续冲击，应力波能量主要在破碎坑底部有效传播。此外，应力波能量在破碎坑底部的有效传播和释放使得破碎坑底部的岩石更易于发生脆性破坏，从而避免了破碎坑底部塑性重度损伤区（红橙色）的出现。另外，柱塞的脉冲幅值对破碎坑下方的应力波能量传播深度并没有产生明显的影响。

图12显示了t=90 μs和t=180 μs时破碎坑的深度和面积与柱塞的脉冲幅值的关系曲线。当柱塞的脉冲幅值较大时，如A_p=30 m/s、t=90 μs时，受载煤岩的破碎坑深度和面积分别为15.75和43.16 mm²，较A_p=5 m/s、t=90 μs时分别增大了27.8%和32.8%；A_p=30 m/s、t=180 μs时，受载煤岩的破碎坑深度和面积分别为10.50和94.06 mm²，较A_p=5 m/s、t=180 μs时分别增大了50.0%和62.0%。在射流冲击前期，如t=90 μs时，破碎坑的深度和面积都随柱塞脉冲幅值的增加呈线性增加；随着冲击时间的增加，如t=180 μs时，破碎坑的深度和面积随柱塞脉冲幅值的增加呈指数型增加，且增长速率随脉冲幅值的增加逐渐增大。主要原因是由于高速水射流冲击作用下煤岩的损伤破坏主要由冲击初期的水锤效应主导^{[4, 17, 20, 27]}，柱塞推动速度的脉冲幅值越大，射流喷出喷嘴后的速度波动范围也越大，即射流速度峰值越高，射流最低速度越低。一方面，射流的每个速度峰值会产生水锤压力，根据式(4)可知，射流速度越大，射流冲击能量越高，对煤岩的损伤破坏效果越好；另一方面，射流的最低速度越低，不但能有效削弱水垫效应对受载煤岩破碎的阻碍作用，还能使作用于煤岩上的加卸载动载作用更明显，进而使煤岩产生疲劳损伤破坏。综上所述，脉冲幅值越大，脉冲射流对受载煤岩的破碎效果越好。

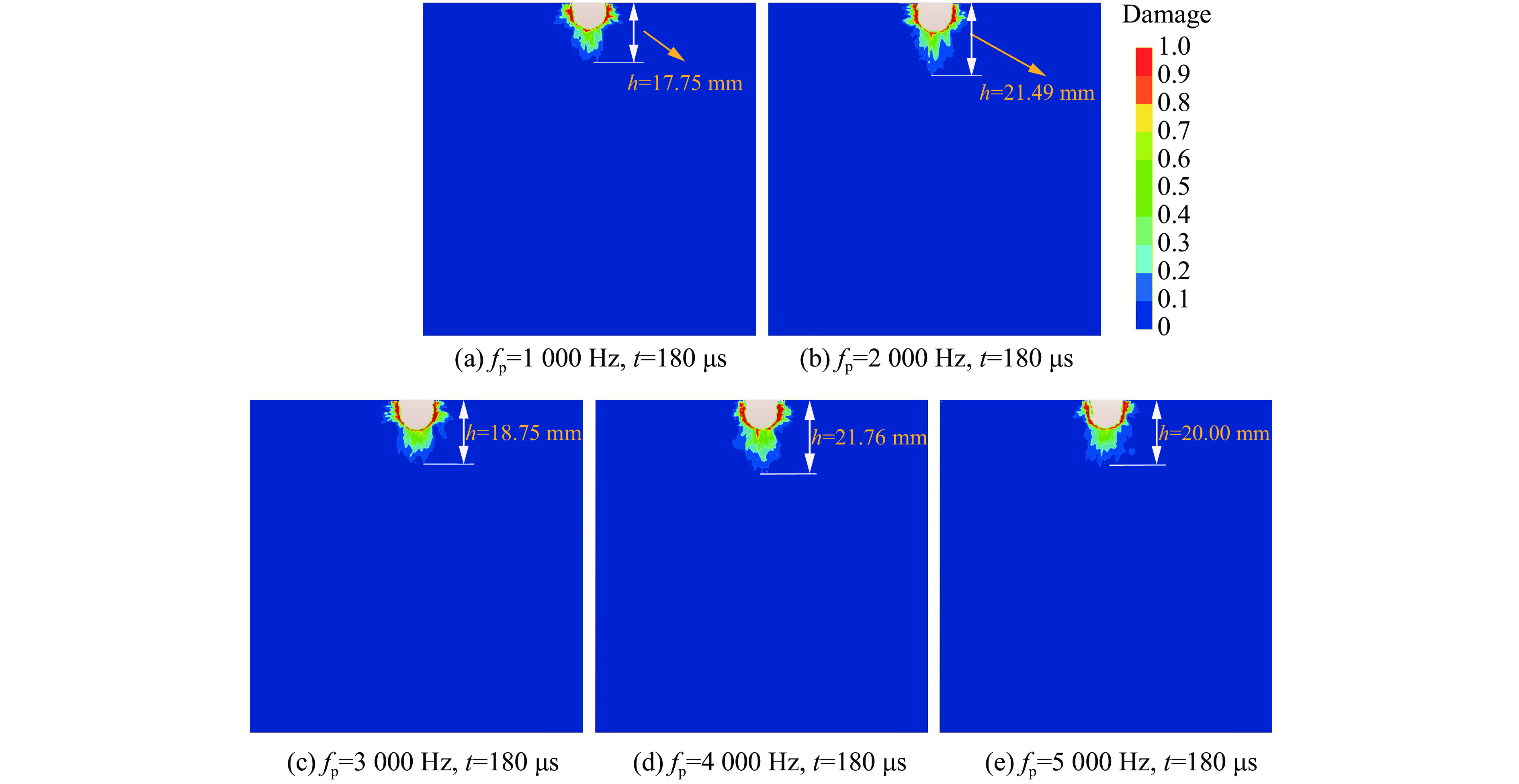
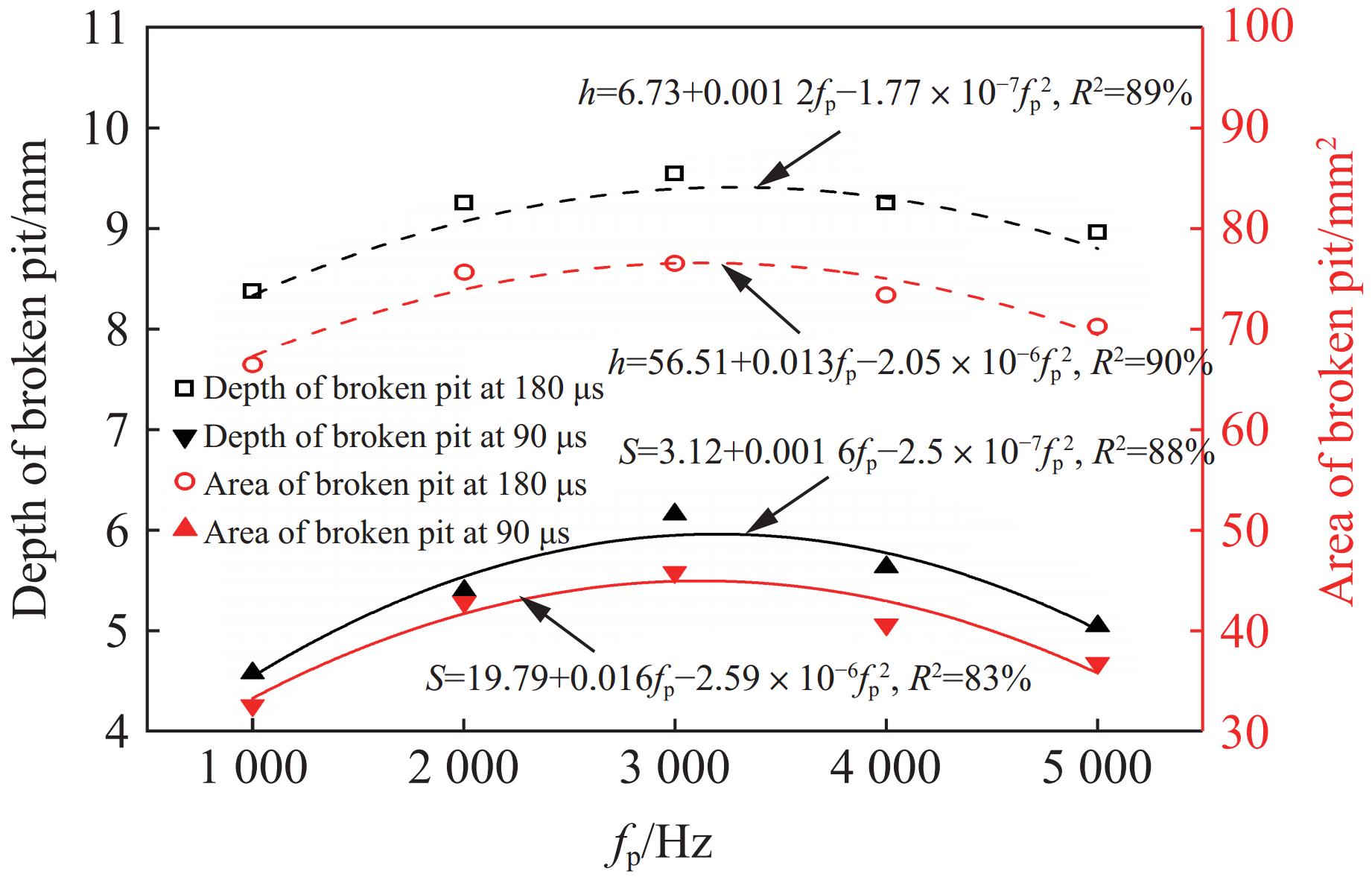
柱塞的脉冲频率反映了射流速度的脉冲周期。将柱塞的平均速度和脉冲幅值分别设定为80 m/s和20 m。180 μs时不同柱塞脉冲频率下受载煤岩的损伤破坏云图如图13所示。由图13可知，柱塞脉冲频率对破碎坑形态的影响并不明显，5种工况下的破碎坑均呈U形。当柱塞的脉冲频率为2000和4000 Hz时，脉冲射流冲击下受载煤岩产生的纵向损伤深度较深，分别为21.49和21.76 mm，表明此脉冲频率更有利于应力波在纵向传播，对煤岩深部产生一定的影响。

图14显示了t=90 μs和t=180 μs时煤岩破碎坑的深度和面积随柱塞脉冲频率的变化关系，可以看到，破碎坑的深度和面积随脉冲频率的增大呈先增大后减小的二次函数变化，当脉冲频率f_p接近3000 Hz时，破碎坑的深度和面积达到最大，t=90 μs和t=180 μs时破碎的深度分别为5.85和8.25 mm，破碎坑的面积分别为36.84和70.25 mm²。综上所述，高压脉冲射流冲击下受载煤岩具有一个破碎的最佳脉冲频率，在该脉冲频率作用下射流具有更好的破煤岩效果。在本研究的模拟条件下，最优脉冲频率f_p约为3000 Hz。主要原因是射流冲击会在煤岩内部产生应力波，应力波以一定的频率传播，当引力波的传播频率与煤岩的固有频率相近时，应力波会发生共振，从而加剧煤岩破坏。由此可见，本研究的最优脉冲频率3000 Hz与模拟的煤岩的固有频率较为接近，其破坏效果最好。值得关注的是，破碎坑的深度和面积等破坏特征是水射流冲击作用下受载煤岩损伤破坏的宏观体现，因此，明确最优脉冲频率对于提高射流破碎受载煤岩效率起着至关重要的作用。因此，在实际工程应用中，应根据破碎对象选择合理的自激频率，从而进一步指导自激振荡脉冲喷嘴设计。

基于SPH-FEM耦合算法，建立了不同工况下脉冲水射流冲击受载煤岩的数值计算模型，通过对柱塞施加正弦速度模拟了水粒子速度的周期性变化，阐明了水粒子在喷嘴内外的速度演化规律，对比分析了无、有应力加载下脉冲射流冲击下煤岩破坏效果的时序特性，探讨了关键脉冲参数对煤岩损伤破坏特征的影响规律，主要结论如下。

(1) 在管路直线段内，当柱塞的挤压作用传递到水粒子时，水粒子的速度突增；进入喷嘴收敛段后，水粒子的速度迅速增加；进入出口直线段后，射流的速度继续增大，并在直线段末端趋于稳定；离开喷嘴后的短距离内，由于能量释放，水粒子的速度微增后达到恒定。当柱塞以正弦速度挤压水粒子时，水粒子的喷出速度也较好地符合正弦变化，其平均速度与连续射流时的速度相差3.3%。

(2) 在无应力加载工况下，脉冲射流冲击下煤岩破坏坑内壁易出现块状剥落体，破碎坑的形状呈畸形，且破碎坑周围衍生出密集的径向裂纹和纵向裂纹。二维应力加载对煤岩内部裂纹的衍生及传播演化具有明显的抑制作用，破碎坑的形态由碗状向U形演变；对于有无应力加载工况，煤岩破坏坑的深度和面积的增长幅度逐渐降低，且脉冲射流对受载煤岩的破碎效率比连续射流更高。

(3) 受载煤岩破碎坑的深度和面积均随柱塞的平均速度或脉冲幅值的增加呈指数增长，但脉冲幅值对破碎坑下方纵向损伤区域无明显影响；脉冲射流冲击受载煤岩时存在煤岩破碎的最佳脉冲频率，本研究的最优脉冲频率约为3000 Hz。