-
砌体填充墙作为最常见的建筑构件被广泛应用于建筑物外立面围护或内部空间的非结构分割。然而,砌体填充墙因其自身材料结构的外载荷抗力不足,在爆炸冲击波作用下极易出现裂缝、破坏和倒塌,产生破片飞屑,并造成严重的人员伤亡和财产损失[1–2]。因此,研究如何提高砌体结构的抗爆性能具有重要意义。
砌体结构具有抗压不抗拉的特点,其加固方式主要围绕增加砌体结构的抗拉强度进行[3],如涂覆聚脲、内置钢筋和加装夹层板等[4]。聚脲具有显著的大拉伸变形能力和应变速率硬化效应,广泛应用于强脉冲载荷下的结构防护。Chen等[5–6]通过试验和理论得到聚脲应变率在10−3~103 s−1范围内的非线性应力-应变曲线,建立了非线性黏-超弹性(nonlinear visco-hyperelastic, NVHE)本构模型,并成功应用于数值模拟。目前,砌体结构涂覆聚脲以加强其承载面外载荷能力被广泛研究。Wang等[7]研究了喷涂聚脲对黏土砖砌体单元墙体抗爆性能的增强作用,发现聚脲层可以有效地防止墙体倒塌和结构破坏,最大限度地减少爆炸过程中加固墙体产生的致命碎片。Zhu等[8–9]对近距离爆炸荷载作用下聚脲喷涂增强黏土砖砌体墙体的损伤行为进行了研究,揭示了聚脲的抗爆机理。Zhang等[10]对喷涂聚脲(spray polyurea, SPUA)加固混凝土空心砌块墙的抗爆过程进行了数值模拟,讨论了边界条件和SPUA涂层厚度对砌体填充墙抗爆性能的影响,研究表明:边界约束条件对墙体抗爆性能的改善作用有限,SPUA涂层厚度对墙体抗爆性能影响显著。Santos等[11]通过实验和仿真对自由远场爆炸作用下未加固砌体墙面外响应进行了研究,分析了边界条件和失效机制以及常用测量技术。Chen等[12]对通长拉结筋加固砌体墙进行了面外准静态均布加载试验,发现墙体的失效形式是钢筋与柱锚固的边缘发生断裂,墙体与框架发生滑移导致倒塌。建筑物典型构件梁板柱墙的抗爆设计一般基于等效单自由度法(equivalent single degree of freedom, ESDOF),在这方面美国已经做了大量的研究,并汇编成了结构抗爆设计手册。PDC TR-06-01[13]和UFC 3-340-02[14]中对单向构件和双向构件的等效分析方法、质量载荷系数取值和不同形式载荷对应的抗力函数都给出了参考,但其主要针对单一构件,忽略了加固材料的抗力问题。许林峰等[15]考虑了聚脲涂层的张力,将墙体和聚脲的抗力分别计算,更好地预测了墙体位移响应。但是,到目前为止,对于采用聚脲和钢筋双重加固砌体墙的抗爆性能研究仍然较少。
针对墙体现有防护形式研究的不足,本工作将对内置拉结筋聚脲涂覆砌体填充墙的近场抗爆性能开展研究,对试件墙体进行3组近距离空爆试验,结合LS-DYNA对墙体在大当量TNT近场爆炸作用下的动力响应和破坏模式进行分析,并构建内置拉结筋聚脲涂覆砌体填充墙的等效单自由度模型和求解方法,实现对近场爆炸荷载作用下墙体位移响应的快速计算分析。
-
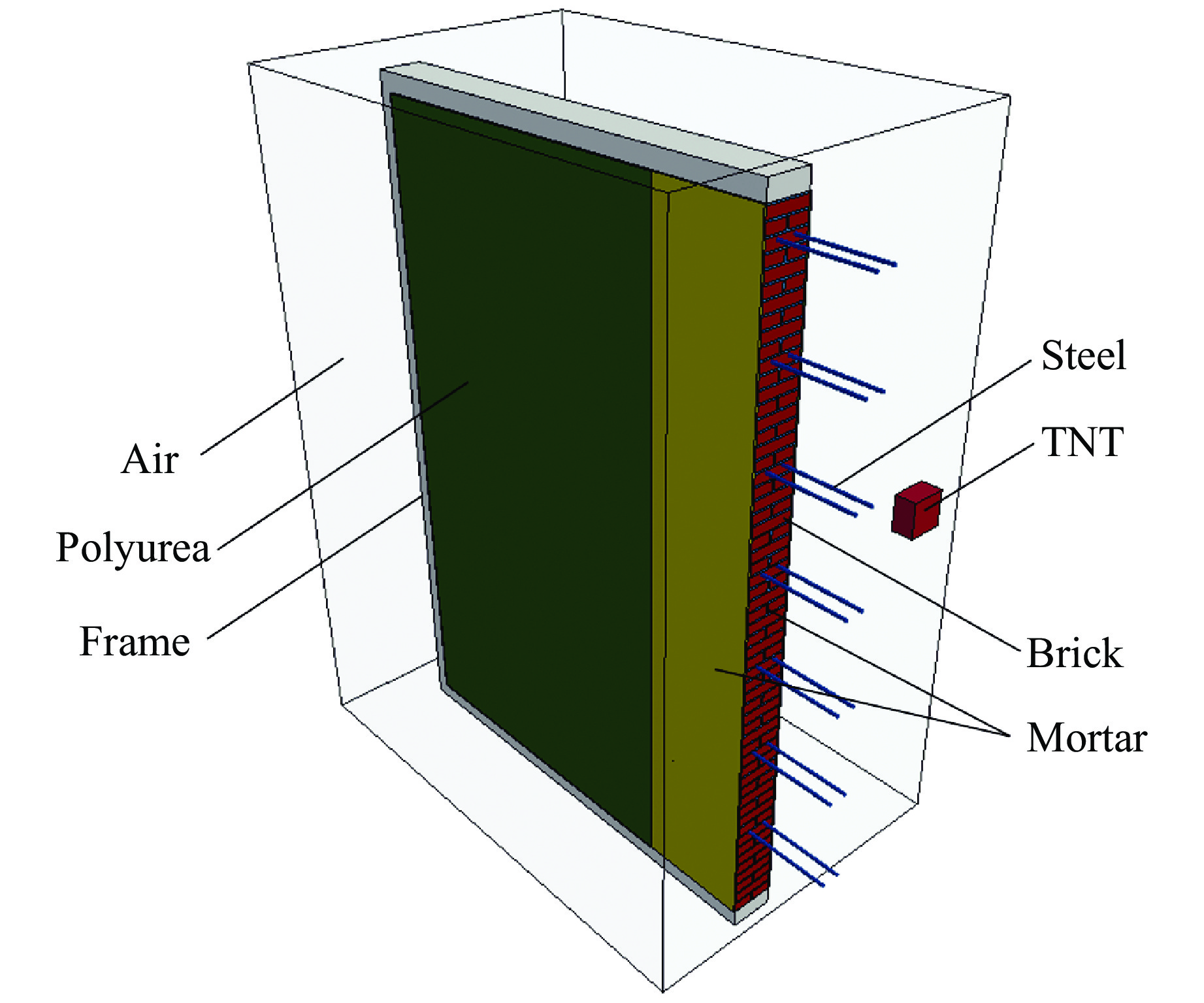
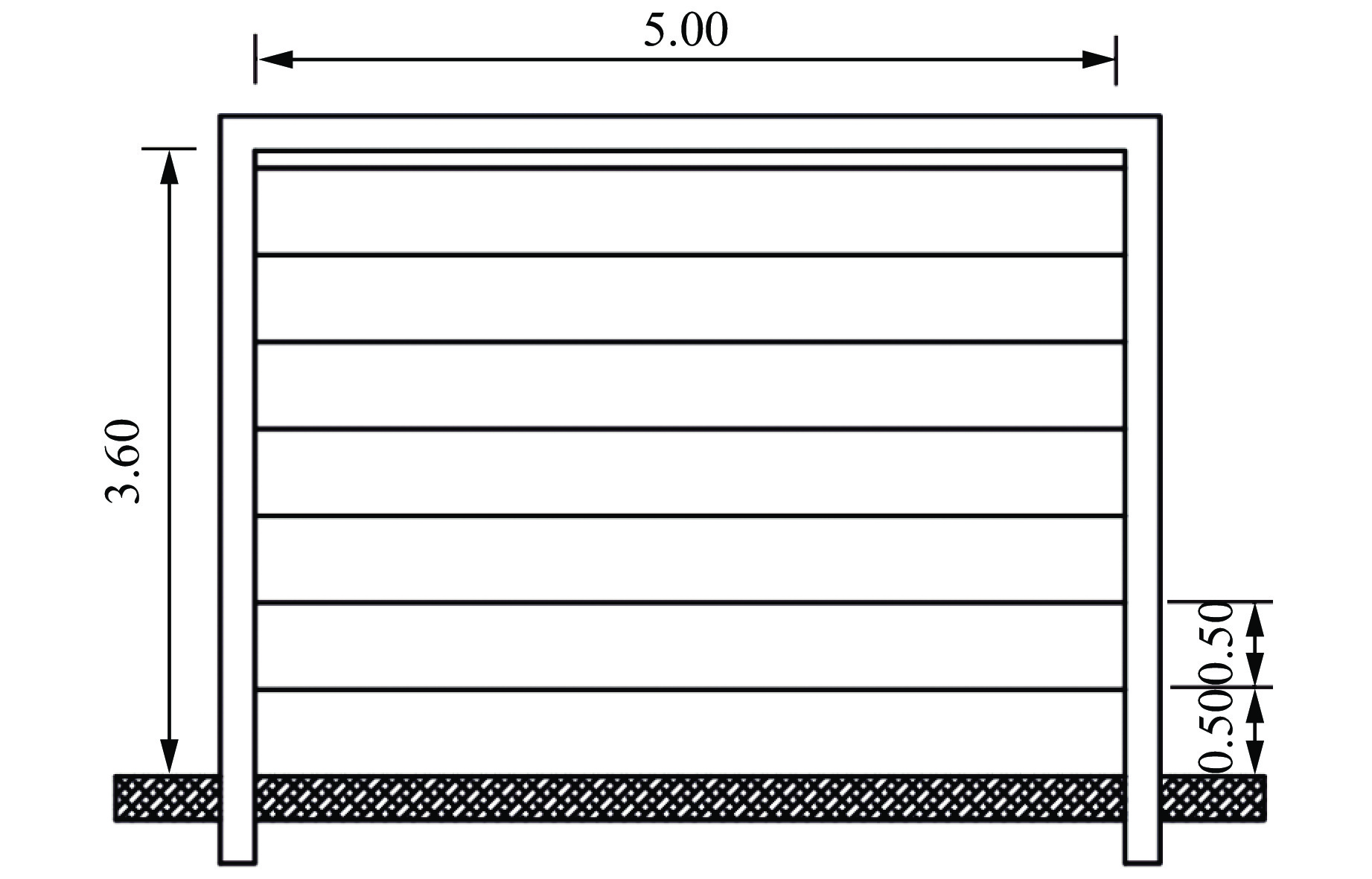
为模拟砌体墙的实际应用情况,将25#C槽钢焊接成宽5.00 m、高3.60 m的框架,在框架内砌筑填充墙,在墙体内部沿高度方向,每隔0.50 m设置2根平行的、直径为6 mm的拉结筋,2根平行拉结筋间隔0.10 m,如图1所示。拉结筋的型号为HRB400,将拉结筋两端焊接在槽钢立柱上,每个立柱后侧均设置斜支撑。
试验墙体均采用MU10蒸压灰砂砖砌筑,单块灰砂砖的尺寸为240 mm×115 mm×53 mm。砌筑墙体的高度为3.60 m,宽度为5.00 m,厚度为0.24 m;墙体的前、后表面均覆10 mm厚的M5.0水泥砂浆层;砂浆的实测抗压强度为5.80 MPa。墙体单面或双面砂浆层上涂覆聚脲。
近距离空爆试验的现场布置如图2所示。将炸药放置在距离墙体中心1.0或1.4 m的位置,在墙体背爆面中心点设置NS-WY03系列位移传感器,线性行程0.30 m,通过墙体背爆面中心点位移和墙体损伤情况来判断其抗爆性能。充分考虑聚脲涂覆方式和比例爆距等因素,设计3组试验工况,如表1所示。
-
对试验墙体开展数值模拟研究,有限元模型如图3所示。为了保证计算精度,采用精细微观的建模方式,即砖块与砂浆缝分开建模。根据砌体的砌筑方式,精细微观模型考虑连续或非连续的砂浆/砌块黏结界面,能够准确地描述砌块与砂浆之间的相互作用以及砌体墙的损伤演化[12]。该模型由砖块、砂浆缝、砂浆层、拉结筋、聚脲涂层、TNT和空气域7部分组成。数值仿真采用全尺寸建模,墙高3.60 m、宽5.00 m、厚0.24 m,砂浆缝和砂浆涂层厚度均设置为0.01 m。空气域长6.00 m、宽2.40 m、高4.00 m,完全包裹住墙体和TNT。
砖块、砂浆缝、砂浆层、聚脲涂层、TNT和空气域采用Solid164单元,拉结筋采用Beam161单元。对于墙体部分,砖块、砂浆缝、砂浆层和聚脲涂层单元网格尺寸均设置为2 mm;拉结筋网格尺寸设置为2 mm;空气和TNT单元网格尺寸均设置为4 mm。空气和TNT采用欧拉网格划分,其余部分采用拉格朗日网格划分,并采用流固耦合算法。对14根钢筋的两端进行全约束,砖块与砂浆层采用共节点处理,聚脲涂层与墙体之间的接触采用*CONTACT_TIEBREAK_SURFACE_TO_SURFACE接触进行定义,它们之间的容许正应力和容许剪应力分别为1.03和6.90 MPa[5]。
聚脲材料模型选用LS-DYNA中的MAT_PIECEWISE_LINEAR_PLATICITY材料模型表示,可以很好地适配聚脲材料韧性强、强度高、伸长率高的特点,聚脲的材料参数[4]如表2所示,其中:E为弹性模量,
$\nu $ 为泊松比,$\rho $ 为密度,$ \sigma\mathrm{_Y} $ 为屈服应力,${E_ {\rm t}}$ 为切线模量。蒸压灰砂砖和水泥砂浆均采用MAT_BRITTLE_DAMAGE材料模型描述,参数选自文献[9],如表3和表4所示,其中:
$ \sigma\mathrm{_{bc}} $ 为抗压强度,$ R\mathrm{_m} $ 为抗拉强度。钢筋采用MAT_PLASTIC_KINEMATIC材料模型描述,应变率通过Cowper-Symonds模型描述,参数选自文献[16],如表5所示,其中:
$ f_{\mathrm{s}} $ 为有效塑性应变。 -
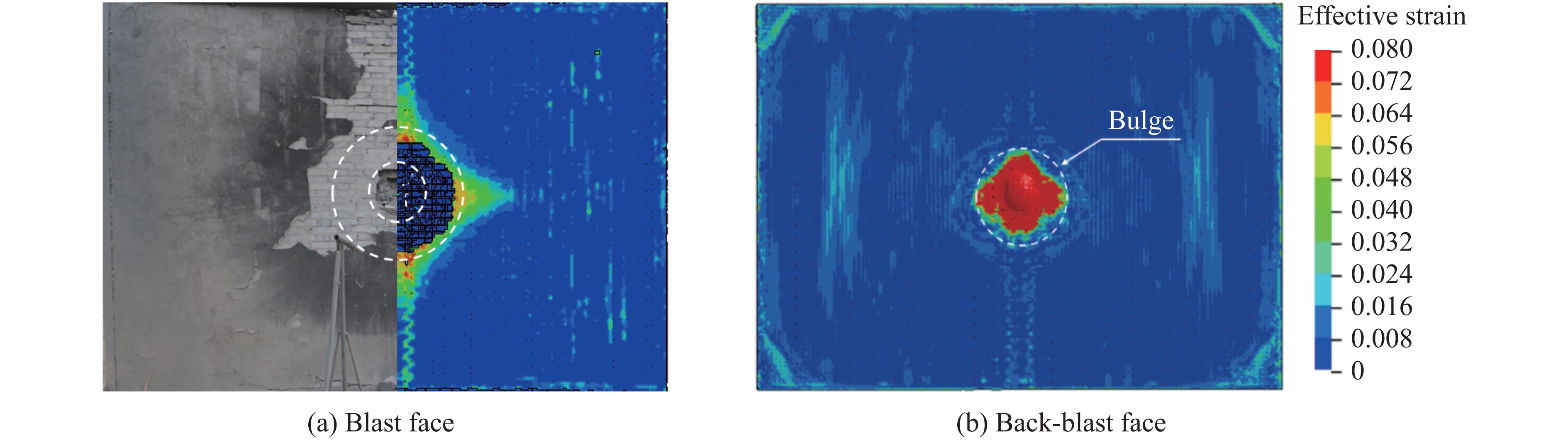
受到爆炸冲击载荷后墙体的毁伤形态如图4所示。工况J-1中,墙体双面喷涂3 mm厚聚脲,爆炸后墙体背爆面中心区域轻微鼓起6 mm,墙体整体完好。工况 J-2中,墙体背爆面喷涂5 mm厚聚脲,迎爆面无涂层,爆炸后墙体背爆面中心区域的最大鼓起厚度达16 mm,迎爆面因无涂层的增强约束效应,出现部分水泥砂浆脱落剥离现象,但墙体整体完好。工况J-3中,墙体仅背爆面涂覆5 mm厚聚脲,爆炸后墙体表面砂浆涂层出现大面积脱落,墙体中心处出现轻微开坑损伤,并未穿透,背爆面聚脲出现鼓包,墙体沿纵向中心线出现明显弯折,墙体迎爆面中心开坑直径约44 mm,墙体未完全穿透。
测得墙体在爆炸过程中的位移时程曲线,如图4所示。在工况J-1 和工况J-2中,墙体背爆面中心的最大位移分别为138和127 mm,工况 J-3的位移数据因传感器故障未采集到。工况J-1和工况J-2的墙体最大位移相差11 mm,砖墙整体完好,无震塌、无剥离、无贯穿、无倾覆。可以得出,仅背爆面涂覆5 mm厚聚脲的内置拉结筋砌体墙的抗爆性能优于双面涂覆3 mm厚聚脲内置拉结筋砌体墙的抗爆性能。
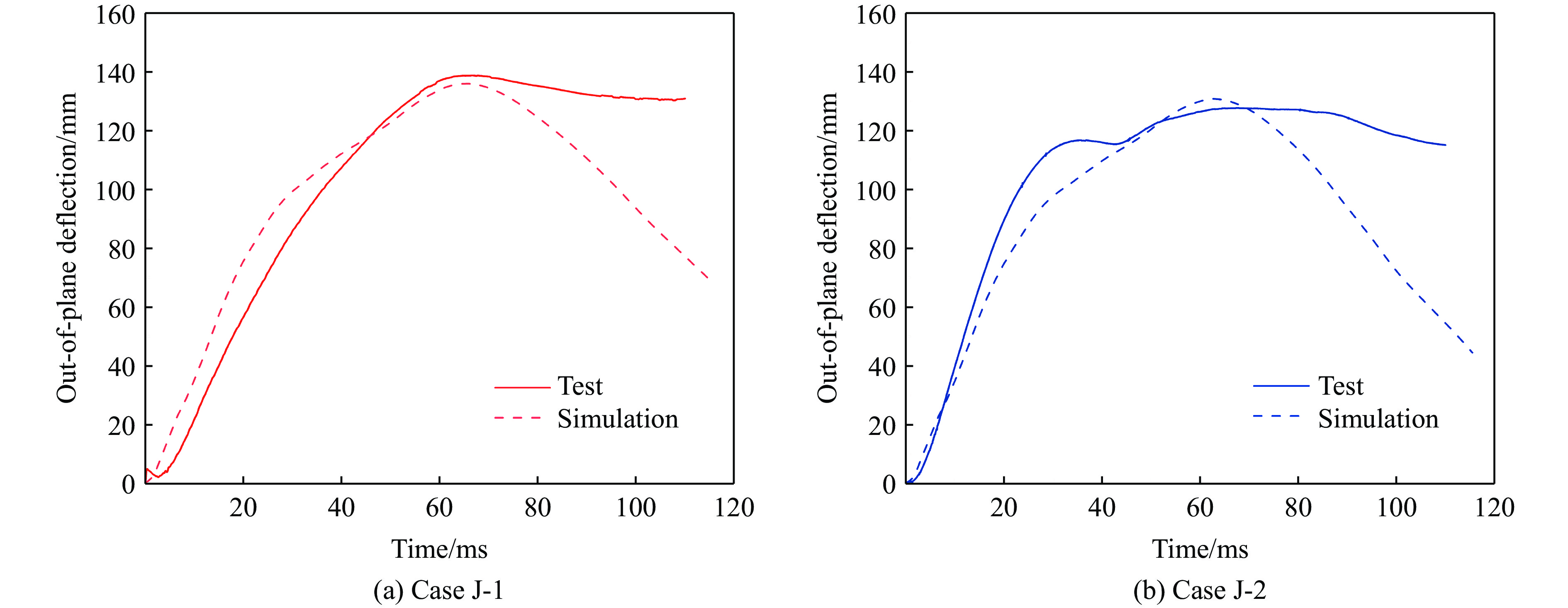
图5为工况 J-1、工况J-2的试验与数值模拟得到的墙体背爆面中心点位移时程曲线。在数值模拟中,墙体在冲击波的作用下达到最大挠度后,受到聚脲涂层和墙体内置钢筋的作用,墙体发生回弹。对于工况J-1,数值模拟的最大位移为134 mm,与试验结果138 mm相差5 mm,相对误差为3.6%;对于工况J-2,数值模拟的最大位移为130 mm,与试验结果127 mm相差3 mm,相对误差为2.4%。试验中使用的位移传感器的拉杆端没有完全固定在墙上,位移传感器在达到最大位移后保持不动,导致未采集到墙体回弹阶段的数据。
工况 J-3中的墙体损伤与数值模拟结果对比如图6所示。数值模拟结果显示,墙体迎爆面水泥砂浆大面积脱落,中心处出现开坑且未贯穿,开坑直径为42 mm,墙体背爆面聚脲鼓包,墙体沿纵向中轴线出现弯折现象。试验与数值模拟结果对比如表6所示,数值计算模型可以较好地描述墙体的损伤情况。
-
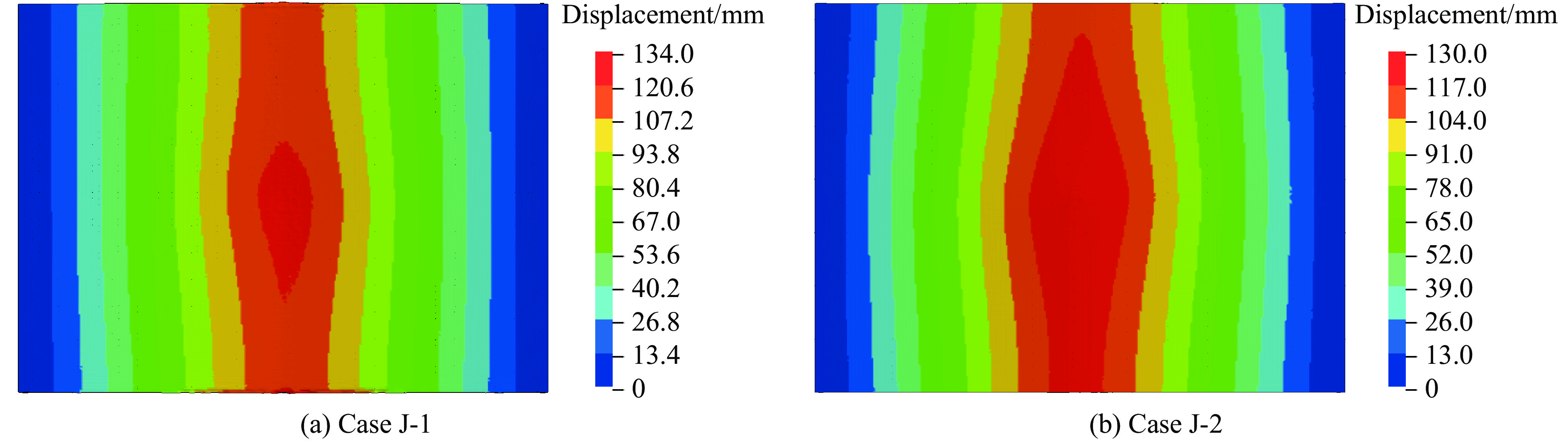
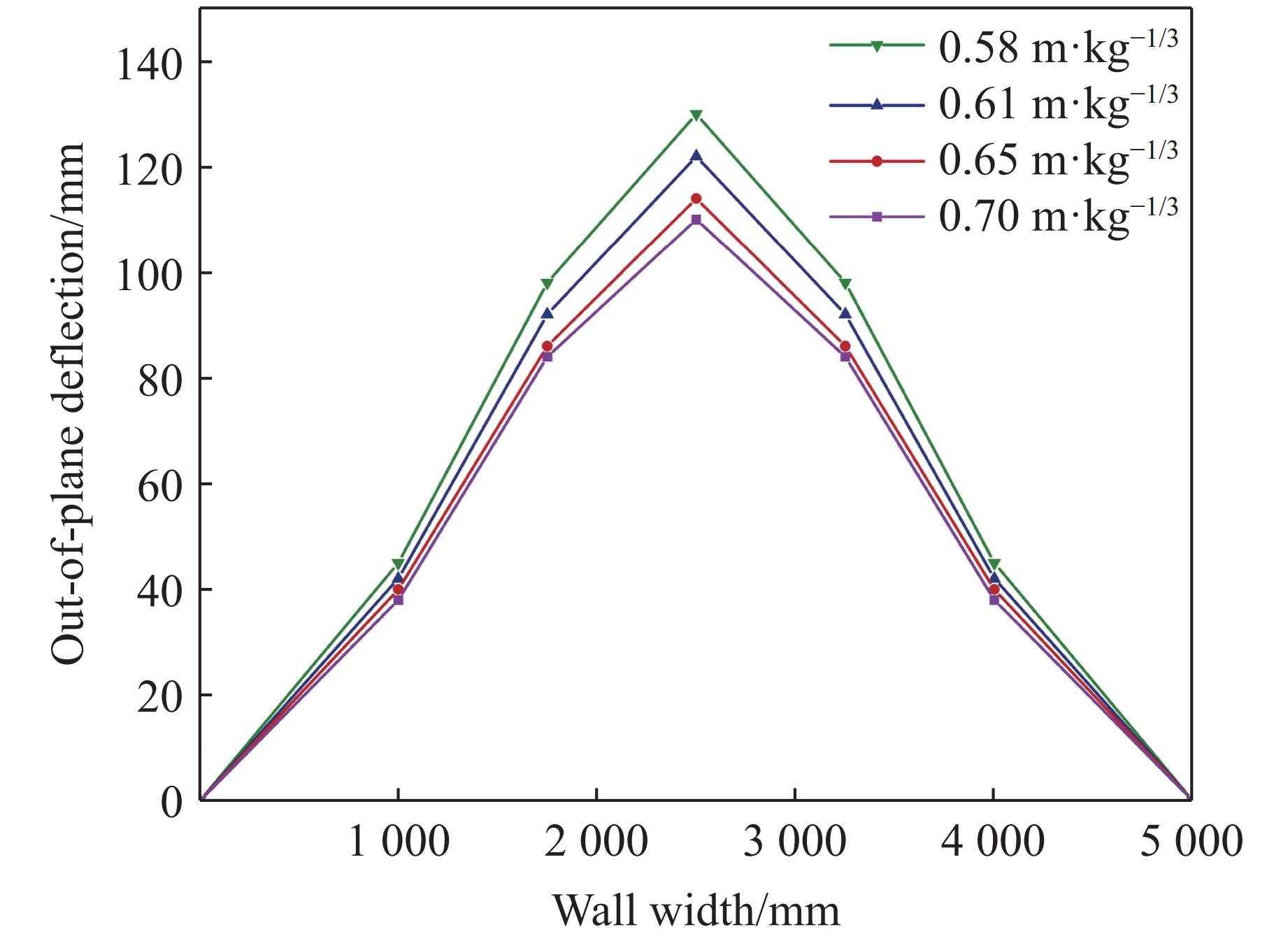
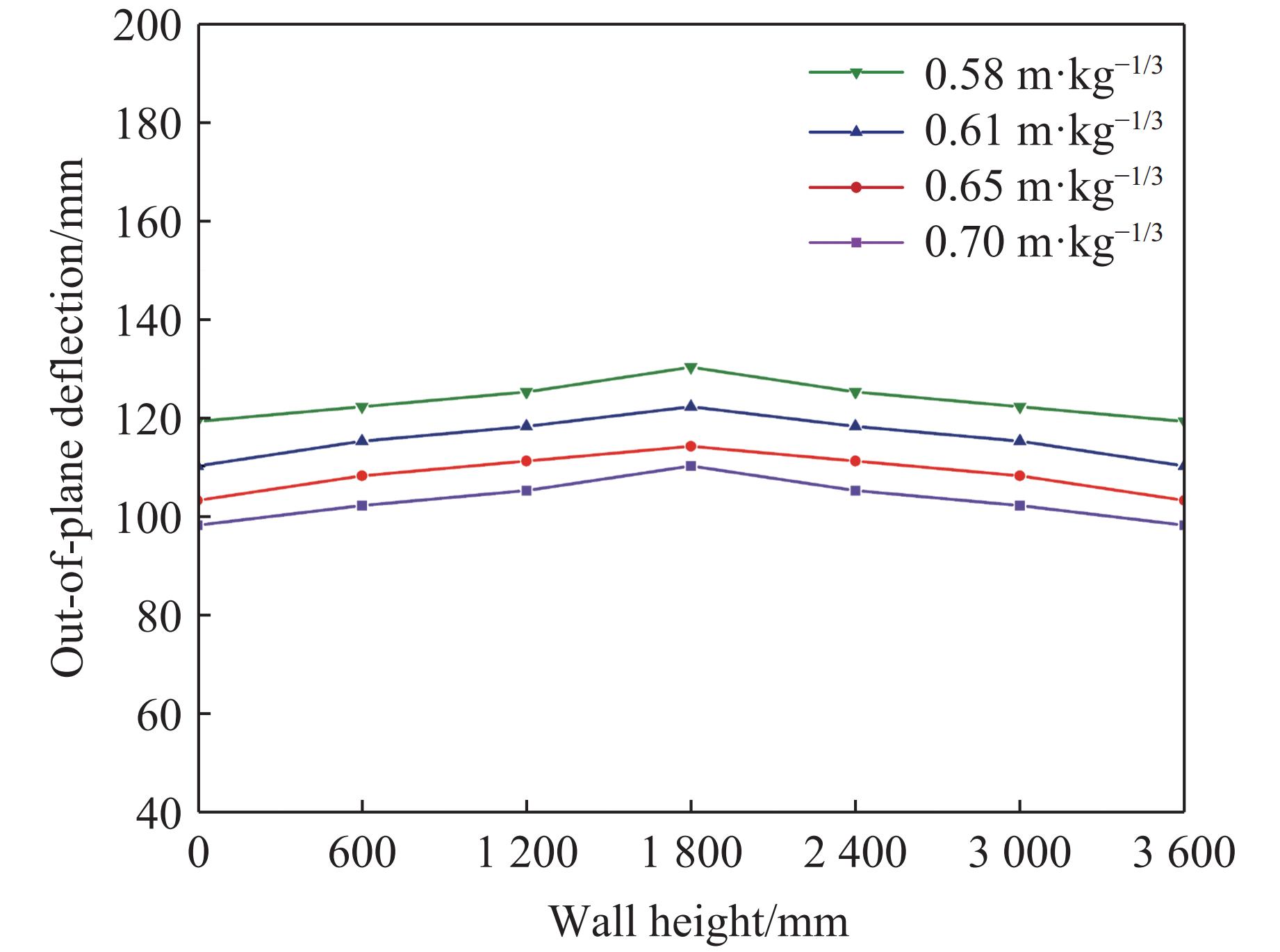
内置拉结筋聚脲涂覆砌体填充墙在近距离爆炸载荷作用下的变形云图如图7所示,中心处位移最大,墙体两端由于拉结筋的作用不会发生位移现象。固定1.4 m爆距,设置TNT药量8~14 kg,通过数值模拟研究不同比例爆距下墙体的变形特征。图8和图9展示了不同爆距下墙体的变形形状。可以看出:墙体基本是对称变形;随着比例爆距的减小,墙体位移逐渐增大;墙体主要是沿纵向中轴线发生弯曲变形,沿横向中轴线的变形不明显。
-
墙体破坏分为弯曲破坏和剪切破坏,试验墙体主要呈现弯曲破坏,本研究采用弯曲等效单自由度分析方法。简化后构件在爆炸载荷作用下的运动方程[14]为
式中:
$ K\mathrm{_{LM}} $ 为等效质量载荷系数;$ m_{\mathrm{t}} $ 为构件质量;$u(t)$ 为垂直于墙面中心点方向的位移,即墙体面外挠度;$c$ 为砌体墙的阻尼系数;$R(u)$ 为构件的抗力函数;$ p(t) $ 为等效爆炸载荷。根据等效载荷对单自由度系统所做的功与实际爆炸载荷对构件所做的功相等,得出等效质量系数$ K\mathrm{_M} $ 和等效载荷系数$ K_{\mathrm{L}} $ ,等效质量荷载系数$ K\mathrm{_{LM}}=K_{\mathrm{M}}/K\mathrm{_L} $ 。式中:
$m(x)$ 为单位长度构件的质量,$\phi (x)$ 为构件在爆炸载荷作用下的变形形状函数,$p(x)$ 为构件所承受的爆炸动荷载,$L$ 为构件长度。UFC-3-340-02规范推荐取值如表7所示。 -
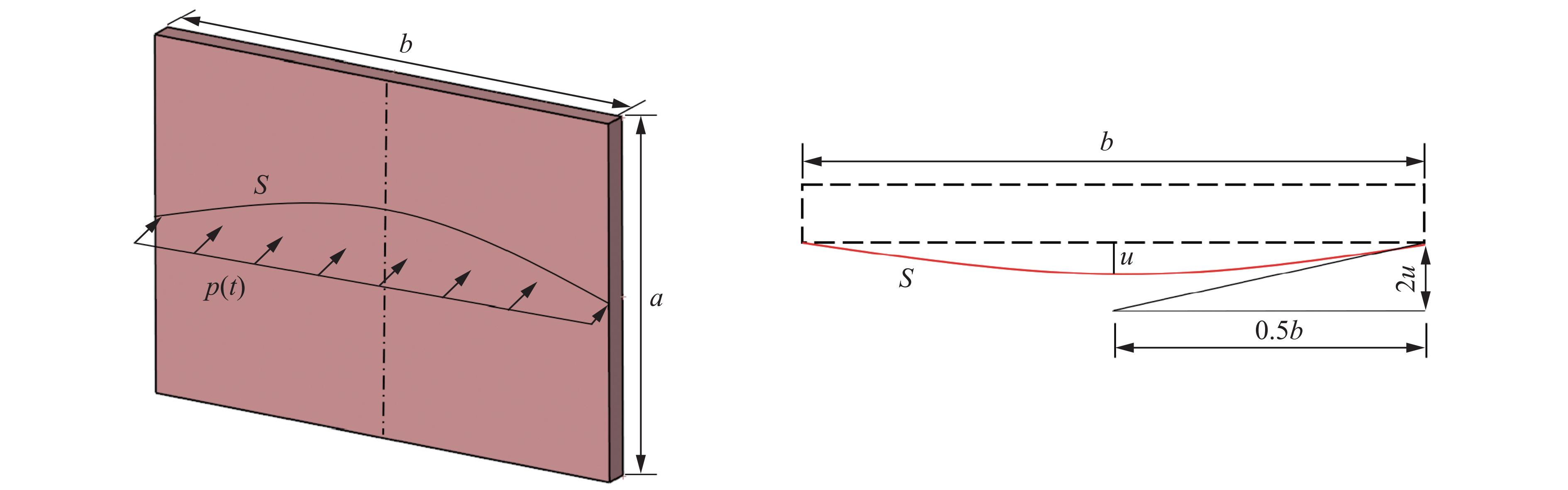
图10为墙体在爆炸载荷作用下的弯曲变形示意图,其中:a、b分别为墙体的短边和长边长度,S为墙体弯曲变形后的挠曲线长度,u为挠度。内置拉结筋聚脲涂覆砌体填充墙由墙体、钢筋和聚脲涂层3部分组成,单独计算各部分抗力再进行累加。
UFC-3-340-02规范中指出:如果支座不能对铅直移动提供抗力,墙中的压力将受到地板以上墙体重量和墙体承受的任何顶部载荷的限制。如果墙体不承受铅直载荷,那么墙体就必须作为简支梁来分析,用砂浆的破裂模量确定最大抵抗力矩。根据试验分析,墙体砌筑在槽钢框架中,大跨度槽钢框架对墙体产生的拱推力相比RC(reinforced concrete)框架而言可以忽略不计,所以墙体可以简化为两端简支梁模型。墙体内部14根拉结筋焊接在外部框架上,在爆炸载荷作用下发生弯曲变形,把拉结筋简化为两端固支结构。背爆面聚脲涂层随墙体发生拉伸变形。
将砖墙简化为简支梁结构,其抗力函数可表示为
式中:
${R_1}(u)$ 为未加固砖墙的抗力函数;$ k\mathrm{_e} $ 为简支结构的弹性刚度,由式(4)计算得到$ k\mathrm{_e} $ =1.53×107 N/m;I为截面惯性矩;Rm为墙体塑性阶段的极限抗力,$ R\mathrm{_m}=8M_{\mathrm{p}}/L^2 $ ,其中极限弯矩$ M_{\mathrm{p}} $ 由砂浆强度决定;$ {\textit{z}_{\rm{e}}}$ 、$ {\textit{z}_{\rm{m}}}$ 分别为弹、塑性极限挠度。将内置14条拉结钢筋简化为两端固支结构,其抗力函数可表示为
式中:
${R_2}(u)$ 为钢筋的抗力函数,$k$ 为固支结构的弹性刚度。试验结果显示,爆炸后拉结筋两端依然是固支状态。因此,钢筋一直处于弹性阶段。聚脲涂层自身的抗弯刚度很小,随着墙体变形,其发生拉伸作用产生抗力,根据胡克定律,可得出
式中:
$\sigma $ 为聚脲长边方向的应力,$E$ 为聚脲材料的弹性模量。抗力函数可表示为式中:
$T$ 为聚脲涂层长边方向的拉应力,$n$ 为应变强化指数[17]。内置拉结筋聚脲砌体填充墙的抗力函数为
-
近距离空爆工况下,爆炸冲击波在墙体上的作用为非均布荷载。为便于计算,可将其等效为均布荷载[18]
式中:
$ p_{\mathrm{m}} $ 为等效均布载荷峰值,$ p_{\mathrm{m}1} $ 为墙体结构中心处反射超压峰值,$ p_{\mathrm{m}2} $ 为墙体短边中心处反射超压峰值,$ p_{\mathrm{m}3} $ 为墙体长边中心处反射超压峰值,$ p_{\mathrm{m}4} $ 为墙体边角处反射超压峰值。载荷作用时间Δt为式中:
${I_1}$ 为墙体中心处爆炸反射冲量。采用预估-校正形式的显示Newmark方法[19]计算等效单自由度系统的位移时程曲线。
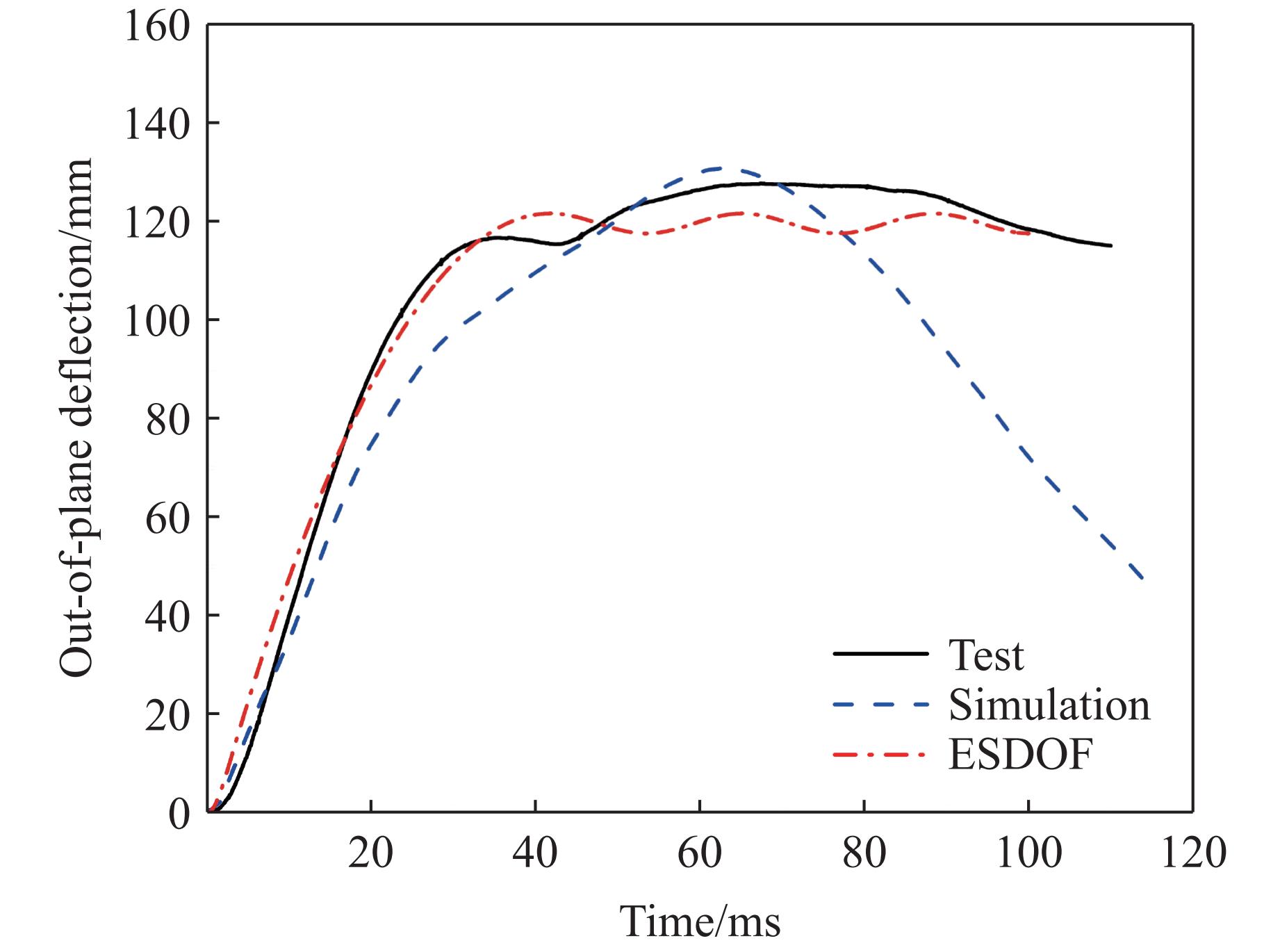
以内置拉结筋背爆面涂覆聚脲墙体为计算对象,选取工况 J-2的试验结果及数值模拟结果来验证等效单自由度模型的准确性。图11为工况 J-2的试验结果、数值模拟结果和等效单自由度模型计算结果的对比。等效单自由度模型计算得到的最大位移为121 mm,数值模拟计算得到的最大位移为130 mm,与试验结果127 mm相比,相对误差分别为4.7%、2.4%。因为等效单自由度模型没有考虑回弹阶段和阻尼问题,所以位移曲线不会回落,停留在最大值。计算结果表明,分别考虑墙体、聚脲涂层和钢筋部分的抗力所建立的等效单自由度模型可以较为准确地描述加固墙体结构在爆炸载荷作用下的动力响应。
-
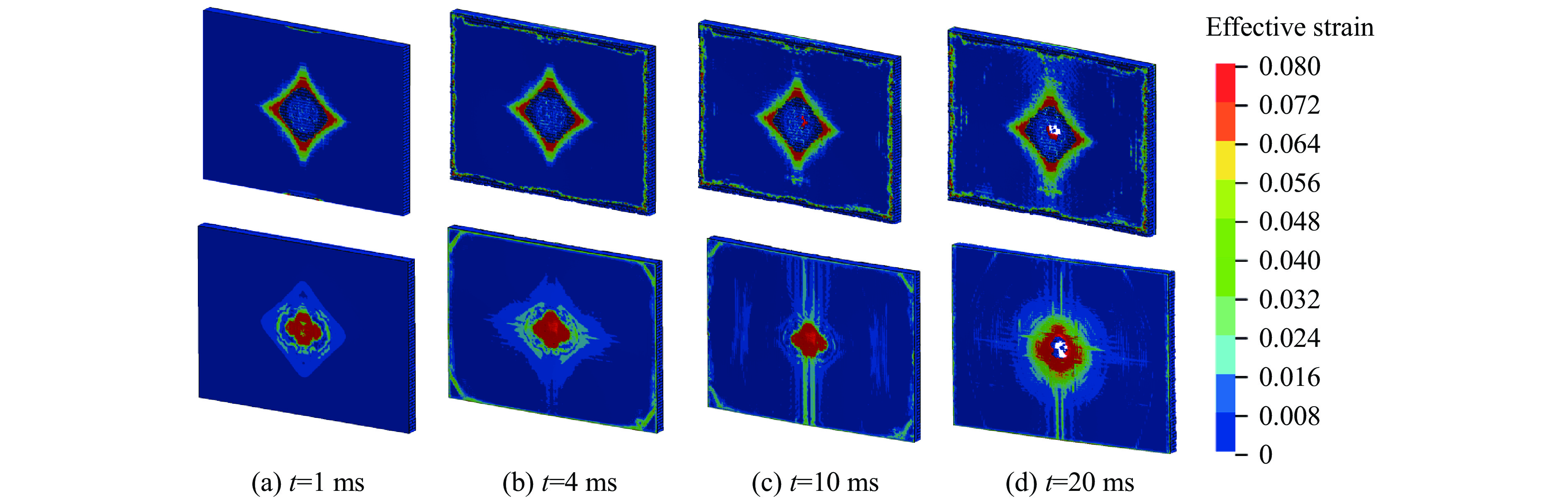
图12显示了加固墙体在典型工况下的毁伤破坏过程。初始阶段,墙体表面砂浆层出现破损,冲击波传播到墙体背面;在4 ms时,冲击波继续在墙体中反射,墙体损伤进一步加大,背面聚脲层开始出现鼓包现象,墙体开始发生弯曲;在10 ms时,墙体正面出现明显的开坑贯穿,聚脲层持续鼓包但未破裂,墙体出现明显的弯曲现象;在20 ms时,墙体完全贯穿,开坑半径增大,聚脲层发生撕裂破坏,内置钢筋裸露出来,且出现弯折现象。
采用聚脲弹性材料加固墙体可以提高砌块之间的连接力,增强墙体结构形变时砌块间的协调性和整体性,降低了结构的局部破坏效果,更均匀地吸收冲击波能量。拉结筋两端固接在框架上,随着墙体发生弯曲变形,可以有效提高框架对墙体的约束作用,增强墙体结构的抗倒塌能力。
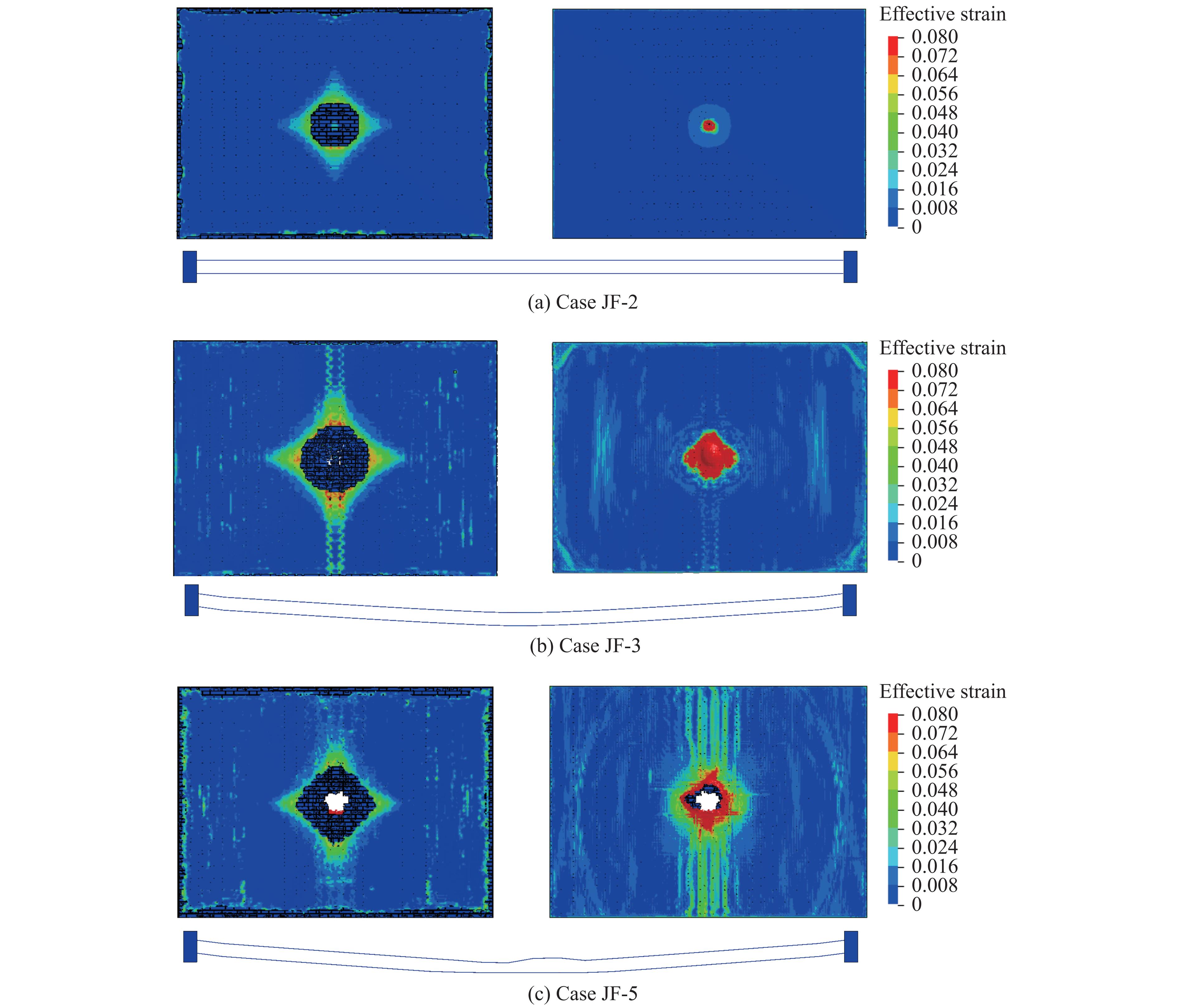
为了研究加固墙体在不同装药量下的破坏模式,在试验工况验证的基础上,固定爆距1.0 m,仅在墙体背爆面涂覆5 mm厚聚脲,对试件装药量10~20 kg下的破坏特征进行数值模拟分析,具体参数及统计结果如表8所示。本研究仅对典型工况展开探讨,如图13所示。
当装药量为12 kg时,墙体结构出现轻微损伤,迎爆面砂浆层损伤,砖块发生轻微破碎,背爆面聚脲涂层出现轻微鼓包,如图13(a) 所示;当装药量增加至14 kg时,墙体迎爆面出现开坑损伤但未贯穿,背爆面聚脲层受砌块和砂浆位错挤压发生大面积鼓包,由于聚脲和钢筋的约束作用,墙体呈明显的弯曲变形模式,如图13(b) 所示;当装药量为18 kg时,墙体中心处出现贯穿损伤,背爆面聚脲涂层发生撕裂破坏,内置钢筋裸露出来,且出现弯折现象,墙体沿纵向中轴线发生大角度弯折,裂缝在纵向中轴线附近延伸扩展,如图13(c) 所示。
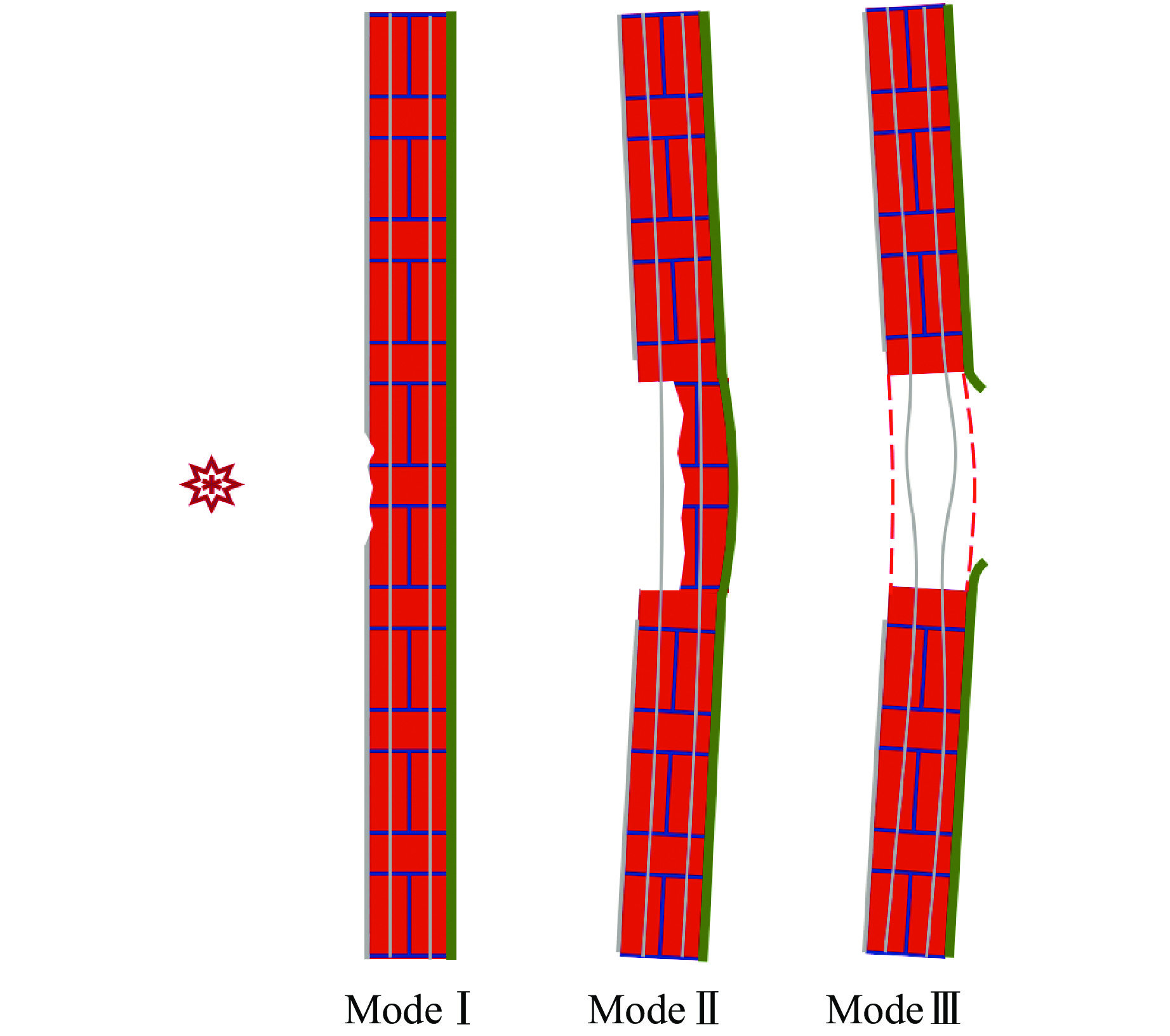
Wu等[20]通过试验研究了在爆炸载荷作用下聚脲加固墙体背爆面出现鼓包时砌块和砂浆的破坏特征,即背爆面中心处砌块与砂浆脱粘发生错位现象。少部分砌块和砂浆缝断裂,在冲击波的作用下,砌块和砂浆整体向后挤压聚脲层形成鼓包。本研究在此基础上,针对内置拉结筋聚脲涂覆砌体填充墙的新型双重加固方式,结合试验与数值模拟结果,根据墙体支座转角将墙体的破坏模式划分为3种,如图14所示。
模式Ⅰ:表面砂浆层损伤。墙体迎爆面砂浆层和砖块发生轻微破损,背爆面聚脲层轻微鼓包,墙体支座转角小于4°。
模式Ⅱ:开坑位错及背面鼓包。墙体迎爆面出现开坑损伤但未贯穿,背爆面聚脲层出现大面积鼓包现象,墙体发生明显弯曲变形,墙体支座转角为4°~8°。
模式Ⅲ:贯穿损伤。墙体出现贯穿损伤,背爆面聚脲涂层发生撕裂破坏,内置钢筋裸露出来且出现弯折现象,墙体沿纵向中轴线发生大角度弯折,墙体支座转角大于8°。
-
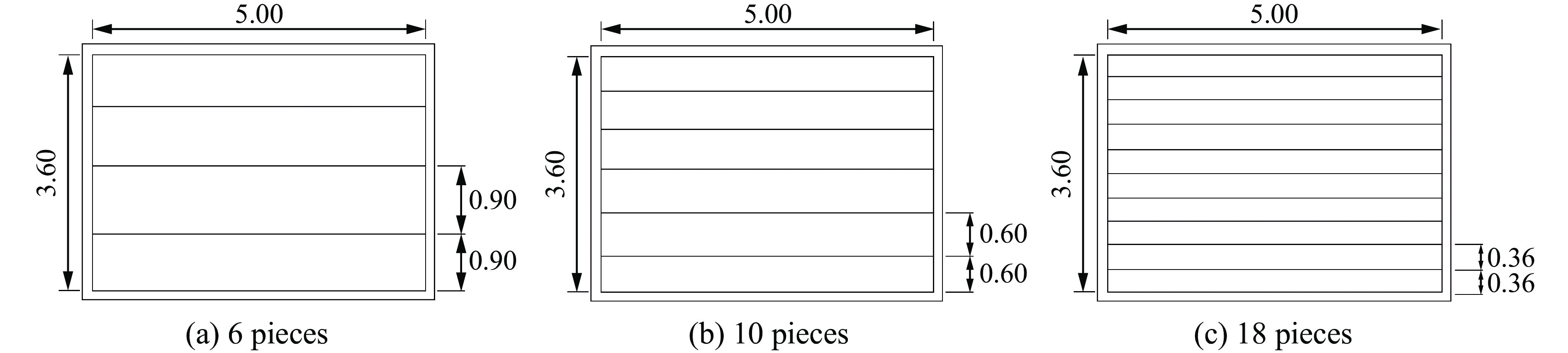
固定1.0 m爆距和墙体背面5 mm厚聚脲涂层参数不变,改变拉结筋数量,拉结筋等距排布,如图15所示。找到墙体达到贯穿损伤等级的临界装药量,研究拉结筋对墙体抗爆性能的影响,工况设置及结果如表9所示。
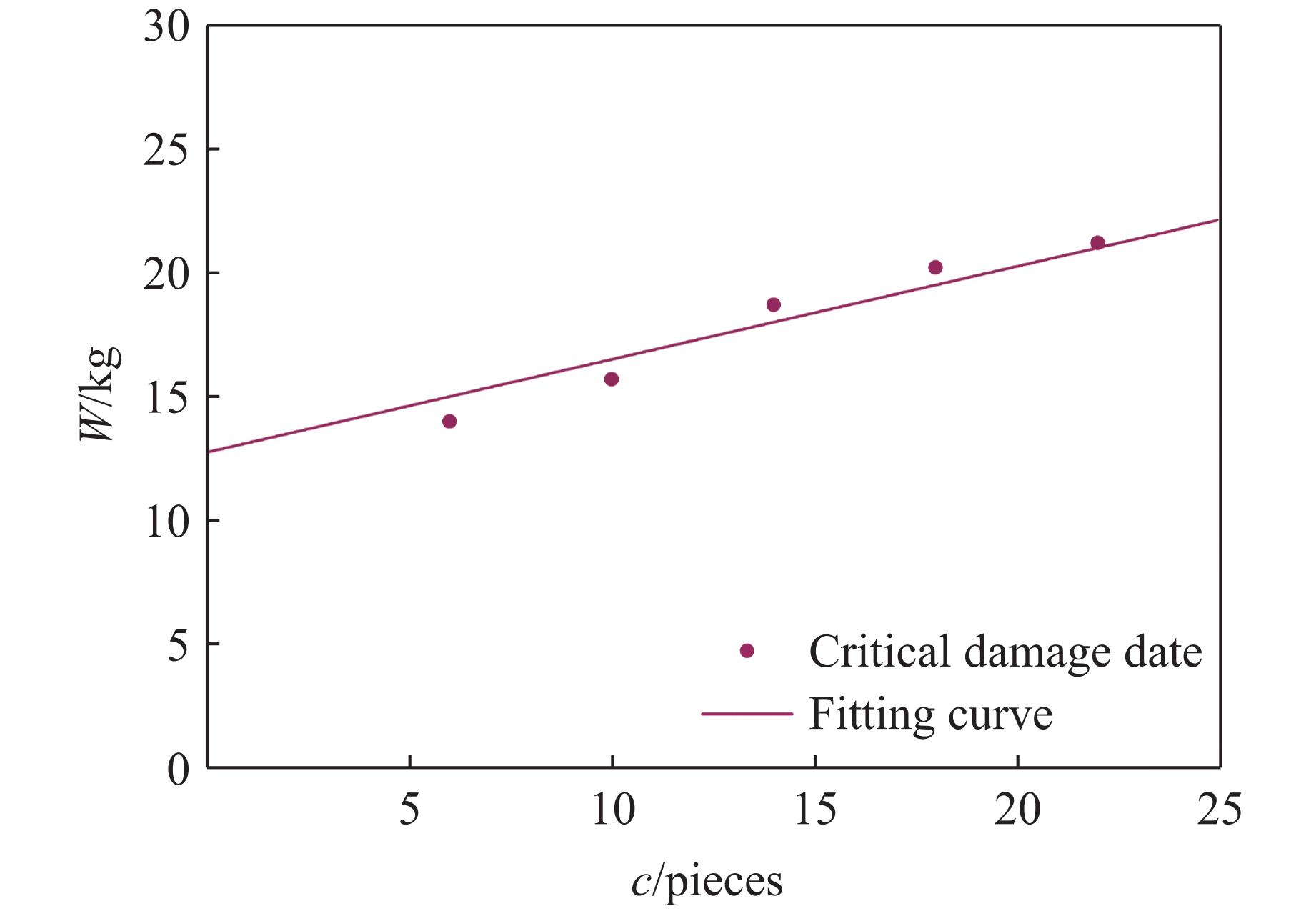
加固墙体达到贯穿损伤等级的临界装药量随着拉结筋数量的增加而逐渐增加,拟合曲线得到的临界装药量
$W$ 与拉结筋数量$c$ 之间的关系如图16所示。可以看到,拉结筋数量对墙体局部毁伤的影响较小。 -
通过近距离空爆试验、全尺寸数值模拟和改进的等效单自由度分析方法研究了内置拉结筋聚脲涂覆砌体填充墙在近场爆炸作用下的毁伤机理,并对其破坏特征进行定量和定性分析,建立了简化计算方法以预测墙体位移响应,得到以下结论。
(1) 内置拉结筋聚脲涂覆砌体填充墙在近距离爆炸载荷作用下的变形特征主要是沿纵向中轴线发生弯曲变形,沿横向中轴线变形不明显。
(2) 本研究提出的改进等效单自由度方法可以准确描述内置拉结筋聚脲涂覆砌体填充墙在近距离爆炸载荷作用下的动力响应,为抗爆工程设计提供理论计算参考。
(3) 近距离空爆作用下,内置拉结筋聚脲涂覆砌体填充墙呈现3种不同的破坏模式:模式Ⅰ为表面砂浆层损伤,墙体支座转角小于4°;模式Ⅱ为开坑位错及背面鼓包,墙体支座转角为4°~8°;模式Ⅲ为贯穿损伤,墙体支座转角大于8°。
(4) 拟合了拉结筋数量与临界装药量的经验公式,墙体达到贯穿损伤等级的临界装药量随拉结筋数量的增加而线性提高,但拉结筋数量对墙体局部毁伤的影响较小。
需要注意的是,本研究划分的破坏模式仅适用于内置拉结筋背爆面涂覆聚脲砌体填充墙结构和近场爆炸工况,对于内置拉结筋双面涂覆聚脲砌体墙结构和远场爆炸工况的破坏模式还有待进一步研究。
内置拉结筋聚脲涂覆砌体填充墙 近场抗爆性能和分析方法
Close-Range Blast Resistance and Analytical Methods of Polyurea Coated Masonry Infill Walls with Built-in Tie Reinforcement
-
摘要: 为研究在近距离爆炸载荷作用下内置拉结筋聚脲涂覆砌体填充墙的动力响应过程、毁伤特征和破坏模式,对不同聚脲涂覆方式和涂覆厚度的砌体墙进行了近距离空爆试验,结合LS-DYNA软件开展了数值模拟研究,基于砖墙、钢筋和聚脲涂层的抗力函数建立了改进的等效单自由度理论计算模型。等效单自由度模型可以准确地描述内置拉结筋涂覆聚脲加固墙体在近场爆炸载荷作用下的位移响应过程。在近场爆炸工况下,根据墙体的面外响应特征,总结出3种近场爆炸破坏模式:表面砂浆层损伤、开坑位错及背面鼓包、贯穿损伤。随着拉结筋数量的增加,墙体的抗爆性能增强,临界贯穿破坏装药量增多。Abstract: In order to investigate the dynamic response process, damage characteristics and damage mode of polyurea coated masonry infill walls with built-in tie reinforcement under close-range explosion load, a series of close-range explosion tests were performed on masonry wall with different polyurea coating methods and thicknesses. Additionally, numerical studies were carried out using the LS-DYNA software. Based on the resistance function of the brick wall, steel bar and polyurea coating, an improved equivalent single degree of freedom (ESDOF) theoretical calculation model was established. This model can accurately describe the displacement response of the polyurea coated masonry infill walls with built-in tie reinforcement under close-range explosion load. Three damage modes: surface mortar layer damage, open pit dislocation with back bulge, and penetration damage were identified according to the wall’s out-of-face response characteristics during close-range explosion load. With the increase of the number of tension reinforcement, the anti-explosion performance of the wall improves and the critical penetration damage charge increases.
-

-
表 1 试验工况
Table 1. Test conditions
Test Rebar pieces Polyurea layer thickness/mm TNT mass/kg Blast distance/m Blast face Back-blast face J-1 14 3 3 14 1.4 J-2 14 0 5 14 1.4 J-3 14 0 5 14 1.0 表 2 聚脲材料参数
Table 2. Material parameters of polyurea
$E/{\text{MPa}}$ $ \nu $ $ \rho /(\text{g}\cdot {\text{cm}}^{{-3}}) $ $ \sigma\mathrm{_Y}/\text{MPa} $ ${E_{\rm t}}/{\text{MPa}}$ 230 0.4 1.19 1.38 3.5 表 3 砖块材料参数
Table 3. Material parameters of brick
$ \rho /(\text{g}\cdot {\text{cm}}^{{-3}}) $ $ E/{\text{MPa}} $ $ \nu $ $ \sigma_{\mathrm{bc} {\rm}}/\text{MPa} $ $ R_{\mathrm{m} {\rm}}/\text{MPa} $ 1.8 8200 0.16 15.5 0.775 表 4 水泥砂浆材料参数
Table 4. Material parameters of mortar
$ \rho /(\text{g}\cdot {\text{cm}}^{{-3}}) $ $ E/{\text{MPa}} $ $ \nu $ $ \sigma\mathrm{_{bc}}/\text{MPa} $ $ R_{\mathrm{m}}/\text{MPa} $ 2.1 4100 0.21 4.9 0.245 表 5 HRB400钢筋材料参数
Table 5. Material parameters of HRB400 rebar
$ \rho/(\text{kg}\cdot\text{m}^{-3}) $ $ E/{\text{GPa}} $ $ \nu $ $ \sigma_{\mathrm{Y}}/\text{MPa} $ $ E\mathrm{_t}/\text{MPa} $ $ f\mathrm{_s} $ 7800 207 0.3 400 1100 0.092 表 6 试验与数值模拟结果对比
Table 6. Comparison of test and simulation results
Case Maximum displacement Pit diameter Test/mm Simulation/mm Error/% Test/mm Simulation/mm Error/% J-1 138 134 3.6 J-2 127 130 2.4 J-3 44 42 4.5 表 7 等效质量系数、等效载荷系数及等效质量载荷系数
Table 7. Equivalent mass, load and mass loading factor
Boundary conditions and load forms Responsive KM KL KLM 
Elasticity 0.50 0.64 0.78 Plasticity 0.33 0.50 0.66 
Elasticity 0.41 0.53 0.77 Elastoplastic 0.50 0.64 0.78 Plasticity 0.33 0.50 0.66 表 8 数值模拟结果
Table 8. Numerical simulation results
Case Blast distance/m TNT mass/kg Scaled distance/(m·kg−1/3) Back polyurea thickness/mm Damage mode JF-1 1.0 10 0.4642 5 Ⅰ JF-2 1.0 12 0.4368 5 Ⅰ JF-3 1.0 14 0.4149 5 Ⅱ JF-4 1.0 16 0.3969 5 Ⅱ JF-5 1.0 18 0.3816 5 Ⅲ JF-6 1.0 20 0.3684 5 Ⅲ 表 9 工况设置及数值模拟结果
Table 9. Test conditions and simulation results
Case Blast distance/m TNT mass/kg Rebar/pieces Back polyurea thickness/mm Damage mode 1 1.0 14.0 6 5 Ⅱ 2 1.0 15.0 6 5 Ⅲ 3 1.0 15.5 10 5 Ⅱ 4 1.0 16.5 10 5 Ⅲ 5 1.0 18.0 10 5 Ⅲ 6 1.0 17.0 14 5 Ⅱ 7 1.0 18.0 14 5 Ⅲ 8 1.0 18.5 18 5 Ⅱ 9 1.0 19.0 18 5 Ⅱ 10 1.0 19.5 18 5 Ⅲ 11 1.0 20.0 22 5 Ⅱ 12 1.0 21.0 22 5 Ⅲ -
[1] 李利莎, 杜建国, 张洪海, 等. 爆炸冲击震动对砖墙破坏作用的数值模拟 [J]. 爆炸与冲击, 2015, 35(4): 459–466. doi: 10.11883/1001-1455(2015)04-0459-08 LI L S, DU J G, ZHANG H H, et al. Numerical simulation of damage of brick wall subjected to blast shock vibration [J]. Explosion and Shock Waves, 2015, 35(4): 459–466. doi: 10.11883/1001-1455(2015)04-0459-08 [2] 曾繁, 肖桂仲, 冯晓伟, 等. 砌体结构长脉宽爆炸荷载损伤等级评估方法 [J]. 爆炸与冲击, 2021, 41(10): 127–137. doi: 10.11883/bzycj-2020-0399 ZENG F, XIAO G Z, FENG X W, et al. A damage assessment method for masonry structures subjected to long duration blast loading [J]. Explosion and Shock Waves, 2021, 41(10): 127–137. doi: 10.11883/bzycj-2020-0399 [3] WANG W, WEI G S, WANG X, et al. Structural damage assessment of RC slab strengthened with POZD coated steel plate under contact explosion [J]. Structures, 2023, 48: 31–39. doi: 10.1016/j.istruc.2022.12.090 [4] WANG W, YANG G R, YANG J C, et al. Experimental and numerical research on reinforced concrete slabs strengthened with POZD coated corrugated steel under contact explosive load [J]. International Journal of Impact Engineering, 2022, 166: 104256. doi: 10.1016/j.ijimpeng.2022.104256 [5] CHEN D, WU H, FANG Q, et al. A nonlinear visco-hyperelastic model for spray polyurea and applications [J]. International Journal of Impact Engineering, 2022, 167: 104265. doi: 10.1016/j.ijimpeng.2022.104265 [6] CHEN D, WU H, WEI J S, et al. Nonlinear visco-hyperelastic tensile constitutive model of spray polyurea within wide strain-rate range [J]. International Journal of Impact Engineering, 2022, 163: 104184. doi: 10.1016/j.ijimpeng.2022.104184 [7] WANG J G, REN H Q, WU X Y, et al. Blast response of polymer-retrofitted masonry unit walls [J]. Composites Part B: Engineering, 2017, 128: 174–181. doi: 10.1016/j.compositesb.2016.02.044 [8] ZHU H J, WANG X, WANG Y T, et al. Damage behavior and assessment of polyurea sprayed reinforced clay brick masonry walls subjected to close-in blast loads [J]. International Journal of Impact Engineering, 2022, 167: 104283. doi: 10.1016/j.ijimpeng.2022.104283 [9] ZHU H J, LUO X N, JI C, et al. Strengthening of clay brick masonry wall with spraying polyurea for repeated blast resistance [J]. Structures, 2023, 53: 1069–1091. doi: 10.1016/j.istruc.2023.05.004 [10] ZHANG Y, HU J H, ZHAO W D, et al. Numerical simulation of the blast resistance of SPUA retrofitted CMU masonry walls [J]. Buildings, 2023, 13(2): 446. doi: 10.3390/buildings13020446 [11] SANTOS A P, CHIQUITO M, CASTEDO R, et al. Experimental and numerical study of polyurea coating systems for blast mitigation of concrete masonry walls [J]. Engineering Structures, 2023, 284: 116006. doi: 10.1016/j.engstruct.2023.116006 [12] CHEN D, WU H, FANG Q. Simplified micro-model for brick masonry walls under out-of-plane quasi-static and blast loadings [J]. International Journal of Impact Engineering, 2023, 174: 104529. doi: 10.1016/j.ijimpeng.2023.104529 [13] Methodology manual for the single degree of freedom blast effects design spreadsheets [R]. PDC-TR 06-01, US Army Corps of Engineers, 2008. [14] Structures to resist the effects of accidental explosions [R]. UFC 3-340-02, Washington DC: US Department of Defence, 2008. [15] 许林峰, 陈力, 李展, 等. 聚脲加固砖填充墙抗爆性能的试验和分析方法研究 [J]. 爆炸与冲击, 2022, 42(7): 126–137. doi: 10.11883/bzycj-2021-0332 XU L F, CHEN L, LI Z, et al. Experimental and analytical study on blast resistance performance of brick infill walls strengthened with polyuria [J]. Explosion and Shock Waves, 2022, 42(7): 126–137. doi: 10.11883/bzycj-2021-0332 [16] YANG C Z, JIA X, HUANG Z X, et al. Damage of full-scale reinforced concrete beams under contact explosion [J]. International Journal of Impact Engineering, 2022, 163: 104180. doi: 10.1016/j.ijimpeng.2022.104180 [17] RAMAN S, NGO T, LU J H, et al. Experimental investigation on the tensile behavior of polyurea at high strain rates [J]. Materials & Design, 2013, 50: 124–129. [18] 汪维. 钢筋混凝土构件在爆炸载荷作用下的毁伤效应及评估方法研究[D]. 长沙: 国防科学技术大学, 2014. WANG W. Study on damage effects and assessments method of reinforced concrete structural members under blast loading [D]. Changsha: National University of Defense Technology, 2014. [19] 陈力, 方秦, 还毅, 等. 爆炸荷载作用下钢筋混凝土梁板结构的面力效应 [J]. 工程力学, 2010, 27(8): 156–163. CHEN L, FANG Q, HUAN Y, et al. Membrane action on reinforced concrete beam-slab structures subjected to blast loads [J]. Engineering Mechanics, 2010, 27(8): 156–163. [20] WU G, JI C, WANG X, et al. Blast response of clay brick masonry unit walls unreinforced and reinforced with polyurea elastomer [J]. Defence Technology, 2022, 18(4): 643–662. doi: 10.1016/j.dt.2021.03.004 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: