首页
登录
注册
-
为缓解地面交通压力，我国各中心城市已掀起地铁建设热潮，因此，地铁结构的安全问题日趋重要。动荡的国际局势和潜在的恐怖主义对地铁结构安全构成了一定的威胁。针对地铁结构的毁伤主要有由外向内和由内向外2种类型：由外向内型毁伤是弹体侵彻贯穿地铁结构上部路基路面进入内部空间引爆，不仅阻断地上交通，而且对地下结构造成毁伤；而由内向外型毁伤则是人为携带易燃易爆物品潜入地铁内部实施爆炸，对乘车人员的人身安全、地铁的正常运行以及地铁结构均会造成威胁。
高金金等[1]总结了恐怖袭击下地铁隧道结构爆炸响应的研究手段、地铁隧道结构的动力响应、毁伤效应及防护对策。目前，对地铁隧道结构毁伤和动力响应的研究主要包含内部爆炸和外部爆炸。在隧道内部爆炸对结构毁伤和动力响应研究方面：孔德森等[2–3]以南京地铁隧道为例，基于LS-DYNA三维流-固耦合算法，开展了10 kg TNT在地铁隧道内爆炸作用下的数值模拟，总结得出了沿地铁隧道纵向的超压衰减规律和冲击响应；李忠献等[4]基于自编制的地铁隧道动力响应非线性动力分析程序，开展了单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应与抗爆分析，一方面总结了爆炸超压、隧道埋深和间距等参数对隧道衬砌应力场的影响规律，另一方面验证了多孔材料泡沫铝覆于隧道外侧具有较好的缓冲吸能作用；王德荣等[5]在经典弹性理论基础上，建立了内爆炸作用下圆柱壳的动力平衡方程，得到了内部冲击荷载作用下各向异性圆柱壳体动力响应的解析解；Zhao等[6]基于任意拉格朗日-欧拉（arbitrary Lagrange Euler, ALE）和有限元耦合算法，对内爆荷载作用下的管片衬砌隧道进行了数值模拟，研究了围岩力学特性和压力水平对隧道结构在内爆作用下动力响应的影响，结果表明，内爆作用下管片衬砌隧道的主要变形模式为带电环节理处的开口变形和相邻环间的剪切变形。
在隧道外部爆炸对结构毁伤和动力响应研究方面：赵敏等[7–8]利用ANSYS/LS-DYNA软件研究了外爆荷载下地铁隧道衬砌结构的动力响应，给出了不同侧爆角度和不同炸药当量下隧道衬砌结构的位移；章毅等[9]利用等效静荷载法对地面爆炸荷载作用下地铁隧道内力的计算方法进行了推导，为地下结构的工程设计提供了参考；马建军等[10]以广州地铁9号线为例，基于4D-LSM（four dimensional-lattice spring model）数值计算模型，分析了不同爆炸压力、爆距、有无衬砌等条件下隧道的动力响应及破坏特征；Zhou等[11]采用玄武岩纤维增强聚合物钢筋对高浅埋混凝土城市综合隧道进行加固，并开展了重复爆破实验，揭示了加固后高浅埋混凝土城市综合隧道在重复爆炸作用下的动力响应、损伤演化和破坏类型，结果表明，隧道顶部是最脆弱的构件，且纵向裂缝沿隧道发展；Zhang等[12]以地铁隧道正上方的人防隧道为研究对象，采用钻孔爆破法开挖人防隧道，监测了人防隧道断面的应变和沿轴线方向的振动，分析了人防隧道断面的应变分布特征和振动传播规律，并采用动态有限元程序LS-DYNA进行了三维有限元模拟，从而确定了人防隧道应力和振动速度最大的位置；Jiang等[13]以深圳沿海地区地铁沿线爆破开挖工程为例，设计并实施了全尺寸埋地燃气管道的现场爆破振动试验，并设计了腐蚀程度、爆破距离、埋深、管径和运行压力等实际工程因素影响下埋地燃气管道爆破振动的正交数值模拟，基于量纲分析法建立了爆破作用下管道及其地表的爆破振动速度预测模型和管道峰值有效应力预测模型；Zhang等[14]结合城市典型管道埋地地层的特点，进行了埋地高密度聚乙烯波纹管的全尺寸爆破试验，监测并分析了爆破振动作用下空管内部的振动加速度和应变特征，并根据最大许用应力准则对管道的安全性进行了评价。
综上所述，目前主要针对地铁隧道衬砌结构开展爆炸作用下的毁伤与动态响应研究，未开展侵彻和爆炸作用下地铁站的毁伤破坏研究。本工作以济南轨道交通7号线“水屯北路站”为工程背景，基于LS-DYNA数值模拟软件，利用已有侵彻爆炸试验对数值建模方法进行验证，并开展地铁结构由外向内的先侵彻后爆炸以及由内向外的内部爆炸荷载作用下结构毁伤破坏效应的数值模拟研究。
-
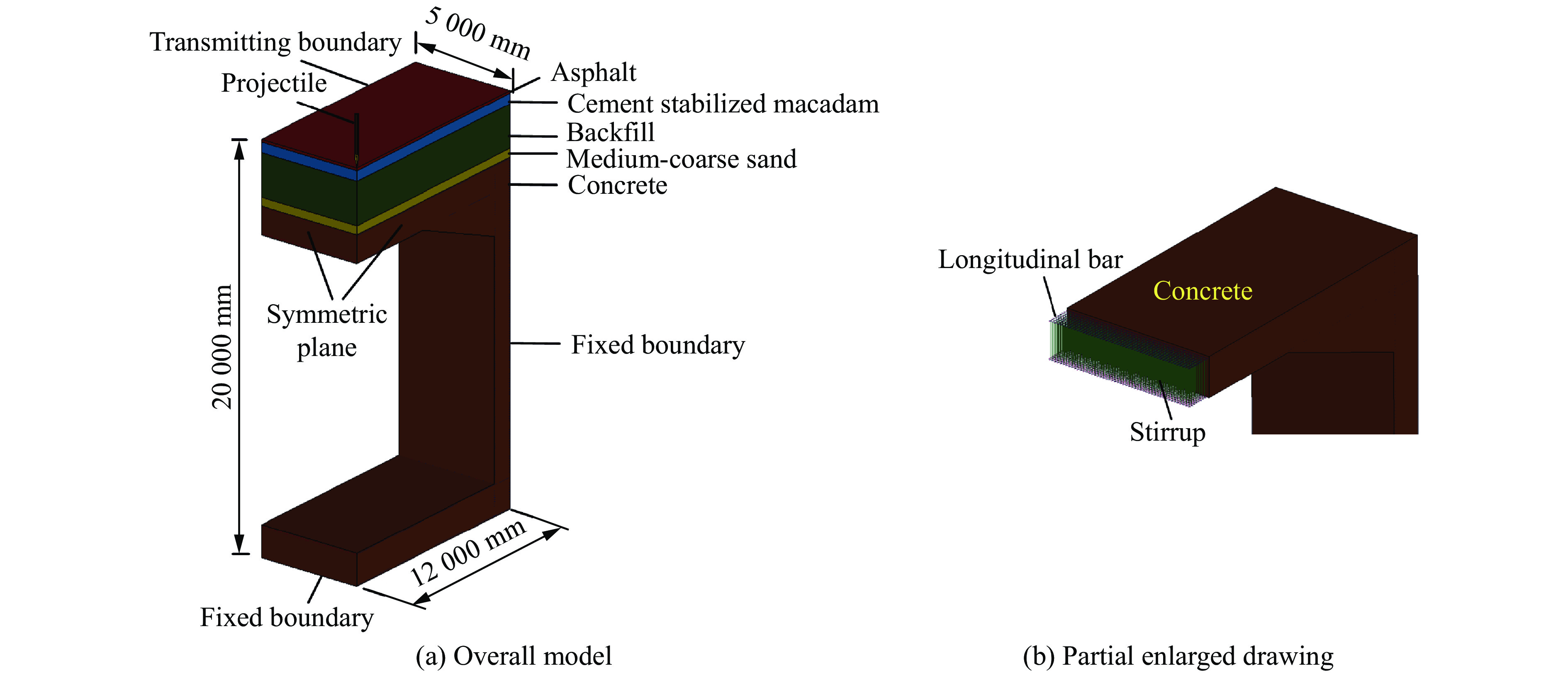
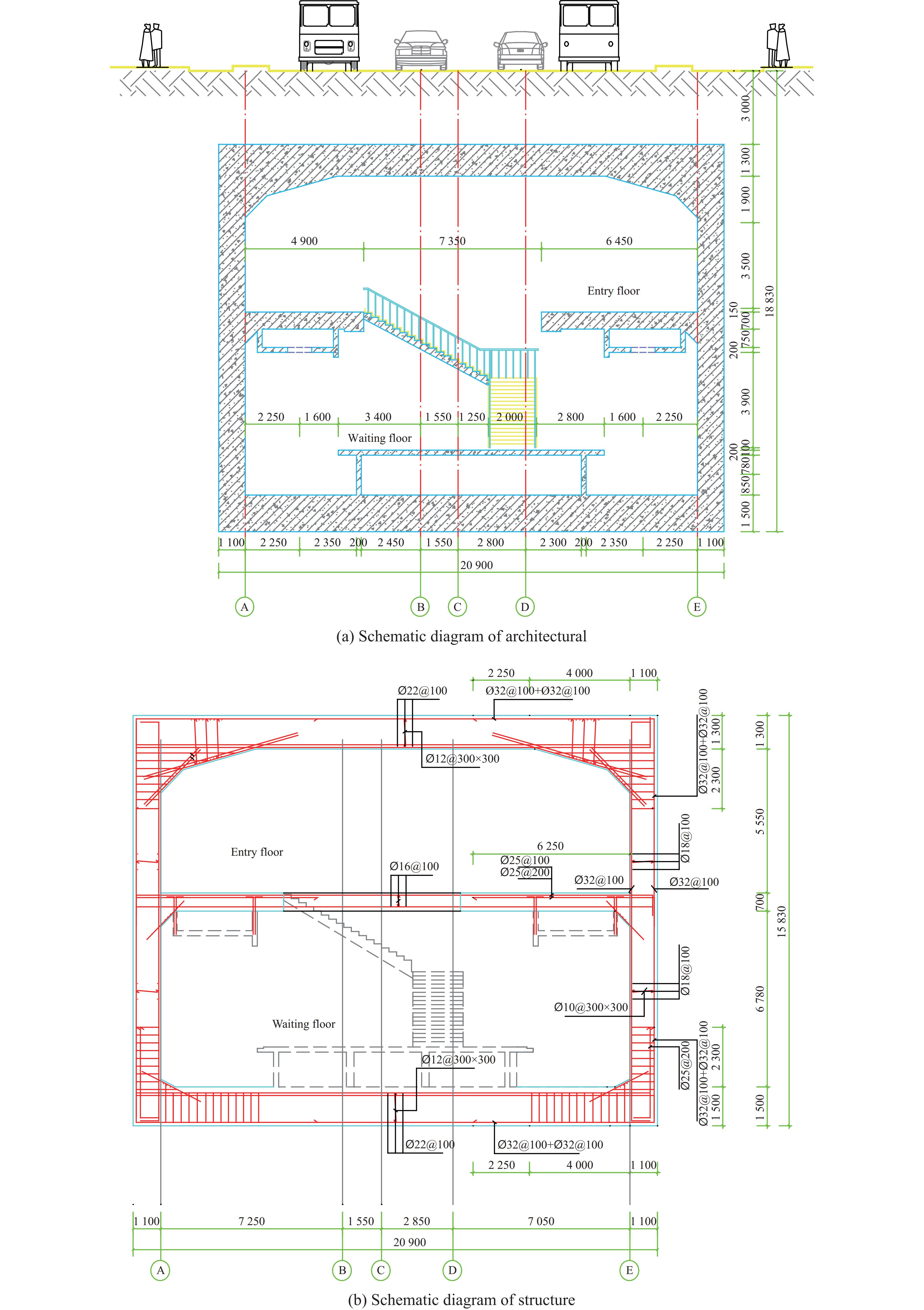
图1为济南轨道交通7号线“水屯北路站”的建筑和结构截面示意图。1 300 mm厚的钢筋混凝土顶板顶部包含4层介质，分别为沥青、水泥碎石、回填土和中粗砂。其中：沥青分为80 mm厚的沥青粗粒和40 mm厚的沥青中粒；水泥碎石分3层铺设，每层厚160 mm，总厚度为480 mm；回填土厚度为2 000 mm；中粗砂厚度为400 mm。地铁站采用传统的岛式站台设计方式，上、下分别为进站层和候站层。地铁结构中混凝土材料的单轴抗压强度为40 MPa，纵筋和箍筋分别选用直径为32和22 mm的HRB 400型三级钢筋，钢筋的屈服强度为400 MPa。考虑到武器是从路面垂直侵入地铁结构内部，整个侵入过程分为侵彻和爆炸2个环节。
-
侵彻过程数值模型采用三维1/4模型，如图2所示。弹体和地铁结构均采用拉格朗日单元描述，两者之间采用侵蚀接触。弹体采用质量约为450 kg的穿甲爆破弹，由弹壳和装药两部分构成，弹体尺寸详见文献[15]，弹壳采用*MAT_RIGID模型[16]描述，装药采用*MAT_PLASTIC_KINEMATIC模型[16]描述。在地铁结构中，沥青采用*MAT_JOHNSON_COOK模型[17]和*EOS_GRÜNEISEN状态方程[17]描述，水泥碎石性质与低强度混凝土类似，采用Kong-Fang混凝土损伤本构模型[15, 18–19]（*MAT_USER_DEFINED_MATERIAL_MODELS）描述，回填土采用*MAT_DRUCKER_PRAGER模型[20]描述，中粗砂采用*MAT_GEOLOGIC_CAP_MODEL模型[20]描述，混凝土结构采用Kong-Fang混凝土损伤本构模型[16]（*MAT_USER_DEFINED_MATERIAL_MODELS）描述，钢筋采用*MAT_PLASTIC_KINEMATIC模型[16]描述。
为保证弹体交界处的计算精度，在直径1 000 mm范围内进行网格加密，网格尺寸为20 mm，网格尺寸选取文献[18]中的尺寸模型。侵彻有限元模型网格数量为5 634 099。
-
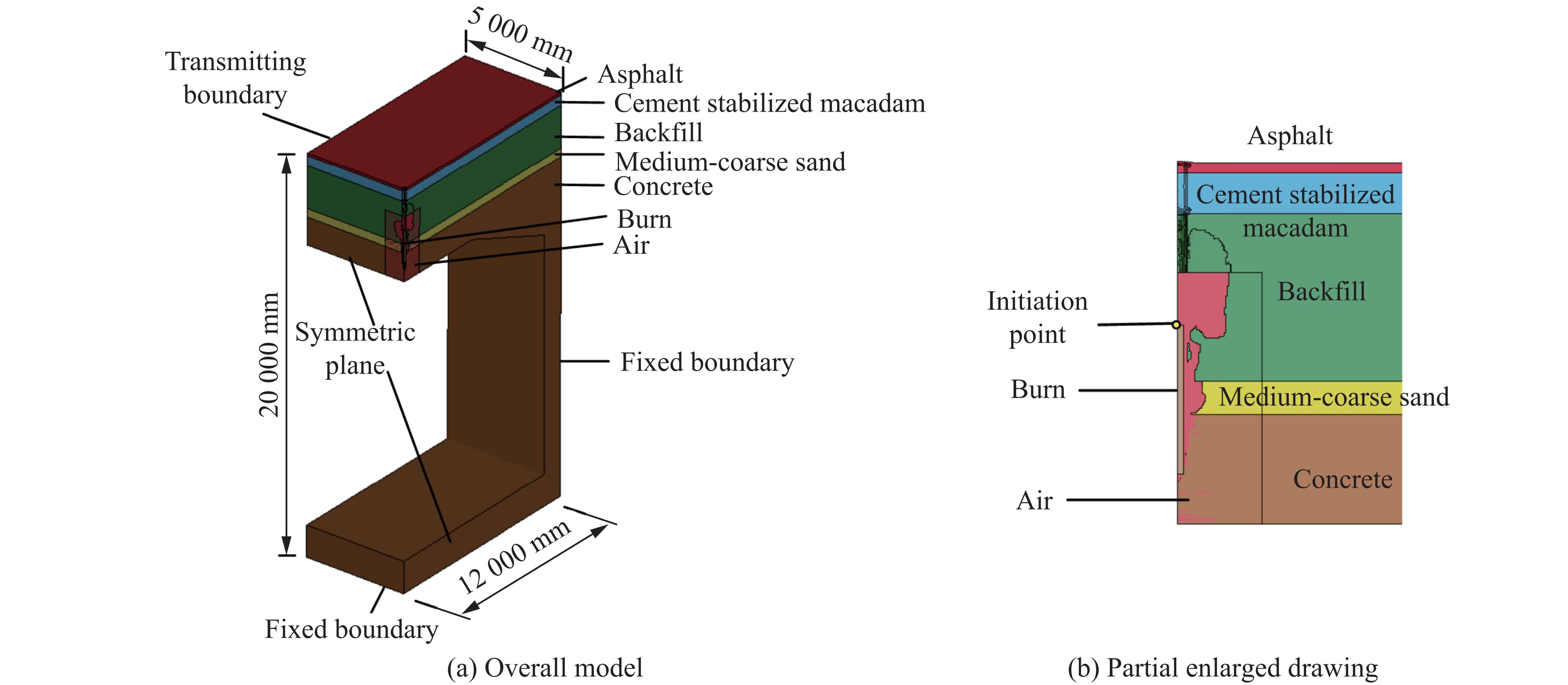
爆炸过程采用完全重启动建模方法，即在图2侵彻有限元模型的基础上删除弹壳和装药部分，增加如图3所示的空气域和装药部分，建立三维1/4模型进行计算，采用局部空气域（图3(b)）设置。爆炸过程中，空气域和装药采用欧拉单元描述且视为流体，侵彻后的沥青、水泥碎石、回填土、中粗砂和混凝土仍然采用拉格朗日单元描述且视为固体，流体与固体之间采用流-固耦合（fluid-structure interaction，FSI）接触方式。装药量为54 kg，尾部起爆。为继承侵彻过程后靶体的损伤破坏状态，采用*STRESS_INITIALIZATION关键字[15]继承地铁结构的部件。空气采用*MAT_NULL模型[15]和*EOS_LINEAR_POLYNOMIAL状态方程[15]描述，装药采用*MAT_HIGH_EXPLOSIVE_BURN模型[15]和*EOS_JWL状态方程[15]描述。地铁结构各材料模型选取不变。空气域和装药网格尺寸均为10 mm，为保证爆炸近区的计算精度，在直径为1 000 mm范围内进行网格加密，网格尺寸为20 mm。爆炸有限元模型网格数量为5 986 003。
-
基于已有混凝土靶体先侵彻后爆炸缩比试验[21]对上述侵彻和重启动爆炸建模方法进行验证。
-
参考文献[21]中的混凝土靶体大口径缩比弹先侵彻后爆炸试验，其中侵彻和爆炸试验分开进行，即先进行侵彻试验，然后在靶体侵彻试验破坏的基础上装药进行爆炸试验，爆炸过程中不考虑弹壳的影响。
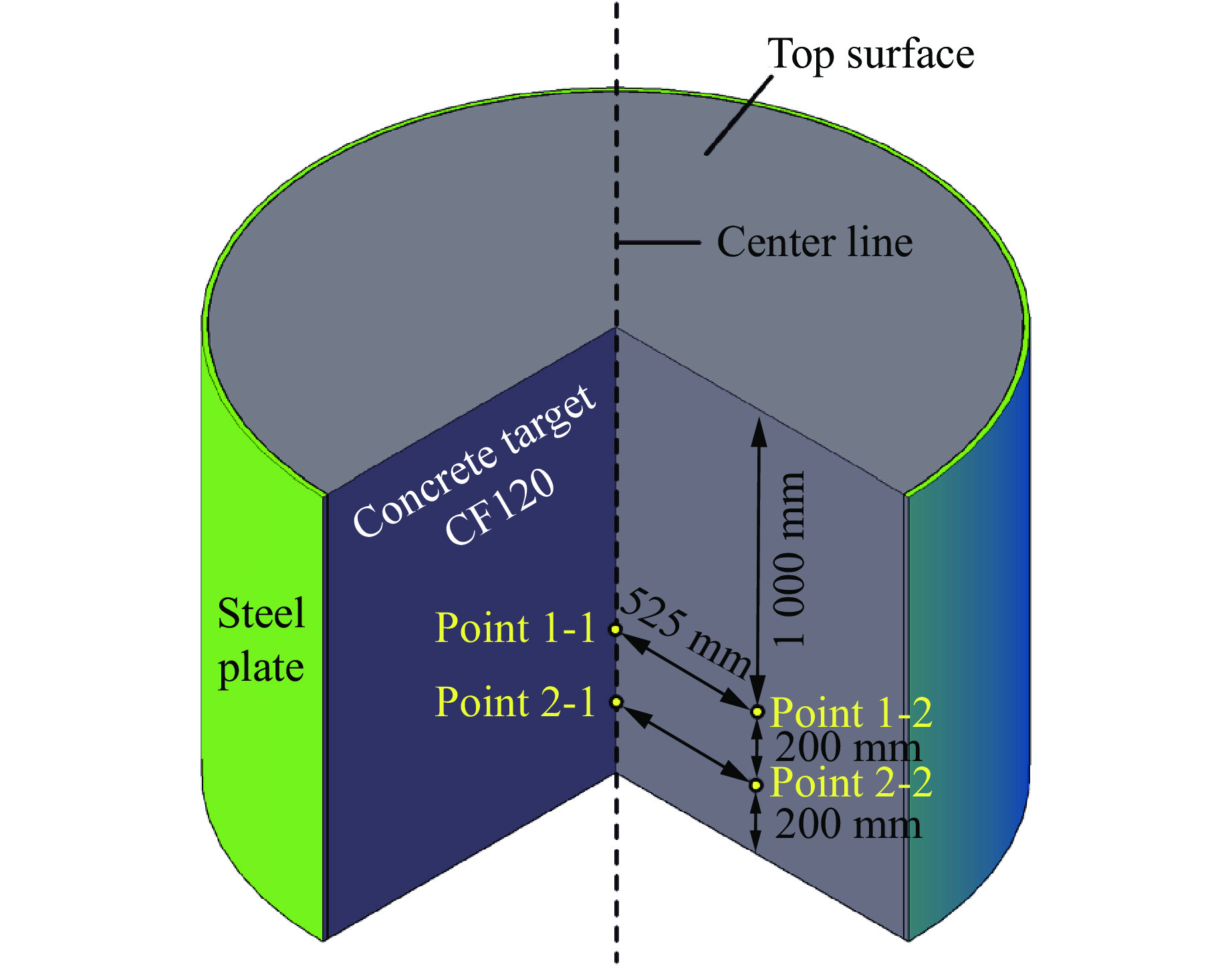
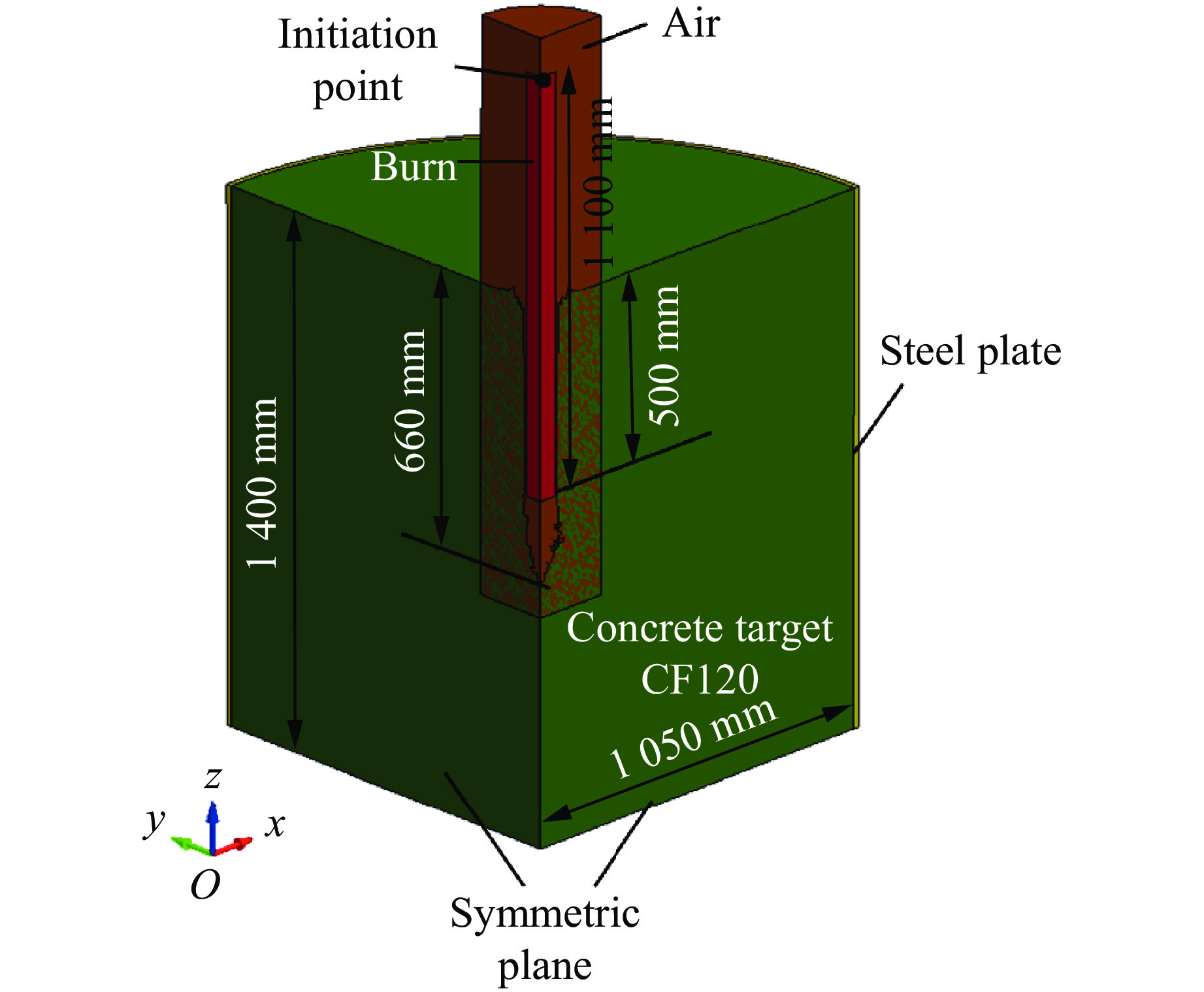
弹体直径为100 mm，弹身长为1 029 mm，质量为34.3 kg，侵彻初速度为365 m/s。靶体尺寸及测点布置如图4所示，靶体直径为2 100 mm，厚1 400 mm，外侧由厚20 mm的钢板约束；在测点处布置聚偏二氟乙烯（polyvinylidene difluoride，PVDF）压力传感器，测点1-1和2-1位于靶体中心线上，埋深分别为1 000和1 200 mm，测点1-2和2-2距中心线525 mm，埋深分别与测点1-1和2-1相同。装药直径为98 mm，长度为1 100 mm，装药密度为1 530 kg/m3，TNT等效装药量为12.77 kg，埋置深度约为500 mm，尾部起爆。
图5给出了混凝土靶先侵彻后爆炸试验前后的宏观损伤破坏[21]。如图5(a)所示，侵彻后混凝土靶的开坑直径约为1 040 mm，弹体变形较小且略有偏转。图5(b)为侵彻后爆炸前装药布置，爆心位于装药顶端。图5(c)为爆炸后靶体的宏观损伤破坏，与侵彻结果相比，开坑区域变化不明显，但上表面裂纹扩展十分明显。试验观测的爆坑深度与侵彻深度相比基本一致。
-
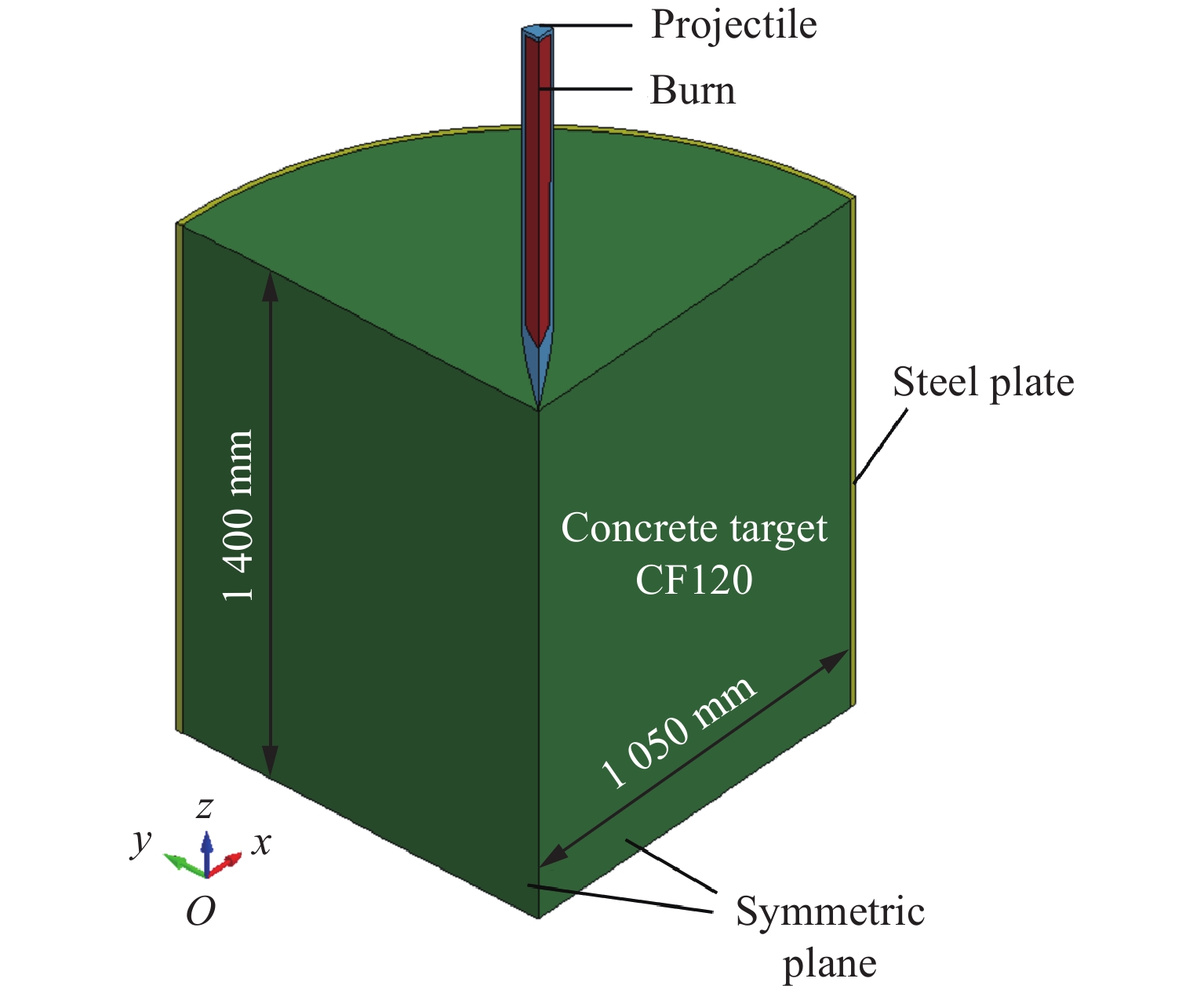
图6为侵彻过程的有限元模型。弹靶尺寸与试验一致，侵彻过程中，弹体、装药、CF120靶体和钢箍均采用拉格朗日单元描述，弹体与靶体之间采用侵蚀接触。考虑对称性，建立1/4模型，并在2个对称面上施加对称约束。图7为爆炸过程的有限元模型。在图6所示的侵彻有限元模型的基础上，删除弹体，增加空气域，装药直径为98 mm，长度为1 100 mm，装药密度为1 530 kg/m3，TNT等效装药量为12.77 kg，埋置深度约为500 mm，尾部起爆。通过*STRESS_INITIALIZATION继承钢箍和CF120超高性能混凝土靶最终时刻的损伤状态。其中，混凝土和钢箍仍采用拉格朗日单元描述，空气和装药则改用欧拉单元描述，两者采用流-固耦合接触算法。
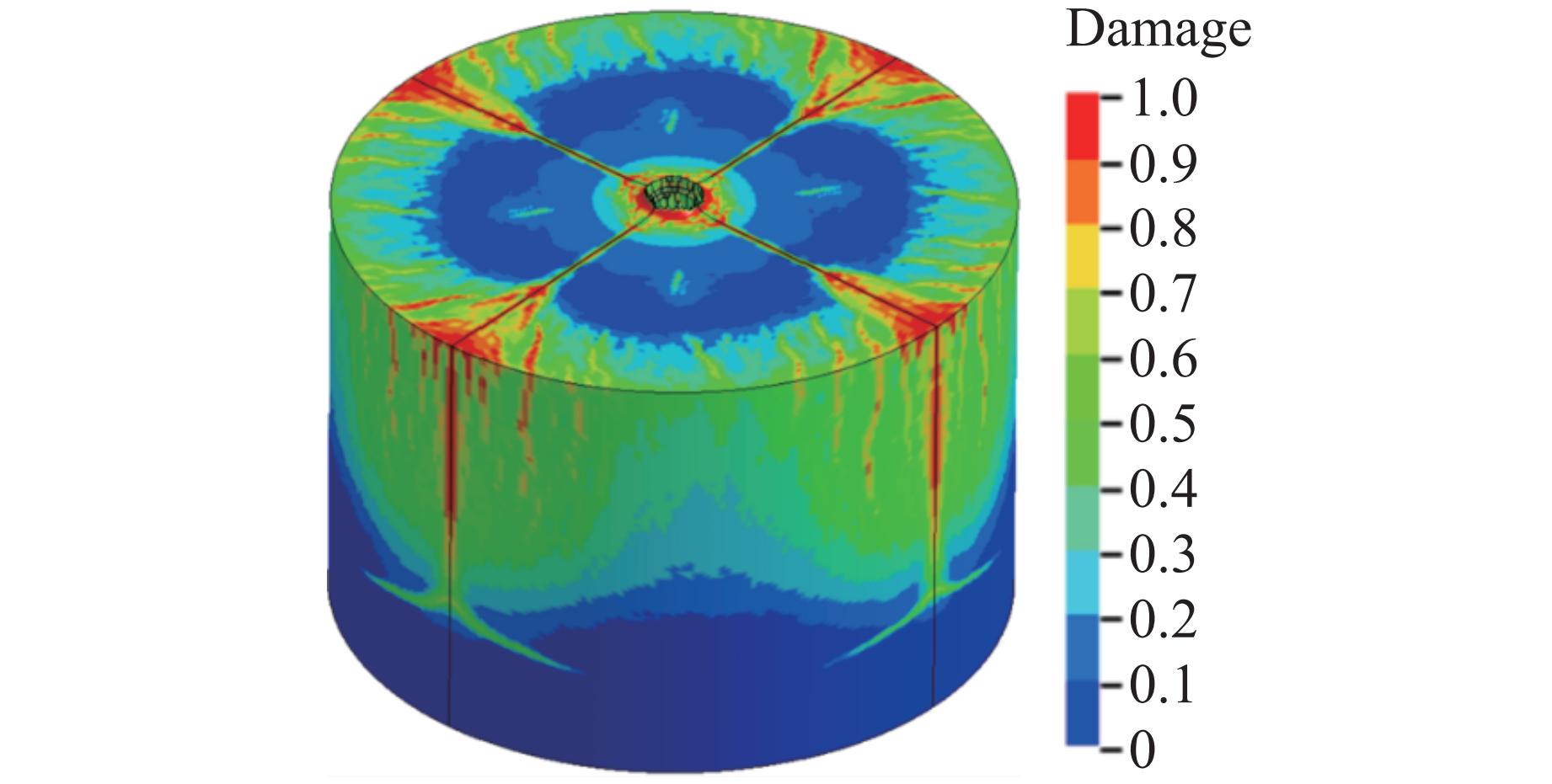
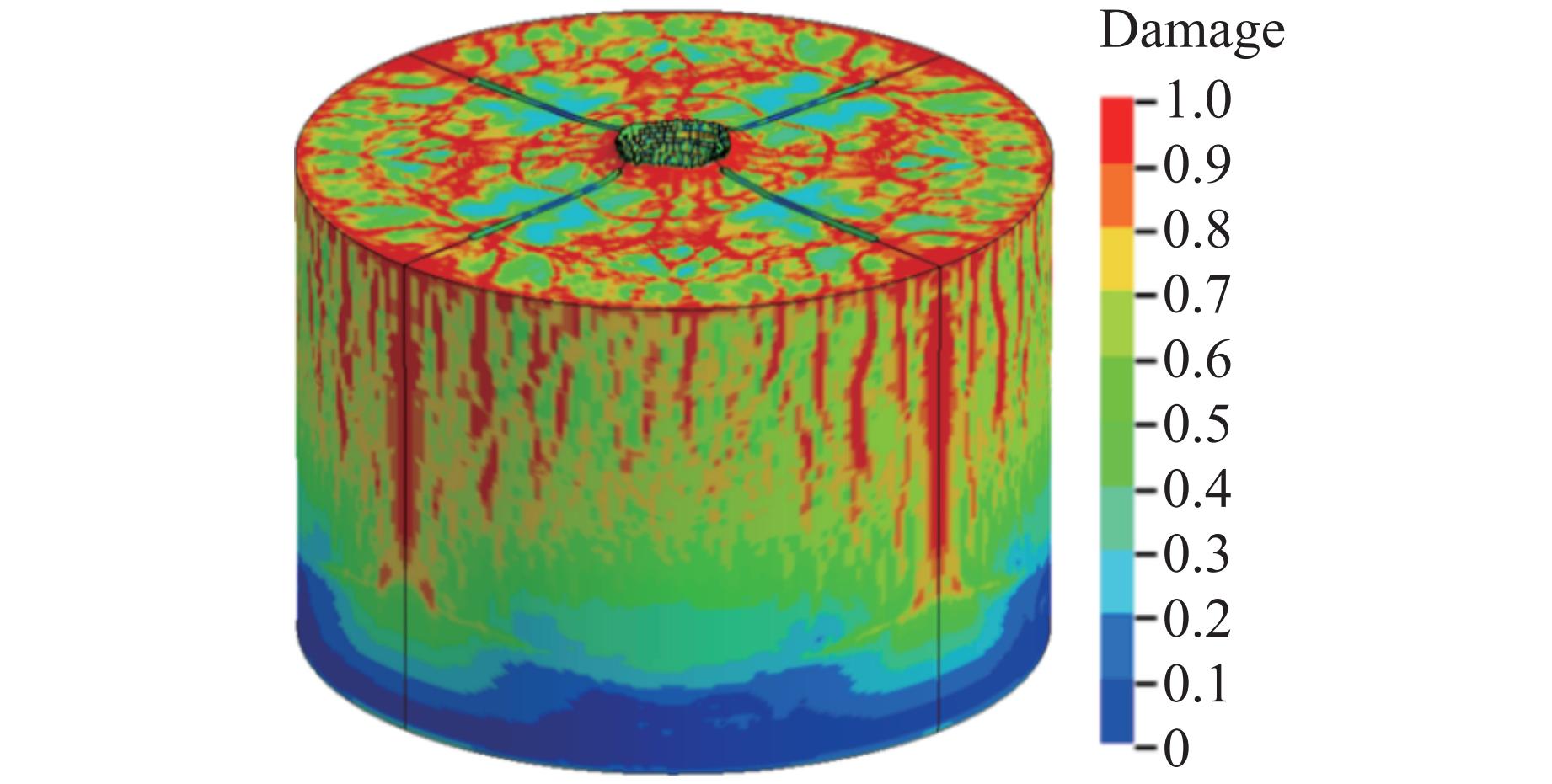
图8为侵彻后靶体损伤破坏的数值预测结果，侵彻深度为660 mm，与试验侵彻深度（700 mm）的相对偏差仅为6%。侵彻过程数值模拟得到的侵彻深度、开坑直径以及损伤破坏效果与侵彻试验结果吻合较好，验证了侵彻过程数值建模方法和模型参数选取的可靠性。图9为爆炸过程靶体损伤破坏的预测结果，爆坑直径在侵彻计算结果的基础上继续增大，但爆坑深度增加不明显。
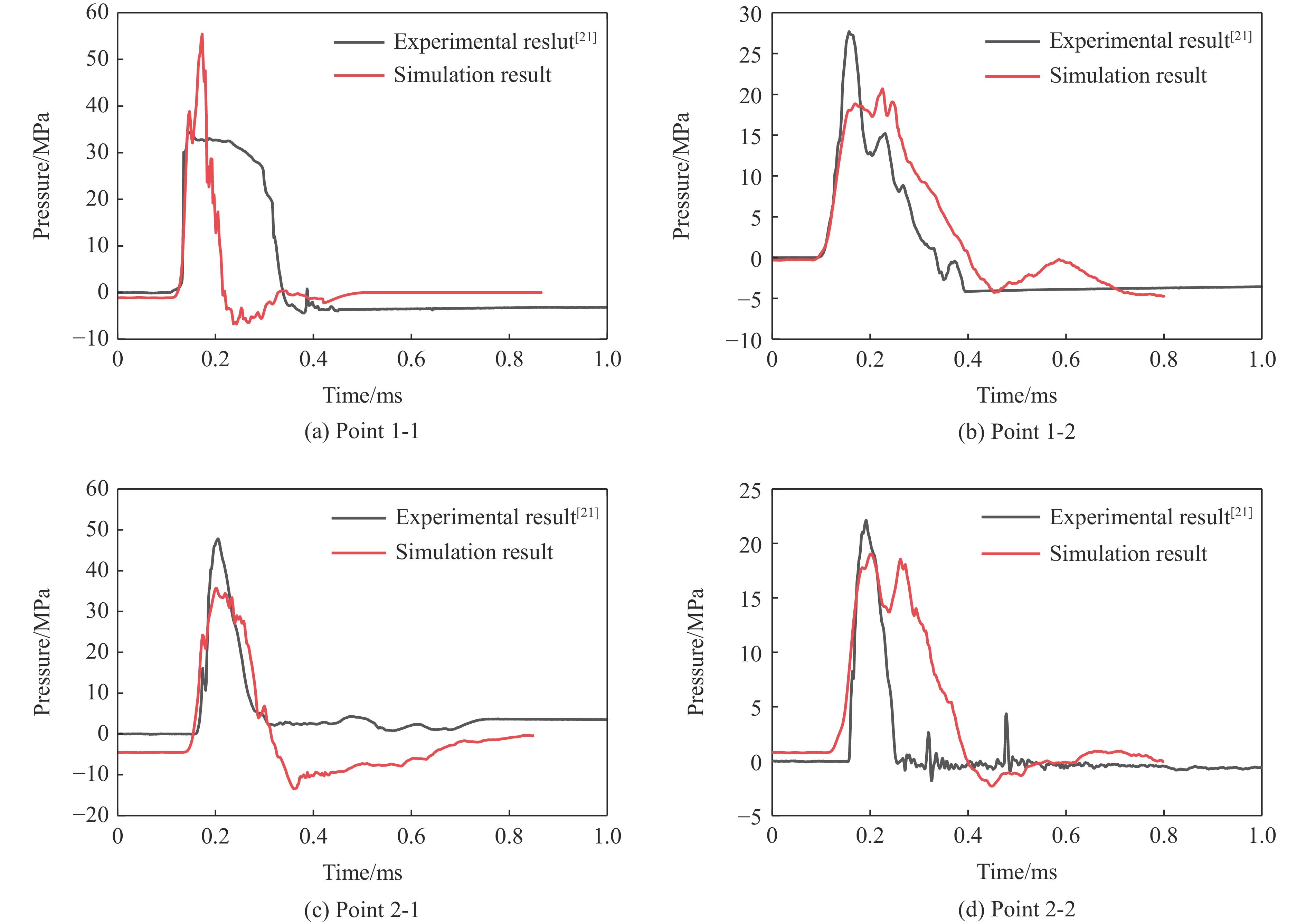
图10给出了爆炸过程靶体内部4个测点压力时程曲线的试验和数值模拟结果。数值计算的各测点压力峰值和压力持时与试验结果吻合较好，相对偏差不超过50%。通过对预制孔装药爆炸和先侵彻后装药爆炸2组试验进行数值模拟验证，认为选用的建模方法、材料模型及参数等均可靠。
-
基于1.1节中的侵彻过程数值建模方法开展侵彻作用下地铁结构毁伤破坏效应数值模拟，基于1.2节中的爆炸过程数值建模方法开展爆炸作用下地铁结构毁伤破坏效应数值模拟。
-
先侵彻后爆炸作用下地铁结构毁伤破坏效应的数值模拟共设计3个工况：工况1的侵彻速度为100 m/s，工况2的侵彻速度为200 m/s，工况3的侵彻速度为300 m/s。侵彻和爆炸过程的有限元模型分别如图2和图3所示。
-
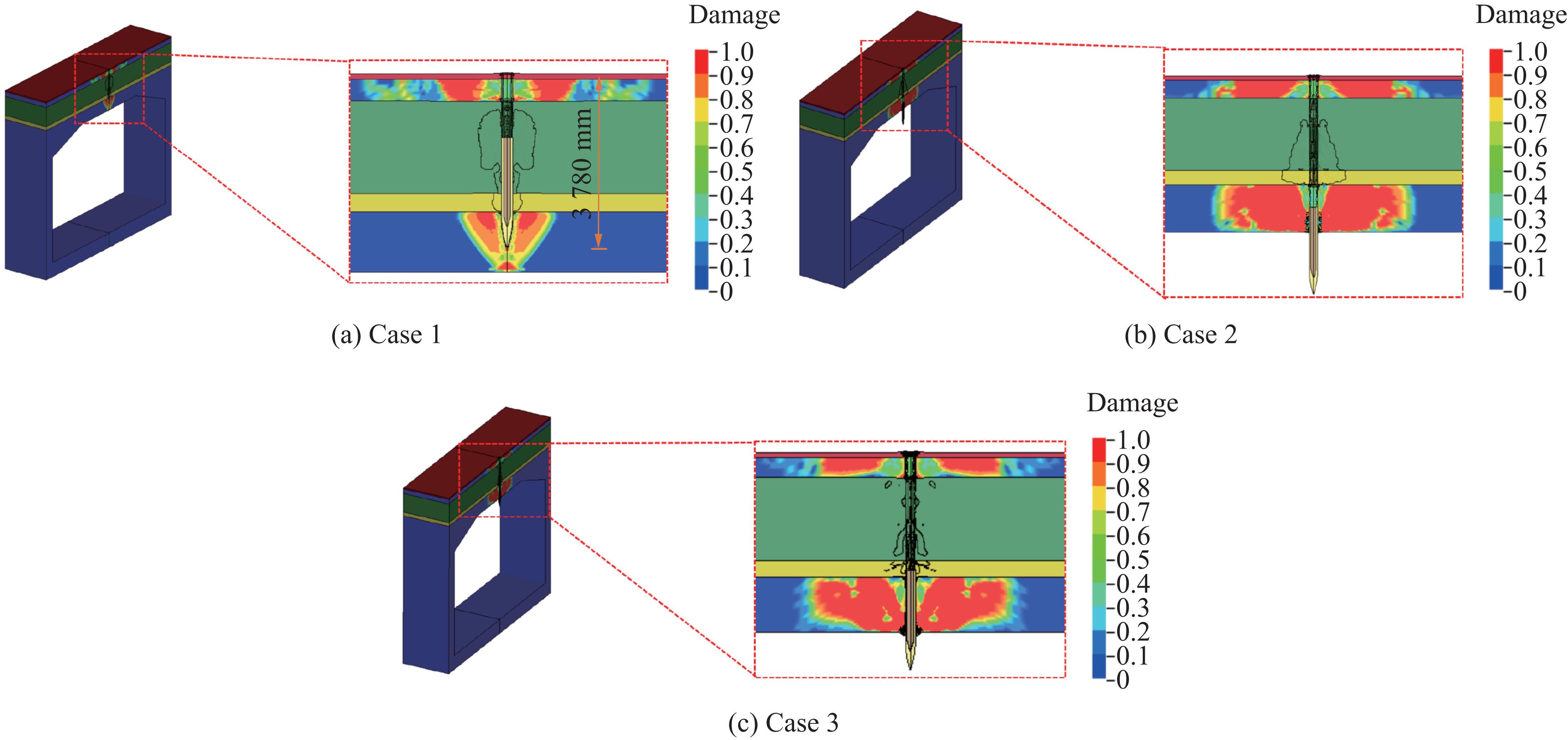
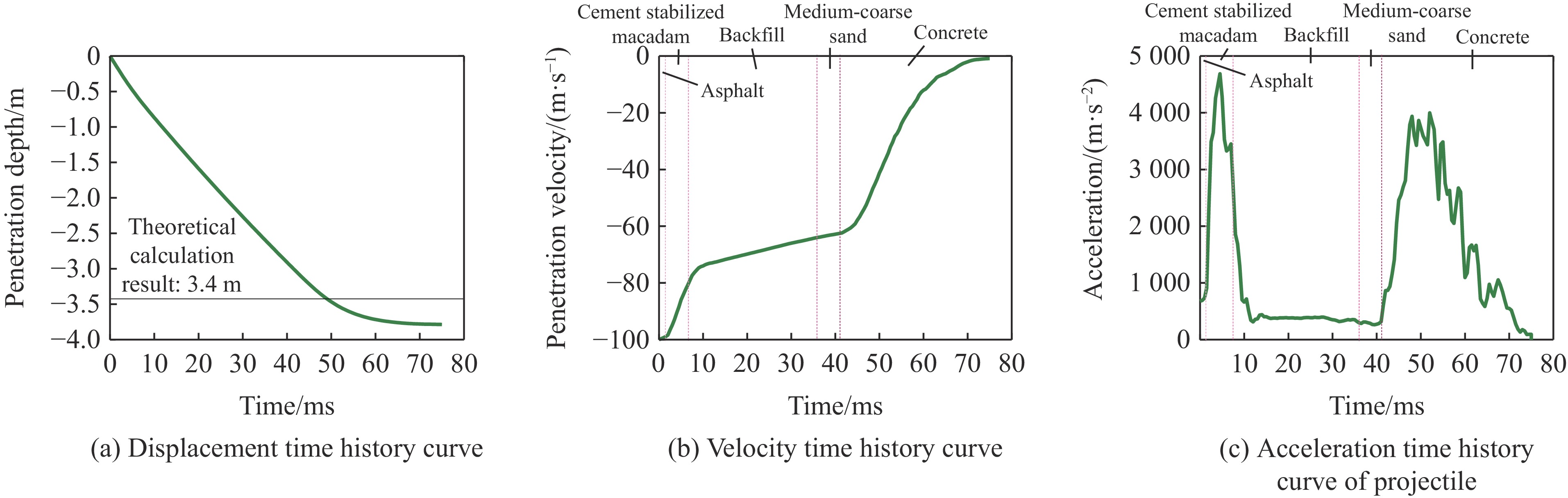
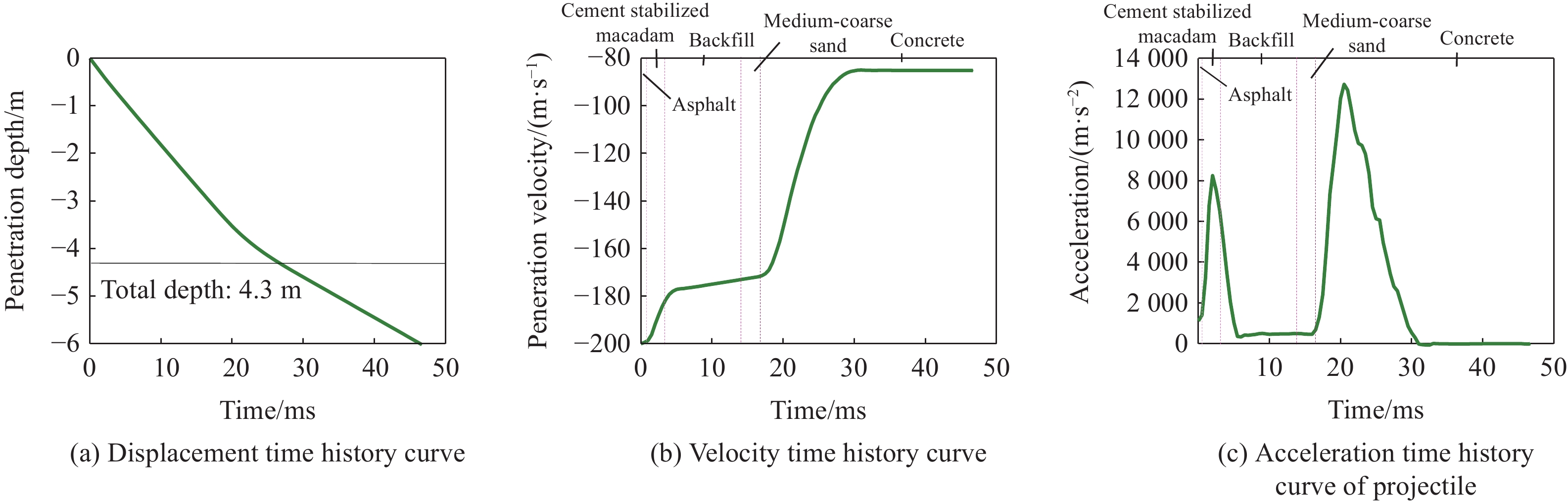
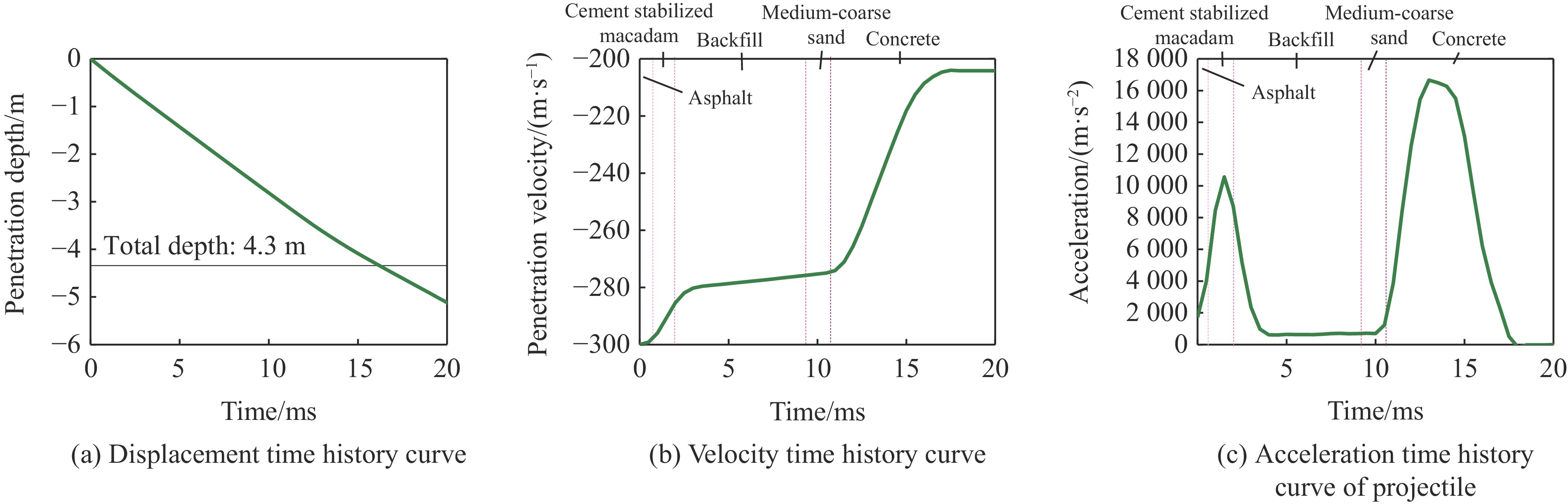
图11给出了3种工况下地铁结构损伤破坏的数值预测结果。由图11可知：工况1中，弹体并未贯穿混凝土结构层，侵彻深度为3 780 mm，与现有防护设计规范[22]中多层介质理论计算结果3 400 mm（图12(a)）的相对偏差为11%；工况2和工况3均发生弹体贯穿混凝土结构层现象，侵彻深度超过4 300 mm（图13(a)和图14(a)），与现有防护设计规范中多层介质理论计算公式的计算结果保持一致。
对比3种工况的计算结果可知：100 m/s侵彻速度下，地铁结构顶板混凝土仅产生局部损伤，开坑直径为弹体直径240 mm，无震塌，水泥碎石产生明显的拉伸损伤裂纹；200 m/s侵彻速度下，地铁结构顶板混凝土被穿透，开坑直径为240 mm，震塌直径为780 mm，震塌高度为550 mm，水泥碎石层也产生了明显的拉伸损伤裂纹；300 m/s侵彻速度下，地铁结构顶板混凝土被穿透，开坑直径为240 mm，震塌直径为800 mm，震塌厚度为420 mm，水泥碎石层也产生明显的拉伸损伤裂纹，但裂纹长度较100和200 m/s侵彻速度下的裂纹长度小。侵彻过程对地铁结构上部顶板和覆土层的毁伤破坏模式为局部破坏。
图12～图14分别为工况1～工况3数值模拟得到的侵彻深度、侵彻速度及弹体加速度时程曲线。可以看出，在弹体侵彻多层介质时，侵彻速度时程曲线的斜率均不一致，侧面反映了介质材料的密度和硬度各异，弹体在沥青、水泥碎石和混凝土介质层的侵彻速度时程曲线斜率较大，而在回填土和中粗砂中侵彻速度时程曲线斜率较小。数值计算结果反映的材料属性与实际材料属性基本一致。
-
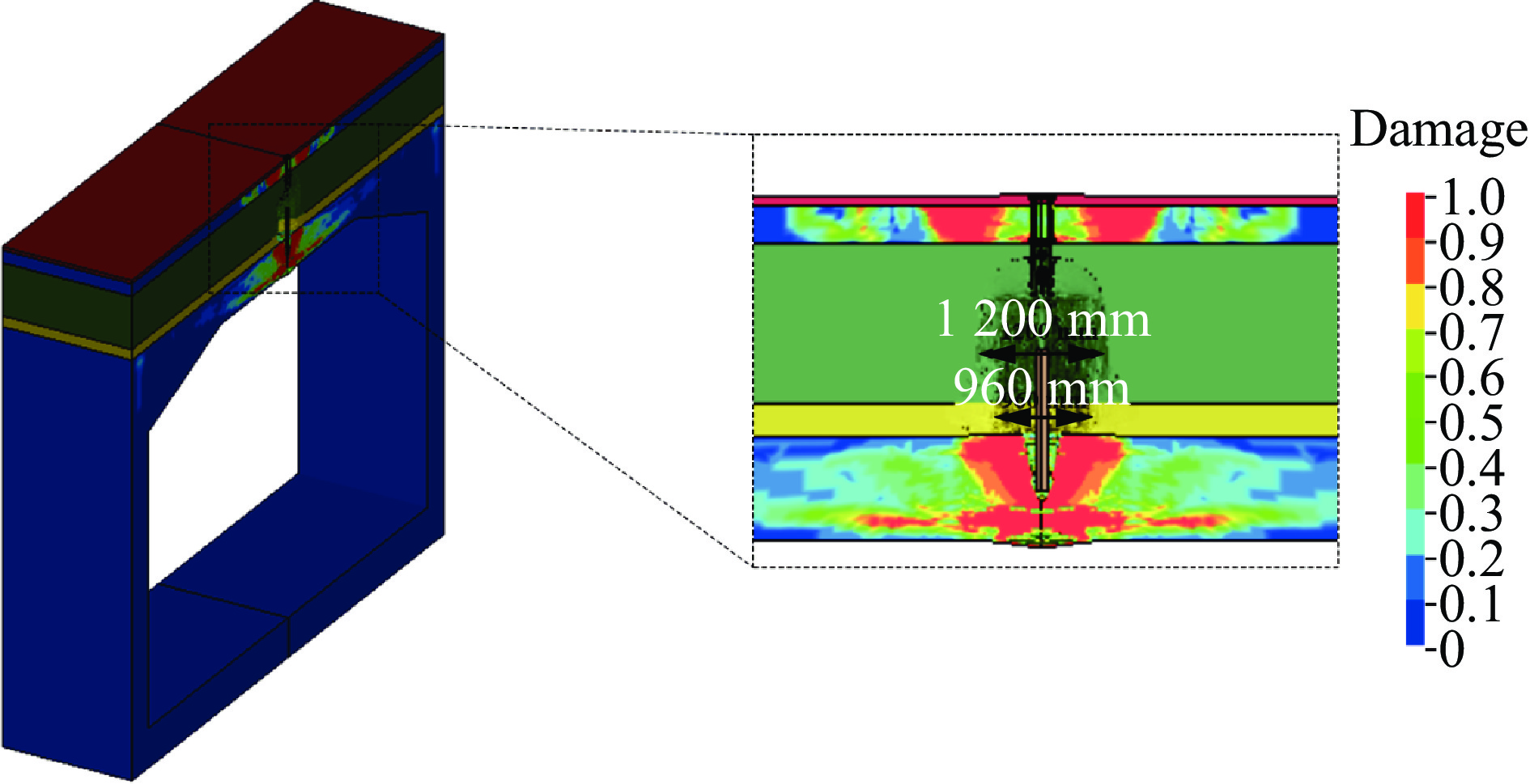
图15为工况1爆炸后的数值计算结果。由图15可知，沥青层、水泥碎石层、回填土层和中粗砂层均发生了不同程度的损伤破坏。由于装药埋置于整个结构内部，因此，起爆后爆轰产物向外扩散，导致沥青层外翻，水泥碎石层拉伸损伤裂纹继续扩展，回填土层弹道最大处直径由240 mm扩至1 200 mm（5倍弹径），中粗砂上表面弹道最大处直径由240 mm扩至960 mm（4倍弹径）。
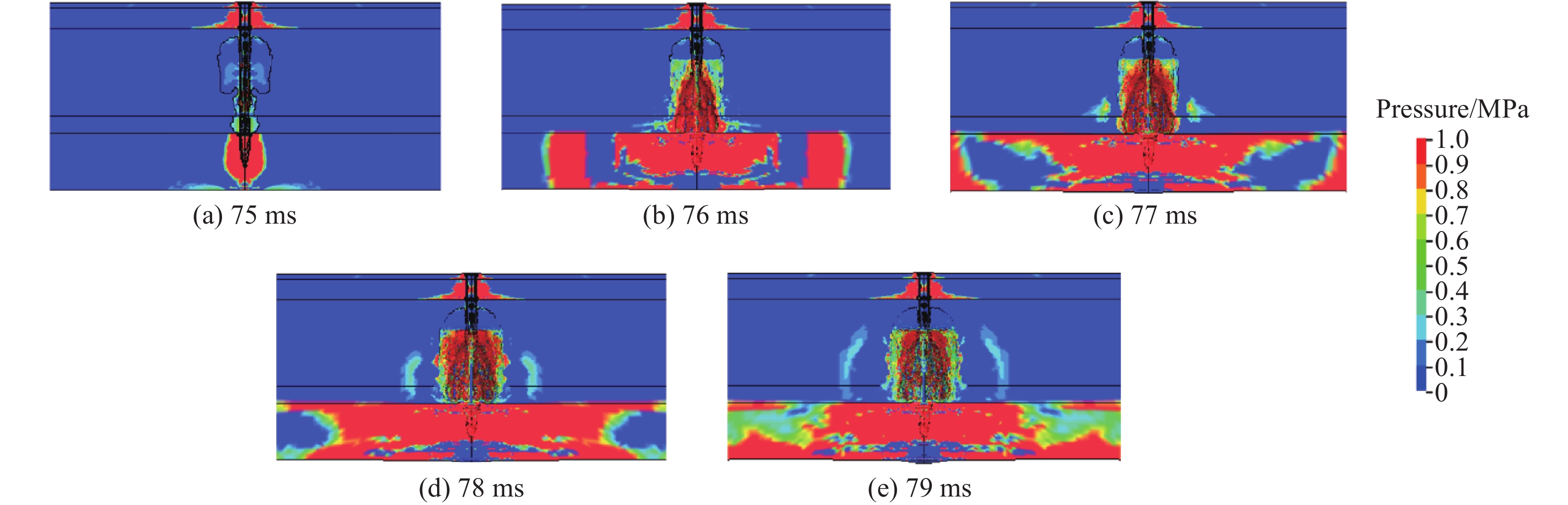
图16为75～79 ms 5个时刻地铁结构上部顶板和覆土层局部区域的压力分布。由图16可知，回填土和中粗砂的侵蚀主要是由爆轰产物与介质界面相互挤压形成，爆炸初始计算时界面压力较大，随着材料被挤压删除，压力逐渐消散。爆炸作用对结构的损伤破坏模式仍然以局部破坏为主。
-
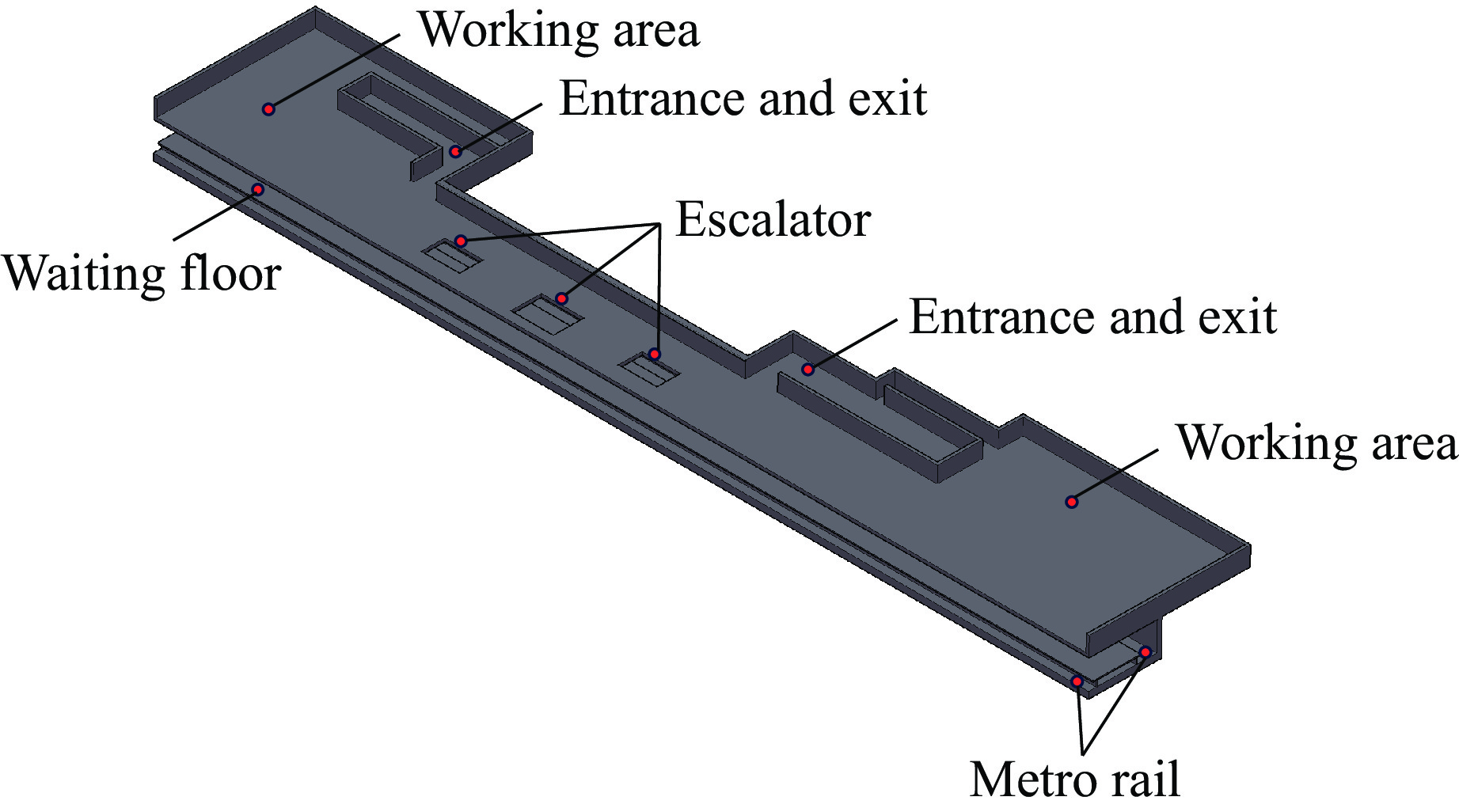
当常规武器的侵彻速度较大时，存在弹体击穿地铁结构上部多层介质进入地铁站台内部的现实可能，应当考虑常规武器在地铁结构内部大当量TNT爆炸的毁伤评估。此时的研究重点转向内部爆炸荷载作用下对地铁结构的毁伤破坏和冲击波的传播规律。图17为济南水屯北路站三维示意图，内部爆炸荷载作用下地铁结构毁伤破坏效应的数值模拟仍以水屯北路站为例。
-
内爆炸作用下城市地铁结构毁伤破坏效应的数值模拟共设计了3种工况：工况A，装药位于候站层；工况B，装药位于进站层；工况C，装药位于楼梯口处。
由于全尺度建模对网格数量、计算精度、计算时间、计算机配置等要求极高，因此，选取地铁结构区段进行三维建模。地铁内部装药质量为1 630 kg，装药形状为立方体，边长1 000 mm。
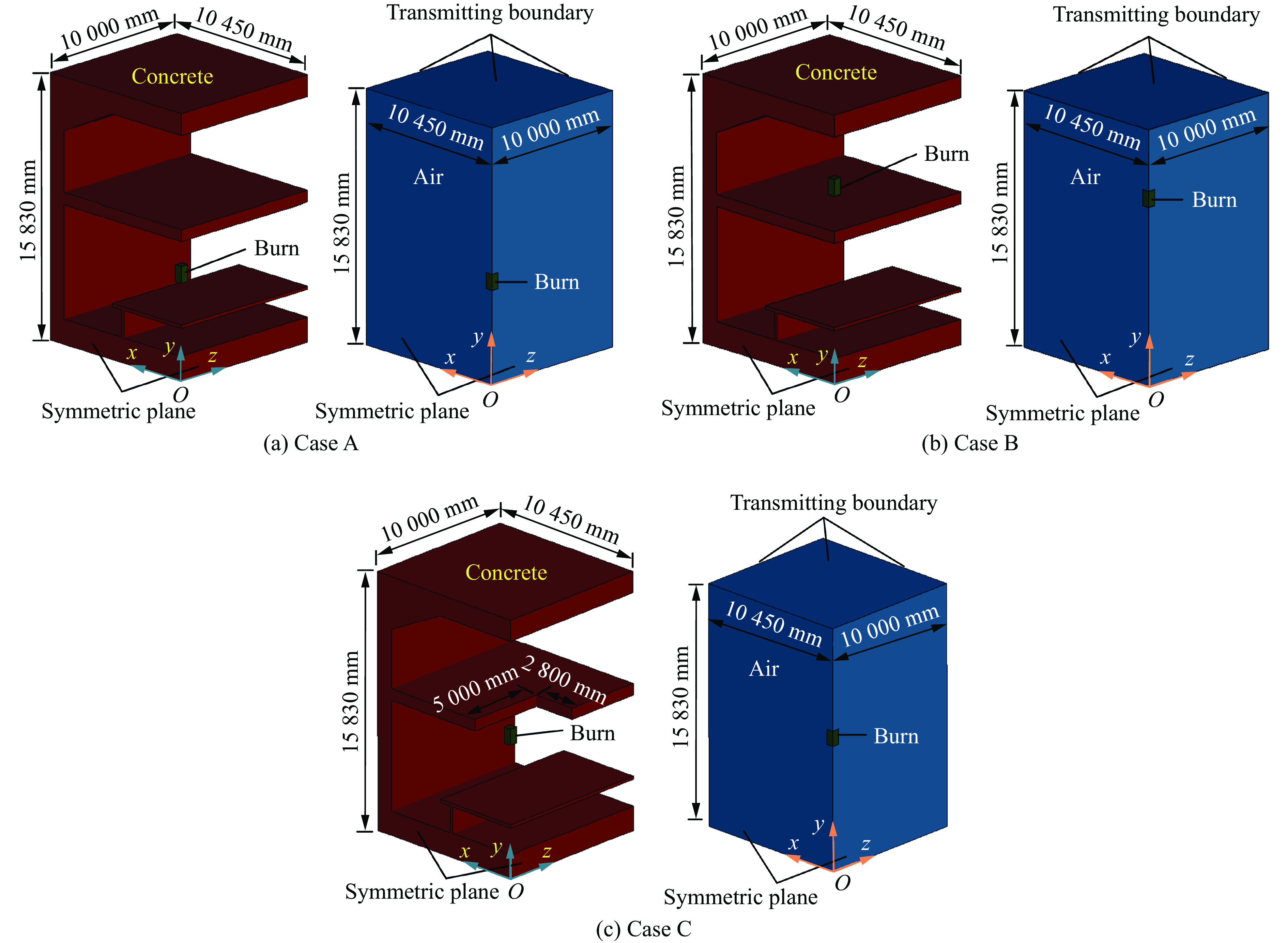
图18(a)给出了工况A的有限元模型。由图18(a)可知，数值模型取1/4结构，xOy和yOz为对称面，地铁结构选取的片段长度为10 m，截面尺寸与图2一致，截面高度为15.83 m，宽度为10.45 m。建立相应尺寸的空气域包裹地铁结构，空气域为长方体，长度为10 m；截面高度为15.83 m，宽度为10.45 m。装药置于地铁结构候站层，且地铁结构进站层与候站层未预留楼梯孔，装药起爆位置坐标为（0，6.3 m，0）。
为提高计算效率，有限元模型网格划分采用渐变网格。地铁结构在距xOy对称面1 m内的单元尺寸为100 mm，在距xOy对称面1～4 m内的单元尺寸为150 mm，在距xOy对称面5～10 m内的单元尺寸为200 mm，共计298 560个单元。空气域在距xOy对称面0.5 m内的单元尺寸为50 mm，在距xOy对称面0.5～2.5 m内的单元尺寸为60 mm，在距xOy对称面2.5～5.5 m内的单元尺寸为75 mm，在距xOy对称面5.5～10.0 m内的单元尺寸为100 mm，共计3 237 625个单元。装药的单元尺寸为50 mm，共计2 000个单元。本模型总计3 538 185个单元。
工况B和工况C的有限元计算模型分别如图18(b)和图18(c)所示。工况B与工况A有限元模型的唯一区别为装药位置，工况B中装药的起爆位置坐标为（0，11.53 m，0）。工况C与工况A的有限元模型相比，存在两点区别：(1) 工况C中，装药起爆位置坐标为（0，8.38 m，0）；(2) 工况C预留了楼梯口，有限元模型中预留楼梯口的截面尺寸为5 000 mm×2 800 mm。
-
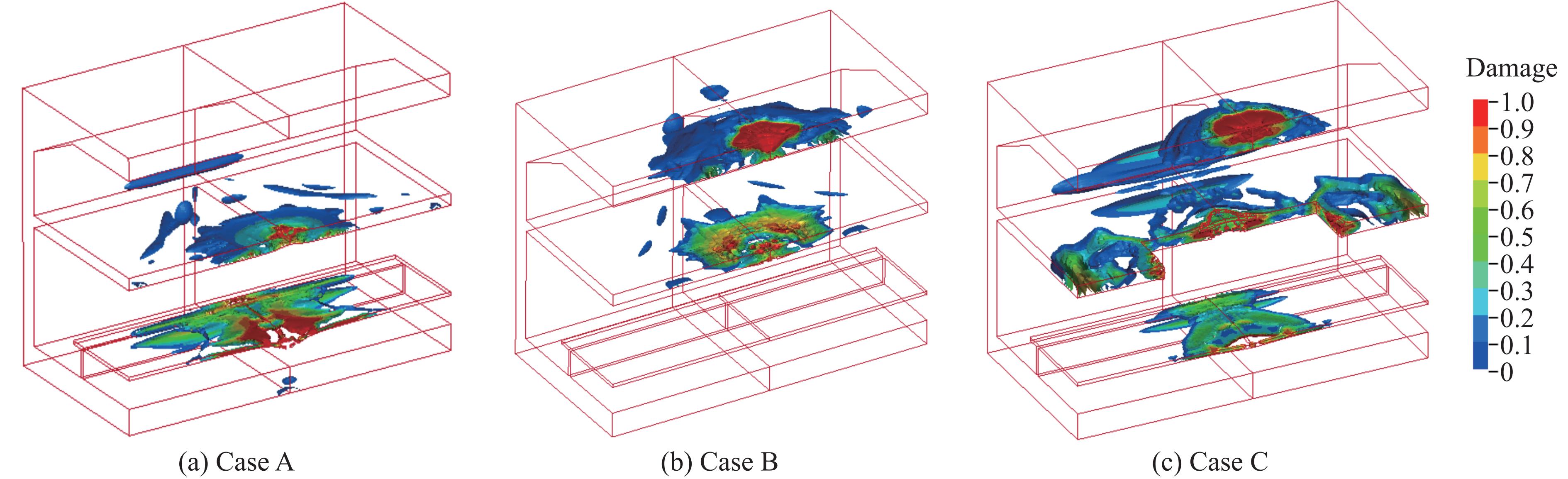
图19给出了爆炸作用下地铁结构的损伤分布。对比3种工况候站层混凝土平台板的损伤破坏情况，发现工况A和工况C中候站层混凝土平台板在爆炸冲击荷载下的损伤破坏程度较大，发生明显炸穿现象，对下方管线等基础设施造成严重威胁；由于工况B中候站层混凝土平台板与爆源不在同一楼层，因此，爆炸冲击荷载对下层影响有限，未发生明显变形。对比3种工况进站层混凝土顶板的损伤破坏情况，发现工况B和工况C中进站层混凝土顶板的上表面主要为拉伸损伤控制，主要由冲击波反射形成拉伸波所致；工况A中进站层混凝土顶板与爆源不在同一楼层，因而爆炸冲击荷载对下层影响有限，未发生明显损伤。对比3种工况进站层混凝土底板的损伤破坏情况，发现工况A中进站层混凝土底板损伤明显，板上表面为拉伸损伤，损伤值已达到1，并伴随混凝土剥落，板下方主要为剪切和体积压缩损伤，损伤值在0.7～0.8之间，结构发生明显变形和位移；工况B中进站层混凝土底板上表面为迎爆面，板上表面以剪切和体积压缩损伤为主，已出现损伤值为1的区域，并伴随混凝土剥落，板下表面主要以拉伸损伤为主，局部损伤值为1，并伴随混凝土剥落；工况C中进站层与候车层存在预留孔洞，进站层混凝土底板的损伤以拉伸损伤为主，主要由于爆炸冲击波在预留孔洞周边混凝土板发生明显绕射，在对称面附近损伤值达到1，伴随混凝土拉伸失效并剥落。
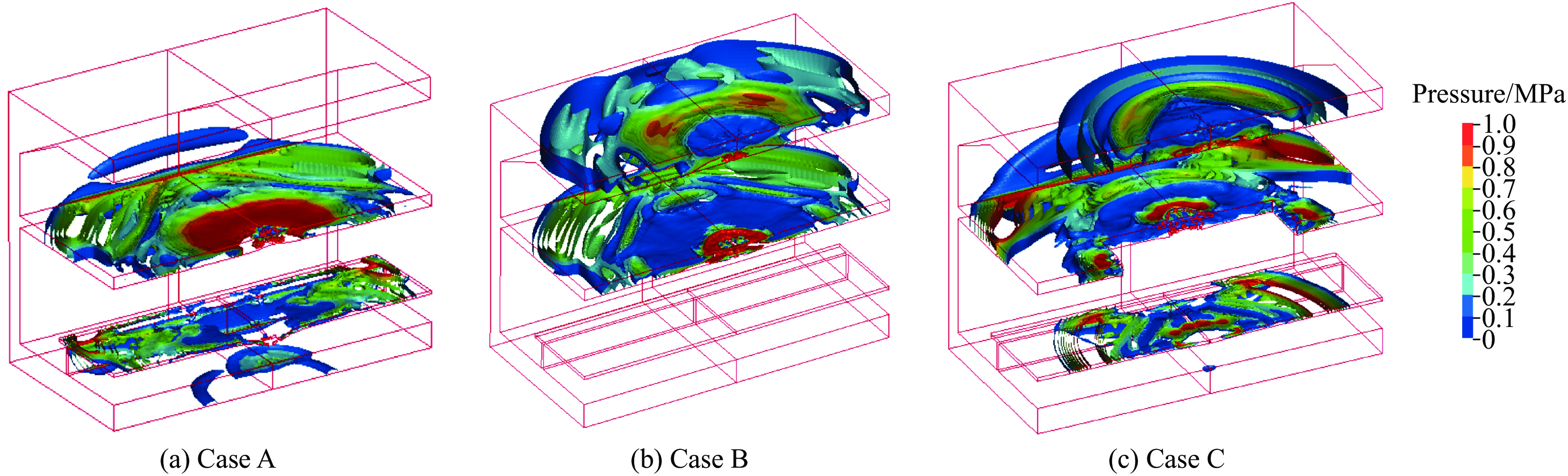
图20给出了爆炸作用下地铁结构的压力分布。在工况A、工况B和工况C中，进站层混凝土底板的压力超过10 MPa，由于普通混凝土的抗拉强度远低于10 MPa，因此，已达到混凝土拉伸开裂界限。在工况A和工况C中，由于候站平台板被炸穿，冲击波进入结构底层，压力幅值在2～3 MPa之间，而工况B未出现此现象。
表1给出了爆炸作用下地铁结构内部压力传播过程。由表1可知，冲击波在地铁结构内部传播分为3个阶段：(1) 冲击波在空气中自由传播（在楼梯口处爆炸时有明显绕射现象）；(2) 冲击波透射进入混凝土板，在固体中传播；(3) 冲击波由混凝土再次进入空气中。
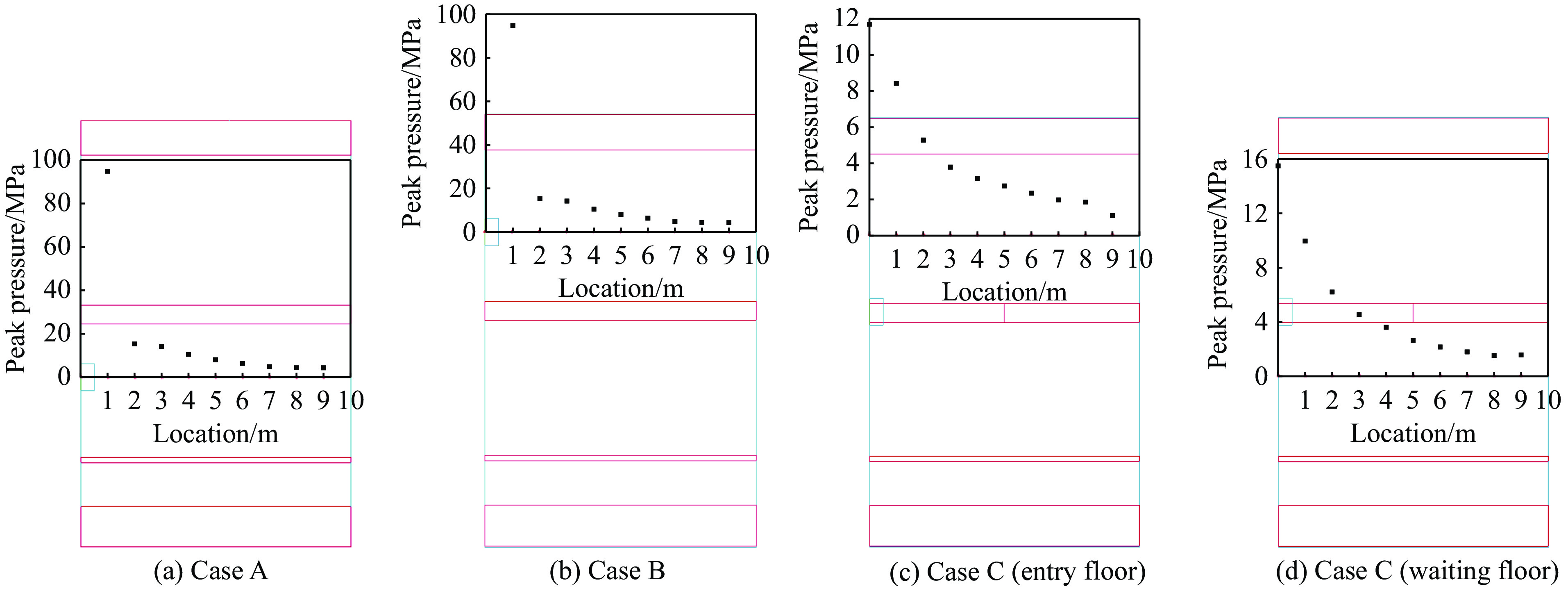
图21给出了爆炸作用下地铁结构内部测点位置与压力峰值。由图21可知，在工况A和工况B中，测点的选取与装药处于同一平面，与爆心的距离为1～9 m，相邻2个测点的间距为1 m。超压在2 m内衰减较快，由1 m处的94.8 MPa衰减至2 m处的15.3 MPa，在2～9 m内衰减较慢，由2 m处的15.3 MPa衰减至9 m处的4.3 MPa。在工况C中，测点位于进站层和候站层，测点中压力峰值呈指数型衰减。
-
以济南轨道交通7号线水屯北路站为例，基于LS-DYNA软件中的流-固耦合算法和完全重启动算法，通过侵彻爆炸试验验证了材料模型和数值建模方法的可靠性，并开展了地铁结构由外向内的钻地弹先侵彻后爆炸以及由内向外的大当量TNT装药内部爆炸作用下结构毁伤破坏效应的数值模拟研究，得到以下主要结论：
(1) 常规武器先侵彻后爆炸作用下，地铁结构顶板的毁伤破坏模式为局部破坏；
(2) 爆炸过程对地铁结构顶板上方覆土层的损伤破坏明显，弹道直径扩大4～5倍；
(3) 装药置于楼梯口处爆炸时，爆炸冲击波在传至同高度的混凝土板时，在板的上下表面发生明显的绕射现象；
(4) 地铁结构内部爆炸时，超压峰值在爆炸近区（小于等于2 m）衰减较快，在爆炸中远区（大于2 m）衰减较慢。
侵彻和爆炸作用下地铁结构毁伤破坏效应的数值模拟
Numerical Simulation on Damage and Failure of Metro Structure under Penetration and Explosion Effects
-
摘要: 以济南轨道交通7号线“水屯北路站”为例，基于LS-DYNA软件中的流-固耦合和完全重启动算法，开展了地铁结构由外及内的钻地弹先侵彻后爆炸以及由内及外的大当量TNT装药内部爆炸作用下结构毁伤破坏效应的数值模拟。首先，对已有弹体先侵彻后爆炸一次打击试验进行了数值模拟，验证了数值建模方法和材料模型参数选取的准确性。在此基础上，建立了3种由外及内的先侵彻后爆炸和3种由内及外的内爆炸三维数值模型，分析了地铁结构损伤破坏模式和对人员及附属构件的毁伤情况。数值模拟结果表明：钻地弹在地铁站上方先侵彻后爆炸作用时，地铁结构的损伤破坏模式为局部损伤；地铁结构内部爆炸时，超压峰值在爆炸近区衰减较快，在爆炸中远区衰减较慢。研究结果可为进一步探究内爆炸作用下地铁结构径向和法向冲击波传播衰减规律提供参考。Abstract: Taking Shuitun North Road Station of Jinan Rail Transit Line 7 as an example, a numerical simulation study was conducted to investigate the structural damage and failure effects of the metro structure based on the fluid-structure couple and full restart algorithm in LS-DYNA software. This study focused on two scenaries: projectile penetration followed by an explosion from outside to inside, and the inner explosion of a large equivalent TNT charge. Firstly, the accuracy of the numerical simulation and the selection of material model parameters were validated through the penetration followed by explosion test. Then, three cases of two-dimensional numerical model for penetration followed by explosion from outside to inside and three cases of three-dimensional numerical models for internal explosion were established. The damage mode of the metro structure and the damage condition for personnel and auxiliary components were analyzed. The simulation results demonstrate that the failure mode of the metro structure subjected to projectile penetration followed by explosion was localized damage. When the explosion occurs inside the metro structure, the peak of overpressure decays faster in the area close to explosion and slower in the middle and far area of the explosion. The present research results can provide a reference for further studies on the radial and normal shock wave propagation attenuation laws of the metro structure subjected to internal explosion.
-
Key words:
- penetration /
- explosion /
- metro structure /
- damage and failure .
-
-
图 1 济南水屯北路站示意图 （单位：mm）
Figure 1. Schematic diagram of Jinan Shuitun North Road Station (Unit: mm)
图 8 数值模拟预测的侵彻后靶体的损伤破坏
Figure 8. Numerical prediction for damage of the target after penetration
图 9 数值模拟预测的爆炸后靶体的损伤破坏
Figure 9. Numerical prediction for damage of the target after explosion
图 10 数值预测的爆炸后的压力时程曲线
Figure 10. Pressure-time history curves after explosion by numerical prediction
图 11 数值预测3种工况侵彻后的损伤云图
Figure 11. Damage nephograms after penetration by numerical prediction of three cases
图 12 工况1的侵彻深度、侵彻速度及弹体加速度时程曲线
Figure 12. Time-dependent curves of penetration depth, penetration velocity, and projectile acceleration in Case 1
图 13 工况2的侵彻深度、侵彻速度及弹体加速度时程曲线
Figure 13. Time-dependent curves of penetration depth, penetration velocity, and projectile acceleration in Case 2
图 14 工况3的侵彻深度、侵彻速度及弹体加速度时程曲线
Figure 14. Time-dependent curves of penetration depth, penetration velocity, and projectile acceleration in Case 3
图 15 数值预测的工况1爆炸后地铁结构损伤
Figure 15. Damage of metro structure after explosion by numerical prediction in Case 1
图 16 数值预测的工况1爆炸后地铁结构上压力分布
Figure 16. Pressure distribution on the metro structure subjected to the explosion by numerical prediction in Case 1
图 17 济南水屯北路站三维示意图
Figure 17. Three-dimensional diagram of Jinan Shuitun North Road Station
图 18 爆炸作用下地铁结构的有限元模型
Figure 18. Finite element model of metro structure subjected to blast
图 19 数值预测的爆炸作用下地铁结构的损伤分布
Figure 19. Damage distribution of metro structure under explosion by numerical prediction
图 20 数值预测的爆炸作用下地铁结构的压力分布
Figure 20. Pressure distribution of metro structure under explosion by numerical prediction
图 21 爆炸作用下地铁结构内部测点位置与压力峰值
Figure 21. Measuring points and peak pressure inside the metro structure subjected to blast
表 1 爆炸作用下地铁结构内部压力传播过程
Table 1. Pressure propagation process in metro structure under explosion
Time/ms Case A Case B Case C 0.17 
0.64 
1.22 
1.90 
2.67 
下载: 导出CSV
-
[1] 高金金, 郭盼盼, 马晶晶, 等. 恐怖袭击下地铁隧道结构爆炸响应与防护对策 [J]. 北京理工大学学报, 2023, 43(6): 549–564. GAO J J, GUO P P, MA J J, et al. Response of metro tunnel to terrorist attack blast and countermeasures [J]. Transactions of Beijing Institute of Technology, 2023, 43(6): 549–564. [2] 孔德森, 孟庆辉, 史明臣, 等. 爆炸冲击波在地铁隧道内的传播规律研究 [J]. 地下空间与工程学报, 2012, 8(1): 48–55, 64. doi: 10.3969/j.issn.1673-0836.2012.01.009 KONG D S, MENG Q H, SHI M C, et al. The dissemination rule of blasting shock-wave in subway tunnel [J]. Chinese Journal of Underground Space and Engineering, 2012, 8(1): 48–55, 64. doi: 10.3969/j.issn.1673-0836.2012.01.009 [3] 孔德森, 孟庆辉, 张伟伟, 等. 爆炸荷载作用下地铁隧道的冲击反应研究 [J]. 振动与冲击, 2012, 31(12): 68–72. doi: 10.3969/j.issn.1000-3835.2012.12.016 KONG D S, MENG Q H, ZHANG W W, et al. Shock responses of a metro tunnel subjected to explosive loads [J]. Journal of Vibration and Shock, 2012, 31(12): 68–72. doi: 10.3969/j.issn.1000-3835.2012.12.016 [4] 李忠献, 刘杨, 田力. 单侧隧道内爆炸荷载作用下双线地铁隧道的动力响应与抗爆分析 [J]. 北京工业大学学报, 2006, 32(2): 173–181. doi: 10.3969/j.issn.0254-0037.2006.02.014 LI Z X, LIU Y, TIAN L. Dynamic response and blast-resistance analysis of double track subway tunnel subjected to blast loading within one side of tunnel [J]. Journal of Beijing University of Technology, 2006, 32(2): 173–181. doi: 10.3969/j.issn.0254-0037.2006.02.014 [5] 王德荣, 冯淑芳, 李杰, 等. 地下隧道在内爆炸荷载作用下的动力响应分析 [J]. 解放军理工大学学报(自然科学版), 2013, 14(5): 511–516. WANG D R, FENG S F, LI J, et al. Dynamic response of underground tunnel to internal explosion loading [J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2013, 14(5): 511–516. [6] ZHAO D B, HUANG Y T, CHEN X S, et al. Numerical investigations on dynamic responses of subway segmental tunnel lining structures under internal blasts [J]. Tunnelling and Underground Space Technology, 2023, 135: 105058. doi: 10.1016/j.tust.2023.105058 [7] 赵敏, 周子豪. 爆炸荷载下地铁盾构隧道动力响应研究 [J]. 科学技术与工程, 2019, 19(34): 302–307. doi: 10.3969/j.issn.1671-1815.2019.34.044 ZHAO M, ZHOU Z H. Study on dynamic response of shield tunnel under explosion load [J]. Science Technology and Engineering, 2019, 19(34): 302–307. doi: 10.3969/j.issn.1671-1815.2019.34.044 [8] 赵敏, 周子豪. 爆炸荷载下地铁隧道损伤规律研究 [J]. 中国安全生产科学技术, 2019, 15(8): 118–123. doi: 10.11731/j.issn.1673-193x.2019.08.019 ZHAO M, ZHOU Z H. Study on damage laws of subway tunnel under explosive load [J]. Journal of Safety Science and Technology, 2019, 15(8): 118–123. doi: 10.11731/j.issn.1673-193x.2019.08.019 [9] 章毅, 周布奎, 于潇, 等. 地面炸药库爆炸对地铁隧道的影响 [J]. 防护工程, 2019, 41(3): 33–37. ZHANG Y, ZHOU B K, YU X, et al. Effect of accidental explosion of ground explosive depot on metro tunnel [J]. Protective Engineering, 2019, 41(3): 33–37. [10] 马建军, 李诚豪, 关俊威, 等. 地铁隧道上方近距离爆炸动力响应研究 [J]. 铁道科学与工程学报, 2023, 20(6): 2246–2255. MA J J, LI C H, GUAN J W, et al. Research on the dynamic response of close-range explosion above a subway tunnel [J]. Journal of Railway Science and Engineering, 2023, 20(6): 2246–2255. [11] ZHOU Q, HE H G, LIU S F, et al. Blast resistance evaluation of urban utility tunnel reinforced with BFRP bars [J]. Defence Technology, 2021, 17(2): 512–530. doi: 10.1016/j.dt.2020.03.015 [12] ZHANG Z, ZHOU C B, REMENNIKOV A, et al. Dynamic response and safety control of civil air defense tunnel under excavation blasting of subway tunnel [J]. Tunnelling and Underground Space Technology, 2021, 112: 103879. doi: 10.1016/j.tust.2021.103879 [13] JIANG N, ZHU B, ZHOU C B, et al. Safety criterion of gas pipeline buried in corrosive saturated soft soil subjected to blasting vibration in a coastal metro line [J]. Thin-Walled Structures, 2022, 180: 109860. doi: 10.1016/j.tws.2022.109860 [14] ZHANG Y Q, JIANG N, ZHOU C B, et al. Mechanical behaviors and failure mechanism of HDPE corrugated pipeline subjected to blasting seismic wave [J]. Alexandria Engineering Journal, 2023, 67: 597–607. doi: 10.1016/j.aej.2022.12.052 [15] 王银, 孔祥振, 方秦, 等. 弹体对混凝土材料先侵彻后爆炸损伤破坏效应的数值模拟研究 [J]. 爆炸与冲击, 2022, 42(1): 013301. doi: 10.11883/bzycj-2021-0132 WANG Y, KONG X Z, FANG Q, et al. Numerical investigation on damage and failure of concrete targets subjected to projectile penetration followed by explosion [J]. Explosion and Shock Waves, 2022, 42(1): 013301. doi: 10.11883/bzycj-2021-0132 [16] 辛春亮, 薛再清, 涂建, 等. 有限元分析常用材料参数手册 [M]. 北京: 机械工业出版社, 2020. XIN C L, XUE Z Q, TU J, et al. Handbook of common material parameters for finite element analysis [M]. Beijing: China Machine Press, 2020. [17] 何兆益, 汪凡, 朱磊, 等. 基于Johnson-Cook黏塑性模型的沥青路面车辙计算 [J]. 重庆交通大学学报(自然科学版), 2010, 29(1): 49–53. HE Z Y, WANG F, ZHU L, et al. Rutting calculation of asphalt pavement based on the Johnson-Cook viscoplastic model [J]. Journal of Chongqing Jiaotong University (Natural Science), 2010, 29(1): 49–53. [18] 宗香华, 王银, 孔祥振, 等. 错位多次打击下UHPC靶体损伤破坏效应的数值模拟研究 [J]. 高压物理学报, 2024, 38(3): 034201. doi: 10.11858/gywlxb.20230834 ZONG X H, WANG Y, KONG X Z, et al. Numerical investigation on damage and failure of UHPC targets subjected to dislocation multi-attacks [J]. Chinese Journal of High Pressure Physics, 2024, 38(3): 034201. doi: 10.11858/gywlxb.20230834 [19] KONG X Z, FANG Q, CHEN L, et al. A new material model for concrete subjected to intense dynamic loadings [J]. International Journal of Impact Engineering, 2018, 120: 60–78. doi: 10.1016/j.ijimpeng.2018.05.006 [20] 赵凯. 分层防护层对爆炸波的衰减和弥散作用研究 [D]. 合肥: 中国科学技术大学, 2007. ZHAO K. The attenuation and dispersion effects on explosive wave of layered protective engineering [D]. Hefei: University of Science and Technology of China, 2007. [21] YANG Y Z, FANG Q, KONG X Z. Failure mode and stress wave propagation in concrete target subjected to a projectile penetration followed by charge explosion: experimental and numerical investigation [J]. International Journal of Impact Engineering, 2023, 177: 104595. doi: 10.1016/j.ijimpeng.2023.104595 [22] 总参谋部工程兵国防工程设计研究所. 防护工程防常规武器结构设计规范: GJB 7404–2023 [S]. 北京: 中国人民解放军总参谋部, 2013. The National Defense Engineering Design Institute of the Headquarters of the General Staff. Design specification for protective engineering anti-conventional weapon structure: GJB 7404–2023 [S]. Beijing: The General Staff Headquarters of the PLA, 2013. -
计量
- 文章访问数: 185
- HTML全文浏览数: 185
- PDF下载数: 0
- 施引文献: 0