本研究的重点是监测现场冲击荷载下岩体产生的振动信号以及对信号进行时频分析，从而获得频谱特征。为此，采用自制光纤振动设备对现场开展监测实验，监测机械冲击钻对岩体施加冲击荷载前后现场不同活动的振动信号。

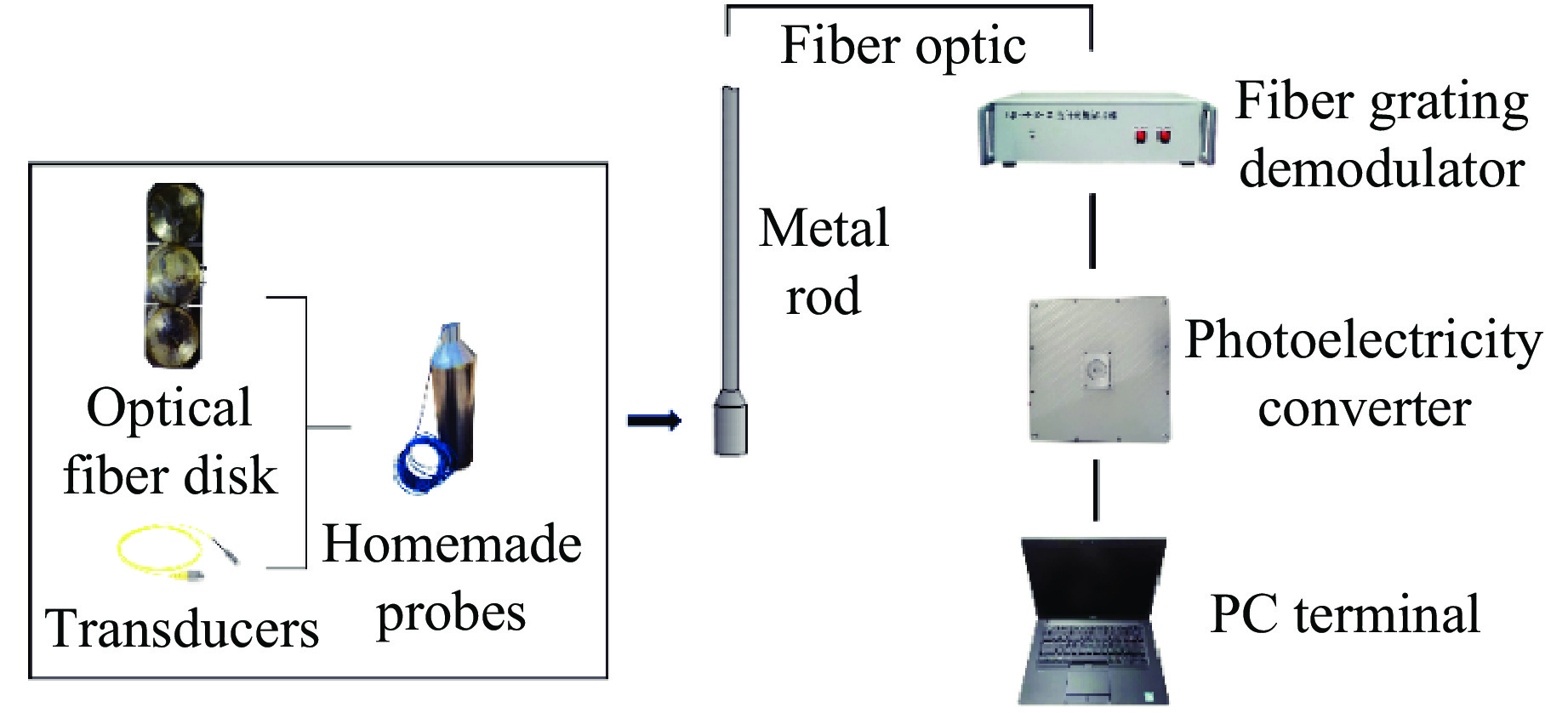
采用自制监测探头及一套光纤振动监测设备开展实验。该监测设备包括一套振动信号采集仪和一套光电转换仪，采样率为8 192 Hz。振动信号采集依据的主要原理为迈克尔逊干涉，即激光器发射激光后进行分光，2条光路经过光纤与监测探头相连；分光到达物体表面后产生干涉和衍射，当物体表面发生形变或机械振动时，干涉条纹也会发生变化。这种光信号的变化通过光电转换仪转变为电压信号的变化，将电压信号收集并存储于电脑上，通过电脑端软件完成对电信号的分析及解算，从而形成振动监测数据。监测末端的探头主要由法拉第旋转镜构成，使用这种结构件的目的是将分光路线更好地反射回来，从而得到最佳干涉效果。探头内部的结构和设备连接方法如图1所示。

为了监测所需信号，在云南某采石场开展实验，该采石场生产的石材以建材常用的灰岩为主，现场实验方案和钻孔布置如图2所示。在采石场边坡平台区域设置4个非等距钻孔，由左至右4个钻孔的深度分别为2、3、6和6 m，后续钻孔与第1个钻孔的距离分别为5、10、30 m，钻孔的孔径为120 mm。这样的测点布置意在探明设备监测信号的有效监测范围以及在哪个钻孔中可以获得更清晰有效的数据。将探头放入4个钻孔中，然后对现场完整地表岩体施加冲击力，在距离破碎位置最近的钻孔中获得了较清晰的信号，随后监测该钻孔一段时间内的所有信号，记录后准备进一步处理。现场实验情况如图3所示。

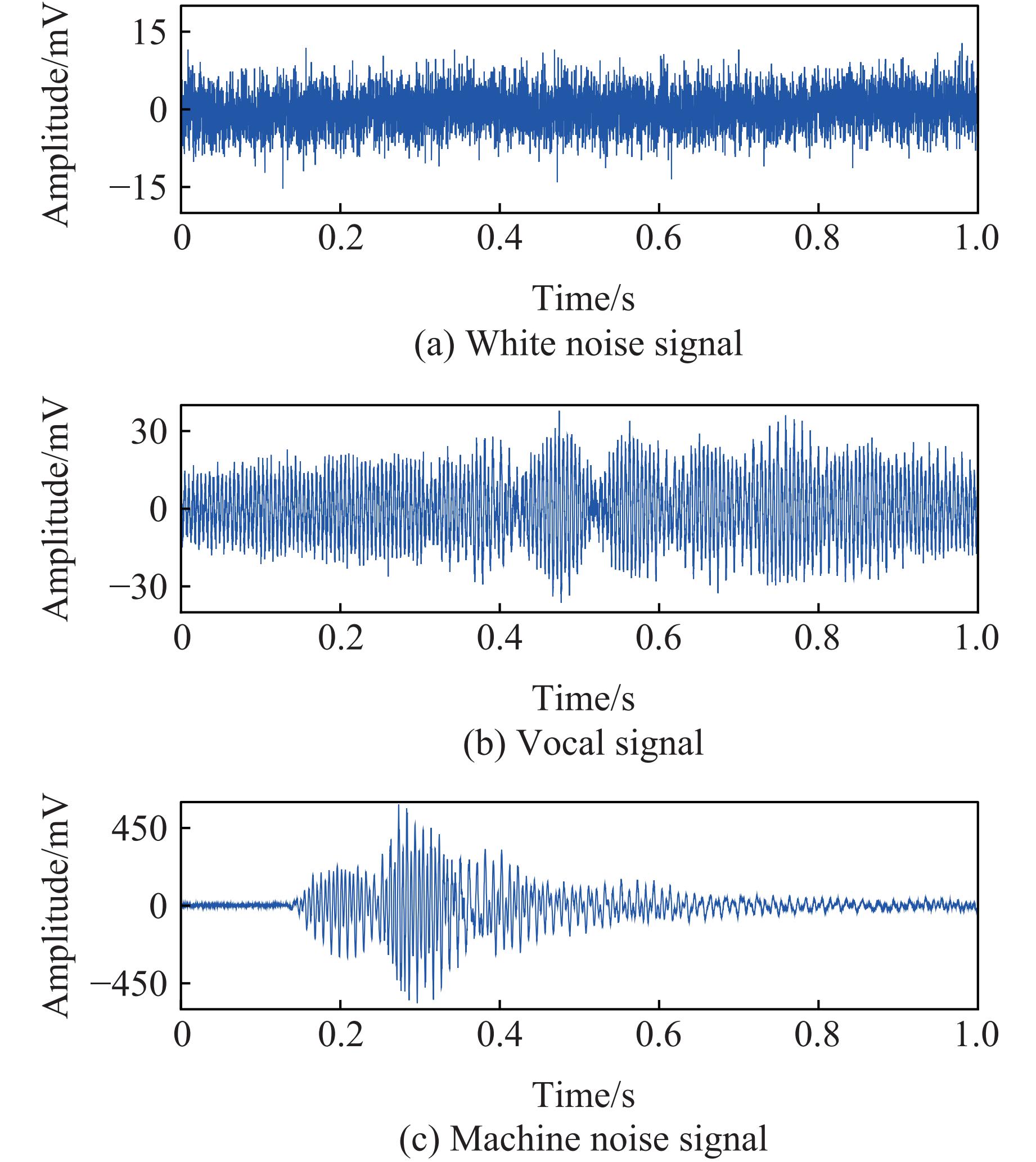
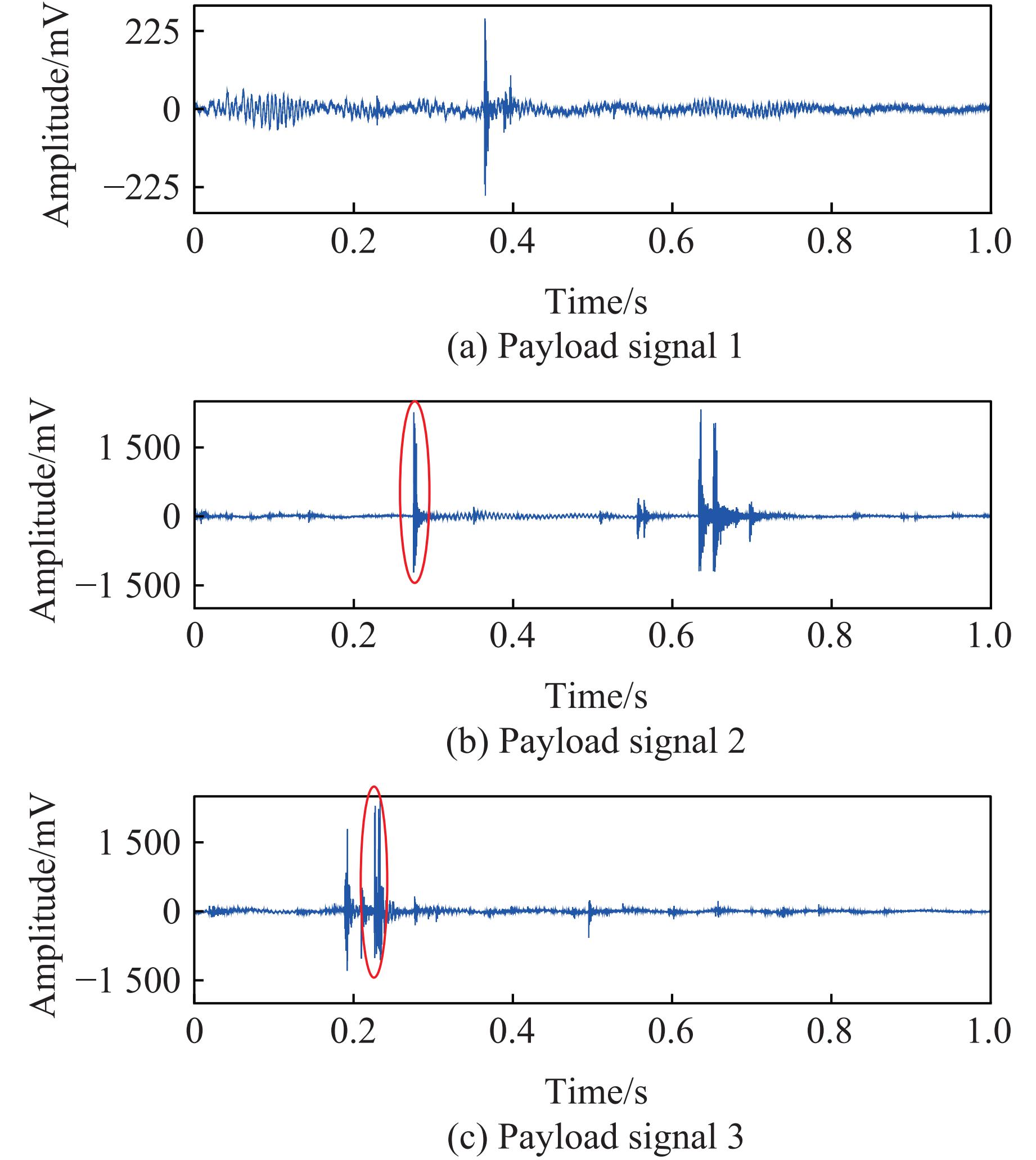
监测开始时，首先需要对外部环境的干扰信号进行监测记录，一段时间后，在图2所示位置开始施加冲击荷载，并对振动信号进行现场记录，获得一组清晰有效的原始监测时域信号数据，得到的噪声信号和施加荷载后的监测信号分别如图4和图5所示。

从图4和图5可以看出，现场噪声信号和干扰信号与冲击荷载产生的信号在形态上完全不同。白噪信号中，最大电压幅值仅为15 mV（图4(a)）；人声信号的最大电压幅值可达30 mV（图4(b)），并且其形态呈现声音信号的规律性特征；机器开动的噪音信号（图4(c)）在启动时幅值达到450 mV，然后逐渐衰减。同时2种噪声信号相比冲击施加信号更加稀疏，而图5中的冲击荷载信号则存续时间较短且振幅大幅增加（高达1 000 mV），施加荷载后的最大振幅达到了噪声信号的50倍，并且存续时间远短于0.1 s，之后出现几个幅值明显衰减但存续时间仍然较短的信号（如图5(b)中红圈所示），表明从时域信号已经可以初步观察到几种信号之间的差异。

为了进一步观察不同信号的频域特征，需要对信号进行时频变换。目前，针对时域信号的分解主要采用傅里叶变换方法。该方法是通过将信号函数分解为不同频率的基本三角函数信号的线性组合，得到时域信号的频域分布^[13–14]。本研究拟采用快速傅里叶变换（fast Fourier transform，FFT）改进方法，同时采用鲁棒性局部均值分解（robust local mean decomposition, RLMD）方法将信号分解为不同频域范围的模态信号，以方便对某一频域范围内的特征信号进行提取。该方法在局部区间内进行多项式拟合，提取局部特征并最终分解为多个局部模态函数，是局部均值分解（local mean decomposition，LMD）方法的改进版本。RLMD分解方法的具体实现过程^[15–17]如下。

(1) 获取原始信号$x(t) $中所有局部振幅极值点，用$t_n $表示其中的所有极值点，$x(t_n) $表示对应的信号振幅极值。

(2) 计算2个相邻振幅极值的局部平均值$\hat m _k $和局部振幅$\hat \alpha_k $，表示为

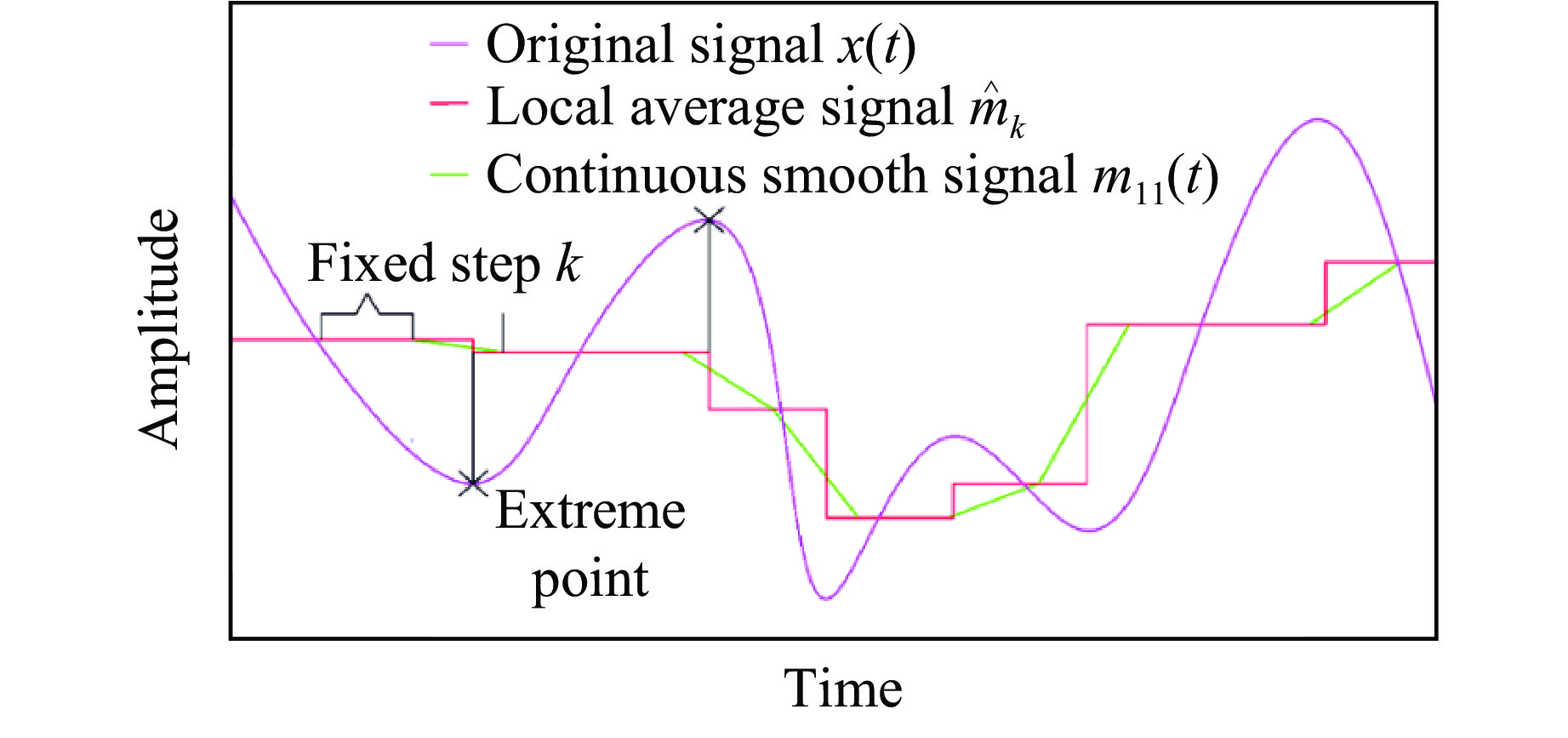
然后用该直线的局部平均值$\hat m _k $代替2个极值点之间的变化信号，连接这些信号并采用统计学中的移动平均法将固定步长k内的局部平均值平滑处理为曲线，获得最初的局部均值函数$m_{11}(t) $，对局部振幅$ {a}_{k} $采用同种方法生成最初包络函数$a_{11}(t) $，过程如图6所示。

(3) 用原始信号$x(t) $减去初始局部均值函数$m_{11}(t) $，得到均零信号$h_{11}(t) $

(4) 用$h_{11}(t) $除以$a_{11}(t) $，得到调频信号$s_{11}(t) $

判断$s_{11}(t) $是否为纯调频信号，即$a_{11}(t) $是否等于1，否则继续循环重复步骤(1)～步骤(4) $ n $次，直到$ n $步之后，包络函数$a_{1n}(t) = 1 $，即

此时总纯调频信号$s_1(t) = s_{1n}(t) $，总包络信号$a_1(t) $为步骤(1)～步骤(4)所有包络信号$a_{1n}(t) $的累乘。

(5) 当式(4)成立时，提取纯调频信号$s_1(t) $和总的包络信号$a_1(t) $，构成模态函数$F_1(t) $

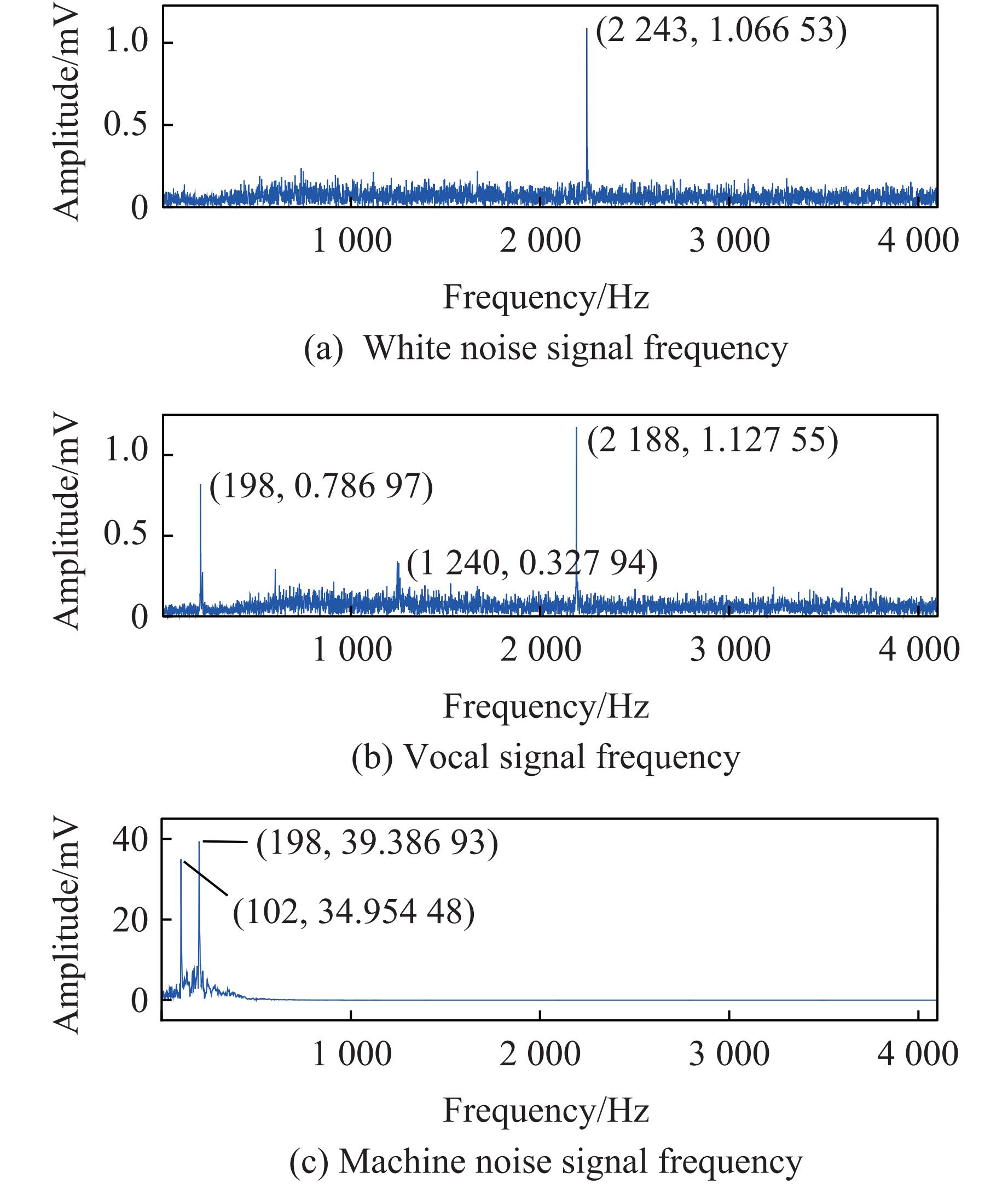
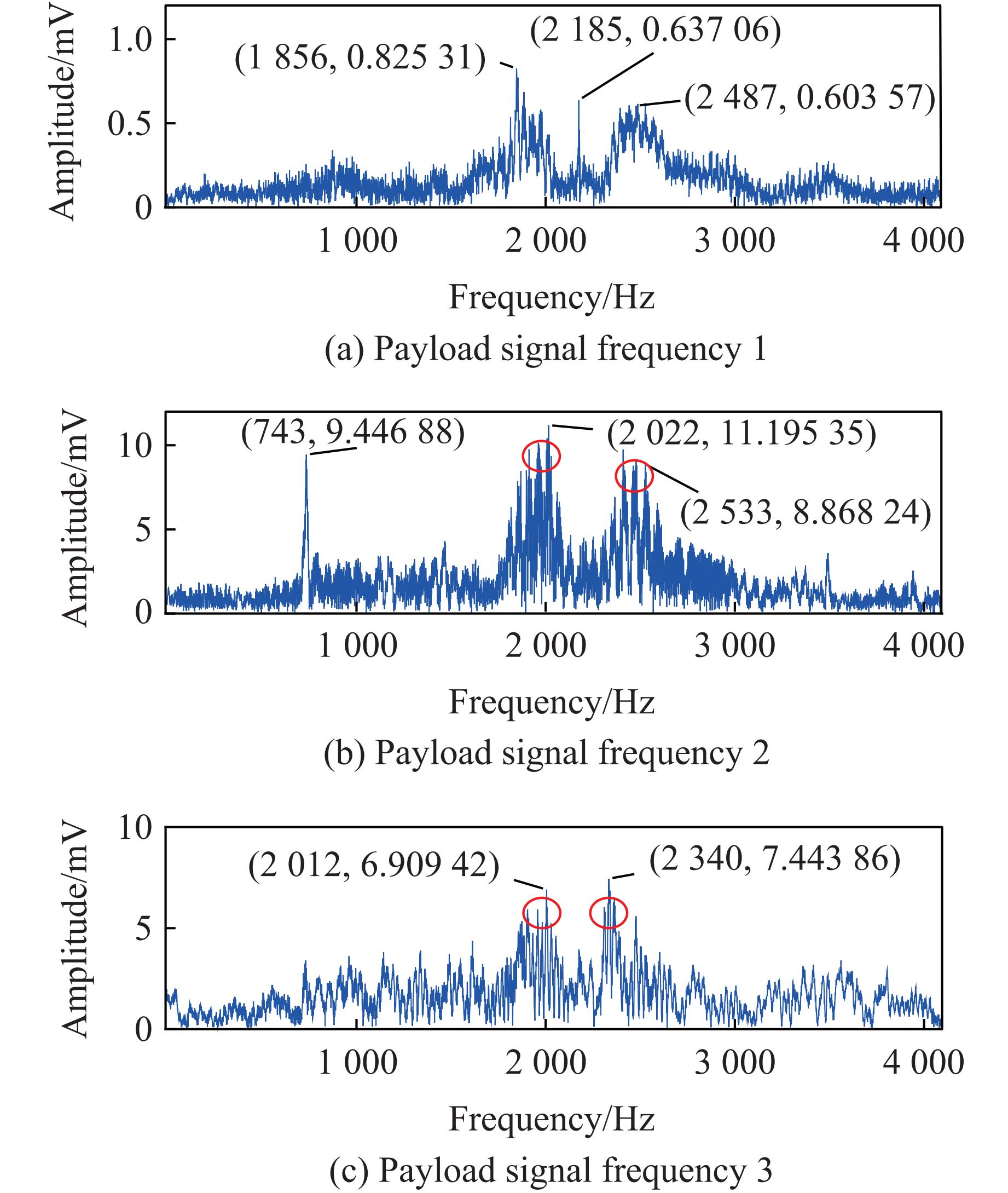
(6) 用原始信号$x(t) $减去$F_1(t) $，得到剩余分量$c_1(t) = x(t) - F_1(t) $。然后，循环上述步骤，直到剩余分量$c_p $为一个常数。信号$x(t) $可分解为k个模态信号函数的总和以及一个单调函数$c_p(t) $，即

同时，为了解决LMD方法的端点效应和模态混叠问题， 采用RLMD方法对其进行优化，具体包括：在边界条件中添加信号左右对称点判定以消除分解方法的端点效应的影响，根据统计理论最优固定移动距离减少包络估计的误差，为了使获得的信号带分量具有实际物理意义而改进筛选停止准则。本研究采用MATLAB代码对原始信号进行分解，并在分解后提取主频率（即分解后振幅最大）所在的模态函数信号进行频域变换，得到的噪声信号主信号带和施加荷载后监测到的信号带分别如图7、图8所示，所有信号频率与图4、图5的时域信号相对应。

从图7和图8可以直观地看出，背景白噪音分解后，仅在2 243 Hz出现最大振幅，此时现场无其他的明显行为，推测为设备本身连接后的电磁噪声信号；人声信号则出现了198和1 240 Hz 2个特征信号；对机械开动的噪声信号进行分解后，发现在102和198 Hz出现2个主要信号，呈几何倍数关系，推测为机械工作产生的谐波。而冲击信号分解后分别在1 800～2 000 Hz以及2 000～2 500 Hz出现多个极大振幅信号，其中一组还出现了743 Hz的峰值频率，并且所有的冲击振动信号都产生了“双峰”现象，该现象的产生一般是由于信号分解中出现了2个主频信号，可能是探测到了2种不同类型的波（P波和S波），也可能是由于被监测岩体本身并非均匀介质，导致信号在其中发生了干涉和衍射，从而使监测的干涉波或衍射波的频率发生了变化。提取几组冲击信号的特征频率并进行对比，发现几类信号频率带也有明显的区别，进一步表明现场监测噪声信号与冲击信号存在明显的不同。

为了进一步验证实验所得的信号监测结果，推断现场监测到的信号是否确实为应力波信号，参考文献[18–19]中的数值模拟方法，模拟现场岩体在受到外力荷载冲击作用下，岩体表面单位岩石的水平方向应力快速变化而产生的应力波，探究模拟应力波的频率与现场监测信号频率的相似性。采用LS-DYNA进行应力分析，在解决动力冲击问题方面，LS-DYNA模块中的显式算法比采用隐性算法求解具有更好的功能性。

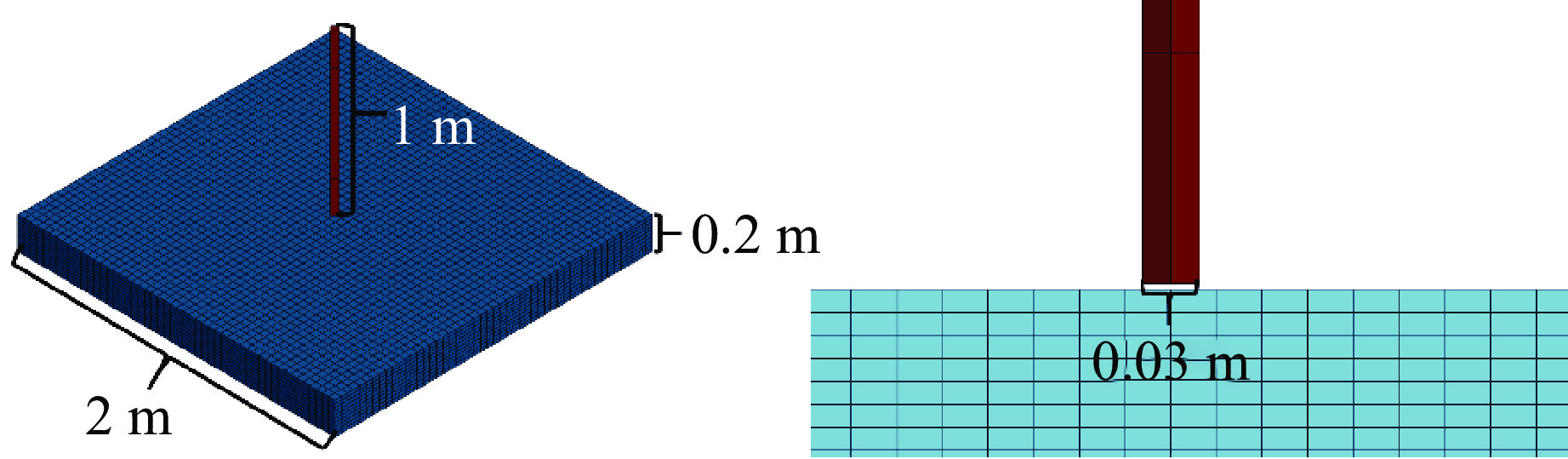
通过施加速度的弹体冲击岩体板模拟现场的实际工况，岩体板的底部和四周设定约束；为了简化计算，假设该模型中岩体板完整均匀，内部不存在节理裂隙面，因此，力和位移等在内部均匀传递，而岩体模型的整体尺寸远大于冲击弹体，可以忽略弹体模型的尺寸效应，据此建立网格模型，如图9所示。设定模型尺寸：冲击杆为边长0.03 m、长1 m的立方柱体，岩层为边长2 m、厚0.2 m的立方柱体。

采用LS-DYNA模拟时，选择基本单位为kg、m、s，其他均为上述基本单位的导出单位；本研究中的岩体选择RHT模型，该模型在解决岩石爆破工程和混凝土靶板侵蚀等问题时均表现出较好的效果，可以很好地反映材料在受冲击等动力作用下的振动特性。

在RHT模型中，采用Mie-Grüneisen状态方程，该方程可以准确地描述材料在高温、高压、高应变率条件下的动态行为。根据文献[20–21]的研究，材料在受到冲击过程中的孔隙度满足

式中：$\alpha $为材料的孔隙度；$\alpha_0 $为材料的初始孔隙度；p(s)为计算过程中任一时刻的压力；$ {p}_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}} $为压实压力；$ {p}_{\mathrm{e}\mathrm{l}} $为初始孔隙挤压压力；N为材料孔隙度指数，用以描述材料孔隙度随压力变化的速率。

物质密度和能量随压力状态变化的方程为

式中：e为内能；ρ为孔隙密度；A₁、A₂、A₃为Hugoniot能量方程的系数；B₀、B₁、T₁、T₂为能量方程的参数；η表示材料受冲击后表现为压缩状态还是膨胀状态，当η>0时，为压缩状态。

模型的弹塑性屈服面模型方程表示为

式中：s为偏应力张量，$\dot{\varepsilon}_{\rm{p}} $为塑性应变率，$\varepsilon_{\rm{p}}^* $为有效塑性应变，$ {R}_{3} $为剪切和拉伸子午线折减函数，$ F_r $为应变率依赖函数，$ {p}^{*} $为归一化压力，f_c为抗压强度，$\sigma_{\rm{y}}^* $为静态屈服面子午线等效应力函数。

通过式(7)～式(10)可以计算本次模拟岩体表面单位岩石在发生振动冲击后一段时间内应力和应变的变化。对RHT模型所涉及的参数进行标定，文献[22]的研究指出：材料密度ρ₀、初始孔隙度$ {\alpha }_{0} $、剪切模量G、单轴压缩模量等可以通过简单的岩石力学实验进行测定，其余部分参数则需要采用分离式霍普金森压杆实验进行参数标定。然而，有些参数只能提供一种近似的经验估计值，且实验测定现场岩石的岩性与参考值基本相同。因此，在允许一定误差存在的情况下，岩石的弹性模量和密度采用采石场的工程报告值，其余采用文献[22]中的参考值，整体参数如表1所示。表1中：A、n为失效面参数，B、Q₀ 为Lode角系数，n_f、A_f为残余强度面参数，$ {g}_{\rm c}^{{*}} $为压缩屈服面参数，$ {g}_{\mathrm{t}}^{*} $为拉伸屈服面参数，$ {{\beta }}_{\rm{c}} $、$ {{\beta}}_{\rm{t}} $分别为压缩应变率和拉伸应变率依赖指数，γ为Grüneisen系数，$ D_1$和${{{D}}}_{2} $为损伤参数，$ {f}_{\rm{t}}^{{*}} $、$ f_{\rm{s}}^{{*}} $为相对抗拉强度和相对剪切强度，$ {\dot{\varepsilon }}^{\mathrm{t}} $、$ {\dot{\varepsilon }}^{\mathrm{c}} $分别为拉伸断裂和压缩断裂时的应变率，$ {\dot{\varepsilon }}_{0}^{\mathrm{c}} $、$ {\dot{\varepsilon }}_{0}^{\mathrm{t}} $分别为参考压缩应变率和参考拉伸应变率，$ {\varepsilon }_{\mathrm{p}}^{\mathrm{m}} $为最小损伤残余应变，$ \xi $为剪切模量折减系数。冲击钻杆的材料模型设定为标准弹性材料结构钢，由于不对其进行分析，依照结构钢参数的取值，其密度为7 850 kg/m³，杨氏模量为200 GPa，泊松比为0.25。

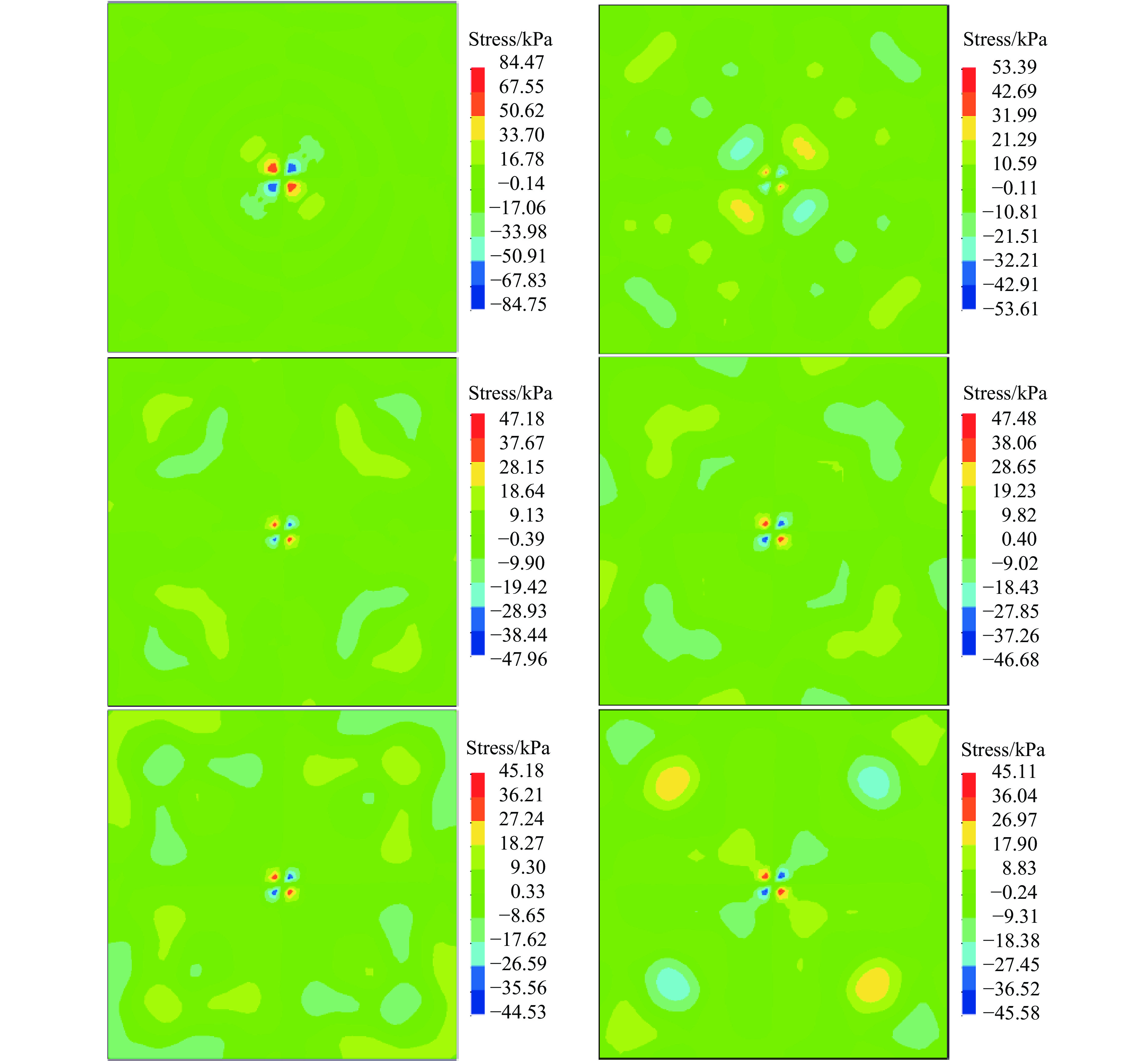
设定冲击钻杆的速度为1 m/s，通过数值模拟计算结构在受到冲击后1 s内表面应力的变化，得到z方向和xy平面的应力云图如图10所示。从图10可以看出：xy平面的应力云图表现出了明显的应力波传递波纹。

观察表面应力云图可以发现：在0.004 s冲击瞬间，xy平面开始产生应力，并从冲击点逐渐以波状向外扩散；之后，该应力波返回，在表面形成干涉波和衍射波，并逐渐形成几个应力波峰与波谷的叠加区，这2个区域关于表面呈对称分布。在对表面应力波建立观测坐标系的过程中，根据观测坐标系为波所作用的质点自身，还是对空间中所有质点进行观测，将观测坐标系分为Lagrange坐标和Euler坐标，本研究采用Lagrange坐标方法，即选择表面网格中的应力波幅值变化明显的一固定点，导出其应力变化数据，并对应力波信号进行频谱分析。

数值模拟得到的应力波曲线及频谱分析结果如图11所示。观察发现，表面应力波数据信号和监测得到的冲击信号在形态上十分相似，即冲击瞬间有一个高振幅短时信号，随后迅速衰减，然后出现数个干涉波或衍射波信号。对1 s内的信号进行频域分析，发现在2 203 Hz左右出现特征振动信号频率，与现场监测实验得到的信号频率段1 800～2 000 Hz、2 000～2 500 Hz基本符合。同时，由于LS-DYNA模型的计算方程参数选取了经验值，因此，采用该方程对现场信号进行模拟时存在一定的误差，造成两者的频率并不完全相等。分析xy面的应力波频率模拟结果，发现模拟结果中并不仅存在单一峰值，存在2 203和2 651 Hz 2个峰值，如图11(b)所示。这是由于数值模拟的平面波在模型边界发生了干涉等现象，因此，推断前述监测结果中的双峰频率也是各种波在表面产生的干涉所致。总体来说，两者频率基本相同，且产生了紧随其后的“二次波”，验证了本研究监测到的表面应力波的变化，同时表明，施加冲击荷载后，确实在表面产生了中高频应力波。

为了更直观地描述不同信号之间的差异，将所有信号的均方根（root mean square，RMS）频率、1 800～2 500 Hz信号能量占总信号能量之比以及所有信号的脉冲因子等信号特征列于表2。其中，RMS频率表示一段信号的平均主频带位置，1 800～2 500 Hz信号能量占总信号能量之比表示冲击频域附近信号能量与信号总能量的比值，脉冲因子则表征该信号是否为冲击信号。

从表2可以看出：模拟信号和冲击信号1、2以及噪声信号的平均主频带在2 000 Hz以上；而人声信号和机械信号的主频带较低，这是因为人声信号和机械信号的主要频率为2 000 Hz以下的低频，由此导致主频带降低。冲击信号附近频带能量占比均达到25%以上，与其他信号的16.87%、12.97%以及3.63%差异较大。所有冲击信号的脉冲因子均达到50以上。可以看出，不同信号在信号特征方面存在较大的差异。

为了进一步探究冲击信号频率变化的影响因素，结合应力波理论展开分析，空间中的应力波波速可以表示为

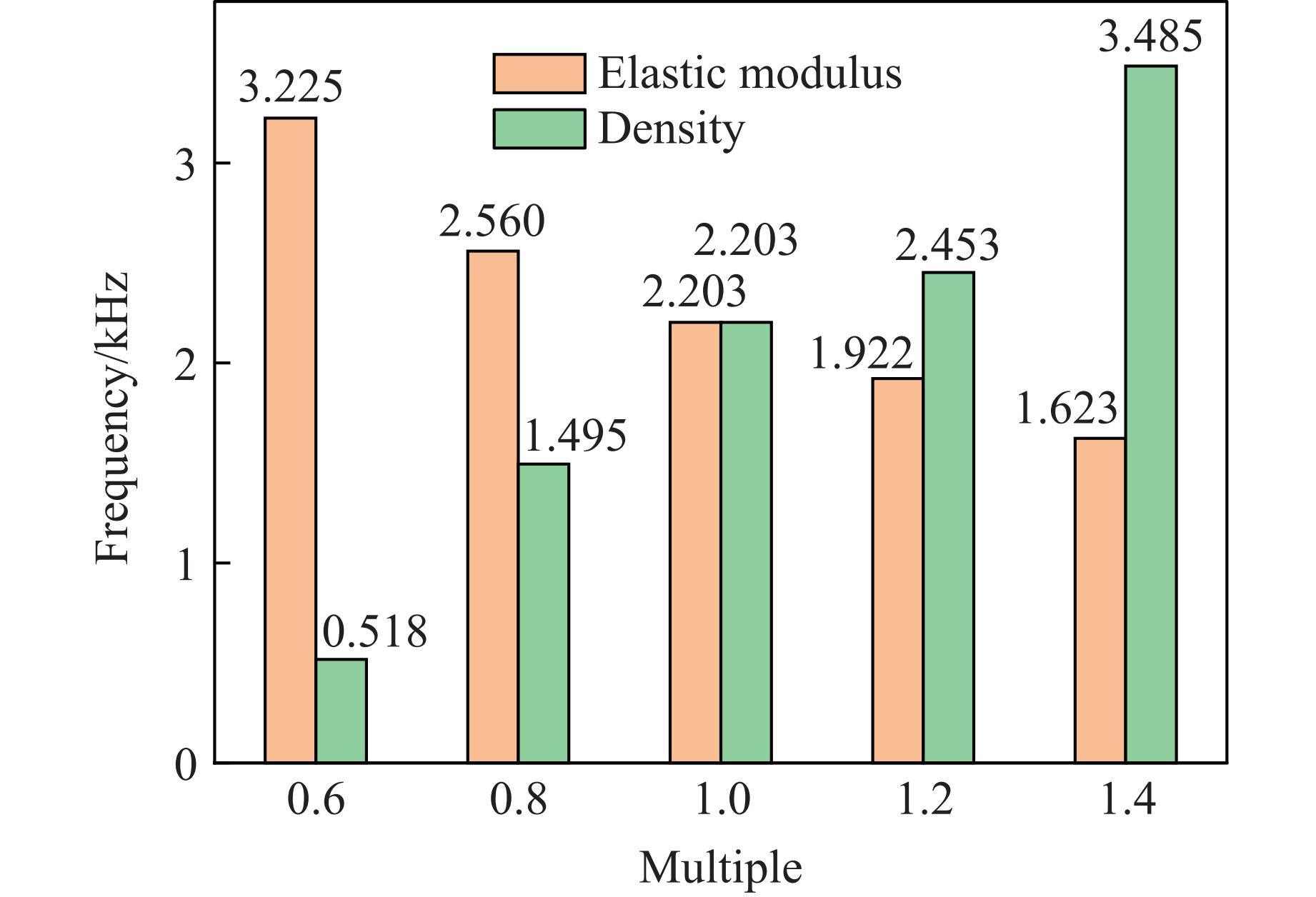
可以看出，应力波的波速只与弹性模量E、材料密度$ \rho_0 $和泊松比$\nu $三者相关。根据波长与波速的关系（$ c=\lambda f $，其中$ \lambda $为波长，$ f $为应力波频率）可以推断，波长一定时，随着弹性模量增加，应力波频率增加，而密度增大时，频率减小。为了验证上述推断，将模拟数据中冲击钻杆的弹性模量和密度分别取原数据的0.6、0.8、1.2和1.4倍，而其余物理量保持不变，计算得到物理参数成倍数改变后的模拟应力波频率分布，如图12所示。这与上述推测呈相反趋势，即频率随着弹性模量的增大而减小，随密度的增大而增大。由此猜测，当这2个量发生改变时，波长的改变速率高于波速的改变速率，导致频率变化呈相反的趋势。导致该趋势产生的内因以及该猜测的理论分析还需要进一步开展研究。

通过建立现场监测方案，探测了岩体在短时间内受冲击荷载作用下的振动信号，并通过数值模拟验证了实验监测分析结果，得到以下主要结论。

(1) 通过冲击实验监测到了确定的冲击信号，冲击信号与噪声信号在时域形态上存在明显的区别。

(2) 通过特征模态信号提取和信号频谱分析，发现冲击信号的频率明显区别于噪声信号，并且冲击信号表现为较高的频带分布，而噪声信号的主要频率相对较低；冲击信号存在双峰现象，推测是波的干涉和衍射等行为产生的二次波所致，而噪声信号则表现为单一峰值。

(3) 通过模拟应力波的产生分析其频率特性，并与监测得到的信号频率进行对比，发现其频率也处在1 800～2 500 Hz范围内。将所有信号主频带、频带能量以及脉冲因子进行对比，也可以进一步区分不同信号。参照一维平面应力波理论分析峰值频率变化的原因，通过等比例改变弹性模量和密度的值，计算冲击荷载应力波与两者之间的关系，发现主频带频率的增大与材料弹性模量和密度均成反比，与应力弹性波波速的推导呈相反的趋势，为此，后续还需要开展更深入的研究。