-
近年来,纤维复合材料因具有高比强度和高比模量等优点被广泛应用在舰船防护领域,其在高速冲击下的动态响应和性能成为当前的研究热点之一。舰船在作战过程中可能遭到弹片或弹体侵彻,纤维复合材料的应用大大提升了舰船结构的防护效能。因此,研究复合材料在弹道侵彻作用下的结构响应和损伤具有重要意义。
目前,针对纤维增强复合材料层合板的抗弹性能,国内外学者已开展较多研究,但大多从宏观角度直接开展,且其参数需要基于大量的材料性能试验。罗锡林等[1]开展了碳纤维编织层合板弹道侵彻研究,从宏观层面给出了失效模式。Du等[2]通过弹道试验研究了超高速冲击下碳纤维层合板的结构响应,从应力波角度分析了高速冲击时层合板背部损伤区域的形成机制。Peng等[3]建立了宏观侵彻有限元模型,模拟研究了弹丸形状和尺寸对碳纤维复合材料层合板的侵彻影响,从宏观角度分析了最大峰值冲击力随弹丸尺寸的变化。Alonso等[4]基于渐进式失效准则,研究了不同厚度玻璃纤维层合板在弹道侵彻作用下的耗能机理。近年来,部分学者从介观尺度研究了纤维复合材料的抗侵彻能力。Meyer等[5]利用宏观结合介观模型,对单层平纹玻璃纤维层合板开展了弹道侵彻数值模拟,取得了较好的模拟效果。牟浩蕾等[6]利用介观模型获取了宏观模型的材料参数,据此研究了芳纶纤维层合板的弹道冲击响应,有效提升了数值模拟精度。
目前,多尺度方法在纤维复合材料中的应用大多集中在纤维增强复合材料静力学性能参数或低速冲击下的损伤预测[7]。王新峰[8]利用多尺度分析方法,研究了纤维束、平纹机织复合材料、三维机织复合材料的应力-应变关系,预测了纤维束和复合材料的静态强度和刚度参数。Madke等[9]采用多尺度分析方法,研究了不同失效准则在预测纤维增强复合材料静力学性能上的适用性。Zhu等[10]通过微观和介观模拟,结合泰勒杆冲击试验,研究了三维编织复合材料的动态力学性能,给出了应力-应变曲线。张洁皓[11]、王涛等[12]针对平纹编织玻璃纤维层合板,通过建立微观、介观和宏观模型,利用不同的失效损伤公式,研究了低速冲击下的损伤行为。赵巧莉等[13]对碳纤维层合板在低速冲击下的压缩性能进行了试验和多尺度数值模拟,研究了不同冲击能量下碳纤维层合板的损伤情况,得到了较为准确的损伤结果。Smojver等[14]建立了多尺度数值模型,对双轴向玻璃纤维层合板的低速冲击进行了研究,得到了与试验结果较为一致的结果。
采用多尺度模拟,可以低成本、短周期地分析纤维组分、分布及体积分数等对纤维增强复合材料层合板宏观力学性能的影响,但是目前大多用来研究纤维复合材料层合板的静态力学性能或低速冲击下的损伤,在弹道侵彻方面的应用较少;在纤维复合材料弹道侵彻数值模拟方面,目前的研究大多从宏观角度出发,未能很好地考虑介观编织结构和应变率效应的影响。因此,本研究利用多尺度模拟的优势,从微观-介观角度出发,考虑纤维编织结构,在无需开展宏观力学性能试验的基础上,直接获得宏观等效参数;同时,通过改进纤维复合材料失效准则,提出考虑纤维材料渐进损伤和应变率效应的纤维增强复合材料层合板弹道侵彻数值模拟方法,给出纤维复合材料弹道侵彻的微观-介观-宏观全流程数值模拟过程,打通多尺度模拟在纤维复合材料弹道侵彻方面应用的“最后一公里”。
-
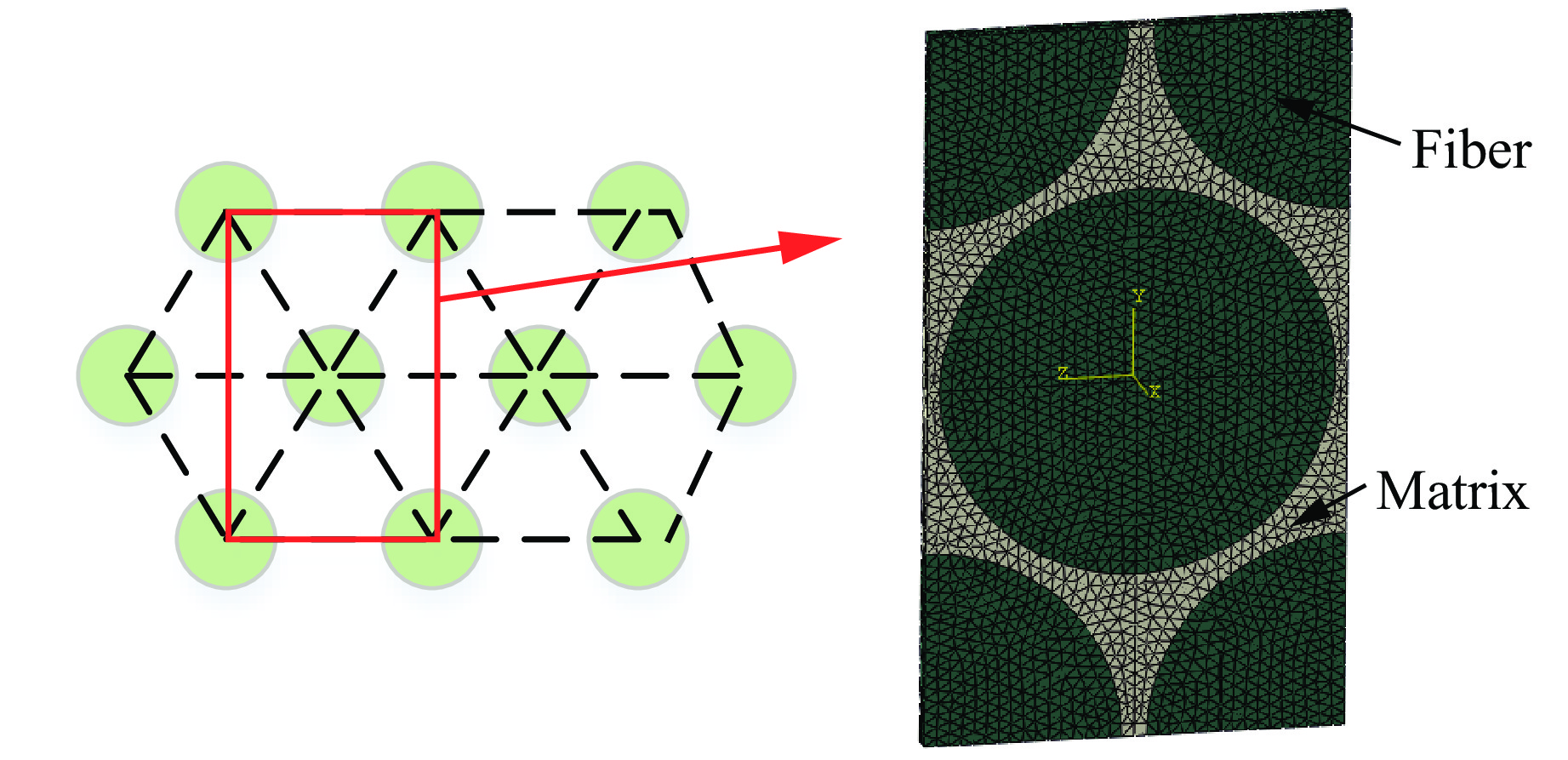
微观尺度的代表性体积单元(representative volume elements,RVE)模型由纤维丝和相邻基体组成。假定纤维丝呈六边形分布,体积分数ϕf=0.8[13],建立微观RVE模型,如图1所示。
在微观尺度RVE模型中,使用四面体单元划分周期性网格,经网格收敛性分析,网格尺寸采用0.03 mm。纤维与基体之间采用共节点连接方式,保证应力和位移连续。根据文献[15–16]中所用碳纤维类型,选择的纤维和基体材料参数如表1和表2所示,其中:E、G和μ分别为材料的弹性模量、剪切模量和泊松比,下标f、m分别表示纤维和基体,Xft、Xfc分别为纤维的拉伸强度和压缩强度,Smt、Smc和Sms分别为基体的拉伸强度、压缩强度和剪切强度。
-
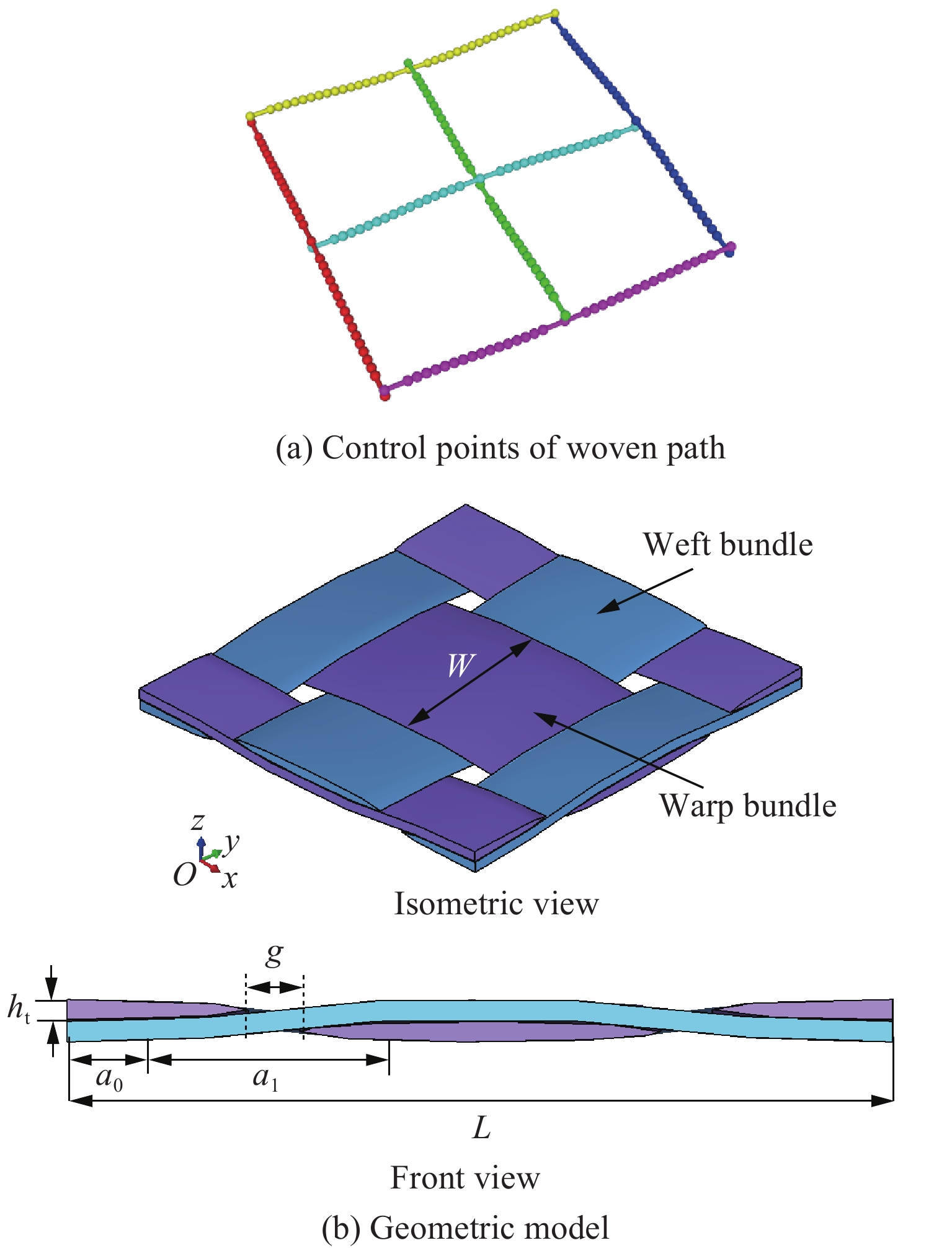
对于编织复合材料,介观尺度RVE模型由相互交织的经纬向纱线及基体组成。为保证介观尺度有限元计算结果的准确性,需要根据其空间特征精准建立几何模型。本研究根据张洁皓[11]对平纹编织碳纤维复合材料的显微镜观察结果进行建模。为避免建模过程中纱线互相穿透、干涉,假设纤维束截面为椭圆形,机织路径由直线段和正弦曲线段组合而成,路径控制点坐标的数学表达式[17]为
式中:ht为纤维束高度,W为纤维束宽度,L为纤维束长度,g为纤维束间隙,a0为直线段长度,a1为曲线段长度,Jx为纤维与基体的间隙。
使用复合材料建模软件Texgen编写Python程序,生成纤维束机织路径控制点,赋予截面属性,建立碳纤维介观尺度RVE模型,如图2所示。在介观RVE模型中,纤维束的体积分数为63.0%,最终纤维的体积分数为50.4%,与文献[15]中的50.6%接近。对于介观尺度RVE模型,基体区域和纤维束区域的空间结构复杂,考虑到采用的网格尺寸既要精准描述其空间构型,保证计算精度,又要兼顾计算效率,因此,结合碳纤维束的实际尺寸,采用四面体单元划分周期性网格,网格尺寸取0.05 mm。将纤维束区域划分为
96296 个单元,基体划分为85128 个单元,能够很好地描述纤维束的空间构型。介观模型中纤维束几何参数的取值见表3。由于纤维束沿路径方向不停波动,材料的主方向也不断改变,为准确描述材料方向的变化,使用ABAQUS中的离散坐标系定义纤维束的主方向。
-
对于周期性RVE模型,为保证应力和位移连续,必须施加周期性边界条件。因此,一对位于相对表面上的对应节点之间的相对位移[18]为
式中:i, j=x, y, z;
$ {u}_{j}^{i+} $ 和$ {u}_{j}^{i-} $ 分别为相对面节点位移;$ {\varepsilon }_{ij}^{0} $ 为单胞宏观应变张量;li为相对表面之间i方向的单胞长度,当单胞模型确定后,li为常数。在ABAQUS中可以使用Equation约束相对的主从节点相对位移。 -
在ABAQUS中,缺乏能够合理描述纤维复合材料三维力学行为的本构关系,因此,利用UMAT子程序接口自定义相关失效准则。
-
在微观尺度有限元计算中,将碳纤维丝视为横观各向同性材料,将基体视为各向同性材料,采用最大应力准则判断纤维丝和基体的损伤起始,即
式中:σi为i方向的应力,τij为ij方向的剪切应力,Xit、Xic和Sijf分别为材料3个主方向的拉伸、压缩和剪切强度。假设纤维丝失效前表现为线弹性,失效后完全不能承受外界载荷,采用刚度折减的退化方案,将其失效后模量折减为原来的0.1。基体的退化方案采用基于断裂韧性的渐进损伤模型。
根据上述损伤模型,编写UMAT子程序,施加周期性边界条件,计算RVE模型在拉压、剪切等位移载荷下的应力-应变关系,获取纤维束的等效力学参数。同时,使用Chamis细观力学公式[19]进行理论预测,2种方法的计算结果如表4和表5所示,其中:Xt和Xc为纤维束的纵向拉伸和压缩强度,Yt和Yc为纤维束的横向拉伸和压缩强度,Zt和Zc为纤维束的法向拉伸和压缩强度,S12、S13、S23为纤维束不同方向的剪切强度。
-
对于介观尺度,需要准确描述纤维束不同方向的损伤情况,因此,采用Hashin和Hou失效准则[11]描述纤维束的损伤起始。
纤维束纵向拉伸失效(
$ {{\sigma _{11}} \geqslant 0} $ )纤维束纵向压缩失效(
$ {{\sigma _{11}} < 0} $ )纤维束横向拉伸失效(
$ {{\sigma _{22}} \geqslant 0} $ )纤维束横向压缩失效(
$ {{\sigma _{22}} < 0} $ )纤维束法向拉伸失效(
$ {{\sigma _{33}} \geqslant 0} $ )纤维束法向压缩失效(
$ {{\sigma _{33}} < 0} $ )式中:σij(i, j=1, 2, 3)为纤维束各个方向的主应力;α为剪切修正因子,根据参数反演法确定α=0.45。采用最大主应力准则描述基体的损伤起始,损伤退化方式均采用基于断裂韧性的渐进损伤模型。
将微观尺度的预测结果作为介观尺度的计算输入。根据上述损伤模型,编写UMAT子程序,施加周期性边界条件,计算RVE模型在拉压、剪切等位移载荷下的应力-应变关系,获取层合板的宏观等效力学参数,结果如表6所示。
由表6可知:介观尺度对纵向拉伸及面外剪切的计算误差在10%以内,说明本方法在预测平纹编织复合材料强度和刚度方面的准确性较高。然而,本方法对于面内剪切强度的预测误差达到43%,这是因为在仿真计算中对RVE模型添加了周期性边界条件,致使仿真过程中材料出现周期性损伤,而试验观测结果表明,材料并不会出现严格的周期性,从而导致仿真计算结果与试验结果之间出现较大的误差[11]。同时,在面内剪切载荷作用下,材料内部损伤具有较强的非线性,使得强度预测值与试验值的误差较大。此外,试验试件本身的缺陷也会导致面内剪切强度预测值的偏差较大。
-
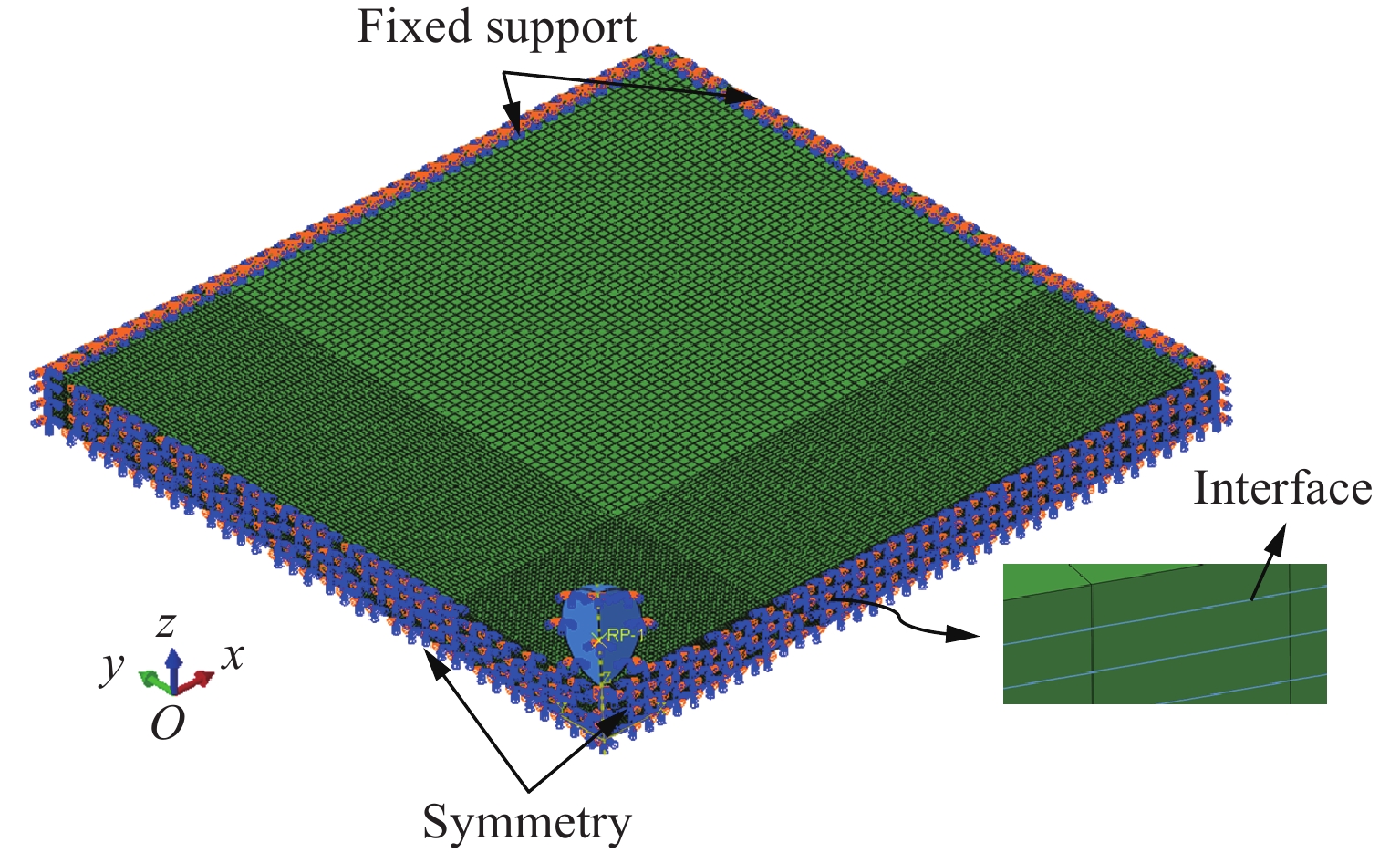
根据文献[15]的弹道侵彻试验建立有限元模型,如图3所示。碳纤维靶板的长和宽均为150 mm,厚度为5.7 mm,采用1/4模型建模,并施加对称边界条件;层合板的单层厚度为0.22 mm,单层的网格尺寸为0.22 mm,在层与层之间插入零厚度的Cohesive单元,用来模拟弹道侵彻过程中的分层现象;对冲击区域进行网格加密,加密区域的面内网格尺寸为0.5 mm×0.5 mm,其余网格尺寸为1.0 mm,采用该网格尺寸能够较好地捕捉靶板的变形情况。球形弹丸的直径为10.3 mm,质量为4.5 g,采用刚体建模。弹丸与靶板之间采用通用接触,法向硬接触,切向罚接触,摩擦因数为0.3。
-
层合板的材料参数来自介观尺度RVE模型的预测结果。对于平纹编织复合材料层合板,纵向及横向损伤以纤维为主,厚度方向上的损伤主要受基体影响。因此,需要提出一种能够同时反映纤维和基体损伤的模型。本节根据连续损伤力学理论,建立碳纤维层合板的损伤本构模型,选用基于应变形式的改进Hashin失效准则[20]来判断纤维和基体的损伤起始,包括纵向及横向的纤维拉伸、压缩损伤以及厚度方向的基体拉伸、压缩损伤,损伤判断公式如下。
纵向纤维的拉伸失效(
$ {{\varepsilon _{11}} \geqslant 0} $ )纵向纤维的压缩失效(
$ {{\varepsilon _{11}} < 0} $ )横向纤维的拉伸失效(
$ {{\varepsilon _{22}} \geqslant 0} $ )横向纤维的压缩失效(
$ {{\varepsilon _{22}} < 0} $ )厚度方向基体的拉伸失效(
$ {{\varepsilon _{33}} \geqslant 0}$ )厚度方向基体的压缩失效(
$ {{\varepsilon _{33}} < 0} $ )式中:Xt和Xc分别为层合板纵向(方向1)的拉伸强度和压缩强度,Yt和Yc分别为层合板横向(方向2)的拉伸强度和压缩强度,Zt和Zc分别为层合板厚度方向(方向3)的拉伸强度和压缩强度,S12、S23和S13分别为层合板xy、yz、xz平面所对应的剪切强度,
$ \varepsilon $ 为积分点应变。利用损伤因子Di(i=1t, 1c, 2t, 2c, 3)识别层内损伤模式,并进行刚度折减,分别表示沿纵向、横向、厚度方向的损伤程度。当满足损伤判据di≥1(i=1t, 1c, 2t, 2c, 3)后,材料点开始发生局部损伤,导致承载能力下降,因此,引入连续损伤变量Di描述这一损伤演化过程,实现单元刚度矩阵的折减,计算公式为
式中:i=1t, 1c, 2t, 2c, 3;n为控制损伤因子演化的无量纲参数,n>0。该损伤模型已在碳纤维层合板冲击有限元模拟[20]中被证明是合理有效的。
-
采用ABAQUS内置的内聚力模型(cohesive zone model)模拟复合材料层间分层损伤,材料参数如表7所示,其中:
$ {t}_{\mathrm{n}}^{0} $ 为法向界面强度,$ {t}_{\mathrm{s}}^{0} $ 和$ {t}_{\mathrm{t}}^{0} $ 分别为第一和第二剪切方向的界面强度,$ {G}_{\mathrm{c}}^{{Ⅰ}} $ 为法向临界断裂能量释放率,$ {G}_{\mathrm{c}}^{{Ⅱ}} $ 和$ {G}_{\mathrm{c}}^{{Ⅲ}} $ 分别为第一和第二剪切方向的临界断裂能量释放率。该模型基于牵引-分离规律,利用节点的牵引应力和分离位移对复合材料层间损伤进行模拟,采用二次名义应力准则定义Cohesive单元的损伤起始,判断准则表示为式中:tn、ts、tt分别为法向、第一剪切方向和第二剪切方向的应力。当法向、第一剪切方向和第二剪切方向的名义应力的平方和为1时,损伤开始。
-
在高速冲击过程中,应变率效应对结果的影响不可忽略,而失效准则中并没有考虑应变率效应,因此,计算结果难免会与试验产生较大误差。本研究采用陈战辉[22]的做法,通过引入动态增强因子
$ {\eta _{{\mathrm{DIF}}}} $ (dynamic increase factor,DIF)修正碳纤维层合板的材料本构,其表达式为式中:
$ \dot \varepsilon $ 为当前应变率,利用子程序进行更新;$ {\dot{\varepsilon }}_{0} $ 为参考应变率,一般取1 s−1;A、B、C为经验参数,仿真计算时根据纤维种类从相关文献中获取。考虑应变率效应后,对模量和强度进行修正,得到式中:S0为参考应变率下的强度参数,SDIF为当前应变率下的强度参数,E0为参考应变率下的模量,EDIF为当前应变率下的模量,
$ {\eta _{{\mathrm{DIF}},S}} $ 和$ {\eta _{{\mathrm{DIF}},E}} $ 分别为模量和强度的动态增强因子。考虑应变率效应后,需要使用当前应变率下的参数进行Hashin失效准则判断。 -
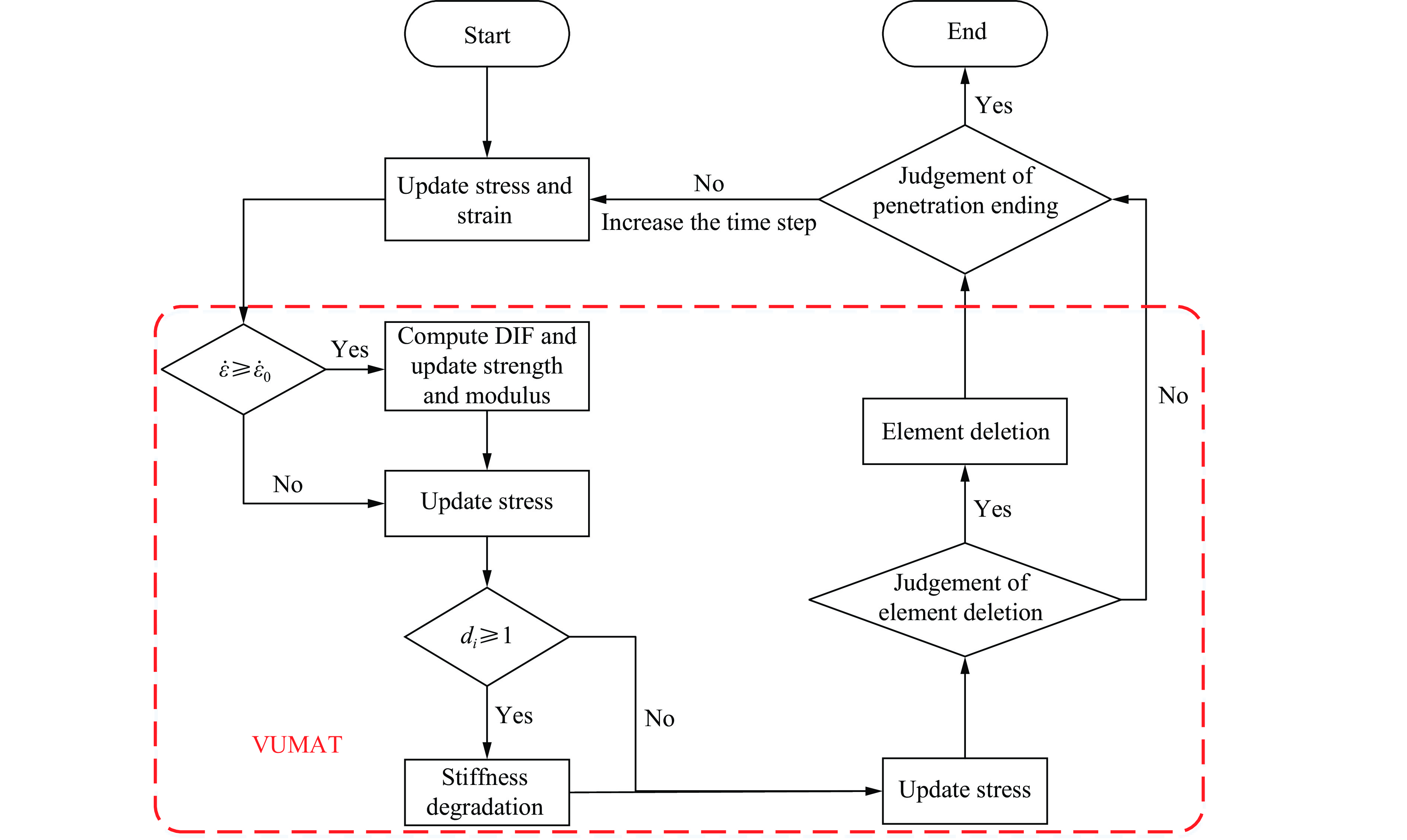
在 ABAQUS/Explict 模块中进行弹道侵彻数值分析,分析流程如图4所示。建立层合板的有限元模型,层内单元采用三维八节点的减缩积分单元(C3D8R),层间单元采用三维八节点零厚度的内聚力单元(COH3D8),定义层合板边界条件和弹丸载荷输入。在宏观尺度的弹道侵彻仿真计算中,已有文献的材料本构和失效模型中大多未考虑应变率效应。本研究通过改进Hashin失效准则,结合渐进式损伤退化模型,同时考虑应变率效应,借助VUMAT进行子程序二次开发。在每一个增量步计算中,通过调用用户自定义材料子程序(VUMAT)来实现碳纤维复合材料层合板的应变率效应和层内渐进损伤过程,并将获得的单元应力-应变和损伤状态等信息反馈至ABAQUS 主程序中,直至侵彻过程结束。
-
质量为4.5 g的球形弹丸以不同速度侵彻靶板时,靶板最终的侵彻形貌如图5所示。从图5可以看出:靶板的损伤模式以剪切破坏和分层损伤为主。迎弹面纤维断裂严重,有明显的剪切孔形成;背弹面铺层剥离脱落,在弹丸动能的作用下,出现不同程度的向外翻折。由于迎弹面的损伤面积小于背弹面的损伤面积,靶板的损伤形貌近似呈喇叭状。随着弹丸侵彻速度的增加,靶板剪切破坏程度加深,分层范围随之减小。仿真得到的靶板隆起高度稍大于试验结果。这是由于:试验中,靶板背部在弹丸侵彻作用下产生一定的隆起鼓包,同时会随着时间变化出现一定的回弹;而在仿真过程中,模型的层间失效未能完全考虑裂纹扩展耗散的能量,更容易出现层间分层和面外变形,另外,由于仿真时间不够长,导致靶板未能充分回弹。
定义单位面密度吸能为弹丸动能变化与靶板面密度的比值
式中:
$ \eta $ 为单位面密度吸能;mp为弹丸的质量;vi为弹丸的入射速度;vr为弹丸的剩余速度;ρa为层合板的面密度,ρa= 8.55 kg/m2。剩余速度和单位面密度吸能的对比结果如表8所示,可以看出,剩余速度的仿真误差在5%以内,单位面密度吸能的仿真误差在15%以内。
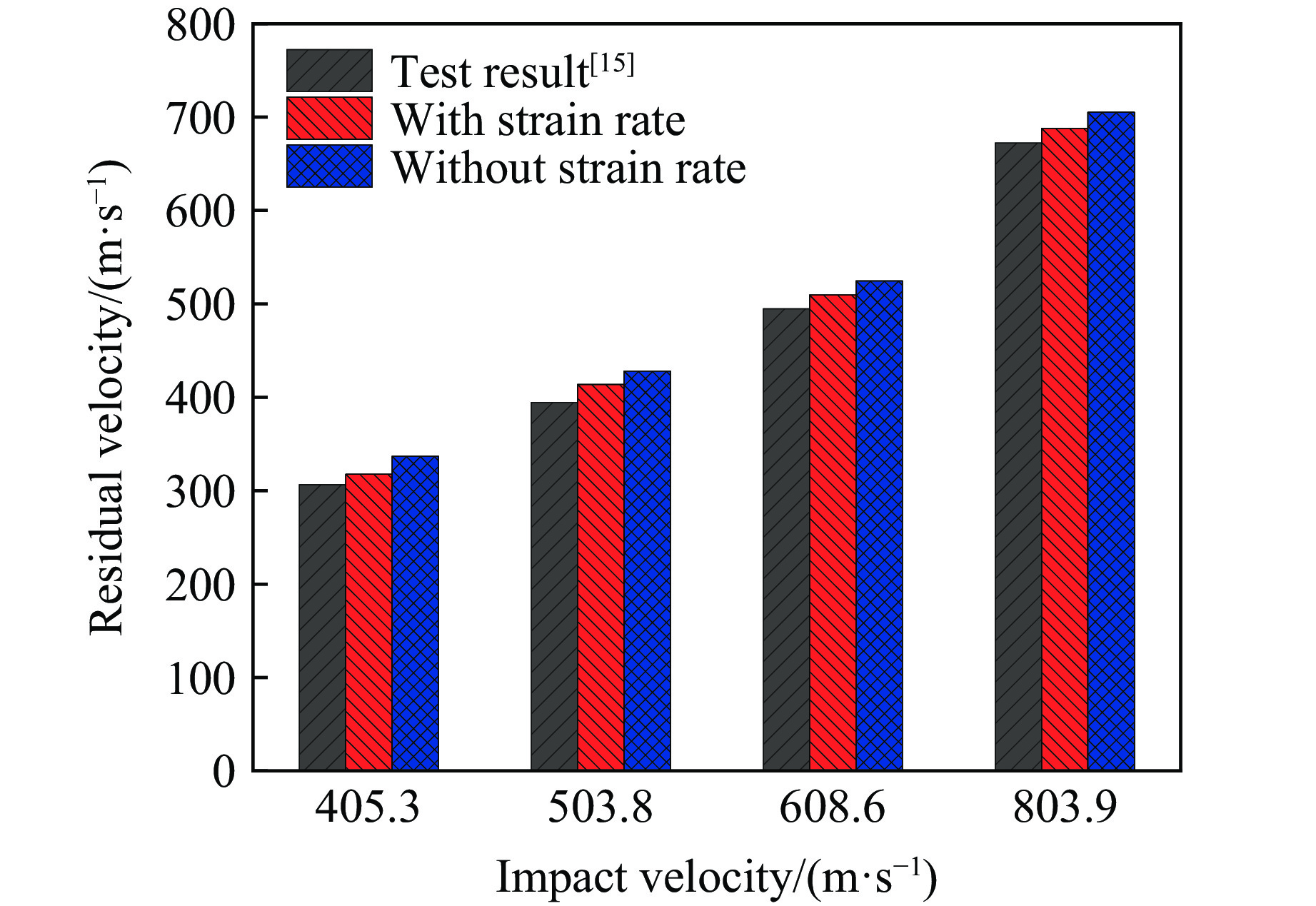
相关研究表明,碳纤维丝的应变率效应不明显,但是基体的应变率效应不可忽略[23]。图6给出了应变率效应对剩余速度的影响,可以看出,不考虑应变率效应时计算结果出现更大的误差。
-
弹道极限速度是指某种弹丸侵彻靶板时恰好穿透靶板且剩余速度为零时的入射速度,是评估材料抗弹性能的重要指标。为了能够以最小板厚实现对侵彻弹丸的有效防御,降低结构冗余,本研究采用Lambert-Jonas方法拟合得到球形弹丸侵彻作用下不同厚度层合板的弹道极限速度,拟合方程为
式中:
$ {v}_{\mathrm{B}\mathrm{L}} $ 为拟合弹道极限速度,a和p为拟合参数。针对研究较多的4~10 mm厚的层合板进行弹道侵彻计算,获取其在不同入射速度下的剩余速度,进而对弹道极限速度进行拟合,不同板厚(h)下的拟合参数如表9所示。
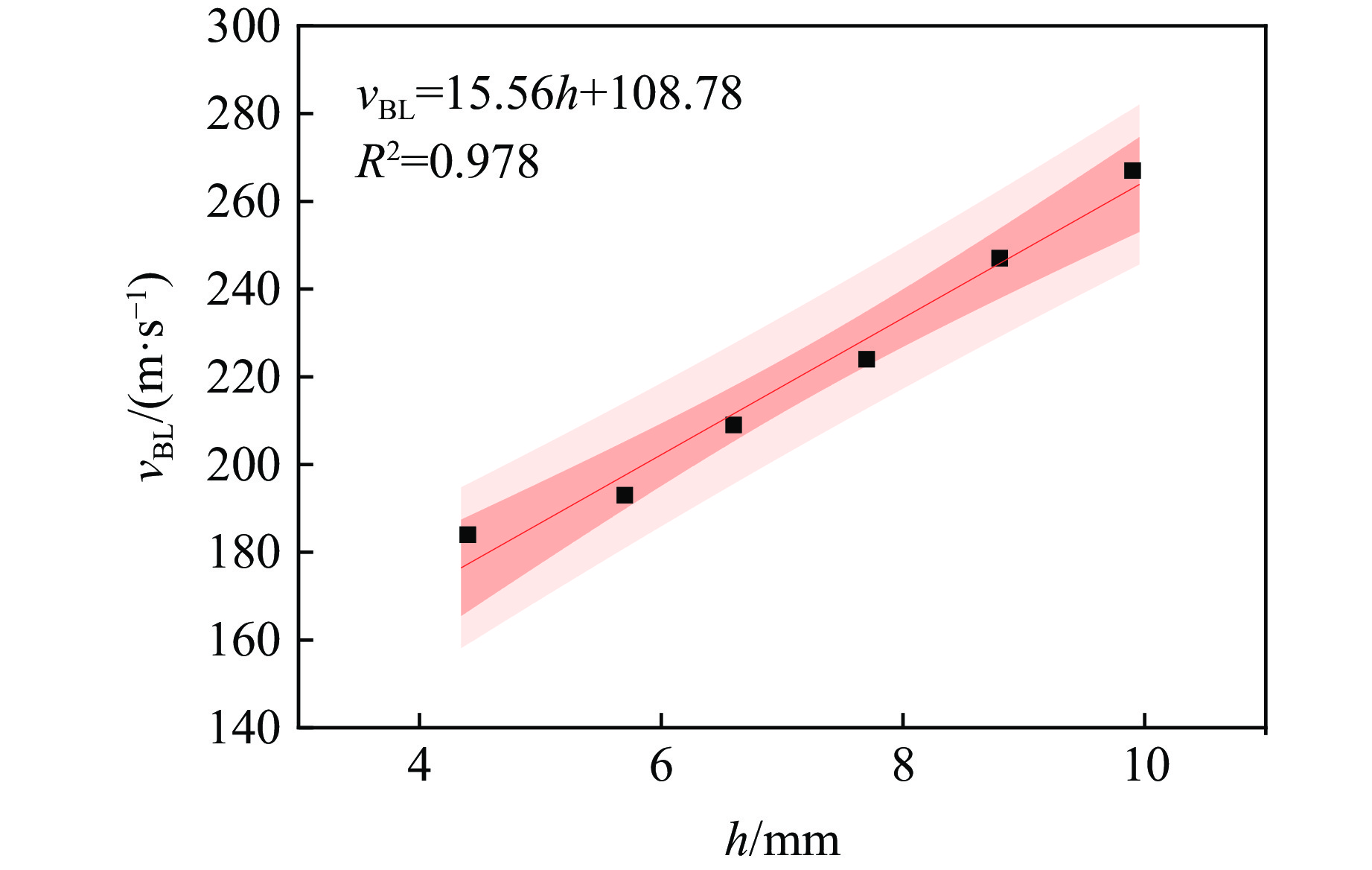
弹道极限速度随层合板厚度的拟合关系如图7所示。可以看出,弹道极限速度与靶板厚度呈线性关系,表达式为
式中:vBL和h的单位分别为m/s和mm。式(23)与Li等[24]关于纤维增强复合材料弹道极限速度的理论模型计算结果相吻合。
进一步对计算结果进行分析,拟合曲线的相关系数R2为0.978,输入的弹道极限点均落在95%置信区间和预测带内,说明拟合结果的可信度较高。需要说明的是,本研究得到的式(23)是根据4~10 mm厚碳纤维层合板得出的,对于较厚的碳纤维层合板,因层合板侵彻失效模型存在差异,式(23)预测的弹道极限速度可能存在较大偏差。
-
根据已发表的试验数据,验证了宏观模型弹道侵彻数值模拟方法的准确性,进而研究了层合板的弹道极限速度随板厚的变化关系,但本研究还存在着一定的局限性:将侵彻弹丸假定为刚体,忽略了实际侵彻过程中弹丸可能出现的镦粗变形等现象;仅对4~10 mm厚层合板进行仿真计算,研究范围较窄。
-
提出了一种用于预测纤维增强复合材料层合板力学性能和抗侵彻能力的多尺度模拟方法,考虑纤维的损伤模式和应变率,采用刚度退化方式,基于UMAT和VUMAT分别进行了静态力学和动态失效准则的二次开发,开展了微观-介观-宏观的力学性能预测和弹道侵彻研究,实现了全流程数值模拟,得到如下主要结论。
(1) 构建了纤维复合材料的拉伸、压缩和剪切等效力学性能的微观和介观模型,通过与理论公式和试验值进行对比,结果显示,微观尺度和介观尺度的力学性能预测结果的误差基本在10%以内,验证了多尺度模型的有效性和准确性。
(2) 提出了考虑应变率效应和不同方向纤维和基体损伤退化的失效准则,建立了层合板弹道侵彻宏观数值模型,准确捕捉到了试验中出现的靶板纤维断裂和层间分层等损伤模式。数值模拟得到的剩余速度与试验结果的相对误差在5%以内,验证了失效准则的合理性和准确性。
(3) 研究了碳纤维复合材料层合板弹道极限速度随板厚的变化规律,给出了不同厚度下剩余速度计算的拟合参数,进而得到了层合板弹道极限速度与板厚的拟合关系式,由此可快速获取不同厚度层合板的弹道极限,为抗侵彻设计提供参考依据。
纤维增强复合材料层合板抗侵彻的多尺度模拟方法
Multiscale Simulation Method for Anti-Penetration of Fiber-Reinforced Composite Laminates
-
摘要: 针对纤维增强复合材料层合板结构设计和抗侵彻数值仿真需要大量材料参数和动态试验数据的问题,以碳纤维增强复合材料层合板为研究对象,采用多尺度模拟方法,实现了纤维丝-纤维束-层合板的微观-介观-宏观力学性能和抗侵彻能力的全流程数值仿真预测。首先,建立微观代表性体积单元(representative volume elements,RVE),基于最大应力准则,预测出纤维束的力学性能;然后,根据编织结构的空间特征建立介观RVE模型,采用Hashin和Hou的失效准则,预测出宏观等效力学性能;最后,根据已发表的试验数据,建立了宏观弹道侵彻数值模型,提出了一种考虑材料应变率效应的改进Hashin失效准则,进而研究了弹道侵彻作用下纤维增强复合材料层合板的剩余速度和损伤特征。结果表明:试验与仿真得到的剩余速度的相对误差在5%以内,宏观数值模型准确捕捉到了纤维断裂、层间分层等损伤模式,验证了多尺度模拟方法的合理性和准确性;拟合得到了弹道极限速度随板厚变化的关系式,两者呈线性关系,且相关系数达0.97以上。研究结果有助于实现纤维增强复合材料层合板抗侵彻的低成本、短周期结构设计,对纤维增强复合材料层合板的正向性能预测和逆向结构设计均具有重要的科学和工程应用价值。Abstract: Aiming at the problem that a large number of material parameters and required for the structural design and numerical simulation of penetration resistance of fiber reinforced composite laminates, this article takes carbon fiber reinforced composite laminates as the research object, and adopts multi-scale simulation method to realize the whole process numerical simulation prediction of micro-, meso-, and macro-scale mechanical properties and penetration resistance of fiber-bundle-laminates. Firstly, microscopic representative volume elements (RVE) were established to predict the mechanical properties of fiber bundles based on the maximum stress criterion. Then, based on Hashin and Hou’s failure criteria, the macroscopic equivalent mechanical properties were predicted by the mesoscopic RVE models established according to the spatial characteristics of braided structures. Finally, an improved Hashin failure criterion considering the strain rate effect was proposed, and the numerical model of ballistic penetration was established based on the literature tests to study the residual velocities and damage characteristics. The results show that the errors of residual velocity results are less than 5%, and the macroscopic numerical models can accurately simulate the damage modes such as fiber fracture as well as interlayer delamination, which verifies the rationality and accuracy of multi-scale simulation method in this article. The relationship between the ballistic limit velocity and the thickness of the plate is linear and the correlation coefficient is above 0.97. The findings of this paper can help to realize the design of low-cost and short-period fiber reinforced composite laminates, which has important scientific and engineering application values for property prediction and inverse structural design of fiber reinforced composite laminates.
-
Key words:
- composite laminate /
- representative volume element /
- multiscale /
- ballistic penetration /
- stiffness degradation .
-

-
Ef1/GPa Ef2/GPa Ef3/GPa Gf12/GPa μf12 μf13 μf23 Xft/MPa Xfc/MPa 221 13.81 13.81 9 0.27 0.27 0.30 3530 2470 Em/GPa μm Smt/MPa Smc/MPa Sms/MPa 3.55 0.33 80 241 60 表 3 介观RVE模型参数
Table 3. Parameters of mesoscopic RVE model
L/mm W/mm ht/mm a0/mm a1/mm 4.00 1.75 0.10 0.25 1.50 表 4 纤维束刚度参数计算结果
Table 4. Results of fiber bundle stiffness parameters
Method Elastic modulus/GPa Shear modulus/GPa Poisson’s ratio E1 E2 E3 G12 G13 G23 $ {\mu }_{12} $ $ {\mu }_{13} $ $ {\mu }_{23} $ Simulation 177.69 10.14 10.14 5.36 5.36 3.51 0.280 0.280 0.350 Equation 177.51 10.58 10.58 5.60 5.60 3.77 0.282 0.282 0.369 Error/% 0.10 −4.17 −4.17 −4.33 −4.33 −6.83 −0.71 −0.71 −5.06 表 5 纤维束强度参数计算结果
Table 5. Results of fiber bundle strength parameters
Method Tension strength/MPa Compressive strength/MPa Shear strength/MPa Xt Yt Zt Xc Yc Zc S12 S13 S23 Simulation 2865.11 72.72 72.72 1938.67 208.44 208.44 64.50 64.50 52.26 Equation 2835.34 74.39 74.39 1983.94 224.09 224.09 Error/% 1.05 −2.24 −2.24 −2.28 −6.99 −6.99 表 6 宏观等效力学参数对比
Table 6. Comparison of macroscopic equivalent mechanical parameters
Method E1/GPa E2/GPa E3/GPa G12/GPa G13/GPa G23/GPa Xt/MPa Simulation 56.50 56.50 7.90 3.59 2.51 2.51 740.37 Test[15] 57.94 57.94 3.59 726 Error/% −2.49 −2.49 0 1.98 Method Yt/MPa Xc/MPa Yc/MPa S12/MPa S13 /MPa S23/MPa Simulation 740.37 630.34 630.34 64.95 62.88 62.88 Test[15] 726 113.29 65.82 65.82 Error/% 1.98 −42.67 −4.47 −4.47 $ {t}_{\mathrm{n}}^{0} $ /MPa$ {t}_{\mathrm{s}}^{0} $ /MPa$ {t}_{\mathrm{t}}^{0} $ /MPa$ {G}_{\mathrm{c}}^{{Ⅰ}} $ /(kJ·m−2)$ {G}_{\mathrm{c}}^{{Ⅱ}} $ /(kJ·m−2)$ {G}_{\mathrm{c}}^{{Ⅲ}} $ /(kJ·m−2)50 90 90 0.52 0.92 0.92 表 8 仿真与试验得到的剩余速度和单位面密度吸能的对比
Table 8. Comparison of residual velocity and energy absorption per unit surface density between simulation and test
表 9 不同板厚下的拟合参数
Table 9. Fitting parameters under different plate thicknesses
h/mm a p 4.4 0.897 2.089 5.7 0.884 2.051 6.6 0.856 2.104 7.7 0.837 2.030 8.8 0.800 2.164 9.9 0.805 2.032 -
[1] 罗锡林, 魏建辉, 李飘, 等. 碳纤维编织复合材料层合板抗侵彻性能研究 [J]. 材料开发与应用, 2023, 38(4): 61–68. doi: 10.19515/j.cnki.1003-1545.2023.04.004 LUO X L, WEI J H, LI P, et al. Study on penetration resistance of carbon fiber braided composite laminates [J]. Development and Application of Materials, 2023, 38(4): 61–68. doi: 10.19515/j.cnki.1003-1545.2023.04.004 [2] DU C L, XIA R Z, LIU P, et al. On the impact damage characteristics of spread-tow woven composites: from high velocity to hyper velocity [J]. Engineering Failure Analysis, 2023, 146: 107109. doi: 10.1016/j.engfailanal.2023.107109 [3] PENG Y, WANG X, CHEN X Z, et al. Numerical simulation of the effect of projectile shape and size on the high-velocity impact of carbon fiber reinforced composite laminates [J]. Journal of Materials Research and Technology, 2024, 30: 5109–5120. doi: 10.1016/j.jmrt.2024.04.218 [4] ALONSO L, MARTÍNEZ-HERGUETA F, GARCIA-GONZALEZ D, et al. A finite element approach to model high-velocity impact on thin woven GFRP plates [J]. International Journal of Impact Engineering, 2020, 142: 103593. doi: 10.1016/j.ijimpeng.2020.103593 [5] MEYER C S, O'BRIEN D J, HAQUE B Z, et al. Mesoscale modeling of ballistic impact experiments on a single layer of plain weave composite [J]. Composites Part B: Engineering, 2022, 235: 109753. doi: 10.1016/j.compositesb.2022.109753 [6] 牟浩蕾, 李仪, 宋东方, 等. 芳纶平纹编织复合材料平板弹道冲击特性及损伤分析 [J]. 复合材料科学与工程, 2024(1): 89–97, 104. doi: 10.19936/j.cnki.2096-8000.20240128.012 MOU H L, LI Y, SONG D F, et al. Ballistic impact characteristics and damage analysis of aramid plain woven composite plates [J]. Composites Science and Engineering, 2024(1): 89–97, 104. doi: 10.19936/j.cnki.2096-8000.20240128.012 [7] 陈玉丽, 马勇, 潘飞, 等. 多尺度复合材料力学研究进展 [J]. 固体力学学报, 2018, 39(1): 1–68. doi: 10.19636/j.cnki.cjsm42-1250/o3.2017.030 CHEN Y L, MA Y, PAN F, et al. Research progress in multi-scale mechanics of composite materials [J]. Chinese Journal of Solid Mechanics, 2018, 39(1): 1–68. doi: 10.19636/j.cnki.cjsm42-1250/o3.2017.030 [8] 王新峰. 机织复合材料多尺度渐进损伤研究 [D]. 南京: 南京航空航天大学, 2007. WANG X F. Multi-scale analyses of damage evolution in woven composite materials [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. [9] MADKE R R, CHOWDHURY R. A multiscale continuum model for inelastic behavior of woven composite [J]. Composite Structures, 2019, 226: 111267. doi: 10.1016/j.compstruct.2019.111267 [10] ZHU Y X, HE C W, ZHAO T, et al. Towards accurate prediction of the dynamic behavior and failure mechanisms of three-dimensional braided composites: a multiscale analysis scheme [J]. Thin-Walled Structures, 2024, 203: 112188. doi: 10.1016/J.TWS.2024.112188 [11] 张洁皓. 开孔平纹机织复合材料低速冲击性能研究 [D]. 郑州: 郑州大学, 2020. ZHANG J H. Study on low-velocity impact performance of plain weave composites with holes [D]. Zhengzhou: Zhengzhou University, 2020. [12] 王涛, 侯玉亮, 铁瑛, 等. 基于ECPL模型的平纹机织复合材料低速冲击多尺度模拟 [J]. 振动与冲击, 2020, 39(20): 295–304. doi: 10.13465/j.cnki.jvs.2020.20.038 WANG T, HOU Y L, TIE Y, et al. Multi-scale simulation of low-velocity impact on plain woven composites based on an ECPL model [J]. Journal of Vibration and Shock, 2020, 39(20): 295–304. doi: 10.13465/j.cnki.jvs.2020.20.038 [13] 赵巧莉, 侯玉亮, 刘泽仪, 等. 碳纤维平纹机织复合材料低速冲击及冲击后压缩性能多尺度分析 [J]. 中国机械工程, 2021, 32(14): 1732–1742. doi: 10.3969/j.issn.1004-132X.2021.14.012 ZHAO Q L, HOU Y L, LIU Z Y, et al. Multi-scale analysis of LVI and CAI behaviors of plain woven carbon-fiber-reinforced composites [J]. China Mechanical Engineering, 2021, 32(14): 1732–1742. doi: 10.3969/j.issn.1004-132X.2021.14.012 [14] SMOJVER I, BREZETIĆ D, IVANČEVIĆ D. Explicit multi-scale modelling of intrinsic self-healing after low-velocity impact in GFRP composites [J]. Composite Structures, 2022, 302: 116213. doi: 10.1016/j.compstruct.2022.116213 [15] BAO J W, WANG Y W, AN R, et al. Investigation of the mechanical and ballistic properties of hybrid carbon/aramid woven laminates [J]. Defence Technology, 2022, 18(10): 1822–1833. doi: 10.1016/j.dt.2021.09.009 [16] ZHENG T, GUO L C, HUANG J Z, et al. A novel mesoscopic progressive damage model for 3D angle-interlock woven composites [J]. Composites Science and Technology, 2020, 185: 107894. doi: 10.1016/j.compscitech.2019.107894 [17] 陈占光. 基于多尺度方法的含孔机织复合材料强度分析研究 [D]. 哈尔滨: 哈尔滨工业大学, 2021. CHEN Z G. Strength analysis of woven composites with holes based on multi-scale method [D]. Harbin: Harbin Institute of Technology, 2021. [18] GAROZ D, GILABERT F A, SEVENOIS R D B, et al. Consistent application of periodic boundary conditions in implicit and explicit finite element simulations of damage in composites [J]. Composites Part B: Engineering, 2019, 168: 254–266. doi: 10.1016/j.compositesb.2018.12.023 [19] CHAMIS C C. Mechanics of composite materials: past, present, and future [J]. Journal of Composites Technology and Research, 1989, 11(1): 3–14. doi: 10.1520/CTR10143J [20] 葛辛辛. 斜纹编织碳纤维层合厚板低速冲击损伤及剩余压缩强度研究 [D]. 武汉: 华中科技大学, 2022. GE X X. Research on low-velocity impact damage and residual compressive strength of twill woven carbon fiber reinforced thick composite laminates [D]. Wuhan: Huazhong University of Science and Technology, 2022. [21] TIE Y, HOU Y L, LI C, et al. Optimization for maximizing the impact-resistance of patch repaired CFRP laminates using a surrogate-based model [J]. International Journal of Mechanical Sciences, 2020, 172: 105407. doi: 10.1016/j.ijmecsci.2019.105407 [22] 陈战辉. 碳纤维平纹织物层合板高速冲击损伤研究 [D]. 西安: 西北工业大学, 2019. CHEN Z H. Investigation on damage in carbon woven composite laminates caused by high velocity impact [D]. Xi’an: Northwestern Polytechnical University, 2019. [23] 方盈盈. 高应变率下碳纤维复合材料动态力学性能研究 [D]. 大连: 大连理工大学, 2018. FANG Y Y. Study on dynamic mechanical properties of carbon fiber reinforced composite materials under high strain rate [D]. Dalian: Dalian University of Technology, 2018. [24] LI J T, LIU M B. An analytical model to predict the impact of a bullet on ultra-high molecular weight polyethylene composite laminates [J]. Composite Structures, 2022, 282: 115064. doi: 10.1016/j.compstruct.2021.115064 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: