首页
登录
注册
-
近年来，榫卯结构作为传统木结构的一种重要连接方式，在现代建筑技术等领域中得到了新的应用与研究[1]。榫卯式结构应用在混凝土结构和传统木结构中，可以提高结构的施工效率[2]和抗震性能[3]。Zhang等[4]研究了木填充墙对传统木结构抗震行为的增强作用，发现传统木结构填充墙可以提高木结构的刚度和极限承载力。Panoutsopoulou等[5]针对传统榫卯T形接头开展了单调和循坏实验，分析了该连接方式对木结构强抗震性能的影响。Zhang等[6]构建了一种榫卯结构摩擦电纳米发电机，发现榫卯结构可以实现高度的坚固性和空间划分。榫卯式结构在现代的应用不仅体现了对传统建筑技术的传承，也展示了现代建筑技术的创新。
周期性多孔结构具有轻质、高强等优异的力学性能和减振、能量吸收等多功能特性[7]。Li等[8]针对球形多孔结构（spherical porous structure，SPS）的研究表明，泡孔的尺寸、层数和厚度均会影响SPS的抗压性能。Yin等[9]研究发现，分层三维多孔（H3DP）结构较传统材料或结构具有相对较高的吸能特性。杜义贤等[10]研究了以负泊松比和刚度为目标的拓扑优化模型，得到了兼具吸能和承载性能的多孔结构。黄浩等[11]研究了多孔结构的抗冲击性能和对冲击波的衰减作用，发现多孔结构能有效衰减冲击波的峰值压力和总能量，孔径和孔隙率的增加可以提高能量吸收能力。Gao等[12]制备并研究了木纤维增强聚甲基丙烯酸甲酯多孔复合材料，发现该材料可以进一步优化透明纤维木材的机械性能和热性能，吸能性能优异。Yan等[13]提出了一种新型的管增强吸收蜂窝夹层结构，发现该结构具有出色的电磁吸收和承载性能。因此，多孔结构被广泛应用于汽车、航空航天等领域。
将榫卯理念引入多孔结构连接中可以有效保护其不受外部机械应力破坏[14]。成瑶[15]研究发现，在多孔材料PAN纤维中预埋ALOOH，可以与水滑石的外延生长在几何构型上形成类似榫卯结构的相互穿插，使水滑石稳定地负载在聚合物纤维上。张宽等[16]研究了复合材料蜂窝夹层结构榫卯胶接T形接头的弯曲破坏机理，发现增加榫头的宽度和数量能显著提高T形接头的弯曲刚度。李腾等[17]研究了多孔柱在准静态压缩下的力学行为和吸能特性。
基于此，本研究将榫卯式结构引入多孔柱中，保持多孔柱的孔隙率相同，使用3D打印熔融丝技术制备模型，探究通过榫卯方式连接的不同高度、孔型、孔数的多孔柱在单轴压缩下的力学行为和能量吸收性能；采用SOLIDWORKS软件建模、ABAQUS软件开展有限元模拟，并与试验结果进行对比验证。
-
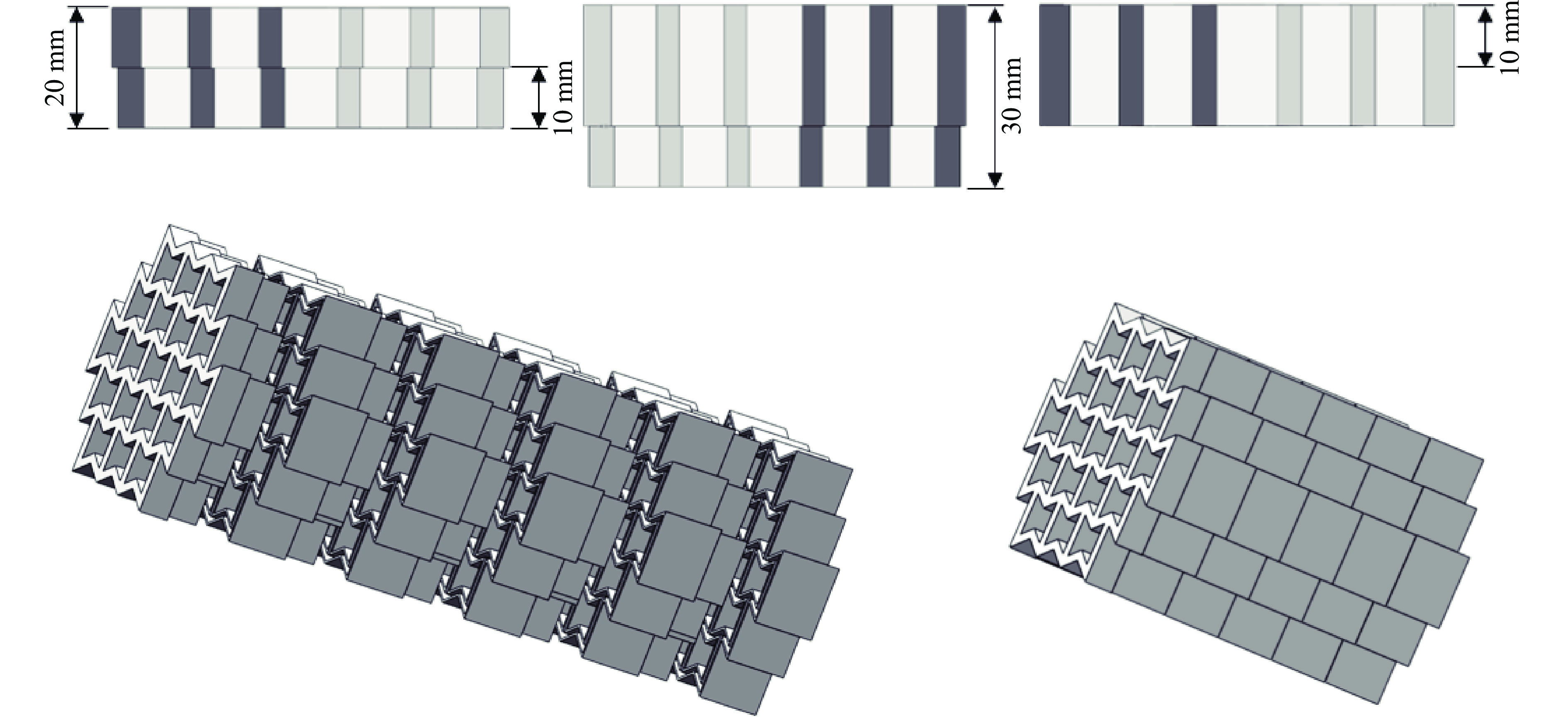
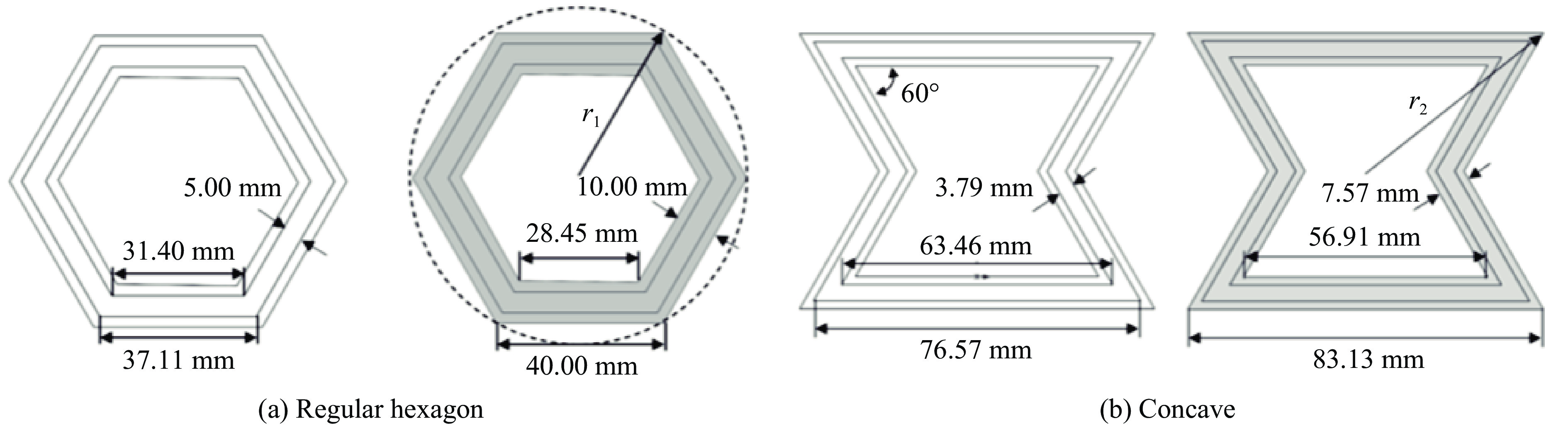
榫卯式多孔柱结构选用具有正、负泊松比效应的正六边形和内凹形2种孔型建立基本模型，如图1所示。确定正六边形基本模型的外边长为40.00 mm，内边长为28.45 mm，壁厚为10.00 mm，连接部分六边形的外边长为37.11 mm，内边长为31.40 mm，壁厚为5.00 mm。保证模型孔隙率均为50.6%，计算得到内凹形基本模型的外边长为83.13 mm，内边长为56.91 mm，壁厚为7.57 mm，连接部分内凹形外边长为76.57 mm，内边长为63.46 mm，壁厚为3.79 mm。
组成榫卯式多孔柱部件的尺寸包括外接圆半径（r）和高度（h）。正六边形的外接圆半径
$ {r}_{1} $ =40.00 mm，内凹形的外接圆半径$ {r}_{2} $ =52.59 mm。榫卯式多孔柱结构由3种基本部件装配组成，中部基本零件的高度$ {h}_{1} $ =30 mm，顶部和底部基本零件的高度$ {h}_{2} $ =20 mm，榫卯式连接部分的凹凸处的高度$ {h}_{3} $ =10 mm。如图2所示，多孔柱结构通过基本部件的榫卯吻合进行拼接，4层结构的高度为70 mm，5层结构的高度为90 mm，6层结构的高度为110 mm。2种榫卯结构的参数如表1所示。模型命名规则如下：以模型Hex-70-1和Con-70-1为例，Hex和Con代表孔型，分别表示正六边形结构和内凹形结构；70表示结构的高度，1表示模型孔数。
-
本研究采用试验测试和有限元模拟两种方法，在孔隙率不变的情况下，分析高度、孔型和孔数等因素的影响，研究榫卯式多孔柱模型在单轴压缩作用下的力学行为和能量吸收性能。
-
试验在室温条件下进行，使用万能试验机CMT5305逐一对试件进行准静态加载，以1 mm/min的速率匀速加载至30 mm，并采用位移传感器采集试验数据，同时用摄像机记录变形过程。试件采用增材制造（additive manufacturing，AM）熔融沉积成形工艺制备：采用聚乳酸（polylacticacid，PLA）材料（密度为1.25 g/cm3，弹性模量为2.3 GPa，泊松比为0.3，屈服强度为45 MPa），通过极光尔沃A6版本3D打印机，设定最佳的打印参数为：打印层高0.2 mm，挤出头温度210 ℃，打印平台温度50 ℃，打印速度30 mm/s，重叠百分比20%。试验加载装置及试件制备如图3所示。
-
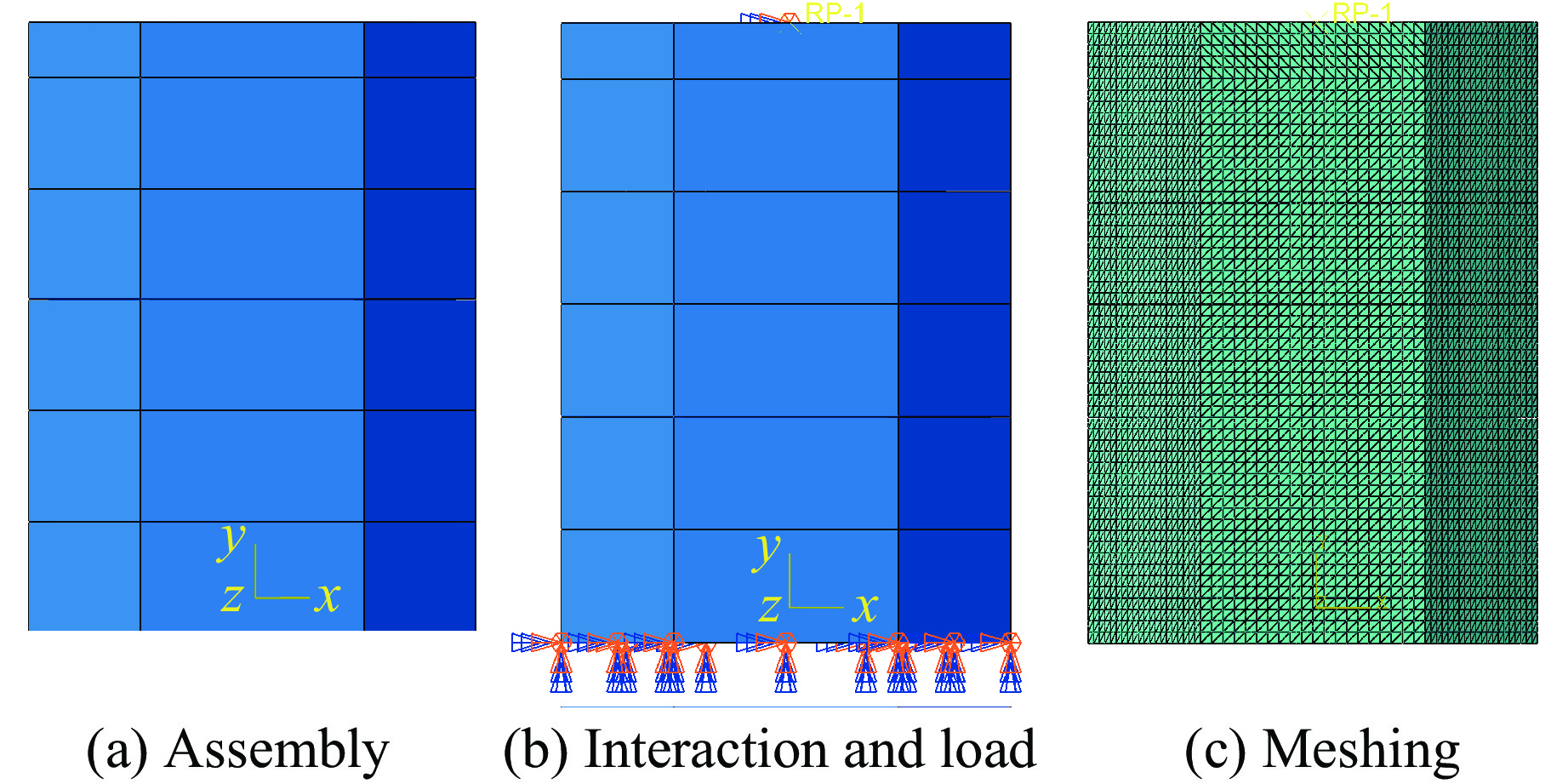
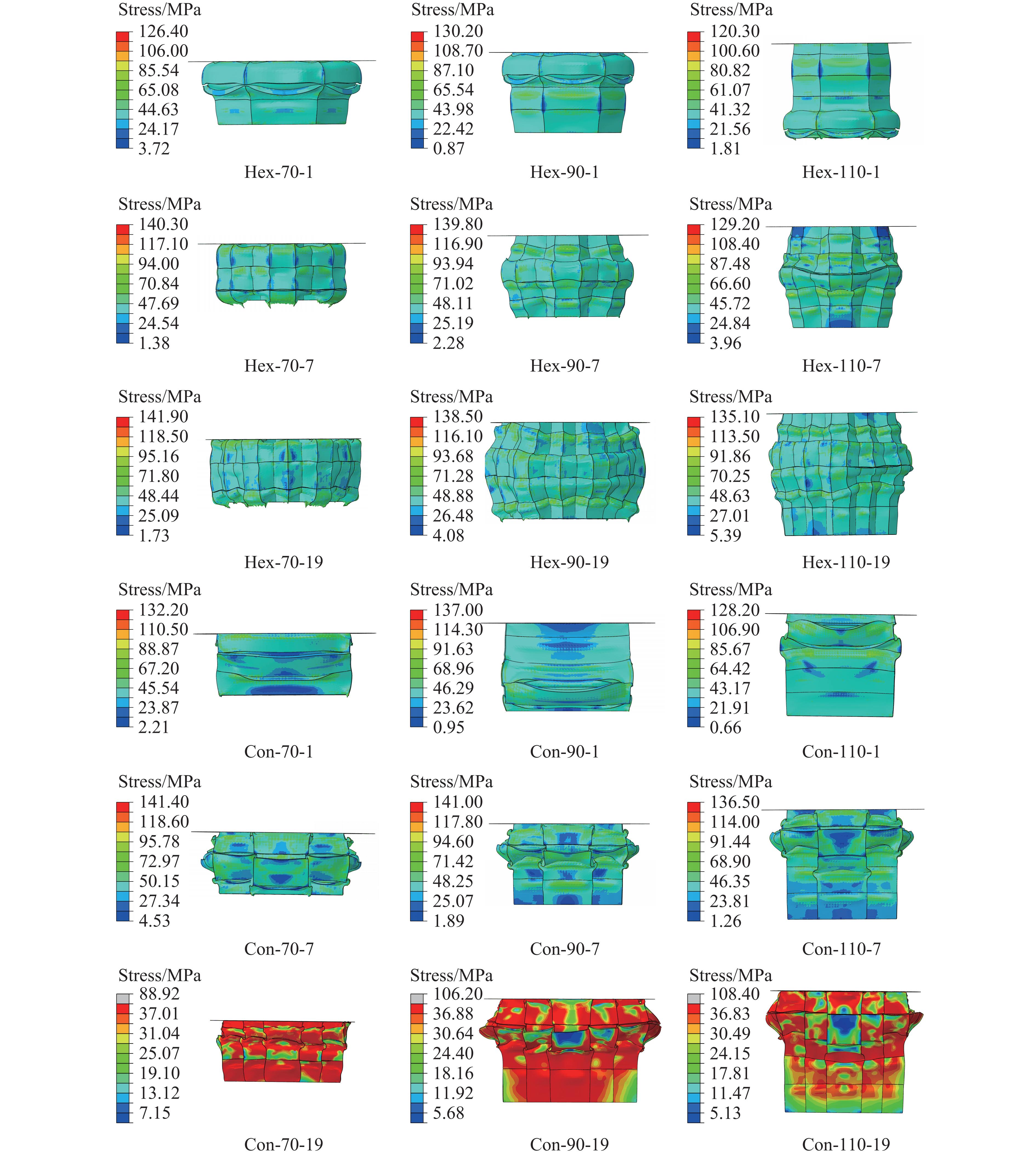
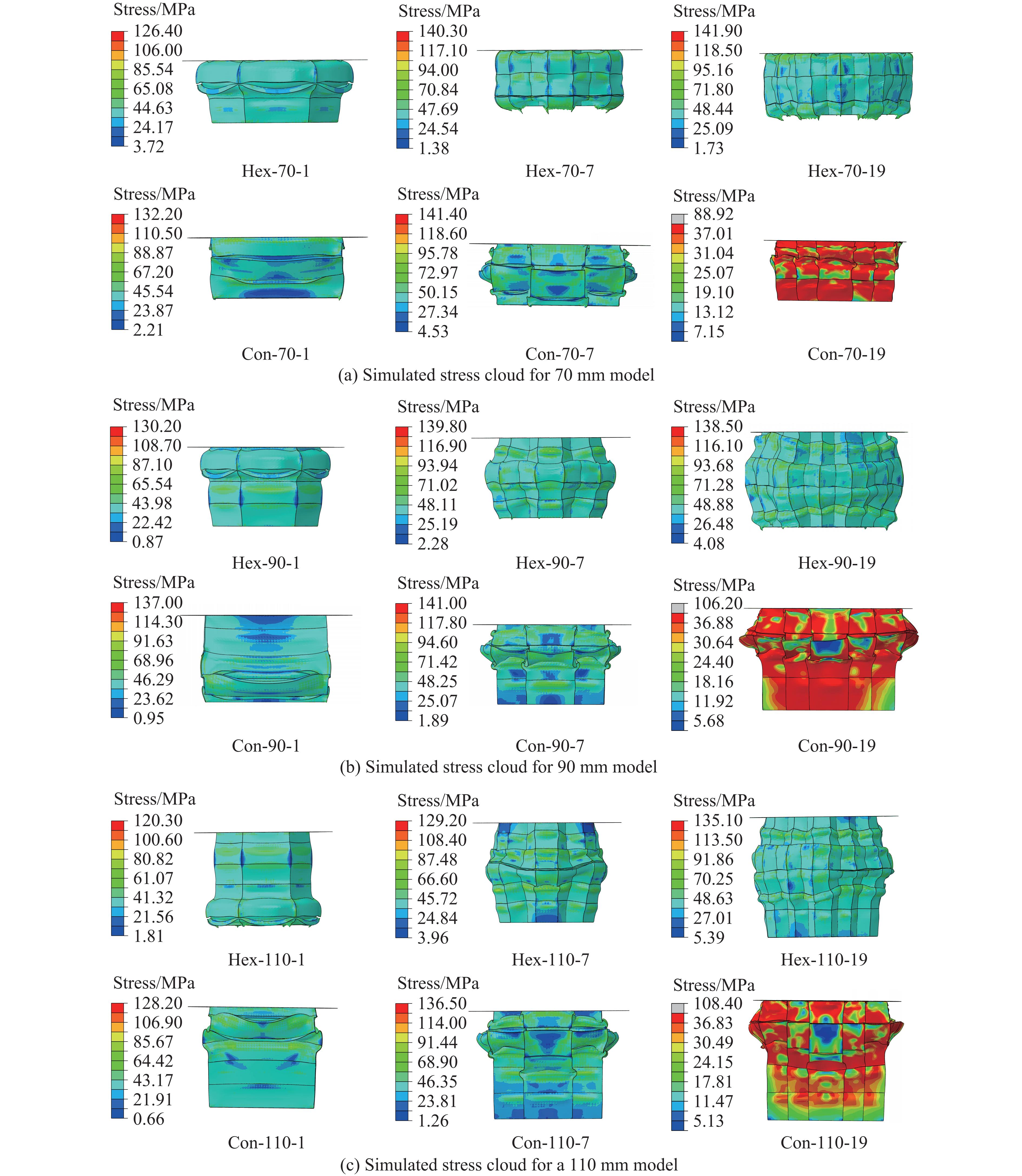
采用ABAQUS软件对榫卯式多孔柱结构进行单轴压缩的动力显式有限元模拟。夹具与模型间的接触形式为铰接和摩擦接触，摩擦因数为0.3，夹具之间的接触形式为铰接，夹具底端固定端约束，顶端在压头处分步施加载荷至30 mm，如图4(b)所示。采用六面体网格对模型进行划分，网格类型选用C3D8R八节点线性六面体单元。在求解过程中，保持约束和载荷不变，逐步细化网格，发现网格疏密对结果的影响可以忽略不计，为此，取网格尺寸为2 mm。采用四面体网格对夹具进行划分，网格尺寸为10 mm，如图4(c)所示。有限元模拟采用弹塑性本构关系，主要观察模型整体的变形及结构破坏形式，模拟结果如图5所示。
分析图5中的模拟结果，所有模型压缩30 mm后均发生明显压缩变形，在单轴压缩的作用下模型长度减小，部分区域宽度增加，且在后续试验中没有发生失稳。在不同参数的条件下，模型发生变形的位置不同，Hex-90-1、Con-110-1、Con-110-7和Con-110-19的初始变形位置位于模型上部，Hex-110-1和Con-90-1的初始变形位置处于模型下部，其余模型的初始变形位置处于模型中部。后续模型其他连接部位也发生轻微变形，并逐渐向模型外部扩展。正六边形模型的初始变形多发生在中部，内凹形模型的初始变形多发生在上下两端。正六边形模型的应力集中处位于侧棱，内凹形模型在负泊松比效应的影响下，应力集中处位于侧面。
-
采取模型下压30 mm时的单轴压缩试验结果与发生相对应压缩变形时的模拟应力云图进行对比，并将试验数据的承载力-位移曲线与拟合的模拟承载力-位移曲线进行对比，探究连接方式、高度、孔型和孔数对抗压强度和吸能特性的影响。
-
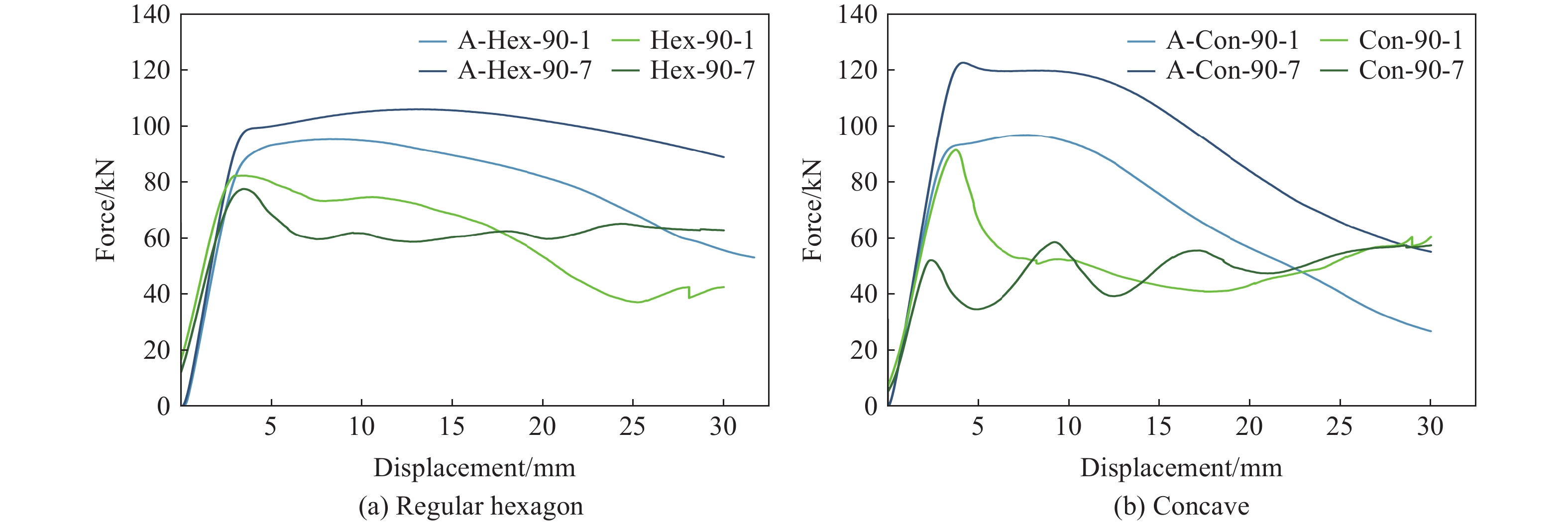
取90 mm的多孔柱一体模型（简称A-Hex或A-Con）和90 mm的榫卯式多孔柱模型进行单轴压缩试验，研究榫卯连接方式对多孔柱结构在单轴压缩试验中的力学行为和吸能特性的影响，分别取正六边形和内凹形2种孔型，并取孔数为1和7，其承载力-位移曲线如图6所示，试验数据如表2所示。
能量吸收是评估结构抵抗压缩性能的主要依据。对比结构吸收的总能量、比吸能和平均压溃力，研究轻质多孔柱的连接方式改变前、后的吸能差异。设能量吸收
$ {E}_{\mathrm{a}} $ 为试件压缩至原高度的66.67%过程中吸收的总能量，表示为式中：L为试件压缩行程，F(s)为试件压缩过程中荷载F关于位移s的函数。
平均压溃力
$ {F}_{\mathrm{m}} $ 是量化试件压溃过程的重要参数之一，为试件在整个准静态压缩过程中的平均承载力，即压缩行程L之内所吸收的总能量$ {E}_{\mathrm{a}} $ 与压缩行程L之比，表示为由式(1)和式(2)计算可得连接方式对模型能量吸收的影响，如表3所示。通过分析图6和表2结果，在高度、孔型和孔数保持一致的情况下，相比多孔柱一体模型，榫卯式多孔柱模型的最大承载力普遍下降，最大承载力对应的位移也较小。在正六边形结构压缩30 mm过程中，Hex-90-1的最大承载力比A-Hex-90-1下降13.77%，发生最大承载力的位移减小64.36%；Hex-90-7的最大承载力比A-Hex-90-7下降26.86%，发生最大承载力的位移减小72.98%。在内凹形结构压缩30 mm过程中，Con-90-1的最大承载力比A-Con-90-1下降5.60%，发生最大承载力的位移减小51.10%；Hex-90-7的最大承载力比A-Hex-90-7下降26.86%，发生最大承载力的位移减小72.98%。对比2种结构模型的最大承载力，除了Hex-90-1外，榫卯式结构模型在30 mm位移附近的承载力高于一体模型，说明榫卯式多孔柱模型在较大受压距离条件下，承载力的表现更加稳定。由表3可知，多孔柱一体模型在单轴压缩试验中的能量吸收能力优于榫卯式多孔柱模型。
通过改变多孔柱的连接方式，从图7可以清楚地看到，多孔柱一体模型发生压缩破坏，从中部发生挤压变形。榫卯式多孔柱结构的各层连接处均发生形变，随着压缩位移的增大，出现脆裂，且模型中力的传递较差。
-
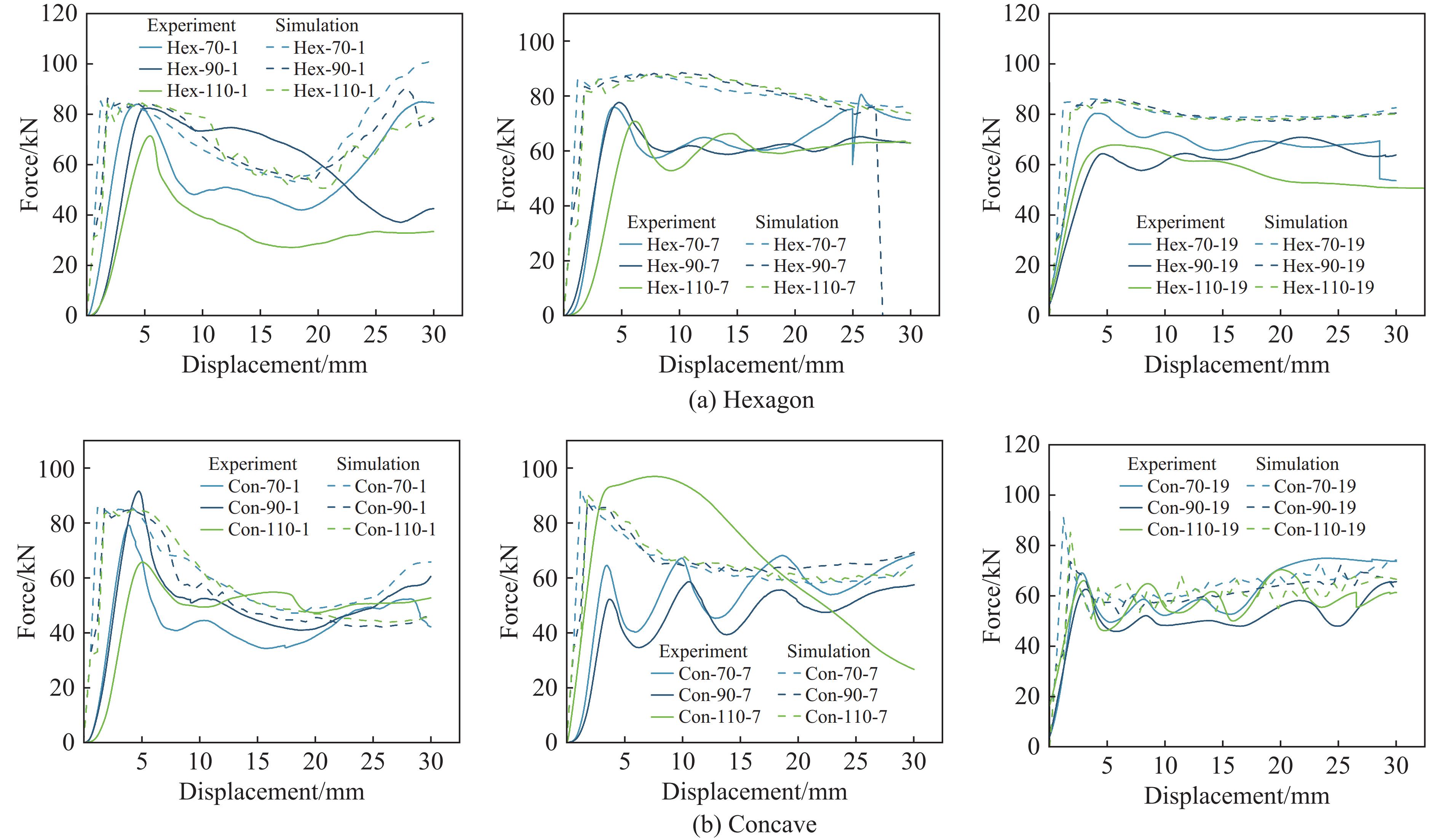
考虑正六边形和内凹形2种孔型及1、7、19这3种孔数，研究高度参数对榫卯式多孔柱抗压能力和吸能特性的影响，高度分别取70、90和110 mm，不同高度下2种模型的承载力-位移曲线如图8所示，最大承载力和位移试验数据如表4所示。由式(1)和式(2)计算可得高度因素对模型能量吸收的影响，如表5所示。
由图8和表4可以看出，随着高度的增大，正六边形孔数为1和19的结构的最大承载力递减，正六边形孔数为7和内凹形单孔的最大承载力先升高后下降，内凹形多孔结构的最大承载力递增。Hex-70/90/110-1的最大承载力先下降1.76%，再下降13.36%；对应位移先增加8.57%，再增加11.22%。Hex-70/90/110-7的最大承载力先升高2.36%，再下降8.86%，对应的位移先增加10.39%，再增加28.24%。Hex-70/90/110-19的最大承载力先下降11.76%，再下降14.18%，对应的位移先增加450.63%，再减少74.57%。Con-70/90/110-1的最大承载力先升高15.71%，再下降28.20%，对应的位移先增加22.56%，再增加6.90%。Con-70/90/110-7的最大承载力先下降14.11%，再升高65.43%，对应的位移先下降64.43%，再下降26.89%。Con-70/90/110-19的最大承载力先下降12.25%，再升高6.34%，对应的位移先增加20.46%，再下降33.17%。对比模拟计算的承载力-位移曲线与试验测试的承载力-位移曲线可以看出，高度对模型抗压性能弹性阶段的影响一致，验证了模拟结果的正确性。分析表5结果，随着高度增加，除Hex-110-19的吸能性能较高以外，其余六边形模型的吸能性能逐渐降低；对于内凹形模型，随着高度增加，除孔数为7的模型的吸能特性先增大后减小以外，其余模型的吸能特性均先减小后增大。由表5可知，当高度取70、90和110 mm时，随高度增加，模型承载力和吸能特性提升。
分析图9和图10结果可以看出：榫卯式多孔柱结构在连接处易发生形变，随着高度增加，六边形单胞在上部发生塑性形变，其余易在中上部发生形变，随后其余部分受力形变，且模型形变更易集中在中上部。
通过建立多元线性回归模型能够定量分析各个自变量对因变量的影响程度，多元线性回归分析结果如表6所示。表中：R2表示该模型的解释能力，显著性值P表示该模型在整体上的统计显著性，B为回归方程中自变量的系数。由表6可知，当高度取70～110 mm时，随高度增加，模型承载力和吸能特性越好。
-
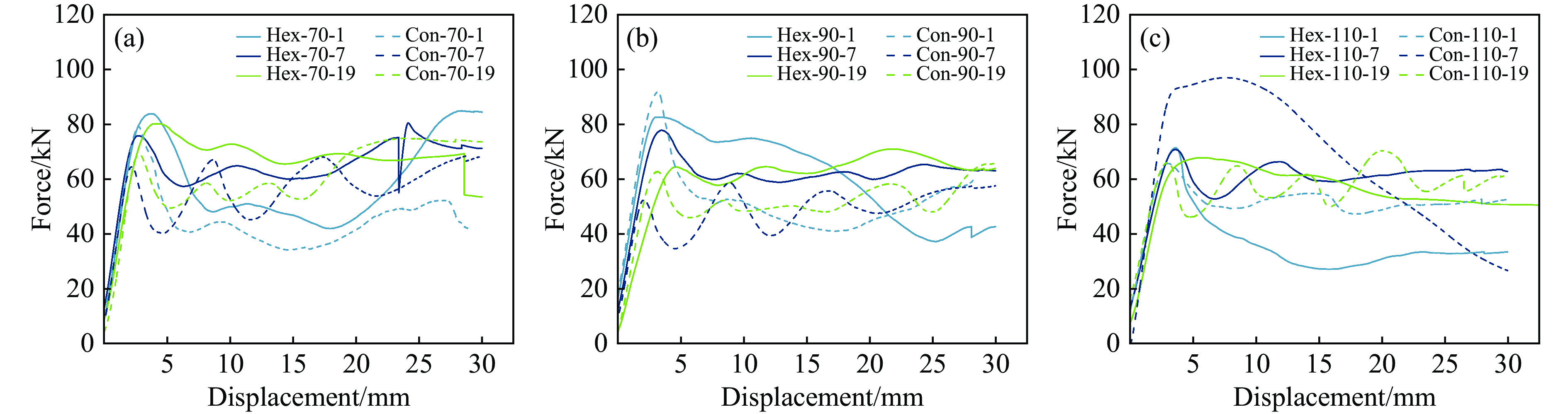
取正六边形和内凹形2种孔型，研究孔型对榫卯式多孔柱抗压能力的影响，并进行吸能分析，榫卯式多孔柱高度分别为70、90和110 mm，孔数分别为1、7和19，进行单轴压缩试验下压30 mm和有限元模拟。考虑孔型因素模型的承载力-位移曲线如图11所示，各模型对应的最大承载力和位移试验结果见表4，吸能情况见表5，模型仿真模拟应力结果如图12所示。
从图11和表4结果可以看出，保持榫卯轻质多孔柱结构的高度和孔数不变，与正六边形孔型对比，按表4中内凹模型的顺序，内凹孔型的最大承载力分别下降5.67%、升高11.10%、下降7.98%、下降10.05%、下降24.52%、升高37.00%、下降6.83%、下降7.34%和升高3.80%，最大承载力对应的位移除孔数为1的模型分别下降12.95%、2.45%和6.24%以外，其他内凹形孔型模型均较正六边形孔型升高588.22%、121.76%、26.43%、529.87%、37.79%和262.21%。六边形孔型的最大承载力普遍优于内凹型，除高度为90 mm的内凹型单胞和高度为110 mm的内凹型多胞的最大承载力优于六边形以外，其余内凹型模型数据均小于六边形孔型模型。因此，正六边形榫卯式多孔柱模型的承载力更好。
由表5可知，除模型Hex-110-1和Hex-110-7的吸能特性弱于对应的内凹模型外，其余六边形孔型模型的吸能均优于内凹型孔型。由图12可知，六边形孔型的初始变形多发生在模型中部，内凹形孔型的初始变形多发生在模型上层，其原因是内凹孔型具有负泊松比属性。由表6可知，正六边形榫卯式多孔柱模型的承载力和吸能特性更好。
-
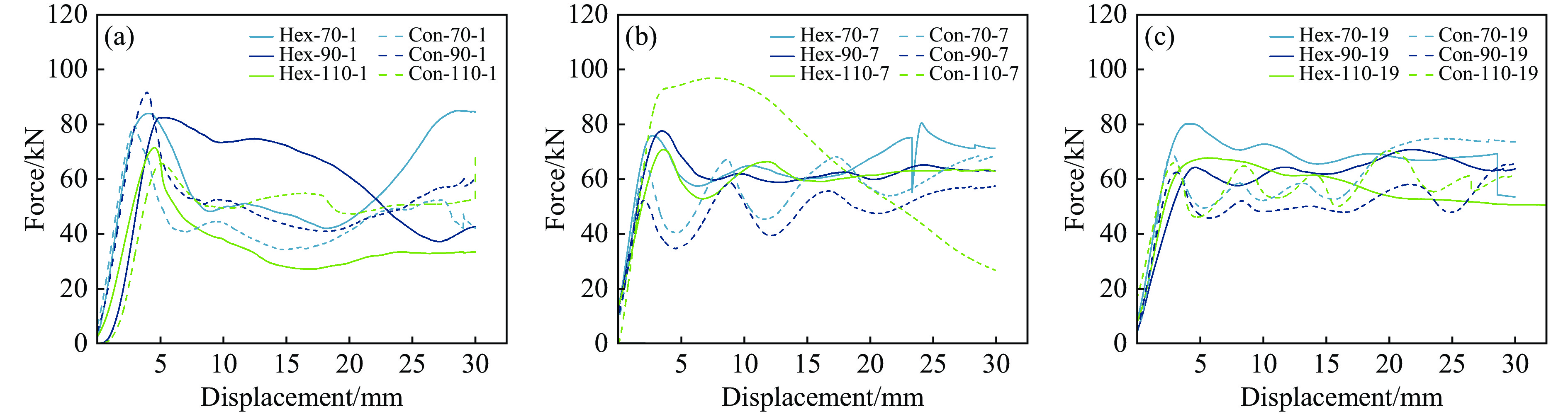
取孔数分别为1、7和19，保持孔型、多孔柱高度不变，研究孔数对榫卯式多孔柱抗压能力的影响，并进行吸能分析，榫卯式多孔柱高度分别为70、90和110 mm，孔型分别为正六边形和内凹形。考虑孔数因素模型的承载力-位移曲线如图13所示，各模型对应的最大承载力和位移试验数据见表4，吸能情况见表5，模拟应力结果如图14所示。
通过分析图13和表4可得，保持榫卯多孔柱结构高度和孔型不变时，随着孔数增加，Hex-70、Con-70、Con-90模型的最大承载力先分别下降9.59%、13.79%和36.01%，再升高5.79%、9.57%和11.95%。Hex-90、Hex-110模型的最大承载力先分别下降5.80%和0.91%，再下降8.81%和4.24%。Con-110模型的最大承载力先升高47.53%，再下降27.44%。除Con-110-7、Con-110-19的最大承载力优于对应孔数为1的模型，其余孔数大于1的模型的最大承载力均小于孔数为1的模型。由表5可知，孔数增大时，模型的能量吸收也增大。正六边形孔型模型和Con-70模型的能量吸收随孔数增加而增加，且单调上升；Con-90模型的能量吸收随孔数增加先减小后增大，Con-110模型的能量吸收则先增大后减小，且非单调上升。由图14可知：孔数为1时，模型的初始变形位置多发生在模型两端；孔数大于1时，模型的初始变形位置多发生在模型中部。由表6可知，孔数与榫卯式多孔柱模型的承载力大小呈负相关，与吸收能量呈正相关。
-
通过对榫卯式多孔柱结构进行单轴压缩试验和数值模拟，研究了连接方式、高度、孔型和孔数对榫卯式多孔柱结构抗压性能和吸能特性的影响规律，得到以下主要结论。
(1) 榫卯式多孔柱结构具有可替换构件，使模型较一体模型具有更好的适应性和可调整性，其中榫卯式内凹模型的后续承载力优于一体模型。
(2) 高度对榫卯式多孔柱模型的承载力影响不明显，但随高度的增加，榫卯式多孔柱结构的初始变形位置更易发生在中上部。
(3) 六边形孔型的最大承载力和吸能特性大多优于内凹形。六边形孔型的初始变形位置多发生在模型中部，内凹形孔型的变形初始位置多发生在模型上部。
(4) 单孔模型的最大承载力普遍优于多孔模型，多孔模型的吸能特性普遍优于单孔模型。单孔模型的初始变形位置多发生在模型两端，多孔模型的初始变形位置多发生在模型中部。
榫卯式多孔柱的单轴压缩力学行为与吸能特性分析
Mechanical Behaviors and Energy Absorption Characteristics of Mortise and Tenon Porous Columns under Uniaxial Compressive Loading
-
摘要: 将传统木结构建筑的榫卯连接方法引入多孔柱中，在保持多孔柱的孔隙率相同的情况下，探究了连接方式、高度、孔型和孔数对结构力学行为和吸能特性的影响；通过试验测试和有限元模拟计算，研究了多孔柱模型在单轴压缩作用下的力学行为和能量吸收性能。结果表明：榫卯式多孔结构在实现快速装配的同时，内凹形模型的后期承载力较好，六边形孔型模型的承载力和吸能特性较好，单孔模型的承载力较好，多孔模型的吸能特性较好。Abstract: By incorporating the traditional mortise-and-tenon structure commonly used in timber structures into the porous column, and the effects of jointing mode, height, hole shape and number on the mechanical behavior and energy absorption characteristics of the structure are investigated under the condition of maintaining a uniform porosity in the porous columns. The mechanical behaviors and energy absorption performance of the porous column model are studied through tests and finite element simulation under uniaxial compression. The results show that the mortise-and-tenon porous structure has a better load carrying capacity in the later stage of the concave shape while realizing rapid assembly. The hexagonal hole model has better load carrying capacity and energy absorption characteristics. The load carrying capacity of the single hole model is higher, and the energy absorption characteristics of the porous model are better.
-
-
图 2 组装模型与基本部件结构示意图（以Con-110-19为例）
Figure 2. Schematic diagram of the assembly model and basic part structure (taking Con-110-19 as an example)
图 4 装配体模型的相互作用和载荷及网格划分示意图
Figure 4. Schematic diagram of the assembly, interaction, and load with meshing
图 5 榫卯式多孔柱结构下压30 mm的模拟结果
Figure 5. Simulation results of mortise-and-tenon porous column structure compressed by 30 mm
图 6 采取不同连接方式的模型的承载力-位移曲线
Figure 6. Load-displacement curves of models with different connection modes
图 8 考虑高度因素时模型的承载力-位移曲线
Figure 8. Force-displacement curves of models with different heights
图 9 考虑高度因素模型的单轴压缩试验
Figure 9. Uniaxial compression tests with modification of the height factor
图 10 考虑高度因素模型下压30 mm的模拟应力云图和试验结果
Figure 10. Stress contour and test results with modification of the height under 30 mm lower pressure
图 11 考虑孔型因素模型的承载力-位移曲线
Figure 11. Load carrying capacity-displacement curve for different hole shape
图 12 不同孔型条件下模型下压30 mm的模拟结果
Figure 12. Simulation results of models with different hole shape compressed by 30 mm
图 13 不同孔数条件下模型的承载力-位移曲线
Figure 13. Load-displacement curves of models with different number of holes
图 14 考虑孔数因素模型下压30 mm的模拟结果
Figure 14. Simulation results of models with different number of holes compressed by 30 mm
表 1 榫卯式多孔柱模型
Table 1. Mortise-and-tenon porous column model
Hole pattern Height/mm Hole number Model Hole pattern Height/mm Hole number Model Regular hexagon 70 1 Hex-70-1 Concave 70 1 Con-70-1 70 7 Hex-70-7 70 7 Con-70-7 70 19 Hex-70-19 70 19 Con-70-19 90 1 Hex-90-1 90 1 Con-90-1 90 7 Hex-90-7 90 7 Con-90-7 90 19 Hex-90-19 90 19 Con-90-19 110 1 Hex-110-1 110 1 Con-110-1 110 7 Hex-110-7 110 7 Con-110-7 110 19 Hex-110-19 110 19 Con-110-19 
下载: 导出CSV
表 2 采取不同连接方式的模型的试验数据
Table 2. Test data of models with different connection modes
Model Maximum force/kN Displacement/mm Model Maximum force/kN Displacement/mm Hex-90-1 82.35 2.94 Con-90-1 91.51 3.77 A-Hex-90-1 95.51 8.25 A-Con-90-1 96.94 7.71 Hex-90-7 77.62 3.51 Con-90-7 58.59 9.17 A-Hex-90-7 106.13 12.99 A-Con-90-7 122.27 4.13
下载: 导出CSV
表 3 采用不同连接方式的模型的能量吸收数据
Table 3. Energy absorption data of models with different jointing modes
Model Ea/kJ Fm/kN Model Ea/kJ Fm/kN Hex-90-1 1.80 60.00 Con-90-1 1.54 51.33 A-Hex-90-1 2.44 81.33 A-Con-90-1 1.97 65.67 Hex-90-7 1.84 61.33 Con-90-7 1.43 47.67 A-Hex-90-7 2.85 95.00 A-Con-90-7 2.70 90.00
下载: 导出CSV
表 4 模型下压30 mm的试验结果
Table 4. Test results of models compressed by 30 mm
Model Maximum force/kN Displacement/mm Model Maximum force/kN Displacement/mm Hex-70-1 83.90 4.48 Con-70-1 79.14 3.90 Hex-90-1 82.42 4.90 Con-90-1 91.57 4.78 Hex-110-1 71.41 5.45 Con-110-1 65.71 5.11 Hex-70-7 75.85 4.33 Con-70-7 68.23 29.80 Hex-90-7 77.64 4.78 Con-90-7 58.60 10.60 Hex-110-7 70.76 6.13 Con-110-7 96.94 7.75 Hex-70-19 80.24 3.95 Con-70-19 74.76 24.88 Hex-90-19 70.80 21.75 Con-90-19 65.60 29.97 Hex-110-19 67.76 5.53 Con-110-19 70.34 20.03
下载: 导出CSV
表 5 模型下压30 mm的能量吸收数据
Table 5. Energy absorption of models compressed by 30 mm
Model Ea/kJ Fm/kN Model Ea/kJ Fm/kN Hex-70-1 1.70 56.67 Con-70-1 1.30 43.33 Hex-90-1 1.73 57.67 Con-90-1 1.48 49.33 Hex-110-1 1.03 34.33 Con-110-1 1.43 47.67 Hex-70-7 1.84 61.33 Con-70-7 1.60 53.33 Hex-90-7 1.76 58.67 Con-90-7 1.36 45.33 Hex-110-7 1.64 54.67 Con-110-7 1.97 65.67 Hex-70-19 2.00 66.67 Con-70-19 1.82 60.67 Hex-90-19 1.82 60.67 Con-90-19 1.53 51.00 Hex-110-19 2.20 73.33 Con-110-19 1.71 57.00
下载: 导出CSV
表 6 多元线性回归分析结果
Table 6. Results of the multiple linear regression analysis
Implicit variable R2/% P B Height Hole patten Hole number Constant Force 19.3 0.375 20.833 –3 888.889 –559.524 85 160.714 Energy uptake 38.4 0.072 2 083.333 –222 222.222 11 111.111 1 734 722.222
下载: 导出CSV
-
[1] LI S C, ZHOU Z C, LUO H Z, et al. Behavior of traditional Chinese mortise-tenon joints: experimental and numerical insight for coupled vertical and reversed cyclic horizontal loads [J]. Journal of Building Engineering, 2020, 30: 101257. doi: 10.1016/j.jobe.2020.101257 [2] ZHU Z G, WU F Q, HAO J. Mechanical behavior of a novel precast concrete beam-column joint using the mortise-tenon connection [J]. Sustainability, 2023, 15(19): 14586. doi: 10.3390/su151914586 [3] 王星, 张献. 榫卯式毂节点半刚性单层球面网壳稳定性及地震响应分析 [J]. 土木工程学报, 2024, 57(10): 1–10. WANG X, ZHANG X. Stability and dynamic performance analysis of semi-rigid single-layer spherical reticulated shell with triodetic joints [J]. China Civil Engineering Journal, 2024, 57(10): 1–10. [4] ZHANG B Z, XIE Q F, LIU Y J, et al. Effects of gaps on the seismic performance of traditional timber frames with straight mortise-tenon joint: experimental tests, energy dissipation mechanism and hysteretic model [J]. Journal of Building Engineering, 2022, 58: 105019. doi: 10.1016/j.jobe.2022.105019 [5] PANOUTSOPOULOU L, MOUZAKIS C. Experimental investigation of the behavior of traditional timber mortise-tenon T-joints under monotonic and cyclic loading [J]. Construction and Building Materials, 2022, 348: 128655. doi: 10.1016/j.conbuildmat.2022.128655 [6] ZHANG H H, ZHANG P, ZHANG W K. A high-output performance mortise and Tenon structure triboelectric nanogenerator for human motion sensing [J]. Nano Energy, 2021, 84: 105933. doi: 10.1016/j.nanoen.2021.105933 [7] 张武昆, 谭永华, 高玉闪, 等. 周期性轻质多孔结构在能量吸收和振动方面的研究进展 [J]. 振动与冲击, 2023, 42(8): 1–19. ZHANG W K, TAN Y H, GAO Y S, et al. Research progress on energy absorption properties and vibration of periodic lightweight porous structures [J]. Journal of Vibration and Shock, 2023, 42(8): 1–19. [8] LI Q Q, GAN W J, HU L, et al. Spherical porous structures for axial compression [J]. International Journal of Mechanical Sciences, 2024, 261: 108681. doi: 10.1016/j.ijmecsci.2023.108681 [9] YIN H F, ZHENG X J, WEN G L, et al. Design optimization of a novel bio-inspired 3D porous structure for crashworthiness [J]. Composite Structures, 2021, 255: 112897. doi: 10.1016/j.compstruct.2020.112897 [10] 杜义贤, 李荣, 田启华, 等. 具有吸能和承载特性的多孔结构拓扑优化 [J]. 华中科技大学学报(自然科学版), 2019, 47(8): 108–113. DU Y X, LI R, TIAN Q H, et al. Topological optimization of porous structure with energy absorption and loading capability [J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2019, 47(8): 108–113. [11] 黄浩, 崔海林, 田晓丽, 等. 多孔结构对冲击波的衰减影响研究 [J]. 机械设计与制造工程, 2024, 53(1): 11–15. doi: 10.3969/j.issn.2095-509X.2024.01.003 HUANG H, CUI H L, TIAN X L, et al. Study on the effect of porous structure on shock wave attenuation [J]. Machine Design and Manufacturing Engineering, 2024, 53(1): 11–15. doi: 10.3969/j.issn.2095-509X.2024.01.003 [12] GAO J S, WANG X, TONG J W, et al. Large size translucent wood fiber reinforced PMMA porous composites with excellent thermal, acoustic and energy absorption properties [J]. Composites Communications, 2022, 30: 101059. doi: 10.1016/j.coco.2022.101059 [13] YAN L L, ZHU K Y, CHEN N, et al. Energy-absorption characteristics of tube-reinforced absorbent honeycomb sandwich structure [J]. Composite Structures, 2021, 255: 112946. doi: 10.1016/j.compstruct.2020.112946 [14] 杜晓晓. 木质衍生碳复合电极在微型超级电容器中的应用研究 [D]. 青岛: 青岛科技大学, 2023. DU X X. Research on the application of wood derived carbon composite electrode in micro-supercapacitors [D]. Qingdao: Qingdao University of Science and Technology, 2023. [15] 成瑶. “预埋种子-外延生长”策略制备无机-有机复合材料及其性能研究 [D]. 北京: 北京化工大学, 2019. CHENG Y. Study of preparation and application of inorganic-organic materials by “seeds embedded epitaxial growth” strategy [D]. Beijing: Beijing University of Chemical Technology, 2019. [16] 张宽, 郭晓宁, 张晓晶. 夹层结构榫卯T型接头弯曲破坏机理试验研究 [J]. 复合材料科学与工程, 2021(8): 95–99. ZHANG K, GUO X N, ZHANG X J. Experimental study on failure mechanism of sandwich T-joint by tenon-and-mortise subjected to flexure [J]. Composites Science and Engineering, 2021(8): 95–99. [17] 李腾, 邓庆田, 李新波, 等. 多孔柱准静态压缩力学行为和吸能特性分析 [J]. 塑性工程学报, 2022, 29(2): 204–211. doi: 10.3969/j.issn.1007-2012.2022.02.029 LI T, DENG Q T, LI X B, et al. Analysis of quasi-static compression mechanical behavior and energy absorption characteristics of porous columns [J]. Journal of Plasticity Engineering, 2022, 29(2): 204–211. doi: 10.3969/j.issn.1007-2012.2022.02.029 -
计量
- 文章访问数: 21
- HTML全文浏览数: 21
- PDF下载数: 0
- 施引文献: 0