-
碳纤维增强聚合物(carbon fibre-reinforced polymer, CFRP)复合材料以其高比强度、高比模量、耐腐蚀、抗疲劳以及良好的可设计性等突出特点,广泛应用于航空航天、发电储能和国防装备等领域[1–4],并逐渐成为警用装备发展的基础性、战略性和先导性材料。然而,CFRP复合材料的固有脆性严重限制了其抗冲击性能[5-6]。随着爆炸袭击形式的多样化,对CFRP构件的抗冲击性能提出了更高的要求。深入理解CFRP复合材料的失效机制进而开展装备研发,是预防爆炸冲击导致的灾难性事故的关键途径。高速破片侵彻破坏是爆炸环境下CFRP复合材料常见的破坏形式,其引发的内部失效往往是导致灾难性事故的重要隐患[7]。然而,CFRP复合材料在冲击载荷下的失效机制十分复杂,主要通过层间分层、基体开裂、纤维断裂、纤维脱粘和纤维滑移等损伤失效模式的协同作用来吸收冲击能量,与传统材料的损伤失效模式存在较大差异[8]。此外,其纤维相与树脂相的应变率敏感性差异较大,可能导致CFRP复合材料在随机破片侵彻下的失效模式呈现显著差异。目前,已有较多关于CFRP复合材料抗侵彻性能的研究。Zhou等[9]研究了冲击角度、冲击器直径、铺层方向和堆叠顺序等因素对CFRP层合板低速冲击响应的影响,通过凹痕深度、分层损伤投影面积和能量耗散等参数评估了损伤特性及其相关性。彭捷等[10]利用单级轻气炮开展了CFRP层合板高速冲击实验,通过高速摄影仪监测撞击过程,采用C-scan技术和显微镜表征损伤区域,探究了CFRP层合板的能量吸收率、损伤形式及能量吸收机制随冲击速度的变化规律。然而,实验手段获取侵彻历程信息的成本高昂,且弹丸穿透靶板后产生的碎片会对弹丸轨迹和剩余速度的监测造成干扰。随着材料本构的发展成熟和计算方法的不断优化,数值模拟的精度和可靠性显著提升,有限元分析(finite element analysis, FEA)方法已成为实验研究的有效补充手段[11]。尽管FEA方法在CFRP复合材料抗冲击性能研究中得到广泛应用[12–13],但其在随机破片侵彻条件下的吸能机制和破坏机制尚不明确。因此,利用FEA方法开展高速破片侵彻CFRP复合材料的仿真研究具有重要意义。本研究基于ABAQUS/Explicit 2017内嵌的CONWEP程序建立爆炸载荷作用下钛合金破片运动分布的FEA模型,设定破片速度和破片倾角;构建CFRP复合材料在破片冲击下的分析模型,考虑速率依赖性并采用三维Hashin失效准则来评估层合板的力学性能,通过自定义的Vumat子程序计算FEA模型;通过与实验结果对比,验证FEA模型的有效性;通过分析破片剩余速度历程,研究冲击速度和破片倾角对高速冲击条件下CFRP层合板吸能效果的影响;通过可视化内部损伤破坏过程和变形区域,揭示CFRP复合材料在不同冲击速度和破片倾角下的吸能机制以及差异化吸能效果的内在原因。
全文HTML
-
由于CFRP层合板的非均质性、界面分层以及冲击速度敏感性等特点,其在高速冲击作用下的动态力学响应十分复杂。为降低实验成本与风险,并可视化复合材料在破片侵彻过程中的内部结构、损伤演化和失效机制以及贯穿后的破坏模式,本研究基于ABAQUS构建了CFRP层合板的弹道冲击模型,并通过自定义的Vumat子程序计算FEA模型。
-
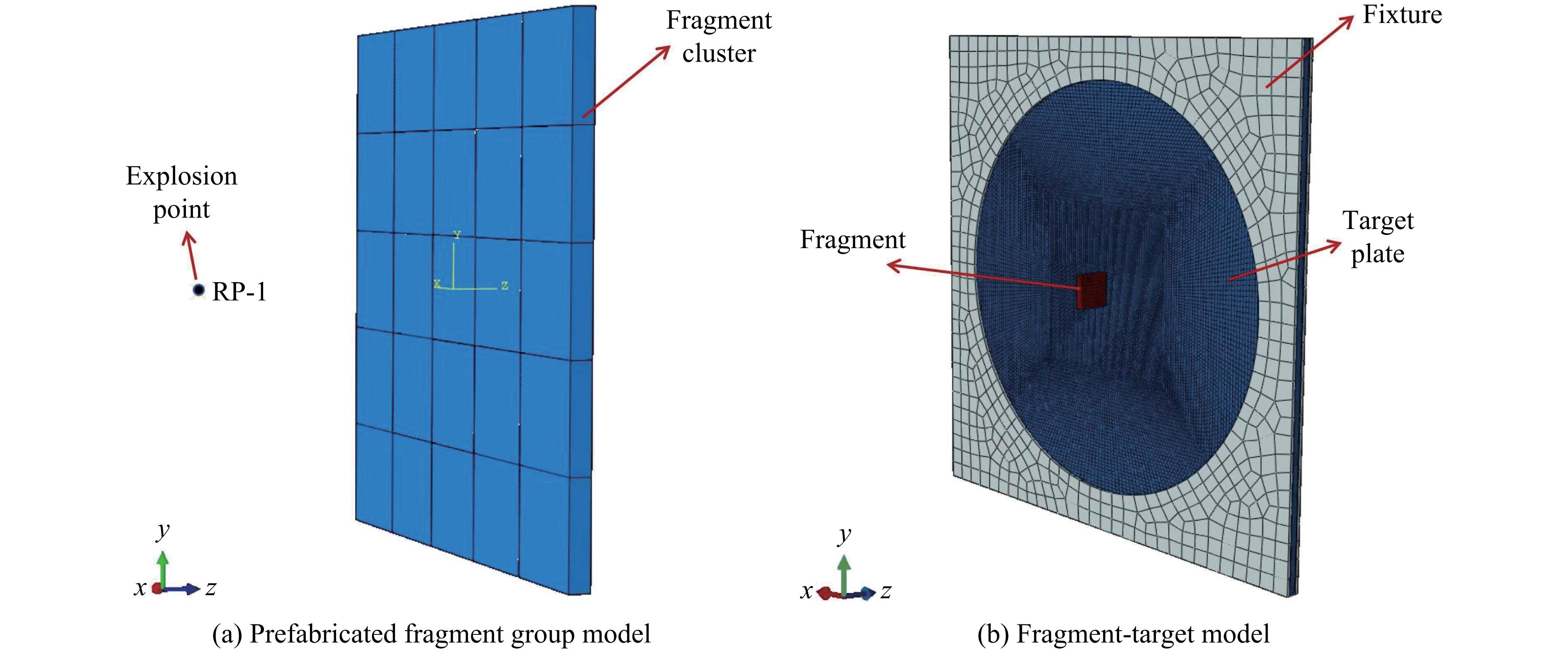
基于ABAQUS内嵌的CONWEP程序建立爆炸载荷作用下钛合金破片运动分布模型,该半经验方法无需考虑炸药类型,可减少计算时间。如图1(a)所示,模型主要由炸点(RP-1)和破片群组成。在爆炸暴恐事件中,常见的爆炸装置为体积小、当量低的简易爆炸装置。为此,设置炸点距破片群中心50 mm,选取500、1 000、1 500和2 000 g的TNT当量,破片尺寸设定为20 mm×20 mm×4 mm,破片密度为4.4 g/cm3,破片之间采用通用接触算法。图1(b)为CFRP层合板的破片冲击模型,主要由破片、靶板和2个夹具组成。参考ASTM 7136M中试样4~6 mm的厚度标准,该工作中靶板由24层纤维/环氧复合材料组成,厚度为4.56 mm,采取[0/90]12铺层方式。另外,为避免尺寸效应的影响(破片与靶板的长度比值应大于1/10),靶板尺寸设定为300 mm×300 mm。基于CONWEP模型的计算结果,赋予单个破片不同的倾角和初速度(vI),初速度范围(195~392 m/s)为不同当量TNT下破片最高速度的集合,使其仅沿z方向自由运动(vx=vy=0)。夹具孔洞的直径设置为250 mm,固定夹具在任意方向的自由度,从而固定靶板并对其施加一定的压力。
CFRP层合板的材料参数如表1 所示,其中:ρ为密度,E11、E22、E33为弹性模量,μ12、μ13、μ23为泊松比,G12、G13、G23为剪切模量,F1T、F2T、F3T为拉伸强度,F1C、F2C、F3C为压缩强度,S12、S13、S23为剪切强度,Gf1、Gf2、Gf3为断裂韧性。由于破片和夹具的刚度远大于靶板,可设定为刚体。模型采用 C3D8R 网格,为提高计算效率,采用差异性网格划分,如图1(b)所示,靶板中间密集区的网格尺寸为2 mm,外围网格尺寸为6 mm。以通用接触算法模拟破片、靶板与夹具之间的相互作用,切向设置摩擦因数为 0.3 的惩罚摩擦公式,法向设置“硬”接触算法。
-
纤维增强聚合物复合材料通常被认为是横观各向同性材料[15]。考虑到CFRP复合材料在高速冲击下的连续应变,采用基于应变的三维Hashin失效准则判断损伤起始。在高速冲击下,CFRP复合材料的力学性能通常会表现出比较明显的应变率效应,其中强度的速率依赖关系为
式中:
$ S $ 为动态强度,MPa;$ {S_0} $ 为准静态强度,MPa;$ \dot \varepsilon $ 为当前时间步的应变率,s−1;$ {\dot \varepsilon _0} $ 为参考应变率,s−1;$ C $ 为应变率硬化修正系数。采用基于连续介质力学的非线性本构模型描述材料损伤的发生与演变过程。为降低高速冲击过程中网格对大变形的敏感性,在损伤演化方程中引入断裂能
$ {G_{i}} $ (i = 1,2,3),损伤演化方程为[16]式中:d为网格损伤;
$ {\sigma _{{ij}}} $ 为材料的二阶应力张量分量,MPa;$ {\varepsilon _{{kl}}} $ 为材料的二阶应变张量分量;f为应力。下标L、T和Z表示网格上正交坐标系的3个方向,下标t和c分别表示拉伸和压缩,上标f,t和f,c分别表示拉应力和压应力。采用Murakami-Ohno模型描述CFRP复合材料的损伤演化,沿L、T和Z方向的损伤分别为
$ \boldsymbol{C}\left(D\right)\mathit{_{ijkl}} $ 为四阶损伤刚度张量,表示为在高速冲击过程中,分层破坏被认为是复合材料层合板的主要破坏模式,对层合板的抗冲击性能有显著影响。因此,设置实际厚度为 0.001 mm 的内聚力单元模拟界面层,采用二次牵引准则确定界面初始损伤,即
式中:
$ {t_{\text{n}}} $ 为内聚力单元的法向应力分量,MPa;$ {t_{\text{s}}} $ 为内聚力单元的第一剪切方向应力分量,MPa;$ {t_{\text{t}}} $ 为内聚力单元的第二剪切方向应力分量,MPa;$ t_{\text{n}}^{\text{0}} $ 为法向界面强度,MPa;$ t_{\text{s}}^{\text{0}} $ 为第一剪切方向界面强度,MPa;$ t_{\text{t}}^{\text{0}} $ 为第二剪切方向界面强度,MPa。当二次应力破坏函数的值达到1.0时,界面开始发生损伤。界面的损伤演化由Benzeggagh-Kenane定律控制
式中:
$ G_{\text{n}}^{\mathrm{C}} $ 为法向临界断裂能量释放速率,N/mm;$ G_{\text{s}}^{\mathrm{C}} $ 为第一剪切方向临界断裂能量释放速率,N/mm;$ G_{\text{t}}^{\mathrm{C}} $ 为第二剪切方向临界断裂能量释放速率,N/mm;$ G_{\text{n}}^{} $ 为$ {t_{\text{n}}} $ 做的功,mJ;$ G_{\text{s}}^{} $ 为$ {t_{\text{s}}} $ 做的功,mJ;$ {G_{\text{t}}} $ 为$ {t_{\text{t}}} $ 做的功,mJ;η为材料系数。 -
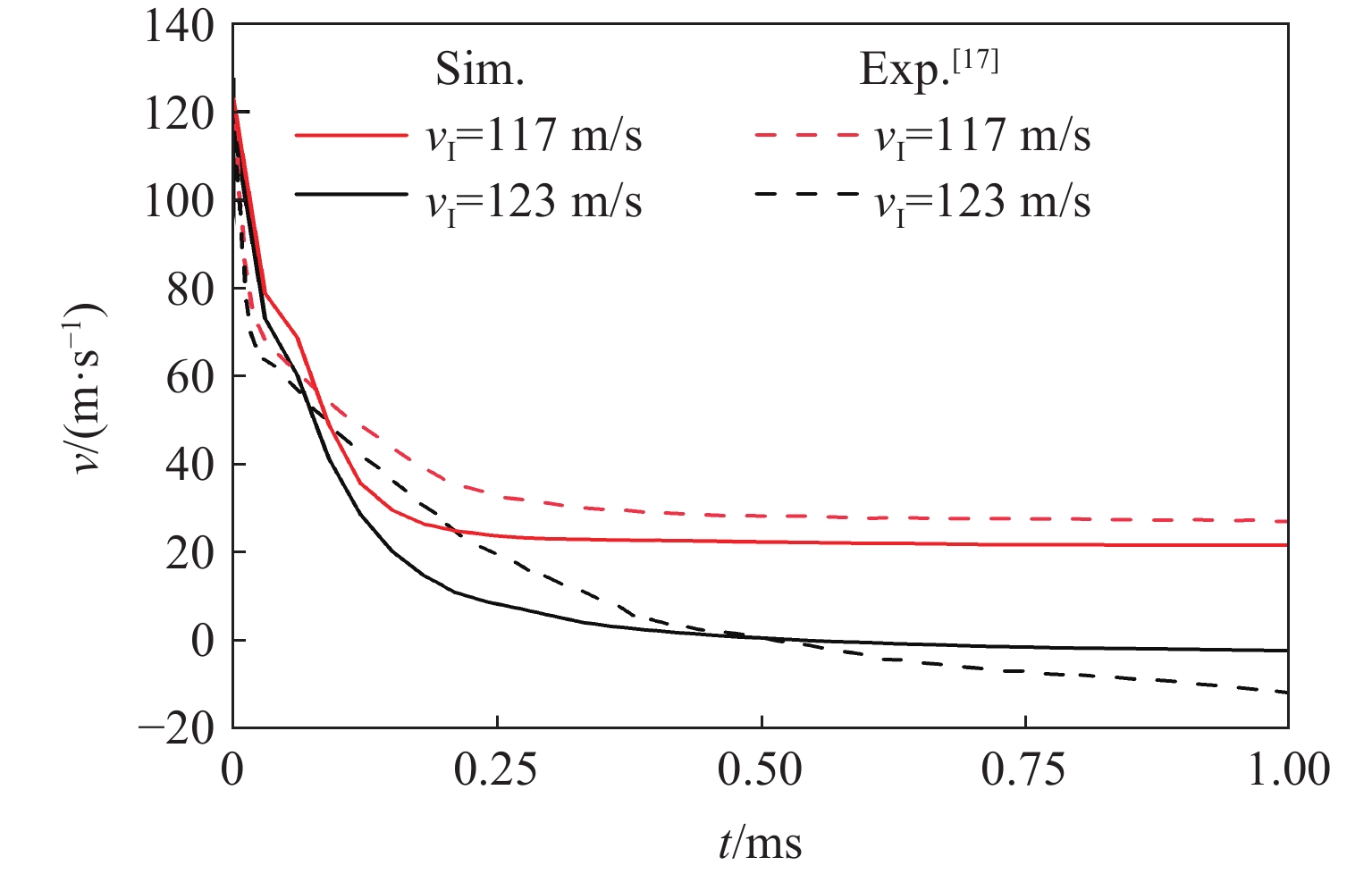
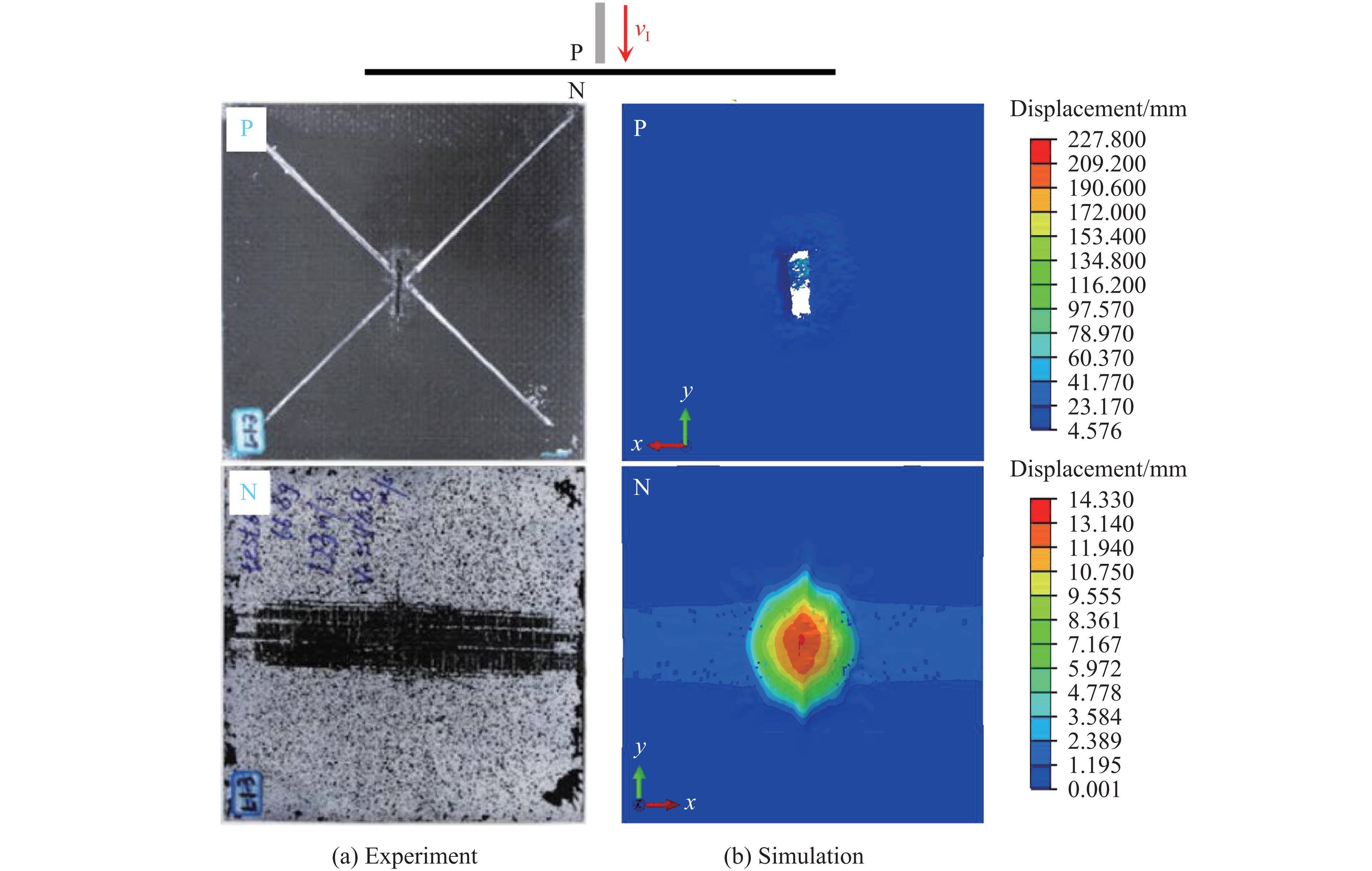
采用数值模拟方法对Du等[17]的靶板类型(L45)和实验工况进行复现,将模拟结果与实验结果进行对比。如图2所示,模拟所得速度阈值与文献[17]一致,模拟与实验得到的速度历程曲线趋同,最大误差为7.3 m/s,相对误差小于10%。值得一提的是,同一时刻两种工况的模拟结果均略小于实验结果,其成因可能是实验中层合板试样存在缺陷以及破片角度难以精准控制。此外,图3展示了L45靶板撞击面和背面的冲击破坏模式。靶板撞击面弹孔呈矩形,破坏区域明显小于背面,靶板背面破坏区域有明显的分层破坏和面外变形,所得破坏特征与文献[17]相同。结果表明,该有限元模型很好地描述了CFRP层合板的弹道冲击响应和损伤破坏行为,验证了有限元模型的有效性。
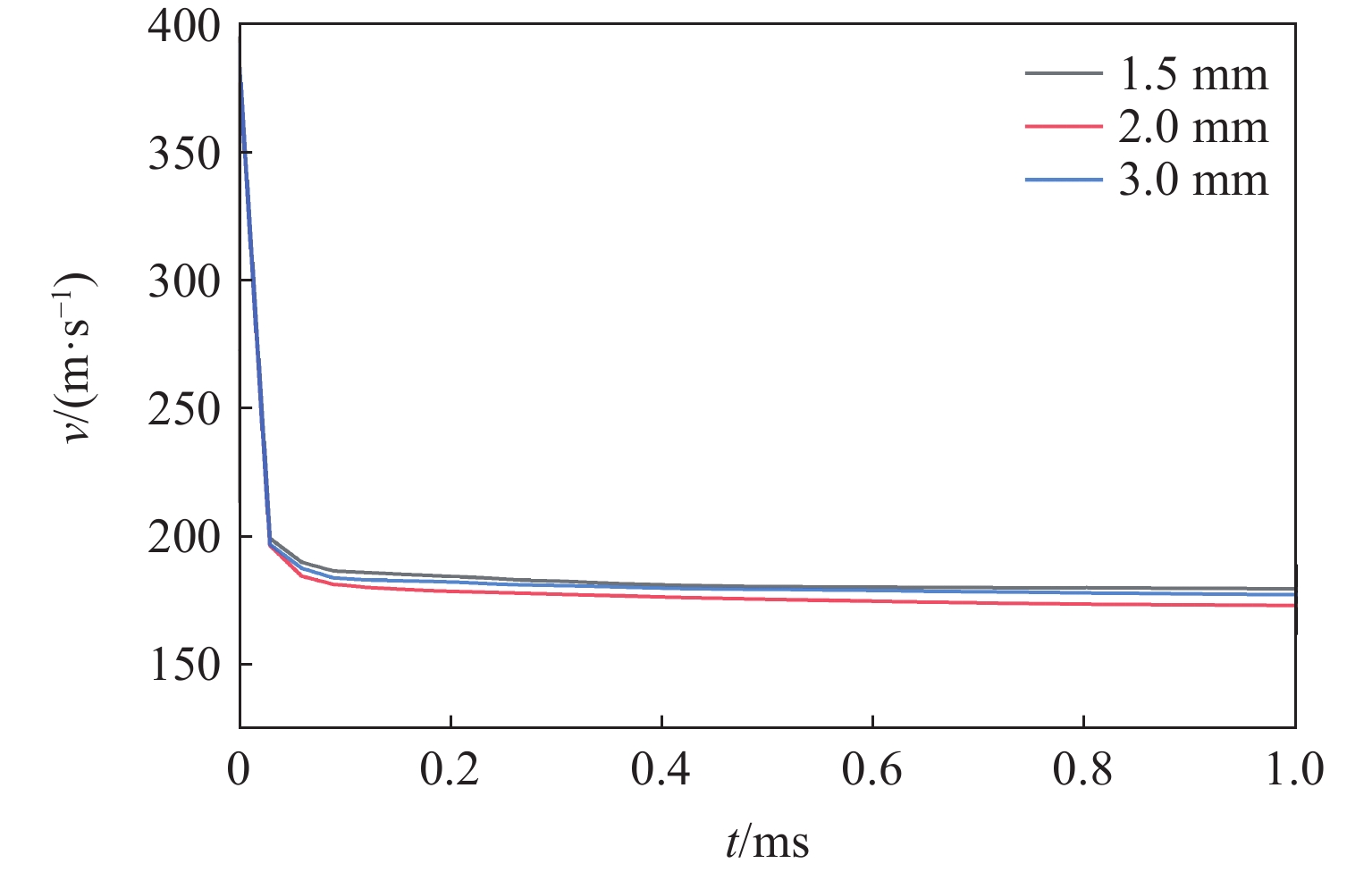
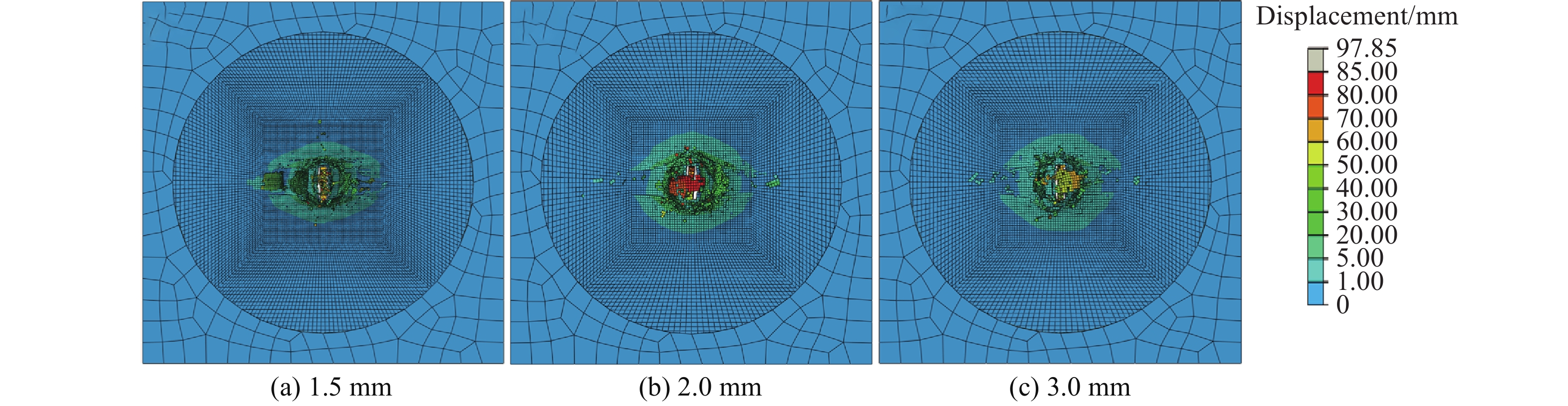
将靶板中心区域的网格尺寸分别设定为1.5、2.0和3.0 mm,对比输出的速度-时间曲线和变形区域,对网格收敛性进行了验证。如图4所示,3种网格密度下的破片速度-时间曲线基本一致。由图5可知,3种网格密度下靶板在0.3 ms时的变形区域和破坏形貌十分接近,可忽略网格尺寸的影响。
1.1. 有限元模型
1.2. 材料模型
1.3. 数值验证
-
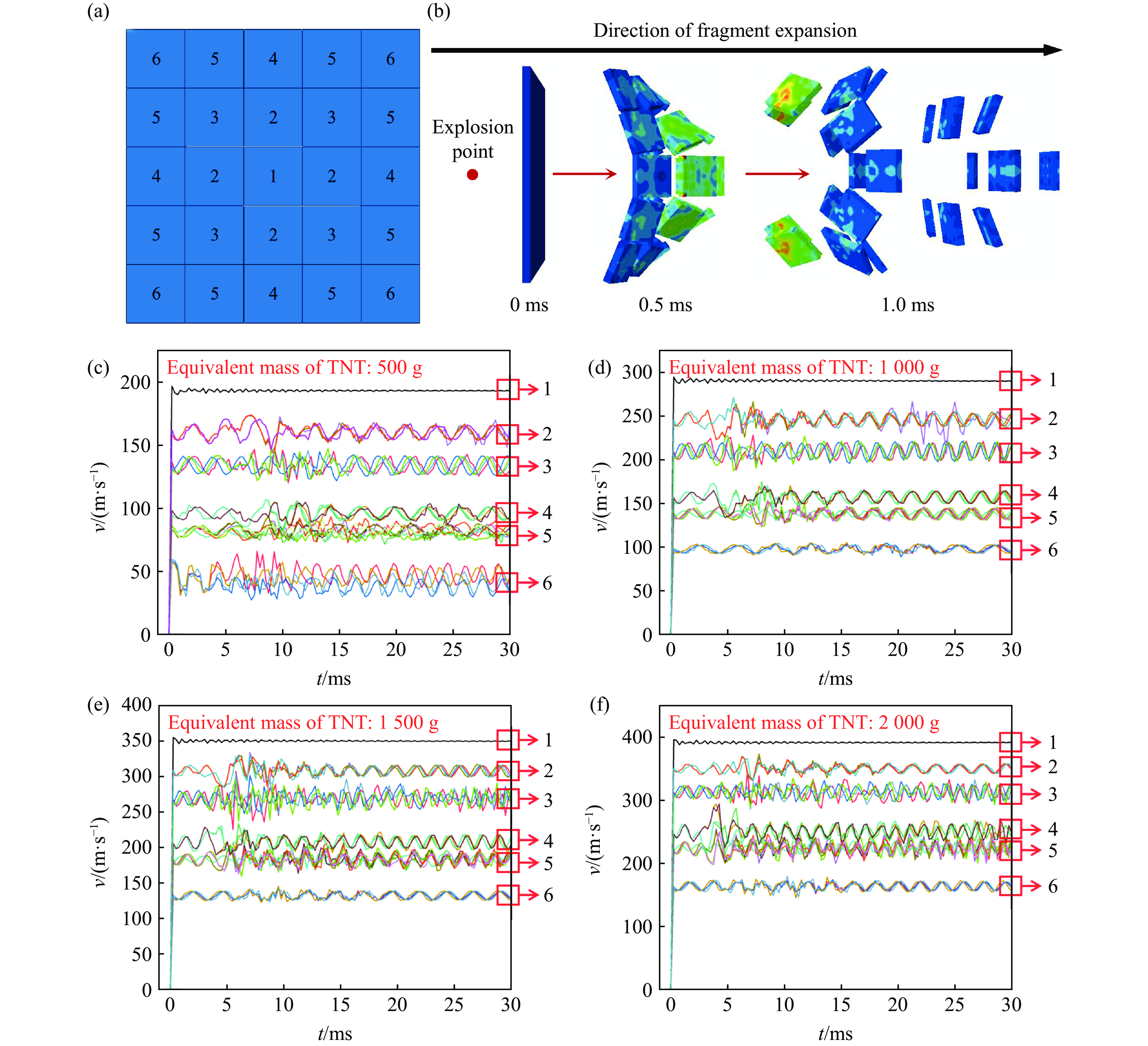
破片是爆炸杀伤的主要形式之一,探究影响破片杀伤效果的因素具有重要价值。为了有效掌握爆炸后破片的扩散特性,还原破片对CFRP层合板的毁伤效果,在模拟时先采用CONWEP程序对预制破片施加爆炸载荷,并设定不同的TNT当量,由此获取特定破片在不同TNT当量下的冲击速度和飞行姿态。在实际爆炸中,破片距爆点的距离不同,可能产生不同的毁伤效果。如图6(a)所示,对预制破片群的破片位置进行标注,破片距爆点的距离随着标注数字的增大而增加。可以发现,不同数字标注对应的破片在爆炸载荷作用下具有不同的飞行姿态(图6(b))。此外,正如图6(c)~图6(f)所示,在500、1 000、1 500和2 000 g的TNT当量下,破片群具有不同的冲击速度,分别为40~195、94~293、128~350和163~392 m/s。在相同TNT当量下,不同位置破片的冲击速度存在明显差异。
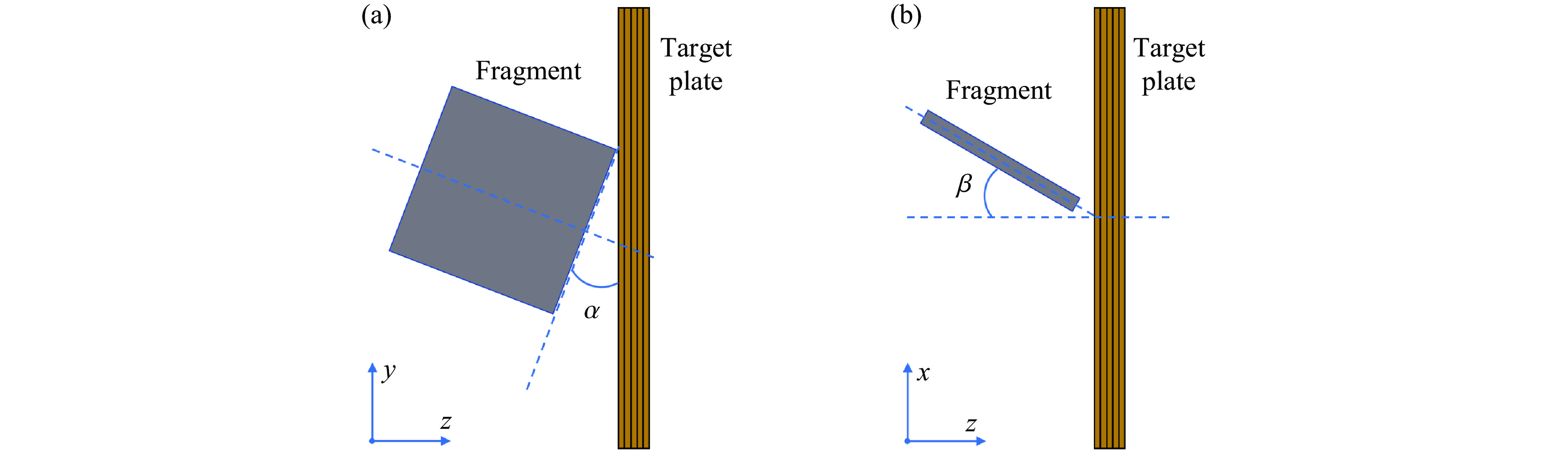
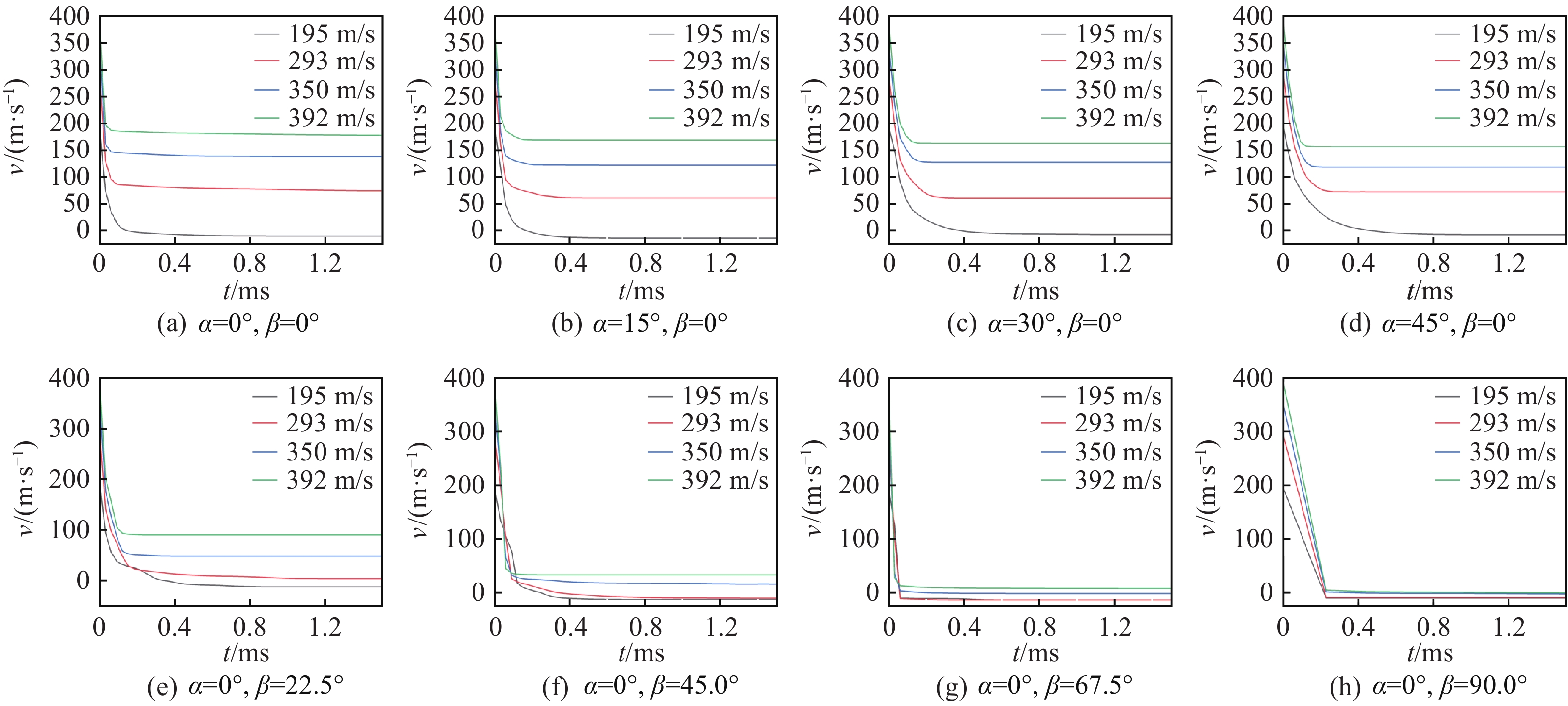
爆炸载荷下破片往往具有随机的飞行姿态,破片撞击靶板时的倾角可能是影响毁伤效果的重要因素。如图7所示,本工作分别考虑了y-z平面和x-z平面上破片与靶板间的倾角,将其定义为α和β,其中,α的取值为0°、15°、30°和45°,β为0°、22.5°、45.0°、67.5°和90.0°。将β=0°时被不同倾角α破片撞击的靶板定义为S-A型试样,将α=0°时被不同倾角β破片撞击的靶板定义为S-B型试样,分别对其进行编号。设破片在500、1 000、1 500和2 000 g的TNT当量下的最高速度为初速度,图8为不同倾角破片的冲击速度-时间曲线。当β=0°时,多种倾角α破片的剩余速度均随着初速度的增大而显著增大,可以认为S-A型试样均具有显著的冲击速度敏感性,如图8(a)~图8(d)所示。另一方面,当α=0°,随着β的增大,破片的剩余速度-时间曲线趋于重合,表明随着β的增加,S-B型试样的冲击速度敏感性逐渐降低,如图8(e)~图8(h)所示。值得一提的是,当β=90°时,195~392 m/s速度范围内的破片均无法穿透靶板(见图8(h))。详细试样信息和模拟结果见表3,其中vR为剩余速度。
-
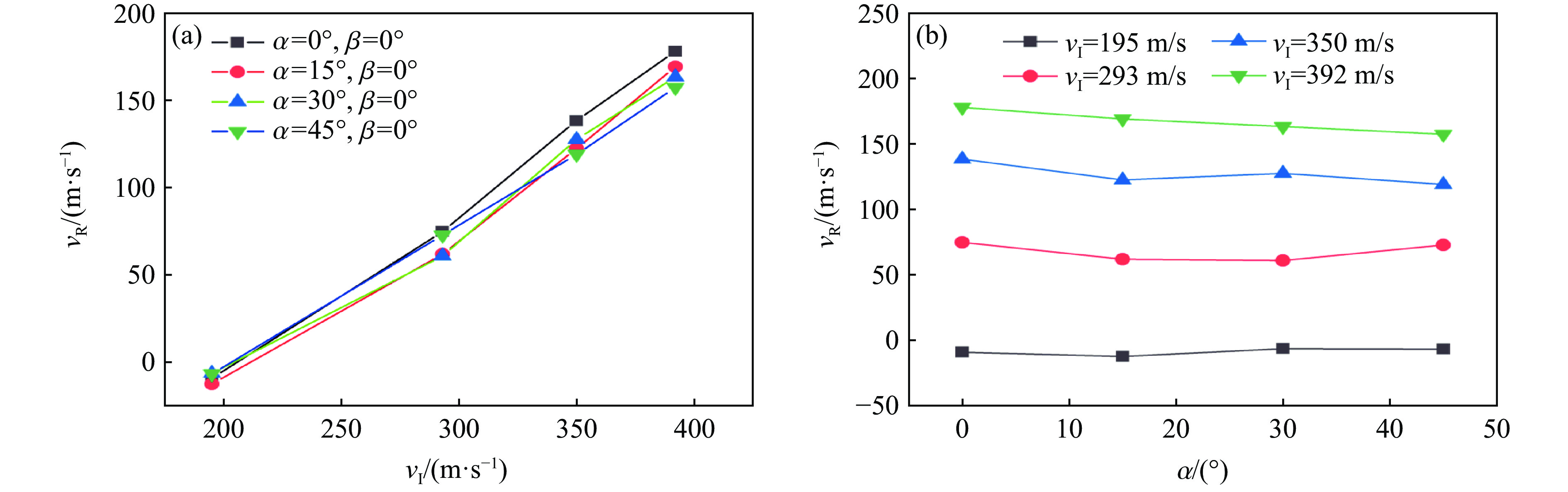
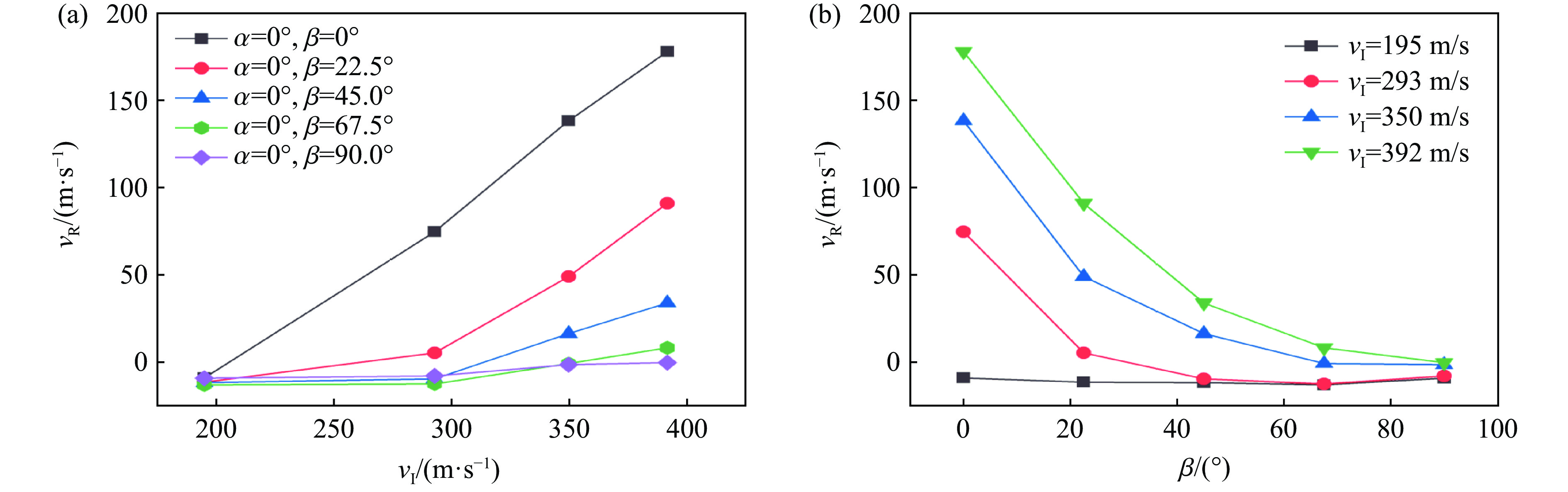
首先,探究了倾角α对CFRP层合板冲击速度敏感性的影响。如图9(a)所示,相同β、不同α下,破片的剩余速度均随着初速度的增大而增大,剩余速度和初速度具有相似的变化趋势。在195、293、350和392 m/s的冲击速度下,不同α的破片间剩余速度的最大差值占初速度的比值分别为3.1%、4.8%、5.5%和5.3%,较小占值意味着相近的剩余速度,同时也表明不同α的破片冲击下靶板相似的冲击速度敏感性。图9(b)展示了不同冲击速度下破片剩余速度随α的变化趋势,可以发现,随着α的增大,破片剩余速度并未展现明显的变化趋势,并且具有相似的值,表明α不是影响层合板试样吸能效果的主要因素。值得注意的是,在195 m/s的冲击速度下,破片剩余速度均为负值,表明在该工况下,500 g的TNT当量炸药不足以使破片击穿CFRP层合板,而1 000、1 500和2 000 g的TNT当量有部分破片击穿CFRP层合板。
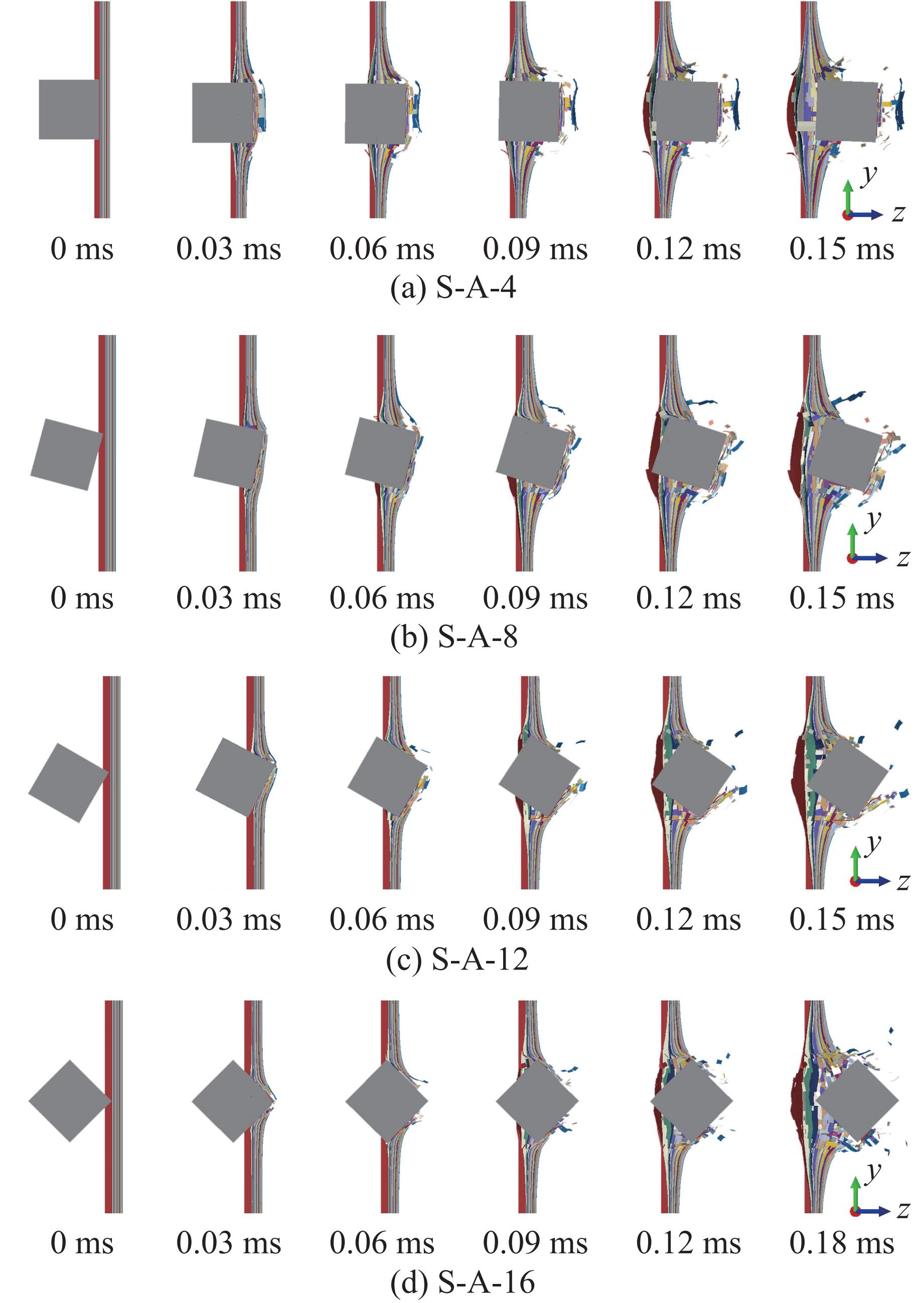
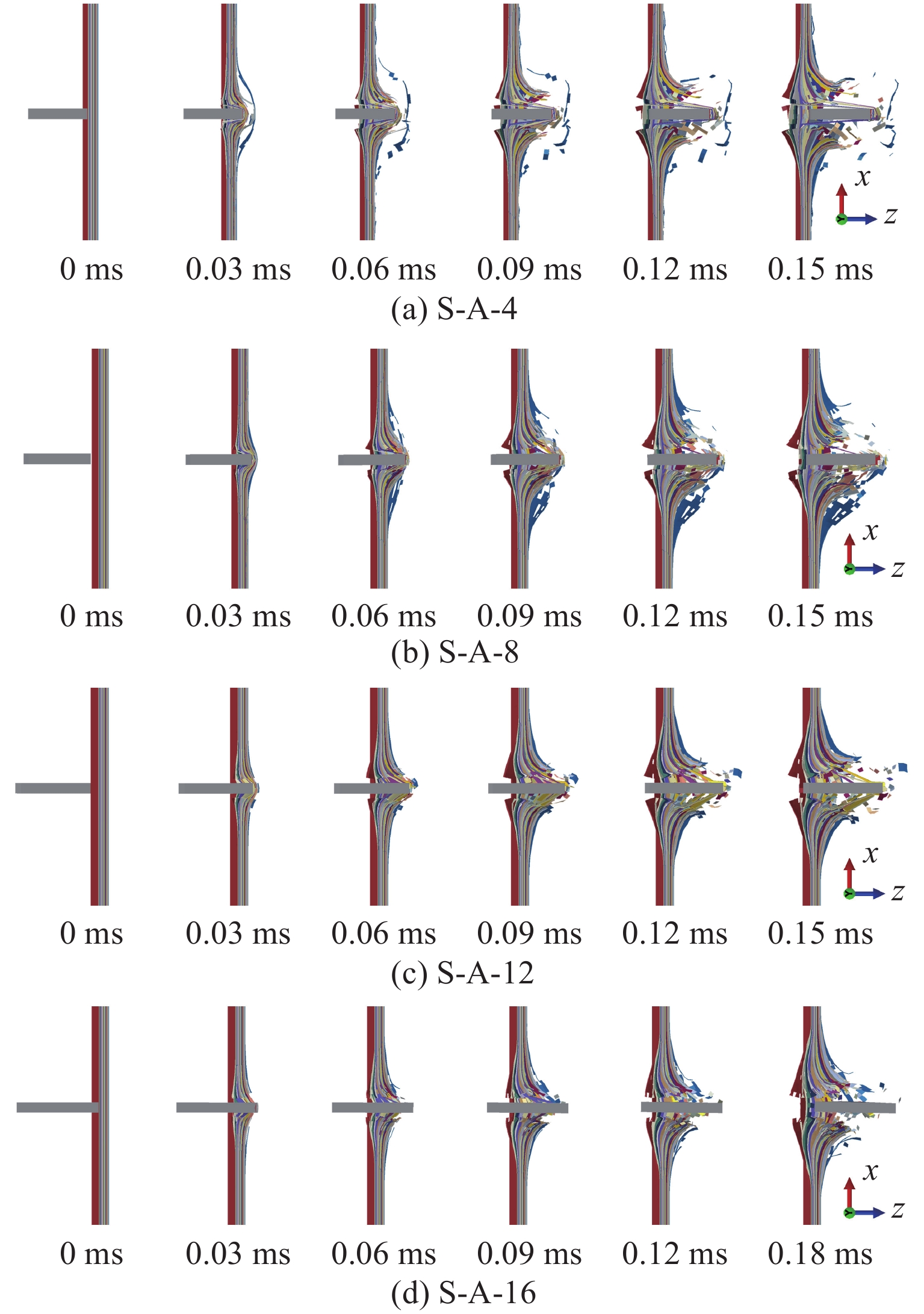
为探究图9所示结果的成因,可视化并分析了392 m/s冲击速度下破片侵彻S-A型试样的破坏过程。如图10所示,不同倾角α的破片在侵彻过程中,α没有发生明显变化。尽管CFRP层合板具有优异的比强度和比刚度,但其固有脆性使其在破片侵彻过程中快速发生失效破坏[18–20],甚至难以对破片的α造成明显改变。从图10和图11可以看出,在破片侵彻过程中,所有倾角α下CFRP层合板试样的破坏模式几乎一致,均为正面压缩破坏和背面拉伸破坏[21],且破坏程度十分相似。可以认为,所有倾角α下CFRP层合板试样具有相似的冲击速度敏感性和吸能效果。
值得一提的是,如图10所示,仅在侵彻初始阶段(0.3~0.6 ms),CFRP层合板试样正面的破坏模式有所差异。其中,S-A-4试样与破片发生面面接触,而其他3种试样则先与破片的一角发生接触,后者更易造成应力集中。然而,4种破片与试样的接触面积并没有显著差异。此外,CFRP层合板试样吸能时的破坏模式主要表现为层间分层和背面纤维的拉伸破坏[22],不同倾角α的破片在侵彻过程中导致的正面破坏模式的差异难以对CFRP层合板的吸能特性造成明显影响。
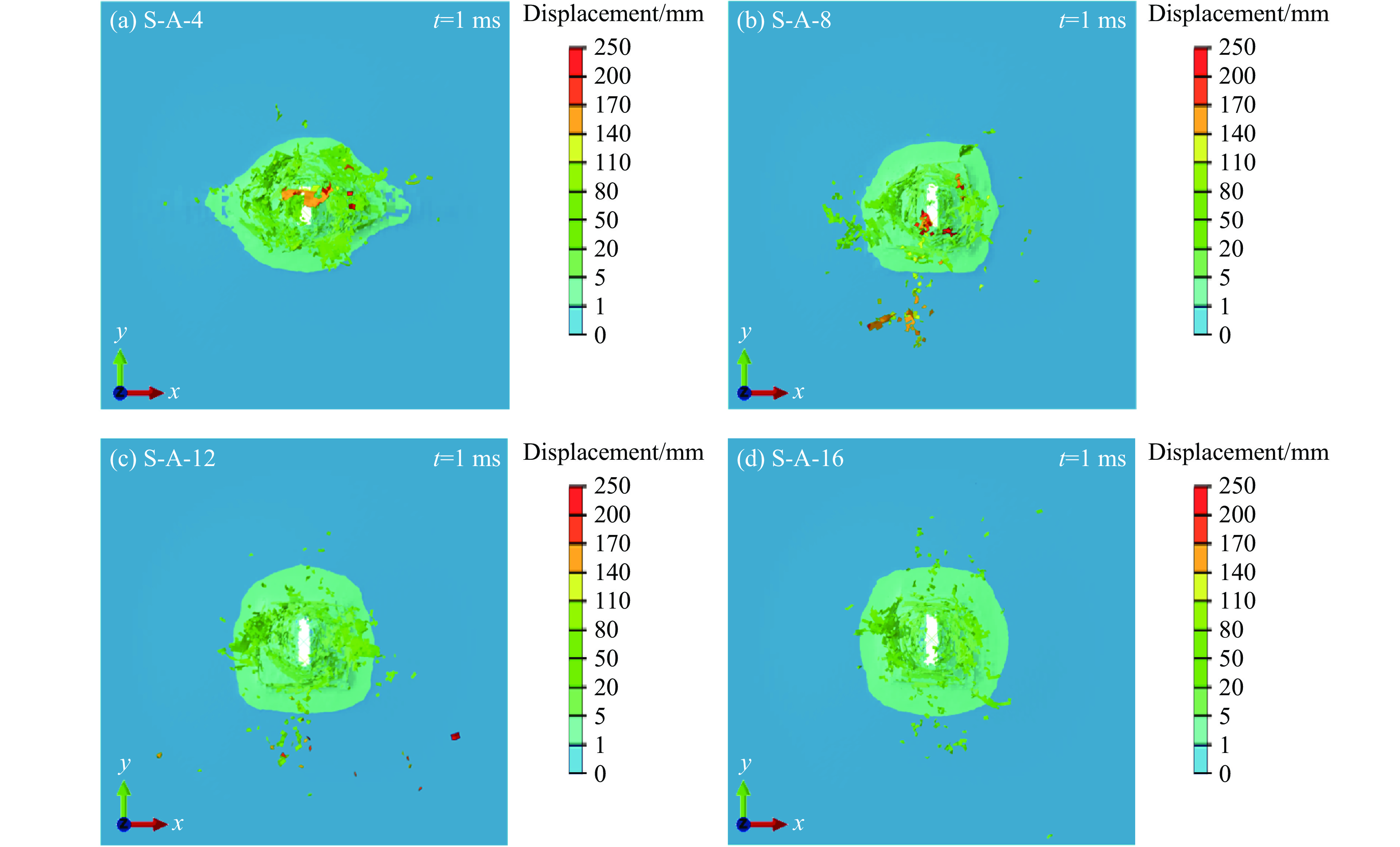
图12给出了试样背面的破坏形态。所有试样都形成了一个由破片冲击引起的压缩破坏导致的小尺寸矩形破坏区域。此外,背面变形区域呈现出相似的变形程度和一致的纤维拉伸破坏特征,变形是CFRP层合板吸收冲击能量的主要机制之一。因此,相似的变形程度是导致不同倾角α的破片冲击下CFRP层合板试样具有相似冲击速度敏感性和吸能性能的重要原因。
-
进一步探究了倾角β对CFRP层合板冲击速度敏感性的影响。如图13(a)所示,具有相同α,不同β的破片,其剩余速度随着初速度的增大而增大;不同于具有倾角α的破片,随着β的增大,破片剩余速度的增长趋势逐渐放缓,呈现出显著差异。可以认为,β对CFRP层合板冲击速度敏感性的影响较大。另一方面,图13(b)展示了不同冲击速度下,破片剩余速度随β的变化趋势。可以发现,在195 m/s的冲击速度下,破片剩余速度均为负值,表明在该工况下500 g的TNT当量炸药不足以使破片击穿CFRP层合板。在293~392 m/s的冲击速度范围内,破片剩余速度均随着β的增大而减小,并在β=90.0°时降为负值,表明倾角β对CFRP层合板的吸能性能具有显著影响。在1 000、1 500和2 000 g的TNT当量炸药爆炸后存在部分破片击穿CFRP层合板。
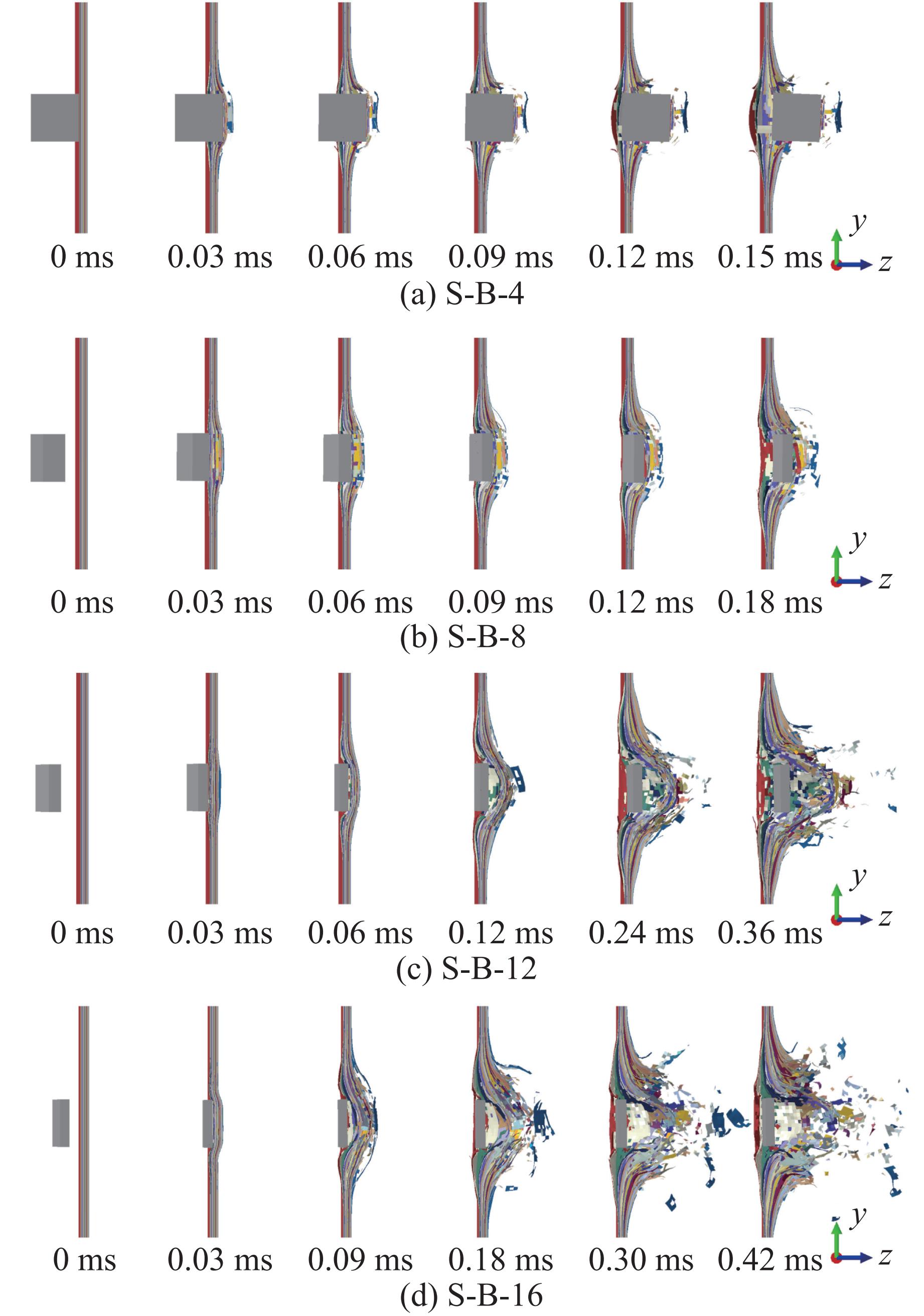
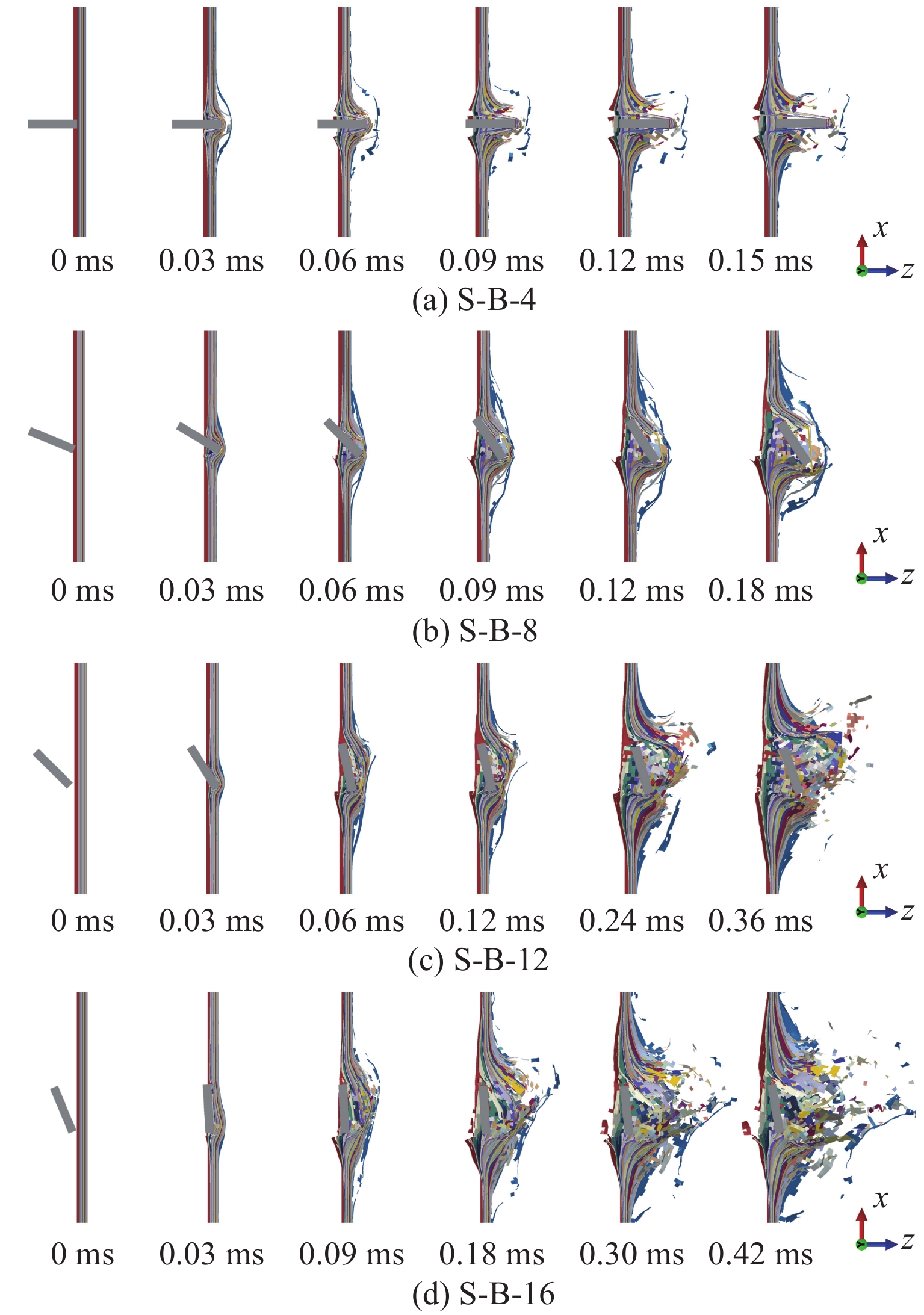
为探究图13所示结果的成因,可视化并分析了392 m/s冲击速度下S-B型试样的破片侵彻破坏过程。由图14可知,尽管4种试样均展现了相似的破坏模式,即正面发生压缩破坏,背面则以拉伸破坏为主[21],但随着β由0°增大到67.5°,破片贯穿层合板所需时间明显增加,层合板的破坏程度显著增大。这种现象与破片剩余速度随β的增大而减小的趋势相符合,表明更大范围的破环区域和更长的破坏过程使得层合板对破片动能的吸收效果更好[23–24]。另一方面,不同于图10在侵彻过程中几乎没有变化的α,图15的侵彻过程中破片的倾角β均发生了明显变化。β的变化导致破片与靶板在撞击初期的接触面积增大,较大的接触面积可有效避免应力集中以及应力集中引起的快速损伤破坏,并促进冲击能量的耗散。其中,β=67.5°时破片与靶板具有更大的接触面积,破片的剩余速度较低。
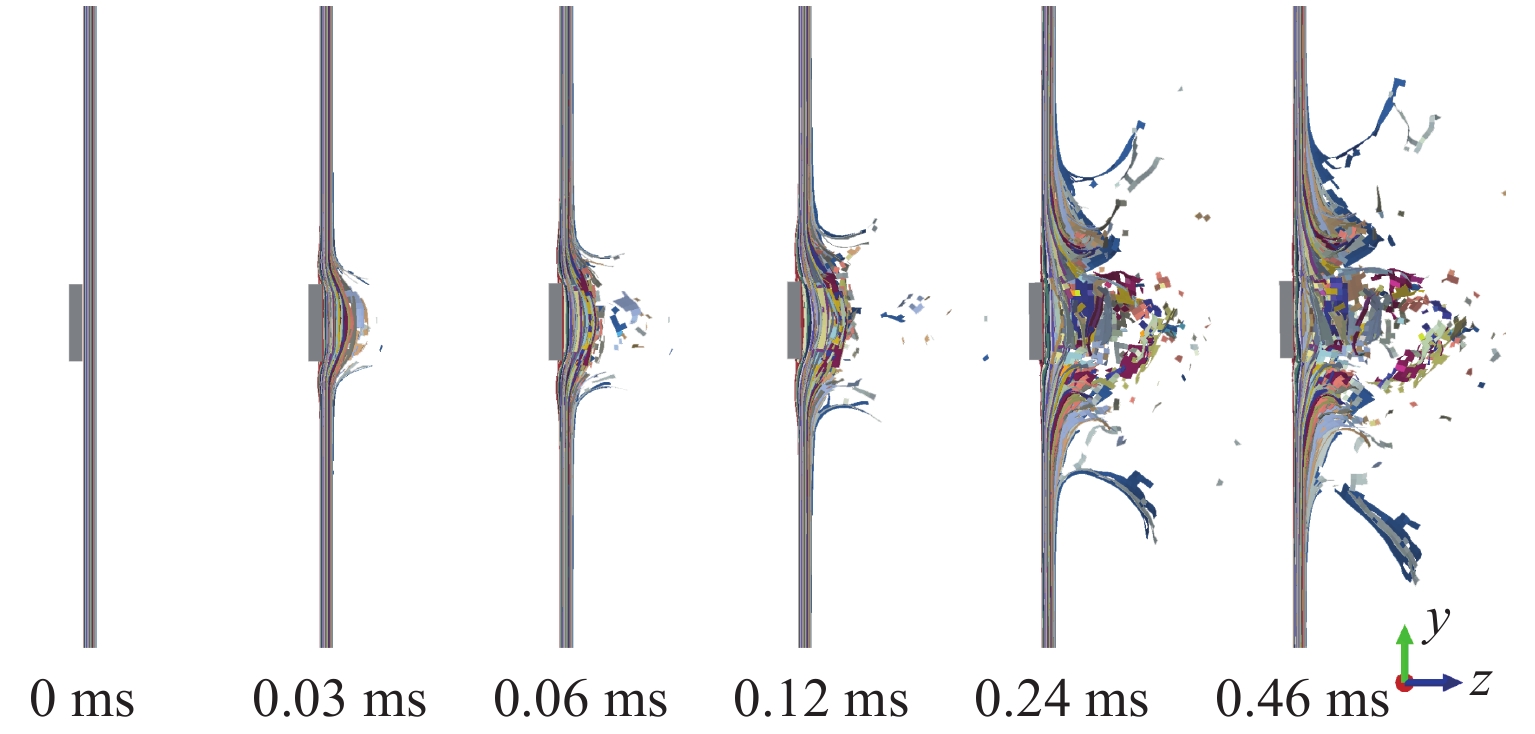
另一方面,如图16所示,S-B-20试样中破片未穿透靶板,靶板正面受破片压力后变形,随后发生回弹。然而,破片撞击靶板产生的应力波传播到靶板背部的自由表面后反射形成拉伸波,导致靶板背面纤维层发生显著的分层破坏和拉伸破坏,造成较大损伤。模拟结果表明,当β=90.0°时,破片以较大的接触面积冲击CFRP层合板,难以将其贯穿,但仍可以使层合板发生严重的损伤破坏。
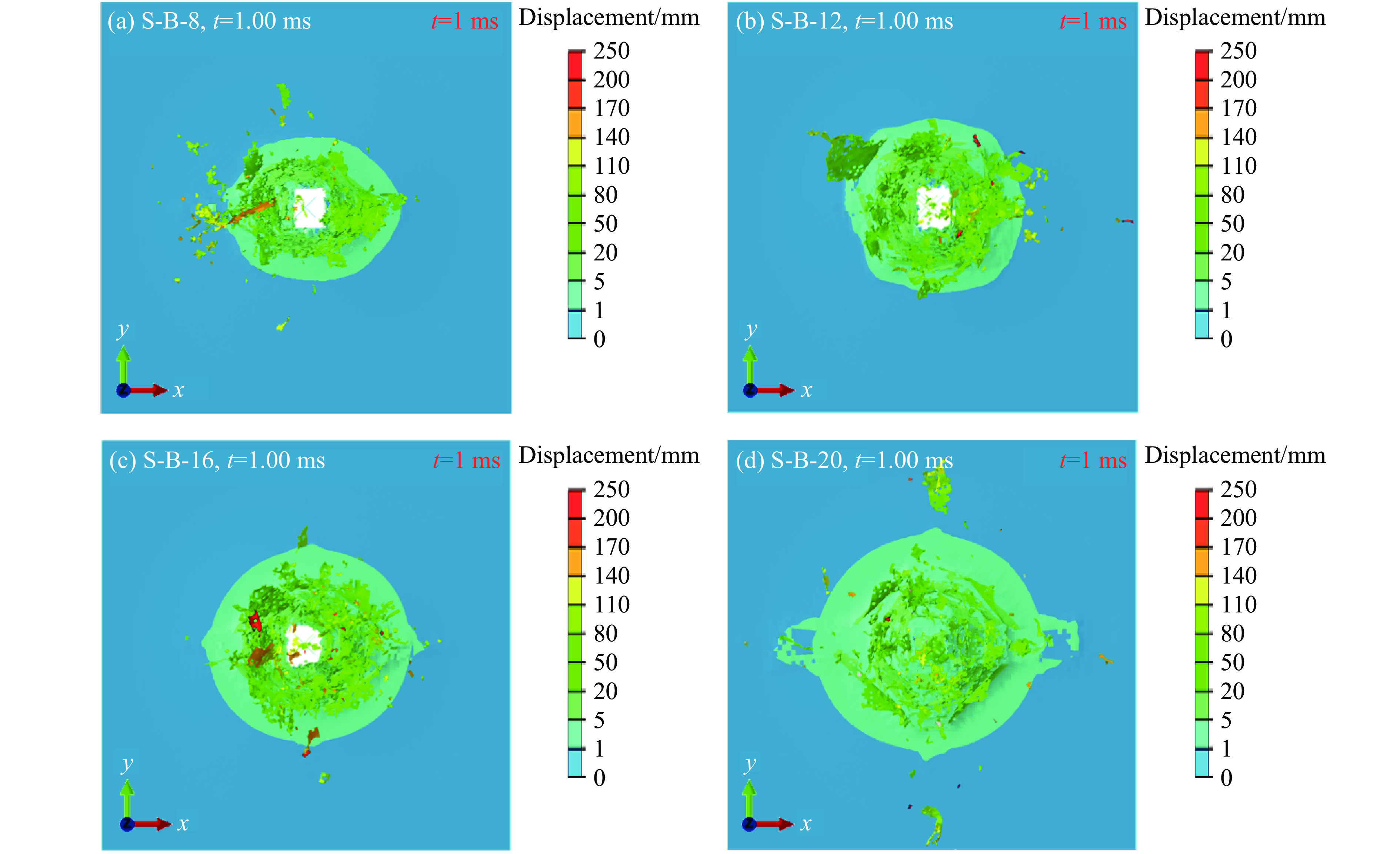
图17展示了不同倾角β的破片冲击下试样背面的变形程度。不同于图12中细长的弹孔形态,图17中的弹孔尺寸更大,表明试样正面在具有倾角β的破片冲击下发生了更大程度的压缩破坏。另一方面,试样背面的变形区域随着β的增大而显著增大,意味着更大程度的能量吸收[25]。因此,较大程度的变形是导致较大倾角β的破片冲击下CFRP层合板试样具有较强吸能效果的重要原因,也是导致S-B型试样间差异化冲击速度敏感性的关键因素。
2.1. 破片扩散状态及能量吸收
2.2. 倾角α对CFRP层合板冲击速度敏感性和吸能效果的影响
2.3. 倾角β对CFRP层合板冲击速度敏感性和吸能效果的影响
-
通过FEA方法研究了破片的冲击速度和倾角对高速冲击下CFRP层合板吸能效果和破坏模式的影响,对其冲击速度敏感性和吸能机制进行了分析。结果表明,FEA模型可有效模拟CFRP层合板的破片冲击响应。预制破片在不同TNT当量和距爆点距离下具有差异明显的初速度和撞击倾角。S-A型试样均具有明显的冲击速度敏感性,CFRP复合材料的吸能效果和冲击速度敏感性未随着破片倾角α的增加表现出明显差异,侵彻过程中层合板难以对α造成明显改变,相似的接触面积、接触时间和变形程度是造成S-A型试样间相似吸能效果和冲击速度敏感性的重要原因。S-B型试样的吸能效果随着破片倾角β的增大而显著增强,其冲击速度敏感性则随β的增大而明显减弱,侵彻过程中β发生了明显改变,由此造成的接触面积、接触时间和变形程度增大是导致S-B型试样间差异化吸能效果和冲击速度敏感性的重要原因。此外,当β=90.0°时,500~2 000 g TNT当量下的破片均无法穿透CFRP层合板,但层合板背面仍表现出更为严重的损伤破坏。

 首页
首页 登录
登录 注册
注册




 下载:
下载: