首页
登录
注册
-
冲击波超压和冲量是评价各类装药爆炸类武器威力的主要指标之一，相关测试方法受到诸多关注。工程中常采用电测传感器对冲击波超压和冲量进行测试，但电测法易受到爆炸场寄生效应干扰，且测试设备易损坏。为应对这一问题，近年来，越来越多的学者开展了基于塑性变形理论的爆炸冲击波测试研究，并取得了一些有价值的研究成果。
将薄板用于毁伤评估最早出现在《水下爆炸》[1]一书中，该书中介绍了几种用于测量水下爆炸的指示器，以薄板或圆板变形作为炸药效果的度量。Jones[2]首次考虑了板内弯矩与膜力的共同作用，在材料刚塑性假设下，忽略材料的应变率效应，建立了上下限理论模型，用于描述简支圆形薄板等轴对称薄板结构在冲击载荷作用下的力学行为，其理论结果与Florence[3]的试验结果吻合良好。Tabata等[4]对矩形薄板开展了研究，给出了均布横向载荷作用下载荷与薄板中心点挠度之间的关系式，并通过该关系式来确定膜片中的残余应力。余同希等[5–6]首次提出了基于能量平衡的“膜力因子法”，有效解决了圆板大变形下弯矩与膜力联合作用问题，成功开展了简支刚塑性圆板在冲击载荷作用下的大挠度塑性响应分析。Wierzbicki等[7]通过试验和理论研究了固支薄板在中心圆形局部冲击载荷作用下的响应，确定了撕裂破坏的位置和临界破坏时的冲量。李家文[8]采用传递函数方法对梁、板、圆柱壳等简单结构在冲击波作用下的瞬态响应进行了理论分析。Brill等[9]将试验与数值模拟相结合，研究了将铜膜片作为应变片测量爆炸冲击波作用下结构动荷载的方法，以及在半球形TNT裸装药爆炸加载结构基础上测量冲量的方法，均未考虑超压与冲量的共同作用。傅辉刚等[10]采用有限元分析方法得到了挠度与爆心距及TNT当量的函数关系，并结合冲击波能量谱发现了自振频率对效应靶毁伤的影响。李丽萍[11]在靶场试验的基础上，建立了薄板变形与交会条件的量纲分析模型，通过引入炸高参量，探讨了冲击波入射角度对薄板变形的影响。荣吉利等[12]利用AUTODYN软件对固支圆板进行建模，建立了其在动爆冲击波作用下的中心挠度理论计算公式。吴迪等[13]基于等效单自由度模型理论，考虑变形过程中弯矩与膜力的联合承载，建立了空中近爆作用下固支弹塑性圆板的动力学模型。翟红波等[14]提出了一种基于Monte-Carlo法的薄板变形稳健性分析方法，结合薄板冲击响应模型，建立了薄板变形稳健性表征方法和极限状态函数。郭佳凯等[15]通过数值模拟方法探究了爆炸冲击波与固支圆板的相互作用过程，推导了变形圆板表面任意一点处爆炸载荷的计算公式，能够较好地计算出变形圆板的表面载荷。
在以往的研究中，大多针对某一特定的冲击波量程或金属材料展开分析，极少考虑冲量对挠度的影响，但在实际情况中，薄板变形是超压与冲量共同作用的结果。基于现有研究的不足，本工作拟对多种材料的圆板在不同冲击载荷下的变形进行探究，考虑超压峰值与冲量对薄板的共同作用，建立普遍适用的挠度-超压峰值/冲量关系模型，并对比分析试验与模型计算结果，评估模型的准确性。
-
为研究冲击载荷作用下圆板的大挠度变形特性，构建冲击载荷作用下的变形关系模型，开展了0.5、1.0、2.0、5.0、10.0 MPa冲击波压力载荷作用下3种材料（2024Al、6061Al、黄铜H62）、4种直径（20、30、40、50 mm）、2种厚度（0.2、0.5 mm）的有限元模拟，相关材料参数如表1所示。其中：ρ为密度，E为材料弹性模量，ν为泊松比，A为单轴拉伸下材料的屈服强度，B为材料的强化系数，n为应变强化系数，C为应变率敏感系数。
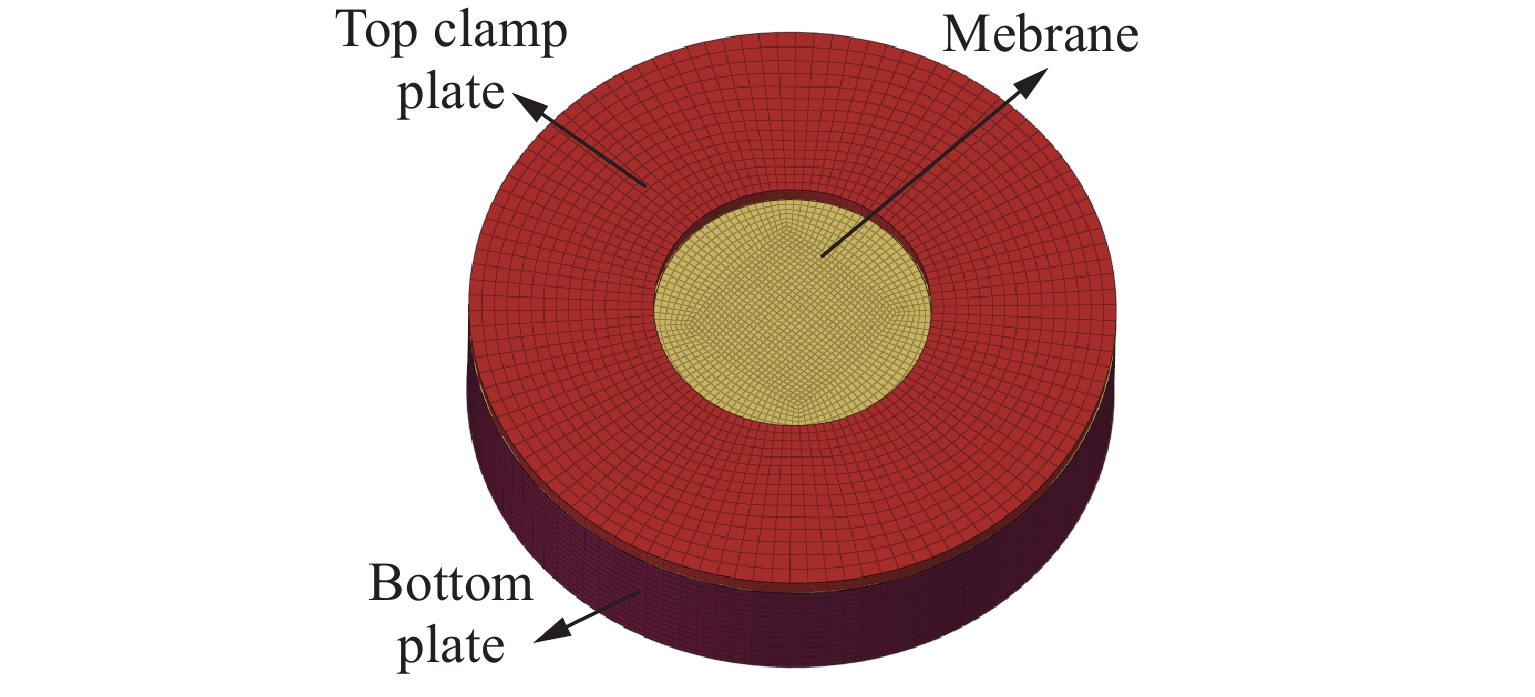
采用LS-DYNA有限元软件建立测压圆板、上压板和底板的数值模型，以圆板直径30 mm为例，构建的模型如图1所示。
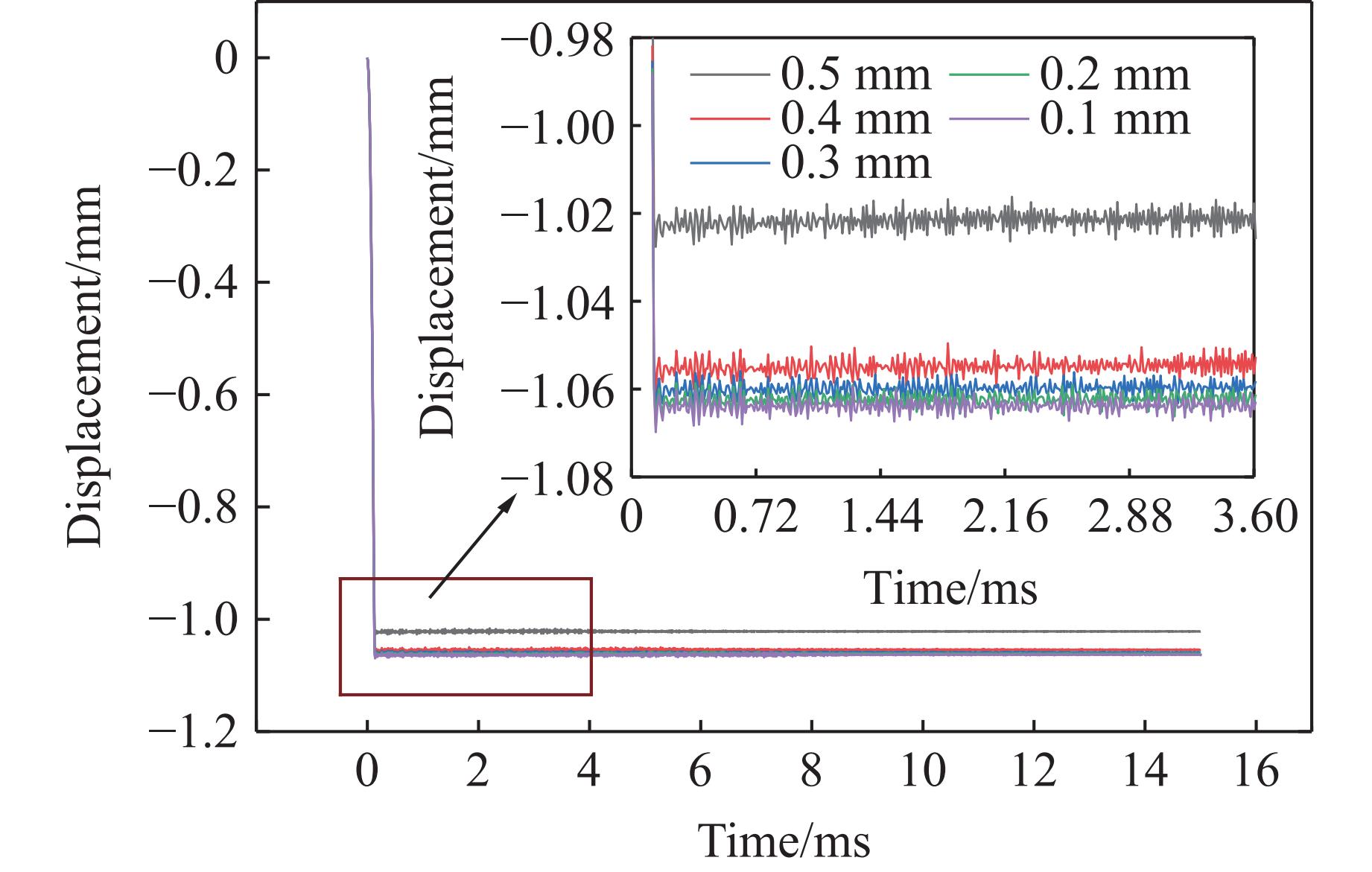
在进行有限元分析时，网格尺寸对数值模拟结果有显著影响，网格尺寸过大会导致数值模拟准确性降低，网格尺寸过小则会大幅降低运算效率，因此，选择合适的网格尺寸至关重要。绘制0.1～0.5 mm共5种尺寸的网格，施加相同载荷，以厚度为0.2 mm的2024Al合金膜片为例进行运算，模拟结束后提取膜片中心节点处的位移，如图2所示。从图2可以看出：采用0.1～0.4 mm的网格尺寸时，网格尺寸对膜片变形几乎没有影响；当网格尺寸增大到0.5 mm时，膜片变形变小，差距为0.3 mm。因此，网格尺寸在0.1～0.4 mm中进行选择。考虑到运行时间问题，当网格尺寸为0.1 mm时，数值模拟所用时间约是网格尺寸为0.4 mm时的3倍，因此，在保证模拟结果准确性的基础上，选择的网格尺寸为0.4 mm。
采用关键字*CONTACT_AUTOMATIC_ SURFACE_TO_SURFACE定义夹板与圆板之间的接触，摩擦系数设置为0.2，圆板材料参数由98号材料模型MAT_SIMPLIFIED_JOHNSON_COOK定义[16]。2个夹板设置为刚体，采用关键字*MAT_RIGID定义，材料的密度为7 800 kg/m3，弹性模量为200 GPa，泊松比为0.30，在下夹板底部设置固定约束。
-
炸药爆炸是一个反应迅速、高温、高压的释能过程，在数值模拟中通常通过建立炸药和空气域，采用流固耦合（fluid-structure interaction, FSI）方法进行模拟。采用流固耦合方法进行数值模拟时，炸药、空气网格尺寸的选取以及无反射边界的设置都会对数值模拟结果产生很大的影响，并且需要大量的计算资源，特别是在空间尺寸较大的爆炸工况下，致使计算效率较低。
为了提高数值模拟的计算效率，采用Conwep算法，该算法应用Conwep程序计算爆炸载荷[17]，考虑了爆炸入射角、入射压力和反射压力的作用，能够实现多种常规武器爆炸效应的计算，计算式为
式中：p(t)为目标界面受到的载荷，pref为反射压力，pin为入射压力，
$ \theta $ 为爆炸冲击波入射角。目前，LS-DYNA数值模拟软件集成了Conwep算法的加载方式，该加载方式不需要构建TNT的几何模型，只需要通过*LOAD_BLAST等关键字调用该算法，在关键字中设置模拟所需要的TNT质量和爆炸点坐标以及受载面即可。
-
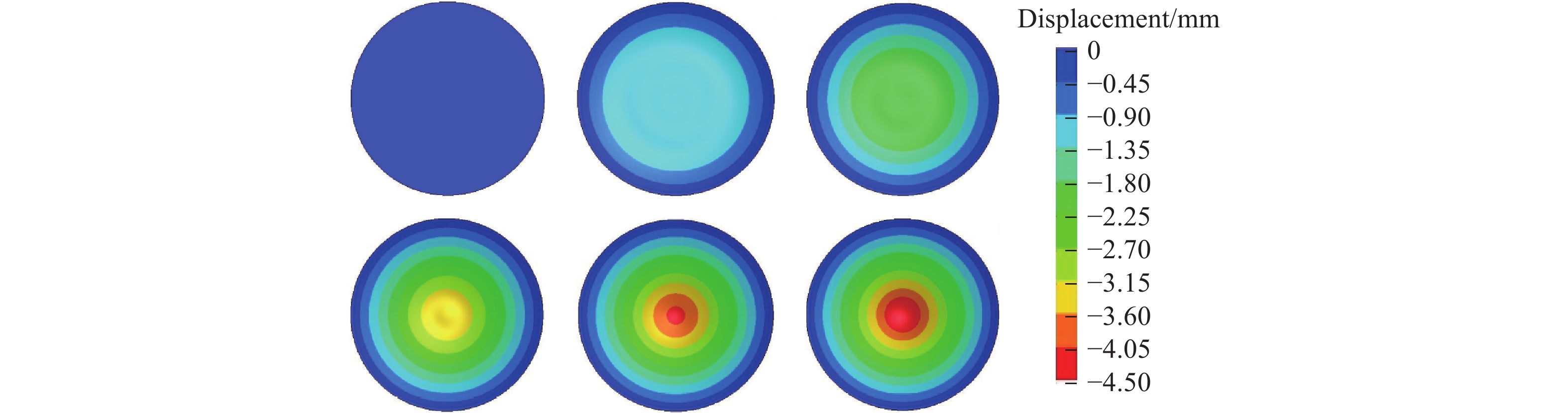
在实际爆炸场中，爆心距远大于圆板直径，因此，可以近似认为作用于圆板受载面的是均匀冲击波。在受到冲击波作用后，圆板中心最先变形并逐渐增大，变形由中心向四周扩散，最终塑性测压圆板在最大变形位置振动，圆板随时间的变形云图如图3所示。图3中，2024Al合金圆板的直径为30 mm、厚度为0.2 mm，TNT质量为50 kg，爆心距为5 m。
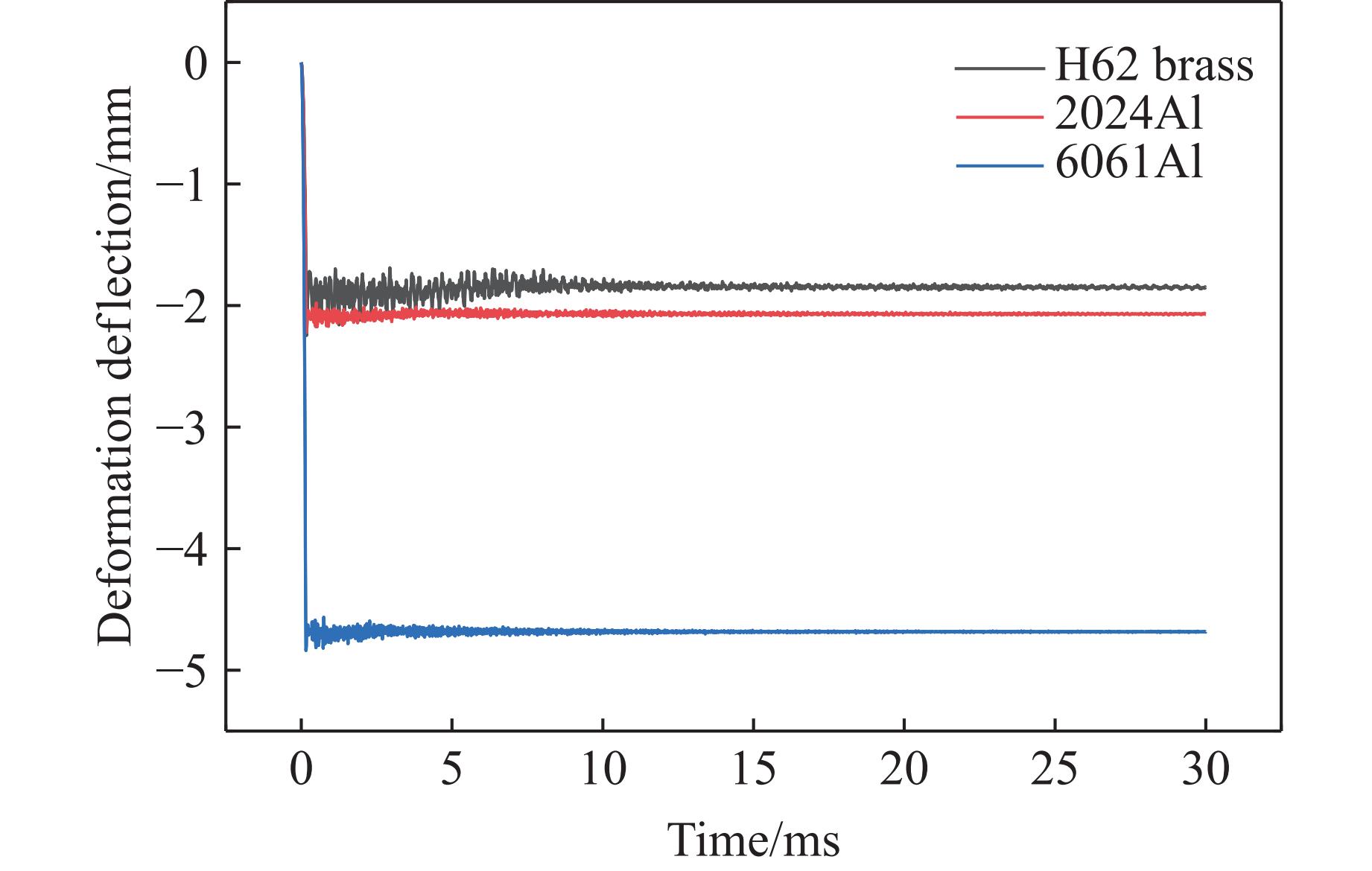
图4展示了直径为30 mm、超压为1.0 MPa、冲量为1 050 Pa·s时3种材料变形挠度的对比，对每种圆板分别进行了5次不同压力载荷的数值模拟，缺少数据点表示圆板破裂，未获得有效数据。从图4可以看出：H62黄铜的变形挠度为1.85 mm；2024Al的变形挠度为2.07 mm，与黄铜变形量的相对偏差约为10%；6061Al的变形挠度达到4.68 mm，约为2024Al变形量的2倍。因此，认为6061Al在冲击载荷下拥有最好的敏感性，2024Al次之，黄铜的敏感性最差。从图4还可以看出：在相同的冲击载荷作用下，相比于2种铝合金材料，H62黄铜从振动状态达到稳定状态需要更长的时间，同时也拥有最大的回弹量，约为0.1 mm；2024Al的回弹量为0.05 mm；6061Al则几乎不产生回弹。因此，可以证明，3种材料中，6061Al更适用于小量程测试，而黄铜更适用于大量程测试。
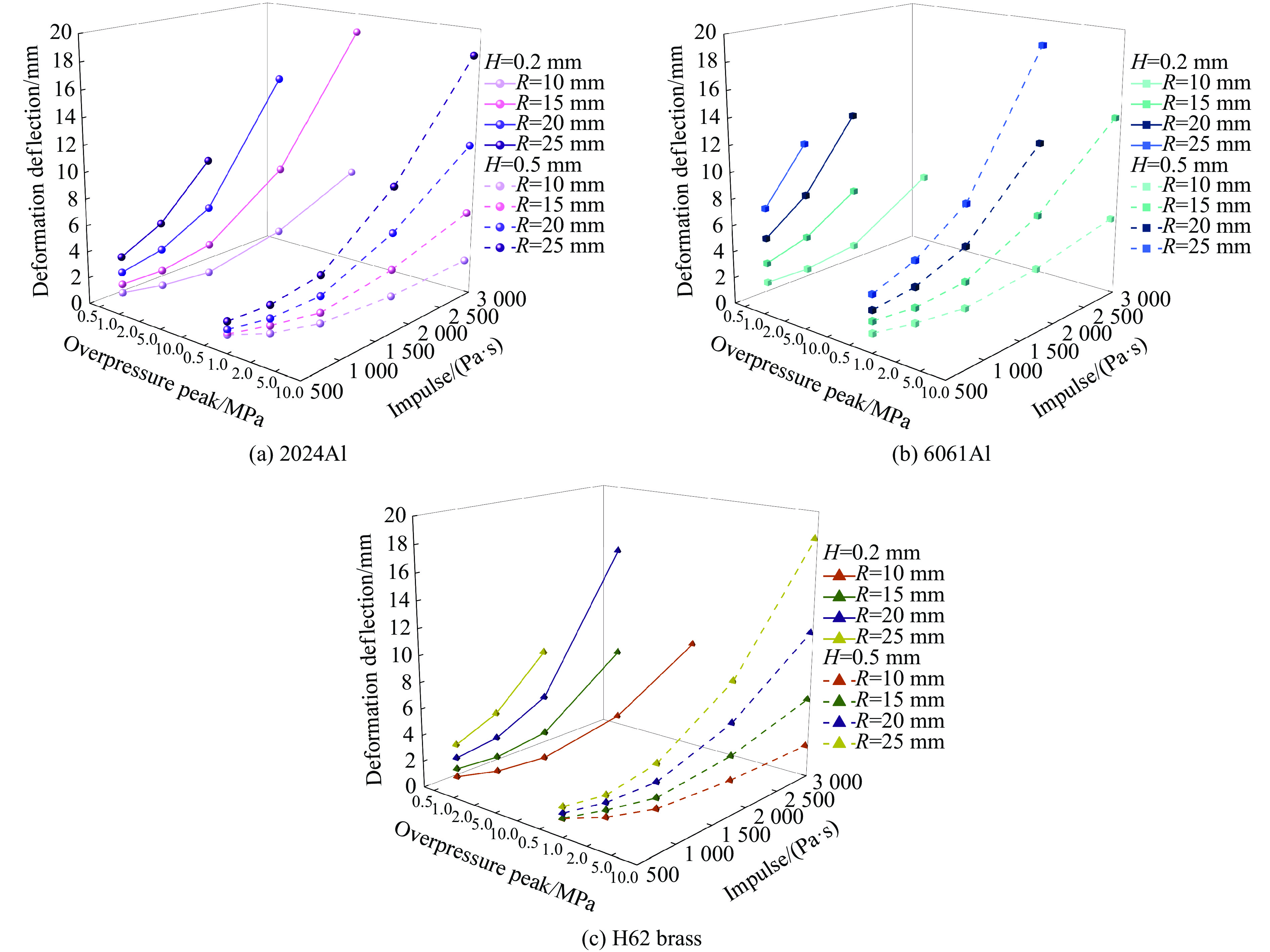
根据数值模拟结果绘制“超压峰值-冲量-变形挠度”曲线，如图5所示。从图5可以看出：无论何种材料，随着冲击载荷压力的增大，圆板最终变形挠度增大；随着冲击载荷冲量的增大，圆板最终变形挠度变大；随着圆板半径（R）增大，圆板最终变形挠度增大；随着圆板厚度（H）增大，圆板最终变形挠度减小。
-
为了能够准确量化圆板变形挠度与冲击波压力峰值、冲量之间的关系，需要建立相应的关系模型，本研究采用量纲分析方法构建数学模型。
根据现有冲击载荷作用下圆板的变形理论[18–20]，影响圆板最终变形挠度的物理量有：冲击压力载荷
$p$ 、冲击载荷冲量$I$ 、圆板半径$R$ 、圆板厚度$H$ 、材料密度$\rho $ 、弹性模量$E$ ，除此之外，还需考虑材料的本构关系。冲击载荷作用下，采用简化的Johnson-Cook模型对材料的本构关系进行描述
式中：
$\sigma _{\rm{y}} $ 为屈服应力，εp为有效塑性应变。因此，冲击载荷作用下圆板最大变形挠度的函数表达式为
由式(3)可知，该问题中有10个物理量，即1个因变量和9个自变量。由
$\prod $ 定理可知，该物理问题中有3个独立的参考物理量，选取材料密度$ \rho $ 、圆板厚度$ H $ 和材料弹性模量$ E $ 作为参考物理量，给出这10个物理量量纲幂次指数的排序情况，如表2所示。将表2进行初等变换，得到初等变换后冲击载荷作用下圆板大变形问题中变量的量纲系数排序，如表3所示。
$\prod $ 定理关系式可以表示为式中：
$ \prod = \dfrac{w}{H},{{\prod} _1} = \dfrac{A}{E},{{\prod} _2} = \dfrac{B}{E},{{\prod} _3} = n, $ $ {{\prod} _4} = \dfrac{R}{H},{{\prod} _5} = \dfrac{p}{E},{{\prod} _6} = \dfrac{I}{{H\sqrt {\rho E} }} $ 。式中：右端第1项、第2项、第3项表示纯材料物理力学性能参数无量纲量，为材料相似条件；右端第4项表示圆板半径与厚度之比，为几何相似条件；右端第5项和第6项为冲击载荷作用下模型的物理量相似条件。
因此，由式(5)可得，基于量纲分析的冲击载荷作用下的塑性变形关系模型为
利用图5的模拟数据，对式(6)进行多元非线性拟合，得到待定系数
${a_1}$ 、${b_1}$ ～${b_5} $ 的值，以决定系数${R^2}$ 为拟合评价指标，${R^2}$ 越接近1，表示拟合度越高，其表达式为式中：
${y_i}$ 为待拟合数值，$\bar y$ 为均值，${\hat y_i}$ 为拟合值。拟合得到冲击载荷作用下圆板塑性变形关系模型
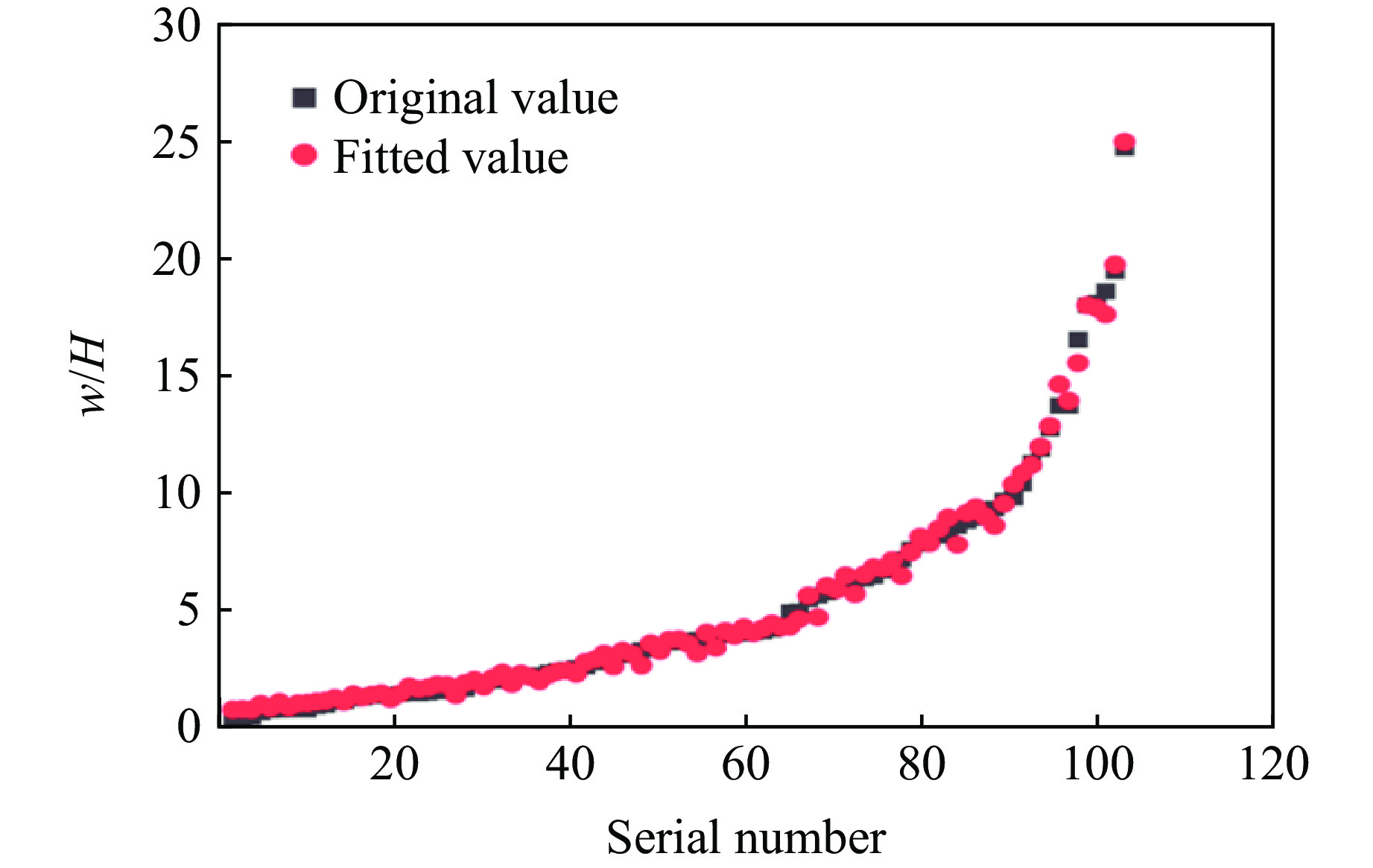
数值模拟与计算结果的对比如图6所示，拟合关系模型的决定系数
$ {R^2} $ 为0.995 0。可以看出，模型具有较高的拟合度，可用来表征冲击载荷作用下的塑性变形。 -
为了验证所建数学模型的准确性，开展了外场爆炸试验。外场爆炸试验是考察爆炸类武器最直接有效的手段，也是塑性测压装置在应用领域最主要的方向。因此，针对圆板的动态特性，在爆炸场中对其进行测试，获得圆板的实际变形挠度，并与理论模型进行对比，以验证模型的可信度。
对质量分别为5.0、10.0和17.5 kg的TNT开展试验，爆高均为1.5 m。在距离爆心4 m处放置塑性测压装置和标准压力传感器，布局如图7所示，图7(b)中左侧为本研究使用的塑性测压装置，右侧为压力传感器。其中，圆板受冲击直径为30 mm，所用的2024Al材料厚度为0.2 mm。
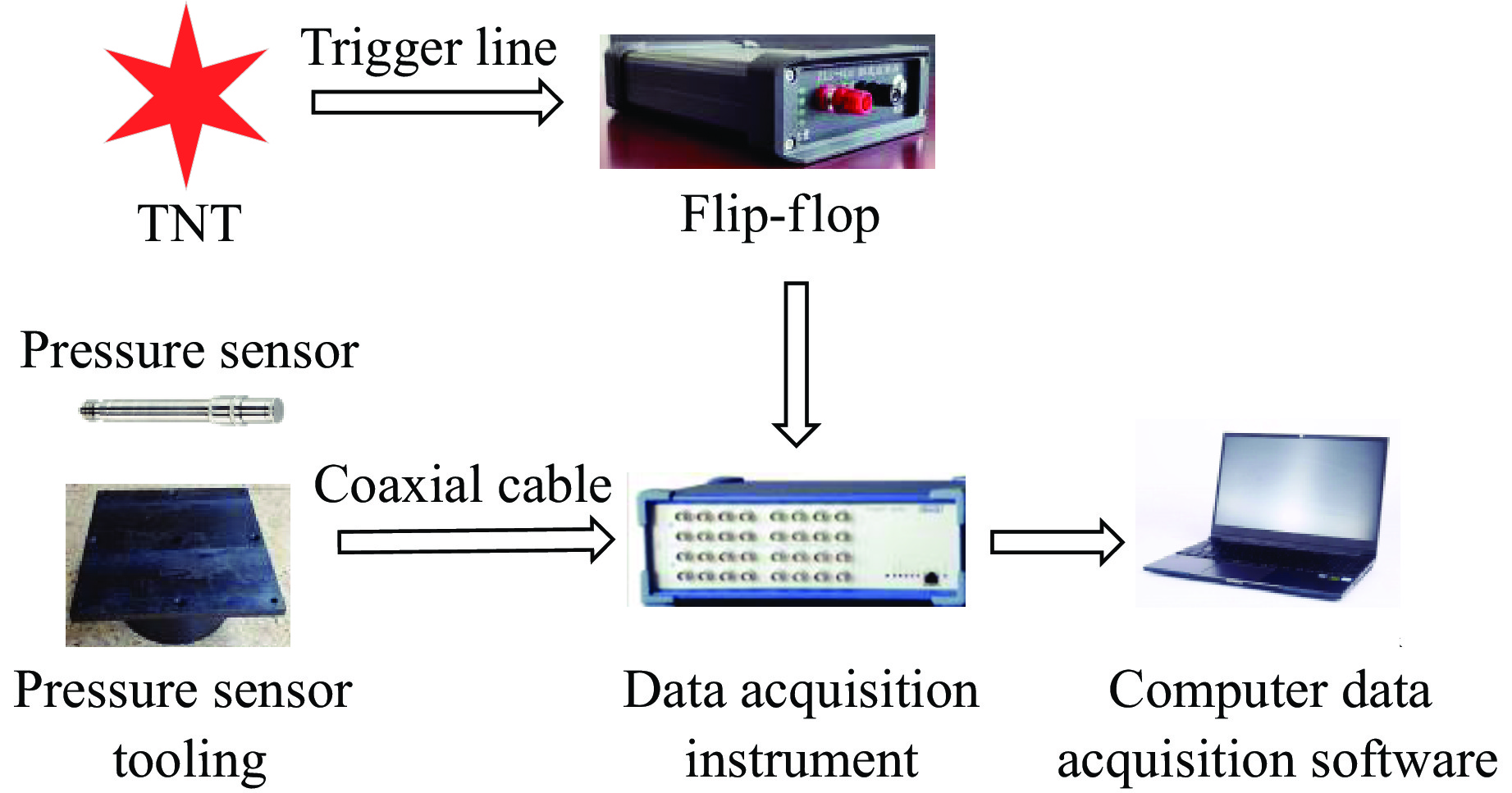
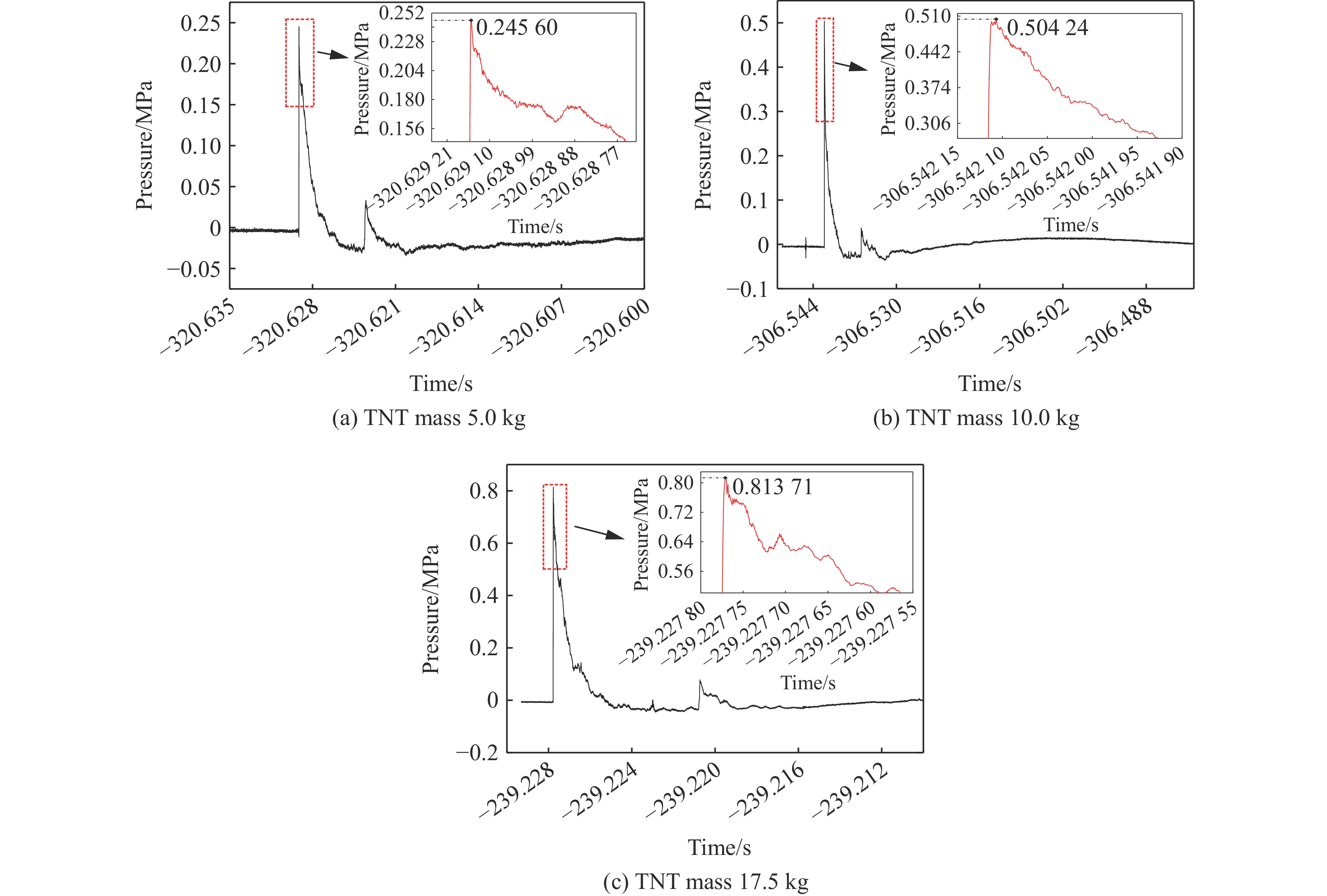
试验中所用的标准传感器为PCB公司113B系列压力传感器，测量系统由传感器及其安装组件、高精度同步触发控制器、信号调理器、数据采集系统及相应的配套软件构成。通过低噪声电缆线连接传感器、信号调理器与数据采集系统。在爆炸场工况下，将信号调理器和数据采集系统放置在指定的掩体内，采用长电缆线将传感器预先与信号调理器连接，如图8所示。3次试验测得的压力曲线如图9所示。
测量并记录3次试验的圆板变形挠度，再将对应的超压峰值、冲量代入式(8)计算得到对应挠度，动态试验与模型计算结果的对比如表4所示。从表4可以看出，与数值模拟结果相比，试验测试结果较大，主要是由于该响应模型未考虑弯矩和薄板受载不均匀性的影响，但计算结果的平均相对误差为4.84%，符合爆炸场冲击波压力测试要求，可以将式(8)作为冲击载荷下的压力/冲量-挠度关系模型，用于实际冲击波压力测试。
-
(1) 采用LS-DYNA有限元软件开展了冲击载荷作用下金属薄板力学特性数值模拟，得到了一定范围内冲击载荷下薄板的变形规律。由数值模拟结果可知：金属薄板在冲击载荷下的变形挠度与冲击波压力、冲量呈正相关；与薄板本身直径、厚度呈负相关；相同载荷下，对于相同尺寸、不同材料的薄板，2024Al薄板的变形挠度约比H62黄铜小10%，6061Al薄板的变形挠度约为2024Al变形量的2倍。
(2) 利用量纲分析方法对数值模拟数据进行拟合，得到了冲击载荷作用下薄板变形挠度与压力/冲量的数学模型。
(3) 为验证关系模型的准确性，开展了冲击载荷下的薄板变形试验，结果表明：动态关系模型的最大相对误差为6.32%，平均相对误差为4.84%，满足实际爆炸场测试精度要求，可以应用于实际压力测量。研究结果可为高能战斗部冲击波毁伤威力测试评估提供测试手段及数据支撑。
超压与冲量综合作用下金属薄板的塑性变形特性分析与建模
Analysis and Modeling of Plastic Deformation Characteristics of Sheet Metal under the Combined Action of Overpressure and Impulse
-
摘要: 当前，基于塑性变形的冲击波压力测试研究往往忽视了超压峰值与冲量对金属薄板的共同作用，导致构建的模型应用范围受限。针对上述问题，开展了不同厚度和直径的3种典型金属圆板在不同冲击载荷作用下的数值模拟分析，揭示了圆板变形量与超压、冲量、直径及厚度的正负相关性。综合考虑超压与冲量共同作用对薄板变形的影响，使用量纲分析方法建立了“圆板变形挠度-超压/冲量”关系模型。试验数据表明，模型的平均误差为4.84%，满足爆炸场测试精度要求，可用于实际冲击波测试。研究成果可为高能战斗部冲击波毁伤威力测试评估提供测试手段及数据支撑。Abstract: The current research of shock wave pressure testing based on plastic deformation neglects the combined effect of overpressure peak and impulse on metal sheet, and the application range of the model is limited. To solve the above problems, the simulation analysis of three typical metal plates with different thicknesses and diameters under different impact loads is carried out, and the positive and negative correlations between the deformation of the plates and overpressure, impulse, diameter and thickness are revealed. Considering the influence of overpressure and impulse on thin plate deformation, the relationship model of deflection of circular plate deformation-overpressure/impulse is established by using dimensional analysis method. The verification test data show that the average error of the model is 4.84%, which meets the requirement of test accuracy in explosion field and can be used for actual shock wave test. The research provides an effective test method and accurate data support for the evaluation of shock wave damage power of high energy warhead.
-
Key words:
- shock wave pressure test /
- metal sheet /
- plastic deformation /
- dimensional analysis .
-
-
图 4 相同条件下不同薄板的变形情况
Figure 4. Deformation of different thin plates under the same conditions
图 5 数值模拟得到的动态载荷下圆板的变形
Figure 5. Simulation deformation of circular plates under dynamic load
表 1 材料参数
Table 1. Material parameters
Material ρ/(kg·m−3) E/GPa ν A/MPa B/MPa n C 2024Al 2 780 69.77 0.33 294.06 481.10 0.881 0 0.008 3 6061Al 2 700 74.31 0.33 96.49 341.11 0.626 6 0.015 0 H62 brass 8 520 101.78 0.31 288.87 167.24 0.435 1 0.017 0 
下载: 导出CSV
表 2 冲击载荷作用下圆板大变形问题中变量的量纲系数排序
Table 2. Dimensional coefficients of variables in large deformation of circular plates under impact loads
Dimension $ \rho $ $ H $ $ E $ $ A $ $ B $ $ n $ $ R $ $ p $ $ I $ $ w $ M 1 0 1 1 1 0 0 1 1 0 L −3 1 −1 −1 −1 0 1 −1 −1 1 T 0 0 −2 −2 −2 0 0 −2 −1 0
下载: 导出CSV
表 3 初等变换后冲击载荷作用下圆板大变形问题中变量的量纲系数
Table 3. Dimensional coefficients of variables in large deformation of circular plates under impact loads after elementary transformations
Dimension $ \rho $ $ H $ $ E $ $ A $ $ B $ $ n $ $ R $ $ p $ $ I $ $ w $ M 1 0 0 0 0 0 0 0 1/2 0 L 0 1 0 0 0 0 1 0 1 1 T 0 0 1 1 1 0 0 1 1/2 0
下载: 导出CSV
表 4 动态试验与模型计算结果的对比
Table 4. Comparison of the dynamic test results with the calculated results of the relational model
TNT mass/kg pm/MPa I/(Pa·s) Deformation deflection Test/mm Calc./mm Relative error/% 5.0 0.246 178.32 0.174 0.163 6.32 10.0 0.504 295.87 0.338 0.325 3.85 17.5 0.816 485.45 0.550 0.526 4.36
下载: 导出CSV
-
[1] 库尔P. 水下爆炸 [M]. 罗耀杰, 韩润泽, 官信, 等, 译. 北京: 国防工业出版社, 1960. KUHL P. Underwater explosion [M]. Translated by LUO Y J, HAN R Z, GUAN X, et al. Beijing: National Defense Industry Press, 1960. [2] JONES N. Impulsive loading of a simply supported circular rigid plastic plate [J]. Journal of Applied Mechanics, 1968, 35(1): 59–65. [3] FLORENCE A L. Circular plate under a uniformly distributed impulse [J]. International Journal of Solids and Structures, 1966, 2(1): 37–47. [4] TABATA O, KAWAHATA K, SUGIYAMA S, et al. Mechanical property measurements of thin films using load-deflection of composite rectangular membrane [C]//IEEE Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines & Robots. Salt Lake City: IEEE, 1989: 152–156. [5] 余同希, 陈发良. 用“膜力因子法”分析简支刚塑性圆板的大挠度动力响应 [J]. 力学学报, 1990, 22(5): 555–565. YU T X, CHEN F L. Analysis of the large deflection dynamic response of simply-supported circular plates by the “membrane factor method” [J]. Chinese Journal of Theoretical and Applied Mechanics, 1990, 22(5): 555–565. [6] 陈发良, 余同希. 计入膜力塑性耗散效应的矩形板塑性动力响应 [J]. 爆炸与冲击, 2005, 25(3): 200–206. CHEN F L, YU T X. Dynamic plastic response of rectangular plates with plastic energy dissipation by membrane force [J]. Explosion and Shock Waves, 2005, 25(3): 200–206. [7] WIERZBICKI T, NURICK G N. Large deformation of thin plates under localised impulsive loading [J]. International Journal of Impact Engineering, 1996, 18(7/8): 899–918. [8] 李家文. 爆炸冲击波作用下结构瞬态响应分析 [D]. 长沙: 国防科学技术大学, 2006. LI J W. Transient response analysis of structures under blast wave [D]. Changsha: National University of Defense Technology, 2006. [9] BRILL A, ME-BAR Y, SADOT O, et al. A method for measuring the impulse on structural foundations due to a blast wave [J]. International Journal of Impact Engineering, 2012, 49: 214–221. [10] 傅辉刚, 孔德仁, 李丽萍, 等. 基于效应靶法评价爆炸冲击波毁伤的数值仿真 [J]. 测试技术学报, 2015, 29(4): 326–331. doi: 10.3969/j.issn.1671-7449.2015.04.010 FU H G, KONG D R, LI L P, et al. Numerical simulation of assessing the damage of explosive blast wave base on effective target’s method [J]. Journal of Test and Measurement Technology, 2015, 29(4): 326–331. doi: 10.3969/j.issn.1671-7449.2015.04.010 [11] 李丽萍. 破片战斗部毁伤威力测试关键技术研究 [D]. 南京: 南京理工大学, 2017. LI L P. Investigation on some key measuring technologies of fragment warhead power field [D]. Nanjing: Nanjing University of Science and Technology, 2017. [12] 荣吉利, 刘东兵, 赵自通, 等. 圆支圆板在动爆冲击波作用下的动力响应 [J]. 北京理工大学学报, 2021, 41(5): 474–479. RONG J L, LIU D B, ZHAO Z T, et al. Dynamic response of fixed circular plate subjected to dynamic explosion shock wave [J]. Transactions of Beijing Institute of Technology, 2021, 41(5): 474–479. [13] 吴迪, 米国, 郭香华, 等. 空爆载荷作用下固支弹塑性圆板的动力学模型 [J]. 高压物理学报, 2022, 36(5): 054202. WU D, MI G, GUO X H, et al. Dynamic model of elastoplastic circular plate with fixed support under air explosion load [J]. Chinese Journal of High Pressure Physics, 2022, 36(5): 054202. [14] 翟红波, 李尚青, 毛伯永, 等. 周边固支效应靶薄板冲击响应的稳健性分析 [J]. 振动、测试与诊断, 2023, 43(5): 1026–1032, 1045. ZHAI H B, LI S Q, MAO B Y, et al. Analysis of shock response robustness for effect target sheet with peripheral fixed support [J]. Journal of Vibration, Measurement & Diagnosis, 2023, 43(5): 1026–1032, 1045. [15] 郭佳凯, 朱春晓, 施锐, 等. 冲击波作用下变形圆板表面载荷研究 [J]. 舰船科学技术, 2024, 46(5): 21–26. GUO J K, ZHU C X, SHI R, et al. Research on surface load of deformation circular plate under blast wave [J]. Ship Science and Technology, 2024, 46(5): 21–26. [16] SIRIGIRI V K R, GUDIGA V Y, GATTU U S, et al. A review on Johnson Cook material model [J]. Materials Today: Proceedings, 2022, 62: 3450–3456. [17] SHIRBHATE P A, GOEL M D. Investigation of effect of perforations in honeycomb sandwich structure for enhanced blast load mitigation [J]. Mechanics of Advanced Materials and Structures, 2023, 30(17): 3463–3478. [18] JACOB N, NURICK G N, LANGDON G S. The effect of stand-off distance on the failure of fully clamped circular mild steel plates subjected to blast loads [J]. Engineering Structures, 2007, 29(10): 2723–2736. [19] GHARABABAEI H, DARVIZEH A, DARVIZEH M. Analytical and experimental studies for deformation of circular plates subjected to blast loading [J]. Journal of Mechanical Science and Technology, 2010, 24(9): 1855–1864. [20] GHARABABAEI H, DARVIZEH A. Experimental and analytical investigation of large deformation of thin circular plates subjected to localized and uniform impulsive loading# [J]. Mechanics Based Design of Structures and Machines, 2010, 38(2): 171–189. -
图( 9) 表( 4)
计量
- 文章访问数: 105
- HTML全文浏览数: 105
- PDF下载数: 0
- 施引文献: 0