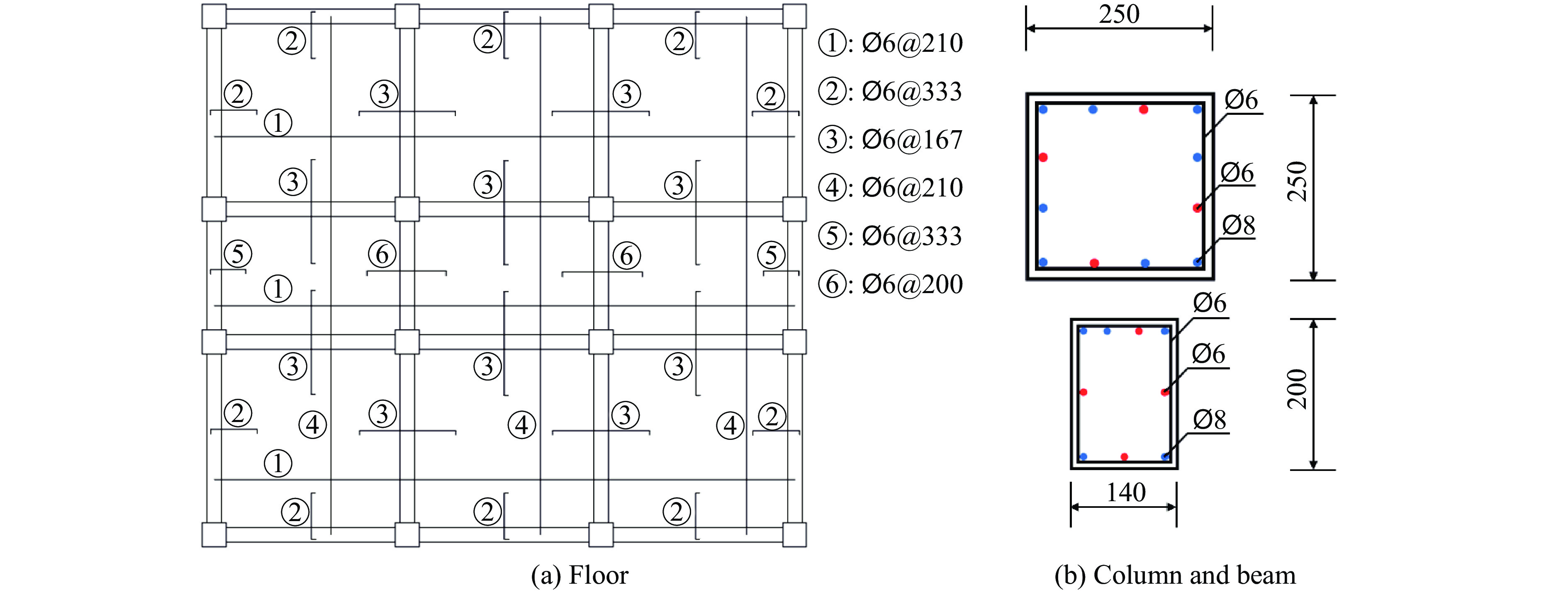
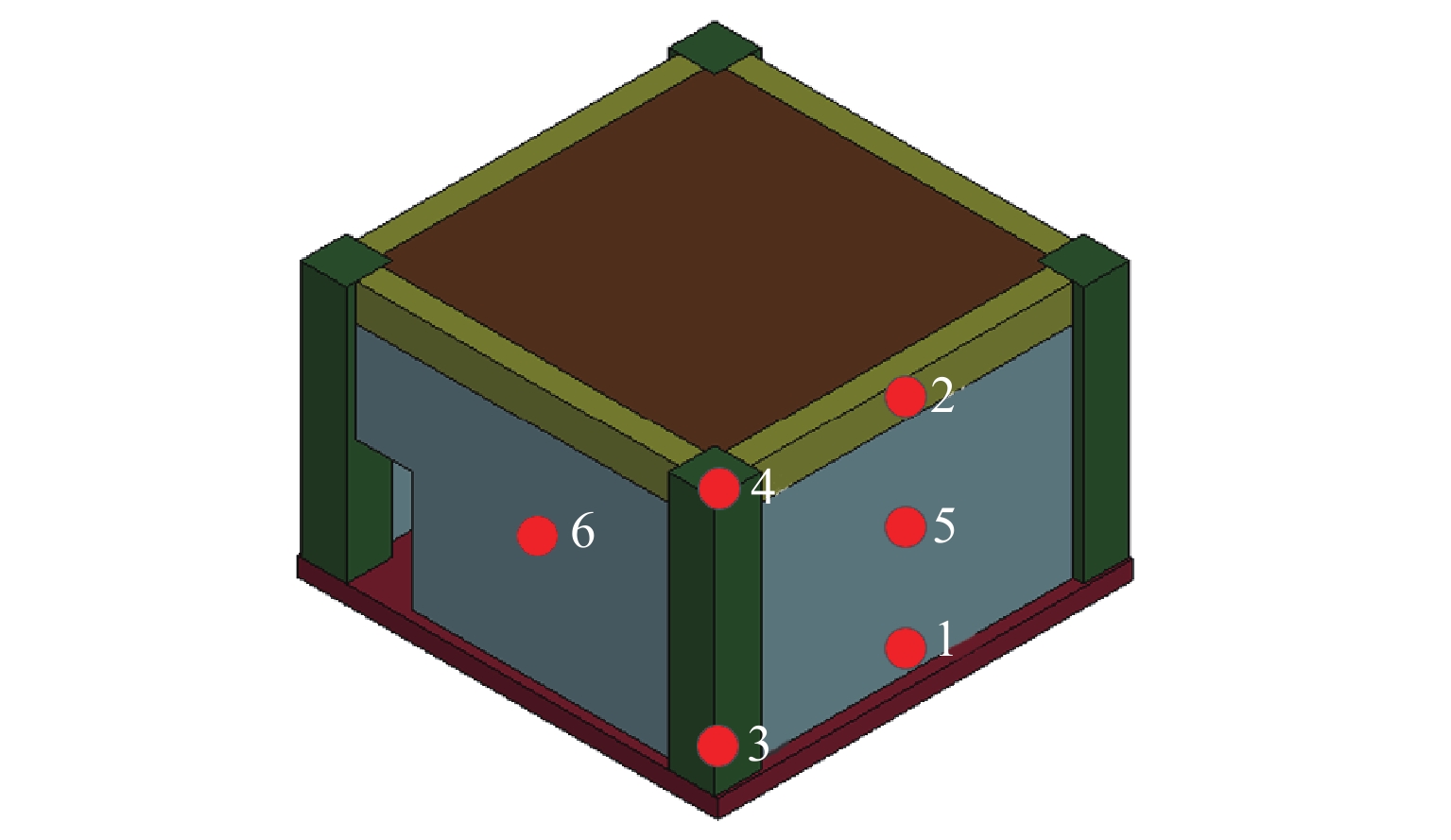
1/3缩尺2层RC框架-砌体墙结构内爆炸试验的框架结构模型如图1所示，每层关键构件编号如图2所示。设置单个房间的长度、宽度均为2.0 m，走廊宽度为1.3 m，一层和二层的层高分别为1.4 m和1.2 m；一层房间中，窗户和门的尺寸分别为800 mm×660 mm和720 mm×330 mm；墙体均为黏土砖填充墙，墙身厚度为115 mm，砖砌块尺寸为240 mm×115 mm×53 mm；柱截面尺寸为250 mm×250 mm，梁截面尺寸为140 mm×120 mm，其保护层厚度均为10 mm；板厚为60 mm，保护层厚度为6 mm。选用HRB400钢筋、C40混凝土建造，钢筋布置如图3所示。结构设计和施工均遵循现行建筑规范，并严格把控建造精度。

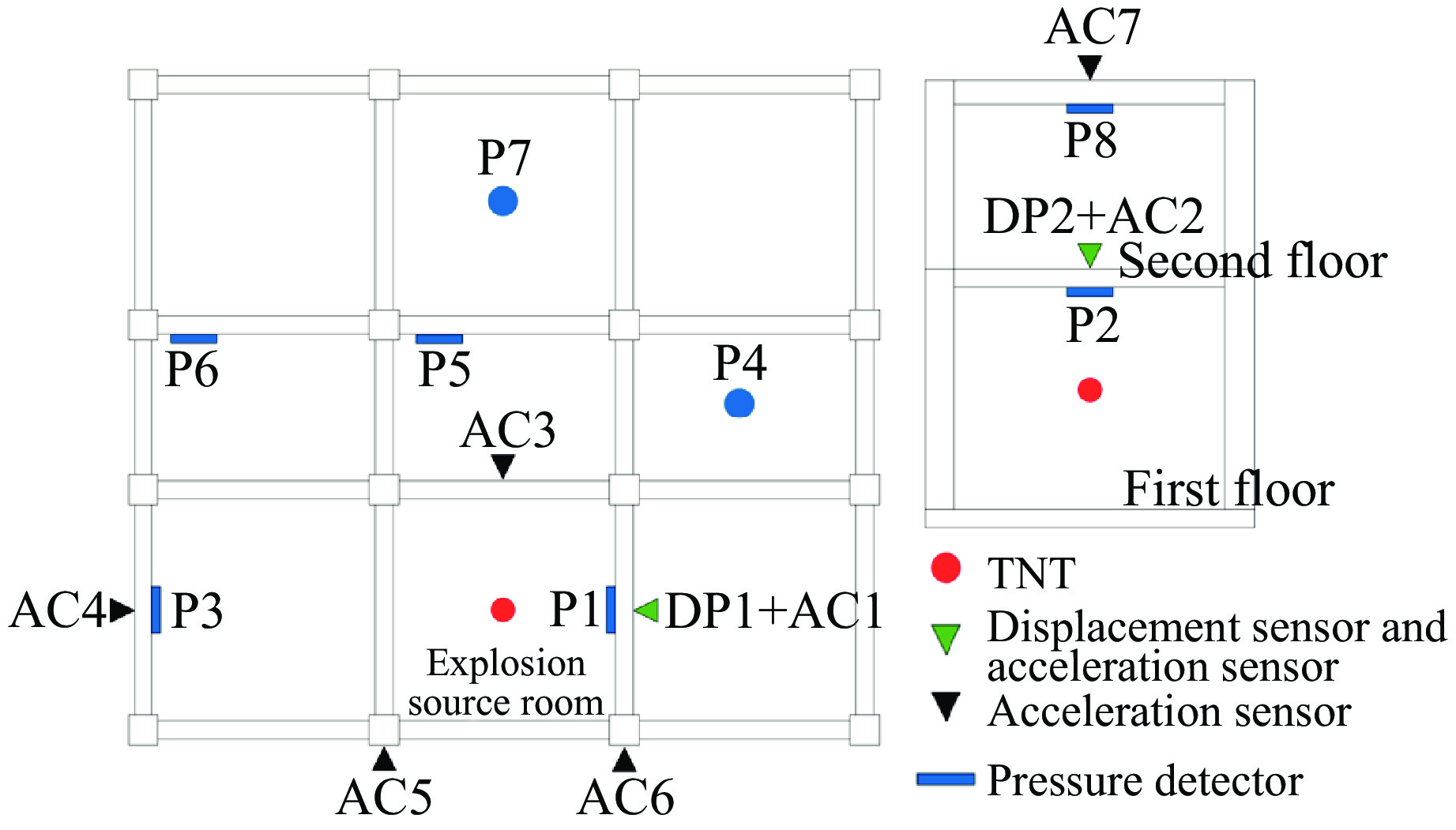
框架结构内爆试验的现场布置如图4所示，测试布局如图5所示。TNT为25 mm×50 mm×125 mm的长方体炸药，当量为0.249 kg，放置于房间的几何中心。在楼板和墙体的迎爆面中心处布置超压传感器，在背爆面中心点布置加速度计和位移计，用于捕捉结构动态响应的详细参数。

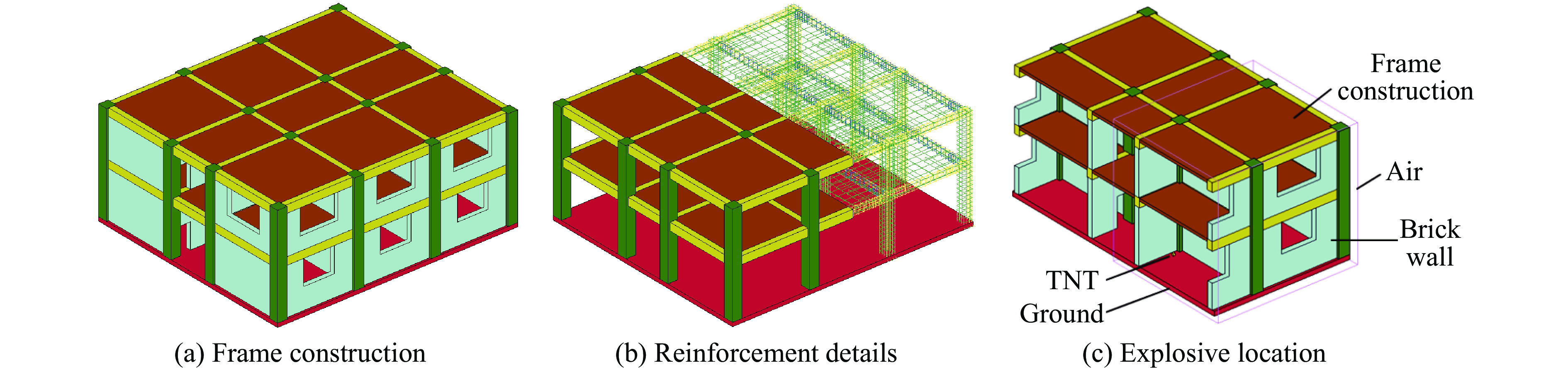
基于试验工况建立如图6所示的有限元模型，模型范围为整个缩比模型，由砌砖墙、混凝土、钢筋、TNT和空气域5部分组成。其中，空气域尺寸为6 750 mm×1 750 mm×2 650 mm。

建立砌体填充墙模型的方法主要有精细化微观模型、简化微观模型和宏观均质模型。精细化微观模型是将砌砖和砂浆分别建模，耦合砂浆和砌块接触面上所有节点的自由度以表征其黏结滑移特性；简化微观模型是不单独建立砂浆模型，将砂浆的厚度和质量整合到砌块上，在砌块之间添加接触来模拟砂浆的黏结作用；宏观均质模型是将砌块和砂浆视作同种材料，将砂浆的效应弥散在整个材料中，统一建立材料的本构模型。前2种方法可以较好地描述砌块与砂浆之间的相互作用，但对计算机CPU和内存等硬件的要求较高，适用于模拟小型试验砌体的破坏行为。本试验的计算模型为整体结构，主要研究构件在内爆炸作用下的动力响应和破坏模式，丁阳等^[14]证实了宏观均质模型在爆炸分析中的可靠性，因此，为提高计算效率，建立砌体填充墙的宏观均质模型。

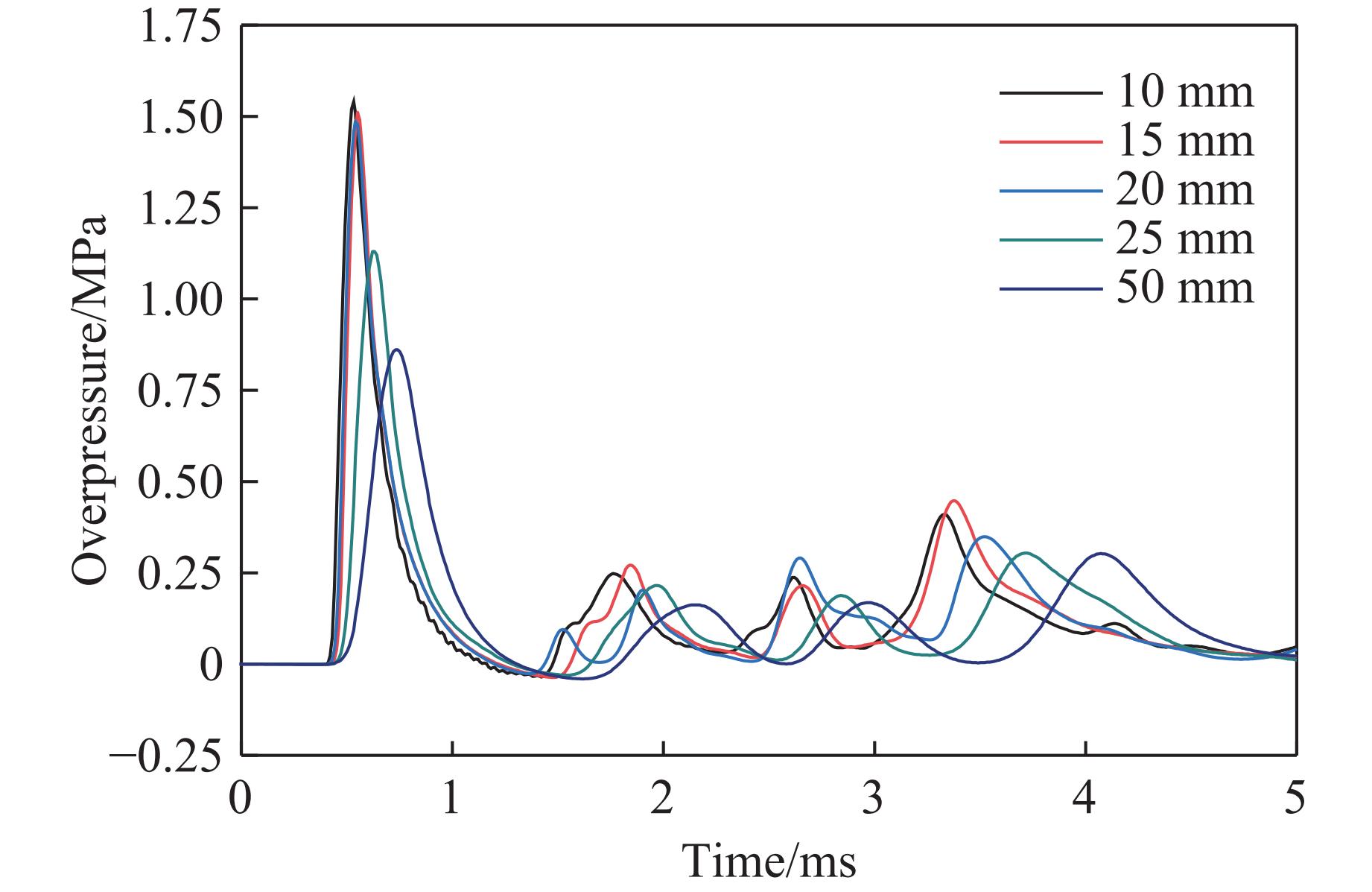
砌砖墙、混凝土和空气域采用Solid164单元，钢筋采用Beam161单元。选取10、15、20、25和50 mm的单元尺寸进行尺寸效应分析。TNT当量为0.249 kg时，分别计算不同单元尺寸模型中测点P1的爆炸荷载，其超压时程曲线如图7所示。单元特征尺寸为10、15、20、25和50 mm的模型对应的峰值超压分别为1.540、1.510、1.479、1.130和0.860 MPa。以10 mm模型为基准，15、20、25和50 mm模型的峰值超压误差分别为1.9%、4.0%、26.6%和44.2%。综合考虑计算精度和计算效率，单元尺寸确定为20 mm。

采用欧拉网格划分空气，采用*INITIAL_VOLUME_FRACTION_GEOMETRY关键字定义炸药在初始阶段ALE（arbitrary Lagrangian-Eulerian）网格中的体积占比，其余部分采用拉格朗日网格划分。通过*CONSTRAINED_LAGRANGE_IN_SOLID关键字描述空气、炸药与RC框架之间的流固耦合。构件之间采用共节点处理，采用*CONSTRAINED_BEAM_IN_SOLID关键字定义混凝土与钢筋之间的相互作用。通过*BOUNDARY_NON_REFLECTING将空气域边界设置为无反射边界。地面通过*MAT_RIGID关键字设置为刚性地面。

混凝土采用RHT模型和p-α状态方程进行表征。该模型将材料的力学特性分为弹性、线性强化和损伤软化3个阶段，通过引进与压力相关的3个不同强度面分别描述混凝土的初始强度、失效强度和残余强度，适用于描述混凝土在爆炸冲击荷载作用下的动态力学行为^[15]。混凝土参数如表1所示，其中：$ \rho $为密度，G为剪切模量，A₁为失效面参数，N为失效面指数，f_c为单轴抗压强度，f_t^*为拉压强度比，f_s^*为剪压强度比。

钢筋采用*MAT_PLASTIC_KINEMATIC塑性随动模型进行表征。该模型考虑了材料以及应变率对材料强度的影响，应变率效应通过Cowper-Symonds模型实现，参数如表2所示，其中：E为弹性模量，$ \nu $为泊松比，σ为屈服应力，E_t为切线模量，C为应变率系数，P为应变率参数。

砖砌墙选用*MAT-BRITTLE-DAMAGE材料模型进行表征，参数引自文献[16]，本研究根据试验确定砖砌墙的材料参数，如表3所示，其中：f_n为初始抗拉极限，f_s为抗剪极限，g_c为断裂韧度，β为剪切保持力，η为体积黏性。

空气视为理想气体，采用*MAT_NULL本构模型描述，采用*EOS_LINEAR_POLYNOMIAL状态方程来描述爆炸后空气的性能，具体参数如表4所示，其中：E₀为初始内能，p_c为截断压力，μ为动态黏性系数，C₀～C₆为状态方程常数。

炸药采用*MAT_HIGH_EXPLOSIVE_BURN材料模型，炸药在爆轰过程中的压力和内能的关系用JWL状态方程描述，具体参数如表5所示，其中：D为爆速，p_CJ为爆压，A₂、B、$ {{R}}_{{1}} $、$ {{R}}_{{2}} $和$ { \omega } $为材料参数，由试验确定。

为模拟混凝土和砌体墙的开裂破坏，添加关键字*MAT_ADD_EROSION定义材料失效，当单元的应力或应变达到失效标准时，该单元被定义为失效并删除，不再承受荷载。以最大主应变为失效判据^[17]，设定混凝土的最大主应变为0.1，砌体墙的最大主应变为0.08。

爆炸后的构件损伤如图8所示，侧墙-1窗下墙体有部分砖砌体脱落，其余两边的墙体明显向外偏转；侧墙-2中上部砖砌体飞出，脱落面积约占面板的30%，水泥砂浆抹灰大面积脱落；侧墙-3存在大面积填充墙倾倒，砖砌体与砂浆之间分离严重，试验中部分砌体墙出现大面积砌块脱落现象，由冲击波作用下砂浆与砖块的黏结效应失效引起。由于楼板中心区域正对爆源，底部正弯矩钢筋通长布置，而顶部负弯矩钢筋仅在支座附近布置，因此，中心区域强度较弱，出现明显变形，外侧混凝土受拉破坏，内侧混凝土局部出现剥蚀区域，钢筋外露，破坏较为严重。梁板交接区域产生冲切裂缝，裂缝沿着梁板交接处开展。此外，框架梁和框架柱产生多道弯曲裂缝。

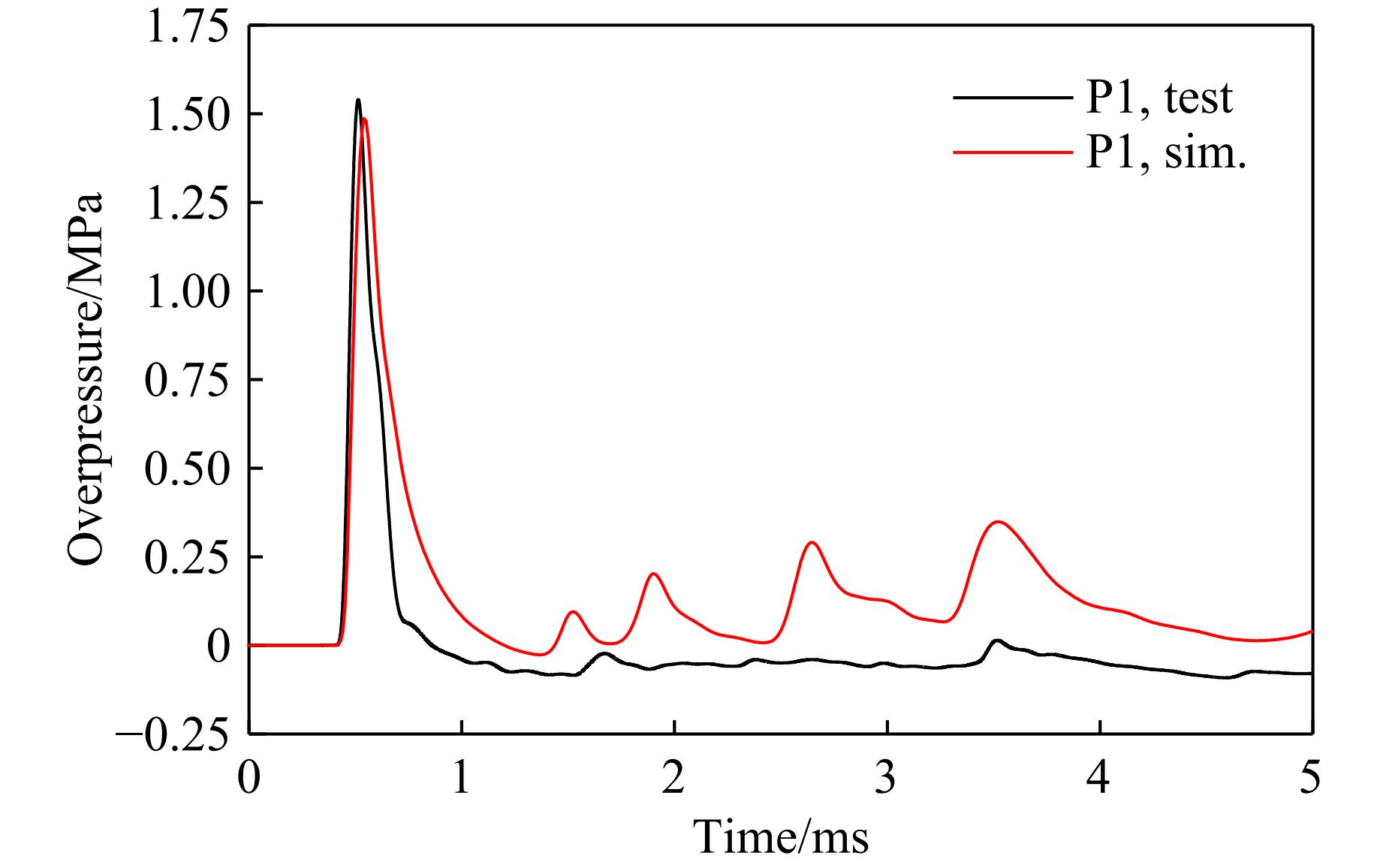
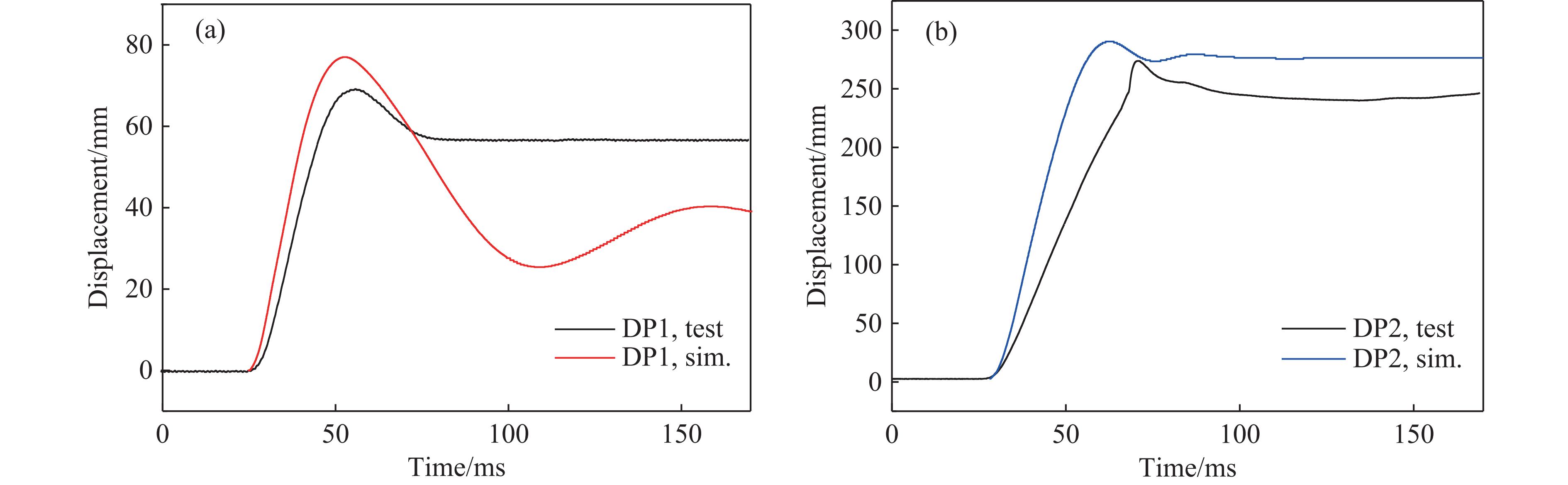
获得测点P1的数值模拟和试验超压时程曲线如图9所示，可以看出，P1的超压峰值为1.479 MPa，与试验结果1.540 MPa相比，相对误差为3.9%。图10给出了DP1和DP2的位移时程曲线对比，其中：DP1的数值模拟最大位移为76 mm，与试验结果69.16 mm相比，相对误差为9.9%；DP2的数值模拟最大位移为289 mm，与试验结果273.34 mm相比，相对误差为5.7%。

破坏形态的试验与模拟对比如图11所示。模拟结果中，侧墙-1窗下墙存在部分砖砌体严重损伤，可观察到与试验墙体相似的裂缝，楼板中心处明显隆起，混凝土损伤严重，梁板交接处产生冲切裂缝，与试验现象相符。综上所述，该数值模型能够较好地描述结构损伤。

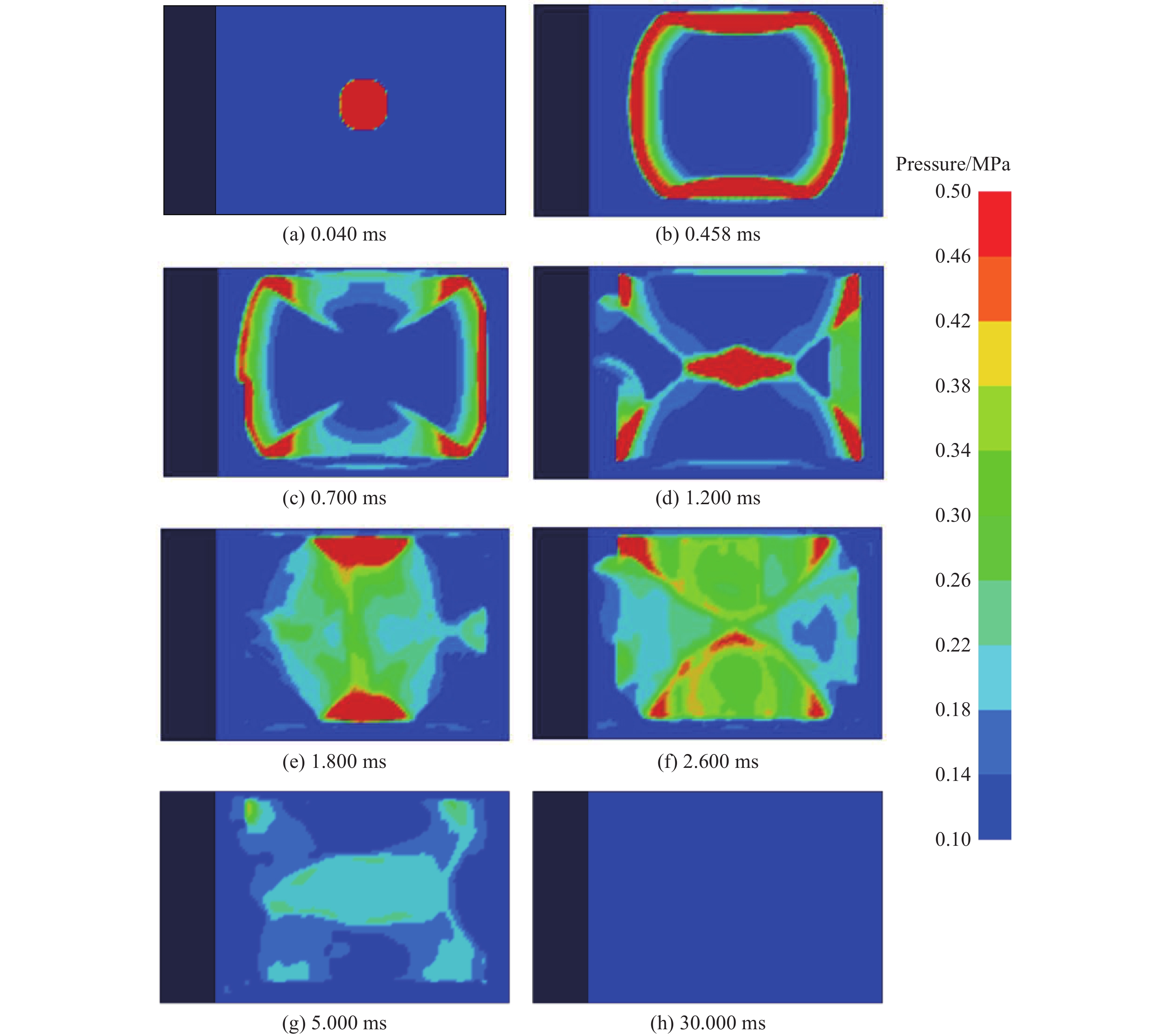
试验得到了框架建筑的最终损伤形态，可通过数值模拟复现0.249 kg炸药在建筑内部爆炸后不同时刻的压力云图，如图12所示。0.040 ms，近似球体的爆炸冲击波迅速向周围传播；0.458 ms，爆炸冲击波传播至楼板和地面，在构件表面反射并向反方向传播，此过程产生的高强反射荷载极易对构件产生冲击破坏效应；0.700 ms，冲击波经过多次反射和叠加，向房间边缘处聚集，形成新的高压区；1.200 ms，房间边缘处冲击波开始向中心汇聚；1.800 ms，爆炸冲击波在中心汇聚后向外传播，并再次传播至房间表面；2.600 ms，冲击波在构件表面发生第2次反射，并向反方向传播；5.000 ms，室内的冲击波经房间内壁的多次反射后，其压力峰值逐渐衰减；30.000 ms，室内流场压力衰减为大气压力。

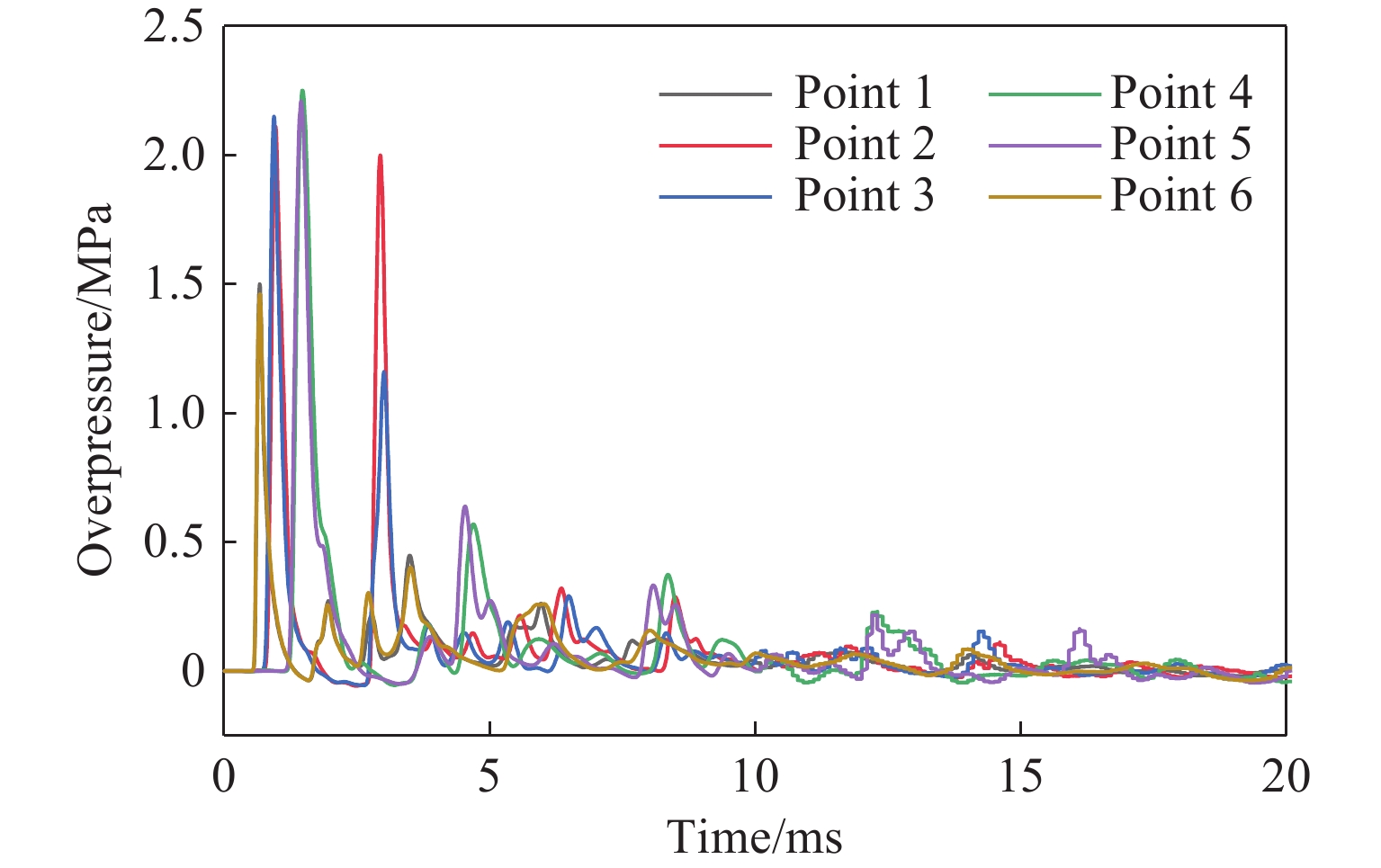
为更准确地了解爆源房间内爆炸冲击波的传播过程，选取图13所示的6个测点，其超压时程曲线如图14所示，每个测点在经过第1个峰值后，均出现负压区，随后出现2个或更多峰值。测点1、2、3和4的峰值超压相差不大，明显高于测点5和测点6的峰值超压，比值约为1.5。

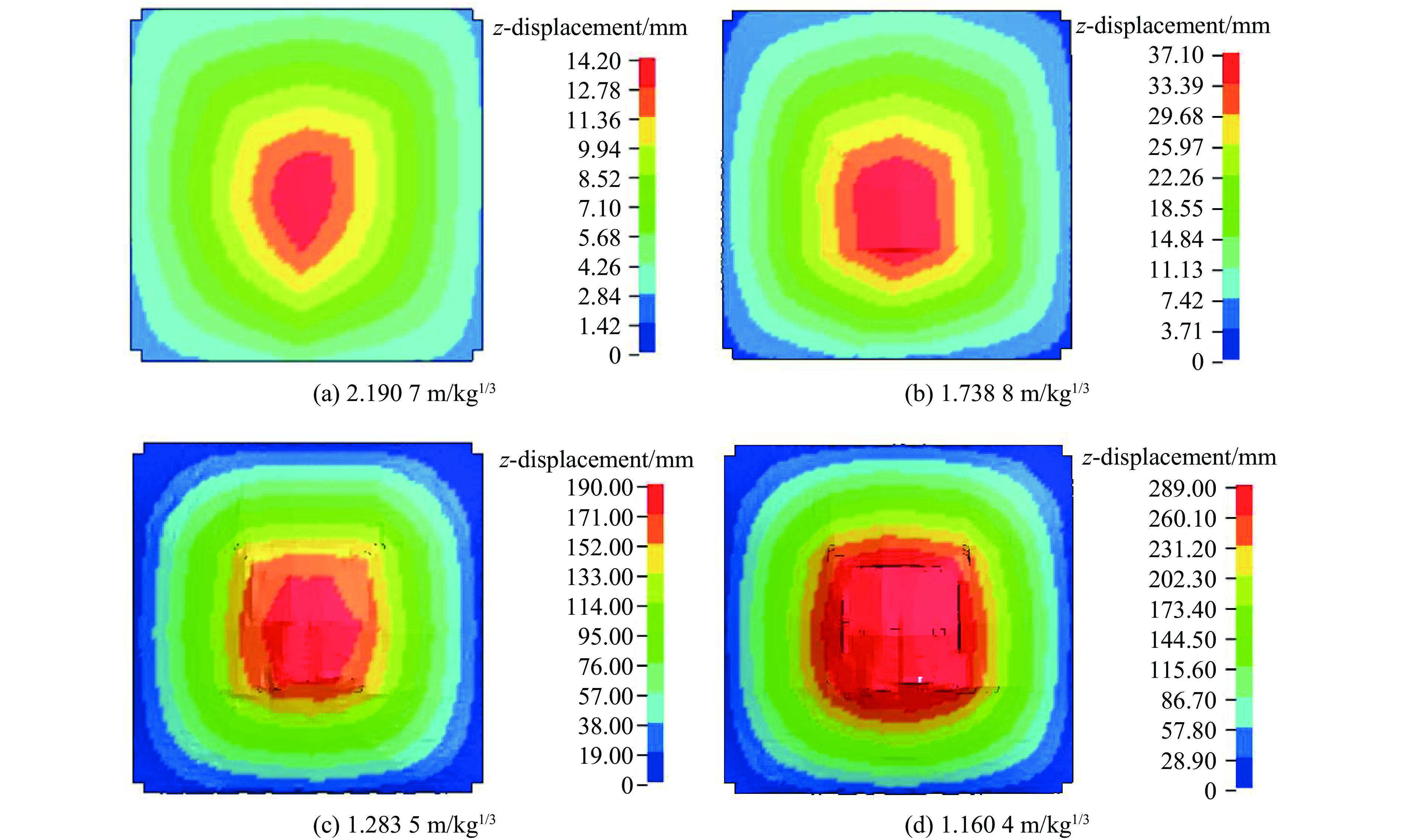
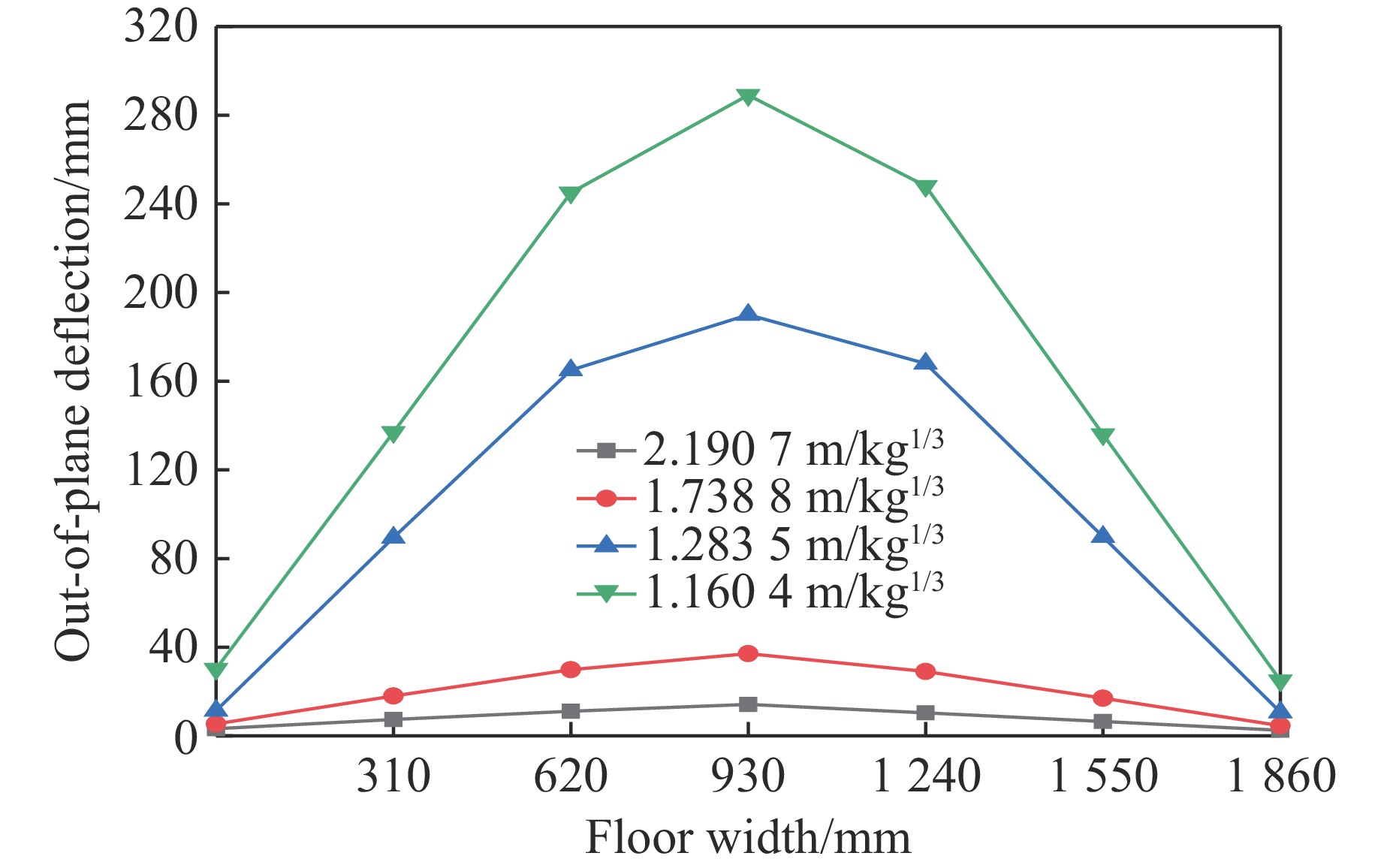
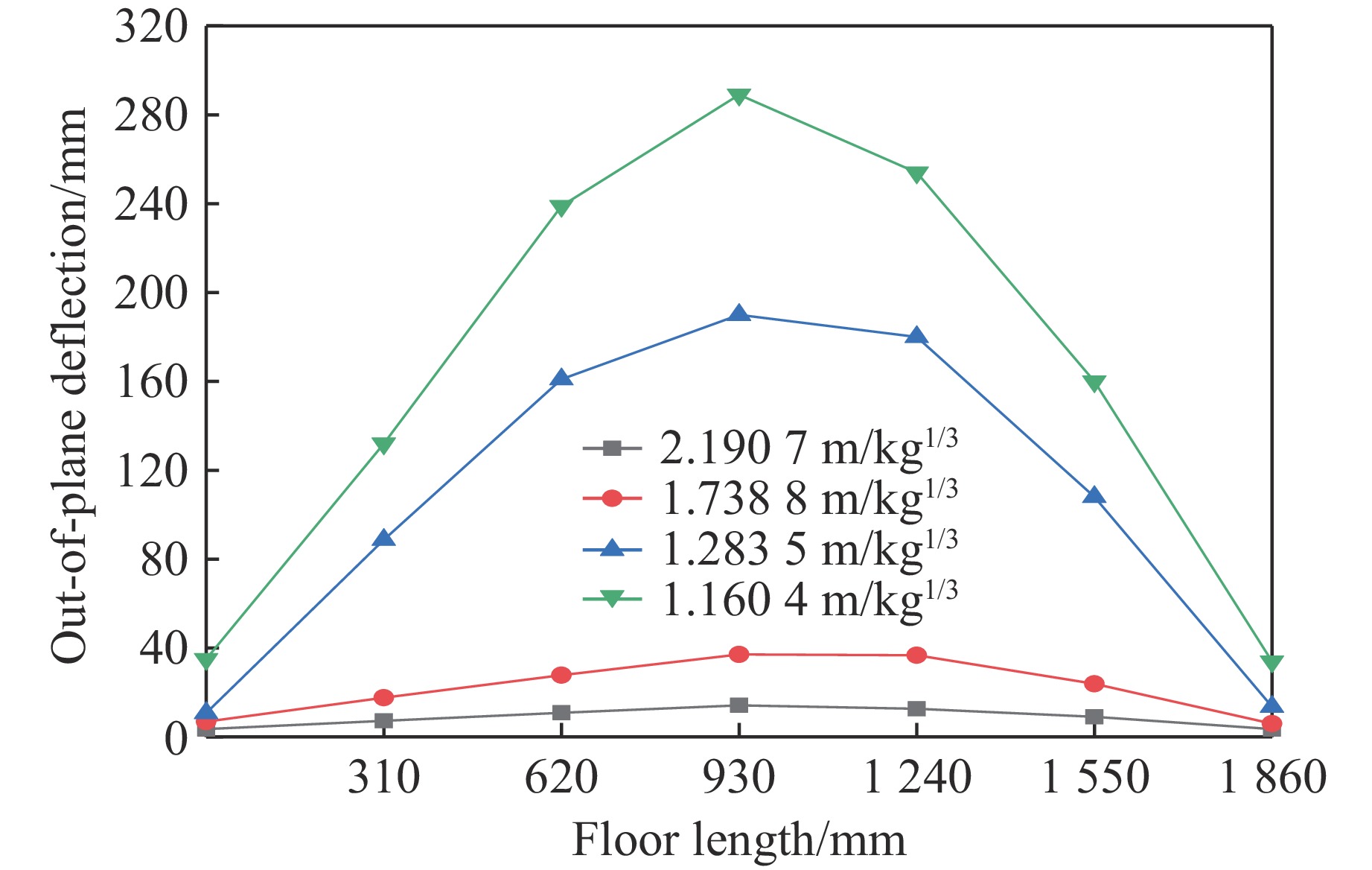
为研究楼板在不同TNT当量内爆炸荷载下的变形特征，固定0.73 m爆距，设置TNT当量为0.037、0.074、0.184和0.249 kg，比例爆距分别为2.190 7、1.738 8、1.283 5和1.160 4 m/kg^1/3进行模拟。不同工况的楼板形变如图15所示。其中，楼板中心区域的位移最大，楼板边缘受梁的连接作用影响，位移较小。图16、图17分别为楼板沿宽度和长度方向的面外挠度变化，结果表明，楼板变形基本沿对称轴对称，随着比例爆距的减小，楼板中心区域位移逐渐增加，弯曲变形的区域也逐渐增大。

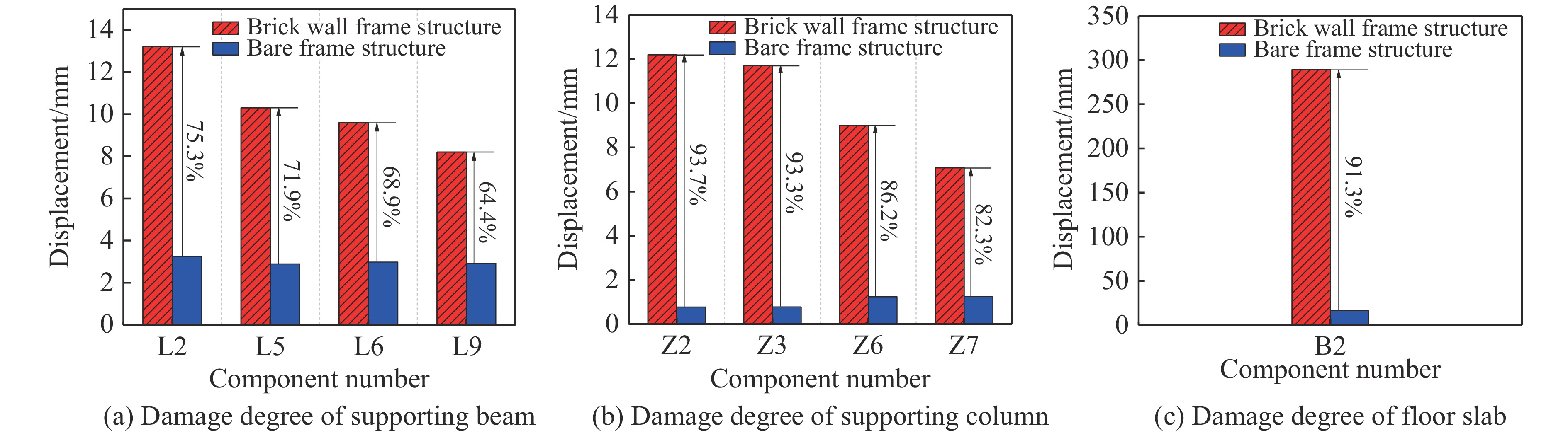
固定TNT当量为0.249 kg，将框架结构中的填充墙全部去除，研究填充墙对建筑构件动力响应的影响。构件的最大位移对比如图18所示，模拟结果中，爆源房间的差异较为明显。在纯框架情况下，无墙体遮挡，爆炸冲击波迅速消散，框架内构件受爆炸荷载的持续时间缩短。纯框架L2、L5、L6和L9梁的峰值位移分别为3.25、2.89、2.98和2.92 mm，较含砌体填充墙框架相应位置的峰值位移（13.20、10.30、9.59和8.20 mm）减少了75.3%、71.9%、68.9%和64.4%。纯框架Z2、Z3、Z6和Z7柱的峰值位移分别为0.77、0.78、1.24 和1.25 mm，较含砌体填充墙框架相应位置的峰值位移（12.20、11.70、9.00和7.08 mm）减少了93.7%、93.3%、86.2%和82.3%。纯框架B2板的峰值位移为25.20 mm，较含砌体填充墙框架相应位置的峰值位移（289.00 mm）减少了91.3%。因此，该工况中典型纯框架结构爆源房间构件的峰值位移相较于含砌体填充墙框架相应位置的峰值位移减少了60%以上。

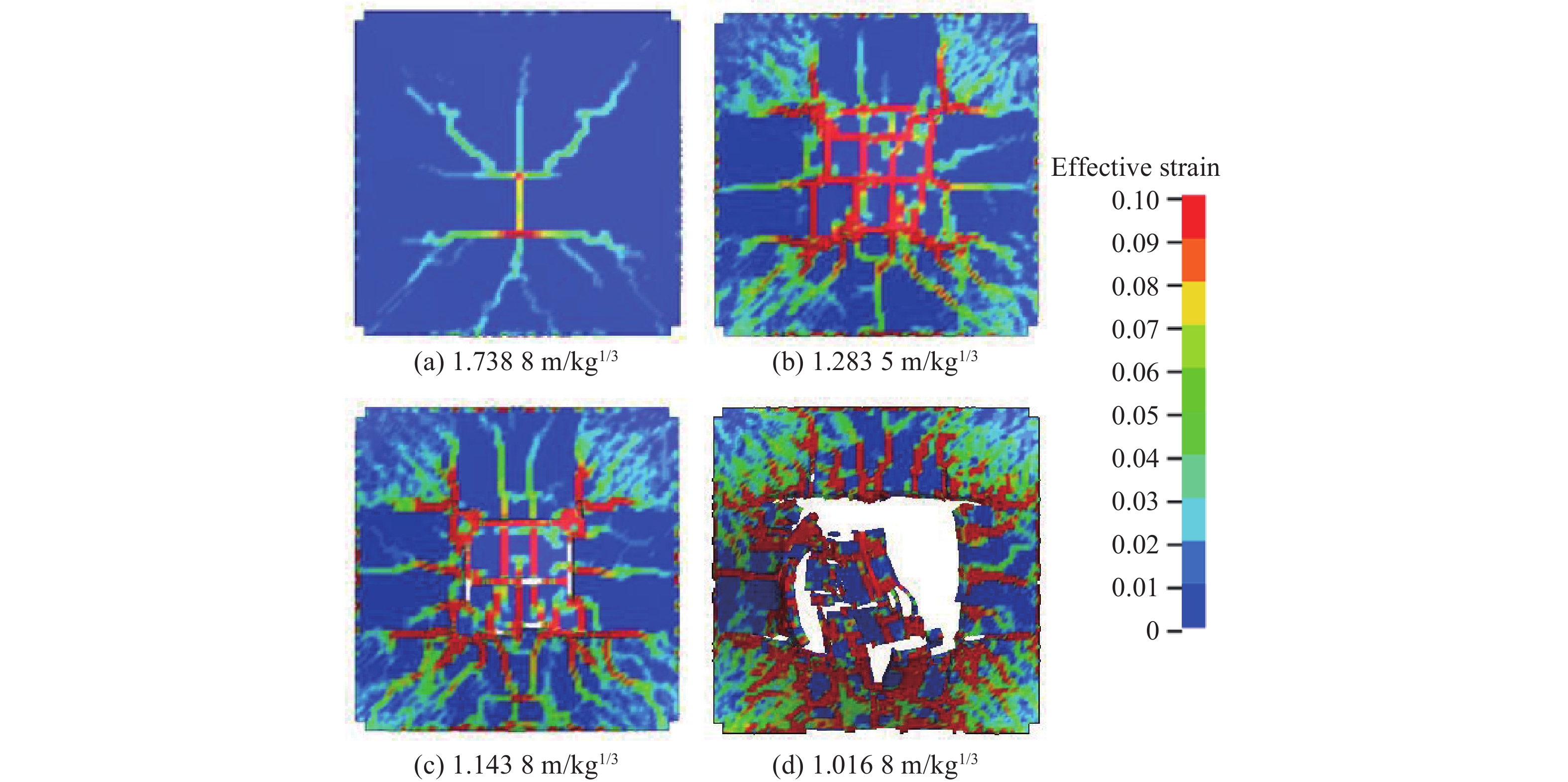
为研究楼板在不同当量内爆炸荷载下的破坏模式，固定爆距0.73 m，模拟分析试件装药量为0.074～0.370 kg时结构的破坏特征。当比例爆距为1.738 8 m/kg^1/3时，楼板轻度弯曲，背爆面出现轻微裂缝，如图19(a)所示；当比例爆距为1.283 5 m/kg^1/3时，楼板明显变形，背爆面中部出现明显的弯曲破坏特征，裂纹尺寸增大，横向裂纹增多，裂缝沿着板的塑性铰线开展，直到梁板交接和梁柱节点区域，如图19(b)所示；当比例爆距为1.143 8 m/kg^1/3时，楼板表现为弯曲冲切破坏，中心区域混凝土发生大变形，产生贯穿裂缝，受拉钢筋屈服，如图19(c)所示；当比例爆距达到1.016 8 m/kg^1/3时，楼板发生冲切破坏，中心区域混凝土贯穿脱落，如图19(d)所示。图20显示了楼板在典型工况下的损伤破坏过程。

为研究框架结构构件在不同当量内爆炸荷载作用下的毁伤程度，保持炸药位置不变，装药量设定为0.037～7.400 kg，模拟得到的框架结构毁伤结果如图21所示。0.037 kg当量作用下，砌体墙出现明显的损伤，梁、板、柱无明显损伤（图21(a)）。装药量为0.184 kg时，砌体墙严重破坏，楼板出现明显的隆起变形，支撑梁和支撑柱轻微损伤（图21(b)）。0.370 kg当量作用下，楼板严重破坏，中心处贯穿脱落，梁板交接区域大部分断开，支撑梁和支撑柱轻度损伤（图21(c)）。装药量为1.840 kg时，楼板完全破坏，梁板交接区域完全断开，支撑梁和支撑柱发生较为明显的毁伤，其中L2和Z2出现明显的向外弯曲变形（图21(d)）。装药量为3.700 kg时，支撑梁L2和支撑柱Z2、Z3明显变形（图21(e)）。装药量为7.400 kg时，支撑梁L2严重弯曲变形，其余梁的毁伤程度加剧，支撑柱Z2、Z3、Z6、Z7的毁伤显著增加，均发生严重变形（图21(f)）。

采用支座转角作为损伤评估准则，通过规定各毁伤等级的支座转角限制，对支撑柱及梁的毁伤情况进行评估。支座转角θ的表达式为

式中：${x_{\max }}$为构件的最大位移， $L{}_{\min }$为峰值位移点距最近支座的距离。

谢奕^[18]基于支撑柱及支撑梁的支座转角范围将其毁伤划分为轻度毁伤、中度毁伤、严重毁伤及完全毁伤4个等级。其中，支撑柱各毁伤等级对应的支座转角为：θ≤1.5°，轻度毁伤；1.5°<θ≤2.5°，中度毁伤；2.5°<θ≤4.0°，严重毁伤；θ>4.0°，完全毁伤。支撑梁各毁伤等级对应的支座转角为：θ≤4°，轻度毁伤；4°<θ≤8°，中度毁伤；8°<θ≤12°，严重毁伤；θ>12°，完全毁伤。支撑柱与支撑梁的毁伤特征大致相同，具体定义如下。

(Ⅰ)轻度毁伤。构件无明显变形，有不贯通裂缝，少量混凝土保护层剥落，满足正常的承载要求。

(Ⅱ)中度毁伤。构件轻微变形，局部混凝土压碎崩落，有少量通裂缝，钢筋外露，无法满足正常承载要求。

(Ⅲ)严重毁伤。构件发生明显变形，部分混凝土破坏崩落，产生大量贯穿裂缝，钢筋屈服或断裂，几乎失去承载能力。

(Ⅳ)完全毁伤。构件发生严重变形、断裂或连接处断裂，大量混凝土破碎剥落，钢筋屈服或断裂，完全丧失承载能力。

工况设置及数值模拟结果如表6所示。装药当量越大，建筑产生毁伤的构件数量越多，且构件毁伤程度也越大。当装药量为0.370 kg时，楼板达到完全毁伤，梁、柱仅发生轻度毁伤；当装药当量达到7.400 kg时，发生毁伤的梁、柱构件数量明显增多，大部分构件的毁伤程度达到严重毁伤以上。

通过缩尺框架结构内爆炸试验和数值模拟方法研究了RC框架-砌体墙结构构件内爆炸荷载作用下的动力响应和破坏模式，并对其破坏特征进行了定量和定性分析，得到如下主要结论。

(1) 对缩尺RC框架-砌体墙结构进行试验，分析了内爆炸时结构构件的破坏情况。在0.249 kg当量作用下，砌体墙和楼板相较于梁、柱破坏更为严重，呈重度毁伤状态，梁板交接区域相较于梁、柱节点更容易发生破坏，产生冲切裂缝。该工况中纯框架结构构件的峰值位移相较于含砌体填充墙框架相应位置峰值位移减小了60%以上。

(2) 楼板的破坏模式随着当量的增大发生转变，当比例爆距为1.283 5 m/kg^1/3时，楼板发生弯曲破坏；当比例爆距减小至1.143 8 m/kg^1/3时，楼板发生弯曲冲切破坏；当比例爆距达到1.016 8 m/kg^1/3时，楼板发生冲切破坏。

(3) 当装药量为0.370 kg时，楼板和砌体墙达到完全毁伤，梁板交接区域大部分断开，梁、柱仅达到轻度毁伤；当装药当量达到7.400 kg时，大部分构件毁伤程度达到严重毁伤以上。对于RC框架结构的抗爆设计，砌体墙宜涂覆防爆材料，防止砌体墙在小当量爆炸荷载作用下大面积倾倒；楼板钢筋宜设计双层双向，避免楼板在小当量内爆炸荷载作用下外侧混凝土受拉破坏；梁板交接区域宜适当加设拉结钢筋，以避免小当量爆炸荷载作用下的冲切破坏。