通过电弧熔炼制备了原子配比为Al_0.3NbTi₃VZr_1.5的高熵合金。为了确保化学成分的化学均匀性，合金锭被反复熔炼5次以上，通过铜模吸铸后在铜坩埚中水冷，从而获得$\varnothing 3\;{\text{mm}} \times 10\;{\text{mm}}$的合金棒，并制备成尺寸为$\varnothing 3\;{\text{mm}} \times 3\;{\text{mm}}$的压缩试样。

采用分离式霍普金森压杆（split Hopkinson pressure bar，SHPB）进行动态加载实验。如图1所示，实验装置主要包括入射杆、透射杆、子弹以及数据采集和记录装置。其中，入射杆和透射杆的直径为19 mm，长度为1 000 mm，子弹长度为200 mm。试样位于入射杆与透射杆之间，通过调节加载气压控制子弹的初始速度v₀，在入射杆的撞击端涂抹凡士林对入射波进行整形。根据入射杆和透射杆上的应变信号，可以计算出样品的应力$\sigma $、应变$\varepsilon $和应变率$\dot \varepsilon $。

式中：${E_{\text{B}}}$和${A_{\text{B}}}$为杆材的弹性模量和横截面积，${A_{\text{S}}}$和${L_{\text{S}}}$为试样的横截面积和高度，${c_{\text{B}}}$为杆材中的弹性波波速，$ {\varepsilon _{\text{R}}} $和$ \varepsilon\mathrm{_T} $分别为动态应变仪采集的入射杆和透射杆应力波信号。

固定实验的加载气压为0.075 MPa，并保持子弹速度恒定（约15 m/s），以排除温度和加载速率对结果的影响。图2展示了Al_0.3NbTi₃VZr_1.5 HEA在动态压缩下的真应力-应变曲线，Test 1、Test 2和Test 3分别对应3次独立测试的结果，应变率约为4 000 s⁻¹。实验表明，该HEA在动态加载下表现出典型的弹塑性变形行为，其应力-应变曲线可分为弹性阶段和塑性阶段。Al_0.3NbTi₃VZr_1.5 HEA在4 000 s⁻¹的应变速率下保持了20%的压缩塑性，并且屈服强度高达1.1 GPa，具有显著的塑性强化效应、高强度与良好塑性等优异特性。

为验证有限元模型的可靠性，对SHPB实验进行有限元分析。利用有限元软件ABAQUS建立SHPB模型，入射杆和透射杆的尺寸与实验一致，材料为高强钢，试件的弹塑性参数参考上述实验设置。如图3(a)所示，由试件变形后的应力云图可以观察到反射波和透射波沿边缘向两端传播。实验和模拟结果的对比如图3(b)所示，数值模拟与实验得到的应力-应变曲线几乎一致，误差小于5%，证明了建立的Al_0.3NbTi₃VZr_1.5 HEA有限元模型的可靠性。

为了提升Al_0.3NbTi₃VZr_1.5 HEA的轻质特性，将该合金与FCCZ点阵结构结合。6061-T6铝合金因其良好的机械性能、加工特性和出色的抗撞性被广泛应用于汽车、航空航天等领域。为了更清晰地展示Al_0.3NbTi₃VZr_1.5 HEA结合FCCZ点阵结构的力学性能，将其与6061-T6铝合金进行对比。所有点阵结构的体积分数均控制在47%，使HEA结合点阵结构的等效密度为2.7 g/cm³，与6061-T6铝合金的密度相同。采用CATIA建立FCCZ点阵结构的几何模型，先建立杆件，进行旋转、镜像和阵列得到单胞，再由单胞沿X、Y、Z 3个方向进行阵列，建立的FCCZ点阵结构如图4所示。

采用有限元软件ABAQUS模拟FCCZ点阵结构的动态压缩响应。选取Johnson-Cook本构模型描述6061-T6铝合金的力学行为，参照材料手册^[21]设定参数。根据Zhou等^[22]对于点阵结构夹芯板低速冲击的研究，将接触面摩擦系数设置为0.2。将模型用四面体网格划分，尺寸为0.1 mm，在刚性板中设置参考点，并提取其位移和反作用力。图5(a)给出了$\varepsilon $分别为0、0.1和0.2时FCCZ点阵结构的应力云图。将反作用力除以初始等效截面，位移除以初始模型厚度得到工程应力-应变曲线，如图5(b)所示。

从图5可以看出，变形刚发生时，如之前的研究^[23]所提到的，FCCZ点阵结构的应力集中发生在竖直杆件和倾斜杆件间的节点上。当应力集中于节点时，点阵结构的压缩过程以弯曲变形为主导，而当应力集中在杆件上时，压缩过程则以轴向压缩变形为主导。点阵结构在压缩过程中的工程应力-应变曲线整体上的表现与6061-T6铝合金类似，均为先迅速线性上升，随后进入缓慢变化的塑性强化阶段，在应变达到0.5时，逐渐进入致密化阶段。屈服强度与点阵结构的等效密度之比即比强度，平台应力取应变0.2～0.5区间内结构应力的算术平均值。FCCZ点阵结构的比强度和平台应力分别达到0.148 N·m/kg和1.175 GPa，对比6061-T6铝合金，分别提升约11%和57%。6061-T6铝合金结合FCCZ点阵结构表现出了较好的轻质高强性能。

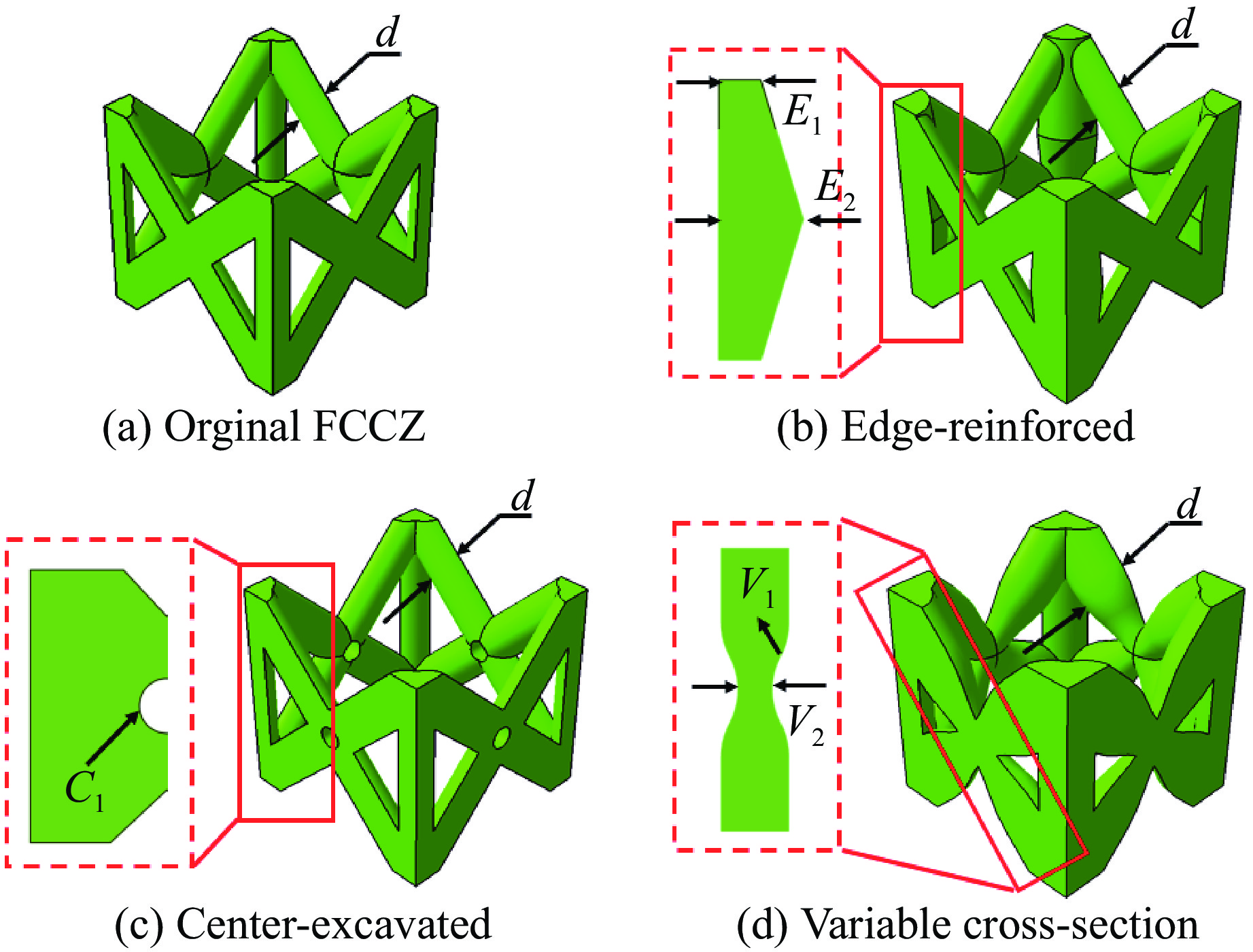
为了平衡点阵结构的应力分布，提升其力学性能，对FCCZ点阵结构进行优化。如图6(a)所示，以直径为d的均匀杆件FCCZ点阵结构为原始结构，在此基础上设计了3类优化结构。根据压缩响应分析和Yang等^[24]对于FCCZ局部优化增强性能的研究，设计了Z向杆件边缘增强（BE）结构，以减少竖直杆件上的应力集中。如图6(b)所示，该结构的Z向杆件呈纺锤形，纺锤大小端尺寸分别为E₁和E₂。根据FCCZ点阵结构在压缩作用下的应力分布以及Cao等^[25]对于改性菱形点阵结构的研究，设计了斜杆交叉支点孔洞（BC）优化结构和变截面斜杆（BV）优化结构，交叉支点孔洞的孔径为C₁，变截面圆角和截面细端尺寸分别为V₁和V₂，如图6(c)和图6(d)所示。

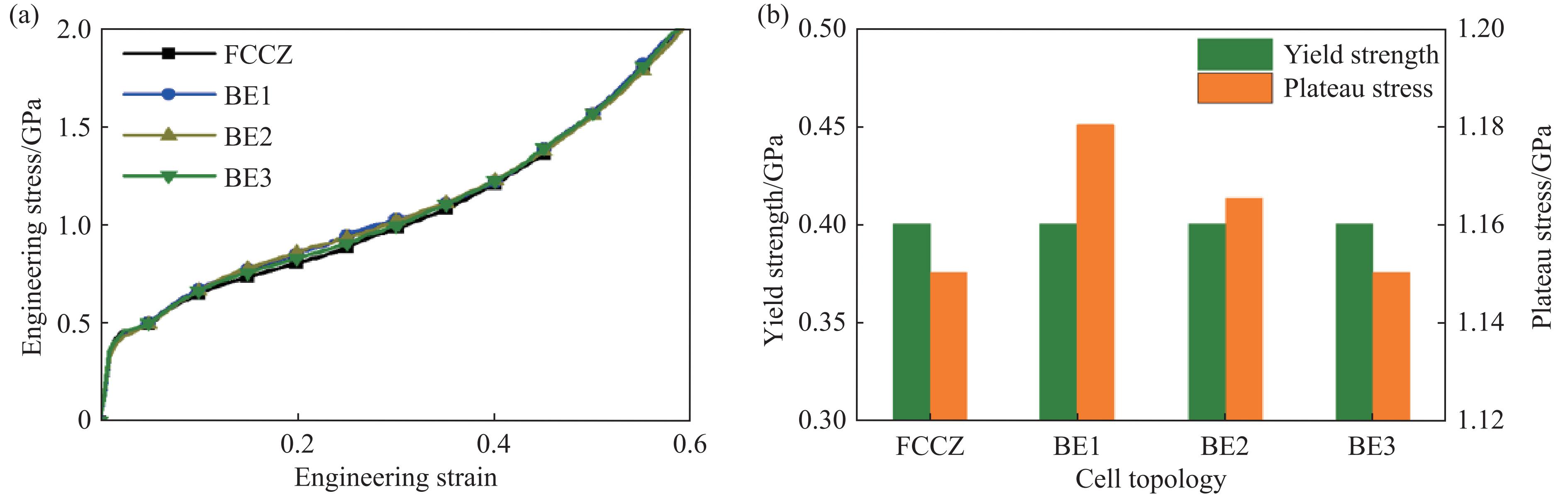
BE结构优化参数为E₁和E₂，根据E₁和E₂取值的不同，可分为BE1型（E₁=$ 0.5d $，E₂=$ 0.5d $）、BE2型（E₁=$ 0.2d $，E₂=$ 1.8d $）、BE3型（E₁=$ 0.8d $，E₂=$ 1.2d $），分别对其进行有限元分析。图7显示了3种BE结构与FCCZ点阵结构的工程应力-应变曲线对比，可以看出，参数E₁、E₂对结构力学性能的影响较小。与初始FCCZ结构相比，该类优化结构仅在应变为0.2时表现出较大的应力。

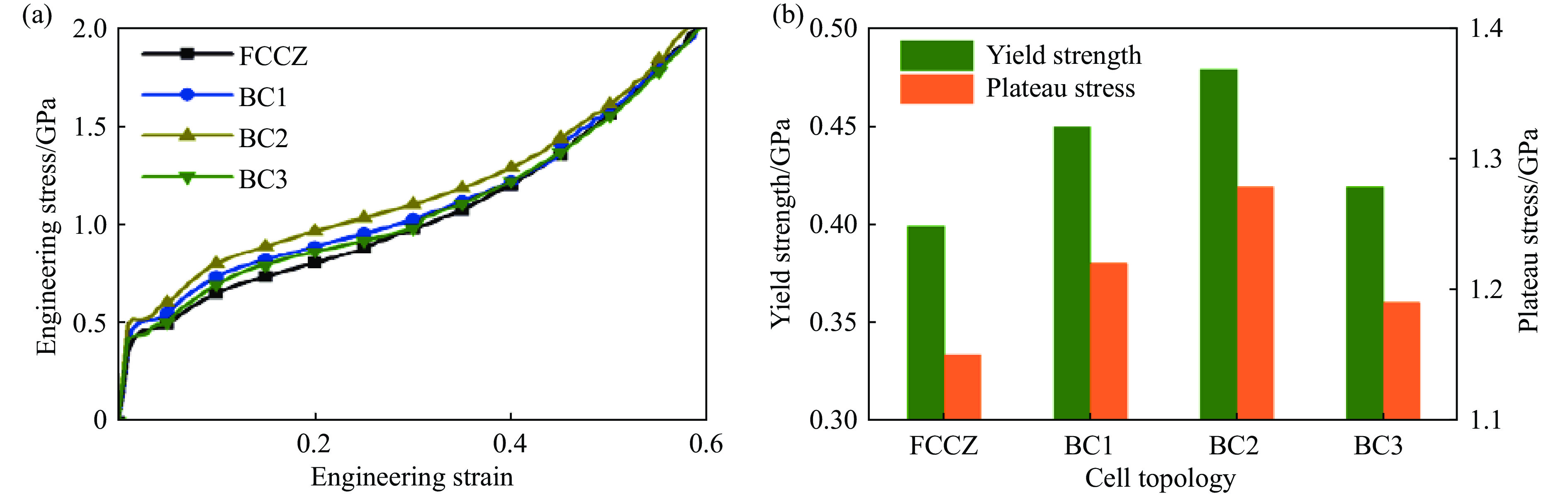
BC结构优化参数为孔径$C_1$，设BC1型、BC2型、BC3型的C₁分别为$ 0.70d $、$ 0.85d $、$ 1.00d $。图8为3种BC结构与初始FCCZ结构的压缩响应对比。可以看出，该优化结构的屈服强度和平台应力显著提升，孔径$C_1$从0.70d增大至1.00d时，力学性能先提升后下降，在$ 0.85d $附近出现峰值。其中，BC2型的屈服强度和平台应力分别为0.48和1.28 GPa，对比初始FCCZ结构，分别提升20%和11%。

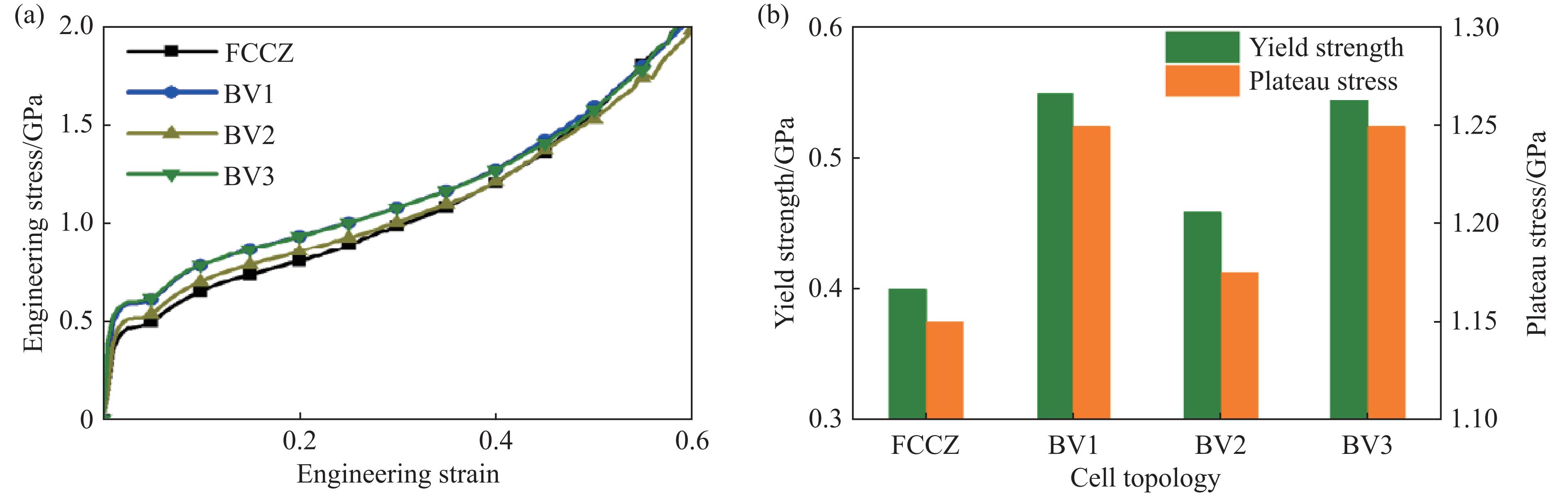
BV结构优化参数为变截面圆角$V_1$和截面细端尺寸$V_2$，设BV1型的V₁和V₂分别为2.0d和0.5d，BV2型为1.0d和0.5d，BV3型为3.0d和0.5d。BV优化结构和初始FCCZ结构的压缩响应对比如图9所示。可以看出，该优化结构和BC优化结构对力学性能的提升效果相近。当$V_2$为$0.5d$，V₁从1.0d增加到3.0d时，优化结构的力学性能先提升后无明显变化，$V_1$取2.0d～3.0d之间时出现峰值。其中，BV1型的屈服强度和平台应力分别为0.52和1.25 GPa，对比初始FCCZ结构，分别提升31%和9%。

对比初始FCCZ结构与3类优化（BE、BC和BV）结构在应变为0、0.1和0.2时的应力云图，可以明显观察到不同结构在应力分布上的差异，如图10所示。边缘增强型BE结构仍然存在显著的应力集中现象，尽管增强了Z向杆件的中间结构，但是杆件中的应力并未得到有效分散，该结构在机械性能上的提升有限，且高应力主要集中在节点区域，导致该区域更易发生塑性变形，应变为0.2时结构的变形行为进一步验证了这一点。与之相比，中心挖孔BC结构和斜杆变截面优化BV结构在斜杆交叉处的应力分布更均匀，表现出较高的屈服强度和平台应力。然而，对于BC结构而言，过大的孔径使得斜杆成为整个结构中最薄弱的环节，易导致失效和断裂。在BV结构中，斜杆交叉处的应力水平较低，表明该区域的承载能力相对较强。综上所述，各优化结构在不同应变条件下的应力分布特征显著不同，不仅影响了材料的力学性能，还在一定程度上决定了结构的失效模式，以上结果为后续的设计与优化提供了重要的参考依据。

为了评估优化结构的吸能特性，研究人员通常使用比吸能（E_SA）、吸能效率（δ_CFE）、峰值力（F_PC）和平均冲击力（F_MC）作为量化优化结构吸能特性的指标^[26–28]。总吸能（E_A）可定义为在压缩过程中吸收的总能量，可由力-位移曲线得到，其数学表达式为

式中：$D$为压缩位移，F为压缩受力。E_SA为单位质量所吸收的能量，通常表示为

式中：$M$为材料的质量。E_SA能有效地比较不同质量的材料，是评估吸能性能的重要指标。δ_CFE通常表示为

式中：F_PC越小，碰撞产生的载荷越小，碰撞过程越稳定；F_MC为压缩过程中施加的平均载荷，能够反映材料承受冲击时的平均受力情况。$F_{\mathrm{MC}} $的常用计算公式为

单一指标无法全面评估材料的吸能特性：E_SA能够衡量单位质量下材料吸收的能量，但不能反映材料在整个冲击过程中的力-位移曲线形状及其变形模式的稳定性；F_MC可描述整个冲击过程中所受载荷的平均水平，但无法反映峰值力或瞬时冲击的剧烈程度；F_PC可反映材料在冲击过程中的最大载荷能力，但不能全面体现材料的能量吸收效率、变形均匀性和吸能稳定性。因此，根据Wang等^[29]对多孔材料耐撞性的研究，将E_SA、δ_CFE、F_PC和F_MC的权重分别设置为0.333、0.333、0.167和0.167，由此可更全面地评估优化结构在能量吸收方面的性能，并采用归一法对每个指标进行标准化

式中：$A$为原始值，$A_{\text{min}}$和$A_{\text{max}}$分别为$A$指标的最小值和最大值。设4类指标标准化后分别为$ E_{{\mathrm{SA}}}' $、$ \delta _{\mathrm{CFE}}' $、$ {F_{\mathrm{MC}}'}$和$ {F_{\mathrm{PC}}'}$，归一后区间为[1, 2]。4类指标中，E_SA、δ_CFE和F_MC是有利因素，F_PC是不利因素，因为过高或过快的峰值力会导致能量吸收效率降低、冲击载荷增加、系统稳定性与安全性下降以及材料失效风险提高。因此，加权得分$ S $的计算公式为

对优化结构进行相同的标准化处理，并计算加权得分，即可得到不同优化结构的吸能特性优劣。

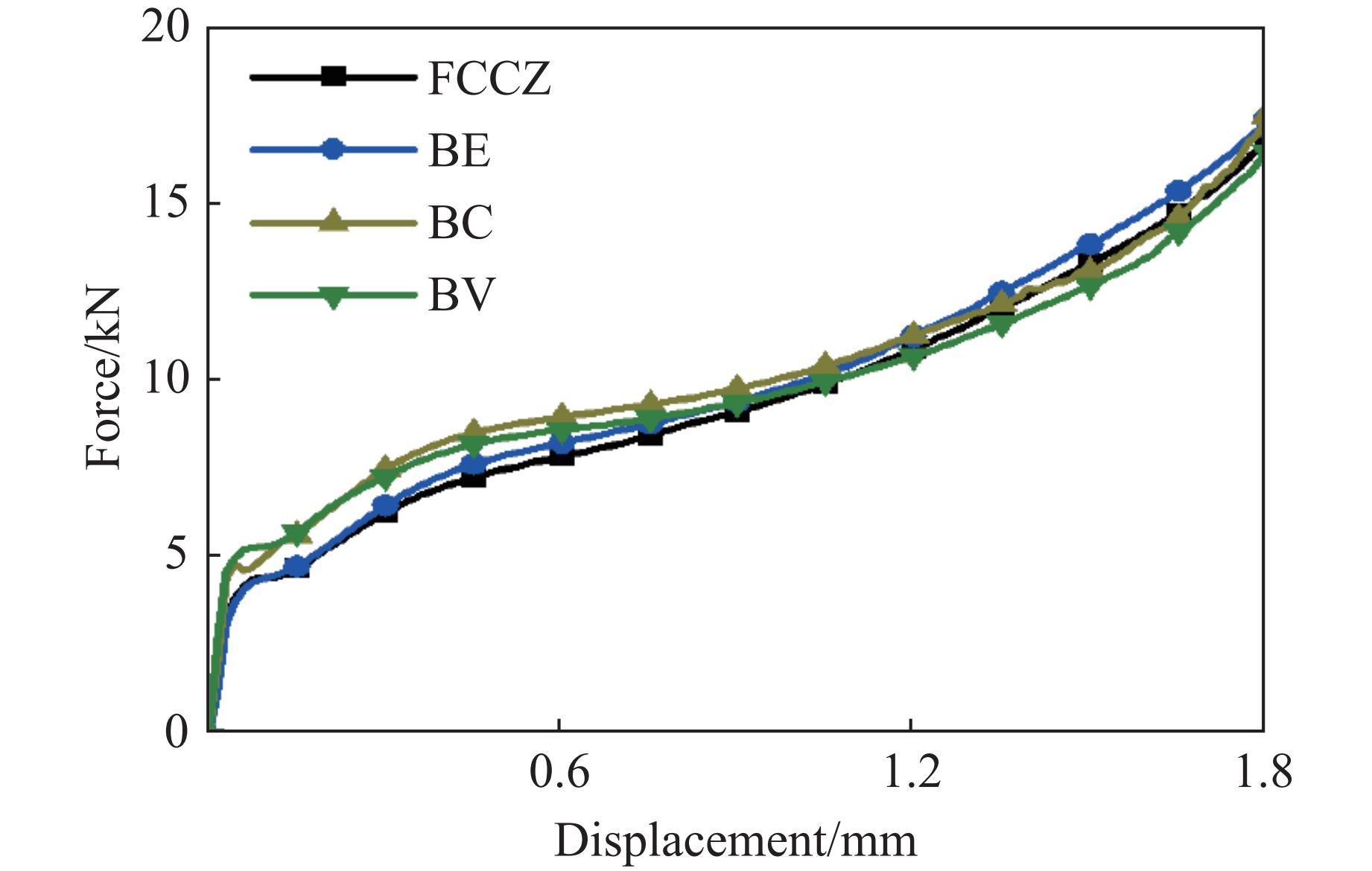
根据第2节的有限元分析，提取了3类优化结构以及原始FCCZ结构的力-位移数据，如图11所示。优化结构旨在增强结构受力时的弹性和平台阶段，延缓或避免迅速进入材料的致密阶段，从而提升其整体的吸能特性。因此，取位移0～1.5 mm计算各种指标，4种结构的吸能特性量化结果如图12所示。BC结构通过优化孔径设计，使得单位面积内的应力分布更加均匀，避免了局部应力集中，在弹性变形后进入缓慢增长的平台应力阶段，能够更高效地吸收能量。BV结构通过适当的变截面设计，引入了局部应变梯度，使得应力在材料内部呈现梯度分布，这种梯度效应能够有效分散应力，同时增加材料的塑性变形，从而提高吸能效率。

图11中4条曲线的变化趋势一致，都经历了3个阶段：首先是线性增长阶段，其次是曲线缓慢上升阶段，最后进入致密化阶段^[30–31]。由于这4种结构的体积分数相同，因此，在达到致密化后，所有曲线几乎重合。

研究表明，BC和BV结构在吸能特性和力学性能方面相较于初始FCCZ结构有明显提升。BC结构的4类吸能指标E_SA、δ_CFE、F_PC和F_MC均达到最优水平，对比FCCZ结构，BC结构在4类指标上分别实现了9%、11%、−2%和9%的提升，其综合评定得分第1。BV结构的吸能特性位列第2，但其比强度表现尤为突出，较FCCZ结构提升了31%，展现了优异的力学性能。这一研究结果为未来材料与结构设计优化提供了重要的理论依据，表明通过合理的几何优化可以有效提升结构的能量吸收性能，增强其在冲击或碰撞等动态载荷下的应用潜力，为材料的安全性和可靠性提升奠定基础。

研究了Al_0.3NbTi₃VZr_1.5 HEA基材结合优化FCCZ点阵结构的动态压缩行为及吸能特性，得出以下主要结论：

(1) 优化结构在压缩载荷下对孔径和变截面圆角2个设计参数敏感，最佳孔径取值约为$ 0.85d $，变截面圆角最佳取值在2.0d～3.0d之间；

(2) BC型和BV型优化结构能够有效改善应力分布，增强FCCZ结构的力学性能。对比初始结构，BV1型的比强度提升31%，BC2型的比吸能提升9%，BC2型优化结构的综合吸能特性最好。